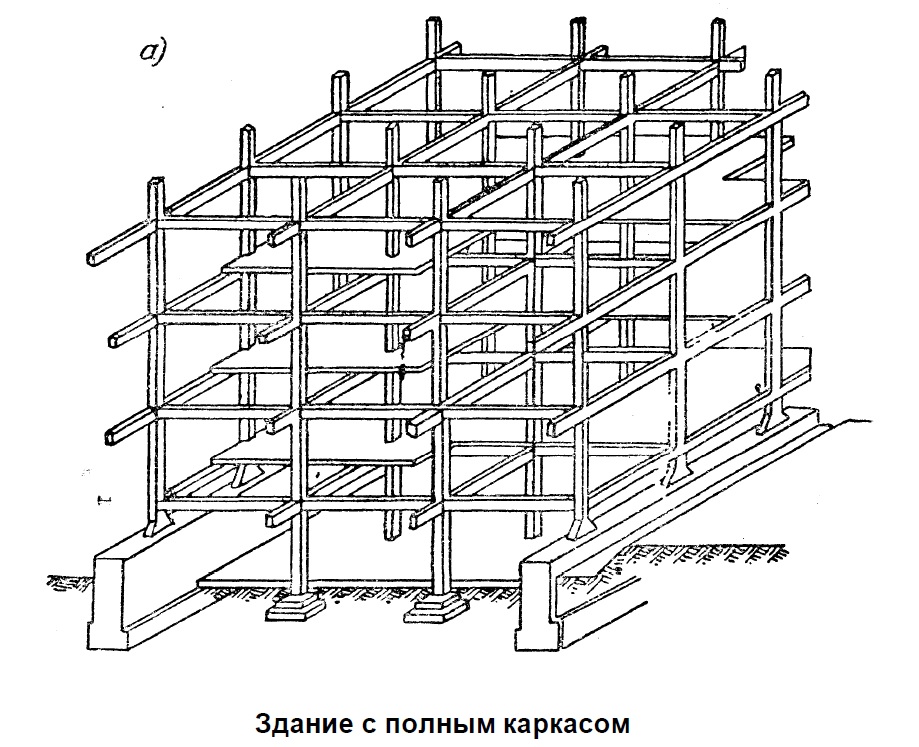
Схема каркаса: Конструктивные схемы и элементы каркаса

Расчет каркасов связевой конструктивной схемы

Главное отличие связевого каркаса от рамного — наличие элементов жесткости, воспринимающих основную часть горизонтальных нагрузок. Под элементами жесткости, в дальнейшем именуемыми как устои, здесь понимаются связевые панели (колонны, объединенные стальной решеткой), сборные железобетонные диафрагмы, стены, лестничные клетки, лифтовые шахты и т.п. конструкции, горизонтальная жесткость которых, как правило, существенно превышает жесткость каркасной части здания, состоящей только из колонн и ригелей. В связи с этим узлы сопряжений колонн и ри­гелей часто выполняются либо шарнирными, либо условно жесткими, т.е. с весьма ограниченной несущей способностью, когда уже при действии не­большой доли вертикальных нагрузок в узлах образуются пластические шарниры. Такие узлы позволяют более рационально использовать напря­гаемую высокопрочную арматуру и обходятся без мощной верхней армату­ры ригелей, необходимой для осуществления жестких узлов.

Расчетные схемы связевых каркасов могут быть двух видов — дискрет­ные и дискретно-континуальные.

Дискретная схема представляет собой устои как консольные стержни, соединенные друг с другом и с каркасной частью здания горизонтальными стержнями на уровне всех перекрытий. Перекрытия, за исключением неко­торых оговоренных случаев, считаются абсолютно жесткими в своей плос­кости, и поэтому горизонтальные смещения устоев и каркасной части будут одинаковыми.

Если конструкция и расположение устоев симметричны, а узлы кар­касной части шарнирные, расчетную схему удобно представить в виде од­ного устоя и одной колонны с жесткостями, равными сумме жесткостей соответственно всех устоев и всех колонн, соединенных на уровне каждого перекрытия жесткими стержнями (рис. ниже).

Если принять жесткость устоя и жесткость колонны в этой схеме изгиб- ной и постоянной по высоте, то устой и колонну на действие горизонталь­ных нагрузок можно рассчитать как отдельные консоли, распределив между ними горизонтальную нагрузку пропорционально их жесткостям. Однако, как правило, в деформациях устоя, в отличие от деформаций колонн, суще­ственную долю составляют деформации сдвига, особенно это имеет место в связевых панелях, а также в диафрагмах с большими проемами. Поэтому такую схему в общем случае рассчитывают методом сил, принимая за неиз­вестные Xj усилия в жестких стержнях, а за коэффициенты при неизвестных 5 у сумму смещений устоя и каркаса как свободных консолей на уровне пе­рекрытия j от действия единичных сил, приложенных к устою и каркасу на уровне перекрытия г. Грузовые члены представляют собой смещения устоя как свободной консоли от действия внешней нагрузки.

Конструктивная (а) и расчетная (б) схемы связевого каркаса с шарнирными узлами и одинаковыми устоями; в — основная система расчета каркаса методом сил

Если узлы каркасной части жесткие, то расчет также можно производить по аналогичной расчетной схеме, принимая обобщенную колонну в виде, показанном на рис. ниже, где жесткости примыкающих ригелей равны суммам жесткостей ригелей этажа. При этом рекомендуется учитывать жесткие опорные участки ригелей и колонн и податливость жестких узлов. Смещения 8у такой колонны определяют методом деформаций, где за неизвестные принимаются углы поворота узлов.

Конструктивная (а) и расчетная (б) схемы связевого каркаса с жесткими узлами и одинаковыми устоями

Если устои имеют различную конструкцию с различными долями сдви­говой и изгибной деформации, например стены* с проемами и без проемов, или связевые панели с различными решетками, между такими устоями уста­навливаются жесткие стержни и число неизвестных увеличивается на число этих стержней. При этом устои, расположенные в разных плоскостях, рас­сматриваются в одной плоскости вместе с обобщенной колонной (рис. ниже).

Конструктивная (я) и расчетная (б) схемы связевого каркаса с различными симметрично расположенными устоями

Расчет может также производиться методом деформаций (рис. ниже), ко­гда за неизвестные принимаются смещения каждого перекрытия от внеш­ней нагрузки. При этом за коэффициенты r_ij при неизвестных принимаются реакции в фиктивных горизонтальных опорах каждого перекрытия j от еди­ничных смещений каждого перекрытия i. Грузовые члены представляют собой внешние горизонтальные силы, приложенные к каждому перекры­тию. Такой расчет более трудоемкий (особенно по сравнению с расчетом каркаса с шарнирными узлами), поскольку определение реакций от еди­ничных смещений требует отдельных расчетов методом деформаций. Од­нако в некоторых случаях такой расчет бывает необходим. В частности, когда при расчете методом сил с учетом деформированной схемы может быть невозможно определение смещений 8

Расчетная схема (а) и основная система расчета методом деформаций (6) связевого каркаса

При несимметричном расположении устоев или при различных их кон­струкциях перекрытия под действием горизонтальных нагрузок, кроме по­ступательных смещений будут поворачиваться, увеличивая смещения неко­торых рам. В общем случае правильно учесть эти повороты можно только методом деформаций, при котором в основной системе кроме горизонталь­ных фиктивных опор, препятствующих поступательным смещениям пере­крытий в направлении нагрузки, устанавливаются в каждом перекрытии также две дополнительные опоры, препятствующие поворотам, но не пре­пятствующие поступательным смещениям. Эти опоры удобней всего уста­навливать по краям перекрытий в их углах (рис. ниже).

Фиктивные горизонтальные опоры перекрытия при расчете связевого каркаса методом деформаций с несимметрично расположенными или неодинаковыми устоями

1 — опора, препятствующая поступательному смещению перекрытия; 2, 3 — опоры, препятствующие повороту перекрытия

Учет поворотов перекрытий методом сил, изложенный в многочислен­ных учебниках и пособиях, основан на фиксации центра жесткости, при приложении к которому внешняя нагрузка не вызывает поворота.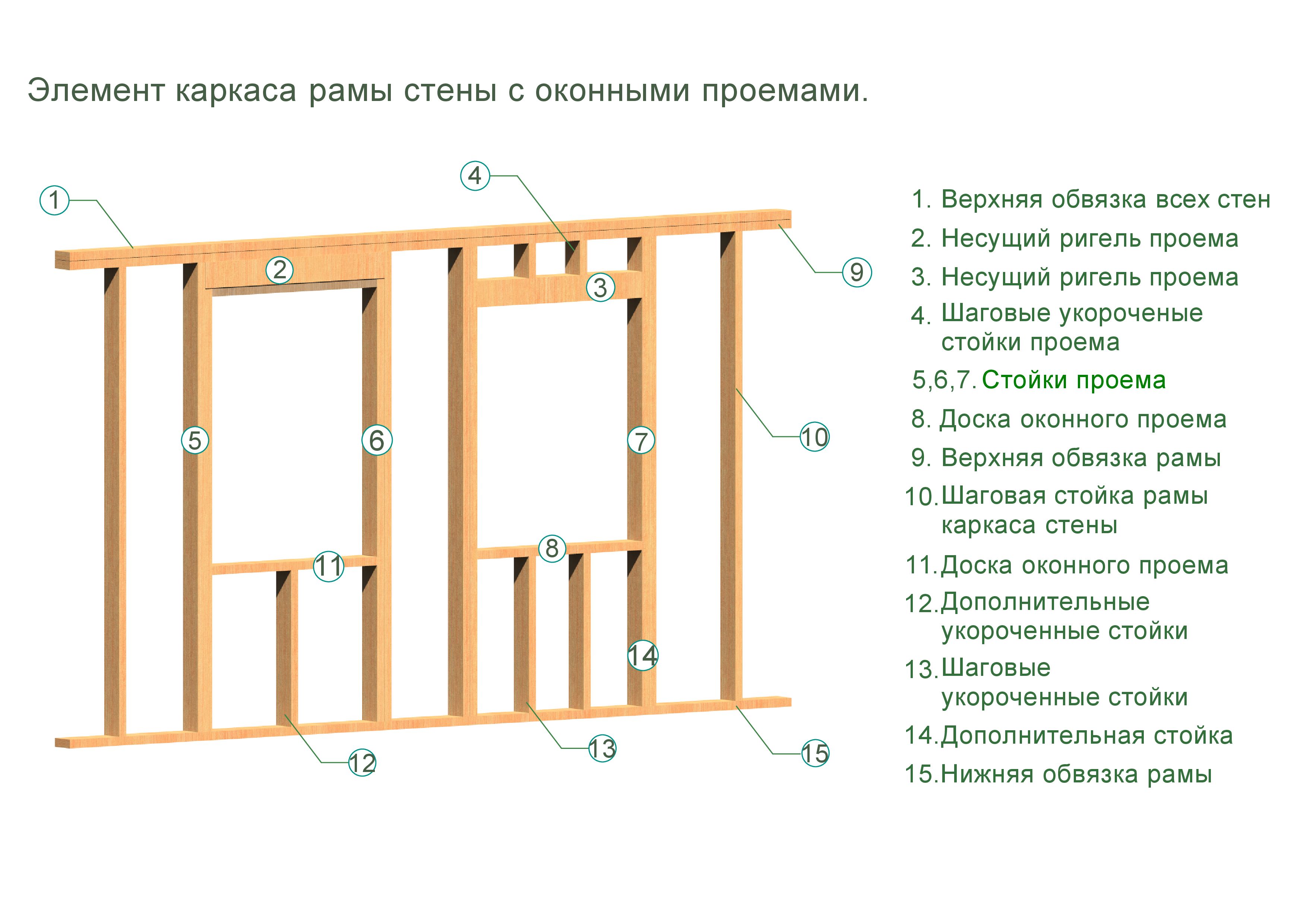

Дискретная расчетная схема имеет универсальный характер. Она мо­жет применяться при расчете каркасов с любыми комбинациями устоев, с любым распределением жесткостей устоев и колонн по высоте, с любым сочетанием высот этажей. Такой расчет, требующий решения систем кано­нических уравнений высокого порядка, может практически выполняться только с помощью компьютерных программ, но при современном распро­странении компьютерной техники это не представляет проблемы.

Дискретно-континуальная расчетная схема отличается от дискретной схемы тем, что горизонтальные нагрузки в виде сосредоточенных сил, а также стержни-связи между устоем и каркасной частью заменяются на рас­пределенные по высоте нагрузки и усилия, а каркасная часть заменяется на стержень, имеющий изгибную и сдвиговую жесткости, аналогичные кар­касной части.

Расчет по этой схеме дает результаты, близкие к результатам расчета по дискретной схеме при следующих условиях:

• число этажей более 6;
• высоты этажей одинаковы;
• жесткость устоев и каркасной части постоянны по высоте.

Результаты решения дифференциального уравнения для частных слу­чаев можно выразить через конкретные формулы, поэтому расчет по этой схеме менее трудоемок и может быть выполнен без использования компью­терных программ. Однако в связи с ограничениями в применении этой схе­мы подробности такого расчета здесь не приводятся. Для наиболее частого случая с симметрично расположенными и одинаковыми устоями при по­стоянной по высоте горизонтальной нагрузке Р, с одинаковыми высотами этажей l и при каркасной части с жесткими узлами приводим без вывода формулы для определения горизонтальных смещений у, изгибающих мо­ментов М и поперечных сил Qdq обобщенного устоя, поперечных сил обоб­щенной колонны Qcol в сечении на расстоянии х от низа:

где В — сумма изгибных жесткостей устоев и колонн каркаса; s_{2 = √B/kv}²

В₀ — изгибная жесткость каркасной части, равная

к = 12/l*(1/Σi_c+1/ Σi_p ) — сдвиговая жесткость каркасной части; Σi_c — сумма

погонных жесткостей колонн этажа; Σi_p — сумма погонных жесткостей ри­гелей этажа;

sh λ и ch λ — гиперболические синус и косинус, равные

е — основание натуральных логарифмов.

Расчетные усилия в отдельных колоннах каркасной части от верти­кальных нагрузок определяются при полном загружении временными на­грузками всех пролетов. Кроме того, для средних колонн следует дополни­тельно провести расчет с учетом отсутствия временной нагрузки на ригеле, примыкающем к нижнему узлу рассматриваемой колонны, а для колонны 1-го этажа — на ригеле, примыкающем к верхнему ее узлу.

инструкция по сборке и монтажу

Можно ли собрать каркас потолка из профиля под гипсокартон своими руками? Какие материалы и инструменты для этого понадобятся, в каком варианте может быть устроена конструкция и главное — как сделать так, чтобы результат радовал годами, не давая повода для ремонта? Обо всем этом ниже.

Каркас под потолок из ГКЛ: каким бывает?

Подвесной и натяжной потолок объединяет нечто общее — каркас. В обоих случаях отделка потребует изначально сделать обрешетку из профилей. Выделяют несколько разновидностей конструкций, разделяемых по разным признакам.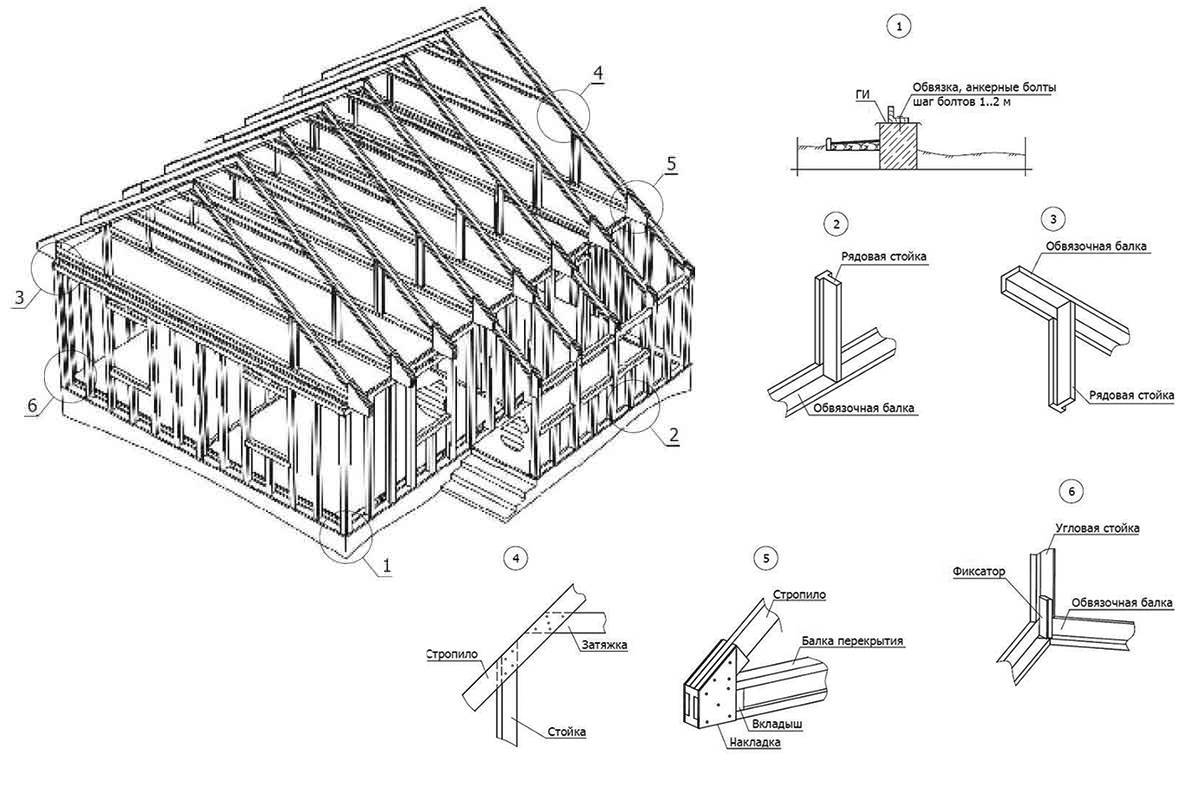

По типу используемых материалов различают каркасы:

• металлические;
• деревянные.

Металлический каркас для гипсокартона на потолок используется чаще из-за отличных эксплуатационных характеристик, простого монтажа и практичности.

Деревянная обрешетка — не исключение, но монтируется не так часто из-за особенностей эксплуатации дерева. Элементы каркаса в этом случае обязательно подлежат обработке против грибков и микроорганизмов и несмотря на это по сроку службы все равно уступают металлическим профилям.

Кроме того, обрешетка под гипсокартон из дерева может потерять форму в результате перепадов температур и повышенного уровня влажности. Практически по всем параметрам деревянный каркас уступает металлическому за исключением одного — полной экологичности.

Деревянный каркас для монтажа гипсокартона

Разделяется каркас подвесного потолка и по структуре. Когда речь идет о металлической конструкции, подразумевают следующие варианты:

• ячеистую;
• поперечную.

В основе ячеистой обрешетки зафиксированные профили и перемычки с одинаковыми ячейками.

Поперечные каркасы чаще становятся выбором опытных мастеров, так как работы потребуют определенных навыков. В случае их устройства листы гипсокартона фиксируются исключительно на поперечно закрепленных профилях.

Разделяют каркас и по количеству уровней на одноуровневые и многоуровневые. Первые монтируют для одноуровневых потолков. Особенность конструкции — профили, закрепленные в одной плоскости.

Многоуровневые каркасы необходимы для монтажа таких же многоуровневых потолков. Самостоятельно собрать конструкцию, учитывая внушительные размеры каркаса, непросто, поэтому ниже рассмотрим простой вариант классической одноуровневой ячеистой обрешетки из металлического профиля.

Что нужно знать об устройстве металлического каркаса

Прежде чем выполнять монтаж каркаса, необходимо проанализировать его устройство в классическом исполнении. Обычно для монтажа используют разные варианты профилей и соединительные элементы.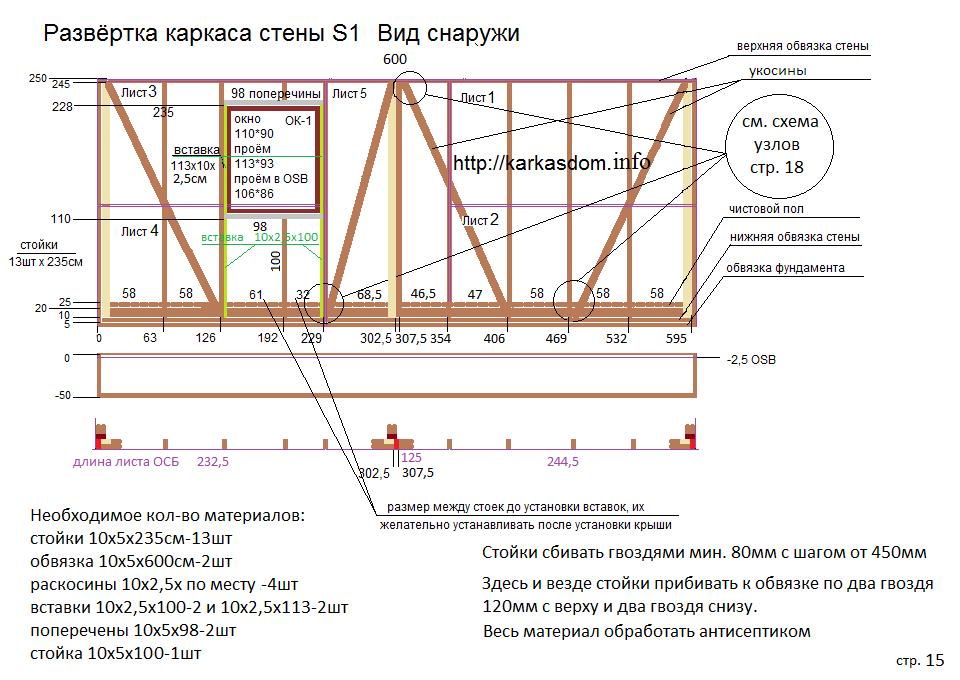 Основные из них:

• CD профиль — играет роль несущего элемента обрешетки, выступает в качестве основы для крепления листов гипсокартона.
• UD — профиль —направляющий, предназначен для создания монтажной плоскости. Используется для соединения отдельных частей обрешетки между собой и с основанием.
• CW и UW — профили с функциями, аналогичными UD и CD профилям, подходят для каркаса не только на потолок, но и на стены, а также используется для монтажа перегородок;
• Соединители — представлены в трех вариантах: прямом, двухуровневом, крестообразном;
• Кронштейн — подходит для крепления CD-профиля к поверхности стен и потолка;
• Быстроподвес — нужен для выравнивания потолочной поверхности по горизонтали;
• Крепежи — дюбели и саморезы для сбора и фиксации конструкции.

Представление об устройстве каркаса упростит непростую задачу, какой является установка профиля на потолок для человека без опыта.

Последовательность проведения работ: краткая схема

Не допустить ошибок в процессе монтажа обрешетки поможет и следование проверенному алгоритму действий. Классический монтаж конструкции для подвесного потолка из гипсокартона представляет собой определенную последовательность работ:

1. Выравнивают углы потолка, тем самым упрощая подгон гипсокартонных листов в дальнейшем.
2. Проводят электромонтажные работы, имея схему расположения осветительных приборов, составленную заранее. Важно, чтобы длина кабеля к точкам расположения приборов была не менее 15 см от гипсокартонного потолка.
3. Составляется схема каркаса для потолка из гипсокартона с нанесением разметки на поверхность потолка.
4. Монтируют горизонтальные направляющие, подвесы, профили.
5. Крепят гипсокартонные листы.
6. Готовую конструкцию отделывают грунтовочными и шпаклевочными смесями под покраску или оклейку обоями.

Монтаж простой ячеистой обрешетки: пошаговая инструкция

На начальном этапе определяют расстояние, на которое «опустится» конструкция. Здесь учитывают особенности планируемых приборов для освещения. Каждый из них потребует определенной высоты и это важно принимать во внимание.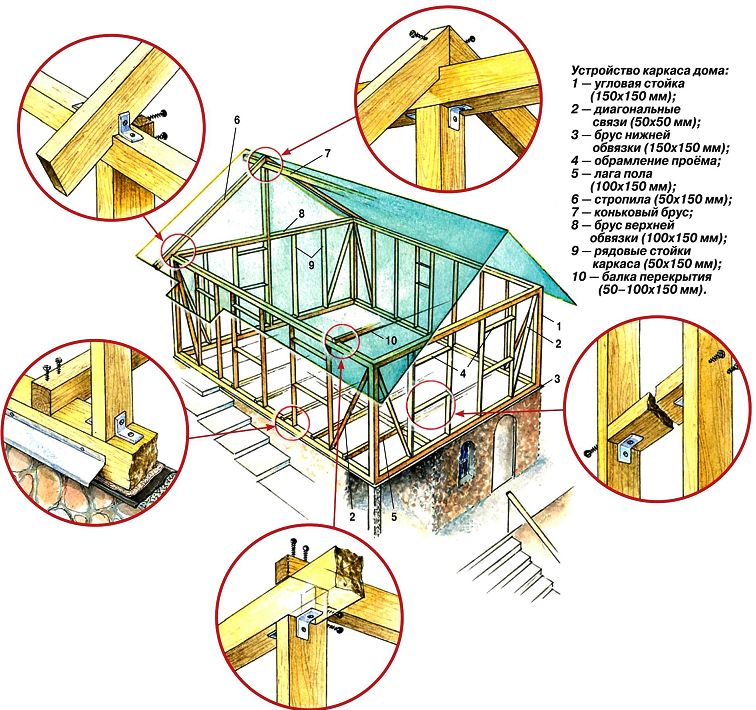

На поверхности стены ставят отметку, от которой будут планировать разметку в дальнейшем. Правильным будет, монтируя потолочный каркас из профиля своими руками, использовать лазерный уровень. Определяют горизонтальную линию, отмечая ее карандашом или отбивочным шнуром.

Используя рулетку, отмеряют необходимую длину металлического профиля, отрезают элемент ножницами по металлу. Отдельные детали должны легко стыковаться друг с другом, поэтому нахлест будет составлять не менее 3 см с фиксацией точки соединения метизом.

На следующем этапе, собирая каркас своими руками, монтируют ПНП на поверхности стен по заранее отмеченным линиям. Большая часть моделей оснащены рабочими отверстиями, в остальных же случаях их делают дополнительно на расстоянии в 50 см друг от друга, используя дрель или перфоратор.

Только после окончания ряда предыдущих работ переходят к разметке потолочных профилей. Для этого от поверхности стены отступают около 60 см, проверяют уровнем точности линий. Отметки должны быть четко обозначены на поверхности. С помощью профиля соединяют линии на противоположных стенах, полученная черта станет «стартовой». Именно о нее начинают наносить параллельные линии по поверхности потолка, учитывая, что шаг обрешетки должен составлять 60 см.

Точно таким же способом проводят линии по длине комнаты, получая в итоге ячейки правильной формы с размерами 60×60 см.

Следующий шаг — крепление прямых подвесов саморезами на расстоянии 60-70 см с центром основания по намеченной ранее линии. В зонах планируемого монтажа приборов дополнительно крепят траверсы.

Чтобы правильно собрать потолок не обязательно нарезать профиль с запасом, так как расстояние от стены до стены может меняться. Каждый профиль измеряется в индивидуальном порядке, при этом важно, чтобы длина его была на несколько сантиметров меньше ширины потолка.

Собирая каркас из металлопрофиля, на следующем этапе крепят потолочные профили в направляющие с центральным желобком, выходящим на риску. Фиксируют его с помощью одного самореза, в отдельных случаях используя муфту.

Ножницами по металлу нарезают перемычки из потолочного профиля по 60 см и поперечины для монтажа от стены до первого продольного профиля на 2-3 см меньше имеющегося расстояния.

Финишный этап для тех, кто решил делать каркас своими руками покажется самым ответственным. Заканчивая устройство конструкции, потолочные профили крепят к подвесам с окончательной фиксацией после проверки и устранения отклонений. Готовую конструкцию обшивают листами гипсокартона.

Модель сетчатой конструктивно-силовой схемы каркаса тестовой панели солнечной батареи космического аппарата

Открытые информационные и компьютерные интегрированные технологии № 58, 2013

96

2. Приведенные результаты выбора рациональных параметров элементов

сетчатой КСС тестовой панели СБ в рамках принятых допущений и исходных

характеристик применяемых ПКМ дают основание рассчитывать на

принципиальную возможность реализации поверхностной массы панели СБ в

пределах 0,64…0,875 кг/м

2

при регламентированной несущей способности и

жесткости, что отвечает мировым тенденциям для объектов данного класса.

Список литературы

1. Композиционные материалы в ракетно-космическом аппаратостроении

[Текст] / Г.П. Гардымов, Е.В. Мешков, А.В. Пчелинцев и др. – СПб.: СпецЛит, 1999.

– 271 с.

2. Коваленко, В.А. [Текст] Применение полимерных композиционных

материалов в изделиях ракетно-космической техники как резерв повышения ее

массовой и функциональной эффективности/ В.А. Коваленко, А.В. Кондратьев //

Авиационно-космическая техника и технология. – 2011. – № 5(82). – С. 14 – 20.

3. Сотовые заполнители и панельные конструкции космического назначения

[Текст]: моногр.: в 2 т. / А.В. Гайдачук, О.А. Карпикова, А.В. Кондратьев,

М.В. Сливинский; под. ред. А.В. Гайдачука – Х.: Нац. аэрокосм. ун-т

им. Н.Е. Жуковского «Харьк. авиац. ин-т», 2012. – Т. 1: Технологические

несовершенства сотовых заполнителей и конструкций. – 279 с.

4. Легкий и прочный конструкционный материал для ракетно-космической

техники [Текст] / В. И. Сливинский, А.В. Кондратьев, В.А. Коваленко,

А.И. Алямовский // Композиционные материалы в промышленности: сб.

материалов 31 междунар. науч.-практ. конф., Ялта 6–10 июня 2011 г. / Украинский

информационный Центр «Наука. Техника. Технология». – К., 2011. – С. 407 – 409.

5. Оптимальное проектирование композитных сотовых конструкций

авиакосмической техники [Текст]: моногр./ В.Е. Гайдачук, А.В. Кондратьев,

В.В. Кириченко, В.И. Сливинский. – Х.: Нац. аэрокосм. ун-т «Харьк. авиац. ин-т»,

2011. – 172 с.

6. К вопросу проектирования сверхлегких панелей солнечных батарей

[Текст] / А.Л. Макаров, А.М. Потапов, В.А. Коваленко и др. // Эффективность

сотовых конструкций в изделиях авиационно-космической техники : сб.

материалов IV междунар. науч.-практ. конф., Днепропетровск 01 – 03 июня 2011 г.

/ Укр. НИИ технологий машиностроения. – Днепропетровск, 2011. – С. 156 – 157.

7. Алферов, Ж.И. [Текст] Тенденции и перспективы развития солнечной

фотоэнергетики / Ж.И. Алферов, В.М. Андреев, В.Д. Румянцев // Физика и техника

полупроводников. – 2004. – Т.38. – Вып. 8. – С. 937 – 948.

8. Выбор рациональных параметров элементов конструктивно-силовой

схемы каркаса тестовой панели солнечной батареи космического аппарата [Текст]

/ В.В. Гаврилко, В.А. Коваленко, А.В. Кондратьев, А.М. Потапов // Открытые

информационные и компьютерные интегрированные технологии: сб. науч. тр. Нац.

аэрокосм. ун-та им. Н.Е. Жуковского «ХАИ». – Вып. 54. – Х., 2012. – С. 5 – 13.

9. Разработка макетного образца и технологии изготовления тестовой

панели солнечной батареи космического аппарата [Текст] / В.В. Гаврилко,

В.А. Коваленко, А.В. Кондратьев, А.М. Потапов // Вопросы проектирования и

производства конструкций летательных аппаратов: сб. науч. тр. Нац. аэрокосм. ун-

та им. Н.Е. Жуковского «ХАИ». – Вып. 3(71).– Х. , 2012. – С. 110 – 117.

Армирование фундаментной плиты – схема, изготовление и монтаж каркаса

Бетонная плита, расположенная в основании дома, принимает на себя неравномерные нагрузки. Места расположения несущих стен или колонн подвергаются большему давлению, нежели на свободные от нагрузок участки. В результате, кроме сжимающих усилий, с которыми великолепно справляется бетонная глыба, появляются разрушающие монолит изгибающие моменты. Справиться с ними помогает армирование фундаментной плиты. Установленные в бетонном теле металлические сетки или каркасы принимают на себя опасные для искусственного камня нагрузки, равномерно распределяя их по всей площади фундамента.

Схема армирования

Монолитные железобетонные плиты считаются одними из самых надежных фундаментов. Их недостатком является высокая себестоимость конструкции, но довольно часто именно плиты становятся единственно возможным вариантом устройства подземной части дома.

Следует сразу же оговориться, что количество, диаметр и шаг арматурных стержней в верхней и нижней сетке определяется согласно произведенным расчетам. В них учитываются постоянные и временные нагрузки, грунтовые условия и другие не менее важные факторы. Кроме того, принимаются во внимание зоны продавливания. Здесь выполняется дополнительное усиление каркаса. Шаг стержней под несущими стенами рекомендуется уменьшать в два раза от аналогичного размера в основных сетках.

Армирование фундаментной плиты толщиной до 150мм допускается выполнять одной сеткой. В более массивные конструкции укладывают каркасы.

Сетка состоит из продольных и поперечных металлических прутьев. Отсутствие тех или иных неминуемо приводит к разрушению бетонного монолита. Шаг арматурных стержней в основных ячейках принимают, как правило, 150-200мм, хотя при малых расчетных нагрузках он может увеличиваться и до 400мм. Существует правило, устанавливающее минимальное расстояние от одного металлического прута до другого. Оно не может превышать толщину фундаментной плиты более чем в полтора раза.

Верхние и нижние арматурные сетки смогут взаимно работать только в том случае, если они будут объединены вертикальными стержнями, которые устанавливают в каждой ячейке или через одну. Для жесткости, на торцах плиты требуется закладывать еще и связанные с каркасом П-образные стержни. Их длина в расправленном состоянии должна составлять не менее удвоенной толщины плиты.

Для сопряжения с монолитными подвальными стенами или цоколем, в местах их стыковки с фундаментной плитой монтируют арматурные выпуски. В зоне расположения основного каркаса их загибают и фиксируют к элементам сеток.

Варианты изготовления каркасов

Для фундаментных плит используются арматурные стержни периодического профиля. Их диаметр принимается, исходя из предварительных расчетов. Как правило, он составляет 8-16мм.

Формирование сеток производится путем фиксации металлических прутков между собой. Существует два способа:

• вязка – с помощью тонкой, податливой проволоки или специальных пластиковых хомутов;
• сварка – быстрый, но менее надежный вариант.

В первом случае выполняется довольно кропотливая работа. Для удобства вязки стержней пользуются специальными приспособлениями (крюками, пистолетами) или плоскогубцами. Проволочное соединение не нарушает структуру металла и дает некоторую свободу при возможном смещении стержней. Сварное крепление является жестким, поэтому при случайных подвижках могут происходить сколы. Кроме того, именно в местах сварки арматура чаще всего начинает ржаветь.

Недостаточно длинные прутья наращивают, укладывая соседние элементы внахлест, размер которого принимают в 40 раз больше диаметра стержней. Стыки размещают вразбежку.

Монтаж каркаса

Нижнюю сетку монтируют на пластиковые фиксаторы, расставленные по всей площади основания. С их помощью обеспечивается образование защитного бетонного слоя толщиной 20-30мм. Именно он предохраняет арматуру от коррозии.

Для удобства укладки верхней сетки устанавливают подставки. Это могут быть деревянные бруски, кирпичи или арматурные «пауки» или «лягушки». Важно, чтобы они были одинаковыми по высоте. Количество опор выбирается с учетом предотвращения горизонтальных прогибов сетки. Верхняя отметка арматурных стержней должна располагаться ниже уровня бетонной плиты на 30-50мм. Данное требование связано с образованием защитного слоя.

На последнем этапе армирования плитного фундамента выполняют установку и крепление вертикальных стержней. После этого деревянные и кирпичные подставки убирают. «Пауки» и «лягушки» могут оставаться в каркасной конструкции в качестве конструктивных распорок.

Напоследок необходимо напомнить о том, что неправильное армирование фундаментной плиты вполне может привести к разрушению бетонного монолита. Поэтому к работам следует подойти ответственно. В этом вопросе экономия или игнорирование технологии вряд ли будут оправданными.

Конструктивные элементы каркаса многоэтажных промышленных и гражданских зданий

Организационные, контрольно-распорядительные и инженерно-технические услуги
в сфере жилой, коммерческой и иной недвижимости. Московский регион. Официально.

Унифицированные сборные железобетонные элементы многоэтажных промышленных зданий

Конструктивная схема стального каркаса производственного здания

Управление недвижимостью: сдача в аренду, работа с арендаторами и поставщиками услуг.
Технический надзор за подрядчиками (мастерами, специалистами), ведение документации.

2007-2021 © remstroyinfo.ru
При цитировании материалов в сети обратная ссылка строго обязательна

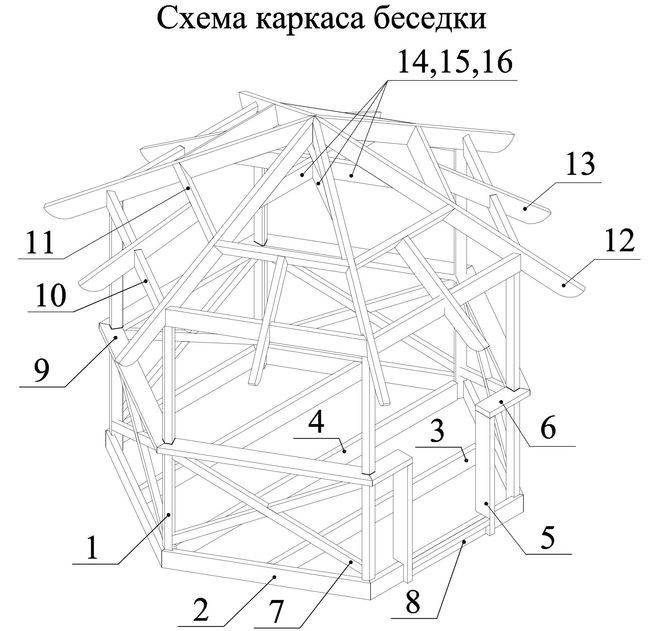
Из чего сделать каркас беседки: обзор материалов

Иметь уютный, комфортный домик загородом или в центре города – мечта многих жителей нашей планеты. Для создания особого уюта на своей территории жилищной площади необходима правильная планировка построения, качественные материалы, квалифицированные специалисты и ваша безграничная фантазия.

Металлический каркас

Уже давно прошли те времена, когда в моде был строгий минимализм и консерватизм. Сейчас комфорт заключается в обилие. Так, частный сектор перестал выглядеть, как обыкновенный дом с садом или огородом. Мы стараемся дополнить жильё функциональностью и разными зонами комфорта, отдыха, работы и просто приятного времяпровождения. Беседка или уютная уличная веранда – то, что нужно для приятного отдыха во дворе собственного дома.

Деревянный каркас

Подготовка к строительству

Обратите внимание, как шикарно выглядит домик с беседкой на фото. Также вы можете посмотреть видео о том, как дополнить свой дом уютными пристройками. Естественно, фото не может передать всех особенностей возведения беседки и раскрыть вопрос о том, как сделать каркас для беседки своими руками. Прежде чем строить каркас беседки для дачи или дома, следует выбрать материал для каркаса.

Итак, первым делом нужно выбрать место, где будет размещаться ваша беседка. К этому вопросу вы должны подойти более чем серьёзно, и для разработки плана использовать схемы и чертежи. Вы должны учитывать расстояние беседки от дома, расстояние беседки от забора, учитывать состояние грунта или асфальта, плитки, чтобы строительная конструкция была надёжной и долговечной.

Схемы и чертежи лучше разрабатывать вместе со специалистами, которые смогут вам помочь во многих строительных вопросах. Также ваши схемы и чертежи помогут вам в дальнейшем корректировать процесс строительства или исправлять неточности выполнения плана рабочими.

Подборка материала для строительства каркаса

Что касается материала для каркаса, то в современное время чаще всего возводят каркас из металла или дерева. Сделать каркас беседки своими руками достаточно просто. Итак, вы изготовили, прежде чем возвести каркас беседки чертёж схем. Схемы и чертежи, на которых вы разместили конкретный, детальный план строительства, также могут вам подсказать, из какого материала лучше строить каркас.

Каркас беседки из металла очень распространён в наши дни. Он может устанавливаться на абсолютно любые виды фундамента, а также металлический каркас для беседки достаточно надёжный и крепкий. Делая металлический каркас своими руками, вы можете подключить фантазию и сделать так, чтобы ваша беседка была изящной, с тонким металлическим переплётом, либо разработать строительство так, чтобы беседка была массивной, крепкой и основательной.

Чтобы возвести металлический каркас, кроме основного материала вам понадобится профильная труба и не один металлический брус. Каркас металлической беседки имеет свои неоспоримые плюсы.

1. Металлический каркас отличается своей мобильностью. Вы с лёгкостью можете передвигать беседку по садовой площади или двору.
2. Беседка из металла противопожарная. Профильная труба из металла позволяет установить внутри камин или мангал.
3. Металлический каркас достаточно лёгкий, но невероятно прочный.
4. Вы можете изготовить крышу для беседки своими руками и придать ей любую форму. Также металлический каркас выдержит любой материал, из которого вы решите изготавливать крышу для беседки.

Единственное, за чем вам придётся пристально следить, так это за тем, чтобы не поржавела профильная труба.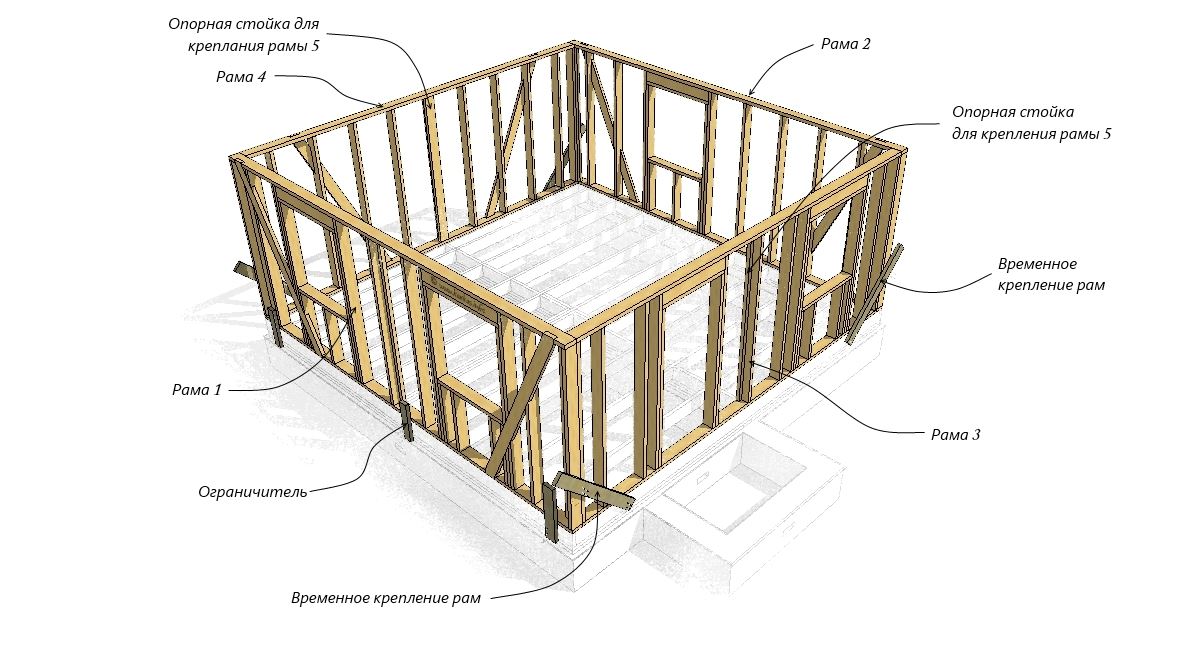 Иначе беседка потеряет общий вид и надёжность.

Особенности деревянного материала для строительства

Каркас деревянной беседки нисколько не проигрывает металлической основе. Вы также с лёгкостью можете построить деревянную беседку своими руками. Каркас, основой которого является деревянный брус, достаточно стойкий к погодным условиям: хорошо выдерживает жару и не размокает в дождь. Такая беседка считается экологически чистой.

Деревянный брус обеспечивает лёгкость монтажа конструкции. Беседка, построенная из деревянных материалов, просто полотно для творчества. Вы можете заняться резьбой по дереву и украсить брус необычным узором. Можете использовать разноцветные краски и дать волю своей фантазии (см. фото).

Каркас деревянной беседки бывает двух видов: решётчатый или сплошной. Вы можете оставлять зазоры между брусьями. Этот вариант больше подходит для летней конструкции, либо использовать деревянный брус для возведения сплошной стены. В такой беседке можно легко укрыться от непогоды, закутаться в тёплый плед, слушать приятную музыку и пить горячий чай.

Для того чтобы деревянный каркас не поддавался нападению вредителей, брусья следует обработать специальным антисептическим раствором. В таком случае, беседка будет надёжно защищена от гниения, повышенной влажности, а каркас прослужит вам долгие годы.

Что необходимо для строительства?

Самыми распространёнными материалами и инструментами, которые вам обязательно пригодятся во время строительства беседки, считаются следующие:

• деревянные брусья либо металлические профильные трубы;
• евровагонки;
• резные карнизы;
• гибкая черепица;
• герметик для черепицы;
• саморезы, гвозди;
• молоток и пила.

Итак, теперь вы видите, беседка, построенная своими руками, это не миф, а реальное достижение. Возвести каркас, абсолютно не составит для вас труда. Главное, правильно выбрать материал для каркаса, обработать его должным образом и тогда ваша беседка станет комфортным, уютным уголком для приятного времяпровождения.

Смотрите также:

Руководство по стилю фреймов UML 2

	Элементы стиля UML 2.0 описывает коллекцию стандартов, соглашений и методические рекомендации для создания эффективных UML-диаграммы . Они основаны на звуке, проверенном принципы разработки программного обеспечения, которые приводят к диаграммам которые легче понять и с которыми работать. Эти соглашения существуют как набор простых, лаконичных руководящие принципы, которые при последовательном применении представляют собой важный первый шаг к повышению производительности модельер.Эта книга ориентирована на средства моделирования UML от среднего до продвинутого уровня, хотя многочисленные примеры в книге, это не было бы быть хорошим способом изучения UML (вместо этого рассмотрите Учебник по предметам ). Книга краткая 188 страницы длинные и удобного карманного размера, так что его легко носить с собой.
	Эта книга, Выбери свой WoW! Дисциплинированное руководство по гибкой разработке для оптимизации вашего способа работы, является незаменимым руководством для agile-коучей и практиков, чтобы определить, какие методы — включая практики, стратегии и жизненные циклы — эффективны в определенных ситуациях и не так эффективен в других.Этот совет основан на проверенном опыте сотен организаций, которые столкнулись с ситуацией, похожей на вашу. Каждая команда уникальна и сталкивается с уникальная ситуация, поэтому они должны выбрать и развивать способ работы (WoW), который эффективен для их. Выбери свой WoW! описывает, как сделать это эффективно, независимо от того, только ли они начинают с agile/lean или если они уже следуют Scrum, Kanban, SAFe, LeSS, Nexus или другим методам.
	The Object Primer, 3-е издание: Agile Model Driven Разработка с использованием UML 2 — важный справочник для разработчиков гибких моделей.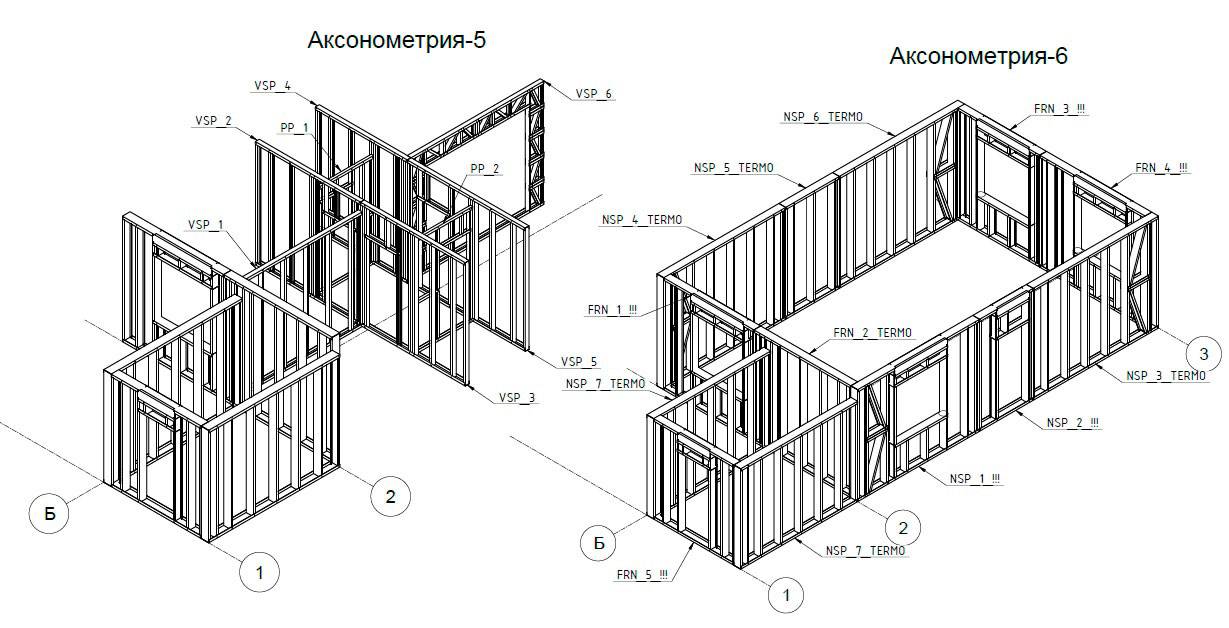 описание того, как разработать 35 типов agile модели включая все 13 UML2-диаграммы.Кроме того, в этой книге описываются фундаментальные методы программирования и тестирования. для успешного предоставления гибкого решения. В книге также показано, как перейти от гибкие модели в исходный код, как преуспеть в таких методах реализации, как рефакторинг и разработка через тестирование (TDD). Учебник по объектам также включает главу, посвященную основным методам разработки баз данных (рефакторинг базы данных, объектно-реляционное отображение, анализ наследия и код доступа к базе данных) из моего отмеченного наградами Справочник по гибким базам данных.

Общая терминология фоторамок | Вермонт Хардвудс

Standards Care and Treatment Standards (FACTS) опубликовал документ, подробно описывающий, как заказывать отбивные и рамы. Вот основные моменты.

При покупке нестандартных рам полезно ознакомиться с терминологией рамок для фотографий. Вот несколько общих терминов для фоторамки с диаграммами, которые помогут вам начать работу.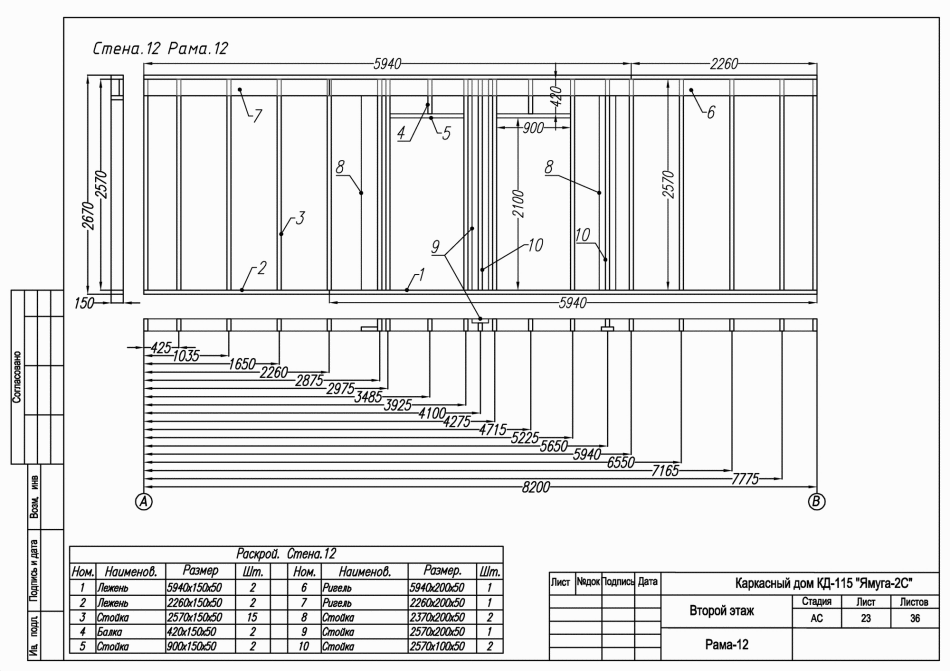

Краткое изложение практики

• Поставщик отбивных или рам должен измерять внутреннюю часть шпунта, если не указано иное.
• Молдинги с двойным шпунтом измеряются по внутренней стороне переднего шпунта
• Ко всем заказанным размерам добавляется стандартный припуск 1/8″. Любые другие инструкции должны использовать обозначенный термин (см. раздел «Как сделать заказ» ниже).

Как заказать

• Размер рамы Заказы должны быть обрезаны до самого внутреннего шпунта с добавлением стандартного припуска 1/8″. Если размер заднего шпунта является наиболее важным, в заказе должно быть указано «Размер рамы по заднему шпунту.«Срез должен иметь стандартный припуск 1/8″. (см. схему 1)
• Точный размер Припуск не добавляется
• Размер прицела Отрежьте внутреннюю молдинговую кромку; припуск не добавляется (см. схему 1 и схему 2)
• Fit Outside Fit Outside Fit вокруг вкладышей или внутренних рам, которые следует заказывать по размеру упаковки художественного произведения/остекления (см. рис. 4 и рис. 5)
• Внешний размер Обрезать по самому внешнему размеру; припуск не добавляется (см. схему 1 и схему 2)

Общая терминология фоторамки

*Схемы ниже для справки .

Должен – Обязательное условие

Следует – Положение не является обязательным, но рекомендуется в качестве хорошей практики

Май – Положение является необязательным

Прибавка – Разница между размером обрамляемых объектов и внутренним размером рамы

Обозначения – Термины, которые следует использовать, когда заказы на отбивные или рамки отличаются от стандартного припуска 1/8″

Размер рамы – Измерение по задней стороне шпунта рамы (см. рис. 1)

Шлиц – Вырезанная часть задней части рамы, которая поддерживает арт-пакет (см.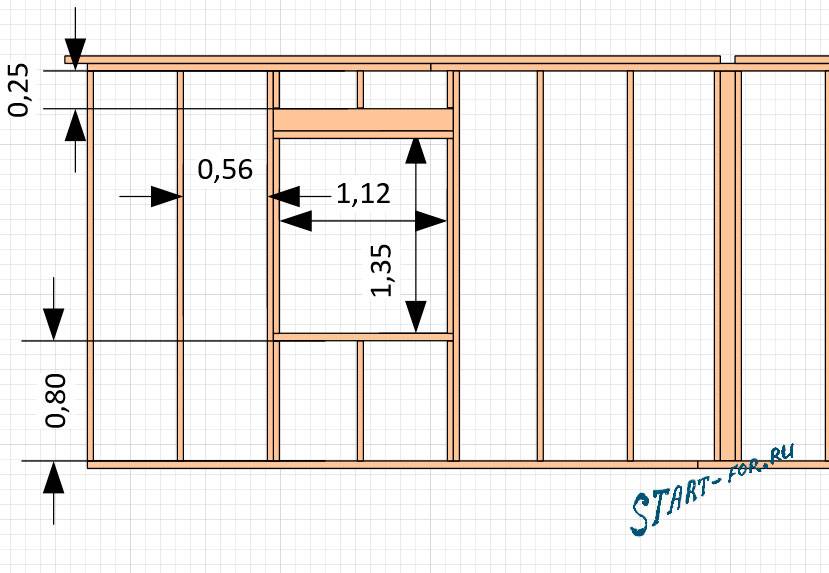 рис. 2)

Задний шлиц – Задний шпунт – самый большой шпунт в молдинге с двойным шпунтом (см. схему 3)

Двойной шпунт – Молдинг с обычным шпунтом спереди и дополнительным шпунтом сзади, который поддерживает художественную или декоративную основу

Внутренняя рама / вкладыш – Дополнительная рама внутри другой рамы

Составная рама – Рама в сборе, состоящая из нескольких рам

Точный размер – Заказанный размер – без припуска

Внешний размер – Общий внешний размер рамы (см. схему 1 или схему 2)

Размер прицела – Измерение (точное, без припуска) через самое внутреннее отверстие рамки (см. схему 1 или схему 2)

Установка снаружи – Установка вокруг вкладыша или рамы (см. схему 4 или схему 5)

Полезные диаграммы

Диаграмма 1:

Диаграмма 2:

Диаграмма 3:

Диаграмма 4:

Диаграмма 5:

Заголовок диаграммы — обзор

3.

Шесть (6) типов диаграмм, являющихся частью SysML-Lite, выделены на рис. 3.2. Каждая диаграмма содержит заголовок диаграммы, который идентифицирует тип диаграммы, и другую информацию о диаграмме, которая объясняется в главе 5, разделе 5.3.2. В частности, SysML-Lite включает:

РИСУНОК 3.2. SysML-Lite включает шесть из девяти диаграмм SysML и подмножество функций языка. Он предназначен для введения нового средства моделирования в SysML, обеспечивая при этом существенные возможности моделирования.

▪

Пакетная диаграмма для захвата модельной организации

▪

▪

Диаграмма требования к захвату Требования к текстовым требованиям

▪

Диаграмма активности для представления поведения системы и его компоненты

▪

Диаграмма определения блока для представления системы иерархии системы

▪

▪

Внутренняя блок-схема для представления системной соединения

▪

Параметрическая диаграмма для захвата взаимоотношений между свойствами системы для поддержки инженерного анализа

Этот набор диаграмм предоставляет пользователю модели существенные возможности для моделирования систем, которые охватывают многие классические схемы системного проектирования и многое другое.

SysML-Lite включает небольшой набор функций языка для каждой из шести диаграмм SysML. Некоторые возможности SysML-Lite представлены на диаграммах на рис. 3.3. Точное подмножество функций языка SysML можно адаптировать к потребностям. На рисунке также показаны толстые линии со стрелками, которые не являются частью языка, но подчеркивают некоторые важные взаимосвязи между диаграммами. Эти отношения обычно согласуются с классическими методами системной инженерии, такими как функциональная декомпозиция и распределение.

РИСУНОК 3.3. Упрощенные диаграммы с выделением некоторых функций языка для каждого типа диаграмм в SysML-Lite.

Диаграмма пакетов, помеченная pkg, используется для организации элементов модели , содержащихся в модели. На этой диаграмме модель системы отображается в заголовке диаграммы и содержит пакеты для требований , поведения , структуры и параметров . Каждый из этих пакетов, в свою очередь, содержит элементы модели, представленные на диаграмме требований, диаграмме действий, диаграмме определения блока, внутренней блок-схеме и параметрической диаграмме соответственно. Обратите внимание, что элементы модели как для схемы определения блока, так и для внутренней блок-схемы содержатся в пакете Structure .

Диаграмма требований помечена как req и представляет собой простую иерархию текстовых требований, которые обычно являются частью документа спецификации. Требование верхнего уровня с именем R1 содержит два требования R1.1 и R1.2. Соответствующий оператор требования для R1.1 фиксируется как текстовое свойство требования и соответствует тексту, который можно найти для этого требования в документе спецификации.

Диаграммы действий помечены как действие. Диаграмма деятельности с именем A0 представляет взаимодействие между System 1 и System 2 . Начальный узел, представленный закрашенным темным кружком, и конечный узел, представленный мишенью, указывают на начало и конец действия соответственно. Действие определяет простую последовательность действий, начиная с выполнения действия :A1 и заканчивая выполнением действия :A2 . Выход :A1 и ввод :A2 представлены прямоугольниками на границе действия, называемыми контактами. Кроме того, разделы действий, помеченные как :Система 1 и :Система 2 , отвечают за выполнение действий, заключенных в этих разделах. Действие под названием :A1 удовлетворяет требованию R1.2 , которое представлено отношением удовлетворяет .

Действие, названное :A1 на диаграмме действий A0 , разложено на диаграмме действий A1 на действия :A1.1 и :A1.2 . Эти действия выполняются :Компонент 1 и :Компонент 2, соответственно. Выход действия A1 , представленный прямоугольником на его границе, соответствует выходному выводу действия :A1 в действии A0. Как показано на диаграммах действий для A0 и A1 , выходные и входные данные непротиворечивы от одного уровня декомпозиции к другому.

Диаграмма определения блока помечена как bdd и часто используется для описания иерархии системы, подобной дереву частей (например, дереву частей). г., дерево снаряжения). Блок используется для определения системы или компонента на любом уровне системной иерархии. Диаграмма определения блока на рисунке показывает блок System Context , состоящий из System 1 и System 2 . Система 1 далее разбивается на Компонент 1 и Компонент 2 . Блоки System 1 и Component 1 содержат свойство значения, которое может соответствовать физической или производительной характеристике, такой как вес или время отклика.

Внутренняя блок-схема обозначена ibd и показывает, как взаимосвязаны части System 1 . Прилагаемая рамка схемы представляет System 1 . Маленькие квадратики на Система 1 и ее части называются портами и представляют их интерфейсы. Система 1 также представлена ​​разделом действия в действии A0 , а компоненты аналогичным образом представлены разделами действия в действии A1 .

Параметрическая диаграмма помечена как par и используется для описания взаимосвязей между свойствами, соответствующими инженерному анализу, такому как производительность, надежность или анализ массовых свойств. В этом примере параметрическая диаграмма включает одно ограничение, называемое Ограничение 1 , которое соответствует уравнению или набору уравнений. Маленькие квадраты на одном уровне с внутренней частью ограничения представляют параметры уравнения. Затем свойства системы и блоков компонентов могут быть привязаны к параметрам, чтобы установить отношение равенства. Таким образом, конкретный анализ может быть приведен в соответствие со свойствами конструкции системы. Часто одно ограничение используется для представления определенного анализа, а параметры представляют входные и выходные данные анализа.

На приведенных выше диаграммах показано лишь небольшое подмножество функций языка SysML для обозначения некоторых ключевых конструкций, используемых для моделирования систем. Следующая упрощенная модель воздушного компрессора иллюстрирует, как можно применять диаграммы и языковые функции SysML-Lite.

Обратите внимание, что некоторые имена содержат двоеточие (:). Это описано в Главе 4, Разделе 4.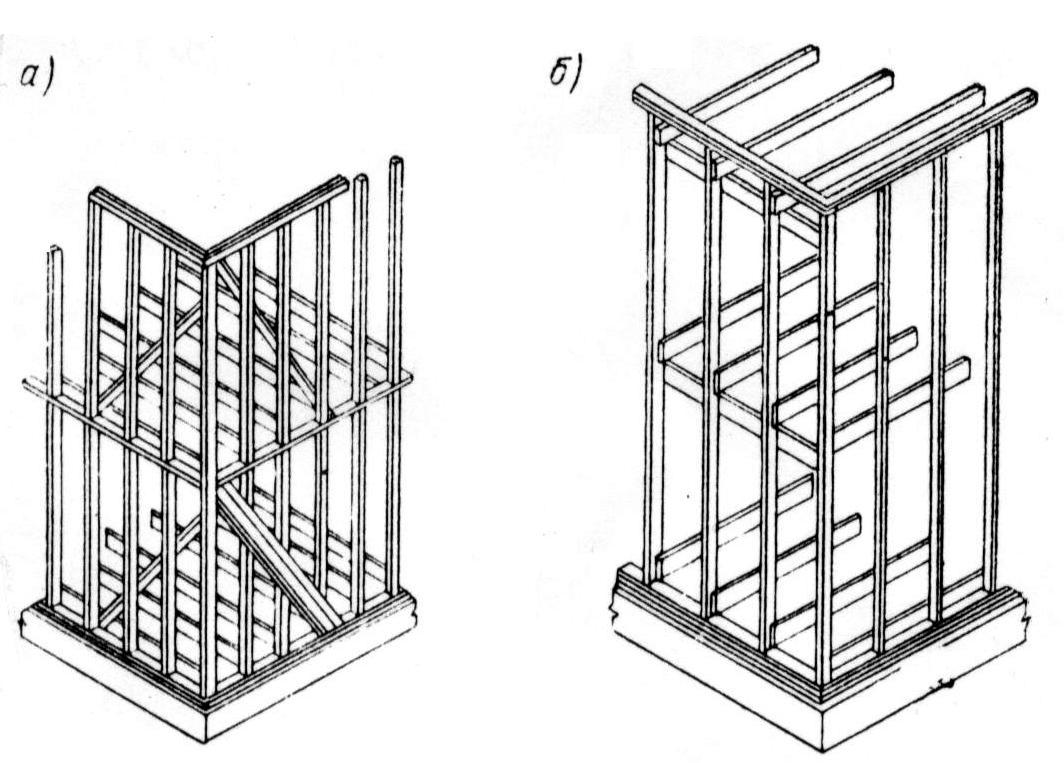 3.12, и более подробно описано в Главе 7, Разделе 7.3.1.

Моделирование сценариев с помощью диаграммы последовательности

Диаграмма последовательности — это разновидность диаграммы поведения, которая представляет динамическое представление варианта использования, требования или системы, представление, выражающее последовательность действий и событий во времени.Вы можете использовать элементы, называемые жизненными линиями, для моделирования поведения участников в системе, а затем использовать сообщения между жизненными линиями для моделирования взаимодействия между этими участниками. Взаимодействие используется, чтобы позволить вам моделировать поведенческую декомпозицию среди набора взаимодействий. Вы также можете указать ограничения по времени и продолжительности взаимодействия.

SysML включает только диаграмму последовательности и исключает диаграмму обзора взаимодействия и диаграмму связи, которые, как считается, предлагают значительно перекрывающиеся функции без добавления значительных возможностей для приложений моделирования системы. Временная диаграмма также исключена из-за опасений по поводу ее зрелости и пригодности для нужд системного проектирования

Зачем моделировать сценарии с помощью диаграммы последовательности?

Вариант использования — это набор взаимодействий между внешними субъектами и системой. Вариант использования — это «спецификация последовательности действий, включая варианты, которые система (или объект) может выполнять, взаимодействуя с действующими лицами системы.

Сценарий — это один путь или поток через прецедент, описывающий последовательность событий, происходящих во время одного конкретного выполнения системы, который часто представляется диаграммой последовательности.

Требования пользователя фиксируются как варианты использования, которые уточняются в сценариях. Вариант использования — это совокупность взаимодействий между внешними субъектами и системой. Обычно каждый вариант использования включает в себя основной сценарий (или основной ход событий) и ноль или более вторичных сценариев, которые представляют собой альтернативные варианты развития событий по отношению к основному сценарию. Часто полезно визуализировать сценарии использования по следующим причинам:

• Более детальное понимание требований путем создания модели проблем конечных пользователей (Моделирование проблемы)
• Однако, как правило, после определения исходной архитектуры системы и изучения возможностей системы (зафиксированных в виде вариантов использования) вы захотите увидеть, как возможности предоставляются компонентами в рамках архитектуры системы (моделирование решения).
• взаимодействия высокого уровня между пользователем системы и системой, между системой и другими системами или между подсистемами (иногда называемые системными диаграммами последовательности)

Краткий обзор диаграмм последовательности

Sequence Diagram — это диаграмма взаимодействия, которая подробно описывает, как выполняются операции — какие сообщения отправляются и когда. Диаграммы последовательности организованы по времени. Время идет по мере того, как вы спускаетесь по странице. Объекты, участвующие в операции, перечислены слева направо в зависимости от того, когда они участвуют в последовательности сообщений.

Диаграммы последовательности показывают взаимодействие элементов во времени и организованы в соответствии с объектом (по горизонтали) и временем (по вертикали):

Объект (спасательный круг) Размер

Линия жизни объекта представляет существование объекта в течение некоторого времени. Объекты, которые существуют во время взаимодействия, должны отображаться в верхней части измерения объектов, а их линии жизни должны быть проведены параллельно измерению времени. Объекты, которые создаются и уничтожаются динамически (переходные объекты), имеют линии жизни объектов, которые начинаются и заканчиваются получением сообщения.

• Горизонтальная ось показывает элементы, участвующие во взаимодействии
• Обычно объекты, участвующие в операции, перечислены слева направо в зависимости от того, когда они участвуют в последовательности сообщений. Однако элементы на горизонтальной оси могут располагаться в любом порядке 90 032

Измерение времени

• Вертикальная ось представляет время (или продвижение) вниз по странице.

Пример ниже представляет собой общую диаграмму последовательности, показывающую последовательность сообщений, взаимодействующих между объектами с кадрами и ограничениями сообщений.

Поток управления и сообщений

Фокус элемента управления , также известный как панель активации, показывает период действия объекта. Действия могут выполняться либо непосредственно объектом, либо через подчиненный объект, которому он отправил сообщения.

Сообщения определяют связь от одного объекта к другому с ожиданием того, что действие будет выполнено объектом-получателем.

Сообщения о вызове операций отображаются горизонтально.Они тянутся от отправителя к получателю. Порядок обозначен вертикальным положением, при этом первое сообщение отображается вверху диаграммы, а последнее сообщение — внизу. В результате порядковые номера являются необязательными.

Тип линии и тип стрелки указывают тип используемого сообщения:

• Асинхронное сообщение (обычно вызов операции) показано сплошной линией с закрашенной стрелкой. Это обычный вызов сообщения, используемый для обычной связи между отправителем и получателем.
  
• В ответном сообщении используется пунктирная линия с открытой стрелкой.
  
• Асинхронное сообщение имеет сплошную линию с открытой стрелкой. Сигнал — это асинхронное сообщение, на которое нет ответа.
  

Сообщения о создании и уничтожении

Участники не обязательно живут в течение всего времени взаимодействия диаграммы последовательности. Участники могут создаваться и уничтожаться в соответствии с передаваемыми сообщениями.

Сообщение конструктора создает получателя. Отправитель, который уже существует в начале взаимодействия, помещается вверху диаграммы. Цели, созданные во время взаимодействия вызовом конструктора, автоматически размещаются ниже по диаграмме.

Сообщение деструктора уничтожает получателя. Есть и другие способы указать, что цель уничтожена во время взаимодействия. Только когда для уничтожения цели установлено значение «после деструктора», вам нужно использовать деструктор.

Немгновенное сообщение

Сообщения часто считаются мгновенными, поэтому время, необходимое для их прибытия к получателю, незначительно. Сообщения отображаются в виде горизонтальной стрелки. Чтобы указать, что требуется определенное время, прежде чем получатель получит сообщение, используется наклонная стрелка .

Пример сообщения диаграммы последовательности

В приведенном ниже примере диаграммы последовательности показано, как можно представлять объекты, линии жизни объектов, фокус управления, ссылки и сообщения в контексте диаграммы последовательности.

Кадры и фрагменты последовательности

Фреймы диаграмм явно определяют границы диаграммы, тогда как комбинированные фреймы фрагментов охватывают части диаграммы или предоставляют ссылки на другие диаграммы или определения методов.

Рама

Нотация кадра последовательности — это графическая нотация, используемая в диаграмме последовательности UML для предоставления границы, включающей все сообщения и линии жизни последовательности связи.

Обозначение кадра последовательности отображается в виде большого прямоугольника с пятиугольником в левом верхнем углу.«sd», за которым следует имя последовательности, написано в пятиугольнике.

Например, обмен коммуникационными сообщениями между пользователем, веб-браузером и веб-сервером для выполнения процесса входа пользователя в систему может быть описан как последовательность коммуникационных сообщений с кадром последовательности.

Фрагменты схемы последовательности

Фрагменты последовательности можно использовать для добавления дополнительной семантики к диаграмме последовательности.

• UML 2.0 вводит фрагменты последовательности (или взаимодействия).Фрагменты последовательности упрощают создание и поддержку точных диаграмм последовательности
• Фрагмент последовательности представлен в виде блока, называемого комбинированным фрагментом, который заключает в себе часть взаимодействий на диаграмме последовательности
• Оператор фрагмента (в левом верхнем углу) указывает тип фрагмента
• Типы фрагментов: ref, assert, loop, break, alt, opt, neg

Моделирование простой логики и алгоритмов

Распространенная проблема с диаграммами последовательности заключается в том, как отобразить зацикливание и условное поведение.Первое, на что следует обратить внимание, — это не то, в чем хороши диаграммы последовательности. Если вы хотите показать подобные структуры управления, вам лучше использовать диаграмму действий или даже сам код. Рассматривайте диаграммы последовательности как визуализацию взаимодействия объектов, а не как способ моделирования логики управления.

Если вы по-прежнему предпочитаете моделировать это на диаграмме последовательности, используйте следующие обозначения. Как в цикле, так и в условном выражении используются фреймы взаимодействия, которые представляют собой способы выделения фрагмента диаграммы последовательности.В приведенном ниже примере диаграммы последовательности показан простой алгоритм, основанный на следующем псевдокоде:

.

	Альтернативные множественные фрагменты: будет выполняться только тот, условие которого истинно.
опция	Необязательно: фрагмент выполняется только в том случае, если предоставленное условие истинно. Эквивалентно альту только с одной трассировкой.
пар	Parallel: каждый фрагмент выполняется параллельно.
петля	Цикл: фрагмент может выполняться несколько раз, и защита указывает основу итерации.
регион	Критическая область: фрагмент может выполняться одновременно только одним потоком.
отрицательный	Отрицательный: фрагмент показывает недопустимое взаимодействие.
номер	Ссылка: относится к взаимодействию, определенному на другой диаграмме.Рамка нарисована, чтобы покрыть линии жизни, участвующие во взаимодействии. Вы можете определить параметры и возвращаемое значение.
сд	Диаграмма последовательности: используется для обозначения всей диаграммы последовательности.

Пример фрагмента последовательности — сценарий размещения заказа

Член корабля, который хотел бы разместить заказ онлайн. Заказанный товар будет отправлен участнику либо курьером, либо обычной почтой в зависимости от статуса участника (VIP, обычное членство). При желании магазин отправит участнику уведомление с подтверждением, если участник выбрал опцию уведомления в заказе.

Подъемная рама Pro-Plough UniMount и схема А-образной рамы — WesternParts.com

	—
	—
	—
	—
	—
	—
	—
	—
	—
	—
	—
	—
	—
	—
	—
	—
	—
	—
	—
	—
	3/4-10 X 3 HEX CS G5
	—
	—
	—
	—
	3/8-16 X 1-1/4 HEX CS G5
	—
	—
	—
	—
	—
	—
	—
	—
	—
	—
	—
	—
	—
	—
	—
	—
	—
	—
	—
	—

Рамка диаграммы — MagicDraw 18.

5

Все диаграммы UML имеют область содержимого, ограниченную рамкой диаграммы, как указано в спецификации UML. Рамка диаграммы в основном используется в тех случаях, когда элемент диаграммы имеет графические граничные элементы (например, порты для классов и компонентов, точки входа/выхода на конечных автоматах).

По умолчанию рамка диаграммы отображается на новой панели диаграммы. Фрейм представляет собой прямоугольник на всех диаграммах, кроме конечного автомата и активности. Рамки конечного автомата и диаграммы действий имеют закругленные углы.

Размер рамки можно изменить вручную, перетащив ее углы или границы.

 

Чтобы скрыть рамку диаграммы, выполните одно из следующих действий.

---

• Щелкните диаграмму правой кнопкой мыши и в контекстном меню отмените выбор Показать рамку диаграммы .
• Откройте диалоговое окно Свойства диаграммы и установите для свойства Показать рамку диаграммы значение false.

 

Чтобы изменить свойства фрейма диаграммы, выполните одно из следующих действий.

---

• В диалоговом окне «Параметры проекта» > «Стили символов» > «Диаграмма» > в группе параметров «Рамка диаграммы» измените нужные параметры.
• В диалоговом окне Свойства диаграммы > группе свойств Рамка диаграммы измените свойства.

 

Чтобы скрыть значок на рамке диаграммы

---

• В диалоговом окне Свойства диаграммы измените значение свойства Показать стереотипы на Текст .
  

Когда создается новая диаграмма, значок стереотипа диаграммы по умолчанию отображается в заголовке фрейма диаграммы, хотя вы можете изменить его на значок стереотипа контекста.

 

Чтобы отобразить значок стереотипа контекста на рамке диаграммы

---

• В диалоговом окне Свойства диаграммы >  Группа свойств Рамка диаграммы измените значение свойства Использовать стереотип на Контекст .

 

Существует возможность отображать аббревиатуру типа диаграммы вместо полного типа диаграммы в заголовке фрейма диаграммы.

 

Чтобы отобразить сокращенный тип диаграммы

---

• В диалоговом окне Свойства диаграммы >  Рамка диаграммы в группе свойств установите флажок Показать сокращенный тип .

 

Сокращенные типы диаграмм перечислены в следующей таблице.

2 Диаграмма

abbruviation	2
UC
UC
	Comm
SD
State Machine	STM
Activity	sct
Композитная структура	cs

4.4 Определение анализа кадров | Learn About Structures

>>Когда вы закончите читать этот раздел, проверьте свое понимание с помощью интерактивного теста в нижней части страницы.

Каркасные конструкции более сложны, чем балки, потому что они не обязательно располагаются вдоль прямой линии, как балки. В рамах могут быть как вертикальные элементы, так и элементы, наклоненные под углом. В первой части этого раздела будут обсуждаться типы нагрузок на наклонные элементы и способы борьбы с ними.Затем будет объяснен метод, который используется для анализа определенных кадров (с использованием тех же методов, которые мы использовали ранее для определенных лучей).

Наклонные нагрузки

Для стержней, наклоненных под углом, часто наиболее удобно анализировать их, сначала преобразовав все нагрузки на стержень в локальное направление оси стержня (перпендикулярно и параллельно наклонному стержню). Этот процесс показан на рисунке 4.7.

Рисунок 4.7: Преобразование нагрузок на наклонные элементы в направления локальной оси

Пример геометрии наклонного элемента показан вверху на рис. 4.7. На рисунке показаны четыре различных типа наклонных нагрузок.

Первый тип показывает преобразование точечных нагрузок на наклонный элемент в параллельные и перпендикулярные составляющие.

Второй тип («ветровой») типичен для распределенных нагрузок, вызванных ветром или другими нагрузками типа давления. Распределенная нагрузка прикладывается прямо перпендикулярно наклонному стержню и распределяется по длине диагонали стержня (в данном случае $L/cos\theta$). Поскольку нагрузка уже перпендикулярна стержню, преобразование не требуется.

Третий тип («стационарный») представляет собой распределенную нагрузку, которая не приложена перпендикулярно элементу. В этом случае он выровнен по направлению глобальной вертикальной оси, чтобы имитировать эффект вертикальной гравитационной (или «стационарной») нагрузки. Этот тип нагрузки также распределяется по длине диагонали элемента, поскольку источник нагрузки (в данном случае собственный вес элемента) также распределяется по длине диагонали. В этом случае можно использовать прямое тригонометрическое преобразование, чтобы разделить вертикальную распределенную нагрузку на две разные составляющие: одну, перпендикулярную элементу (что вызовет сдвиг и изгиб), и одну, параллельную элементу (вызвавшую осевую нагрузку), как показано на рисунке. на рисунке.

Четвертый и последний тип («снежный») представляет собой распределенную нагрузку, которая не перпендикулярна к элементу и также распределяется не по длине элемента, а по горизонтальной проекции элемента (в этом случае расстояние $ л$). В случае снеговой нагрузки с определенного участка неба может выпасть только определенное количество снега, поэтому, чем больше наклон элемента, тем больше длина, на которую будет распределен снег (что делает нагрузку на единицу длины элемента ниже).Полная вертикальная нагрузка здесь будет равна $w_{snow}L$, что меньше, чем соответствующая полная вертикальная нагрузка от стационарной нагрузки, которая была равна $w_{dead}L/\cos\theta$. Прежде чем распределенную нагрузку снежного типа можно будет разделить на перпендикулярную и параллельную составляющие, она должна быть равномерно распределена по длине диагонали элемента (вместо равномерного распределения по горизонтальной проекции элемента). Если мы разделим общую вертикальную нагрузку $w_{snow}L$ на общую длину диагонали $L/\cos\theta$, то получим новую распределенную вертикальную нагрузку, равную $w_{snow}\cos\theta$, которая теперь равна распределяется по длине диагонали элемента. Отсюда нагрузку можно разделить на перпендикулярную и параллельную составляющие, как это было сделано для стационарной нагрузки, что приводит к составляющим, показанным на рисунке 4.7.

Метод анализа определенных кадров

Анализ определенных рам очень похож на анализ определенных балок, за исключением того, что вам нужно разделить раму на отдельные элементы, чтобы каждый из них можно было проанализировать отдельно как балку. Рамы также имеют дополнительную сложность из-за потенциально наклонных элементов, а также включения в расчет осевых сил, которыми мы ранее пренебрегали при анализе балок.

Общие шаги для анализа детерминированного кадра:

1. Используйте равновесие, чтобы найти все силы реакции.
2. Разделить раму на отдельные элементы.

   Любая точечная нагрузка или момент, действующие непосредственно на соединение между двумя или более элементами, должны быть возложены только на ОДИН из элементов, когда они разделены. Неважно, какой член получает точечную нагрузку, главное, чтобы она была только на одном.

3. Найдите все силы на концах каждого элемента (на концах любого элемента или в разрезах между этим элементом и соседним элементом), используя равновесие на диаграммах свободного тела каждого элемента по отдельности.
4. Распределите все нагрузки на стержень (концевые нагрузки и моменты, а также нагрузки по длине стержня) в направлениях локальной оси стержня (т. е. перпендикулярно и параллельно стержню).
5. Теперь диаграммы осевого момента, поперечной силы и изгибающего момента могут быть найдены путем решения каждого элемента, как если бы это была отдельная балка (см. раздел 4.3).
6. (При необходимости) Используйте результаты каждого элемента для построения диаграмм общей осевой силы, поперечной силы и изгибающего момента для всей конструкции рамы.

Пример

Анализ детерминированных кадров будет продемонстрирован на примере структуры, показанной на рисунке 4.8. Начертите диаграммы осей, сдвига и моментов для всех элементов конструкции.

Рисунок 4.8: Пример определения структуры кадра

В качестве первого шага мы можем проверить стабильность и детерминированность структуры, используя методы из главы 2. Используя уравнение \eqref{eq:deg-indet}:

\begin{equation} \boxed{i_e = 3m + r — (3j + e_c) } \label{eq:deg-indet} \tag{1} \end{equation} \begin{align*} i_e &= 3m + r — (3j + e_c) \\ &= 3(3) + 3 — (3(4) + 0) \\ & = 0 \end{align*}

Так как $i_e = 0$, то структура определена.Он также стабилен, поскольку отсутствуют механизмы коллапса.

Следующим шагом анализа является определение сил реакции. В этой конструкции есть три силы реакции: $A_x$ и $A_y$ на левом штифте и $D_y$ на правом ролике. Найдем реакции, используя равновесие на всей структуре. Схема свободного тела конструкции показана на рисунке 4.9.

Рисунок 4.9: Пример схемы корпуса без рамы

Начиная с момента равновесия относительно точки A найти вертикальную реакцию в точке D ($D_y$):

\begin{align*} \curvearrowleft \sum M_A &= 0 \\ -75(5)-25(7)(3. 5)+D_y(7) &= 0 \\ D_y &= +141,1\mathrm{\,kN} \end{align*} \begin{equation*} \boxed{D_y = 141,1\mathrm{\,kN} \ стрелка вверх} \end{уравнение*}

Для горизонтального равновесия горизонтальная реакция в точке A ($A_x$) первоначально считается положительной (указывая вправо):

\begin{align*} \rightarrow \sum F_x &= 0 \\ A_x + 75 &= 0 \\ A_x &= -75\mathrm{\,kN} \end{align*}

Но отрицательное решение говорит нам, что $A_x$ на самом деле указывает влево (как показано на рисунке 4.9):

\begin{equation*} \boxed{A_x = 75\mathrm{\,kN} \leftarrow} \end{equation*}

Вертикальное равновесие:

\begin{align*} \uparrow \sum F_y &= 0 \\ A_y — 25(7) + D_y &= 0 \\ A_y — 25(7) + 141.1 &= 0 \\ A_y &= +33.9\mathrm {\,kN} \end{align*} \begin{equation*} \boxed{A_y = 33,9\mathrm{\,kN} \uparrow} \end{equation*}

Теперь структуру необходимо разделить на отдельные элементы. Наша структура будет разделена на трех членов: AB, BC и CD.Мы пройдемся по каждому по очереди, решив все неизвестные концевые силы, осевую силу, силу сдвига и момент, прежде чем перейти к следующему элементу. Диаграмма свободного тела и решение для стержня AB показаны на рисунке 4.10.

Рисунок 4.10: Пример элемента рамы AB

Диаграмма свободного тела (FBD) в левой части рисунка 4.10 показывает всю информацию, которая на данный момент известна о члене AB. Он содержит известные реакции на базе $A_x$ и $A_y$. Кроме того, показаны неизвестные силы на разрезе в точке В.{AB} = 33,9\mathrm{\,kN} \downarrow} \end{уравнение*}

Результирующий решенный FBD показан на рисунке 4.10.

Теперь, когда мы знаем все силы, действующие на стержень AB, мы можем использовать методы анализа балки, чтобы найти диаграммы осей, сдвига и моментов, которые показаны на рисунке 4.10.

Построение диаграммы осевых сил аналогично диаграмме поперечных сил, начиная с одного конца, силы, параллельные элементу, которые вызывают сжатие, перемещают диаграмму осевых сил в одну сторону, а силы, вызывающие растяжение, перемещают ее в другую способ.Неважно, какой путь на диаграмме указан, если на диаграмме указаны стороны сжатия и растяжения. Сторона сжатия на диаграмме осевой силы обозначена на рисунке буквой «С». В этом случае мы можем начать с точки А, предполагая, что стержень закреплен на другом конце (точка В). Вертикальная сила реакции в точке A, равная $49,5\mathrm{\,kN}$, заставляет стержень сжиматься, поэтому мы смещаем диаграмму осевой силы вправо на ту же величину и указываем, что эта сторона сжимается.Никакой другой нагрузки, параллельной стержню, нет до точки B, которая имеет силу $49,5\mathrm{\,kN}$, которая вызовет натяжение стержня, если оттолкнет его от B (предположим, что сила действует чуть ниже точки Б). Это сдвигает диаграмму осевой силы обратно влево, встречая ось стержня в точке 0,

.

Диаграммы сдвига и момента для этого стержня просты и построены снизу вверх. Диаграмма моментов «нарисована со стороны сжатия». Это означает, что с какой бы стороны стержня на моментной диаграмме не возникал момент, крайнее волокно на этой стороне балки будет сжиматься.Для этого члена AB весь момент приходится на левую сторону члена. Следовательно, левая сторона элемента сжимается (а правая — растягивается).

В месте разреза стрелки моментов всегда указывают на сжатую сторону элемента.

Теперь, когда элемент AB полностью решен, мы можем перейти к следующему элементу, элементу BC, показанному на рис. 4.11.

Рисунок 4.11: Пример элемента рамы BC Равновесие и разрешение сил в направлении локальной оси

Часть (а) рисунка 4.11 показана свободная диаграмма тела элемента BC со всей известной на данный момент информацией. Поскольку элементы AB и BC находятся по обе стороны от разреза в точке B, силы и моменты должны передаваться в этой точке. Итак, мы можем взять силы в точке B от стержня AB и приложить их к точке B на стержне BC; однако мы должны обязательно изменить направление сил, поскольку силы и моменты должны быть равными и противоположными по обе стороны от разреза (как обсуждалось ранее в разделе 1.6). Горизонтальная сила на разрезе в B меняет направление справа налево, вертикальная сила изменяется снизу вверх, а момент меняется с направления против часовой стрелки на направление по часовой стрелке. {ВС} = 141,1\mathrm{\,кН} \стрелка вверх} \конец{уравнение*}

Полученная решенная диаграмма свободного тела показана в части (b) рисунка 4.11. Поскольку стержень BC является наклонным стержнем, нам нужно разделить все силы на локальные направления стержня (т. е. перпендикулярные и параллельные стержню), прежде чем мы сможем найти осевой, поперечный и момент на стержне. Этот процесс показан в частях (c) и (d) рисунка. В части (c) показано, как преобразовать горизонтальные и вертикальные силы в точке B в силы, перпендикулярные и параллельные стержню BC.\circ} \\ P_{para} &= 62,8\mathrm{\,kN} \swarrow \text{ (параллельно BC)} \end{align*}

Тот же процесс выполняется для точечных нагрузок в точке C.

В части (d) рисунка 4.11 показаны результирующие точечные нагрузки (параллельные и перпендикулярные) на любом конце элемента. Он также показывает распределенную нагрузку, разрешенную по направлениям локальной оси (стержня). Распределенная нагрузка снежного типа на балку разлагается на перпендикулярное и параллельное направления с использованием выражений, ранее показанных на рисунке 4. 2} = 7,28\mathrm{\,m}$) длиннее горизонтальной проекции ($7\mathrm{\,m}$).

Теперь, когда известны все нагрузки на стержень BC, осевые диаграммы, диаграммы сдвига и моментов могут быть построены с использованием методов расчета балки. Этот процесс показан на рисунке 4.12.

Рисунок 4.12: Пример элемента рамы BC Осевой, сдвиг и момент

Диаграмма осевой силы непостоянна для стержня BC, как показано на рисунке 4.12, поскольку распределенная нагрузка снежного типа на стержень имеет параллельную составляющую, действующую по длине стержня.Эта параллельная распределенная нагрузка может быть названа тягой по длине элемента. Двигаясь слева направо, элемент начинает с натяжения $62,8\mathrm{\,kN}$, которое затем неуклонно увеличивается за счет натяжения в том же направлении $6,59\mathrm{\,kN/m}$, которое перемещает диаграмма осевой силы дальше в сторону растяжения. Это приводит к тому, что наклон на диаграмме осевых сил также равен $6,59\mathrm{\,kN/m}$. На правом конце члена окончательное сжатие (в противоположном направлении) на 110 долларов.8\mathrm{\,kN}$ возвращает диаграмму осевой силы к нулю.

Диаграммы поперечной силы и изгибающего момента строятся, как и раньше, с особым вниманием к тому, чтобы наклон диаграммы момента в любой точке был прямо равен значению диаграммы поперечной силы в той же точке. Диаграмма момента, показанная на рисунке 4.12, начинается со скачка вверх из-за момента по часовой стрелке в точке B, затем перемещается еще выше из-за сдвига между точками B и B’, прежде чем снова опуститься между точками B’ и C.Важно определить максимальный момент и место возникновения этого максимального момента. Значение максимального момента легко найти, добавив момент в точке B ($600\mathrm{\,kNm}$) к площади под диаграммой поперечной силы между точками B и B’ (треугольник высотой $53,2\). матрм{\,кН}$). Чтобы найти площадь этого треугольника, нам нужно знать длину основания. Это можно найти, используя подобные треугольники, как показано (общая длина элемента, умноженная на высоту маленького треугольника, разделенная на общую высоту обоих треугольников). В этом случае длина меньшего треугольника составляет $2,303\mathrm{\,m}$, как показано. Это местонахождение точки максимального момента, которую следует определить на моментной диаграмме. Используя эту длину, площадь под диаграммой поперечной силы между точками B и B’ равна $0,5(53,2)(2,303)=61,2\mathrm{\,kNm}$. Это дает максимальный момент $600 + 61,2 = 661,2\mathrm{\,kNm}$ в месте $2,303\mathrm{\,m}$ от точки B (как показано на рисунке 4.12).

Поскольку форма диаграммы поперечной силы является линейной, то форма диаграммы моментов должна быть параболической.Форму параболы можно легко определить, нарисовав наклон диаграммы момента на обоих концах, как показано на рисунке 4.12, и указав места нулевого наклона, которые являются точками, где диаграмма поперечной силы равна нулю. Эта диаграмма моментов снова нарисована на сжатой стороне стержня, и можно видеть, что, как упоминалось ранее, точечные моменты на концах стержня указывают на сжатую сторону балки на каждом конце.

Теперь, когда элемент BC полностью решен, мы можем перейти к последнему элементу, элементу CD, показанному на рис.  4.13.

Рисунок 4.13: Пример элемента рамы CD

Диаграмма свободного тела элемента CD, показанная на рисунке 4.13, включает всю информацию, известную до этого момента (включая силы противоположного направления от элемента BC на другой стороне разреза в точке C). Как видно из этого рисунка, неизвестных сил, которые необходимо найти для элемента CD, не существует. Обычно это происходит с последним элементом в анализе кадра. Мы уже определили силы в точке D, когда нашли реакции, используя глобальное равновесие; тем не менее, мы можем использовать равновесие на элементе CD в качестве проверки того, что мы правильно решили остальную часть фрейма.Если мы делаем эту проверку и равновесие не соблюдается, значит, мы допустили ошибку на одном из предыдущих шагов. Итак, давайте проверим равновесие для члена CD:

.

\begin{align*} \curvearrowleft \sum M_C &= 0 \\ -374,8 + 75(5) &= 0 \; \checkmark \end{align*} \begin{align*} \rightarrow \sum F_x &= 0 \\ 75 — 75 &= 0 \; \checkmark \end{align*} \begin{align*} \uparrow \sum F_y &= 0 \\ 141.