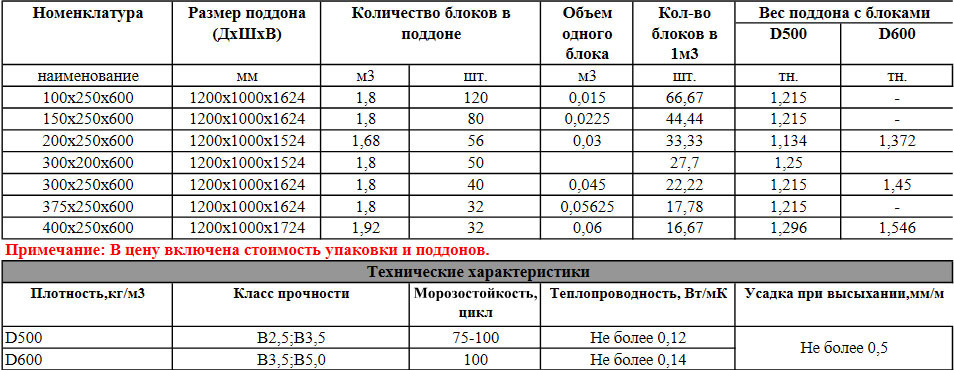
Сколько в 1 кубе силикатных блоков: Сколько газосиликатных блоков в кубе
Сколько силикатного кирпича в 1 м3
Содержание
- Зачем знать количество штук силикатного кирпича в кубе материала
- Как это работает на стройке
- Считаем по стандарту
- Особенности расчета на практике
- Выводы
Начиная любое дело, нужно хорошенько продумать все детали и составить подробный план необходимых работ. Это касается и строительства. Чем больше внимания вы уделите продумыванию всех аспектов будущей новостройки, тем лучший получите результат.
Стройка – дело масштабное и требующее значительных материальных затрат. Поэтому, чтобы не застрять на полпути с недостроенным домом, нужно заранее рассчитать необходимое количество стройматериалов, прежде всего для кладки кирпича. При этом расчеты выложенной площади в квадратных метрах зачастую зависят от того, сколько кубов материала использовано.
Зачем знать количество штук силикатного кирпича в кубе материала
Любая стройка – это работа с калькулятором в руках.
Дополнительные расходы на укладке силикатного кирпича. Логистика стройки требует точно знать, сколько чего нужно, и какой транспорт потребуется для доставки определенного количества кубов силикатного кирпича.
От этого зависят вспомогательные расходы и оплата за обработку силикатного кирпича:
- Каменщики на кладке получают оплату за количество уложенных кубов силикатного кирпича, и они всячески будут спорить с тем, сколько силикатного материала уложено;
- От кубатуры зависит, сколько раз будет работать транспорт по доставке силикатного кирпича;
- Сколько силикатного материала было потеряно, украдено или разбито.
Совет! Определение веса одного силикатного блока вычисляют, как усредненную величину веса десяти кирпичей или блоков из каждой пачки.
Как это работает на стройке
С одной стороны, закупка сразу всего необходимого стройматериала, точное знание, сколько весит тот или иной стройматериал для строительства, позволит сэкономить на транспортных расходах и затратах времени.
С другой стороны, тщательный расчет площади в квадратных метрах позволит избежать в будущем проблем с несовпадающими по внешнему виду партиями облицовочных блоков, с необходимостью срочно привезти на стройплощадку пару мешков цемента или куб материала. К тому же, при закупке лишнего камня или других стройматериалов будут выброшены лишние деньги, которые можно и нужно потратить на более необходимые расходы.
Весит силикатный блок немало. От того, сколько конкретно весит тысяча штук или куб камня, зависят ваши транспортные расходы. В справочнике куб полнотелого силикатного кирпича весит от 1700 до 1900 кг. Такой силикатный кирпич весит 3,7-3,8 кг.
Поэтому к вопросу расчета, сколько необходимо объемов строительных материалов, нужно подходить особенно внимательно. Ведь лишние пару кубов камня затем будут головной болью, где их хранить, куда девать, хорошо, если получится продать или использовать в хозяйстве. Поэтому, если планируется строительство дома из кирпича, придется рассчитывать объем и площадь в квадратных метрах будущих стен, сколько кирпича будет необходимо для возведения всех стен необходимой толщины и высоты.
Считаем по стандарту
Отдельно необходимо рассчитать, сколько потребуется стройматериала, и площадь в квадратных метрах стен, которые предполагается обкладывать облицовочным кирпичом. Не забывайте учитывать ширину кладочного раствора. Затем полученные значения количества штук пересчитываем в количество кубов камня, которое нужно будет закупить.
Эти данные нам понадобятся и для последующих расчетов с каменщиками.
К счастью для нас, прошли те времена, когда каждый владелец кирпичного завода мог изготавливать кирпич таких размеров, какие были удобны ему. С началом массового использования силикатных кирпичей в высотном строительстве размеры выпускаемых кирпичей были приведены в соответствие требованиям ГОСТа.
Рассчитывая, сколько блоков в одном кубе, и сколько понадобится для строительства, необходимо знать размеры одного камня.
Согласно стандартам ГОСТа кирпичи изготавливаются в следующих основных вариантах размеров: одинарный, полуторный и двойной. Первый имеет размеры 250х120х65 мм.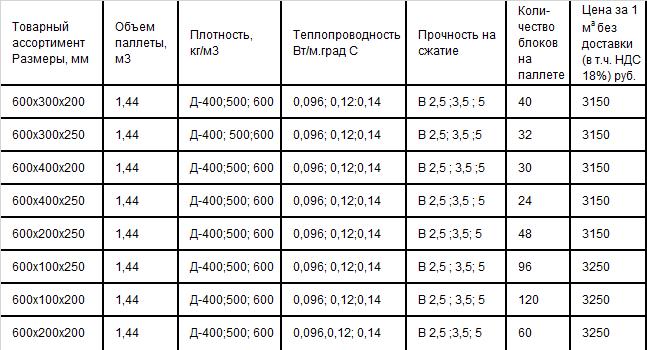
Объем одного кирпича, если вспомнить школьные уроки, можно вычислить, последовательно перемножив три приведенные величины. Для удобства расчета нужно привести их в метры. Объем одного камня получается 0,00195 м3. Чтобы определить, сколько силикатных камней помещается в одном кубе, необходимо разделить 1 м3 на объем одного кирпича. Получается 512 блоков в одном кубе.
Полуторный блок – 250х120х88 мм, отличается только по высоте. Аналогично перемножаем линейные размеры полуторного кирпича, получаем объем одной единицы – 0,00264 м3. Разделим куб на объем одного полуторного блока, получим 378 штук в 1 м3.
Двойной блок имеет размеры 250х120х138 мм. В одном кубе помещается 255 двойных кирпичей.
Еще бывают камни нестандартных размеров, которые относятся к декоративным облицовочным камням, здесь иногда важнее знать площадь кладки в квадратных метрах. Их число в кубе вы можете определить, измерив линейные размеры одного блока, а затем, пользуясь примерами, указанными выше, посчитать требуемые значения.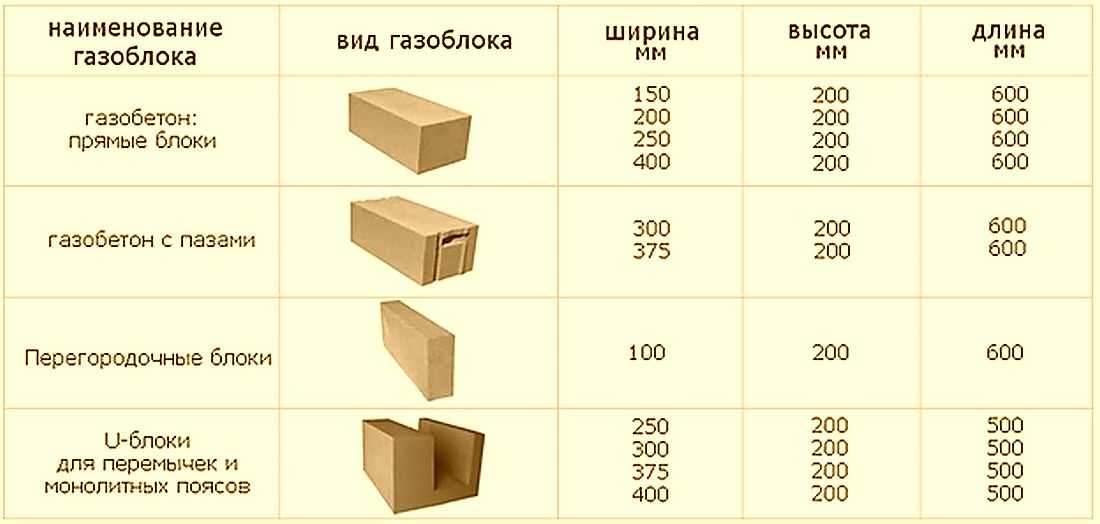
Особенности расчета на практике
Особо дотошным и педантичным застройщикам следует иметь в виду, что рассчитать, сколько требуется стройматериала, с точностью до нескольких штук не удастся, так как нужно делать поправку на некоторый процент битого и бракованного материала (в среднем это 5% от общего объема). В случае использования кладки с тычковыми перевязками стен процент отбракованного материала может вырасти до 12%. Если вы включаете в конструкцию здания различные декоративные арки, выступы, полукруглые своды, ориентируйтесь на убыль битого кирпича до 15%.
Число силикатных блоков в 1 м3 кирпичной кладки по понятным причинам не совпадет с величиной в 1м,3 упакованного на заводе.
Чтобы правильно подсчитать, сколько блоков на возведение конкретной стены, необходимо знать размеры стены, которую нужно выложить (длина, ширина, высота), а также, какой кладкой ее необходимо выложить, и учесть толщину швов. Толщина швов у разных каменщиков может незначительно отличаться, нужно иметь это в виду, рассчитывая необходимое число штук.
Кроме того, сколько швов выполнено, зависит от размеров кирпичей, чем больше размер блока, тем меньшее число швов придется на квадратный метр кладки.
Выводы
Можно рассчитывать вручную, сколько камней с учетом толщины швов и вида кладки будет в одном кубе выложенной стены. Но лучше воспользоваться готовыми таблицами, в которых приведены данные по количеству штук с учетом растворных швов и толщины стены.
- Состав и пропорции раствора для кладки кирпича
- Как сделать цветной раствор для кирпича
- Размер и вес белого силикатного кирпича
- Кирпич облицовочный силикатный
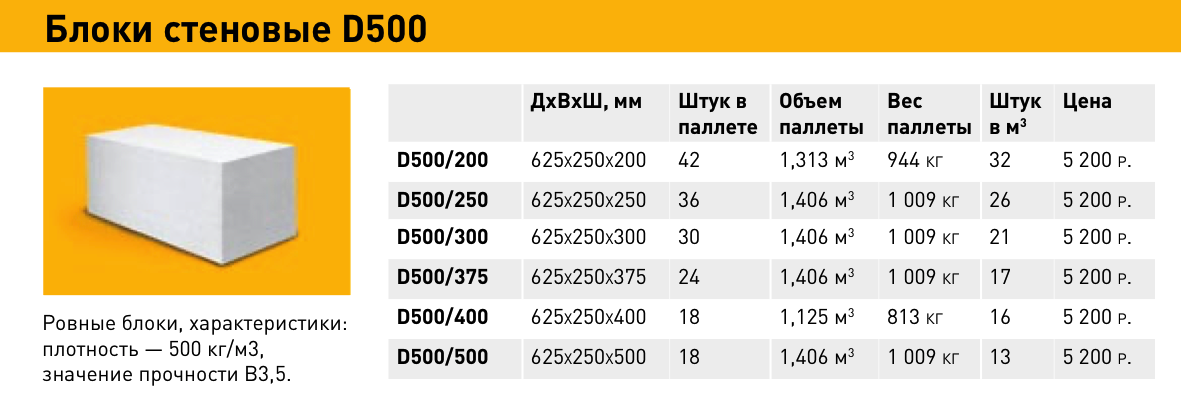
Сколько газобетонных блоков в кубе / 1м3? Пример расчета
Пример расчета для определения количества газобетонных блоков в 1м3.
За основу возьмем самый распространенный размер газобетонных блоков — 600х200х300 мм.
Для начала определимся с его геометрическими составляющими блока. Где:
- 600 — длина;
- 200 — высота;
- 300 — ширина (обычно ширину указывают последней и именно такой толщины получится возведенная стена).
Далее пошаговый план расчета
1. Так как геометрические размеры указаны в миллиметрах, для удобства расчета и приведения к единой системе измерения необходимо их перевести в метры. Для этого все величины делим на 1000.
600/1000 = 0,6 м.
200/1000 = 0,2 м.
300/1000 = 0,3 м.
2. Перемножаем полученные значения между собой, тем самым получив объем 1 блока.
0,6*0,2*0,3 = 0,036 м3
3. Один кубический метр делим на объем одного блока
1/0,036 = 27,77 шт.
Основные размеры газобетонных блоков и их количество в 1 куб. метре
Сколько блоков в 1м3 при высоте блока 200 мм.
Размер при длине 600 мм. |
Количество штук |
| 600х200х50 | 167 |
| 600х200х75 | 111 |
| 600х200х100 | 83 |
| 600х200х125 | 67 |
| 600х200х150 | 56 |
| 600х200х175 | 48 |
| 600х200х250 | 33 |
| 600х200х300 | 28 |
| 600х200х375 | 22 |
| 600х200х400 | 21 |
| 600х200х500 | 17 |
| Размер при длине 625 мм. | Количество штук |
| 625х200х50 | 160 |
| 625х200х75 | 107 |
| 625х200х100 | 80 |
| 625х200х125 | 64 |
| 625х200х150 | 53 |
| 625х200х175 | 46 |
| 625х200х250 | 32 |
| 625х200х300 | 27 |
| 625х200х375 | 21 |
| 625х200х400 | 20 |
| 625х200х500 | 16 |
Сколько блоков в 1м3 при высоте блока 250 мм.
| Размер при длине 600 мм. | Количество штук |
| 600х250х50 | 133 |
| 600х250х75 | 89 |
| 600х250х100 | 67 |
| 600х250х125 | 53 |
| 600х250х150 | 44 |
| 600х250х175 | 38 |
| 600х250х200 | 33 |
| 600х250х300 | 22 |
| 600х250х375 | 18 |
| 600х250х400 | 17 |
| 600х250х500 | 13 |
| Размер при длине 625 мм. | Количество штук |
| 625х250х50 | 128 |
| 625х250х75 | 85 |
| 625х250х100 | 64 |
| 625х250х125 | 51 |
| 625х250х150 | 43 |
| 625х250х175 | 37 |
| 625х250х200 | 32 |
| 625х250х300 | 21 |
| 625х250х375 | 17 |
| 625х250х400 | 16 |
| 625х250х500 | 13 |
Сколько требуется бетонных блоков на 1 кубометр?
Сколько бетонных блоков требуется на 1 кубометр? | сколько 8-дюймовых блоков требуется на 1 кубометр? | сколько 6-дюймовых блоков требуется на 1 кубометр? | сколько 4-х дюймовых блоков требуется на 1 кубометр? | сколько 10-дюймовых блоков требуется на 1 кубометр? | сколько 12-дюймовых блоков требуется на 1 кубометр?.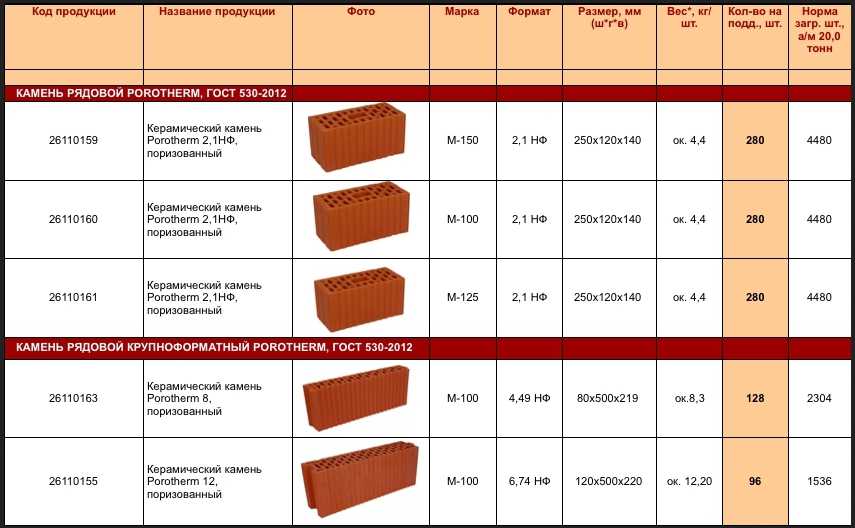
Бетонные блоки, изготовленные из смеси цемента, песка, заполнителя, золы-уноса и воды, также известные как блоки бетонной кладки (CMU), шлакоблоки (изготовленные из золы-уноса) и бетонные блоки, цементные блоки, бывают разных размеров, форма, сплошная или полая в зависимости от страны происхождения.
Необходимое количество бетонных блоков на м3 зависит от размера и объема одного блока. Он используется во многих проектах для общих стен, подпорных стен, нового гаража, фундамента или других строительных работ.
Стандартные бетонные или шлакоблоки США, используемые в большинстве стран мира, имеют длину 16 дюймов, ширину 8 дюймов и высоту 8 дюймов, что дает 1024 кубических дюйма, что эквивалентно 0,01678 кубических метров. Таким образом, на один кубический метр вам понадобится 60 единиц бетонного блока (1/0,01678 = 60).
Стандартные британские бетонные или газобетонные блоки имеют длину 440 мм, ширину 100 мм и высоту 215 мм, что дает 577 кубических дюймов, что эквивалентно 0,00946 кубических метров.
Таким образом, на один кубический метр вам понадобится 106 единиц бетонного блока (1/0,00946 = 106).
Как рассчитать, сколько блоков мне нужно на один кубический метр?, перевести все измерения в метры, рассчитать объем блока, умножив его высоту, ширину и толщину в кубических метрах. Разделите один кубический метр на объем одного блока. В результате получается общее количество блоков, необходимое вам на кубический метр.
Бетонный блок бывает разных размеров, в зависимости от толщины. Как правило, цельные бетонные блоки или CMU имеют номинальные размеры лицевой стороны 200 мм в высоту и 400 мм в длину, доступные с номинальной толщиной 100 мм, 150 мм, 200 мм, 250 мм и 300 мм.
Половина бетонного блока или CMU имеют номинальные размеры лицевой стороны 200 мм в высоту и 200 м в длину соответственно.
Как правило, размер CMU, представленный толщиной × высота × длина, при нормальной высоте и длине одинаков для всех типов, но их толщина различна, поэтому они классифицируются по толщине, например, 100 мм, 150 мм, 200 м, 250 мм и 300мм.
Он также подразделяется на полный блок и полублок.
Стандартные блоки США, измеряемые в дюймах, цельные шлакоблоки или CMU, имеют номинальные размеры лицевой стороны 8 дюймов в высоту и 16 дюймов в длину, доступны с номинальной толщиной 4, 6, 8, 10 и 12 дюймов.
◆ Вы Можете подписаться на меня в Facebook и
Подпишитесь на наш канал Youtube
Согласно стандарту США, на 1 кубический метр требуется 60 шт. бетонных блоков или шлакоблоков. Блок имеет длину 16 дюймов, ширину 8 дюймов и высоту 8 дюймов, что дает 1024 кубических дюйма, что эквивалентно 0,01678 кубических метров. Таким образом, на один кубический метр вам понадобится 60 единиц бетонного блока (1/0,01678 = 60). Таким образом, 60 стандартных блоков США составляют один кубический метр.
Сколько 8-дюймовых блоков требуется на 1 кубический метр? На 1 кубический метр требуется 60 штук 8-дюймовых бетонных блоков или шлакоблоков.
Блок размером 8 дюймов имеет размер 16 дюймов × 8 дюймов × 8 дюймов, что дает 1024 кубических дюйма, что эквивалентно 0,01678 кубических метров. Таким образом, на один кубический метр вам понадобится 60 единиц бетонного блока (1/0,01678 = 60).
На 1 кубический метр требуется 80 штук 6-дюймовых бетонных блоков или шлакоблоков. Блок размером 6 дюймов имеет размеры 16 дюймов × 8 дюймов × 6 дюймов, что дает 768 кубических дюймов, что эквивалентно 0,01258 кубических метров. Таким образом, на один кубический метр вам понадобится 80 штук 6-дюймовых бетонных блоков (1/0,01258 = 80).
Сколько 4-дюймовых блоков требуется на 1 кубический метр? На 1 кубический метр требуется 120 шт.
4-дюймовых бетонных блоков или шлакоблоков. Блок размером 4 дюйма имеет размеры 16 дюймов × 8 дюймов × 4 дюйма, что дает 512 кубических дюймов, что эквивалентно 0,00839 кубических метров. Таким образом, на один кубический метр вам понадобится 120 штук 4-дюймовых бетонных блоков (1/0,00839 = 120).
На 1 кубический метр требуется 48 шт. 10-дюймовых бетонных блоков или шлакоблоков. Блок размером 10 дюймов имеет размер 16 дюймов × 8 дюймов × 10 дюймов, что дает 1280 кубических дюймов, что эквивалентно 0,0210 кубических метров. Таким образом, на один кубический метр вам понадобится 48 штук 10-дюймовых бетонных блоков (1/0,0210 = 48).
Сколько 12-дюймовых блоков требуется на 1 кубический метр? На 1 кубический метр требуется 40 шт. 12-дюймовых бетонных блоков или шлакоблоков. Блок размером 12 дюймов имеет размер 16 дюймов × 8 дюймов × 12 дюймов, что дает 1536 кубических дюймов, что эквивалентно 0,0252 кубических метра.
Таким образом, на один кубический метр вам понадобится 40 штук 10-дюймовых бетонных блоков (1/0,0252 = 40).
● Расчет блочной стены | Узнайте, сколько блоков вам нужно
● Сколько шлакоблоков мне нужно, чтобы построить гараж
● Размеры шлакоблоков в соответствии со стандартом ASTM
● Сколько бетонных блоков на м2
● Из скольких блоков можно построить комнату 14 на 14
3 Сколько блоковНа 1 м3 требуется 125 шт. бетонных блоков толщиной 100 мм. Блок 100 мм имеет размер 400 мм × 200 мм × 100 мм, что дает 0,008 кубических метра. Таким образом, на один кубический метр вам понадобится 125 штук 100-мм бетонных блоков (1/0,008 = 125).
Выводы:
На 1 кубометр требуется 60 штук 8-дюймовых бетонных блоков или шлакоблоков. 4-дюймовый блок будет стоить 120 шиллингов за м3. 6-дюймовый блок будет стоить 80 шиллингов за м3.
10-дюймовый блок будет стоить 48 центов за м3.
Ионная координация и правила Полинга
Ионная координация и правила Полинга| ЭЭНС 2110 | Минералогия |
| Тулейнский университет | Проф. Стивен А. Нельсон |
Координация и правила Полинга | |
Расположение атомов в кристаллической структуре зависит не только от заряд иона и тип связи между атомами, но и размер атомы или ионы. В любой данной молекуле или кристаллической структуре каждый атом или ион будет окружен другими атомами или ионами. Число ионов или атомов, которые непосредственно окружают интересующий атом или ион, называется  Н. Как мы увидим, координация
число зависит от относительного размера атомов или ионов. Итак, мы
должны сначала обсудить их размеры.Атомные и ионные радиусы Размер атома или иона зависит от размера ядра и количество электронов. Как правило, атомы с большим числом электронов имеют больший радиус, чем с меньшим числом электронов. Таким образом, ионы будут иметь радиусы отличается от атомов, потому что ионы будут либо приобретать, либо терять электроны. Количество положительных зарядов в ядре определяет количество электронов, окружающих атом, и количество электроны, которые могут быть потеряны или приобретены с образованием ионов.
Атомные и ионные радиусы также зависят от типа связи, которая принимает
место между составляющими, и на координационное число.
Таким образом, атомные и ионные радиусы будут несколько различаться в зависимости от
среда, в которой находятся атомы или ионы. |
Здесь мы видим эффект увеличения атомного номера (и общего числа
электронов) для ионов одинакового заряда и эффект изменения
координационный номер. Радиусы увеличиваются с увеличением общего количества
электронов вниз в табл. Ионный радиус также увеличивается с увеличением координации
число,
электронное облако вытягивается за счет присутствия большего количества окружающих ионов. |
|
Затем мы исследуем одну строку Периодической таблицы, чтобы увидеть, как радиусы
зависит от заряда иона.
Здесь мы видим, что по мере того, как заряд становится более положительным, радиус катион уменьшается. Это связано с тем, что электронов меньше. внешние оболочки ионов. Размеры анионов относительно велики. потому что на их внешних оболочках больше электронов. |
|
Координация ионов Координационный номер, C. |
N. зависит от родственника
размер ионов. Если все атомы в кристалле одинаковы
размер, то есть два способа упаковать атомы, чтобы сформировать кристалл
состав. В этом случае максимальное количество атомов
координируется вокруг любого человека, равно 12. Мы называем это 12-кратным
координация. Есть два способа упаковать атомы в 12-кратном порядке.
координация.| Сначала исследуйте один слой атомов одинакового размера. Обратите внимание, что
между атомами есть два вида пустот, которые имеют своего рода
треугольную форму с треугольниками, направленными вверх, мы назовем пустотами B, а
те, у которых треугольники направлены вниз, мы назовем С-пустотами. Если мы добавим следующий слой атомов так, чтобы они заняли пространство выше
пустоты B, а затем добавьте следующий слой над атомами A, это
приводит к последовательности стекирования, которая выполняет AB AB AB . Если после добавления слоя атомов В разместить следующий слой так, чтобы атомы занимают положения над пустотами C в слое A и продолжают вверх, мы получаем последовательность стекирования, которая выполняет ABC ABC ABC…. и т. д. Этот тип упаковки называется кубическим упаковка. Это приводит к кубической или изометрической решетке с ось перпендикулярна слоям. |
…и т.д. Этот тип
плотнейшей упаковки называется гексагональной плотнейшей упаковкой. Это
приводит к гексагональной решетке с осью c, ориентированной перпендикулярно
слои AB AB. Чтобы увидеть, что происходит, когда один из вовлеченных ионов или атомов становится
меньше, нам нужно исследовать относительные размеры атомов.
относительные размеры указаны отношением радиусов координирующих атомов
или ионы. В кристаллических структурах мы обычно рассматриваем катионы, окруженные
анионами, поэтому отношение радиусов определяется как Rx/Rz, где Rx — радиус
катиона, а Rz — радиус окружающих анионов. С
анионы обычно представляют собой более крупные ионы, что приводит к уменьшению значений
Rx/Rz по мере уменьшения размера катиона.Если мы уменьшим размер катиона в таком расположении, все равно позволяя окружающим анионам соприкасаться друг с другом и соприкасаться катион, с уменьшением размера катиона координация сначала в результате 8 анионов окружают катион. |
| Это называется 8-кратной координацией или кубической координацией, потому что
форма объекта, построенная путем проведения линий через центры
более крупные ионы представляют собой куб. Если размер координированного катиона станет меньше, он станет
слишком мал, чтобы касаться окружающих анионов. Таким образом, есть
отношение предельного радиуса, которое произойдет, когда Rx/Rz станет слишком
небольшой. Чтобы увидеть, каков этот предел, мы должны посмотреть на вертикальную плоскость
проходят через центры анионов, обозначенных A и B. |
| В этой конструкции мы можем определить соотношение радиусов для предельное состояние, часто называемое «пределом отсутствия дребезжания», потому что если отношение радиусов становится меньше, чем это, катион будет «погремушка» на своем сайте. Используя теорему Пифагора, мы можем написать: |
Предоставление Rx/Rz = 0,732 |
Таким образом, при Rx/Rz < 0,732 катион будет слишком маленьким или будет дребезжать
на своем участке и структуре придется перейти на 6-кратную координацию.
|
| Шестикратная координация также называется октаэдрической координацией, потому что форма, определяемая рисованием плоскостей, проходящих через центр более крупных ионов, октаэдр. Октаэдрическая координация стабильна при Rx/Rz , 0,732, но уменьшение радиуса катиона Rx в конечном итоге приведет к предел, где снова меньший ион будет греметь на своем месте. |
| Предел отсутствия дребезга можно определить, взглянув на горизонтальную плоскость проходящий через ионы, обозначенные C и D. В этом случае мы можем написать: |
|
При Rx/Rz < 0,414 структура переходит в 4-кратную координацию. Плоскости, проходящие через центры более крупных атомов, в этом случае будут образовывать
тетраэдра, поэтому 4-кратная координация также называется тетраэдрической
координация. |
| Расчет для определения предела «бесшумности» для тетраэдрическая координация сложна (см. текст Кляйн и Дутроу, стр. 70). Результат показывает, что предел достигается, когда Rx/Rz = 0,225. Когда отношение радиусов становится меньше этого, треугольные координация становится стабильной конфигурацией. |
| Для треугольной координации координационное число равно трем, то есть 3 анионы окружают меньший катион. Лимит «без стука» достигается для треугольной координации, когда Rx/Rz становится меньше 0,155. |
При значениях Rx/Rz < 0,155 меньший ион может быть
координируется более крупными ионами, состоит в том, чтобы иметь 2 более крупных иона на любой
сторона. Эта двойная координация называется линейной координацией. |
| В таблице приведены соотношения радиусов катионов и анионов, Rx/Rz, для различные координационные числа и дает название координации многогранника для каждого координационного числа. |
|
При описании строения кристаллов и расположения различных
ионов или атомов внутри кристаллов часто ссылаются на
кристаллографический узел, на котором находится атом. |
Такие сайты
обычно упоминается в терминах координационного числа или координационного
многогранник, окружающий ион. Например, в силикате.
минералы Si окружены 4 атомами кислорода в тетраэдрической координации.
Таким образом, часто говорят, что Si занимает тетраэдрические позиции в силикате.
минералы. Мы рассмотрим эти концепции более подробно позже в
курс.| Эти общие отношения координации применяются только в том случае, если соединение
преимущественно ионный. В ковалентных структурах атомы перекрываются, потому что
они делят электроны. Также следует отметить, что 5-, 7-, 9- и
10-кратная координация также возможна в сложных структурах. Для элементов, которые встречаются в обычных минералах земной коры,
наиболее распространенным координирующим анионом является кислород. Следующая таблица
дает ионный радиус и координацию этих обычных катионов металлов
координируется с кислородом. |
Ион К.Н.
(с кислородом)Координ. Многогранник Ионный радиус, К + 8 — 12 куб. до ближайшего 1,51 (8) — 1,64 (12) Нет данных + 8 — 6 кубический в октаэдрический 1,18 (8) — 1,02 (6) Ca +2 8 — 6 1,12 (8) — 1,00 (6) Пн +2 6 Октаэдрический 0,83 Fe +2 6 0,78 Мг +2 6 0,72 Fe +3 6 0,65 Ти +4 6 0,61 Аль +3 6 0,54 Аль +3 4 Тетраэдрический 0,39 Si +4 4 0,26 P +5 4 0,17 С +6 4 0,12 С +4 3 Треугольный 0,08
Правила Полинга Лайнус Полинг изучал кристаллические структуры и типы
связи и координации, которые происходят в них. Правило 1 Около каждого катиона образуется координационный полиэдр анионов, в котором катион-анионное расстояние определяется суммами радиусов и координационное число определяется отношением радиусов. Это правило просто излагает то, что мы обсуждали выше, заявляя, что разные типы координационных полиэдров определяются радиусом отношение Rx/Rz катиона к аниону.
|
Его исследования обнаружили
что кристаллические структуры подчиняются следующим правилам, теперь известным как правило Полинга.
Правила.Правило 2, Принцип электростатической валентности
Ан
ионная структура будет стабильной до такой степени, что сумма сил
электростатических связей, которые достигают иона, равны заряду этого иона. В чтобы понять это правило, мы должны сначала определить электростатическую валентность, э.в. э.в = заряд иона/C.N. |
| Например, в NaCl каждый Na + окружен 6 Cl — ионы. Таким образом, Na имеет 6-кратную координацию, и C.N. = 6. Таким образом, э.в. = 1/6. Таким образом, 1/6 часть отрицательного заряда достигает иона Na от каждого Кл. Таким образом, +1 заряд иона Na уравновешивается 6*1/6 =1 отрицательным зарядом. заряд от ионов 6 Cl. |
Аналогично, в структуре CaF 2 каждый ион Ca +2 окружен 8 ионами F — в кубической или 8-кратной координации.
э.в. таким образом, достижение иона Ca от каждого из ионов F составляет 1/4.
Поскольку имеется 8 ионов F, общий заряд, достигающий иона Ca, составляет 8*1/4 или
2. Итак, снова заряд сбалансирован. |
| Обратите внимание, что в NaCl каждый ион Cl также окружен 6 ионами Na в
октаэдрическая координация. Итак, опять же, 1/6 положительного заряда
от каждого Na достигает иона Cl, и, таким образом, ион Cl видит 6*1/6 = 1
положительный заряд, который точно уравновешивает заряд -1 на
Кл. В случае NaCl заряд точно сбалансирован на обоих катионах и анионы. В таком случае мы говорим, что связи равны силы со всех сторон. Когда это происходит, говорят, что облигации быть изодесмическим . |
Это не так для иона C +4 в треугольной координации
с О -2 . Здесь, напр. = 4/3 (C имеет заряд +4
и координируется 3 атомами кислорода). Таким образом, по 3 кислорода каждый
вносят 4/3 заряда в ион углерода, а заряд углерода составляет
сбалансированный. Но у каждого Oxygen все еще есть 2/3 заряда, который он
не использовал. Таким образом, образуется карбонатная структурная группа — СО 3 -2 .В подобных случаях, когда электростатическая валентность больше 1/2 заряд на анионе (4/3 > 1/2*2), анион будет сильнее связан с центральным координирующим катионом, чем он может быть связан с другим структурные группы. Когда это происходит, связь считается равной 9.0119 анизодесмический . |
Третий случай возникает, когда э.в. достигает катиона ровно 1/2
заряд на анионе. Это относится к Si +4 в
тетраэдрическая координация с O -2 . Здесь э.в.
достижения Si составляет 4/4 =1. Это оставляет каждый кислород с зарядом -1.
что не поделился. Так как это -1 ровно 1/2 оригинала
заряд на О -2 Кислород в SiO 4 -4 группа может быть так же прочно связана с ионами вне группы, как и с
центрально-координированный Si. В этом случае связь называется мезодесмической .Группа SiO 4 -4 является основным строительным блоком самые распространенные минералы в земной коре, силикаты.
|
Правило 3 Общие ребра и особенно грани двух анионных полиэдров в
кристаллическая структура снижает его стабильность. |
Причина этого в том, что совместное использование только углов многогранников
размещает положительно заряженные катионы на наибольшем расстоянии от каждого
Другой. В показанном здесь примере для тетраэдрической координации, если
расстояние между катионами в многогранниках, имеющих общие вершины, равно
принимается равным 1, то общие ребра уменьшают расстояние до 0,58, а совместное использование
лиц уменьшает расстояние до 0,38. |
