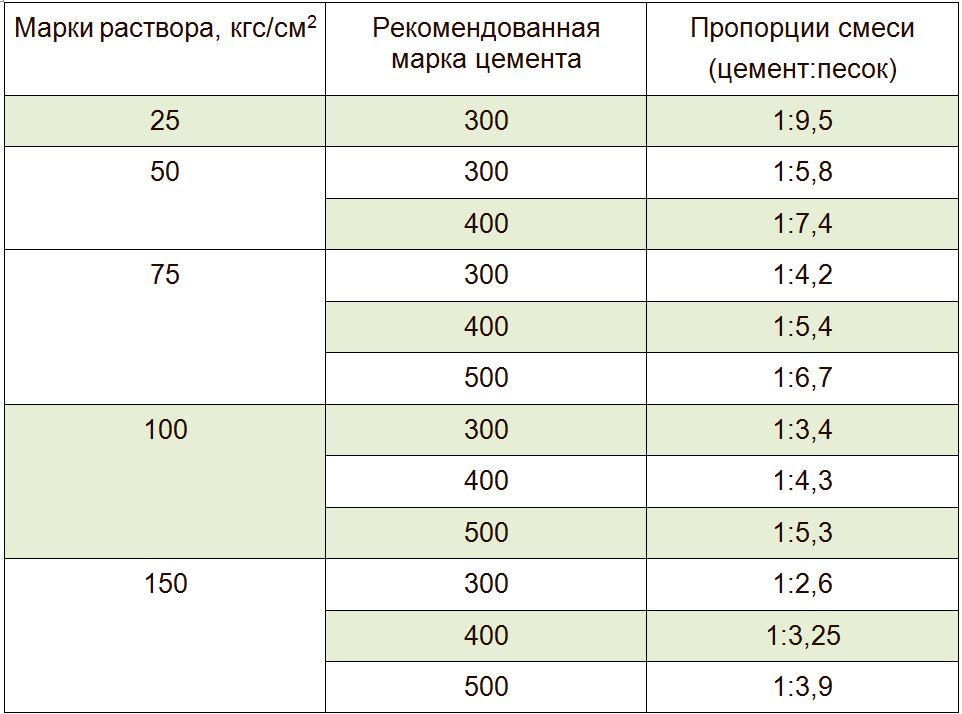
Раствор 1 к 3: как развести и сколько песка и цемента в 1 м3, соотношение частей и расход

Цементный раствор – незаменимый материал в строительстве

Цемент является основным строительным материалом. В основном используется для изготовления бетона и строительных растворов. Цемент представляет собой вяжущее вещество, которое при взаимодействии с водой, водными растворами солей и другими жидкостями образует пластичную массу,  затем затвердевает и становится очень прочным материалом, незаменимым в строительных работах.

На сегодняшний день, как в монолитном, так и в сборном строительстве незаменимым материалом является цементный раствор. Цементные заводы на сегодня представляют из себя наиболее бурно развивающиеся производства. Цементно-бетонные изделия пользуются на сегодня повышенным спросом. Ведь они нужны практически на любой стройке. Это и плиты перекрытия, и готовые лестничные марши, и стеновые панели, цементный шифер.

Строительный раствор получают в результате затвердевания смеси вяжущего вещества (цемент), мелкого заполнителя (песок), затворителя (вода) и специальных добавок.

В процессе твердения вяжущий материал прочно связывает между собой отдельные частицы заполнителя. В качестве вяжущего используют цемент, известь, глину, а в качестве заполнителя — песок.

По виду применяемого вяжущего вещества строительные растворы делятся на:

• простые — один вяжущий элемент (цемент, известь, гипс и др.)
• сложные — с использованием смешанных вяжущих элементов (известково-гипсовый, известково-зольный, цементно-известковый раствор, и др.)

Составы простых растворов обозначают двумя числами. Первое число показывает в частях пропорцию вяжущего материала в растворе. Второе число в соотношении с первым показывает, сколько частей заполнителя приходится на одну часть вяжущего материала. Например, известковый раствор состава 1:3 обозначает, что в данном растворе на 1 часть извести приходится 3 части заполнителя.

 Для сложных растворов соотношение состоит из трех чисел, из которых первое число (единица) выражает объемную часть основного вяжущего материала, а второе число показывает, каково количество дополнительного вяжущего нужно взять на одну часть. Для примера, состав известково-цементного раствора в пропорциях 1:2:3 говорит о том, что на 1 часть извести приходится 2 части цемента и 3 части заполнителя.

Применение цементно-известкового раствора целесообразно при оштукатуривании как фасадов зданий (конструкций, не подвергающихся систематическому увлажнению), так и внутренних помещений. Введение извести резко повышает пластичность растворов. Основной недостаток известковых растворов — медленное твердение. Для повышения их водостойкости в раствор вводят гидравлические добавки: трепел, диатомит, золы и др.

Цементно-песчаный раствор также часто используется, как экономичный вариант в строительстве. Так как эта разновидность раствора придает покрытию дополнительную прочность и позволяет расходовать его экономно. Очень часто в строительных и отделочных работах используется цемент с добавлением песка. Данный раствор применяется для заполнения неровностей и трещин покрытия, укладки плит, заполнения швов, отделки стен.

Раствор М100 — низкая цена за м3 с доставкой

Компания «Трансбетон» производит и доставляет строительный раствор марки М100 к строительной площадке.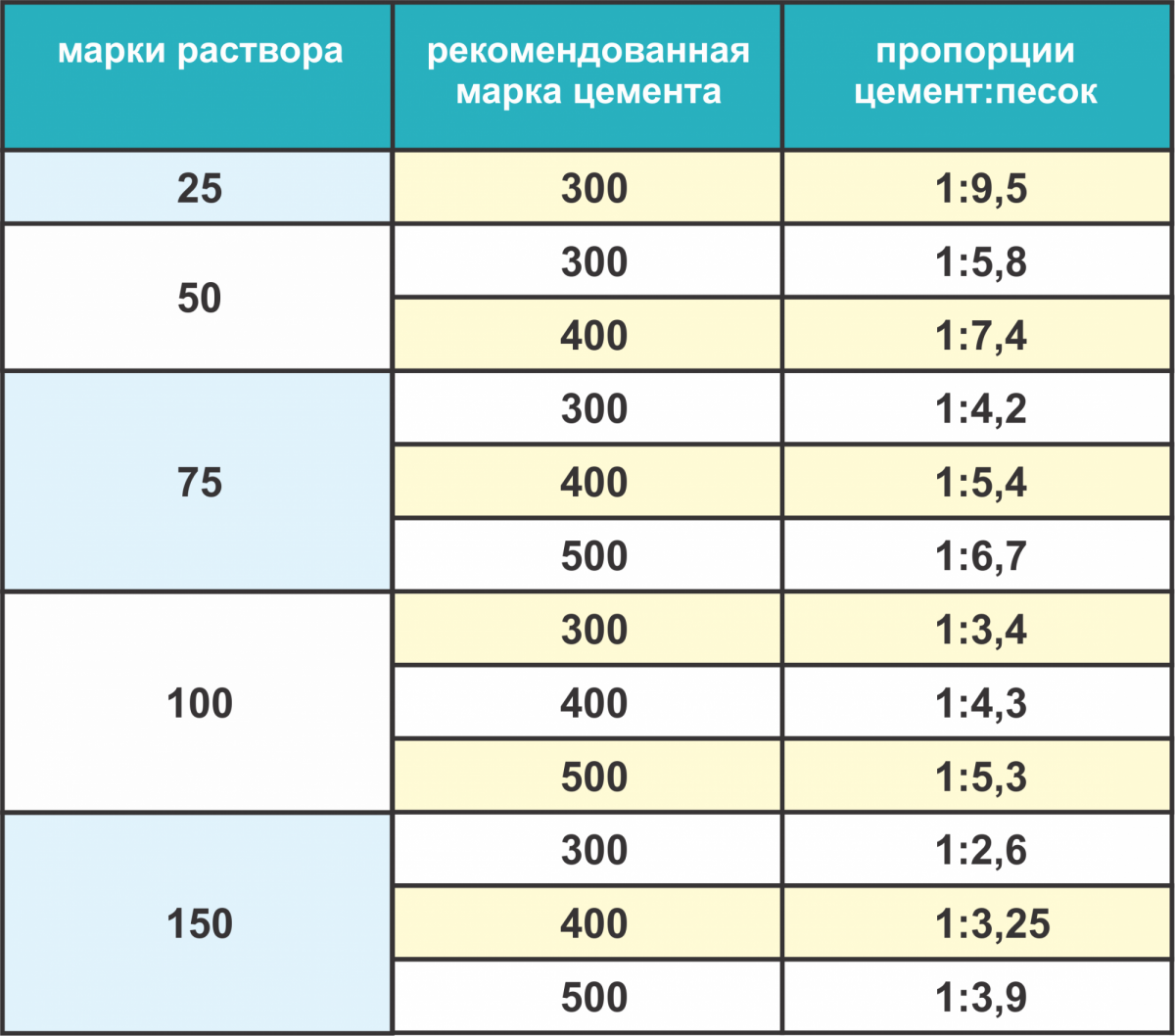 Эта пластичная кладочная смесь полностью соответствует требованиям ГОСТа. Она прочна и водонепроницаема, поэтому популярна среди наших заказчиков. Каждый из них получает качественный раствор М100 с доставкой по Москве недорого и оперативно. Этому способствует эффективная логистика с использованием собственных автомиксеров. Мы не нанимаем посредников для доставки продукции, поэтому стоимость строительного раствора М100 для наших клиентов ниже, чем у конкурентов.

расчет приблизительный, для окончательного расчёта обратитесь к менеджеру

Доставка в пределах МКАД

Цены за 1 м3, указанные выше, приведенны с учетом НДС, но не включают в себя затраты на доставку. Итоговая стоимость растрвора будет зависеть от расстояния между заводом и вашим объектом. Цена доставки рассчитывается индивидуально в каждом случае. Позвоните по многоканальному телефону +7 (495) 540-59-68, чтобы уточнить итоговую стоимость доставки куба цементного раствора м100 по столице и Московской области.

Что отличает нас от других компаний

Область применения раствора марки М100

Кладочный раствор марки М100 применяется для выравнивания поверхностей в сухих помещениях, устройства стяжки полов.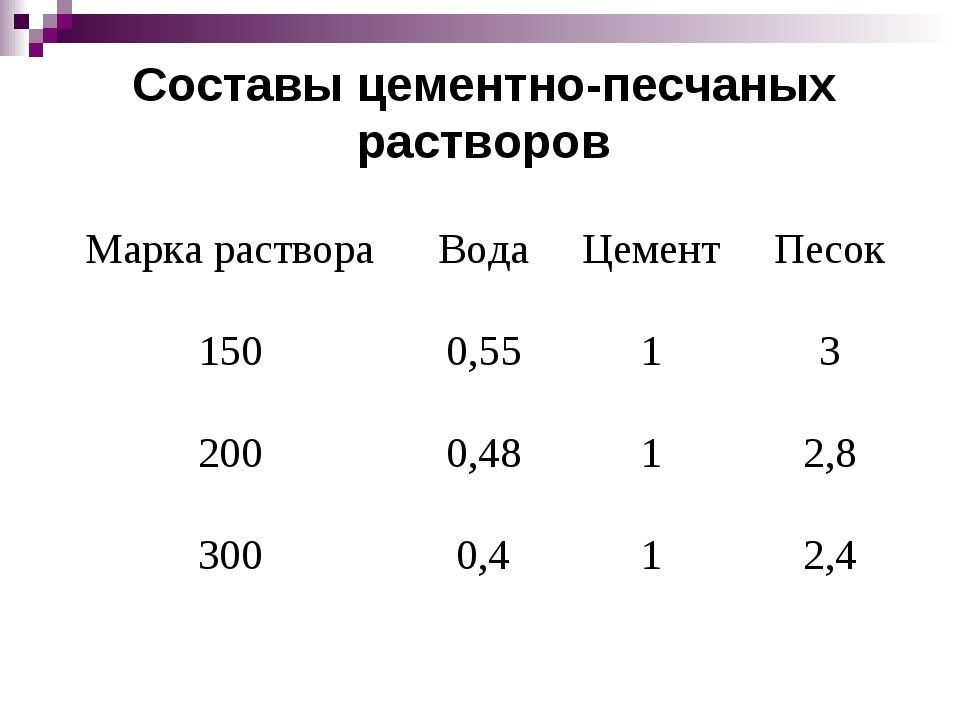 Обладая высокой прочностью и адгезивностью, эта смесь хорошо подходит для заделки швов, укладки керамической, гипсовой, стеклянной, каменной плитки и мозаики.

М100 нередко используется при возведении конструкций, перегородок и колонн из кирпича, бетонных и пенобетонных блоков. Его применение позволяет значительно сэкономить на гидроизоляционных материалах при возведении основания под кровлю.

Состав и свойства смеси

Раствор марки М100 состоит из 1 части цемента, 6 частей песка и 1,3 – воды. Его состав определяет характеристики и свойства смеси: класс прочности – В-7,5, подвижность – от П2 до П4, прочность на сжатие — не менее 100 кг/м3, морозостойкость – F50, водонепроницаемость – W2, средний рабочий диапазон температур – от 0 до +30 С.

Для повышения прочности смеси при ее изготовлении используется заполнитель, отличающийся более плотной структурой. Это специально отобранный горный песок без обломков раковин и гладких песчинок, наличие которых может снижать прочность готового раствора или бетона.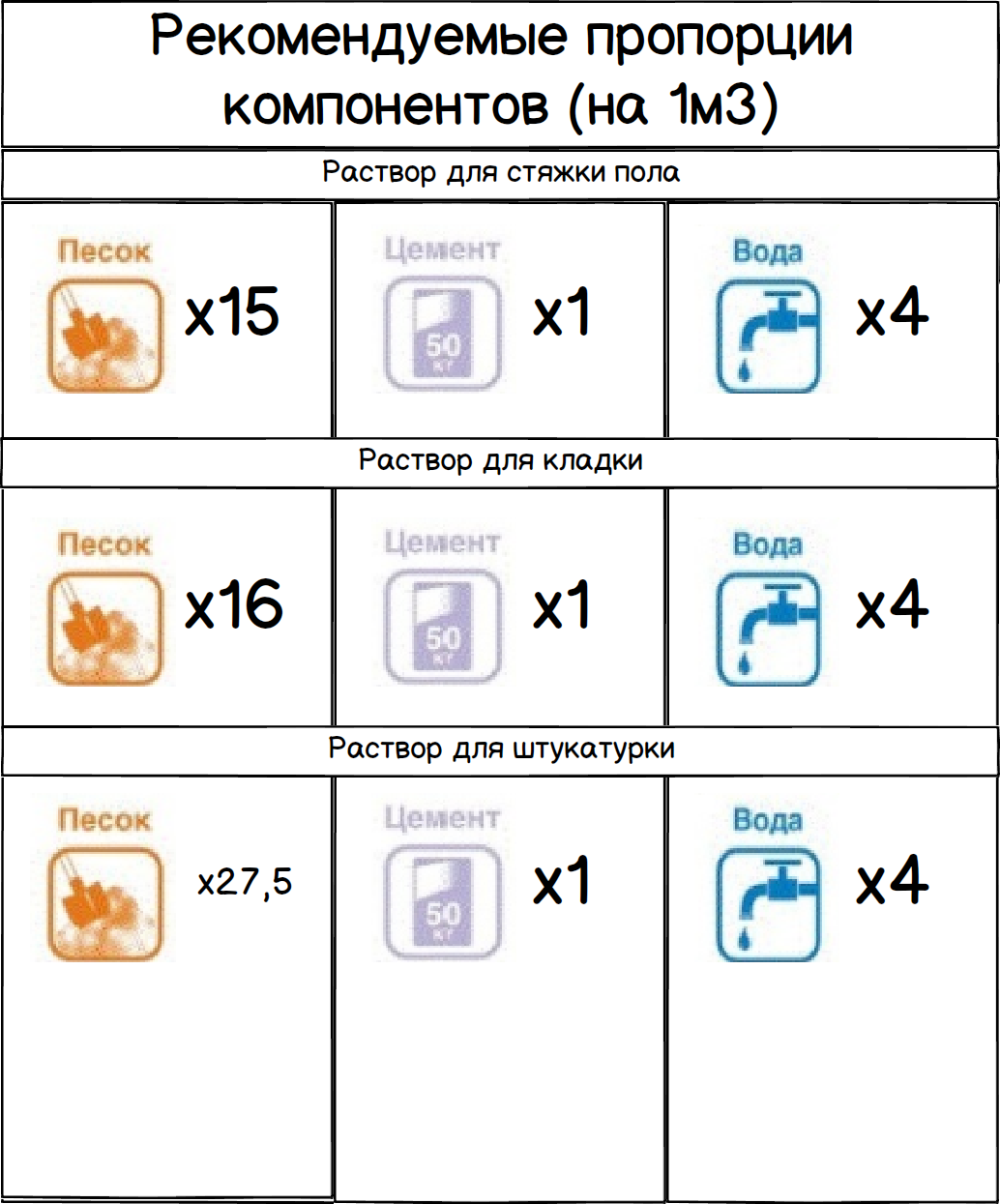

Для улучшения характеристик раствора используются пластификаторы и добавки, замедляющие затвердевание материала. Это позволяет перевозить его на дальние расстояния, повышает его эластичность и прочность. Выбор добавок осуществляется с учетом необходимых характеристик смеси. При этом цена цементного раствора М100 с учетом транспортировки остается самой низкой в столичном регионе.

Как мы работаем

1.

Оставляете заявку

2.

Уточняем детали

3.

Согласовываем сроки

5.

Изготавливаем бетонную смесь

6.

Доставляем ваш заказ

Заказать бетонный раствор М100

Чтобы дешево купить строительный раствор М100 с доставкой по Москве и Московской области, достаточно заполнить форму обратной связи. В течение 10 минут менеджер вам перезвонит и оформит заказ. Он также расскажет о различиях между марками бетона и других смесей, поможет определиться с выбором. Или позвоните по телефону +7 (495) 540-59-68, чтобы недорого заказать раствор прямо сейчас.

Решение неравенств с помощью пошагового решения математических задач

В этой главе мы разработаем некоторые приемы, помогающие решать задачи, сформулированные словами. Эти методы включают переписывание задач в виде символов. Например, поставленная задача

«Найдите число, которое при прибавлении к 3 дает 7»

можно записать так:

3 + ? = 7, 3 + n = 7, 3 + x = 1

и т. д., где символы ?, n и x представляют число, которое мы хотим найти. Такие сокращенные версии поставленных задач мы называем уравнениями или символическими предложениями. Такие уравнения, как x + 3 = 7, являются уравнениями первой степени, поскольку показатель степени равен 1. Члены слева от знака равенства составляют левый член уравнения; те, что справа, составляют правый член. Таким образом, в уравнении x + 3 = 7 левая часть равна x + 3, а правая часть равна 7.

РЕШЕНИЕ УРАВНЕНИЙ

Уравнения могут быть истинными или ложными, так же как словесные предложения могут быть истинными или ложными.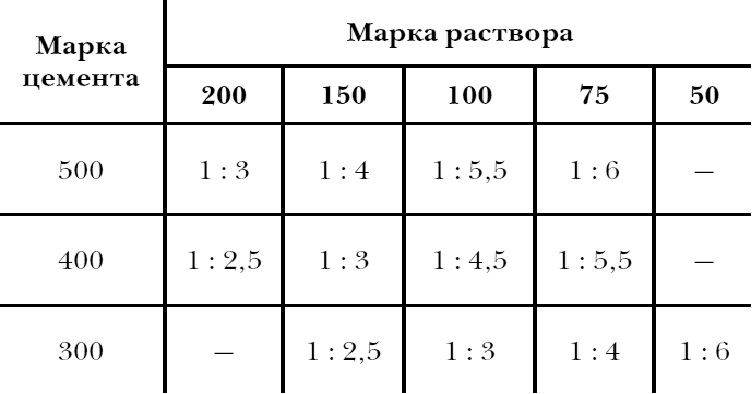 Уравнение:

3 + x = 7

будет ложным, если вместо переменной подставить любое число, кроме 4. Значение переменной, для которой уравнение верно (4 в этом примере), называется решением уравнения. Мы можем определить, является ли данное число решением данного уравнения, подставив число вместо переменной и определив истинность или ложность результата.

Пример 1. Определить, является ли значение 3 решением уравнения член.

4(3) — 2 = 3(3) + 1

12 — 2 = 9 + 1

10 = 10

Ответ. 3 это решение.

Уравнения первой степени, которые мы рассматриваем в этой главе, имеют не более одного решения. Решения многих таких уравнений можно определить путем проверки.

Пример 2 Найдите решение каждого уравнения путем проверки.

а. х + 5 = 12
б. 4 · x = -20

Решения а. 7 является решением, так как 7 + 5 = 12,
b. -5 является решением, поскольку 4(-5) = -20.

РЕШЕНИЕ УРАВНЕНИЙ С ИСПОЛЬЗОВАНИЕМ СВОЙСТВ СЛОЖЕНИЯ И ВЫЧИТАНИЯ

В разделе 3. 1 мы решили некоторые простые уравнения первой степени путем проверки. Однако решения большинства уравнений не сразу очевидны при осмотре. Следовательно, нам нужны некоторые математические «инструменты» для решения уравнений.

ЭКВИВАЛЕНТНЫЕ УРАВНЕНИЯ

Эквивалентные уравнения – это уравнения, имеющие одинаковые решения. Таким образом,

3x + 3 = x + 13, 3x = x + 10, 2x = 10 и x = 5

эквивалентны уравнениям, поскольку 5 является единственным решением каждого из них. Обратите внимание, что в уравнении 3x + 3 = x + 13 решение 5 не очевидно при проверке, но в уравнении x = 5 решение 5 очевидно при проверке. При решении любого уравнения мы преобразуем данное уравнение, решение которого может быть неочевидным, в эквивалентное уравнение, решение которого легко заметить.

Следующее свойство, иногда называемое свойством сложения-вычитания , является одним из способов генерирования эквивалентных уравнений.

Если к обоим элементам добавляется или вычитается одно и то же количество уравнения, полученное уравнение эквивалентно исходному уравнение.

В символах

a — b, a + c = b + c и a — c = b — c

являются эквивалентными уравнениями.

Пример 1 Напишите уравнение, эквивалентное

x + 3 = 7

путем вычитания 3 из каждого члена.

Решение Вычитание 3 из каждого члена дает

x + 3 — 3 = 7 — 3

или

x = 4

Обратите внимание, что x + 3 = 7 и x = 4 являются эквивалентными уравнениями, поскольку решение одно и то же. для обоих, а именно 4. Следующий пример показывает, как мы можем сгенерировать эквивалентные уравнения, сначала упростив один или оба члена уравнения.

Пример 2 Напишите уравнение, эквивалентное

4x- 2-3x = 4 + 6

путем объединения одинаковых терминов, а затем добавления 2 к каждому элементу.

Объединение одинаковых членов дает

x — 2 = 10

Добавление 2 к каждому члену дает

x-2+2 =10+2

x = 12

Чтобы решить уравнение, мы используем сложение-sub тяга свойство преобразовывать данное уравнение в эквивалентное уравнение формы x = a, из которого мы можем найти решение путем проверки.

Пример 3 Решить 2x + 1 = x — 2.

Мы хотим получить эквивалентное уравнение, в котором все члены, содержащие x, находятся в одном члене, а все члены, не содержащие x, — в другом. Если мы сначала прибавим -1 к каждому элементу (или вычтем из него 1), мы получим

2x + 1- 1 = x — 2- 1

2x = x — 3

Если мы теперь прибавим -x к каждому члену (или вычтем x из него), мы получим

2x-x = x — 3 — х

х = -3

где решение -3 очевидно.

Решением исходного уравнения является число -3; однако ответ часто отображается в виде уравнения x = -3.

Поскольку каждое уравнение, полученное в процессе, эквивалентно исходному уравнению, -3 также является решением 2x + 1 = x — 2. В приведенном выше примере мы можем проверить решение, подставив — 3 вместо x в исходном уравнение

2(-3) + 1 = (-3) — 2

-5 = -5

Симметричное свойство равенства также полезно при решении уравнений. Это свойство указывает

Если a = b, то b = a

Это позволяет нам менять местами члены уравнения в любое время, не заботясь о смене знака. Таким образом,

Если 4 = x + 2, то x + 2 = 4

Если x + 3 = 2x — 5, то 2x — 5 = x + 3

Если d = rt, то rt = d

Может быть несколько различные способы применения вышеуказанного свойства сложения. Иногда один метод лучше другого, а в некоторых случаях также полезно симметричное свойство равенства.

Пример 4 Решите 2x = 3x — 9. (1)

Решение Если мы сначала прибавим -3x к каждому элементу, мы получим

2x — 3x = 3x — 9 — 3x

-x = -9

где переменная имеет отрицательный коэффициент. Хотя при проверке мы видим, что решение равно 9, поскольку -(9) = -9, мы можем избежать отрицательного коэффициента, добавляя -2x и +9 к каждому члену уравнения (1). В этом случае получаем

2х-2х + 9 = 3х- 9-2х+ 9

9 = х

откуда решение 9очевидно. Если мы хотим, мы можем записать последнее уравнение как x = 9 по симметричному свойству равенства.

Решенные уравнения с использованием Свойства Отдела

Рассмотрим уравнение

3x = 12

Решение этого уравнения равно 4.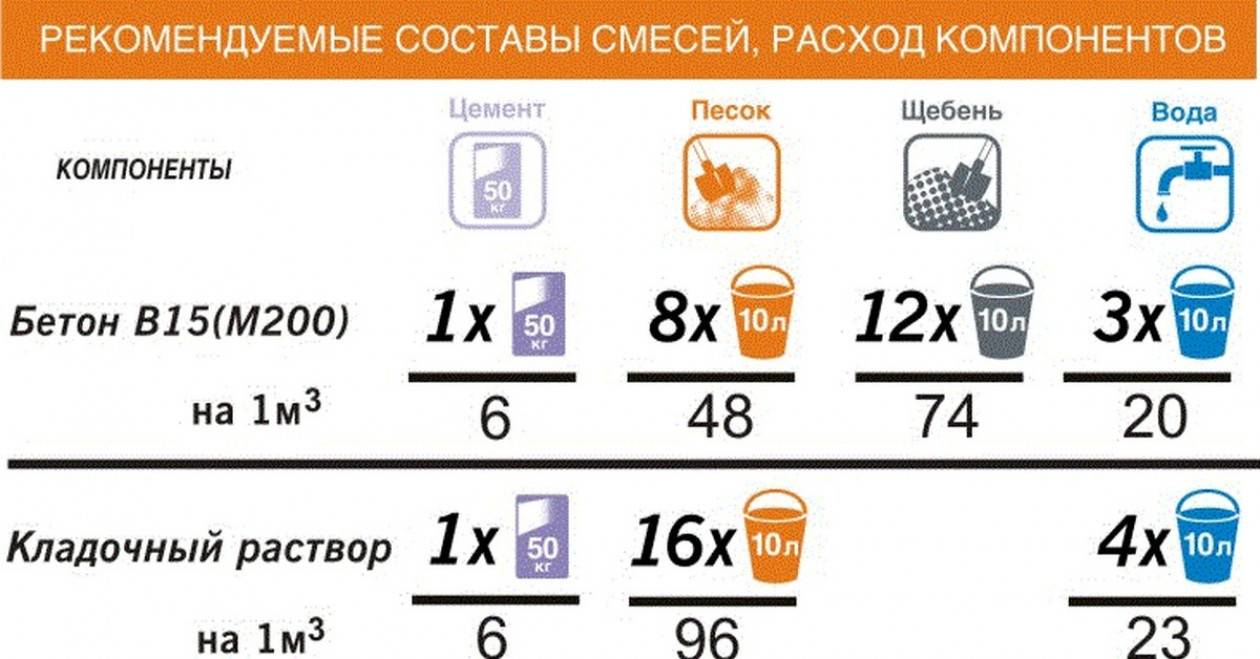 Также обратите внимание, что если мы разделим каждый член уравнения на 3, мы получаем уравнения

, решение которого также равно 4. В общем случае мы имеем следующее свойство, которое иногда называют свойством деления.

Если оба члена уравнения разделить на одно и то же (отличное от нуля) полученное уравнение эквивалентно исходному уравнению.

В символах

эквивалентны уравнениям.

Пример 1 Напишите уравнение, эквивалентное

-4x = 12

, разделив каждый член на -4.

Решение Деление обоих членов на -4 дает

При решении уравнений мы используем вышеуказанное свойство для получения эквивалентных уравнений, в которых переменная имеет коэффициент 1.

Пример 2 Решите 3y + 2y = 20.

Сначала мы объединяем одинаковые члены, чтобы получить

5y = 20

Затем, разделив каждый член на 5, мы получаем

В следующем примере мы используем дополнение — свойство вычитания и свойство деления для решения уравнения.

Пример 3 Решить 4x + 7 = x — 2.

Решение Сначала мы добавляем -x и -7 к каждому члену, чтобы получить

4x + 7 — x — 7 = x — 2 — x — 1

Далее , объединение одинаковых членов дает

3x = -9

Наконец, мы делим каждый член на 3, чтобы получить

РЕШЕНИЕ УРАВНЕНИЙ, ИСПОЛЬЗУЯ СВОЙСТВО УМНОЖЕНИЯ решение этого уравнения равно 12. Также обратите внимание, что если умножая каждый член уравнения на 4, мы получаем уравнения

, решение которых также равно 12. В общем случае мы имеем следующее свойство, которое иногда называют свойством умножения.

Если оба члена уравнения умножить на одну и ту же ненулевую величину, полученное уравнение эквивалентно исходному уравнению.

В символах

a = b и a·c = b·c (c ≠ 0)

являются эквивалентными уравнениями.

Пример 1 Напишите уравнение, эквивалентное

, умножив каждый член на 6.

Решение Умножив каждый член на 6, получим

дроби.

Пример 2 Решить

Решение Сначала умножьте каждый член на 5, чтобы получить

Теперь разделите каждый член на 3,

Пример 3 Решите .

Решение Сначала упростим над дробной чертой, чтобы получить

Затем умножим каждый член на 3, чтобы получить

Наконец, разделив каждый член на 5, получим

ДОПОЛНИТЕЛЬНОЕ СОЛНЦЕ РЕШЕНИЯ УРАВНЕНИЙ

Теперь мы знаем все методы, необходимые для решения большинства уравнений первой степени. Нет определенного порядка, в котором следует применять свойства. Любой один или несколько из следующих шагов, перечисленных на странице 102, могут быть подходящими.

Шаги для решения уравнений первой степени:

1. Объедините одинаковые члены в каждом члене уравнения.
2. Используя свойство сложения или вычитания, напишите уравнение со всеми членами, содержащими неизвестное в одном члене, и всеми членами, не содержащими неизвестного в другом.
3. Объедините одинаковые термины в каждом элементе.
4. Используйте свойство умножения для удаления дробей.
5. Используйте свойство Division, чтобы получить коэффициент 1 для переменной.

Пример 1 Решите 5x — 7 = 2x — 4x + 14.

Решение Сначала мы объединяем одинаковые члены, 2x — 4x, чтобы получить

5x — 7 = -2x + 14

Затем мы добавляем +2x и +7 к каждому члену и объединяем одинаковые члены, чтобы получить

5x — 7 + 2x + 7 = -2x + 14 + 2x + 1

7x = 21

Наконец, мы делим каждый член на 7, чтобы получить

В следующем примере мы упрощаем дробную черту перед применением свойств, которые мы изучали.

Пример 2 Решить

Решение Сначала мы объединяем одинаковые члены, 4x — 2x, чтобы получить

Затем мы добавляем -3 к каждому члену и упрощаем

Затем мы умножаем каждый член на 3, чтобы получить

Наконец, мы делим каждый член на 2, чтобы получить

РЕШЕНИЕ ФОРМУЛ

Уравнения, которые включают переменные для измерения двух или более физических величин, называются формулами. Мы можем найти любую переменную в формуле, если известны значения других переменных. Мы подставляем известные значения в формулу и находим неизвестную переменную методами, которые мы использовали в предыдущих разделах.

Пример 1 В формуле d = rt найдите t, если d = 24 и r = 3.

Решение Мы можем найти t, подставив 24 вместо d и 3 вместо r. То есть

d = rt

(24) = (3)t

8 = t

Часто бывает необходимо решать формулы или уравнения, в которых имеется более одной переменной для одной из переменных в терминах другие. Мы используем те же методы, которые были продемонстрированы в предыдущих разделах.

Пример 2 В формуле d = rt найдите t через r и d.

Решение Мы можем найти t через r и d, разделив оба члена на r, чтобы получить

, откуда по симметричному закону

В приведенном выше примере мы нашли t, применив свойство деления для создания эквивалентного уравнения. Иногда необходимо применить более одного такого свойства.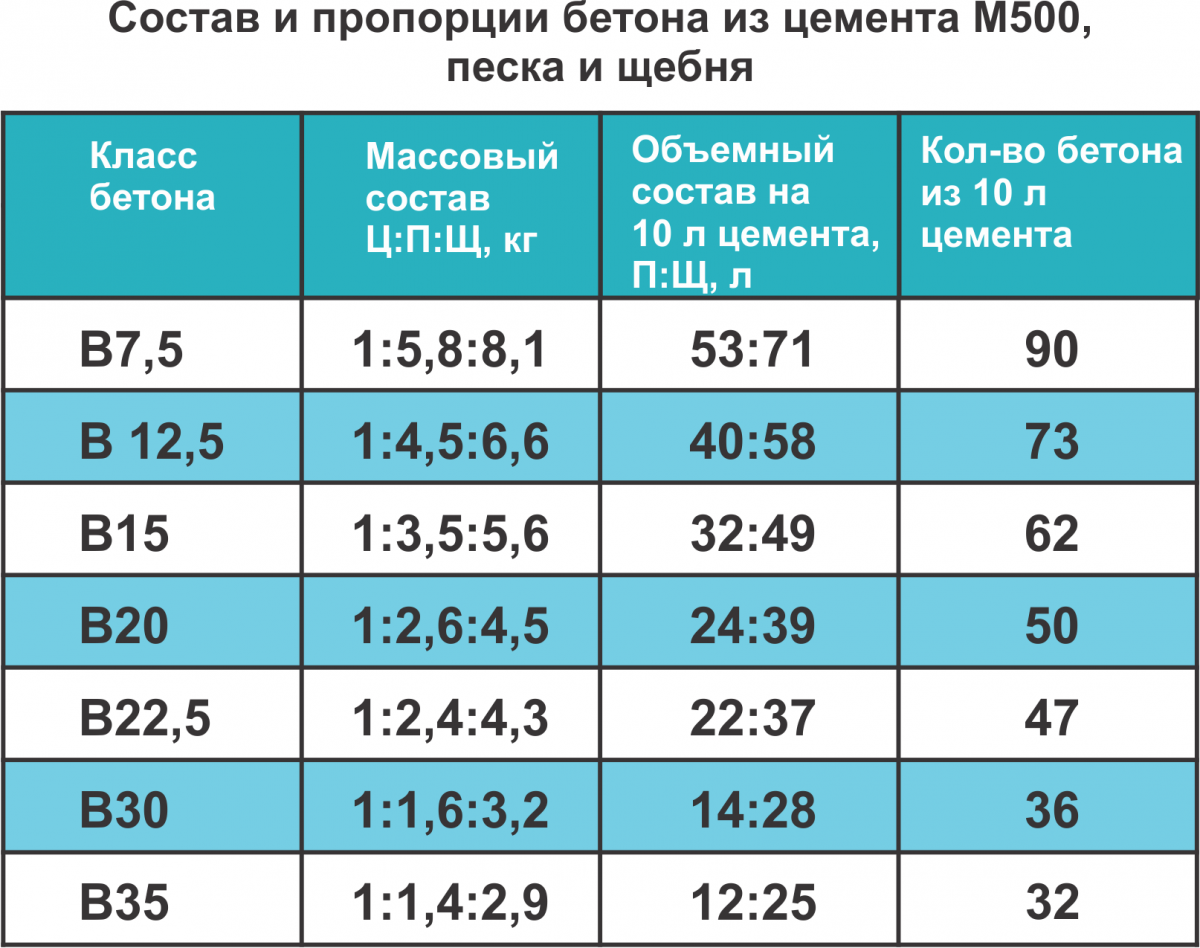

Пример 3 В уравнении ax + b = c найдите x через a, b и c.

Решение Мы можем найти x, сначала добавив -b к каждому члену, чтобы получить

затем разделив каждый член на a, мы получим

13.7: Разбавление раствора — Химия LibreTexts

1. Последнее обновление

2. Сохранить как PDF

• Эд Витц, Джон В. Мур, Джастин Шорб, Ксавьер Прат-Ресина, Тим Вендорф и Адам Хан
• Цифровая библиотека химического образования (ChemEd DL)

Цели обучения

• Объяснить, как можно изменить концентрацию в лаборатории.
• Понять, как используются стандартные растворы в лаборатории.

Нас часто интересует, сколько растворенного вещества растворено в заданном количестве раствора. Мы начнем обсуждение концентрации раствора с двух связанных и относительных терминов: разбавленный и концентрированный .

• Разбавленный раствор — это раствор, в котором растворено относительно небольшое количество растворенного вещества.
• Концентрированный раствор содержит относительно большое количество растворенного вещества.

Эти два термина не предоставляют никакой количественной информации (фактических чисел), но они часто полезны для сравнения решений в более общем смысле. Эти термины также не говорят нам, является ли раствор насыщенным или ненасыщенным, является ли раствор «сильным» или «слабым». Эти два последних термина будут иметь особое значение, когда мы будем обсуждать кислоты и основания, поэтому будьте осторожны, чтобы не перепутать их.

Стандартные растворы

Часто необходимо иметь раствор с очень точно известной концентрацией. Растворы, содержащие точную массу растворенного вещества в точном объеме раствора, называются маточными (или стандартными) растворами . Для приготовления стандартного раствора следует использовать такое лабораторное оборудование, как мерная колба. Эти колбы имеют объем от 10 мл до 2000 мл и тщательно откалиброваны до единого объема. На узком стержне имеется калибровочная метка 9.0409 . Точную массу растворенного вещества растворяют в небольшом количестве растворителя и добавляют в колбу. Затем в колбу добавляют достаточное количество растворителя, пока уровень не достигнет калибровочной отметки.

Часто бывает удобно приготовить серию растворов известных концентраций, сначала приготовив один исходный раствор , как описано в предыдущем разделе. Аликвоты (тщательно измеренные объемы) исходного раствора можно затем разбавить до любого желаемого объема. В других случаях может быть неудобно достаточно точно взвешивать небольшую массу образца для приготовления небольшого объема разбавленного раствора. Каждая из этих ситуаций требует разбавления раствора для получения желаемой концентрации.

Разведения стандартных (или стандартных) растворов

Представьте, что у нас есть раствор соленой воды определенной концентрации. Это означает, что у нас есть определенное количество соли (определенная масса или определенное количество молей), растворенное в определенном объеме раствора. Далее мы разбавим этот раствор. Это делается добавлением большего количества воды, а не соли:

\(\rightarrow\)

Перед разбавлением и после разбавления

Молярность раствора 1 равна

\[ M_1 = \dfrac{\text{моли }_1}{\text{литр}_1} \номер\]

и молярность раствора 2 равна

\[ M_2 = \dfrac{\text{moles}_2}{\text{литр}_2} \nonumber \]

переставьте уравнения, чтобы найти моли:

\[ \text{моль}_1 = M_1 \text{литр}_1 \номер \]

и

\[ \text{моль}_2 = M_2 \text{литр}_2 \неномер \]

Что осталось прежним и что изменилось между двумя решениями? Добавляя больше воды, мы изменяли объем раствора. Это также изменило его концентрацию. Однако число молей растворенного вещества не изменилось. Итак,

\[moles_1 = moles_2 \nonnumber \]

Поэтому

\[ \boxed{M_1V_1= M_2V_2 } \label{diluteEq} \]

где

90 283 \(M_1\) и \(M_2 \) — концентрации исходного и разбавленного растворов
• \(V_1\) и \(V_2\) — объемы двух растворов

Приготовление растворов является обычным делом в химической лаборатории и других местах. Как только вы поймете приведенную выше взаимосвязь, расчеты станут простыми.

Предположим, что у вас есть \(100. \: \text{mL}\) раствора \(2.0 \: \text{M}\) \(\ce{HCl}\). Вы разбавляете раствор, добавляя достаточное количество воды, чтобы сделать объем раствора \(500. \: \text{мл}\). Новую молярность можно легко рассчитать, используя приведенное выше уравнение и решив \(M_2\).

\[M_2 = \dfrac{M_1 \times V_1}{V_2} = \dfrac{2.0 \: \text{M} \times 100. \: \text{mL}}{500. \: \text{мл}} = 0,40 \: \text{M} \: \ce{HCl} \nonumber \]

Раствор разбавлен на одну пятую, так как новый объем в пять раз превышает исходный.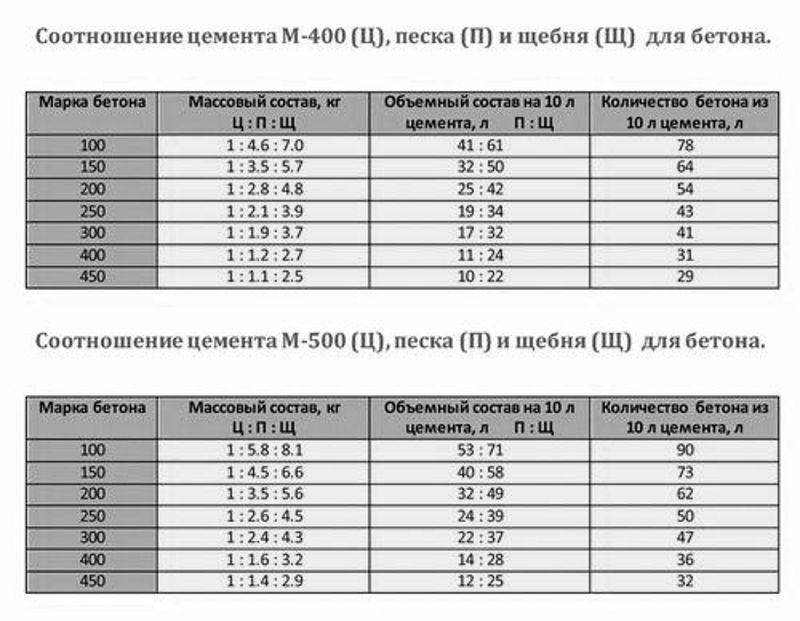 оригинальный объем. Следовательно, молярность составляет одну пятую от первоначального значения.

Еще одна распространенная проблема с разбавлением заключается в расчете количества высококонцентрированного раствора, необходимого для получения желаемого количества раствора меньшей концентрации. Высококонцентрированный раствор обычно называют исходным раствором.

Пример \(\PageIndex{1}\): Разбавление азотной кислоты

Азотная кислота \(\left( \ce{HNO_3} \right)\) является сильной и агрессивной кислотой. При заказе в компании-поставщике химикатов его молярность составляет \(16 \: \text{M}\). Сколько исходного раствора азотной кислоты нужно использовать, чтобы получить \(8,00 \: \text{L}\) из \(0,50 \: \text{M}\) раствора?

Решение

Решения примера 13.7.1

Действия по решению проблем
Определите «данную» информацию и то, что проблема просит вас «найти».	Дано: M 1 , Запас \(\ce{HNO_3} = 16 \: \text{M}\) \(V_2 = 8.00 \: \text{L}\) \(М_2 = 0,50 \: \текст{М}\) Найти: Объем запаса \(\ce{HNO_3} \left( V_1 \right) = ? \: \text{L}\)
Перечислите другие известные количества.	нет
Спланируйте задачу.	Сначала перестройте уравнение алгебраически, чтобы решить для \(V_1\). \[V_1 = \dfrac{M_2 \times V_2}{M_1} \номер\]
Расчет и отмена единиц.	Теперь подставьте известные величины в уравнение и решите. \[V_1 = \dfrac{0,50 \: \text{M} \times 8,00 \: \text{L}}{16 \: \text{M}} = 0,25 \: \text{L}\]
Подумайте о своем результате.	\( 0,25 \: \text{L} \: (250 \: \text{мл})\) исходного раствора \(\ce{HNO_3}\) необходимо разбавить водой до конечного объема \( 8.00 \: \text{L}\). Разведение производится в 32 раза, чтобы перейти от \(16 \: \text{M}\) до \(0,5 \: \text{M}\).

Упражнение \(\PageIndex{1}\)

К 0,885 М раствору KBr с начальным объемом 76,5 мл добавляют воду до тех пор, пока его концентрация не станет 0,500 М. Каков новый объем раствора?

Ответ

135,4 мл

Обратите внимание, что расчетный объем будет иметь те же размеры, что и входной объем, и анализ размерностей говорит нам, что в этом случае нам не нужно преобразовывать в литры, так как L сокращается при делении М (моль/л) на М (моль/л).

Растворы для разбавления и смешивания

Эта страница под названием 13.