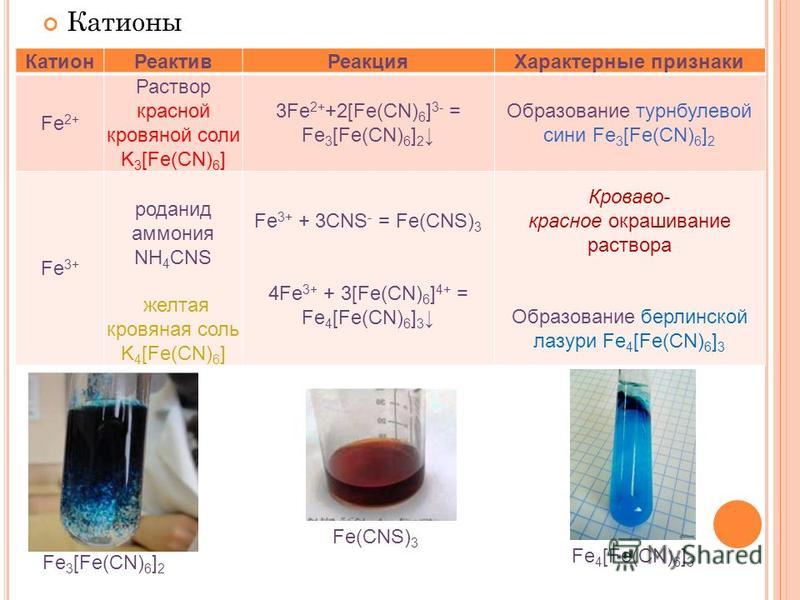
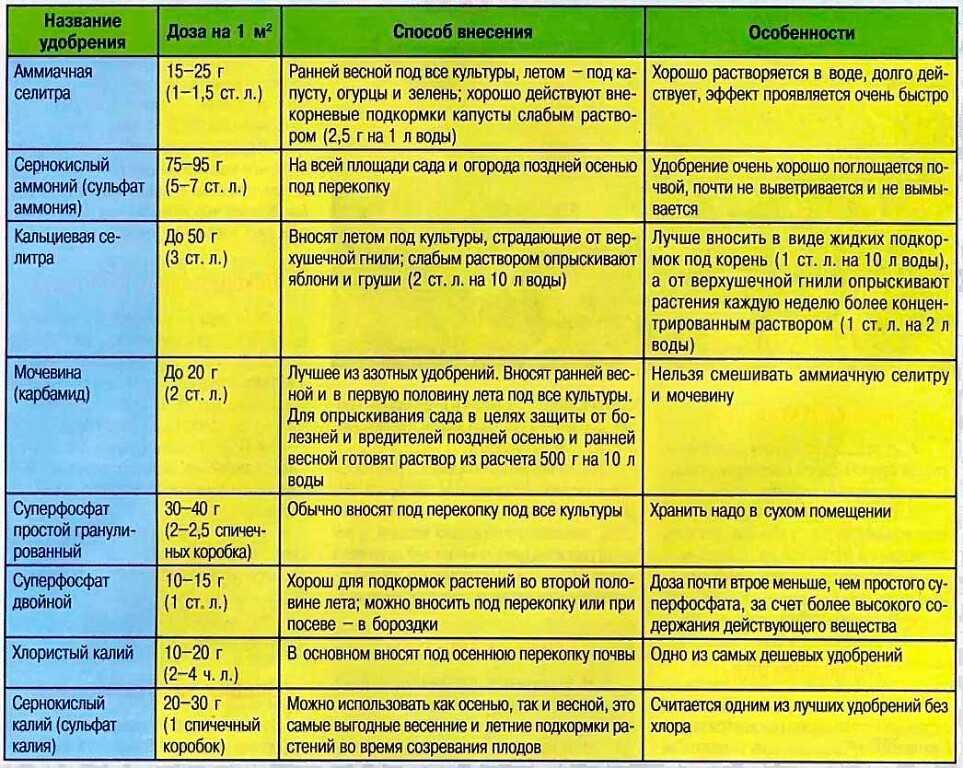
Раствор 1 к 3: как развести и сколько песка и цемента в 1 м3, соотношение частей и расход
описание, технические характеристики, пропорции, цена готовых смесей
Цементно-известковый раствор используется для кладочных и штукатурных работ. Состав у него такой же, как и у смеси с цементом, но с добавлением гашеной извести. В зависимости от пропорций внесенных компонентов меняются его характеристики и назначение, применяется для отделочных работ как снаружи, так и внутри помещений. Сделать его можно своими руками или купить готовый.
Оглавление:
- Разновидности и технические параметры
- Руководство по самостоятельному изготовлению
- Цена готовых известковых смесей
Виды и характеристики
Известковый раствор имеет повышенную степень адгезии. Он хорошо пристает практически к любым поверхностям, в том числе к дереву и к бетону. Благодаря бактерицидным свойствам извести исключается вероятность появления плесени или грибков. Такой состав способен пропускать влагу, не нарушая микроклимат в помещении. Выдерживает перепады температур от -50°С до +65°С.
В отличие от цементной смеси, известковая более эластичная. Она отлично заполняет все щели и впадины. Нанесенную штукатурку можно поправить в течение 1-3 часов. Раствор с цементом же только до одного часа. Благодаря такому длительному высыханию вероятность появления трещин минимальна.
Для различия составов с известью и цементом существует такая техническая характеристика раствора как жирность. Именно по ней определяется область его применения.
Существуют следующие степени жирности:
- нормальная;
- тощая;
- жирная.
Чаще всего используется раствор с нормальным уровнем жирности, так как он обладает наиболее оптимальной пластичностью, крайне редко садится и не дает трещины. Тощие подходят для облицовки поверхностей и имеют минимальную усадку. Жирные состоят из большого количества вяжущего компонента, поэтому высокоэластичные.
Характеристика жирности зависит от соотношения компонентов раствора. Чтобы получить тощий, вносят больше песка, жирный – больше извести. Различаются они и по плотности: низкие (до 1500 кг/м3) и средние (от 1500). На область применения раствора влияет соотношение компонентов. Чаще всего используются марки М50 (для штукатурных работ) и М75 (для кладки кирпича).
Также цементно-известковые штукатурные растворы делятся на следующие виды:
- базовые;
- декоративные;
- специального назначения.
Первый вариант используется для выравнивания любых поверхностей и применяется в качестве чернового слоя. Декоративные высыхают длительное время, благодаря чему их удобно обрабатывать и придавать нужную форму и узоры. Смеси специального назначения обладают повышенными влагозащитными характеристиками, хорошо поглощают шум и теплоизолируют.
Приготовление раствора своими руками
По сравнению с цементно-песчаным раствором, известковый имеет более низкую цену.
Также пропорции раствора зависят от толщины слоя нанесения. Для черновых работ (обрызг) замешивают в следующих соотношениях – 6,7:1,5:1:2,2 (песок, известь, портландцемент, вода). Для слоя средней толщины – 9:2,2:1:2,8, в качестве финишного покрытия – 13,5:3:1:4.
Для замешивания известковой смеси обычно требуется не более 0,8 части воды к одной части портландцемента. На это соотношение также влияет сухость компонентов. Главное, чтобы цементный раствор по консистенции был похож на густую сметану.
Перед тем как замешивать, известь нужно погасить. Если не сделать этого заранее, то из-за химической реакции в растворе появятся вздутия. Для гашения используется отдельная емкость. Технология гашения зависит от типа извести. Она может быть быстрогасящейся, средней и медленной. Первый тип гасят следующим образом: в емкость, заполненную водой, засыпается порошок. Как только начинается химическая реакция, доливается вода и все перемешивается. Процесс гашения закончится через 8 мин.
Если не сделать этого заранее, то из-за химической реакции в растворе появятся вздутия. Для гашения используется отдельная емкость. Технология гашения зависит от типа извести. Она может быть быстрогасящейся, средней и медленной. Первый тип гасят следующим образом: в емкость, заполненную водой, засыпается порошок. Как только начинается химическая реакция, доливается вода и все перемешивается. Процесс гашения закончится через 8 мин.
Известь средней скорости гашения гасят таким же образом, но это занимает больше времени – около получаса. Медленногасящийся известковый порошок не заливают водой, а лишь сбрызгивают. Гашение длится до тех пор, пока весь объем не увеличится в 3 раза. Реакция происходит более получаса.
Чтобы известковый раствор получился качественным, главное – соблюсти пропорции, так как именно от соотношения компонентов зависят все его характеристики и конечный результат. Для замешивания рекомендуется портландцемент, а не обычный цемент, так как он имеет лучшую прочность.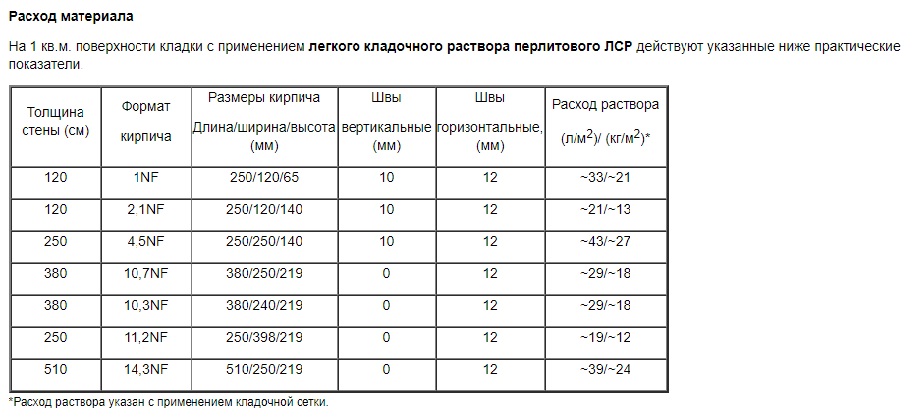
Если смесь замешивается для кладки большого количества кирпича, то рекомендуется использовать бетономешалку. Она сделает ее абсолютно однородной. Сначала вливается вода, после чего засыпается портландцемент, известковый порошок и песок. Как только все тщательно перемешалось, снова добавляется вода и все доводится до нужной консистенции.
Если раствор замешивается вручную, то рекомендуется дрель со специальной насадкой – миксером. Технология приготовления вручную может быть проведена двумя способами:
- Гашеную известь процеживают через сито с диаметром ячеек до 3 мм. В полученное известковое молоко засыпается песок и портландцемент. Все компоненты тщательно перемешиваются, и смесь доводится до необходимой степени жирности.
- В сухом виде перемешиваются песок с портландцементом до однородного состояния. Медленно заливается процеженная гашеная известь. До нужной консистенции доводят с помощью воды.
Для повышения технических характеристик добавляются пластификаторы, добавки, которые делают раствор морозоустойчивым, ускорители или замедлители времени затвердевания и так далее.
Обзор производителей и цены
Наиболее известными производителями известковых растворов являются Besto, Основит, Knauf и Henkel.
Цементно-штукатурный состав Besto марки М100 выпускается в бумажных мешках весом 25 и 50 кг. В него входят портландцемент М500д0, гашеная известь, влагоудерживающие компоненты, песок разных фракций – 1 и 0,6 мм и полипропиленовая фибра, которая повышает прочностные свойства раствора, а точнее, армирует его. Применяется Besto для внутренних и внешних работ. Наносить можно как вручную, так и с помощью оборудования. Готовый порошок нужно развести количеством воды, указанным в инструкции. При толщине слоя в 1 см потребуется 18 кг смеси на 1 м2.
Сухой Основит PC21 Стартвэлл фасуется в мешки весом 25 кг. Содержит компоненты, повышающие морозоустойчивость известкового раствора. Также имеет влагоудерживающие добавки, благодаря чему его можно использовать для отделки помещений с повышенной влажностью или для фасадов. Марка прочности – В10. Расход такой же, как и у Besto – 18 кг/м2 при толщине 10 мм. Разведенный раствор можно применять в течение двух часов при температуре от +5 до +30°С.
Расход такой же, как и у Besto – 18 кг/м2 при толщине 10 мм. Разведенный раствор можно применять в течение двух часов при температуре от +5 до +30°С.
Момент Henkel предназначен для обработки поверхностей только внутри помещений. Порошок Хенкель можно использовать в качестве промежуточного слоя, на который в последствие наносится финишное покрытие. Затворенную смесь нужно нанести в течение часа. Толщина слоя за одно нанесение не должна быть больше 2 см. Фасуется в упаковки весом 25 кг.
Сухой порошковый МП Ляйхт Цемент содержит в себе перлит и полимерные добавки. Применяется в качестве выравнивающего слоя. Может использоваться как снаружи, так и внутри помещений. Фасуется в мешках по 30 кг. На 1 м2 толщиной слоя 1 см потребуется 13,4 кг. Наносится либо вручную, либо техникой.
Стоимость цементного раствора с известью зависит от объема мешка, назначения и производителя.
Таблица с ценами, по которым можно купить готовые сухие известковые смеси:
| Название | Цена, рубли |
| Основит PC21 Стартвэлл 25 кг | 220 |
| Стройбриг Танилит 25 кг | 250 |
| Besto 25 кг | 110 |
| Besto 50 кг | 185 |
| Геркулес GP-31 25 кг | 280 |
Известковый раствор продается в бумажных мешках с разным весом. Приобретая его, следует проверить целостность мешка, на нем не должно быть дыр или склеенных мест. Также нужно обратить внимание на условия хранения. Он не должен храниться в сыром помещении, так как цемент быстро теряет свои прочностные характеристики. К тому же порошок схватывается, и образуются комки. Если использовать такой материал для кладки или штукатурки, то в нем после высыхания проявятся трещины. Чтобы повысить степень адгезии отделываемой поверхности, нужно очистить ее от грязи, старых финишных покрытий и жирных масляных пятен. Также можно обработать грунтовкой или бетоноконтактом.
Приобретая его, следует проверить целостность мешка, на нем не должно быть дыр или склеенных мест. Также нужно обратить внимание на условия хранения. Он не должен храниться в сыром помещении, так как цемент быстро теряет свои прочностные характеристики. К тому же порошок схватывается, и образуются комки. Если использовать такой материал для кладки или штукатурки, то в нем после высыхания проявятся трещины. Чтобы повысить степень адгезии отделываемой поверхности, нужно очистить ее от грязи, старых финишных покрытий и жирных масляных пятен. Также можно обработать грунтовкой или бетоноконтактом.
Цементный раствор с доставкой по СПб. Характеристики и виды цементного раствора
Прежде чем купить цементный раствор, необходимо определиться — какой именно цементный раствор вам нужен!
Цементный (строительный) раствор — это смесь воды, цемента (связующий элемент) и песка (наполнитель) в определенной пропорции. Например, для раствора М100 эта пропорция составит 1 : 6,0 : 1,3 (цемент : песок : вода).
Характеристики цементного раствора
Первой характеристикой является марка (М) цементного раствора (как и марка бетонного) показывает среднюю прочность на сжатие куба бетона через 28 суток после укладки.
Второй характеристикой цементного раствора является подвижность (Пк). Подвижность показывает способность цементного раствора проникать в поры и другие труднодоступные участки. Подвижность определяют путем погружения эталонного конуса в раствор. Если конус под собственной массой погрузился на 4-8 см, то Пк = 2, если на 8-12 см, то Пк = 3.
Виды цементного раствора
Встречаются разные названия строительного раствора: цементно-песчаный раствор или просто раствор цемента (по названию составляющих). Во всех этих случаях имеется ввиду одно и тот же.
В зависимости от целей цементный раствор подразделяют на монтажный и кладочный.
Монтажный раствор используется, например, чтобы заполнять горизонтальные швы между тяжелыми бетонными панелями, а также щели или стыки между блоками при строительстве зданий.
Кладочный раствор применяется в строительстве зданий и других сооружений, когда используется небольшие блоки, такие как кирпич, различные бетонные и каменные элементы.
Сделать заявку и/или проконсультироваться можно по телефону +7 (812) 703-90-66 (отдел продаж) или +7 (812) 333-11-55 (отдел строительства) (Прием звонков: с 8:00 до 21:00)
Почему стоит купить цементный раствор у нас?
Гарантия качества — завод ЛенБетон на рынке уже более пяти и зарекомендовал себя как надежный партнер
Низкие цены — наши цены на монтажный и кладочный растворы одни из самых низких в городе
Всегда в срок — мы доставляем точно по графику!
Заявка на скидку
Отправьте заявку на доставку бетона и получите скидку на доставку.
Заполните правильно Имя
Заполните правильно Телефон
Если вы заказываете бетон в первый раз — ознакомьтесь с правилами отгрузки
Заказ и доставка цементного раствора с любого производства ЛенБетон:
* Офис ЛенБетон
Адрес: Ленинградская область, п. Новоселье,
Новоселье,
с 9:00 до 18:00 (Пн-Пт)
80 м³/час
Адрес: Ленинградская область, п. Новоселье.
Круглосуточно
100 м³/час
Адрес: Лен. обл., дер. Янино, центральный проезд 16.
Круглосуточно
100 м³/час
Адрес: Ленинградская обл., дер. Порошкино.
Круглосуточно
Заводы «ЛенБетон» на карте Санкт-Петербурга
Задайте вопрос.
+7 (812) 703-90-66
Быстрый расчет и консультация!
Решение неравенств с помощью пошагового решения математических задач
В этой главе мы разработаем некоторые приемы, помогающие решать задачи, сформулированные словами. Эти методы включают переписывание задач в виде символов. Например, поставленная задача
Эти методы включают переписывание задач в виде символов. Например, поставленная задача
«Найдите число, которое при прибавлении к 3 дает 7»
можно записать так:
3 + ? = 7, 3 + n = 7, 3 + x = 1
и т. д., где символы ?, n и x представляют число, которое мы хотим найти. Такие сокращенные версии поставленных задач мы называем уравнениями или символическими предложениями. Такие уравнения, как x + 3 = 7, являются уравнениями первой степени, поскольку показатель степени равен 1. Члены слева от знака равенства составляют левый член уравнения; те, что справа, составляют правый член. Таким образом, в уравнении x + 3 = 7 левая часть равна x + 3, а правая часть равна 7.
РЕШЕНИЕ УРАВНЕНИЙ
Уравнения могут быть истинными или ложными, так же как словесные предложения могут быть истинными или ложными. Уравнение:
3 + x = 7
будет ложным, если вместо переменной подставить любое число, кроме 4. Значение переменной, для которой уравнение верно (4 в этом примере), называется решением уравнения. Мы можем определить, является ли данное число решением данного уравнения, подставив число вместо переменной и определив истинность или ложность результата.
Мы можем определить, является ли данное число решением данного уравнения, подставив число вместо переменной и определив истинность или ложность результата.
Пример 1. Определить, является ли значение 3 решением уравнения член.
4(3) — 2 = 3(3) + 1
12 — 2 = 9 + 1
10 = 10
Ответ. 3 это решение.
Уравнения первой степени, которые мы рассматриваем в этой главе, имеют не более одного решения. Решения многих таких уравнений можно определить путем проверки.
Пример 2 Найдите решение каждого уравнения путем проверки.
а. х + 5 = 12
б. 4 · x = -20
Решения а. 7 является решением, так как 7 + 5 = 12,
b. -5 является решением, поскольку 4(-5) = -20.
РЕШЕНИЕ УРАВНЕНИЙ С ИСПОЛЬЗОВАНИЕМ СВОЙСТВ СЛОЖЕНИЯ И ВЫЧИТАНИЯ
В разделе 3.1 мы решили некоторые простые уравнения первой степени путем проверки. Однако решения большинства уравнений не сразу очевидны при осмотре. Следовательно, нам нужны некоторые математические «инструменты» для решения уравнений.
ЭКВИВАЛЕНТНЫЕ УРАВНЕНИЯ
Эквивалентные уравнения – это уравнения, имеющие одинаковые решения. Таким образом,
3x + 3 = x + 13, 3x = x + 10, 2x = 10 и x = 5
эквивалентны уравнениям, поскольку 5 является единственным решением каждого из них. Обратите внимание, что в уравнении 3x + 3 = x + 13 решение 5 не очевидно при проверке, но в уравнении x = 5 решение 5 очевидно при проверке. При решении любого уравнения мы преобразуем данное уравнение, решение которого может быть неочевидным, в эквивалентное уравнение, решение которого легко заметить.
Следующее свойство, иногда называемое свойством сложения-вычитания , является одним из способов генерирования эквивалентных уравнений.
Если к обоим элементам добавляется или вычитается одно и то же количество уравнения, полученное уравнение эквивалентно исходному уравнение.
В символах
a — b, a + c = b + c и a — c = b — c
являются эквивалентными уравнениями.
Пример 1 Напишите уравнение, эквивалентное
x + 3 = 7
путем вычитания 3 из каждого члена.
Решение Вычитание 3 из каждого члена дает
x + 3 — 3 = 7 — 3
или
x = 4
Обратите внимание, что x + 3 = 7 и x = 4 являются эквивалентными уравнениями, поскольку решение одно и то же. для обоих, а именно 4. Следующий пример показывает, как мы можем сгенерировать эквивалентные уравнения, сначала упростив один или оба члена уравнения.
Пример 2 Напишите уравнение, эквивалентное
4x- 2-3x = 4 + 6
путем объединения одинаковых терминов, а затем добавления 2 к каждому элементу.
Объединение одинаковых членов дает
x — 2 = 10
Добавление 2 к каждому члену дает
x-2+2 = 10+2
x = 12
Чтобы решить уравнение, мы используем сложение-вычитание свойство преобразовывать данное уравнение в эквивалентное уравнение формы x = a, из которого мы можем найти решение путем проверки.
Пример 3 Решить 2x + 1 = x — 2.
Мы хотим получить эквивалентное уравнение, в котором все члены, содержащие x, находятся в одном члене, а все члены, не содержащие x, — в другом. Если мы сначала прибавим -1 к каждому элементу (или вычтем из него 1), мы получим
2x + 1- 1 = x — 2- 1
2x = x — 3
Если мы теперь прибавим -x к каждому члену (или вычтем x из него), мы получим
2x-x = x — 3 — х
х = -3
где решение -3 очевидно.
Решением исходного уравнения является число -3; однако ответ часто отображается в виде уравнения x = -3.
Поскольку каждое уравнение, полученное в процессе, эквивалентно исходному уравнению, -3 также является решением 2x + 1 = x — 2. В приведенном выше примере мы можем проверить решение, подставив — 3 вместо x в исходном уравнение
2(-3) + 1 = (-3) — 2
-5 = -5
Симметричное свойство равенства также полезно при решении уравнений. Это свойство указывает
Если a = b, то b = a
Это позволяет нам менять местами члены уравнения, когда нам угодно, не заботясь о смене знака. Таким образом,
Таким образом,
Если 4 = x + 2, то x + 2 = 4
Если x + 3 = 2x — 5, то 2x — 5 = x + 3
Если d = rt, то rt = d
Может быть несколько различные способы применения вышеуказанного свойства сложения. Иногда один метод лучше другого, а в некоторых случаях также полезно симметричное свойство равенства.
Пример 4 Решите 2x = 3x — 9. (1)
Решение Если мы сначала прибавим -3x к каждому элементу, мы получим
2x — 3x = 3x — 9 — 3x
-x = -9
где переменная имеет отрицательный коэффициент. Хотя при проверке мы видим, что решение равно 9, поскольку -(9) = -9, мы можем избежать отрицательного коэффициента, добавляя -2x и +9 к каждому члену уравнения (1). В этом случае получаем
2х-2х + 9 = 3х- 9-2х+ 9
9 = х
откуда решение 9очевидно. Если мы хотим, мы можем записать последнее уравнение как x = 9 по симметричному свойству равенства.
РЕШЕНИЕ УРАВНЕНИЙ С ИСПОЛЬЗОВАНИЕМ СВОЙСТВА ДЕЛЕНИЯ
Рассмотрим уравнение
3x = 12
Решением этого уравнения является 4. Также обратите внимание, что если мы разделим каждую часть уравнения на 3, мы получим уравнения
Также обратите внимание, что если мы разделим каждую часть уравнения на 3, мы получим уравнения
, решение которого также равно 4. В общем случае мы имеем следующее свойство, которое иногда называют свойством деления.
Если оба члена уравнения разделить на одно и то же (отличное от нуля) полученное уравнение эквивалентно исходному уравнению.
В символах
эквивалентны уравнениям.
Пример 1 Напишите уравнение, эквивалентное
-4x = 12
, разделив каждый член на -4.
Решение Деление обоих членов на -4 дает
При решении уравнений мы используем вышеуказанное свойство для получения эквивалентных уравнений, в которых переменная имеет коэффициент 1.
Пример 2 Решите 3y + 2y = 20.
Сначала мы объединяем одинаковые члены, чтобы получить
5y = 20
Затем, разделив каждый член на 5, мы получаем
В следующем примере мы используем сложение — свойство вычитания и свойство деления для решения уравнения.
Пример 3 Решить 4x + 7 = x — 2.
Решение Сначала мы добавляем -x и -7 к каждому члену, чтобы получить
4x + 7 — x — 7 = x — 2 — x — 1
Далее , объединение одинаковых членов дает
3x = -9
Наконец, мы делим каждый член на 3, чтобы получить
РЕШЕНИЕ УРАВНЕНИЙ С ИСПОЛЬЗОВАНИЕМ СВОЙСТВА УМНОЖЕНИЯ
Рассмотрим уравнение
Решение этого уравнения умножая каждый член уравнения на 4, мы получаем уравнения
, решение которых также равно 12. В общем случае мы имеем следующее свойство, которое иногда называют свойством умножения.
Если оба члена уравнения умножить на одну и ту же ненулевую величину, полученное уравнение эквивалентно исходному уравнению.
В символах
a = b и a·c = b·c (c ≠ 0)
являются эквивалентными уравнениями.
Пример 1 Напишите уравнение, эквивалентное
, умножив каждый член на 6.
Решение Умножив каждый член на 6, получим
дроби.
Пример 2 Решить
Решение Сначала умножьте каждый член на 5, чтобы получить
Теперь разделите каждый член на 3,
Пример 3 Решите .
Решение Сначала упростим над дробной чертой, чтобы получить
Затем умножим каждый член на 3, чтобы получить
Наконец, разделив каждый член на 5, получим
ДОПОЛНИТЕЛЬНЫЕ РЕШЕНИЯ 90 все методы, необходимые для решения большинства уравнений первой степени. Нет определенного порядка, в котором следует применять свойства. Любой один или несколько из следующих шагов, перечисленных на странице 102, могут быть подходящими.
Шаги для решения уравнений первой степени:
- Объедините одинаковые члены в каждом члене уравнения.
- Используя свойство сложения или вычитания, напишите уравнение со всеми членами, содержащими неизвестное в одном члене, и всеми членами, не содержащими неизвестного в другом.
- Объедините одинаковые термины в каждом элементе.

- Используйте свойство умножения для удаления дробей.
- Используйте свойство Division, чтобы получить коэффициент 1 для переменной.
Пример 1 Решите 5x — 7 = 2x — 4x + 14.
Решение Сначала мы объединяем одинаковые члены, 2x — 4x, чтобы получить
5x — 7 = -2x + 14
Затем мы добавляем +2x и +7 к каждому члену и объединяем одинаковые члены, чтобы получить
5x — 7 + 2x + 7 = -2x + 14 + 2x + 1
7x = 21
Наконец, мы делим каждый член на 7, чтобы получить
В следующем примере мы упрощаем дробную черту перед применением свойств, которые мы изучали.
Пример 2 Решить
Решение Сначала мы объединяем одинаковые члены, 4x — 2x, чтобы получить
Затем мы добавляем -3 к каждому члену и упрощаем
Затем мы умножаем каждый член на 3, чтобы получить
Наконец, мы делим каждый член на 2, чтобы получить
РЕШЕНИЕ ФОРМУЛ
Уравнения, которые включают переменные для измерения двух или более физических величин, называются формулами. Мы можем найти любую переменную в формуле, если известны значения других переменных. Мы подставляем известные значения в формулу и находим неизвестную переменную методами, которые мы использовали в предыдущих разделах.
Мы можем найти любую переменную в формуле, если известны значения других переменных. Мы подставляем известные значения в формулу и находим неизвестную переменную методами, которые мы использовали в предыдущих разделах.
Пример 1 В формуле d = rt найдите t, если d = 24 и r = 3.
Решение Мы можем найти t, подставив 24 вместо d и 3 вместо r. То есть
d = rt
(24) = (3)t
8 = t
Часто бывает необходимо решать формулы или уравнения, в которых имеется более одной переменной для одной из переменных в терминах другие. Мы используем те же методы, что и в предыдущих разделах.
Пример 2 В формуле d = rt найдите t через r и d.
Решение Мы можем найти t через r и d, разделив оба члена на r, чтобы получить
, откуда по симметричному закону
В приведенном выше примере мы нашли t, применив свойство деления для создания эквивалентного уравнения. Иногда необходимо применить более одного такого свойства.
Пример 3 В уравнении ax + b = c найдите x через a, b и c.
Решение Мы можем найти x, сначала добавив -b к каждому члену, чтобы получить
затем разделив каждый элемент на a, мы получим
наборов решений
Горячая математикаНаборы решений для уравнений
поставил содержащий все решения уравнения называется множеством решений этого уравнения.
Если уравнение не имеет решений, пишем ∅ для набора решений. ∅ означает нулевой набор (или пустой набор).
Уравнение | Набор решений |
3 Икс + 5 знак равно 11 | { 2 } |
Икс 2 знак равно Икс | { 0 , 1 } |
Икс + 1 знак равно 1 + Икс | р (набор всех действительных чисел) |
Икс + 1 знак равно Икс | ∅ (пустой набор) |
Иногда вам могут дать набор для замены и попросить проверить, верно ли уравнение для всех значений в наборе для замены.
Пример 1:
Найдите множество решений уравнения г + г знак равно г × г если сменный комплект { 0 , 1 , 2 , 3 , } .
Одним из способов решения этой проблемы является проверка всех значений в замещающем наборе с помощью таблицы.
г г + г знак равно г × г Результат 0 0 + 0 знак равно ? 0 × 0 0 знак равно 0 1 1 + 1 знак равно ? 1 × 1 2 ≠ 1 2 2 + 2 знак равно ? 2 × 2 4 знак равно 4 3 3 + 3 знак равно ? 3 × 3 6 ≠ 9
Таким образом, набор решений этого уравнения равен
{
0
,
2
}
.