Рассчитать угол наклона: Онлайн калькулятор расчета угла наклона и стропильной системы двухскатной крыши
Как рассчитать угол наклона крыши
Как рассчитать угол наклона крыши от компании Світ ПокрівліКрыша приватного здания, которое возводится по индивидуальному плану, может встречаться в разном формате. При этом наклонный размер скатовсоразмерен конструкционным особенностям, присутствию чердачного помещения, а также погодным условиям окружающей среды. Этот параметр являет собой размер между горизонтальным сегментом конструкции и верхней частью крыши. В расчетной документации он показан в градусах или процентном соотношении.
Измерять уклон можно при содействии специальных приспособлений или математическим способом. В первом случае задействуется специальный рейковый уклономер, хотя в последнее время появились и более современные инструменты — геодезические приборы, уровни в капсулами или электронного типа.
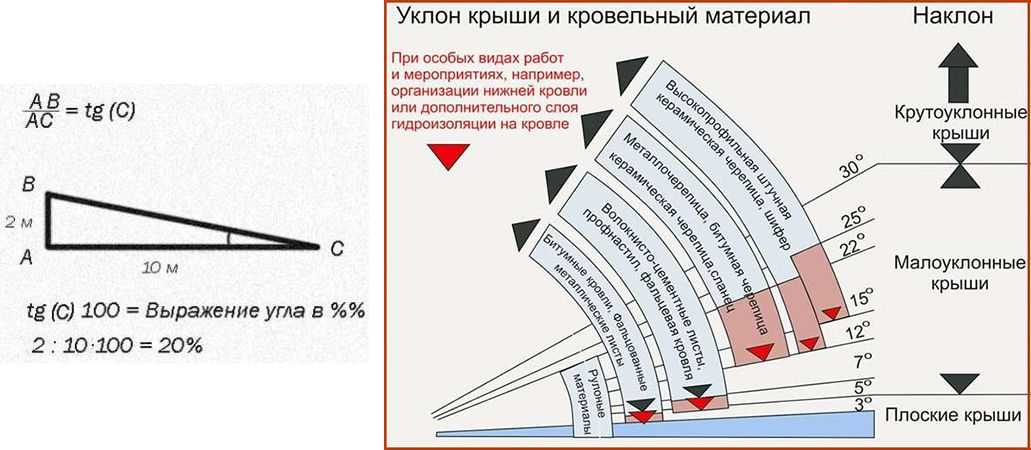
Математический расчетСамым простым методом обозначения наклонности углов является тот, которые не предусматривает использования специальных геодезических приборов. Чтобы обозначить этот параметр, достаточно знать два показателя:
Чтобы обозначить этот параметр, достаточно знать два показателя:
Н — высоту по вертикали –зачастую от карнизной части до конька;
L – величину по горизонтали – от низа ската до верхней части.
Формула основных расчетов в данной ситуации выглядит следующим образом:
i = Н : L
Полученная в результате цифра умножается на 100 –тогда будет известен наклонный угол в процентном показателе . Если же данные требуются в градусах, то тогда необходимо воспользоваться особой таблицей, в которой наведены соотношения:
|
градусы |
% |
градусы |
% |
градусы |
% |
||
|
1° |
1,75% |
16° |
28,68% |
31° |
60,09% |
||
|
2° |
3,50% |
17° |
30,58% |
32° |
62,48% |
||
|
3° |
5,24% |
18° |
32,50% |
33° |
64,93% |
||
|
4° |
7,00% |
19° |
34,43% |
34° |
67,45% |
||
|
5° |
8,75% |
20° |
36,39% |
35° |
70,01% |
||
|
6° |
10,51% |
21° |
38,38% |
36° |
72,65% |
||
|
7° |
12,28% |
22° |
40,40% |
37° |
75,35% |
||
|
8° |
14,05% |
23° |
42,45% |
38° |
78,13% |
||
|
9° |
15,84% |
24° |
44,52% |
39° |
80,98% |
||
|
10° |
17,64% |
25° |
|
40° |
83,90% |
||
|
11° |
19,44% |
26° |
48,78% |
41° |
86,92% |
||
|
12° |
21,25% |
27° |
50,95% |
42° |
90,04% |
||
|
13° |
23,09% |
28° |
53,18% |
43° |
93,25% |
||
|
14° |
24,94% |
29° |
55,42% |
44° |
96,58% |
||
|
15° |
26,80% |
30° |
57,73% |
45° |
100% |
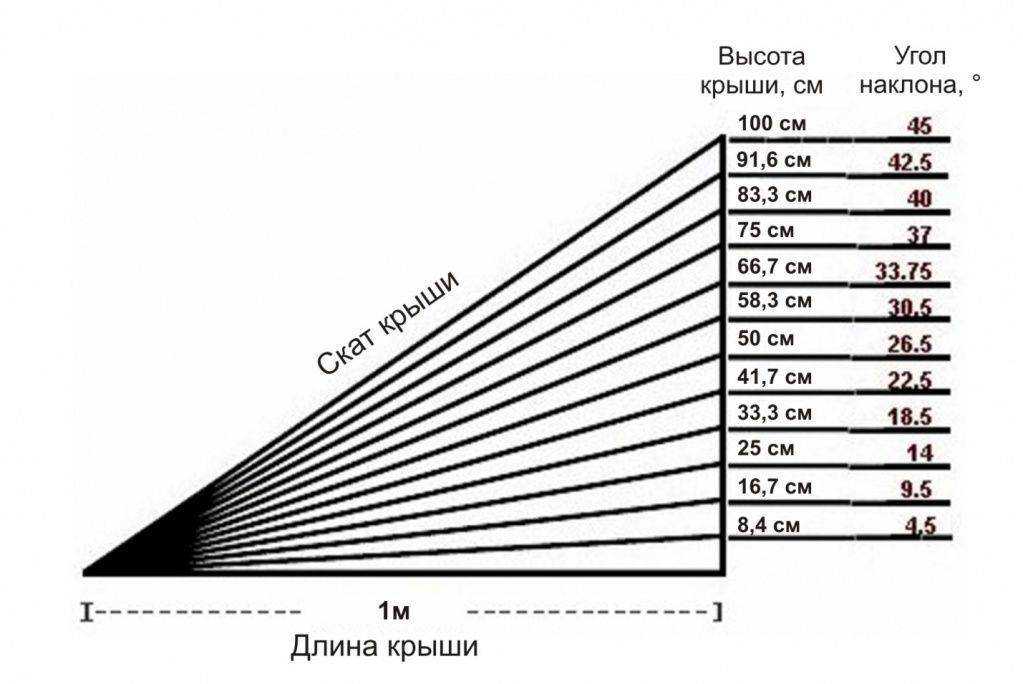
Каждый тип конструкции крыши имеет свои преимущества и недостатки. Некоторые из них требуют усиленной гидроизоляции, некоторые менее сложные в монтаже. Все это желательно учесть при подборе материалов, которые будут использованы в работе. Как правило, изготовители дают детальную информацию по поводу рекомендуемого уклона кровли. Например, на пологих крышах обычно задействуют рулонные материалы, а при крутизне в 15 градусов штучные изделия будут недопустимы. Более подробные сведения по этому вопросу можно найти в таблице, которая наводится ниже.
Некоторые из них требуют усиленной гидроизоляции, некоторые менее сложные в монтаже. Все это желательно учесть при подборе материалов, которые будут использованы в работе. Как правило, изготовители дают детальную информацию по поводу рекомендуемого уклона кровли. Например, на пологих крышах обычно задействуют рулонные материалы, а при крутизне в 15 градусов штучные изделия будут недопустимы. Более подробные сведения по этому вопросу можно найти в таблице, которая наводится ниже.
Расчет высоты крыши предусматривает прямую связь с размером полезной площади пространства под скатами. Чем она выше, тем просторнее будет полезная площадь внутри дома.
Изменение полезной площади в зависимости от высоты кровли
Поскольку показатель полезной высоты мансардного помещения обычно находится на уровне 2, 5 — 3 м, то и поднятие кровли с учетом используемого материала выше 5 метров считается невыгодным.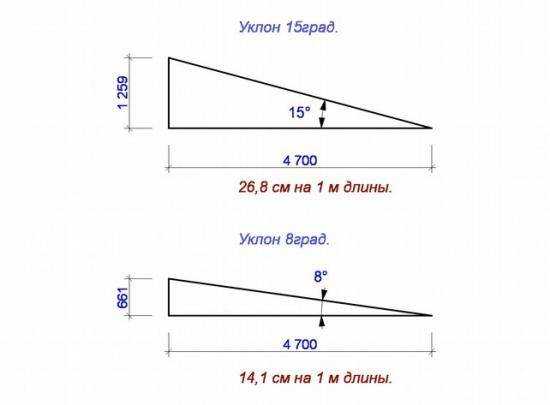 Если принимать во внимание эти данные, то величина в 25 градусов для зданий с одно- либо двухскатной крышей можно считать самой оптимальной. При необходимости возведения кровли мансардного типа ее часть вверху может допускать уклон в 10 — 20 градусов, а внизу – 50 — 80. При этом размещение самого пространства под крышей предусматривает большую вариативность, которая зависит от того, какая система кровли будет применена.
Если принимать во внимание эти данные, то величина в 25 градусов для зданий с одно- либо двухскатной крышей можно считать самой оптимальной. При необходимости возведения кровли мансардного типа ее часть вверху может допускать уклон в 10 — 20 градусов, а внизу – 50 — 80. При этом размещение самого пространства под крышей предусматривает большую вариативность, которая зависит от того, какая система кровли будет применена.
Из всего вышесказанного можно сделать вывод, что для большей части нашей страны наиболее подходящим будет считаться уклон кровли в пределах 25 — 35 градусов. Такая конструкция не даст снегу и дождю задерживаться на поверхности, и прекрасно выдержит сильные ветра. А правильно разработанный проект будет гарантировать большой объем площади мансардного помещения.
Заказывайте только у нас — самые качественные кровельные материалы: Сланцевая кровля, Модульная металлочерепица, Фальцевая кровля, Металлопрофиль (профнастил), Битумная черепица, Композитная черепица, Натуральная черепица, Цементно-песчаная черепица
Все виды монтажных работ от лучших специалистов: Монтаж металлочерепицы, Монтаж металлопрофиля, Монтаж модульной металлочерепицы, Монтаж натуральной черепицы, Монтаж фальцевой кровли, Монтаж битумной черепицы, Монтаж композитной черепицы, Монтаж цементно-песчаной черепицы, Монтаж сланцевой кровли
Как рассчитать угол наклона крыши — минимальный и оптимальный
- Что нужно учитывать при выборе угла наклона
- Зависимость уклона от используемого кровельного материала
- Как рассчитать угол наклона дома
Как рассчитать угол наклона крыши — важный вопрос, который встает при расчете стропильной системы и при выборе кровельного материала.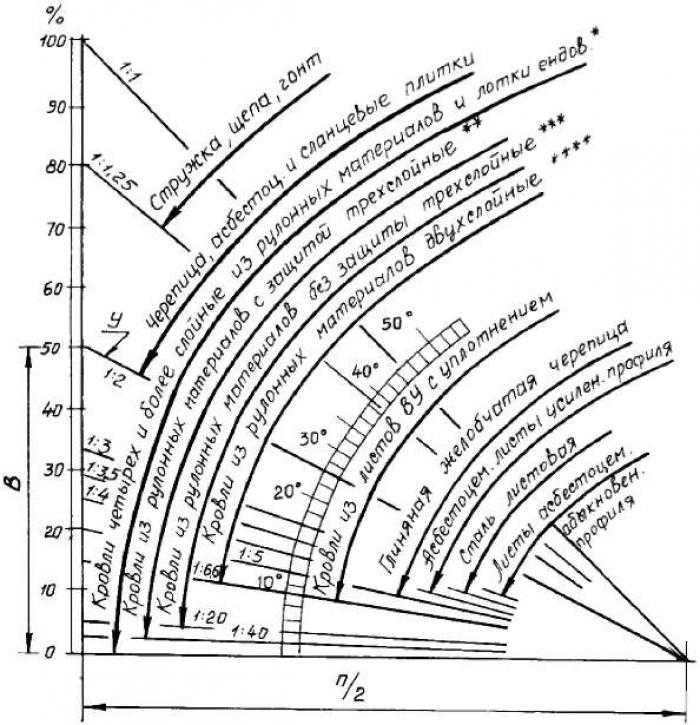 Если правильно вычислить угол наклона крыши, он обеспечит надежность и функциональность всей конструкции, а допущенные ошибки могут привести к различным неблагоприятным последствиям: протечки и застаивание воды при слишком малом наклоне или опрокидывание из-за ветра при слишком большом.
Если правильно вычислить угол наклона крыши, он обеспечит надежность и функциональность всей конструкции, а допущенные ошибки могут привести к различным неблагоприятным последствиям: протечки и застаивание воды при слишком малом наклоне или опрокидывание из-за ветра при слишком большом.
Чтобы подобных неприятностей не произошло, давайте разберемся, как рассчитать угол наклона крыши в градусах.
Что нужно учитывать при выборе угла наклона
Угол наклона крыши напрямую влияет на эксплуатационные параметры конструкции. Всего выделяют 4 типа кровельных конструкций:
- плоские — уклон меньше 10°;
- пологие — уклон до 30°;
- скатные — уклон до 45°;
- крутые — уклон до 60°.
Чтобы выбрать угол наклона правильно, необходимо учитывать целый ряд важных параметров.
Ветровая нагрузка
В процессе эксплуатации дома на крышу сильно влияют ветры, особенно в регионах, где ветровые нагрузки могут достигать очень высоких значений.
В таких областях оптимальными считаются кровли с углом наклона 25-30°. Если выбрать другой вариант, в процессе эксплуатации дома возможны неприятные сюрпризы:
- Если выбрать крышу с уклоном более 30°, стропильная система будет испытывать экстремальные нагрузки, способные в итоге привести к опрокидыванию конструкции.
- При выборе уклона меньше 25° ветровые нагрузки будут преимущественно воздействовать на фасад и фундамент дома, что также может привести к различным деформациям.
Чтобы выбрать оптимальный наклон нужно ориентироваться не только на величину ветровой нагрузки, необходимо одновременно учитывать и другие факторы. Например, направленность ветра, наличие дополнительных препятствий в виде зданий или иных барьеров, общую высоту здания.
Нагрузка снеговая
Не меньшее значение при выборе угла наклона имеет и среднее количество осадков в холодные месяцы. Если в регионе выпадает много снега каждую зиму, то выбирать необходимо крутую крышу, с которой снежный покров будет своевременно сходить, не накапливаясь и не создавая излишней нагрузки на здание.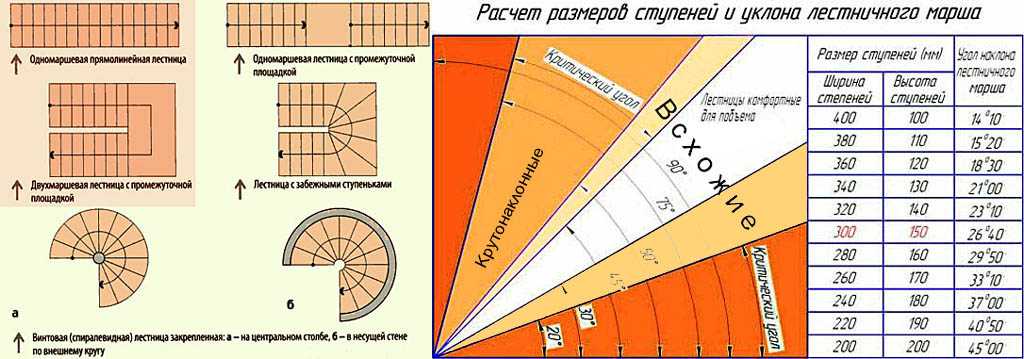
Пологие кровли подходят для домов только в тех регионах, где в зимнее время не выпадает слишком большое количество снега.
Зависимость уклона от используемого кровельного материала
При строительстве частных домов рекомендуется возводить крыши с углом наклона до 90°, но это больше в теории. На практике крайне редко встречаются стропильные системы с уклоном более 50°. Острые крыши преимущественно создаются в декоративных целях — при строительстве различных башен.
Делая расчет угла наклона крыши, необходимо учитывать, что производители облицовочных материалов далеко не всегда указывают необходимые параметры и требования к стропильной системе в градусах, иногда они используют процентное выражение.
Согласно действующим строительным нормативам 100% соответствует углу в 45°, а 1° соответствует 1,7%. Располагая этими данными, без труда можно перевести один показатель в другой.
Минимальный
В техдокументации на все без исключения кровельные материалы указывается допустимый наклон. При этом у разных покрытий данная характеристика индивидуальна:
При этом у разных покрытий данная характеристика индивидуальна:
- гибкая или мягкая черепица: от 12°, покрытие также требует создания надежной сплошной обрешетки;
- металлочерепица: от 14°, это минимальный угол наклона крыши для металлочерепицы, однако на практике материал рекомендуется использовать на кровлях с углом от 35°, так как на пологих покрытиях из металлочерепицы могут скапливаться большие снеговые массы зимой;
- профнастил: от 12°, при монтаже на основания с углом до 15° материал требует двухволновый нахлест листов;
- композитная черепица: от 15° и при условии монтажа на редкую обрешетку;
- фальцевая кровля: от 11°;
- керамочерепица: от 22°, материал требует устройства усиленной крыши, так как характеризуются большой массой.
Независимо от кровельного материала нужно помнить, что чем меньшим будет уклон, тем большие снеговые нагрузки будет испытывать стропильная система и все здание.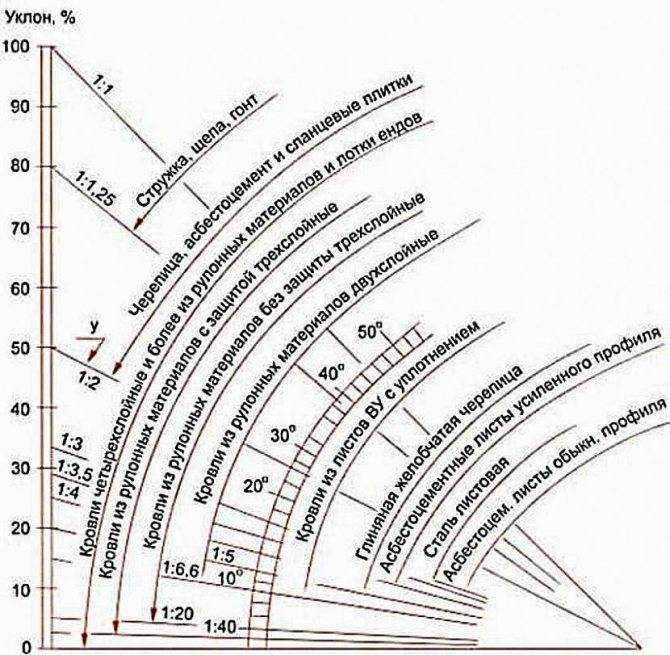
Оптимальный наклон
Чтобы разобраться, какой должен быть угол наклона крыши, необходимо также рассмотреть оптимальные характеристики данного параметра для объектов, эксплуатируемых в разных условиях.
Если нужно вычислить угол наклона крыши исключительно из соображений экономии, очевидно, что лучшим является минимальный, так как таким стропильным системам требуется меньше всего строительных материалов. Однако нельзя ориентироваться только на экономию при строительстве кровли, так как от нее будет зависеть удобство и безопасность эксплуатации строения в целом.
Оптимальные параметры уклона для регионов с различными условиями:
- Регионы с частыми осадками. Если в вашем населенном пункте дожди и снег случаются чаще, чем хотелось бы, выбирать рекомендуется уклон в диапазоне 45-60°. Эти рекомендации даются, так как с крутых поверхностей дождевая и талая вода, а также снег будут сходить максимально быстро — до того, как осадки смогут создать большую нагрузку или навредить строительным конструкциям здания.

- Регионы с сильными ветровыми нагрузками. Для таких населенных пунктов оптимальными называются значения уклона от 15 до 20°. Эти конструкции характеризуются минимальной парусностью, поэтому полностью исключается вероятность разрушения конструкций из-за сильных порывов ветра.
- Ветряные регионы с обильными осадками. Оптимален угол от 20 до 45°.
Как рассчитать угол наклона крыши
Вычислить угол наклона крыши в градусах можно самостоятельно в домашних условиях, не обращаясь за помощью к профессионалам. Достаточно использовать простую формулу.
Односкатная
В данной ситуации расчет должен производиться по формуле:
I = (H/L)×100
В ней:
- I — угол наклона;
- H — высота крыши;
- L — ширина объекта.
Если провести расчет для дома со стропильной системой высотой 3 м и шириной 10 м, мы получим:
I = (3/10) ×100
I = 30%.
Теперь, чтобы определить угол наклона в градусах, необходимо обратиться к таблице соответствия градуса угла процентному соотношению. Мы получим величину около 17°.
Двускатная
Расчет угла наклона двускатной крыши производится по несколько другой формуле, а именно:
I = (H/(0,5L))×100
Здесь 0,5 — это поправочный коэффициент, призванный вычислить разницу между двумя катетами треугольной конструкции.
Если мы возьмем за основу те же характеристики: 3 м — высота в месте конька и 10 м — ширина, то получим следующее значение:
I = (3/(0,5×10)×100 = 60%.
Снова воспользуемся конвертером величин и получим угол наклона примерно 31°.
Выводы
Вычислить угол наклона крыши возможно самостоятельно, если учитывать все соответствующие факторы, включая климатические условия в регионе и характеристики здания.
Однако специалисты советуют не упускать возможности предварительно проконсультироваться с профессионалами и заказывать у них услуги проектирования и измерения, чтобы гарантировать высокую надежность, функциональность и долговечность кровельной системы.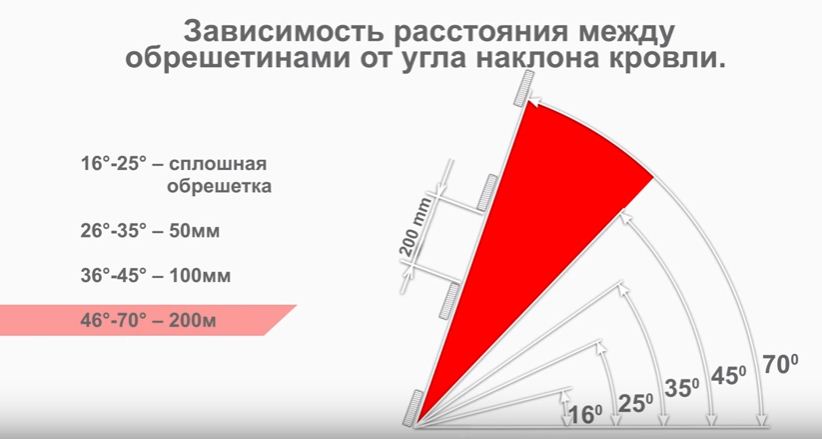
Заказать строительство дома вы можете в компании Render House. Типовые варианты представлены на сайте, также мы занимаемся возведением коттеджей по индивидуальным проектам.
Угол наклона и наклон линии
Пусть прямая l пересекает ось x в точке A. Угол между положительной осью x и линией l, измеренный в направлении против часовой стрелки, называется углом наклона прямая л.
На приведенном выше рисунке, если θ – это угол прямой линии l, то мы имеем следующие важные моменты.
(i) 0° ≤ θ ≤ 180°
(ii) Для горизонтальных линий θ = 0° или 180°, а для вертикальных линий θ = 90°
(iii) Если прямая линия первоначально лежит вдоль оси х и начинает вращаться вокруг неподвижной точки А на оси х против часовой стрелки и, наконец, совпадает с осью х, то угол наклона прямой линии в начальном положении равно 0°, а линии в конечном положении равно 0°.
(iv) Линии, перпендикулярные оси x, называются вертикальными линиями.
(v) Линии, перпендикулярные оси Y, называются горизонтальными линиями.
(vi) Другие линии, которые не перпендикулярны ни оси x, ни оси y, называются наклонными линиями.
Угол наклона и наклон линии – приложение
Основное применение угла наклона прямой линии – определение уклона.
Если θ – угол наклона прямой линии l, то tanθ называется наклоном градиента линии и обозначается буквой «m».
Следовательно, наклон прямой равен
м = tan θ
для 0° ≤ θ ≤ 180°
Найдем наклон прямой по приведенной выше формуле
(i) Для горизонтальных линий угол наклона равен 0° или 180°.
То есть
θ = 0° или 180°
Следовательно, наклон прямой линии равен
м = tan0° или tan 180° = 0
(ii) Для вертикальных линий угол наклона равен 90°.
То есть
θ = 90°
Следовательно, наклон прямой равен
м = tan90° = Не определено
(iii) Для наклонных линий, если θ имеет острую форму, наклон положительный. Если же θ тупой, то наклон отрицательный.
Если же θ тупой, то наклон отрицательный.
Наклон линии — положительный или отрицательный, нулевой или неопределенный
Когда мы смотрим на прямую линию визуально, мы можем легко определить знак наклона.
Чтобы узнать знак наклона прямой, всегда нужно смотреть на прямую слева направо.
Это иллюстрируют приведенные ниже рисунки.
Решенные задачи
Задача 1 :
Найдите угол наклона прямой, наклон которой равен 1/√3.
Решение :
Пусть θ — угол наклона линии.
Тогда наклон линии составляет
M = TANθ
Дано: наклон = 1/√3
Затем,
1/√3 = tanθ
θ = 30 °
Итак, угол угла наклон 30°.
Задача 2 :
Если угол наклона прямой равен 45°, найдите ее наклон.
Решение :
Пусть θ — угол наклона линии.
Тогда, наклон линии,
M = TANθ
Дано: θ = 45 °
Затем,
M = TAN 45 °
M = 1
Итак, склон — 1.
Задача 3 :
Если угол наклона прямой равен 30°, найдите ее наклон.
Решение :
Пусть θ — угол наклона линии.
Затем, наклон линии,
м = tanθ
Дано: θ = 30°
Тогда
м = tan30°
м = 1/√3
Итак, уклон равен √3
.
Задача 4 :
Найдите угол наклона прямой, наклон которой равен √3.
Решение :
Пусть θ — угол наклона линии.
Затем, наклон линии,
м = tanθ
Дано: Уклон = √3
Тогда,
√3 = tanθ
θ = 60°
Итак, угол наклона равен 60°.
Задача 5 :
Найдите угол наклона прямой, уравнение которой y = x + 32.
Решение :
Пусть θ — угол наклона линии.
Данное уравнение находится в форме пересечения наклона.
То есть
y = mx + b
Сравнивая
y = x + 32
и
y = mx + b,
получаем наклон 1. m = 9.0004
Мы знаем, что наклон линии равен
м = tanθ
Тогда
1 = tanθ
θ = 45°
Итак, угол наклона равен 45°.
Пожалуйста, отправьте ваш отзыв на [email protected]
Мы всегда ценим ваши отзывы.
©Все права защищены. onlinemath5all.com
4.3 Наклон линии | Аналитическая геометрия
4.3 Наклон линии (EMBGD)
На диаграмме показано, что прямая образует угол \(\theta\) с положительной осью \(x\). Это называется угол наклона прямой.
Мы замечаем, что если градиент изменяется, то значение \(\theta\) также изменяется, поэтому угол наклон линии связан с ее градиентом. Мы знаем, что градиент – это отношение изменения \(y\)-направление на изменение \(x\)-направления:
\[m=\frac{\Delta y}{\Delta x}\]Из тригонометрии мы знаем, что функция тангенса определяется как отношение:
\[\tan \theta = \frac{\text{противоположная сторона}}{\text{прилегающая сторона}}\]
А из схемы мы видим, что
\начать{выровнять*} \tan \theta &= \dfrac{\Delta y}{\Delta x} \\ \поэтому m &= \tan \theta \qquad \text{ for } \text{0}\text{°} \leq \theta < \текст{180}\текст{°} \конец{выравнивание*}
Следовательно, градиент прямой линии равен тангенсу угла, образованного между прямой и
положительное направление оси \(x\).
Вертикальные линии
- \(\тета = \текст{90}\текст{°}\)
- Градиент не определен, поскольку значения \(x\) не изменились (\(\Delta x = 0\)).
- Следовательно, \(\tan \theta\) также не определено (график \(\tan \theta\) имеет асимптоту в \(\theta = \text{90}\text{°}\)).
Горизонтальные линии
- \(\тета = \текст{0}\текст{°}\)
- Градиент равен \(\text{0}\), поскольку значения \(y\) не изменяются (\(\Delta y = 0\)).
- Следовательно, \(\tan \theta\) также равно \(\text{0}\) (график \(\tan \theta\) проходит через происхождение \((\text{0}\text{°};0))\).
Линии с отрицательным уклоном
Если прямая имеет отрицательный наклон (\(m < 0\), \(\tan \theta < 0\)), то угол, образованный
между прямой и положительным направлением оси \(х\) тупая.
Из диаграммы CAST в тригонометрии мы знаем, что функция тангенса отрицательна во втором и четвертом квадрант. Если мы вычисляем угол наклона для линии с отрицательным градиентом, мы должны добавить \(\text{180}\text{°}\), чтобы изменить отрицательный угол в четвертом квадранте на тупой угол в второй квадрант:
Если нам дана прямая с градиентом \(m = -\text{0,7}\), то мы можем определить угол наклон с помощью калькулятора: 9{-1}(-\текст{0,7}) \\ &= -\текст{35,0}\текст{°} \конец{выравнивание*}
Этот отрицательный угол лежит в четвертом квадранте. Мы должны добавить \(\text{180}\)\(\text{°}\) чтобы получить тупой угол во втором квадранте:
\начать{выровнять*} \тета &= -\текст{35,0}\текст{°} + \текст{180}\текст{°} \\ &= \текст{145}\текст{°} \конец{выравнивание*}
И мы всегда можем использовать наш калькулятор, чтобы проверить, что тупой угол \(\theta = \text{145}\text{°}\)
дает градиент \(m = -\text{0,7}\).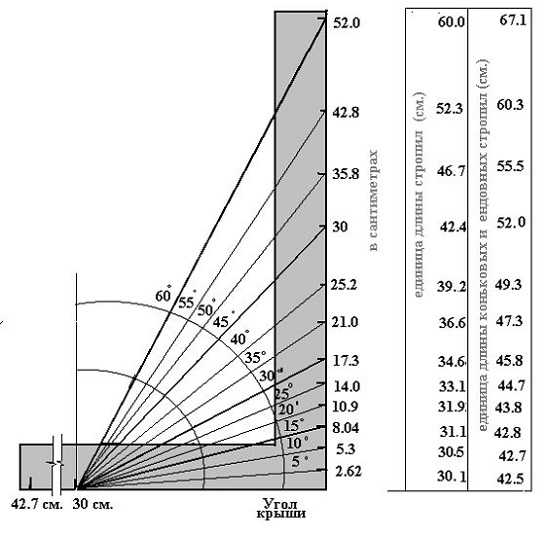
Угол наклона
Учебник Упражнение 4.5
\(\text{60}\text{°}\)
\begin{align*} м &= \загар \тета\\ &= \tan \text{60}\text{°} \\ \поэтому m &= \text{1,7} \end{align*}
\(\text{135}\text{°}\)
\begin{align*} м &= \загар \тета\\ &= \tan \text{135}\text{°} \\ \поэтому m &= -\text{1} \end{выравнивание*}
\(\text{0}\text{°}\)
\begin{align*} м &= \загар \тета\\ &= \tan \text{0}\text{°} \\ \поэтому m &= \text{0} \end{align*}
\(\text{54}\text{°}\)
\begin{align*} м &= \загар \тета\\ &= \загар \текст{54}\текст{°} \\ \поэтому m &= \text{1,4} \end{выравнивание*}
\(\text{90}\text{°}\)
\begin{align*} м &= \загар \тета\\ &= \загар \текст{90}\текст{°} \\ \поэтому m & \text{ не определено} \end{align*}
\(\text{45}\text{°}\)
\begin{align*} м &= \загар \тета\\ &= \tan \text{45}\text{°} \\ \поэтому m &= \text{1} \end{выравнивание*}
\(\text{140}\text{°}\)
\begin{align*} м &= \загар \тета\\ &= \tan \text{140}\text{°} \\ \поэтому m &= -\text{0,8} \end{align*}
\(\text{180}\text{°}\)
\begin{align*} м &= \загар \тета\\ &= \tan \text{180}\text{°} \\ \поэтому m &= \text{0} \end{выравнивание*} 9{-1} \влево( \text{0,75} \вправо) \\ \поэтому \тета &= \text{36,8}\text{°} \end{align*}
\(2y — x = 6\)
\begin{align*} 2у — х&=6\ 2у &= х + 6 \\ y &= \frac{1}{2}x + 3 \\ \загар \тета &= м \\ &= \фракция{1}{2} \\ \theta &= \tan^{-1} \left( \text{0,5} \right) \\ \поэтому \тета &= \текст{26,6}\текст{°} \end{выравнивание*} 9{-1} \влево( \текст{1} \вправо) \\ \поэтому \тета &= \text{45}\text{°} \end{align*}
\(y=4\)
Горизонтальная линия
\(x = 3y + \frac{1}{2}\)
\begin{align*} х &= 3y + \frac{1}{2} \\ x — \frac{1}{2} &= 3y \\ \frac{1}{3}x — \frac{1}{6} &= y \\ \поэтому m &= \frac{1}{3} \\ \theta &= \tan^{-1} \left( \frac{1}{3} \right) \\ \поэтому \тета &= \text{18,4}\text{°} \end{выравнивание*} 9{-1} \влево( \текст{0,577} \вправо) \\ \поэтому \тета &= \text{30}\text{°} \конец{выравнивание*}
Рабочий пример 8: Наклон прямой линии
Определить угол наклона (с точностью до \(\text{1}\) десятичного знака) прямой линии
проходящей через точки \((2;1)\) и \((-3;-9)\). {-1}2\\
&= \текст{63,4}\текст{°}
\end{выравнивание*}
{-1}2\\
&= \текст{63,4}\текст{°}
\end{выравнивание*}
Важно: убедитесь, что ваш калькулятор находится в режиме DEG (градусы).
Напишите окончательный ответ
Угол наклона прямой равен \(\text{63,4}\)\(\text{°}\).
temp textРабочий пример 9: Наклон прямой линии
Определите уравнение прямой, проходящей через точку \((3;1)\) и с углом наклон \(\text{135}\text{°}\).
Используйте угол наклона для определения градиента линии
\begin{align*} м &= \загар \тета\\ &= \tan \text{135}\text{°} \\ \поэтому m &= -1 \конец{выравнивание*}
Запишите уравнение прямой линии в форме точки градиента. x — x_1)\]
Подставить заданную точку \((3;1)\)
\begin{выравнивание*} у — 1 & = -(х — 3) \\ у&=-х+3+1\ &= -х + 4 \конец{выравнивание*}
Напишите окончательный ответ
Уравнение прямой линии \(y = -x + 4\).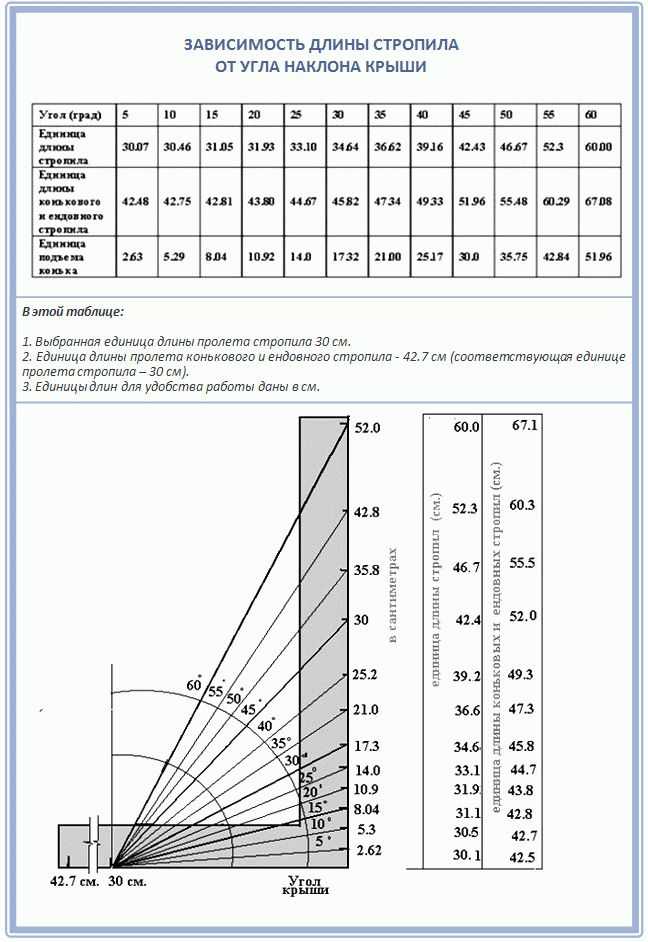
Рабочий пример 10: Наклон прямой линии
Определить острый угол (с точностью до \(\text{1}\) десятичного знака) между прямой, проходящей через точки \(M(-1;1\frac{3}{4})\) и \(N(4;3)\) и прямая \(y = — \frac{3}{2}x + 4\).
Нарисуйте эскиз
Проведите прямую через точки \(M(-1;1\frac{3}{4})\) и \(N(4;3)\) и прямую \(y = — \ дробь{3}{2}x + 4\) в подходящей системе координат. Обозначьте \(\alpha\) и \(\beta\) углы наклона две линии. Обозначьте \(\theta\) острый угол между двумя прямыми.
Обратите внимание, что \(\alpha\) и \(\theta\) — острые углы, а \(\beta\) — тупой угол.
\[\begin{массив}{rll}
\hat{B}_1 &= \text{180}\text{°} — \beta & (\angle \text{на строке}) \\
\text{and} \theta &= \alpha + \hat{B}_1 \quad & (\text{ext.} \angle \text{ of } \triangle =
\text{ сумма внутр. опп}) \\
\поэтому \тета &= \альфа + (\текст{180}\текст{°} — \бета) \\
&= \text{180}\text{°} + \alpha — \beta
\конец{массив}\]
9{-1} \left(-\frac{3}{2}\right) &= -\text{56,3}\text{°}
\конец{выравнивание*}
опп}) \\
\поэтому \тета &= \альфа + (\текст{180}\текст{°} — \бета) \\
&= \text{180}\text{°} + \alpha — \beta
\конец{массив}\]
9{-1} \left(-\frac{3}{2}\right) &= -\text{56,3}\text{°}
\конец{выравнивание*}
Этот отрицательный угол лежит в четвертом квадранте. Мы знаем, что угол наклона \(\beta\) равен тупой угол лежит во второй четверти, поэтому
\начать{выравнивать*} \beta &= -\text{56,3}\text{°} + \text{180}\text{°}\\ &= \текст{123,7}\текст{°} \конец{выравнивание*}
Определить градиент и угол наклона линии через \(M\) и \(N\)
Определение градиента \начать{выравнивать*} m & = \frac{y_2 — y_1}{x_2 — x_1} \\ & = \dfrac{3 — \frac{7}{4}}{4-(-1)} \\ & = \dfrac{\frac{5}{4}}{5} \\ &= \фракция{1}{4} \end{align*}
Определить угол наклона \начать{выравнивать*} \загар \альфа & = м\\ & = \фракция{1}{4} \\ \поэтому \alpha & = \tan^{-1} \left( \frac{1}{4} \right) \\ &= \текст{14,0}\текст{°} \end{выравнивание*}
Напишите окончательный ответ
\begin{align*} \тета & = \текст{180}\текст{°} + \альфа — \бета\\ & = \text{180}\text{°} + \text{14,0}\text{°} — \text{123,7}\text{°} \\ & = \текст{70,3}\текст{°} \end{align*}
Острый угол между двумя прямыми равен \(\text{70,3}\)\(\text{°}\).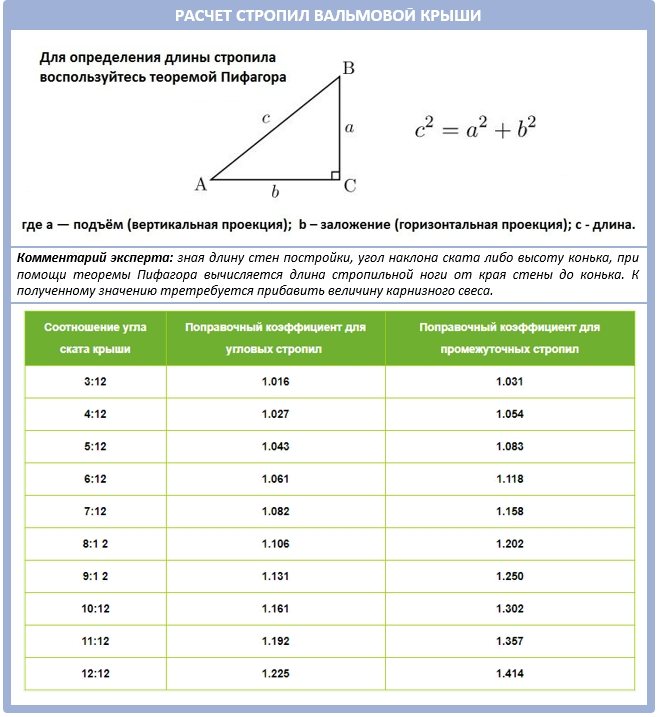 {-1} \left( -\text{2} \right) \\
&= -\текст{63,4}\текст{°} \\
\поэтому \theta &= \text{180}\text{°} — \text{63,4}\text{°} \\
\поэтому \тета &= \text{80}\text{°}
\end{выравнивание*} 9{-1} \влево(-\frac{9}{2} \вправо) \\
&= -\текст{77,5}\текст{°} \\
\поэтому \тета &= \text{180}\text{°} — \text{77,5}\text{°} \\
\поэтому \тета &= \текст{102,5}\текст{°}
\end{align*}
{-1} \left( -\text{2} \right) \\
&= -\текст{63,4}\текст{°} \\
\поэтому \theta &= \text{180}\text{°} — \text{63,4}\text{°} \\
\поэтому \тета &= \text{80}\text{°}
\end{выравнивание*} 9{-1} \влево(-\frac{9}{2} \вправо) \\
&= -\текст{77,5}\текст{°} \\
\поэтому \тета &= \text{180}\text{°} — \text{77,5}\text{°} \\
\поэтому \тета &= \текст{102,5}\текст{°}
\end{align*}
линия, проходящая через \((-1;-6)\) и \((-\frac{1}{2};-\frac{11}{2})\)
\begin{выравнивание*} m &= \frac{y_2 -y_1}{x_2 — x_1} \\ &= \frac{-\frac{11}{2}+ 6}{-\frac{1}{2}+1} \\ &= \ гидроразрыва {\ гидроразрыва {1} {2}} {\ гидроразрыва {1} {2}} \\ \поэтому m &= 1 \\ \theta &= \tan^{-1} \left( 1 \right) \\ \поэтому \тета &= \text{45}\text{°} \end{выравнивание*} 9{-1} \влево(-\frac{1}{3} \вправо) \\ \поэтому \тета &= -\текст{18,4}\текст{°} \\ \поэтому \тета &= \text{180}\text{°} — \text{18,4}\text{°} \\ \поэтому \тета &= \текст{161,6}\текст{°} \end{align*}
Градиент undefined
Определить острый угол между линией, проходящей через точки \(A(-2;\frac{1}{5})\)
и \(B(0;1)\) и прямой, проходящей через точки \(C(1;0)\) и \(D(-2;6)\). {-1} \left(-2 \right) \\
\поэтому \alpha &= -\text{63,4}\text{°} \\
\поэтому \alpha &= \text{180}\text{°} — \text{63,4}\text{°} \\
\поэтому \alpha &= \text{116,6}\text{°} \\
\text{And } \theta &= \beta + (\text{180}\text{°} — \alpha) \quad (\text{ext. } \angle
\треугольник)\\
\поэтому \theta &= \text{21,8}\text{°} + (\text{180}\text{°} —
\text{116,6}\text{°} ) \\
&= \текст{85,2}\текст{°}
\конец{выравнивание*}
{-1} \left(-2 \right) \\
\поэтому \alpha &= -\text{63,4}\text{°} \\
\поэтому \alpha &= \text{180}\text{°} — \text{63,4}\text{°} \\
\поэтому \alpha &= \text{116,6}\text{°} \\
\text{And } \theta &= \beta + (\text{180}\text{°} — \alpha) \quad (\text{ext. } \angle
\треугольник)\\
\поэтому \theta &= \text{21,8}\text{°} + (\text{180}\text{°} —
\text{116,6}\text{°} ) \\
&= \текст{85,2}\текст{°}
\конец{выравнивание*}
Определить угол между прямой \(y + x = 3\) и прямой \(x = y + \frac{1}{2}\).
Пусть угол наклона линии \(y + x = 3\) равен \(\alpha\), а угол наклона наклон линии \(x = y + \frac{1}{2}\) равен \(\beta\). Пусть угол между двумя строки будут \(\тета\):
\начать{выравнивать*}
у &= — х + 3 \\
\поэтому m &= — 1 \\
\alpha &= \tan^{-1} \left(-1\right) \\
\поэтому \alpha &= -\text{45}\text{°} \\
\поэтому \alpha &= \text{180}\text{°} — \text{45}\text{°} \\
\поэтому \alpha &= \text{135}\text{°} \\
х &= у + \ гидроразрыва {1} {2} \\
х — \фракция{1}{2} &= у \\
\поэтому m &= 1 \\
\beta &= \tan^{-1} \left(1 \right) \\
\поэтому \бета &= \text{45}\text{°} \\
\text{And } \theta &= \beta + (\text{180}\text{°} — \alpha) \quad (\text{ext.