Рассчитать угол наклона: Онлайн калькулятор расчета угла наклона и стропильной системы двухскатной крыши
Калькулятор угла уклона пандуса
Калькулятор для пандуса
В соответствии с СП 59.13330.2020 «Доступность зданий и сооружений для маломобильных групп населения. Актуализированная редакция СНиП 35-01-2001» максимальный перепад высот для установки пандуса не должен превышать 6,0 м, а уклон одного марша пандуса — не более 1:12,5 (80‰). В стеснённых условиях допускается увеличение уклона до 1:10 (100‰).
| Соотношение | Проценты (%) | Промилле (‰) | Градусы (°) |
| 1:33 | 3% | 30‰ | 1,7° |
| 1:20 | 5% | 50‰ | 2,9° |
| 1:12,5 | 8% | 80‰ | 4,8° |
| 1:10 | 10% | 100‰ | 5,7° |
Введите параметры будущего пандуса, исходя из данных объекта. Параметры необходимо вводить в миллиметрах. Нажмите кнопку «Рассчитать». Соответственно, длина наклонной площадки рассчитывается в миллиметрах. Также Вы получите рекомендации относительно параметров, которые у Вас получились.
Параметры необходимо вводить в миллиметрах. Нажмите кнопку «Рассчитать». Соответственно, длина наклонной площадки рассчитывается в миллиметрах. Также Вы получите рекомендации относительно параметров, которые у Вас получились.
Основным действующим нормативным документом для определения уклона пандуса и его длины в РФ является СП 59.13330.2020 «Доступность зданий и сооружений для маломобильных групп населения»
| Продольный уклон марша пандуса | Длина одного марша пандуса, м,не более | Суммарная длина наклонных поверхностей пандуса, м, не более |
| От 30 до 40 ‰ (от 1:33 до 1:25) (включительно) | 15 | 110 |
| От 40 до 50 ‰ (от 1:25 до 1:20) (включительно) | 12 | |
| От 50 до 60 ‰ (от 1:20 до 1:16,7) (включительно) | 9 | |
| От 61 до 80 ‰ (от 1:16 до 1:12,5) (включительно) | 6 | 36 |
П р и м е ч а н и я
| ||
Пандус – это устройство для адаптации социально-значимых объектов и открытых пространств: вход в здание, сопровождение лестницы, пешеходный переход и т.д. Пандус необходим, чтобы сделать жизнь маломобильных групп населения комфортнее: пожилые люди, с коляской или тяжелой поклажей, с костылями после травм, инвалиды-колясочники.
Активное развитие и продвижение федеральной программы «Доступная среда» сподвигло многие организации установить пандусы на входной группе. Однако зачастую это делается либо для галочки, либо организациями, не владеющими навыками и знаниями существующих нормативов. Поэтому не всегда готовое изделие соответствует государственным стандартам. Как результат — недоступность для людей с ограничениями.
Нормативы для пандусов 2023
По нормативам СП 59. 13330.2020 (с учетом вступивших в силу изменений 01 июля 2021 года) пандус должен иметь следующие характеристики:
13330.2020 (с учетом вступивших в силу изменений 01 июля 2021 года) пандус должен иметь следующие характеристики:
Список документации, рекомендуемой к ознакомлению:
- СНиП 35-01-2001 содержит предписания по адаптации жилых домов и социально-значимых объектов для маломобильных групп населения. А так же конкретные ограничения по установке и параметрам пандусов.
- ГОСТ Р 51261-2022 содержит технические требования к стационарным опорным устройствам.
- СП 30-102-99 содержит требования к входной площадке.
- СП 59.13330.2020 содержит предписания по доступности зданий и сооружений для маломобильных групп населения
Угол наклона пандуса не должен превышать уклон в отношении 1:20 (5%). В данном случае очень часто проценты путают с градусами. В результате чего подъем/спуск получается в разы выше. Угол наклона — это соотношение длины к высоте подъема.
Запомните При перепаде высоты от трех метров, вместо пандусов применяются подъемные устройства. В данном случае наличие пандуса будет бесполезным и недоступным для инвалида-колясочника.
В данном случае наличие пандуса будет бесполезным и недоступным для инвалида-колясочника.
Справка!
- При временном сооружении пандуса (ремонте или реконструкции здания). Если его высота не превышает 0,5 м, а промежуток между площадками не более 6 м, уклон может быть 8% или 1:12
- Если высота подъема не достигает 0,2 м, уклон допустим в пропорции 1:10 (10%).
- Длина непрерывного движения марша пандуса не должна превышать 9,0 м, далее необходимо организовывать разворотную площадку или площадку отдыха.
- Длина горизонтальной площадки прямого пандуса должна быть не менее 1,5 м.
- Пандусы должны иметь двухстороннее ограждение с поручнями на высоте 0,9 и 0,7 м.
- Поверхность пандуса должна быть нескользкой текстурой.
- Поверхность марша пандуса должна визуально контрастировать с горизонтальной поверхностью в начале и конце пандуса.

Поручни для пандуса
- В начале и конце поручни должны быть длиннее на 300 мм и иметь закруглённую форму.
- Верхний поручень расположен на высоте 900 мм.
- Расстояние между поручнями 900-1000 мм.
- Перила должны быть круглого сечения с диаметром от 30 до 50 мм.
- Начало и конец маркируются предупредительными полосами.
- Нижний поручень должен быть на высоте 700 мм.
- По продольным краям марша пандуса следует устанавливать бортики высотой не менее 0,05 м.
- Покрытие пандуса должно обладать противоскользящим эффектом.
- Минимальное расстояние от гладкой стены 45 мм, от неровной 60 мм.
- Поручни с внутренней стороны не должны прерываться.
- Поручни изготавливаются из металла и устанавливаются с обеих сторон наклонной площадки.
Если пандус изначально соответствует всем строительным параметрам, то его можно оснастить необходимыми дополнительными устройствами при их отсутствии:
- Опорными поручнями.

- Контрастной тактильной разметкой (для незрячих и слабовидящих людей). Разметкой следует обозначать сами поручни и подстилающую поверхность. С внутренней стороны поручней можно приклеить тактильные наклейки для обозначения начала и конца препятствия.
Если пандус изначально не соответствует конструкторским параметрам в соответствии со сводами правил, то его следует демонтировать, а на его месте организовать доступный пандус.
Вопросы по адаптации
Автопарковка для МГН
Адаптация тротуаров для незрячих
Адаптация лестниц для МГН
Адаптация входной группы
Адаптация холла в помещении
Адаптация санузела для незрячих
Адаптация лифтов для МГН
НАШЕ ПРЕИМУЩЕСТВО — ДОЛГОЛЕТНИЙ ОПЫТ и КАЧЕСТВО!
Расчет угла наклона пандуса
Расчет угла наклона пандусаБезбарьерная среда для
людей с ограничениями
Поддержать нас
+7 (915) 746-45-05
Оставить заявку на
паспортизацию объекта
Одна из самых распространённых ошибок при создании доступной среды это неверный уклон пандуса. К сожалению, исполнители, то есть подрядные строительные организации, которые разрабатывают проект и выполняют установку пандуса, не всегда компетентны в вопросе создания доступной среды и не знают норм и правил организации пандуса.
С помощью нашего калькулятора вы сможете проверить, соответствует ли угол наклона пандуса нормам доступности.
Инструкция:
Введите параметры пандуса: высоту — максимальную цифру, длину непрерывного марша пандуса. Параметры необходимо вводить в сантиметрах. Нажмите кнопку «рассчитать». Калькулятор выдаст результат рассчитанного угла уклона проверяемого пандуса в процентах (%).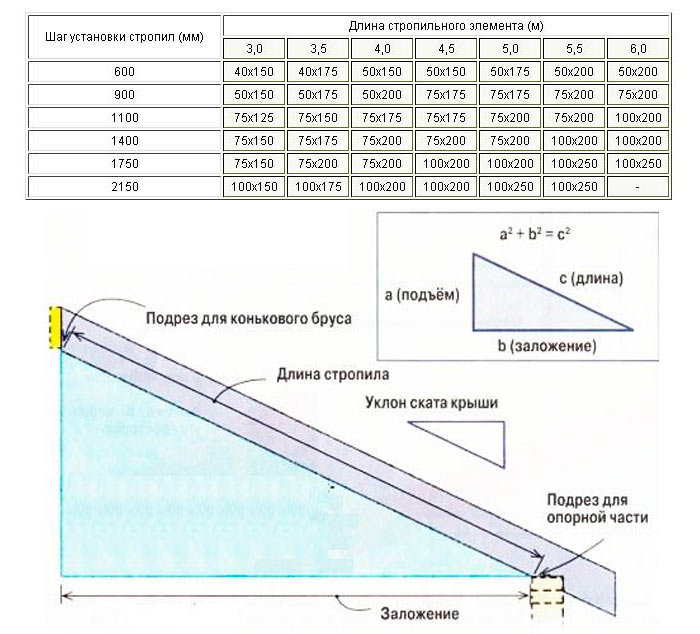 Так будут указаны рекомендации соответствует ли угол наклона проверяемого пандуса нормам доступности.
Так будут указаны рекомендации соответствует ли угол наклона проверяемого пандуса нормам доступности.
Основным действующим нормативным документом для определения уклона пандуса и его длины в РФ является СП 59.13330.2016 «Доступность зданий и сооружений для маломобильных групп населения».
Допустимые значения угла наклона пандуса. Адаптация входной группы для людей с инвалидностью
Максимальная высота одного подъема (марша) пандуса не должна превышать 0,45 м при уклоне не более 1:20 (5%).
При перепаде высот пола на путях движения 0,2 м и менее допускается увеличивать уклон пандуса до 1:10 = 10%
Внутри зданий и на временных сооружениях или объектах временной инфраструктуры допускается максимальный уклон пандуса 1:12 (8%) при условии, что подъем по вертикали между площадками не превышает 0,5 м. При проектировании реконструируемых, подлежащих капитальному ремонту и приспосабливаемых существующих зданий, и сооружений уклон пандуса принимается в интервале от 1:20 (5%) до 1:12 (8%).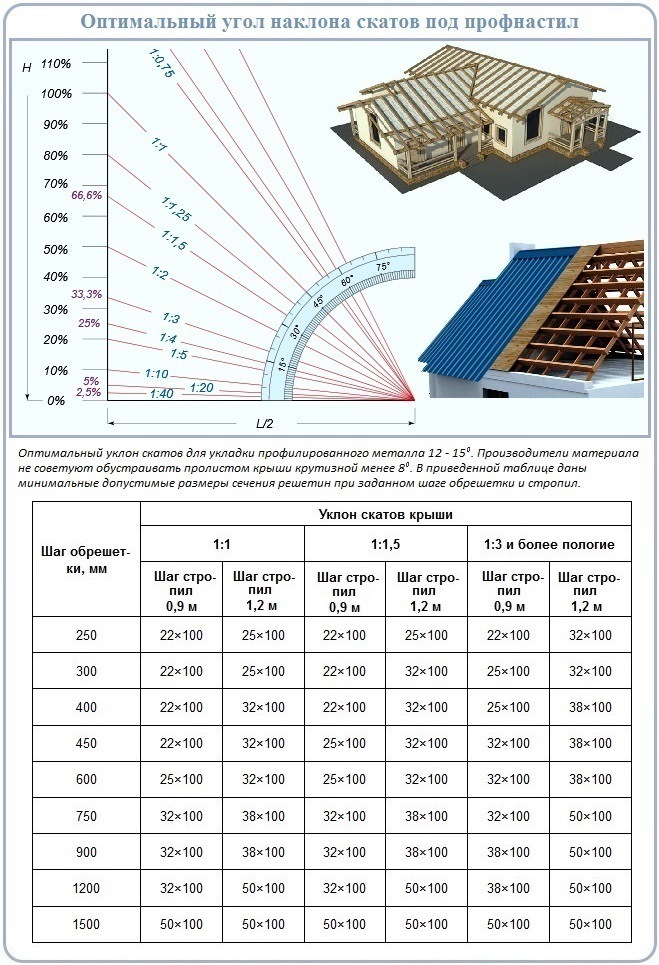
Пандусы при перепаде высот более 3,0 м следует заменять лифтами, подъемными платформами и т.п.
В соответствии с приказом Минстроя России №750/ приказ от 21 октября 2015 г. «Об утверждении изменений №1 к СП 59.13330.2016 «Доступность зданий и сооружений для маломобильных групп населения» «При проектировании реконструируемых, подлежащих капитальному ремонту и приспосабливаемых существующих зданий, и сооружений уклон пандуса принимается в интервале от 1:20 (5%) до 1:12 (8%)».
Что обозначают цифры:
1:20 = 5% т.е. при перепаде высот 1 м, длина пандуса должна быть 20 м, при высоте 0,5 м — 10 м.
1:12 = 8% — т.е. при перепаде высоты в 1 м, длина пандуса должна быть 12 м, при высоте 0,5 м — длина пандуса должна быть не менее 6 метров и т.д.
1:10 = 10% — т.е. при перепаде высот в 1 м, длина пандуса должна быть 10 м, при высоте 0,5 м — длина пандуса должна быть 5 м и т.д.
Я хочу принять участие в Исследовании
Принять участие как:
?ВолонтерИсследователь
Город:
Выберите городБлаговещенскАрхангельскАстраханьБелгородБрянскВладимирВолгоградВологдаВоронежИвановоИркутскКалининградКалугаКемеровоКировКостромаКурганКурскСанкт-ПетербургЛипецкМагаданМоскваМурманскНижний НовгородВеликий НовгородНовосибирскОмскОренбургОрёлПензаПсковРостов-на-ДонуРязаньСамараСаратовЮжно-СахалинскЕкатеринбургСмоленскТамбовТверьТомскТулаТюменьУльяновскЧелябинскЯрославль
Мероприятие:
Выберите мероприятиеПосещение общепитаОбщественный транспортПолучение гос. услугСоциальные услуги
услугСоциальные услуги
Группа инвалидности:
Выберите группу инвалидностиНет123
Телефон или e-mail:
Прикрепить файлы
Согласие на обработку персональных данных:
Условия участия в мероприятии
Контент временно отсутствует!
Я хочу принять участие в мероприятии
Группа инвалидности
Выберите группу инвалидностиНет123
Согласие на обработку персональных данных
Прикрепить файлы
Условия участия в мероприятии
Контент временно отсутствует!
Заявка на паспортизацию
Организация:
Город:
Выберите городБлаговещенскАрхангельскАстраханьБелгородБрянскВладимирВолгоградВологдаВоронежИвановоИркутскКалининградКалугаКемеровоКировКостромаКурганКурскСанкт-ПетербургЛипецкМагаданМоскваМурманскНижний НовгородВеликий НовгородНовосибирскОмскОренбургОрёлПензаПсковРостов-на-ДонуРязаньСамараСаратовЮжно-СахалинскЕкатеринбургСмоленскТамбовТверьТомскТулаТюменьУльяновскЧелябинскЯрославль
Объект паспортизации:
Контактное лицо:
Телефон
Прикрепить файлы
Согласие на обработку персональных данных:
Рассчитать элементыдоступной среды
на калькуляторе
Выделите опечатку и нажмите Ctrl + Enter, чтобы отправить сообщение об ошибке.
Угол наклона и наклон линии
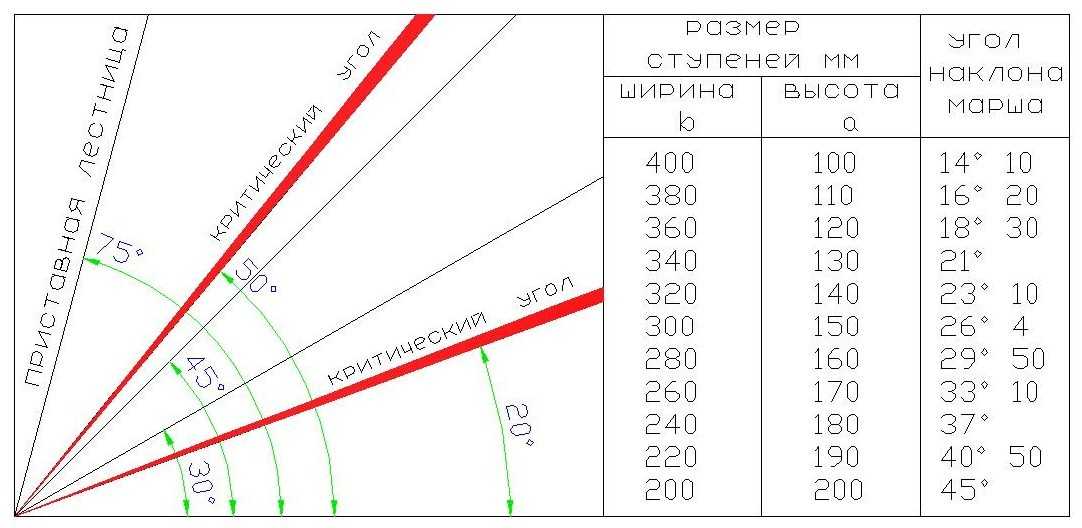
Пусть прямая l пересекает ось x в точке A. Угол между положительной осью x и линией l, измеренный в направлении против часовой стрелки, называется углом наклона прямая л.
На приведенном выше рисунке, если θ – это угол прямой линии l, то мы имеем следующие важные моменты.
(i) 0° ≤ θ ≤ 180°
(ii) Для горизонтальных линий θ = 0° или 180° и для вертикальных линий θ = 90°
(iii) Если прямая линия изначально лежит вдоль оси х и начинает вращаться вокруг неподвижной точки А на оси х против часовой стрелки и, наконец, совпадает с осью х, то угол наклона прямой линии в начальном положении равно 0°, а линии в конечном положении равно 0°.
(iv) Линии, перпендикулярные оси x, называются вертикальными линиями.
(v) Линии, перпендикулярные оси Y, называются горизонтальными линиями.
(vi) Другие линии, которые не перпендикулярны ни оси x, ни оси y, называются наклонными линиями.
Угол наклона и наклон линии – приложение
Основное применение угла наклона прямой линии – определение уклона.
Если θ – угол наклона прямой линии l, то tanθ называется наклоном градиента линии и обозначается буквой «m».
Следовательно, наклон прямой равен
м = tan θ
для 0° ≤ θ ≤ 180°
Найдем наклон прямой по приведенной выше формуле
(i) Для горизонтальных линий угол наклона равен 0° или 180°.
То есть
θ = 0° или 180°
Следовательно, наклон прямой линии равен
м = tan0° или tan 180° = 0
(ii) Для вертикальных линий угол наклона равен 90°.
То есть
θ = 90°
Следовательно, наклон прямой равен
м = tan90° = Не определено
(iii) Для наклонных линий, если θ имеет острую форму, наклон положительный. Если же θ тупой, то наклон отрицательный.
Наклон линии — положительный или отрицательный, нулевой или неопределенный
Когда мы смотрим на прямую линию визуально, мы можем легко определить знак наклона.
Чтобы узнать знак наклона прямой, всегда нужно смотреть на прямую слева направо.
Это иллюстрируют приведенные ниже рисунки.
Решенные задачи
Задача 1 :
Найдите угол наклона прямой, наклон которой равен 1/√3.
Решение :
Пусть θ — угол наклона линии.
Тогда наклон линии составляет
M = tanθ
Дано: наклон = 1/√3
Затем,
1/√3 = tanθ
θ = 30 °
Таким наклон 30°.
Задача 2 :
Если угол наклона прямой равен 45°, найдите ее наклон.
Решение :
Пусть θ — угол наклона линии.
Тогда, наклон линии,
M = TANθ
Дано: θ = 45 °
Затем,
M = TAN 45 °
M = 1
Итак, склон — 1.
Задача 3 :
Если угол наклона прямой равен 30°, найдите ее наклон.
Решение :
Пусть θ — угол наклона линии.
Затем, наклон линии,
м = tanθ
Дано: θ = 30°
Тогда
м = tan30°
м = 1/√3
Итак, уклон равен √3
.
Задача 4 :
Найдите угол наклона прямой, наклон которой равен √3.
Решение :
Пусть θ — угол наклона линии.
Затем, наклон линии,
м = tanθ
Дано: Уклон = √3
Тогда,
√3 = tanθ
θ = 60°
Итак, угол наклона равен 60°.
Задача 5 :
Найдите угол наклона прямой, уравнение которой y = x + 32.
Решение :
Пусть θ — угол наклона линии.
Данное уравнение находится в форме пересечения наклона.
То есть
y = mx + b
Сравнивая
y = x + 32
и
y = mx + b,
получаем наклон 1. m = 9.0004
Мы знаем, что наклон линии равен
м = tanθ
Тогда
1 = tanθ
θ = 45°
Итак, угол наклона равен 45°.
Пожалуйста, отправьте свой отзыв на [email protected]
Мы всегда ценим ваши отзывы.
©Все права защищены. onlinemath5all.com
4.3 Наклон линии | Аналитическая геометрия
4.
 3 Наклон линии (EMBGD)
3 Наклон линии (EMBGD)На диаграмме показано, что прямая образует угол \(\theta\) с положительной осью \(x\). Это называется угол наклона прямой.
Мы замечаем, что если градиент изменяется, то значение \(\theta\) также изменяется, поэтому угол наклон линии связан с ее градиентом. Мы знаем, что градиент – это отношение изменения \(y\)-направление на изменение \(x\)-направления:
\[m=\frac{\Delta y}{\Delta x}\]Из тригонометрии мы знаем, что функция тангенса определяется как отношение:
\[\tan \theta = \frac{\text{противоположная сторона}}{\text{прилегающая сторона}}\]
А из схемы мы видим, что
\начать{выровнять*} \tan \theta &= \dfrac{\Delta y}{\Delta x} \\ \поэтому m &= \tan \theta \qquad \text{ for } \text{0}\text{°} \leq \theta < \текст{180}\текст{°} \конец{выравнивание*}
Следовательно, градиент прямой линии равен тангенсу угла, образованного между прямой и
положительное направление оси \(x\).
Вертикальные линии
- \(\тета = \текст{90}\текст{°}\)
- Градиент не определен, так как значения \(x\) не изменились (\(\Delta x = 0\)).
- Следовательно, \(\tan \theta\) также не определено (график \(\tan \theta\) имеет асимптоту в \(\theta = \text{90}\text{°}\)).
Горизонтальные линии
- \(\тета = \текст{0}\текст{°}\)
- Градиент равен \(\text{0}\), поскольку значения \(y\) не изменяются (\(\Delta y = 0\)).
- Следовательно, \(\tan \theta\) также равно \(\text{0}\) (график \(\tan \theta\) проходит через происхождение \((\text{0}\text{°};0))\).
Линии с отрицательным уклоном
Если прямая имеет отрицательный наклон (\(m < 0\), \(\tan \theta < 0\)), то угол, образованный
между прямой и положительным направлением оси \(х\) тупая.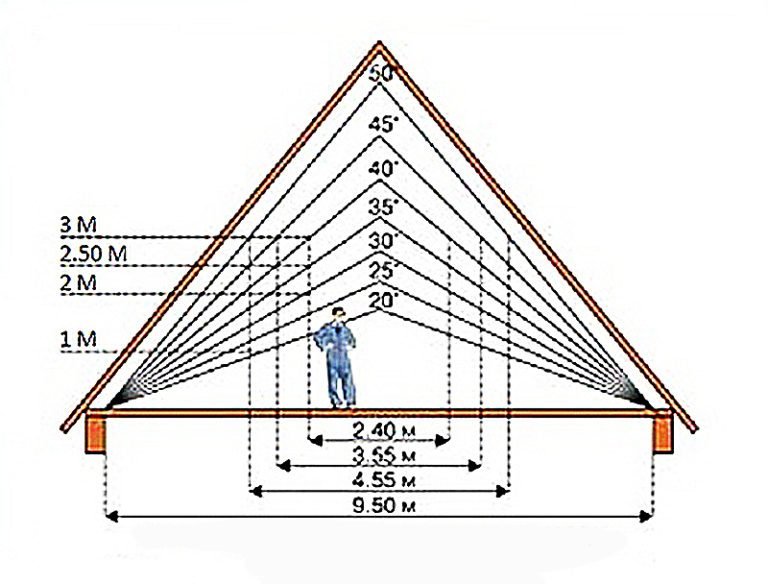
Из диаграммы CAST в тригонометрии мы знаем, что функция тангенса отрицательна во втором и четвертом квадрант. Если мы вычисляем угол наклона для линии с отрицательным градиентом, мы должны добавить \(\text{180}\text{°}\), чтобы изменить отрицательный угол в четвертом квадранте на тупой угол в второй квадрант:
Если нам дана прямая с градиентом \(m = -\text{0,7}\), то мы можем определить угол наклон с помощью калькулятора: 9{-1}(-\текст{0,7}) \\ &= -\текст{35,0}\текст{°} \конец{выравнивание*}
Этот отрицательный угол лежит в четвертом квадранте. Мы должны добавить \(\text{180}\)\(\text{°}\) чтобы получить тупой угол во втором квадранте:
\начать{выровнять*} \тета &= -\текст{35,0}\текст{°} + \текст{180}\текст{°} \\ &= \текст{145}\текст{°} \конец{выравнивание*}
И мы всегда можем использовать наш калькулятор, чтобы проверить, что тупой угол \(\theta = \text{145}\text{°}\)
дает градиент \(m = -\text{0,7}\).
Угол наклона
Учебник Упражнение 4.5
\(\text{60}\text{°}\)
\begin{align*} м &= \загар \тета\\ &= \tan \text{60}\text{°} \\ \поэтому m &= \text{1,7} \end{align*}
\(\text{135}\text{°}\)
\begin{align*} м &= \загар \тета\\ &= \tan \text{135}\text{°} \\ \поэтому m &= -\text{1} \end{выравнивание*}
\(\text{0}\text{°}\)
\begin{align*} м &= \загар \тета\\ &= \tan \text{0}\text{°} \\ \поэтому m &= \text{0} \end{align*}
\(\text{54}\text{°}\)
\begin{align*} м &= \загар \тета\\ &= \загар \текст{54}\текст{°} \\ \поэтому m &= \text{1,4} \end{выравнивание*}
\(\text{90}\text{°}\)
\begin{align*} м &= \загар \тета\\ &= \загар \текст{90}\текст{°} \\ \поэтому m & \text{ не определено} \end{align*}
\(\text{45}\text{°}\)
\begin{align*} м &= \загар \тета\\ &= \tan \text{45}\text{°} \\ \поэтому m &= \text{1} \end{выравнивание*}
\(\text{140}\text{°}\)
\begin{align*} м &= \загар \тета\\ &= \tan \text{140}\text{°} \\ \поэтому m &= -\text{0,8} \end{align*}
\(\text{180}\text{°}\)
\begin{align*} м &= \загар \тета\\ &= \tan \text{180}\text{°} \\ \поэтому m &= \text{0} \end{выравнивание*} 9{-1} \влево( \text{0,75} \вправо) \\ \поэтому \тета &= \text{36,8}\text{°} \end{align*}
\(2y — x = 6\)
\begin{align*} 2у — х&=6\ 2у &= х + 6 \\ y &= \frac{1}{2}x + 3 \\ \загар \тета &= м \\ &= \фракция{1}{2} \\ \theta &= \tan^{-1} \left( \text{0,5} \right) \\ \поэтому \тета &= \текст{26,6}\текст{°} \end{выравнивание*} 9{-1} \влево( \текст{1} \вправо) \\ \поэтому \тета &= \text{45}\text{°} \end{align*}
\(y=4\)
Горизонтальная линия
\(x = 3y + \frac{1}{2}\)
\begin{align*} х &= 3y + \frac{1}{2} \\ x — \frac{1}{2} &= 3y \\ \frac{1}{3}x — \frac{1}{6} &= y \\ \поэтому m &= \frac{1}{3} \\ \theta &= \tan^{-1} \left( \frac{1}{3} \right) \\ \поэтому \тета &= \text{18,4}\text{°} \end{выравнивание*} 9{-1} \влево( \текст{0,577} \вправо) \\ \поэтому \тета &= \text{30}\text{°} \конец{выравнивание*}
Рабочий пример 8: Наклон прямой линии
Определить угол наклона (с точностью до \(\text{1}\) десятичного знака) прямой линии
проходящей через точки \((2;1)\) и \((-3;-9)\).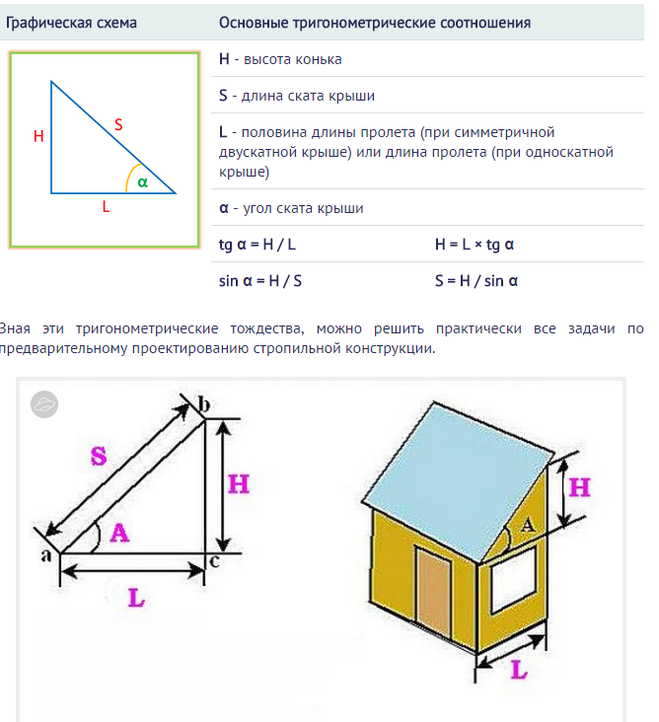 {-1}2\\
&= \текст{63,4}\текст{°}
\end{выравнивание*}
{-1}2\\
&= \текст{63,4}\текст{°}
\end{выравнивание*}
Важно: убедитесь, что ваш калькулятор находится в режиме DEG (градусы).
Напишите окончательный ответ
Угол наклона прямой равен \(\text{63,4}\)\(\text{°}\).
temp textРабочий пример 9: Наклон прямой линии
Определите уравнение прямой, проходящей через точку \((3;1)\) и с углом наклон \(\text{135}\text{°}\).
Используйте угол наклона для определения градиента линии
\begin{align*} м &= \загар \тета\\ &= \tan \text{135}\text{°} \\ \поэтому m &= -1 \конец{выравнивание*}
Запишите уравнение прямой линии в форме точки градиента. x — x_1)\]
Подставить заданную точку \((3;1)\)
\begin{выравнивание*} у — 1 & = -(х — 3) \\ у&=-х+3+1\ &= -х + 4 \конец{выравнивание*}
Напишите окончательный ответ
Уравнение прямой линии \(y = -x + 4\).
Рабочий пример 10: Наклон прямой линии
Определить острый угол (с точностью до \(\text{1}\) десятичного знака) между прямой, проходящей через точки \(M(-1;1\frac{3}{4})\) и \(N(4;3)\) и прямая \(y = — \frac{3}{2}x + 4\).
Нарисуйте эскиз
Проведите прямую через точки \(M(-1;1\frac{3}{4})\) и \(N(4;3)\) и прямую \(y = — \ дробь{3}{2}x + 4\) в подходящей системе координат. Обозначьте \(\alpha\) и \(\beta\) углы наклона две линии. Обозначьте \(\theta\) острый угол между двумя прямыми.
Обратите внимание, что \(\alpha\) и \(\theta\) — острые углы, а \(\beta\) — тупой угол.
\[\begin{массив}{rll}
\hat{B}_1 &= \text{180}\text{°} — \beta & (\angle \text{на строке}) \\
\text{and} \theta &= \alpha + \hat{B}_1 \quad & (\text{ext.} \angle \text{ of } \triangle =
\text{ сумма внутр.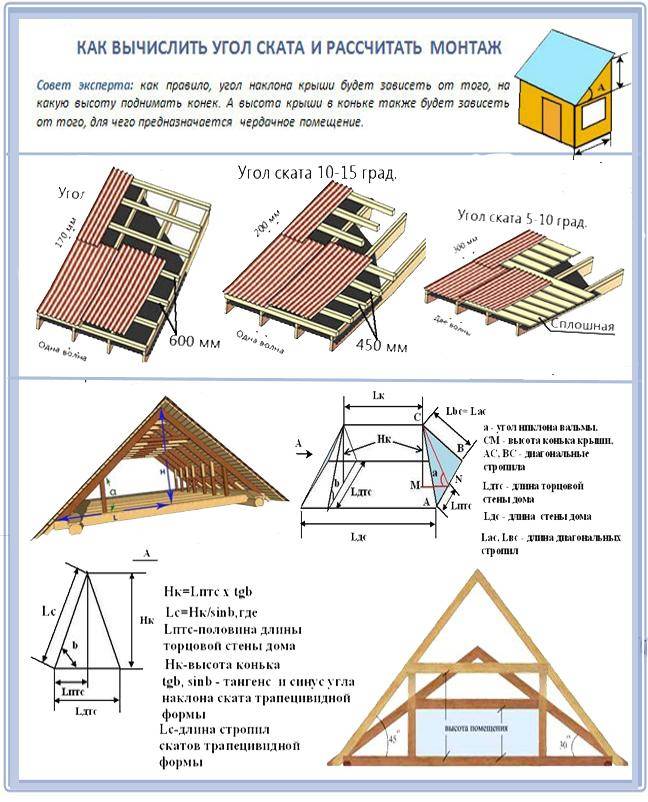 опп}) \\
\поэтому \тета &= \альфа + (\текст{180}\текст{°} — \бета) \\
&= \text{180}\text{°} + \alpha — \beta
\конец{массив}\]
9{-1} \left(-\frac{3}{2}\right) &= -\text{56,3}\text{°}
\конец{выравнивание*}
опп}) \\
\поэтому \тета &= \альфа + (\текст{180}\текст{°} — \бета) \\
&= \text{180}\text{°} + \alpha — \beta
\конец{массив}\]
9{-1} \left(-\frac{3}{2}\right) &= -\text{56,3}\text{°}
\конец{выравнивание*}
Этот отрицательный угол лежит в четвертом квадранте. Мы знаем, что угол наклона \(\beta\) равен тупой угол лежит во второй четверти, поэтому
\начать{выравнивать*} \beta &= -\text{56,3}\text{°} + \text{180}\text{°}\\ &= \текст{123,7}\текст{°} \конец{выравнивание*}
Определить градиент и угол наклона линии через \(M\) и \(N\)
Определение градиента \начать{выравнивать*} m & = \frac{y_2 — y_1}{x_2 — x_1} \\ & = \dfrac{3 — \frac{7}{4}}{4-(-1)} \\ & = \dfrac{\frac{5}{4}}{5} \\ &= \фракция{1}{4} \end{align*}
Определить угол наклона \начать{выравнивать*} \загар \альфа & = м\\ & = \фракция{1}{4} \\ \поэтому \alpha & = \tan^{-1} \left( \frac{1}{4} \right) \\ &= \текст{14,0}\текст{°} \end{выравнивание*}
Напишите окончательный ответ
\begin{align*} \тета & = \текст{180}\текст{°} + \альфа — \бета\\ & = \text{180}\text{°} + \text{14,0}\text{°} — \text{123,7}\text{°} \\ & = \текст{70,3}\текст{°} \end{align*}
Острый угол между двумя прямыми равен \(\text{70,3}\)\(\text{°}\).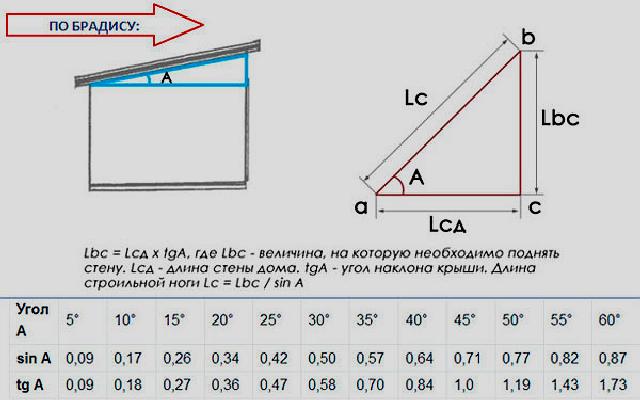 {-1} \left( -\text{2} \right) \\
&= -\текст{63,4}\текст{°} \\
\поэтому \theta &= \text{180}\text{°} — \text{63,4}\text{°} \\
\поэтому \тета &= \text{80}\text{°}
\end{выравнивание*} 9{-1} \влево(-\frac{9}{2} \вправо) \\
&= -\текст{77,5}\текст{°} \\
\поэтому \тета &= \text{180}\text{°} — \text{77,5}\text{°} \\
\поэтому \тета &= \текст{102,5}\текст{°}
\end{align*}
{-1} \left( -\text{2} \right) \\
&= -\текст{63,4}\текст{°} \\
\поэтому \theta &= \text{180}\text{°} — \text{63,4}\text{°} \\
\поэтому \тета &= \text{80}\text{°}
\end{выравнивание*} 9{-1} \влево(-\frac{9}{2} \вправо) \\
&= -\текст{77,5}\текст{°} \\
\поэтому \тета &= \text{180}\text{°} — \text{77,5}\text{°} \\
\поэтому \тета &= \текст{102,5}\текст{°}
\end{align*}
линия, проходящая через \((-1;-6)\) и \((-\frac{1}{2};-\frac{11}{2})\)
\begin{выравнивание*} m &= \frac{y_2 -y_1}{x_2 — x_1} \\ &= \frac{-\frac{11}{2}+ 6}{-\frac{1}{2}+1} \\ &= \ гидроразрыва {\ гидроразрыва {1} {2}} {\ гидроразрыва {1} {2}} \\ \поэтому m &= 1 \\ \theta &= \tan^{-1} \left( 1 \right) \\ \поэтому \тета &= \text{45}\text{°} \end{выравнивание*} 9{-1} \влево(-\frac{1}{3} \вправо) \\ \поэтому \тета &= -\текст{18,4}\текст{°} \\ \поэтому \тета &= \text{180}\text{°} — \text{18,4}\text{°} \\ \поэтому \тета &= \текст{161,6}\текст{°} \end{align*}
Градиент undefined
Определить острый угол между линией, проходящей через точки \(A(-2;\frac{1}{5})\)
и \(B(0;1)\) и прямой, проходящей через точки \(C(1;0)\) и \(D(-2;6)\).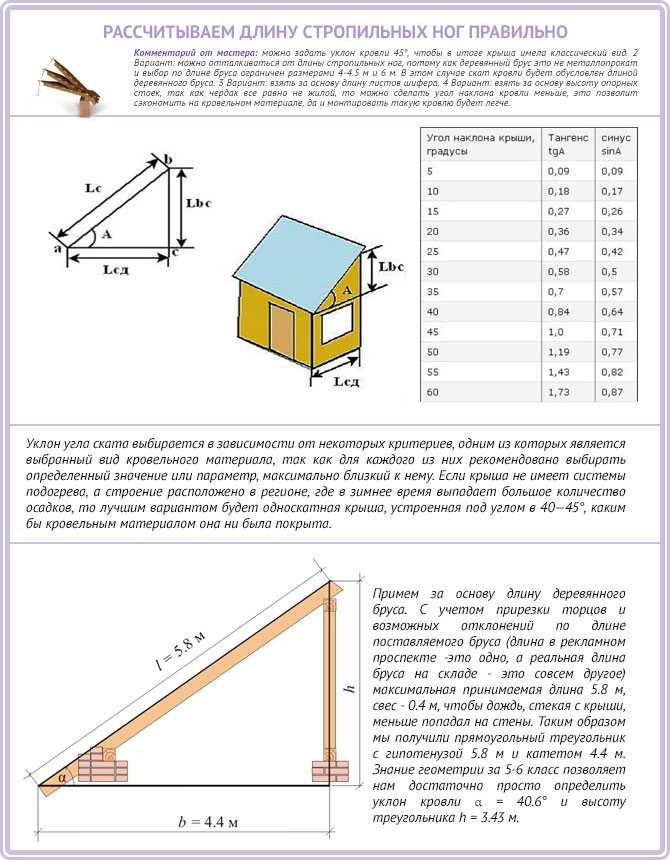 {-1} \left(-2 \right) \\
\поэтому \alpha &= -\text{63,4}\text{°} \\
\поэтому \alpha &= \text{180}\text{°} — \text{63,4}\text{°} \\
\поэтому \alpha &= \text{116,6}\text{°} \\
\text{And } \theta &= \beta + (\text{180}\text{°} — \alpha) \quad (\text{ext. } \angle
\треугольник)\\
\поэтому \theta &= \text{21,8}\text{°} + (\text{180}\text{°} —
\text{116,6}\text{°} ) \\
&= \текст{85,2}\текст{°}
\конец{выравнивание*}
{-1} \left(-2 \right) \\
\поэтому \alpha &= -\text{63,4}\text{°} \\
\поэтому \alpha &= \text{180}\text{°} — \text{63,4}\text{°} \\
\поэтому \alpha &= \text{116,6}\text{°} \\
\text{And } \theta &= \beta + (\text{180}\text{°} — \alpha) \quad (\text{ext. } \angle
\треугольник)\\
\поэтому \theta &= \text{21,8}\text{°} + (\text{180}\text{°} —
\text{116,6}\text{°} ) \\
&= \текст{85,2}\текст{°}
\конец{выравнивание*}
Определить угол между прямой \(y + x = 3\) и прямой \(x = y + \frac{1}{2}\).
Пусть угол наклона линии \(y + x = 3\) равен \(\alpha\), а угол наклона наклон линии \(x = y + \frac{1}{2}\) равен \(\beta\). Пусть угол между двумя строки будут \(\тета\):
\начать{выравнивать*}
у &= — х + 3 \\
\поэтому m &= — 1 \\
\alpha &= \tan^{-1} \left(-1\right) \\
\поэтому \alpha &= -\text{45}\text{°} \\
\поэтому \alpha &= \text{180}\text{°} — \text{45}\text{°} \\
\поэтому \alpha &= \text{135}\text{°} \\
х &= у + \ гидроразрыва {1} {2} \\
х — \фракция{1}{2} &= у \\
\поэтому m &= 1 \\
\beta &= \tan^{-1} \left(1 \right) \\
\поэтому \бета &= \text{45}\text{°} \\
\text{And } \theta &= \beta + (\text{180}\text{°} — \alpha) \quad (\text{ext.