Расчет ж б балки: Расчет железобетонной балки. — Доктор Лом
Расчёт железобетонной балки
Не смотря на то, что заводы железобетонных изделий производят большое количество готовой продукции, все же иногда приходится делать железобетонную балку перекрытия или железобетонную перемычку самому. Практически все видели строителей-монтажников, засовывающих в опалубку какие-то железяки, и почти все знают, что это — арматура, обеспечивающая прочность конструкции, вот только определять количество и диаметр арматуры, закладываемой в железобетонные конструкции, хорошо умеют только инженеры-технологи. Железобетонные конструкции, хотя и применяются вот уже больше сотни лет, но по-прежнему остаются загадкой для большинства людей, точнее, не сами конструкции, а расчет железобетонных конструкций.
Расчёт железобетонной балки — это одна из наиболее часто встречающихся задач в частном секторе. Столкнувшись с задачей расчёта фундамента для своего дома я разложил его на множество «условно» отдельных балок, посчитал все возможные нагрузки и принялся за расчёты.
С 12,01,2021 flash не поддерживается по умолчанию.
Вот способ от одного из подписчиков:
Шаг 2. Скачать и установить флэшплеер версии 27 или ниже.
Метод работает в браузере Яндекс. Говорят, что ещё на Мозиле работает. Правда, в Хроме не работает всё равно.
После ввода любых числовых значений не забываем нажимать Enter, чтобы калькулятор их посчитал!
Процесс расчёта
Основная идея расчёта сводится к тому, чтобы добиться баланса между прочностью бетона на сжатие и прочностью арматуры на растяжение.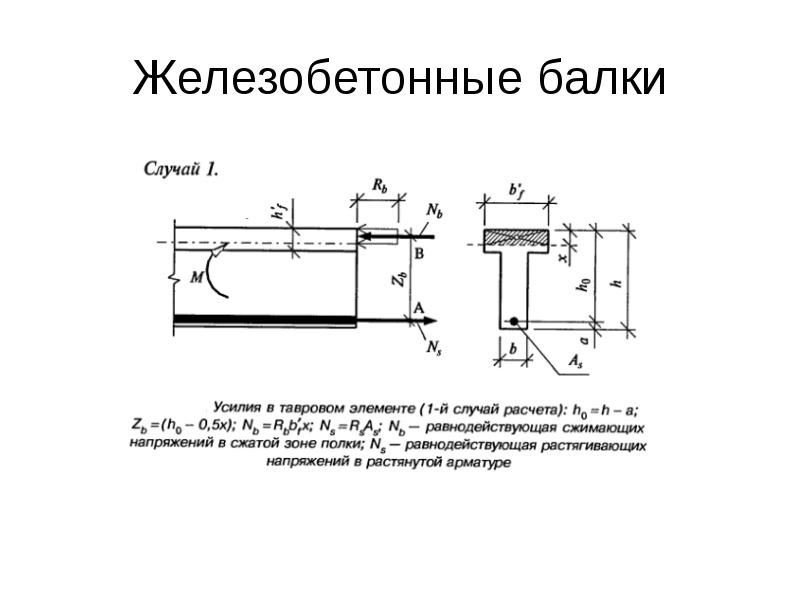 Иногда, в процессе расчётов каких-нибудь явно нереальных балок и нагрузок, можно увидеть, что калькулятор предлагает какое-то расчётное армирование, но при этом прочность балки не обеспечивается. Это следует понимать как то, что при таком сечении балки обеспечить прочность только арматурой невозможно. Т.е. калькулятор выдаёт сечение арматуры, при котором и бетон и арматура разрушатся одновременно и при этом наращивание армирования уже не приведёт к желаемому результату. Нужно либо уменьшать нагрузки/пролёты, либо увеличивать высоту/ширину сечения бетона.
Иногда, в процессе расчётов каких-нибудь явно нереальных балок и нагрузок, можно увидеть, что калькулятор предлагает какое-то расчётное армирование, но при этом прочность балки не обеспечивается. Это следует понимать как то, что при таком сечении балки обеспечить прочность только арматурой невозможно. Т.е. калькулятор выдаёт сечение арматуры, при котором и бетон и арматура разрушатся одновременно и при этом наращивание армирования уже не приведёт к желаемому результату. Нужно либо уменьшать нагрузки/пролёты, либо увеличивать высоту/ширину сечения бетона.
1. Геометрические параметры балки
Некоторые программки, типа «Строитель+», расчитывают балку исходя из того, что известны длина пролёта, распределённая нагрузка на балку и марка бетона. В результате расчёта мы получим высоту, ширину и количество арматуры для обеспечения прочности балки. Это на начальном этапе не так и плохо, но зачастую геометрию нам диктуют условия строительства. Например, имея газобетонную стену шириной 290мм целесообразно сделать и балку перекрытия, скажем, над гаражными воротами шириной 290мм.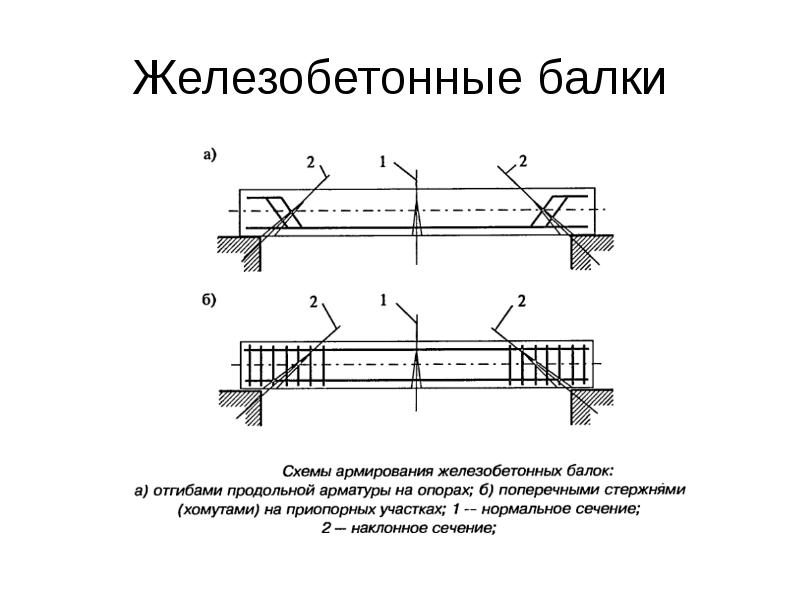
Итак, всеми этими примерами я хотел сказать то, что геометрические параметры зачастую нам заданы внешними факторами и порой требуется посчитать, сможем ли мы вложиться в отведённое нам пространство, а если не сможем, то сколько нужно арматуры, чтобы это стало возможным.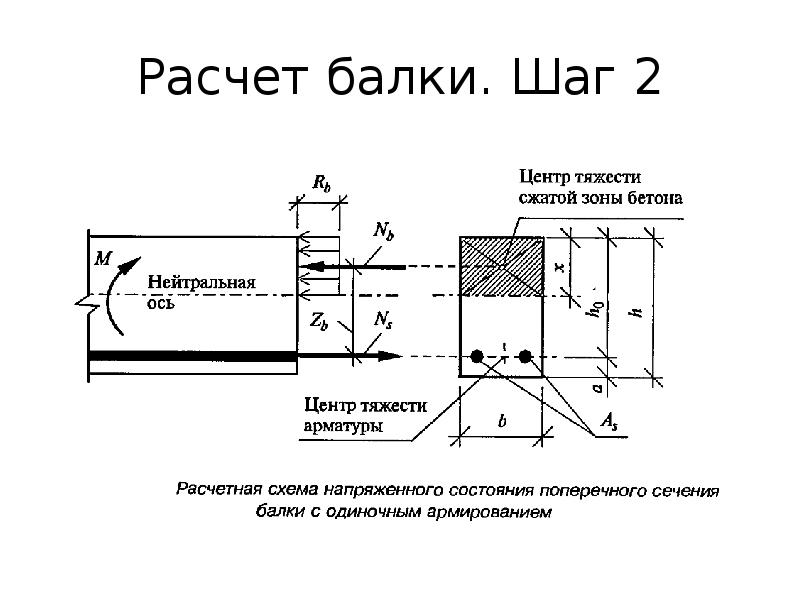
Пример из моей стройки. Я, не зная ещё ничего о форме своей ленты-ростверка на столбах ТИСЭ, размышлял следующим образом. Диаметр столбов ТИСЭ у меня 200мм. В процессе их заливки я местами немного ошибался, то они на пару миллиметров толще, то уже, то при бурении бур увело в сторону на 5мм, то ветер сдувал разметочную верёвочку и т.п. В общем, я принял ширину ленты 220мм (200мм — столб + 20мм запас). Далее, высота балки обычно принимается как b / 0.3 ÷ 0.5, т.е. высота лежит в диапазоне 440 ÷ 730 мм. Нагрузки от каркасного дома у меня не большие, максимум 2500кг/м.п., а максимальный пролёт между столбами равен 2800мм в свету (ограничен несущей способностью грунта и диаметром расширения столба ТИСЭ).
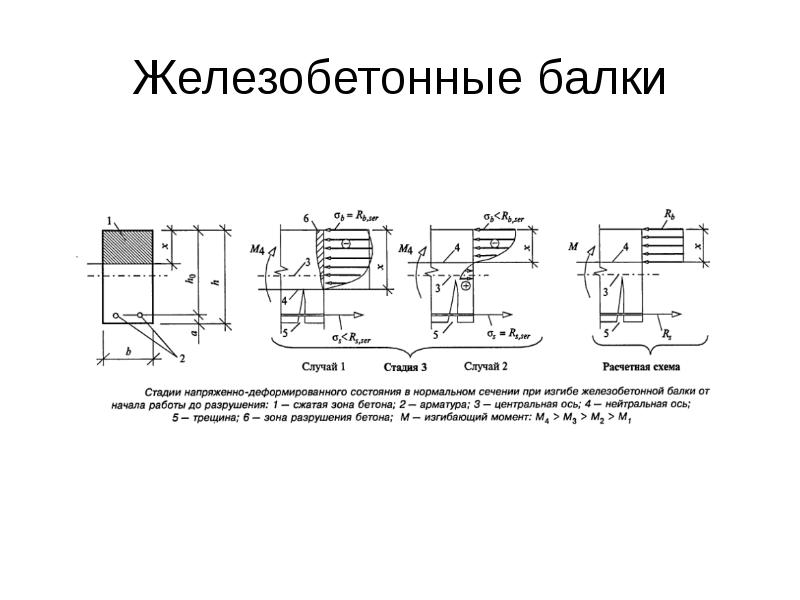
2. Определение опор балки
С точки зрения сопромата, будет ли это перемычка над дверным или оконным проемом или балка перекрытия, значения не имеет. А вот то как именно балка будет опираться на стены имеет большое значение. С точки зрения строительной физики любую реальную опору можно рассматривать или как шарнирную опору, вокруг которой балка может условно свободно вращаться или как жесткую опору. Определить расчётную схему не сложно:
Балка на шарнирных опорах. Если железобетонная балка устанавливается в проектное положение после изготовления, ширина опирания балки на стены меньше 200 мм, при этом соотношение длины балки к ширине опирания больше 15/1 и в конструкции балки не предусмотрены закладные детали для жесткого соединения с другими элементами конструкции, то такая железобетонная балка однозначно должна рассматриваться как балка на шарнирных опорах.

Защемлённая на концах балка. Если железобетонная балка изготавливается непосредственно в месте установки, то такую балку можно рассматривать, как защемленную на концах только в том случае, если и балка и стены, на которые балка опирается, бетонируются одновременно или при бетонировании балки предусмотрены закладные детали для жесткого соединения с другими элементами конструкции. Во всех остальных случаях балка рассматривается, как лежащая на двух шарнирных опорах.
Консольная балка. Балка, один или два конца которой не имеют опор, а опоры находятся на некотором расстоянии от концов балки, называется консольной. Например плиту перекрытия над фундаментом, выступающую за пределы фундамента на несколько сантиметров, можно рассматривать как консольную балку.
Многопролетная балка. Иногда возникает необходимость рассчитать железобетонную балку перекрытия, которая будет перекрывать сразу две или даже три комнаты, монолитное железобетонное перекрытие по нескольким балкам перекрытия или перемычку над несколькими смежными проемами в стене.
 В таких случаях балка рассматривается как многопролетная на шарнирных опорах. Это уже значительно более сложная в расчёте конструкция. Её, конечно, можно рассматривать как отдельные шарнирно опёртые балки, но это совсем не так! При равных по длине пролётах самый большой изгибающий момент образуется не в пролётах, а над опорами и в этом случае особое значение приобретает рассчёт арматуры именно верхнего ряда. Мой калькулятор пока умеет рассчитывать лишь двухпролётные балки.
В таких случаях балка рассматривается как многопролетная на шарнирных опорах. Это уже значительно более сложная в расчёте конструкция. Её, конечно, можно рассматривать как отдельные шарнирно опёртые балки, но это совсем не так! При равных по длине пролётах самый большой изгибающий момент образуется не в пролётах, а над опорами и в этом случае особое значение приобретает рассчёт арматуры именно верхнего ряда. Мой калькулятор пока умеет рассчитывать лишь двухпролётные балки.
Лента-ростверк в фундаменте ТИСЭ однозначно относится к Многопролётным балкам, однако, я её рассчитывал, как набор несвязанных между собой шарнирно опёртых балок, нагруженных равномерной нагрузкой от стен дома. В реальности, конечно, все сегменты ленты армированы максимально длинными кусками арматуры (12 метров), соблюдая все правила армирования по расположению стыков, нахлёстов, примыканий, длин анкеровки и установке поперечных хомутов. Что даёт мне значительный запас по прочности в условиях очень «ажурного» сечения балки. Такую конструкцию целесообразнее расчитывать в два прохода: все центральные элементы — это балки с двумя защемлёнными концами, а пролёты возле углов и Т-образные примыкающие пролёты — по схеме с одним защемлённым и одним шарнирно-опираемым концами. Чем больше пролётов в балке, тем ближе она будет к подобному упрощению (начиная с 5 пролётов — разбежка ).
Такую конструкцию целесообразнее расчитывать в два прохода: все центральные элементы — это балки с двумя защемлёнными концами, а пролёты возле углов и Т-образные примыкающие пролёты — по схеме с одним защемлённым и одним шарнирно-опираемым концами. Чем больше пролётов в балке, тем ближе она будет к подобному упрощению (начиная с 5 пролётов — разбежка ).
3. Определение нагрузки на балку
Нагрузки бывают распределёнными и сосредоточенными. В жизни, конечно, всё сложнее: распределённые нагрузки могут быть равномерно и неравномерно изменяющимися, сосредоточенные нагрузки почти всегда сопровождаются некоторыми распределёнными, а ещё все эти сочетания могут быть статическими или динамическими, или обоими одновременно! С одной стороны конструкцию следует рассчитывать на максимально неблагоприятное сочетание нагрузок, с другой стороны теория вероятности говорит о том, что вероятность такого сочетания нагрузок крайне мала и рассчитывать конструкцию на максимально неблагоприятное сочетание нагрузок, значит неэффективно тратить строительные материалы и людские ресурсы.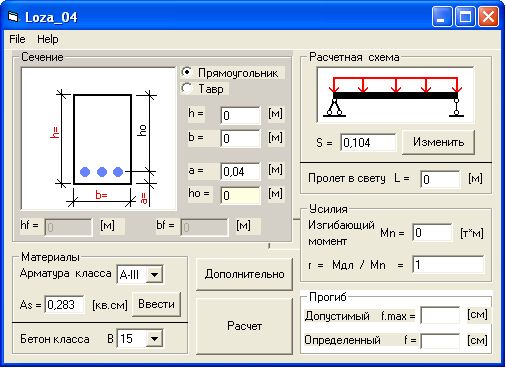 Поэтому при расчете конструкций динамические нагрузки используются с различными поправочными коэффициентами, учитывающими вероятность сочетания нагрузок, но как показывает практика, учесть все невозможно. Для примера я покажу вам свои расчёты нагрузки на ленту-ростверк:
Поэтому при расчете конструкций динамические нагрузки используются с различными поправочными коэффициентами, учитывающими вероятность сочетания нагрузок, но как показывает практика, учесть все невозможно. Для примера я покажу вам свои расчёты нагрузки на ленту-ростверк:
Как видите, динамическая нагрузка вносит очень ощутимый вклад в суммарное значение всех нагрузок, хотя она вряд ли когда-нибудь случится. Для дальнейших расчётов я округлил нагрузку в 2242кг*м.п. до 2500кг*м.п., Вдруг я на старости лет увлекусь роялем и бильярдом одновременно =)
К этой же нагрузке стоит добавить ещё и нагрузку от собственного веса балки. При размерах 0,22 х 0,3 х 3 метров объём балки составит 0,198 м³, что при плотности железобетона 2500кг на кубометр составит 495кг. В калькуляторе эти величины так-же вычисляются, и автоматически добавляются к полезной нагрузке, если стоит галочка напротив строчки «Добавлять вес балки?»
Поскольку стены дома конструктивно обшиты ОСП-плитами, равномерно распределяющими нагрузку от стоек каркаса по всему обвязочному брусу я принимаю нагрузку, как равномерно распределённую.
4. Класс арматуры
В последнее время я несколько раз уже покупал арматуру, и ни разу не видел арматуру диаметров 10 — 16мм другого класса, кроме как А500С. Это самая подходящая арматура, рекомендованная современными правилами. Тем не менее, в программу-калькулятор я включил почти всю линейку современных классов арматуры (от А240 до А1000) и те классы, которые были в старых сводах правил (типа А-I, A-II, A-III). Мало ли, кто где какую арматуру раздобудет. Для расчётов и на практике я использовал арматуру класса А500С диаметром 12мм.
5. Армирование
Этот пункт в калькуляторе находится в разделе исходных данных, однако имеет некоторую «обратную связь» от расчётов. Задавая количество прутов арматуры в растянутой зоне балки программа рассчитает требуемый диаметр этих прутов и если выбранный диаметр меньше расчётного, покажет это. Как выбрать количество прутов? Для этого в раздлах СНиП есть ряд правил, которые я описал в статье «правила армирования». В общем случае, если это не узенькая слабонагруженная перемычка над окном, рекомендуется не менее двух прутов. Есть ограничения и на максимальное количество прутов, обусловленное расстоянием между прутами. Это минимальное расстояние определено необходимостью свободного протекания бетонной смеси в тело ленты между стержнями арматуры фундамента при заливке бетона, возможностью его уплотнения и хорошей связи бетона с арматурой для совместной работы под нагрузкой. Минимальное расстояние между стержнями продольной арматуры не может быть меньше наибольшего диаметра стержней арматуры и не менее 25 мм для нижнего ряда арматуры и 30 мм — для арматуры верхнего ряда при двух рядах армирования. Таким образом, максимальное количество прутов:
Есть ограничения и на максимальное количество прутов, обусловленное расстоянием между прутами. Это минимальное расстояние определено необходимостью свободного протекания бетонной смеси в тело ленты между стержнями арматуры фундамента при заливке бетона, возможностью его уплотнения и хорошей связи бетона с арматурой для совместной работы под нагрузкой. Минимальное расстояние между стержнями продольной арматуры не может быть меньше наибольшего диаметра стержней арматуры и не менее 25 мм для нижнего ряда арматуры и 30 мм — для арматуры верхнего ряда при двух рядах армирования. Таким образом, максимальное количество прутов:
N=b-2a/(D+25)
округлённое до меньшего целого. В моём примере ширина балки b=220мм, толщина защитного слоя a=35мм (задана пластиковыми фиксаторами арматуры типа «звёздочка»), диаметр арматуры D=12мм:
N=220-2*35/(12+25)=4
С целью уменьшения арматурных работ я выбрал 3 прута. До расчётов диаметра мы еще дойдём.
6. Максимально допустимый относительный прогиб
Все строительные, и не строительные тоже, конструкции прогибаются! Не бывает таких материалов, которые не гнутся совсем. Железобетон не исключение, он может прогибаться под нагрузками в некоторых пределах без разрушительных последствий, причём порой на достаточно большие величины. СНиП 2.01.07-85 «Нагрузки и воздействия» регламентирует максимально допустимые прогибы, причем часть из этих ограничений связаны не с конструктивными проблемами бетонных балок, а просто с эстетическими (некрасиво, если плита перекрытия над головой прогибается на 10см, не смотря на то, что прочность обеспечена!) Выбираем требуемый в конкретном случае прогиб. В моём примере выбран прогиб 1/200, что означает, что при пролёте 3 м максимальный прогиб может составить 15 мм.
Железобетон не исключение, он может прогибаться под нагрузками в некоторых пределах без разрушительных последствий, причём порой на достаточно большие величины. СНиП 2.01.07-85 «Нагрузки и воздействия» регламентирует максимально допустимые прогибы, причем часть из этих ограничений связаны не с конструктивными проблемами бетонных балок, а просто с эстетическими (некрасиво, если плита перекрытия над головой прогибается на 10см, не смотря на то, что прочность обеспечена!) Выбираем требуемый в конкретном случае прогиб. В моём примере выбран прогиб 1/200, что означает, что при пролёте 3 м максимальный прогиб может составить 15 мм.
7. Изгибающий момент (начало расчётов)
Определение изгибающего момента — ключевое действие в расчёте. Все последующие вычисления будут опираться на эту величину. К сожалению, существует очень много самых разнообразных случаев приложения нагрузки к балке, да и балки бывают на разных опорах, да ещё и балки бывают статически определимые и неопределимые. Потому нету одной универсальной формулы, по которой можно вычислить изгибающий момент в любой ситуации (возможно, математики скажут, что я не прав, но двойные интегралы в уравнениях общего вида лежат за гранью моего понимания). Для определения наиболее подходящей для каждого конкретного случая формулы я порекомендую вот этот сайт, формулами которого я пользовался для написания своего калькулятора. В моём примере с равномерно распределённой нагрузкой (2500кг/м + собственный вес балки 495 кг / 3 м = 2665 кг/м) и шарнирно опёртой балкой изгибающий момент считается по формуле:
Потому нету одной универсальной формулы, по которой можно вычислить изгибающий момент в любой ситуации (возможно, математики скажут, что я не прав, но двойные интегралы в уравнениях общего вида лежат за гранью моего понимания). Для определения наиболее подходящей для каждого конкретного случая формулы я порекомендую вот этот сайт, формулами которого я пользовался для написания своего калькулятора. В моём примере с равномерно распределённой нагрузкой (2500кг/м + собственный вес балки 495 кг / 3 м = 2665 кг/м) и шарнирно опёртой балкой изгибающий момент считается по формуле:
М=ql²/8
М=2665 х 3²/8=2998 кгс*м
Если бы нагрузка была сосредоточенной посередине балки, то: М=Ql/4.
8. Высота сжатой зоны
Следующим важным шагом является определение высоты сжатой зоны бетона и сравнение её с граничным условием.
Железобетон — это композитный материал, прочностные свойства которого зависят от множества факторов, точно учесть которые при расчете достаточно сложно. Кроме того бетон хорошо работает на сжатие, а арматура хорошо работает на растяжение, а при сжатии возможно вспучивание арматуры. Поэтому конструирование железобетонной конструкции сводится к определению сжатых и растянутых зон. В растянутых зонах устанавливается арматура. При этом высота сжатой и растянутой зоны зараннее неизвестна и потому применять обычные методы подбора сечения, как для деревянной или металлической балки, не получится.
Кроме того бетон хорошо работает на сжатие, а арматура хорошо работает на растяжение, а при сжатии возможно вспучивание арматуры. Поэтому конструирование железобетонной конструкции сводится к определению сжатых и растянутых зон. В растянутых зонах устанавливается арматура. При этом высота сжатой и растянутой зоны зараннее неизвестна и потому применять обычные методы подбора сечения, как для деревянной или металлической балки, не получится.
Для начала определяем граничную высоту сжатой зоны. Это такая высота бетона, при которой его предельное напряжение на сжатие наступает одновременно с предельным напряжением в арматуре на растяжение. Т.е. при такой высоте сжатой зоны будет достигнут баланс между двумя разнонаправленными силами, сжатием и растяжением, и при превышении нагрузки произойдет одновременное разрушение бетона и обрыв арматуры. Граничная высота считается по следующей формуле:
ξr= ω/(1+Rs/Rpr*(1- ω/1,1))
где ω — характеристика сжатой зоны бетона, определяемая по формуле:
ω = k — 0,008 · Rb
где в свою очередь k — коэффициент, принимаемый равным для бетона: тяжёлого — 0,85; мелкозернистого — 0,80;
Rb — сопротивление бетона класса В25 сжатию: 14. 5 МПа.
5 МПа.
Итого: ω = 0,85 — 0,008 · 14,5 = 0,734.
Rpr — предельное напряжение в арматуре сжатой зоны сечения, принимаемое равным 500 Н / мм²
Rs — сопротивление арматуры класса А500 растяжению, 435 МПа.
ξr=0,734/(1+435/500*(1-0,734/1,1))=0,57
Поскольку это относительная высота, её можно перевести в абсолютную: ξr*h=171мм.
Высота сжатой зоны бетона c учётом сжатых стержней арматуры:
x=(RsAs-RscAsc)/(Rb*b)
где As — площадь сечений растянутой арматуры, в нашем примере 3 прута по 12мм, Asc — площадь сжатой арматуры (2 прута 10мм):
As=пR²*N;
As=3,14*0,6²*3=3,39 см² Asc=3,14*0,5²*2=1,57 см²
x=(435*3,39-400*1,57)/(14,5*22)=2,66 см
9. Коэффициенты Аm и Ar
Расчёт требуемой площади арматуры можно вести по алгоритму, изображённому ниже:
Для расчёта необходимого сечения арматуры нужно вычислить коэффициент Аm.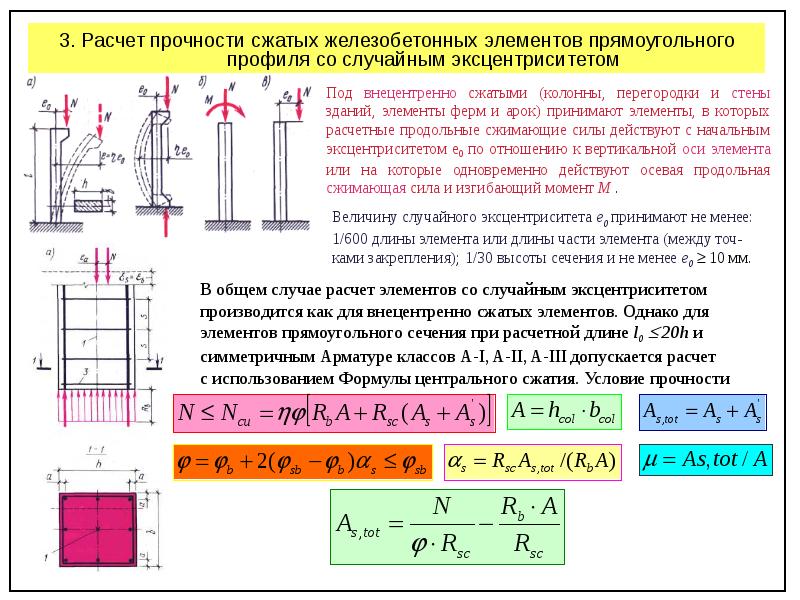
Аm=М/(Rb*h0²*b)
Поскольку М у нас в кг*м, Rb в Мпа, а величины b и h0 в см нужно всё привести к единым размерностям. М=2998 кг*м=299800 кг*см, Rb=14.5 МПа=147,86 кг/см² , теперь можно считать:
Am=299800/(147,86*26,5²*22)=0,131
Если значение Am будет больше Ar, то потребуется увеличить сечение бетонной балки, или повысить класс бетона. Если же таких возможностей или желаний нет, то необходимо устанавливать арматуру в сжатой зоне бетона!
Коэффициент Ar вычисляется по формуле:
Ar=ξr(1-0,5ξr)
Ar=0,57(1-0,5*0,57)=0,408
Условие Am<Ar у нас выполняется, значит сжатой арматуры добавлять не требуется.
10. Площадь растянутой арматуры
Расчёт необходимой площади сечения растянутой арматуры ведётся по формуле:
Fa=M/(Rs*h0*η)
где η = 0,5*(1+√(1-2*Am)) = 0,5*(1+√0,738) = 0,93
Поскольку у нас в расчёте опять размерности не совпадают, приведём все данные к единой системе, для удобства — к сантиметрам.
Rb=14.5 МПа=147,86 кг/см², Rs=435 МПа=4435,76 кг/см² .
Fa=299800/(4435,76*26,5*0,93)=2,74 см²
Поскольку количество стержней мы уже предварительно выбрали (N=3), то площадь сечения одного стержня должна быть не менее Fa/N = 2,74 / 3 = 0,914 см². Несложно посчитать диаметр этого стержня:
D=√(S/π)*20 D=10,79 мм
Округляем до ближайшего большего значения из номенклатурного ряда — 12мм. Итого, получается для армирования балки из моего примера достаточно 3 прута арматуры диаметром 12мм.
11. Проверка
Поскольку площадь растянутой арматуры отличается от расчётной, можно провести обратный расчёт для того, чтобы узнать, насколько большой у нас получился запас прочности. Сначала вновь пересчитываем площадь арматуры:
As=N*π*(D/2)² = 3,39 см²
Затем считаем максимальный изгибающий момент. Если условие Am<Ar выполняется и высота сжатой зоны х>0, то используется формула:
Mmax=Rb*b*х*(h0-0.5*х)+Rsс*Asс*(h0-a)
Mmax=147,86*22*2,66*(26,5-0,5*2,66)+4078,86*1,57*(26,5-3,5) =365078 кг*см (3650,7 кг*м = 35,8 кН*м)
где a — толщина защитного слоя бетона 3,5 см, Rsc — Предел прочности арматуры на сжатие Rsc=400 МПа=4078,86 кг/см²
Если х меньше или равен нулю, то используется другая формула: Mmax=Rs*As*(h0-а)
А если не выполняется условие Am<Ar, то: Mmax=Ar*Rb*b*h0²+Rsс*Asс*(h0-a)
Для того, чтобы перевести это значение в распределённую нагрузку, воспользуемся формулой из пункта 7:
q=8M/l²
q=8*3650,7/3²=3245 кг*м
Поскольку наша расчётная нагрузка составляет 2665 кг*м (с учётом собственного веса), то получается запас по прочности 21%.
12. Процент армирования
Процент армирования балки, это не самая критически важная величина в расчёте, потому я её оставил на последнем месте. Считается эта величина по формуле:
μ = (Fa+Fa’)/b*h0*100
μ=(3,39+1,57)/(22*26,5)*100=0,85%
Существуют рекомендованные диапазоны процента армирования балок от 0,3 до 4% (для колонн до 5%), выведенные изходя из экономических и конструктивных соображений, и наш результат отлично вписывается в этот диапазон.
13. Прогиб
Нередко бывает так, что прочность балки по первой группе предельных состояний достаточна, а вот расчёт по второй группе выходит за пределы допустимых деформаций. Потому расчёт на прогиб мне показался достаточно необходимым, чтобы потратить своё время и включить его в калькулятор. Приводимый ниже расчет не совсем соответствует рекомендациям СНиП 2.03.01-84 и СП 52-101-2003, тем не менее позволяет приблизительно определить значение прогиба по упрощенной методике. И хотя шарнирно опертая безконсольная однопролетная балка c прямоугольной формой поперечного сечения, на которую действует равномерно распределенная нагрузка — это частный случай на фоне множества возможных видов нагрузок, расчетных схем и геометрических форм сечения, тем не менее это очень распространенный частный случай в малоэтажном строительстве.
Прогиб балки для моего примера считается по формуле:
f = k5qlᶣ/384EIp
Эта формула очень похожа на класическую формулу прогибов, как в расчётах деревянных элементов и отличается наличием коэффициента k. Этот коэффициент учитывает изменение высоты сжатой области сечения по длине балки при действии изгибающего момента. При равномерно распределенной нагрузке и работе бетона в области упругих деформаций значение коэффициента для приближенных расчетов можно принимать k = 0.86. Использование этого коэффициента позволяет определять прогиб балки (плиты) переменного сечения, как для балки постоянного сечения с высотой hmin. Таким образом в приведенной формуле остается только 2 неизвестных величины — расчетное значение модуля упругости бетона и момент инерции приведенного сечения Ip в том месте, где высота сечения минимальна. Остается только определить этот самый момент инерции, а модуль упругости примем равный начальному. Момент инерции приведённого сечения Ip вычисляется довольно сложным и запутанным методом, в процессе которого необходимо решать кубическое уравнение, поэтому, если очень хочется вникнуть в суть и пересчитать всё самому, отправлю вас на сайт, где этот метод описан по шагам с картинками, чтобы совсем уж не копировать сайт автора )
Момент инерции балки J и момент сопротивления W калькулятор расчитывает по методике, описанной на указанном сайте и выдаёт результат в двух первых строчках правого столбца с расчётами.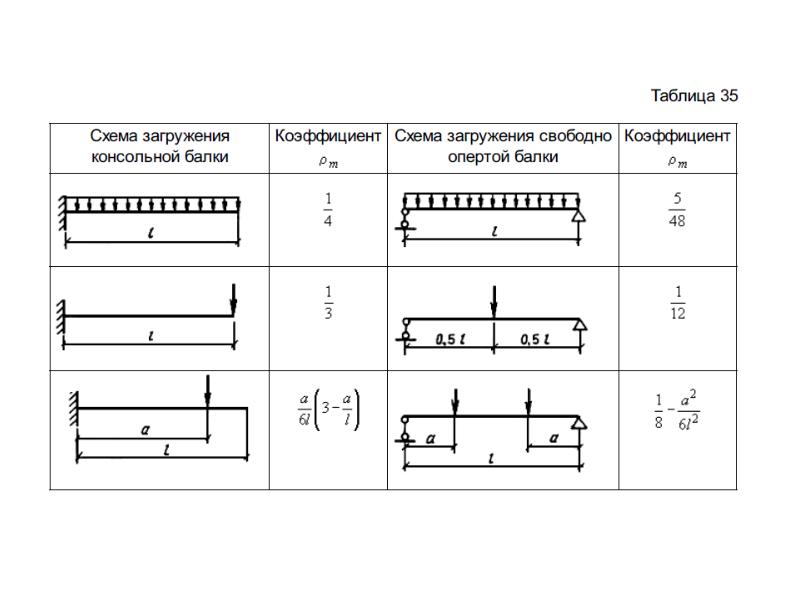
14. Прочность по наклонным сечениям
Этим расчётом никогда нельзя пренебрегать, поскольку бетон не переносит
растягивающих усилий, а возле опор, на которые опирается балка, создаются
именно такие усилия, которые к тому-же не скомпенсированы никакой арматурой
(если не ставить хомуты). Если расчёт по прогибу и по прочности проходит, то это
совсем не означает, что балка не разрушится возле опоры из-за наклонной трещины.
Суть возникновения этой трещины изображена на картинке справа.
Для начала нам нужно определить реакции опор.
Поскольку мы рассматриваем нашу балку как шарнирно опёртую, то реакции левой и правой опор будут равны между собой, т.е. нагрузка между ними распределиться поровну.
Qопоры = q*L*0,5 = 2665 * 3 * 0,5 = 3998 кг = 39,2 кН (4т на каждую опору)
Прочность балки по наклонным сечениям обеспечивается прочностью бетона и поперечной арматуры, расположенной в теле балки.
Выясняем необходимость постановки поперечного армирования по расчету из условия:
Qопоры ≤ Qmin
где Qmin — расчетная поперечная сила, воспринимаемая железобетонным элементом без поперечной арматуры.
Расчетную поперечную силу Qmin, воспринимаемую элементом без вертикальной и (или) наклонной арматуры, допускается определять по формуле (7.78a) п.п. 7.2.1.6 СНБ 5.03.01-02 :
Qmin = ϕс * Rbt * b * ho
где коэффициент ϕс принимается равным:
для тяжелого бетона — 0,6;
для мелкозернистого — 0,5.
Rbt — сопротивление бетона растяжению Rbt=1,05 МПа=1050 кПа, а b и h0 выражены в миллиметрах.
Qmin = 0,6 * 1,05 * 220 * 265 = 36729 H = 36,7 кН
Поскольку Qопоры (39,2 кН) > Qmin (36,7 кН), бетон возле опоры не выдерживает нагрузки и требуется расчёт поперечного армирования.
15. Поперечное армирование
Диаметр хомутов в вязанных каркасах должен быть не менее 5 мм при h ≤ 800 мм и 8 мм при h > 800 мм. Высота нашего сечения 300 мм, но для хомутов у нас запасена арматура диаметром 6мм. Хомуты представляют из себя изогнутую рамочку, обхватывающую продольную арматуру, а значит площадь сечения хомута является удвоенной площадью сечения арматуры диаметром 6мм:
Asw = 3,14*0,3²*2 = 0,5652 см².
Максимально допустимый расчётный шаг хомутов определяем по формуле (Пособие по проектированию жбк, к СНиП 2.03.01-84 п.п. 3.29 (46)):
Smax = ϕb4 * Rbt * b * ho²/Q
Smax = 1,5 * 1050 кПа * 0,22 м * 0,265² м / 39,2 кН = 0,62 м
где фb4 | фb3 | фb2:
— для тяжёлого бетона: 1,5 | 0,6 | 2,00
— для мелкозернистого и лёгкого плотностью выше D 1900: 1,2 | 0,5 | 1,7
— для лёгкого D < 1900 и пористого: 1,0 | 0,4 | 1,5
Однако, согласно СНБ 5.03.01-02 п.п. 11.2.21, в железобетонных элементах, в которых поперечная сила не может быть воспринята только бетоном, поперечную арматуру следует устанавливать с выполнением следующих конструктивных требований, определяющих шаг поперечных стержней:
— при h ≤ 450 мм — не более h/2 и 150 мм;
— при h > 450 мм — не более h/3 и 300 мм;
— не более 3/4h и 500 мм;
Таким образом, в средней части пролета шаг поперечных стержней принимаем S = 3/4*30 = 22 см, (что не превышает 3/4h = 3/4*30 = 22,5 см). Исходя из равномерного распределения по длине центральной части у меня получилось 25 см, что, в принципе, допустимо в виду незначительного превышения Qопоры над Qmin.
Исходя из равномерного распределения по длине центральной части у меня получилось 25 см, что, в принципе, допустимо в виду незначительного превышения Qопоры над Qmin.
В приопорных участках шаг поперечных стержней не должен превышать 15 см и не более h/2 = 30/2 = 15 см. Принимаем 15 см.
Вычисляем интенсивность усилий в поперечных стержнях на единицу длины балки:
qs = Rsw * Asw / S
qs = 290 000 кПа * 0,00005652 м² / 0,15 м = 109,27 кН/м
где Rsw — сопротивление растянутой поперечной арматуры класса АIII = 290 МПа;
Asw — площадь сечения арматуры хомута;
S — расстояние между хомутами в этой проекции, S = 15 cм.
Минимальная интенсивность:
qsmin = фb3 * Rbt * b / 2
qsmin = 0,6 * 1050 * 0,22 /2 = 69,3 кН/м
Требуемая интенсивность:
qsтр = Q² / (4 * Mb)
где Mb = фb2 * Rbt * b * ho²
Mb = 2 * 1050 * 0,22 * 0,265² = 32,44 кН·м
qsтр = 39,2² / (4 * 32,44) = 11,84 кН/м
Так как принятая интенсивность (109 кН/м) больше требуемой (11,84 кН/м) и больше минимальной (69,3 кН/м), оставляем шаг S = 15 см.
16. Ширина приопорных участков
Ширину приопорных участков вычислим по длине проекции опасной наклонной трещины на продольную ось балки:
с0 = √(Mb/qs) = √(32,44 / 109,27) = 0,55 м
Учитывая границы с0 в расчёте (ho < c0 < 2ho), принимаем с0 = 53 см. Несущую способность наклонного сечения проверяем по условию:
Qmax = Mb / c0 + qs * c0 = 32,44 / 0,55 + 109,27 * 0,55 = 119 кН
Qmax (119 кН) > Qопоры (39,2 кН)
Условие выполняется! Такой запас несущей способности у нас образовался благодаря хомутам диаметром 6 мм. Для данного случая можно было использовать хомуты диаметром 5мм, которые даже в приопорных учасках можно было бы ставить на расстоянии, как и в средней части пролёта — 25 см, но требования СНБ написаны не просто так!
P.S.: Если у вас балка планируется неразрезная многопролётная и с более-менее равными пролётами (+/-10%), и вы её надеетесь посчитать самостоятельно, то вам может пригодиться график эпюр изгибающих моментов.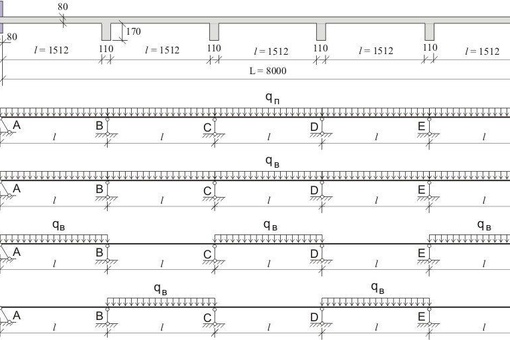 Для совсем ручного счёта рекомендую пролистать статейку про монолитное реблисто-балочное перекрытие.
Для совсем ручного счёта рекомендую пролистать статейку про монолитное реблисто-балочное перекрытие.
Расчет ж/б балки прямоугольного сечения. Занятие 56. Практическая работа 8
1. Практическая работа № 8
«Расчет ж/б балки прямоугольного сечения• Основная идея расчёта сводится к тому, чтобы добиться баланса
между прочностью бетона на сжатие и прочностью арматуры на
растяжение.
3. Расчет:
•1. Геометрические параметры балки•1.1. Определение длины балки.
• Рассчитать реальную длину балки проще всего. Главное, что мы
заранее знаем пролет, который должна перекрыть балка. Пролет это расстояние между несущими стенами для балки перекрытия
или ширина проема в стене для перемычки. Длина балки должна
быть больше пролета на ширину опирания на стены. Ширина опор
зависит от прочности материала конструкции под балкой и от
длины балки, чем прочнее материал конструкции под балкой и
чем меньше пролет, тем меньше может быть ширина опоры.
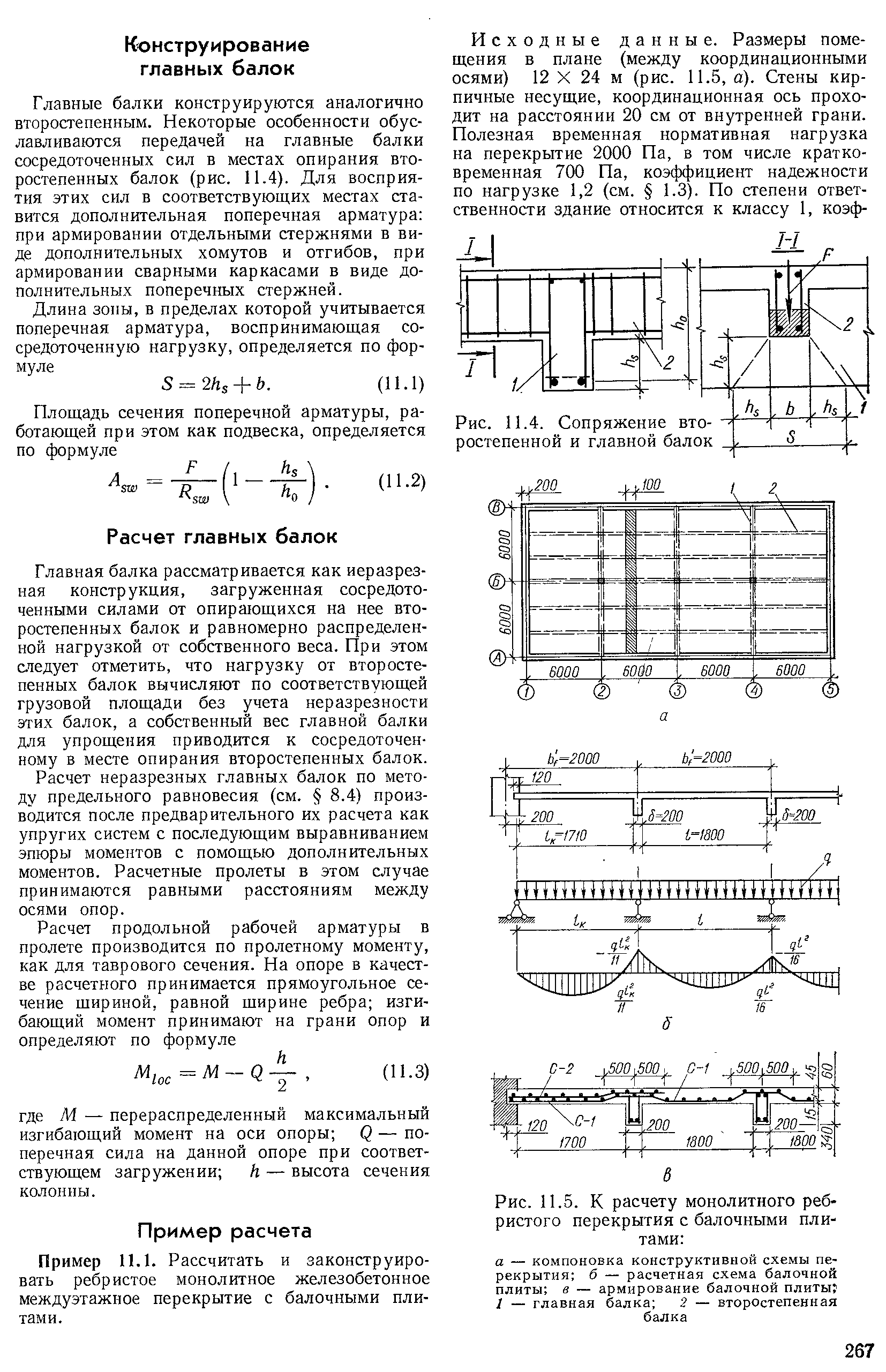
Теоретически рассчитать ширину опоры, зная материал
конструкции под опорой можно точно также, как и саму балку, но
обычно никто этого не делает, если есть возможность опереть
балку на кирпичные, каменные и бетонные (железобетонные)
стены на 150-300 мм при пролетах 2-10 метров. Для стен из
пустотелого кирпича и шлакоблока может потребоваться расчет
ширины опоры.
5. 1.2. Предварительное определение ширины и высоты балки и класс бетона, арматуры.
• «геометрические параметры зачастую нам заданы внешними факторамии порой требуется посчитать, сможем ли мы вложиться в отведённое
нам пространство, а если не сможем, то сколько нужно арматуры»
• Для балок перекрытия ширина может быть какой угодно, но обычно
принимается не менее 10 см и кратной 5 см (для простоты расчетов).
• Высота балки принимается из конструктивных или эстетических
соображений. Можно использовать пропорции: от 1/8L до 1/12L
• Класс бетона В20-В30
6.
 2. Расчетная схема. Определение опор • С точки зрения сопромата, будет ли это перемычка над
2. Расчетная схема. Определение опор • С точки зрения сопромата, будет ли это перемычка наддверным или оконным проемом или балка перекрытия,
значения не имеет. А вот то как именно балка будет
опираться на стены имеет большое значение. С точки
зрения строительной физики любую реальную опору
можно рассматривать или как шарнирную опору, вокруг
которой балка может условно свободно вращаться или
как жесткую опору. Другими словами жесткая опора
называется защемлением на концах балки.
7. 1. Балка на двух шарнирных опорах.
Если железобетонная балка устанавливается в проектноеположение после изготовления, ширина опирания балки
на стены меньше 200 мм, при этом соотношение длины
балки к ширине опирания больше 15/1 и в конструкции
балки не предусмотрены закладные детали для жесткого
соединения с другими элементами конструкции, то такая
железобетонная балка однозначно должна
рассматриваться как балка на шарнирных опорах.
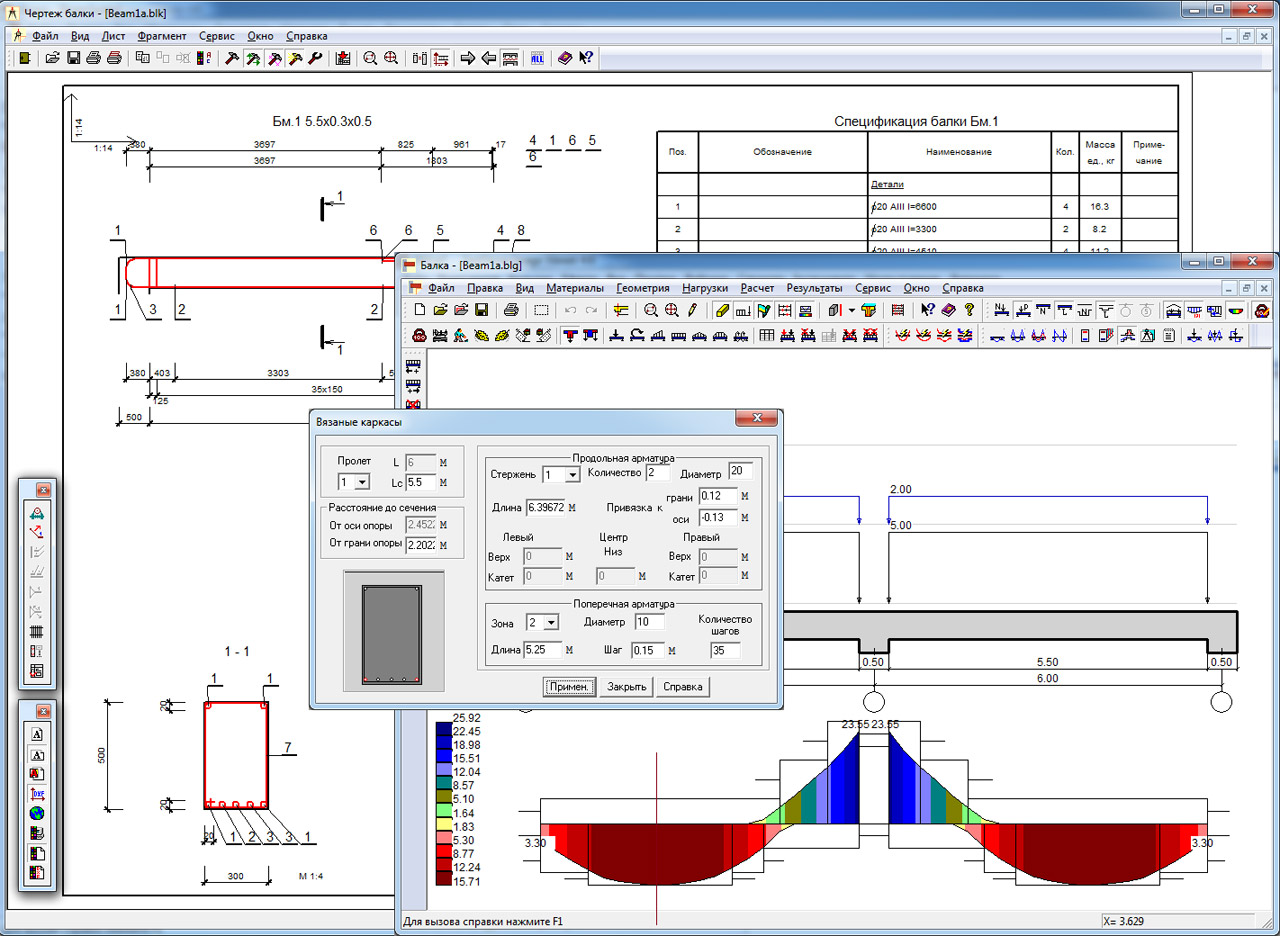 Для
Длятакой балки принято следующее условное обозначение:
8. Балка на двух шарнирных опорах
9. 2. Балка с жестким защемлением на концах
• Если железобетонная балка изготавливается непосредственно вместе установки, то такую балку можно рассматривать, как
защемленную на концах только в том случае, если и балка и
стены, на которые балка опирается, бетонируются
одновременно или при бетонировании балки предусмотрены
закладные детали для жесткого соединения с другими
элементами конструкции. Во всех остальных случаях балка
рассматривается, как лежащая на двух шарнирных опорах. Для
такой балки принято следующее условное обозначение:
10. 2. Балка с жестким защемлением на концах
11. 3. Многопролетная балка.
• Иногда возникает необходимость рассчитать железобетоннуюбалку перекрытия, которая будет перекрывать сразу две или даже
три комнаты, монолитное железобетонное перекрытие по
нескольким балкам перекрытия или перемычку над несколькими
смежными проемами в стене.
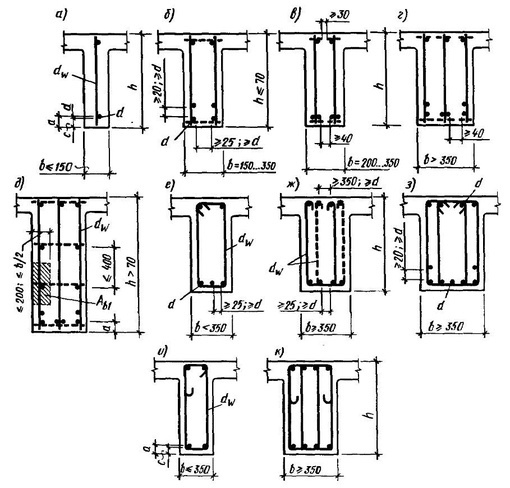 В таких случаях балка
В таких случаях балкарассматривается как многопролетная, если опоры шарнирные. При
жестких опорах количество пролетов значения не имеет, так как
опоры жесткие, то каждая часть балки может рассматриваться и
рассчитываться как отдельная балка.
13. 4. Консольная балка
• Балка, один или два конца которой не имеют опор, аопоры находятся на некотором расстоянии от концов
балки, называется консольной. Например плиту
перекрытия над фундаментом, выступающую за
пределы фундамента на несколько сантиметров,
можно рассматривать как консольную балку, кроме
того перемычку, опорные участки которой больше l/5
также можно рассматривать как консольную и так
далее.
14. Консольная балка.
15. 3. Определение нагрузки на балку 4. 5.
16. Проверка прочности по касательным напряжениям.
17. Прочность по наклонным сечениям
18. Ширина приопорных участков
19. Прогиб
•f = k5qlᶣ/384EIpСП 20.
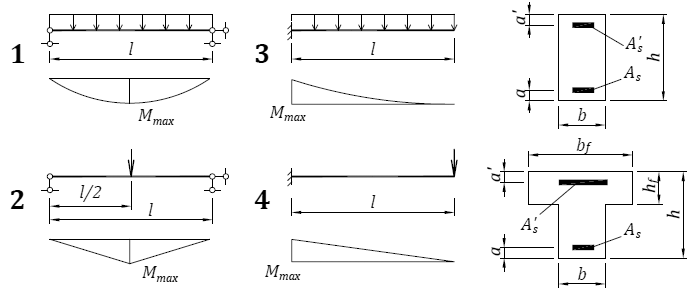 13330.2016 Нагрузки и воздействия.
13330.2016 Нагрузки и воздействия.Актуализированная редакция СНиП 2.01.07-85*
(с Изменениями N 1, 2)
т. Д.1
Расчет ж.б. балки (добавлен exe), стойки и рамы + исходники и пособие по работе.
Васькин Влад
размещено: 15 Ноября 20103. Программа расчёта внецентренно-сжатых ж/б элементов WinStoika.
3.1. Общее описание
Программа предназначена для расчёта внецентренно-сжатых ж/б элементов по предельным состояниям I и II групп и производит следующие расчёты :
1) — учёт влияния длительности действия нагрузки;
2) — учёт случайного эксцентриситета;
3) — учёт влияния прогиба элемента на величину изгибающего момента;
4) — расчёт элементов по I группе предельных состояний :
• — проверку прочности сечения;
• — подбор продольной арматуры
5) — расчёт элементов по II группе предельных состояний :
• — по образованию трещин, нормальных к продольной оси элемента;
• — по раскрытию трещин, нормальных к продольной оси элемента;
• — определение кривизны элемента :
— на участке без трещин в растянутой зоне;
— на участке с трещинами в растянутой зоне
4.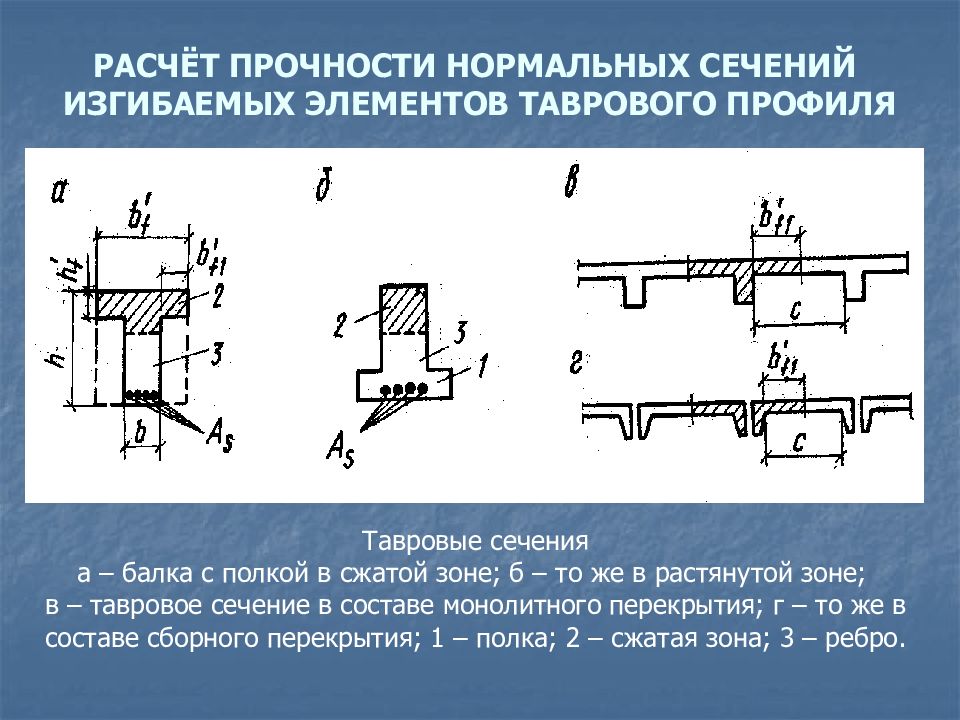 Программа расчёта изгибаемых ж/б элементов WinBalka.
Программа расчёта изгибаемых ж/б элементов WinBalka.
4.1. Общее описание
Программа предназначена для расчёта изгибаемых ж/б элементов по пре-дельным состояниям I и II групп и производит следующие расчёты :
1) — расчёт элементов по I группе предельных состояний :
• — проверка прочности нормальных сечений, подбор продольной арматуры;
• — проверка прочности наклонных сечений по сжатой полосе и по наклонной трещине, подбор поперечной арматуры;
2) — расчёт элементов по II группе предельных состояний :
• — по образованию трещин, нормальных и наклонных к продольной оси элемента;
• — по раскрытию трещин, нормальных и наклонных к продольной оси элемента;
• — по деформациям;
— определение кривизны элемента :
— на участке без трещин в растянутой зоне;
— на участке с трещинами в растянутой зоне;
— определение прогибов элемента;
5. Программа расчёта поперечной ж/б рамы одноэтажного промышленного здания WinRama.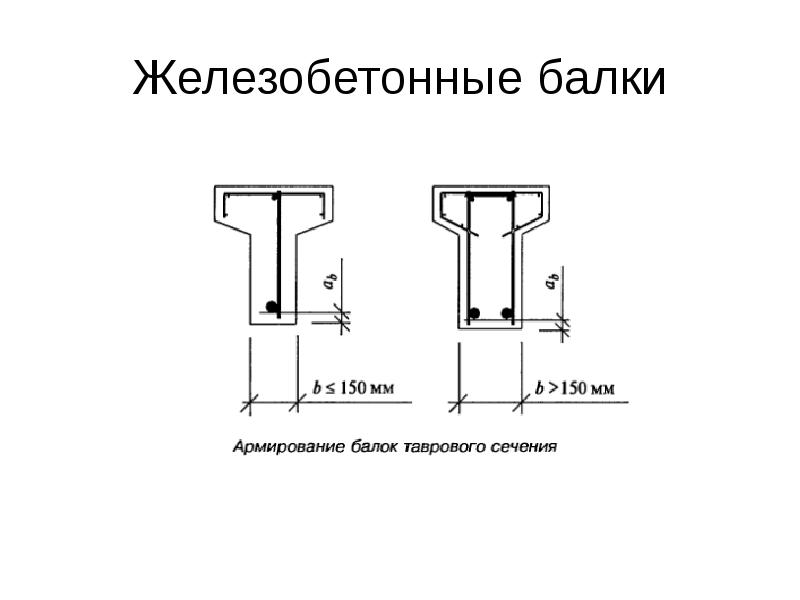
5.1. Общее описание
Программа предназначена для расчёта ж/б поперечных рам одноэтажных промышленных зданий с различным количеством пролётов.
| ||||||||||||||||||||||
Расчёт железобетонной балки по допускаемым напряжениям
Содержание:
Расчёт железобетонной балки по допускаемым напряжениям
- Расчет железобетонных балок на допустимые напряжения.
 На практике часто встречаются балки, изготовленные из разнородных материалов. Деревянные балки могут быть укреплены снизу стальными пластинами. В железобетонных балках стальная арматура размещается в растянутой зоне.§ 105] расчет
На практике часто встречаются балки, изготовленные из разнородных материалов. Деревянные балки могут быть укреплены снизу стальными пластинами. В железобетонных балках стальная арматура размещается в растянутой зоне.§ 105] расчет
допустимого напряжения 345 В этих случаях предполагается, что разрозненные элементы, из которых изготовлены балки, будут соединены между собой, и их совместная работа будет обеспечена. Он считает, что поперечное сечение такой сложной балки
остается плоским при деформации и вращается вокруг нейтральной оси. Людмила Фирмаль
В результате этого положения следует линейный закон распределения удлинения и укорочения по высоте балки: Z формула для вычисления-p’нормального напряжения имеет вид а=ее=Е-;Р’ При этом в расчетах, конечно, необходимо учитывать различные значения модуля Е для такого сложного балочного материала. Приведена структурная схема железобетонной балки. В нижней
(растянутой) части 271 балки размещена арматура в виде трех стальных стержней. Я 1-1 / ; з—————————————————— /1 Семь. Но. Один. Фигура. 271. При расчете такой балки, 1) бетон не испытывает растягивающих напряжений;2) благодаря сцеплению крюка и бетона арматура работает совместно с последней, и все это делается таким же образом. Для того чтобы получить расчетную формулу для рассматриваемой балки, необходимо в основном повторить выводы, изложенные в§ 78 и 79. Верхние волокна пучка
Я 1-1 / ; з—————————————————— /1 Семь. Но. Один. Фигура. 271. При расчете такой балки, 1) бетон не испытывает растягивающих напряжений;2) благодаря сцеплению крюка и бетона арматура работает совместно с последней, и все это делается таким же образом. Для того чтобы получить расчетную формулу для рассматриваемой балки, необходимо в основном повторить выводы, изложенные в§ 78 и 79. Верхние волокна пучка
- сжимаются, нижние волокна растягиваются, и нейтральный слой проходит через расстояние Zq, которое находится от верхнего края пучка. Если предположить, что поперечное сечение остается плоским при изгибе, то можно видеть, что удлинение и укорочение изменяются по закону прямых линий(рис. 272). Умножение модуля упругости материала, соответствующего относительной деформации в каждой точке, дает график распределения нормального напряжения(рис. 273). Напряжение стальной арматуры значительно больше, чем у бетона, так как модуль упругости стали EC примерно в 10-15 раз больше, чем у бетона E$модуль упругости.
 Среднее
Среднее
значение EC=210E kg] cm2; E$=140 000 — [200 000 K g] можно считать в cm2. 346 расчет железобетонных балок[гл. XVII Максимальное напряжение сжатия бетона показывает ад. Растягивающие напряжения в Стали можно считать одинаковыми по всей площади арматуры, так как ее диаметр меньше высоты поперечного сечения; эти напряжения показаны. Назовем расстояние от сжатого края сечения до центра тяжести поперечного сечения арматуры Fa rebar; высота сечения до ширины S\fre h- В § 91. Область Отношение модуля упругости — =g — =I=10 4-15. Из состояния равновесия отрезанной части балки получают нейтральное осевое расстояние от
вершины балки и величину напряжения. 1)сумма сжимающих напряжений Людмила Фирмаль
равна сумме напряжений, а 2) сумма моментов внутренней силы относительно нейтральной оси O равна изгибающему моменту. Сила сжатия D может быть рассчитана тем же методом, что и расчет силы Ntbdz на расстоянии Z от нейтральной оси (рис. 274) AB dz\сумма сжимающих сил имеет равную силу (£) = В Abdz; Но согласно линейному закону напряжения И так оно и есть. Сила растяжения якоря равна Z C=F1, и AC » первое уравнение равновесия принимает форму(рис. 273): — D+Zz=0, или D=Zc, Или — ’+Л А С=°-(17.1) Напряжение переменного тока может быть выражено через ad. Из линейного закона деформации (рис. 272) имеют: Но С»2. • OS=E SGS и sd=£6ed ,
274) AB dz\сумма сжимающих сил имеет равную силу (£) = В Abdz; Но согласно линейному закону напряжения И так оно и есть. Сила растяжения якоря равна Z C=F1, и AC » первое уравнение равновесия принимает форму(рис. 273): — D+Zz=0, или D=Zc, Или — ’+Л А С=°-(17.1) Напряжение переменного тока может быть выражено через ad. Из линейного закона деформации (рис. 272) имеют: Но С»2. • OS=E SGS и sd=£6ed ,
И так оно и есть., E h z h g§ 106] расчет допустимой нагрузки 347 Уравнение равновесия (17.1) принимает вид −1+Фаадн-о. Преобразование, мы получаем: Из этого уравнения находим положение нейтрального слоя z0′. (17.2) Зная Z0, мы можем составить второе уравнение равновесия. Но учтите, что сила D приложена к центру масс треугольника. Мощность D и Z равны — — — — — второе уравнение: o Или (17.3) Таким образом, получаем формулу для напряжения бетона: 2L4 (17.4) Зная АРФ, находим напряжение переменного тока, а именно якорь: Zc D vd zj) M С=~/1a1A п сек. (17.5)) Испытание на прочность в этом случае следует проводить в соответствии с формулами maxar f^[A clK]и shahas * ^[C], где [asj] — допустимое напряжение сжатия бетона, а[a] — случай растяжения стали.
Смотрите также:
СП63. Расчет минимального и максимального армирования балок прямоугольного сечения
Минимальное и максимальное как продольное, так и поперечное армирование балок прямоугольного сечения вычислено на основе конструктивных требований Раздела 10 СП63.13330.2018.
Минимальное и максимальное армирование балок прямоугольного сечения согласно СП63.13330.2018
Конструктивные требования Раздела 10 СП63.13330.2018 определяют диапазоны значений площадей как продольной As, так и поперечной Aswарматуры в сечениях железобетонных элементов.
Конструктивные требования к геометрическим размерам и армированию железобетонных элементов являются обязательными к выполнению в соответствии с пунктом 10.1.1 СП63.
Расчет минимального и максимального продольного армирования реализован на основе требований пунктов 10.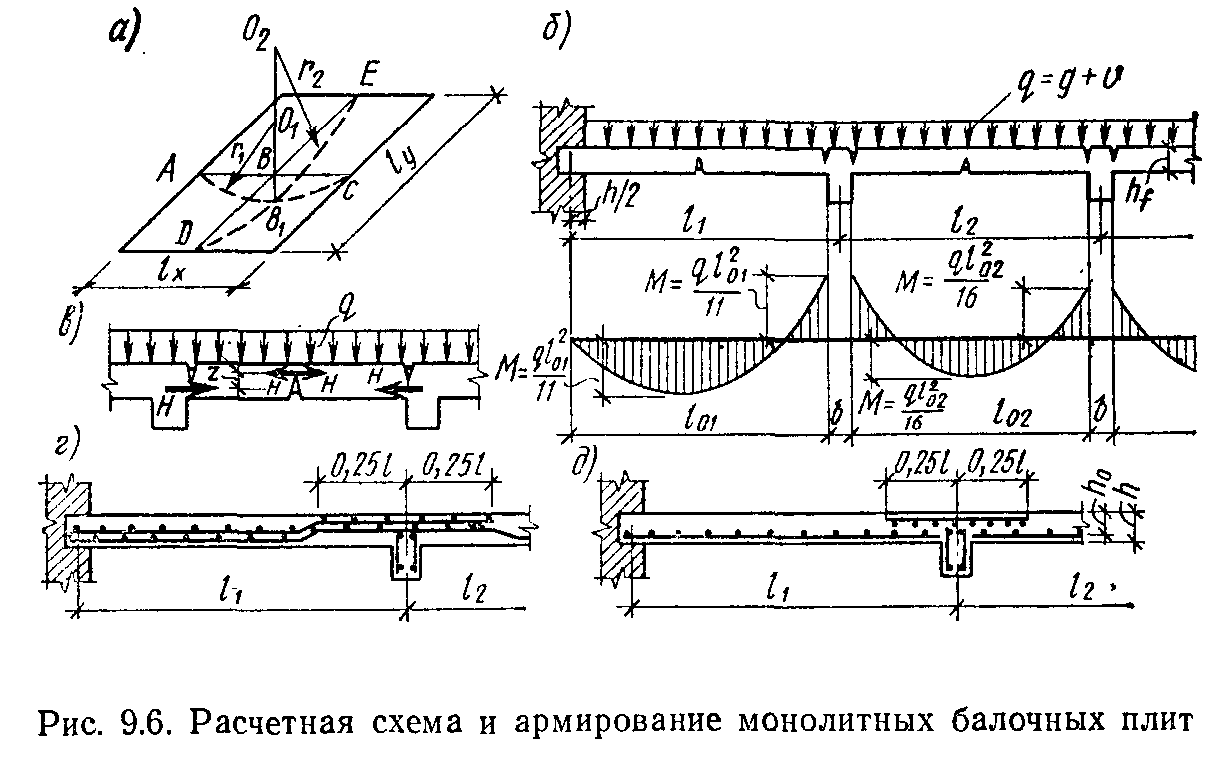 2.1, 10.2.2, 10.3.5, 10.3.6, 10.3.8 и 10.3.9; расчет поперечного – 10.3.11, 10.3.12, 10.3.13, 10.3.14, 10.3.16 и 10.3.33.
2.1, 10.2.2, 10.3.5, 10.3.6, 10.3.8 и 10.3.9; расчет поперечного – 10.3.11, 10.3.12, 10.3.13, 10.3.14, 10.3.16 и 10.3.33.
СОДЕРЖАНИЕ
1. Продольное армирование балок прямоугольного сечения
1.1 Комментарии и ограничения в реализации
1.2. Минимальное продольное армирование As,min
1.3. Расчет максимального продольного армирования As,max
2. Поперечное армирование балок прямоугольного сечения
2.1. Комментарии и ограничения в реализации
2.2. Минимальное поперечное армирование Asw,min
2.3. Расчет максимального поперечного армирования Asw,max
1. Продольное армирование балок прямоугольного сечения
Расчет выполняется для продольных стержней арматуры фиксированного диаметра, расположенных в один ряд*. Арматурный ряд располагается вдоль стороны “b” прямоугольного сечения балки, см. Рисунок 1.1.
Принят номинальный диаметр арматурных стержней ds, без учета высоты рифов в случае периодического профиля. **
**
Центрально растянутые элементы в данном расчете не рассматриваются.
Требования пунктов 10.2.1 и 10.3.5 не имеют количественных критериев выполнения (в части возможности размещения арматуры, качественного уплотнения бетонной смеси и др.), потому их реализация обеспечивается субъективным решением проектировщика в каждой конкретной проектной ситуации.
Осуществляется входной контроль величины защитного слоя бетона в рамках пункта 10.3.2 СП63.13330.2018. Более строгие требования к величине защитного слоя могут быть предъявлены со стороны других нормативных документов в части условий обеспечения долговечности, требуемой огнестойкости и др.
* – результаты расчетов возможно распространить на случай многорядного армирования, при этом необходимо контролировать соблюдение пункта 10.3.5 и учитывать смещение центра тяжести растягиваемых/сжимаемых арматурных стержней.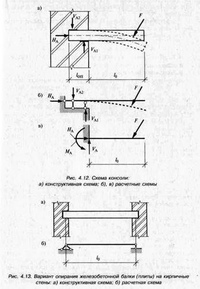
** – в рамках данного расчета высота рифов влияет на расстояние между продольными стержнями “в свету” smin и величину бокового защитного слоя бетона cs. Учет высоты рифов возможен косвенно, через задание соответствующих значений smin и cs.
1.2. Минимальное продольное армирование
As,minМинимальный процент продольной растянутой арматуры μmin, а также требуемой по расчету сжатой, в явном виде определен пунктом 10.3.6 в зависимости от вида напряженно-деформированного состояния (НДС) и формы поперечного сечения. Соответствующая площадь минимального армирования вычисляется по формуле As,min = μmin · b · (h – c)*.
Конструирование минимального армирования не осуществляется. Результаты расчета содержат вычисленную As,min и максимальное расстояния между осями стержней в соответствии с СП63.
В случае неопределенности выбора вида НДС (работа на множество сочетаний нагрузок, статическая неопределимость ЖБК) рекомендуется принимать внецентренное сжатие, так как при прочих равных условиях минимальное армирование будет наибольшим.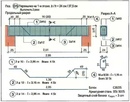
* – в “запас” надежности рабочая высота сечения принята равной h0 = h – c вместо h0 = h – c – 0.5⋅ds, где ds – диаметр арматурных стержней при конструировании минимального армирования.
1.3. Расчет максимального продольного армирования
As,maxМаксимальный процент армирования μmax в явном виде не определен нормами СП63, но может быть вычислен* на основе нормируемого пунктом 10.3.5 минимального расстояния между арматурными стержнями smin и диаметра ds,max, назначенного проектировщиком.
Максимальный процент растянутой или сжатой арматуры μmax достигается при размещении по полезной ширине сечения b – 2·cs максимума площади армирования As,max, соответствующей целому числу арматурных стержней с расстоянием “в свету” не более smin.
Диапазон диаметров арматурных стержней при поиске максимума As,max имеет границы от 6 мм до ds,max, где ds,max по умолчанию не превышает 1/10 высоты сечения h. Значение верхней границы диапазона может быть переопределено.
Значение верхней границы диапазона может быть переопределено.
Минимальное расстояние между стержнями “в свету” smin по умолчанию принято наименьшему возможному значению, определенному пунктом 10.3.5. Рекомендуется переопределять smin в сторону увеличения для обеспечения требований по размещению арматуры и качества уплотнения бетонной смеси.
Учитывая неопределенности в назначении smin и соответствующего ds,max, в первую очередь из-за необходимости выполнения качественных конструктивных требований (см. Раздел 1.1), процент армирования μmax носит субъективный характер. Вычисляемый μmax может, в том числе, рассматриваться просто как процент армирования балки прямоугольного сечения μ при заданном диаметре стержней ds не превышающих расстояния s между ними.
* – результаты расчета зависят от субъективного решения проектировщика по обеспечению выполнения конструктивных требований не имеющих количественных критериев.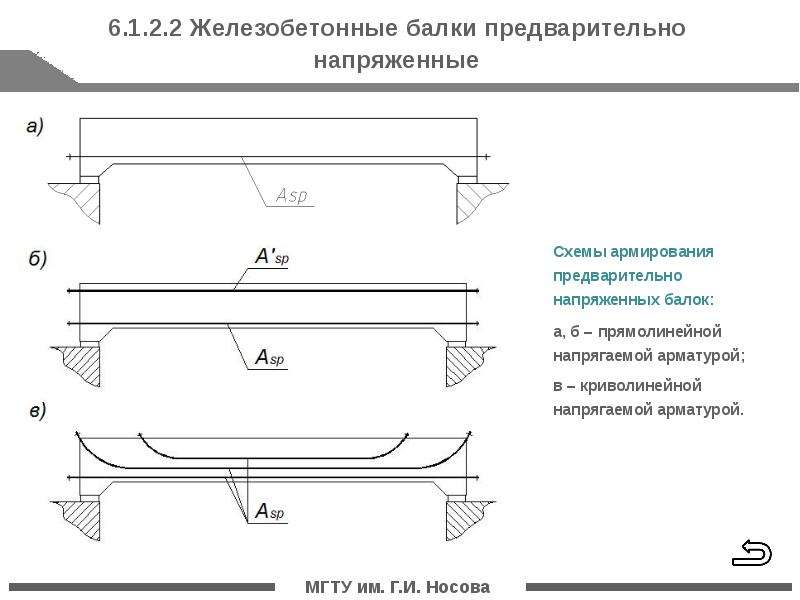 У разных проектировщиков могут быть получены различные результаты в одной и той же проектной ситуации.
У разных проектировщиков могут быть получены различные результаты в одной и той же проектной ситуации.
2. Поперечное армирование балок прямоугольного сечения
Поперечное армирование устанавливается у всех поверхностей железобетонных элементов, вблизи которых расположены стержни продольной арматуры, пункт 10.3.11 СП63.13330.2018. Армирование должно образовывать замкнутый контур в случае воздействия крутящих моментов, пункт 10.3.16 СП63.
Рисунок 2.1 – Поперечное армирование: шпилька, открытый и замкнутый хомутКонструирование поперечного армирования напрямую зависит от продольного, так как расположение поперечной арматуры привязано к продольным стержням, см. Рисунок 2.1. Таким образом, установлено следующее взаимодействие пользователя с программой.
По умолчанию для поперечного армирования установлен переключатель “Расчет не требуется”. При нажатии “Расчет” результаты продольного армирования замораживаются и передаются в расчет поперечного армирования как исходные данные.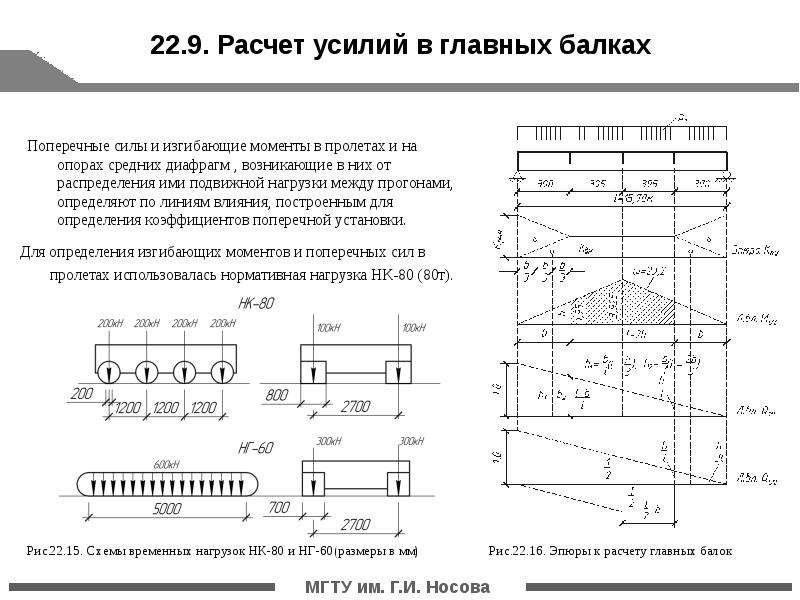 “Коррекция продольного” позволяет разморозить и изменить данные по продольному армированию, при этом соответствующие изменения в поперечном армировании будут учтены при последующем нажатии на “Расчет”.
“Коррекция продольного” позволяет разморозить и изменить данные по продольному армированию, при этом соответствующие изменения в поперечном армировании будут учтены при последующем нажатии на “Расчет”.
Минимальные Asw,min и максимальные Asw,max площади и соответствующие им μsw,min и μsw,max проценты поперечного армирования явным образом не определены в СП63. Значения Asw,min и Asw,max вычислены косвенно, на основе конструктивных требований к минимальному диаметру dsw,min и минимальному/максимальному шагу поперечных стержней sw,min / sw,max, см. пункты 10.3.12, 10.3.5 и 10.3.13 соответственно.
Стержни поперечного армирования (шпильки и/или ветви хомутов) расположены с фиксированным шагом sw вдоль стороны сечения “b” и ориентированы под углом 90° к продольной оси балки. Все стержни приняты одинаковыми, с номинальным диаметром dsw.
Шаг sw определяется по центрам стволов поперечных стержней, загиб шпилек при определении минимального расстояния не учитывается, см.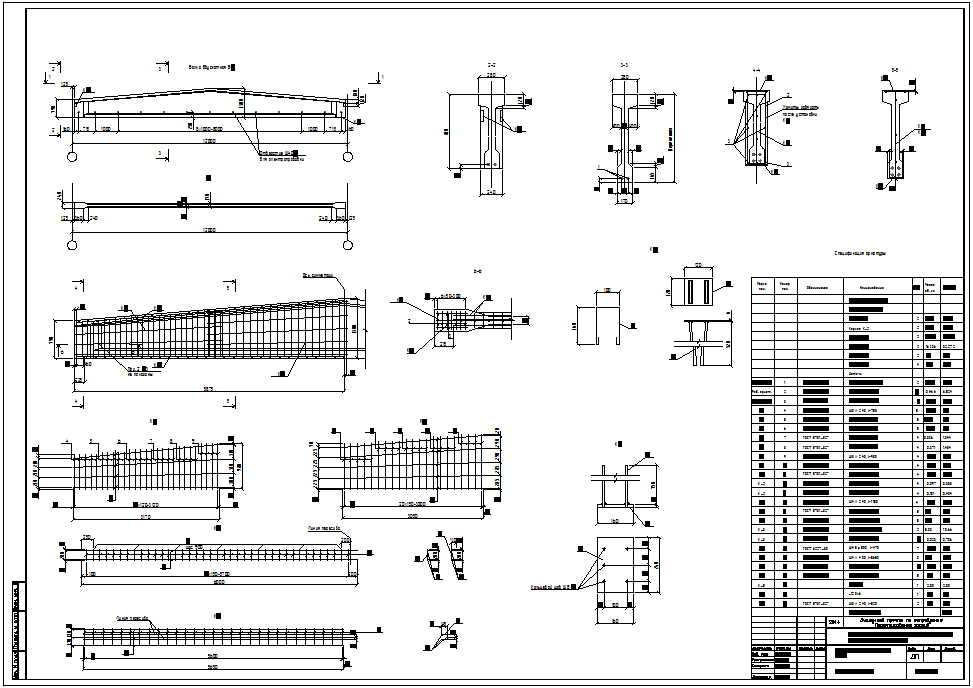 Рисунок 2.1.1.
Рисунок 2.1.1.
Площади поперечного армирования Asw,min и Asw,max вычислены в см2 на погонный метр длины балки.
Минимальный и максимальный процент поперечного армирования определен формулами μsw,min = Asw,min / (b · sw,max) и μsw,max = Asw,max / (b · sw,min) соответственно.
Нижний и верхний защитный слой поперечного армирования csw вычислен как csw = c – dsw, боковой csw,s = cs – dsw – 0.5·(dоп – ds,max), где dоп – диаметр оправки согласно пункту 10.3.33. Если ds,max ≥ dоп, то поперечный стержень изгибается по продольному (пунктир на Рисунке 2.1.2) и третье слагаемое в csw,s принимается равным нулю.
Рисунок 2.1.2 – Защитный слой бетонаМинимальная величина защитных слоев бетона поперечного армирования csw и csw,s контролируется программой и составляет не менее dsw и 10 мм согласно требованиям пункта 10.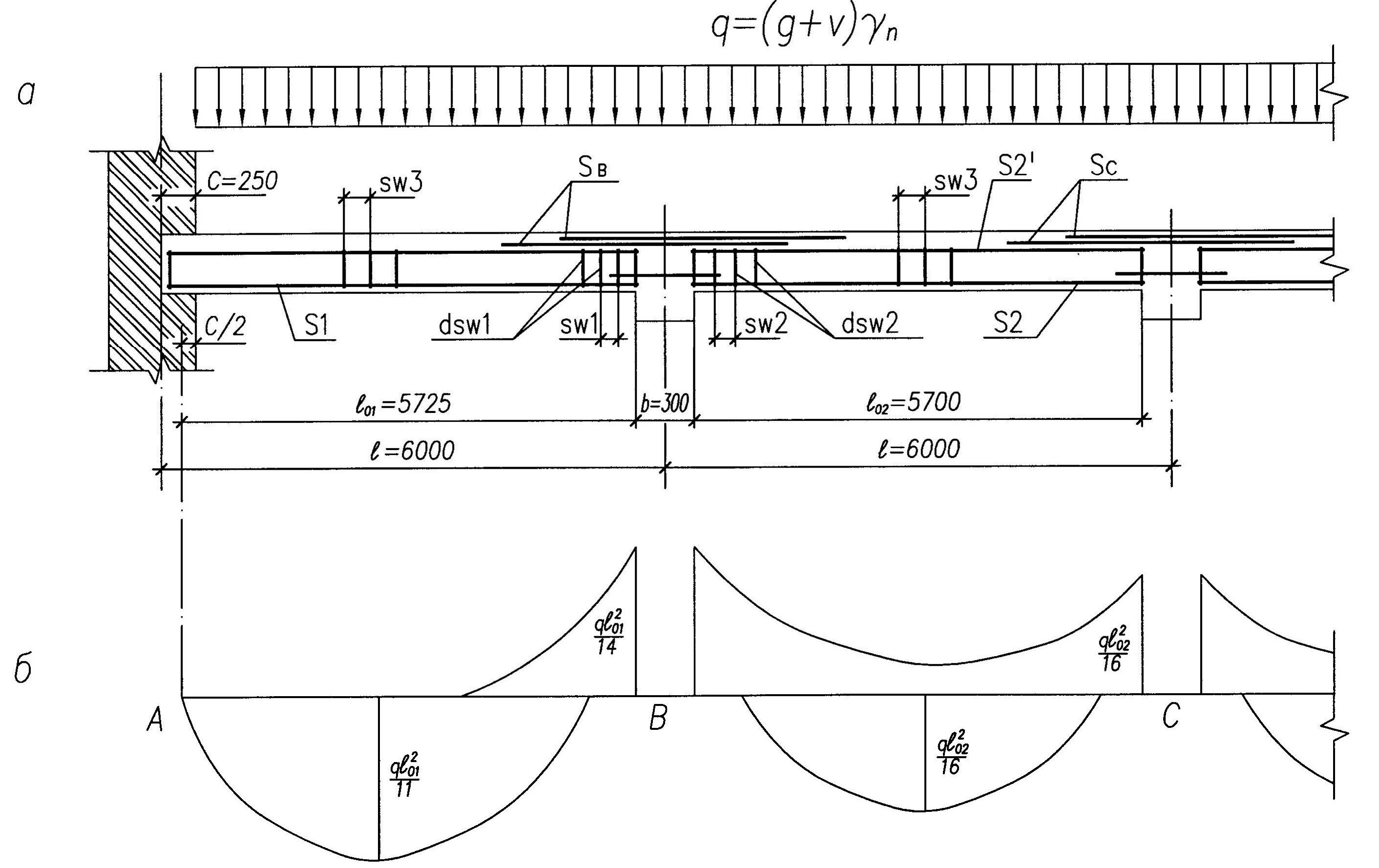 3.2. Требуемый в каждой конкретной проектной ситуации защитный слой назначается проектировщиком и обеспечивается через соответствующее задание с, cs, dsw и ds,max.
3.2. Требуемый в каждой конкретной проектной ситуации защитный слой назначается проектировщиком и обеспечивается через соответствующее задание с, cs, dsw и ds,max.
В балках прямоугольного сечения шириной более 150 мм устанавливается замкнутый внешний хомут, обрамляющий сечение по крайним продольным стержням.
2.2. Минимальное поперечное армирование
Asw,minМинимальное армирование балок Asw,min вычислено* из условия размещения по полезной ширине прямоугольного сечения b – 2·(cs – dsw,min) целого числа поперечных стержней минимального диаметра dsw,min с шагом, cтремящимся к наибольшему шагу по СП63, sw -> sw,max. Шаг поперечных стержней по направлению вдоль балки принят sw,max, см. Рисунок 2.2.1.
Рисунок 2.2.1 – Схема к расчету минимального поперечного армирования балки прямоугольного сечения* – для простоты, не учтена взаимная увязка расположения стержней продольного и поперечного армирования.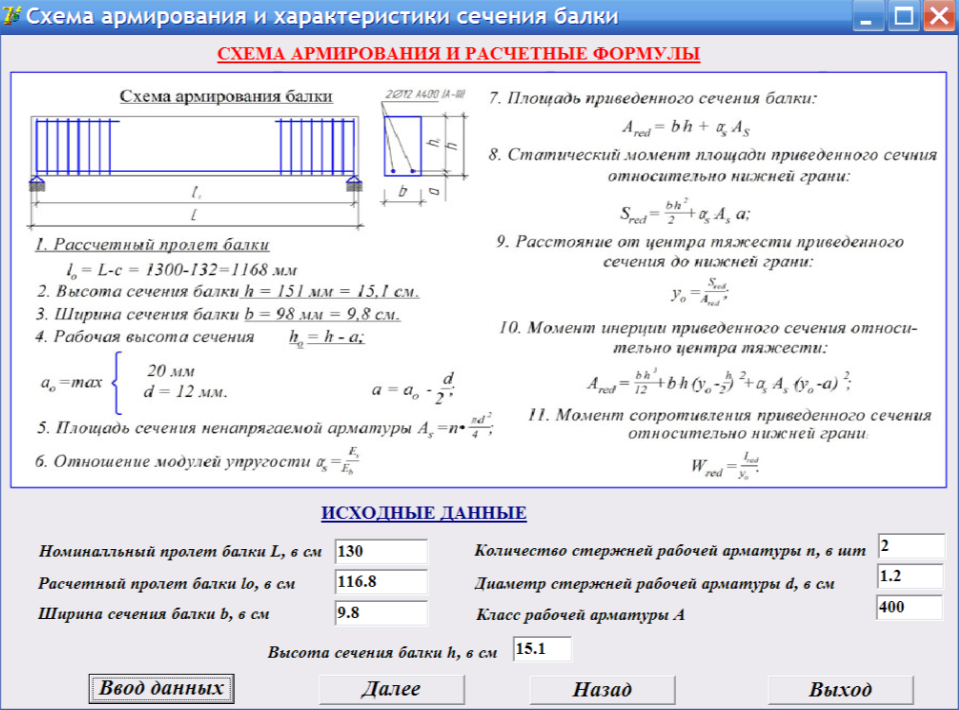 Таким образом, армирование вычисляется “с запасом”, его абсолютный минимум достигается при sw = sw,max.
Таким образом, армирование вычисляется “с запасом”, его абсолютный минимум достигается при sw = sw,max.
2.3. Расчет максимального поперечного армирования
Asw,maxРасчет Asw,max выполнен на основе результатов расчета продольного армирования As,max из Раздела 1.3. В качестве исходных данных принято расстояние между центрами продольных стрежней s, их количество и диаметр ds.
Рисунок 2.2.2 – Схема к расчету максимального поперечного армирования балки прямоугольного сеченияМаксимальное поперечное армирование соответствует* расположению поперечных стержней заданного диаметра dsw,max с шагом sw=s, то есть, на каждом продольном стержне. В случае, если шаг поперечного армирования менее минимального нормативного sw < sw,min, то sw увеличивается кратно s вплоть до выполнения условия sw ≥ sw,min.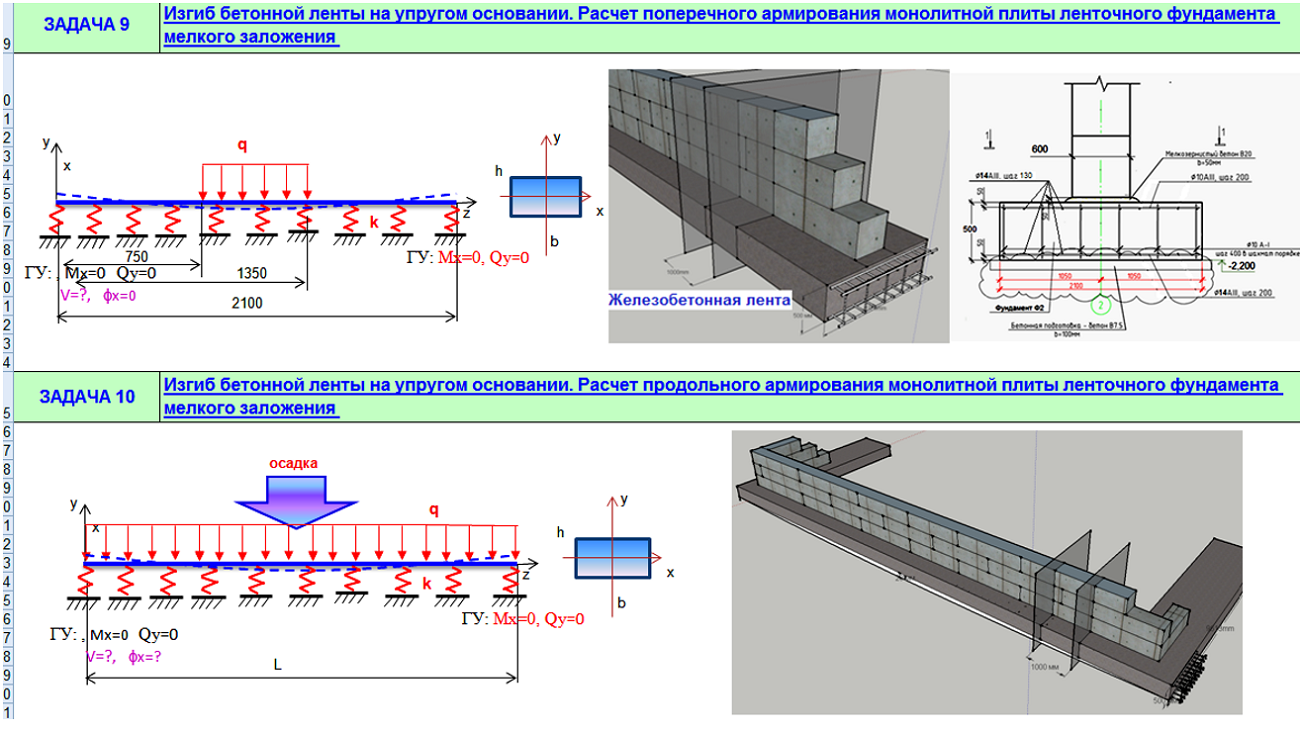
Крайние поперечные стержни соответствуют ветвям замкнутого внешнего хомута, обрамляющего сечение по крайним продольным стержням (b > 150 мм).
Максимальный диаметр dsw,max ограничен условием размещения внешнего замкнутого хомута учитывая радиуса оправки по пункту 10.3.33 СП63.
По аналогии с Разделом 1.3, вычисляемый процент армирования μsw,max может, в том числе, рассматриваться просто как процент армирования балки прямоугольного сечения μsw при заданном диаметре стержней dsw не превышающих расстояния sw между ними.
* – результаты расчета зависят от субъективного решения проектировщика по обеспечению выполнения конструктивных требований не имеющих количественных критериев, см. Раздел 1.1.
Использование данного расчета означает факт согласия с Отказом от ответственности.
Актуальность СП63.13330.2018 рекомендуется проверять на официальном сайте ФАУ ФЦС.
Замечания и предложения по данному расчету можно направить через форму обратной связи.
Любое использование материалов сайта допускается лишь с разрешения правообладателя и только со ссылкой на источник: www.RConcreteDesign.com
Общие положения по конструктивным требованиям
Конструктивные требования к геометрическим размерам железобетонных элементов
Минимальные размеры сечений внецентренно сжатых элементов
Минимальный защитный слой бетона
Минимальные расстояния в свету между арматурными стержнями
Минимальный процент продольного армирования
Максимальное расстояние между продольными арматурными стержнями
Минимальное количество продольных стержней в балках и ребрах в зависимости от ширины сечения
Установка и расположение поперечного армирования
Минимальный диаметр стержней поперечного армирования
Максимальный шаг поперечного армирования
Максимальный шаг поперечного армирования в случае требуемой по расчету сжатой продольной арматуры
Конструкция хомутов во внецентренно сжатых линейных элементах
Поперечное армирование при действии крутящих моментов
Минимальный диаметр загиба арматурного стержня
Калькулятор прочности и прогиба балки
Балка или стержень – это любой конструктивный элемент, длина которого значительно превышает его ширину или глубину. Однако термин «значительно» означает разные вещи для разных людей. Некоторым достаточно вдвое большей длины, другие сочтут пятикратную длину слишком короткой и поэтому сочтут такой элемент пластиной, рамой или конструкцией. Процедуры расчета балок не налагают таких ограничений или различий.
Однако термин «значительно» означает разные вещи для разных людей. Некоторым достаточно вдвое большей длины, другие сочтут пятикратную длину слишком короткой и поэтому сочтут такой элемент пластиной, рамой или конструкцией. Процедуры расчета балок не налагают таких ограничений или различий.
Балки обычно используются для несущей нагрузки, в то время как опоры перекрываются на большом расстоянии друг от друга, например, пол (см. Калькулятор этажей CalQlata).При указании балки необходимо определить ее максимальную грузоподъемность (т. е. ее прочность) и ее максимально допустимый прогиб.
Прочность и жесткость балки
Прочность балки зависит от предела текучести материала, из которого изготовлена балка, тем самым определяя максимальную нагрузку, которая может быть приложена до того, как балка окончательно деформируется (или сломается, если она изготовлена из хрупкого материала), и
его жесткость зависит от второго момента площади поперечного сечения балки (т.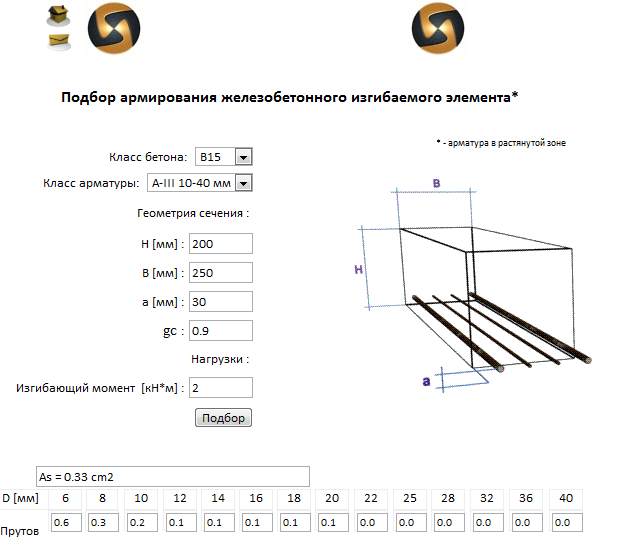 г. Швеллер, двутавровая балка, двутавровая балка, угол и т. д.) вместе с модулем Юнга его материала, тем самым определяя ожидаемый прогиб балки для любой заданной нагрузки
г. Швеллер, двутавровая балка, двутавровая балка, угол и т. д.) вместе с модулем Юнга его материала, тем самым определяя ожидаемый прогиб балки для любой заданной нагрузки
Обе вышеуказанные характеристики определяют поведение балки под нагрузкой.
Дизайн балки
Предположим, у вас есть равномерно распределенная нагрузка в 4000 Н на балке длиной 4 м (1 Н/мм) и максимально допустимый прогиб, скажем, 1/200 длины балки (20 мм).
Используя Балки, вы вводите известную информацию и изменяете второй момент площади (I), пока не получите желаемое отклонение (20 мм в середине балки, где ее отклонение будет наибольшим), что в данном случае дает вам значение для I около 800000 мм⁴.
Предполагая, что вы планируете использовать секцию швеллера, отсортировав швеллеры в базе данных стальных секций CalQlata, вы обнаружите, что размер вашей балки должен быть секции «3×6», которая является наименьшей секцией балки со значением I выше 800000 мм⁴, и найдите значение для « y’ (расстояние от нейтральной оси луча до внешней стороны его сечения), которое в данном случае составляет 38,1 мм.
Вы возвращаетесь к Балкам, вводите правильное значение I (863 264 мм⁴), а также вводите значение 38,1 мм для d, чтобы установить максимальное напряжение в материале балки, которое в данном случае составляет 88 Н/мм².
Если это значение находится в пределах ваших требований к безопасности, то ваш луч приемлем. Если нет, но приходится работать с данным материалом, то следует изменить (увеличить) сечение балки, тем самым уменьшая допустимый прогиб до тех пор, пока напряжение не станет приемлемым.
Калькулятор отклонения балки — Техническая помощь
Рис. 1. Схема нагрузки на балку
Предполагается, что любая нагрузка в калькуляторе прочности балок действует одинаково через плоскость или сечение балки во всех направлениях, перпендикулярных (другими словами, под углом 90° к) ее продольной оси.
Если нагрузка локализована в поперечном сечении балки (т. е. распределена по ней неравномерно), могут потребоваться дополнительные расчеты для определения местных (сосредоточенных) реакций и напряжений (см.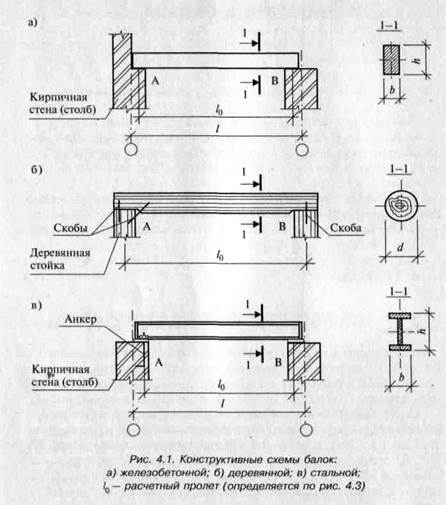 калькуляторы плит и листов CalQlata).
калькуляторы плит и листов CalQlata).
Напряжение при изгибе
Изгибающие напряжения в балках применяются к балке на заданном расстоянии (‘d’) от ее нейтральной оси. Эта входная переменная (‘d’) используется только в расчетах напряжения (σx) и деформации (ex). Если вы оставите это поле пустым или установите его равным нулю, Beams не будет рассчитывать напряжение или деформацию в указанном вами месте вдоль балки (рис. 1 «x»).Никакие другие результаты не будут затронуты.
Условия многократной/одновременной загрузки
Если у вас есть балка с более чем одной приложенной нагрузкой, вы просто суммируете результаты вместе в указанном месте.
Пример расчета прочности балки (рис. 2):
Детали балки:
L = 2000 мм
I = 1,2E+08 мм⁴
E = 2,07E+05 Н/мм²
y = 200 мм
Условия нагрузки 1:
wA и wB = 450 Н/мм
l = 0
Условия нагрузки 2:
F = 150000 Н
l = 700 мм
Расстояние вдоль луча до выхода:
x = 1000
Шаг 1:
Введите данные для балки и условия нагрузки 1 (простая фиксированная / распределенная нагрузка), установив wA (/L) и wB (/L) на 450 футов, скопируйте список данных и вставьте в электронную таблицу.
Шаг 2:
Введите условие нагрузки 2 (простая фиксированная / точечная нагрузка), установив F на 150000, скопируйте список данных и вставьте в ту же таблицу.
Шаг 3:
Добавьте результаты обоих калькуляторов, и вы получите условия в нужном месте.
Рис. 2. Процедура расчета составной нагрузки
Ограничения
Эти расчеты действительны только в том случае, если материал по всей длине и толщине сечения подчиняется закону Гука.
Результаты остаются действительными для этого калькулятора, если прогиб таков, что на длину балки условия нагрузки не оказывают существенного влияния.
Калькулятор больших прогибных балок CalQlata (Flexible Beams) следует использовать, если длина балки изменяется более чем на 5% в результате приложенной нагрузки.
Дополнительное чтение
Дополнительную информацию по этому вопросу можно найти в справочных публикациях (2, 3 и 4)
Калькулятор и таблица веса двутавровой и двутавровой балок (бесплатно)
Что я лучу
Двутавровая балка также называется стальной балкой (Универсальная балка), которая представляет собой длинную стальную полосу с двутавровым поперечным сечением. Двутавр делится на обычный двутавр и легкий двутавр.
Двутавр делится на обычный двутавр и легкий двутавр.Что такое двутавровая балка
Двутавровая балка разработана путем оптимизации двутавровой стали. Название происходит от того, что его сечение совпадает с английской буквой H.Это экономичный высокоэффективный профиль с более разумным соотношением прочности и веса и более оптимизированным распределением площади поперечного сечения.
Каждая часть H-образной стали расположена под прямым углом, поэтому она обладает такими преимуществами, как сильное сопротивление изгибу, экономия затрат, простая конструкция и легкий вес во всех направлениях.
Часто используется в больших зданиях, где требуется большая пропускная способность и хорошая устойчивость поперечного сечения, таких как высотные здания и мастерские.
Кроме того, он также широко используется в судах, мостах, подъемно-транспортных машинах, кронштейнах, фундаментах оборудования, фундаментных сваях и т. д.
Двутавровая балка против двутавровой балки
Что касается разницы между двутавровой и двутавровой балкой, вы можете обратиться к статье ниже.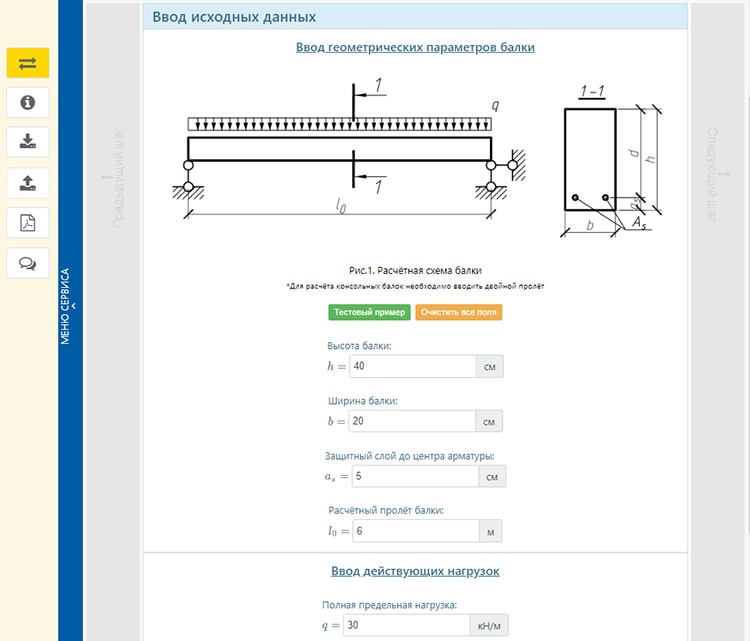
Расчет веса двутавровой балки и двутавровой балки
В этой статье мы в основном обсуждаем, как рассчитать вес двутавровой и двутавровой балки.Для удобства расчета мы создали два калькулятора: калькулятор веса двутавра и калькулятор веса двутавра.
Используя эти два калькулятора, вы можете легко рассчитать вес двутавровой и двутавровой балки. Конечно, для получения дополнительных расчетов различных весов металлов вы можете обратиться к следующей статье.
Теперь начните использовать калькулятор для расчета веса профиля.
Если вам надоело использовать калькулятор для расчета веса двутавровой и двутавровой балок, вы можете обратиться к следующей таблице веса двутавровой и двутавровой балок.Это позволяет быстрее проверять вес двутавровых и двутавровых балок разных размеров.
Расчет несущей способности двутавровой балки
Я полагаю, вы все еще хотите знать, какой вес может выдержать стальная балка? Как рассчитать грузоподъемность стальной балки? Или вы можете узнать, какой размер двутавровой балки вам нужен для вашего строительного проекта.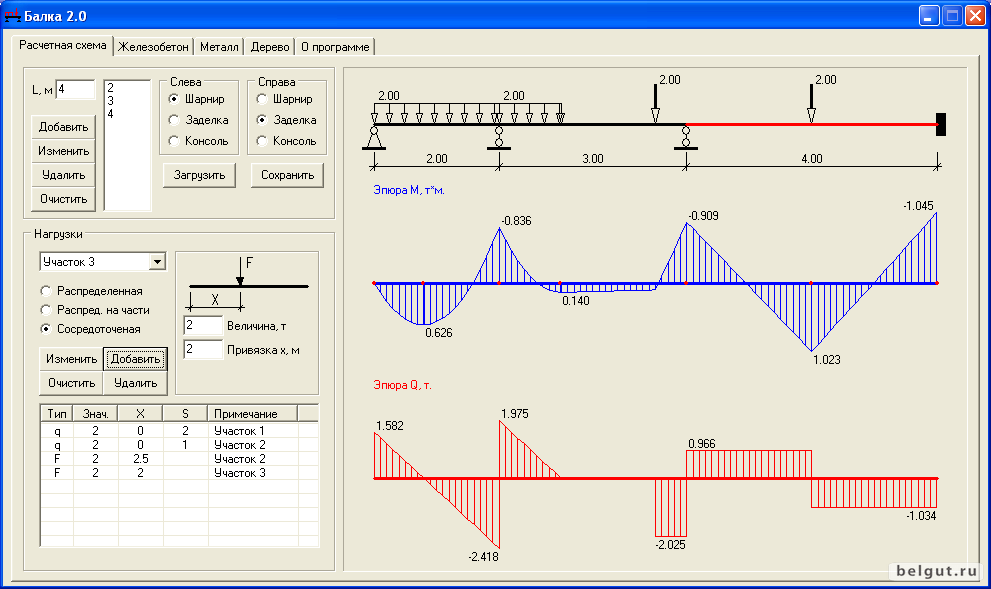
Поэтому мы подготовили для вас этот очень мощный калькулятор грузоподъемности балки, а также диаграмму грузоподъемности, как показано на снимке экрана ниже:
И он в формате Excel, который может быть рассчитан автоматически после ввода необходимых данных.Вы можете загрузить этот инструмент, нажав на ссылку ниже, и не забудьте включить функцию макроса вашего Excel, чтобы он работал правильно.лучей
Приложение для расчета балок
Приложение Beam поддерживает
- расчет размеров
- проверочный расчет
На этапе определения размеров детальный чертеж вала не требуется, выполнить расчет поможет сделанный от руки эскиз.Балка поддерживает также расчет балок с неизменным сечением, таких как стандартные
профили I, U, L, T, прямоугольные и круглые сплошные и полые профили и трубы.
Приложение поддерживает также расчет сварных балок в виде двутавровых и коробчатых балок с переменным или постоянным поперечным сечением.
Пользовательский интерфейс
Beam — это приложение для Microsoft Windows с пользовательским интерфейсом и выводом в только язык английский .Пользователь должен иметь базовые знания в области сопротивления материалов.
Идентификация проекта расчета
При запуске нового проекта расчета открывается диалоговое окно для ввода некоторых данных для идентификации проекта расчета. Это диалоговое окно содержит элементы управления редактированием для ввода в виде: порядка, проекта, подпроекта, элемента, идентификатора луча, рассчитанного, организации, и дата расчета. Предусмотрен элемент управления редактированием для хранения заметки о проекте расчета.
Свойства материалов
Для управления записями материалов предусмотрено диалоговое окно со списком.
Краткое описание записи материала: ID, Cl, Обозначение, E, HBW, d, R m , R p , σ wb , τ wt ,
р, ν
Конфигурация балки
Декартова система координат используется для определения положения поперечного сечения. Ввод начальной и конечной точки луча, количества
опоры и расчетный интервал D z , координат опор и типа опоры.
Ввод начальной и конечной точки луча, количества
опоры и расчетный интервал D z , координат опор и типа опоры.
Короче говоря, на этом веб-сайте в качестве примера рассматривается только проблема проверки.
Перейти на следующую веб-страницу для выбора типа поперечного сечения.
Компоненты подключения
Панель стенки колонны при сдвиге
Компонент рассчитывается в соответствии со статьей 6.2.6.1 стандарта EN 1993-1-8.
Примечания:
(1) Не реализовано.
(2) Расчет в Scia Engineer действителен также для двустороннего соединения, в котором толщина балки неодинакова, или для усиленной панели стенки колонны.
(4) Чтобы учесть дополнительное сопротивление, в настройках соединения должен быть активирован параметр «Использовать ребра жесткости в сопротивлении панели стенки колонны», а в соединении присутствуют как верхний, так и нижний ребра жесткости.
Для расчета сопротивления пластическому моменту полки колонны используется отдельный расчет для каждой полки:
Для расчета сопротивления пластическому моменту ребра жесткости учитывается ширина колонны.
Предполагается, что оба элемента жесткости одинаковы и соответствуют минимальным критериям, основанным на соединении балки. Значения t f,stif и f y,stif принимаются равными балке t f и f y .
Сопротивление V wp,Rd рассчитывается как:
, который должен быть меньше:
(5) Когда диагональный прямоугольный элемент жесткости активируется в соединении, предполагается, что компонент не разрушается, а сопротивление компонента принимается равным бесконечности.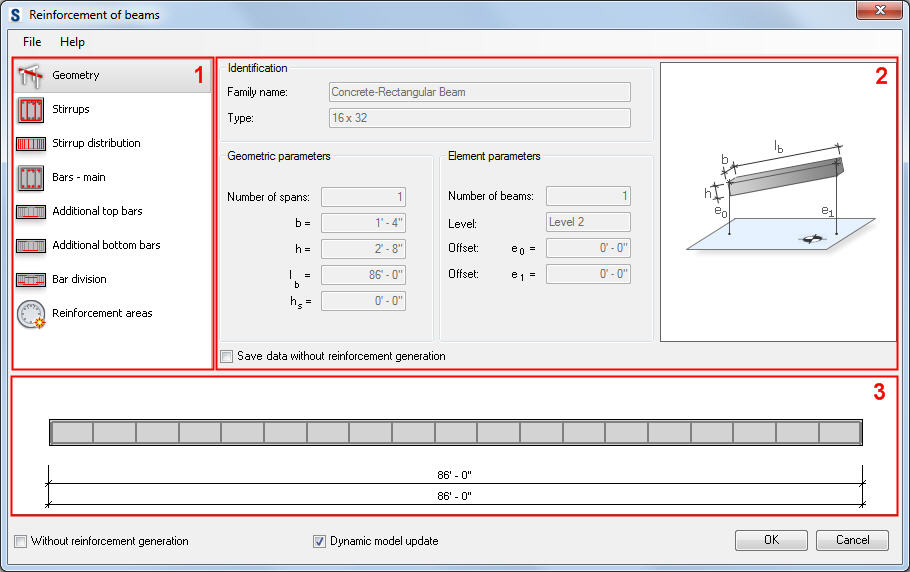
(6) Увеличение площади A vc за счет наличия удвоителя полотна выполнено по артикулу как b s *t w также для корпуса 2 пластины полотна.
(8) — (13) Проверки не реализованы.
Стенка колонны в поперечном сжатии
Компонент рассчитывается в соответствии со статьей 6.2.6.2 стандарта EN 1993-1-8.
Примечания:
(1) Величина b eff , c,wc для болтовых соединений рассчитывается по формуле (6.11), где:
с:
| с p_top | увеличение разброса из-за рассеивания через торцевую пластину в верхней части прижимного фланца |
| с p_bot | увеличение разброса из-за рассеивания через торцевую пластину в нижней части прижимного фланца |
Для болтовых соединений торцевой пластины, как правило, оба расстояния s p_top и s p_bot равны e p из-за отклонения под углом 45°, но если:
- при перпендикулярном соединении нижний выступ торцевой пластины ниже фланца не обеспечивает достаточного пространства для прохода через концевую пластину, т.
 е.e.: расширение меньше, чем (√2)*a + e p ), s p_bot вычисляется как:
е.e.: расширение меньше, чем (√2)*a + e p ), s p_bot вычисляется как:
Эффективная ширина b eff,c,wc для болтового перпендикулярного соединения:
с:
| е р | толщина торцевой пластины |
| и | размер сварного шва фланца |
| т фб | толщина полки балки |
| т фк | толщина полки колонны |
| Пластина bot_ext | нижнее удлинение торцевой пластины |
Та же логика будет использоваться в случае определения вута плиты, так как центр сжатия расположен в пределах полки нижней балки (см. также главу: «Центр сжатия»).
также главу: «Центр сжатия»).
- в ветке с фланцевым соединением, выступ днища торцевой пластины ниже полки не обеспечивает достаточного пространства для распространения от конца сварного шва переменным током (см. также главу: «Веточка с фланцем») через концевую пластину, т.е. : расширение меньше, чем (e p — ( t fl / sin(α) — ac )) в случае ac < t fl / sin(α), или чем ( e p + ( ac — t fl / sin(α) ) ) в случае ac >= t fl / sin(α, s p_bot вычисляется как:
Эффективная ширина b eff,c,wc для болтового соединения вута:
с:
| е р | толщина торцевой пластины |
| т фб | толщина полки балки |
| т фк | толщина полки колонны |
| а в | размер сварного шва между вутом и торцевой пластиной/колонной |
| α | угол между колонной и полкой (градус ввода вута) |
| Пластина bot_ext | нижнее удлинение торцевой пластины |
(2) Чтобы учесть влияние осевой силы и изгибающего момента в колонне на расчетное сопротивление стенки колонны при сжатии, пользователь должен установить флажок «Включить снижение напряжения в стенке» в настройка подключения. Коэффициент уменьшения k wc рассчитывается с учетом расчетных внутренних сил для определения напряжения сжатия σ com,E . Силы снимаются с того же сечения, где расположен центр сжатия.
Коэффициент уменьшения k wc рассчитывается с учетом расчетных внутренних сил для определения напряжения сжатия σ com,E . Силы снимаются с того же сечения, где расположен центр сжатия.
(5) Когда ребро жесткости в месте расположения угла сжатия активируется на стороне колонны соединения, предполагается, что компонент не разрушается, а сопротивление компонента принимается равным бесконечности.
(6) Толщина стенки колонны t wc принимается отдельно, или как 1,5*t wc или 2*t wc , исходя из наличия одного или двух удвоителей стенки. Область сдвига A vc для определения значений ω берется из «Стабильной стенки колонны в компоненте сдвига» (см. также главу: «Панель стенки колонны в сдвигаемой части»).
Стенка колонны при поперечном растяжении
Компонент рассчитывается в соответствии со статьей 6 EN 1993-1-8. 2.6.3.
2.6.3.
Примечания:
(3) Расчетная ширина b eff,t,wc используемая в формуле (6.15) для расчета расчетного сопротивления растяжению стенки колонны F t,wc,Rd для болтового соединения, принимается равна расчетной длине компонента «Полка колонны при поперечном изгибе» с учетом вида разрушения (см. также главу: «Полка колонны при поперечном изгибе»).
(6) Если поперечное ребро жесткости находится в растянутой зоне колонны, считается, что элемент не разрушается, а сопротивление элемента принимается равным бесконечности.
(8) Для расчета t w,eff при наличии дублера стенки принимается, что продольные швы являются угловыми швами с толщиной шва, удовлетворяющей данному условию, поэтому коэффициент 1,4 соответственно 1,3, исходя из используемого материала.
Фланец колонны при поперечном изгибе
Компонент рассчитывается в соответствии со статьей 6. 2.6 стандарта EN 1993-1-8.4.
2.6 стандарта EN 1993-1-8.4.
В EN 1993-1-8 проводится различие между неусиленной (6.2.6.4.1) и усиленной (6.2.6.4.2) полкой колонны, но, поскольку содержание статьи 6.2.6.4.1 может быть также в статье 6.2.6.4.2, приведенные ниже замечания относятся к этой статье.
Примечания:
(1) + (3) См. главу: «Группа рядов болтов».
(2) Альтернативный метод, указанный в статье 6.2.4.1 по таблице 6.2 можно использовать, установив флажок «Использовать альтернативный метод для F t,1,Rd » в настройках подключения. (См. также главу: «Удлинение болта»)
(5) Эффективная длина l eff эквивалентного фланца с Т-образной вставкой основана на значениях для каждого ряда болтов, приведенных в Таблице 6.5, за одним исключением. Это исключение касается расчета некруговой схемы для рядов болтов, классифицируемых как «концевой ряд болтов, примыкающий к элементу жесткости».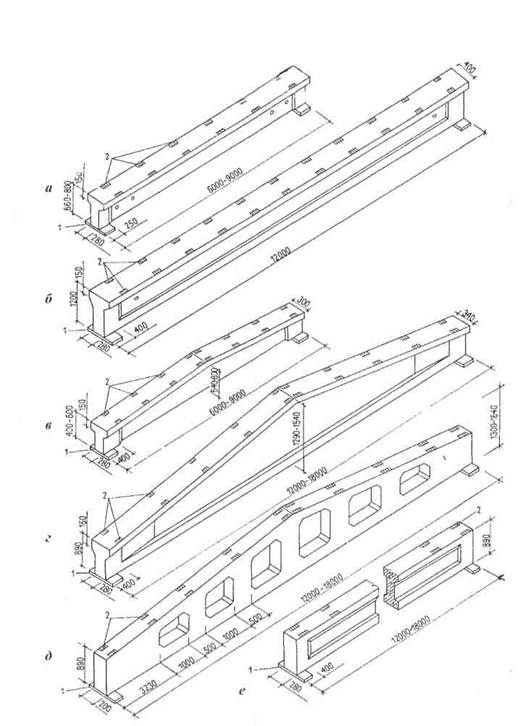 В дополнение к формуле «е 1 +α*m-(2*m + 0,625*e)» используется дополнительный критерий «α*m».Затем минимальное из этих значений используется как l eff,nc . (См. также главы: «Классификация болтовых рядов», «Альфа-коэффициент»)
В дополнение к формуле «е 1 +α*m-(2*m + 0,625*e)» используется дополнительный критерий «α*m».Затем минимальное из этих значений используется как l eff,nc . (См. также главы: «Классификация болтовых рядов», «Альфа-коэффициент»)
Примечание: Вертикальное расстояние e1
EN 1993-1-8, статья 3.5, рисунок 3.1 определяет e1 как конечное расстояние от центра отверстия до соседнего конца полки колонны, измеренное в направлении передачи нагрузки.
В SCIA Engineer это расстояние e1 измеряется от центра краевого болта до соответствующего конца колонны, где определено соединение.Все внутренние узлы с возможными балками и соединениями игнорируются.
(6) Не реализовано.
Торцевая пластина при изгибе
Компонент рассчитывается в соответствии со статьей 6.2.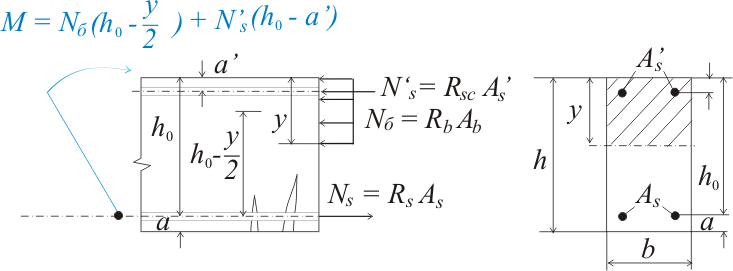 6.5 стандарта EN 1993-1-8.
6.5 стандарта EN 1993-1-8.
Примечания:
(1) Альтернативный метод, указанный в ст. 6.2.4.1 таблицы 6.2, можно использовать, активировав флажок «Использовать альтернативный метод для F t,1,Rd » в настройках подключения.(См. также главу: «Удлинение болта»)
(2) См. главу: «Группа рядов болтов».
(4) В таблице 6.6 не приведены формулы для таких рядов болтов, классифицированных как «ряд болтов вне балки», для расчета эффективных длин l eff для ряда болтов, рассматриваемых как часть группы болтов. ряды. В рамках Scia Engineer это означает, что для конструкции соединения на натянутой стороне торцевой пластины не допускается наличие более одного ряда болтов, классифицированных как «Вне балки».Если на натянутой стороне соединенной балки обнаруживается больше рядов болтов, классифицированных как «Вне балки», отображается сообщение об ошибке, и процесс проектирования соединения прекращается.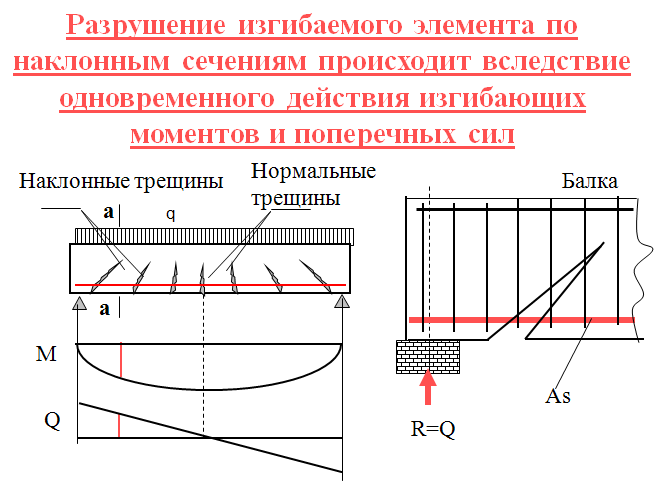 (См. также главы: «Классификация болтовых рядов», «Альфа-коэффициент»)
(См. также главы: «Классификация болтовых рядов», «Альфа-коэффициент»)
Если расширение торцевой пластины находится за пределами высоты существующей ветки пластины, а ряд болтов определен внутри или даже снаружи этой ветки, программное обеспечение распознает эту геометрию как несовместимую со схемами линий текучести, и печатается предупреждение на выходе.В этом случае может произойти возможный «скачок» паттернов линии доходности, на который EN не распространяется. Предполагается, что зазор вута пластины возле полки балки не влияет на схемы линий текучести.
Полка и стенка балки при сжатии
Компонент рассчитывается в соответствии со статьей 6.2.6.7 стандарта EN 1993-1-8.
Примечания:
(1) Сопротивление компонента F c,fb,Rd рассчитывается по уравнению (6.21), используя расчетное сопротивление моменту поперечного сечения балки M c,Rd .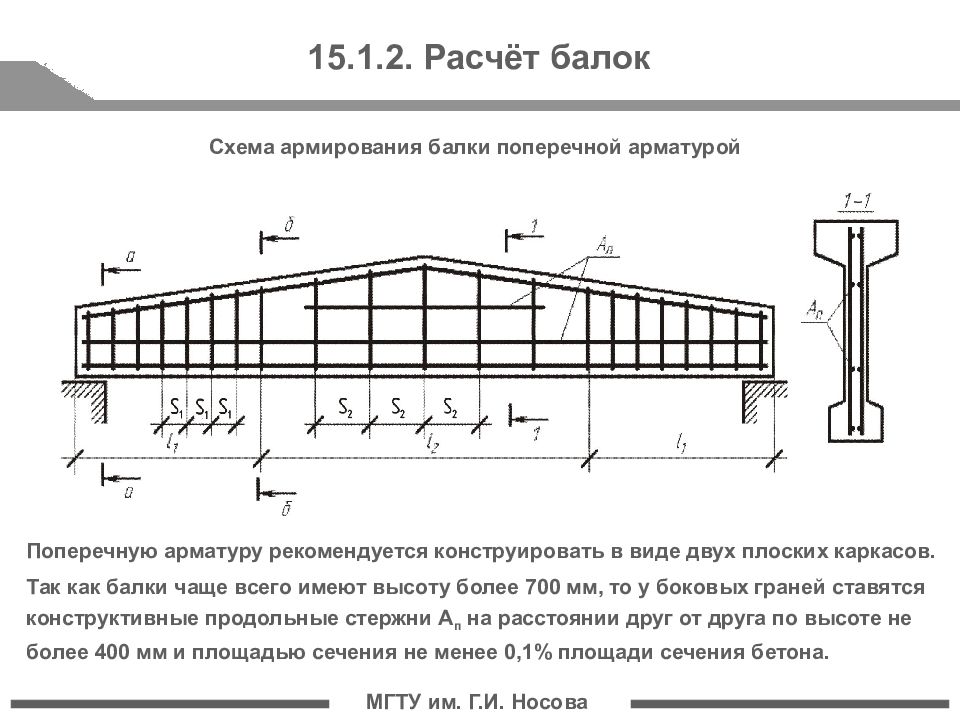
— Учтен возможный наклон присоединяемой балки.
— Скругление основного поперечного сечения не учитывается в случае наличия вута или наклона соединенной балки.
— Вуты без фланцев не учитываются.
При расчете плеча рычага h b -t fb также не учитывается влияние наклонной секции и наклонной полки вута.
— Однако учитывается различная толщина полки балки и вута.
При расчете сечения с одной РЕАЛЬНОЙ веткой с фланцем плечо рычага h b -t fb .задается как:
с:
| (ч б -т ф б ) | рычаг |
| ч б | высота балки без вута |
| т фб | толщина полки балки |
| ч полный | высота бедра на полном конце |
| л полный | длина бедра от начала до конца |
| т левый | толщина фланца вута |
| л лицевая сторона | длина вута от начала до соединительной поверхности |
Правило, описанное в последнем предложении этой части, так называемое правило 20%, полностью выполняется.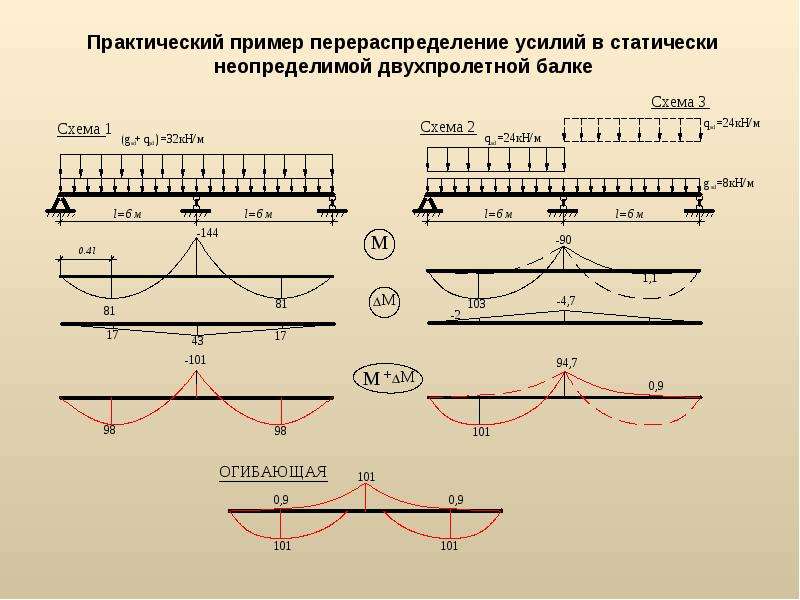 Предельная высота 600 мм сравнивается с общей высотой секции, исключая возможные вуты без полки. Расчетный лимит рассчитывается по формуле ниже:
Предельная высота 600 мм сравнивается с общей высотой секции, исключая возможные вуты без полки. Расчетный лимит рассчитывается по формуле ниже:
с:
| б ч | ширина полки балки |
| т ч | толщина полки балки |
| f yb | предел текучести материала балки |
Сопротивление конечного компонента принимается как минимум начального значения и предельного значения.
(2) Веточка с фланцем должна соответствовать критериям, указанным ниже, указанным в статье:
– ширина и толщина полки, а также толщина стенки вута должны быть не менее толщины элемента;
– угол между полкой вута и полкой элемента не должен быть больше 45°
Если критерии не выполняются, отображается предупреждение.
(3) Как указано в этой статье, если балка усилена вантами, расчетное сопротивление стенки балки на сжатие следует определять в соответствии с 6.2.6.2. В Scia Engineer проводится различие между вузом с фланцем и без него.
В случае наличия вута без полки на сжатой стороне балки центр сжатия считается на сжатой полке балки и предполагается, что усилие сжатия будет направлено непосредственно на полку балки.Поэтому нет необходимости проверять сопротивление какого-либо другого компонента, и рассчитывается только компонент «Полка балки и стенка при сжатии».
В случае наличия вута с полкой на сжатой стороне балки исходный компонент «Полка и стенка балки на сжатие» заменяется двумя компонентами: «Сжатая полка вута» и «Сжатая стенка балки». Эти два компонента позже используются по отдельности в таблице «Оценка сдвига и сжатия» для определения предельного компонента сжатия, а также при определении сопротивления нормальному сжатию Nj,Rd.
(См. также разделы: «Полка вута на сжатие», «Сетка балки на сжатие»)
Фланец вута на сжатие
Компонент рассчитан в соответствии с Еврокодом 3: Bemessung und Construktion von Stahlbauten, Band 2: Anschlüsse – DIN EN 1993-1-8 mit Nationalem Anhang – Kommentar und Beispiele von Prof. Dr.-Ing. Дитер Унгерманн, профессор, д.т.н. Томас Умменхофер, профессор, д.т.н. Рамгопал Путли, Др.-инж. Клаус Вейнанд, опубликовано в 2015-09 гг. Сопротивление компонента рассчитывается по следующей формуле:
с:
| 16_1″> б фх | ширина полки вута, ограниченная b max |
| т фх | толщина фланца вута |
| f yb | предел текучести балки |
| β | угол между фланцем вута и направлением, перпендикулярным торцевой пластине |
| γ M0 | частичный запас прочности для стали |
Компонент всегда рассчитывается вместе с компонентом «Сжатая стенка балки», как замена компонента «Полка балки и сжатая стенка» в случае наличия сжатого вута с полкой на сжатой стороне соединяемой балки.(См. также главу: «Полка и стенка балки при сжатии»)
Стенка балки при сжатии
Компонент рассчитывается в соответствии со статьей 6.2.6.2 стандарта EN 1993-1-8 в отношении Еврокода 3: Bemessung und Construktion von Stahlbauten, Band 2: Anschlüsse – DIN EN 1993-1-8 mit Nationalem Anhang – Kommentar und Beispiele von Prof. д-р инж. Дитер Унгерманн, профессор, д.т.н. Томас Умменхофер, профессор, д.т.н. Рамгопал Путли, д-р инж. Клаус Вейнанд, опубликовано в 2015-09 гг.
Как правило, сопротивление компонента «Сетка балки при сжатии» F c,wb,Rd рассчитывается по той же формуле, что и компонент «Сетка колонны при сжатии» (см.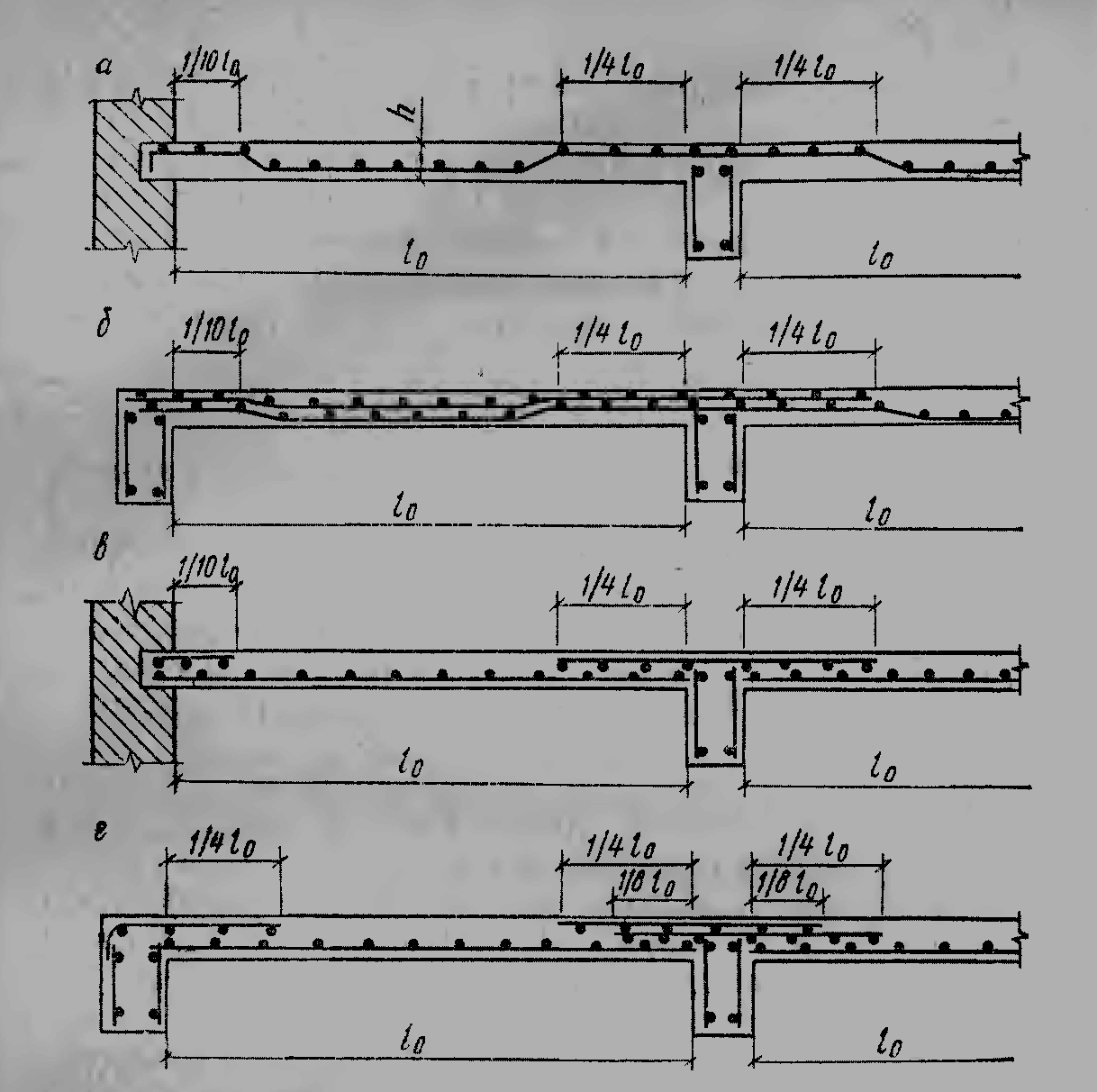 также главу: «Сетка колонны при поперечном сжатии» ). Однако используются значения из соединенной балки вместо колонны, и также необходимы некоторые модификации.
также главу: «Сетка колонны при поперечном сжатии» ). Однако используются значения из соединенной балки вместо колонны, и также необходимы некоторые модификации.
Стенка балки в элементе сопротивления сжатию F c,wb,Rd рассчитывается как:
Для распространения в стенке балки скорректированная формула для b eff,c,wb дана по ссылке:
с:
| т фх | толщина фланца вута |
| 16_1″> т фб | толщина полки балки |
| с | согласно EN 1993-1-8 Статья 6.2.6.2 (1) |
| α | — угол определения вута (угол между полкой балки и полкой вута)e |
Параметр преобразования Бета для определения ω следует принимать как для одностороннего соединения, т.е.: β = 1.
Внутренние усилия для определения σ com, принимают так же, как и при проверке компонента «Стинка колонны на сжатие», в том месте сечения, которое должно быть проверено (где заканчивается веток, т.е. где действует сила).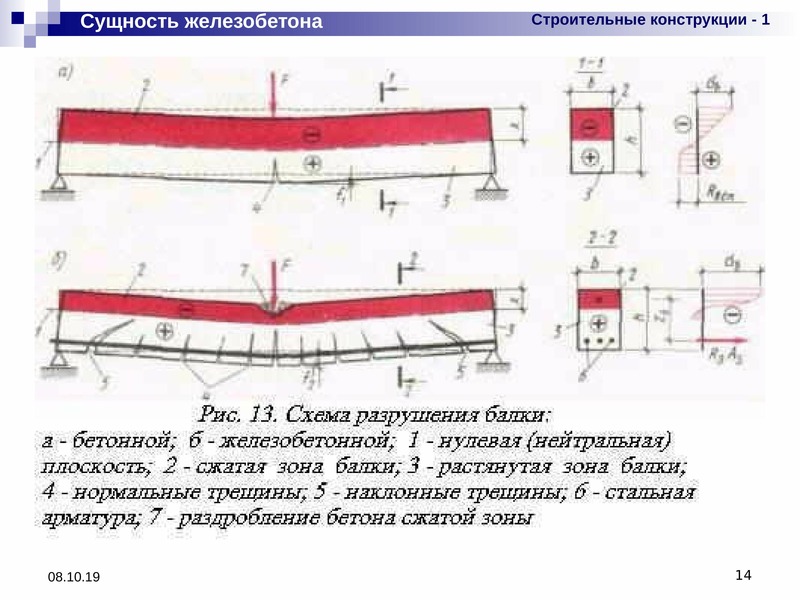 Использование уменьшения и, следовательно, расчет коэффициента уменьшения k wb зависит от активации флажка «Включить уменьшение напряжения в перемычке» в настройках соединения.
Использование уменьшения и, следовательно, расчет коэффициента уменьшения k wb зависит от активации флажка «Включить уменьшение напряжения в перемычке» в настройках соединения.
При расчете сопротивления F c,wb,Rd компонента требуется преобразование в направлении, перпендикулярном колонне.
Поэтому используется следующее уравнение:
Если элемент жесткости на конце вута присутствует на конце сжатого вута, считается, что компонент не разрушается, а сопротивление компонента принимается равным бесконечности.
Компонент всегда рассчитывается вместе с компонентом «Полка вута на сжатие», как замена компонента «Полка и стенка балки на сжатие» в случае наличия сжатого вута с полкой на сжатой стороне соединяемой балки.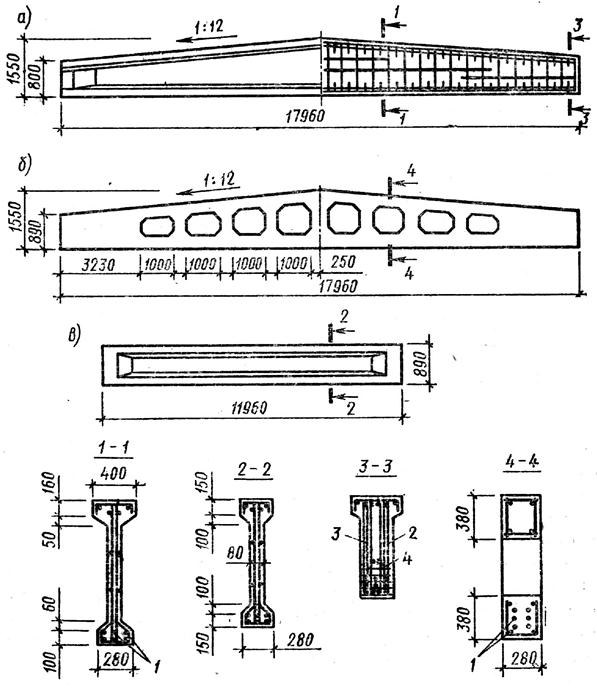 (См. также главу: «Полка и стенка балки при сжатии»)
(См. также главу: «Полка и стенка балки при сжатии»)
Стенка балки на растяжение
Компонент рассчитывается в соответствии со статьей 6.2.6.8 стандарта EN 1993-1-8.
Примечания:
(2) Эффективная ширина b eff,t,wb , используемая в формуле (6.22) для расчета расчетного сопротивления растяжению стенки балки F t,wb,Rd для болтового соединения принимаются равными расчетной длине элемента «Концевая плита на изгиб» с учетом вида разрушения (См. также главу: «Концевая пластина при изгибе»).
Проблемы измерения широких и расходящихся лучей
VCSEL, светодиоды, краевое излучение и волоконные лазеры используются во многих чувствительных приложениях на быстрорастущих рынках.Чтобы гарантировать высокое качество устройств, необходимо анализировать профиль луча, но эти широкие расходящиеся лучи предъявляют особые требования к измерительной системе.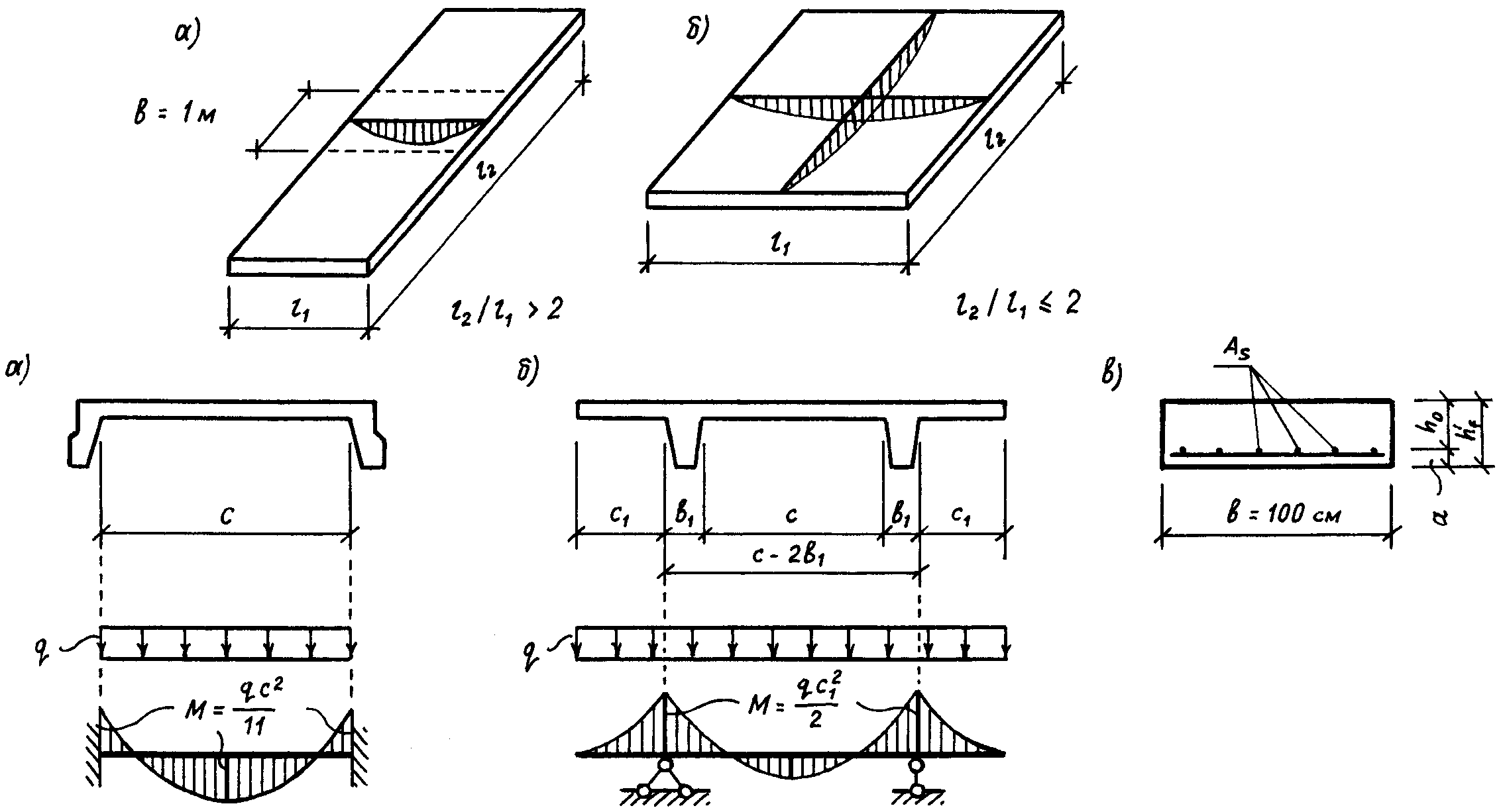 С одной стороны, апертуры обычных профилировщиков луча слишком малы, чтобы собрать все пятно больших или расходящихся источников света. С другой стороны, расходящиеся лучи нельзя точно измерить с помощью обычных детекторов, поскольку квантовая эффективность детектора сильно зависит от угла падения. Эти проблемы были решены с помощью Ophir Wide Beam Imager – WB-I, откалиброванного оптического аксессуара для камер с профилированием луча, на основе рассеивателя с апертурой диаметром 45 мм и формирователя изображения, предназначенного для измерения дальнего поля.
С одной стороны, апертуры обычных профилировщиков луча слишком малы, чтобы собрать все пятно больших или расходящихся источников света. С другой стороны, расходящиеся лучи нельзя точно измерить с помощью обычных детекторов, поскольку квантовая эффективность детектора сильно зависит от угла падения. Эти проблемы были решены с помощью Ophir Wide Beam Imager – WB-I, откалиброванного оптического аксессуара для камер с профилированием луча, на основе рассеивателя с апертурой диаметром 45 мм и формирователя изображения, предназначенного для измерения дальнего поля.
Рис. 1. Ophir Wide Beam-Imager (WB-I)
Области применения и ограничения
Существует несколько типов широких или расходящихся источников света, таких как светодиоды или оптоволоконные осветители, которые можно измерять с помощью WB-I, но его основное применение — измерение VCSEL в дальней зоне. Лазеры с поверхностным излучением с вертикальным резонатором (VCSEL) представляют собой тип полупроводникового лазерного диода.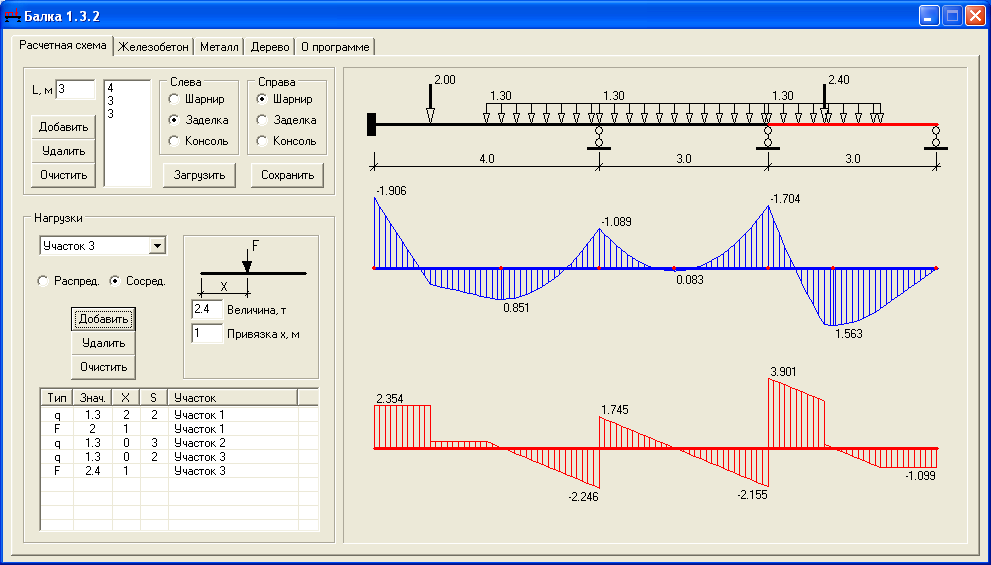 В отличие от лазерных диодов с краевым излучением, лазеры VCSEL излучают вверх и поэтому могут быть легко упакованы в виде массивов излучателей, содержащих сотни излучателей на одном кристалле.
В отличие от лазерных диодов с краевым излучением, лазеры VCSEL излучают вверх и поэтому могут быть легко упакованы в виде массивов излучателей, содержащих сотни излучателей на одном кристалле.
Маломощные VCSEL используются для высокоскоростной передачи данных, 3D-зондирования (например, распознавания жестов и лиц) и датчиков приближения, в то время как высокомощные VCSEL предназначены для лидаров и других приложений дистанционного зондирования. Многие из этих приложений работают от батарей, поэтому потребление энергии должно быть сведено к минимуму. Чтобы обеспечить правильную работу устройств VCSEL, важно измерять и анализировать мощность VCSEL, профиль луча и шум. Хотя существует множество методов измерения мощности излучения VCSEL, для профилирования их выходного луча обычно требуется громоздкое лабораторное оборудование, которое не помещается в производственные линии и неудобно для испытаний «на месте».
Вторая проблема связана с углом падения: Квантовая эффективность стандартных детекторов (таких как кремниевые фотодиоды или ПЗС-сенсоры) сильно зависит от угла падения — на целых 10 % на каждые 15 градусов. Таким образом, они не могут точно измерить расходящиеся лучи. WB-I захватывает луч и отображает распределение его мощности на камеру с точностью лучше 5%. Давайте посмотрим, как достигается эта точность.
Таким образом, они не могут точно измерить расходящиеся лучи. WB-I захватывает луч и отображает распределение его мощности на камеру с точностью лучше 5%. Давайте посмотрим, как достигается эта точность.
Отображение широкого луча
Устройство WB-I улавливает широкие лучи на диффузионном экране и повторно отображает их для получения полной и точной карты распределения интенсивности света.Компактная оптическая система предназначена для использования с системами профилирования луча на основе камеры вместе с измерительным программным обеспечением Ophir BeamGage. WB-I — прочный, компактный, пыленепроницаемый, «готовый к использованию» аксессуар, предназначенный как для производственных условий, так и для обслуживания у заказчика. Благодаря апертуре диаметром 45 мм и углу падения 140 градусов можно отображать лучи любой формы (круглые, линейные или квадратные), которые слишком расходятся и слишком велики для сенсора камеры (рис. 2) с заданным масштабированием. фактор.Само измерение происходит мгновенно и требует минимальных настроек для оптимизации под различную интенсивность освещения. Расстояние между измеряемым источником света и рассеивателем WB-I варьируется от одного мм до нескольких десятков мм в зависимости от типа испытания и применения.
Расстояние между измеряемым источником света и рассеивателем WB-I варьируется от одного мм до нескольких десятков мм в зависимости от типа испытания и применения.
Рис. 2. Схема установки при использовании Ophir WB-I с камерой SP920s
Компоненты WB-I (рис. 2):
- Непрозрачная рассеивающая поверхность (1) с 45 мм CA
- Объектив изображения (2)
- Камера (3), e.г. Ophir SP920s с программным обеспечением BeamGage (приобретается отдельно)
- Два фильтра нейтральной плотности (4)
Давайте подробнее рассмотрим, что и как использовать WB-I.
Профилирование луча VCSEL
Как уже говорилось, распределение энергии VCSEL напрямую зависит от таких параметров, как ток, ширина импульса и частота повторения, температура и срок службы устройства. Следовательно, важно измерять угловое распределение VCSEL на различных этапах производственного процесса, а также в ходе исследований и разработок и полевого обслуживания.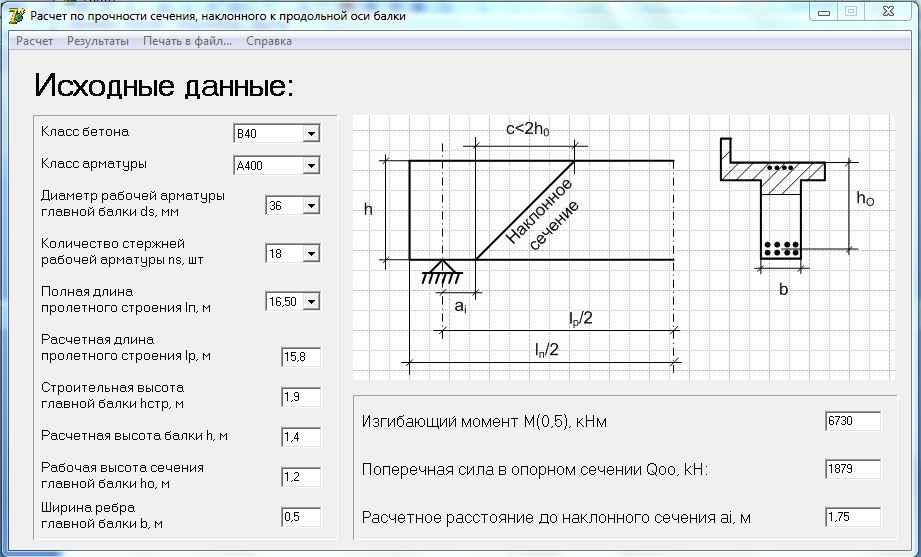 Аксессуар WB-I обеспечивает гибкое измерение расходящихся лучей и предоставляет ценную информацию в различных сценариях:
Аксессуар WB-I обеспечивает гибкое измерение расходящихся лучей и предоставляет ценную информацию в различных сценариях:
Поведение VCSEL при тесте развертки LIV
VCSEL находятся в так называемом «режиме светодиодов», когда подается только слабый ток. Как только ток, подаваемый на VCSEL, увеличивается, его профиль луча меняется на «лазерный режим». Этот сдвиг происходит очень быстро, и определение точных электрооптических значений во время этого процесса очень важно. Это одна из причин, по которой «испытание развертки светового тока-напряжения (LIV)» используется для определения характеристик лазерного диода в работе.Наблюдение за изменениями профиля луча во время такого испытания дает важную дополнительную информацию. Поскольку аксессуар WB-I вместе с камерой и программным обеспечением BeamGage обеспечивает анализ и визуализацию формы луча в реальном времени, можно легко обнаружить изменения формы луча из-за различных приложенных токов.
VCSEL без крышки диффузора
В зависимости от области применения и стадии производства VCSEL можно измерять с крышкой диффузора или без нее.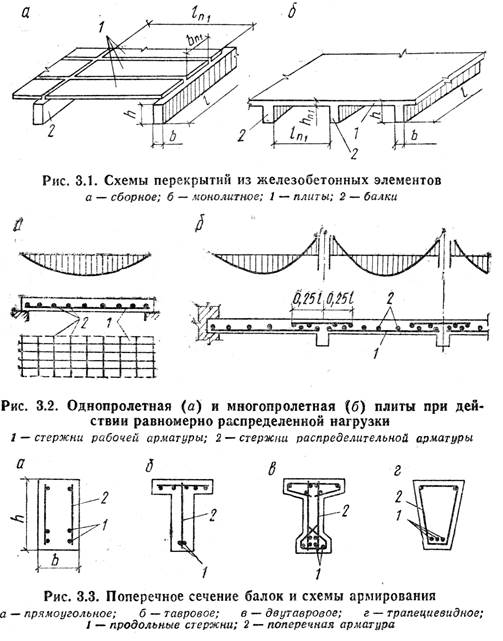 В обоих случаях измерение можно проводить с помощью прибора WB-I.Ниже приведены два примера массивов VCSEL с крышкой диффузора и без нее.
В обоих случаях измерение можно проводить с помощью прибора WB-I.Ниже приведены два примера массивов VCSEL с крышкой диффузора и без нее.
Рис. 3. Образец источника VCSEL без диффузора: изменение формы пучка в зависимости от приложенного тока.
Поскольку изменения формы луча можно отслеживать в зависимости от приложенного тока, можно легко диагностировать любые электронные или оптические отклонения продукта.
Рис. 4. Профиль образца источника VCSEL (показан на рис. 3)
На рис. 4 представлен график изменения формы луча в зависимости от тока.На нем ясно видно, что гауссов пучок становится плоской вершиной и переходит в двойную моду при изменении тока с 0,74 А до 0,92 А.
VCSEL с крышкой диффузора
Ниже приведен пример профиля луча другого образца матрицы VCSEL с диффузором, который показывает другое угловое распределение энергии.
Рис. 5. VCSEL с крышкой диффузора: форма луча изменяется в зависимости от приложенного тока.
Рис. 6. Поперечное сечение профиля пучка образца VCSEL с крышкой диффузора.
Поперечное сечение профиля луча образца VCSEL с крышкой диффузора (см. рис. 6) иллюстрирует изменение формы от гауссовой к квадратной. Цилиндр и общая мощность увеличиваются с приложенным током.
Измерение расходимости луча
Для измерения расходимости луча, что важно для оценки качества VCSEL, светодиодов и волоконных осветительных приборов, необходимо точное измерение угловой освещенности.
Непрозрачный диффузор, используемый в WB-I, позволяет измерять расходящиеся лучи до 140° AOI, что намного лучше, чем другие методы, такие как лезвие ножа, основанные на использовании измерителя мощности.На рис. 7 показаны различия между измерениями фотодиодного датчика и WB-I с камерой. С увеличением угла показания мощности фотодиодов перестают быть достоверными.
Рис. 7. Линейность распределения энергии WB-I для направленного света по сравнению с измерениями фотодиодного датчика.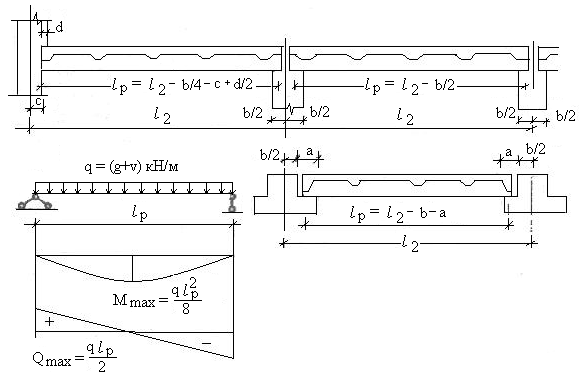
Благодаря равномерному рассеиванию света при широких углах падения, WB-I позволяет измерять сильно расходящиеся лучи до 70° AOI (угол раскрытия 140°°)
Рис.8. Диаметр луча как функция расстояния.
Как показано на рис. 8, анализ диаметра луча как функции расстояния между источником и WB-I дает дополнительную информацию. В нашем примере он показывает линейное поведение во всем диапазоне. Это позволяет точно измерять углы расхождения источников света. Для расчета расходимости необходимо ввести в программу BeamGage расстояние между источником света и рассеивателем аксессуара WB-I.На основе этого ввода и измеренной ширины луча (или предварительно выбранной пользователем) алгоритм вычисляет расхождение, отображаемое в мрадах или градусах °.
Опять же, при измерении VCSEL могут появиться различия: они показывают разное расхождение для разных токов при переходе от «светодиодного режима» к «лазерному режиму».
Рис.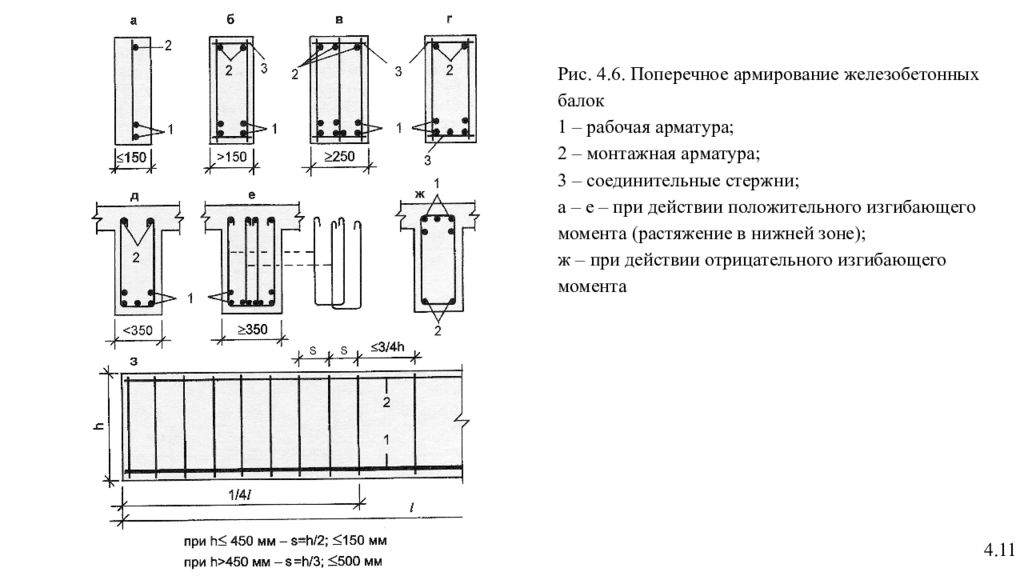 9. VCSEL, расположенный на расстоянии 60 мм от WB-I, показывает расходимость 472 мрад при токе 0,4 А и 381 мрад при токе 0,8 А.
9. VCSEL, расположенный на расстоянии 60 мм от WB-I, показывает расходимость 472 мрад при токе 0,4 А и 381 мрад при токе 0,8 А.
Измерение дивергенции светодиодов с помощью WB-I
Как уже упоминалось, WB-I измеряет не только VCSEL, но и светодиоды.Поскольку их расходимость обычно намного выше, чем у VCSEL, тесты проводились с двумя разными светодиодными источниками. Результаты можно увидеть на рисунках 10 и 11.
Рис. 10. Расчетная расходимость луча 1303 мрад для образца красного светодиода, расположенного на расстоянии 8 мм от WB-I.
Рис. 11. Расчетная расходимость луча 1236 мрад для синего светодиода, расположенного на расстоянии 8 мм от WB-I.
Расчет дивергенции – советы и рекомендации
Для получения надежных измерений, особенно с очень расходящимися лучами, мы хотим поделиться некоторыми советами, связанными с программным обеспечением:
- На вкладке расчета BeamGage мы рекомендуем использовать расчет ширины луча по полувысоте — 50% пика.
 Параметр
Параметр - «Оптическое масштабирование» должен быть равен 8,15, что соответствует объективу видеонаблюдения WB-I.
- Расчет дивергенции должен производиться в соответствии с параметром «Широкий угол FF» (Дальнее поле) и должно быть указано расстояние от рассеивателя WB-I до источника света. * В случае сильно расходящихся источников света, таких как светодиоды, мы рекомендуем располагать их рядом с рассеивателем WB-I. Выше 8 мм расчет расхождения может показать неверные результаты. Для менее рассеивающих источников света, таких как лазеры или VCSEL, расстояние для расчета расходимости может достигать десятков миллиметров.
Измерение WB-I источников света, показывающих спекл-структуру
Спекл-проблемы
При измерении коллимированных лазерных лучей взаимодействие между лазером и диффузной структурой поверхности WB-I может вызвать спекл-структуру на датчике профиля луча. Это явление вызвано интерференцией монохроматического лазерного излучения и рассеивающей поверхности. Его можно легко сгладить программным алгоритмом программы BeamGage.
Его можно легко сгладить программным алгоритмом программы BeamGage.
С помощью функции фильтра нижних частот (ФНЧ) в программном обеспечении BeamGage можно значительно уменьшить наблюдаемую зернистость, поскольку она превращает профиль луча с большим количеством пространственных шумов в оптимизированное изображение.
Чтобы узнать больше об алгоритме свертки сглаживания данных, см. эту презентацию.
Функция LPF программного обеспечения BeamGage находится на вкладке «Захват» > и находится на панели «Обработка»:
Пример применения с использованием функции LPF
В описанной ниже ситуации с помощью системы WB-I измерялся расходящийся пучок гелий-неонового лазера с длиной волны 632 нм. Наблюдалась выраженная спекл-структура. Для сглаживания спекл-эффекта использовались различные фильтры нижних частот.
Рис. 12. Спекл-эффект, сглаженный функцией LPF
Рис. 13. Сравнение профилей функций ФНЧ различных матриц, демонстрирует сглаживание спекл-эффекта.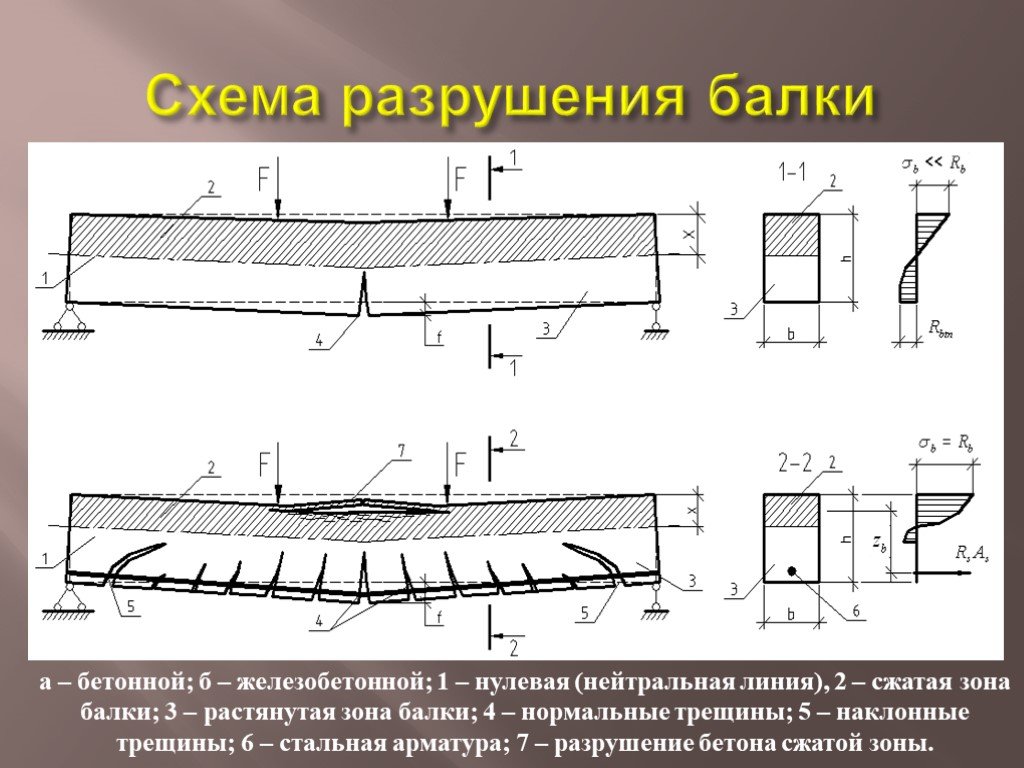
Как показано, функция LPF сгладила спекл-эффект без ущерба для ширины луча (D4σ), интенсивности и других параметров луча.
Кроме того, обратите внимание на этот совет по применению:
Установка WB-I может располагаться как горизонтально, так и вертикально.Таким образом, и камеру, и всю установку можно легко повернуть, чтобы она соответствовала любой ориентации источника света.
Заключение
Разработав аксессуар WB-I, компания Ophir упростила измерение широко расходящихся источников света. VCSEL и светодиоды теперь можно легко измерить в производственном процессе, в исследованиях и разработках, а также на объектах заказчика. Комбинация прибора WB-I с камерой для профилирования луча и программным обеспечением BeamGage позволяет быстро получать надежные результаты измерений.Профилирование луча в дальней зоне от расходящихся или широких источников больше не требует обширной подготовки или индивидуального изготовления оборудования, а может выполняться с помощью калиброванного измерительного устройства.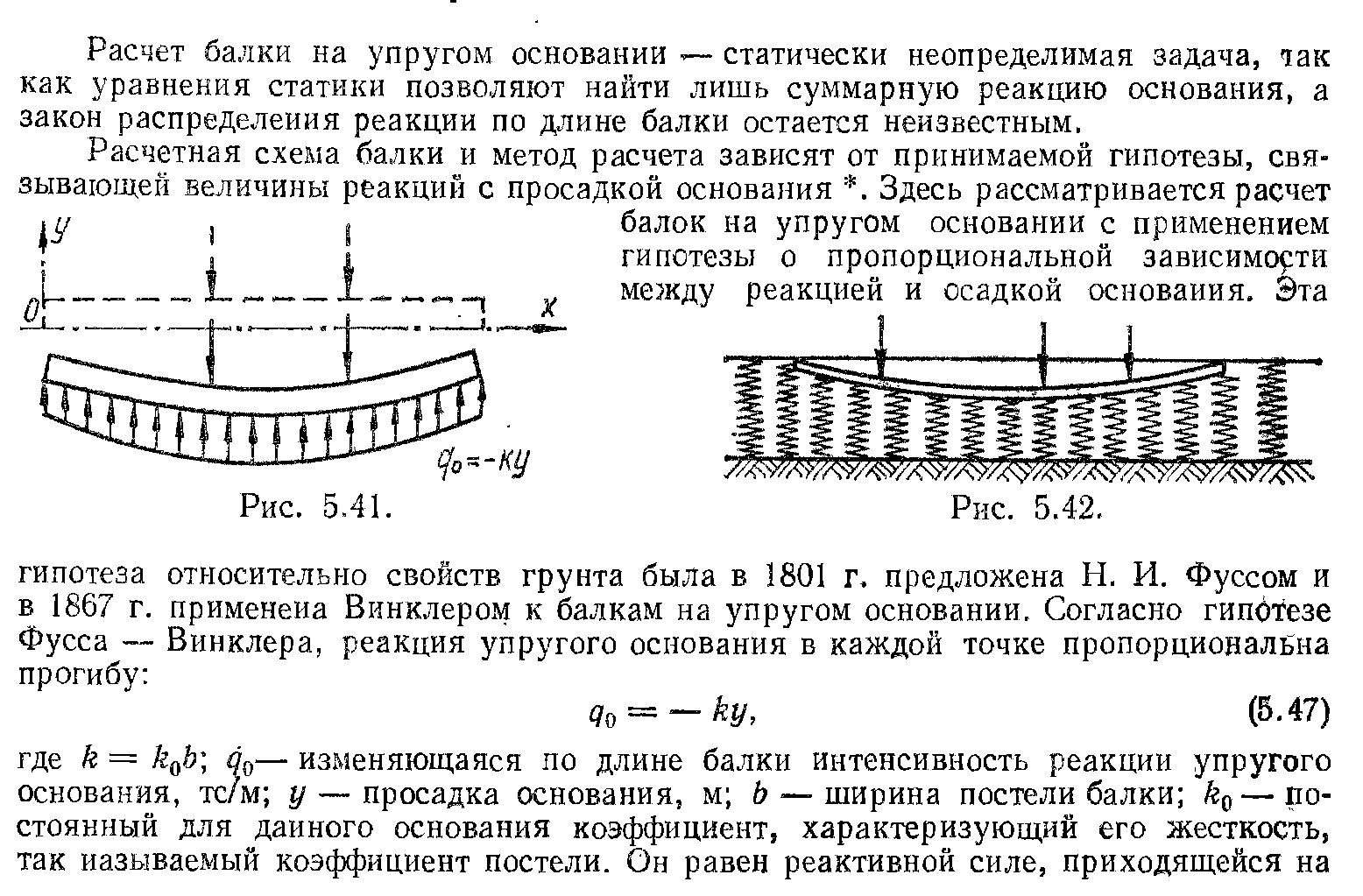
Читать как PDF
Численный анализ гибридных стальных балок с трапециевидной гофрированной стенкой, несварными наклонными фальцами
Гибридные балки дают возможность реализовать характерные стальные сечения путем набора материалов на основе предела текучести и типа приложенного напряжения.Предыдущие исследования показали, что стальные балки с трапециевидной гофрированной стенкой (SBCW) подвержены как усталостным трещинам, зарождающимся вдоль наклонного фальца (IF), так и максимальным дополнительным напряжением, расположенным в середине IF. В данной работе представлено численное исследование гибридных СБКВ и несварных ВС. Представлено численное моделирование методом конечных элементов (КЭ) с помощью пакета программ ANSYS. Трехмерные модели КЭ были разработаны с учетом нелинейных свойств материалов и геометрических несовершенств и проверены с использованием пяти гибридных образцов, которые были изготовлены и испытаны авторами экспериментально. Поведение нагрузки-прогиба и механизм отказа численных результатов хорошо согласовывались с экспериментальными результатами. Сравнение моделей КЭ и экспериментальных результатов показывает хорошие возможности использования модели КЭ в качестве основы для параметрического исследования. Параметрическое исследование было сосредоточено на влиянии толщины стенки, толщины полки, высоты стенки и марки стали полки и стенки. Кроме того, проводятся параметрические исследования для изучения влияния количества и глубины ребер жесткости на поведение гибридных SBCW.Мы пришли к выводу, что толщина фланца, толщина стенки, высота стенки и марки стали фланцев существенно влияют на производительность и режим отказа гибридных SBCW. Мы также пришли к выводу, что ребра жесткости фланцев оказывают значительное влияние на общее поведение, ударную вязкость и грузоподъемность SBCW. Наконец, новое уравнение предлагается для прогнозирования способности к сдвигу несварных IF SBCW на основе длины сварной горизонтальной складки.
Поведение нагрузки-прогиба и механизм отказа численных результатов хорошо согласовывались с экспериментальными результатами. Сравнение моделей КЭ и экспериментальных результатов показывает хорошие возможности использования модели КЭ в качестве основы для параметрического исследования. Параметрическое исследование было сосредоточено на влиянии толщины стенки, толщины полки, высоты стенки и марки стали полки и стенки. Кроме того, проводятся параметрические исследования для изучения влияния количества и глубины ребер жесткости на поведение гибридных SBCW.Мы пришли к выводу, что толщина фланца, толщина стенки, высота стенки и марки стали фланцев существенно влияют на производительность и режим отказа гибридных SBCW. Мы также пришли к выводу, что ребра жесткости фланцев оказывают значительное влияние на общее поведение, ударную вязкость и грузоподъемность SBCW. Наконец, новое уравнение предлагается для прогнозирования способности к сдвигу несварных IF SBCW на основе длины сварной горизонтальной складки.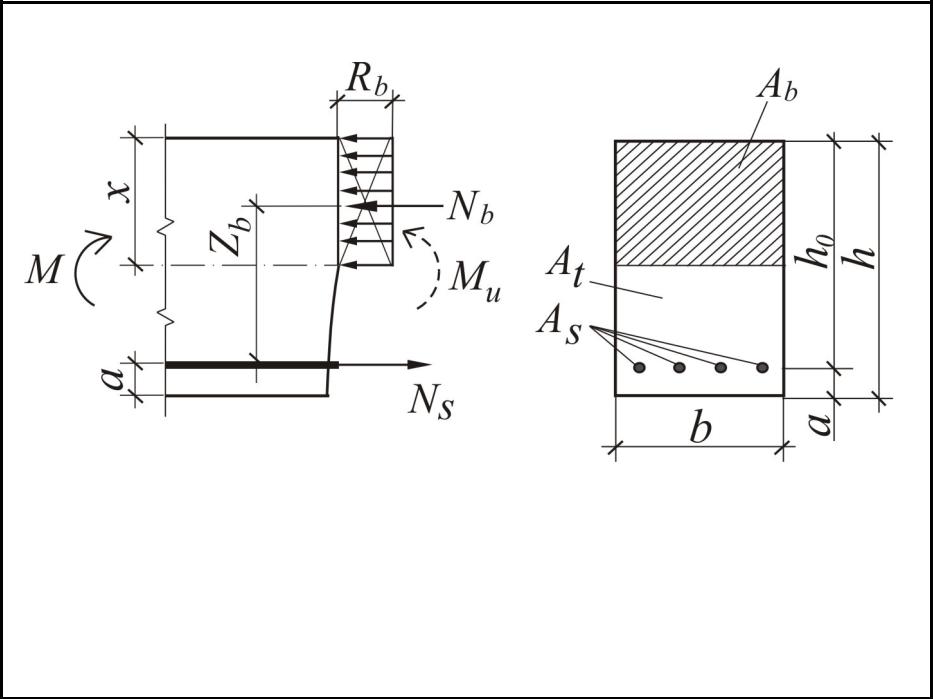
1. Введение
Стальные балки с гофрированными стенками (SBCW) широко использовались в последние четыре десятилетия в мостах и обычных стальных конструкциях.SBCW можно использовать как главную балку или как второстепенную балку. Основные SBCW могут быть загружены одной (средняя нагрузка) или несколькими сосредоточенными нагрузками, передаваемыми от второстепенных балок. Это исследование касается SBCW, несущего второстепенную балку в середине пролета (трехточечный изгиб). Основным преимуществом трапециевидного гофрированного полотна является опорное состояние, обеспечиваемое как продольными, так и наклонными складками друг к другу. Это свойство увеличивает внеплоскостную жесткость SBCW. Однако геометрические характеристики CWSB имеют три недостатка: во-первых, выдающаяся длина полки сжатия; во-вторых, эксцентриситет стенки из-за глубины гофра; и в-третьих, прочность на изгиб сопротивлялась только вкладу фланцев.
SBCW имеют два разных режима отказа: первый вид отказа определяется напряжением сдвига стенки (выпучивание стенки), а второй — напряжением текучести полки (выпучивание полки).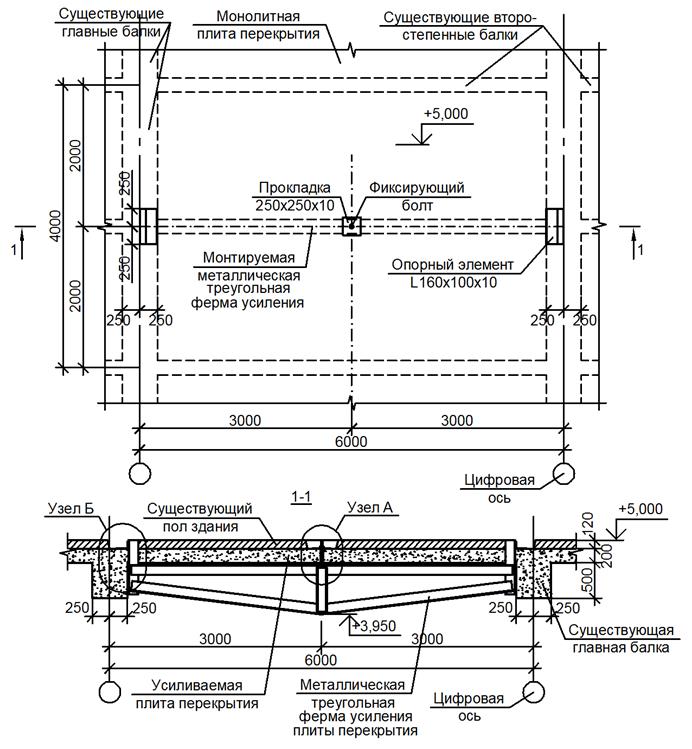 В 2005 году Anami и Sause [1] аналитически оценили усталостную прочность сварных швов гофрированных стенок и фланцев. Результаты показали, что на мощность балки значительно повлияли усталостные трещины, возникающие вдоль наклонных складок (IFs), а затем распространяющиеся перпендикулярно направлению главного напряжения.Таким образом, это исследование аналитически представляет влияние несварных IFs. В нескольких предыдущих экспериментальных или аналитических исследованиях сообщалось о гибридных SBCW или случае несварных IF. Таким образом, в этом разделе представлены общие сведения о предыдущем исследовании поведения SBCW при сдвиге и изгибе.
В 2005 году Anami и Sause [1] аналитически оценили усталостную прочность сварных швов гофрированных стенок и фланцев. Результаты показали, что на мощность балки значительно повлияли усталостные трещины, возникающие вдоль наклонных складок (IFs), а затем распространяющиеся перпендикулярно направлению главного напряжения.Таким образом, это исследование аналитически представляет влияние несварных IFs. В нескольких предыдущих экспериментальных или аналитических исследованиях сообщалось о гибридных SBCW или случае несварных IF. Таким образом, в этом разделе представлены общие сведения о предыдущем исследовании поведения SBCW при сдвиге и изгибе.
Реакция на сдвиг гофрированных стеновых балок подвергалась многочисленным экспериментальным и теоретическим исследованиям потери устойчивости при сдвиге и прочности на сдвиг SBCW [2–23].Это исследование было начато в 1965 г. Шимадой [2]. Бергфельт и Лейва в 1984 г., Луо и Эдлунд в 1996 г. и Аббас в 2003 г. сообщили, что прочность на сдвиг SBCW определяется податливостью к сдвигу и короблением полотна [2–5]. На основе аналитического метода, проведенного Луо и Эдлундом [4], была предложена эмпирическая формула для прогнозирования сдвиговой способности SBCW. Аналитические и экспериментальные исследования SBCW, нагруженных в основном поперечной силой, были проведены Elgaaly et al. [6] и др. [7–18].Эти исследования были посвящены локальному и глобальному упругому выпучиванию и взаимодействию между ними, а также соответствующей теории. В центре внимания исследований было предсказать три типа потери устойчивости при сдвиге путем разработки формул. Линднер [18] предложил использовать 70% напряжения потери устойчивости при сдвиге при расчете номинальной прочности на сдвиг SBCW. Все эти исследования показали, что касательное напряжение равномерно распределяется по высоте стенки и постепенно увеличивается до потери устойчивости.Кроме того, локальное и глобальное выпучивание стенок чаще всего наблюдалось в грубых и плотных гофрах соответственно.
На основе аналитического метода, проведенного Луо и Эдлундом [4], была предложена эмпирическая формула для прогнозирования сдвиговой способности SBCW. Аналитические и экспериментальные исследования SBCW, нагруженных в основном поперечной силой, были проведены Elgaaly et al. [6] и др. [7–18].Эти исследования были посвящены локальному и глобальному упругому выпучиванию и взаимодействию между ними, а также соответствующей теории. В центре внимания исследований было предсказать три типа потери устойчивости при сдвиге путем разработки формул. Линднер [18] предложил использовать 70% напряжения потери устойчивости при сдвиге при расчете номинальной прочности на сдвиг SBCW. Все эти исследования показали, что касательное напряжение равномерно распределяется по высоте стенки и постепенно увеличивается до потери устойчивости.Кроме того, локальное и глобальное выпучивание стенок чаще всего наблюдалось в грубых и плотных гофрах соответственно.
Что касается исследований изгибающего момента, несколько предыдущих исследований были сосредоточены на определении сопротивления изгибу стальных или композитных SBCW [19, 24]. Аббас и др. [19] сообщили, что SBCW под действием плоскостного сдвига и изгибающего момента имели два типа смещения: вертикальное смещение (прогиб в плоскости) и смещение вне плоскости (скручивание) одновременно.Эти смещения вызывают поперечный изгиб полки, что означает напряжения полки, которые должны быть добавлены к напряжениям, возникающим при изгибе в плоскости. Чтобы рассчитать этот поперечный изгиб, Abbas et al. [20] представили метод С-фактора в качестве аналитического метода. Линднер [24] в 1992 г. и Ашингер и Линднер [25] в 1997 г. были первыми, кто наблюдал поперечный изгиб полки SBCW.
Аббас и др. [19] сообщили, что SBCW под действием плоскостного сдвига и изгибающего момента имели два типа смещения: вертикальное смещение (прогиб в плоскости) и смещение вне плоскости (скручивание) одновременно.Эти смещения вызывают поперечный изгиб полки, что означает напряжения полки, которые должны быть добавлены к напряжениям, возникающим при изгибе в плоскости. Чтобы рассчитать этот поперечный изгиб, Abbas et al. [20] представили метод С-фактора в качестве аналитического метода. Линднер [24] в 1992 г. и Ашингер и Линднер [25] в 1997 г. были первыми, кто наблюдал поперечный изгиб полки SBCW.
Кроме того, некоторые исследователи изучали сочетание реакции на изгиб и прочности на сдвиг SBCW [26].В исследованиях сварки было проведено несколько исследований сварки между стенкой и фланцами, первое исследование было проведено Шерманом и Фишером [27]. Экспериментально в этом исследовании изучались три различные толщины стенки 25 SBCW, чтобы определить длину соединения, необходимую между стенкой и полками. Результаты показали, что горизонтальные складки нужно было соединить только с фланцами. Кроме того, наблюдалось незначительное влияние на жесткость и максимальную грузоподъемность балки из-за связи между полками и наклонными складками.
Результаты показали, что горизонтальные складки нужно было соединить только с фланцами. Кроме того, наблюдалось незначительное влияние на жесткость и максимальную грузоподъемность балки из-за связи между полками и наклонными складками.
Несмотря на то, что существует множество исследований, посвященных SBCW, только небольшое количество предыдущих исследований касается гибридных SBCW, и небольшое количество исследований изучало влияние ребер жесткости полки на несущую способность балки. Кроме того, предыдущие исследования показали необходимость дальнейших исследований в случае несварных наклонных складок. Эти исследования, по существу, указывают на наиболее важные параметры, влияющие на общее поведение и характер разрушения гибридных SBCW с несварными наклонными фальцами, а также на то, как полочные ребра жесткости влияют на грузоподъемность и поведение такого типа балок.В настоящем исследовании было проведено аналитическое исследование поведения при изгибе гибридной SBCW несварной наклонной складки.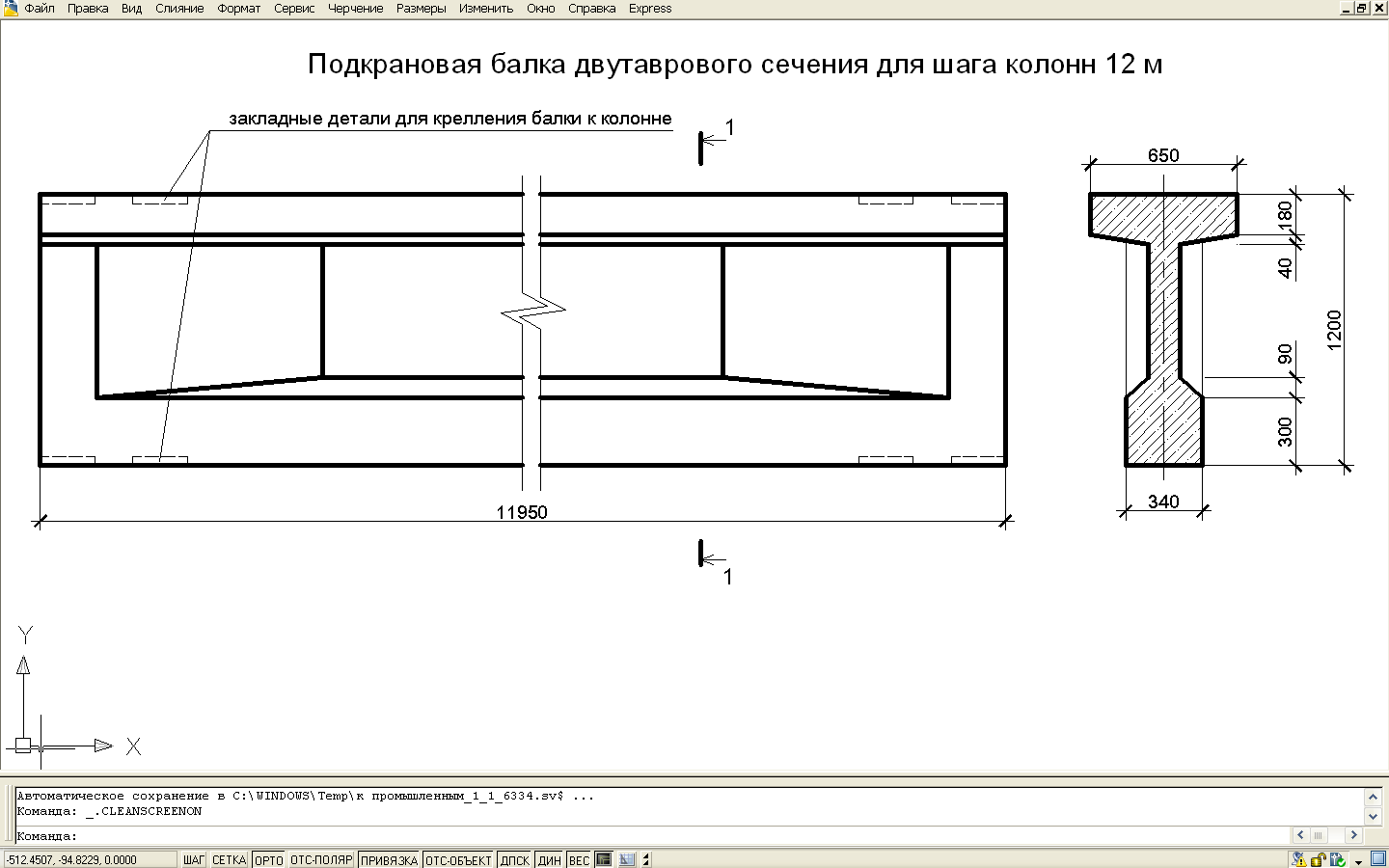
На основе результатов экспериментальных испытаний пяти гибридных SBCW при трехлинейных нагрузках, проведенных авторами [28], модели конечных элементов были проверены. Наблюдалось многообещающее согласие между КЭ и экспериментальными результатами. Трехмерное (3D) параметрическое КЭ исследование было выполнено на основе проверенной модели. Исследование было сосредоточено на шести параметрах, которые могут повлиять на механизм разрушения несварных наклонных складок SBCW.Изученными факторами были толщина стенки, толщина полки, высота стенки, марки стали полки и стенки, а также поперечные ребра жесткости полки. Наконец, предлагается уравнение для прогнозирования максимальной силы сдвига для SBCW класса 4 на основе длины горизонтальной складки.
2. Экспериментальная программа
Экспериментальная работа была проведена для выявления факторов, которые могут повлиять на поведение при изгибе и прочность гибридных SBCW. Краткое изложение экспериментальной работы представлено в этом разделе, а более подробная информация доступна в [28].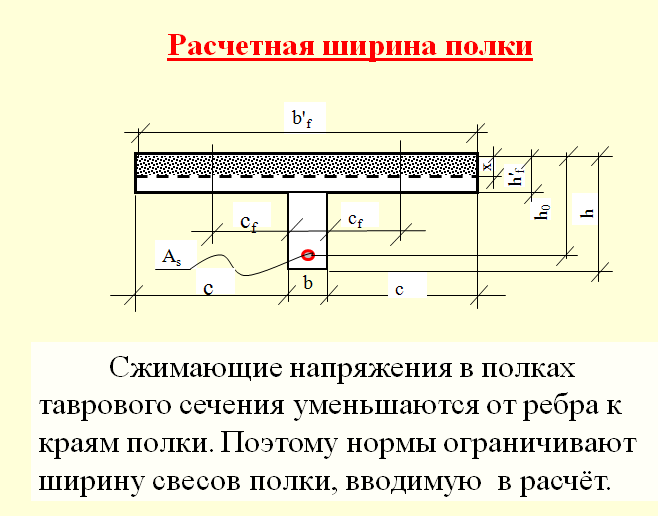 Было изготовлено шесть натурных балок: пять SBCW и одна плоская перемычка. Все балки имели длину 1900 мм с эффективным пролетом 1800 мм и были испытаны при трехлинейных нагрузках. Высота стенки (), толщина стенки (), ширина полки () и толщина полки () составляли 400, 3, 200 и 8 мм соответственно. Соотношение (/) гофрированной стенки составляло 133. Компактность фланцев в испытанных образцах измерялась по отношению к максимальной выдающейся длине (( + )/2). В этом экспериментальном исследовании изучалось влияние длины горизонтальной складки 200, 260 и 350 мм на поведение SBCW.Глубина гофра ( h ) и длина горизонтальной проекции наклонной складки ( d ) были равны 100 мм. Угол гофра ( α ) составлял 45°. Профили гофра образцов показаны на рис. 1.
Было изготовлено шесть натурных балок: пять SBCW и одна плоская перемычка. Все балки имели длину 1900 мм с эффективным пролетом 1800 мм и были испытаны при трехлинейных нагрузках. Высота стенки (), толщина стенки (), ширина полки () и толщина полки () составляли 400, 3, 200 и 8 мм соответственно. Соотношение (/) гофрированной стенки составляло 133. Компактность фланцев в испытанных образцах измерялась по отношению к максимальной выдающейся длине (( + )/2). В этом экспериментальном исследовании изучалось влияние длины горизонтальной складки 200, 260 и 350 мм на поведение SBCW.Глубина гофра ( h ) и длина горизонтальной проекции наклонной складки ( d ) были равны 100 мм. Угол гофра ( α ) составлял 45°. Профили гофра образцов показаны на рис. 1.
Для каждого образца использовали три ребра жесткости из стальных пластин (400 мм × 200 мм × 8 мм): по одному над каждой опорой и один под сосредоточенная нагрузка. Гофрированная стенка была соединена с полками непрерывными угловыми швами диаметром 4 мм с одной стороны с углом соединения 45° с использованием дуговой сварки металлическим электродом.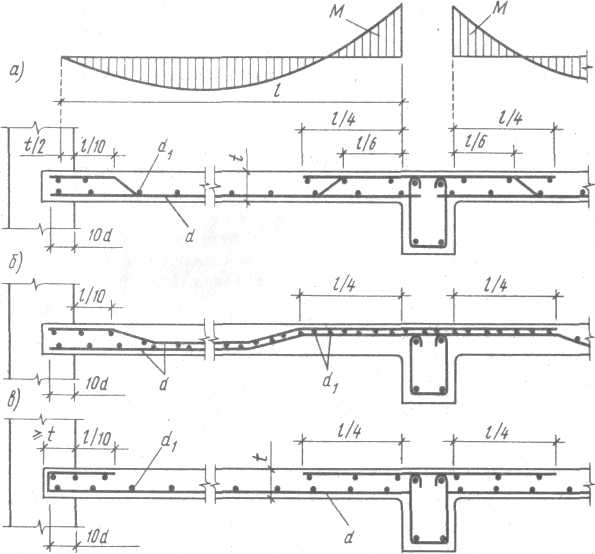 Образцы были названы кодом, обозначающим тестируемые параметры, где «CW», «FW», «IF», «FS», «W» и «NW» означают «гофрированное полотно», «плоское полотно», «наклонная складка». », «ребра жесткости полки», «сварные» и «несварные» соответственно. Число, следующее за «CW» или «FW», указывает длину линии ВЧ или прерывистой сварки (в см) соответственно. Подробная информация о каждом образце представлена в таблице 1, а дополнительные сведения о сварке и ребрах жесткости фланцев доступны в [28]. Свойства стали стенки и полки представлены в таблице 2.
Образцы были названы кодом, обозначающим тестируемые параметры, где «CW», «FW», «IF», «FS», «W» и «NW» означают «гофрированное полотно», «плоское полотно», «наклонная складка». », «ребра жесткости полки», «сварные» и «несварные» соответственно. Число, следующее за «CW» или «FW», указывает длину линии ВЧ или прерывистой сварки (в см) соответственно. Подробная информация о каждом образце представлена в таблице 1, а дополнительные сведения о сварке и ребрах жесткости фланцев доступны в [28]. Свойства стали стенки и полки представлены в таблице 2.
3. Численный анализ3.1. Разработка численной модели Численное моделирование, описанное в этом разделе, было выполнено с использованием нелинейной программы FE ANSYS для проведения параметрического анализа для SBCW с фланцевыми ребрами жесткости. Для моделирования SBCW было проведено четыре моделирования с использованием ячеек с размером ячеек 100, 50, 25 и 10 мм. Результаты показали, что средний процент ошибки относительно экспериментальной предельной нагрузки составил 2,5% и 3,5% для элементов размером 10 мм и 25 мм соответственно. В этом исследовании размер сетки для моделирования поведения пучка был выбран равным 25 мм, чтобы минимизировать время вычислений. За исключением базового стального цилиндра и исполнительного механизма, средний размер ячейки 20 мм оказался подходящим, как показано на рисунке 2(b). Чтобы получить уникальное решение, модель была ограничена с помощью граничных условий смещения. Чтобы убедиться, что модель ведет себя так же, как экспериментальные образцы, при нагрузке и опорах применялись граничные условия. Опоры выполнены в виде роликовых опор. Все узлы на нижней части базового стального цилиндра были защемлены во всех направлениях. Защемленные узлы из модели расположены в следующих положениях: (1) призма, имитирующая привод, защемлена от перемещений в осях x и z по длине призмы с обеих сторон положения загрузки. Тип области контакта определяется как контакт без трения. Контактная грань оболочки и целевая грань определяются как верхние грани, чтобы заставить целевую грань и контактную грань быть обращены друг к другу, чтобы уточнить обнаружение контакта. Свойства контакта контролируются радиусом пинбола, который указан как 10 мм, где в качестве метода обнаружения используется «Узел-нормально к цели», а обработка интерфейса выбрана как «Настроить на прикосновение».Сила, приложенная к верхним узлам блока привода, представляла собой фактическую приложенную силу, деленную на количество узлов. Общее значение нагрузки, приложенной к каждой модели, предполагалось в соответствии с предельной нагрузкой на балку, достигаемой каждым образцом из испытаний, которая была выше почти на 20%. Метод автоматического временного шага (или автоматической загрузки) — это метод, при котором приложенные нагрузки определяются автоматически в ответ на текущее состояние рассматриваемого анализа. 3.2. Прикладные несовершенства В литературе подчеркивается значительное влияние несовершенства на численные результаты [16]. Поэтому особое внимание уделялось форме прикладного несовершенства в текущем численном моделировании.Исходными несовершенствами являются структурные (остаточные напряжения) и геометрические несовершенства, которые можно смоделировать эквивалентными геометрическими несовершенствами. В модели для анализа модели применяются два загружения.Первый случай заключается в наведении начального несовершенства в виде начального внеплоскостного смещения по ГРП без приложения внешней нагрузки. Второй случай применяется в конце этого первого случая, пока не будет достигнута предельная нагрузка. Таким образом, модель подвергается двум вариантам нагрузки во время запуска, а именно: (1) от начала до применения начального несовершенства и (2) от обновления геометрии с начальным несовершенством до окончательного разрушения. 3.3. Проверка модели Для проверки модели КЭ было проведено сравнение характеристик нагрузки и вертикального отклонения, грузоподъемности и механики разрушения с экспериментальными результатами. В таблице 3 показано сравнение экспериментальных и численных результатов. Следовательно, на рис. 5(а)-5(е) представлены графики экспериментальной и численной нагрузки в зависимости от вертикального прогиба в середине пролета смоделированных образцов.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

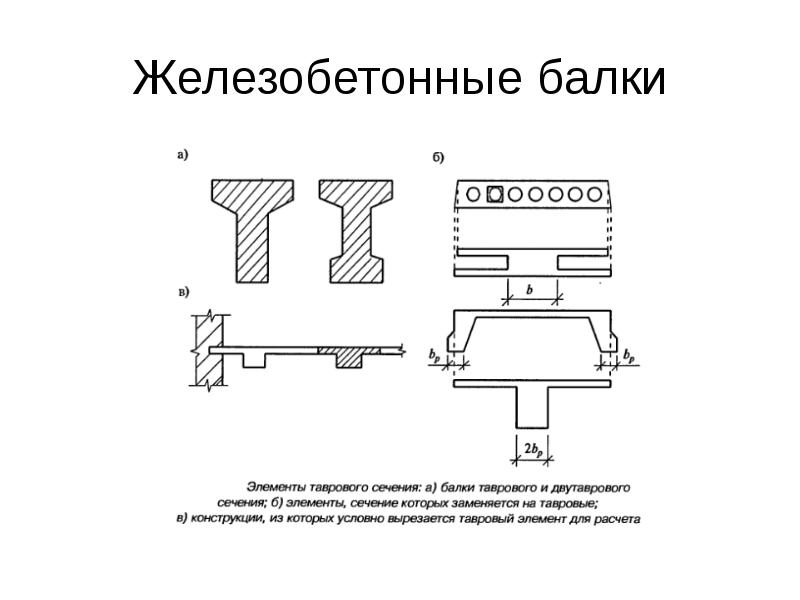 В таких случаях балка рассматривается как многопролетная на шарнирных опорах. Это уже значительно более сложная в расчёте конструкция. Её, конечно, можно рассматривать как отдельные шарнирно опёртые балки, но это совсем не так! При равных по длине пролётах самый большой изгибающий момент образуется не в пролётах, а над опорами и в этом случае особое значение приобретает рассчёт арматуры именно верхнего ряда. Мой калькулятор пока умеет рассчитывать лишь двухпролётные балки.
В таких случаях балка рассматривается как многопролетная на шарнирных опорах. Это уже значительно более сложная в расчёте конструкция. Её, конечно, можно рассматривать как отдельные шарнирно опёртые балки, но это совсем не так! При равных по длине пролётах самый большой изгибающий момент образуется не в пролётах, а над опорами и в этом случае особое значение приобретает рассчёт арматуры именно верхнего ряда. Мой калькулятор пока умеет рассчитывать лишь двухпролётные балки.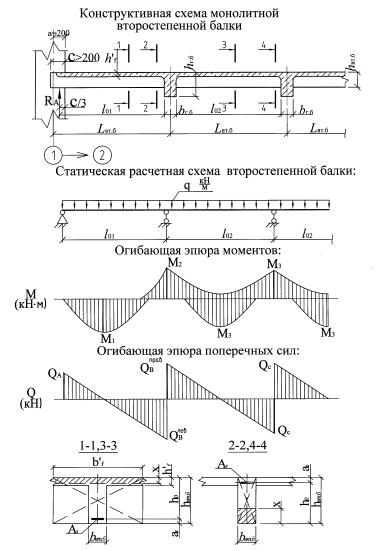
 ..». Так вот, там почти в полном составе указан наш старый добрый «снип со звездочкой» + ГОСТ Р 52748, т.е. про актуализированные — ничего (кто в теме — пишите в комментах ваше мнение).
..». Так вот, там почти в полном составе указан наш старый добрый «снип со звездочкой» + ГОСТ Р 52748, т.е. про актуализированные — ничего (кто в теме — пишите в комментах ваше мнение).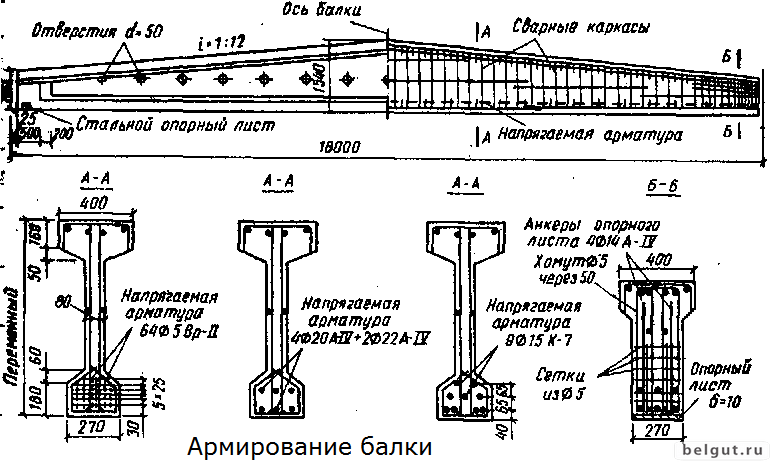 Кстати, выполнил сравнительный расчет «до и после 20 мая» — хоть и ввели к тележке фиксированный коэффициент надежности, а ко всей АК — к-т динамичности 1.4, но к-т полосности к тележке 0.6 все вернул на свои места, так что по АК изменения в пределах + 5-10% в зависимости от длины пролета.
Кстати, выполнил сравнительный расчет «до и после 20 мая» — хоть и ввели к тележке фиксированный коэффициент надежности, а ко всей АК — к-т динамичности 1.4, но к-т полосности к тележке 0.6 все вернул на свои места, так что по АК изменения в пределах + 5-10% в зависимости от длины пролета. 0,8 к Н-14 при расчете по IIгр
0,8 к Н-14 при расчете по IIгр 0,8 к Н-14 при расчете по IIгр
0,8 к Н-14 при расчете по IIгр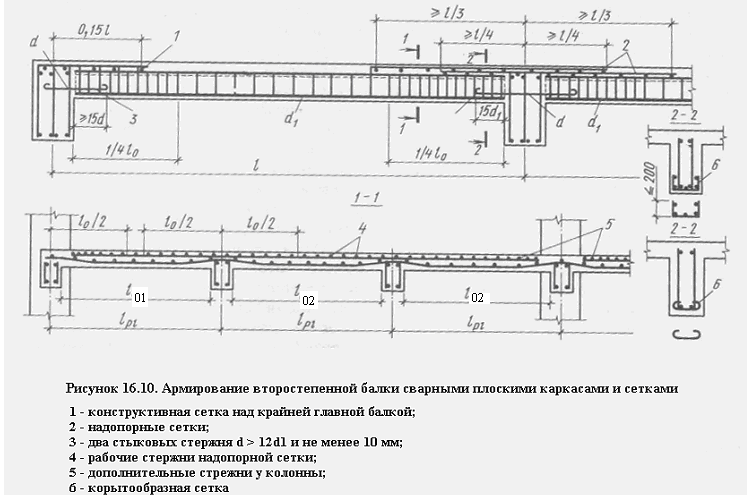 0,8 к Н-14 при расчете по IIгр
0,8 к Н-14 при расчете по IIгр Литература по этому вопросу осталась на работе, после выходных отсканирую и выложу отдельной темой. В двух словах — у меня есть методичка, по-моему СГТУ, где довольно четко прорисована эпюра передачи усилий и определяющие факторы. Там определяется длина переходного участка, на котором совместно учитывается анкеровка и сцепление, и вот этот участок считается таким «комплексным анкером». В типовом СДП я так и не разобрался, почему в местах близ обрыва пучков они уменьшают площадь рабочей арматуры, причем коэффициенты разные. В моих расчетах это нигде не учитывалось, и точку приложения силы натяжения я располагал где диафрагма анкера. В недобетонированных балках получалось следующее: хоть опорное сечение и меньше, но эксцентриситет преднапряжения тоже невелик, поэтому ни недопустимых растягивающих напряжений в верхнем поясе, ни касательных в стенке не возникало.
Литература по этому вопросу осталась на работе, после выходных отсканирую и выложу отдельной темой. В двух словах — у меня есть методичка, по-моему СГТУ, где довольно четко прорисована эпюра передачи усилий и определяющие факторы. Там определяется длина переходного участка, на котором совместно учитывается анкеровка и сцепление, и вот этот участок считается таким «комплексным анкером». В типовом СДП я так и не разобрался, почему в местах близ обрыва пучков они уменьшают площадь рабочей арматуры, причем коэффициенты разные. В моих расчетах это нигде не учитывалось, и точку приложения силы натяжения я располагал где диафрагма анкера. В недобетонированных балках получалось следующее: хоть опорное сечение и меньше, но эксцентриситет преднапряжения тоже невелик, поэтому ни недопустимых растягивающих напряжений в верхнем поясе, ни касательных в стенке не возникало.  На практике часто встречаются балки, изготовленные из разнородных материалов. Деревянные балки могут быть укреплены снизу стальными пластинами. В железобетонных балках стальная арматура размещается в растянутой зоне.§ 105] расчет
На практике часто встречаются балки, изготовленные из разнородных материалов. Деревянные балки могут быть укреплены снизу стальными пластинами. В железобетонных балках стальная арматура размещается в растянутой зоне.§ 105] расчет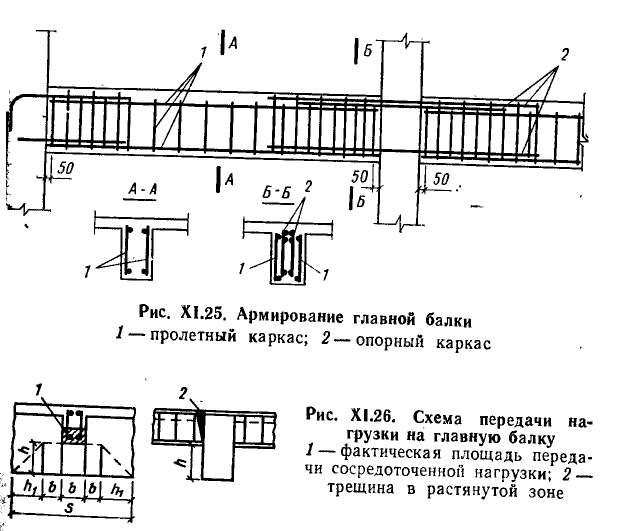 Среднее
Среднее 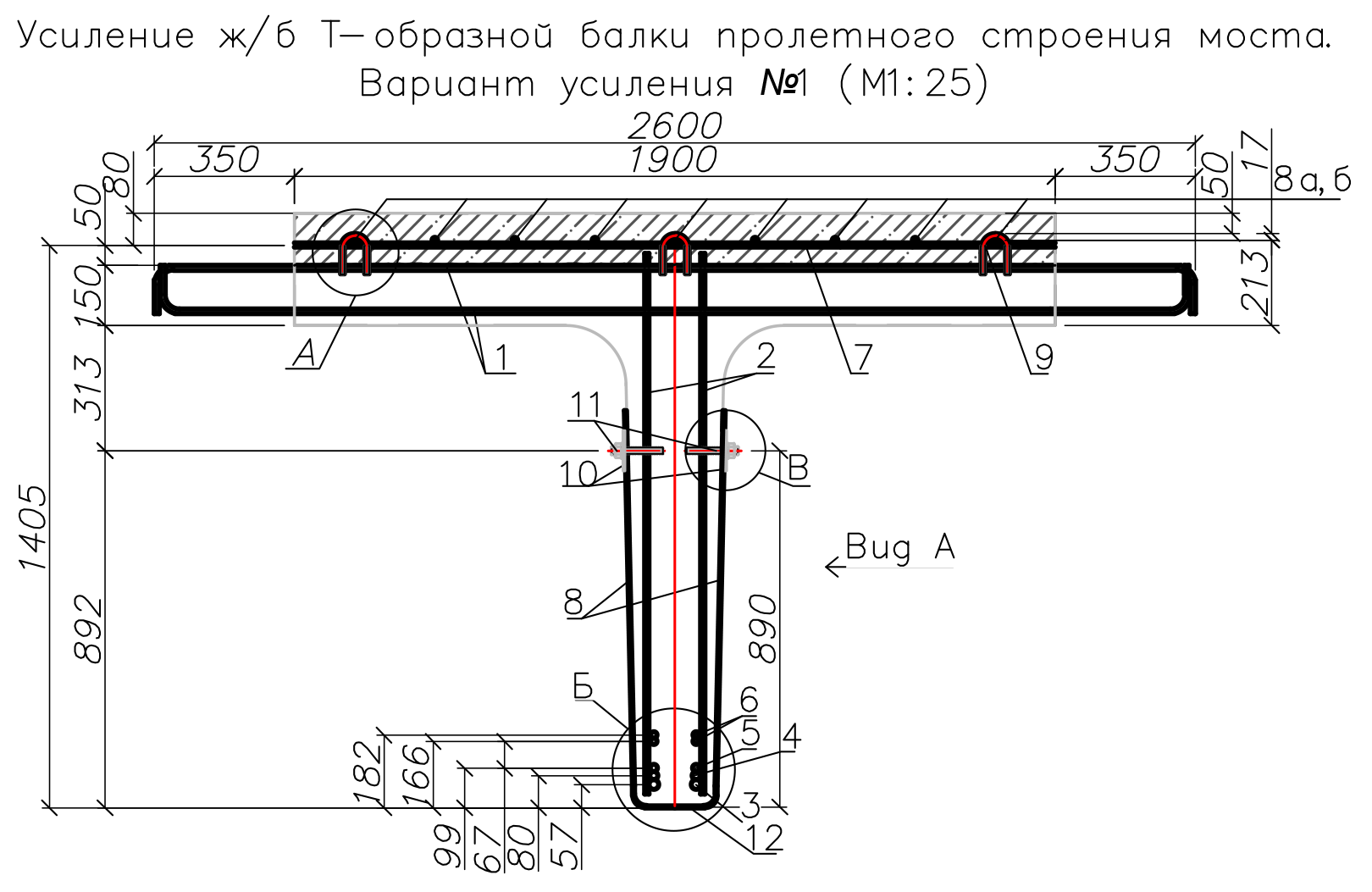 е.e.: расширение меньше, чем (√2)*a + e p ), s p_bot вычисляется как:
е.e.: расширение меньше, чем (√2)*a + e p ), s p_bot вычисляется как: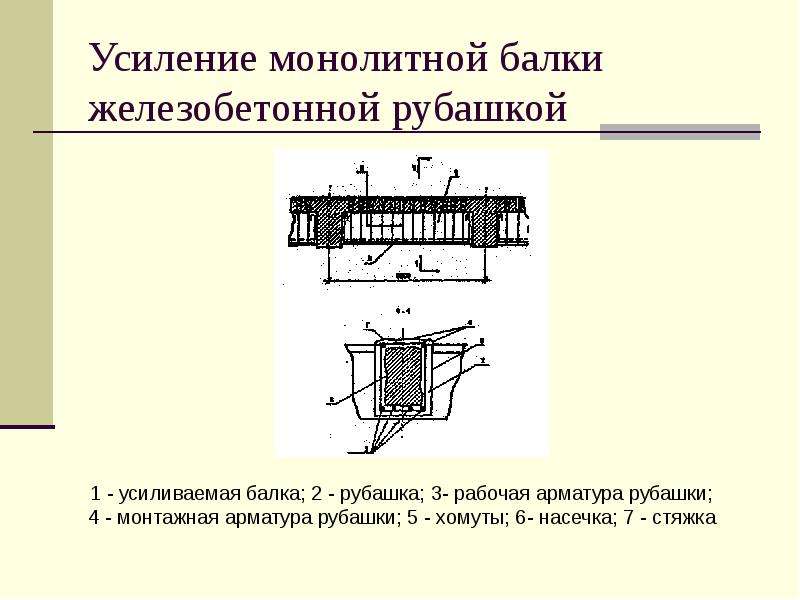

 В исходной модели КЭ были использованы размеры экспериментально испытанных СПКВ в Таифском университете ( b = 200 мм, горизонтальная проекция IF = 100 мм, α = 45°, = 2,8 мм, = 400мм). Для имитации стали использовалась упругопластическая оболочка КЭ (SHELL181). Элемент SHELL181 задавался четырьмя узлами с шестью степенями свободы в каждом узле: перемещения в узловых x , y и z направлениях и повороты вокруг узловых x , y и z оси.Элемент допускал пластичность, ползучесть, жесткость под напряжением, большие прогибы и способность выдерживать большие деформации. Опоры и привод были смоделированы с использованием твердотельных элементов, где контактные элементы использовались для моделирования контактных поверхностей между фланцами и опорами или приводом, как показано на рисунке 2(а). Некоторые элементы использовались для имитации контакта между полками балки и опорой или приводом (CONTA173, чтобы представить деформируемую поверхность) и (TARGE170, чтобы представить целевую поверхность).
В исходной модели КЭ были использованы размеры экспериментально испытанных СПКВ в Таифском университете ( b = 200 мм, горизонтальная проекция IF = 100 мм, α = 45°, = 2,8 мм, = 400мм). Для имитации стали использовалась упругопластическая оболочка КЭ (SHELL181). Элемент SHELL181 задавался четырьмя узлами с шестью степенями свободы в каждом узле: перемещения в узловых x , y и z направлениях и повороты вокруг узловых x , y и z оси.Элемент допускал пластичность, ползучесть, жесткость под напряжением, большие прогибы и способность выдерживать большие деформации. Опоры и привод были смоделированы с использованием твердотельных элементов, где контактные элементы использовались для моделирования контактных поверхностей между фланцами и опорами или приводом, как показано на рисунке 2(а). Некоторые элементы использовались для имитации контакта между полками балки и опорой или приводом (CONTA173, чтобы представить деформируемую поверхность) и (TARGE170, чтобы представить целевую поверхность).
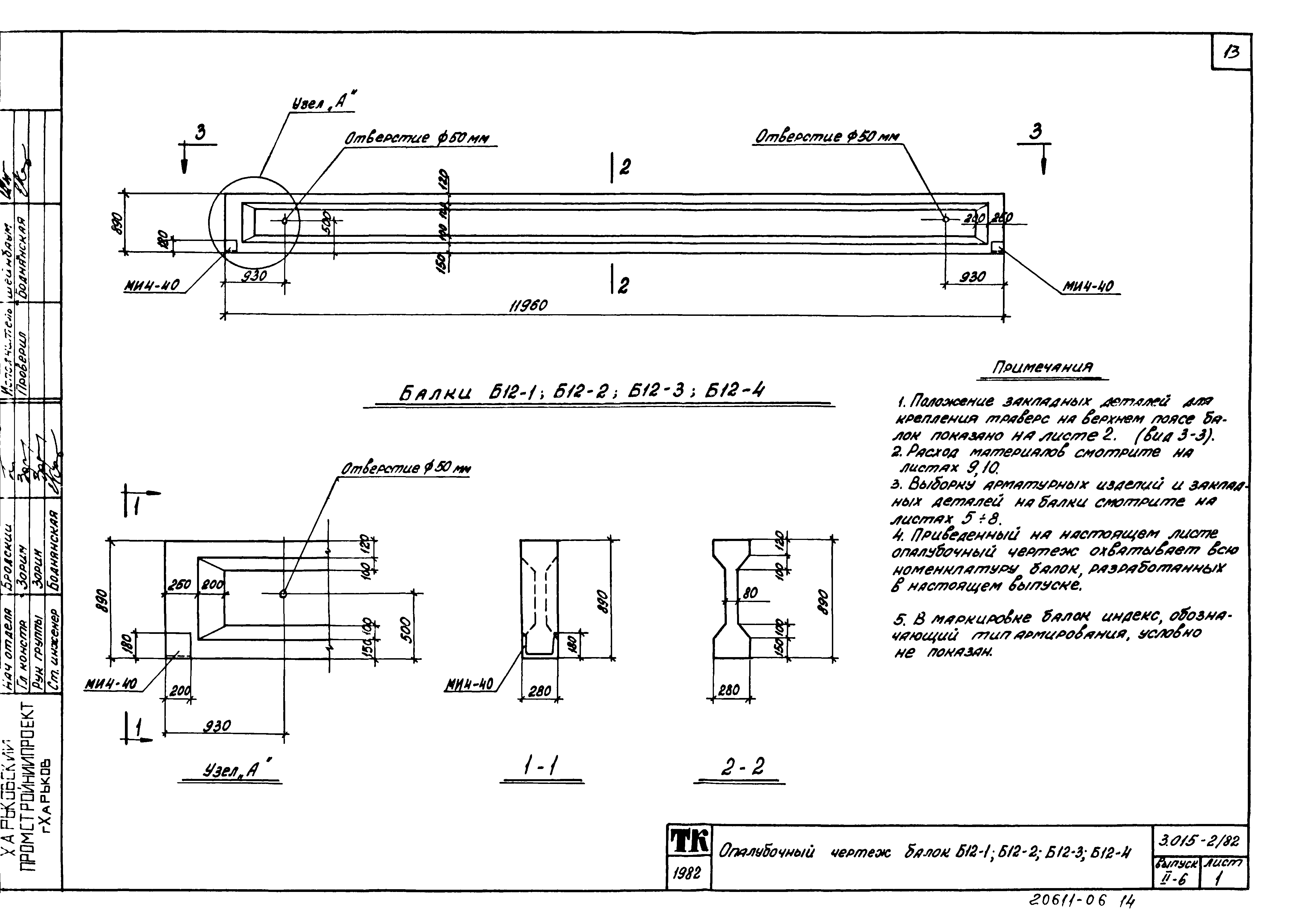 (2) Нижняя часть цилиндров, представляющих опоры, полностью защищена от перемещений и вращений в осях x , y и z , как показано на рисунке 3.
(2) Нижняя часть цилиндров, представляющих опоры, полностью защищена от перемещений и вращений в осях x , y и z , как показано на рисунке 3. В программу встроена технология автоматического пошагового расчета по времени, позволяющая регулировать соотношение силы и смещения модели, чтобы найти оптимальное приращение времени для достижения баланса.Этот метод использует нелинейный статический анализ с постепенным увеличением нагрузки, и тангенциальная жесткость рассчитывается до тех пор, пока силы дисбаланса (которые также называются остаточными силами/моментами R ) не станут приемлемо малыми. Максимальный и минимальный выбранные временные шаги составляли от 10% до 1% от общей приложенной нагрузки соответственно. Значения, измеренные в ходе экспериментальных испытаний свойств материала стальных компонентов (стенок и фланцев), были использованы в анализе КЭ (рис. 4 и таблица 2).Коэффициент Пуассона для стали был равен 0,3. В модели сталь представляет собой изотропный материал, который следует полилинейной кривой напряжения-деформации (рис. 4). Удлинение при текучести варьировалось от 0,001 до 0,0021 в зависимости от значения текучести для фланцев и стенки балки.
В программу встроена технология автоматического пошагового расчета по времени, позволяющая регулировать соотношение силы и смещения модели, чтобы найти оптимальное приращение времени для достижения баланса.Этот метод использует нелинейный статический анализ с постепенным увеличением нагрузки, и тангенциальная жесткость рассчитывается до тех пор, пока силы дисбаланса (которые также называются остаточными силами/моментами R ) не станут приемлемо малыми. Максимальный и минимальный выбранные временные шаги составляли от 10% до 1% от общей приложенной нагрузки соответственно. Значения, измеренные в ходе экспериментальных испытаний свойств материала стальных компонентов (стенок и фланцев), были использованы в анализе КЭ (рис. 4 и таблица 2).Коэффициент Пуассона для стали был равен 0,3. В модели сталь представляет собой изотропный материал, который следует полилинейной кривой напряжения-деформации (рис. 4). Удлинение при текучести варьировалось от 0,001 до 0,0021 в зависимости от значения текучести для фланцев и стенки балки.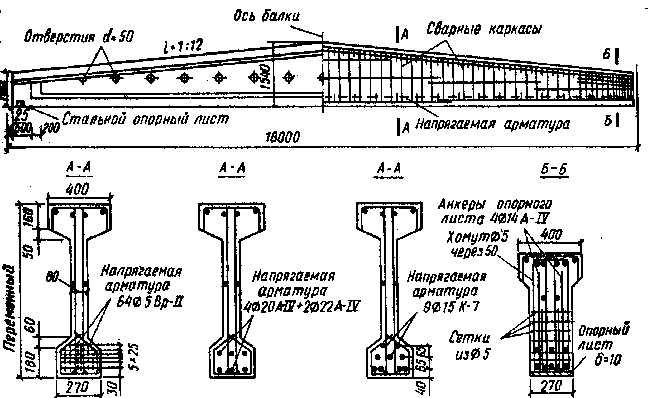 Изотропное поведение упрочнения с использованием приведенного модуля ( E r ) используется для моделирования свойств стали после достижения предела текучести, и это поведение продолжается до достижения предельного напряжения ( f u ).После предельного напряжения модель материала следует идеально пластичному поведению. Общее количество степеней свободы для каждой модели варьируется от 7500 до 9000 в зависимости от длины горизонтальной складки и изучаемых параметров. Техника решения Ньютона-Рафсона реализована для итеративного решения нелинейной задачи.
Изотропное поведение упрочнения с использованием приведенного модуля ( E r ) используется для моделирования свойств стали после достижения предела текучести, и это поведение продолжается до достижения предельного напряжения ( f u ).После предельного напряжения модель материала следует идеально пластичному поведению. Общее количество степеней свободы для каждой модели варьируется от 7500 до 9000 в зависимости от длины горизонтальной складки и изучаемых параметров. Техника решения Ньютона-Рафсона реализована для итеративного решения нелинейной задачи.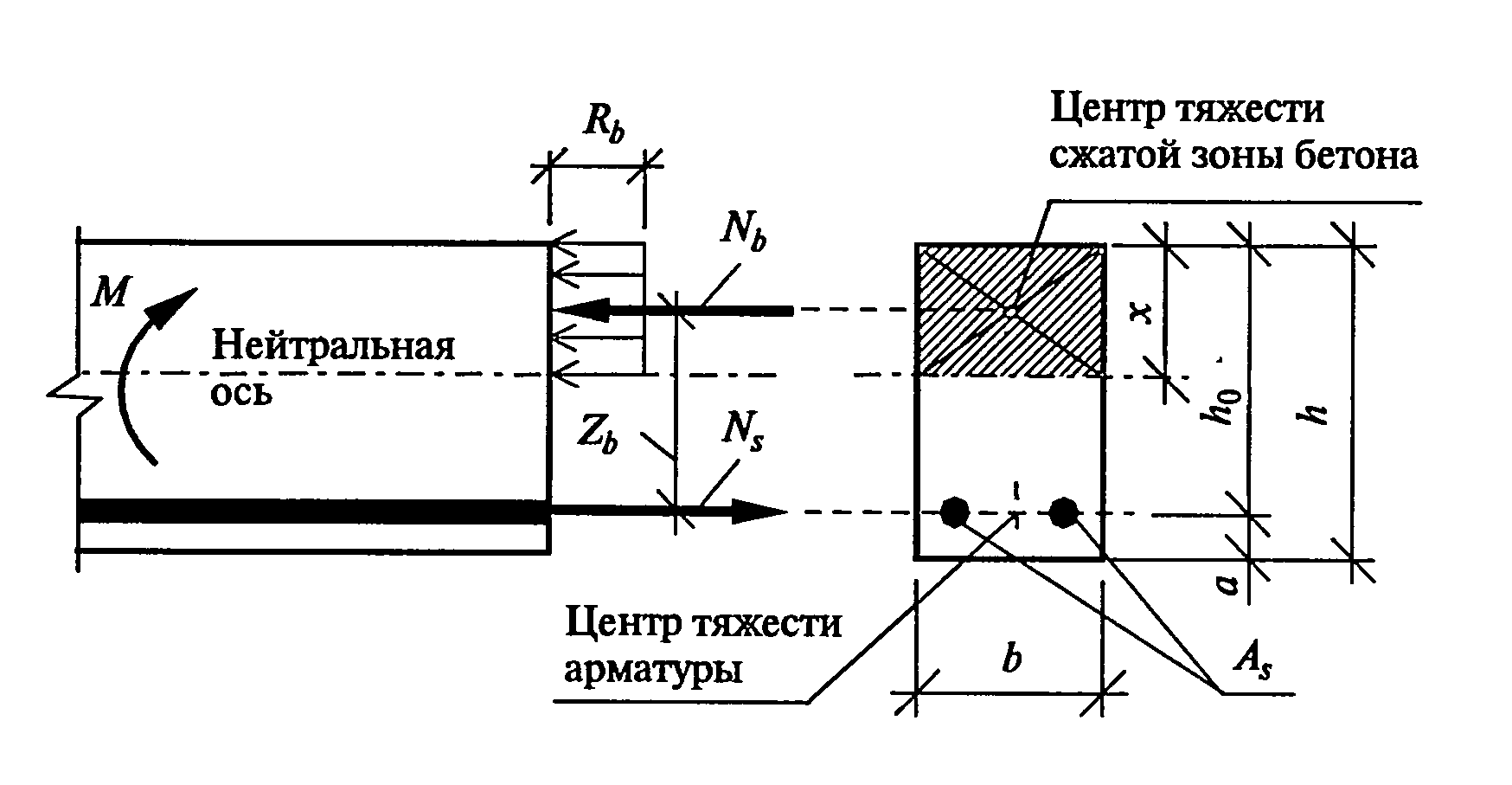 Формы и величины эквивалентного геометрического несовершенства могут быть определены с использованием различных альтернатив; одной из этих альтернатив является применение формы первой собственной моды. Этот метод используется главным образом потому, что он содержит соответствующий вид отказа, что также разрешено EN1993-1-5 [29]. Кроме того, стандарт разрешает использовать геометрические несовершенства на основе собственных форм.Из-за технологической обработки геометрические допуски на изготовление в сочетании с остаточными напряжениями представлены профилями напряжений с амплитудами, эквивалентными средним значениям. Начальные геометрические несовершенства в сетке обычно можно оценить как величину, значительно меньшую /200 [30]. Леблуба и др. В [14] рекомендуется рассматривать первую форму формы потери устойчивости как источник геометрического несовершенства с величиной, равной толщине стенки. На основе экспериментальной программы, проведенной для испытания шести стальных балок с гофрированной стенкой, было также сообщено, что на остаточную прочность не оказывает существенного влияния режим потери устойчивости при сдвиге, и она оценивается примерно в 50% от предельной несущей способности испытанной конструкции.
Формы и величины эквивалентного геометрического несовершенства могут быть определены с использованием различных альтернатив; одной из этих альтернатив является применение формы первой собственной моды. Этот метод используется главным образом потому, что он содержит соответствующий вид отказа, что также разрешено EN1993-1-5 [29]. Кроме того, стандарт разрешает использовать геометрические несовершенства на основе собственных форм.Из-за технологической обработки геометрические допуски на изготовление в сочетании с остаточными напряжениями представлены профилями напряжений с амплитудами, эквивалентными средним значениям. Начальные геометрические несовершенства в сетке обычно можно оценить как величину, значительно меньшую /200 [30]. Леблуба и др. В [14] рекомендуется рассматривать первую форму формы потери устойчивости как источник геометрического несовершенства с величиной, равной толщине стенки. На основе экспериментальной программы, проведенной для испытания шести стальных балок с гофрированной стенкой, было также сообщено, что на остаточную прочность не оказывает существенного влияния режим потери устойчивости при сдвиге, и она оценивается примерно в 50% от предельной несущей способности испытанной конструкции.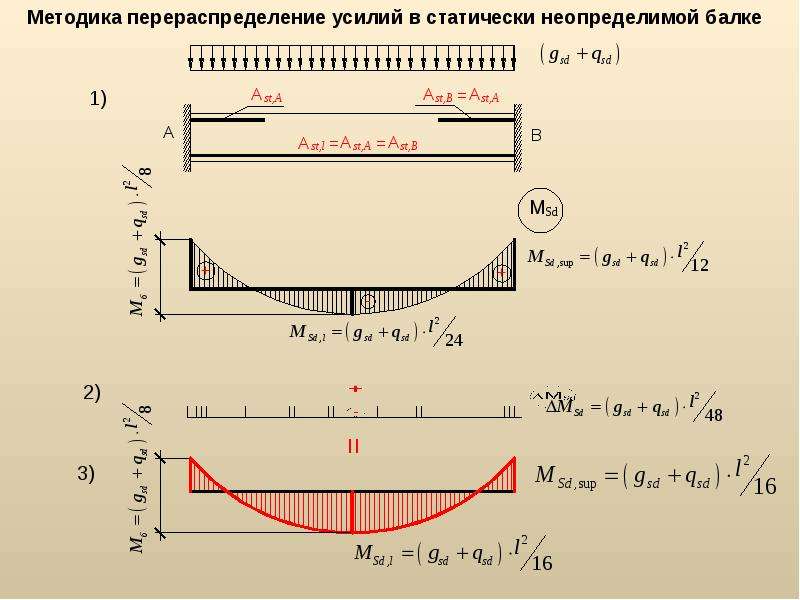 лучи.В настоящем исследовании были созданы и проверены нелинейные модели КЭ с учетом геометрических несовершенств. Расчеты были основаны на эквивалентных геометрических несовершенствах, рекомендованных стандартом EN 1993-1-5:2006. Был проведен анализ потери устойчивости по собственным значениям, чтобы получить первую моду потери устойчивости, а затем формы потери устойчивости были масштабированы для имитации начального дефекта. Таким образом, в текущем моделировании начальное несовершенство учитывается только при изгибе стенки с амплитудой, равной 2 мм.Различные режимы отказов были исследованы по отдельности и объединены для обеспечения надлежащего и безопасного решения. Изменения режима отказа в области взаимодействия обрабатывались с помощью такого типа несовершенства. Под действием одной сосредоточенной нагрузки были выполнены опытные прогоны пяти свободно опертых балок с гофрированными стенками, имеющих те же размеры пролета и полки, что и экспериментально исследуемые образцы с гофрированными стенками.
лучи.В настоящем исследовании были созданы и проверены нелинейные модели КЭ с учетом геометрических несовершенств. Расчеты были основаны на эквивалентных геометрических несовершенствах, рекомендованных стандартом EN 1993-1-5:2006. Был проведен анализ потери устойчивости по собственным значениям, чтобы получить первую моду потери устойчивости, а затем формы потери устойчивости были масштабированы для имитации начального дефекта. Таким образом, в текущем моделировании начальное несовершенство учитывается только при изгибе стенки с амплитудой, равной 2 мм.Различные режимы отказов были исследованы по отдельности и объединены для обеспечения надлежащего и безопасного решения. Изменения режима отказа в области взаимодействия обрабатывались с помощью такого типа несовершенства. Под действием одной сосредоточенной нагрузки были выполнены опытные прогоны пяти свободно опертых балок с гофрированными стенками, имеющих те же размеры пролета и полки, что и экспериментально исследуемые образцы с гофрированными стенками.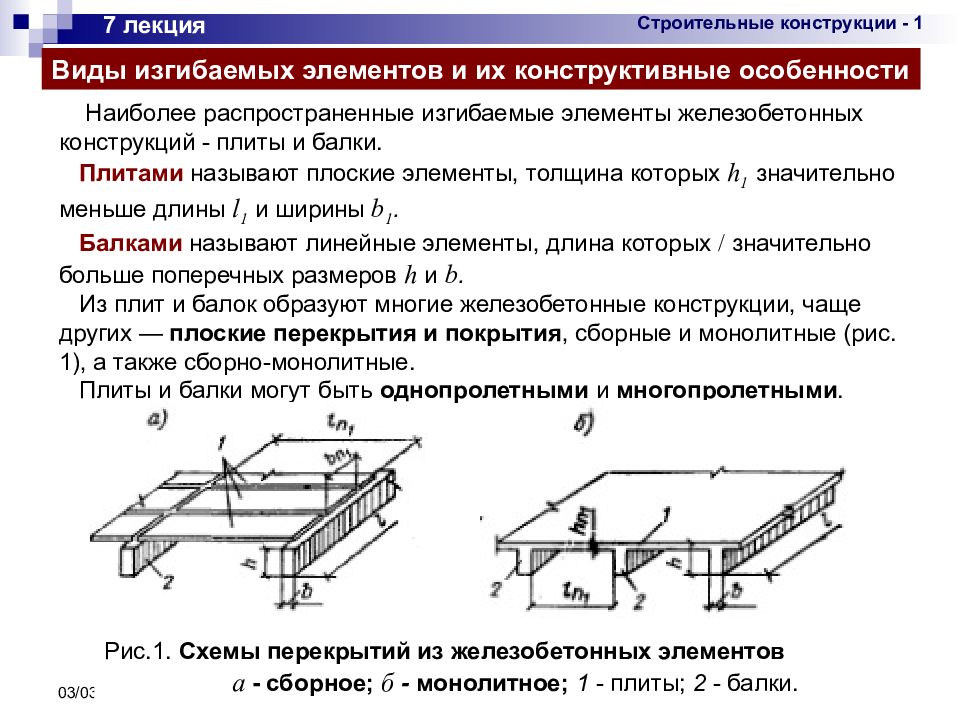 Нагрузки применялись к модели путем определения различных шагов нагрузки.
Нагрузки применялись к модели путем определения различных шагов нагрузки.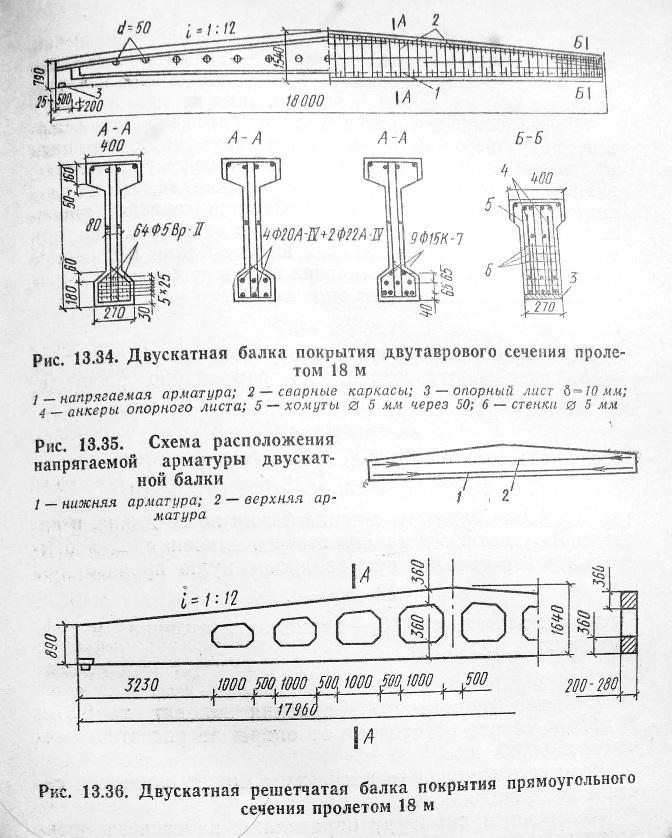 Таблица 3 ясно показывает, что модель может точно предсказать доходность и максимальную нагрузку, а также режимы отказа испытанных балок.Максимальные ошибки прогнозируемой урожайности и максимальных нагрузок были менее 12,8% и 5,6% соответственно (для нагрузки текучести среднее значение ( µ ) = 8,1% и стандартное отклонение ( σ ) = 3,6, а для максимальной нагрузки µ = 3,2% и σ = 1,7). Следовательно, кривые нагрузка-прогиб, полученные из модели FE, также хорошо согласуются с экспериментальными данными для гофрированных стальных балок (рис. 5). График нагрузка-прогиб в линейном диапазоне из анализа КЭ совпал с графиком нагрузка-прогиб в линейном диапазоне на основе экспериментальных результатов.Модель КЭ стала немного жестче, чем фактическая балка после упругой стадии. Кривые показывают, что в процессе решения конструкция находится в равновесии, если остаточные силы/моменты полностью исчезают; и приращение смещения/поворота ∆u на каждой итерации обновляется.
Таблица 3 ясно показывает, что модель может точно предсказать доходность и максимальную нагрузку, а также режимы отказа испытанных балок.Максимальные ошибки прогнозируемой урожайности и максимальных нагрузок были менее 12,8% и 5,6% соответственно (для нагрузки текучести среднее значение ( µ ) = 8,1% и стандартное отклонение ( σ ) = 3,6, а для максимальной нагрузки µ = 3,2% и σ = 1,7). Следовательно, кривые нагрузка-прогиб, полученные из модели FE, также хорошо согласуются с экспериментальными данными для гофрированных стальных балок (рис. 5). График нагрузка-прогиб в линейном диапазоне из анализа КЭ совпал с графиком нагрузка-прогиб в линейном диапазоне на основе экспериментальных результатов.Модель КЭ стала немного жестче, чем фактическая балка после упругой стадии. Кривые показывают, что в процессе решения конструкция находится в равновесии, если остаточные силы/моменты полностью исчезают; и приращение смещения/поворота ∆u на каждой итерации обновляется.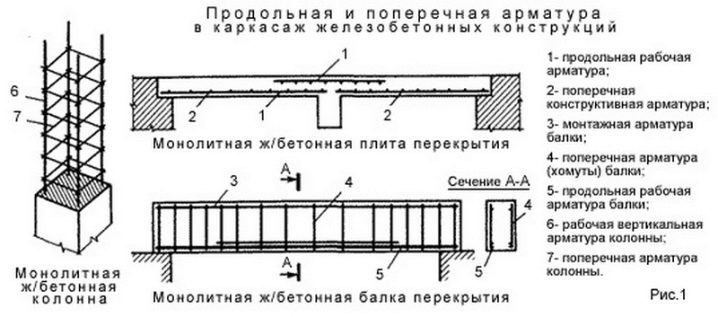 Наконец, на уровне нагрузки, когда структура становится неустойчивой (не достигается сходимость), в этот момент программа останавливала процесс решения. В некоторых случаях, как показано на рисунках 5(b) и 5(e)), программа останавливалась при меньшем отклонении, чем отклонение, полученное по результатам испытаний, возможно, из-за методов решения, реализованных в этом анализе.Кроме того, на рисунке 6 показано сравнение экспериментальных и расчетных механизмов разрушения для смоделированных образцов CW20IFNW, CW20IFNFS, CW35IFW и FW35WL. Вышеприведенные результаты и сравнения обеспечили способность смоделированной модели с хорошей точностью прогнозировать общее поведение, нагрузки и режимы отказов испытанного SBCW, а также SBCW с плоской стенкой.
Наконец, на уровне нагрузки, когда структура становится неустойчивой (не достигается сходимость), в этот момент программа останавливала процесс решения. В некоторых случаях, как показано на рисунках 5(b) и 5(e)), программа останавливалась при меньшем отклонении, чем отклонение, полученное по результатам испытаний, возможно, из-за методов решения, реализованных в этом анализе.Кроме того, на рисунке 6 показано сравнение экспериментальных и расчетных механизмов разрушения для смоделированных образцов CW20IFNW, CW20IFNFS, CW35IFW и FW35WL. Вышеприведенные результаты и сравнения обеспечили способность смоделированной модели с хорошей точностью прогнозировать общее поведение, нагрузки и режимы отказов испытанного SBCW, а также SBCW с плоской стенкой.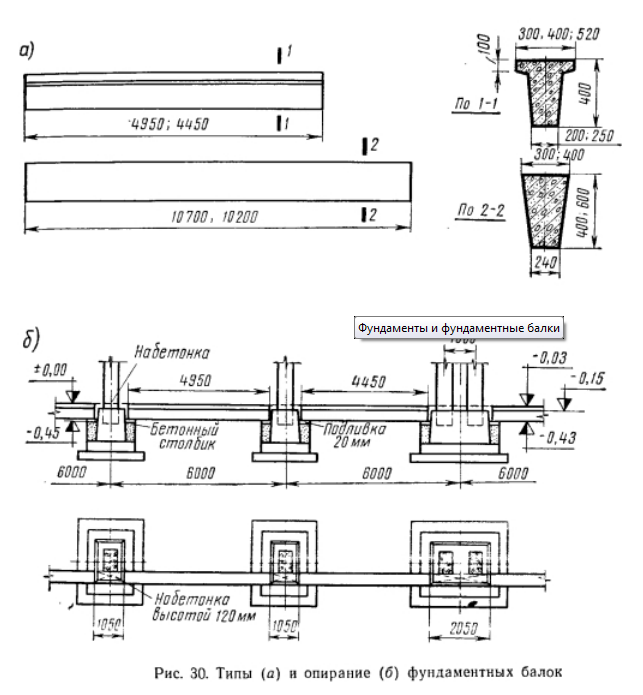 (кН)
(кН) 6
6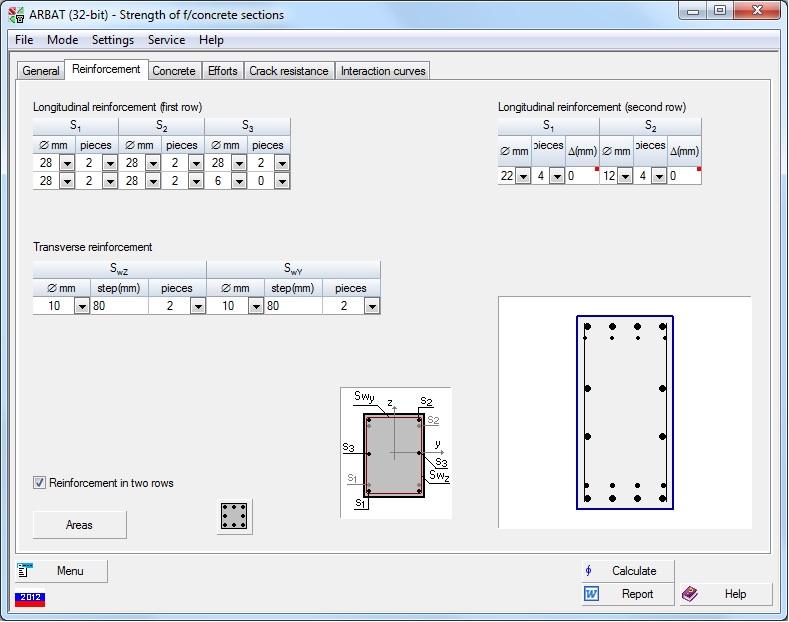 Сжимающее напряжение, полученное из модели КЭ на верхней полке, составило 138,14 МПа при полной нагрузке на изгиб полки (рис. 6 (а) и 7 (а)).Процент ошибки между моделью КЭ и экспериментальными результатами был менее 4%. Этот результат показал, что модель может имитировать поведение CWSB с приемлемой степенью точности.
Сжимающее напряжение, полученное из модели КЭ на верхней полке, составило 138,14 МПа при полной нагрузке на изгиб полки (рис. 6 (а) и 7 (а)).Процент ошибки между моделью КЭ и экспериментальными результатами был менее 4%. Этот результат показал, что модель может имитировать поведение CWSB с приемлемой степенью точности. Кроме того, была построена деформация верхней полки смоделированной балки CW20IFNW для различных стадий нагружения (рис. 6 (а)). Поведение фланца можно разделить на две основные стадии.На первом этапе наблюдалась линейная зависимость между напряжением и деформацией от нуля почти до почти 50-60% предела текучести полки (на основе горизонтальной длины сгиба), тогда как на второй стадии деформация увеличивалась быстрее, чем напряжение, до видимого коробления полки. произошел. На рисунке 7 (б) показано соотношение между напряжением и деформацией, полученное в результате экспериментальных испытаний и модели конечного элемента на верхней полке балки CW20IFNW. Рисунок обеспечил хорошее соответствие между численными и экспериментальными кривыми напряжения-деформации для верхней полки.Это сравнение подчеркнуло способность предложенной численной модели точно фиксировать общее поведение элементов CWSB, таких как грузоподъемность, отказоустойчивость, пятна и т. д.
Кроме того, была построена деформация верхней полки смоделированной балки CW20IFNW для различных стадий нагружения (рис. 6 (а)). Поведение фланца можно разделить на две основные стадии.На первом этапе наблюдалась линейная зависимость между напряжением и деформацией от нуля почти до почти 50-60% предела текучести полки (на основе горизонтальной длины сгиба), тогда как на второй стадии деформация увеличивалась быстрее, чем напряжение, до видимого коробления полки. произошел. На рисунке 7 (б) показано соотношение между напряжением и деформацией, полученное в результате экспериментальных испытаний и модели конечного элемента на верхней полке балки CW20IFNW. Рисунок обеспечил хорошее соответствие между численными и экспериментальными кривыми напряжения-деформации для верхней полки.Это сравнение подчеркнуло способность предложенной численной модели точно фиксировать общее поведение элементов CWSB, таких как грузоподъемность, отказоустойчивость, пятна и т. д.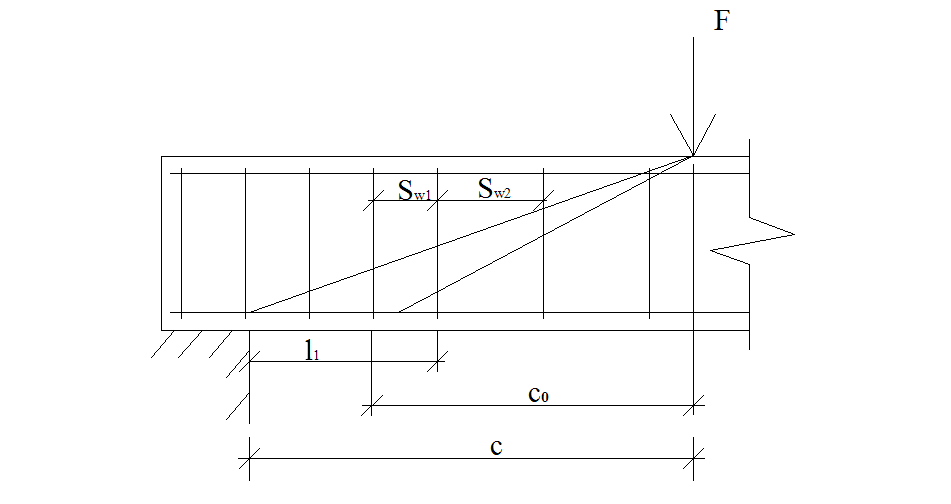 Соответственно, эту предыдущую модель FE можно использовать для исследования влияния различных параметров, влияющих на поведение и мощность SBCW, с более глубоким пониманием. В этом параметрическом исследовании изучалось влияние толщины стенки, предела текучести стенки, глубины стенки, толщины полки, предела текучести полки и ребер жесткости на поведение и нагрузки SBCW.Детали смоделированных балок и изученные параметры перечислены в таблице 4. Следовательно, целью этого параметрического исследования было исследование различных аспектов поведения системы, таких как жесткость, предельная грузоподъемность и режим разрушения, путем изменения изучаемые параметры. Исследуемые параметры были разделены на 6 групп (табл. 4). В группе 1 были смоделированы четыре SBCW с различной толщиной стенки (2, 4, 5 и 6 мм). Во 2-й группе моделировались три SBCW с разным пределом текучести полотна (400, 450 и 500 МПа).В группе 3 были смоделированы три SBCW с различной высотой полотна (450, 550 и 650 мм). Наоборот, в группе 4 моделировались четыре SBCW с различной толщиной полки (7, 9, 10 и 12 мм).
Соответственно, эту предыдущую модель FE можно использовать для исследования влияния различных параметров, влияющих на поведение и мощность SBCW, с более глубоким пониманием. В этом параметрическом исследовании изучалось влияние толщины стенки, предела текучести стенки, глубины стенки, толщины полки, предела текучести полки и ребер жесткости на поведение и нагрузки SBCW.Детали смоделированных балок и изученные параметры перечислены в таблице 4. Следовательно, целью этого параметрического исследования было исследование различных аспектов поведения системы, таких как жесткость, предельная грузоподъемность и режим разрушения, путем изменения изучаемые параметры. Исследуемые параметры были разделены на 6 групп (табл. 4). В группе 1 были смоделированы четыре SBCW с различной толщиной стенки (2, 4, 5 и 6 мм). Во 2-й группе моделировались три SBCW с разным пределом текучести полотна (400, 450 и 500 МПа).В группе 3 были смоделированы три SBCW с различной высотой полотна (450, 550 и 650 мм). Наоборот, в группе 4 моделировались четыре SBCW с различной толщиной полки (7, 9, 10 и 12 мм).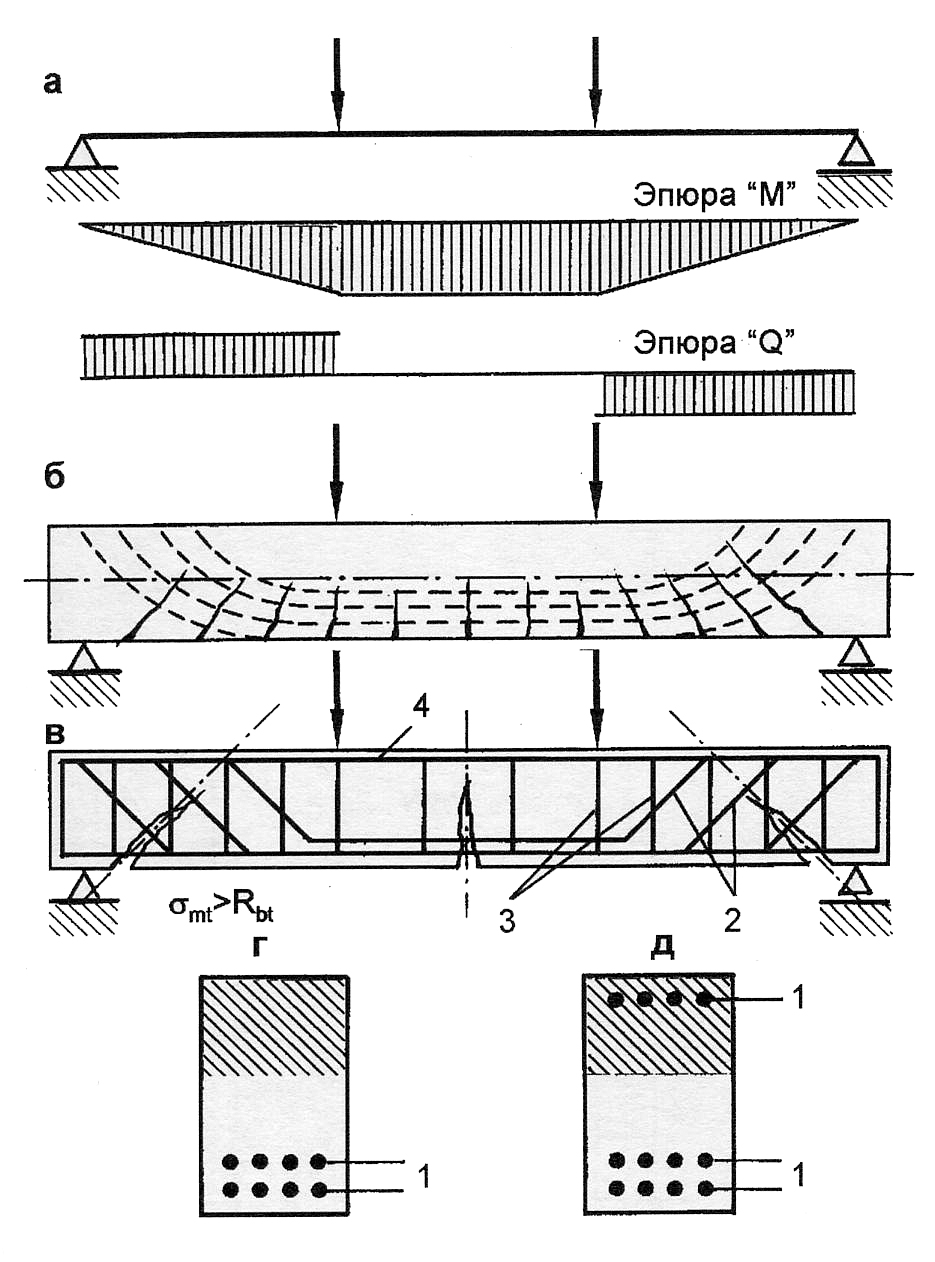 В группе 5 также были смоделированы четыре SBCW с различными пределами текучести полки (250, 275 и 300 МПа). Наконец, в группе 6 с использованием проверенной модели КЭ были рассмотрены два случая с разной высотой элементов жесткости (рис. 8 (а) и 8 (б)) и количеством элементов жесткости (рис. 8 (в) и 8 (г)). В этом исследовании значение варьировалось от 35% до 85%, чтобы исследовать влияние высоты полки-ребра жесткости на сопротивление полки.В параметрическом исследовании КЭ согласованность моделей поддерживалась таким образом, что единственным переменным параметром были условия жесткости. При параметрическом исследовании луч CW20IFNW был зафиксирован в качестве контрольного луча. Результаты для смоделированных балок в параметрическом исследовании сравнивались с результатами для рассматриваемой контрольной балки.
В группе 5 также были смоделированы четыре SBCW с различными пределами текучести полки (250, 275 и 300 МПа). Наконец, в группе 6 с использованием проверенной модели КЭ были рассмотрены два случая с разной высотой элементов жесткости (рис. 8 (а) и 8 (б)) и количеством элементов жесткости (рис. 8 (в) и 8 (г)). В этом исследовании значение варьировалось от 35% до 85%, чтобы исследовать влияние высоты полки-ребра жесткости на сопротивление полки.В параметрическом исследовании КЭ согласованность моделей поддерживалась таким образом, что единственным переменным параметром были условия жесткости. При параметрическом исследовании луч CW20IFNW был зафиксирован в качестве контрольного луча. Результаты для смоделированных балок в параметрическом исследовании сравнивались с результатами для рассматриваемой контрольной балки. 5. Результаты параметрического исследования
5. Результаты параметрического исследования и максимальное, так как отказ произошел из-за потери устойчивости полки.Увеличение высоты стенки также увеличило грузоподъемность SBCW, поскольку оно задержало или предотвратило растрескивание полки и уменьшило сжимающее напряжение на полках. Увеличение высоты стенки с 384 мм до 450, 550 и 650 мм увеличило предельную нагрузку SBCW на 9%, 18% и 20% соответственно, а предельную нагрузку SBCW увеличил на 10%, 16% и 22%, соответственно. Таким образом, увеличение высоты стенки до 69 % по сравнению с CB увеличило грузоподъемность SBCW на 22 %. Исследуемые параметры, связанные с характеристиками стенки (размеры и свойства материала), имели максимальное увеличение несущей способности на 22% для балок с высотой стенки 650 мм.
и максимальное, так как отказ произошел из-за потери устойчивости полки.Увеличение высоты стенки также увеличило грузоподъемность SBCW, поскольку оно задержало или предотвратило растрескивание полки и уменьшило сжимающее напряжение на полках. Увеличение высоты стенки с 384 мм до 450, 550 и 650 мм увеличило предельную нагрузку SBCW на 9%, 18% и 20% соответственно, а предельную нагрузку SBCW увеличил на 10%, 16% и 22%, соответственно. Таким образом, увеличение высоты стенки до 69 % по сравнению с CB увеличило грузоподъемность SBCW на 22 %. Исследуемые параметры, связанные с характеристиками стенки (размеры и свойства материала), имели максимальное увеличение несущей способности на 22% для балок с высотой стенки 650 мм.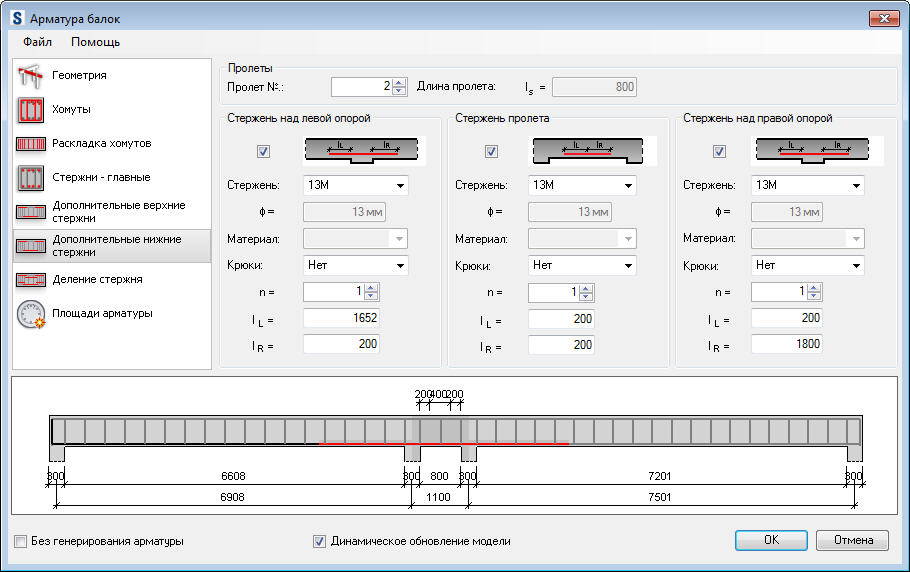 5
5 5981
5981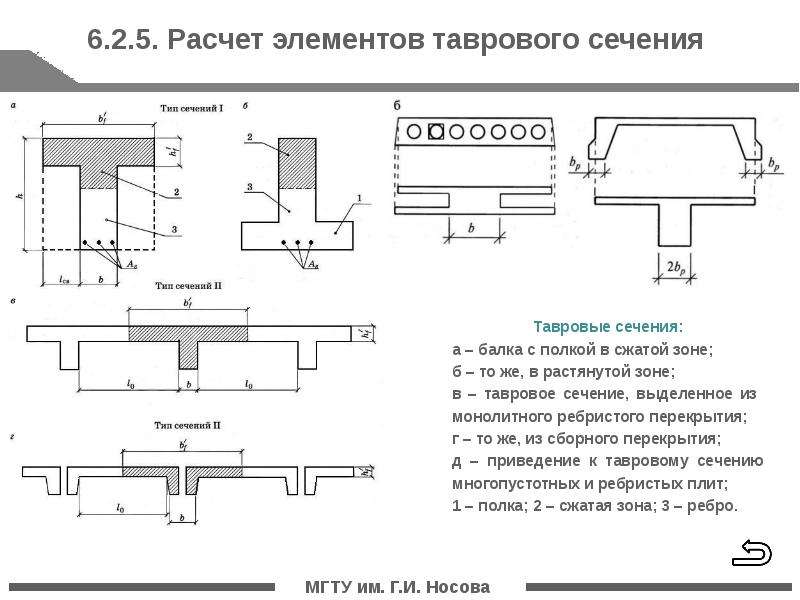 Более того, увеличение толщины полки изменило вид разрушения с WB + FB на только WB. Таким образом, увеличение толщины фланца примерно на 67% по сравнению с CB увеличило предел текучести и предельные нагрузки на 95% и 55%, соответственно, по сравнению с CB. Кроме того, увеличение предела текучести полки с 225 МПа (CB) до 250, 275 и 300 МПа увеличило предел текучести на 13%, 21% и 26% соответственно, в то время как предельные нагрузки увеличились на 10%, 15%, и 20%, соответственно, по сравнению с CB, так как режим отказа изменился с WB + FB на только WB.Сравнение размеров стенки и полки на поведение CWSB показало более высокую эффективность размеров полки на грузоподъемность и режимы отказа CWSB. И наоборот, влияние свойств материала стенки и фланцев имело почти такое же влияние на поведение CWSB.
Более того, увеличение толщины полки изменило вид разрушения с WB + FB на только WB. Таким образом, увеличение толщины фланца примерно на 67% по сравнению с CB увеличило предел текучести и предельные нагрузки на 95% и 55%, соответственно, по сравнению с CB. Кроме того, увеличение предела текучести полки с 225 МПа (CB) до 250, 275 и 300 МПа увеличило предел текучести на 13%, 21% и 26% соответственно, в то время как предельные нагрузки увеличились на 10%, 15%, и 20%, соответственно, по сравнению с CB, так как режим отказа изменился с WB + FB на только WB.Сравнение размеров стенки и полки на поведение CWSB показало более высокую эффективность размеров полки на грузоподъемность и режимы отказа CWSB. И наоборот, влияние свойств материала стенки и фланцев имело почти такое же влияние на поведение CWSB.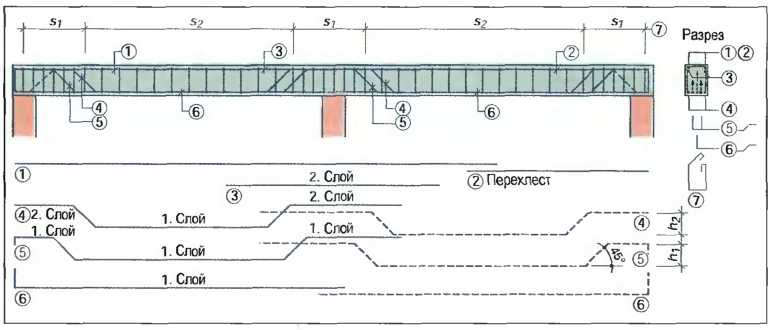 Предел текучести SBCW с 1, 2 и 3 фланцевыми ребрами жесткости высотой 150 мм увеличился на 12%, 42% и 49% соответственно, а предельные нагрузки увеличились на 14%, 41% и 92%, соответственно, больше, чем у CB. И наоборот, использование одного элемента жесткости высотой 250 и 350 мм увеличило предельные нагрузки на 34% и 48% соответственно, а предельные нагрузки увеличились на 29% и 67% соответственно по сравнению с CB. Из приведенных выше результатов увеличение толщины полки или использование ребер жесткости полки оказало большее влияние на повышение предела текучести и предельных нагрузок SBCW, чем увеличение размеров стенки или предела текучести стенки и полки.Влияние высоты полки-ребра жесткости на нормальное напряжение и коробление полки показано на рисунках 9 (а) и 9 (б). Кроме того, было исследовано влияние количества ребер жесткости полки на изгиб полки и предельное нормальное напряжение путем изменения расположения и количества ребер жесткости полки. Фланцевые ребра жесткости рекомендовалось располагать только в РП, близких к линейной нагрузке.
Предел текучести SBCW с 1, 2 и 3 фланцевыми ребрами жесткости высотой 150 мм увеличился на 12%, 42% и 49% соответственно, а предельные нагрузки увеличились на 14%, 41% и 92%, соответственно, больше, чем у CB. И наоборот, использование одного элемента жесткости высотой 250 и 350 мм увеличило предельные нагрузки на 34% и 48% соответственно, а предельные нагрузки увеличились на 29% и 67% соответственно по сравнению с CB. Из приведенных выше результатов увеличение толщины полки или использование ребер жесткости полки оказало большее влияние на повышение предела текучести и предельных нагрузок SBCW, чем увеличение размеров стенки или предела текучести стенки и полки.Влияние высоты полки-ребра жесткости на нормальное напряжение и коробление полки показано на рисунках 9 (а) и 9 (б). Кроме того, было исследовано влияние количества ребер жесткости полки на изгиб полки и предельное нормальное напряжение путем изменения расположения и количества ребер жесткости полки. Фланцевые ребра жесткости рекомендовалось располагать только в РП, близких к линейной нагрузке.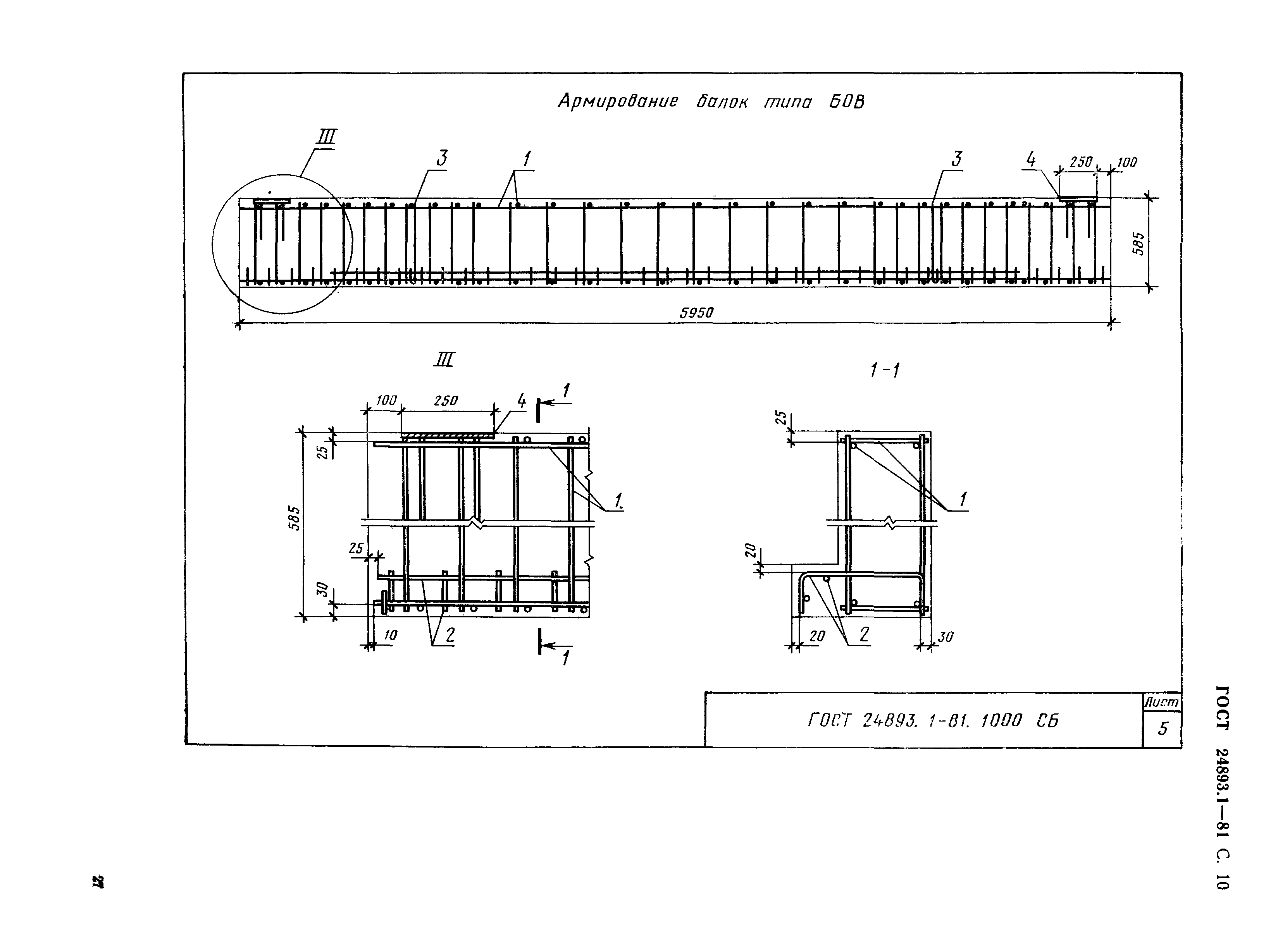 Три ребра жесткости были использованы, чтобы максимально увеличить количество ребер жесткости полки вдоль ВЧ. Первое и второе ребра жесткости располагались на линиях пересечения ВЧ и ВЧ, а третье закреплялось на середине длины ВЧ.Количество поперечных ребер жесткости значительно повлияло на коробление полки и предельное нормальное напряжение SBCW, как показано на рисунках 9 (c) и 9 (d). Балка БС3Хс150 (с тремя ребрами жесткости полки 150 мм) испытала наибольшую грузоподъемность смоделированных балок из-за влияния ребер жесткости на замедление или предотвращение потери устойчивости полки (таблица 5 и рисунок 9 (г)). Количество ребер жесткости или увеличение высоты ребра жесткости оказали большое влияние на грузоподъемность и режим отказа SBCW (таблица 5).Более того, использование трех фланцевых ребер жесткости предотвратило разрушение НК.
Три ребра жесткости были использованы, чтобы максимально увеличить количество ребер жесткости полки вдоль ВЧ. Первое и второе ребра жесткости располагались на линиях пересечения ВЧ и ВЧ, а третье закреплялось на середине длины ВЧ.Количество поперечных ребер жесткости значительно повлияло на коробление полки и предельное нормальное напряжение SBCW, как показано на рисунках 9 (c) и 9 (d). Балка БС3Хс150 (с тремя ребрами жесткости полки 150 мм) испытала наибольшую грузоподъемность смоделированных балок из-за влияния ребер жесткости на замедление или предотвращение потери устойчивости полки (таблица 5 и рисунок 9 (г)). Количество ребер жесткости или увеличение высоты ребра жесткости оказали большое влияние на грузоподъемность и режим отказа SBCW (таблица 5).Более того, использование трех фланцевых ребер жесткости предотвратило разрушение НК. Жесткость SBCW увеличивалась по мере увеличения толщины стенки, поскольку увеличение толщины стенки увеличивало инерцию луча и уменьшало прогиб луча при сдвиге (рис. 10 (а)). Напротив, хотя увеличение предела текучести стенки увеличило нагрузки на балку, предел текучести стенки оказал незначительное влияние на жесткость SBCW, поскольку инерция балки зависела только от размеров балки (рис. 10 (б)).И наоборот, по мере увеличения высоты стенки жесткость SBCW увеличивалась, поскольку увеличение высоты стенки увеличивало инерцию балки и уменьшало прогиб балки при сдвиге, тем самым увеличивая жесткость SBCW (рис. 10 (c)). Кроме того, увеличение толщины фланца значительно увеличило жесткость SBCW, поскольку это сильно повлияло на инерцию балки (рис. 10 (d)). Кроме того, увеличение предела текучести полки увеличило жесткость SBCW (рис. 10 (e)). Наконец, соотношение значительно повлияло на кривую нагрузки-прогиба SBCW, как показано на рисунке 10 (f).Использование фланцевого ребра жесткости увеличило жесткость SBCW, поскольку ребра жесткости могли задержать или предотвратить смещение SBCW вне плоскости.
Жесткость SBCW увеличивалась по мере увеличения толщины стенки, поскольку увеличение толщины стенки увеличивало инерцию луча и уменьшало прогиб луча при сдвиге (рис. 10 (а)). Напротив, хотя увеличение предела текучести стенки увеличило нагрузки на балку, предел текучести стенки оказал незначительное влияние на жесткость SBCW, поскольку инерция балки зависела только от размеров балки (рис. 10 (б)).И наоборот, по мере увеличения высоты стенки жесткость SBCW увеличивалась, поскольку увеличение высоты стенки увеличивало инерцию балки и уменьшало прогиб балки при сдвиге, тем самым увеличивая жесткость SBCW (рис. 10 (c)). Кроме того, увеличение толщины фланца значительно увеличило жесткость SBCW, поскольку это сильно повлияло на инерцию балки (рис. 10 (d)). Кроме того, увеличение предела текучести полки увеличило жесткость SBCW (рис. 10 (e)). Наконец, соотношение значительно повлияло на кривую нагрузки-прогиба SBCW, как показано на рисунке 10 (f).Использование фланцевого ребра жесткости увеличило жесткость SBCW, поскольку ребра жесткости могли задержать или предотвратить смещение SBCW вне плоскости.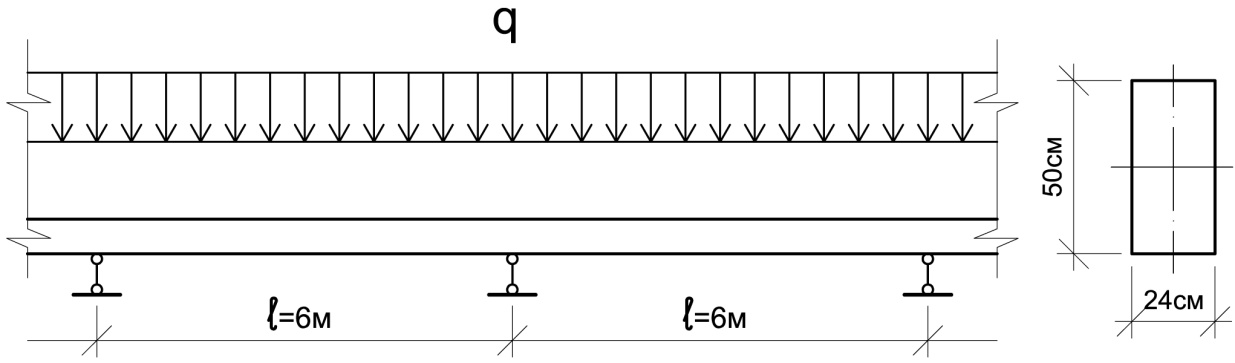 Напротив, увеличение количества ребер жесткости фланцев и их высоты незначительно повлияло на жесткость SBCW, хотя сильно повлияло на грузоподъемность и ударную вязкость SBCW (рис. 10(f)).
Напротив, увеличение количества ребер жесткости фланцев и их высоты незначительно повлияло на жесткость SBCW, хотя сильно повлияло на грузоподъемность и ударную вязкость SBCW (рис. 10(f)).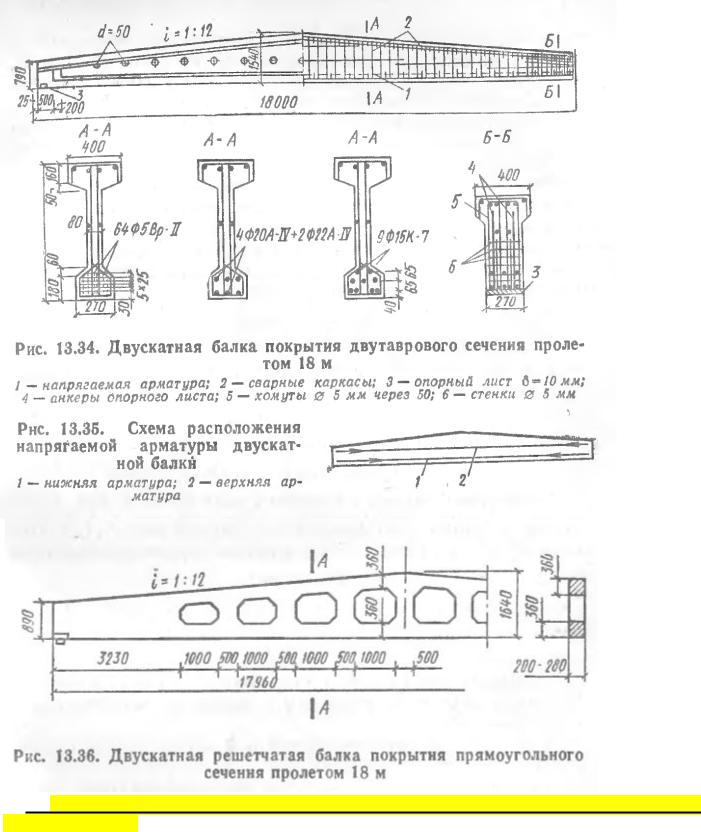 Это уравнение предсказало максимальное усилие сдвига, которое могло быть выдержано несварными наклонными складчатыми SBCW с классом гибкости стенки и полки 4 в зависимости от длины горизонтальной складки. Предлагаемое уравнение было следующим: где V — максимальная сила сдвига в кН, а b — длина горизонтальной складки в (мм). На рисунке 11 показано сравнение результатов испытаний и результатов модели КЭ со значениями сдвига, полученными из предложенного уравнения. На графике показано, что уравнение оценивает максимальное усилие сдвига, полученное в результате экспериментального анализа и анализа КЭ, с приемлемой степенью точности.
Это уравнение предсказало максимальное усилие сдвига, которое могло быть выдержано несварными наклонными складчатыми SBCW с классом гибкости стенки и полки 4 в зависимости от длины горизонтальной складки. Предлагаемое уравнение было следующим: где V — максимальная сила сдвига в кН, а b — длина горизонтальной складки в (мм). На рисунке 11 показано сравнение результатов испытаний и результатов модели КЭ со значениями сдвига, полученными из предложенного уравнения. На графике показано, что уравнение оценивает максимальное усилие сдвига, полученное в результате экспериментального анализа и анализа КЭ, с приемлемой степенью точности.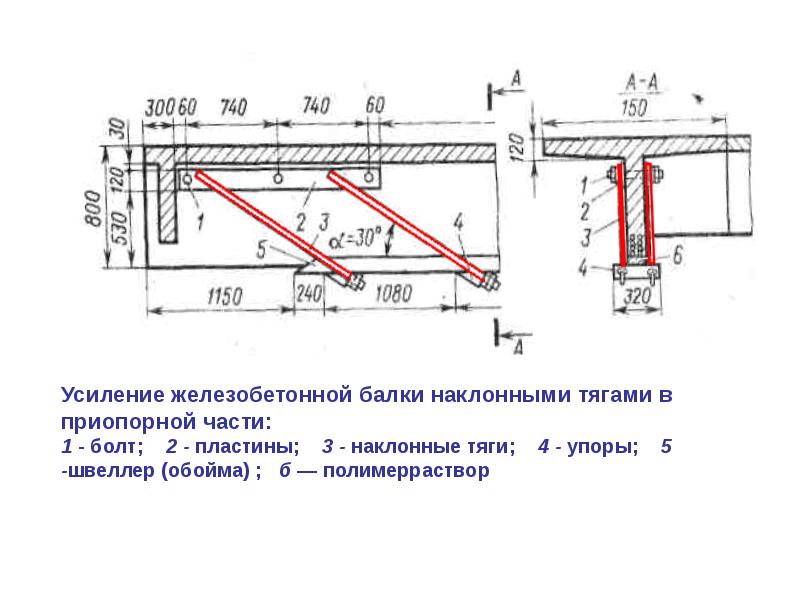
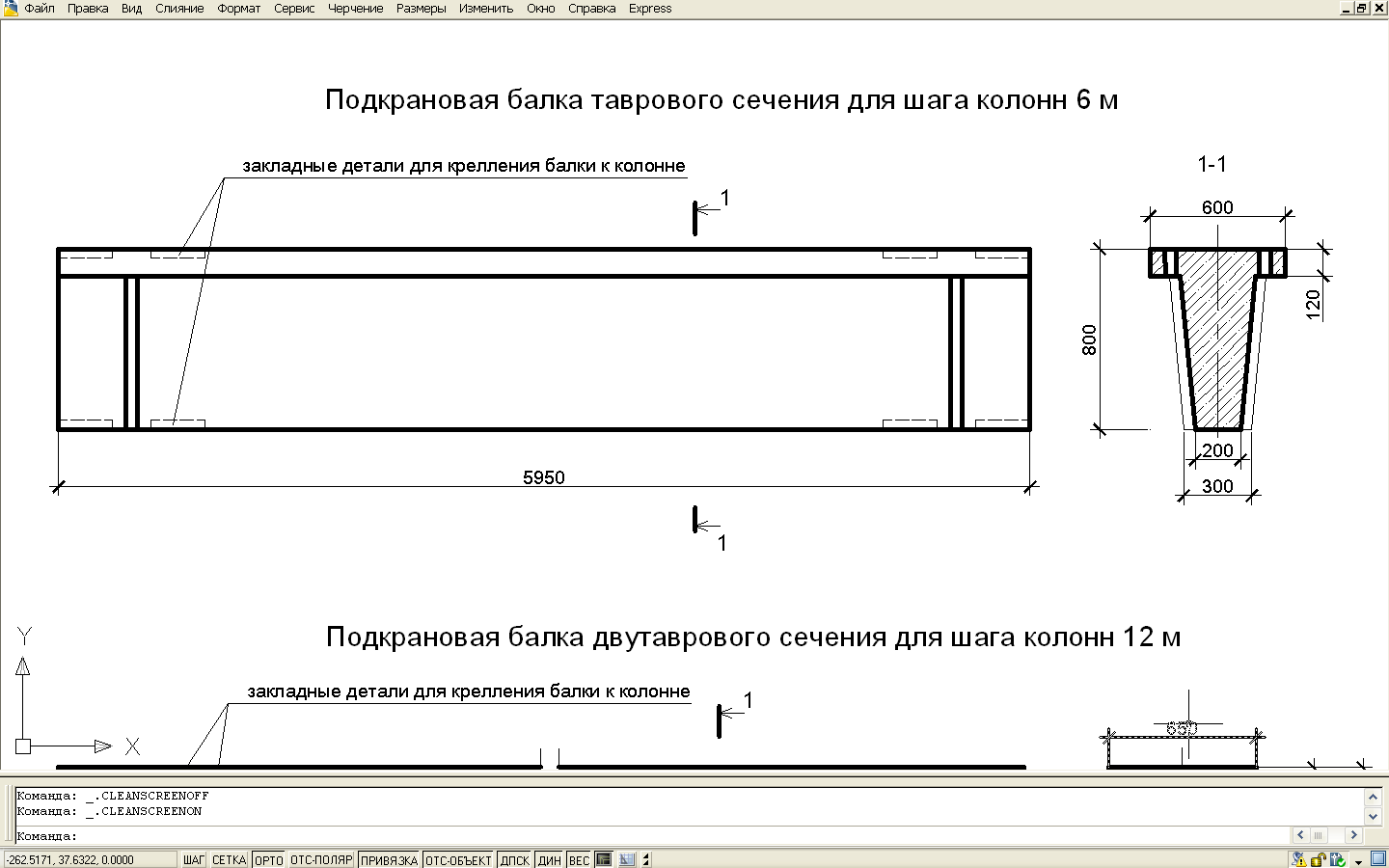 И наоборот, увеличение предела текучести полки с 225 МПа до 300 МПа увеличило предел текучести и предельные нагрузки на 26% и 20%, соответственно, по сравнению с пределом текучести и предельной нагрузкой CB, а вид разрушения изменился с WB + FB только на WB.
И наоборот, увеличение предела текучести полки с 225 МПа до 300 МПа увеличило предел текучести и предельные нагрузки на 26% и 20%, соответственно, по сравнению с пределом текучести и предельной нагрузкой CB, а вид разрушения изменился с WB + FB только на WB.
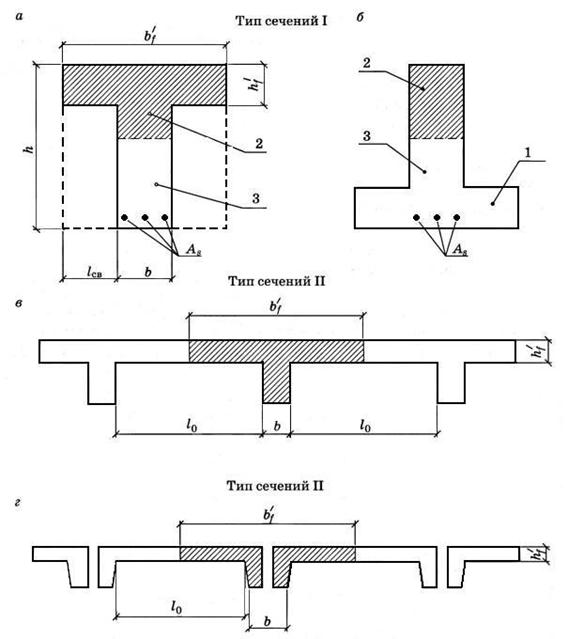 Тем не менее, детекторы на основе кремниевых диодов имеют тенденцию к чрезмерному отклику в малых полях из-за их высокой плотности по сравнению с водой. По этой причине рекомендуются поправочные коэффициенты луча для конкретного детектора () не только для коррекции общих коэффициентов рассеяния, но также для коррекции отношения максимума ткани и внеосевого отношения. Однако применение к углубленным и внеосевым местоположениям не изучалось. Целью данной работы является рассмотрение влияния поправочных коэффициентов на расчетное распределение дозы в статических нетрадиционных пучках фотонов (в частности, в стереотаксической радиохирургии с круговыми коллиматорами).Для достижения этой цели были измерены общие коэффициенты рассеяния, тканевой максимум и внеосевое отношение с помощью диода стереотаксического поля для круглых коллиматоров диаметром 4,0, 10,0 и 20,0 мм. Облучение проводили на линейном ускорителе Novalis® с использованием фотонного пучка с энергией 6 МВ. Поправочные коэффициенты для конкретного детектора были рассчитаны и применены к экспериментальным данным дозиметрии для глубинного и внеосевого местоположений.
Тем не менее, детекторы на основе кремниевых диодов имеют тенденцию к чрезмерному отклику в малых полях из-за их высокой плотности по сравнению с водой. По этой причине рекомендуются поправочные коэффициенты луча для конкретного детектора () не только для коррекции общих коэффициентов рассеяния, но также для коррекции отношения максимума ткани и внеосевого отношения. Однако применение к углубленным и внеосевым местоположениям не изучалось. Целью данной работы является рассмотрение влияния поправочных коэффициентов на расчетное распределение дозы в статических нетрадиционных пучках фотонов (в частности, в стереотаксической радиохирургии с круговыми коллиматорами).Для достижения этой цели были измерены общие коэффициенты рассеяния, тканевой максимум и внеосевое отношение с помощью диода стереотаксического поля для круглых коллиматоров диаметром 4,0, 10,0 и 20,0 мм. Облучение проводили на линейном ускорителе Novalis® с использованием фотонного пучка с энергией 6 МВ. Поправочные коэффициенты для конкретного детектора были рассчитаны и применены к экспериментальным данным дозиметрии для глубинного и внеосевого местоположений. Скорректированные и нескорректированные данные дозиметрии были использованы для ввода в эксплуатацию системы планирования лечения для планирования радиохирургии.Были рассчитаны различные планы с смоделированными поражениями с использованием нескорректированной и скорректированной дозиметрии. Полученные в результате расчеты дозы сравнивались с использованием теста гамма-индекса с несколькими критериями. Результаты этой работы представили важные выводы относительно использования поправочных коэффициентов луча для конкретного детектора (в системе планирования лечения. Использование для коэффициентов полного рассеяния оказывает важное влияние на расчет блока монитора. Напротив, использование для ткани — максимальное и внеосевое отношения не оказывают существенного влияния на расчет распределения дозы системой планирования лечения.Этот вывод справедлив только для комбинации системы планирования лечения, детектора и поправочных коэффициентов, используемых в данной работе; однако этот метод можно применять к другим системам планирования лечения, детекторам и поправочным коэффициентам.
Скорректированные и нескорректированные данные дозиметрии были использованы для ввода в эксплуатацию системы планирования лечения для планирования радиохирургии.Были рассчитаны различные планы с смоделированными поражениями с использованием нескорректированной и скорректированной дозиметрии. Полученные в результате расчеты дозы сравнивались с использованием теста гамма-индекса с несколькими критериями. Результаты этой работы представили важные выводы относительно использования поправочных коэффициентов луча для конкретного детектора (в системе планирования лечения. Использование для коэффициентов полного рассеяния оказывает важное влияние на расчет блока монитора. Напротив, использование для ткани — максимальное и внеосевое отношения не оказывают существенного влияния на расчет распределения дозы системой планирования лечения.Этот вывод справедлив только для комбинации системы планирования лечения, детектора и поправочных коэффициентов, используемых в данной работе; однако этот метод можно применять к другим системам планирования лечения, детекторам и поправочным коэффициентам.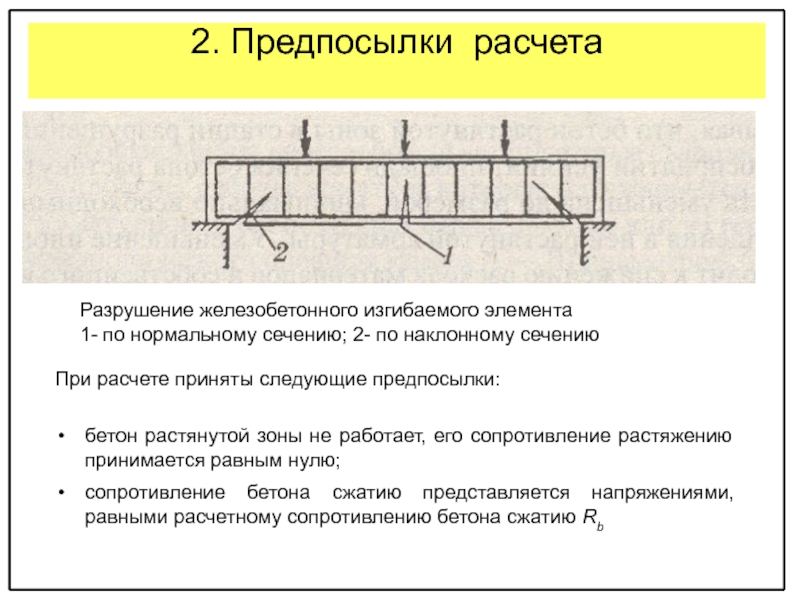
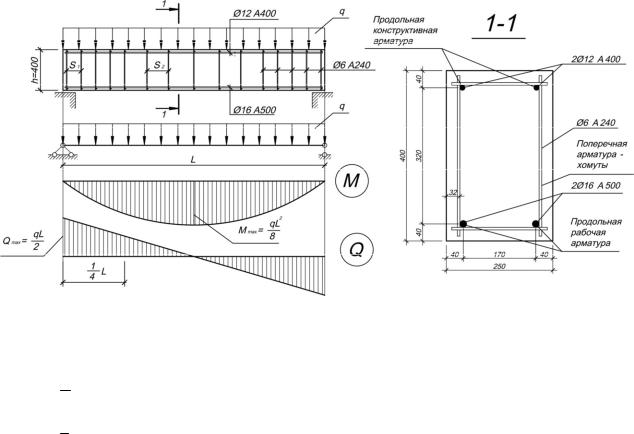 Пожалуйста, направляйте запросы по адресу: ING. АНЖЕЛИКА ГАРСИА ГУСМАН, Jefa del Departamento de Apoyo a la Investigacion Instituto Nacional de Neurologia y Neurocirugía Тел. +52 (55) 5606-3822 доб. 3517; электронная почта:
Пожалуйста, направляйте запросы по адресу: ING. АНЖЕЛИКА ГАРСИА ГУСМАН, Jefa del Departamento de Apoyo a la Investigacion Instituto Nacional de Neurologia y Neurocirugía Тел. +52 (55) 5606-3822 доб. 3517; электронная почта: