Расчет раствора на фундамент: Калькулятор ленточного фундамента
Расчет бетона на фундамент
Строительство дома требует немалых затрат, поэтому крайне важно заранее спланировать все расходы, особенно связанные с приобретением строительных материалов. Поскольку закладка основания дома выполняется с использованием большого количества цементно-песчаного раствора, очень важно провести грамотный расчет бетона на фундамент, который позволит определиться с его объемом и качественными показателями.
Строительство дома требует немалых затрат, поэтому крайне важно заранее спланировать все расходы, особенно связанные с приобретением строительных материалов. Поскольку закладка основания дома выполняется с использованием большого количества цементно-песчаного раствора, очень важно провести грамотный расчет бетона на фундамент, который позволит определиться с его объемом и качественными показателями.
Расход бетона для закладки разных видов оснований
Количество расходуемого бетона измеряется в кубометрах, а его объем, необходимый для заливки фундамента, рассчитывается по формулам с учетом типа основания и его геометрии:
Кроме того расчет объема бетона для фундамента каждого вида должен осуществляться, исходя из его индивидуальных особенностей.
- Для ленточного фундамента:
исчисляется суммарная длина всего основания и умножается на его ширину и высоту. Ширина фундамента зависит от двух параметров – необходимой площади опоры и характера грунта: чем больше вес здания и слабее грунт, тем шире должна быть подошва основания. Высота фундамента включает в себя глубину его заложения и высоту надземной части. Общая длина основания – это сумма периметра внешних стен и длины фундамента под стенами внутри постройки.
- Для столбчатого фундамента:
определяется объем бетона для одной опоры и умножается на общее количество столбиков. Для проведения расчета необходимо знать диаметр и длину каждого элемента столбчатого фундамента.
- Для плитного основания:
расчет количества бетона для фундамента без ребер жесткости осуществляется по самой простой формуле – путем умножения высоты плиты на ее ширину и длину. Чтобы определить количество бетона, необходимое для установки ребер жесткости, следует вычислить их суммарную длину и площадь поперечного сечения. Высота каждого ребра жесткости соответствует толщине фундамента, ширина составляет 0,8 высоты в прямоугольном сечении и 0,8/1,5 – в трапециевидном (меньшее и большее основание).
Высота каждого ребра жесткости соответствует толщине фундамента, ширина составляет 0,8 высоты в прямоугольном сечении и 0,8/1,5 – в трапециевидном (меньшее и большее основание).
- Для свайного фундамента:
нужное количество бетона рассчитывается отдельно для свай и отдельно для ростверка, поскольку их заливка производится не одновременно. Для расчета объема сваи используется формула для столбчатого фундамента. Объем ростверка определяется по формуле для ленточного фундамента.
Рассчитывая количество бетона, которое потребуется для заливки фундамента любого типа, следует учитывать вероятность небольших погрешностей, поскольку даже самая точная формула расчета бетона на фундамент в данном случае не может гарантировать абсолютную точность выполнения работ. В некоторых местах опалубка может быть установлена на пару сантиметров шире или углы могут немного отойти. Поэтому специалисты рекомендуют приобретать на 10% больше раствора или материалов для его изготовления, учитывая также остатки в бетономешалке или неполную выгрузку бетона.
Расчет состава бетонной смеси
Чтобы самостоятельно приготовить именно такое количество бетона, которое необходимо для заливки конкретного фундамента, следует помнить, что при расчете состава бетонной смеси не бывает мелочей. Качественный раствор в нужном объеме может быть получен при соблюдении трех факторов:
- соотношения воды и цемента
- характеристик заполнителей (песок, щебень)
- марки цемента.
К примеру, требуется приготовить бетон марки М250 из портландцемента М400. По таблице 1 водоцементное соотношение в данном случае должно быть равным 0,57. В этой таблице приведены коэффициенты для раствора, который приготовлен на основе заполнителей с модулем крупности максимум 2,5, то есть его компоненты (песок и щебень) имеют зерна среднего размера.
При приготовлении бетонной смеси без добавления щебня указанный в таблице показатель соотношения вода/цемент следует уменьшить на 0,1.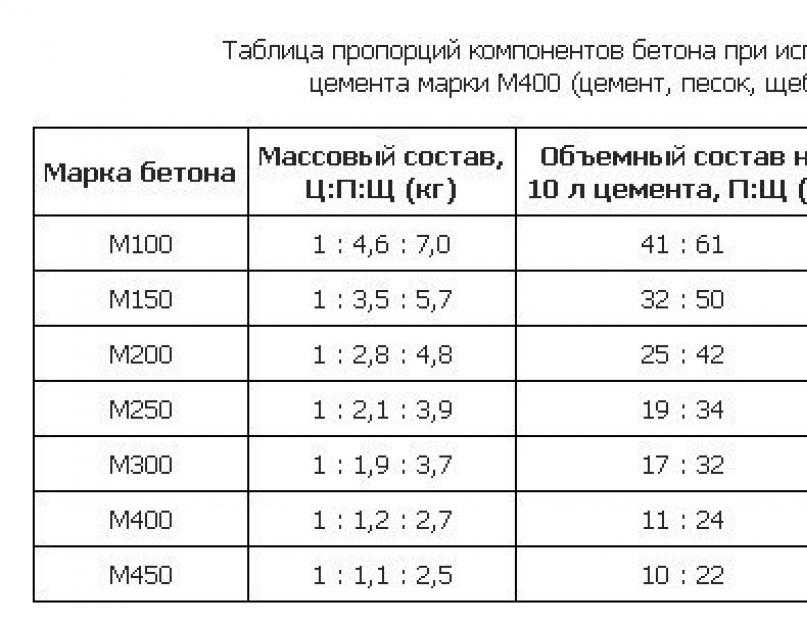
После определения необходимого соотношения воды и цемента требуется определить часть, которую занимают заполнители в общем объеме бетонной смеси. Данный расчет кубов бетона на фундамент и количество в них песочно-щебневой смеси можно выполнить, пользуясь таблицей 2. Определив объемы наполнителей и показатели плотности, можно рассчитать их массу. Полученные результаты помогут произвести корректировку расчета фундамента.
Пользуясь приведенной ниже схемой оценки подвижности бетонной смеси и данными из таблицы 3, можно проверить, что расчетная масса цемента соответствует значениям, указанным для приготовления конкретной бетонной смеси с подходящей осадкой конуса.
Расчет объема и компонентов для замеса бетона
Самостоятельный замес бетонной смеси в том объеме, который необходим для заливки всего фундамента, невозможно произвести вручную.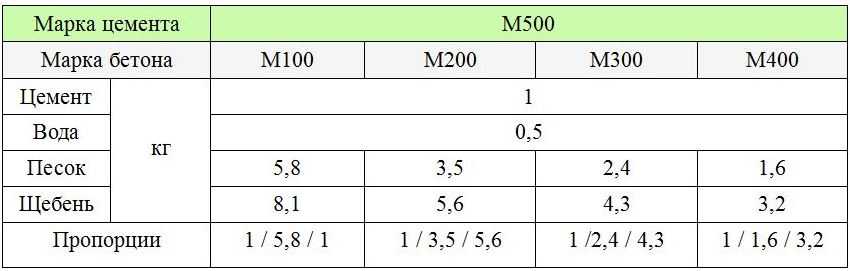 Для выполнения данного вида работ обычно используется бетономешалка. Но поскольку расчет расхода бетона на фундаментпозволяет получить суммарный объем необходимого количества смеси, которую невозможно приготовить за один раз, то возникает необходимость проведения еще одного расчета. В этом случае необходимо определить, сколько ингредиентов нужно загружать для одного замеса.
Для выполнения данного вида работ обычно используется бетономешалка. Но поскольку расчет расхода бетона на фундаментпозволяет получить суммарный объем необходимого количества смеси, которую невозможно приготовить за один раз, то возникает необходимость проведения еще одного расчета. В этом случае необходимо определить, сколько ингредиентов нужно загружать для одного замеса.
Наиболее распространенными являются бетономешалки объемом на 500 литров. Для расчета одной нормы загрузки следует воспользоваться полученными данными расходования материалов для приготовления 1 м3 раствора. Кроме того следует учитывать показатели объемного веса цемента (1300 кг/м3), щебня (1500 кг/м3) и песка (1600 кг/м3).
Сначала нужно рассчитать коэффициент выхода бетона по формуле:
Кб =1/((Кц/1300)+Кв+(Кп/1600)+(Кщ/1500)),
где Кц – общее количество цемента
Кв – количество воды
Кп – количество песка
Кщ – количество щебня.
Расчет каждого ингредиента на один замес выполняется с учетом емкости бетономешалки (500 л):
Цемента – 500×Кб×Кц/1000
Воды: 500×Кб×Кв/1000
Песка: 500×Кб×Кп/1000
Щебня: 500×Кб×Кщ/1000.
Используя описанный выше принцип расчета объема и качественного состава компонентов, можно самостоятельно приготовить необходимое количество бетонного раствора с нужными характеристиками. Изготовленный из такого бетона фундамент будет не только прочным и надежным, но и наиболее экономным в плане расходования стройматериалов.
Читайте также:
Расчет цемента для бетона на фундамент или пол.
Расчет цемента для бетона на фундамент или пол. — строительный блог- Главная
- Блог
- Расчет цемента для бетона на фундамент или пол.
Основа любого блочного дома – строительный раствор, который заливается и в фундамент, и соединяет кирпичи, и нужно точно знать, как рассчитать расход цемента, чтобы получить качественный бетон для заливки или добротный крепежный состав.
Как рассчитать расход цемента, исходя из его марки
Трудно недооценить важность для строительных работ такого материала, как цемент, однако его популярность по большей части зависит от марок, среди которых есть наиболее и наименее используемые. В частности, очень часто отдается предпочтение для малоэтажного частного строительства маркам 300 и 400. Расход у них различный, к примеру, на один квадратный метр заливки толщиной 10 сантиметров понадобится 50-килограммовый мешок цемента М400, и пятая часть останется, а вот М300 потребуется 51 килограмм, то есть мешка не хватит. Логично, что это для раствора марки М150, поскольку для М200 чаще используется цемент 400 и 500.
Обычно расчет расхода цемента ведется в кубометрах. Зная, что для получения 1 м3 бетона М300 из цемента марки М400 нужно 600 килограммов, имеем расчетное количество основной составляющей раствора для заливки 10 квадратов пола стяжкой толщиной 10 сантиметров. Очень важно перед тем, как рассчитать расход цемента, узнать рецептуру смесей в точных пропорциях, для чего существуют СНиПы, из которых нужно брать все данные. Так, согласно СП 82-101-98, для получения растворов 150 и 200 при использовании определенных марок материала необходимо соблюсти соотношение:
Очень важно перед тем, как рассчитать расход цемента, узнать рецептуру смесей в точных пропорциях, для чего существуют СНиПы, из которых нужно брать все данные. Так, согласно СП 82-101-98, для получения растворов 150 и 200 при использовании определенных марок материала необходимо соблюсти соотношение:
| Пропорции цемента песка и известкового (глиняного) теста для смеси М200 | |
| М500 | 1:3:0.2 |
| М400 | 1:25:0.1 |
| Пропорции цемента, песка и известкового (глиняного) теста для смеси М150 | |
| М500 | 1:4:0.3 |
| М400 | 1:3:0.2 |
| М300 | 1:2.5:0.1 |
Как рассчитать расход цемента, исходя из его марки
Трудно недооценить важность для строительных работ такого материала, как цемент, однако его популярность по большей части зависит от марок, среди которых есть наиболее и наименее используемые. В частности, очень часто отдается предпочтение для малоэтажного частного строительства маркам 300 и 400. Расход у них различный, к примеру, на один квадратный метр заливки толщиной 10 сантиметров понадобится 50-килограммовый мешок цемента М400, и пятая часть останется, а вот М300 потребуется 51 килограмм, то есть мешка не хватит. Логично, что это для раствора марки М150, поскольку для М200 чаще используется цемент 400 и 500.
Расход у них различный, к примеру, на один квадратный метр заливки толщиной 10 сантиметров понадобится 50-килограммовый мешок цемента М400, и пятая часть останется, а вот М300 потребуется 51 килограмм, то есть мешка не хватит. Логично, что это для раствора марки М150, поскольку для М200 чаще используется цемент 400 и 500.
Обычно расчет расхода цемента ведется в кубометрах. Зная, что для получения 1 м3 бетона М300 из цемента марки М400 нужно 600 килограммов, имеем расчетное количество основной составляющей раствора для заливки 10 квадратов пола стяжкой толщиной 10 сантиметров. Очень важно перед тем, как рассчитать расход цемента, узнать рецептуру смесей в точных пропорциях, для чего существуют СНиПы, из которых нужно брать все данные. Так, согласно СП 82-101-98, для получения растворов 150 и 200 при использовании определенных марок материала необходимо соблюсти соотношение:
| Пропорции цемента песка и известкового (глиняного) теста для смеси М200 | |
| М500 | 1:3:0. 2 2 |
| М400 | 1:25:0.1 |
| Пропорции цемента, песка и известкового (глиняного) теста для смеси М150 | |
| М500 | 1:4:0.3 |
| М400 | 1:3:0.2 |
| М300 | 1:2.5:0.1 |
Как рассчитать цемент – простая математика
Допустим, нам нужен ленточный фундамент, ситуация довольно распространенная. Параметры его мы знаем, пусть они будут следующими: длина 20, ширина 0.4 и глубина 0.5 метров. Раствор возьмем цементно-песчаный в стандартной пропорции 1:3, а не бетон с щебнем в качестве наполнителя, чтобы проще было посчитать. Объем фундамента составит 4 кубометра, для раствора нам столько цемента, конечно, не нужно, большую часть займут песок и вода, которой нам нужно не более 6 долей (столько и возьмем).
Итак, в растворе у нас должно получиться в целом 10 долей компонентов, что на куб раствора дает 0.1 куба порошка, а для фундамента нам понадобится 0.4 куба материала. Однако кроме как рассчитать цемент в объемном отношении, нужно учесть и его плотность, которая для приведенного в примере раствора составляет 3000 килограмм на кубический метр. Если умножить необходимый нам объем материала на его плотность, получим требуемую массу, то есть 0.4*3000 = 1200 килограммов. Если материал расфасован в мешки по полцентнера, нам нужно 24 мешка.
Однако кроме как рассчитать цемент в объемном отношении, нужно учесть и его плотность, которая для приведенного в примере раствора составляет 3000 килограмм на кубический метр. Если умножить необходимый нам объем материала на его плотность, получим требуемую массу, то есть 0.4*3000 = 1200 килограммов. Если материал расфасован в мешки по полцентнера, нам нужно 24 мешка.
16.02.2018, 686 просмотров.
Расчет цемента для бетона на фундамент или пол., блог, статья, строительный магазин, липецк
Расчет цемента для бетона на фундамент или пол., блог, статья, строительный магазин, липецк
Расчет цемента для бетона на фундамент или пол., блог, статья, строительный магазин, липецк
Расчет цемента для бетона на фундамент или пол., блог, статья, строительный магазин, липецк Расчет цемента для бетона на фундамент или пол., блог, статья, строительный магазин, липецк Расчет цемента для бетона на фундамент или пол. , блог, статья, строительный магазин, липецк
, блог, статья, строительный магазин, липецк
Расчетные модули > Фундамент > Фундамент общего назначения
Нужно больше? Задайте нам вопрос
Этот модуль обеспечивает расчет прямоугольного фундамента с приложенной осевой нагрузкой, перекрывающей нагрузкой, моментом и поперечной нагрузкой. Нажмите здесь, чтобы просмотреть видео:
Модуль позволяет перемещать положение приложения осевой нагрузки вне центра фундамента и обеспечивает автоматический расчет допустимого увеличения несущей способности грунта на основе размеров фундамента и/или глубины под поверхностью.
Модуль проверяет рабочую нагрузку, давление грунта, устойчивость к опрокидыванию, устойчивость к скольжению, изгиб на каждой из четырех поверхностей опоры, сдвиг в одном направлении в точке «d» с каждой из четырех сторон опоры и сдвиг на продавливание по расположенному периметру. ‘d/2’ от граней пьедестала.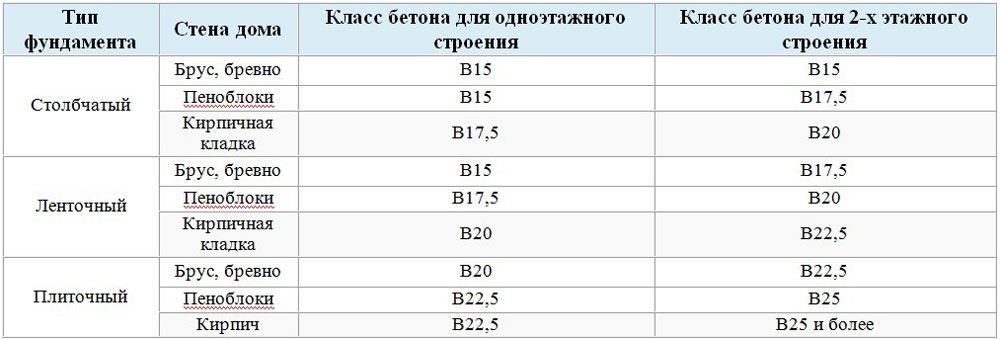
Общие
f’c
Прочность бетона на сжатие через 28 дней.
fy
Предел текучести арматуры.
Ec
Модуль упругости бетона.
Плотность бетона
Плотность бетона используется для расчета собственного веса пьедестала и фундамента, если выбран этот параметр.
Phi Values
Введите значения снижения производительности, применяемые к Vn и Mn.
Двухосный анализ
Выберите «Да» или «Нет», чтобы указать, следует ли выполнять двухосный анализ. Если выполняется двухосный расчет, в решении будут учитываться моменты, действующие одновременно относительно двух ортогональных осей фундамента. Если двухосный анализ НЕ выполняется, решение будет считать, что моменты, приложенные к двум ортогональным осям, действуют не одновременно.
Величина длины кромки для M и V (отображается только при выборе двухосного расчета)
При расчете сдвига и момента для фундаментов, где максимальные значения давления ) размера основания от края для использования при расчете моментов и сдвигов из-за переменного давления грунта в этом регионе. Меньшее значение этой переменной приведет к более консервативному расчету, поскольку он будет сфокусирован на более узкой полосе, которая испытывает наибольшее давление грунта.
Меньшее значение этой переменной приведет к более консервативному расчету, поскольку он будет сфокусирован на более узкой полосе, которая испытывает наибольшее давление грунта.
Нажмите, чтобы рассчитать (кнопка отображается только при выборе двухосного анализа)
Из-за итеративного характера расчетов, необходимых для двухосного анализа, было бы нежелательно повторно выполнять весь анализ и проектирование каждый раз, когда изменяется входной параметр. Таким образом, из соображений эффективности программа автоматически переходит в режим ручного пересчета при выборе двухосного анализа. Щелкайте по этой кнопке в любое время, когда вы хотите пересчитать с текущими входными параметрами.
Учитывать вес фундамента при определении несущей способности грунта
Выберите этот параметр, чтобы модуль рассчитывал собственный вес фундамента и применял его как нисходящую нагрузку при определении несущей нагрузки грунта. Собственный вес будет умножен на коэффициент статической нагрузки в каждой из комбинаций нагрузок от давления на грунт.
Примечание. Обычно следует выбирать этот параметр. Отключение этой опции может привести к неправильным расчетам несущей способности грунта в фундаментах с моментом. Если цель состоит в том, чтобы попытаться сравнить опорное давление грунта с чистым допустимым давлением, то было бы целесообразно использовать параметр на вкладке «Допуски грунта» «Увеличить опорную нагрузку на вес основания».
Учитывать вес основания при определении скольжения, опрокидывания и подъема
Выберите этот параметр, чтобы модуль рассчитывал собственный вес основания и применял его как нисходящую нагрузку при определении коэффициентов безопасности скольжения, опрокидывания и подъема. Собственный вес будет умножен на коэффициент статической нагрузки в каждой из комбинаций нагрузки на устойчивость.
Игнорировать проверки на скольжение
Выберите этот вариант, если скольжение по какой-либо конкретной причине не рассматривается при проектировании.
Минимальное отношение стали – температура/усадка
Введите минимальное отношение температуры/усадки стали, рассчитанное с использованием полной толщины фундамента. Это вызовет предупреждающее сообщение, если секция недостаточно армирована.
Примечание. Эта проверка выполняется при условии, что будет предоставлен только один мат из заданного арматурного стержня. Если конструкция имеет чистое поднятие, так что верхний мат является гарантией, или если верхний мат будет предоставлен в любом случае, имейте в виду, что программа по-прежнему будет учитывать вклад только одного мата в соответствие требованиям к температуре и усадке. В этом случае может оказаться более удобным установить соотношение T&S равным половине общего количества, зная, что двух матов будет достаточно для обеспечения полного требуемого количества.
Минимальный коэффициент безопасности при опрокидывании
Введите минимально допустимое отношение момента сопротивления к опрокидывающему моменту. Если фактическое соотношение меньше указанного минимального соотношения, появится сообщение о том, что устойчивость к опрокидыванию неудовлетворительна.
Если фактическое соотношение меньше указанного минимального соотношения, появится сообщение о том, что устойчивость к опрокидыванию неудовлетворительна.
Минимальный коэффициент запаса прочности при скольжении
Введите минимально допустимое отношение силы сопротивления к силе скольжения. Если фактическое отношение меньше заданного минимального отношения, появится сообщение о том, что стабильность скольжения неудовлетворительна.
Учитывать ACI 10.5.1 и 10.5.3 в качестве минимального усиления
Установите этот флажок, если вы хотите, чтобы модуль учитывал разделы 10.5.1 и 10.5.3 ACI 318 при определении минимального усиления.
Допустимые значения грунта
Допустимое давление грунта
Введите допустимое давление грунта, которому может противостоять грунт. Это сопротивление рабочей нагрузке, которое будет сравниваться с расчетным давлением грунта при рабочей нагрузке (нагрузки не учитываются, как при расчете прочности).
Увеличить опору на вес основания
Нажмите [Да], чтобы модуль рассчитал вес одного квадратного фута (вид сверху) веса основания и добавил его к допустимому значению несущей способности грунта. Это приводит к тому, что грунт не подвергается штрафу за собственный вес основания, и полезен в ситуациях, когда в инженерно-геологическом отчете указаны допустимые чистые несущие нагрузки.
Пассивное сопротивление грунта скольжению
Введите значение пассивного сопротивления грунта скольжению. Это значение будет использоваться для определения компонента сопротивления скольжению, создаваемого пассивным давлением грунта. Сопротивление скольжению из-за пассивного давления затем добавляется к сопротивлению скольжению из-за трения, чтобы определить общее сопротивление скольжению для каждой комбинации нагрузок.
Коэффициент трения между грунтом и бетоном
Введите коэффициент трения между грунтом и основанием для использования в расчетах сопротивления скольжению.
Увеличение несущей способности грунта
В этом разделе можно указать некоторые размеры, превышение которых автоматически увеличивает допустимое давление несущей способности грунта.
Глубина основания фундамента ниже поверхности почвы: расстояние от нижней части фундамента до верхней части почвы. Это значение используется для определения допустимого увеличения несущей способности грунта и пассивного сопротивления грунта скольжению, но не используется ни в каких других расчетах в этом модуле.
Увеличения на основе глубины фундамента: Предоставляет метод автоматического увеличения базового допустимого несущего давления грунта на основе глубины фундамента ниже некоторой опорной глубины. Собирает следующие параметры:
Допустимое увеличение давления на фут: указывает величину, на которую базовое допустимое опорное давление грунта может быть увеличено на каждый фут глубины ниже некоторой контрольной глубины.
Если основание фундамента ниже: Указывает требуемую глубину, чтобы начать постепенное увеличение допустимого опорного давления грунта на основе глубины фундамента.
Пример: Предположим следующее: Базовое допустимое давление грунта на опору = 3 кгс. Основание фундамента находится на глубине 6 футов-0 дюймов ниже поверхности почвы. В геотехническом отчете указано, что допускается увеличение опорного давления на 0,15 тыс. футов на каждый фут глубины, когда основание находится глубже, чем на 4 фута ниже поверхности почвы. Поскольку вы указали, что если фундамент находится на 6 футов ниже поверхности почвы, модуль автоматически рассчитает скорректированное допустимое давление на грунт как 3 тыс.фут + (6 — 4 фута) * 0,15 тыс.фунт = 3,30 тыс.фунт.0003
Увеличения на основе размера фундамента: Предоставляет метод автоматического увеличения базового допустимого несущего давления грунта на основе размеров фундамента, превышающих какой-либо контрольный размер. Собирает следующие параметры:
Собирает следующие параметры:
Допустимое увеличение давления на фут: указывает величину, на которую базовое допустимое опорное давление грунта может быть увеличено на каждый фут длины или ширины, превышающей некоторый эталонный размер.
Когда максимальная длина или ширина больше: Указывает требуемый размер, чтобы начать поэтапное увеличение допустимого несущего давления грунта на основе размера фундамента.
Пример: Предположим следующее: Базовое допустимое давление грунта на опору = 3 кгс. Фундамент измеряет 12′-0″ x 6′-0″. В геотехническом отчете указывается, что допустимо увеличение опорного давления грунта на 0,15 тыс. футов на каждый фут, если наибольший размер фундамента в плане превышает 4 фута. Модуль автоматически рассчитает скорректированное допустимое давление на грунт как 3 тыс. футов + (12 футов — 4 фута) * 0,15 тыс. футов = 4,2 тыс. футов.
Примечание. Увеличение в зависимости от глубины фундамента и размеров в плане является кумулятивным.
Размеры основания
На этой вкладке вы вводите размеры основания и пьедестала.
Ширина, длина и толщина: определяет габаритные размеры основания.
Расположение нагрузки: определяет смещение от центра основания, в котором действует осевая нагрузка. Если двухосный анализ НЕ используется, то можно использовать только одно направление.
Размеры пьедестала: Если бетонный пьедестал опирается на фундамент, его размеры можно указать здесь. Размеры px и pz используются для определения мест на всех четырех сторонах, где рассчитывается односторонний сдвиг, двусторонний сдвиг и изгибающий момент. Если вы введете ненулевую высоту, вы можете выбрать, чтобы вес этой призмы был рассчитан и добавлен как статическая нагрузка. Любые приложенные нагрузки от вскрыши будут исключены из области, определяемой как размер основания по осям xx и yy, независимо от заданной высоты призмы.
Примечание. Если пьедестал не определен, то центр фундамента будет рассматриваться как поверхность пьедестала при определении критических мест для проверки на сдвиг и изгиб.
Если пьедестал не определен, то центр фундамента будет рассматриваться как поверхность пьедестала при определении критических мест для проверки на сдвиг и изгиб.
Учитывать вес опоры при определении: этот параметр позволяет пользователю указать, следует ли учитывать собственный вес опоры при определении несущей — при проверках на скольжение, опрокидывание и подъем следует учитывать вес пьедестала.
Армирование фундамента
На этой вкладке можно указать армирование в каждом направлении фундамента.
Приложенные ВЕРТИКАЛЬНЫЕ нагрузки
На этой вкладке можно указать осевую нагрузку, приложенную к расположению пьедестала, и нагрузку от вскрыши, приложенную ко всему размеру фундамента в плане (за исключением области, обозначенной как пьедестал).
Введите нагрузки с положительным знаком для направления вниз.
Внимание! Этот модуль не допускает поднятия сетки на фундаменте. Если результат факторизованных осевых нагрузок (стационарная, динамическая, ветровая и т. д.) дает отрицательный знак нагрузки, модуль не будет пересчитывать и уведомит вас о том, какая комбинация нагрузок привела к чистому подъему.
Если результат факторизованных осевых нагрузок (стационарная, динамическая, ветровая и т. д.) дает отрицательный знак нагрузки, модуль не будет пересчитывать и уведомит вас о том, какая комбинация нагрузок привела к чистому подъему.
Приложенные изгибающие нагрузки
На этой вкладке можно ввести приложенные моменты.
Приложенные сдвиговые нагрузки
На этой вкладке можно ввести приложенные поперечные силы. Эти нагрузки приложены в месте расположения пьедестала. Если указана высота пьедестала, сдвиг будет применяться на этой высоте и создаст момент на основании, равный поперечной нагрузке * (толщина основания + высота пьедестала).
Сочетания нагрузок — обслуживание
Это типичная вкладка сочетаний нагрузок, используемая в библиотеке проектирования конструкций. Вкладка «Комбинации услуг» используется для расчета давления на грунт, которое необходимо сравнить с допустимым давлением на грунт. «Увеличение грунта» — это коэффициент, который можно указать отдельно для каждой комбинации нагрузок и который применяется к допустимому давлению на грунт.
«Увеличение грунта» — это коэффициент, который можно указать отдельно для каждой комбинации нагрузок и который применяется к допустимому давлению на грунт.
Сочетания нагрузок — с учетом фактора
Это типичная вкладка сочетаний нагрузок, используемая в Библиотеке проектирования конструкций для расчета прочности. Эти комбинации нагрузок используются для расчета моментов и сдвигов в фундаменте для определения напряжений и требуемой арматуры.
Примечание. Модуль «Общее основание» применяет факторизованные нагрузки к основанию и определяет другой эксцентриситет, чем тот, который был определен с использованием эксплуатационных нагрузок для проверки опорного давления грунта.
Вкладка «Результаты»
На этой вкладке представлена сводка всех рассчитанных значений. Сообщаются коэффициенты напряжений, применяемые и допустимые значения, а также сочетания нагрузок для этих основных значений.
Вкладка «Давление грунта»
На этой вкладке приведены расчетные значения давления грунта на рабочую нагрузку для моментов и сдвигов, приложенных к указанной оси, для каждой комбинации нагрузок.
Вкладка «Устойчивость к опрокидыванию»
На этой вкладке представлены расчеты устойчивости фундамента к опрокидыванию и моменту сопротивления относительно каждой оси и для каждого сочетания нагрузок. Обратите внимание, что используемые здесь сочетания нагрузок генерируются внутренними силами, а НЕ из сочетаний эксплуатационных нагрузок, которые вы ввели для оценки несущего давления грунта.
Обратите внимание, что программа настроена на индивидуальный поиск сил опрокидывания и сопротивления. Например, возьмем ситуацию, когда основание подвергается равным и противоположным сдвигам на заданной высоте. Здравый смысл подсказывает, что эти силы компенсируют друг друга, и основание не испытывает от них чистого приложенного опрокидывающего момента. Но программа рассматривает одну из двух равных и противоположных сил как опрокидывающую силу, а другую — как противодействующую. Таким образом, для этих двух сил сообщается чистый опрокидывающий момент, но момент сопротивления ТАКЖЕ учитывает влияние противодействующей нагрузки, поэтому учет, используемый для определения коэффициента опрокидывания, является правильным.
Но программа рассматривает одну из двух равных и противоположных сил как опрокидывающую силу, а другую — как противодействующую. Таким образом, для этих двух сил сообщается чистый опрокидывающий момент, но момент сопротивления ТАКЖЕ учитывает влияние противодействующей нагрузки, поэтому учет, используемый для определения коэффициента опрокидывания, является правильным.
Вкладка «Устойчивость к скольжению»
На этой вкладке представлены расчеты приложенной и сопротивляющейся устойчивости фундамента к скольжению в каждом направлении оси и для каждого сочетания нагрузок. Обратите внимание, что используемые здесь сочетания нагрузок генерируются внутренними силами, а НЕ из сочетаний эксплуатационных нагрузок, которые вы ввели для оценки несущего давления грунта.
Вкладка для изгиба основания
На этой вкладке представлены сводные данные расчетного момента нагрузки с учетом факторов на всех четырех краях периметра опоры для каждого сочетания нагрузок.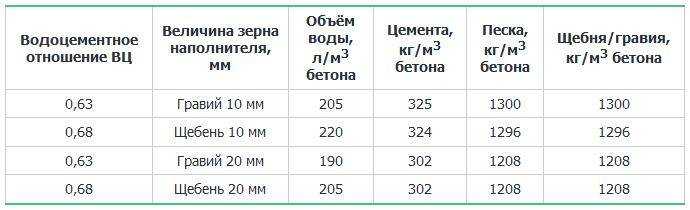 Он указывает, вызывает ли указанное сочетание нагрузок растяжение верхней или нижней поверхности фундамента.
Он указывает, вызывает ли указанное сочетание нагрузок растяжение верхней или нижней поверхности фундамента.
Примечание. В случаях, когда напряжение возникает в верхней части фундамента, проверка на изгиб будет основываться на предположении, что на верхней поверхности фундамента предусмотрен определенный арматурный мат. Пользователь должен просмотреть результаты и определить, действительно ли для каких-либо комбинаций нагрузок требуется армирующий верхний мат или можно ли усилить основание только нижним матом.
Вкладка «Сдвиг основания»
На этой вкладке представлены сводные данные расчетного сдвига с учетом факторов нагрузки на всех четырех краях периметра опоры для каждой комбинации нагрузок. Также рассчитывается двухсторонний или продавливающий сдвиг.
Вкладка «Эскиз»
Методика расчета оптимизации несущей способности двухслойного глиняного фундамента
1 Введение
В области инженерно-геологических работ расчет предельной несущей способности фундаментов всегда был большой проблемой (Терзаги и Пек, 1967; Дэвис и Букер, 1974; Чен, 1975; Гриффитс, 1982; Михаловски и Лей, 1996). существенные последствия для подземного пространства и инженерной безопасности. Анализ верхнего предела, основанный на механике пластической механики, является мощным подходом к расчету предельной несущей способности фундаментов (Лямин и Слоан, 2002; Хуан и Цинь, 2009).; Осман 2019; Шамлу и Имани 2020). Он в основном состоит из конечного элемента предельного анализа и подхода предельного анализа, основанного на дискретизации жесткого блока с точки зрения различных подходов дискретизации, используемых в расчетной модели. Этот метод не требует введения слишком большого количества допущений, имеет строгую теоретическую основу и имеет преимущества при расчете несущей способности фундамента.
существенные последствия для подземного пространства и инженерной безопасности. Анализ верхнего предела, основанный на механике пластической механики, является мощным подходом к расчету предельной несущей способности фундаментов (Лямин и Слоан, 2002; Хуан и Цинь, 2009).; Осман 2019; Шамлу и Имани 2020). Он в основном состоит из конечного элемента предельного анализа и подхода предельного анализа, основанного на дискретизации жесткого блока с точки зрения различных подходов дискретизации, используемых в расчетной модели. Этот метод не требует введения слишком большого количества допущений, имеет строгую теоретическую основу и имеет преимущества при расчете несущей способности фундамента.
В последнее время многие исследователи предложили метод предельного анализа конечного элемента с верхней границей решения несущей способности фундамента путем объединения пластической механики теории предельного анализа и метода конечных элементов (Alkhafaji et al., 2020; Pham et al., 2020; Shamloo и Имани 2020). Подход, основанный на теореме о верхней оценке пластической механики, может компенсировать неточность теоретической основы традиционного подхода предельного равновесия. Однако это может привести к большой рабочей нагрузке и низкой эффективности расчетов, так как конечно-элементная дискретизация должна проводиться на объекте исследования, а скорость каждого узла элемента считается неизвестной величиной. Кроме того, большое количество неизвестных величин и высокая степень свободы усложняют процесс расчета. В целом, его широкое внедрение и применение в сложной практической инженерии будет сложной задачей (Wang et al., 2019).; Ван и др., 2020).
Подход, основанный на теореме о верхней оценке пластической механики, может компенсировать неточность теоретической основы традиционного подхода предельного равновесия. Однако это может привести к большой рабочей нагрузке и низкой эффективности расчетов, так как конечно-элементная дискретизация должна проводиться на объекте исследования, а скорость каждого узла элемента считается неизвестной величиной. Кроме того, большое количество неизвестных величин и высокая степень свободы усложняют процесс расчета. В целом, его широкое внедрение и применение в сложной практической инженерии будет сложной задачей (Wang et al., 2019).; Ван и др., 2020).
В подходе к анализу предельной несущей способности фундамента, основанном на дискретизации жестких блоков, исходя из предположения, что скорость соседнего блока соответствует совместимости скоростей, а скорость поверхности раздела удовлетворяет уравнению соотношения принципа связанного потока, поле скоростей скользящее тело сначала получают путем рекурсии поля скоростей скользящей массы при рекурсии, а затем решают предельную нагрузку в соответствии с уравнением функционального равновесия, согласно которому диссипация внутренней энергии равна внешней работе. Подход также предполагает допущение касательного направления относительной скорости и может решить проблему введения значительного количества допущений в традиционном подходе предельного равновесия.
Подход также предполагает допущение касательного направления относительной скорости и может решить проблему введения значительного количества допущений в традиционном подходе предельного равновесия.
В этом исследовании оптимизированная математическая модель несущей способности фундамента была построена непосредственно в соответствии с теоремой о верхней границе вместо принятия идеи о введении значительного количества допущений в традиционном подходе предельного равновесия. Таким образом, задача о несущей способности фундамента может быть преобразована в задачу оптимизации решения. На основании этого было предложено решение верхней границы анализа предельной несущей способности фундамента (FLU) для определения несущей способности фундамента с использованием решателя нелинейного математического программирования. При этом предложен принцип определения интервала значений глубины наиболее опасного проскальзывания двухслойного глиняного основания путем изучения влияния различных глубин на несущую способность двухслойного глиняного основания. Аналогичным образом был предложен расчетный подход итеративной оптимизации с использованием дихотомии для несущей способности двухслойного глиняного фундамента для достижения цели достижения минимальной несущей способности фундамента. Кроме того, на математическом примере доказана рациональность предлагаемого метода.
Аналогичным образом был предложен расчетный подход итеративной оптимизации с использованием дихотомии для несущей способности двухслойного глиняного фундамента для достижения цели достижения минимальной несущей способности фундамента. Кроме того, на математическом примере доказана рациональность предлагаемого метода.
2 Расчет предела несущей способности фундамента Верхнее решение (FLU)
2.1 Дискретизация жесткого блока
Как показано на рисунке 1, в этом исследовании предлагается усовершенствованный дискретный подход жесткого блока, который может автоматически генерировать модель разделения на блоки на основе геологических данных. условия и режим разрушения фактического фундамента. С помощью сегмента интерфейса или набора блоков, составляющих систему блочного разделения, модель системы блочного разделения может быть определена следующим образом:
{V=L1 L2…Lj…Lhl-1LhlV=B0B1 B2…Bk…Bhb-1Bhb(1)
, где j – порядковый номер сегментов интерфейса в системе блочного разделения; hl – общее количество интерфейсных сегментов в системе блочного разделения; hl′ – общее количество всех участков интерфейса, исключая земную поверхность; k — порядковый номер блоков в системе блочного деления; hb – общее количество блоков, содержащихся в шликерной массе; B1~Bhb – механизмы разрушения; и B0 указывает на грунт без пластического разрушения.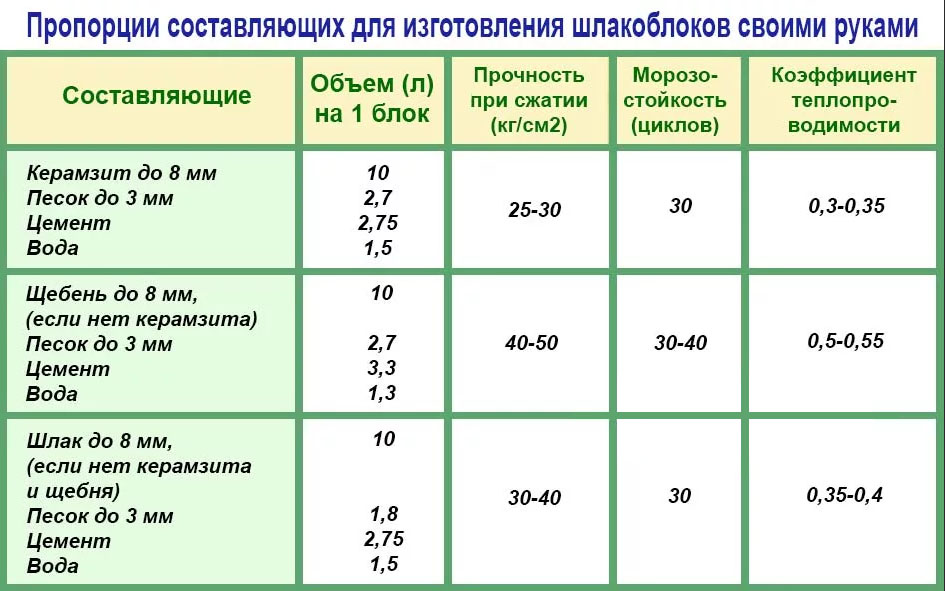
РИСУНОК 1 . Улучшенная модель жесткого блочного деления.
Вектор нормали в сегменте интерфейса определяется как облегчающий создание оптимизированной математической модели решения верхней границы предельного анализа в системе блочного деления. Кроме того, ниже кратко представлен подход к вычислению вектора внутренней нормали.
Любой блок Bk в системе блочного деления может быть образован серией узлов или интерфейсных сегментов, расположенных последовательно, как показано ниже в уравнении. 2
{BK=ak1,ak2…aki…akh2−1,akh2BK=ak1ak2…akiaki+1…akh2−1akh2(2)
где aki – вершины, составляющие многоугольник BK и расположенные по часовой стрелке, а последняя точка многоугольник BK совпадает с первой точкой, или akh2=ak1, что обеспечивает замыкание многоугольника; i — порядковый номер вершины; h2 — общее количество вершин; а akiaki+1 — это сегмент интерфейса.
Внутренний вектор нормали сегмента линии интерфейса akiaki+1 получается с использованием уравнения 3и.
mki=(aki+1−aki)×(aki−aki−1)×(aki+1−aki)/|mki|(3i)
, где mki — вектор внутренней нормали akiaki+1 сегмента интерфейса в блок БК. Вектор нормали, рассчитанный с помощью приведенного выше уравнения в граничном сегменте, всегда указывает на внутреннюю часть многоугольника, независимо от направления вращения вершины, и уникален в геометрическом пространстве. Кроме того, как показано на рис. 2, внутренние векторы нормалей интерфейса, разделяемые двумя соседними блоками, равны по величине и противоположны по направлению.
РИСУНОК 2 . Определение вектора нормали в сегменте интерфейса.
2.2 Система переменных
Переменные, используемые в модели оптимизации решения верхней границы несущей способности фундамента, состоят из предельной несущей способности ( P ), скорости VBk(VBxk,VByk) каждого блока в системе разделения на блоки , а промежуточная переменная относительной скорости Vj(VTj,VNj) участка интерфейса введена для упрощения оптимизационного решения. Для описания направленных характеристик интерфейсной силы на всех интерфейсах устанавливается локальная система координат с направлением сегмента в качестве положительной оси и вектором направления в качестве tj. Как показано на рисунке 3, 9Ось 0429 N перпендикулярна граничному сегменту с вектором направления nj=lz×tj, где lz=(0,0,1). Затем относительная скорость границы раздела может быть выражена с помощью уравнения. 3ii:
Для описания направленных характеристик интерфейсной силы на всех интерфейсах устанавливается локальная система координат с направлением сегмента в качестве положительной оси и вектором направления в качестве tj. Как показано на рисунке 3, 9Ось 0429 N перпендикулярна граничному сегменту с вектором направления nj=lz×tj, где lz=(0,0,1). Затем относительная скорость границы раздела может быть выражена с помощью уравнения. 3ii:
{VTj=VTj∗tjVNj=VNj∗nj(3ii)
РИСУНОК 3 . Общие подходы к представлению силы на границе раздела двух соседних блоков.
В блоке направление локальной системы координат в Bk должно быть определено с помощью вектора внутренней нормали сегмента интерфейса Lj, как показано в уравнении. 4:
{VTki=VTj∗tj∗(nj·mki)VNki=VNj∗nj∗(nj·mki)(4)
Когда nj и mki находятся в одном направлении, тогда nj·mki=1. Когда nj и mki направлены в противоположные стороны, тогда nj·mki=−1.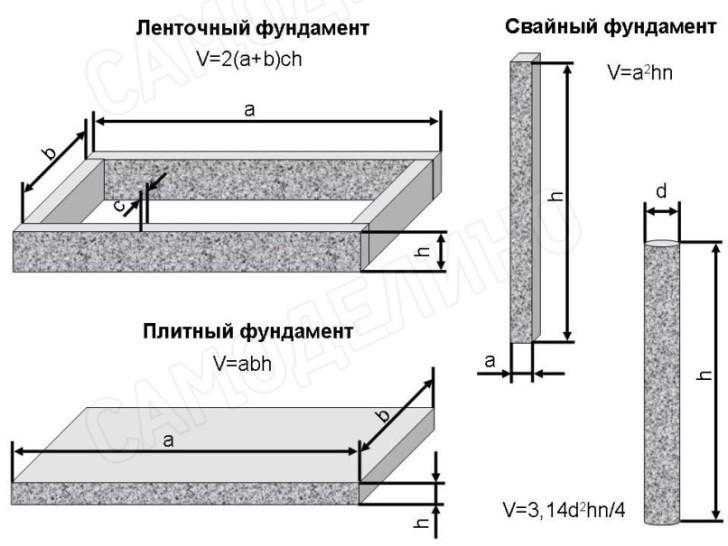 В соответствии с этим определением, векторы направления локальных координат, установленные на общем интерфейсе l12, противоположны друг другу для двух соседних блоков (таких как B6 и B8 на фиг.3). В этом случае требуется только набор переменных V12(VT12,VN12) на общем интерфейсе l12 для описания характеристик действующей силы между равными по величине и противоположными по направлению блоками.
В соответствии с этим определением, векторы направления локальных координат, установленные на общем интерфейсе l12, противоположны друг другу для двух соседних блоков (таких как B6 и B8 на фиг.3). В этом случае требуется только набор переменных V12(VT12,VN12) на общем интерфейсе l12 для описания характеристик действующей силы между равными по величине и противоположными по направлению блоками.
Очевидно, что переменные, требуемые системой переменных, установленной этим методом, меньше конечного элемента предельного анализа. Основные причины следующие: 1) количество блоков после блочной дискретизации меньше количества конечных элементов; 2) метод в этой статье основан на блочном интерфейсе, конечный элемент предельного анализа основан на узлах и должен учитывать ситуацию с перекрывающимися узлами, а количество блочных интерфейсов меньше, чем количество узлов.
2.3 Уравнения ограничений
Согласно теореме о верхней границе предельного анализа, уравнения ограничений включают связанное правило потока, уравнения совместимости скоростей и уравнения функционального равновесия.
2.3.1 Связанное правило потока
Относительная скорость границы раздела также должна соответствовать связанному правилу потока или угол между относительной кинематической скоростью и границей раздела должен быть равен внутреннему углу трения φj:
VNj=tan φj|VTj|(5)
Чтобы лучше описать характеристики |VTj| и уменьшить сложность поиска оптимизационного решения, две промежуточные переменные, VTaj и VTbj, вводятся и определяются следующим образом:
Уравнение 5 можно переписать следующим образом:
VNj=tanφj(VTaj+VTbj)(7)
Решение с верхней границей, предложенное Chen et al. (2003), например, предположили, что направление VTjVTj на нижней поверхности скольжения определено. Однако рациональность предположения о направлении VTj на границе раздела блоков не может быть гарантирована в некоторых сложных инженерных задачах. Кроме того, необоснованные предположения о направлении могут привести к неточным результатам. Направление VTj в предлагаемом подходе определяется непосредственно через оптимизацию, а не через предположения, что теоретически является более строгим.
Направление VTj в предлагаемом подходе определяется непосредственно через оптимизацию, а не через предположения, что теоретически является более строгим.
2.3.2 Условие совместимости скоростей
Смежные блоки должны соответствовать условию совместимости скоростей, т. е. треугольник скоростей состоит из относительной скорости скорости границы раздела и скорости двух соседних блоков и может быть выражен математически как следующие:
{VNj=(Vj1−Vj2)·njVTj=VTaj−VTbj=(Vj1−Vj2)·tj(8)
, где Vj1 и Vj2 — блоки, ограниченные общим сегментом интерфейса lj. В Vj1 вектор внутренней нормали внутреннего сегмента интерфейса lj равен mj1=nj. В Vj2 вектор внутренней нормали внутреннего сегмента интерфейса lj равен mj1=-nj. Что касается граничного сегмента, Vj2=VB0=(0,0,0) на поверхности скольжения Vj=Vj1, как показано на рисунке 4.9.0003
РИСУНОК 4 . Диаграмма совместимости скоростей.
2.3.3 Уравнение функционального равновесия
В соответствии с соответствующим законом течения диссипация внутренней энергии на многоугольнике интерфейса Lj может быть выражена как:
E1=∑j=1hl′|VTj|cjlj=∑j=1hl′ (VTaj+VTbj)cjlj(9)
где cj и lj — сила сцепления и длина сегмента интерфейса Lj соответственно.
Сила тяжести, действующая на блок, равна
E2=∑k=1hbVk·Gdk(10)
, где G — вектор направления силы тяжести, принимая (0, −9,81, 0) в целом, а dk — плотность блока, Bk.
Внешняя работа равна
E3=∑i=1hqQi·Vi(11)
, где Qi — внешняя нагрузка, включающая неизвестные переменные, такие как несущая способность фундамента (P) и перекрывающая нагрузка q; i – порядковый номер внешней нагрузки; hq – общее количество внешних нагрузок; Vi — скорость блока, в котором находится Qi.
На этой основе можно получить уравнение функционального равновесия для всей массы шликера:
∑j=1hl'(VTaj+VTbj)cjlj=∑k=1hbVk·Gdk+∑i=1hqQi·Vi(12)
2.3.4 Другие ограничения
Чтобы гарантировать, что блоки не встраиваются, относительная нормаль скорость должна также удовлетворять уравнению связи уравнения (1). 13:
VNj≥0(13)
2.
 4 Модель оптимизации
4 Модель оптимизацииВ соответствии с теоремой о верхней границе несущая способность фундамента, рассчитанная по любому виду разрушения, удовлетворяющему ограничениям, больше реальной несущей способности фундамента. Чем меньше расчетная несущая способность фундамента, тем ближе она к реальному решению. Таким образом, целевая функция модели оптимизации состоит в том, чтобы минимизировать уравнение несущей способности. 14. Целевая функция (уравнения 5, 6, 9)., 14 в качестве стандартных моделей оптимизации условий ограничений показаны на рисунке 5.
FLU=Min(P)(14)
РИСУНОК 5 . Модель оптимизации.
2.5 Проверка уравнения для несущей способности фундамента
Для фундаментов с негравитированной средой Прандтль-Рейсснер предполагает, что основание фундамента полностью гладкое с режимом разрушения (как показано на рис. 6A), и уравнение расчета для предельной несущей способности задано, используя характеристический подход:
{P=qNq+cNcNq=tan2(π4+φ2)eπtanφNc=(Nq−1)cotφ(15)
где Nq — коэффициент давления грунта для вышележащей нагрузки q; Nc – коэффициент давления Земли; c – сцепление грунта.
РИСУНОК 6 . Режим отказа Прандтля-Рейснера и жесткий дискретный блок. (A) Режим отказа Прандтля-Рейсснера. (B) Дискретные модели жесткого блока с φ=0° и φ=30°
Как показано на рисунке 6B, дискретная модель жесткого блока генерируется автоматически в соответствии с геометрическим соотношением в режиме разрушения (когда углы трения в грунтовой массы 0° и 30°). Затем создается оптимизированная математическая модель для получения предельной несущей способности фундамента с гравийной средой при различных параметрах (табл. 1). Для простого фундамента с гравийной средой результаты расчетов, полученные с помощью предложенного в данном исследовании ГПЗ, согласуются с теоретическим решением, что свидетельствует о рациональности предложенного подхода.
ТАБЛИЦА 1 . Сравнение предельной несущей способности и характеристических параметров при различных углах внутреннего трения.
3 Исследование диапазона значений глубины оползания двухслойного глиняного основания
Несущая способность двухслойного глиняного основания трудно поддается расчету. Многие исследователи проводили аналитические исследования по этому поводу. Чтобы лучше представить преимущества жесткого дискретного блока в этом исследовании, режимы скольжения, подобные тем, которые использовались Прандтлем-Рейсснером и Терцаги, отдаются на усмотрение твердого тела, как показано на рисунке 7. Коэффициент глубины скольжения H/b на рисунке 7 – глубина слоя; h/b – глубина скольжения. Точная блочная дискретная модель может быть получена по характеристикам режима скольжения путем определения h/b и автоматически сгенерирована с использованием предложенного подхода; c1/c2 – отношение сил сцепления верхнего и нижнего грунта; hb – количество блоков.
Многие исследователи проводили аналитические исследования по этому поводу. Чтобы лучше представить преимущества жесткого дискретного блока в этом исследовании, режимы скольжения, подобные тем, которые использовались Прандтлем-Рейсснером и Терцаги, отдаются на усмотрение твердого тела, как показано на рисунке 7. Коэффициент глубины скольжения H/b на рисунке 7 – глубина слоя; h/b – глубина скольжения. Точная блочная дискретная модель может быть получена по характеристикам режима скольжения путем определения h/b и автоматически сгенерирована с использованием предложенного подхода; c1/c2 – отношение сил сцепления верхнего и нижнего грунта; hb – количество блоков.
РИСУНОК 7 . Расчетная модель несущей способности двухслойного глиняного фундамента.
Для определения диапазона значений глубины оползания двухслойных глиняных фундаментов исследовано влияние глубины оползания hb на несущую способность фундамента при различных сочетаниях c1c2=1, c1c2<1(0,2,0,25,0,33,0,5), c1c2>1(2,3,4,5), а Hb=0,2、0,5、1,0、1,5, как показано на рисунке 8. По результатам расчета:
По результатам расчета:
1) При c1c2=1 задача расчета несущая способность двухслойных глиняных фундаментов сводится к задаче расчета несущей способности однородных и несвязных оснований. Коэффициент несущей способности фундамента Pc1b сначала уменьшается, а затем увеличивается с увеличением hb, достигая минимального значения 5,14 при hb=0,71, что является теоретическим решением Прандтля.
2) При c1c2<1 и Hb<0,71(Hb=0,2、0,5) происходит местное разрушение верхнего слоя грунта из-за его низкой прочности.
3) При c1c2<1 и Hb>0,71(Hb=1,0、1,5) закон изменения до достижения слоистой границы раздела Hb такой же, как и у однородного основания, и Pc1b достигает минимального значения 5,14 при hb =0,71. Низкое значение Pc1b не может быть получено в диапазоне нижнего грунта, потому что прочность нижнего грунта больше, чем прочность верхнего грунта при увеличении hb. В этом случае его можно считать равномерным основанием.
4) При c1c2>1 и Hb<0,71(Hb=0,2、0,5) коэффициент несущей способности фундамента сначала уменьшается, а затем увеличивается с ростом hb. Кроме того, минимальное значение будет отставать из-за меньшей прочности нижнего грунта, hb>0,71.
Кроме того, минимальное значение будет отставать из-за меньшей прочности нижнего грунта, hb>0,71.
5) Когда c1c2>1 и Hb<0,71 (Hb=1,0、1,5), по обеим сторонам от Hb можно наблюдать нисходящий и восходящий тренд с двумя отчетливыми впадинами. При реальном поиске следует сравнивать значения Pc1b, соответствующие двум впадинам, при этом меньшая из них используется в качестве предельной нагрузки.
РИСУНОК 8 . hb−Pc1b. Изгиб. (А) с1с2=1, (Б) с1с2>1, (В) с1с2>1.
В соответствии с диапазоном значений hb, полученным в приведенных выше результатах (Таблица 2), уменьшение диапазона поиска при расчете предельной нагрузки может повысить эффективность расчета.
ТАБЛИЦА 2 . Диапазон глубины скольжения.
4 Оптимизированный метод расчета несущей способности двухслойного глиняного фундамента
На основании таблицы 2 и FLU предлагается оптимизированный метод расчета несущей способности двухслойного глиняного фундамента. Предлагаемый подход сначала рассчитывает диапазон глубины проскальзывания в соответствии с таблицей 2, а затем получает окончательную глубину проскальзывания и несущую способность фундамента, используя дихотомию в итерации. Рисунок 9показывает конкретный процесс.
Предлагаемый подход сначала рассчитывает диапазон глубины проскальзывания в соответствии с таблицей 2, а затем получает окончательную глубину проскальзывания и несущую способность фундамента, используя дихотомию в итерации. Рисунок 9показывает конкретный процесс.
РИСУНОК 9 . Оптимизирован подход к расчету несущей способности двухслойного глиняного фундамента. (A) Блок-схема, (B) Итеративное решение с использованием дихотомии
Как показано на рисунке 9, L (min, max) — это модель оптимизации итеративного решения с использованием дихотомии, где min — это минимум начальный интервал итерации, а max — максимальное значение начального интервала итерации. FLU (hb) — предельная несущая способность, соответствующая глубине проскальзывания hb (полученная с помощью верхней границы решения предельного анализа), FLU(Δhb)=FLU(hb)−FLU(hb+Δ) и Δ= 0,001 – шаг анализа расчета.
Различные подходы к расчету оптимизации несущей способности двухслойного глиняного фундамента используются для расчета предельной нагрузки при различных сочетаниях c1c2 и Hb в соответствии с несущей способностью двухслойного глиняного фундамента. В таблице 3 показаны результаты предельной нагрузки и сравнение литературы. На рис. 10 показаны типичные виды отказов, полученные в результате поиска. Как видно из результатов расчета, при c1c2<1 и Hb<0,71(Hb=0,2、0,5) в верхнем мягком грунте происходит локальное разрушение, и результат расчета находится между решением Терцаги (5.71) и решением Прандтля ( 5.14) однородной и агравовой глины, что подтверждается литературными данными. При c1c2<1 и Hb>0,71 (Hb=1,0、1,5) решения с верхней и нижней границами, рассчитанные с использованием предложенного подхода к расчету, составляют 5,14, что находится в пределах диапазона решений верхней и нижней границ, приведенных в литературе. . Рациональность предложенного подхода в определенной степени доказана. При c1c2> и Hb<0,71 (Hb=0,2、0,5) увеличивается глубина проскальзывания и быстро снижается предельная несущая способность; соответствующий коэффициент предельной несущей способности Pc1b, соответствующий Hb=0,2 и c1c2=5, равен 1,80. При c1c2> и Hb<0,71 (Hb=1,0、1,5) возможны два режима нестабильности.
В таблице 3 показаны результаты предельной нагрузки и сравнение литературы. На рис. 10 показаны типичные виды отказов, полученные в результате поиска. Как видно из результатов расчета, при c1c2<1 и Hb<0,71(Hb=0,2、0,5) в верхнем мягком грунте происходит локальное разрушение, и результат расчета находится между решением Терцаги (5.71) и решением Прандтля ( 5.14) однородной и агравовой глины, что подтверждается литературными данными. При c1c2<1 и Hb>0,71 (Hb=1,0、1,5) решения с верхней и нижней границами, рассчитанные с использованием предложенного подхода к расчету, составляют 5,14, что находится в пределах диапазона решений верхней и нижней границ, приведенных в литературе. . Рациональность предложенного подхода в определенной степени доказана. При c1c2> и Hb<0,71 (Hb=0,2、0,5) увеличивается глубина проскальзывания и быстро снижается предельная несущая способность; соответствующий коэффициент предельной несущей способности Pc1b, соответствующий Hb=0,2 и c1c2=5, равен 1,80. При c1c2> и Hb<0,71 (Hb=1,0、1,5) возможны два режима нестабильности. Один из них заключается в том, что глубина погребения почвы велика в нижнем мягком грунте (например, Hb = 1,5) и не сильно отличается от верхнего слоя почвы (например, c1c2 = 2, 3, 4). Нижний грунт не влияет на предельную несущую способность. В этом случае рассматривается равномерный фундамент с предельным коэффициентом нагрузки Pc1b=5,14 и глубиной проскальзывания hb=0,71. Во-вторых, слабый нижний грунт влияет на предельную несущую способность при глубоком проскальзывании. При Hb=1,5 и c1c2=5 глубина скольжения hb достигает 2,9.3.
Один из них заключается в том, что глубина погребения почвы велика в нижнем мягком грунте (например, Hb = 1,5) и не сильно отличается от верхнего слоя почвы (например, c1c2 = 2, 3, 4). Нижний грунт не влияет на предельную несущую способность. В этом случае рассматривается равномерный фундамент с предельным коэффициентом нагрузки Pc1b=5,14 и глубиной проскальзывания hb=0,71. Во-вторых, слабый нижний грунт влияет на предельную несущую способность при глубоком проскальзывании. При Hb=1,5 и c1c2=5 глубина скольжения hb достигает 2,9.3.
ТАБЛИЦА 3 . Статистика коэффициента предельной несущей способности.
РИСУНОК 10 . Типичные режимы отказа.
5 Заключение
1) Сначала создается оптимизированная математическая модель на основе жесткой блочной дискретной системы с минимальной несущей способностью в качестве целевой функции, скоростью блока в качестве основной переменной и удовлетворением совместимости скоростей, связанным правилом потока, и уравнения функционального равновесия соседнего блока как основные ограничения жесткой блочной дискретной системы. Затем предлагается FLU после получения верхней границы несущей способности фундамента с помощью оптимизационного решения.
Затем предлагается FLU после получения верхней границы несущей способности фундамента с помощью оптимизационного решения.
2) Влияние глубины проскальзывания (hb) на несущую способность фундамента исследуется для сложного двухслойного глиняного основания, прежде чем предлагать диапазон значений глубины проскальзывания при различных комбинациях параметров (c1c2) и различной глубине слоев (Hb).
3) На основании приведенных выше результатов предлагается оптимизированный подход к расчету несущей способности двухслойного глиняного фундамента путем введения итеративного решения с использованием дихотомии. Кроме того, рациональность подхода проверяется на расчетном примере.
Заявление о доступности данных
Первоначальные материалы, представленные в исследовании, включены в статью/дополнительный материал; дальнейшие запросы можно направлять соответствующему автору.
Вклад авторов
Все перечисленные авторы внесли существенный, непосредственный и интеллектуальный вклад в работу и одобрили ее для публикации.
Финансирование
Это исследование финансировалось Национальной ключевой программой исследований и разработок Китая (№ 2018YFC0407000), Национальным фондом естественных наук Китая (№ 51809).289, U1965204) и Программу поддержки исследований и разработок IWHR (№ GE0199A082021, GE110145B0022021). Исследовательский проект Китайской корпорации «Три ущелья» (контракт № JG/19055J).
Конфликт интересов
XW и YF работали в компании PowerChina Kunming Engineering Corporation Limited, а GZ работала в компании Beijing Glory PKPM Technology Co., Ltd.
Остальные авторы заявляют, что исследование проводилось в отсутствие каких-либо коммерческих или финансовых отношений, которые могут быть истолкованы как потенциальный конфликт интересов.
Примечание издателя
Все претензии, изложенные в этой статье, принадлежат исключительно авторам и не обязательно представляют претензии их дочерних организаций, издателя, редакторов и рецензентов. Любой продукт, который может быть оценен в этой статье, или претензии, которые могут быть сделаны его производителем, не гарантируются и не поддерживаются издателем.
Ссылки
Алхафаджи Х., Имани М. и Фахимифар А. (2020). Предельная несущая способность фундаментов из массива горных пород, подверженных действию фильтрационных сил, с использованием модифицированного критерия Хука–Брауна. Рок Мех. Рок инж. 53 (1), 251–268. doi:10.1007/s00603-019-01905-6
CrossRef Full Text | Google Scholar
Чен Дж., Инь Дж.-Х. и Ли К.Ф. (2003). Анализ верхней границы устойчивости откосов с использованием жестких конечных элементов и нелинейного программирования. Кан. Геотех. J. 40 (4), 742–752.
Полнотекстовая перекрестная ссылка | Google Scholar
Chen, WF (1975). Предельный анализ и пластичность грунта . Нью-Йорк: Научное издательство Elsevier.
Google Scholar
Дэвис, Э. Х., и Букер, Дж. Р. (1974). Влияние увеличения прочности с глубиной на несущую способность глин: 14F, 6R. ГЕОТЕХНИКА, В23, N4, ДЕКАБРЬ. 1973, стр. 551–563. Междунар. Дж. Рок Мех. Горная наука. Геомеханика. 11 (3), 62. doi:10.1016/0148-9062(74)91688-x
11 (3), 62. doi:10.1016/0148-9062(74)91688-x
CrossRef Full Text | Google Scholar
Гриффитс, Д. В. (1982). «Расчет несущей способности слоистых грунтов», в сб., 4-я межд. конф. на Нум Мет. В геомеханике, Vol. 1, 163–170.
Google Scholar
Хуан М. и Цинь Х.-Л. (2009). Многожесткоблочные решения с верхней границей несущей способности двухслойных грунтов. Вычисл. Геотехника 36 (3), 525–529. doi:10.1016/j.compgeo.2008.10.001
Полный текст CrossRef | Google Scholar
Лямин А.В., Слоан С.В. (2002). Анализ верхней границы с использованием линейных конечных элементов и нелинейного программирования. Междунар. Дж. Нумер. Анальный. Методы геомех. 26 (2), 181–216.
Полнотекстовая перекрестная ссылка | Google Scholar
Мерифилд, Р. С., Слоан, С. В., и Ю, Х. С. (1999). Жесткие решения по пластичности несущей способности двухслойных глин. Геотехника 49 (4), 471–490. doi:10.1680/geot.1999.49.4.471
Полный текст CrossRef | Google Scholar
Михаловски Р.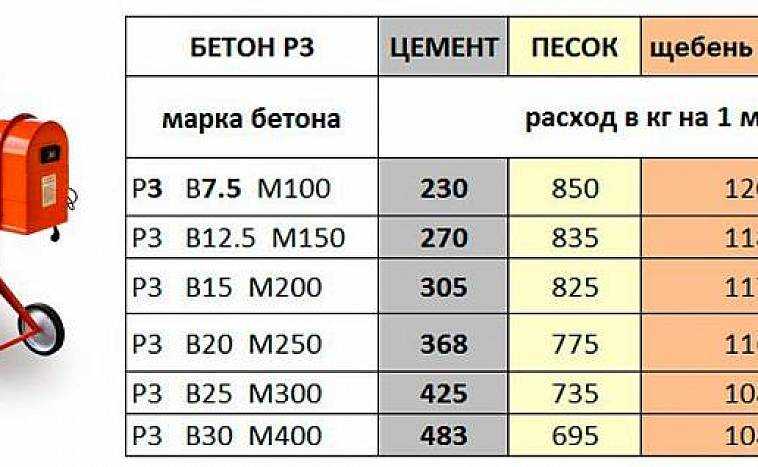 Л. и Лей С. (1996). Несущая способность оснований на двухслойных грунтах основания. J. Инженер-геотехник. 121 (5), 421–428. дои: 10.1061 / (нач.) 0733-9410(1995)121:5(421)
Л. и Лей С. (1996). Несущая способность оснований на двухслойных грунтах основания. J. Инженер-геотехник. 121 (5), 421–428. дои: 10.1061 / (нач.) 0733-9410(1995)121:5(421)
Полнотекстовая перекрестная ссылка | Google Scholar
Осман А.С. (2019). Верхние граничные решения для коэффициентов формы гладких прямоугольных оснований на трущихся материалах. Вычисл. Geotechnics 115 (ноябрь), 103177. doi:10.1016/j.compgeo.2019.103177
CrossRef Полный текст | Google Scholar
Фам, К. Н., Оцука, С., Исобе, К., и Фукумото, Ю. (2020). Предельная грузоподъемность жесткого основания при внецентренно наклонной нагрузке . Токио: почвы и фундаменты.
Google Scholar
Шамлу С. и Имани М. (2020). Решение верхней границы несущей способности горных массивов с учетом глубины залегания. Океанский инж. 218 (6), 108169. doi:10.1016/j.oceaneng.2020.108169
CrossRef Полный текст | Google Scholar
Терцаги, К., и Пек, Р.
