Расчет плиты перекрытия пустотной: Кафедра промышленного и гражданского строительства — Методические указания, задания, вопросы
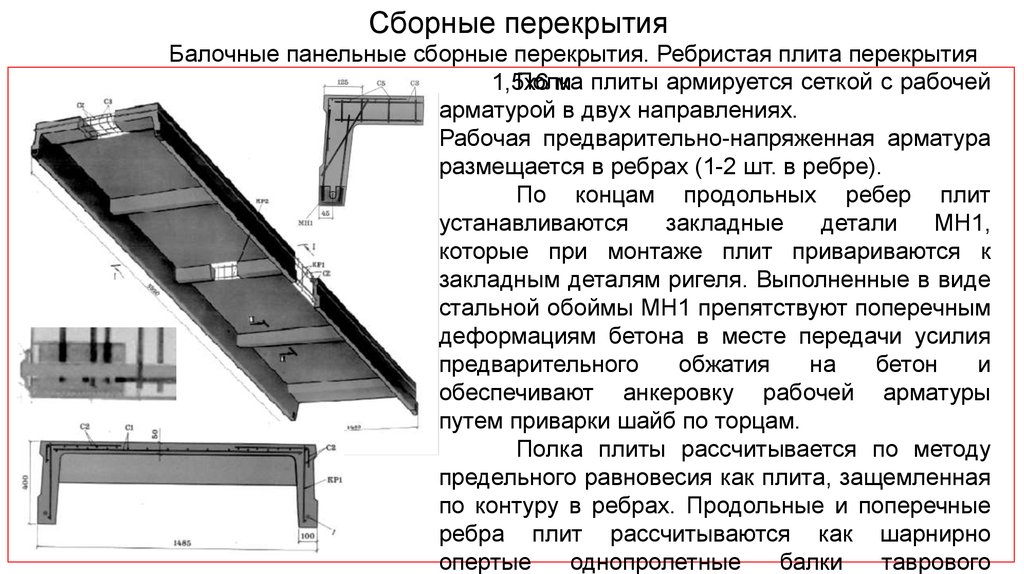
2. Расчет многопустотной плиты перекрытия.
2.2.1. Расчет многопустотной плиты по предельным состояниям
первой группы.
2.2.1.1. Расчетный пролет и нагрузки.
Расчетный пролет lо=6960 м.
Нормативные и расчетные нагрузки на 1 м2 перекрытия.
Нагрузка | Нормативная нагрузка, Н/м2 | Коэффициент надежности по нагрузке | Расчетная Нагрузка, Н/м2 |
Постоянная: Собственный вес много-пустотной плиты с круглыми пустотами Стяжка из цементно-песчаного раствора М150 (t=35 мм) =1800 кг/м3; Прослойка и заполнение швов из цементно-песчаного раствора М 150 (t=15 мм) =1800 кг/м3; Собственный вес керамических плиток (t=35 мм) =1800 кг/м3; | 3000 270 630 162 | 1,1 1,3 1,3 1,1 | 3300 351 178,2 |
Итого: Временная В том числе: длительная кратковременная | 4062 1500 300 1200 | — 1,2 1,2 1,2 | 4648,2 1800 360 1440 |
Полная нагрузка В том числе: Постоянная и длительная кратковременная | 5562 4362 1200 | — — — | 6448. — — |
Расчетная нагрузка на 1 м при ширине плиты 1,5 м с учетом коэффициента надежности по назначению здания
Постоянная g=4,648*1,5*0,95=6,62 кН/м;
Полная g+v=6.448*1,5*0,95=9.18 кН/м; v=1.8*1.5*0.95=2.565 кН/м;
Нормативная нагрузка на 1 м:
Постоянная g=4,062*1,5*0,95=5,79 кН/м;
Полная g+v=5,562*1,5*0,95=7,93 кН/м;
В том числе постоянная и длительная 4,362*1,5*0,95=6,22кН/м;
2.2.1.2. Усилия от расчетных и нормативных нагрузок.
От расчетной нагрузки
М=(g+v)l02/8=9.18*6.962/8=55.5 кН*м;
 18*6.96/2=31.95
кН*м;
18*6.96/2=31.95
кН*м;От нормативной нагрузки
М=(g+v)l02/8=7,93*6.962/8=48 кН*м;
Q=(g+v)l0/2=7,93*6.96/2=27.6 кН*м;
От нормативной постоянной и длительной нагрузок
М=(g+v)l02/8=6.22*6.962/8=37.66 кН*м;
Высота сечения многопустотной (7 круглых пустот диаметром 15,9 см) предварительно напряженной плиты h 220 мм. Рабочая высота сечения h0=h—a=220-30=190 мм.
Размеры: толщина верхней и нижней полок (22-15,9)/2=3,05 см.
Ширина ребер: средних – 33см,
крайних
– 79. 5см.
5см.
В расчетах по предельным состояниям первой группы расчетная толщина сжатой полки таврового сечения
отношение h’f /h=3,05/22=0,1380,1, при этом в расчет вводится вся ширина полки b’f=146 см;
Расчетная ширина ребра b=146-7*15,9=35 см.
2.2.1.4. Характеристики прочности бетона и арматуры.
Пустотную предварительно напряженную плиту армируют стержневой арматурой класса А-IV с электротермическим натяжением на упоры форм. К трещиностойкости плиты принимаются требования 3-ей категории. Изделие подвергают тепловой обработке при атмосферном давлении.
Бетон тяжелый класса В20, соответствующий напрягаемой арматуре. Призменная прочность нормативная
Расчетное
сопротивление сжатию Rb=11,5
МПа.
Нормативное сопротивление при растяжении Rbtn=Rbt,ser=1.4 МПа.
Расчетное сопротивление при растяжении Rbt=15 МПа.
Начальный модуль упругости бетона Е
Передаточная прочность бетона Rbp устанавливается так, чтобы при обжатии отношение напряжений bp/Rbp 0.75
Арматура класса А-IV:
Нормативное сопротивление Rsn=590 МПа.
Расчетное сопротивление Rs=510 МПа.
Модуль упругости Еs=190000 МПа.
Предварительное
напряжение арматуры равно: sp=0.75*Rsn=0.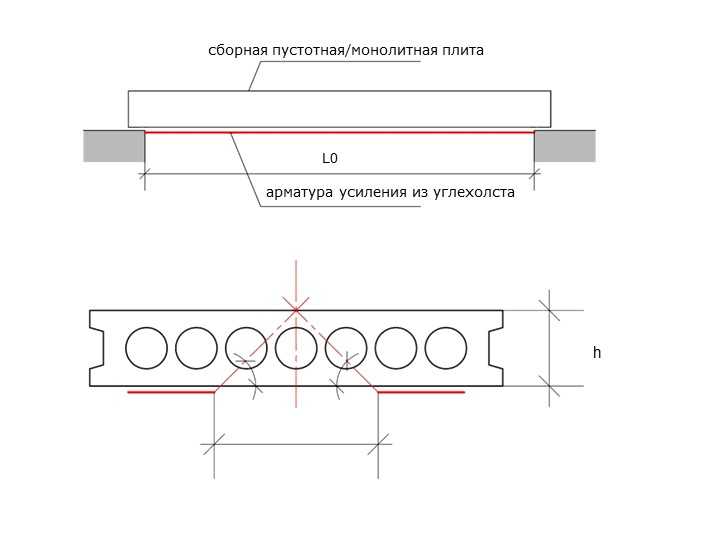
При электротермическом способе натяжения
р=30+360/l=30+360/7,2=80 МПа.
sp+ р=442,5+80=522,5 Rsn=590 МПа. – условие sp+ р Rsn выполняется.
Вычисляем предельное отклонение предварительного напряжения при числе напрягаемых стержней nр=5.
sp=0.5
Коэффициент
точности натяжения: sp
При проверке по образованию трещин в верхней зоне плиты при обжатии принимают sp=1+ sp=1+0,13=1,13.
Предварительные
напряжения с учетом точности натяжения sp=0,87*442,5=385
МПа.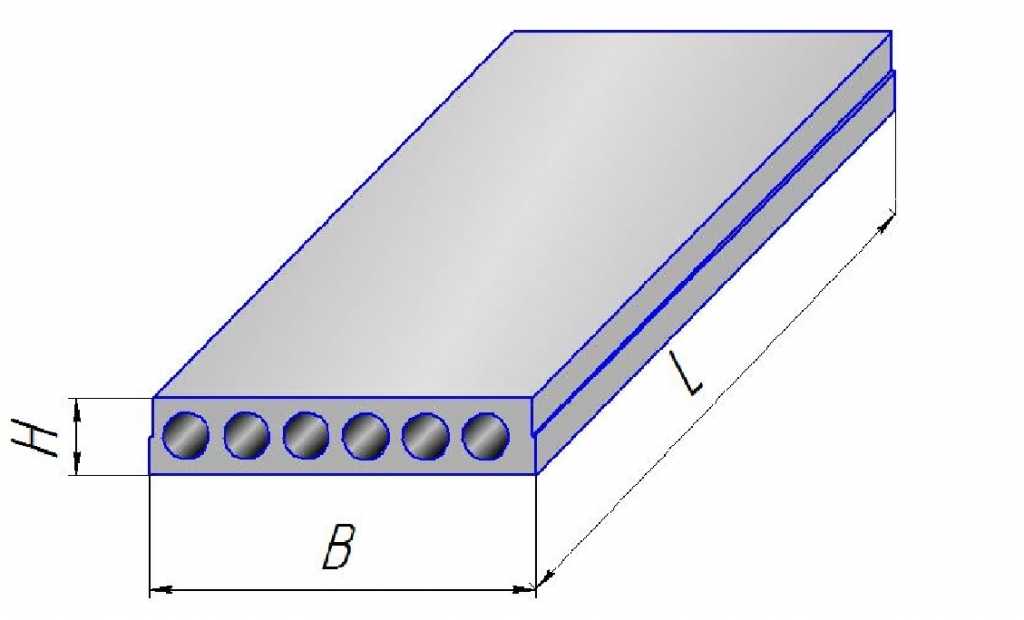
Расчёт многопустотной плиты по предельным состояниям первой группы
2. Расчёт многопустотной плиты по предельным состояниям первой группы
Исходные данные. Многопустотная плита из тяжелого бетона класса В40 опирается поверху на железобетонные ригели каркаса, пролет ригелей – lp=5,9м. Нормативное значение временной нагрузки 3,5кПа. Требуется рассчитать и законструировать плиту перекрытия. Класс рабочей арматуры принять А-V.
2.1 Расчет плиты по предельным состояниям первой группы
2.1.1 Расчётный пролёт и нагрузки
Для установления расчётного пролёта плиты предварительно задаёмся размерами сечения ригеля:
hp=(1/12)*lp=(1/12)*590=50см, bp=0.5*hp=0.4*50=20см.
При опирании на ригель поверху расчётный пролёт плиты составит:
lo=l-bp/2=6,4-0,2/2=6,3м.
Рекомендуемые материалы
Подсчёт нагрузок на 1м2 перекрытия сводим в таблицу 1.
Таблица 1 – Нормативные и расчётные нагрузки на 1м2 перекрытия
На 1м длины плиты шириной плиты 2,1м действуют следующие нагрузки, Н/м: кратковременная нормативная pn=1050*2,1=2205; кратковременная расчетная р=1260*2,1=2646; постоянная и длительная нормативная qn=6130*2,1=12873; постоянная и длительная расчетная q=7074*2,1=14855,4; итого нормативная qn+pn=12873+2205=15078; итого расчетная q+p=14855,4+2646=17501,4.
2.1.2 Усилия от расчётных и нормативных нагрузок
Расчётный изгибающий момент от полной нагрузки:
M=(q+p)*l20*gn/8=17501,4*6,32*0.95/8=82487,4Н.м.
Расчетный изгибающий момент от полной нормативной нагрузки:
Mn=(qn+pn)*l20*gn/8=15078*6,32*0.95/8=71065,4Н.м.
То же, от нормативной постоянной и длительной временной нагрузок:
Mld=qn*l20*gn/8=12873*6,32*0. 95/8=60672,9Н.м.
95/8=60672,9Н.м.
То же, от нормативной кратковременной нагрузки:
Mсd=рn*l20*gn/8=2205*6,32*0.95/8=10392,6Н.м.
Максимальная поперечная сила на опоре от расчетной нагрузки:
Q=(q+p)*l0*gn/2=17501,4*6,3*0.95/2=52372,9Н.
То же, от нормативной нагрузки:
Qn=(qn+pn)*l0*gn/2=15078*6,3*0.95/2=45120,9Н.
То же, от нормативной нагрузки:
Qnld=qn*l0*gn/2=12873*6,3*0.95/2=38522,5Н.
2.1.3 Установление размеров сечения плиты
Плиту рассчитываем как балку прямоугольного сечения с заданными размерами bxh=210х22см (где b – номинальная ширина, h – высота плиты). Проектируем плиту одинадцатипустотной. В расчете поперечное сечение пустотной плиты приводим к эквивалентному двутавровому сечению. Заменяем площадь круглых пустот прямоугольниками той же площади и того же момента инерции.
Вычисляем:
h1=0.9*d=0.9*15.9=14.3см;
hf=hf’=(h-h1)/2=(22-14.3)/2=3.8см;
тогда приведенная толщина ребер равна:
bp=b=bf’-n*h1=207-11*14.3=49,7см,
где bf’=207см – расчетная ширина сжатой полки.
Приведенная толщина бетона плиты:
hred=h-(n*p*d2)/4b=22-(11*p*15.92)/(4*207)=11.5см>10 см.
Рабочая высота сечения h0=22-3=19см.
Толщина верхней и нижней полок hf=(22-15.9).0.5=3см.
Ширина ребер: средних – 2.9см, крайних – 3см.
Плита изготавливается из тяжелого бетона класса В40, имеет предварительно напрягаемую рабочую арматуру класса А-VI с электротермическим натяжением на упоры форм. К трещиностойкости плиты предъявляются требования 3-ей категории. Изделие подвергают тепловой обработке при атмосферном давлении.
Бетон тяжёлый класса В40
Призменная прочность бетона нормативная: Rbn=Rb,ser=29МПа, расчётная Rb=22МПа, коэффициент условий работы бетона gb2=0. 9; нормативное сопротивление при растяжении Rbtn=Rbt,ser=2.1МПа, расчётное Rbt=1.4МПа; начальный модуль упругости бетона Eb=32.5*103МПа.
9; нормативное сопротивление при растяжении Rbtn=Rbt,ser=2.1МПа, расчётное Rbt=1.4МПа; начальный модуль упругости бетона Eb=32.5*103МПа.
Передаточная прочность бетона Rbp устанавливается так, чтобы при обжатии отношение напряжений sbp/Rbp£0.75.
Арматура продольная класса A—VI
Нормативное сопротивление Rsn=Rs,ser=980МПа,
Расчётное сопротивление Rs=225МПа,
Модуль упругости Es=1.9*105МПа.
Предварительное напряжение арматуры назначаем таким образом, чтобы выполнялись условия . При электротермическом способе натяжения:
Принимаем ssp=600МПа.
Определяем коэффициент точности натяжения арматуры
где n – число стержней напрягаемой арматуры, принимаем n=8.
.
При благоприятных влияниях предварительного напряжения gsp=1-0.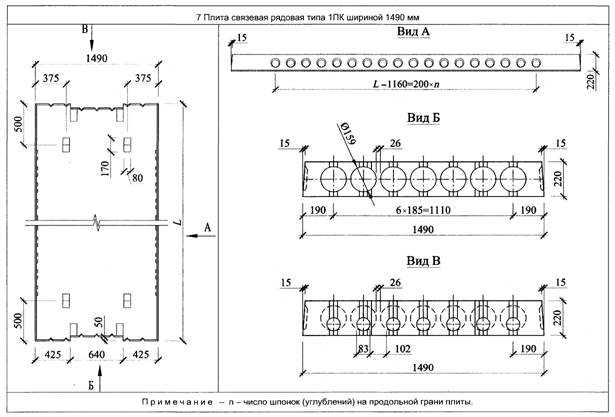 1=
1=
=0.9. При проверке по образованию начальных трещин в верхней зоне плиты g’sp =1+0.1=1.1. Значение предварительного напряжения с учётом точности натяжения арматуры составит 0.9*600=540МПа.
2.1.5 Расчёт прочности плиты по сечению, нормальному к продольной оси
При расчёте прочности, сечение плиты принимается тавровым (полка нижней растянутой зоны в расчёт не вводится). Размеры сечения показаны на рисунке 2б.
Вычисляем:
Находим
Высота сжатой зоны сечения:
следовательно, нейтральная ось проходит в пределах сжатой полки, и сечение рассчитывается как прямоугольное шириной bf’=207см. Вычисляем характеристики сжатой зоны
ω=0,85-0,008·Rb=0,85-0,008·22·0,9=0,69
Вычисляем граничную высоту сжатой зоны
ξR=
где σSR=Rs+400- σSP2
σSP=0,6Rsn=0,6·785=471 МПа
σSP2=γsp· σSP·0,7=0,84·471·0,7=276,95 МПа
σSR=680+400-276,95=803,1 МПа
Поскольку соблюдается условие x<xR (0. 034<0.43), то расчётное сопротивление арматуры умножается на коэффициент условий работы gs6:
034<0.43), то расчётное сопротивление арматуры умножается на коэффициент условий работы gs6:
где h=1.15 – коэффициент, принимаемый равным для арматуры класса A-V.
Требуемую площадь сечения рабочей арматуры определяем по формуле:
где h=1-0.5x=1-0.5*0.058=0.971.
Принимаем в качестве предварительно напряжённой продольной рабочей арматуры три стержня арматуры класса A-V 3Æ16мм с общей площадью Asp=6,03см2. Арматура устанавливается в четвертом слева и крайних рёбрах плиты.
2.1.6 Расчёт прочности плиты по наклонным сечениям
По конструктивным требованиям в многопустотных плитах высотой не более 30см поперечная арматура не устанавливается, если она не нужна по расчету. Проверим необходимость постановки поперечной арматуры расчетом. Проверяем условие: Q£ 0.3jw1jb1Rb b h0,
где Q – поперечная сила на опоре от расчетной нагрузки; Q=52,37кН,
jw1=1, так как поперечная арматура отсутствует;
jb1=1-0. 01Rb=1-0.01*22=0.78.
01Rb=1-0.01*22=0.78.
Условие:
52,37<0.3*1*0.78*22*10-1*49,7*19,
52,37кН<486,13кН, выполняется,
следовательно, прочность плиты по наклонной полосе между наклонными трещинами обеспечена.
Поперечную арматуру в плите можно не устанавливать, если выполняются условия:
а) Qmax£2.5*Rbt*b*h0; Qmax=Q.
52,37<2.5*1.4*10-1*49,7*19,
52,37кН<330,51кН, условие выполняется.
б) Q1£Mb1/c, Q1=Qmax-q1*c=52,37-11,88*0.475=46,73кН,
где с — проекция наклонного сечения, принимаем:
с=2,5h0=2,5*19=47,5см;
q=gp*b*gf=8,334*1,5*0,95=11,88кН/м,
Мb1=jb4(1+jn)gb2Rbt*b*h02;
jb4=1.5- для тяжелого бетона; jn=0;
где Р=Asp(ssp-100)=5,96*(540-100)*0.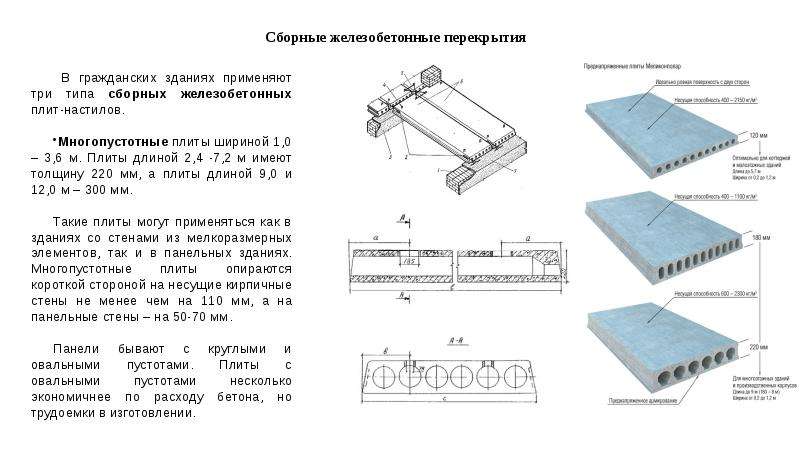 1=262кН – усилие предварительного обжатия,
1=262кН – усилие предварительного обжатия,
100МПа – минимальное значение суммарных потерь предварительного напряжения.
Принимаем jn=0.5.
Мb1=1,5*(1+0,22)*0,9*1,4*10-1*49,7*192=4137кН*см.
Мb1/с=4137/47,5=87,09кН.
Условие Q1£Мb1/с:
46,73кН<87,09кН выполняется,
следовательно, поперечную арматуру в плите не устанавливаем.
На приопорных участках длиной l/4 арматуру устанавливаем конструктивно Æ4 Вр-I с шагом S=h/2=22/2=11см, в средней части пролёта поперечную арматуру не устанавливаем.
2.2 Расчет плиты по предельным состояниям второй группы
2.2.1 Геометрические характеристики сечения
При расчёте по 2-ой группе предельных состояний в расчёт водится двутавровое сечение плиты (рисунок 2в).
Площадь приведённого сечения:
расстояние от нижней грани до центра тяжести приведённого сечения:
момент инерции сечения:
момент сопротивления сечения:
упругопластический момент сопротивления по растянутой зоне
здесь g=1. 5 для двутаврового сечения при 2<bf/b=207/49,7=4,2<6,0.
5 для двутаврового сечения при 2<bf/b=207/49,7=4,2<6,0.
Упругопластический момент по растянутой зоне в стадии изготовления и обжатия Wpl’=Wpl=20343см3.
Расстояния от ядровых точек – наиболее и наименее удалённой от растянутой зоны (верхней и нижней) – до центра тяжести сечения:
2.2.2 Потери предварительного напряжения
Расчёт потерь выполняем в соответствии с требованиями СНиП 2.03.01-84*. Коэффициент точности натяжения арматуры принимаем gsp=1.0.
Потери s1 от релаксации напряжений при электротермическом натяжении высокопрочных канатов:
s1=0.03*ssp=0.03*600=18МПа.
Потери s2 от температурного перепада между натянутой арматурой и упорами равны нулю, так как при пропаривании форма с упорами нагревается вместе с изделием.
Потери от деформации анкеров s3 и формы s5 при электротермическом способе равны нулю. Поскольку арматура не отгибается, потери от трения арматуры s4 также равны нулю.
Усилие обжатия
Эксцентриситет силы Р1 относительно центра тяжести сечения еор=у0-а=11-3=8см. Определим сжимающие напряжения в бетоне:
где Mg=q*l2/8=(2,07*3,0)*6,42/8=31,8кНм – изгибающий момент в середине пролета плиты от собственного веса,
l=6,4м – расстояние между прокладками при хранении плиты.
Устанавливаем значение передаточной прочности бетона из условия sbp/Rbp£0.75, но не менее 0.5В (В — класс бетона):
0,78МПа,
0,5 B=0,5*40=20МПа.
Принимаем Rbp=20МПа, тогда:
при расчёте потерь от быстронатекающей ползучести s6 при
<
Итак, первые потери slos1=s1+s6=18+0,79=18,79МПа.
С учётом потерь slos1:
Р1=Аsp(ssp-slos1)=5,96*(600-18,79)*10-1=346,4МПа.
Отношение .
Из вторых потерь s7…s11 при принятом способе натяжения арматуры учитываются только потери s8 от усадки бетона и потери s9 от ползучести бетона.
Для тяжёлого бетона классов В40 и ниже s8=40МПа.
Так как sbp/Rbp<0.75 то s9=127.9*sbp/Rbp=112,5*0,029=3,26МПа.
Вторые потери slos2=s8+s9=40+3,26=43,26МПа.
Полные потери slos=slos1+slos2=18,79+43,26=62,05МПа<100МПа, принимаем slos=100МПа.
Усилие обжатия с учётом полных потерь:
Р2=Аsp(ssp-slos)=5,96*(600-100)*10-1=298кН.
2.2.3 Расчёт по образованию нормальных трещин
Образование нормальных трещин в нижней растянутой зоне плиты не происходит, если соблюдается условие Mn=71,065кН*м£Mcrc(Mcrc – момент образования трещин):
Поскольку Mn<Mcrc (71,065<79,52), то в нижней зоне плиты трещины не образуются.
Проверим, образуются ли начальные трещины в верхней зоне плиты от усилия предварительного обжатия. Расчётное условие:
здесь Rbt,p=1МПа – нормативное сопротивление бетона растяжению, соответствующее передаточной прочности бетона Rbp=20МПа;
Р1 — принимается с учётом потерь только s1, Р1=346,4кН;
Mg – изгибающий момент в середине пролёта плиты от собственного веса, Mg=31,8кН*м.
Вычисляем: 1.12*346,4*(8-5,72)£1*10-1*20343,5+31,8, 884,57кН*см<2066,2кН*см.
Условие выполняется, значит, начальные трещины в верхней зоне плиты от усилия предварительного обжатия не образуются.
2.2.4 Расчёт прогиба плиты
Для однопролётной шарнирно опертой балочной плиты прогиб можно определить по формуле:
где 1/r – кривизна оси элемента при изгибе. Кривизна оси элемента, где не образуются трещины при длительном действии нагрузки:
где jb1=0. 85 – коэффициент, учитывающий снижение жесткости под влиянием неупругих деформаций бетона растянутой зоны;
85 – коэффициент, учитывающий снижение жесткости под влиянием неупругих деформаций бетона растянутой зоны;
jb2 – коэффициент, учитывающий снижение жёсткости (увеличение кривизны) при длительном действии нагрузки под влиянием ползучести бетона сжатой зоны при средней относительной влажности воздуха выше 40%, равна 2; jb2 – то же, при кратковременной нагрузке равна 1.
Так как в растянутой зоне плиты трещины не образуются, то кривизна оси (без учета влияния выгиба):
где – кривизна соответственно от кратковременных и от постоянных и длительных нагрузок,
Тогда прогиб будет равен:
От постоянной и длительной временной нагрузок:
Тогда прогиб будет равен:
Тогда полный прогиб будет равен:
2.3 Проверка панели на монтажные нагрузки
Панель имеет четыре монтажные петли из стали класса А-1, расположенные на расстоянии 70см от концов панели (рисунок 3а). С учётом коэффициента динамичности kd=1.4 расчётная нагрузка от собственного веса панели:
С учётом коэффициента динамичности kd=1.4 расчётная нагрузка от собственного веса панели:
где собственный вес панели; bп – конструктивная ширина панели; hred – приведённая толщина панели; r — плотность бетона.
Расчётная схема панели показана на рисунке 3б. Отрицательный изгибающий момент консольной части панели:
Этот момент воспринимается продольной монтажной арматурой каркасов. Полагая, что z1=0.9*h0=0.9*19=17.1см, требуемая площадь сечения указанной арматуры составляет:
Если Вам понравилась эта лекция, то понравится и эта — 49 Кавитация.
что значительно меньше принятой конструктивно арматуры 3Æ16 А-II, Аs=5,96см2.
При подъёме панели вес её может быть передан на две петли. Тогда усилие на одну петлю составляет
Площадь сечения арматуры петли
принимаем конструктивно стержни диаметром 14 мм, Аs=1,539см2.
Конструкция многопустотной плиты — ПРЕДВАРИТЕЛЬНОЕ НАПРЯЖЕНИЕ
Перейти к содержимомуDollowcore Slab Design-Pre-StressPaul TATE2022-07-15T13: 47: 30+02: 00
Программное обеспечение для проектирования и анализа для
.
Веб-семинары
YouTube
Документы
Благодаря последним дополнениям в PRE-Stress 6.7 программное обеспечение стало лучше, чем когда-либо, и стало идеальным инструментом для проектирования и анализа предварительно напряженных пустотных (HC) плит.
Посмотрите краткий обзорный видеоролик о конструкции многопустотных плит
Конструктивные особенности многопустотных плит
Вы можете выбрать поперечные сечения многопустотных плит из предопределенного списка или создать свой собственный. Если у вас есть CAD-чертеж вашего сечения, вы можете использовать функцию импорта, и программа найдет профиль пустотного сердечника и автоматически создаст для вас сечение. Вам нужно будет сконфигурировать предварительно напряженные проволоки/пряди, используя Диспетчер моделей прядей.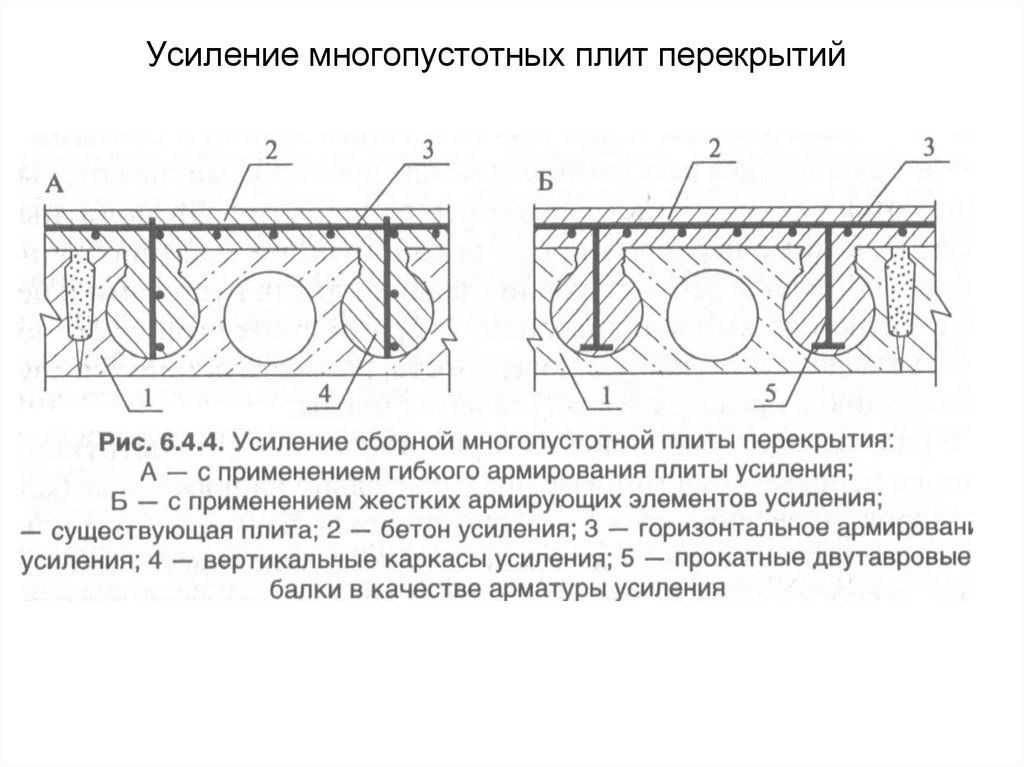
Добавьте топпинг к вашему сборному элементу и сделайте полный расчет с учетом слоя монолитного бетона. Вы можете добавить армирование к верхнему слою и заставить его работать вместе с предварительно напряженным пустотелым заполнителем. Также можно выполнить пожарный расчет.
Очень легко добавить предварительно напряженные арматуры/проволоки/пряди и стандартную арматуру к вашему элементу. Применение полос можно выполнить вручную или с помощью диспетчера шаблонов, и вы можете настроить и сохранить любой макет для будущих проектов.
Вы также можете спроектировать углубления отверстий и заполнение стержней в многопустотных плитах, указав точное расположение и размеры.
Учет долгосрочных эффектов путем введения коэффициентов ползучести и усадки. У вас есть доступ к нашему онлайн-инструменту гибкой поддержки, который рассчитывает эти факторы в соответствии с вашим типом бетона.
Собственный вес автоматически применяется к элементу и любому покрытию, если оно имеется. В зависимости от типа, выбранного для нагрузки, программа автоматически добавит правильные коэффициенты в соответствии с Национальным приложением и создаст комбинации нагрузок.
В зависимости от типа, выбранного для нагрузки, программа автоматически добавит правильные коэффициенты в соответствии с Национальным приложением и создаст комбинации нагрузок.
Рассчитайте многопустотную плиту в соответствии с Еврокодом и получите быстрое и точное представление всего срока службы элемента. Проверка кода выполняет все проверки в соответствии с Еврокодом, включая проверку на растрескивание. Вы можете проверить конкретные проверки для каждого этапа. За считанные секунды получите полную документацию по расчету пустотелых элементов со всеми проверками, включая расчет пожарной безопасности.
Нажмите кнопку «Получить бесплатную пробную версию», чтобы подать заявку на пробную версию, или свяжитесь с местным торговым представителем для получения дополнительной информации.
Проектирование многопустотных плит в IMPACT
ПРЕДВАРИТЕЛЬНОЕ НАПРЯЖЕНИЕ Пользователи, работающие с программным обеспечением IMPACT Design, также могут импортировать данные и получать выгоду от полной интеграции расчетов пустотных плит при детализации компоновок перекрытий из многопустотных плит в AutoCAD и BricsCAD, а теперь и в полном 3D с менеджер проекта IMPACT.
Зачем ждать? Подайте заявку ниже, чтобы загрузить пробную лицензию PRE-Stress и начать свое путешествие уже сегодня!
Подать заявку на пробную версию
PRE-Stress Wiki
Для получения полной технической информации и руководств пользователя по проектированию многопустотных плит посетите веб-сайт PRE-Stress Wiki, нажав здесь.
Блог до стресса
Paul Tate2022-07-15T13:25:35+02:002022-07-15|Категории: Блог, FEM-Design, Pre-Stress, StruSoft Portal, WIN-Statik|Теги: Ползучесть бетона, Усадка бетона, Онлайн-калькулятор , сборные конструкции, предварительно напряженные конструкции, конструкции из железобетона|
StruSoft рада поддержать вас, предоставив бесплатный онлайн-инструмент, который поможет вам рассчитать ползучесть и усадку бетона для вашего конструкционного бетона […]
Пол Тейт2022-02-02T23:19:51+01:002020-12-15|Категории: Блог, Предстресс|Теги: Hollowcore|
Компания StruSoft рада объявить о выпуске гибкой поддержки PRE-Stress. Это онлайн-инструмент, который поможет вам рассчитать использование предварительно напряженных […]
Это онлайн-инструмент, который поможет вам рассчитать использование предварительно напряженных […]
Пол Тейт2022-04-19T11:23:39+02:002020-02-08|Категории: Блог, Предварительное напряжение|Теги: Проверка на наличие трещин, Импорт DWG, Полый сердечник, Наклонная балка, Топпинг|
Компания StruSoft взяла интервью у Богдана Бузаяну из компании Gapa Projects в Румынии, чтобы узнать, как они используют программное обеспечение PRE-Stress при проектировании предварительно напряженных […]
Ссылка для загрузки страницы ‘; }Перейти к началу
Огнестойкость прессованных многопустотных плит
Чтобы прочитать полную версию этого контента, выберите один из вариантов ниже:
Кристиан Герц (Кафедра гражданского строительства, Датский технический университет, Люнгбю, Дания)
Луиза Джулиани (кафедра гражданского строительства, Danmarks Tekniske Universitet, Lyngby, Дания)
Lars Schiøtt Sørensen (ВОО, Ольборгский университет, Ольборг, Дания)
Журнал структурной пожарной техники
«> ISSN : 2040-2317 гг.
Дата публикации статьи: 7 июля 2017 г.
Дата публикации номера: 16 августа 2017 г.
Загрузки
Аннотация
Назначение
Сборные экструдированные многопустотные плиты являются предпочтительными строительными элементами для перекрытий в нескольких странах. Поэтому важно иметь возможность задокументировать огнестойкость этих плит, подтверждающую выполнение стандартных требований огнестойкости 60 и 120 минут, установленных в большинстве национальных строительных норм. В работе представлен подробный анализ механизмов, ответственных за потерю несущей способности многопустотных плит при воздействии огня.
Проект/методология/подход
Кроме того, теоретические расчеты и оценки в соответствии со структурными нормами сравниваются с данными, полученными в результате стандартного испытания на огнестойкость и тщательного изучения доступной комплексной документации по испытаниям многопустотных плит, подверженных возгоранию.
Выводы
Выяснены механизмы потери несущей способности, обнаружены признаки огнестойкости.
Значение оригинальности
Впервые выявлены механизмы, ответственные за потерю несущей способности, а результаты испытаний и расчетный подход впервые применены в соответствии друг с другом для оценки огнестойкости конструкции.
Ключевые слова
- Прессованные многопустотные плиты
- Огневое испытание
- Несущая способность
- Стандартная огнестойкость
Цитата
Герц К., Джулиани Л. и Соренсен Л.С. (2017), «Огнестойкость экструдированных многопустотных плит», Journal of Structural Fire Engineering , Vol.
