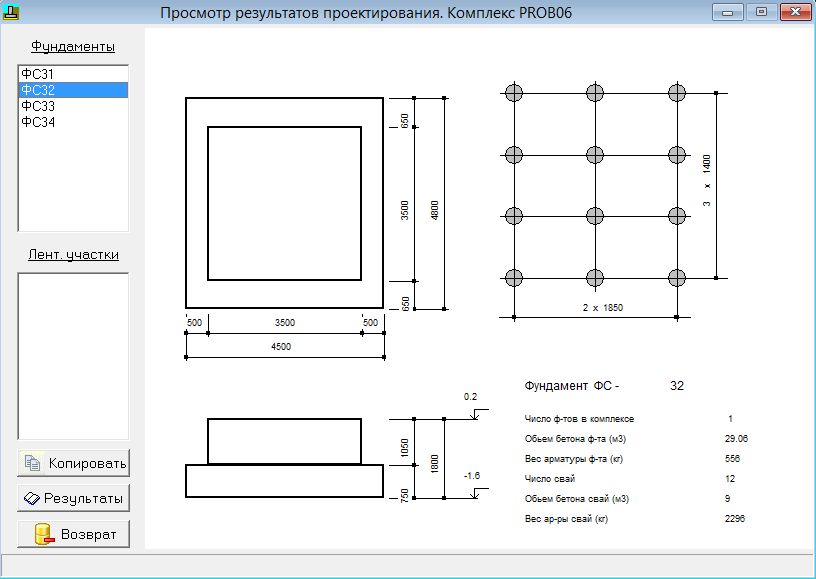
Расчет нагрузки на фундамент калькулятор онлайн: Калькулятор Вес-Дома-Онлайн v.1.0 — Сбор нагрузок на фундамент
Расчет нагрузки на фундамент. Расчет подошвы фундамента
РЕКЛАМА
Из статьи «Грунты в основании фундаментов» известно, что фундамент дома может опираться на грунт с разной несущей способностью.
Несущая способность грунта — это сила давления от веса здания, которую выдерживает грунт длительное время при допустимой деформации.
Несущая способность грунта характеризуется величиной расчетного сопротивления грунта — R, т/м2.
Ширина подошвы фундамента — размер в.Толщина противопучинистой песчаной подушки — размер t.
Цель расчета – подобрать ширину подошвы фундамента (в) и толщину песчаной подушки между грунтом и фундаментом (t) так, чтобы удельное давление от веса здания было меньше расчетного сопротивления грунта.
Расчет ведем в следующей последовательности:
- Выбираем размеры фундамента исходя из конструктивных соображений.

- Определяем вес здания, приходящийся на один погонный метр длины стены.
- По характеристикам грунта в основании фундамента определяем R – расчетное сопротивление грунта.
- Расчитываем необходимую ширину подошвы фундамента на один погонный метр длины (площадь фундамента под 1 погонным метром стены).
- Корректируем размеры фундамента по результатам расчета.
- Определяем толщину песчаной подушки между грунтом и подошвой фундамента.
Для выполнения расчета удобно использовать программу – калькулятор (книга Excel), которую можно скачать по ссылке «Калькулятор – расчет фундамента». Со скачанным файлом калькулятора удобно работать в онлайн редакторе «Google Таблицы».
На листе «Расчет» в разделе «1. Определение нагрузки от веса здания на 1 погонный метр подошвы фундамента» в первых столбцах вводим исходные данные по конструкции здания.
Данные берем из чертежей проекта. Для наглядности руководствуемся конструктивной схемой здания.
Затем заполняем столбцы «Удельная нагрузка конструкций». Нагрузки определяем из таблиц на листе «Справочник». При заполнении исходных данных важно отличать вертикальные конструкции стен (нагрузка — т/м
После ввода исходных данных программа выдает результат расчета – нагрузку на 1 погонный метр по каждой оси здания.
В разделе «2. Расчет ширины подошвы фундамента» вводятся исходные данные по грунту и песчаной подушке.
Расчетное сопротивление грунта определяется по таблицам на листе «Справочник». Для мелкозаглубленных фундаментов используется таблица «Расчетное сопротивление грунта R на глубине заложения фундамента 0,3  » Программа выдает результат расчета – ширину подошвы фундамента по каждой оси.
» Программа выдает результат расчета – ширину подошвы фундамента по каждой оси.
С учетом результатов расчета и конструктивных соображений в строке «Принимаем:» назначаем ширину подошвы. Принятые размеры вводим в исходные данные по фундаменту раздела 1. Программа пересчитывает нагрузки и ширину подошвы. Добиваемся, чтобы принятая ширина подошвы была не меньше расчетной величины.
В разделе «3. Расчет толщины песчаной подушки» производится расчет толщины песчаной подушки по исходным данным, взятым из раздела 2. С учетом результатов расчета и конструктивных соображений в строке «Принимаем:» назначаем толщину подушки.
Следующая статья:
Глубина промерзания грунта на карте.
Предыдущая статья:
Выбор фундамента устойчивого к морозному пучению грунта
Выбери тип фундамента для своего дома
Прочитайте статью
Выбор фундамента для частного дома на пучинистом грунте
Какой фундамент выбрали Вы? Голосуйте!
Узнайте, что выбрали другие.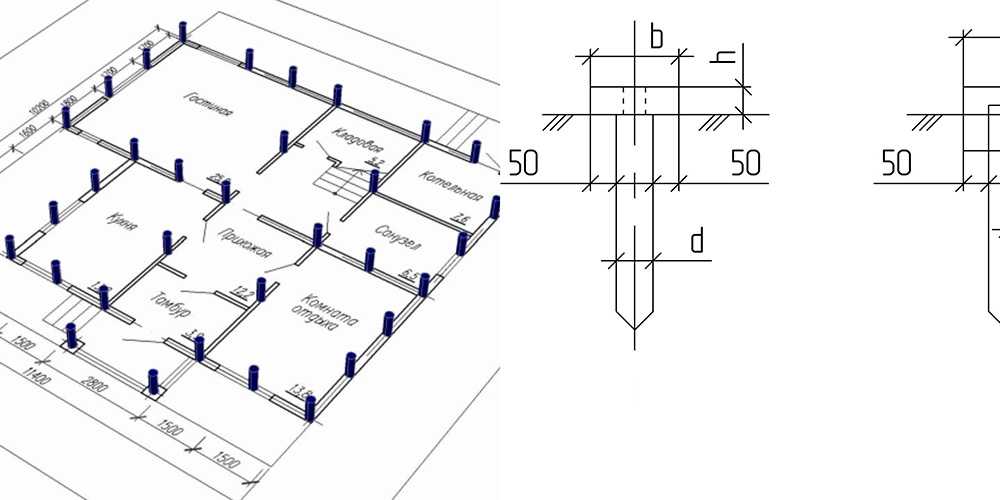
Фундамент для дома на пучинистых грунтах?
Смотреть! — все опросы
Опубликовано Автор Igor PazdnikovРубрики Фундамент ленточный, Фундамент теплоизолированный, Фундаменты — выборПостроили дешевый дом своими руками
Калькулятор расчета количества винтовых свай
Калькулятор
Сторона А Менее 3м3 м4 м5 м6 м7 м8 м9 м10 м11 м12 м13 м14 м15 м
Сторона B Менее 3м3 м4 м5 м6 м7 м8 м9 м10 м11 м12 м13 м14 м15 м
Тип строения БеседкаБытовкаГаражПристройкаБаняДом
Выбор грунта
ПесокСуглинокТорф, толщина 1.5 метраТорф, толщина 3 метраТорф, толщина 5 метраТорф, толщина 7 метраТорф, толщина 9 метраТорф, толщина 10. 5 метра
5 метра
Количество
углов дома
456789101112131415
Планируемая
высота пола
над землей
менее 50 смболее 50 см
Печка в доме
Если вам необходимо рассчитать количество винтовых свай, которые потребуются для строительства фундамента на вашем объекте, вы можете сделать это, не выходя из дома. Вам нужно только знать первичные параметры.
Воспользуйтесь онлайн-калькулятором расчета количества свай на нашем сайте. Помимо необходимого количества, вы сможете узнать также их предварительный диаметр и длину.
Расчет свайного поля онлайн достаточно прост. Для этого не нужно иметь специальное образование и читать литературу. Вам требуется только внести данные в существующие графы.
Расчет количества винтовых свай с помощью калькулятора
- Укажите длину сторон вашего строения, выбрав по форме от 3-х до 15-ти метров.
- Укажите тип строения – дом, гараж, бытовое сооружение и пр.
- Укажите «этажность», если появляются соответствующие графы.

Заполняя графы, обратите внимание на то, что дом с мансардой будет считаться полутора этажным строением. - Выбирайте материал вашего строения.
- Укажите тип грунта на участке.
- Укажите количество углов планируемого дома.
- Укажите высоту цокольного этажа из предложенных вариантов.
- Отметьте, собираете ли вы устанавливать камин/печку.
- Кликнете «Рассчитать».
Через несколько секунд появится результат подсчета необходимого количества свай для вашего объекта.
Рассмотрим пример
Имеется торфяной участок с глубиной торфа 3 метра. Вы решили построить деревянный дом (брус 150х150), площадью 10 на 10 метров. Дом планируется оригинальной формой с девятью углами и мансардой. На высоте 50 см над землей будет расположен пол. Чтобы зимой вам было тепло, было решение установить в доме камин.
После того, как были внесены все данные, калькулятор подсчета количества винтовых свай выдал нам результат – 32 сваи, диаметром 108 мм и длиной в 4,5 метра.
Конечно, данный расчет является предварительным. Он служит ориентиром при планировании бюджета и дальнейшего заказа. Для более точного результата необходим выезд специалиста на объект для детального осмотра участка под планируемую застройку, где будут учтены все факторы.
Самостоятельный расчет на месте
Такой же расчет можно сделать самостоятельно и без использования калькулятора. Полученный таким способом результат в большинстве случаев менее точный. Вам нужно будет определить тип и плотность грунта, проанализировать природный рельеф, определить расстояние, на котором находятся более плотные слои почвы.
Еще одним вариантом, как можно узнать необходимое количество свай – это рассчитать их по плану первого этажа. Здесь вам необходимо посчитать количество углов и стыки внешних стен с несущими перегородками. В указанных местах и должны располагаться сваи, они должны идти по периметру с шагом не более трех метров. Если вы планируете установить камин, то, в зависимости от его веса, вам необходимо установить под него от одной до четырех свай.
Проведите расчет на калькуляторе и по плану первого этажа и сравните результаты.
Расчет осадок в геотехнике
Конструкции своими нагрузками вызывают изменение напряжения в грунте. Чтобы иметь возможность рассчитать осадки в грунте из-за этого изменения напряжения, необходимо знать распространение и распределение напряжений в грунте основания.
Напряжения рассчитаны для так называемого упруго-изотропного полупространства. Трехмерное пространство разделено на две половины горизонтальной бесконечно протяженной плоскостью. Верхняя часть пуста, нижняя часть заполнена однородным материалом, который ведет себя упруго. Двойным перпендикулярным разрезом из этого полупространства вырезается полусрез, который используется для решения всех плоских задач.
Полупространство обладает следующими свойствами:
- собственный вес полупространства не учитывается,
- полупространство однородно, модуль упругости Е и коэффициент Пуассона ν везде одинаковы в одном направлении внутри полупространства,
- полупространство изотропно, механические свойства E и ν одинаковы во всех направлениях,
- полупространство упруго, применим закон Гука.
 Компоненты напряжения могут накладываться линейно
Компоненты напряжения могут накладываться линейно
1.1 Распределение напряжений в грунте
Напряжения в грунте из-за нагрузок распространяются с увеличением глубины. Они оказываются больше под центром структуры, чем по краям. Доступны аналитические решения для различных нагрузок для упругого изотропного полупространства. Различные авторы приводят коэффициенты влияния «i» для расчета напряжений в грунте в зависимости от величины нагрузки, рассматриваемой глубины и расстояния до места приложения нагрузки в виде таблицы.
Для дальнейшего рассмотрения необходимо различать нагрузки от жестких и гибких оснований.
Гибкий фундамент вместе с нагруженным грунтом образует осадочную депрессию. Давление на подстилающий грунт известно и соответствует нагрузке выше (например, засыпанная земляная насыпь, свежезалитый бетон).
Для жестких фундаментов вертикальное смещение фундамента в грунт одинаково для всего фундамента. Поселенческая депрессия больше не может образовываться. Поэтому вертикальные напряжения должны увеличиваться к краям. Теоретически здесь возникают пики напряжений, но они корректируются до уровня предельных напряжений, допустимых для грунта (несущей способности).
Поэтому вертикальные напряжения должны увеличиваться к краям. Теоретически здесь возникают пики напряжений, но они корректируются до уровня предельных напряжений, допустимых для грунта (несущей способности).
1.2 Решение для различных типов нагрузки
Аналитические решения для различных типов нагрузки приведены, среди прочего, в Справочнике по инженерно-геологическим работам. К ним относятся решения для вертикальных и горизонтальных нагрузок, точечных, линейных и площадных нагрузок. Факторы влияния «i» приведены в табличной форме или с помощью уравнений, с помощью которых можно рассчитать напряжения в грунте на разных глубинах и расстояниях от приложения нагрузки. Среди авторов этих таблиц Терзаги, Елинек, Гилбой, Ньюмарк, Буссинеск, Кани и Стейнбреннер.
Часто используется раствор Штейнбреннера. Осадкообразующее напряжение σ z на глубине z при однородной гибкой поверхностной нагрузке с размерами a и b под ее угловой точкой может быть определено как: вне области нагрузки рассчитывается путем деления нагруженной базовой площади на подпрямоугольники таким образом, что рассматриваемая точка (P) является угловой точкой каждого из смежных подпрямоугольников. Затем компоненты напряжения частичных прямоугольников накладываются друг на друга. Таким образом, при нагружении фундамента равномерно распределенным напряжением σ 0 , напряжение σ z,P ниже точки P внутри или снаружи области нагружения определяется с помощью следующих правил наложения: с самыми разнообразными геометриями можно найти в статье глоссария «Расчет осадок с напряжениями по таблице Штейнбреннера».
Затем компоненты напряжения частичных прямоугольников накладываются друг на друга. Таким образом, при нагружении фундамента равномерно распределенным напряжением σ 0 , напряжение σ z,P ниже точки P внутри или снаружи области нагружения определяется с помощью следующих правил наложения: с самыми разнообразными геометриями можно найти в статье глоссария «Расчет осадок с напряжениями по таблице Штейнбреннера».
1.3 Напряжения под жестким основанием
Места, где осадки гибкого и жесткого оснований одинаковы, называются «характерными точками», СР. Поэтому осадки жестких фундаментов также можно определить с помощью расчетов для гибких фундаментов, если напряжения σ z,CP ниже характерные точки известны.
В случае прямоугольника характеристическая точка CP находится на расстоянии 0,74 • a/2 или 0,74 • b/2, в случае круга на расстоянии 0,845 • r от центра, как показано ниже.
Коэффициенты влияния «i» по Кани доступны для расчета напряжений ниже характерной точки. В этих влияющих факторах уже учтено разделение общей площади нагрузки на подпрямоугольники.
В этих влияющих факторах уже учтено разделение общей площади нагрузки на подпрямоугольники.
2.1 Расчет осадки в результате вертикальных напряжений
Осадку s из-за нагрузки грунта можно рассчитать как интеграл деформаций ε по глубине z с помощью следующего уравнения:
Следовательно, для определения осадки необходимо знать:
- ход вертикальных напряжений σ z с глубиной. Осадкообразующее напряжение основания σ 1 = σ 0 — γ • h должно использоваться с учетом снижения напряжения за счет разгрузки земляных работ для глубины заложения фундаментов.
- зависящие от напряжения модули связей слоев грунта
- значение предельной глубины
Для приближенного расчета осадок ход вертикальных (осадкообразующих) напряжений разбивается на учитываемые подслои , так называемые ламели, толщиной Δz и . Для хорошего приближения ход напряжений в этих частичных слоях должен быть примерно линейным. Нагружение поверхности приводит к увеличению напряжения в каждой отдельной ламели. Для расчета коэффициентов осадки используются средние постоянные напряжения σ konst,i определяются для всех i ламелей. Общая осадка равна сумме частичных осадок всех ламелей. Пример с 6 ламелями показан ниже.
Нагружение поверхности приводит к увеличению напряжения в каждой отдельной ламели. Для расчета коэффициентов осадки используются средние постоянные напряжения σ konst,i определяются для всех i ламелей. Общая осадка равна сумме частичных осадок всех ламелей. Пример с 6 ламелями показан ниже.
2.2 Расчет осадок по замкнутым формулам
Метод расчета осадок s от напряжения в основании фундамента σ 0 основан на значениях среднего модуля упругости E m и уравнении
Член σ 0 ⋅b⋅f обозначает интеграл хода напряжения до предельной глубины. ДИН 4019относится к таблицам для определения коэффициента осадки f по Кани. Эта таблица применима для неслоистого грунта со средним стесненным модулем упругости. Если этот метод предполагается использовать для расчета осадок в слоистых грунтах, коэффициенты осадок определяют для каждого отдельного слоя; доля осадки отдельных слоев определяется разницей в коэффициентах осадки:
2.
 3 Предельная глубина
3 Предельная глубинаDIN 4019 ограничивает толщину сжимаемого слоя на глубине, где напряжения, вызывающие осадку σ z становятся менее 20% напряжений вскрышных пород σ 0 . Эта глубина обозначается предельной глубиной, t limit .
За пределами этой предельной глубины компоненты осадки больше не принимаются во внимание, если, например, ниже предельной глубины нет сильно чувствительных к осадке слоев почвы, которые все еще вносят значительный вклад в общую осадку.
В предыдущих главах был представлен расчет общих окончательных расчетов. Однако связные грунты реагируют с замедленной осадкой, которая зависит от зернового состава и содержания воды. Осадки в почвенных слоях состоят из трех компонентов:
S i – это осадки, возникающие мгновенно и не связанные с изменением объема грунта. Почва отклоняется в сторону под нагрузкой. Это часто называют упругой осадкой.
S c называется консолидацией расчетов. Это связано с изменением объема почвы. Вода, присутствующая в связном грунте, выдавливается, и грунт приобретает более высокую плотность. Из-за очень низкой водопроницаемости связных грунтов равновесие давления зерен на зерна не может установиться сразу после загрузки, но в процессе выдавливания воды это равновесие установится по мере уменьшения содержания воды. Таким образом, со временем избыточное поровое давление воды, создаваемое нагрузкой, будет уменьшаться. Таким образом, осадки образуются за счет снижения избыточного порового давления воды. С c также называют первичным расчетом. В несвязных грунтах первичные осадки происходят в момент времени t = 0 из-за высокой водопроницаемости.
Это связано с изменением объема почвы. Вода, присутствующая в связном грунте, выдавливается, и грунт приобретает более высокую плотность. Из-за очень низкой водопроницаемости связных грунтов равновесие давления зерен на зерна не может установиться сразу после загрузки, но в процессе выдавливания воды это равновесие установится по мере уменьшения содержания воды. Таким образом, со временем избыточное поровое давление воды, создаваемое нагрузкой, будет уменьшаться. Таким образом, осадки образуются за счет снижения избыточного порового давления воды. С c также называют первичным расчетом. В несвязных грунтах первичные осадки происходят в момент времени t = 0 из-за высокой водопроницаемости.
Вторичные осадки S s вызываются процессами ползучести в грунте, а также явлениями длительной вязкотекучести зернистой структуры. На временной диаграмме видно, что вторичные поселения неуклонно растут после первичных поселений. Таким образом, линия расчетов по времени не приближается асимптотически к горизонтальной линии.
Сразу после непосредственного расчета S и (t = 0) начинается процесс консолидации, растут расчеты консолидации S c . Переход от первичных и вторичных расчетов определяется — в логарифмическом масштабе — пересечением касательной к точке поворота временной расчетной линии для первичного расчета и продолжением прямой линии, описывающей вторичные расчеты, как показано на следующий рисунок.
По Терзаги (1923), дифференциальное уравнение, описывающее процесс одномерной консолидации, имеет вид:
Это уравнение представляет собой линейное и однородное дифференциальное уравнение в частных производных 2 -го -го порядка. Член c v является так называемым коэффициентом консолидации. При проницаемости грунта k f , собственном весе воды γ w и условном модуле E s получается: t) — функция, зависящая только от времени, а ψ(z) — функция, зависящая только от глубины.
Разделяет дифференциальное уравнение в частных производных на два обыкновенных дифференциальных уравнения. Для решения необходимы начальное условие (изохрона при t = 0) и два однородных граничных условия (условия дренирования). После некоторых преобразований получаются два обыкновенных дифференциальных уравнения
Для решения необходимы начальное условие (изохрона при t = 0) и два однородных граничных условия (условия дренирования). После некоторых преобразований получаются два обыкновенных дифференциальных уравнения
, которые имеют следующие решения:
Для решения в эти уравнения необходимо включить граничные условия обезвоживания, чтобы можно было определить константы C1-C3. С помощью полученных уравнений для избыточного порового давления воды Δu как функции времени и глубины z можно рассчитать изохроны для различных начальных и граничных условий. Они доступны в виде графиков во многих стандартных учебниках.
3.1 Степень консолидации
Первичная осадка связного грунта s(t) определяется объемом выжатой воды. Они стремятся к предельному значению s(t = ∞), которое представляет собой общий окончательный расчет. Их соотношение называется степенью консолидации u K .
с
дает:
Наглядно, степень консолидации u K представляет собой отношение заштрихованной (белой) площади F σ'(z,t) как эффективное напряжение в момент времени «t» к общая площадь 1234 как эффективное напряжение в момент времени t = ∞. В качестве примера здесь показан слой глины, подлежащий осушению двухходовым дренажем.
В качестве примера здесь показан слой глины, подлежащий осушению двухходовым дренажем.
Для примера, показанного насыпи длиной 100 м и шириной 35 м с высотой 5 м над поверхностью земли, в следующем видео показано, как можно выполнить анализ осадки с помощью компьютерной программы GGU-SETTLE. Для этого примера упрощенно предполагается, что показанная стратификация грунта не меняется вдоль продольной оси насыпи.
Для показанного примера слоя глины толщиной 8 м, нагруженного неограниченной поверхностной нагрузкой p = 25 кН/м², время для степени уплотнения U k = 85 % и соответствующую осадку поверхности грунта определяют в соответствии с теорией одномерного уплотнения с использованием компьютерной программы GGU-CONSOLIDATE.
Все тексты, изображения и медиафайлы, перечисленные здесь, защищены авторским правом и являются интеллектуальной собственностью Civilserve GmbH. Использование разрешено только при наличии соответствующей ссылки и ссылки на этот источник.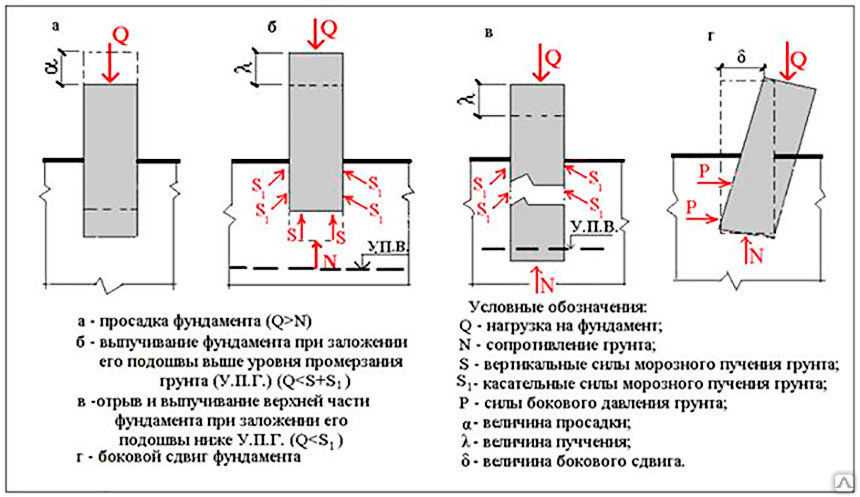
КАК РАССЧИТАТЬ НЕСУЩУЮ СПОСОБНОСТЬ ГРУНТА ИЗ ИСПЫТАНИЙ НА НАГРУЗКУ ПЛИТЫ?
Сурьяканта | 8 ноября 2015 г. | Фонд, Геотехнический, Как | 34 комментария
Испытание плитой под нагрузкой — это полевое испытание, которое обычно используется для определения несущей способности и осадки грунта при заданных условиях нагрузки.
В этом испытании квадратная или круглая жесткая пластина стандартного размера (обычно 300 мм2 для квадратной или 300 мм в диаметре для круглой) помещается на уровне фундамента, и нагрузка прикладывается поэтапно. Затем фиксируют осадку плиты, соответствующую каждому приращению нагрузки, для расчета несущей способности грунта.
Чтобы узнать подробную процедуру проверки, нажмите на ссылку, указанную ниже.
Как выполнить тест на нагрузку плиты на месте?
Весь процесс расчета несущей способности грунта с использованием данных испытаний на нагрузку плиты состоит из следующих 4 основных этапов.
- Шаг 1 (построение кривой осадки нагрузки)
- Шаг 2 (Определение предельной несущей способности)
- Шаг 3 (Расчет безопасной несущей способности)
- Этап 4 (Расчет осадки предлагаемого фундамента)
1.
 Шаг 1 (построение кривой стабилизации нагрузки)
Шаг 1 (построение кривой стабилизации нагрузки)После выполнения испытания на нагрузку пластины постройте кривую стабилизации нагрузки (см. рис. 1) в арифметическом масштабе с приложенным давлением в кН/м 2 по оси абсцисс и соответствующий расчет (в мм) по оси у .
В зависимости от типа грунта под испытательной пластиной кривая установления нагрузки может быть четырех различных типов, как показано ниже.
Рис-1 Типы кривых оседания нагрузкиКривая A: Эта типовая кривая получена в случае рыхлого до среднесвязного грунта (т.е. 15 < N < 30 ). Этот тип кривой не показывает четкой точки отказа.
Кривая B: Эта типовая кривая получена для связного грунта . По мере увеличения нагрузки кривая наклоняется к кривой осадки.
Кривая C: Эта типовая кривая получена для частично связного грунта (т. е. грунта C-phi) . Этот тип кривой также не показывает четкой точки отказа.
е. грунта C-phi) . Этот тип кривой также не показывает четкой точки отказа.
Кривая D: Эта типовая кривая получена для плотного несвязного грунта (т.е. N > 30) . Этот тип кривой распространен в случае плотных отложений песка или гравия.
2. Шаг 2 (Определение предельной несущей способности)
После построения кривой расчета нагрузки следующим шагом является определение точки отказа на кривой расчета нагрузки.
В случае кривой B и D , точку отказа можно легко определить по резкому падению кривой. Или начертите две касательные линии от начального прямого участка кривой и конечного прямого участка кривой. Точка, в которой эти две касательные пересекаются, называется точкой отказа . Давление, соответствующее этой точке, называется предельной несущей способностью грунта.
Но в случае кривой A & C трудно найти четкую точку отказа на кривой расчета нагрузки. Чтобы преодолеть эту проблему, ученый Abbet ввел еще один метод построения кривой расчета нагрузки. В соответствии с его методом логарифмическая диаграмма строится с осадкой по оси абсцисс и соответствующей интенсивностью давления по оси ординат. Такое построение даст две прямые линии, пересечение которых и будет считаться точкой отказа. Найдите соответствующее значение давления в точке разрушения. Это считается предельной несущей способностью грунта.
Чтобы преодолеть эту проблему, ученый Abbet ввел еще один метод построения кривой расчета нагрузки. В соответствии с его методом логарифмическая диаграмма строится с осадкой по оси абсцисс и соответствующей интенсивностью давления по оси ординат. Такое построение даст две прямые линии, пересечение которых и будет считаться точкой отказа. Найдите соответствующее значение давления в точке разрушения. Это считается предельной несущей способностью грунта.
3. Шаг 3 (Расчет безопасной несущей способности)
Чтобы рассчитать безопасную несущую способность грунта, разделите предельную несущую способность грунта на подходящий коэффициент запаса прочности.
Безопасная несущая способность грунта = Предельная несущая способность / Коэффициент запаса прочности
Обычно используемые значения коэффициента запаса прочности: 2 , 2,5 или 3 в зависимости от состояния площадки и важности сооружения.
4. Этап 4 (Расчет осадки предлагаемого фундамента)
Следующая формула, предложенная Terzaghi и Peck , используется для расчета осадки фундамента для гранулированного грунта .
S f = S p {[B*(B p +0,3)] / [B p *(B+0,3)]} 2
3 90 Для 6 глины можно использовать следующее уравнение.
S f = S p *(B/B p )
Где,
S P = расселение пластины, мм
S F = Settlemnt of Feting, MM
B P = ширина или диапазон пластины, M
9002 B = ширина или диапазона, M 9002 B = ширина или диапазона. м Для расчета осадки фундамента заданного размера, подвергающегося заданной нагрузке , сначала рассчитайте соответствующую интенсивность нагрузки, разделив площадь основания на нагрузку, т. е.
е.
Интенсивность нагрузки = нагрузка (кН) / Площадь основания (м 2 )
Затем из кривой осадки нагрузки, построенной с использованием данных PLT, найдите осадку плиты, соответствующую расчетной интенсивности нагрузки, и используйте это значение осадки в формуле для расчета осадки фундамента.
Было проведено испытание на нагрузку плиты размером 0,75 м * 0,75 м на однородном слое песка, и были получены следующие данные:
Рассчитайте безопасную несущую способность грунта, приняв коэффициент запаса 2,5.
Расчет осадки квадратного фундамента размером 2 м x 2 м при безопасной несущей способности
Ответ
Расчет безопасной несущей способности
Из кривой расчета нагрузки (см.


 Компоненты напряжения могут накладываться линейно
Компоненты напряжения могут накладываться линейно