Расчет нагрузки на фундамент калькулятор онлайн: Калькулятор Вес-Дома-Онлайн v.1.0 — Сбор нагрузок на фундамент
Расчет фундамента калькулятор
Завод быстровозводимых зданий. Проектирование строительство зданий, ангаров, складов, магазинов / Это интересно
03.09.2018
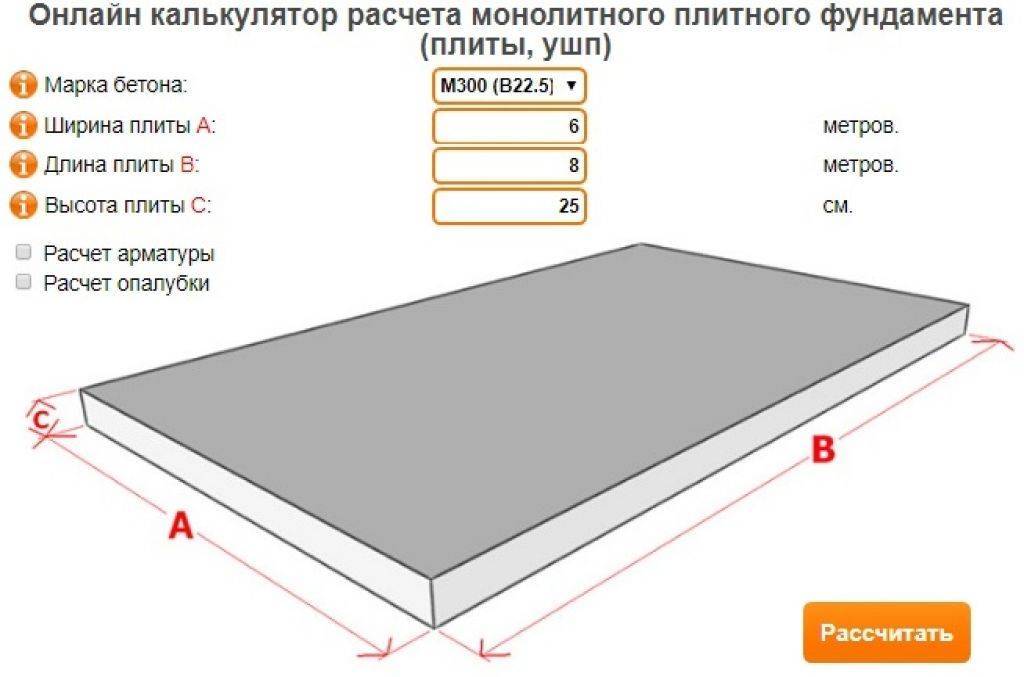
Расчет фундамента, калькулятор которого учитывает разные показатели, понадобится нам при возведении здания или сооружения. Поэтому важно научиться его правильно формировать. Эта информация будет ценной только для тех, кому она по-настоящему интересна.
Производить расчет фундамента на калькуляторе можно при помощи специалистов или же самостоятельно в онлайн режиме. Рассмотрим самое главное, не меняя методов онлайн расчетов и не тестируя способы обмена идей на деньги. Все дело в том, что в онлайн режиме расчет фундамента калькулятор производит бесплатно. Проектировщик, подрядчик по-прежнему рекомендуют учитывать их советы, повышать эффективность и инвестиционную привлекательность проекта. Разумеется с их помощью. А вот пользоваться онлайн калькулятором пользователь может и без них. Что тоже очень удобно.
Чтобы решить проблему и достучаться до клиента, мы выстраиваем две схемы расчетов — сначала подкидываем идею с онлайн сервисом, а затем обрабатываем полученные результаты и формируем сметный расчет фундамента, калькулятор же необходим, в этом случае, для подтверждения полученных сумм.
Чтобы начать строительство быстровозводимого здания нужно спроектировать фундамент, а затем вычислить количество строительных материалов, необходимых для его возведения. В нашем случае расчет фундамента калькулятор сделает, то есть вычислит количество бетона для создания фундамента. Но после определения типа и различных параметров, по которым в дальнейшем вычисляется нужное количество бетона.
Какой же расчет фундамента калькулятор нам предлагает в онлайн режиме и что в него входит? В него включены:
- расчеты нагрузки,
- объем фундаментного котлована,
- подсказки, которые необходимо учитывать при создании проекта фундамента.
В настоящее время онлайн калькуляторы являются ключевыми инструментами, которые выполняют функцию, связанную с управлением проектом в сфере финансов.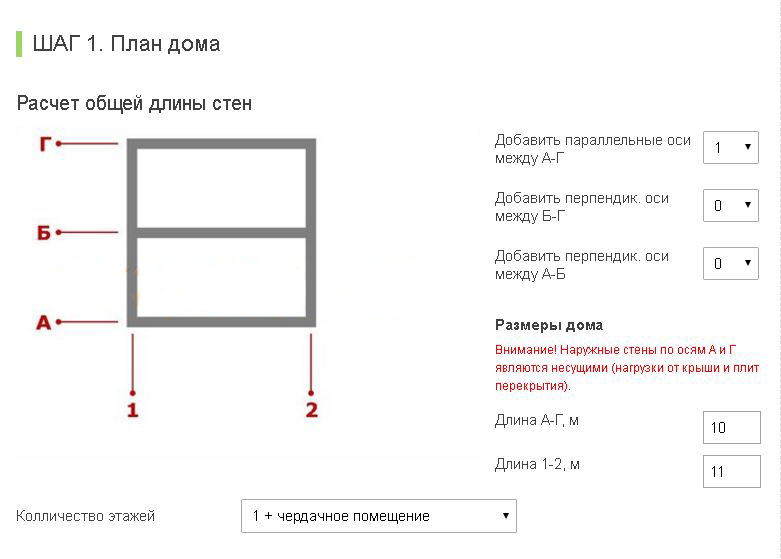 Поэтому перед тем как переходить к сделке, рекомендуем произвести расчет фундамента на калькуляторе самостоятельно.
Поэтому перед тем как переходить к сделке, рекомендуем произвести расчет фундамента на калькуляторе самостоятельно.
Мы строим быстровозводимые здания из металлоконструкций собственного производства и используем в своих проектах столбчатый или свайный фундаменты.
Чтобы определить нужное количество бетона для столбчатого фундамента, необходимо знать такие параметры, как площадь поперечного сечения и высота столба. Формула нахождения поперечного сечения круга следующая: S=3.14*R2, где R – радиус круга. Если поперечное сечение столба, к примеру, будет диаметром 15 сантиметров, то расчет окажется следующим: 3,14м2*0,075м2=0,2355 м2. Аналогично производит расчет фундамента калькулятор для столба высотой 1,5 метра. Его объем будет равен 0,2355*1,5=0,353 м3. Необходимое количество столбов онлайн калькулятор сможет вычислить еще быстрей. После чего формируются остальные вычисления, и определяется количество арматуры и вязальной проволоки.
- Вы можете выбрать более удобный способ вычислений и оставить заявку на расчеты фундамента нашему менеджеру по телефону или письменно.
 После того, как все расчеты будут сформированы, мы с вами обязательно свяжемся!
После того, как все расчеты будут сформированы, мы с вами обязательно свяжемся!
Если вы собираетесь производить расчет фундамента, калькулятор, находящийся в онлайн сервисе расчетов всегда к вашим услугам! Также вы можете воспользоваться более точными расчетами и обратиться за помощью к консультантам компании по телефону 391 251-82-82!
Вернуться к списку
Расчет нагрузки на фундамент — Самая лучшая система расчета нагрузки
Содержание
- 1 Определение глубины заложения фундамента
- 2 Расчет нагрузки кровли
- 3 Расчет снеговой нагрузки
- 4 Расчет нагрузки перекрытий
- 5 Расчет нагрузки стен
- 6 Предварительный расчет нагрузки фундамента на грунт
- 7 Расчет общей нагрузки на 1 м2 грунта
Расчет нагрузки на фундамент необходим для правильного выбора его геометрических размеров и площади подошвы фундамента. В конечном итоге, от правильного расчета фундамента зависит прочность и долговечность всего здания.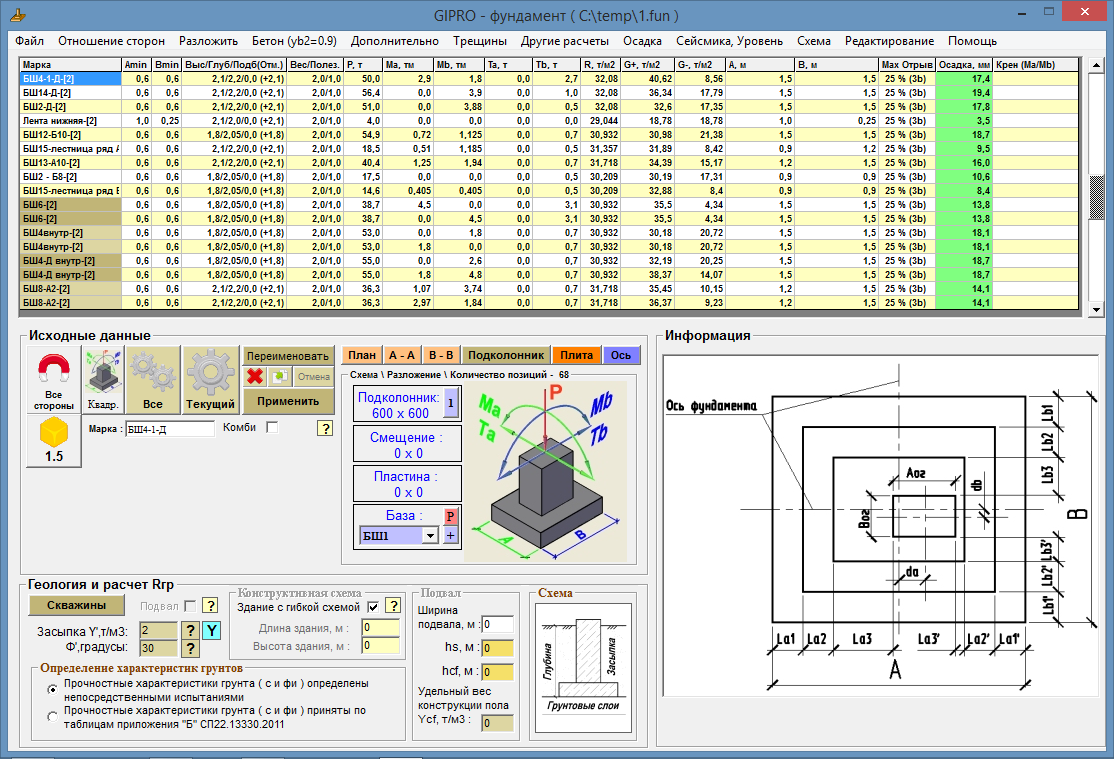 Расчет сводится к определению нагрузки на квадратный метр грунта и сравнению его с допустимыми значениями.
Расчет сводится к определению нагрузки на квадратный метр грунта и сравнению его с допустимыми значениями.
Для расчета необходимо знать:
- Регион, в котором строится здание;
- Тип почвы и глубину залегания грунтовых вод;
- Материал, из которого будут выполнены конструктивные элементы здания;
- Планировку здания, этажность, тип кровли.
Исходя из требуемых данных, расчет фундамента или его окончательная проверка производится после проектирования строения.
Попробуем рассчитать нагрузку на фундамент для одноэтажного дома, выполненного из полнотелого кирпича сплошной кладки, с толщиной стен 40 см. Габариты дома – 10х8 метров. Перекрытие подвального помещения – железобетонные плиты, перекрытие 1 этажа – деревянное по стальным балкам. Крыша двускатная, покрытая металлочерепицей, с уклоном 25 градусов. Регион – Подмосковье, тип грунта – влажные суглинки с коэффициентом пористости 0,5. Фундамент выполняется из мелкозернистого бетона, толщина стенки фундамента для расчета равна толщине стены.
Определение глубины заложения фундамента
Глубина заложения зависит от глубины промерзания и типа грунта. В таблице приведены справочные величины глубины промерзания грунта в различных регионах.
Таблица 1 – Справочные данные о глубине промерзания грунта
Справочная таблица для определения глубины заложения фундамента по регионам
Глубина заложения фундамента в общем случае должна быть больше глубины промерзания, но есть исключения, обусловленные типом грунта, они указаны в таблице 2.
Таблица 2 – Зависимость глубины заложения фундамента от типа грунта
Зависимость глубины заложения фундамента от типа грунта
Глубина заложения фундамента необходима для последующего расчета нагрузки на почву и определения его размеров.
Определяем глубину промерзания грунта по таблице 1. Для Москвы она составляет 140 см. По таблице 2 находим тип почвы – суглинки. Глубина заложения должна быть не менее расчетной глубины промерзания.
Исходя из этого глубина заложения фундамента для дома выбирается 1,4 метра.
Расчет нагрузки кровли
Нагрузка кровли распределяется между теми сторонами фундамента, на которые через стены опирается стропильная система. Для обычной двускатной крыши это обычно две противоположные стороны фундамента, для четырехскатной – все четыре стороны. Распределенная нагрузка кровли определяется по площади проекции крыши, отнесенной к площади нагруженных сторон фундамента, и умноженной на удельный вес материала.
Таблица 3 – Удельный вес разных видов кровли
Справочная таблица – Удельный вес разных видов кровли
- Определяем площадь проекции кровли. Габариты дома – 10х8 метров, площадь проекции двускатной крыши равна площади дома: 10·8=80 м2.
- Длина фундамента равна сумме двух длинных его сторон, так как двускатная крыша опирается на две длинные противоположные стороны. Поэтому длину нагруженного фундамента определяем как 10·2=20 м.
- Площадь нагруженного кровлей фундамента толщиной 0,4 м: 20·0,4=8 м2.

- Тип покрытия – металлочерепица, угол уклона – 25 градусов, значит расчетная нагрузка по таблице 3 равна 30 кг/м2.
- Нагрузка кровли на фундамент равна 80/8·30 = 300 кг/м2.
Расчет снеговой нагрузки
Снеговая нагрузка передается на фундамент через кровлю и стены, поэтому нагружены оказываются те же стороны фундамента, что и при расчете крыши. Вычисляется площадь снежного покрова, равная площади крыши. Полученное значение делят на площадь нагруженных сторон фундамента и умножают на удельную снеговую нагрузку, определенную по карте.
Таблица – расчет снеговой нагрузки на фундамент
- Длина ската для крыши с уклоном в 25 градусов равна (8/2)/cos25° = 4,4 м.
- Площадь крыши равна длине конька умноженной на длину ската (4,4·10)·2=88 м2.
- Снеговая нагрузка для Подмосковья по карте равна 126 кг/м2. Умножаем ее на площадь крыши и делим на площадь нагруженной части фундамента 88·126/8=1386 кг/м2.

Расчет нагрузки перекрытий
Перекрытия, как и крыша, опираются обычно на две противоположные стороны фундамента, поэтому расчет ведется с учетом площади этих сторон. Площадь перекрытий равна площади здания. Для расчета нагрузки перекрытий нужно учитывать количество этажей и перекрытие подвала, то есть пол первого этажа.
Площадь каждого перекрытия умножают на удельный вес материала из таблицы 4 и делят на площадь нагруженной части фундамента.
Таблица 4 – Удельный вес перекрытий
Таблица расчет веса перекрытий и их нагрузка на фундамент
- Площадь перекрытий равна площади дома – 80 м2. В доме два перекрытия: одно из железобетона и одно – деревянное по стальным балкам.
- Умножаем площадь железобетонного перекрытия на удельный вес из таблицы 4: 80·500=40000 кг.
- Умножаем площадь деревянного перекрытия на удельный вес из таблицы 4: 80·200=16000 кг.
- Суммируем их и находим нагрузку на 1 м2 нагружаемой части фундамента: (40000+16000)/8=7000 кг/м2.

Расчет нагрузки стен
Нагрузка стен определяется как объем стен, умноженный на удельный вес из таблицы 5, полученный результат делят на длину всех сторон фундамента, умноженную на его толщину.
Таблица 5 – Удельный вес материалов стен
Таблица – Удельный вес стен
- Площадь стен равна высоте здания, умноженной на периметр дома: 3·(10·2+8·2)=108 м2.
- Объем стен – это площадь, умноженная на толщину, он равен 108·0,4=43,2 м3.
- Находим вес стен, умножив объем на удельный вес материала из таблицы 5: 43,2·1800=77760 кг.
- Площадь всех сторон фундамента равна периметру, умноженному на толщину: (10·2+8·2)·0,4=14,4 м2.
- Удельная нагрузка стен на фундамент равна 77760/14,4=5400 кг.
Предварительный расчет нагрузки фундамента на грунт
Нагрузку фундамента на грунт расчитывают как произведение объема фундамента на удельную плотность материала, из которого он выполнен, разделенное на 1 м2 площади его основания. Объем можно найти как произведение глубины заложения на толщину фундамента. Толщину фундамента принимают при предварительном расчете равной толщине стен.
Объем можно найти как произведение глубины заложения на толщину фундамента. Толщину фундамента принимают при предварительном расчете равной толщине стен.
Таблица 6 – Удельная плотность материалов фундамента
Таблица – удельная плотность материало для грунта
- Площадь фундамента – 14,4 м2, глубина заложения – 1,4 м. Объем фундамента равен 14,4·1,4=20,2 м3.
- Масса фундамента из мелкозернистого бетона равна: 20,2·1800=36360 кг.
- Нагрузка на грунт: 36360/14,4=2525 кг/м2.
Расчет общей нагрузки на 1 м
2 грунтаРезультаты предыдущих расчетов суммируются, при этом вычисляется максимальная нагрузка на фундамент, которая будет больше для тех его сторон, на которые опирается крыша.
Условное расчетное сопротивление грунта R0 определяют по таблицам СНиП 2.02.01—83 «Основания зданий и сооружений».
- Суммируем вес крыши, снеговую нагрузку, вес перекрытий и стен, а также фундамента на грунт: 300+1386+7000+5400+2525=16 611 кг/м2=17 т/м2.

- Определяем условное расчетное сопротивление грунта по таблицам СНиП 2.02.01—83. Для влажных суглинков с коэффициентом пористости 0,5 R0 составляет 2,5 кг/см2, или 25 т/м2.
Из расчета видно, что нагрузка на грунт находится в пределах допустимой.
Расчет осадок в геотехнике
Конструкции своими нагрузками вызывают изменение напряжения в грунте. Чтобы иметь возможность рассчитать осадки в грунте из-за этого изменения напряжения, необходимо знать распространение и распределение напряжений в грунте основания.
Напряжения рассчитаны для так называемого упруго-изотропного полупространства. Трехмерное пространство разделено на две половины горизонтальной бесконечно протяженной плоскостью. Верхняя часть пуста, нижняя часть заполнена однородным материалом, который ведет себя упруго. Двойным перпендикулярным разрезом из этого полупространства вырезается полусрез, который используется для решения всех плоских задач.
Полупространство обладает следующими свойствами:
- собственный вес полупространства не учитывается,
- полупространство однородно, модуль упругости Е и коэффициент Пуассона ν везде одинаковы в одном направлении внутри полупространства,
- полупространство изотропно, механические свойства E и ν одинаковы во всех направлениях,
- полупространство упруго, применим закон Гука.
 Компоненты напряжения могут накладываться линейно
Компоненты напряжения могут накладываться линейно
1.1 Распределение напряжений в грунте
Напряжения в грунте из-за нагрузок распространяются с увеличением глубины. Они оказываются больше под центром структуры, чем по краям. Доступны аналитические решения для различных нагрузок для упругого изотропного полупространства. Различные авторы приводят коэффициенты влияния «i» для расчета напряжений в грунте в зависимости от величины нагрузки, рассматриваемой глубины и расстояния до места приложения нагрузки в виде таблицы.
Для дальнейшего рассмотрения необходимо различать нагрузки от жестких и гибких оснований.
Гибкий фундамент вместе с нагруженным грунтом образует осадочную депрессию. Давление на подстилающий грунт известно и соответствует нагрузке выше (например, засыпанная земляная насыпь, свежезалитый бетон).
Для жестких фундаментов вертикальное смещение фундамента в грунт одинаково для всего фундамента. Поселенческая депрессия больше не может образовываться. Поэтому вертикальные напряжения должны увеличиваться к краям. Теоретически здесь возникают пики напряжений, но они корректируются до уровня предельных напряжений, допустимых для грунта (несущей способности).
Поэтому вертикальные напряжения должны увеличиваться к краям. Теоретически здесь возникают пики напряжений, но они корректируются до уровня предельных напряжений, допустимых для грунта (несущей способности).
1.2 Решение для различных типов нагрузки
Аналитические решения для различных типов нагрузки приведены, среди прочего, в Справочнике по инженерно-геологическим работам. К ним относятся решения для вертикальных и горизонтальных нагрузок, точечных, линейных и площадных нагрузок. Факторы влияния «i» приведены в табличной форме или с помощью уравнений, с помощью которых можно рассчитать напряжения в грунте на разных глубинах и расстояниях от приложения нагрузки. Среди авторов этих таблиц Терзаги, Елинек, Гилбой, Ньюмарк, Буссинеск, Кани и Стейнбреннер.
Часто используется раствор Штейнбреннера. Осадкообразующее напряжение σ z на глубине z при однородной гибкой поверхностной нагрузке с размерами a и b под ее угловой точкой может быть определено как: вне области нагрузки рассчитывается путем деления нагруженной базовой площади на подпрямоугольники таким образом, что рассматриваемая точка (P) является угловой точкой каждого из смежных подпрямоугольников. Затем компоненты напряжения частичных прямоугольников накладываются друг на друга. Таким образом, при нагружении фундамента равномерно распределенным напряжением σ 0 , напряжение σ z,P ниже точки P внутри или снаружи области нагружения определяется с помощью следующих правил наложения: с самыми разнообразными геометриями можно найти в статье глоссария «Расчет осадок с напряжениями по таблице Штейнбреннера».
Затем компоненты напряжения частичных прямоугольников накладываются друг на друга. Таким образом, при нагружении фундамента равномерно распределенным напряжением σ 0 , напряжение σ z,P ниже точки P внутри или снаружи области нагружения определяется с помощью следующих правил наложения: с самыми разнообразными геометриями можно найти в статье глоссария «Расчет осадок с напряжениями по таблице Штейнбреннера».
1.3 Напряжения под жестким основанием
Места, где осадки гибкого и жесткого оснований одинаковы, называются «характерными точками», СР. Поэтому осадки жестких фундаментов также можно определить с помощью расчетов для гибких фундаментов, если напряжения σ z,CP ниже характерные точки известны.
В случае прямоугольника характеристическая точка CP находится на расстоянии 0,74 • a/2 или 0,74 • b/2, в случае круга на расстоянии 0,845 • r от центра, как показано ниже.
Коэффициенты влияния «i» по Кани доступны для расчета напряжений ниже характерной точки. В этих влияющих факторах уже учтено разделение общей площади нагрузки на подпрямоугольники.
В этих влияющих факторах уже учтено разделение общей площади нагрузки на подпрямоугольники.
2.1 Расчет осадки в результате вертикальных напряжений
Осадку s из-за нагрузки грунта можно рассчитать как интеграл деформаций ε по глубине z с помощью следующего уравнения:
Следовательно, для определения осадки необходимо знать:
- ход вертикальных напряжений σ z с глубиной. Осадкообразующее напряжение основания σ 1 = σ 0 — γ • h должно использоваться с учетом снижения напряжения за счет разгрузки земляных работ для глубины заложения фундаментов.
- зависящие от напряжений модули связей слоев грунта
- значение предельной глубины
Для ориентировочного расчета осадок ход вертикальных (осадкообразующих) напряжений разбивается на учитываемые подслои , так называемые ламели, толщиной Δz и . Для хорошего приближения ход напряжений в этих частичных слоях должен быть примерно линейным. Нагружение поверхности приводит к увеличению напряжения в каждой отдельной ламели. Для расчета коэффициентов осадки используются средние постоянные напряжения σ konst,i определяются для всех i ламелей. Общая осадка равна сумме частичных осадок всех ламелей. Пример с 6 ламелями показан ниже.
Нагружение поверхности приводит к увеличению напряжения в каждой отдельной ламели. Для расчета коэффициентов осадки используются средние постоянные напряжения σ konst,i определяются для всех i ламелей. Общая осадка равна сумме частичных осадок всех ламелей. Пример с 6 ламелями показан ниже.
2.2 Расчет осадок по замкнутым формулам
Метод расчета осадок s от напряжения в основании фундамента σ 0 основан на значениях среднего модуля упругости E m и уравнении
Член σ 0 ⋅b⋅f обозначает интеграл хода напряжения до предельной глубины. ДИН 4019относится к таблицам для определения коэффициента осадки f по Кани. Эта таблица применима для неслоистого грунта со средним стесненным модулем упругости. Если этот метод предполагается использовать для расчета осадок в слоистых грунтах, коэффициенты осадок определяют для каждого отдельного слоя; доля осадки отдельных слоев определяется разницей в коэффициентах осадки:
2.
 3 Предельная глубина
3 Предельная глубинаDIN 4019 ограничивает толщину сжимаемого слоя на глубине, где напряжения, вызывающие осадку σ z становятся менее 20% напряжений вскрышных пород σ 0 . Эта глубина обозначается предельной глубиной, t limit .
За пределами этой предельной глубины компоненты осадки больше не принимаются во внимание, если, например, ниже предельной глубины нет сильно чувствительных к осадке слоев почвы, которые все еще вносят значительный вклад в общую осадку.
В предыдущих главах был представлен расчет общих окончательных расчетов. Однако связные грунты реагируют с замедленной осадкой, которая зависит от зернового состава и содержания воды. Осадки в почвенных слоях состоят из трех компонентов:
S i – это осадки, возникающие мгновенно и не связанные с изменением объема грунта. Почва отклоняется в сторону под нагрузкой. Это часто называют упругой осадкой.
S c называется консолидацией расчетов. Это связано с изменением объема почвы. Вода, присутствующая в связном грунте, выдавливается, и грунт приобретает более высокую плотность. Из-за очень низкой водопроницаемости связных грунтов равновесие давления зерен на зерна не может установиться сразу после загрузки, но в процессе выдавливания воды это равновесие установится по мере уменьшения содержания воды. Таким образом, со временем избыточное поровое давление воды, создаваемое нагрузкой, будет уменьшаться. Таким образом, осадки образуются за счет снижения избыточного порового давления воды. С c также называют первичным расчетом. В несвязных грунтах первичные осадки происходят в момент времени t = 0 из-за высокой водопроницаемости.
Это связано с изменением объема почвы. Вода, присутствующая в связном грунте, выдавливается, и грунт приобретает более высокую плотность. Из-за очень низкой водопроницаемости связных грунтов равновесие давления зерен на зерна не может установиться сразу после загрузки, но в процессе выдавливания воды это равновесие установится по мере уменьшения содержания воды. Таким образом, со временем избыточное поровое давление воды, создаваемое нагрузкой, будет уменьшаться. Таким образом, осадки образуются за счет снижения избыточного порового давления воды. С c также называют первичным расчетом. В несвязных грунтах первичные осадки происходят в момент времени t = 0 из-за высокой водопроницаемости.
Вторичные осадки S s вызываются процессами ползучести в грунте, а также явлениями длительной вязкотекучести зернистой структуры. На временной диаграмме видно, что вторичные поселения неуклонно растут после первичных поселений. Таким образом, линия расчетов по времени не приближается асимптотически к горизонтальной линии.
Сразу после непосредственного расчета S и (t = 0) начинается процесс консолидации, растут расчеты консолидации S c . Переход от первичных и вторичных расчетов определяется — в логарифмическом масштабе — пересечением касательной к точке поворота временной расчетной линии для первичного расчета и продолжением прямой линии, описывающей вторичные расчеты, как показано на следующий рисунок.
По Терзаги (1923), дифференциальное уравнение, описывающее процесс одномерной консолидации, имеет вид:
Это уравнение представляет собой линейное и однородное дифференциальное уравнение в частных производных 2 -го -го порядка. Член c v является так называемым коэффициентом консолидации. При проницаемости грунта k f , собственном весе воды γ w и условном модуле E s получается: t) — функция, зависящая только от времени, а ψ(z) — функция, зависящая только от глубины.
Разделяет дифференциальное уравнение в частных производных на два обыкновенных дифференциальных уравнения. Для решения необходимы начальное условие (изохрона при t = 0) и два однородных граничных условия (условия дренирования). После некоторых преобразований получаются два обыкновенных дифференциальных уравнения
Для решения необходимы начальное условие (изохрона при t = 0) и два однородных граничных условия (условия дренирования). После некоторых преобразований получаются два обыкновенных дифференциальных уравнения
, которые имеют следующие решения:
Для решения в эти уравнения необходимо включить граничные условия обезвоживания, чтобы можно было определить константы C1-C3. С помощью полученных уравнений для избыточного порового давления воды Δu как функции времени и глубины z можно рассчитать изохроны для различных начальных и граничных условий. Они доступны в виде графиков во многих стандартных учебниках.
3.1 Степень консолидации
Первичная осадка связного грунта s(t) определяется объемом выжатой воды. Они стремятся к предельному значению s(t = ∞), которое представляет собой общий окончательный расчет. Их соотношение называется степенью консолидации u K .
с
дает:
Наглядно, степень консолидации u K представляет собой отношение заштрихованной (белой) площади F σ'(z,t) как эффективное напряжение в момент времени «t» к общая площадь 1234 как эффективное напряжение в момент времени t = ∞. В качестве примера здесь показан слой глины, подлежащий осушению двухходовым дренажем.
В качестве примера здесь показан слой глины, подлежащий осушению двухходовым дренажем.
Для примера, показанного насыпи длиной 100 м и шириной 35 м с высотой 5 м над поверхностью земли, в следующем видео показано, как можно выполнить анализ осадки с помощью компьютерной программы GGU-SETTLE. Для этого примера упрощенно предполагается, что показанная стратификация грунта не меняется вдоль продольной оси насыпи.
Для показанного примера слоя глины толщиной 8 м, нагруженного неограниченной поверхностной нагрузкой p = 25 кН/м², время для степени уплотнения U k = 85 % и соответствующую осадку поверхности грунта определяют в соответствии с теорией одномерного уплотнения с использованием компьютерной программы GGU-CONSOLIDATE.
Все тексты, изображения и медиафайлы, перечисленные здесь, защищены авторским правом и являются интеллектуальной собственностью Civilserve GmbH. Использование разрешено только при наличии соответствующей ссылки и ссылки на этот источник.
Несущая способность грунта – типы и расчеты
🕑 Время чтения: 1 минута
Несущая способность грунта определяется как способность грунта выдерживать нагрузки, исходящие от фундамента. Давление, которое грунт может легко выдержать при нагрузке, называется допустимым опорным давлением.
Состав:
- Типы несущей способности грунта
- 1. Предельная несущая способность (qu)
- 2. Чистая предельная несущая способность (qnu)
- 3. Чистая безопасная несущая способность (qns) 9000 9 4. Валовая безопасная несущая способность (qs)
- 5. Чистое безопасное расчетное давление (qnp)
- 6. Чистое допустимое опорное давление (qna)
- 1. Теория несущей способности Терцаги
- 2. Подшипник Хансена теория емкости
Ниже приведены некоторые виды несущей способности грунта:
1.
 Предельная несущая способность (q u )
Предельная несущая способность (q u )2. Чистая предельная несущая способность (q
nu )Пренебрегая давлением вскрыши из предельной несущей способности, мы получим чистую предельную несущую способность.
Где = удельный вес грунта, D f = глубина фундамента
3. Чистая допустимая несущая способность (q
ns )При рассмотрении только разрушения при сдвиге чистая предельная несущая способность делится на определенный коэффициент безопасности, что дает чистую безопасную несущую способность.
q нс = q
Где F = коэффициент безопасности = 3 (обычное значение)
4.
 Полная безопасная несущая способность (q s )
Полная безопасная несущая способность (q s )Когда предельная несущая способность делится на коэффициент безопасности, это дает общую безопасную несущую способность.
q s = q u /F
5. Чистое безопасное расчетное давление (q
np )Давление, которое может нести грунт без превышения допустимой осадки, называется чистым безопасным давлением осадки.
6. Чистое допустимое давление на подшипник (q
na ) Это давление мы можем использовать для проектирования фундаментов. Это равно чистому безопасному давлению на подшипник, если q
Расчет несущей способности
Для расчета несущей способности грунта существует очень много теорий. Но все теории заменены теорией несущей способности Терцаги.
Но все теории заменены теорией несущей способности Терцаги.
1. Теория несущей способности Терцаги
Теория несущей способности Терцаги полезна для определения несущей способности грунтов под ленточным фундаментом. Эта теория применима только к неглубоким основаниям. Он рассмотрел некоторые предположения, которые заключаются в следующем.
- Основание ленточного фундамента черновое.
- Глубина основания меньше или равна его ширине, т. е. мелкое основание.
- Он пренебрег прочностью грунта на сдвиг над основанием фундамента и заменил ее равномерной надбавкой. ( Д ф )
- Нагрузка, действующая на фундамент, распределена равномерно и действует в вертикальном направлении.
- Он предположил, что длина фундамента бесконечна.
- Он рассматривал уравнение Мора-Кулона как определяющий фактор прочности грунта на сдвиг.
Как показано на рисунке выше, AB является основанием фундамента.
Нагрузка от основания x вес клина = пассивное давление + сцепление x CB sin
Где P p = результирующее пассивное давление = (P  Поэтому, Заменив, Итак, в итоге получаем q u = c’N c + y D f N q + 0,5 y B N y 9003 4 Приведенное выше уравнение называется уравнением несущей способности Терцаги. Где q
Поэтому, Заменив, Итак, в итоге получаем q u = c’N c + y D f N q + 0,5 y B N y 9003 4 Приведенное выше уравнение называется уравнением несущей способности Терцаги. Где q
| Нк | № | Нью-Йорк | |
| 0 | 5,7 | 1 | 0 |
| 5 | 7,3 | 1,6 | 0,5 |
| 10 | 9,6 | 2,7 | 1,2 |
| 15 | 12,9 | 4,4 | 2,5 |
| 20 | 17,7 | 7,4 | 5 |
| 25 | 25,1 | 12,7 | 9,7 |
| 30 | 37,2 | 22,5 | 19,7 |
| 35 | 57,8 | 41,4 | 42,4 |
| 40 | 95,7 | 81,3 | 100,4 |
| 45 | 172,3 | 173,3 | 297,5 |
| 50 | 347,5 | 415,1 | 1153,2 |
Наконец, для определения несущей способности под ленточным фундаментом можно использовать
q u = c’N c + D f N q + 0,5 B N 9003 3 года
По модификация приведенного выше уравнения, уравнения для квадратных и круглых фундаментов также приведены и они. Для квадратного метра
Для квадратного метра
q u = 1,2 c’N c + D f N q + 0,4 B N у
Для кругового фундамента
q u = 1,2 c’N c + D f N q + 0,3 B N y
2. Теория несущей способности Хансена
Для связных грунтов значения, полученные по теории несущей способности Терцаги, превышают экспериментальные значения. Но, тем не менее, он показывает те же значения для несвязных грунтов. Поэтому Хансен изменил уравнение, приняв во внимание факторы формы, глубины и наклона. По мнению Хансена
Где Nc, Nq, Ny = коэффициенты несущей способности Хансена
Sc, Sq, Sy = коэффициенты формы
dc, dq, dy = коэффициенты глубины
ic, iq, iy = коэффициенты наклона
Коэффициенты несущей способности рассчитываются по следующим уравнениям. Для различных значений несущей способности Хансена коэффициенты несущей способности рассчитаны в таблице ниже.
Для различных значений несущей способности Хансена коэффициенты несущей способности рассчитаны в таблице ниже.
| Нк | № | Нью-Йорк | |
| 0 | 5,14 | 1 | 0 |
| 5 | 6,48 | 1,57 | 0,09 |
| 10 | 8,34 | 2,47 | 0,09 |
| 15 | 10,97 | 3,94 | 1,42 |
| 20 | 14,83 | 6,4 | 3,54 |
| 25 | 20,72 | 10,66 | 8.11 |
| 30 | 30,14 | 18,40 | 18.08 |
| 35 | 46,13 | 33,29 | 40,69 |
| 40 | 75,32 | 64,18 | 95,41 |
| 45 | 133,89 | 134,85 | 240,85 |
| 50 | 266,89 | 318,96 | 681,84 |
Факторы формы для различных форм фундамента приведены в таблице ниже.
| Форма фундамента | Sc | Кв. | Си |
| Непрерывный | 1 | 1 | 1 |
| Прямоугольный | 1+0,2Б/л | 1+0,2Б/л | 1-0.4Б/л |
| Квадрат | 1,3 | 1,2 | 0,8 |
| Циркуляр | 1,3 | 1,2 | 0,6 |
Факторы глубины учитываются в соответствии со следующей таблицей.
| Факторы глубины | Значения |
| постоянный ток | 1+0,35(Д/Б) |
| дк | 1+0,35(Д/Б) |
| дв | 1,0 |
Аналогично учитываются коэффициенты наклона из таблицы ниже.

 После того, как все расчеты будут сформированы, мы с вами обязательно свяжемся!
После того, как все расчеты будут сформированы, мы с вами обязательно свяжемся! 
 Исходя из этого глубина заложения фундамента для дома выбирается 1,4 метра.
Исходя из этого глубина заложения фундамента для дома выбирается 1,4 метра.



 Компоненты напряжения могут накладываться линейно
Компоненты напряжения могут накладываться линейно