Расчет мелкозаглубленного ленточного фундамента: Мелкозаглубленный ленточный фундамент — расчёт и устройство
Расчет мелко заглубленного ленточного фундамента
РЕКЛАМА
Особенности, преимущества и недостатки мелкозаглубленного ленточного фундамента (МЗЛФ) описаны в статье здесь.
Расчет мелкозаглубленного ленточного фундамента производится в следующей последовательности:
- На основе материалов изысканий определяется несущая способность и степень пучинистости грунта основания.
- Задаются предварительные размеры подошвы фундамента, глубина его заложения, толщина песчаной (песчано-гравийной) подушки (минимум 20 см.). Первоначально ширина подошвы фундамента и толщина подушки, высота ленты задаются исходя из конструктивных соображений.
Производится расчет и проверка фундамента по трем условиям:
b — ширина подошвы фундамента; t — толщина песчаной подушки; 1. Выполняется проверка несущей способности грунта в основании фундамента.
Несущая способность грунта характеризуется величиной расчетного сопротивления грунта — R,
2. При проектировании мелкозаглубленных фундаментов на пучинистых грунтах обязательным является расчет оснований по деформациям пучения грунта. Для этого выполняется расчет деформации морозного пучения грунта и их влияние на фундамент, определяются параметры армирования фундамента, его прогиб (выгиб).
Рассчитываются предельно допустимые для конструкции деформации. При расчётах допускается изгиб (прогиб) ВСЕЙ системы: фундамент — стены — пояс жёсткости
В нормативных документах по строительству указаны предельно — допустимые деформации различных типов зданий.
Например, «несущая стена здания из кирпича или блоков без армирования», допускает относительную деформацию лишь 0,0005. Это значит, что при длине элемента рамы фундамента в 15 м. допускается всего 7,5 мм. абсолютный прогиб (выгиб) такой стены
3. Кроме этого, осуществляется расчёт прочности железобетонной рамы фундамента по напряжениям в арматурных стержнях. Напряжения, возникающие в конструкциях фундамента должны быть меньше напряжений, при которых происходят необратимые процессы потери упругости в арматуре фундамента.
Если первоначально выбранные размеры и параметры армирования фундамента не удовлетворяют хотя-бы одному условию, то размеры меняют и производят повторный расчет.
Неоднократно изменяя размеры (ширину и высоту подушки, ленты, армирование) подбирают оптимальный вариант фундамента, удовлетворяющего всем трем условиям и наименее затратного.
Расчёт воздействия касательных сил морозного пучения не производится из-за малой глубины заложения фундамента и соответственно малой площади соприкосновения боковой поверхности с грунтом.
Советы застройщику:
Не стремитесь сделать фундамент максимально жестким, увеличивая, например, высоту ленты. Это приводит к неоправданному увеличению армирования и росту напряжений. Чем больше высота ленты фундамента, тем выше напряжения в арматуре, тем больше её сечение. В меру гибкий фундамент экономичней и надежней.
Расчет деформации морозного пучения грунта и их влияния на фундамент достаточно сложен. Точность расчетов определяется прежде всего оценкой грунта в основании фундамента. Точная оценка грунта также сложная инженерная задача. К тому же, пучинистые свойства грунта могут со временем меняться (например, при изменении уровня грунтовых вод, временных подтоплений).
Снижение деформаций до допустимого уровня требует затрат на усиление фундамента, цоколя и стен здания.
Ежегодно подвергать дом ломке морозом – согласитесь, на лучшее решение. Теплоизоляция фундамента снимает все эти проблемы и риски. Расчет конструкции теплоизолированного ленточного фундамента мелкого заложения производится по условиям 1 и 3.
Читайте: «Теплоизолированный фундамент — лучший для дома».
Оценку грунтов в основании, расчет фундамента лучше поручить специалистам, особенно для пучинистых грунтов или близком залегании грунтовых вод.
Если рискнете делать это самостоятельно, а также для оценки принятых проектировщиками решений рекомендую использовать программы-калькуляторы.
Прочитав статью «Расчет нагрузок и площади подошвы фундамента» Вы сможете с помощью программы — калькулятора выполнить расчет нагрузки на грунт от веса здания, определить необходимые ширину подошвы фундамента (b) и толщину песчаной подушки (t).
Этого расчета обычно достаточно для выбора конструкции фундамента на непучинистом грунте, фундамента, закладываемого на глубину промерзания (для дома с подвалом) или теплоизолированного фундамента ТФМЗ.
Например, этот онлайн калькулятор МЗЛФ проверяет фундамент по всем трем условиям, правда для конкретного региона. Для проверки по 2-му условию в других регионах программу можно использовать путем изменения коэффициента надежности, изменяя его в соответствии с отличиями глубины промерзания регионов.
Товары для строительства и ремонта
⇆
Профессиональные программы, например BASE — блок расчета фундаментов ( http://www.basegroup.su/index.php?Page=money.html ), требуют для применения специальных знаний.
Следующая статья:
Фундамент малозаглубленный теплоизолированный.
Предыдущая статья:
Фундамент малозаглубленный ленточный
Выбери тип фундамента для своего дома
Прочитайте статью:
Выбор фундамента для частного дома на пучинистом грунте
Какой фундамент выбрали Вы? Голосуйте!
Узнайте, что выбрали другие.
Смотреть! — все опросы
|
Ленточный мелкозаглубленный монолитный фундамент на песчаной подушке. (Вариант «А» на схеме №4). Самый простой и распространенный вариант ленточного монолитного фундамента на песчаной подушке. Поверх песчаной подушки укладывается слой гидроизоляции (толстая полиэтиленовая пленка или битумно-полимерный рулонный материал) и в опалубке, после выполнения армирования, отливается сама лента фундамента. Хотя мы подробно будем говорить об особенностях армирования мелкозаглубленного ленточного фундамента ниже, обратите внимание на толщину защитного слоя бетона ленты со стороны песчаной подушки. Требования отечественных норм [пункт 12.8.5 СП 50-101-2004]и американских норм Института бетона ACI 318 почти единодушны – толщина защитного слоя бетона со стороны песчаной подушки должна быть 70 мм (76 мм по ACI 318). Дальнейшие работы на фундаменте начинаются после того, как бетон наберет 50% от марочной прочности. При средней температуре воздуха +20°С такая марочная прочность бетона на портландцементе достигается на 3-4 сутки. (70% — в течение 6-10 суток и 100% в течение 28 суток). Несмотря на бытующие в среде народных строителей предубеждения о необходимости выжидать 28 суток, при наборе 50% марочной прочности бетоном на нем можно начинать производить работы (в том числе и постепенно нагружать кладкой стен). Гарантированно безопасная отметка начала работ – набор бетоном 70% расчетной прочности. Отметим, что при среднесуточной (а не дневной) температуре +10 °С срок набора 50% прочности бетоном растягивается до 5-6 суток. Подробнее мы рассмотрим особенности бетонирования мелкозаглубленного ленточного фундамента ниже.  После того как бетон наберет марочную прочность как минимум 50%, ленту мелкозаглубленного ленточного фундамента можно покрывать постоянной наружной вертикальной и горизонтальной битумно-полимерной гидроизоляцией. Вертикальную гидроизоляцию наружных стен следует во всех случаях поднимать выше на 0,5 м наибольшего прогнозируемого уровня подземных вод. Более подробно о нормативных безопасных сроках снятия опалубки написано разделе «Опалубка» главы «Строительство фундамента».  После проведения работ по гидроизоляции, мелкозаглубленный ленточный фундамент утепляется со стороны улицы экструдированным пенополистиролом и вокруг фундамента устраивается кольцевой дренаж. Продольные уклоны дренажей должны обеспечить скорость воды в трубах, при которой не происходит их заиливание. Для глинистых грунтов рекомендуется принимать уклон не менее 0,002, а для песков — не менее 0,003. Для обеспечения фильтрационной способности трубчатых дренажей, а также дренажных галерей предусматривают обсыпку из дренирующих материалов (щебня, гравия, песка или их смесей) толщиной не менее 30 см, изолированной от грунтов геотекстилем.  При условии хорошей дренированности грунта, или при устройстве кольцевого дренажа, и при глубине промерзания грунтов до 1 м ширина пазухи может составлять всего 0,2 м. При глубинах промерзания грунта от 1 до 1,5 м минимально допустимая ширина пазухи составляет не менее 0,3 м. На грунтах с глубиной промерзания от 1,5 до 2,5 м пазуху желательно засыпать на ширину не менее 0,5 м. Глубина засыпки пазух в данном случае принимается не менее 3/4 глубины заложения мелкозаглубленного ленточного фундамента, считая от планировочной отметки. При плохой дренированности грунта и невозможности отвода воды из непучинистого грунта, засыпку пазух можно рекомендовать на ширину, равную на уровне подошвы фундамента 0,25-0,5 м. От основания фундамента ширина пазухи должна увеличиваться и на уровне поверхности земли (планировочной отметки) быть равной глубине промерзания грунта.  Рекомендуется засыпать пазухи только не мерзлым грунтом, слоями толщиной не более 20 см, с тщательным трамбованием каждого слоя в отдельности. При выполнении работ по обратной засыпке пазух и котлованов следует предусмотреть меры, позволяющие избежать повреждения дренажных труб, стен подвалов и нанесенных на них теплоизоляционных, влагоизоляционных, гидроизоляционных и пароизоляционных слоев. Использовать при засыпке пазух в одном слое грунты разных типов не допускается, если это не предусмотрено проектом [пункт 4.2 СНиП 3.02.01-87]. В пределах обратной засыпки твердые включения, должны быть равномерно распределены в отсыпаемом грунте и расположены не ближе 0,2 м от фундамента. Пазуха, засыпанная непучинистым грунтом, должна быть обязательно укрыта поверхностной водонепроницаемой отмосткой (жесткой или мягкой с гидроизоляцией) для отвода осадков, поступающих с кровли. Схема №5. Размеры засыпаемых пазух на плохо дренированных грунтах или при невозможности водоотвода |
В обычных условиях при наличии дренажа пазухи в грунте засыпаются крупным или средним песком (в смеси с керамзитом фракции 10-20 или без него), щебнем, гравием. |
Засыпка пазух непучинистым грунтом и его уплотнение должны выполняться с обеспечением сохранности гидроизоляции фундамента и подземных коммуникаций (кабелей, трубопроводов). Работы по засыпке пазух следует производить сразу после устройства гидроизоляции и утепления мелкозаглубленного ленточного фундамента. Не допускается оставлять открытыми пазухи длительное время. Засыпку пазух рекомендуется доводить до отметок, гарантирующих надежный отвод поверхностных вод. В зимних условиях грунт для засыпки пазух должен быть талым. Засыпанный песок требуется уплотнить [пункт 6.4 ВСН 29-85]. После окончания работ по устройству фундаментов следует незамедлительно закончить вокруг здания планировку с обеспечением стока атмосферных вод от здания и устройством отмосток. Не допускается оставлять мелкозаглубленные (незаглубленные) фундаменты незагруженными на зимний период. Если это условие по каким-либо обстоятельствам оказывается невыполнимым, вокруг фундаментов следует устраивать временно теплоизоляционные покрытия из опилок, шлака, керамзита, шлаковаты, соломы и других материалов, предохраняющих грунт от промерзания.
Запрещается устраивать мелкозаглубленные фундаменты на промерзшем основании. В зимнее время допускается устраивать ленточные фундаменты только при условии глубокого залегания грунтовых вод с предварительным оттаиванием мерзлого грунта и обязательной засыпкой пазух непучинистым материалом. Поверх засыпки устраивается кольцевое утепление грунта и мягкая (щебень, керамзит, грунт) или жесткая (мощение, отливка) отмостка.Расчет сейсмической несущей способности ленточных фундаментов мелкого заложения с использованием метода сглаженных конечных элементов на основе ячеек
Бхоумик С., Лю Г.Р. (2018) Моделирование фазового поля для хрупкого разрушения и распространения трещин на основе сглаженного метода конечных элементов на основе ячеек метод. Eng Fract Mech 204:369–387
Статья Google Scholar
Bolton MD, Lau CK (1993) Факторы вертикальной несущей способности для круговых и ленточных фундаментов на грунте Мора-Кулона.
Кан Геотех Дж. 30:1024–1033
Артикул Google Scholar
Будху М., Аль-Карни А. (1993) Сейсмическая несущая способность грунтов. Геотехника 43(1):181–187
Статья Google Scholar
Cascone E, Casablanca O (2016) Статическая и сейсмическая несущая способность неглубоких ленточных фундаментов. Soil Dyn Earthq Eng 84:204–223
Статья Google Scholar
Cui X, Han X, Duan SY, Liu GR (2020) Реализация ABAQUS метода сглаженных конечных элементов на основе ячеек (CS-FEM). Int J Comput Methods 17(2):1850127
Статья MathSciNet Google Scholar
Frydman S, Burd HJ (1997) Численные исследования коэффициента несущей способности N γ . Journal of Geotechnical and Geoenvironmental Engineering 123(1):20–29
Статья Google Scholar
«>Гаян С., Каттер Б.Л., Фален Дж.Д., Хатчинсон Т.С., Мартин Г.Р. (2005) Центрифужное моделирование деформационно-нагрузочного поведения качающихся неглубоких фундаментов. Soil Dyn Earthq Eng 25(7–10):773–783
Статья Google Scholar
Гриффитс Д.В. (1982) Расчет коэффициентов несущей способности с использованием конечных элементов. Геотехника 32(3):195–202
Статья Google Scholar
Hansen JB (1970) Пересмотренная и расширенная формула для несущей способности. Датская геотех. Инст Булл 28:5–11
Google Scholar
He T (2019) Изучение сглаженного метода конечных элементов на основе ячеек для течений с преобладанием конвекции. Comput Struct 212:215–224
Статья Google Scholar
«>He T (2020) Искажение истинной сетки позволило реализовать сглаженный метод конечных элементов на основе ячеек для потоков несжимаемой жидкости с фиксированными и подвижными границами. Int J Numer Meth Eng 121 (14): 3227–3248
Артикул MathSciNet Google Scholar
Кнаппет Дж.А., Хей С.К., Мадабхуши С.Г. (2006) Механизмы разрушения неглубоких фундаментов при землетрясении. Soil Dyn Earthq Eng 26(2–4):91–102
Статья Google Scholar
Le CV (2017) Оценка коэффициентов несущей способности связно-фрикционного грунта с использованием клеточного сглаженного метода конечных элементов. Компьютерная геотехника 83: 178–183
Артикул Google Scholar
Li M, Zhou L, Liu C (2020) Мультифизический метод сглаженных конечных элементов на основе ячеек для анализа переходного поведения функционально качественных магнитоэлектроупругих тонкостенных структур в термической среде.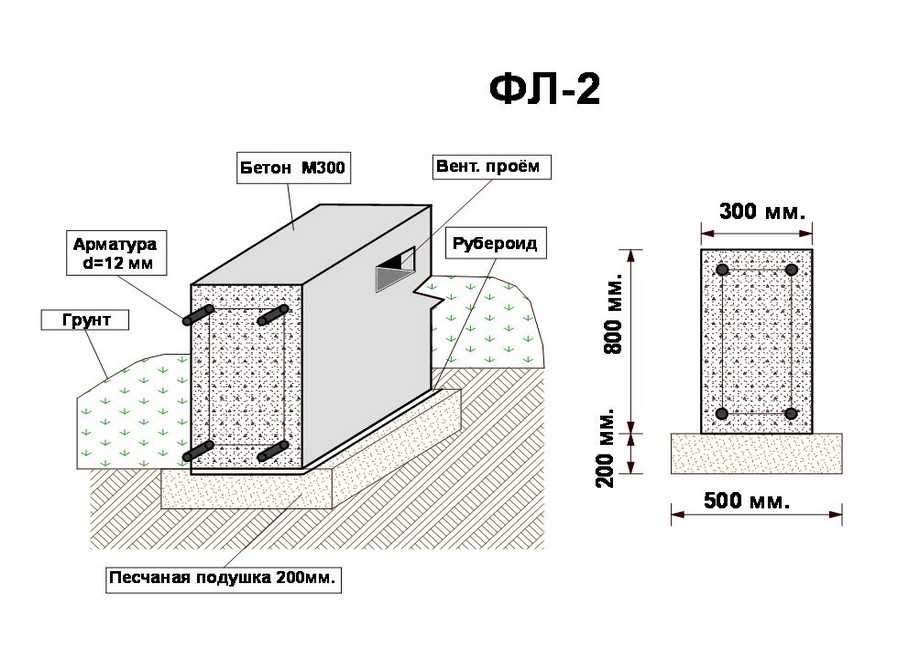
Тонкостенная конструкция 155:106876
Артикул Google Scholar
Лю Г.Р., Нгуен Т.Т., Дай К.И., Лам К.Ю. (2007) Теоретические аспекты метода сглаженных конечных элементов (SFEM). Int J Numer Meth Eng 71 (8): 902–930
Артикул MathSciNet Google Scholar
Лю Г.Р., Трунг Н.Т. (2016) Сглаженные методы конечных элементов. CRC Пресс
Книга Google Scholar
Luong-Van H, Nguyen-Thoi T, Liu GR, Phung-Van P (2014) Метод сглаженных конечных элементов на основе ячеек с использованием трехузлового пластинчатого элемента Mindlin без блокировки сдвига (CS-FEM-MIN3) для динамический отклик слоистых композитных пластин на вязкоупругой основе. Eng Анальная граница Элемент 42: 8–19
Артикул MathSciNet Google Scholar
«>Makrodimopoulos A, Martin CM (2006) Анализ предела нижней границы когезионно-фрикционных материалов с использованием программирования конуса второго порядка. J Numer Methods Eng 66(4):604–634
Статья Google Scholar
Makrodimopoulos A, Martin CM (2007) Анализ верхней границы с использованием симплексных элементов деформации и программирования конуса второго порядка. Int J Numer Anal Meth Geomech 31(6):835–865
Артикул Google Scholar
Martin CM (2005) Точные расчеты несущей способности методом характеристик. проц. ИАКМАГ. Турин: 441–450
Мэтью Т.В., Бекс Л., Бордас С.П., Натараджан С. (2020) Стохастический метод сглаженных конечных элементов на основе ячеек Галеркина (SGCS-FEM). Int J Comput Methods 17(08):1950054
Статья MathSciNet Google Scholar
«>Могери М., Мусумечи Г., Новита Д., Тейлор К.А. (2000) Испытание на разрушение неглубокого фундамента под действием внецентренной нагрузки на вибростенде. Soil Dyn Earthq Eng 20(5–8):435–444
Статья Google Scholar
Мейерхоф Г.Г. (1963) Некоторые недавние исследования несущей способности фундаментов. Can Geotech J 1(1):16–26
Артикул Google Scholar
Мосек А (2015) Набор инструментов оптимизации MOSEK для руководства по MATLAB
Нгуен, С.Н., Труонг Т.Т., Чо М., Трунг, Н.Т. (2020) Формула сглаженных конечных элементов на основе ячеек для вязкоупругих многослойных композитных пластин с учетом гигротермических эффектов . J Композитный материал, 0021998320980054
Нгуен-Суан Х., Нгуен Х.В., Бордас С., Рабчук Т., Дюфлот М. (2012) Сглаженный метод конечных элементов на основе ячеек для трехмерных твердых структур.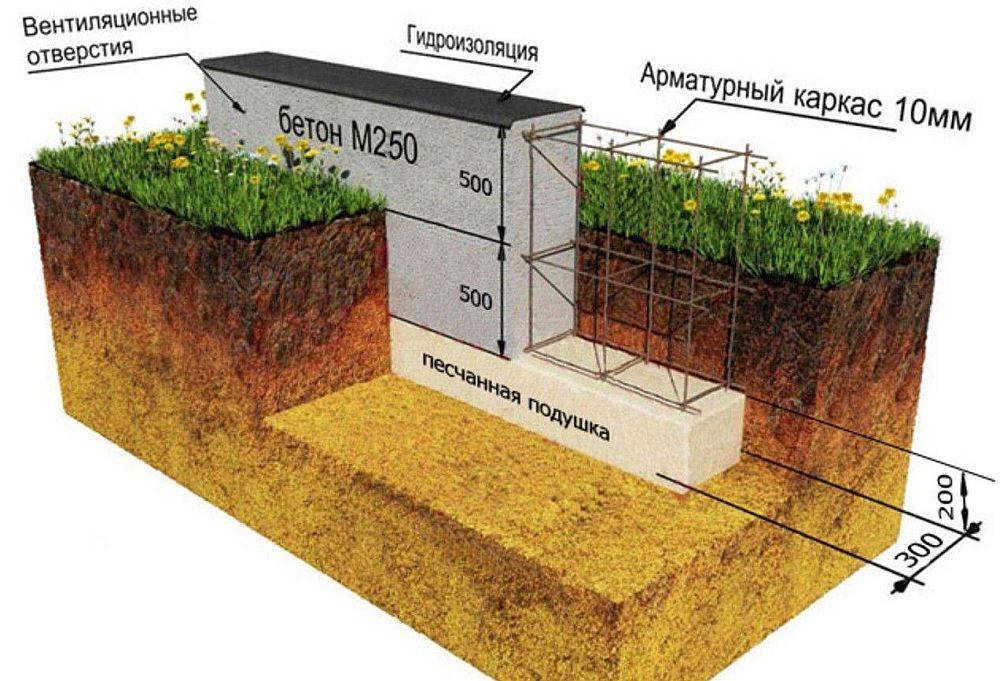
KSCE J Civ Eng 16 (7): 1230–1242
Артикул Google Scholar
Нгуен Х.К., Ле К.В., Нгуен Т.М. (2011) Оценка несущей способности и механизма разрушения ленточного фундамента с использованием анализа предела верхней границы. На 1-й Международной конференции по вычислительной науке и инженерии в Хошимине, Вьетнам
Нгуен Х.К. (2020 г.) Коэффициент безопасности и механизм отказа в геотехническом проектировании: численное исследование. Достижения в области компьютерных методов и геомеханики, Springer, Сингапур, стр. 121–129.
Нгуен Х.К. (2020a) Использование адаптивного сглаженного анализа предельных значений конечных элементов для сейсмостойкости туннелей. 10-й Международный симпозиум по геотехническим аспектам подземного строительства в мягком грунте (принято)
Нгуен Х.К. (2020b) Анализ верхней границы сейсмостойкости туннелей с использованием сглаженных конечных элементов на основе ячеек.
10-й Международный симпозиум по геотехническим аспектам подземного строительства в слабых грунтах (принято)
Prandtl L (1920) Uber die Eindringungs-festigkeit (Harte) plastischer Baustoffe und die Festigkeit von Schneiden. Zeitschrift fur Angewandte Mathematik und Mechanik 1:15–20
Статья Google Scholar
Reissner H (1924) Проблема Зумерддрака. В материалах 1-й международной конференции по прикладной механизации, Делфт, с. 295–311
Ричардс-младший Р., Элмс Д.Г., Будху М. (1993) Сейсмическая несущая способность и осадки фундаментов. J Geotech Eng 119(4):662–674
Сарма С.К., Йоссифелис И.С. (1990) Коэффициенты сейсмической несущей способности ленточных фундаментов мелкого заложения. Геотехника 40(2):265–273
Статья Google Scholar
«>Ширато М., Коно Т., Асаи Р., Накатани С., Фукуи Дж., Паолуччи Р. (2008) Крупномасштабные эксперименты по нелинейному поведению неглубоких фундаментов, подверженных сильным землетрясениям. Почвы Найдено 48(5):673–692
Статья Google Scholar
Соколовский В. (1960) Статика почвенных сред. Баттервортс
Google Scholar
Soubra AH (1999) Решения по верхней границе несущей способности фундаментов. J Geotech Geoenviron Eng 125(1):59–68
Статья Google Scholar
Сурендран М., Чанкье Л., Нгуен-Суан Х., Лю Г.Р., Натараджан С. (2020) Сглаженный метод конечных элементов на основе ячеек для моделирования межфазных трещин с несовпадающими сетками. Eng Fract Mech 242:107476
Артикул Google Scholar
«>Терзаги К. (1943) Теоретическая механика грунтов. John Wiley & Sons Inc, Нью-Йорк
Книга Google Scholar
Весич А.С. (1973) Расчет предельных нагрузок мелкозаглубленных фундаментов. J Soil Mech Found Div 68(1):45–73
Статья Google Scholar
Во-Минь Т., Нгуен Т.М., Чау А.Н., Нгуен Х.К. (2017) Устойчивость сдвоенных кольцевых туннелей в связном фрикционном грунте с использованием метода сглаженных конечных элементов на основе узлов (NS-FEM). J Вибрация 19(1):520–538
Артикул Google Scholar
Vo-Minh T, Nguyen-Son L (2021) Метод сглаженных конечных элементов на основе стабильных узлов для анализа устойчивости двух кольцевых туннелей на разной глубине в связных грунтах. Comput Geotech 129:103865
Статья Google Scholar
«>Vo-Minh T (2020) Расчет коэффициентов несущей способности ленточного фундамента с использованием метода сглаженных конечных элементов на основе узлов (NS-FEM). В области геотехники для устойчивого развития инфраструктуры Springer, Сингапур. стр. 1127–1134.
Zeng X, Steedma RS (1998) Нарушение несущей способности неглубоких фундаментов при землетрясениях. Геотехника 48(2):235–256
Статья Google Scholar
Zhou L, Li M, Chen B, LiLi FX (2019) Метод сглаженных конечных элементов на основе неоднородных ячеек для нелинейной переходной реакции функционально градиентных магнитоэлектроупругих структур с коэффициентами демпфирования. J Intell Mater Syst Struct 30(3):416–437
Артикул Google Scholar
Zhu D (2000) Наименьшая верхняя граница решений для коэффициента несущей способности N γ .
Почвы Найдено 40(1):123–129
Статья Google Scholar
ГК | Несущая способность мелкозаглубленных фундаментов в грунте
{{appTitle}}c (кПа)
φ ( 0 )
Д ф (м)
Б (м)
γ (кН/м 3 )
Тип Fndn StripCircularSquare
Весовая тонна (м)
ФС ст
ФС нержавеющая сталь
F ст (кПа)
F нержавеющая сталь (кПа)
N c
{{nc | раунд:2}}
N q
{{nq | раунд: 2}}
N γ
{{ngamma | раунд:2}}
S c
{{sc | round:2}}
S γ
{{sgamma | раунд:2}}
Q ULT = C N C S C + Q N Q + 0,5 γ E B N γ S γ
Q Ult = (r | ZON ZNSHONE Q .
}})({{nc | ряд:2}})({{sc | ряд:2}}) + ({{efektifStres | ряд:2}})({{nq | ряд:2}}) + ( 0,5)({{gamma_efficient | раунд:2}})({{tg | раунд:2}})({{ngamma | раунд:2}})({{sgamma | раунд:2}})
q ульта = {{qult | round:0}} кПа
q все — st = q ult / FS st
q all — st = {{qult | раунд:0}} / {{guvenlikSayisiSt | round:0}}
q all — st = {{qallst | раунд:0}} кПа (✔) (✘)
q all — ss = q ult / FS ss
q all — ss = {{qult | раунд:0}} / {{guvenlikSayisiSs | раунд:0}}
q все — сс = {{qallss | раунд:0}} кПа (✔) (✘)
Процедура и составы для Terzaghi (1943) Расчет несущей способности Приведенный выше инструмент расчета несущей способности мелкозаглубленного фундамента следует процедуре, приведенной в «Анализе и проектировании фундамента», 5-е издание (Джозеф Э.