Расчет кубатуры фундамента калькулятор: Калькулятор ленточного фундамента
расчет бетона на фундамент калькулятор ингридиентов
Частное строительство, которое реализуется собственными руками, не отменяет проведения точных расчетов. Такой подход помогает оптимизировать расходы и ускорить ход работ. Расчет бетона на фундамент калькулятором позволит купить точное количество нужного материала, без огромных нереализуемых остатков.
Содержание
- 1 Марка бетона для фундамента частного дома
- 2 Калькулятор бетона
- 3 Расчет материалов на ленточный фундамент
- 4 Расчет бетона на столбчатый фундамент калькулятор
- 5 Расчет кубатуры бетона для монолитной плиты
- 6 Расчет цемента на куб бетона
- 7 Стоимость
- 8 Книги по теме:
Марка бетона для фундамента частного дома
Выбор железобетона по прочности опирается на особенности будущей конструкции. Если нагрузка на основание будет небольшой, как от дачных построек или каркасно-щитовых сооружений, можно использовать материал марки М200.
Более массивные строения, в том числе двухэтажные, с мансардами, выполненные из бруса, бревна, пеноблоков, требуют обустройства более крепких оснований на марках М 250/300. Кирпичные, ж/б стены выдерживают системы, изготовленные на основе материалов М350/М400. Оперируя маркой рабочего раствора, можно провести расчёт объема бетона для фундамента, калькулятор позволит получить все данные.
Кирпичные, ж/б стены выдерживают системы, изготовленные на основе материалов М350/М400. Оперируя маркой рабочего раствора, можно провести расчёт объема бетона для фундамента, калькулятор позволит получить все данные.
Ключевое значение имеет плотность бетона, используемого для возведения несущих конструкций. Она варьируется от 1300 до 2500 кг/м³
Калькулятор бетона
Сервис предназначен для вычисления размеров основания, опалубки, диаметра и количества арматуры и объёма рабочего раствора, который используется для обустройства несущей конструкции.
Расчет бетона для фундамента (калькулятор) опирается на строительные нормы и правила, регулирующие устройство конструкций из бетона и железобетона (СНиП) 52-01-2003, государственный стандарт ГОСТ Р 52086-2003, СНиП 3.03.01-87.
Расчет материалов на ленточный фундамент
Несущая конструкция данного типа является замкнутой монолитной железобетонной полосой, которая размещается под несущими стенами объекта, распределяя нагрузку по всей площади лент.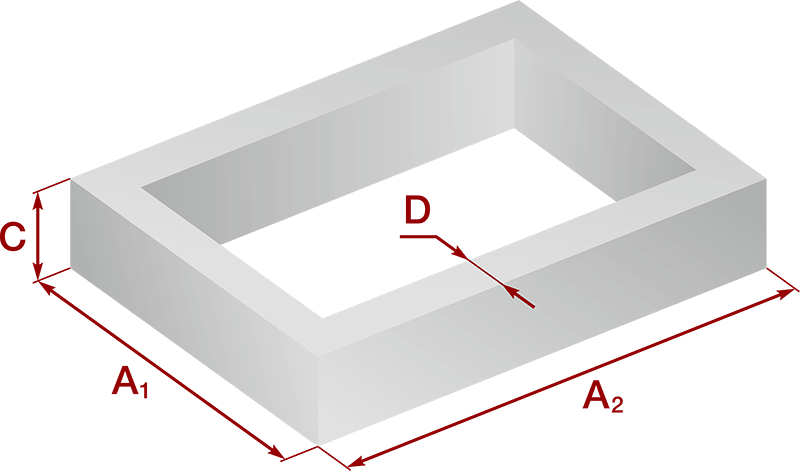
Система блокирует изменение формы постройки и ее проседание, что происходит из-за вспучивания почв, высокие нагрузки передаются на углы.
Ленточные основания могут быть сборными или монолитными, глубокозаглубленными и мелкозаглубленными. Выбор типа конструкции опирается на характеристики почвенного слоя, расчётную нагрузку и прочие параметры, рассматриваемые индивидуально. Система подходит для всех типов построек и применяется при обустройстве цоколя и подвалов.
Вычисления основаны на указанных исходных данных:
- марка железобетона;
- ширина ленты, в метрах;
- длина ленты, в метрах;
- высота ленты, в см;
- толщина ленты, в см;
Показательный расчет бетона на монолитный фундамент (калькулятор)
Если обустраивается ленточное основание на растворе марки М300, класса 22. 5, со следующими линейными параметрами конструкции:
5, со следующими линейными параметрами конструкции:
- ширина – 6.00 м;
- длина – 8.00 м;
- высота – 70.00 см;
- толщина – 40.00 см, то необходимый объём бетона составит 7.4 м³ общей массой 18500 кг (при плотности материала 2500 кг/м³).
Расчет бетона на фундамент — общие сведения по расшифровке результатов
Определить количество материала в кг легко. Достаточно умножить показатель объёма м³ на плотность кг/м³
Используя калькулятор, можно получить указанные данные. Их трактовка осуществляется следующим образом:
- совокупная длина ленты – периметр основания;
- площадь подошвы ленты – указывает на площадь опоры основания на грунты. Параметр соответствует требуемым размерам гидроизоляции;
- площадь боковой поверхности с внешней стороны – указывает площадь требуемого утеплителя для внешней стороны основания;
- расчет объёма бетона – калькулятор позволяет определить кубатуру материала, требуемого для заливки всего основания с исходными параметрами.

- количество раствора – примерный вес материала при средней плотности;
- расчёт нагрузки на фундамент – калькулятор позволяет определить параметры нагрузки на всю площадь опоры, в кг/см²;
- толщина доски опалубки – ГОСТ Р 52086-2003 при заданном шаге опор и исходных параметрах несущей конструкции;
- количество досок – число досок для опалубки исходного размера.
Расчёт бетона на ленточный фундамент с учетом всех параметров строительства готов.
Расчет бетона на столбчатый фундамент калькулятор
При вычислении количества материалов на столбчатый фундамент
- марка бетона;
- количество столбов, шт;
- диаметр столба, см;
- высота, см;
- диаметр его основания, см;
- высота основания, см;
- ширина ростверка, м;
- длина ростверка, м;
- высота ростверка, м;
- толщина ростверка, м;
Конструктивные элементы подобных систем – столбы – располагаются в грунте. Вершины столбов связаны между собой монолитом (железобетонной лентой, которая называется ростверк). Расчет кубов бетона на фундамент (калькулятор) такого типа позволяет получить искомые данные, согласно действующим строительным нормам и правилам.
Вершины столбов связаны между собой монолитом (железобетонной лентой, которая называется ростверк). Расчет кубов бетона на фундамент (калькулятор) такого типа позволяет получить искомые данные, согласно действующим строительным нормам и правилам.
Примерный расчет
Точное определение арматуры и ее количества производится на основании сложных инженерных расчетов фундамента на прочность
Исходные данные:
- система содержит 12 столбов;
- диаметр каждого – 30 см;
- высота – 300 см;
- диаметр основания столба – 40 см;
- высота основания – 20 см;
- ширина ростверка – 6м;
- длина – 8 м;
- высота – 70 см;
- толщина – 40 см.
Для обустройства фундамента понадобится 10.2 м³ материала (М300), весом 24059 кг.
Расчет кубатуры бетона для монолитной плиты
Разработка подобных оснований позволяет получить основание прямоугольной формы.
- длина плиты;
- ширина;
- высота.

Примерный расчет количества бетона для фундамента дома (калькулятор) выглядит таким образом: исходные данные — габариты ростверка 12.0 х 10.0 м, высота плиты 0.40 м. Вычисление на куб материала – 12.0 х 10.0 х 0.40 = 48.0 м³, что соответствует 120.000 кг
Арматура для фундамента (монолитных плит)
Расчет позволяет определить следующие параметры:
- min допустимый диаметр продольно и поперечно расположенных стержней, мм;
- min количество рядов в верхнем и нижнем поясе, шт.;
- величину нахлёста, в см;
- совокупная длина, м;
- общая масса, кг.
Расчет опалубки для монолитной плиты
Калькулятор позволяет определить минимальную толщину доски, при установке опалубки с шагом 1 м, в мм и количество досок исходного размера в шт.
Расчет цемента на куб бетона
Марка материала должна в 1.5-2 р превышать требуемую марку рабочего раствора. Например, для получения М 200 понадобится связующее М400.
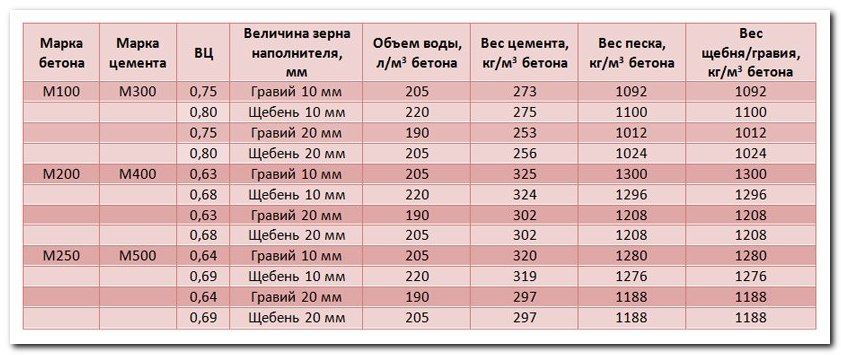
Чтобы определить требуемое количество цемента на м³ железобетона, необходимо разделить используемое количество воды на водоцементное соотношение.
Таблица – расход воды в зависимости от фракции заполнителя
| Расход жидкости, л/м³ | ||||||||
| Гравий, мм | Щебень, мм | |||||||
| 10.00 | 20.00 | 40.00 | 80.00 | 10.00 | 20.00 | 40.00 | 80.00 | |
| Высокая | 215.00 | 200.00 | 185.00 | 170.00 | 230.00 | 215.00 | 200.00 | 185.00 |
| Средняя | 205.00 | 190.00 | 175.00 | 160.00 | 220.00 | 205.00 | 190.00 | 175.00 |
| Низкая | 195.00 | 180.00 | 165.00 | 150. 00 00 | 210.00 | 195.00 | 180.00 | 165.00 |
| Непластичный бетон | 185.00 | 170.00 | 155.00 | 140.00 | 200.00 | 185.00 | 170.00 | 155.00 |
Выбор водоцементного соотношения опирается на срок созревания железобетона (согласно условиям строительства) и марку цемента. Если для приготовления смеси используется щебень, к указанному в таблице показателю прибавляется 0.05
| Цемент, М | ||||
| Марки железобетона | ||||
| 200.0 | 250.0 | 300.0 | 400.0 | |
| 300.0 | 0.550 | 0.500 | 0.400 | — |
| 400.0 | 0.630 | 0.560 | 0.500 | 0.400 |
| 500.0 | 0.710 | 0.640 | 0.600 | 0.460 |
Например, при заданном объёме жидкости, равном 205 литрам и ВЦ, равном 0. 61, для замеса потребуется 336 кг цемента (205.0/0.610).
61, для замеса потребуется 336 кг цемента (205.0/0.610).
Стоимость
Реализовав расчет бетона на фундамент (калькулятор онлайн) можно определить затраты на строительство. Чем выше марка материала, тем выше уровень издержек. В среднем 1 м³ самого ходового раствора марки М300 оценивается в 3100-3300 т.р. Если подача материала будет производиться через бетононасос, наблюдается незначительное удорожание.
В этом видео рассказывают как расчет количества бетона для фундамента калькулятором изобличает мошенничество поставщиков бетона:
Книги по теме:
Вы не знаете, как рассчитать кубатуру фундамента? Не беда! Просто изучите наши рекомендации и заполните пробелы в ваших знаниях. Ведь для того, чтобы подсчитать кубатуру основания достаточно освежить воспоминания о школьном курсе алгебры и геометрии. Словом, это очень простая задача и мы готовы подсказать вам самый короткий путь к ее решению.
Причем кубатуру опалубки можно определить на этапе расчетов, по чертежам и по данным, снятым с готовой конструкции. Причем последний вариант, будет немного точнее первого. Впрочем, любители простых решений могут использовать особый калькулятор-расчет кубатуры фундамента – специальную программу, которой скармливают предполагаемые габариты основания (длину, ширину, высоту, толщину стенки). В итоге, пользователи программы получают не только точный расчет объема используемого раствора, но и рекомендации по самостоятельному приготовлению бетона из песка цемента и щебня. Как видите, существует множество способов вычислить кубатуру основания и объем раствора, используемого для заливки фундамента. Расчет кубатуры монолитной плитыТакое основание представляет собой монолитный, прямоугольный параллелепипед, грани которого можно замерить по готовой опалубке или по чертежам. Объем такой опалубки вычисляется просто – для этого нужно перемножить площадь подошвы фундамента и высоту опалубки. При этом площадь подошвы равна произведению ширины и длины будущего ростверка. Если перейти от формулировок к цифрам, то кубатура фундамента с габаритами ростверка 10х12 метров и высотой плиты в 0,4 метра равняется 48 кубическим метрам (10м х 12м х 0,4м = 48 м3). Разумеется, при точных расчетах из этого объема требуется вычесть кубатуру армирующей сетки, но такие размеры делают подобные вычисления бессмысленными. Расчет кубатуры ленточного основанияЛенточное основание это тот же прямоугольный параллелепипед, только с полой внутренней частью. Впрочем, несмотря на немного усложненную форму, объем ленточной опалубки можно вычислить без особых усилий. Для этого нужно вычесть из объема прямоугольного параллелепипеда, образованного внешними стенками опалубки, объемы такой же геометрической фигуры, образованной внутренними стенками опалубки. После этого к полученному результату можно добавить объемы внутренних лент, поддерживающих межкомнатные перегородки. Причем поперечные, внутренние ленты (относительно лицевой стороны фасада) считают, как один параллелепипед, а продольные – как два параллелепипеда, примыкающие к поперечной ленте. И если перейти от формул к цифрам, то объемы основания 10х12 метров с шириной ленты в 0,4 метра, заглубленного в грунт на 2 метра и дополненного одной внутренней лентой, толщиной в 0,5 метра, вычисляются следующим образом:
Расчет кубатуры столбчатого основанияКубатура столбчатого основания определяется как сумма двух геометрических фигур – широкого и низкого параллелепипеда-подошвы и высокого и узкого параллелепипеда-столба. Указанное значение умножается на общее количество столбов в основании, расположенных вдоль периметра фасада с шагом в 2 метра. В цифрах объем столбчатого основания под дом в 6х6 метров, с общим количеством столбов в 20 штук (четыре угловых и 16 промежуточных), основания которых имеют габариты в 0,5х0,5х0,2 метра, а столбы 0,3х0,3х0,8 метра, рассчитывается следующим образом:
Расчеты буронабивного основания с монолитным ростверкомКубатура этого типа основания вычисляется, как сумма кубатур столбов (цилиндров) и плиты ростверка (прямоугольного параллелепипеда). То есть, как и в предыдущих случаях, мы разбиваем сложную заливку на множество простых фигур и, вычислив их объем, добираемся до искомого результата. Причем объем колонны вычисляется как произведение площади ее основания на высоту от подошвы до нижней границы ростверка. А площадь основания (круга) равна одной четверти от произведения удвоенного диаметра и константы ? (3,14) В числовом выражении кубатура фундамента на 20 столбах диаметром 0,4 метра и глубиной погружения в грунт в 2,5 метра, которые поддерживают ростверк с габаритами 10х12х0,3 метра, вычисляется следующим образом:
|
Методы Монте-Карло на практике
Интеграция методом Монте-Карло
Время считывания: 14 мин.Если вы понимаете и знаете о наиболее важных понятиях вероятности и статистики, которые мы представили в Уроке 16, вы увидите, что понимание интегрирования по методу Монте-Карло невероятно просто. Этот метод часто используется при рендеринге (в частности, трассировке лучей) и затенении. В этой главе мы поговорим о теории, а в следующей главе мы фактически изучим практический пример. Чтобы понять, как интеграция MC используется в рендеринге, вам сначала нужно узнать об уравнении рендеринга (это тема следующего урока). Затем мы покажем, как этот метод используется на следующем уроке (Введение в легкий транспорт).
Оценщик Монте-Карло: вычисление интегралов
Прежде чем вы начнете читать эту главу, вы должны понять закон бессознательного статистика , который мы объяснили в этой главе из урока 16. Он гласит, что математическое ожидание функции случайной величины f(X) может быть определено как :
Он гласит, что математическое ожидание функции случайной величины f(X) может быть определено как :
Где \(P_X\) — распределение вероятностей случайной величины X. Надеюсь, вы хорошо это понимаете. Если нет, настоятельно рекомендуем внимательно прочитать главу, посвященную этому понятию. Вы должны полностью усвоить эту идею, чтобы понять интеграцию Монте-Карло.
К этому моменту вы также должны быть знакомы с концепцией дисперсии и стандартного отклонения , о которых мы здесь не будем говорить (если вы этого не сделаете, вы найдете их объяснение в уроке 16). Однако в качестве быстрого напоминания напомним, что дисперсию можно определить двумя эквивалентными способами (второй чуть более удобен): 92. \конец{массив} $$
Мы будем использовать эти формулы далее, поэтому также важно, чтобы вы их поняли (они объясняются в уроке Математические основы методов Монте-Карло).
Рисунок 1: интеграл по области [a,b] можно рассматривать как площадь под кривой. Рисунок 2: кривую можно вычислить по x и результат можно умножить на (b — a). Это определяет прямоугольник, который можно рассматривать как очень грубое приближение интеграла. 9б f(x)\;dx.$$
Рисунок 2: кривую можно вычислить по x и результат можно умножить на (b — a). Это определяет прямоугольник, который можно рассматривать как очень грубое приближение интеграла. 9б f(x)\;dx.$$ Как вы помните, интеграл функции f(x) можно интерпретировать как вычисление площади под кривой функции. Эта идея проиллюстрирована на рисунке 1\. Теперь представьте, что мы просто берем случайное значение, скажем, x в диапазоне [a,b], оцениваем функцию f(x) в x и умножаем результат на (b-a). На рис. 2 показано, как выглядит результат: это еще один прямоугольник (где f(x) — высота этого прямоугольника, а (b-a) — его ширина), в некотором смысле вы также можете посмотреть на очень грубую аппроксимацию площади под прямоугольником. изгиб. Конечно, мы можем понять это более или менее правильно. Если мы оцениваем функцию в x1 (рисунок 3), мы довольно сильно недооцениваем эту область. Если мы оцениваем функцию в x2, мы переоцениваем площадь. Но поскольку мы продолжаем оценивать функцию в разных случайных точки между a и b, суммируя площади прямоугольников и усредняя сумму, полученное число становится все ближе и ближе к фактическому результату интеграла. В этом нет ничего удивительного, поскольку слишком большие прямоугольники компенсируют слишком маленькие прямоугольники. И действительно, скоро мы приведем доказательство того, что суммирование их и усреднение их площадей сходится к интегральной «площади» по мере увеличения числа отсчетов, используемых при расчете. Эта идея проиллюстрирована на следующем рисунке. Функцию оценивали в четырех разных местах. Результат функции в виде этих четырех случайно выбранных значений x затем умножается на (b-a), суммируется и усредняется (мы делим сумму на 4). Результат можно считать аппроксимацией реального интеграла. 9N \rangle \) является аппроксимацией F с использованием N отсчетов. Это эквивалентно условному обозначению среднего \(\bar X_n\), которое мы использовали в уроке 16, и оба эквивалентны). Это уравнение называется базовой оценкой Монте-Карло . Случайная точка в интервале [a,b] может быть легко получена путем умножения результата генератора случайных чисел, производящего равномерно распределенные числа в интервале [0,1], на (b-a):
В этом нет ничего удивительного, поскольку слишком большие прямоугольники компенсируют слишком маленькие прямоугольники. И действительно, скоро мы приведем доказательство того, что суммирование их и усреднение их площадей сходится к интегральной «площади» по мере увеличения числа отсчетов, используемых при расчете. Эта идея проиллюстрирована на следующем рисунке. Функцию оценивали в четырех разных местах. Результат функции в виде этих четырех случайно выбранных значений x затем умножается на (b-a), суммируется и усредняется (мы делим сумму на 4). Результат можно считать аппроксимацией реального интеграла. 9N \rangle \) является аппроксимацией F с использованием N отсчетов. Это эквивалентно условному обозначению среднего \(\bar X_n\), которое мы использовали в уроке 16, и оба эквивалентны). Это уравнение называется базовой оценкой Монте-Карло . Случайная точка в интервале [a,b] может быть легко получена путем умножения результата генератора случайных чисел, производящего равномерно распределенные числа в интервале [0,1], на (b-a):
\(X_i = a + \xi (b — a)\), где \(\xi\) равномерно распределено между нулем и единицей. 9б f(x)\:dx,\\
&=&Ф\\
\конец{массив}
$$
9б f(x)\:dx,\\
&=&Ф\\
\конец{массив}
$$
Помните, что PDF равна 1/(b-a), таким образом, она отменяет член (b-a) справа внутри знака интеграла (строка 3).
Обобщение до произвольного PDF
Теперь, как упоминалось выше, формула, которую мы использовали для оценки методом Монте-Карло, является базовой. Почему? Потому что это работает только в том случае, если PDF случайной величины X однороден. Однако мы можем распространить интеграцию Монте-Карло на случайные величины с произвольными PDF. Тогда более общая формула: 9{N-1} \dfrac{f(X_i)}{pdf(X_i)}.$$
Это более обобщенная форма оценки методом Монте-Карло, которую вам следует запомнить (если в последних двух главах нужно запомнить только одно уравнение, то это оно).
Для ясности, плотность вероятности в знаменателе совпадает с плотностью вероятности случайной величины X.
Как и в случае с базовой оценкой Монте-Карло, чтобы убедиться, что эта формула верна, нам нужно проверить, что эта оценщик имеет правильное ожидаемое значение. Проверим: 9{N-1} \int_\omega f(x) \; дх, \\
& = & Ф.
\конец{массив}
$$
Проверим: 9{N-1} \int_\omega f(x) \; дх, \\
& = & Ф.
\конец{массив}
$$
Хитрость здесь в замене (строка 2):
$$E \влево[f(X_i)\вправо],$$для (строка 3):
$$E[f(x)] = \int_{\Omega} f(x) pdf(x) \;dx.$$ в третьей строке (и не забудьте разделить f(x) на pdf(x)). Потратьте время, чтобы понять эти уравнения. Как мы только что сказали, это самый важный результат всего, что мы изучали до сих пор, и он является основой почти каждого алгоритма, который мы собираемся изучать на следующих уроках. Если вы не понимаете этот алгоритм, вы не поймете трассировку лучей Монте-Карло . С уравнением рендеринга это, вероятно, второе по важности уравнение. Теперь вы спросите , зачем мне брать образцы из какого-либо другого распределения, кроме равномерного распределения? И это был бы очень хороший вопрос. Слабый ответ: «Потому что, возможно, вы можете использовать данный генератор случайных чисел только для создания образцов, и этот генератор имеет неоднородный PDF». Таким образом, по крайней мере, если это так, мы только что продемонстрировали, что вы все еще можете использовать интеграцию Монте-Карло, если вы не забываете делить \(f(X_i)\) на \(pdf(X_i)\) . Но вы также увидите, что этот результат пригодится, когда мы будем изучать снижение дисперсии в следующей главе. Так что продолжайте читать, и вы скоро поймете, почему этот результат важен!
Но вы также увидите, что этот результат пригодится, когда мы будем изучать снижение дисперсии в следующей главе. Так что продолжайте читать, и вы скоро поймете, почему этот результат важен!
Давайте поймем, зачем нужно делить f(x) на pdf(x) (для непостоянных PDF). Как вы знаете, PDF дает вероятность того, что случайная величина X получит некоторое значение \(x_i\). Когда вы берете образцы из произвольного PDF, образцы распределяются неравномерно: больше образцов генерируется там, где PDF высокий, и наоборот, меньше образцов создается там, где PDF низкий (см. рисунок рядом). Однако при интеграции по методу Монте-Карло образцы должны быть распределены равномерно. Если вы создадите высокую концентрацию выборок в некоторых областях функции (поскольку PDF в этой области высока), результат интегрирования Монте-Карло будет смещен.
Разделение f(x) на pdf(x) уравновесит этот эффект. В самом деле, когда плотность вероятности высока (где также генерируется больше выборок), деление f(x) на pdf(x) уменьшит «вес» этих выборок в сумме. Таким образом, по сути, мы компенсируем более высокую концентрацию образцов, уменьшая их вклад. С другой стороны, при низкой плотности вероятности генерируется меньше выборок (плотность выборок ниже, чем в области с высокой плотностью вероятности). Но если мы разделим f(x) на низкое значение (например, 1, деленное на 0,1), вклад этих выборок увеличится. Мы компенсируем меньшую плотность образцов, придавая им больший вес.
Таким образом, по сути, мы компенсируем более высокую концентрацию образцов, уменьшая их вклад. С другой стороны, при низкой плотности вероятности генерируется меньше выборок (плотность выборок ниже, чем в области с высокой плотностью вероятности). Но если мы разделим f(x) на низкое значение (например, 1, деленное на 0,1), вклад этих выборок увеличится. Мы компенсируем меньшую плотность образцов, придавая им больший вес.
По сути, это то, что делает деление f(x) на pdf(x). Он взвешивает вклад выборок, чтобы компенсировать тот факт, что выборки, сгенерированные из произвольной PDF, не будут распределены равномерно (при условии, конечно, что PDF не постоянна): он уменьшает выборки, сгенерированные в областях с более высокой плотностью (где PDF высокой) и масштабирует выборки, созданные в областях с меньшей плотностью (где PDF низкая).
Мы подробно рассмотрим эту концепцию в следующей главе, посвященной уменьшению дисперсии и выборке по важности.
Свойства интеграции Монте-Карло
Как видите, оценка Монте-Карло — это не что иное, как выборочное среднее, только мы заменяем население произвольной функцией с действительным значением.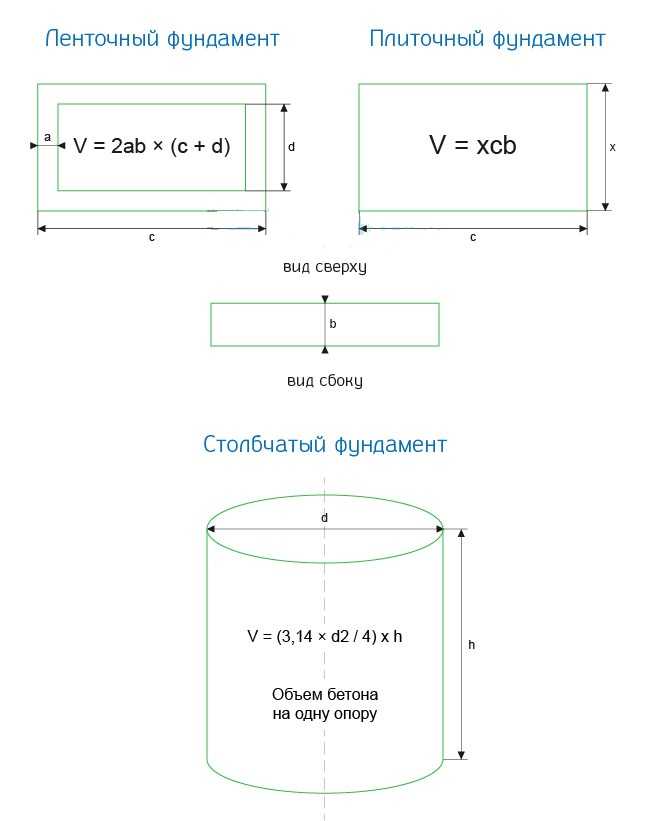 По этой причине оценки Монте-Карло и выборочные средства имеют одни и те же свойства:
По этой причине оценки Монте-Карло и выборочные средства имеют одни и те же свойства:
Оценка методом Монте-Карло сходится к ожидаемому значению функции f(x), когда размер выборки приближается к бесконечности. Это, как вы можете догадаться, очень важное свойство. Он говорит, как и в случае с выборочным средним, что чем выше N, тем больше вероятность того, что мы сойдемся, по вероятности, к правильному ответу (F). 9N \угол\).
Преимущества интегрирования методом Монте-Карло по сравнению с детерминированными методами
Идея оценки методом Монте-Карло проста и, вероятно, известна уже очень давно, но получила широкое распространение только с появлением компьютерных технологий в конце 1940-х годов. Многократное вычисление функций и усреднение результатов — это задача, которую компьютер может выполнить в бессчетное количество раз быстрее, чем мы, люди, когда-либо могли достичь. Возможность эффективно запускать эти симуляции (чего у нас не было до компьютерной эры) помогла решить множество важных и сложных задач во многих областях науки (математика, физика, биология, химия и т.
 d\) отсчетов).
d\) отсчетов).Пример кратного интеграла: \(\int \cdots \int_D f(x_1, x_2, \cdots, x_n) dx_1 \cdots dx_n\).
С другой стороны, принцип интегрирования Монте-Карло может быть легко распространен на более высокое измерение, а скорость сходимости метода не зависит от количества измерений. Как вы увидите на следующих уроках, при рендеринге нам иногда приходится решать интегралы функций со многими переменными (или множественные интегралы), для которых лучше подходит интегрирование MC. Конечно, для фиксированного количества отсчетов качество аппроксимации снижается с увеличением количества измерений, но тем не менее вы гарантированно получите решение за фиксированную стоимость (количество отсчетов N).
Одним из ключевых элементов оценки методом Монте-Карло является возможность использовать и, таким образом, генерировать последовательности случайных чисел, которые мы можем использовать для оценки функции f(x) для «случайных» значений x в желаемом интервале [a,b ]. Таким образом, как и во всех других методах, генерация случайных чисел.
 В этой главе мы рассмотрим только случай, когда эти числа генерируются с равномерным распределением, но в некоторых случаях выгодно генерировать случайные числа с очень специфическими PDF. Мы объясним почему позже в этой главе и уроке по выборке важности. Однако суть здесь в том, что овладение искусством генерации случайных чисел очень важно, если вы хотите использовать методы Монте-Карло. Этой теме посвящена глава данного урока.
В этой главе мы рассмотрим только случай, когда эти числа генерируются с равномерным распределением, но в некоторых случаях выгодно генерировать случайные числа с очень специфическими PDF. Мы объясним почему позже в этой главе и уроке по выборке важности. Однако суть здесь в том, что овладение искусством генерации случайных чисел очень важно, если вы хотите использовать методы Монте-Карло. Этой теме посвящена глава данного урока.Улучшение интеграции методом Монте-Карло: уменьшение отклонений
В этой главе мы представили только базовую оценку методом Монте-Карло. Этот наивный метод хорошо работает для простых случаев, но мы заинтересованы в его использовании для решения практических задач, которые, как правило, более сложны. Как мы объясняли ранее, проблема с интегрированием по методу Монте-Карло заключается в его скорости сходимости, которая, несмотря на то, что она постоянна, также довольно низка (\(O\sqrt{N}\)). По этой причине было проведено много исследований по разработке методов уменьшения ошибки (или дисперсии).
 Мы часто говорим о уменьшение отклонения . Например, выборка по важности, термин, о котором вы, возможно, уже слышали, является примером такой стратегии.
Мы часто говорим о уменьшение отклонения . Например, выборка по важности, термин, о котором вы, возможно, уже слышали, является примером такой стратегии.Резюме
Подведем итог тому, что мы узнали о методе интегрирования Монте-Карло.
Преимущества:
Простота (хорошо адаптируется к многомерным интегралам).
Беспристрастный и последовательный.
Параллельный характер: каждому процессору компьютера может быть назначена задача выполнения случайного испытания (по крайней мере, обработка испытаний пакетами) и, таким образом, работа над решением интегрирования параллельно.
Недостатки:
Медленная скорость сходимости.
Трудно оценить дисперсию функции f(x) и трудно понять, какова ошибка аппроксимации.
формул строительства — Google Поиск0009
Buch
Строительные формулы — расчет количества
www.
 quantity-takeoff.com › полезность для строительства…
quantity-takeoff.com › полезность для строительства…Полезность строительных формул и уравнений для строительных проектов; Бетон: ширина х длина х высота, деленное на 27 = необходимое количество метров бетона.
Распространенные расчетные преобразования и формулы — 1build
1build.com › blog › common-estimating-conversion…
13.04.2022 · 1build — это простое в использовании программное обеспечение для расчета стоимости строительства, которое позволяет подрядчикам участвовать в торгах с уверенностью и в режиме реального времени, местные данные о затратах. Итак…
Горизонтальные стойки: По количеству: Количество горизонтальных стоек = (Высота стены в линейных футах / Расстояние между горизонтальными стойками)
Горизонтальные стойки: По линейным футам: Общее количество стоек = Количество стоек * Длина стойки +
Вертикальных стоек: По количеству: Количество вертикальных стоек = (длина стены / расстояние между стойками по вертикали)Математические формулы для главы 10 класса – Формула построения
www.
 pw.live › Математические формулы
pw.live › Математические формулыКонструкции , получить все формулы Конструкций для быстрого пересмотра и подведения итогов всего …
Базовая математика от Construction Knowledge.net
www.constructionknowledge.net › general_tech_bas…
Что такое основные формулы площади и объема? Чтобы рассчитать, сколько бетона заказать для плиты по марке, вам нужно знать некоторые основные формулы площади и объема.
Основные области и… · Как изучить основы…
Наиболее важные формулы, используемые инженером-строителем на строительной площадке…
civilsuccessonline.com › top-important-formules -использовать…
22.11.2020 · Важные формулы ; Периметр или периферийная длина (P) = L + B + L + B = 2 x (L + B). · Объем прямоугольника (V) = площадь прямоугольника x высота …
Строительные формулы Quick-Card — Книги строителя
$ Auf Lager
В этой единственной 6-страничной ламинированной карточке вы найдете все основные математические сведения, необходимые для заключения контрактов.
 Формулы и эмпирические правила расчета конструкции …
Формулы и эмпирические правила расчета конструкции …Строительные расчетные математические формулы | Расчет бетонной смеси …
www.pinterest.com › Исследовать › Образование
17 февраля 2015 г. — Математические формулы оценки строительства необходимы профессионалам в области строительства для расчета стоимости строительства и промежуточных итогов …
Строительные формулы Карта Quick-Card: Builders Book, Inc., Мэри …
www.amazon.com › Construction-Formulas-Quick-…
Bewertung 4,7
(65) · 9,05 $ · Auf Lager
Construction Formulas Quick-Card [Builders Book, Inc., Mary Jorgensen, Kevin Choi, Kevin Choi] на Amazon.com. *БЕСПЛАТНАЯ* доставка по соответствующим предложениям.
Обучение оценке строительства: основные формулы
build-ed.com › обучение-оценка строительства-…
Ниже приведены четыре основные формулы, используемые при обучении оценке строительства, а также в строительной отрасли в целом.





 И далее по тексту мы приведем самые простые способы расчетов, адаптированных под конкретные конструкции оснований.
И далее по тексту мы приведем самые простые способы расчетов, адаптированных под конкретные конструкции оснований. Причем внутри основания могут располагаться еще и элементы для поддержки межкомнатных перегородок.
Причем внутри основания могут располагаться еще и элементы для поддержки межкомнатных перегородок.

 d\) отсчетов).
d\) отсчетов). В этой главе мы рассмотрим только случай, когда эти числа генерируются с равномерным распределением, но в некоторых случаях выгодно генерировать случайные числа с очень специфическими PDF. Мы объясним почему позже в этой главе и уроке по выборке важности. Однако суть здесь в том, что овладение искусством генерации случайных чисел очень важно, если вы хотите использовать методы Монте-Карло. Этой теме посвящена глава данного урока.
В этой главе мы рассмотрим только случай, когда эти числа генерируются с равномерным распределением, но в некоторых случаях выгодно генерировать случайные числа с очень специфическими PDF. Мы объясним почему позже в этой главе и уроке по выборке важности. Однако суть здесь в том, что овладение искусством генерации случайных чисел очень важно, если вы хотите использовать методы Монте-Карло. Этой теме посвящена глава данного урока.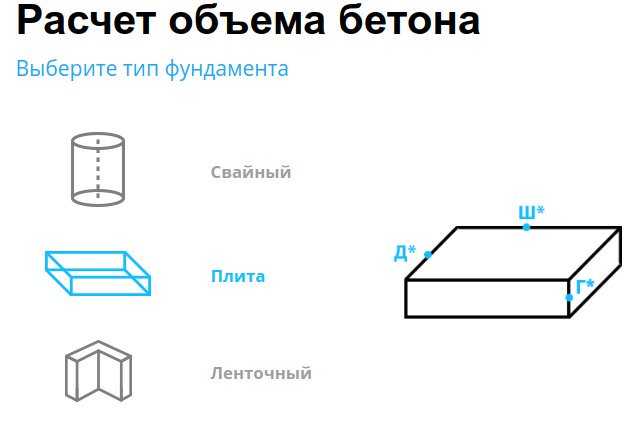 Мы часто говорим о уменьшение отклонения . Например, выборка по важности, термин, о котором вы, возможно, уже слышали, является примером такой стратегии.
Мы часто говорим о уменьшение отклонения . Например, выборка по важности, термин, о котором вы, возможно, уже слышали, является примером такой стратегии. quantity-takeoff.com › полезность для строительства…
quantity-takeoff.com › полезность для строительства… pw.live › Математические формулы
pw.live › Математические формулы Формулы и эмпирические правила расчета конструкции …
Формулы и эмпирические правила расчета конструкции …