Расчет количества пеноблоков: Онлайн калькулятор расчета количества газобетонных блоков
Сколько пеноблоков в 1м3? Расход их количества для кладки
Всё о пеноблоках
В последние годы очень популярно стало использование при строительстве пеноблоков, они имеют массу преимуществ, такие как быстрая кладка и хорошая теплоизоляция, но подробнее об этом ниже.
Расчет для строительства и перевозки
Пеноблоки для строительства стен имеют размер 600х300х200 мм, встречаются и другие размеры, но этот самый распространенный и по этой причине будем опираться именно на этот размер. Таких пенобетонных блочков в одном кубе 28 штук, без учёта раствора.
Поскольку при работе с пеноблоками получается не очень много швов, расчет с учетом раствора не ведется. Расчет пеноблоков может вестись как поштучно так и в кубометрах. Разберем на примере.
Скажем, нам необходимо построить строение. Пусть это будет двухэтажное здание, будущего кафе. Каждый этаж будет иметь 4 метра высотой, итого у нас 8 метров высоты. А размеры будут 6х12 метров. У нас там, допустим, будут большие окна размером 1.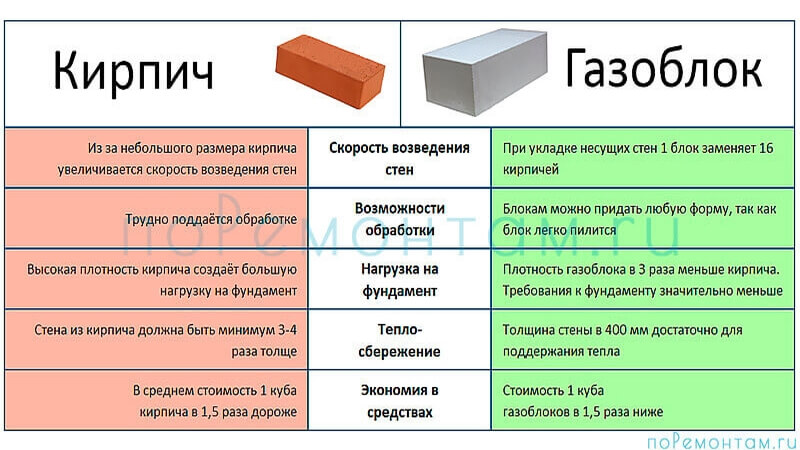
Для подсчета необходимого материала нам нужно будет выполнить следующие пункты:
- Считаем кубатуру здания. Перемножаем периметр высоту и толщину 36х8х0.3 и получаем примерно 87 кубических метров блочков.
- Вычисляем размеры проемов. На окна у нас получается 20 кубов (0.3х1.5х3х15), на маленькую дверь примерно 0.6 куба (2х0.9х0.3) а на две большие 1.8 кубов (2х1.4х0.3х2). итого вместе у нас на проёмы получится примерно 23 куба.
- Вычитаем. Из 87 мы вычитаем 23 и получаем 64 кубометра чистой кладки.
- Переводим, если требуется, в штучное количество. 64 умножаем на 28 и получаем 1792 блочка для строительства здания нам необходимо.
Вес пеноблоков также может быть различным, в зависимости от марки блочка. Самым легким блочком является блок марки Д-300 он весит всего лишь 11. 7кг, а самым тяжелым является блочок марки Д-1200 и он весит почти 50кг.
7кг, а самым тяжелым является блочок марки Д-1200 и он весит почти 50кг.
Вес зависит от плотности и количества пенообразователя, добавленного при изготовлении. Чем тяжелее пеноблок, тем он прочнее.
Основные марки и виды пеноблоков
Виды блоков по назначению:
- Теплоизоляционные
- Конструкционно-теплоизоляционные. Для производства этих блочков используют бетон марок: М-600, М-700, М-800, М-900 и имеют прочность на сжатие от 16 до 35 кг на 1 сантиметр квадратный. Возможно строительство небольших зданий из этих блочков без использования каркаса и более прочных материалов. Эти блочки не сильно уступают кирпичу в плотности, но при этом превосходят его в теплоизоляционных свойствах.

- Конструкционные. Для изготовления этих блочков используют бетон марок М-1000, М-1100 и М-1200, по своим параметрам прочности не уступает кирпичу, имеют запас прочности до 90кг на 1 квадратный сантиметр.
Также блоки различают по способу использования:
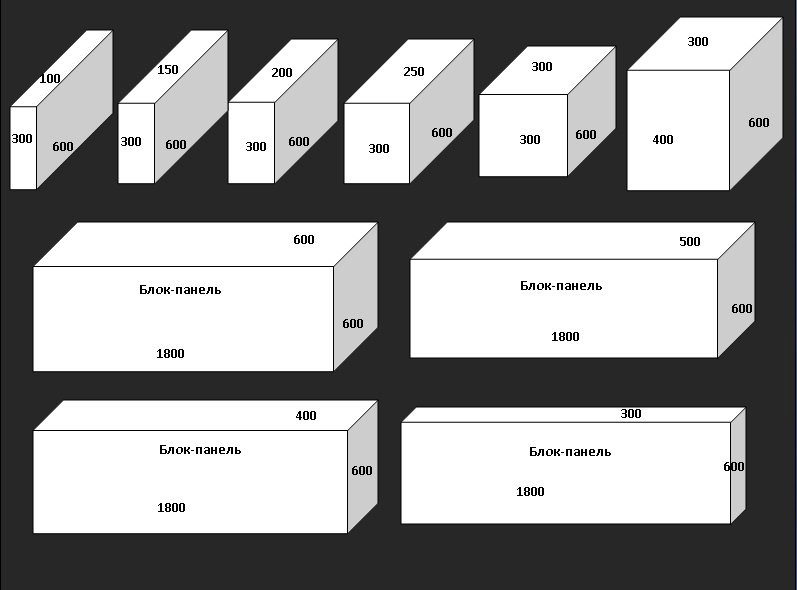
- Стеновые. Эти блочки имеют размер 200х300х600 мм.
Относительно плотности есть следующие марки:
| Название марки | Вес, кг |
| Д300 | 11.7 |
| Д400 | 15.7 |
| Д500 | 19.4 |
| Д600 | 23.3 |
| Д700 | 27.3 |
| Д800 | 31.7 |
| Д900 | 35.6 |
| Д1000 | 39.6 |
| Д1100 | 43.2 |
| Д1200 | 47.5 |
- Перегородочные блочки.
 Они имеют размер 100х300х600мм.
Они имеют размер 100х300х600мм.
Также согласно прочности и весу разделяются на следующие марки:
| Название марки | Вес, кг |
| Д300 | 5.8 |
| Д400 | 7.8 |
| Д500 | 9.7 |
| Д600 | 11.7 |
| Д700 | 13.6 |
| Д800 | 15.8 |
| Д900 | 17.8 |
| Д1000 | 19.8 |
| Д1100 | 21.8 |
| Д1200 | 23.8 |
Этот вес принято считать при влажности воздуха не более 75%, плюс у разных производителей он может различаться.
Основные плюсы и минусы пеноблоков перед другими материалами
Сперва о достоинствах:
- Практичность применения. Блочки крупные и по этой причине работа идет очень быстро. Значительно быстрее кирпичной кладки.
- Долгий срок службы
 Не меньше 50 лет.
Не меньше 50 лет. - Дополнительная теплоизоляция. Благодаря пористой структуре блочки замечательно держат тепло. Плюс из-за малого количества швов минимальное количество температурных мостиков.
- Шумоизоляция. Опять же из-за пористой структуры.
- Минимальный расход клеящего раствора. Особенно когда используют клей и наносят его гребенчатым шпателем.
- Малый вес. Один блочок заменяет 20 кирпичей. Самый тяжелый блочок весит 50 кг, а 20 кирпичей не меньше 80 кг.
- Не подвержен гниению.
- Доступная цена.
Ну, а теперь небольшие недостатки:
- Боязнь сырости. Это, пожалуй, главный недостаток, при возведении наружных стен необходимо последующие работы по закрытию блочков от внешних воздействий.
- Прочность. Относительно этой характеристики блочки уступают кирпичу.
Производство блочков
- Начинается всё с приготовления смеси для будущих пенобетонных блочков.
 Она состоит из бетона и пенообразователя. Пропорции зависят от необходимой марки.
Она состоит из бетона и пенообразователя. Пропорции зависят от необходимой марки. - Далее, идет образование блочков из готовой субстанции.
Есть два способа:- Заливка смеси в специальные формы. Является более быстрым но менее качественным методом производства.
- Резка формованной смеси с помощью струны. Такой метод более трудоёмкий но блочки обладают более хорошими гранями.
- Последний этап — это сушка и набор пеноблоков необходимой прочности.
Есть два варианта:- Естественная сушка, тратится 12 часов.
- Пропаривание блочков в специальной комнате. Происходит всё за пару часов.
Прочитав эту статью, вы узнали всю необходимую информацию о пеноблоках. И теперь с уверенностью можете приобрести именно то, что вам нужно.
| Единица измерения | Размер кирпича | Без учета растворных швов, шт.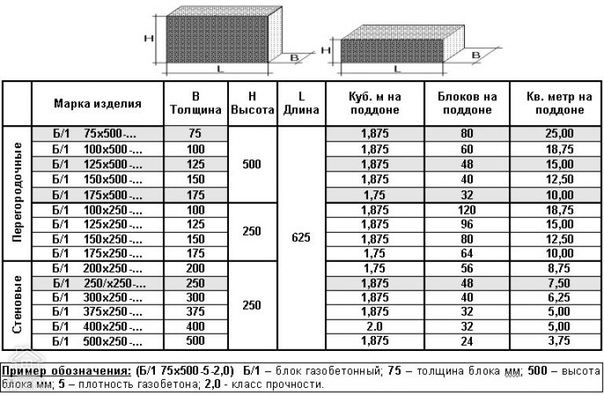 | С учетом растворных швов, шт. |
| 1 куб.м. кладки | Одинарный | 512 | 400 |
| Утолщенный | 302 | ||
| Двойной | 242 | 200 | |
| 1 кв.м. кладки в 0,5 кирпича (толщина кладки 12 см) | Одинарный | 61 | 51 |
| Утолщенный | 45 | 39 | |
| Двойной | 30 | 26 | |
| 1 кв.м. кладки в 1 кирпич (толщина кладки 25 см) | Одинарный | 128 | 102 |
| Утолщенный | 78 | ||
| Двойной | 60 | 52 | |
1 кв. м. кладки в 1,5 кирпича м. кладки в 1,5 кирпича(толщина кладки 38 см) | Одинарный | 189 | 153 |
| Утолщенный | 140 | 117 | |
| Двойной | 90 | 78 | |
| 1 кв.м. кладки в 2 кирпича (толщина кладки 51 см) | Одинарный | 256 | 204 |
| Утолщенный | 190 | 156 | |
| Двойной | 120 | 104 | |
| 1 кв.м. кладки в 2,5 кирпича (толщина кладки 64 см) | Одинарный | 317 | 255 |
| Утолщенный | 235 | 195 | |
| Двойной | 150 | 130 |
Расчет количества пеноблоков для строительства дома
Когда речь идет о строительстве дома, следует не только спроектировать дом, но и подобрать строительный материал, из которого он будет возведен, и рассчитать их сумму. На данный момент достаточно популярным является строительство дома из пенобетона, на это имеется немалое множество причин: он обладает высокой прочностью, высокой влагостойкостью, низкой теплопроводностью, простотой возведения. Однако, прежде чем начать строительство, необходимо произвести расчет количества пеноблоков. Сделать это не составит особых сложностей, ведь для просчета нужно только знать простые математические правила.
На данный момент достаточно популярным является строительство дома из пенобетона, на это имеется немалое множество причин: он обладает высокой прочностью, высокой влагостойкостью, низкой теплопроводностью, простотой возведения. Однако, прежде чем начать строительство, необходимо произвести расчет количества пеноблоков. Сделать это не составит особых сложностей, ведь для просчета нужно только знать простые математические правила.
Преимущества пеноблока.
Расчет пеноблоков производится с небольшим запасом, но погрешность должна быть невелика.
Исходные данные
Схема расчета пеноблока для строительства дома.
- размеры строения: длина высота, толщина стен, включая внутренние;
- количество и размеры дверных и оконных проемов.
В среднем толщина стен составляет 30 см, что является равным ширине стандартного блока из пенобетона или газобетона.
Рассчитывая пенобетон, не стоит забывать и про то, что при транспортировке материал может повредиться. Конечно, точно сказать о процентном соотношении сложно. Но вы всегда можете узнать у продавца примерный процент, что даст вам возможность правильно рассчитать необходимую сумму пенобетонных блоков.
Конечно, точно сказать о процентном соотношении сложно. Но вы всегда можете узнать у продавца примерный процент, что даст вам возможность правильно рассчитать необходимую сумму пенобетонных блоков.
Несколько способов расчета
1 способ. Для этого следует перемножить периметр сооружения на его высоту, благодаря чему вы получите квадратуру наружных стен. Из полученного значения необходимо вычесть квадратуру оконных и дверных проемов. Данные, которые получились в итоге, нужно разделить на размер блока из пенобетона. Сколько необходимо пенобетона, вычислить несложно, для этого нужно высоту умножить на ширину блока.
Схема возведения стен из пенобетонных блоков.
Однако мы высчитали только, сколько пенобетонных блоков нужно для строительства самой коробки дома без учета внутренних перегородок. Для вычисления необходимого их числа для внутренних перегородок нужно воспользоваться той же схемой, что и для внешних несущих стен. Эти просчеты делаются отдельно, вследствие того что внутренние перегородки в основном имеют меньшую толщину, а значит, вам понадобится пенобетон других размеров. Иными словами, в конце расчетов вы получите нужное количество материала для внешних стен и для внутренних, то есть две цифры. Зная нужный объем, вы сможете приобрести строительный материал, но не забудьте о проценте лома.
2 способ. По большому счету этот способ также сводится к вычислению суммы пенобетона для строительства дома, но в данном варианте немного другая суть. Вам также нужно вычислить объем для внутренних и внешних стен. Делается это таким образом: ширина пеноблока умножается на высоту, дальше нужно 1 м2 разделить на полученную цифру. Таким образом вы получите количество материала для строительства 1 м2 дома. Затем следует разделить квадратуру наружных стен на полученный объем материала на 1 м2 и квадратуру внутренних перегородок – на объем пенобетона, необходимый на строительство 1 м2. Для второго способа тоже нужно делать просчеты с вычетом дверных и оконных проемов и, конечно же, взять погрешность на лом.
Если же поставщик реализует пенобетон в кубах, то необходимо просчитать нужный объем материала в м3. Это сделать несложно, нужно высчитать габаритные размеры 1-го пенобетонного блока, для этого необходимо перемножить ширину, высоту и длину блока. Затем следует 1 м3 разделить на полученный объем, соответственно, вы получите количество строительного материала в 1 м3, после чего общее количество для постройки дома делите на полученную цифру. Таким простым способом вы получите кубический объем пенобетонного материала.
Помните! При просчете кубического объема расчет для наружных и внутренних стен нужно производить отдельно.
Если вы не хотите заморачиваться с просчетами и вычислениями, то вы всегда можете построить дом с использованием материала одного размера. При расчете в данном случае вы делаете все то же самое, причем можете выбрать как первый, так и второй вариант вычисления, только считаете сразу для внутренних и внешних стен одновременно, с вычетом объема оконных и дверных проемов.
Макет дома из газобетонных блоков.
Иными словами, пенобетон – это достаточно удобный стройматериал, причем не только для возведения сооружения, но и для просчетов. А что касается постройки, то с помощью этого стройматериала дома строятся достаточно быстро, более того, они характеризуются надежными и качественными сооружениями.
Такими простыми способами вы можете легко и просто сделать все необходимые просчеты и, самое главное, не прибегая к посторонней помощи. Для этого нужно только вооружиться рулеткой, листом бумаги, ручкой или калькулятором.
Конечно, можно воспользоваться онлайн-калькуляторами, которые в автоматическом режиме просчитают нужное вам число пенобетонных блоков для постройки дома, но если вы знаете все необходимые параметры, а вы их должны знать, то и самостоятельно рассчитать количество пеноблоков не составит никакого труда.
Кстати, некоторые профессионалы-строители утверждают о том, что для каждого помещения имеются свои стандарты просчетов, но в то же время вы сами решаете, какой толщины будут ваши стены и какую высоту будет иметь дом. Ведь вы можете построить дом в два пеноблока либо в один, хотя для пеноблочного строительства два камня не используется, так как вы всегда можете приобрести блок того размера, который вам необходим. А здесь есть где разгуляться, ведь рынок стройматериалов изобилует не только широким ассортиментом моделей и фирм, но и габаритных размеров.
Удачного вам строительства дома из пено- и газобетона и изначально правильных расчетов!
РАСЧЁТ ПЕНОБЛОКОВ ДЛЯ СТРОИТЕЛЬСТВА ДОМА. Пример расчета
С чего начинается строительство дома? Конечно же, с проектирования и всевозможных расчетов. Особенно важен для хозяина расчет пеноблоков для строительства дома, ведь от их количества зависит финансовая сторона возведения жилища.
На самом деле, вычислить количество пеноблоков, которые потребуются для строительства любого обособленного объекта, вовсе не так сложно. Для этого нужно просто разобраться с принципами расчёта.
Вполне очевидно, что количество необходимых для строительства блоков прямо пропорционально зависит от размеров запланированного сооружения. Не следует забывать, что из этого материала можно выстроить здание, имеющее не более трёх этажей. Важен также и состав пеноблоков.
Исходные данные
Рассмотрим пример расчёта для гипотетического двухэтажного здания со сторонами в 15 метров и не имеющего мансарды. Определяясь с высотой этажей, следует иметь в виду, что первый этаж обычно имеет несколько большую высоту, чем второй. Примем в качестве исходных следующие основные величины:
- Высота цокольного этажа 2,8 м, а второго лишь 2,65 м.
- Основные стены дома будут толщиной 40 см.
- Общая длина внутренних перегородок первого этажа 15 м.
- Общая длина внутренних перегородок второго этажа 15 м.
- Толщину всех перегородок на обоих этажах примем за 30 см.
Пример расчёта
Условимся, что расчёт пеноблоков для строительства дома будем проводить в метрах:
- Для расчёта объёма пеноблоков, потребующихся на строительство первого этажа здания, периметр здания умножается на толщину, заданную для внешних стен и высоту первого этажа:
4 х 15 х 0,4 х 2,8 = 67,2 куб. м блоков. Из полученного объёма можно было бы вычесть пустоты оконных и дверных проёмов, но этого лучше не делать, поскольку сэкономленные блоки могут быть востребованы в качестве запасных. Ведь некоторые блоки придётся резать и придавать им необходимую форму. - Для второго этажа объём блоков рассчитывается точно так же – путём перемножения соответствующих параметров, в результате чего получается совокупный необходимый объём материала:
4 х 15 х 0,4 х 2,65 = 63,6 куб. м блоков.
- Дальше рассчитывается объём пеноблоков, необходимых для возведения перегородок. Это также простейшая задача: длина перегородки умножается на её толщину и высоту:
для первого этажа 15 х 0,3 х 2,8 = 12,6 куб. м блоков
для второго этажа 15 х 0,3 х 2,65 = 11,93 куб. м блоков
На оба этажа для перегородок потребуется в сумме 24,53 куб. м материала. - Суммируем объёмы блоков для определения общего количества блоков для возведения дома:
Для наружных стен понадобится 130,8 куб. м (67,2 + 63,6) блоков толщиной 40 см.
Для межкомнатных перегородок потребуется 24,53 куб. м более тонких блоков (30 см).
Для кладки газобетонных или пеноблоков можно использовать не только стандартный цементный раствор, но и специальный кладочный клей. Расход последнего на кубометр блоков составляет примерно 25 кг, значит, его общая необходимая масса равна:25 х (130,8 + 24,63) ≈ 3886 кг.
Поделиться этой статьей в социальных сетях
Калькулятор для расчета пеноблоков для строительства дома онлайн
Для чего нужен калькулятор для расчета пеноблоков
Калькулятор расчета пеноблоков для строительства дома используется для того, чтобы подсчитать число и особенности блоков из пеноблока, чтобы возводить стену жилых строений и нежилых, и иных строений, учитывая фронтонные, и так далее. Подсчет числа используемых тканей, среди которых песчанно-цементный смесей и цена материалов.
Пенобетонные блоки представляют собой разновидности ячеистого характера бетона, в основе которых кроме жидкости, цемента с песком добавляются химического характера пенообразователь. С помощью пенообразователя, этот материал можно получить простым и обладает высокой надежностью, чтобы препятствовать внешней нагрузке.
Пенобетон получил широкое применение в следующих видах строительных работ:
- Блочное строение стен
- Монолитная заливка
- Применение как тепло- и звукоизоляционный материал.
Надежность этого бетона основана из его плотности, чем этот показатель более, тем выше надежность. Однако это правило может работать лишь, если соблюдать все нормы в производственном процессе. От типа изготовления основано качество смеси. Процесс производства очень простой, вследствие чего он очень популярен. Однако в этом случае это большой недостаток, потому что можно осуществить производство в «гаражных» условиях, отрицательно может отражаться на качественных характеристиках.
Пенобетон имеет ряд достоинств:
- Пониженная теплопроводность
- Пониженная объемная масса
- Простота обработки механическим способом
Инструкция по подсчету числа пеноблока
Можно подсчитать цену пеноблоков благодаря необыкновенному онлайн калькулятору например для гаража или бани. Для правильных подсчетов вводим габариты строения и численные данные пеноблока: стоимость кубометра и габариты блока. Стоимость кладки можно посчитать очень быстро
Вводим информацию в ячейки онлайн калькулятора для расчета стен:
- Периметр стен строения.
- Примерную высоту вместе с толщиной стены.
- Толщину кладки и смеси.
- Число, ширину и высоту дверей и окон.
Программа, благодаря которой подсчитывается число пеноблоков — имеет загруженные базы оо обыкновенных габаритах пеноблоков , толщины смеси в кладке. Подбирайте материал лишь когда работает настоящий мастер.
Как рассчитать количество пеноблоков для строительства дома
Строительство любого объекта начинается с составления проекта и сметы. И если расчетом нужного количества материалов на производстве занимаются специалисты, то при самостоятельном возведении частного дома или других построек застройщику приходится заниматься этим самому. Как правильно рассчитать количество пеноблоков при возведении частного здания именно из этого материала? Решить столь важную задачу при возведении дома или хозпостройки совсем не сложно, если знать и учитывать при этом несколько важных нюансов.
Преимущества материала
Вспененный бетон в настоящее время — достаточно популярный материал. Он незаменим там, где невозможно использовать другие виды стройматериалов – кирпич, камень, дерево. Используют пеноблоки, в зависимости от их марки, для решения разного вида задач:- Строительства цокольных уровней.
- Возведения несущих внутренних и наружных стен.
- Создания перегородок.
- Кладки контурного дополнительного слоя.
Причиной столь высокой популярности блоков из вспененного бетона являются их достоинства. Это:
- Экологическая чистота – для изготовления блоков используется песок, цемент и вспенивающее вещество.
- Теплосберегающие свойства. Пористая структура – отличное препятствие для холода и тепла, благодаря этому в доме сохраняется стабильная температура.
- Стойкость против воздействия химических смесей, огня, перепадов температуры.
- Небольшой вес, что позволяет использовать материал для возведения зданий на нестабильных грунтах и не создавать под них тяжелые мощные фундаменты.
- Быстрота укладки. Изделия гораздо больше по размерам чем кирпич, поэтому кладка стен будет осуществляться гораздо быстрее.
- Простота обработки. Пеноблоки при необходимости легко укоротить для получения элемента нужного размера. Кроме того, в них несложно создавать каналы, чтобы проложить трубы, электрическую проводку и другие коммуникации.
Подсчет материалов
Чтобы рассчитать количество пеноблоков для строительства дома, необходимо учитывать следующие параметры:
- Объем несущих элементов.
- Площадь здания. Конкретно – площадь стен.
- Количество погонных метров.
Так как стандартных показателей по данным замерам нет, поэтому при подсчетах придется исходить из габаритов здания и самих блоков.
Выпускаются пеноблочные изделия разных габаритов. Для внешних стен используются блоки размером 20 х 30 х 60 см. Для возведения несущих стен их укладывают на ребро рядами так, чтобы слой был толщиной в 2 элемента. Тогда толщина стен будет достаточной (40 см) и выдержит все нагрузки. Если выкладывать в один слой, толщина стены будет всего 30 см и этого недостаточно для поддержания веса самих стен и кровли.
Далее предстоит рассчитать количество пеноблоков для внутренних перегородок, которые не являются несущими. Для их возведения подойдут изделия размером 10 х 30 х 60 см.
Особенности подсчета нужного количества материала
Чтобы правильно и грамотно рассчитать количество пеноблоков, необходимо участки здания разделить на группы:
- Первая – несущие внешние стены.
- Вторая – несущие внутренние стены.
- Третья – внутренние перегородки, которые не несут никаких нагрузок.
При выборе материала необходимо учитывать и этажность будущего здания. Для внутренних простенков, на которые выпадает небольшая нагрузка, подойдет пенобетонные изделия марки D400 или D500. Для двухэтажного дома понадобится приобретать более прочные пеноблоки — марки D600 либо D700. Если строится здание трехэтажное, нужны пеноблоки марки D800 и D900.
Чтобы рассчитать количество пеноблоков, разбивают объект на группы, подсчитывают параметры каждого из них. Из данных показателей вычисляют площадь, которую занимают окна и двери. Причем двери как наружные, так и внутренние.
К полученной цифре обязательно нужно добавлять определенное количество блоков их вспененного бетона – на случай, если попадутся поврежденные изделия или будет неправильно сделан срез и блок не подойдет, понадобится использовать следующий. Другими словами, небольшой запас всегда должен быть.
Варианты подсчета
Рассчитать количество пеноблоков для строительства можно двумя способами – по рядам и по объему. Каждый из них обладает своими преимуществами. Выбор конкретного способа совсем не обязателен: можно воспользоваться обеими и сравнить полученные результаты.Если они совпадут, значит, все посчитано правильно, если нет – где-то допущена ошибка и понадобится перепроверить все цифры. Как подсчитать, используя каждый способ? Об этом далее.
Подсчет по квадратуре
Чтобы было проще понять, как рассчитать количество пеноблоков на дом, лучше всего разобрать особенности этого действия на примере. Для начала высчитывают площадь здания. Вычет оконных и дверных проемов делают позже. Для начала подсчет выполняют первого этажа:- Вычислить периметр: 8 х 2 + 8 х 2 = 32 м.
- Поделить полученную цифру на длину пеноблока (0,6м). 32 м : 0,6 м = 54 шт.
- Посчитать, сколько будет рядов – высоту этажа (3 м) поделить на высоту блока (0,2): 3,0 : 0,2 = 15.
- Теперь осталось количество блоков одного ряда умножить на количество рядов: 54 х 15 = 810 шт.
Теперь осталось вычесть из полученной цифры те изделия, которые будут лишними из-за наличия окон и дверей. Так как изначально планируется запас в размере 8-10%, то можно проемы не высчитывать. Но для примера все же высчитать стоит. Если общий объем окон на первом этаже составляет 20 кв. м, эту цифру умножают на 5,56 и получают минус 111 штук от общей цифры. Точно так же производят расчет остальных этажей, если постройка классическая. Если планируется строительство мансарды, подсчет нужно будет изменить, высчитав только треугольные фронтоны. Для этого длину мансарды (8 м) умножить на высоту (3 м) и полученный показатель поделить на 2, получится 12 м : 0,6 м = 20 штук на одну сторону.
Подсчет по объему
Чтобы рассчитать количество пеноблоков по объему, используют те же данные размеров дома: высота 3 м, периметр 32 м. После умножения данных получается объем 96 м. Теперь осталось умножить этот показатель на 0,3 – высоту кладки. Получится 28,8 кубометров. Один кубометр – это 27,7 стандартных пеноблоков. Умножив на количество необходимых кубов можно получить показатель нужного количества изделий – 798 штук. Это – на возведение первого этажа.
Вывод
Рассчитать количество пеноблоков на дом совсем не сложно, если имеются данные всех показателей – площади, объема, ширины и высоты уровней, размеры мансарды, габариты проемов. Благодаря знанию всех цифр можно идеально точно высчитать, сколько материала понадобится. Запас не должен превышать 10-12 % от общего количества материала. Это позволит узнать и сумму средств, необходимых на приобретение материала для строительства, и особенности его транспортировки, складирования и хранения.Если же не хочется производить никаких расчетов, можно воспользоваться калькулятором на любом из строительных сайтов в Сети или обратиться в проектное бюро.
Бесплатный калькулятор для линейных функций
- Анализ
- Область между функциями
- Изменение знаков
- Набросок кривой
- Деривация
- Функции поиска
- Функции
- Точки перегиба
- Интегральное вычисление
- 000
- Пересечение
- функций Монотонность
- Корни
- Касательные
- Точки поворота
- Уравнения и термины
- Биномиальные формулы
- Уравнения
- Дробные уравнения
- Дробные члены
- Уравнения с дробными числами
- Решение уравнений
- Системы уравнений
- p, q-Формула
- Функции
- Функции возведения в степень
- Линейные функции
- Полиномиальные развлечения ctions
- Квадратичные функции
- Функции преобразования
- Вершинная форма
- Дроби
- Сложение дробей
- Отмена дробей
- Десятичные дроби
- Вычисление дробей
- 000
- 000 Дробные вычисления
- 000 Дроби
- Вычислить gcd
- Делимость
- Факторизация на простые множители
- Набор делителей
- lcm
- Геометрия
- Дуга окружности
- Расчет площади
- Cone
- 0003 Cone
- Cuboid Цилиндр
- Теорема о пересечении
- Линии
- Призмы
- Пирамида
- Четырехугольник
- Прямоугольник
- Ромб
- Калькулятор ромбов
- Прямоугольный треугольник
- Сфера
- Квадрат
- Трапеция
- Калькулятор треугольников
- Тригонометрия
- Объем
- Векторный анализ
- Поперечное произведение
- Плоскость точек расстояния
- 9000 Линия пересечения 9000 9000 Линия пересечения через точки
- Нормирующие векторы
- Уравнения плоскости
- Пересечение плоскости
- Точка на прямой
- Точка на плоскости
- Калькулятор четырехугольника (векторы)
- Преобразование уравнений плоскости
- Угол пересечения вектора Стохастик
- Модель урны
- Базовая арифметика
- Сложение
- Деление чисел
- Умножение
- Вычитание
- Математика для повседневной жизни 900 05
- Антипропорциональность
- Расчет процентов
- Система счисления
- Процент
- Пропорциональность
- Римские числа
- Правило трех
- Единицы
Мужчины
Число протонов и нейтронов
Число протонов и нейтронов — атом определяет элемент
Самый чистый тип атома называется элементом.Атомы состоят из трех видов более мелких частиц: протонов, нейтронов и электронов. Протоны и нейтроны состоят из еще более мелких частиц, называемых кварками. Количество протонов, количество нейтронов и количество электронов в атоме определяют, что это за элемент.
- Атомы состоят из трех видов маленьких частиц: протонов, нейтронов и электронов
- Атомы должны иметь одинаковое количество протонов и электронов
Ядро находится в середине атома и содержит протоны и нейтроны.Эти более мелкие частицы — протоны, нейтроны и электроны — обладают разными свойствами.
Число протонов и нейтронов
Число протонов и нейтронов — что такое электроны?
Напоминание об определении перед тем, как научиться вычислять числа. Электроны — это крошечные, очень легкие частицы, имеющие отрицательный электрический заряд. В атомах должно быть равное количество протонов и электронов.
Число протонов и нейтронов — что такое протоны?
Протоны намного крупнее и тяжелее электронов и имеют положительный заряд.В атомах должно быть равное количество протонов и электронов.
Число протонов и нейтронов — что такое нейтроны?
Нейтроны большие и тяжелые, как протоны, однако нейтроны не имеют электрического заряда.
Число протонов и нейтронов — Как найти атомный номер элемента
Каждый элемент имеет уникальный символ элемента и уникальный атомный номер, доступ к которому можно получить через Периодическую таблицу с атомной массой.
- Определение: атомный номер — это количество протонов в атоме элемента.
Периодическая таблица — действительно важный инструмент для студентов-химиков, позволяющий им узнавать названия элементов по их атомному номеру. Химические элементы периодической таблицы перечислены в порядке атомного номера. Вы также можете найти в нижней части этой страницы краткую таблицу всех элементов и их атомных номеров в числовом порядке.
Число протонов и нейтронов — Как найти число протонов — Примеры
Атомный номер основан на количестве протонов в атоме элемента.(Примечание: атомы также должны иметь равное количество протонов и электронов.) Итак, если мы знаем атомный номер элемента, то мы также знаем, сколько протонов в элементе.
- Пример 1 — Число протонов в золоте: элемент Золото (символ Au) имеет атомный номер 79. Любой атом, который содержит ровно 79 протонов в своем ядре, является атомом золота. Таким образом, число протонов в атоме золота составляет 79.
- Пример 2 — Число протонов в серебре: элемент Серебро (символ Ag) имеет атомный номер 47.Любой атом, который содержит в своем ядре ровно 47 протонов, является атомом серебра. Таким образом, число протонов в атоме серебра равно 47.
- Пример 3 — Число протонов в неоне: элемент Неон (символ Ne) имеет атомный номер 10. Любой атом, который содержит ровно 10 протонов в своем ядре, является атомом. из золота. Таким образом, число протонов в атоме золота равно 10.
Добавление или удаление протонов из ядра атома создает другой элемент. Например, , удалив одного протона из атома Золота, создает атом Платины (Платина имеет атомный номер 78, следовательно, количество протонов = 78.) Добавление одного протона из атома Золота создает атом Меркурия (Меркурий имеет атомный номер 80, следовательно, количество протонов = 80.). Обратитесь к таблице ниже и определите количество протонов в различных элементах.
Число протонов и нейтронов — Как найти число атомной массы
Расчет числа нейтронов в атоме или элементе немного сложнее. Для этого расчета вам необходимо установить атомный вес, исходя из которого вы сможете установить томическое массовое число A .Атомный вес или масса — это, по сути, измерение общего числа частиц в ядре атома. Атомное массовое число определяется округлением атомного веса до ближайшего целого числа. Периодическая таблица с атомной массой даст вам атомный вес или атомную массу элементов.
Атомное массовое число = атомный вес элемента, округленное до ближайшего целого числа
Итак, если мы знаем количество протонов и нейтронов в атоме (элементе), мы можем определить атомное массовое число
- Пример 1 — Атомная масса золота: элемент Золото (символ Au) имеет атомный номер 79.Таким образом, число протонов в атоме золота составляет 79. Атомная масса золота составляет 196,97. Округлить до ближайшего целого числа. Следовательно, атомное массовое число золота составляет 197.
- Пример 2 — Атомная масса серебра: элемент Серебро (символ Ag) имеет атомный номер 47. Таким образом, количество протонов в атоме серебра равно 47. Серебро имеет атомный номер Масса масса 107,87. Округлить до ближайшего целого числа. Следовательно, атомное массовое число серебра составляет 108.
- Пример 3 — Атомная масса неона: элемент Неон (символ Ne) имеет атомный номер 10.Таким образом, количество протонов в атоме неона равно 10. Неон имеет атомную массу 20,18. Округлить до ближайшего целого числа. Следовательно, атомное массовое число неона равно 20.
Число протонов и нейтронов — как найти число нейтронов
Мы можем определить количество нейтронов в атоме или элементе, используя уже имеющуюся информацию. Чтобы найти количество нейтронов, вычтите атомное массовое число из атомного номера.
Количество нейтронов = массовое число — атомное число
- Пример 1 — Элемент Золото (символ Au).Атомное массовое число золота составляет 197 и имеет атомный номер 79. Число нейтронов в золоте составляет 197 — 79 = 118
- Пример 2 — Элемент Серебро (символ Ag). Число нейтронов в серебре: № атомной массы. серебра 108 и имеет атомный номер 47. Число нейтронов в неоне 108 — 47 = 61
- Пример 3 — Элемент Неон (символ Ne). Атомное массовое число неона 20 и атомный номер из 10. Число нейтронов в неоне составляет 20-10 = 10
Добавление или удаление протонов из ядра атома создает другой элемент, но добавление или удаление нейтронов из ядра атома не создать другой элемент.Сравните количество нейтронов и протонов в таблице ниже.
Числовой список атомных номеров элементов
Числовой список атомных номеров элементов
Максимальные и минимальные значения — подход к исчислению
10
Поворотные точки графика
МЫ ГОВОРИМ, ЧТО ФУНКЦИЯ f ( x ) имеет относительное максимальное значение при x = a ,
, если f ( a ) на больше , чем любое значение, непосредственно предшествующее или последующее.
Мы называем это «относительным» максимумом, потому что другие значения функции на самом деле могут быть больше.
Мы говорим, что функция f ( x ) имеет относительное минимальное значение в x = b ,
, если f ( b ) на меньше , чем любое значение, непосредственно предшествующее или последующее.
Опять же, другие значения функции могут быть меньше. С таким пониманием мы откажемся от термина «относительный».
Значение функции, значение y , максимальное или минимальное, называется экстремальным значением.
Теперь, что характеризует график при экстремальном значении?
Касательная к кривой горизонтальна . Мы видим это в точках A и B . Наклон каждой касательной линии — производной при вычислении a или b — равен 0.
f ‘ ( x ) = 0.
Более того, в точках непосредственно к слева от максимума — в точке C — наклон касательной положительный: f ‘ ( x )> 0. В то время как в точках непосредственно к справа — в точке D — наклон отрицательный: f ‘ ( x )
Другими словами, максимум f ‘ ( x ) меняет знак с + на -.
Как минимум, f ‘ ( x ) меняет знак с — на +. Мы видим, что в точках E и F .
Мы также можем наблюдать, что максимум при A график вогнут вниз. (Тема 14 Precalculus.) Хотя, как минимум, на B , она вогнута вверх.
Значение x , при котором функция имеет максимум или минимум, называется критическим значением.На рисунке —
— критические значения: x = a и x = b .
Критические значения определяют точки поворота, в которых касательная параллельна оси x . Критические значения — если таковые имеются — будут решений от до f ‘ ( x ) = 0.
Пример 1. Пусть f ( x ) = x 2 — 6 x + 5.
Есть ли критические значения — какие-нибудь поворотные моменты? Если да, то определяют ли они максимум или минимум? И каковы координаты на графике этого максимума или минимума?
Решение . f ‘ ( x ) = 2 x — 6 = 0 означает x = 3. (Урок 9 алгебры)
x = 3 — единственное критическое значение. Это x — координата поворотной точки.Чтобы определить y -coordinate, оцените f при этом критическом значении — оцените f (3):
| f ( x ) | = | x 2 — 6 x + 5 |
| f (3) | = | 3 2 — 6 · 3 + 5 |
| = | −4. | |
Крайнее значение — 4. Чтобы увидеть, является ли он максимумом или минимумом, в этом случае мы можем просто посмотреть на график.
f ( x ) — парабола, и мы видим, что точка поворота минимальна.
Найдя значение x , где производная равна 0, мы обнаружили, что вершина параболы находится в точке (3, −4).
Но мы не всегда сможем посмотреть на график.Алгебраическим условием минимума является то, что f ‘ ( x ) меняет знак с — на +. Мы видим это в точках E , B , F выше. Величина наклона увеличивается.
Теперь сказать, что наклон увеличивается, значит сказать, что при критическом значении вторая производная (Урок 9), которая представляет собой скорость изменения наклона, равна положительным .
Опять же, вот f ( x ):
| f ( x ) | = | x 2 — 6 x + 5. |
| f ‘ ( x ) | = | 2 x — 6. |
| f ‘ ( x ) | = | 2. |
f » при критическом значении 3 — f » (3) = 2 — положительно. Это алгебраически говорит нам, что критическое значение 3 определяет минимум.
Достаточные условия
Теперь мы можем сформулировать эти достаточные условия для экстремальных значений функции при критическом значении a :
Функция имеет минимальное значение x = a , если f ‘ ( a ) = 0
и f’ ‘ ( a ) = положительное число.
Функция имеет максимальное значение x = a , если f ‘ ( a ) = 0,
и f’ ‘ ( a ) = отрицательное число.
В случае максимума наклон касательной равен , при уменьшении — наклон от положительного к отрицательному. Мы видим, что в точках C , A , D .
Пример 2. Пусть f ( x ) = 2 x 3 — 9 x 2 + 12 x — 3.
Есть ли крайние значения? Во-первых, существуют ли какие-либо критические значения — решения для f ‘ ( x ) = 0 — и определяют ли они максимум или минимум? И каковы координаты на графике этого максимума или минимума? Где поворотные моменты?
| Решение . f ‘ ( x ) = 6 x 2 -18 x + 12 | = | 6 ( x 2 -3 x + 2) |
| = | 6 ( x — 1) ( x — 2) | |
| = | 0 | |
подразумевает:
x = 1 или x = 2.
(Урок алгебры 37.)
Это критические значения. Каждый определяет максимум или минимум? Чтобы ответить, мы должны оценить вторую производную для каждого значения.
| f ‘ ( x ) | = | 6 x 2 -18 x + 12. |
| f ‘ ( x ) | = | 12 x — 18. |
| f ‘ (1) | = | 12-18 = −6. |
Вторая производная отрицательна. Таким образом, функция имеет максимум x = 1.
Чтобы найти y -coördinate — крайнее значение — на этом максимуме мы оцениваем f (1):
| f ( x ) | = | 2 x 3 — 9 x 2 + 12 x — 3 |
| f (1) | = | 2–9 + 12–3 |
| = | 2. | |
Максимум происходит в точке (1, 2).
Затем, x = 2 определяет максимум или минимум?
| f ‘ ( x ) | = | 12 x — 18. |
| f ‘ (2) | = | 24 — 18 = 6. |
Вторая производная положительна.Таким образом, функция имеет минимум x = 2.
Чтобы найти y -coördinate — экстремальное значение — на этом минимуме, мы оцениваем f (2):
| f ( x ) | = | 2 x 3 — 9 x 2 + 12 x — 3. |
| f (2) | = | 16–36 + 24–3 |
| = | 1. | |
Минимум находится в точке (2, 1).
Вот собственно график f ( x ):
Решения для f » ( x ) = 0 указывают точку перегиба в этих решениях, а не максимум или минимум. Пример: y = x 3 . y » = 6 x = 0 подразумевает x = 0. Но x = 0 является точкой перегиба на графике y = x 3 , а не максимум или минимум .
Другой пример: y = sin x . Решения для y » = 0 являются умножениями π, которые являются точками перегиба.
Задача 1. Найти координаты вершины параболы,
y = x 2 — 8 x + 1.
Чтобы увидеть ответ, наведите указатель мыши на цветную область.
Чтобы закрыть ответ еще раз, нажмите «Обновить» («Reload»).
Сначала решите проблему сами!
y ‘ = 2 x — 8 = 0.
Это подразумевает x = 4. Это x -кординация вершины. Чтобы найти координату y , оцените y при x = 4:
y = 4 2 -8 · 4 + 1 = −15.
Вершина находится в точке (4, −15).
Задача 2. Проверьте каждую функцию на наличие максимумов и минимумов.
a) y = x 3 — 3 x 2 + 2.
y ‘ = 3 x 2 — 6 x = 3 x ( x — 2) = 0 означает
x = 0 или x = 2.
y ‘ ( x ) = 6 x — 6.
у » (0) = −6.
Вторая производная отрицательна. Это означает, что существует максимум x = 0. Это максимальное значение составляет
.y (0) = 2.
Далее,
y ‘ (2) = 12 — 6 = 6.
Вторая производная положительна. Это означает, что существует минимум x = 2.Это минимальное значение —
.y (2) = 2 3 -3 · 2 2 + 2 = 8-12 + 2 = −2.
b) y = −2 x 3 — 3 x 2 + 12 x + 10.
При x = 1 получается максимум y = 17.
При x = −2 минимум y = −10.
c) y = 2 x 3 + 3 x 2 + 12 x — 4.
Поскольку f ‘ ( x ) = 0 не имеет реальных решений, нет крайних значений.
d) y = 3 x 4 — 4 x 3 — 12 x 2 + 2.
При x = 0 получается максимум y = 2.
При x = −1 минимум y = −3.
При x = 2 минимум y = −30.
Следующий урок: Применение максимальных и минимальных значений
Содержание | Дом
Сделайте пожертвование, чтобы TheMathPage оставался в сети.

 Они имеют размер 100х300х600мм.
Они имеют размер 100х300х600мм.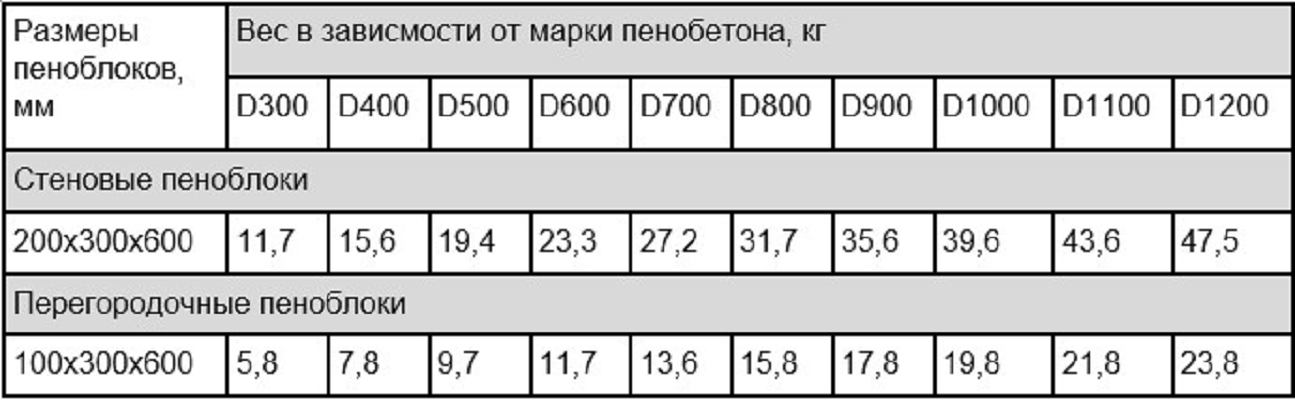 Не меньше 50 лет.
Не меньше 50 лет.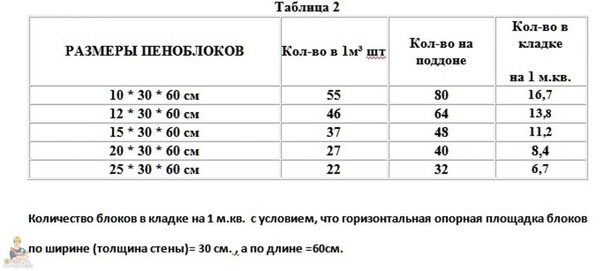 Она состоит из бетона и пенообразователя. Пропорции зависят от необходимой марки.
Она состоит из бетона и пенообразователя. Пропорции зависят от необходимой марки.