Расчет арматуры ростверка: Калькулятор Столбы-Онлайн v.1.0 — расчет столбчатого фундамента, ростверка. Расчет свайного фундамента.
Расчета свайного фундамента, столбчатого фундамента
Онлайн калькулятор по расчету буронабивных свайно-ростверковых и столбчатых фундаментов. Определение нагрузки на свайный фундамент.
Выберите тип ростверка:
Параметры ростверка:
Параметры столбов и свай:
Расчет арматуры:
Расчет опалубки ростверк:
Рассчитать
Результаты расчетов
Фундамент:
Общая длина ростверка: 0 м.
Площадь подошвы ростверка: 0 м2.
Площадь внешней боковой поверхности ростверка: 0 м2.
Общий объем бетона для ростверка и столбов (с 10% запасом): 0 м3.
Вес бетона: 0 кг.
Нагрузка на почву от фундамента в местах основания столбов: 0 кг/см2.
Расчет арматуры ростверка:
Расчет арматуры для столбов и свай:
Минимальный диаметр поперечной арматуры (хомутов):
Максимальный шаг поперечной арматуры (хомутов) для ростверка: 0 мм.
Общий вес хомутов: 0 кг.
Опалубка:
Минимальная толщина доски при опорах через каждый 1 метр: 0 мм.
Максимальное расстояние между опорами: 0 м.
Количество досок для опалубки: 0 шт.
Периметр опалубки: 0 м.
Объем досок для опалубки: 0 м3.
Примерный вес досок для опалубки: 0 кг.
Дополнительная информация о калькуляторе
Онлайн калькулятор монолитного буронабивного (свайного и столбчатого) ростверкового фундамента предназначен для расчетов размеров, опалубки, диаметра арматуры, ее количества и объема расходуемого бетона. Для определения подходящего типа конструкции фундамента обязательно проконсультируйтесь со специалистами.
Обратите внимание! В расчётах используются нормативы, приведенные в ГОСТ Р 52086-2003, СНиП 3.03.01-87 и СНиП 52-01-2003 «Бетонные и железобетонные конструкции».
Данный тип фундамента основывается на сваях или столбах, поэтому его также часто называют столбчатым либо свайным. Глубина установки и несущая способность отличает сваи от столбов.
Вершины столбов или свай связывают между собой сплошной железобетонной лентой, так называемым ростверком. Между ростверком и поверхностью земли остаётся воздушная прослойка некоторой высоты.
Основная причина для выбора ростверкового фундамента – глубокое промерзание или слабость грунта. Этот тип фундамента востребован в местах, где из-за погодных условий другие виды фундамента создавать проблематично. Забивка свай не зависит от климата, что является несомненным преимуществом ростверковой технологии. Другой её плюс – высокая скорость возведения сооружений, поскольку сваи можно подготовить заранее, а их вбивание – ускорить, пробурив в земле отверстия.
На тип ростверкового фундамента влияет материал и форма свай, характер действия на грунт, способы установки и виды непосредственно ростверка. Трудно давать типовые рекомендации, не зная самого сооружения и специфики местности, где оно строится. Перед началом проектирования следует учесть климат местности, свойства грунта, расчётные нагрузки. Безусловно, лучше всего обратиться к специалистам и последовать их рекомендациям, так как есть риск «доэкономиться» до деформации или разрушения будущего строения. Чтобы этого избежать, советуем внимательно ознакомиться с данным калькулятором. Он поможет вам рассчитать расходы при возведении стандартных конструкций и обдумать составляющие будущего фундамента.
Вы можете задать вопрос или предложить идею по улучшению данного калькулятора. Будем рады вашим комментариям!
Пояснения к результатам расчетов
Общая длина ростверка
Внешний периметр ростверка, включая длину внутренних перегородок
Площадь подошвы ростверка
Площадь нижней поверхности ростверка, которая нуждается в гидроизоляции.
Площадь внешней боковой поверхности ростверка
Площадь наружной поверхности фундамента, которая нуждается в утеплении специальными материалами.
Общий объем бетона для ростверка
Суммарный объём бетона, нужный для полной заливки фундамента с обозначенными вами параметрами. При заказе бетона возьмите запас приблизительно в 10%. При заливке могут возникнуть уплотнения, ведущие к повышенному расходу, а доставка может привезти несколько меньший объём, чем вы заказали фактически.
Вес бетона
Примерный вес бетона, который понадобится вам для фундамента. Рассчитан для бетона средней плотности.
Нагрузка на почву от фундамента в местах основания столбов
Давление, которое фундамент оказывает на почву в основании свай или столбов.
Минимальный диаметр продольных стержней арматуры для ростверка
Рассчитывается с учётом содержания продольной арматуры в площади сечения ростверка и нормативов СНиП.
Минимальное количество рядов арматуры для ростверка
Количество стержней продольной арматуры в верхнем и нижнем поясах ленты ростверка, необходимое для предотвращения естественной деформации ленты силами растяжения и сжатия.
Общий вес арматуры
Вес арматурного каркаса.
Величина нахлеста арматуры
При креплении отрезков стержней внахлест следует использовать данное значение.
Длина продольной арматуры
Общая длина арматуры для всего каркаса (с учетом нахлеста).
Минимальное количество продольных стержней арматуры для столбов и свай
Число продольных стержней арматуры располагаемое в каждом столбе или свае.
Минимальный диаметр арматуры для столбов и свай
Предельный минимальный диаметр арматуры столбов, исчисляется в соответствии с нормативами СНиП.
Минимальный диаметр поперечной арматуры (хомутов)
Минимально допустимый диаметр поперечной арматуры в соответствии с нормативами СНиП исходя из заданных параметров.
Максимальный шаг поперечной арматуры (хомутов)
Максимальный шаг хомутов, при котором арматурный каркас будет должным образом выполнять свою функцию. Следует использовать данное значение, либо уменьшить шаг хомутов.
Общий вес хомутов
Общий вес хомутов, необходимых при строительстве фундамента.
Минимальная толщина доски опалубки (при опорах через каждый метр)
Расчетная толщина досок опалубки в соответствии с ГОСТ Р 52086-2003, для заданных параметров фундамента и при заданном шаге опор. Опалубка рассчитывается для ростверка.
Количество досок для опалубки
Количество материала для опалубки заданного размера. За основу берется доска длиной 6 метров.
Периметр опалубки
Общий периметр опалубки для ростверка, включая внутренние перегородки.
Объем и примерный вес досок для опалубки
Требуемый объем пиломатериала для опалубки в кубических метрах и килограммах.
Расчёт свайного ростверка для свайного фундамента, примеры, формулы
Долговечность и надежность свайного ростверка зависит не только от соблюдения технологии его монтажа, но и от правильных расчетов. Все полученные результаты проверки переносятся на проект, который передается строителям.
Основные правила расчёта свайного ростверка, формулы и СНИП нормативы, полная информация далее на странице.
Расчет свайного фундамента с ростверком
Для проведения расчетов такого плана следует обращаться к специалистам, специализирующихся в этом профиле. Перед этим проводятся геологические изыскания, позволяющие разработать проект, соответствующий почве на стройплощадке.
Совет эксперта! Если работы по геодезическому изысканию проведены не будут, то произвести точные расчеты основания с ростверком будет невозможно. Объясняется это тем, что несущая способность определяется только на основании силы сопротивления почвы.
Рис: Схема свайно-ростверкового фундамента
Для проведения изысканий на участке бурится отверстие в почве для ее пробы и анализа. Только потом можно проводить важные расчеты.
При разработке проекта учитываются такие параметры по сваям:
- Глубина погружения.
- Диаметр сваи.
- Количество свай.
- Схема их расположения.
По ростверку:
- Форма ростверка (3 вида: высокий, повышенный, низкий).
- Диаметр.
- Устойчивость на изгиб и продавливание.
- Метод армирования.
Рис: Схематическое положения ростверка свайного фундамента
Совет эксперта! Определить высоту ростверка следует исходя из веса будущего сооружения и уровня пучинистости грунта.
Как делается расчет
Существует 2 группы, благодаря которым происходит расчет свайного фундамента.
- Прочность используемых материалов, несущая способность почвы и оснований.
- Осадка вследствие трещин, нагрузки вертикальной и движения свай.
Процесс проектирования по указанным предельным выполняется при помощи следующих формул.
Устойчивость к продавливанию:
Устойчивость на изгиб:
Устойчивость к поперечным нагрузкам:
СНиП для проведения полного расчета свайного ростверка
За основу берется два СНиПа:
- Для ростверка СНиП №2.03.01.
- Для свай СНиП №2.17.77.
Совет эксперта! Соблюдение всех рекомендаций в СНиПе является обязательным условием.
Что учитывается при расчетах
Крайне важно учитывать такие аспекты:
- Все предполагаемы нагрузки и воздействия по СНиПу.
- Несущая способность опор и основания на основе особых и сочетаемых нагрузок.
- Сочетание всех используемых материалов с почвой на стройплощадке. В этом случае берутся во внимание геодезические изыскания на предмет исследования почвы и динамических/статических испытаний ЖБИ свай. Опять же, в расчет берутся показания в СНиП.
- Обращается внимание на тип свай, они могут быть висячими или стойки. Обязательно учитывается общий вес. Не менее важны и нагрузка воздушных масс.
- В процессе расчетов, основание с ростверком представляет собой единой рамной конструкцией. Она должна воспринимать нагрузку по вертикали и горизонтали. Также изгибающая сила.
- Если почва сложная (грунтовые воды очень высоко и тому подобное), а проектная нагрузка высокая, то учитывается негативная сила трения в процессе осадки строения.
- Учитываются и другие немаловажные факторы при проектировании. Особенно те, которые непосредственно связаны с разными грунтами.
Пример расчета
Предлагаем рассмотреть пример расчета ростверкового фундамента на основе свай. Хотя в интернете есть множество подобных расчетов, если вы не имеете достаточного опыта в этом вопросе, то будет крайне сложно со всем разобраться. Хотя и так, лучше обращаться к профильным специалистам, но для общего понимания стоит узнать важные детали.
Так, учитываются при расчетах следующие данные:
- Масса постройки. Чтобы получить конкретную и точную сумму массы, то необходимо сложить массу каждого элемента строения, а, в частности: стены, стяжка пола, стропильная система, кровля, перекрытия и прочее. Для определения этой суммы необходимо использовать средний показатель конкретного строительного материала.
Рис: Вес конструктивных элементов здания
- Полезная нагрузка. В этом случае учитывается вся создаваемая нагрузка от мебели, отделки стен, бытовых приспособлений, количество проживающих человек и тому подобное. Согласно установленным нормам, на 1 м2 приходится нагрузки до 100 кг на перекрытие.
Совет эксперта! Определение полезной нагрузки происходит путем умножения площади перекрытия на 100 кг.
- Снеговая нагрузка. Для этого используются данные и нормативы для конкретного региона страны. Полученную сумму необходимо умножить на площадь всей крыши.
Рис: Карта снеговых нагрузок РФ
- Вся нагрузка на фундамент строения. В этом случае следует сложить всю массу будущего строения, нагрузку от снега в вашем регионе и полезную нагрузку. Полученный результат умножается на коэффициент надежности 1,2 (для жилого дома).
- Грузонесущая способность ЖБИ свай. Подобные расчеты выполняются согласно следующей формуле на основании геологических изысканий:
- Сколько будет опор и какая их длина. Для этого необходима информация обо всей предполагаемой нагрузке на будущее основание. Что касается длины, то она вычисляется, отталкиваясь от характера почвы. Всегда к полученному результату следует добавить 400 мм по длине.
- Это позволит выполнить сопряжение ростверка со сваями. Что касается шага между опорами, то преимущественно шаг колеблется от 2 до 2,5 метров. Свая всегда устанавливается по углам и в местах соединения стен.
Рис: Схема заглубления ЖБ свай
- Расчет ростверка. Итак, все расчеты выполняются согласно предоставленным формулам.
Совет эксперта! Помните, самостоятельно делать такие расчеты не рекомендуется, необходимо обращаться исключительно к профильным специалистам, которые имеют опыт в этом вопросе.
В большинстве случаев ростверк имеет сечение 400×300 мм. Для изготовления бетона используется цемент М200 и 300. Для армирования применяются прутья А2 и 1 Ø10-15 мм.
В нашей компании работает команда высококвалифицированных специалистов, которые обладают достаточным опытом по разработке свайного фундамента с ростверком. При этом учитываются все ГОСТы и СНиПы. За счет этого достигается высочайшее качество и надежность построенного строения.
Поможем с расчётами и работами по свайному фундаменту
Мы опытная компания по погружению железобетонных свай и шпунтов, с большим парком техники и большим количеством сданных объектов. Поможем Вам с возведением свайного фундамента любой сложности, примеры наших работ на фото. Видео наших работ. Ждём Вашего обращения по заявке:
Оставить заявку
Расчет столбчатого фундамента, расчет свайного фундамента
Расчет столбчатого фундамента, свайный фундамент с ростверком
Простой онлайн калькулятор рассчитает точное количество требуемых строительных материалов для монолитного свайно-ленточного фундамента. Начните расчет сейчас!
Столбчато-ленточный фундамент
Чаще всего в загородном строительстве используют буронабивные сваи фундамента, которые идеально дополняются монолитной лентой – это самый простой и экономичный способ. Сваи берут на себя несущую функцию, тогда как ростверк (лента) берет на себя соединяющую функцию и таким образом равномерно распределяет нагрузку на столбы. Столбчатый монолитный железобетонный фундамент отлично подходит для пучинистых грунтов, когда земля промерзает и расширяется, при этом строение должно быть легким или средней тяжести. Фундамент на столбах идеальное решения для возведения деревянных, каркасных и дачных домов, а так же гаражей и хозяйственных построек. Столбчатый фундамент лучше не использовать при строительстве каменных или кирпичных домов.
Столбчатый фундамент своими руками
Онлайн калькулятор столбчатого фундамента позволяет вам не только произвести расчет количества столбов, количества арматуры и объема бетона, но и получить наглядные чертежи фундамента с ростверком и полную стоимость буронабивного фундамента с ростверком.
Технология предполагает заливку бетонного раствора в опалубку, для этого нужно заранее пробурить отверстия, при возведении частного дома земляные работы можно провести в ручную, без привлечения бурильной установки. Диаметр сваи рассчитывается из расчета давления, которое будет оказывать вес загородного дома. Сваи фундамента должны быть углублены ниже, чем уровень промерзания грунта в вашем регионе. Бетонные столбы подойдут для любой глубины, они могут быть монолитными, как в нашем случае, важно чтобы их ширина была минимум 400 мм. Асбестобетонные или металлические трубы подходящего диаметра можно залить бетоном, при этом исключаются работы по опалубке. Рекомендуемое расстояние между столбами не более 3 метров.
Несущая способность фундамента на сваях с ростверком
Учтите, что данный онлайн калькулятор предполагает только расчет материалов и затрат по вашему фундаменту, но не дает возможность просчитать несущую способность фундамента, так как для подобного расчета потребуется геодезия вашего участка, сбор нагрузок и прочее.
17.Расчет ростверков
Принимаем материалы для изготовления ростверков:
— монолитный бетон класса по прочности В25, Rb= 14,5 МПа;Rbt= 1,05 МПа;γb2= 0,9;Rb= 13,05 МПа;Rbt= 0,945 МПа;Eb= 30000 МПа;
— арматура класса А-III,Rs=Rsc= 365 МПа;Es= 200000 МПа;
— арматура класса А-I,Rsw= 175 МПа;Es= 210000 МПа.
Ростверк фундамента ФС1.
Расчет на продавливание.
Поскольку ростверк является высоким, отпор грунта под его подошвой при расчете на продавливание не учитывается. Анализ опалубочного чертежа фундамента СВ1 (рис. 6) приводит к выводу, что рассчитываемый ростверк является балочным. В балочном ростверке пирамида продавливания вырождается в фигуру с двумя наклонными плоскостями, по которым происходит продавливание под колонной. Указанные плоскости пересекают ростверк в верхнем сечении по граням колонны, а в нижнем сечении по граням свай. Здесь имеется полная аналогия с разрушением балки по наклонному сечению при действии поперечной силы. Расчеты на продавливание выполняются по формуле (107) норм /6/:
где N– максимальная нагрузка на сваю, равная 1256,6 кН;α— коэффициент, принимаемый для тяжелого бетона равным 1,0;um– средняя линия боковой поверхности пирамиды продавливания, равная в нашем случае ширине ростверка 0,9 м;h0– высота пирамиды продавливания, равная в нашем случае высоте ростверка за вычетом защитного слоя бетона в нижней зонеa= 0,05 м,h0= 0,6 – 0,05 = 0,55 м.
Из опалубочного чертежа фундамента следует, что боковая грань пирамиды продавливания наклонена к горизонтали на угол, больший 450. При этом проекция ее высоты на горизонтальную плоскостьс= 0,25 м. Вычисляем минимальное значение этой проекции, учитываемое в расчетах на продавливание (п. 3.42 норм /6/):
Поскольку c>cmin, в качестве расчетного значения принимаемc= 0,25 м. При наклоне боковой грани пирамиды продавливания к горизонтали на угол, больший 450, расчетное сопротивление батонаFbумножают на коэффициент, равныйh0/c. С учетом сделанных замечаний расчет на продавливание ростверка выполняем по формуле:
Условие прочности при продавливании ростверка не выполняется. Увеличение несущей способности ростверка на продавливание может быть выполнено одним из следующих способов:
— применение поперечного армирования;
— увеличение толщины ростверка;
— увеличение класса бетона по прочности.
Недостаток несущей способности составляет 18,1 %. Несущая способность минимального расчетного поперечного армирования (п. 3.42 норм /6/) должно составлять не менее 50 % несущей способности бетонного сечения. В связи с этим способ повышения несущей способности ростверка на продавливание за счет применения поперчного армирования следует признать экономически нецелесообразным.
Принимаем толщину ростверка 0,7 м. Переопределяем величину cmin:
Поскольку c<cmin, в качестве расчетного значения принимаемc= 0,26 м.
Проверяем несущую способность ростверка на продавливание:
Условие прочности ростверка на продавливание выполнено. Корректируем по результатам расчета опалубочный чертеж фундамента ФС1 (рис. 7).
Вставить рис. 7, чертеж ФС1, окончательный вариант
Расчет на изгиб.
Нижнюю продольную арматуру в ростверке подбираем из расчета на изгиб нормального сечения по грани колонны. Отпор Pсо стороны сваи равен нагрузке на сваю и составляет 1256,6 кН. Плечо приложения силыlизмеряется от оси сваи до грани колонны и составляет 0,4 м. Изгибающий момент в расчетном сечении будет равен:
Находим предварительное сечение продольной арматуры:
Принимаем 4Ф28А-III,As= 0,002463 м2или 24,63 см2. Проверяем достаточность принятого армирования по нормам /6/:
Принятое армирование является достаточным.
Верхнюю продольную арматуру определяем из расчета на изгиб нормального сечения ростверка по грани колонны при действии изгибающего момента, передавемого колонной на ростверк, М= 179,0 кНм. При этом ростверк рассматривается как балка, свободно опертая на сваи и загруженная расчетным изгибающим моментом в центре пролета. Определяем по правилам строительной механики изгибающий момент в расчетном сечении ростварка:
где xi– расстояние от оси сваи до центра колонны или ростверка;lc— размер поперечного сечения колонны.
Находим предварительное сечение продольной арматуры:
Минимальное сечение растянутой арматуры по таб. 38 норм /6/ составляет 0,05 % от площади поперечного сечения b∙h0или 0,0002925 м2.
Принимаем 4Ф10А-III,As= 0,000314 м2или 3,14 см2. Проверяем достаточность принятого армирования по нормам /6/:
Принятое армирование является достаточным и удовлетворяет требованиям норм /6/ по минимальному армированию.
Поперечное армирование принимаем конструктивно с учетом требований п. 5.29 норм /6/ в виде замкнутых хомутов 4Ф6А-I, устанавливаемых с шагом 200 мм.
0
Ростверк фундамента ФС2.
Расчет на продавливание.
Поскольку ростверк является высоким, отпор грунта под его подошвой при расчете на продавливание не учитывается. Анализ опалубочного чертежа фундамента СВ2 (рис. 4) приводит к выводу, что рассчитываемый ростверк является плитным. В плитном ростверке пирамида продавливания имеет верхнее основание, совподающее с опорным сечением колонны, и нижнее основание в форме прямоугольника, углы которого совпадают с внутренними углами поперечных сечений свай. Расчеты на продавливание выполняются по формуле (107) норм /6/:
где N– максимальная нагрузка от колонны на ростверк, равная 3412,7 кН;α— коэффициент, принимаемый для тяжелого бетона равным 1,0;um– среднеарифметическое значение периметров верхнего и нижнего оснований пирамиды продавливания;h0– высота пирамиды продавливания, равная в нашем случае высоте ростверка за вычетом защитного слоя бетона в нижней зонеa= 0,05 м,h0= 0,6 – 0,05 = 0,55 м.
Из опалубочного чертежа фундамента следует, что боковые грани пирамиды продавливания наклонены к горизонтали на угол, больший 450. При этом проекция высоты боковой грани на горизонтальную плоскостьс= 0,1 м. Вычисляем минимальное значение этой проекции, учитываемое в расчетах на продавливание (п. 3.42 норм /6/):
Поскольку c<cmin, в качестве расчетного значения принимаемc= 0,22 м.
Вычисляем среднеарифметическое значение периметров оснований пирамиды продавливания:
При наклоне боковой грани пирамиды продавливания к горизонтали на угол, больший 450, расчетное сопротивление батонаFbумножают на коэффициент, равныйh0/c. С учетом сделанных замечаний расчет на продавливание ростверка выполняем по формуле:
Условие прочности при продавливании ростверка не выполняется. Увеличение несущей способности ростверка на продавливание может быть выполнено увеличение толщины ростверка.
Принимаем толщину ростверка 0,7 м. Переопределяем величину cmin:
Поскольку c<cmin, в качестве расчетного значения принимаемc= 0,26 м.
Проверяем несущую способность ростверка на продавливание:
Условие прочности ростверка на продавливание выполнено. Корректируем по результатам расчета опалубочный чертеж фундамента ФС2 (рис. 8).
Вставить рис. 8, чертеж ФС2, окончательный вариант
Расчет на изгиб.
Применяем для расчета пространственного ростверка упрощенную схему, в соответствии с которой он рассчитывается по балочной схеме в двух направлениях. Поскольку ростверк симметричен по геометрии и нагрузкам, расчет выполняем в одном направлении, а результаты этого расчета распространяем на оба направления. Нижнюю продольную арматуру в ростверке подбираем из расчета на изгиб нормального сечения по грани колонны. Отпор Pсо стороны свай равен сумме нагрузок на сваи, расположенные по одну сторону от колонны, и составляет 899,1∙2 = 1798,2 кН. Плечо приложения силыlизмеряется от оси сваи до грани колонны и составляет в соответствии с опалубочным чартежом (рис. 8) 0,25 м. Изгибающий момент в расчетном сечении будет равен:
Находим предварительное сечение продольной арматуры:
Принимаем 7Ф20А-III,As= 0,002199 м2или 21,99 см2. Проверяем достаточность принятого армирования по нормам /6/:
Принятое армирование является достаточным.
Верхнюю продольную арматуру определяем из расчета на изгиб нормального сечения ростверка по грани колонны при действии изгибающего момента, передавемого колонной на ростверк, М= 82,7 кНм. При этом ростверк рассматривается как балка, свободно опертая на сваи и загруженная расчетным изгибающим моментом в центре пролета. Определяем по правилам строительной механики изгибающий момент в расчетном сечении ростварка:
Находим предварительное сечение продольной арматуры:
Минимальное сечение растянутой арматуры по таб. 38 норм /6/ составляет 0,05 % от площади поперечного сечения b∙h0или 0,000585 м2.
Принимаем 8Ф10А-III,As= 0,000628 м2или 6,28 см2. Проверяем достаточность принятого армирования по нормам /6/:
Принятое армирование является достаточным и удовлетворяет требованиям норм /6/ по минимальному армированию.
Поперечное армирование принимаем по технологическим соображениям для фиксации в проектном положении продольной арматуры. Применяем отдельные стержни Ф10А-I, устанавливаемые с шагом в продольном и поперечном направлении 600 мм (по 4 стержня в каждом продольном и поперечном ряду).
Окончательно принимаем:
— нижняя продольная арматура в виде сетки Ф 20А-III по 7 стержней в каждом направлении;
— верхняя продольная арматура в виде сетки Ф 10А-III по 8 стержней в каждом направлении.
Рекомендуется 7 стержней верхней сетки разместить по аналогии с нижней арматурной сеткой, а 8-й стержень установить как спаренный в центре сечения. Это позволит систематизировать установку поперечной арматуры, стержни которой будут размещаться в узлах сеток и крепиться к продольной арматуре на сварке.
18.Анкеровка арматуры колонн
По проектному заданию в колонне применена арматура периодического профиля класса А-IIIс максимальным диаметром 25 мм. Вычисляем длину зоны анкеровки по формуле (186) норм /6/:
где входящие в формулу коэффициенты принимаются по таб. 37 норм /6/, а расчетное сопротивление бетона берется без учета коэффициента γb2. Поскольку расчетная длина анкеровки арматуры превышаетh0= 650 мм, требуется применение конструктивных мероприятий по обеспечению надежной анкеровки рабочей арматуры колонн в ростверке. Рекомендуется применить анкер в виде поперечного стержня (коротыша) диаметром 16 мм, который привариваетсы к рабочей арматуре на расстоянии 100 мм от конца, заделанного в ростверке (тип анкеровки № 5 по таб. 9 Рекомендаций /27/). При использовании такой анкеровки вводится понижающий коэффициент на расчетную длину анкеровки, равный 0,7. При этом получаем:
Надежность анкеровки рабочей арматуры колонны в ростверке обеспечена.
| На главную | База 1 | База 2 | База 3 |
| Поиск по реквизитамПоиск по номеру документаПоиск по названию документаПоиск по тексту документа |
| Искать все виды документовДокументы неопределённого видаISOАвиационные правилаАльбомАпелляционное определениеАТКАТК-РЭАТПЭАТРВИВМРВМУВНВНиРВНКРВНМДВНПВНПБВНТМ/МЧМ СССРВНТПВНТП/МПСВНЭВОМВПНРМВППБВРДВРДСВременное положениеВременное руководствоВременные методические рекомендацииВременные нормативыВременные рекомендацииВременные указанияВременный порядокВрТЕРВрТЕРрВрТЭСНВрТЭСНрВСНВСН АСВСН ВКВСН-АПКВСПВСТПВТУВТУ МММПВТУ НКММПВУП СНЭВУППВУТПВыпускГКИНПГКИНП (ОНТА)ГНГОСТГОСТ CEN/TRГОСТ CISPRГОСТ ENГОСТ EN ISOГОСТ EN/TSГОСТ IECГОСТ IEC/PASГОСТ IEC/TRГОСТ IEC/TSГОСТ ISOГОСТ ISO GuideГОСТ ISO/DISГОСТ ISO/HL7ГОСТ ISO/IECГОСТ ISO/IEC GuideГОСТ ISO/TRГОСТ ISO/TSГОСТ OIML RГОСТ ЕНГОСТ ИСОГОСТ ИСО/МЭКГОСТ ИСО/ТОГОСТ ИСО/ТСГОСТ МЭКГОСТ РГОСТ Р ЕНГОСТ Р ЕН ИСОГОСТ Р ИСОГОСТ Р ИСО/HL7ГОСТ Р ИСО/АСТМГОСТ Р ИСО/МЭКГОСТ Р ИСО/МЭК МФСГОСТ Р ИСО/МЭК ТОГОСТ Р ИСО/ТОГОСТ Р ИСО/ТСГОСТ Р ИСО/ТУГОСТ Р МЭКГОСТ Р МЭК/ТОГОСТ Р МЭК/ТСГОСТ ЭД1ГСНГСНрГСССДГЭСНГЭСНмГЭСНмрГЭСНмтГЭСНпГЭСНПиТЕРГЭСНПиТЕРрГЭСНрГЭСНсДИДиОРДирективное письмоДоговорДополнение к ВСНДополнение к РНиПДСЕКЕНВиРЕНВиР-ПЕНиРЕСДЗемЕТКСЖНМЗаключениеЗаконЗаконопроектЗональный типовой проектИИБТВИДИКИМИНИнструктивное письмоИнструкцияИнструкция НСАМИнформационно-методическое письмоИнформационно-технический сборникИнформационное письмоИнформацияИОТИРИСОИСО/TRИТНИТОсИТПИТСИЭСНИЭСНиЕР Республика КарелияККарта трудового процессаКарта-нарядКаталогКаталог-справочникККТКОКодексКОТКПОКСИКТКТПММ-МВИМВИМВНМВРМГСНМДМДКМДСМеждународные стандартыМетодикаМетодика НСАММетодические рекомендацииМетодические рекомендации к СПМетодические указанияМетодический документМетодическое пособиеМетодическое руководствоМИМИ БГЕИМИ УЯВИМИГКМММНМОДНМонтажные чертежиМос МУМосМРМосСанПинМППБМРМРДСМРОМРРМРТУМСанПиНМСНМСПМТМУМУ ОТ РММУКМЭКННАС ГАНБ ЖТНВННГЭАНДНДПНиТУНКНормыНормы времениНПНПБНПРМНРНРБНСПНТПНТП АПКНТП ЭППНТПДНТПСНТСНЦКРНЦСОДМОДНОЕРЖОЕРЖкрОЕРЖмОЕРЖмрОЕРЖпОЕРЖрОКОМТРМОНОНДОНКОНТПОПВОПКП АЭСОПНРМСОРДОСГиСППиНОСНОСН-АПКОСПОССПЖОССЦЖОСТОСТ 1ОСТ 2ОСТ 34ОСТ 4ОСТ 5ОСТ ВКСОСТ КЗ СНКОСТ НКЗагОСТ НКЛесОСТ НКМОСТ НКММПОСТ НКППОСТ НКПП и НКВТОСТ НКСМОСТ НКТПОСТ5ОСТНОСЭМЖОТРОТТПП ССФЖТПБПБПРВПБЭ НППБЯПВ НППВКМПВСРПГВУПереченьПиН АЭПисьмоПМГПНАЭПНД ФПНД Ф СБПНД Ф ТПНСТПОПоложениеПорядокПособиеПособие в развитие СНиППособие к ВНТППособие к ВСНПособие к МГСНПособие к МРПособие к РДПособие к РТМПособие к СНПособие к СНиППособие к СППособие к СТОПособие по применению СППостановлениеПОТ РПОЭСНрППБППБ-АСППБ-СППБВППБОППРПРПР РСКПР СМНПравилаПрактическое пособие к СППРБ АСПрейскурантПриказПротоколПСРр Калининградской областиПТБПТЭПУГПУЭПЦСНПЭУРР ГазпромР НОПРИЗР НОСТРОЙР НОСТРОЙ/НОПР РСКР СМНР-НП СРО ССКРазъяснениеРаспоряжениеРАФРБРГРДРД БГЕИРД БТРД ГМРД НИИКраностроенияРД РОСЭКРД РСКРД РТМРД СМАРД СМНРД ЭОРД-АПКРДИРДМРДМУРДПРДСРДТПРегламентРекомендацииРекомендацияРешениеРешение коллегииРКРМРМГРМДРМКРНДРНиПРПРРТОП ТЭРС ГАРСНРСТ РСФСРРСТ РСФСР ЭД1РТРТМРТПРУРуководствоРУЭСТОП ГАРЭГА РФРЭСНрСАСанитарные нормыСанитарные правилаСанПиНСборникСборник НТД к СНиПСборники ПВРСборники РСН МОСборники РСН ПНРСборники РСН ССРСборники ценСБЦПСДАСДАЭСДОССерияСЗКСНСН-РФСНиПСНиРСНККСНОРСНПСОСоглашениеСПСП АССП АЭССправочникСправочное пособие к ВСНСправочное пособие к СНиПСправочное пособие к СПСправочное пособие к ТЕРСправочное пособие к ТЕРрСРПССНССЦСТ ССФЖТСТ СЭВСТ ЦКБАСТ-НП СРОСТАСТКСТМСТНСТН ЦЭСТОСТО 030 НОСТРОЙСТО АСЧМСТО БДПСТО ВНИИСТСТО ГазпромСТО Газпром РДСТО ГГИСТО ГУ ГГИСТО ДД ХМАОСТО ДОКТОР БЕТОНСТО МАДИСТО МВИСТО МИСТО НААГСТО НАКССТО НКССТО НОПСТО НОСТРОЙСТО НОСТРОЙ/НОПСТО РЖДСТО РосГеоСТО РОСТЕХЭКСПЕРТИЗАСТО САСТО СМКСТО ФЦССТО ЦКТИСТО-ГК «Трансстрой»СТО-НСОПБСТПСТП ВНИИГСТП НИИЭССтП РМПСУПСССУРСУСНСЦНПРТВТЕТелеграммаТелетайпограммаТематическая подборкаТЕРТЕР Алтайский крайТЕР Белгородская областьТЕР Калининградской областиТЕР Карачаево-Черкесская РеспубликаТЕР Краснодарского краяТЕР Мурманская областьТЕР Новосибирской областиТЕР Орловской областиТЕР Республика ДагестанТЕР Республика КарелияТЕР Ростовской областиТЕР Самарской областиТЕР Смоленской обл.ТЕР Ямало-Ненецкий автономный округТЕР Ярославской областиТЕРмТЕРм Алтайский крайТЕРм Белгородская областьТЕРм Воронежской областиТЕРм Калининградской областиТЕРм Карачаево-Черкесская РеспубликаТЕРм Мурманская областьТЕРм Республика ДагестанТЕРм Республика КарелияТЕРм Ямало-Ненецкий автономный округТЕРмрТЕРмр Алтайский крайТЕРмр Белгородская областьТЕРмр Карачаево-Черкесская РеспубликаТЕРмр Краснодарского краяТЕРмр Республика ДагестанТЕРмр Республика КарелияТЕРмр Ямало-Ненецкий автономный округТЕРпТЕРп Алтайский крайТЕРп Белгородская областьТЕРп Калининградской областиТЕРп Карачаево-Черкесская РеспубликаТЕРп Краснодарского краяТЕРп Республика КарелияТЕРп Ямало-Ненецкий автономный округТЕРп Ярославской областиТЕРрТЕРр Алтайский крайТЕРр Белгородская областьТЕРр Калининградской областиТЕРр Карачаево-Черкесская РеспубликаТЕРр Краснодарского краяТЕРр Новосибирской областиТЕРр Омской областиТЕРр Орловской областиТЕРр Республика ДагестанТЕРр Республика КарелияТЕРр Ростовской областиТЕРр Рязанской областиТЕРр Самарской областиТЕРр Смоленской областиТЕРр Удмуртской РеспубликиТЕРр Ульяновской областиТЕРр Ямало-Ненецкий автономный округТЕРррТЕРрр Ямало-Ненецкий автономный округТЕРс Ямало-Ненецкий автономный округТЕРтр Ямало-Ненецкий автономный округТехнический каталогТехнический регламентТехнический регламент Таможенного союзаТехнический циркулярТехнологическая инструкцияТехнологическая картаТехнологические картыТехнологический регламентТИТИ РТИ РОТиповая инструкцияТиповая технологическая инструкцияТиповое положениеТиповой проектТиповые конструкцииТиповые материалы для проектированияТиповые проектные решенияТКТКБЯТМД Санкт-ПетербургТНПБТОИТОИ-РДТПТПРТРТР АВОКТР ЕАЭСТР ТСТРДТСНТСН МУТСН ПМСТСН РКТСН ЭКТСН ЭОТСНэ и ТЕРэТССЦТССЦ Алтайский крайТССЦ Белгородская областьТССЦ Воронежской областиТССЦ Карачаево-Черкесская РеспубликаТССЦ Ямало-Ненецкий автономный округТССЦпгТССЦпг Белгородская областьТСЦТСЦ Белгородская областьТСЦ Краснодарского краяТСЦ Орловской областиТСЦ Республика ДагестанТСЦ Республика КарелияТСЦ Ростовской областиТСЦ Ульяновской областиТСЦмТСЦО Ямало-Ненецкий автономный округТСЦп Калининградской областиТСЦПГ Ямало-Ненецкий автономный округТСЦэ Калининградской областиТСЭМТСЭМ Алтайский крайТСЭМ Белгородская областьТСЭМ Карачаево-Черкесская РеспубликаТСЭМ Ямало-Ненецкий автономный округТТТТКТТПТУТУ-газТУКТЭСНиЕР Воронежской областиТЭСНиЕРм Воронежской областиТЭСНиЕРрТЭСНиТЕРэУУ-СТУказУказаниеУказанияУКНУНУОУРврУРкрУРррУРСНУСНУТП БГЕИФАПФедеральный законФедеральный стандарт оценкиФЕРФЕРмФЕРмрФЕРпФЕРрФормаФорма ИГАСНФРФСНФССЦФССЦпгФСЭМФТС ЖТЦВЦенникЦИРВЦиркулярЦПИШифрЭксплуатационный циркулярЭРД |
| Показать все найденныеПоказать действующиеПоказать частично действующиеПоказать не действующиеПоказать проектыПоказать документы с неизвестным статусом |
| Упорядочить по номеру документаУпорядочить по дате введения |
Сравнение расчета балочного ростверка с расчетом с использованием ортотропных плит
Рисунок 01 — Автомобильный мост через L55 возле Шварцхайде, Германия
Например, [2] часто рекомендует определять балочный ростверк. Ростверк очень хорошо отображает двухосное структурное поведение бетонной плиты из композитной балки. Однако в этом случае требуется больше усилий по моделированию, и ростверк неточен в локальных дискретных точках.Ниже моделирование балочного ростверка сравнивается с моделированием ортотропной плиты.
Рисунок 02 — «Редактировать жесткость поверхности — ортотропия» в RFEM
Сначала описывается определение балочного ростверка с использованием простой конструкции, а затем определяется ортотропная пластина. Наконец, объясняются результаты и отклонения.
Система
Рисунок 03 — Конструктивная система
- Сталь поперечного сечения: HE-A 200
- Материал стали: S235
- Поперечное сечение бетона: d = 100 мм
- Материал бетон: C30 / 37
- Нагрузка: 5 кН / м²
Рисунок 04 — Поперечное сечение, включая полезную ширину
Составное поперечное сечение создается в SHAPE-MASSIVE и импортируется в RFEM с заданным эксцентриситетом поперечного сечения относительно бетонной плиты.Эффективная ширина поперечного сечения принята 60 см. Центроид поперечного сечения немного смещен вверх на 0,8 см к стыку между бетоном и сталью. Поэтому стык опор учитывается. Опоры смещены вниз на 5 см.
Рисунок 05 — Расположение опоры
Сама схема опоры подобрана таким образом, чтобы не возникало ограничений из-за сдерживаемой деформации.
Нагрузка одинакова для обеих систем.
- LC1 = 5 кН / м²
- LC2 = 10 кН (направление x = середина пролета, направление y = внешний край)
Рисунок 06 — Вариант нагружения 2
Балка ростверк Структура
Требования к балочному ростверку (из [1]):
- высоты постоянной конструкции
- прямой балочный мост
- простого симметричное поперечное сечение
- Оба главных балки поддерживаются на каждую оси опоры, которая перпендикулярно продольной оси моста.\ mathrm I \; = \; \ mathrm k \; \ cdot \; ({\ mathrm {GI}} _ \ mathrm T) \\ {\ mathrm G} _ \ mathrm c \; = \; \ frac {{ \ mathrm E} _ \ mathrm c} {2 \; \ cdot \; (1 \; + \; \ mathrm \ mu)} \; = \; \ frac {3,300} {2 \; \ cdot \; (1 \; + \; 0.2)} \; = \; 1,375 \; \ mathrm {kNcm} ² \ end {array} $$
Свойства поперечного сечения:
- I T = 0 см 4
- I y = 6250 см 4
- A = 1000 см²
- A y = 833 см²
Ввод осуществляется в программе с использованием свойств эффективного сечения.Учитывается жесткость элементов на сдвиг.
Ортотропная пластинчатая конструкция
В ортотропной пластинчатой конструкции основные балки моделируются таким же образом, как и в балочном ростверке. Эти балки затем интегрируются в бетонный фланец. Жесткость полностью передается основными балками в продольном направлении и бетонным фланцем в поперечном направлении. Размер ячейки FE определяется идентично расстоянию до вторичной балки в 50 см.
Матрица жесткости ортотропной пластины симметрична и применяется только к главным диагоналям. Жесткости на изгиб в продольном направлении плиты и кручение определены идентично поперечным стержням балочного ростверка с почти нулевым значением.
Расчетное значение жесткости на изгиб:
$$ \ mathrm D22 \; = \; \ frac {{\ mathrm E} _ \ mathrm c \; \ cdot \; \ mathrm d³} {12 \; \ cdot \; ( 1 \; — \; \ mathrm \ mu²)} \; = \; 206,000 \; \ mathrm {kNcm} / \ mathrm {cm} $$Расчетное значение крутильной жесткости:
$$ \ mathrm D33 \; = \; {\ mathrm G} _ \ mathrm {xy} \; \ cdot \; \ frac {\ sqrt {\ mathrm d_ \ mathrm x ^ 3 \; \ cdot \; \ mathrm d_ \ mathrm y ^ 3}} { 12} \; = \; 13.8 \; \ mathrm {kNcm} / \ mathrm {cm} $$В программе данные вводятся с использованием значений жесткости, определенных пользователем.
Рисунок 07 — Матрица жесткости плоскости плиты
Заключение
Рисунок 08 — Сравнение результатов
Рисунок 09 — Деформации при нагружении 2
Литература
.[1] Unterweger, H.: Globale Systemberechnung von Stahl- und Verbundbrücken, Modellbildung und Leistungsfähigkeit verbesserter einfacher Stabmodelle. Грац: IBK при Технологическом университете Граца, 2007 [2] Standsicherheitsnachweise für Kunstbauten: Anforderungen an den Inhalt den Umfang und die Form. Бонн-Бад Годесберг: Федеральный министр транспорта, Департамент дорожного строительства, 1987 Устойчивость Метод расчета наклона, армированных предварительно напряженного Якорь в процессе раскопок
Эта статья имеет эффект опорной конструкции и якорь на устойчивость откосов процесса землеройной в рассмотрение; представлена модель расчета устойчивости уклона, усиленного предварительно напряженным анкером и балкой ростверка, а также предложена модель динамического поиска критической поверхности скольжения. Также предоставляется расчетная модель решения оптимальной устойчивости каждого натяжения анкера всего процесса, с помощью которой можно в реальном времени проводить анализ и проверку устойчивости откоса в процессе земляных работ.Примеры расчетов показывают, что устойчивость откоса изменяется при динамическом изменении конструктивных параметров анкерной и ростверковой балки. Таким образом, относительно более точно и разумно использовать модель динамического поиска для определения критической поверхности скольжения откоса, усиленного предварительно напряженным анкером и балкой ростверка. Путем соотношения каждой компоновки анкеров и высоты откоса на различных этапах выемки можно получить оптимальное решение по устойчивости расчетного значения натяжения предварительно напряженного болта на различных этапах выемки.Расположение его предварительно напряженной анкерной силы отражает то, что расположение нижней части болта и расчет арматуры откоса соответствуют фактическим. Это указывает на то, что метод разумный и практичный.
1. Введение
В конструкции предварительно напряженной анкерной балки рамы механизм усиления комбинации анкерной и рамной балки проходит через мощное предварительное напряжение для усиления наклона предармирования. Когда склон находится под действием предварительного напряжения, во-первых, физические и механические характеристики породы и тела грунта под действием предварительного напряжения могут быть улучшены до определенной степени, и он может полностью использовать возможности породы и почвы. кузов и повысить устойчивость на склоне.Во-вторых, давление скользящего тела, вертикального по отношению к скользящей поверхности, увеличивается незаметно, поэтому сила трения скольжения на поверхности скольжения увеличивается, и, таким образом, улучшается устойчивость наклонного тела. Балка заземления рамы в основном может передавать анкерную силу; в то же время он может повысить эффективность конструкции.
Что касается исследования предварительно напряженной анкерной балки рамы, оно в основном сосредоточено на предварительном напряжении анкерного механизма, методе расчета внутренней силы балки рамы и некоторых исследованиях полевых испытаний, но все они в основном направлены на расчет внутренней силы балки рамы [1 –5].Исходя из функции предварительно напряженной анкерной балки ростверка, устойчивость усиленного откоса должна быть основным элементом расчета, обоснованность конструкции и расчета каркасной конструкции следует оценивать по устойчивости откоса после его усиления. Если конструкция армирования и устойчивость откоса относительно независимы друг от друга, с одной стороны, это может привести к нестабильности откоса, а с другой стороны, приведет к ненужным расходам.
Что касается этих проблем, исследования моделирования проводятся с помощью соответствующего программного обеспечения, но количественная оценка и расчет устойчивости откоса не могут быть выполнены, особенно для нового типа анкерной конструкции, которая похожа на предварительно напряженную анкерную рамную балку [6, 7 ].
Укрепляющие откосы имеют большие изменения по сравнению с традиционными откосами, анализ устойчивости системы напряжений откосов является относительно более сложным, а соответствующие исследования проводятся редко. Автор провел некоторое исследование проблемы [8], но этот метод не учитывает взаимосвязь между расположением болтов и высотой выемки в процессе выемки откоса, и анализ устойчивости откоса при выемке на разных этапах процесса не может быть сделано в реальном времени.
Когда устойчивость откоса рассчитывается с использованием теории предельного равновесия, наиболее важной проблемой является режим разрушения откоса и наиболее опасная поверхность скольжения при положении откоса; в общем, эта проблема уже не сложная. Однако, что касается новой предварительно напряженной конструкции усиления балки анкерного каркаса, при выполнении анализа устойчивости откоса анализ устойчивости является более сложным. В настоящее время основной проблемой становится влияние дополнительной функции удерживающей конструкции на устойчивость откоса, и общие проблемы устойчивости откоса имеют те же моменты, а также выделяют свои собственные характеристики.Таким образом, взаимодействие грунтовой конструкции и анкера при условии предварительно напряженного анкерного решетчатого каркаса следует учитывать при создании расчетной модели устойчивости усиленного откоса, а расчет устойчивости также следует принимать в качестве основного. В исследовании приводится методика анализа различных стадий откоса выемки грунта в критическом напряженном состоянии, а также анализ программной конструкции и примеры.
2. Механизм усиления предварительно напряженного анкерного каркаса
Каркасная балка представляет собой предварительно напряженную анкерную балочную конструкцию каркаса; он состоял из якоря и тела почвы, и она относится к легкой конструкции подпорной почвы.Часть рамы образует систему каркасной конструкции балки, головка стержня анкера соединена с рамой на пересечении колонны и балок, анкер внутреннего конца закреплен в грунте, грунт балки каркаса передается от головки анкера к стальному стержню, и затем, за счет трения, он передается в окружающий грунт зоны анкеровки, чтобы поддерживать силу давления грунта на каркасную конструкцию. В процессе работы конструкция может усилить анкерную балку рамы и гарантировать однородность болтов в сопротивлении скольжению, непрерывность и целостность, а также достичь цели полностью устойчивого наклона.Якорь предварительно напряженный кадр луч опорного конструкции модели показан на рисунке 1.
3. Устойчивость Расчет Модели Рамы несущей конструкцию с предварительно напряженным Якорем
Основываясь на режиме отказа наклона почвы, он принимает почвы, структуры кадра, и якорь стержневое (канатное) взаимодействие и, согласно литературным данным, для откосов грунта и крупномасштабных горных откосов целесообразен метод кругового скольжения. Расчетная модель устойчивости предварительно напряженной балки анкерного каркаса представлена на рисунке 2.
За основание склона берется точка, и мы устанавливаем систему координат; представляет центр круговой поверхности скольжения круга, представляет координату слоя точки привязки рычага, представляет координату пересечения слоя точки привязки и плоскости скольжения, представляет собой высоту уклона; конструкция зубчатого колеса и плоскость скольжения в грунте рассматриваются как единое целое, якорь на поверхности скольжения называется сегментом свободы, а внешняя поверхность скольжения называется сегментом крепления.
Основная сила откоса — это его гравитация, натяжение в направлении анкерного действия анкерного стержня и горизонтальная тяга в его основании.
Из коэффициента устойчивости можно рассчитать решение наиболее опасной поверхности скольжения и слоев напряжения анкерного стержня. Метод расчета включает три аспекта; Устойчивость арматуры предварительно напряженного анкерного каркаса представлена ниже.
3.1. Определение коэффициента устойчивости
Как показано на рисунке 2, с помощью теории ограничивающего равновесия в отношении определенного заданного положения плоскости скольжения следует учитывать влияние балки рамы и анкера на устойчивость склона; для повышения устойчивости принят метод епископа, а типы расчета коэффициентов следующие:
Среди них представляет коэффициент безопасности; представляет собой полный момент сопротивления скользящей поверхности; представляет собой общий снижающийся крутящий момент на скользящей поверхности; представляет собой момент противоскольжения грунта и верхнюю нагрузку; представляет собой эквивалентный момент сопротивления, создаваемый сопротивлением растяжению; представляет собой расчетные значения горизонтальной тяги внизу рамной конструкции; представляет собой расстояние от центра окружности поверхности дуги скольжения до низа каркасной конструкции.представляет собой число скольжения скользящего тела; представляет номер слоя якоря; представляет собой коэффициент интегральной скользящей подстатьи; представляет собой коэффициент важности; представляет собой массу слоя почвы; представляет ширину слоя; представляет собой стандартные значения когезионной прочности на критической поверхности скольжения; представляет собой стандартное значение угла внутреннего трения по скользящей поверхности; представляет собой угол между касательной и горизонтальной плоскостью в любой точке критической поверхности скольжения.представляет собой угол между анкерной штангой и горизонтальной плоскостью; представляет длину дуги поверхности скольжения; представляет собой толщину блока скользящего тела; представляет радиус дуги плоскости скольжения; представляет собой расчетное значение горизонтальной тяги внизу балки рамы; представляет собой сопротивление растяжению анкерного рычага слоя.
3.2. Модель поиска потенциальной поверхности скольжения
В соответствии с основными характеристиками поверхности скольжения, такими как форма, размер и местоположение, когда происходит проскальзывание откосов грунта, она выдвигает два допущения в качестве квалификации поиска поверхности скольжения, основанной на этих предположениях, поиск поверхность скольжения может быть реализована, и может быть получена реальная ситуация плоскости скольжения.(1) Два допущения. (A) Если мы предположим, что под действием удерживающей конструкции уклона плоскость скольжения проходит через точки основания откоса, как показано на рисунке 3. (b) Поверхность склона и касательная дуга плоскости скольжения точка пересечения должна иметь горизонтальный угол не более. (2) Модель поиска скользящей поверхности.
Следующая модель предварительно напряженной анкерной балки рамы и пути поиска скользящей поверхности такая же, как модель, предложенная в статье [6], которая показана на рисунке 3; линии обозначают поверхность откоса, точки обозначают нижнюю точку откоса, дуга окружности — точка плоскости откоса, проходящая через точку и пересекающуюся с поверхностью откоса в точке, а точка — центр окружности плоскости скольжения.
Возьмем и в качестве исходной точки двух прямоугольных систем координат; система координат с началом координат принимается за основную систему координат, а система координат с началом координат — за вспомогательную; линии и — проекции в направлении и направлении соответственно в основной системе координат. Линии и являются проекцией в направлении и вспомогательной системы координат.
Точки представляют собой точки пересечения первого слоя с наклонной поверхностью и круговой плоскостью скольжения; можно рассчитать по проектным параметрам; можно получить через привязку в уравнении прямой и уравнении дуги.На рисунке 3,, представляют горизонтальный угол и дугу; обе три переменные связаны с точкой. Производный процесс модели поиска скользящей поверхности описан в статье [6]. Функция переменных представлена в следующем виде
Модель уклона показана на рисунке 3, когда скользящая поверхность выполняет поиск, каждая поисковая переменная изменяется в соответствии со следующей формулой где представляет угол между поверхностью уклона и горизонтальной плоскостью, — высота уклона, — угол между дугой плоскости скольжения и горизонтальной плоскостью.
3.3. Устойчивость процесса земляных работ на основе растяжения анкера каждого слоя
В поддерживающей конструкции предварительно напряженного анкерного каркаса устойчивость является основным содержанием конструкции; конструкция должна быть основана на стабильности несущей конструкции и принять его в качестве предварительного условия. Следовательно, при анализе устойчивости первым шагом является расчет натяжения анкера и конструкция анкера, а затем расчет системы несущей способности рамы.
С изменением подпорной стенки, анкерного стержня анкерной силы, и влияние структуры, коэффициент безопасности будет соответствующим образом изменен.Анализ устойчивости предварительно напряженной балки анкерной рамы в процессе выемки грунта значительно увеличит неопределенность устойчивости, это не соответствие реальной ситуации по значению коэффициента безопасности, чтобы определить, является ли уклон устойчивым или нет.
Стремясь решить эти проблемы, на основе коэффициента безопасности, на всех этапах выемки откоса может быть дано определенное ограничение на взаимосвязь между положением и силой каждого анкерного крепления, в конечном итоге теоретический метод расчета и оптимальное решение могут быть получено.
Конструкция слоев растяжения анкерной штанги должна соответствовать требованиям устойчивости, а именно:
.Исследования по устойчивости Методы расчета для ростверка Несущая конструкция с Pre-напряженное Anchor
[1] Институт планирования и проектирования водных ресурсов и гидроэнергетики. Технология предварительно напряженного анкера [M]. Пекин: China Water Conservancy and Hydropower Press, (2001).
[2] Ся Сюн, Чжоу Депэй. Предварительно напряженная балка заземления анкерного кабеля при армировании откосов [J]. Механика горных пород и грунтов, 2002, 23 (2): 242-245.
[3] Ян Мин, Ху Хутянь, Лу Дж. К. и др. Расчет внутренних сил предварительно напряженного анкерного канатного каркаса, армированного откосом грунта [Дж].Китайский журнал механики горных пород и инженерии, 2002, 21 (9): 1383-1386.
[4] Чжоу Юнцзян, Хэ Сымин, Ян Сюэлянь.Исследование механизма потери предварительного напряжения предварительно напряженного анкерного кабеля [J]. Механика горных пород и грунтов, 2006, 27 (8), 1353-1356.
.(IUCr) Введение в расчет структурных факторов
S. C. Wallwork
В рентгеновской кристаллографии структурный фактор F ( hkl ) любого отражения рентгеновских лучей (дифрагированный луч) hkl — это величина, которая выражает как амплитуду, так и фазу этого отражения. Он играет центральную роль в решении и уточнении кристаллических структур, поскольку представляет величину, связанную с интенсивностью отражения, которая зависит от структуры, вызывающей это отражение, и не зависит от метода и условий наблюдения отражения.Набор структурных факторов для всех отражений hkl является первичными величинами, необходимыми для вывода трехмерного распределения электронной плотности, которое представляет собой изображение кристаллической структуры, рассчитанное методами Фурье. Это изображение является кристаллографическим аналогом изображения, сформированного в микроскопе путем рекомбинации лучей, рассеянных объектом. В микроскопе эта рекомбинация физически осуществляется линзами микроскопа, но в кристаллографии соответствующая рекомбинация дифрагированных лучей должна производиться математическим расчетом.
Способ, которым отдельные рассеянные или дифрагированные лучи объединяются для формирования изображения, зависит от трех факторов, связанных с каждым лучом:
- (a)
- направление,
- (b)
- амплитуда,
- ( в)
- фаза.
При физической рекомбинации лучей линзами микроскопа эти три части информации о каждом луче сохраняются и автоматически используются в процессе рекомбинации. В рентгеновской кристаллографии дифрагированные пучки наблюдаются отдельно, а их интенсивности измеряются как черные пятна на рентгеновской пленке или путем прямого квантового счета на дифрактометре.Путем определения индексов Миллера ( hkl ) плоскости кристалла, дающей начало каждому дифрагированному лучу, задается направление луча. По измеренной интенсивности пучка легко определить его амплитуду. Таким образом, известны две из трех необходимых частей информации о каждом луче, но, к сожалению, пока нет доступного метода для наблюдения фазы каждого дифрагированного луча, что является третьей частью информации, необходимой для того, чтобы математическая рекомбинация могла создать изображение структура.Это составляет так называемую фазовую проблему в кристаллографии.
Таким образом, решение кристаллической структуры состоит из применения некоторой техники для получения приблизительных фаз, по крайней мере, некоторых рентгеновских отражений, а процесс уточнения структуры — это процесс, при котором знание фаз распространяется на все отражения и сделан максимально точным для всех отражений. Помимо прямых методов получения некоторых начальных фаз, процессы решения и уточнения зависят от способности вычислить структурные факторы для предлагаемого приблизительного расположения некоторых или всех атомов в кристаллической структуре.Это тема данной брошюры. Видно, что можно одновременно рассчитать как амплитуду
 , так и фазу
, так и фазу  каждого луча, который будет дифрагировать на предлагаемой структуре. Поскольку фазы не могут быть сопоставлены ни с какими наблюдаемыми величинами, справедливость предложенной структуры должна быть проверена путем сравнения рассчитанных значений амплитуд структурного фактора F c с наблюдаемыми амплитудами | Факс 0 |.Это делается путем вычисления коэффициента надежности или R, фактора, определяемого как
каждого луча, который будет дифрагировать на предлагаемой структуре. Поскольку фазы не могут быть сопоставлены ни с какими наблюдаемыми величинами, справедливость предложенной структуры должна быть проверена путем сравнения рассчитанных значений амплитуд структурного фактора F c с наблюдаемыми амплитудами | Факс 0 |.Это делается путем вычисления коэффициента надежности или R, фактора, определяемого как
, где суммирование обычно проводится по всем отражениям, дающим значительные интенсивности. Из-за случайных ошибок в наблюдаемых амплитудах структурных факторов | F 0 |, и приближения, сделанные в модели, на которой основаны расчетные структурные факторы, никогда не смогут получить набор | F c | которые точно воспроизводят | F 0 |, поэтому уточнение структуры никогда не уменьшает R до нуля.Для качественных данных дифрактометра значения R в районе 0,05 являются обычными для полностью уточненных структур. Для начальных приближенных структур, возникающих в процессе структурного решения, R обычно не должно быть больше примерно 0,5, чтобы можно было удовлетворительно улучшить качество.
Структурный фактор представляет собой результирующую рассеивающую способность рентгеновских лучей всей кристаллической структуры, однако, поскольку вся структура состоит из большого количества элементарных ячеек, все рассеянные в фазе друг с другом, результирующая рассеивающая способность фактически рассчитывается для содержания только одной элементарной ячейки.Таким образом, структурный фактор представляет собой результирующую амплитуду и фазу рассеяния всего распределения электронной плотности одной элементарной ячейки. Амплитуда рассчитывается как во сколько раз больше амплитуды рассеяния от изолированного электрона. Фаза вычисляется относительно фазы нуля для гипотетического рассеяния точкой в начале координат элементарной ячейки. Результирующий результат вычисляется как наложение волн, по одной от каждого атома в элементарной ячейке, каждая волна имеет амплитуду, которая зависит от количества электронов в атоме, и фазу, которая зависит от положения атома в элементарной ячейке.
Прежде чем подробно рассмотреть, как выполнить этот расчет, мы должны сначала увидеть, как можно комбинировать волновые движения разных амплитуд и фаз. Мы рассматриваем простейший случай сложения волны амплитуды f 1 и фазы
 и волны амплитуды f 2 и фазы
и волны амплитуды f 2 и фазы  . Каждую волну можно рассматривать как функцию косинуса, генерируемую путем проецирования на горизонтальный диаметр окружности — положение точки ( P 1 или P 2 ), вращающейся с постоянной скоростью вокруг окружности, (рис.1). Смещение выступа по горизонтальному диаметру можно принять равным x . Если бы каждая волна имела нулевую фазу, радиус, соединяющий точки P 1 или P 2 с центром каждого круга, составлял бы тот же угол
. Каждую волну можно рассматривать как функцию косинуса, генерируемую путем проецирования на горизонтальный диаметр окружности — положение точки ( P 1 или P 2 ), вращающейся с постоянной скоростью вокруг окружности, (рис.1). Смещение выступа по горизонтальному диаметру можно принять равным x . Если бы каждая волна имела нулевую фазу, радиус, соединяющий точки P 1 или P 2 с центром каждого круга, составлял бы тот же угол  с горизонтальным диаметром в один и тот же момент времени, как показано на рис. 1 ( a ), а смещения по горизонтальным диаметрам будут заданы следующим образом:
с горизонтальным диаметром в один и тот же момент времени, как показано на рис. 1 ( a ), а смещения по горизонтальным диаметрам будут заданы следующим образом:
Рисунок 1: Генерация и комбинация двух сигналов, (а) оба с нулевой фазой, (б) с фазами  и
и  .
.
Сумма этих двух волновых движений представляет собой просто волну одной фазы с амплитудой ( f 1 + f 2 ). В любой момент времени полное смещение определяется как:

Когда первая волна имеет фазовый угол
 относительно радиуса под углом
относительно радиуса под углом  , а вторая волна имеет фазовый угол
, а вторая волна имеет фазовый угол  относительно того же радиуса, двухкомпонентные волны и их равнодействующая показаны на рис.1 ( б ). Результирующая теперь имеет амплитуду, которая меньше чем ( f 1 + f 2 ), потому что составляющие волны больше не полностью усиливают друг друга, и ее фаза отличается от фазы любого из компонентов. Смещения x 1 и x 2 для двух составляющих волн теперь задаются как:
относительно того же радиуса, двухкомпонентные волны и их равнодействующая показаны на рис.1 ( б ). Результирующая теперь имеет амплитуду, которая меньше чем ( f 1 + f 2 ), потому что составляющие волны больше не полностью усиливают друг друга, и ее фаза отличается от фазы любого из компонентов. Смещения x 1 и x 2 для двух составляющих волн теперь задаются как:
, а смещение для результирующей волны определяется как
При разложении косинусных членов это становится


Как видно из рис.1 результирующая волна является другой косинусоидальной волной той же частоты, что и составляющие волны, но другой фазы, которую мы назовем
 . Следовательно, его можно представить как:
. Следовательно, его можно представить как:
Расширяя это, мы имеем
Сравнивая уравнение (2) с уравнением (1), мы видим, что


Чтобы найти амплитуду | F | и фаза
 результирующей волны, мы заметим, что:
результирующей волны, мы заметим, что:
и

В общем, чтобы найти результирующую амплитуду и фазу для волны, состоящей из n косинусоидальных волн, из которых типичная составляющая j имеет амплитуда f j и фаза
 , имеем
, имеем
и | F | и
 относятся к A ‘и B ‘, как и в случае двух компонентов.
относятся к A ‘и B ‘, как и в случае двух компонентов.Это добавление компонентов может быть удобно представлено на векторной диаграмме, как на фиг. 2, где снова показан пример сложения тех же двух компонентов. На этой диаграмме можно увидеть, что A ‘- это алгебраическая сумма
 членов, а B ‘ — алгебраическая сумма
членов, а B ‘ — алгебраическая сумма  членов. Результирующий вектор F представляет собой векторную сумму двух компонентов и квадрат ее амплитуды, | F 2 |, по теореме Пифагора задается формулой ( A ‘) 2 + ( B ‘) 2 .Направление или фаза результирующего задается углом
членов. Результирующий вектор F представляет собой векторную сумму двух компонентов и квадрат ее амплитуды, | F 2 |, по теореме Пифагора задается формулой ( A ‘) 2 + ( B ‘) 2 .Направление или фаза результирующего задается углом  , тангенс которого равен B ‘/ A ‘.
, тангенс которого равен B ‘/ A ‘.Рисунок 2: Комбинация составляющих волн с амплитудой f 1 и f 2 и фаз  и
и  для получения результирующей волны амплитуды | F | и фаза
для получения результирующей волны амплитуды | F | и фаза  , представленная как процесс сложения вектора.
, представленная как процесс сложения вектора.
Обычно амплитуду и фазу волны представляют комплексным числом, которое может быть выражено в форме a + ib или

 .В этих представлениях , или
.В этих представлениях , или  — действительная часть комплексного числа, а ib или
— действительная часть комплексного числа, а ib или  — мнимая часть. Это вполне согласуется с векторным представлением на рис. 2 в том, что A ‘представляет собой действительную часть a комплексной волны F , а iB ‘ является мнимой частью ib . Следовательно, горизонтальную ось на рис. 2 следует рассматривать как действительную ось, а вертикальную ось — как мнимую ось традиционной диаграммы Аргана для представления комплексных чисел.В экспоненциальной форме комплексной волны
— мнимая часть. Это вполне согласуется с векторным представлением на рис. 2 в том, что A ‘представляет собой действительную часть a комплексной волны F , а iB ‘ является мнимой частью ib . Следовательно, горизонтальную ось на рис. 2 следует рассматривать как действительную ось, а вертикальную ось — как мнимую ось традиционной диаграммы Аргана для представления комплексных чисел.В экспоненциальной форме комплексной волны  угол
угол  соответствует фазовому углу
соответствует фазовому углу  на фиг. 2, а x соответствует амплитуде | F |.
на фиг. 2, а x соответствует амплитуде | F |.Увидев, как волны могут быть добавлены, чтобы дать результирующую волну, мы теперь в состоянии применить эту процедуру к суммированию волн, рассеянных различными атомами элементарной ячейки, чтобы получить результирующий структурный фактор F . Нам необходимо рассмотреть амплитуду f рассеяния от каждого атома и его фазу
 .Обе эти величины лучше всего подходят с точки зрения брэгговской трактовки дифракции рентгеновских лучей, которая будет описана вначале.
.Обе эти величины лучше всего подходят с точки зрения брэгговской трактовки дифракции рентгеновских лучей, которая будет описана вначале.Брэгги, отец и сын, считали, что дифракцию рентгеновских лучей на кристалле удобнее рассматривать в терминах отражения от равномерно расположенных параллельных плоскостей в кристалле. Как и любой процесс отражения, угол
 между падающим лучом и отражающей плоскостью равен углу между отраженным лучом и плоскостью.Однако, в отличие от зеркального отражения, только определенные углы падения и отражения вызывают заметную интенсивность отраженного луча. Это углы, при которых лучи, отраженные последовательными плоскостями в кристалле, различаются по фазе на целое число длин волн. (Это ограничение возникает из-за того, что на самом деле проблема заключается в дифракции.) Разница в фазе находится путем вычисления разницы в длине пути для двух последовательных лучей.
между падающим лучом и отражающей плоскостью равен углу между отраженным лучом и плоскостью.Однако, в отличие от зеркального отражения, только определенные углы падения и отражения вызывают заметную интенсивность отраженного луча. Это углы, при которых лучи, отраженные последовательными плоскостями в кристалле, различаются по фазе на целое число длин волн. (Это ограничение возникает из-за того, что на самом деле проблема заключается в дифракции.) Разница в фазе находится путем вычисления разницы в длине пути для двух последовательных лучей.Рассмотрим первые два луча падающего луча, которые попадают в последовательные плоскости кристалла в точках O и B соответственно, где OB перпендикулярно плоскостям кристалла (рис.3 а ). Дополнительное расстояние, пройденное нижним лучом, вычисляется путем рисования перпендикулярных волновых фронтов OA и OC падающему и дифрагированному лучам соответственно. Видно, что это AB + BC . Поскольку
 — это угол между AB и плоскостью кристалла и между BC и плоскостью кристалла,
— это угол между AB и плоскостью кристалла и между BC и плоскостью кристалла,  также является углом между перпендикуляром к AB (т.е. OA ) или к BC (т.е.е. OC ) и перпендикулярно плоскостям кристалла (т.е. OB ). Это показано на увеличенной части диаграммы на рис. 3 b . Теперь из треугольников ABO и BCO :
также является углом между перпендикуляром к AB (т.е. OA ) или к BC (т.е.е. OC ) и перпендикулярно плоскостям кристалла (т.е. OB ). Это показано на увеличенной части диаграммы на рис. 3 b . Теперь из треугольников ABO и BCO :
, поскольку OB = d , перпендикулярное расстояние между плоскостями кристалла. Таким образом, общая разница в пути между двумя лучами ( AB + BC ) равна
 . Для усиления последовательных лучей эта разность хода должна составлять целое число длин волн.
. Для усиления последовательных лучей эта разность хода должна составлять целое число длин волн.
Это известно как уравнение Брэгга или закон Брэгга.
Рис. 3: Брэгговское отражение от равноотстоящих параллельных плоскостей кристалла. (а) Построение для расчета относительных фаз лучей, отраженных в точках O , B и P . (б) Расширение части (а). 
Во-вторых, мы должны показать, что разница в пути одинакова для двух лучей, отраженных от двух последовательных плоскостей кристалла, независимо от точек на плоскостях, в которых они падают на плоскости.Рассмотрим два луча, отраженные от верхней плоскости в точках P и O . Чтобы проверить, нет ли разницы в пути между этими двумя лучами, мы построим перпендикуляры PQ и OR . Расстояние, проходимое лучом, отраженным от O между перпендикулярными волновыми фронтами PQ и OR , составляет QO . Это равно
 . Расстояние, пройденное лучом, отраженным от P между теми же двумя волновыми фронтами, составляет PR .Однако, поскольку угол RPO также равен
. Расстояние, пройденное лучом, отраженным от P между теми же двумя волновыми фронтами, составляет PR .Однако, поскольку угол RPO также равен  , PR также равен
, PR также равен  . Таким образом, два луча находятся в фазе друг с другом. Это также означает, что если разность фаз между лучами, отраженными на O и B , составляет
. Таким образом, два луча находятся в фазе друг с другом. Это также означает, что если разность фаз между лучами, отраженными на O и B , составляет  после отражения, то разность фаз между лучами, отраженными на P и B , также будет
после отражения, то разность фаз между лучами, отраженными на P и B , также будет  после отражения. Это устанавливает принцип, согласно которому разность фаз между лучами, отраженными от параллельных плоскостей в кристалле, зависит от расстояний до точек отражения, измеренных перпендикулярно плоскостям, а не от расстояния между точками отражения, измеренных параллельно плоскостям.Этот принцип используется как при рассмотрении того, как амплитуда рассеяния атома зависит от угла Брэгга
после отражения. Это устанавливает принцип, согласно которому разность фаз между лучами, отраженными от параллельных плоскостей в кристалле, зависит от расстояний до точек отражения, измеренных перпендикулярно плоскостям, а не от расстояния между точками отражения, измеренных параллельно плоскостям.Этот принцип используется как при рассмотрении того, как амплитуда рассеяния атома зависит от угла Брэгга  , так и при вычислении зависимости фазы рассеянного пучка от каждого атома от его положения в элементарной ячейке.
, так и при вычислении зависимости фазы рассеянного пучка от каждого атома от его положения в элементарной ячейке.Если бы все электроны в атоме были сосредоточены в одной точке, амплитуда рентгеновских лучей, рассеянных атомом, была бы просто в Z раз больше амплитуды, рассеянной одним свободным электроном, где Z — атомный номер атома.Фактически, электроны образуют диффузное облако различной плотности, сферическое по симметрии в первом приближении, но с довольно высокой плотностью электронов, скажем, на расстоянии половины обычного атомного радиуса от центра атома. Рентгеновские лучи, рассеянные от одной части атома, могут быть не в фазе с рассеянными от другой части, так что их вклады в общее рассеяние сокращаются, а не складываются. Таким образом, полная амплитуда рассеяния атомом будет, как правило, меньше Z и будет зависеть от расстояния между параллельными дифракционными плоскостями для рассматриваемого отражения рентгеновских лучей.
Рисунок 4: Зависимость относительных фаз рассеяния рентгеновских лучей от двух точек O и P в атоме от межплоскостного расстояния d последовательных плоскостей Брэгга AB и CD (или C ‘ D ‘). 
Это можно понять, обратившись к рис. 4. Слева показана ситуация, когда расстояние d 1 между плоскостями Брэгга AB и CD является большим по сравнению с атомом с центром в O .Если рентгеновские лучи, отраженные на CD , на одну длину волны не совпадают по фазе с рентгеновскими лучами, отраженными на AB , тогда луч, отраженный от P , будет только на небольшую часть длины волны не в фазе с отраженным лучом. с О . Следовательно, рассеянные лучи из этих двух точек будут в значительной степени усиливать друг друга. Фактически, рассеяние от всех частей атома будет в значительной степени складываться, давая общую амплитуду f не намного меньше, чем Z .На рис.4 ( b ), с другой стороны, рассматривается другое отражение рентгеновского излучения, где расстояние между плоскостями Брэгга, d 2 , теперь того же порядка размера, что и атом . Теперь луч, отраженный от точки P , будет почти точно не в фазе с лучом, отраженным от точки O . Между ними будет деструктивная интерференция (однако не сводя к нулю, потому что плотность электронов и, следовательно, амплитуда рассеяния при P будет меньше, чем при O ).В этой ситуации полная амплитуда рассеяния f от всего атома будет намного меньше Z . Поскольку d и угол Брэгга
 связаны уравнением Брэгга (5), ситуация на фиг.4 ( a ) соответствует отражению под малым углом
связаны уравнением Брэгга (5), ситуация на фиг.4 ( a ) соответствует отражению под малым углом  , а ситуация на фиг.4 ( b ) ) соответствует большому углу Брэгга
, а ситуация на фиг.4 ( b ) ) соответствует большому углу Брэгга  . Фактически, амплитуда рассеяния на атоме f плавно изменяется с
. Фактически, амплитуда рассеяния на атоме f плавно изменяется с  , как показано для некоторых типичных атомов на рис.5. Амплитуда f для атома называется атомным фактором рассеяния. Он экстраполируется на Z , поскольку
, как показано для некоторых типичных атомов на рис.5. Амплитуда f для атома называется атомным фактором рассеяния. Он экстраполируется на Z , поскольку  стремится к нулю, потому что d стремится к бесконечности, а разности фаз рассеяния от разных частей атомов стремятся к нулю. При вычислении структурного фактора для конкретного отражения рентгеновских лучей hkl расчет в первую очередь выполняется так, как если бы рассеяние для каждого атома происходило из одной точки — атомного центра. Влияние распределения электронной плотности по значительному объему затем учитывается путем умножения члена для каждого атома на атомный коэффициент рассеяния f , соответствующий углу Брэгга
стремится к нулю, потому что d стремится к бесконечности, а разности фаз рассеяния от разных частей атомов стремятся к нулю. При вычислении структурного фактора для конкретного отражения рентгеновских лучей hkl расчет в первую очередь выполняется так, как если бы рассеяние для каждого атома происходило из одной точки — атомного центра. Влияние распределения электронной плотности по значительному объему затем учитывается путем умножения члена для каждого атома на атомный коэффициент рассеяния f , соответствующий углу Брэгга  отражения.
отражения.Рисунок 5: Коэффициенты атомного рассеяния f для водорода, углерода и фтора, построенные против  .
.
Теперь мы должны рассмотреть, как фаза
 рассеяния на атоме как вклад в общий структурный фактор F зависит от положения атома в элементарной ячейке. Принцип метода заключается в том, что лучи, отраженные последовательными плоскостями Брэгга, имеют фазу на одну длину волны, отличную друг от друга, и поэтому их фазовый угол отличается на
рассеяния на атоме как вклад в общий структурный фактор F зависит от положения атома в элементарной ячейке. Принцип метода заключается в том, что лучи, отраженные последовательными плоскостями Брэгга, имеют фазу на одну длину волны, отличную друг от друга, и поэтому их фазовый угол отличается на  радиан или 360
радиан или 360  .Гипотетический луч, отраженный от начала координат ячейки, всегда определяет нулевой фазовый угол, поэтому точки пересечения плоскости hkl с осями ячейки соответствуют фазе
.Гипотетический луч, отраженный от начала координат ячейки, всегда определяет нулевой фазовый угол, поэтому точки пересечения плоскости hkl с осями ячейки соответствуют фазе  радиан или 360
радиан или 360  . Фаза для рассеяния любым атомом в элементарной ячейке (рассматриваемой для этой цели как находящаяся в точке своего центра) поэтому определяется его расстоянием, измеренным перпендикулярно между плоскостью, проходящей через начало координат, параллельной плоскости hkl , и плоскостью гкл сама.(Следует помнить, что фаза не зависит от положения, параллельного плоскостям Брэгга.) Расчет фазы лучше всего проиллюстрировать в двух измерениях, как на рис. 6.
. Фаза для рассеяния любым атомом в элементарной ячейке (рассматриваемой для этой цели как находящаяся в точке своего центра) поэтому определяется его расстоянием, измеренным перпендикулярно между плоскостью, проходящей через начало координат, параллельной плоскости hkl , и плоскостью гкл сама.(Следует помнить, что фаза не зависит от положения, параллельного плоскостям Брэгга.) Расчет фазы лучше всего проиллюстрировать в двух измерениях, как на рис. 6.Рис. 6: Конструкция для расчета фаза рассеяния от точки x , y в двух измерениях для отражения h , k . 
Оси x и y двухмерной ячейки показаны пересеченными плоскостью Брэгга (фактически линией), определенной индексами Миллера h , k .Из определения индексов Миллера, пересечение по оси x происходит на расстоянии a / h от начала координат O , а пересечение по оси y происходит на b / k где a и b — размеры элементарной ячейки по осям x и y соответственно. Расстояние по перпендикуляру d между этой плоскостью и параллельной плоскостью через начало координат определяется расстоянием OR .Рассмотрим атом в точке T , имеющий координаты x и y в ячейке. Мы хотим знать, как далеко T перпендикулярно плоскости через O к плоскости через a / h , b / k , по сравнению с общим перпендикулярным расстоянием между этими плоскостями. Удобно измерять все перпендикулярные расстояния вдоль линии ИЛИ , поэтому составляющая расстояния по координате x получается путем проецирования расстояния x на OR как OP , а составляющая из-за y координата получается путем проецирования y на OR как PQ .Общее перпендикулярное расстояние T от плоскости через O , следовательно, составляет OQ , и оно рассчитывается следующим образом:


Но, из треугольника, определенного как O , R и точка a / h ,
и из треугольника, определенного как O , R и точка b / k ,

So


Теперь OR или расстояние d соответствует изменению фазы на
 радиан.Таким образом, OQ соответствует изменению фазы на
радиан.Таким образом, OQ соответствует изменению фазы на  радиан. Следовательно, это равно
радиан. Следовательно, это равно  радиан и представляет собой фазу рассеяния от точки T по сравнению с нулевой фазой в начале координат ячейки.
радиан и представляет собой фазу рассеяния от точки T по сравнению с нулевой фазой в начале координат ячейки.Когда это вычисление распространяется на три измерения, пересечение плоскости hkl с кристаллографической осью z в точке c / l и проекция z на перпендикуляр от O к самолету также необходимо учитывать.Фаза рассеяния атомом в точке x , y , z тогда задается как
Это, следовательно, выражение для рассчитанного фазового угла
 для использования в уравнениях, таких как (3) и (4). Амплитуда f j для рассеяния атома, которая учитывает количество электронов в атоме и тот факт, что они фактически не сконцентрированы в точке x , y , z , но распределенный вокруг него, является уже обсуждавшимся атомным фактором рассеяния f .Уравнения для действительной части ( A ‘) и мнимой части ( B ‘) структурного фактора, соответствующие уравнениям (3) и (4), поэтому:
для использования в уравнениях, таких как (3) и (4). Амплитуда f j для рассеяния атома, которая учитывает количество электронов в атоме и тот факт, что они фактически не сконцентрированы в точке x , y , z , но распределенный вокруг него, является уже обсуждавшимся атомным фактором рассеяния f .Уравнения для действительной части ( A ‘) и мнимой части ( B ‘) структурного фактора, соответствующие уравнениям (3) и (4), поэтому:
Или, в экспоненциальной форме, структурный фактор может быть выражен как:
В каждом случае суммирование проводится по n атомов в элементарной ячейке.
На практике любой один атом в элементарной ячейке связан с другими атомами в ячейке за счет действия различных элементов симметрии.Принимая во внимание взаимосвязь между координатами этих связанных с симметрией атомов, можно вывести формулы, выражающие сумму факторов
 и сумму факторов
и сумму факторов  для всей этой группы связанных с симметрией атомов. Эти суммы обычно называются A и B соответственно. Вся сумма, A или B , затем умножается на коэффициент атомного рассеяния, который снова на практике корректируется с учетом теплового движения атомов, которое еще больше размывает электронное облако и вызывает более быстрое падение f. j с
для всей этой группы связанных с симметрией атомов. Эти суммы обычно называются A и B соответственно. Вся сумма, A или B , затем умножается на коэффициент атомного рассеяния, который снова на практике корректируется с учетом теплового движения атомов, которое еще больше размывает электронное облако и вызывает более быстрое падение f. j с  , чем показано на рис.5. Затем:
, чем показано на рис.5. Затем:
, где сумма берется только по атомам одной асимметричной единицы. Подробности этих расширений основных принципов расчета структурных факторов выходят за рамки данной брошюры, но формулы для A и B приведены в Международных таблицах для рентгеновской кристаллографии , том 1, 1969. , (Бирмингем, Kynoch Press). Расчеты обычно производятся на компьютере.
Наконец, следует упомянуть, что всякий раз, когда набор атомов, для которого выполняется расчет структурного фактора, имеет центр симметрии, результирующий структурный фактор всегда полностью реален, и, следовательно, соответствующие фазовые углы всегда равны 0 или
. .В том, что это так, легко убедиться, разделив структуру на центросимметрично связанные пары. Для каждого атома при x , y , z будет один атом при — x , — y , — z и, следовательно, мнимые части, B ‘, структурного фактора , поскольку они содержат синусоидальный член, будут иметь противоположный знак и сокращаться.
.В том, что это так, легко убедиться, разделив структуру на центросимметрично связанные пары. Для каждого атома при x , y , z будет один атом при — x , — y , — z и, следовательно, мнимые части, B ‘, структурного фактора , поскольку они содержат синусоидальный член, будут иметь противоположный знак и сокращаться.

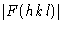 , так и фазу
, так и фазу 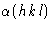 каждого луча, который будет дифрагировать на предлагаемой структуре. Поскольку фазы не могут быть сопоставлены ни с какими наблюдаемыми величинами, справедливость предложенной структуры должна быть проверена путем сравнения рассчитанных значений амплитуд структурного фактора F c с наблюдаемыми амплитудами | Факс 0 |.Это делается путем вычисления коэффициента надежности или R, фактора, определяемого как
каждого луча, который будет дифрагировать на предлагаемой структуре. Поскольку фазы не могут быть сопоставлены ни с какими наблюдаемыми величинами, справедливость предложенной структуры должна быть проверена путем сравнения рассчитанных значений амплитуд структурного фактора F c с наблюдаемыми амплитудами | Факс 0 |.Это делается путем вычисления коэффициента надежности или R, фактора, определяемого как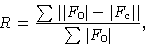
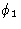 и волны амплитуды f 2 и фазы
и волны амплитуды f 2 и фазы 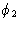 . Каждую волну можно рассматривать как функцию косинуса, генерируемую путем проецирования на горизонтальный диаметр окружности — положение точки ( P 1 или P 2 ), вращающейся с постоянной скоростью вокруг окружности, (рис.1). Смещение выступа по горизонтальному диаметру можно принять равным x . Если бы каждая волна имела нулевую фазу, радиус, соединяющий точки P 1 или P 2 с центром каждого круга, составлял бы тот же угол
. Каждую волну можно рассматривать как функцию косинуса, генерируемую путем проецирования на горизонтальный диаметр окружности — положение точки ( P 1 или P 2 ), вращающейся с постоянной скоростью вокруг окружности, (рис.1). Смещение выступа по горизонтальному диаметру можно принять равным x . Если бы каждая волна имела нулевую фазу, радиус, соединяющий точки P 1 или P 2 с центром каждого круга, составлял бы тот же угол 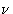 с горизонтальным диаметром в один и тот же момент времени, как показано на рис. 1 ( a ), а смещения по горизонтальным диаметрам будут заданы следующим образом:
с горизонтальным диаметром в один и тот же момент времени, как показано на рис. 1 ( a ), а смещения по горизонтальным диаметрам будут заданы следующим образом: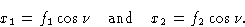
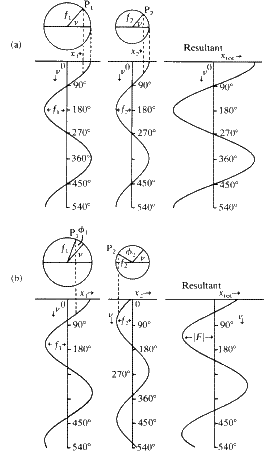
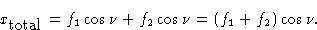
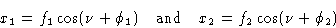
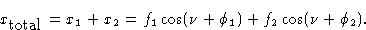
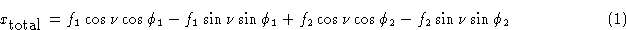
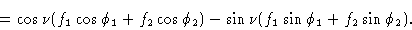
 . Следовательно, его можно представить как:
. Следовательно, его можно представить как: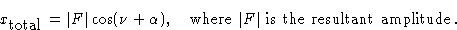
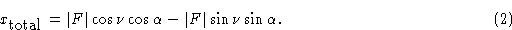
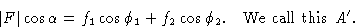
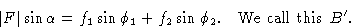
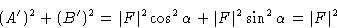
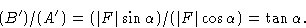
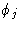 , имеем
, имеем

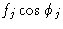 членов, а B ‘ — алгебраическая сумма
членов, а B ‘ — алгебраическая сумма 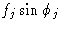 членов. Результирующий вектор F представляет собой векторную сумму двух компонентов и квадрат ее амплитуды, | F 2 |, по теореме Пифагора задается формулой ( A ‘) 2 + ( B ‘) 2 .Направление или фаза результирующего задается углом
членов. Результирующий вектор F представляет собой векторную сумму двух компонентов и квадрат ее амплитуды, | F 2 |, по теореме Пифагора задается формулой ( A ‘) 2 + ( B ‘) 2 .Направление или фаза результирующего задается углом 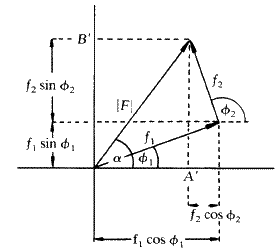
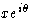
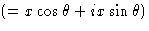 .В этих представлениях , или
.В этих представлениях , или 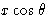 — действительная часть комплексного числа, а ib или
— действительная часть комплексного числа, а ib или 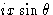 — мнимая часть. Это вполне согласуется с векторным представлением на рис. 2 в том, что A ‘представляет собой действительную часть a комплексной волны F , а iB ‘ является мнимой частью ib . Следовательно, горизонтальную ось на рис. 2 следует рассматривать как действительную ось, а вертикальную ось — как мнимую ось традиционной диаграммы Аргана для представления комплексных чисел.В экспоненциальной форме комплексной волны
— мнимая часть. Это вполне согласуется с векторным представлением на рис. 2 в том, что A ‘представляет собой действительную часть a комплексной волны F , а iB ‘ является мнимой частью ib . Следовательно, горизонтальную ось на рис. 2 следует рассматривать как действительную ось, а вертикальную ось — как мнимую ось традиционной диаграммы Аргана для представления комплексных чисел.В экспоненциальной форме комплексной волны 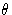 соответствует фазовому углу
соответствует фазовому углу 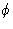 .Обе эти величины лучше всего подходят с точки зрения брэгговской трактовки дифракции рентгеновских лучей, которая будет описана вначале.
.Обе эти величины лучше всего подходят с точки зрения брэгговской трактовки дифракции рентгеновских лучей, которая будет описана вначале.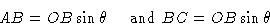

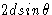 . Для усиления последовательных лучей эта разность хода должна составлять целое число длин волн.
. Для усиления последовательных лучей эта разность хода должна составлять целое число длин волн.
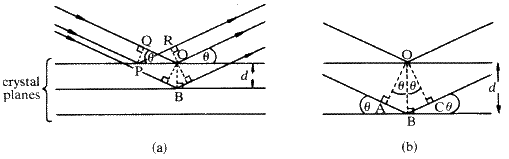
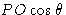 . Расстояние, пройденное лучом, отраженным от P между теми же двумя волновыми фронтами, составляет PR .Однако, поскольку угол RPO также равен
. Расстояние, пройденное лучом, отраженным от P между теми же двумя волновыми фронтами, составляет PR .Однако, поскольку угол RPO также равен 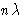 после отражения, то разность фаз между лучами, отраженными на P и B , также будет
после отражения, то разность фаз между лучами, отраженными на P и B , также будет 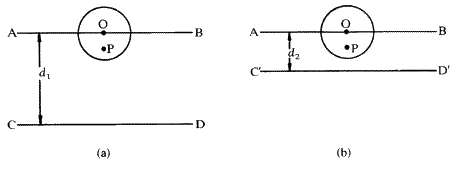
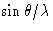 , как показано для некоторых типичных атомов на рис.5. Амплитуда f для атома называется атомным фактором рассеяния. Он экстраполируется на Z , поскольку
, как показано для некоторых типичных атомов на рис.5. Амплитуда f для атома называется атомным фактором рассеяния. Он экстраполируется на Z , поскольку 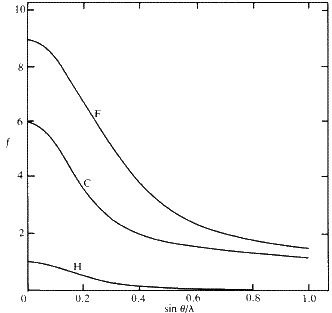
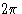 радиан или 360
радиан или 360 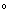 .Гипотетический луч, отраженный от начала координат ячейки, всегда определяет нулевой фазовый угол, поэтому точки пересечения плоскости hkl с осями ячейки соответствуют фазе
.Гипотетический луч, отраженный от начала координат ячейки, всегда определяет нулевой фазовый угол, поэтому точки пересечения плоскости hkl с осями ячейки соответствуют фазе 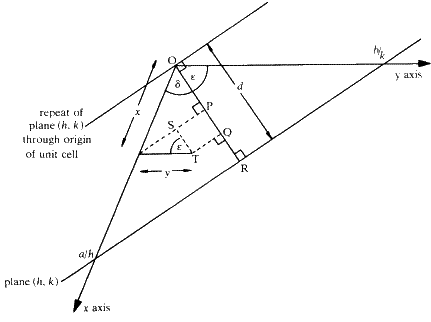
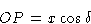
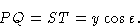
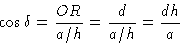
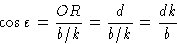
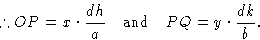
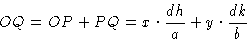
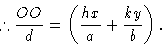
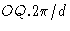 радиан. Следовательно, это равно
радиан. Следовательно, это равно 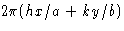 радиан и представляет собой фазу рассеяния от точки T по сравнению с нулевой фазой в начале координат ячейки.
радиан и представляет собой фазу рассеяния от точки T по сравнению с нулевой фазой в начале координат ячейки.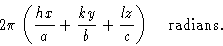
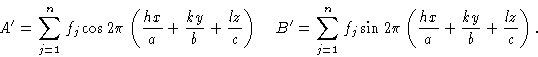
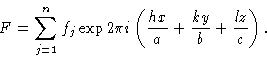
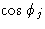 и сумму факторов
и сумму факторов 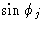 для всей этой группы связанных с симметрией атомов. Эти суммы обычно называются A и B соответственно. Вся сумма, A или B , затем умножается на коэффициент атомного рассеяния, который снова на практике корректируется с учетом теплового движения атомов, которое еще больше размывает электронное облако и вызывает более быстрое падение f. j с
для всей этой группы связанных с симметрией атомов. Эти суммы обычно называются A и B соответственно. Вся сумма, A или B , затем умножается на коэффициент атомного рассеяния, который снова на практике корректируется с учетом теплового движения атомов, которое еще больше размывает электронное облако и вызывает более быстрое падение f. j с 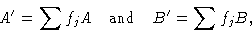
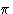 .В том, что это так, легко убедиться, разделив структуру на центросимметрично связанные пары. Для каждого атома при x , y , z будет один атом при — x , — y , — z и, следовательно, мнимые части, B ‘, структурного фактора , поскольку они содержат синусоидальный член, будут иметь противоположный знак и сокращаться.
.В том, что это так, легко убедиться, разделив структуру на центросимметрично связанные пары. Для каждого атома при x , y , z будет один атом при — x , — y , — z и, следовательно, мнимые части, B ‘, структурного фактора , поскольку они содержат синусоидальный член, будут иметь противоположный знак и сокращаться.