Процент армирования изгибаемых балок прямоугольного сечения: Карта сайта
Как определить минимальный процент армирования конструкции?
Нормы дают нам ограничение в армировании любых конструкций в виде минимального процента армирования – даже если по расчету у нас вышла очень маленькая площадь арматуры, мы должны сравнить ее с минимальным процентом армирования и установить арматуру, площадь которой не меньше того самого минимального процента армирования.
Где мы берем процент армирования? В «Руководстве по конструированию железобетонных конструкций», например, есть таблица 16, в которой приведены данные для всех типов элементов.
Но вот есть у нас на руках цифра 0,05%, а как же найти искомое минимальное армирование?
Во-первых, нужно понимать, что ищем мы обычно не площадь всей арматуры, попадающей в сечение, а именно площадь продольной рабочей арматуры. Иногда эта площадь расположена у одной грани плиты (в таблице она обозначена как А – площадь у растянутой грани, и А’ – площадь у сжатой грани), а иногда это вся площадь элемента.
На примерах, думаю, будет нагляднее.
Пример 1. Дана монолитная плита перекрытия толщиной 200 мм (рабочая высота сечения плиты h₀ до искомой арматуры 175 мм). Определить минимальное количество арматуры у нижней грани плиты.
1) Найдем площадь сечения бетона 1 погонного метра плиты:
1∙0,175 = 0,175 м² = 1750 см²
2) Найдем в таблице 16 руководства минимальный процент армирования для плиты (изгибаемого элемента):
0,05%
3) Составим известную со школы пропорцию:
1750 см² — 100%
Х – 0,05%
4) Из пропорции найдем искомую минимальную площадь арматуры:
Х = 0,05∙1750/100 = 0,88 см²
5) По сортаменту арматуры находим, что данная площадь соответствует 5 стержням диаметром 5 мм. То есть меньше этого мы устанавливать не имеем права.
Обратите внимание! Мы определяем площадь арматуры у одной грани плиты (а не площадь арматуры всего сечения плиты), именно она соответствует минимальному проценту армирования.
Пример 2. Дана плита перекрытия шириной 1,2 м, толщиной 220 мм (рабочая высота сечения плиты h₀ до искомой арматуры 200 мм), с круглыми пустотами диаметром 0,15м в количестве 5 шт. Определить минимальное количество арматуры в верхней зоне плиты.
Заглянув в примечание к таблице, мы увидим, что в случае с двутавровым сечением (а при расчете пустотных плит мы имеем дело с приведенным двутавровым сечением), мы должны определять площадь плиты так, как описано в п. 1:
1) Найдем ширину ребра приведенного двутаврового сечения плиты:
1,2 – 0,15∙5 = 0,45 м
2) Найдем площадь сечения плиты, требуемую условиями расчета:
0,45∙0,2 = 0,09 м² = 900 см²
3) Найдем в таблице 16 руководства минимальный процент армирования для плиты (изгибаемого элемента):
0,05%
4) Составим пропорцию:
900 см² — 100%
Х – 0,05%
5) Из пропорции найдем искомую минимальную площадь арматуры:
Х = 0,05∙900/100 = 0,45 см²
6) По сортаменту арматуры находим, что данная площадь соответствует 7 стержням диаметром 3 мм. То есть меньше этого мы устанавливать не имеем права.
То есть меньше этого мы устанавливать не имеем права.
И снова обратите внимание! Мы определяем площадь арматуры у одной грани плиты (а не площадь арматуры всего сечения плиты), именно она соответствует минимальному проценту армирования.
Пример 3. Дан железобетонный фундамент под оборудование сечением 1500х1500 мм, армированная равномерно по всему периметру. Расчетная высота фундамента равна 4 м. Определить минимальный процент армирования.
1) Найдем площадь сечения фундамента:
1,5∙1,5 = 2,25 м² = 22500 см²
2) Найдем в таблице 16 руководства минимальный процент армирования для фундамента, предварительно определив l₀/h = 4/1.5 = 4,4 < 5 (для прямоугольного сечения):
0,05%
3) Из пункта 2 примечаний к таблице 16 (см. рисунок выше) определим, что мы должны удвоить процент армирования, чтобы найти минимальную площадь арматуры всего сечения фундамента (а не у одной его грани!), т.е. минимальный процент армирования у нас будет равен:
2∙0,05% = 0,1%
4) Составим пропорцию:
22500 см² — 100%
Х – 0,1%
4) Из пропорции найдем искомую минимальную площадь арматуры:
Х = 0,1∙22500/100 = 22,5 см²
5) Принимаем шаг арматуры фундамента 200 мм, значит по периметру мы должны установить 28 стержней, а площадь одного стержня должна быть не меньше 22,5/28 = 0,8 см²
6) По сортаменту арматуры находим, что мы должны принять диаметр арматуры 12 мм. То есть меньше этого мы устанавливать не имеем права.
То есть меньше этого мы устанавливать не имеем права.
И снова обратите внимание! В данном примере мы определяем площадь арматуры не у одной грани фундамента, а сразу для всего фундамента, т.к. он заармирован равномерно по всему периметру.
Пример 4.
1) Найдем площадь сечения колонны:
0,46∙1,6 = 0,736 м² = 7360 см²
2) Найдем в таблице 16 руководства минимальный процент армирования для колонны (внецентренно-сжатого элемента с l₀/h = 8/0.5 = 16):
0,2%
3) Составим известную со школы пропорцию:
7360 см² — 100%
Х – 0,2%
4) Из пропорции найдем искомую минимальную площадь арматуры:
Х = 0,2∙7360/100 = 14,72 см²
5) Из руководства по проектированию находим, что максимальное расстояние между продольной арматурой в колонне не должно превышать 400 мм.
6) По сортаменту находим, что у каждой грани нам нужно установить 4 стержня диаметром 22 мм. Если считаем, что диаметр великоват, увеличиваем количество стержней, уменьшая тем самым диаметр каждого.
Обратите внимание! Мы определяем площадь арматуры у каждой из двух граней
Пример 5. Дана стена и толщиной 200 мм (рабочая высота сечения плиты h₀ до искомой арматуры 175 мм), рабочая высота стены l₀ = 5 м. Определить минимальное количество арматуры у обеих граней стены.
1) Найдем площадь сечения бетона 1 погонного метра стены:
1∙0,175 = 0,175 м² = 1750 см²
2) Найдем в таблице 16 руководства минимальный процент армирования для стены, предварительно определив l₀/h = 5/0.
0,25%
3) Составим пропорцию:
1750 см² — 100%
Х – 0,25%
4) Из пропорции найдем искомую минимальную площадь арматуры:
Х = 0,25∙1750/100 = 4,38 см²
5) По сортаменту арматуры находим, что данная площадь соответствует 5 стержням диаметром 12 мм, которые нужно установить у каждой грани на каждом погонном метре стены.
Заметьте, если бы стена была толще, минимальный процент армирования резко бы упал. Например, при толщине стены 210 мм потребовалось бы уже 5 стержней диаметром 10 мм, а не 12.
60. Каковы особенности расчета переармированных сечений? Чем определяется максимальный и минимальный процент армирования?
Предельный процент армирования
изгибаемых элементов с одиночной
арматурой (расположенной только в
растянутой зоне) определяют из уравнения
равновесия предельных усилий RbbxR -RsAsp =0 при высоте сжатой зоны, равной
граничной. При этом для прямоугольного
сечения RbbxR-RsAsp=0.
Предельный процент армирования с учетом значения ξrпо формуле для предварительно напряженных элементов
µ=100ωRb/[(1+(σsr/σscu)(1-ω/1.1)Rs] для элементов без предварительного напряжения при σsr=σscu=Rs :
µ=100ωRb/[2(1-
Предельный процент армирования с повышением класса арматуры уменьшается. Сечения изгибаемых элементов, имеющие процент армирования, превышающий предельный, называют переармированными.
Нижний предел процента
армирования установлен в нормах из
конструктивных соображений для восприятия
не учитываемых расчетом различных
усилий (усадочных, температурных и
т. п.). Для изгибаемых и внецентренно
растянутых прямоугольных сечений
шириной b, высотой h минимальный процент
армирования продольной растянутой
арматурой µ1 =0,05 %; для внецентренно растянутых
элементов в случае
п.). Для изгибаемых и внецентренно
растянутых прямоугольных сечений
шириной b, высотой h минимальный процент
армирования продольной растянутой
арматурой µ1 =0,05 %; для внецентренно растянутых
элементов в случае
В тавровых сечениях с полкой в сжатой зоне минимальный процент армирования относится к площади сечения ребра, равной b*h.
61. Выведите формулы для расчета прямоугольных сечений изгибаемых элементов с двойной арматурой. Какие условия обеспечивают прочность изгибаемых элементов прямоугольного профиля с двойной арматурой (рассмотрите 2 типа задач)?
Элементы с двойной арматурой – это такие элементы, у которых арматуру по расчету устанавливают в растянутой и сжатой зонах.
Сжатую арматуру устанавливают по расчету, когда прочность бетона сжатой зоны недостаточна, т.е. когда x£xR.
Элементы с двойной арматурой требуют
повышенного расхода стали, поэтому их
применение должно быть обосновано. Двойную арматуру приходиться принимать,
когда сечение элемента ограничено и
невозможно увеличение класса бетона.
Сжатую арматуру устанавливают также
при воздействии на элемент изгибающих
моментов двух знаков (неразрезные
конструкции и т.д.), а также для уменьшения
эксцентриситета предварительного
обжатия в преднапряженных элементах.
Двойную арматуру приходиться принимать,
когда сечение элемента ограничено и
невозможно увеличение класса бетона.
Сжатую арматуру устанавливают также
при воздействии на элемент изгибающих
моментов двух знаков (неразрезные
конструкции и т.д.), а также для уменьшения
эксцентриситета предварительного
обжатия в преднапряженных элементах.
Формулы для расчета нормальных сечений элементов с двойной арматурой получены из тех же условий, что и для элементов с одиночной.(рис)
Прочность сечения будет обеспечена, если расчетный момент от внешней нагрузки не превысит расчетного момента внутренних усилий, или, иначе, SМ = 0.
Уравнение равенства моментов относительно центра тяжести растянутой арматуры:
M £ Nb × (h0 — x/2) + Ns’ × (h0 – a’) или M £ Rb × b × x × (h0 — x/2) + Rsc × As’ × (h0 – a’)
и уравнение равенства моментов относительно центра тяжести сжатой зоны бетона:
M £ Ns × (h0 — x/2) + Ns’ × (x/2 — a’) или M £ ss × As × (h0 — x/2) + Rsc × As’ × (x/2 — a’)
где а’ – расстояние от сжатой грани сечения до центра тяжести сжатой арматуры;
As’
– площадь сечения сжатой арматуры.
Составляется также вспомогательное уравнение равенства нулю суммы проекций усилий на продольную ось элемента:
Nb × b × x + Ns’ × As’ – Ns × As = 0 или ss × As = Rb × b × x + Rsc × As’ .
Исследования показали, что сечение будет наиболее экономичным, когда на бетон передается максимально возможное сжимающее усилие. Это будет иметь место при x=xR. В этом случае площади сжатойAs’ и растянутойAsарматуры определяют приведенных уравнений, принимаяx=xR=xR×h0. Таким образом:
Rsc×As’×(h0–a’) =M-Rb×b×xR×(h0-xR/2)
Rs × As = Rb × b × xR + Rsc × As’
Задача
типа 1. Заданы размеры b
и h.
Требуется определить площадь сечения
арматуры As и As’.
Заданы размеры b
и h.
Требуется определить площадь сечения
арматуры As и As’.
As’= [M — Rb × b × xR × (h0 — xR/2)]/[ Rsc-(h0 – a’)]
As= [Rb × b × xR + Rsc × As’]/Rs
Задача 2 типа. Заданы размеры сечения b и h и площадь сечения сжатой арматуры As’. Определить площадь сечения арматуры As
αm = (M-Rsc·A’S·zs)/(b·h20·Rb) по таблице находим ξ, проверяя условие ξ< ξR.
AS=M/(ξ·h0·RS)=[As’·Rsc +ξ·b·h0·Rb]/Rs
Если αm> αR, заданного количества арматуры по площади сечения As’ недостаточно.
ACI 318-11: Расчетные параметры железобетонных балок
США: Тел. : 1-206-279-3300
: 1-206-279-3300
ЕС: Тел.: +30 6986 007 252
Коэффициент армирования в бетонных элементах
Количество стальных арматурных элементов должно быть ограничено . Чрезмерное армирование (размещение слишком большого количества арматуры) не позволит стали деформироваться до разрушения бетона и внезапного разрушения.
Коэффициент армирования в конструкции бетонной балки представляет собой следующую дробь:
Коэффициент армирования, ρ, должен быть меньше значения, определенного при деформации бетона 0,003 и деформации растяжения 0,004 (минимум). Когда деформация арматуры составляет 0,005 или больше, секция контролируется натяжением. (Для меньших деформаций коэффициент сопротивления уменьшается до 0,65, поскольку напряжение меньше, чем предел текучести в стали.)
Максимальное армирование
Исходя из предельной деформации 0,005 в стали, x(или c) = 0,375d SO
α = β 1 (0,375D), чтобы найти AS-MAX
даже если бетон может противостоять натяжению, чтобы предотвратить растрескивание.
Минимальное необходимое армирование:
, но не менее
где:
f y — предел текучести в psi
b w — ширина стенки поперечного сечения бетонной тавровой балки
d — эффективная глубина от вершины железобетонной балки до центра тяжести растянутой стали
Покрытие для арматуры
Бетонное покрытие над/под арматурой должно быть предусмотрено для защиты стали от коррозии. Для внутреннего воздействия для балок и колонн типично 1,5 дюйма, для плит — 0,75 дюйма, а для бетона, залитого в грунт, требуется минимум 3 дюйма.
Расстояние между стержнями
Минимальное расстояние между стержнями указано для обеспечения надлежащего уплотнения бетона вокруг арматуры. Минимальное расстояние составляет максимум 1 дюйм, диаметр стержня, или в 1,33 раза больше максимального размера заполнителя.
Эффективная ширина b eff
В случае тавровых или гамма-балок эффективная плита может быть рассчитана следующим образом: наименьшее из:
L/4, bw + 16t, или от центра к центру балок
Для наружных T-образных профилей, bE или bw + ½ (расстояние в свету до следующей балки)
Когда стенка находится в напряжении, минимальное требуемое армирование такое же, как и для прямоугольных профилей
с шириной стенки ( bw ) вместо б .
Когда фланец находится в состоянии растяжения (отрицательный изгиб),
минимальная требуемая арматура равна большему значению
, где:
f y — предел текучести в фунтах на квадратный дюйм
b w — ширина 90 стенка поперечного сечения бетонной тавровой балки
b eff – эффективная ширина полки
Армирование на сжатие
Если сечение двойно армировано , это означает, что в балке наблюдается сжатие из стали. Сила в сжимающей стали, которая может быть не податливой, составляет
Cs = As´(f´s — 0,85f´c)
Полное сжатие, которое уравновешивает натяжение, составляет теперь: T = Cc + Cs .
Момент относительно центра тяжести напряжения сжатия равен Mn = T(d-a/2)+Cs(a-d’)
, где As ‘ — площадь сжатой арматуры
d’ – эффективная глубина до центра масс сжимаемой арматуры
Поскольку сжатая сталь может не поддаваться деформации, нейтральная ось x должно быть найдено из соотношений равновесия сил, а напряжение может быть найдено на основе деформации, чтобы увидеть, податливо ли оно.
Copyright © 2003 — 2022 ООО «Глубокие раскопки». Все права защищены.
Веб-разработка от RedMob
. 2020 20 мая;13(10):2350.
дои: 10.3390/ma13102350.
Михал Марчин Бакалаж 1 , Павел Гжегож Косаковский 1 , Павел Творжевский 1
принадлежность
- 1 Кафедра прочности материалов, бетонных конструкций и мостов, Факультет строительства и архитектуры, Келецкий технологический университет, ул.
- PMID: 32443770
- PMCID: PMC7287615
- DOI:
10.
 3390/ма13102350
3390/ма13102350
Бесплатная статья ЧВК
Михал Марцин Бакаларз и др. Материалы (Базель). .
Бесплатная статья ЧВК
. 2020 20 мая;13(10):2350.
дои: 10.3390/ma13102350.
Авторы
Михал Марцин Бакаларж 1 , Павел Гжегож Косаковский 1 , Павел Творжевский 1
принадлежность
- 1 Кафедра прочности материалов, бетонных конструкций и мостов, Факультет строительства и архитектуры, Келецкий технологический университет, ул.

- PMID: 32443770
- PMCID: PMC7287615
- DOI: 10.3390/ма13102350
Абстрактный
Темой статьи является анализ статической работы неармированных и армированных композитным материалом деревянных балок при испытаниях на изгиб. Представлены результаты экспериментальных испытаний и краткая характеристика внутреннего армирования деревянных конструкций. Экспериментальные испытания проводились на натурных балках из клееного бруса (ЛВЛ) с номинальными размерами 45×200×3400 мм. Две полосы армированного углеродным волокном полимера (CFRP) были вклеены в прямоугольные канавки в нижней части компонента с помощью двухкомпонентной эпоксидной смолы (процент армирования 0,62%). Армирование в основном повлияло на повышение максимальных значений изгибающего момента, оцененных в точках приложения как имеющие сосредоточенные силы 32% и 24% по сравнению с неармированными элементами. Было достигнуто увеличение на 11% и 7% общего модуля упругости в коэффициентах изгиба и жесткости соответственно. Выход из строя эталонных балок был вызван превышением предела прочности LVL. Усиленные элементы характеризовались большей вариабельностью режима разрушения в результате растяжения, сжатия или поперечного выпячивания при кручении. Показание профиля деформации показало более высокое использование характеристики сжатия шпона в образцах, армированных углеродными ламинатами.
Армирование в основном повлияло на повышение максимальных значений изгибающего момента, оцененных в точках приложения как имеющие сосредоточенные силы 32% и 24% по сравнению с неармированными элементами. Было достигнуто увеличение на 11% и 7% общего модуля упругости в коэффициентах изгиба и жесткости соответственно. Выход из строя эталонных балок был вызван превышением предела прочности LVL. Усиленные элементы характеризовались большей вариабельностью режима разрушения в результате растяжения, сжатия или поперечного выпячивания при кручении. Показание профиля деформации показало более высокое использование характеристики сжатия шпона в образцах, армированных углеродными ламинатами.
Ключевые слова: 4-х точечный изгиб; углеродные волокна; армирование; шпон; деревянные конструкции.
Заявление о конфликте интересов
w3.org/1998/Math/MathML» xmlns:p1=»http://pubmed.gov/pub-one»> Авторы заявляют об отсутствии конфликта интересов. Спонсоры не участвовали в разработке исследования; при сборе, анализе или интерпретации данных, при написании рукописи или при принятии решения о публикации результатов.Цифры
Рисунок 1
Схема усиления балки серии Е с…
Рисунок 1
Схема усиления балки серии Е с обозначенными осями опоры и защиты.
фигура 1Схема усиления балки серии Е с обозначенными осями опоры и защиты.
Рисунок 2
Просмотр статического теста…
Рисунок 2
Вид статической тестовой установки.
Вид статической тестовой установки.
Рисунок 3
Диаграмма суммарной нагрузки-прогиба для…
Рисунок 3
Диаграмма полной нагрузки-прогиба для выбранных балок.
Рисунок 3Диаграмма суммарной нагрузки-прогиба для выбранных балок.
Рисунок 4
Диаграмма суммарная нагрузка-время для…
Рисунок 4
Диаграмма суммарная нагрузка-время для выбранных балок.
Рисунок 4 Диаграмма суммарная нагрузка-время для выбранных балок.
Рисунок 5
Зарегистрировано изменение значений силы…
Рисунок 5
Изменение значений усилия, зафиксированное во время испытания балки E1.
Рисунок 5Изменение значений усилия, записанное во время испытания балки E1.
Рисунок 6
Типичный вид отказа…
Рисунок 6
Типичный вид разрушения эталонной балки (растяжение).
Рисунок 6Типичный вид отказа эталонной балки (натяжение).
Рисунок 7
Пример усиленного…
Рисунок 7
Пример разрушения усиленной балки (растяжение + сжатие).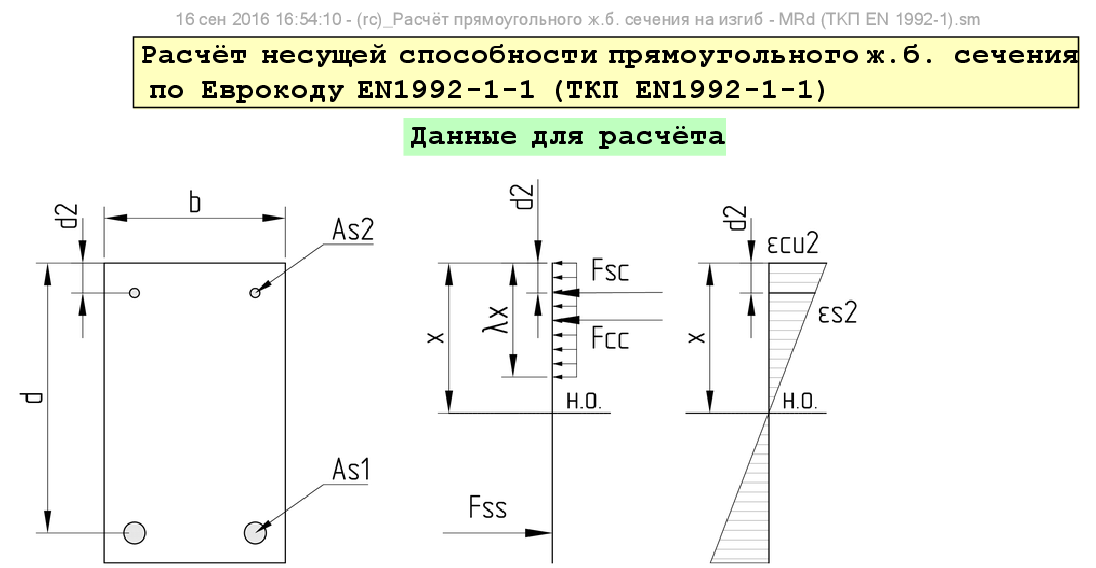
Пример разрушения усиленной балки (растяжение + сжатие).
Рисунок 8
Диаграмма нагрузка-деформация для балки A1.
Рисунок 8
Диаграмма нагрузка-деформация для балки A1.
Рисунок 8Диаграмма нагрузка-деформация для балки A1.
Рисунок 9
Профиль деформации для балки A1.
Рисунок 9
Деформационный профиль для балки A1.
Рисунок 9 Профиль деформации для балки A1.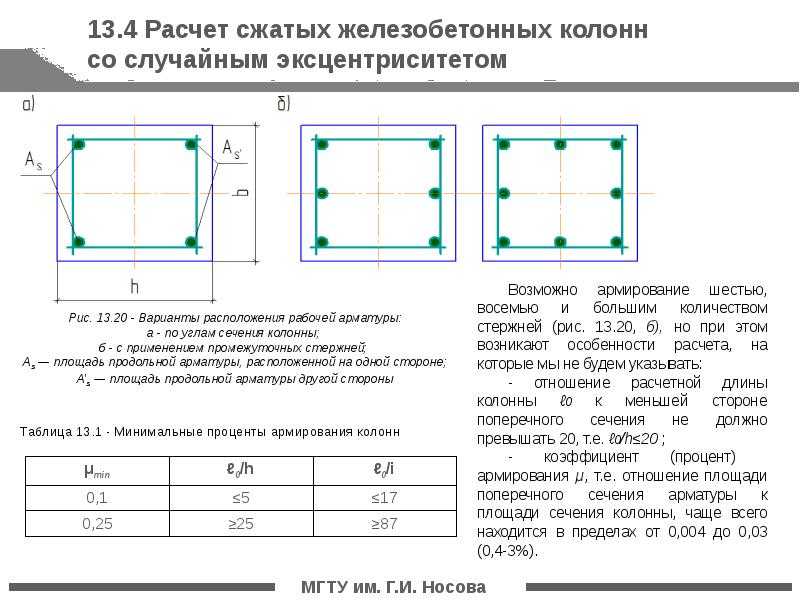
Рисунок 10
Диаграмма нагрузка-деформация для балки E5.
Рисунок 10
Диаграмма нагрузка-деформация для балки E5.
Рисунок 10Диаграмма нагрузка-деформация для балки E5.
Рисунок 11
Деформационный профиль для балки E5.
Рисунок 11
Деформационный профиль для балки E5.
Рисунок 11Профиль деформации для балки E5.
См. это изображение и информацию об авторских правах в PMC
Похожие статьи
Усиление полноразмерных балок из клееного бруса листами углепластика.

Бакаларз М.М., Коссаковски П.Г. Бакаларз М.М. и соавт. Материалы (Базель). 2022 сен 20;15(19):6526. дои: 10.3390/ma15196526. Материалы (Базель). 2022. PMID: 36233868 Бесплатная статья ЧВК.
Влияние углепластиковых листов на несущую способность балок из клееного бруса при испытании на изгиб.
Слива-Вечорек К., Островски К.А., Ясковска-Леманьска Ю., Каролак А. Слива-Вечорек К. и соавт. Материалы (Базель). 2021 18 июля; 14 (14): 4019. дои: 10.3390/ma14144019. Материалы (Базель). 2021. PMID: 34300938 Бесплатная статья ЧВК.
Пластичность зоны растяжения гнутых деревянных балок, усиленных материалами из углепластика.
Вдовяк-Постулак А., Брол Дж. Вдовяк-Постулак А. и соавт.
 Материалы (Базель). 2020 30 ноября; 13 (23): 5451. дои: 10.3390/ma13235451.
Материалы (Базель). 2020.
PMID: 33266003
Бесплатная статья ЧВК.
Материалы (Базель). 2020 30 ноября; 13 (23): 5451. дои: 10.3390/ma13235451.
Материалы (Базель). 2020.
PMID: 33266003
Бесплатная статья ЧВК.Влияние предварительной нагрузки на эффективность усиления железобетонных балок, усиленных полосами NSM без и с предварительным натяжением.
Котыня Р., Пшигоцка М. Котыня Р. и соавт. Полимеры (Базель). 2018 3 февраля; 10 (2): 145. doi: 10.3390/polym10020145. Полимеры (Базель). 2018. PMID: 30966181 Бесплатная статья ЧВК.
Армированное волокном полимерное усиление конструкций методом приповерхностного монтажа.
Парвин А., Сайед Шах Т. Парвин А. и др. Полимеры (Базель). 2016 11 августа; 8 (8): 298. doi: 10.3390/polym8080298. Полимеры (Базель). 2016.
 PMID: 30974575
Бесплатная статья ЧВК.
Обзор.
PMID: 30974575
Бесплатная статья ЧВК.
Обзор.
Посмотреть все похожие статьи
Цитируется
Усиление полноразмерных балок из клееного бруса листами углепластика.
Бакаларз М.М., Коссаковски П.Г. Бакаларз М.М. и соавт. Материалы (Базель). 2022 сен 20;15(19):6526. дои: 10.3390/ma15196526. Материалы (Базель). 2022. PMID: 36233868 Бесплатная статья ЧВК.
Экспериментальное исследование болтовых соединений алюминиево-деревянного композита, усиленных зубчатыми пластинами.
Чибински М, Полус Л. Чибинский М. и соавт. Материалы (Базель). 2022 30 июля; 15 (15): 5271. дои: 10.3390/ma15155271. Материалы (Базель). 2022. PMID: 35955205 Бесплатная статья ЧВК.

Изменение жесткости на кручение прямоугольных профилей при напряжении на изгиб.
Мациковски К., Варда Б., Митукевич Г., Димитрова З., Баторий Д. Мачиковски К. и соавт. Материалы (Базель). 2022 31 марта; 15 (7): 2567. дои: 10.3390/ma15072567. Материалы (Базель). 2022. PMID: 35407899 Бесплатная статья ЧВК.
Механическое поведение композитных соединений алюминия и дерева с помощью винтов и зубчатых пластин.
Чибински М, Полус Л. Чибинский М. и соавт. Материалы (Базель). 2021 22 декабря; 15 (1): 68. дои: 10.3390/ma15010068. Материалы (Базель). 2021. PMID: 35009215 Бесплатная статья ЧВК.
Экспериментальный и численный анализ армированного деревянного соединения внахлестку.

Е Л., Ван Б., Шао П. Йе Л и др. Материалы (Базель). 2020 16 сентября; 13 (18): 4117. дои: 10.3390/ma13184117. Материалы (Базель). 2020. PMID: 32948038 Бесплатная статья ЧВК.
использованная литература
- Де Лоренцис Л., Тенг Дж.Г. Приповерхностное армирование FRP: новый метод усиления конструкций. Композиции Часть Б. 2007; 38:119–143. doi: 10.1016/j.compositesb.2006.08.003. — DOI
- Jasieńko J. Połączenia Klejowe w Rehabilitacji i Wzmacnianiu Zginanych belek Drewnianych. Oficyna Wydawnicza Politechniki Wrocławskiej; Вроцлав, Польша: 2002 г.
- Борри А.
 , Корради М. Метод усиления на изгиб старых деревянных балок материалами из углепластика. Композиции Часть Б. 2005; 36: 143–153. doi: 10.1016/j.compositesb.2004.04.013.
—
DOI
, Корради М. Метод усиления на изгиб старых деревянных балок материалами из углепластика. Композиции Часть Б. 2005; 36: 143–153. doi: 10.1016/j.compositesb.2004.04.013.
—
DOI
- Борри А.
- Ян Х., Джу Д., Лю В., Лу В. Предварительно напряженные клееные балки, армированные стержнями из углепластика. Констр. Строить. Матер. 2016;109:73–83. doi: 10.1016/j.conbuildmat.2016.02.008. — DOI
- Сориано Дж., Пелиис Б.П., Маскиа Н.Т. Механические характеристики балок из клееного бруса, симметрично армированных стальными стержнями.

- Сориано Дж., Пелиис Б.П., Маскиа Н.Т. Механические характеристики балок из клееного бруса, симметрично армированных стальными стержнями.

 3390/ма13102350
3390/ма13102350
 Материалы (Базель). 2020 30 ноября; 13 (23): 5451. дои: 10.3390/ma13235451.
Материалы (Базель). 2020.
PMID: 33266003
Бесплатная статья ЧВК.
Материалы (Базель). 2020 30 ноября; 13 (23): 5451. дои: 10.3390/ma13235451.
Материалы (Базель). 2020.
PMID: 33266003
Бесплатная статья ЧВК. PMID: 30974575
Бесплатная статья ЧВК.
Обзор.
PMID: 30974575
Бесплатная статья ЧВК.
Обзор.
 , Корради М. Метод усиления на изгиб старых деревянных балок материалами из углепластика. Композиции Часть Б. 2005; 36: 143–153. doi: 10.1016/j.compositesb.2004.04.013.
—
DOI
, Корради М. Метод усиления на изгиб старых деревянных балок материалами из углепластика. Композиции Часть Б. 2005; 36: 143–153. doi: 10.1016/j.compositesb.2004.04.013.
—
DOI