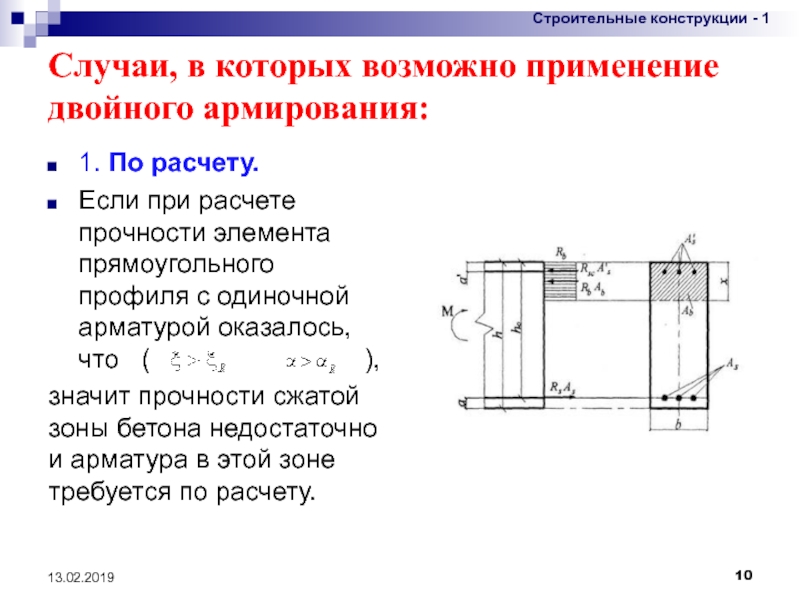
Процент армирования изгибаемых балок прямоугольного сечения: Как определить минимальный процент армирования конструкции?
Как определить минимальный процент армирования конструкции?
Нормы дают нам ограничение в армировании любых конструкций в виде минимального процента армирования – даже если по расчету у нас вышла очень маленькая площадь арматуры, мы должны сравнить ее с минимальным процентом армирования и установить арматуру, площадь которой не меньше того самого минимального процента армирования.
Где мы берем процент армирования? В «Руководстве по конструированию железобетонных конструкций», например, есть таблица 16, в которой приведены данные для всех типов элементов.
Но вот есть у нас на руках цифра 0,05%, а как же найти искомое минимальное армирование?
Во-первых, нужно понимать, что ищем мы обычно не площадь всей арматуры, попадающей в сечение, а именно площадь продольной рабочей арматуры. Иногда эта площадь расположена у одной грани плиты (в таблице она обозначена как А – площадь у растянутой грани, и А’ – площадь у сжатой грани), а иногда это вся площадь элемента.
На примерах, думаю, будет нагляднее.
Пример 1. Дана монолитная плита перекрытия толщиной 200 мм (рабочая высота сечения плиты h₀ до искомой арматуры 175 мм). Определить минимальное количество арматуры у нижней грани плиты.
1) Найдем площадь сечения бетона 1 погонного метра плиты:
1∙0,175 = 0,175 м² = 1750 см²
2) Найдем в таблице 16 руководства минимальный процент армирования для плиты (изгибаемого элемента):
0,05%
3) Составим известную со школы пропорцию:
1750 см² — 100%
4) Из пропорции найдем искомую минимальную площадь арматуры:
Х = 0,05∙1750/100 = 0,88 см²
5) По сортаменту арматуры находим, что данная площадь соответствует 5 стержням диаметром 5 мм. То есть меньше этого мы устанавливать не имеем права.
Обратите внимание! Мы определяем площадь арматуры у одной грани плиты (а не площадь арматуры всего сечения плиты), именно она соответствует минимальному проценту армирования.
Пример 2. Дана плита перекрытия шириной 1,2 м, толщиной 220 мм (рабочая высота сечения плиты
Заглянув в примечание к таблице, мы увидим, что в случае с двутавровым сечением (а при расчете пустотных плит мы имеем дело с приведенным двутавровым сечением), мы должны определять площадь плиты так, как описано в п. 1:
1) Найдем ширину ребра приведенного двутаврового сечения плиты:
1,2 – 0,15∙5 = 0,45 м
2) Найдем площадь сечения плиты, требуемую условиями расчета:
0,45∙0,2 = 0,09 м² = 900 см²
3) Найдем в таблице 16 руководства минимальный процент армирования для плиты (изгибаемого элемента):
0,05%
4) Составим пропорцию:
900 см² — 100%
Х – 0,05%
5) Из пропорции найдем искомую минимальную площадь арматуры:
Х = 0,05∙900/100 = 0,45 см²
6) По сортаменту арматуры находим, что данная площадь соответствует 7 стержням диаметром 3 мм. То есть меньше этого мы устанавливать не имеем права.
То есть меньше этого мы устанавливать не имеем права.
И снова обратите внимание! Мы определяем площадь арматуры у одной грани плиты (а не площадь арматуры всего сечения плиты), именно она соответствует минимальному проценту армирования.
Пример 3. Дан железобетонный фундамент под оборудование сечением 1500х1500 мм, армированная равномерно по всему периметру. Расчетная высота фундамента равна 4 м. Определить минимальный процент армирования.
1) Найдем площадь сечения фундамента:
1,5∙1,5 = 2,25 м² = 22500 см²
2) Найдем в таблице 16 руководства минимальный процент армирования для фундамента, предварительно определив l₀/h = 4/1.5 = 4,4 < 5 (для прямоугольного сечения):
0,05%
3) Из пункта 2 примечаний к таблице 16 (см. рисунок выше) определим, что мы должны удвоить процент армирования, чтобы найти минимальную площадь арматуры всего сечения фундамента (а не у одной его грани!), т.
2∙0,05% = 0,1%
4) Составим пропорцию:
22500 см² — 100%
Х – 0,1%
4) Из пропорции найдем искомую минимальную площадь арматуры:
Х = 0,1∙22500/100 = 22,5 см²
5) Принимаем шаг арматуры фундамента 200 мм, значит по периметру мы должны установить 28 стержней, а площадь одного стержня должна быть не меньше 22,5/28 = 0,8 см²
6) По сортаменту арматуры находим, что мы должны принять диаметр арматуры 12 мм. То есть меньше этого мы устанавливать не имеем права.
И снова обратите внимание! В данном примере мы определяем площадь арматуры не у одной грани фундамента, а сразу для всего фундамента, т.к. он заармирован равномерно по всему периметру.
Пример 4. Дана железобетонная колонна сечением 500х1600 (рабочая высота сечения колонны в коротком направлении h₀= 460 мм). Расчетная высота колонны равна 8 м. Определить минимальный процент армирования у длинных граней колонны.
Определить минимальный процент армирования у длинных граней колонны.
1) Найдем площадь сечения колонны:
0,46∙1,6 = 0,736 м² = 7360 см²
2) Найдем в таблице 16 руководства минимальный процент армирования для колонны (внецентренно-сжатого элемента с l₀/h = 8/0.5 = 16):
0,2%
3) Составим известную со школы пропорцию:
7360 см² — 100%
Х – 0,2%
4) Из пропорции найдем искомую минимальную площадь арматуры:
Х = 0,2∙7360/100 = 14,72 см²
5) Из руководства по проектированию находим, что максимальное расстояние между продольной арматурой в колонне не должно превышать 400 мм. Значит, у каждой грани мы можем установить по 4 стержня (между угловой арматурой колонны, которая является рабочей, и ее площадь определялась расчетом), площадь каждого из стержней равна 14,72/4 = 3,68 см²
6) По сортаменту находим, что у каждой грани нам нужно установить 4 стержня диаметром 22 мм. Если считаем, что диаметр великоват, увеличиваем количество стержней, уменьшая тем самым диаметр каждого.
Если считаем, что диаметр великоват, увеличиваем количество стержней, уменьшая тем самым диаметр каждого.
Обратите внимание! Мы определяем площадь арматуры у каждой из двух граней колонны, именно она соответствует минимальному проценту армирования в данном случае.
Пример 5. Дана стена и толщиной 200 мм (рабочая высота сечения плиты
1) Найдем площадь сечения бетона 1 погонного метра стены:
1∙0,175 = 0,175 м² = 1750 см²
2) Найдем в таблице 16 руководства минимальный процент армирования для стены, предварительно определив l₀/h = 5/0.2 = 25 > 24:
0,25%
3) Составим пропорцию:
1750 см² — 100%
Х – 0,25%
4) Из пропорции найдем искомую минимальную площадь арматуры:
Х = 0,25∙1750/100 = 4,38 см²
5) По сортаменту арматуры находим, что данная площадь соответствует 5 стержням диаметром 12 мм, которые нужно установить у каждой грани на каждом погонном метре стены.
Заметьте, если бы стена была толще, минимальный процент армирования резко бы упал. Например, при толщине стены 210 мм потребовалось бы уже 5 стержней диаметром 10 мм, а не 12.
class=»eliadunit»>Железобетонные конструкции (II часть)
Предисловие 8
РАЗДЕЛ I ИЗГИБ И СКАЛЫВАНИЕ ПРИ ИЗГИБЕ 10
Глава I. Конструкции, работающие на изгиб и скалывание при изгибе. Плоские покрытия и перекрытия 10
Глава II. Статический расчет изгибаемых элементов железобетонных конструкций 23
1. Предварительные сведения 23
2. Расчет балочных плит 25
4. Расчет балок 40
Глава III. Работа балки на изгиб. Три стадии напряженности 48
Глава IV. Расчет прочности балок на изгиб 53
А. Прямоугольная балка или плита с одиночной арматурой 53
1. Формулы для определения Мр и плеча пары внутренних сил z 53
2.
 Опытная проверка расчетной формулы Мр 56
Опытная проверка расчетной формулы Мр 563. Предельные значения процента армирования балок 60
4. Оптимальный процент армирования прямоугольных балок и плит 62
5. Таблицы для расчета плит и балок прямоугольного сечения с одиночной арматурой 64
Б. Прямоугольная балка или плита с двойной арматурой 70
1. Формулы для определения Мр 70
2. Армирование при различном соотношении площадей сжатой и растянутой арматуры. Армирование при условии min (Fa+Fa’) 75
3. Примеры расчета плит и балок с двойной арматурой 79
В. Балка таврового сечения 83
1. Работа тавровой балки на изгиб 83
2. Наименьший процент армирования растянутой зоны балок таврового сечения 87
3. Расчет 0алок таврового сечения на отрицательный момент 88
4. Расчет балок таврового сечения на положительный момент 89
5. Выбор высоты балок таврового сечения 93
6.
 Примеры расчета балок таврового сечения 98
Примеры расчета балок таврового сечения 98Глава V. Расчет и конструирование арматуры плит перекрытий (балочные плиты и плиты, опертые по контуру) 99
1. Конструктивные указания по проектированию балочных плит и плит, опертых по контуру 99
2. Пример расчета и конструирования балочных плит ребристого перекрытия 105
3. Пример расчета и конструирования плиты кессонного перекрытия 110
Глава VI. Расчет изгибаемых элементов, на поперечную силу 116
1. Работа балок при поперечном срезе по данным опытов 116
2. Скалывающие напряжения и главные напряжения в балке 125
3. Расчетные эпюры огл = т вдоль балки 131
4. Оценка по эпюре огл = о сопротивляемости балки главным растягивающим напряжениям. Распределение эпюры на части с передачей их на продольную арматуру, хомуты и косые стержни 136
5. Расчет и конструирование хомутов 144
6. Расчет и конструирование отогнутой арматуры 148
7.
 Эпюра арматуры. Прочность балки по нормальным и косым сечениям 154
Эпюра арматуры. Прочность балки по нормальным и косым сечениям 154Глава VII. Расчет и конструирование балок по изгибу и поперечному срезу 159
1. Конструктивные указания по проектированию балок 159
2. Пример расчета и конструирования однопролетных свободно лежа¬щих балок с равномерно распределенной нагрузкой 161
3. Пример расчета и конструирования однопролетных свободно лежащих балок под действием сосредоточенных сил 166
4. Пример расчета и конструирования неразрезных балок ребристого перекрытия 169
5. Применение вутов в неразрезных балках ребристого перекрытия 190
Глава VIII. Консоли, их расчет и конструирование 197
1. Примеры применения консолей в строительстве 197
2. Расчет и конструирование консолей с большим вылетом 200
3. Расчет и конструирование коротких консолей 202
Глава IX. Расчет изгибаемых элементов, к которым предъявляются требования непроницаемости бетона 209
1.
 Изгибаемые элементы с обыкновенной арматурой и с арматурой, имеющей предварительное натяжение 209
Изгибаемые элементы с обыкновенной арматурой и с арматурой, имеющей предварительное натяжение 209А. Расчет на изгиб бетонных неармированных балок 214
2. Расчет бетонных неармированных балок на изгиб по ТУ и Н проектирования бетонных конструкций (ОСТ 90040-39) 214
3. Расчет бетонных неармированных балок на изгиб по стадии напряженности IIa 215
Б. Расчет на изгиб железобетонных балок с обыкновенной арматурой 220
4. Расчет железобетонных балок на изгиб по стадии напряженности I 220
5. Расчет на изгиб железобетонных балок прямоугольного сечения с одиночной или с двойной арматурой по стадии напряженности IIa 222
6. Расчет на изгиб железобетонных балок прямоугольного сечения по стадии напряженности IIb 227
7. Примеры расчета и сопоставление различных приемов расчета 232
В. Расчет на изгиб балок с предварительно напряженной арматурой 238
8. Определение Mm для балок прямоугольного сечения с двойной арматурой, имеющей предварительное натяжение 238
9.
 Определение Mm для балок прямоугольного сечения с одиночной или двойной арматурой, часть стержней которой имеет предвари¬тельное натяжение 242
Определение Mm для балок прямоугольного сечения с одиночной или двойной арматурой, часть стержней которой имеет предвари¬тельное натяжение 24210. Потеря арматурой первоначального (монтажного) напряжения 244
11. Сравнение результатов расчета по выведенным формулам с опытными данными для железобетонных балок прямоугольного сечения с одиночной арматурой, имеющей предварительное натяжение 245
12. Графики и таблицы для расчета Mm. Примеры расчёта на изгиб балок с предварительно напряженной арматурой 248
13. Расчет на положительный момент балок таврового сечения с арматурой, имеющей предварительное натяжение 258
РАЗДЕЛ II ОСЕВОЕ И ВНЕЦЕНТРЕННОЕ СЖАТИЕ 263
Глава X. Элементы железобетонных конструкций, работающие на осевое и внецентренное сжатие (колонны и стойки, рамные и арочные конструкции) 263
1. Общие сведения 263
2. Конструкции, работающие на осевое и внецентренное сжатие 267
Глава XI. Осевое сжатие 272
А.
 Колонны с продольной арматурой и обык¬новенными хомутами 272
Колонны с продольной арматурой и обык¬новенными хомутами 2721. Расчет коротких колонн с продольной арматурой и обыкновенными хомутами 272
2. Конструктивные указания по проектированию на осевое сжатие колонн с продольной арматурой и обыкновенными хомутами 274
3. Продольный изгиб и его учет в расчетах прочности колонн 276
4. Примеры расчета колонн на осевое сжатие с продольной арматурой и обыкновенными хомутами 283
Б. Колонны со спиральной арматурой 285
5. Расчетные формулы и их обоснование 285
6. Конструктивные указания по проектированию «бетона в обойме» 291
7. Примеры расчета и конструирования колонн со спиральной арматурой («бетона в обойме») 294
Глава XII. Внецентренное сжатие колонн и стоек прямоуголь¬ного сечения с продольной арматурой и обыкно¬венными хомутами 297
1. Общие предпосылки к расчету внецентренно сжатых сечений. Принятые обозначения 297
2. Расчетные формулы для первого случая внецентренного сжатия 299
3.
 Расчетные формулы для второго случая внецентренного сжатия 306
Расчетные формулы для второго случая внецентренного сжатия 3064. Указания по конструированию и расчету внецентренно сжатых элементов 316
5. Учет гибкости колонн и стоек при расчете их на внецентренное сжатие 323
6. Примеры подбора сечений внецентренно сжатых элементов 328
7. Расчет на внецентренное сжатие элементов таврового сечения 347
8. Расчет на внецентренное сжатие при соблюдении требования непроницаемости бетона 353
РАЗДЕЛ III ОСЕВОЕ И ВНЕЦЕНТРЕННОЕ РАСТЯЖЕНИЕ 358
Глава XIII. Элементы конструкций, работающие на осевое и внецентренное растяжение 358
Глава XIV. Осевое растяжение 361
1. Расчет прочности при осевом растяжении 361
2. Расчет, обеспечивающий требование непроницаемости бетона 362
3. Мероприятия, предотвращающие образование волосных трещин в бетоне растянутых элементов конструкции 364
Глава XV. Внецентренное растяжение 367
1. Первый случай внецентренного растяжения 367
2.
 Второй случай внецентренного растяжения 368
Второй случай внецентренного растяжения 3683. Примеры расчета сечений на внецентренное растяжение 371
4. Расчет на внецентренное растяжение при соблюдении требования непроницаемости бетона 374
РАЗДЕЛ IV КРУЧЕНИЕ В ЖЕЛЕЗОБЕТОНЕ 381
Глава XVI. Опыты и расчеты 381
1. Возникновение крутящих моментов в элементах конструкции и учет их в расчетах 381
2. Кручение бетонных круглых цилиндрических образцов. Определение огл = ткр. Опытные данные 385
3. Кручение бетонных элементов прямоугольного сечения. Определение огл = ткр 390
4. Армирование железобетонных элементов при кручении. Расчетные формулы. Пример расчета 394
5. Опытные данные при кручении армированных образцов 399
6. Совместное действие кручения и изгиба 403
Приложения 406
Приложение I. Таблицы для статического расчета железо¬бетонных конструкций 406
А. Таблица для расчета на изгиб плит, опертых по контуру, при сплошной равномерно распределенной нагрузке q 406
Б.
 Таблица М и Q для неразрезных балок с равными пролетами и постоянного сечения при равномерной постоянной нагрузке g и временной р 408
Таблица М и Q для неразрезных балок с равными пролетами и постоянного сечения при равномерной постоянной нагрузке g и временной р 408В. Таблица М и Q для неразрезных балок с равными пролетами и постоянного сечения при сосредоточенной нагрузке: постоянной G и временной Р 412
Г. Таблица пролетных и опорных моментов и поперечных сил в опор¬ных сечениях неразрезных балок с равными пролетами 420
Д. Таблица опорных моментов для неразрезных балок с равными пролетами и постоянного сечения при любых нагрузках, симметричных по отношению к пролету. Концы балок могут быть свободно положены на опоры (схема I) или жестко заделаны в опорах (схема II) 430
Е. Таблица грузовых коэфициентов s балок с симметричной нагрузкой 433
Ж. Таблица моментов, поперечных сил и эквивалентных по моменту нагрузок для свободно лежащих балок 434
З. Таблица моментов в равнопролетной балке на упруго вращающихся опорах 435
Приложение 2. Таблицы и графики для расчета элементов железобетонных конструкций.
 442
442Iа. Таблица круглого железа 442
Iб. Таблица площадей арматуры в 1 пог. м плиты при различном расстоянии между стержнями 443
II. Таблица для расчета на изгиб плит и балок прямоугольного сечения с одиночной арматурой 444
III. Таблица для подбора прямоугольных сечений с одиночной арматурой 446
IV. График для расчета прямоугольных сечений на изгиб 447
V. Таблица для подбора сечений на изгиб с одиночной или двойной арматурой и на внецентренное сжатие и растяжение 448
VI. а, б, в, г, д. Графики расчета Мт для балок прямоугольного сечения с одиночной арматурой 450
VII. Таблица для подбора внецентренно сжатых прямоугольных се¬чений с двойной симметричной арматурой 455
VIII. График значении n1 Np/Rubh в зависимости от с0 = e0/h и о1 = a1’ = omFa/Rubh при внецентренном сжатии прямоугольных сечении с двойной симметричной арматурой при б1 = 0,08 458
IX. График для расчета внецентренно сжатых элементов прямоугольного сечения (б1 = б1’ = 0,08) 459
X.
 а, б. Графики для расчета внецентреьно сжатых прямоугольных сечений с двойной симметричной арматурой 460
а, б. Графики для расчета внецентреьно сжатых прямоугольных сечений с двойной симметричной арматурой 460XI. График для определения моментов инерции тавровых сечений 462
XII. График для определения коэффициента m при расчете внецентренно сжатых сечений с учетом гибкости элемента 463
X.IIа. Таблица для расчета на изгиб балок прямоугольного сечения с предварительно напряженной арматурой. Марка бетона 250 кг/см2 464
XIIIб. То же. Марка бетона 300 кг/см2 465
ХIIIв. То же. Марка бетона 350 кг/см2 466
Приложение 3. Принятые обозначения 467
Приложение 4. Свод формул и правил расчета и конструирования железобетонных элементов 471
Железобетонные конструкции. II часть. Бушков В.А. 1941 | Библиотека: книги по архитектуре и строительству
Предисловие
Раздел I. Изгиб и скалывание при изгибе
Глава I. Конструкции, работающие на изгиб и скалывание при изгибе. Плоские покрытия и перекрытия
Глава II. Статический расчет изгибаемых элементов железобетонных конструкций
Статический расчет изгибаемых элементов железобетонных конструкций
1. Предварительные сведения
2. Расчет балочных плит
3. Расчет плит, опертых по контуру (плиты с перекрестной арматурой)
4. Расчет балок
Глава III. Работа балки на изгиб. Три стадии напряженности
Глава IV. Расчет прочности балок на изгиб
A. Прямоугольная балка или плита с одиночной арматурой
1. Формулы для определения Mp и плеча пары внутренних сил z
2. Опытная проверка расчетной формулы Mp
3. Предельные значения процента армирования балок
4. Оптимальный процент армирования прямоугольных балок и плит
5. Таблицы для расчета плит и балок прямоугольного сечения с одиночной арматурой
6. Примеры расчета прямоугольных сечений балок с одиночной арматурой
Б. Прямоугольная балка или плита с двойной арматурой
1. Формулы для определения Mp
2. Армирование при различном соотношении площадей сжатой и растянутой арматуры. Армирование при условии min (Fa + F’a)
Армирование при условии min (Fa + F’a)
3. Примеры расчета плит и балок с двойной арматурой
B. Балка таврового сечения
1. Работа тавровой балки на изгиб
2. Наименьший процент армирования растянутой зоны балок таврового сечения
3. Расчет балок таврового сечения на отрицательный момент
4. Расчет балок таврового сечения на положительный момент
5. Выбор высоты балок таврового сечения
6. Примеры расчета балок таврового сечения
Глава V. Расчет и конструирование арматуры плит перекрытий (балочные плиты и плиты, опертые по контуру)
1. Конструктивные указания по проектированию балочных плит и плит, опертых по контуру
2. Пример расчета и конструирования балочных плит ребристого перекрытия
3. Пример расчета и конструирования плиты кессонного перекрытия
Глава VI. Расчет изгибаемых элементов, на поперечную силу
1. Работа балок при поперечном срезе по данным опытов
2. Скалывающие напряжения и главные напряжения в балке
3. Расчетные эпюры σгл = τ вдоль балки
Расчетные эпюры σгл = τ вдоль балки
4. Оценка по эпюре σгл = σ сопротивляемости балки главным растягивающим напряжениям. Распределение эпюры на части с передачей их на продольную арматуру, хомуты и косые стержни
5. Расчет и конструирование хомутов
6. Расчет и конструирование отогнутой арматуры
7. Эпюра арматуры. Прочность балки по нормальным и косым сечениям
Глава VII. Расчет и конструирование балок по изгибу и поперечному срезу
1. Конструктивные указания по проектированию балок
2. Пример расчета и конструирования однопролетных свободно лежащих балок с равномерно распределенной нагрузкой
3. Пример расчета и конструирования однопролетных свободно лежащих балок под действием сосредоточенных сил
4. Пример расчета и конструирования неразрезных балок ребристого перекрытия
5. Применение вутов в неразрезных балках ребристого перекрытия
Глава VIII. Консоли, их расчет и конструирование
1. Примеры применения консолей в строительстве
Примеры применения консолей в строительстве
2. Расчет и конструирование консолей с большим вылетом
3. Расчет и конструирование коротких консолей
Глава IX. Расчет изгибаемых элементов, к которым предъявляются требования непроницаемости бетона
1. Изгибаемые элементы с обыкновенной арматурой и с арматурой, имеющей предварительное натяжение
А. Расчет на изгиб бетонных неармированных балок
2. Расчет бетонных неармированных балок на изгиб по ТУ и Н проектирования бетонных конструкций (ОСТ 90040—39)
3. Расчет бетонных неармированных балок на изгиб по стадии напряженности IIa
Б. Расчет на изгиб железобетонных балок с обыкновенной арматурой
4. Расчет железобетонных балок на изгиб по стадии напряженности I
5. Расчет на изгиб железобетонных балок прямоугольного сечения с одиночной или с двойной арматурой по стадии напряженности IIa
6. Расчет на изгиб железобетонных балок прямоугольного сечения по стадии напряженности IIb
7. Примеры расчета и сопоставление различных приемов расчета
Примеры расчета и сопоставление различных приемов расчета
В. Расчет на изгиб балок с предварительно напряженной арматурой
8. Определение Mm для балок прямоугольного сечения с двойной арматурой, имеющей предварительное натяжение
9. Определение Mm для балок прямоугольного сечения с одиночной или двойной арматурой, часть стержней которой имеет предварительное натяжение
10. Потеря арматурой первоначального (монтажного) напряжения
11. Сравнение результатов расчета по выведенным формулам с опытными данными для железобетонных балок прямоугольного сечения с одиночной арматурой, имеющей предварительное натяжение
12. Графики и таблицы для расчета Mm. Примеры расчёта на изгиб балок с предварительно напряженной арматурой
13. Расчет на положительный момент балок таврового сечения с арматурой, имеющей предварительное натяжение
Раздел II. Осевое и внецентренное сжатие
Глава X. Элементы железобетонных конструкций, работающие на осевое и внецентренное сжатие (колонны и стойки, рамные и арочные конструкции)
1. Общие сведения
Общие сведения
2. Конструкции, работающие на осевое и внецентренное сжатие
Глава XI. Осевое сжатие
А. Колонны с продольной арматурой и обыкновенными хомутами
1. Расчет коротких колонн с продольной арматурой и обыкновенными хомутами
2. Конструктивные указания по проектированию на осевое сжатие колонн с продольной арматурой и обыкновенными хомутами
3. Продольный изгиб и его учет в расчетах прочности колонн
4. Примеры расчета колонн на осевое сжатие с продольной арматурой и обыкновенными хомутами
Б. Колонны со спиральной арматурой
5. Расчетные формулы и их обоснование
6. Конструктивные указания по проектированию «бетона в обойме»
7. Примеры расчета и конструирования колонн со спиральной арматурой («бетона в обойме»)
Глава XII. Внецентренное сжатие колонн и стоек прямоугольного сечения с продольной арматурой и обыкновенными хомутами
1. Общие предпосылки к расчету внецентренно сжатых сечений. Принятые обозначения
Принятые обозначения
2. Расчетные формулы для первого случая внецентренного сжатия
3. Расчетные формулы для второго случая внецентренного сжатия
4. Указания по конструированию и расчету внецентренно сжатых элементов
5. Учет гибкости колонн и стоек при расчете их на внецентренное сжатие
6. Примеры подбора сечений внецентренно сжатых элементов
7. Расчет на внецентренное сжатие элементов таврового сечения
8. Расчет на внецентренное сжатие при соблюдении требования непроницаемости бетона
Раздел III. Осевое и внецентренное растяжение
Глава XIII. Элементы конструкций, работающие на осевое и внецентренное растяжение
Глава XIV. Осевое растяжение
1. Расчет прочности при осевом растяжении
2. Расчет, обеспечивающий требование непроницаемости бетона
3. Мероприятия, предотвращающие образование волосных трещин в бетоне растянутых элементов конструкции
Глава XV. Внецентренное растяжение
1. Первый случай внецентреиного растяжения
Первый случай внецентреиного растяжения
2. Второй случай внецентреиного растяжения
3. Примеры расчета сечений на внецентренное растяжение
4. Расчет на внецентренное растяжение при соблюдении требования непроницаемости бетона
Раздел IV. Кручение в железобетоне
Глава XVI. Опыты и расчеты
1. Возникновение крутящих моментов в элементах конструкции и учет их в расчетах
2. Кручение бетонных круглых цилиндрических образцов. Определение σгл = τкр. Опытные данные
3. Кручение бетонных элементов прямоугольного сечения. Определение σгл = τкр
4. Армирование железобетонных элементов при кручении. Расчетные формулы. Пример расчета
5. Опытные данные при кручении армированных образцов
6. Совместное действие кручения и изгиба
Приложения
Приложение 1. Таблицы для статического расчета железобетонных конструкций
A. Таблица для расчета на изгиб плит, опертых по контуру, при сплошной равномерно распределенной нагрузке q
Б. Таблица М и Q для неразрезных балок с равными пролетами и постоянного сечения при равномерной постоянной нагрузке g и временной p
Таблица М и Q для неразрезных балок с равными пролетами и постоянного сечения при равномерной постоянной нагрузке g и временной p
B. Таблица М и Q для неразрезных балок с равными пролетами и постоянного сечения при сосредоточенной нагрузке: постоянной G и временной P
Г. Таблица пролетных и опорных моментов и поперечных сил в опорных сечениях неразрезных балок с равными пролетами
Д. Таблица опорных моментов для неразрезных балок с равными пролетами и постоянного сечения при любых нагрузках, симметричных по отношению к пролету. Концы балок могут быть свободно положены на опоры (схема I) или жестко заделаны в опорах (схема II)
Е. Таблица грузовых коэфициентов s балок с симметричной нагрузкой
Ж. Таблица моментов, поперечных сил и эквивалентных по моменту нагрузок для свободно лежащих балок
З. Таблица моментов в равнопролетной балке на упруго вращающихся опорах
Приложение 2. Таблицы и графики для расчета элементов железобетонных конструкций
Iа. Таблица круглого железа
Таблица круглого железа
I6. Таблица площадей арматуры в 1 пог. м плиты при различном расстоянии между стержнями
II. Таблица для расчета на изгиб плит и балок прямоугольного сечения с одиночной арматурой
III. Таблица для подбора прямоугольных сечений с одиночной арматурой
IV. График для расчета прямоугольных сечений на изгиб
V. Таблица для подбора сечений на изгиб с одиночной или двойной арматурой и на внецентренное сжатие и растяжение
VI. а, б, в, г, д. Графики расчета Mm для балок прямоугольного сечения с одиночной арматурой
VII. Таблица для подбора внецентренно сжатых прямоугольных сечений с двойной симметричной арматурой
VIII. График значении n1 = Np / Rubh в зависимости от c0 = e0 / h и σ1 = α’1 = σmFα / Rubh при внецентренном сжатии прямоугольных сечении с двойной симметричной арматурой при δ1 = 0,08
IX. График для расчета внецентренно сжатых элементов прямоугольного сечения (δ1 = δ’1 = 0,08)
X. а, б. Графики для расчета внецентреьно сжатых прямоугольных сечений с двойной симметричной арматурой
а, б. Графики для расчета внецентреьно сжатых прямоугольных сечений с двойной симметричной арматурой
XI. График для определения моментов инерции тавровых сечений
XII. График для определения коэфициента m при расчете внецентренно сжатых сечений с учетом гибкости элемента
XIIIa. Таблица для расчета на изгиб балок прямоугольного сечения с предварительно напряженной арматурой. Марка бетона 250 кг/см2
XIIIб. То же. Марка бетона 300 кг/см2
XIIIв. То же. Марка бетона 350 кг/см2
Приложение 3. Принятые обозначения
Приложение 4. Свод формул и правил расчета и конструирования железобетонных элементов
Предисловие
Современный курс железобетонных конструкций, отражая с максимальной полнотой достижения в области теории железобетона, должен также достаточно удовлетворять запросам практики.
Совершенно очевидно также, что в курсе должна быть дана и перспектива развития теории и практики железобетона.
Автор не считает, что в этой книге с достаточной полнотой получили разрешение перечисленные выше задачи. Материал, использованный при написании данной второй части курса, настолько обширен, многообразен и по существу нов, что некоторые положения, приведенные в курсе, нуждаются еще в серьезной дополнительной теоретической и экспериментальной проверке.
Насущные потребности текущей учебной и производственной практики однако столь важны и неотложны, что автор не счел возможным откладывать написание курса впредь до окончания разработки этих положений.
Все указания и пожелания читателей, касающиеся улучшения качества книги, будут приняты автором с благодарностью и учтены при переиздании книги.
Вторая часть курса, в которой излагаются расчет и конструирование элементов железобетонных конструкций, построена на базе действующих ТУ и Н 1939 г. (ОСТ 90003—38). Применительно к этим нормам, с использованием теоретического и экспериментального материала ЦНИПС и других научно-исследовательских организаций, нашей и иностранной технической литературы, а также личных исследований автора построено изложение курса.
При составлении курса была также учтена «Инструкция по применению норм и технических условий проектирования железобетонных конструкций», которая разрабатывалась во время написания книги.
Расположение материала в книге, трактующей о сопротивляемости железобетонных элементов при различном воздействии усилий, соответствует в основном обычно принятому расположению материала в курсе сопротивления материалов.
Раздел I курса излагает сопротивляемость железобетона изгибу и скалыванию при изгибе; здесь же приведены данные по расчету и конструированию таких элементов.
В разделе II рассмотрены вопросы расчета и конструирования элементов, работающих на осевое и внецентренное сжатие.
В раздел III вошли главы, посвященные осевому и внецентренному растяжению.
Раздел IV посвящен вопросам расчета и конструирования при наличии кручения в элементах конструкции.
Все изложение теоретических вопросов сопровождается примерами расчета и конструирования. Для облегчения расчетов даются графики и таблицы.
Каждому разделу предшествует обзор применяемых в практике конструкций.
Одним из недочетов новых норм является отсутствие в них указаний по расчету изгибаемых, внецентренно сжатых и внецентренно растянутых элементов, к которым предъявляются требования непроницаемости бетона. Этот пробел устранен в курсе. Все указания по этим расчетам, сопровождаемые графиками, таблицами и примерами практического применения, изложены достаточно полно. Кроме того уделено внимание расчету изгибаемых элементов с предварительно напряженной арматурой.
В заключение автор считает своим долгом принести глубокую благодарность доктору технических наук проф. В.М. Келдыш за его ценные указания при написании книги и при ее рецензировании, а также доктору технических наук проф. А.А. Гвоздеву за его ценные замечания при рецензировании книги.
Проф. В. Бушков
Расчет диаметра и количества арматуры на ленточный фундамент | Строю сам
То, что фундамент дома необходимо армировать – знают все, а вот как правильно это сделать – знает меньшинство. И армирует наш честной народ как придется – любой диаметр от 6 до 24 мм, любое количество арматуры. Особенно умиляют персонажи, которые считают, что чем больше они напихают металла в фундамент – тем лучше.
И армирует наш честной народ как придется – любой диаметр от 6 до 24 мм, любое количество арматуры. Особенно умиляют персонажи, которые считают, что чем больше они напихают металла в фундамент – тем лучше.
На самом деле, в армировании ленточного фундамента для дома в 1-2 этажа нет ничего сложного.
Для армирования ленточного фундамента используют 2 основные схемы армирования:
1. Четырьмя стержнями;
2. Шестью стержнями.
Далее, СП 52-101-2003 нам глаголет, что расстояние между двумя продольными стержнями не должно превышать 40 см (400 мм), потому выбранная схема зависит от ширины ленты фундамента, если ее ширина – 40 см, то первая схема ваша, если 50-60 см – то вторая. Кроме того, согласно СП, расстояние между крайними продольными арматуринами и стенками опалубки должно составлять 50-70 мм.
Диаметр вертикальной и поперечной арматуры обычно составляет 8 мм, и этого вполне достаточно для 1-2 этажного дома.
Диаметр продольной арматуры, согласно тому же СНиП 52-01-2003, рассчитывается так: площадь сечения арматуры равна 0,1% от площади сечения фундамента. То есть, ширину ленты, допустим, 40 см, умножаем на высоту ленты, допустим, 1 метр (100 см).
Получается 4000 см2, делим это на 1000, получаем – 4 см2.
Теперь просто воспользуемся таблицей:
Из таблицы видим, что диаметр продольной арматуры для нашего фундамента должен быть 12 мм.
Как рассчитать количество арматуры
Расчет количества важен, поскольку как меньшее, так и большее количество арматуры – это дополнительные затраты. Итак, начнем с 12 мм арматуры, то есть, продольной.
Исходные данные: лента фундамента 6 на 6 метров, 4-х стержневая схема армирования. Высота ленты – 1 м, ширина – 40 см.
4*6= 24 м, умножаем на 4 (стержни), получаем 96 метров. Но это в идеале, но нужно учитывать стыки в перехлест, обрезки. А это еще 10%. В Итоге нам нужно 12 мм арматуры 105,6 метров, округляем до 110, например.
Но это в идеале, но нужно учитывать стыки в перехлест, обрезки. А это еще 10%. В Итоге нам нужно 12 мм арматуры 105,6 метров, округляем до 110, например.
Поперечная и вертикальная арматура рассчитывается примерно также:
0,35*2 + 0,90*2 = 2,5 метра на точку. Теперь нам нужно узнать, сколько таких узлов у нас будет.
Примем за шаг вертикальных прутков 60 см, тогда на 6 м стену у нас выйдет 10 узлов. То есть, 40 узлов на все четыре стены.
Теперь 40*2,5 и получаем 100 метров. Берем запас в 10 метров, и получаем 110 метров 8 мм арматуры.
Вот так все просто и правильно.
Друзья! Буду рад лайку и подписке!
Прямоугольное поперечное сечение – обзор
4.1.1 Пластометрические испытания
В этом разделе обсуждаются основные типы пластометрических испытаний и указываются их преимущества и ограничения. Знание устойчивости материалов к деформации и их способности безопасно выдерживать нагрузку до разрушения имело первостепенное значение для людей с тех пор, как были построены первые конструкции. В шестнадцатом веке найдены документальные свидетельства из сочинений Леонардо да Винчи, свидетельствующие о том, что количественные методы применялись для измерения различий в свойствах материалов [352].Галилео Галилей [95] представил первую серьезную математическую трактовку упругой прочности материала в конструкции, подвергаемой изгибу. В последующие века поиск связи между приложенной нагрузкой и деформацией материала продолжался, и были разработаны машины для измерения прочности на растяжение. Испытание на растяжение было основным методом, применяемым в то время. Среди ряда вкладов в развитие методов испытания материалов следует упомянуть Уильяма Фэйрберна [85] в Англии, а затем Адольфа Мартенса [222] в Германии.Бывший ученый внес значительный вклад в систематическую оценку прочности материалов при высоких температурах.
В шестнадцатом веке найдены документальные свидетельства из сочинений Леонардо да Винчи, свидетельствующие о том, что количественные методы применялись для измерения различий в свойствах материалов [352].Галилео Галилей [95] представил первую серьезную математическую трактовку упругой прочности материала в конструкции, подвергаемой изгибу. В последующие века поиск связи между приложенной нагрузкой и деформацией материала продолжался, и были разработаны машины для измерения прочности на растяжение. Испытание на растяжение было основным методом, применяемым в то время. Среди ряда вкладов в развитие методов испытания материалов следует упомянуть Уильяма Фэйрберна [85] в Англии, а затем Адольфа Мартенса [222] в Германии.Бывший ученый внес значительный вклад в систематическую оценку прочности материалов при высоких температурах.
Иоганн Баушингер [27] был еще одним участником испытаний материалов, которому приписывают введение двусторонних экстензометров, которые позволяют компенсировать кривизну или смещение испытуемого образца. Это позволило значительно улучшить измерение деформации растяжения и обеспечить достаточную точность измерений, чтобы наблюдать, что предел текучести снижается, когда за деформацией в одном направлении следует деформация в противоположном направлении.Сейчас это известно как эффект Баушингера. Многочисленные исследования и сравнения испытаний на растяжение были проведены в течение следующих десятилетий, и результаты были впоследствии обобщены Анвином [358]. ASTM E8-24T «Стандартные методы испытаний металлических материалов на растяжение» были опубликованы в 1924 году.
Это позволило значительно улучшить измерение деформации растяжения и обеспечить достаточную точность измерений, чтобы наблюдать, что предел текучести снижается, когда за деформацией в одном направлении следует деформация в противоположном направлении.Сейчас это известно как эффект Баушингера. Многочисленные исследования и сравнения испытаний на растяжение были проведены в течение следующих десятилетий, и результаты были впоследствии обобщены Анвином [358]. ASTM E8-24T «Стандартные методы испытаний металлических материалов на растяжение» были опубликованы в 1924 году.
В настоящее время испытания на растяжение считаются наиболее распространенными и простыми в выполнении испытаниями. Прочность материала при растяжении долгое время считалась одной из наиболее важных характеристик, необходимых для проектирования, производства, контроля качества и прогнозирования срока службы промышленного предприятия.Стандарты испытаний на растяжение были одними из первых опубликованных стандартов, и разработка таких стандартов продолжается и сегодня. Эти тесты тщательно разрабатывались в течение почти столетия, и было опубликовано большое количество научных статей и руководств по передовой практике. Последние собраны в отчете проекта 6-й рамочной программы «Испытания металлических материалов на растяжение: обзор», аббревиатура TENSTAND.
Эти тесты тщательно разрабатывались в течение почти столетия, и было опубликовано большое количество научных статей и руководств по передовой практике. Последние собраны в отчете проекта 6-й рамочной программы «Испытания металлических материалов на растяжение: обзор», аббревиатура TENSTAND.
Образцы цилиндрического или прямоугольного сечения используются при испытаниях на растяжение.Преимущества этих испытаний можно резюмировать следующим образом:
- •
не нужно учитывать проблемы трения,
- •
испытания регулируются стандартами, поэтому межлабораторная изменчивость сведена к минимуму.
Недостатки указывают на то, что испытание на растяжение не является наиболее подходящим испытанием, когда используемая информация предназначена для изучения процессов объемной штамповки металла. Они следующие:
- •
возможны малые деформации, не более 40–50 %,
- •
одноосный характер распределения напряжений теряется, когда начинается локальное деформирование.

Теперь доступна обширная информация о методах и стандартах испытаний на растяжение, и читатель может ознакомиться с обзорными публикациями в Refs. [118,212][118][212], стандарты ASTM E8/E8M-13a «Стандартные методы испытаний металлических материалов на растяжение» и к упомянутому отчету проекта 6-й рамочной программы TENSTAND.
Испытание на сжатие было разработано гораздо позже испытания на растяжение. Это испытание определяет поведение материалов при сжимающих нагрузках.Подробный обзор процедуры и стандартов для испытания на сжатие можно найти в Ref. [178]. Испытание может проводиться на цилиндрических или плоских образцах. Первое называется одноосным сжатием (UC), второе — PSC. В некоторых практических приложениях также используется испытание на сжатие кольца (RC). Схематическая иллюстрация основных испытаний на сжатие представлена на рисунке 4.1. Сжатие в канальных штампах также показано на рис. 4.1, но это испытание посвящено скорее исследованию механизма деформирования при плоском состоянии деформации. Общими преимуществами всех испытаний на сжатие являются:
Общими преимуществами всех испытаний на сжатие являются:
Рисунок 4.1. Схематическое изображение пластометрических тестов.
- •
возможны большие деформации, чем при растяжении, обычно более 1 при сжатии цилиндров и до 2 при испытании плоских образцов, формирование.
Недостатками испытаний на сжатие являются:
- •
Силы трения на границе раздела ползун-образец возрастают по мере прохождения испытания, и их влияние необходимо устранить.
- •
Растяжение цилиндрических поверхностей или краев плоских образцов ограничивает уровень деформации.
- •
Достижение постоянной истинной скорости деформации во время испытаний требует тщательного контроля обратной связи, что делает неизбежным использование кулачкового пластометра или сервогидравлической испытательной системы.
- •
Распределение деформации в нормальном направлении неравномерно.
 При плоскодеформированном сжатии трудно достичь изотермических условий.
При плоскодеформированном сжатии трудно достичь изотермических условий.
В тесте UC образец располагается между двумя параллельными плитами (рис. 4.1). Образцы обрабатываются с учетом того, что остаточные напряжения должны быть сведены к минимуму. Ориентация образца относительно исходного материала должна быть записана. Рекомендуемое соотношение сторон (высота к диаметру) должно быть около 1,5. Перед горячей деформацией образец должен быть подвергнут определенному циклу предварительного нагрева. Целью предварительного нагрева является гомогенизация микроструктуры и получение однородной температуры в начале испытания.Применение различных температур предварительного нагрева позволяет получить различную микроструктуру перед деформацией [270]. Образец сжимается между плитами, и во время испытания регистрируются силы, текущая высота и температура. Напряжение течения рассчитывается как отношение силы к контактной поверхности ( F / A ), а деформация рассчитывается по изменению высоты как 2 ), где h 1 и h 2 — начальная и конечная высоты соответственно.
Трение является основным фактором, влияющим на результаты этого теста. Из-за трения деформация неоднородна. Кроме того, деформационный нагрев и передача тепла плите и окружающей среде еще больше затрудняют интерпретацию результатов испытаний. Неоднородность теста хорошо видна на рис. 4.2. На этом рисунке видно, что распределение деформаций и температуры неравномерно. Таким образом, прямая интерпретация результатов испытаний может привести к ошибкам.
Рисунок 4.2. Распределение деформации (а) и температуры (б) в испытании UC для стали C-Mn.
PSC является одним из пластометрических тестов, который используется в основном для физического моделирования процессов многоступенчатой формовки, но также часто применяется для определения напряжения течения. В этом тесте прямоугольный образец сжимается между двумя плоскими матрицами; см. рис. 4.1. Это испытание допускает большую пластическую деформацию, а состояние деформации аналогично тому, которое имеет место в процессе плоской прокатки. Состояние плоской деформации достигается за счет двух факторов. Небольшое отношение ширины (b) образца к ширине матрицы (w) предотвращает течение материала в направлении ширины. Это похоже на плоскую прокатку, где малое отношение длины контакта к ширине полосы способствует удлинению и предотвращает растекание. Влияние так называемых жестких концов является еще одним фактором, ограничивающим распространение и включающим плоскодеформированное состояние. Жесткие концы – это части образца, находящиеся за пределами площади под штампом. Эти части не сжаты, поэтому не имеют склонности к растеканию.Кроме того, при нагреве образцов резистивным нагревом (например, на тренажере Gleeble 3800) эти детали имеют более низкую температуру, чем область под штампом, и их сопротивление деформации выше. Из-за всех этих обсуждаемых фактов PSC часто используется в качестве физического моделирования процесса плоской прокатки.
Состояние плоской деформации достигается за счет двух факторов. Небольшое отношение ширины (b) образца к ширине матрицы (w) предотвращает течение материала в направлении ширины. Это похоже на плоскую прокатку, где малое отношение длины контакта к ширине полосы способствует удлинению и предотвращает растекание. Влияние так называемых жестких концов является еще одним фактором, ограничивающим распространение и включающим плоскодеформированное состояние. Жесткие концы – это части образца, находящиеся за пределами площади под штампом. Эти части не сжаты, поэтому не имеют склонности к растеканию.Кроме того, при нагреве образцов резистивным нагревом (например, на тренажере Gleeble 3800) эти детали имеют более низкую температуру, чем область под штампом, и их сопротивление деформации выше. Из-за всех этих обсуждаемых фактов PSC часто используется в качестве физического моделирования процесса плоской прокатки.
Плоское состояние деформации, недостижимое в других пластометрических тестах, в течение многих лет вдохновляло ученых на различные применения тестов PSC. Одним из таких приложений является идентификация модели напряжения течения, а другим примером является исследование эволюции микроструктуры.Среди нескольких исследовательских лабораторий, участвовавших в исследованиях на основе тестов PSC, группа под руководством К.М. Следует упомянуть Селларса из Университета Шеффилда. В 1950-х и 1960-х годах этот тест широко использовался там для исследования материалов, и результатом этих исследований стали фундаментальные работы по эволюции микроструктуры [322] и по моделям напряжения течения [58].
Одним из таких приложений является идентификация модели напряжения течения, а другим примером является исследование эволюции микроструктуры.Среди нескольких исследовательских лабораторий, участвовавших в исследованиях на основе тестов PSC, группа под руководством К.М. Следует упомянуть Селларса из Университета Шеффилда. В 1950-х и 1960-х годах этот тест широко использовался там для исследования материалов, и результатом этих исследований стали фундаментальные работы по эволюции микроструктуры [322] и по моделям напряжения течения [58].
Некоторые аспекты теста PSC, такие как подготовка образца, предварительный нагрев и т. д., аналогичны тем, которые используются в тестах UC.Следует, однако, подчеркнуть, что различные помехи сильно затрудняют интерпретацию результатов тестов PSC. Эти испытания характеризуются большой неоднородностью деформации (рис. 4.3а), что обусловлено сложной формой очага деформации (рис. 4.1) и действием трения. Кроме того, тепло, выделяющееся за счет пластической работы и трения, а также передача тепла инструментам и окружающей среде, вызывает сильную неоднородность температуры в образце (рис. 3б).
3б).
Рисунок 4.3. Распределение деформации (а) и температуры (б) в испытании PSC для медного сплава.
Техника RC, изначально разработанная для холодной штамповки, была адаптирована Мале и Кокрофтом [218] для горячей обработки. Течение металла в этом испытании зависит от трения. Для низкого трения увеличиваются как внутренний, так и внешний диаметры. При большом трении внутренний диаметр течет внутрь, а внешний диаметр течет наружу, и нейтральная точка возникает без проскальзывания. Это хорошо видно на рисунке 4.4, где показаны результаты расчетов формы кольца для различных коэффициентов трения в модели Трески. Поскольку положение нейтральной точки является функцией трения, этот тест обычно используется для измерения коэффициента трения. Для определения этого коэффициента достаточно измерить только изменение формы кольца. Традиционный метод интерпретации RC основан на измерении внутреннего диаметра только после сжатия. Специальные диаграммы, см., например, Шей [317], используются для определения коэффициента трения на основе этого измерения. Однако испытание RC дает больше информации, чем изменение внутреннего диаметра кольца. Обратный анализ позволяет учесть эту информацию, которая обычно включает результаты измерений внутреннего и внешнего диаметра в нескольких точках по высоте кольца. Кроме того, измерение нагрузок при деформации кольца дает информацию, которая дополнительно позволяет оценить параметры напряжения течения. Следовательно, этот тест может быть выбран для оценки как фрикционных, так и реологических параметров.
Однако испытание RC дает больше информации, чем изменение внутреннего диаметра кольца. Обратный анализ позволяет учесть эту информацию, которая обычно включает результаты измерений внутреннего и внешнего диаметра в нескольких точках по высоте кольца. Кроме того, измерение нагрузок при деформации кольца дает информацию, которая дополнительно позволяет оценить параметры напряжения течения. Следовательно, этот тест может быть выбран для оценки как фрикционных, так и реологических параметров.
Рисунок 4.4. Форма четверти поперечного сечения кольца, измеренная до и после сжатия (сплошные линии) и рассчитанная после сжатия для различных коэффициентов трения.
Тщательный анализ преимуществ и недостатков тестов UC и PSC, а также стандарты для этих тестов можно найти в Руководствах по эффективной практике Национальной физической лаборатории [197,304][197][304]. Применение обратного анализа для интерпретации результатов испытаний UC, RC и PSC представлено в разделе 4.2.2.
Испытания материалов на кручение проводятся для определения таких свойств, как модуль упругости при сдвиге, предел текучести при кручении и модуль разрыва. Эти испытания особенно полезны для определения характеристик технологической пластичности материалов, которые отражают свойства материалов в процессах обработки металлов давлением. Они также используются для сравнительной оценки пластичности материалов в зависимости от их химического состава, фазового состава и технологии производства.Результаты испытаний на кручение могут быть использованы для оценки силовых параметров в процессах обработки металлов давлением и для определения оптимальных диапазонов технологических параметров в этих процессах. Эти тесты также позволяют оценить влияние условий деформации на эволюцию микроструктуры.
Эти испытания особенно полезны для определения характеристик технологической пластичности материалов, которые отражают свойства материалов в процессах обработки металлов давлением. Они также используются для сравнительной оценки пластичности материалов в зависимости от их химического состава, фазового состава и технологии производства.Результаты испытаний на кручение могут быть использованы для оценки силовых параметров в процессах обработки металлов давлением и для определения оптимальных диапазонов технологических параметров в этих процессах. Эти тесты также позволяют оценить влияние условий деформации на эволюцию микроструктуры.
Испытания на кручение также часто используются для испытаний хрупких материалов и для испытаний полноразмерных деталей, т. е. валов, осей и спиральных сверл, которые в процессе эксплуатации подвергаются скручивающей нагрузке.При испытании на кручение стандартные цилиндрические образцы на кручение изготавливают из поставляемого исследуемого материала и подвергают испытаниям на специальной установке на кручение, оснащенной радиационной печью.
Испытание на кручение лучше всего подходит для процессов с большими деформациями. Можно получить конечные деформации 5, что позволяет моделировать всю историю горячей прокатки, включая явления на черновом стане и на чистовой линии прокатных станов горячей прокатки. Преимущества испытаний на кручение:
- •
возможны очень большие деформации,
- •
постоянная скорость деформации легко достигается,
Недостатки:
- •
напряжения и деформации при кручении различаются по поперечному сечению, и для получения данных одноосного нормального напряжения-деформации необходим значительный объем анализа,
- •
- вариация во времени. В результате для разных участков поперечного сечения требуется разное время для проявления металлургических явлений, в частности динамической рекристаллизации (DRX).
Крутящий момент является основным выходным параметром при испытании на кручение. Существует несколько помех, которые затрудняют надежное измерение крутящего момента. Разгон скорости крутки от нуля до номинального значения занимает некоторое время. Температура образца увеличивается во время испытания. Эти два явления вызывают необходимость проведения коррекции записанного теста. Типичное поправочное уравнение имеет вид:
Существует несколько помех, которые затрудняют надежное измерение крутящего момента. Разгон скорости крутки от нуля до номинального значения занимает некоторое время. Температура образца увеличивается во время испытания. Эти два явления вызывают необходимость проведения коррекции записанного теста. Типичное поправочное уравнение имеет вид:
(4.1)M=Mrec(N˙NN˙)m
где M rec — зарегистрированный крутящий момент, M — скорректированный крутящий момент, m — чувствительность к скорости деформации. , N˙N номинальная скорость скручивания, а N˙ зарегистрированная скорость скручивания.
Расчет истинной деформации ε , скорости деформации ε˙ и напряжения течения σ p по измеренному крутящему моменту является еще одной проблемой при интерпретации результатов испытаний. Следующие соотношения были предложены в работе [1]. [127]:
(4.2)ε=23πRNL
(4.3)ε˙=23πRN˙L
(4.4)σp=(3M2πR3)2(3+p+m)2+(FπR2)2
где L длина образца, R радиус образца, M крутящий момент, N количество скручиваний, N˙ скорость скручивания, м чувствительность к скорости деформации и p дифференциальная составляющая, определяемая из уравнения:
(4. 5)p=NM∂M∂N
5)p=NM∂M∂N
В литературе можно найти несколько других методов интерпретации испытания на кручение, позволяющих рассчитать напряжение течения по крутящему моменту, зарегистрированному во время испытания [117]. Моделирование этого теста методом конечных элементов (КЭ) представлено в [1]. [257], а попытка применения обратного анализа к интерпретации результатов испытаний на кручение представлена в [2]. [157]. КЭ-модель испытания на кручение также использовалась в качестве модели прямой задачи в этой публикации. Поскольку КЭ-моделирование деформации материала при кручении, которое связано со значительным напряжением сдвига, было затруднено, применение обратного анализа для интерпретации результатов испытаний на кручение представляло трудности и никогда не становилось таким популярным, как для испытаний на сжатие.Обзор методов расчета напряжения течения по крутящему моменту, зарегистрированному во время испытания, был разработан Хадасиком [127] и не описывается в этой книге.
Подводя итог, можно констатировать, что разнообразие конструкции торсионных пластометров, гибкость метода испытаний, трудности учета теплового эффекта и неоднородности окраски привели к существенным расхождениям между результатами, полученными в разных лабораториях. Это также затрудняет сравнение результатов испытаний на кручение с результатами испытаний на сжатие.Все эти трудности с интерпретацией результатов испытаний на кручение являются основными ограничениями в применении испытаний на кручение для количественного определения напряжения течения. Тест скорее посвящен сравнению различных материалов и физическому моделированию многостадийных процессов.
Это также затрудняет сравнение результатов испытаний на кручение с результатами испытаний на сжатие.Все эти трудности с интерпретацией результатов испытаний на кручение являются основными ограничениями в применении испытаний на кручение для количественного определения напряжения течения. Тест скорее посвящен сравнению различных материалов и физическому моделированию многостадийных процессов.
Минимальный процент стали в зависимости от толщины балки
Контекст 1
… бетонные балки подвергаются различным механизмам разрушения из-за различной гибкости балки и/или коэффициента армирования и/или масштаба балки.Три основных механизма обрушения следующие: • Образование наклонных трещин сдвига; Сжатие и дробление на кромке при сжатии; • Зарождение и распространение трещин на кромке при растяжении. Что касается разрушения при растяжении, минимальное количество армирования может быть определено с помощью концепций механики разрушения, в то время как максимальная неупругая вращательная способность может быть получена, даже когда разрушение смещается в сторону сжатия. Многие экспериментальные тесты подтвердили, что обе эти величины подвержены заметному размерному эффекту.Хорошо известно, что минимальное армирование (минимальное количество стали, предотвращающее хрупкое разрушение) должно быть достаточным для поглощения сил растяжения, присутствующих в бетоне непосредственно перед разрушением. Другими словами, минимальный процент армирования должен гарантировать, что при сопротивлении бетона растяжению одним из способов выражения пластичности железобетонной балки является предельный пластический поворот. Как правило, это определяется как неупругое вращение в соответствии с предельным изгибающим моментом.При обычном определяющем законе стали и бетона максимальный момент достигается при меньших значениях кривизны. При более реалистичном предположении пиковое значение будет достигнуто для дальнейшего искривления. В последующем анализе мы вычисляем предельные значения вращения в соответствии с относительной кривизной в момент, равный 90% пикового значения нисходящей ветви.
Многие экспериментальные тесты подтвердили, что обе эти величины подвержены заметному размерному эффекту.Хорошо известно, что минимальное армирование (минимальное количество стали, предотвращающее хрупкое разрушение) должно быть достаточным для поглощения сил растяжения, присутствующих в бетоне непосредственно перед разрушением. Другими словами, минимальный процент армирования должен гарантировать, что при сопротивлении бетона растяжению одним из способов выражения пластичности железобетонной балки является предельный пластический поворот. Как правило, это определяется как неупругое вращение в соответствии с предельным изгибающим моментом.При обычном определяющем законе стали и бетона максимальный момент достигается при меньших значениях кривизны. При более реалистичном предположении пиковое значение будет достигнуто для дальнейшего искривления. В последующем анализе мы вычисляем предельные значения вращения в соответствии с относительной кривизной в момент, равный 90% пикового значения нисходящей ветви. Вращение, полученное таким образом, было очищено от перегрузки, все еще можно встретить более стабильный отклик того же луча.Согласно некоторым исследованиям (Ozbolt and Bruckner, 1999), основанным на механике разрушения, было выявлено, что минимальное армирование зависит от размеров балки, в отличие от норм проектирования, где минимальное армирование не зависит от размера h, рис. 1. от значения упругости, принятого в соответствии с пределом текучести арматуры. Испытание проводят до разрушения с контролем смещения для процентной доли стальной арматуры более 0,25, а контроль прогиба используют для значений, меньших или равных 0.25. Результат нелинейного анализа зависит от проектных значений, принятых для свойств материала в различных частях конструкции. Без учета эффекта второго порядка и с учетом нелинейного поведения материала и жесткости при растяжении код (CEB, 1993) указывает, что для положения предполагаемой нагрузки среднее значение свойств материала остается неизменным до предела текучести.
Вращение, полученное таким образом, было очищено от перегрузки, все еще можно встретить более стабильный отклик того же луча.Согласно некоторым исследованиям (Ozbolt and Bruckner, 1999), основанным на механике разрушения, было выявлено, что минимальное армирование зависит от размеров балки, в отличие от норм проектирования, где минимальное армирование не зависит от размера h, рис. 1. от значения упругости, принятого в соответствии с пределом текучести арматуры. Испытание проводят до разрушения с контролем смещения для процентной доли стальной арматуры более 0,25, а контроль прогиба используют для значений, меньших или равных 0.25. Результат нелинейного анализа зависит от проектных значений, принятых для свойств материала в различных частях конструкции. Без учета эффекта второго порядка и с учетом нелинейного поведения материала и жесткости при растяжении код (CEB, 1993) указывает, что для положения предполагаемой нагрузки среднее значение свойств материала остается неизменным до предела текучести. значение стали было достигнуто в критическом сечении. Как только этот предел достигнут, для свойств материала расчетное значение должно быть принято в соответствии с критическим сечением, а максимальная емкость принята равной емкости в предельном состоянии.Критические сечения локализованы в соответствии с максимальным значением изгибающего момента по зонам, где эти характеристики имеют один и тот же знак. В отсутствие осевой силы и при наличии определяющего закона упругопластического упрочнения стали можно считать, что при достижении предела текучести стали критические сечения действуют как пластические шарниры вплоть до значения предельного момента, а пластическое вращение достигает своего предельного значения. Указанная модель соответствует предположению третьего отрезка определяющего закона сечения, определенного в справочнике переводной системы с началом в пределе текучести стали, в котором его наклон определяется как отношение разности значений предельного момента и допустимое пластическое вращение, как указано выше.
значение стали было достигнуто в критическом сечении. Как только этот предел достигнут, для свойств материала расчетное значение должно быть принято в соответствии с критическим сечением, а максимальная емкость принята равной емкости в предельном состоянии.Критические сечения локализованы в соответствии с максимальным значением изгибающего момента по зонам, где эти характеристики имеют один и тот же знак. В отсутствие осевой силы и при наличии определяющего закона упругопластического упрочнения стали можно считать, что при достижении предела текучести стали критические сечения действуют как пластические шарниры вплоть до значения предельного момента, а пластическое вращение достигает своего предельного значения. Указанная модель соответствует предположению третьего отрезка определяющего закона сечения, определенного в справочнике переводной системы с началом в пределе текучести стали, в котором его наклон определяется как отношение разности значений предельного момента и допустимое пластическое вращение, как указано выше. Интересно отметить, что при высоком проценте стальной арматуры большие деформации бетона происходят до того, как сталь поддастся. В этом случае приведенное выше соображение должно быть изменено, даже если с общей точки зрения мы можем сослаться на конститутивный закон с тремя сегментами. Было проведено испытание на трехточечный изгиб 17 железобетонных балок. Балки были разделены на классы А, В и С с площадью поперечного сечения b×h, равной 100×100, 100×200 и 200×400 мм соответственно, с различным коэффициентом стали, 0.125, 0,25, 0,50, 1,00 и 2,00 % (расположение основной стали и хомутов см. рис. 2), а также различные значения гибкости (отношение пролета l/h к глубине) 6, 12 и 18. Балки были испытаны в Лаборатория факультета строительной инженерии Туринского университета. Используемая испытательная машина представляла собой машину с сервоуправлением с обратной связью. Испытания проводились в условиях контролируемого перемещения, чтобы можно было записать нисходящую ветвь кривой нагрузка-перемещение, если таковая имеется.
Интересно отметить, что при высоком проценте стальной арматуры большие деформации бетона происходят до того, как сталь поддастся. В этом случае приведенное выше соображение должно быть изменено, даже если с общей точки зрения мы можем сослаться на конститутивный закон с тремя сегментами. Было проведено испытание на трехточечный изгиб 17 железобетонных балок. Балки были разделены на классы А, В и С с площадью поперечного сечения b×h, равной 100×100, 100×200 и 200×400 мм соответственно, с различным коэффициентом стали, 0.125, 0,25, 0,50, 1,00 и 2,00 % (расположение основной стали и хомутов см. рис. 2), а также различные значения гибкости (отношение пролета l/h к глубине) 6, 12 и 18. Балки были испытаны в Лаборатория факультета строительной инженерии Туринского университета. Используемая испытательная машина представляла собой машину с сервоуправлением с обратной связью. Испытания проводились в условиях контролируемого перемещения, чтобы можно было записать нисходящую ветвь кривой нагрузка-перемещение, если таковая имеется. Датчики перемещения, используемые для контроля процесса нагружения, были размещены в середине пролета на нижней кромке образца.Диапазон измерения был больше, чем максимальное ожидаемое отклонение образца при разрушении, чтобы избежать сопротивления сигнала; для перестановки датчика (см. рис. 3 и рис. 8). Значения экспериментальных параметров балок приведены в таблице 1. Пластическое вращение формально выражается как уникальная функция отношения x / d между глубиной нейтральной оси и полезной глубиной балки без игнорирования того, что это отношение связано к коэффициенту армирования, в то время как в недавних исследованиях также учитывался эффект пластичности стали (Lounis et al., 2010). Влияние пластичности стали, по сути, стало важным из-за технологической эволюции производства стали, которая снижает отношение f t / f y по отношению к прошлому. С другой стороны, на пластическое поведение железобетонных конструкций большое влияние оказывают другие факторы, такие как: — условия удержания в зоне сжатия сечения балки; — Условия связи между стальными стержнями и бетоном; — Градиент изгибающего момента; — Эффект масштаба; — Тестовая процедура; — площадь зоны контакта между приложенной нагрузкой и поверхностью балки.
Датчики перемещения, используемые для контроля процесса нагружения, были размещены в середине пролета на нижней кромке образца.Диапазон измерения был больше, чем максимальное ожидаемое отклонение образца при разрушении, чтобы избежать сопротивления сигнала; для перестановки датчика (см. рис. 3 и рис. 8). Значения экспериментальных параметров балок приведены в таблице 1. Пластическое вращение формально выражается как уникальная функция отношения x / d между глубиной нейтральной оси и полезной глубиной балки без игнорирования того, что это отношение связано к коэффициенту армирования, в то время как в недавних исследованиях также учитывался эффект пластичности стали (Lounis et al., 2010). Влияние пластичности стали, по сути, стало важным из-за технологической эволюции производства стали, которая снижает отношение f t / f y по отношению к прошлому. С другой стороны, на пластическое поведение железобетонных конструкций большое влияние оказывают другие факторы, такие как: — условия удержания в зоне сжатия сечения балки; — Условия связи между стальными стержнями и бетоном; — Градиент изгибающего момента; — Эффект масштаба; — Тестовая процедура; — площадь зоны контакта между приложенной нагрузкой и поверхностью балки. Что касается определения, пластическое вращение не имеет однозначного определения, но оно всегда связано с методом расчета, адаптированным к структурному анализу. В неопределенной структуре используется определение, данное в (CEB, 1993). Пластический поворот θ p будет получен интегрированием по зоне пластичности lp (где напряжение в растянутой стали больше ее предела текучести) как разность между полной кривизной 1/rm и кривизной, полученной на пределе текучести точка стали 1 / р как …
Что касается определения, пластическое вращение не имеет однозначного определения, но оно всегда связано с методом расчета, адаптированным к структурному анализу. В неопределенной структуре используется определение, данное в (CEB, 1993). Пластический поворот θ p будет получен интегрированием по зоне пластичности lp (где напряжение в растянутой стали больше ее предела текучести) как разность между полной кривизной 1/rm и кривизной, полученной на пределе текучести точка стали 1 / р как …
(PDF) Минимальная арматура на изгиб в прямоугольных и тавровых бетонных балках
371
A. Carpinteri/E. Кадамуро/М. Corrado · Минимальная арматура на изгиб в прямоугольных и тавровых бетонных балках
Structural Concrete 15 (2014), № 3
Модель. Она оказывается функцией h–0,15 для прямоугольных балок и h–0,08 для тавровых балок вместо h–0,50, полученной с помощью LEFM. Такая разница хорошо видна на
рис.8, где кривая Боско и Карпинтери [11] составляет
по сравнению с настоящим предложением. Предлагаемые формулы
Предлагаемые формулы
, уравнения. (19) и (20), могут быть далее переставлены для практических целей путем выражения fctm и KIC как функций
fck в соответствии с соотношениями, доступными в литературе
и/или в нормах проектирования (см., например, fib Код модели
2010 [2]). В качестве альтернативы, очень похожие результаты можно получить, применяя предписание, предусмотренное Еврокодом
2 и Модельным кодом fib 2010 (ур.(4)), в котором прочность на одноосное растяжение
al заменена прочностью на растяжение при изгибе
, заданной уравнением. (21). Полученная формула, безусловно, пригодна для практических целей.
Наконец, следует отметить, что для полного решения проблемы минимального
армирования необходимо также тщательно изучить условия работоспособности.
В соответствии с подходом модели FIB 2010, например,
, более строгие предписания для минимального
количества арматуры могут быть получены из ограничений
на смещение устья трещины, необходимое для
предотвращения коррозии стали и повысить долговечность. Ожидается, что эффекты размера также повлияют на раскрытие трещины в
Ожидается, что эффекты размера также повлияют на раскрытие трещины в
этом случае и, следовательно, на минимальное армирование, как показали эксперименты Yasir Alam et al. [27].
Благодарности
Финансовая поддержка, оказанная Министерством университетов и научных исследований (MIUR) для проекта «Объявление
передовых приложений механики разрушения для изучения
целостности и долговечности материалов и конструкций ” is
с благодарностью.
Обозначение
Площадь поперечного сечения
Площадь стальной арматуры
bwширина растянутой стороны балки
эффективная глубина балки
DMкоэффициент влияния для приложенного момента
—
места размещения
Модуль упругости бетона
Модуль упругости стали
fck характеристическая прочность бетона на сжатие
fcm средняя прочность бетона на сжатие
fctm средняя прочность бетона на одноосное растяжение, на изгиб
05 бетон
fyk характеристический предел текучести стали
{F} вектор узловых сил
GCэнергия разрушения бетона
GFэнергия разрушения бетона
габаритная глубина балки
KIC вектор вязкости разрушения бетона
90} коэффициенты влияния для приложенияment
[Kw] матрица коэффициентов влияния для узловых смещений
мест размещения
Lпролет балки
lдлина рассматриваемой части балки
нанесенный на карту момент изгиба —
Inforcent X Moment Arms)
MCR Cracking Момент простых бетонных секции
NPREINFORPORPLIONGING CRISTLESTY NOUM
NPC Критическое значение для армирования Crittlenity NUM-
BER, соответствующий минимальному армирую
Summer
Нагрузка на панте
PCR Максимальная трещина нагрузки
Тюзамная нагрузка относительно данной стали и
полностью треснувшего поперечного сечения
Sstreness Crittless Number
{W} Вектор узловых смещений
WC
CR критические перекрывающиеся смещения
WT
CR критические смещение раскрытия трещины
δ
прогиб в середине пролета
ϑ
локализованное вращение рассматриваемой части балки
ρ
(As/bwd) ×100, процент стальной арматуры
коэффициент φсопротивления
ЛитератураБалаш, Г.
 Л.: Проектирование SLS в соответствии с кодом модели fib
Л.: Проектирование SLS в соответствии с кодом модели fib2010. Конструкционный бетон, 2013, 14, № 2, стр. 99–123.
2. Federation International du Beton (ed.): Model Code 2010 –
Первый полный проект, vol. 1, Thomas Telford Ltd, Lausanne,
fib Bulletin No. 55, 2010.
3. Комитет 318 Американского института бетона (ред.): Building
Требования к конструкционному бетону (ACI 318-95)
и комментарий (ACI 318R-95), Детройт, Мичиган, 1995 г.
4. Комитет 318 Американского института бетона (ред.): Building
Кодекс требований к конструкционному бетону (ACI 318-08)
и комментарий (ACI 318R-08), Farmington Hills, MI,
2008.
5
5. Seguirant, SJ, Brice, R., Khaleghi, B.: Обоснование минимальных требований к арматуре на изгиб для железобетонных элементов
. Журнал PCI, 2010, 55, № 3, стр. 64–85.
6. Европейский комитет по стандартизации (ред.): Еврокод 2:
Проектирование бетонных конструкций, Часть 1-1: Общие правила и
Правила для зданий, Брюссель, 2004.
7. Норвежский стандарт, NS 3473 E (английский перевод): Бетон
бетон Конструкции, правила проектирования, Норвежский совет по строительной стандартизации
, Олсо, Норвегия, 1989 г.
8. Карпинтери, А.: Стабильность процесса разрушения железобетонных балок.
Journal of Structural Engineering, 1984, 110, № 3, стр.
544–558.
9. Боско, К., Карпинтери, А.: Размягчение и проламывание
армированных элементов. Журнал инженерной механики
—, 1992, 118, № 8, стр. 1564–1577.
10. Боско, К., Карпинтери, А., Дебернарди, П.Г.: Минимальное усилие
в высокопрочном бетоне. Журнал Structural
Engineering, 1990, 116, № 2, стр. 427–437.
11. Боско, К., Карпинтери, А.: Оценка механики разрушения
минимальной арматуры в бетонных конструкциях.В: Приложения
механики разрушения железобетона, Карпин-
тери, А. (ред.), Elsevier Applied Science, Лондон, 1992, стр.
347–377.
12. Хокинс, Н.М., Хьорсетет, К.: Минимальные требования к
Хокинс, Н.М., Хьорсетет, К.: Минимальные требования к
арматуре для бетонных изгибаемых элементов. В: Приложения
механики разрушения железобетона, Carpinteri,
A. (ред.), Elsevier Applied Science, Лондон, 1992, стр.
379–412.
13.Gerstle, W.H., Dey, P.P., Prasad, N.N.V., Rahulkumar, P.,
Xie, M.: Рост трещины в изгибаемых элементах – разрушение ме-
Расчет допустимого момента ж/б балки
Поведение балки: допустимый момент балкиПрежде чем обсуждать расчет допустимого момента, давайте рассмотрим поведение простой железобетонной балки при увеличении нагрузки на балку от нуля до величины, которая может привести к разрушению. Балка будет подвергаться нагрузке вниз, что вызовет положительный момент в балке.Стальная арматура расположена в нижней части балки, которая является растянутой стороной. Здесь мы можем выбрать три основных режима поведения луча:
1. Поведение при изгибе при очень малой нагрузке При условии, что бетон не треснул, а сталь выдержит растяжение. Также бетон наверху будет сопротивляться сжатию. Распределение напряжения будет линейным:
Также бетон наверху будет сопротивляться сжатию. Распределение напряжения будет линейным:
В этом случае предел прочности бетона на растяжение будет превышен, и бетон растрескается в зоне растяжения.Поскольку бетон не может передавать какое-либо напряжение через трещину, стальные стержни будут сопротивляться всему напряжению. Распределение напряжения сжатия бетона по-прежнему предполагается линейным.
3. Поведение при изгибе при предельной нагрузкеЗдесь сжимающие деформации и напряжения увеличиваются с некоторой нелинейной кривой напряжения на стороне сжатия балки. Эта кривая напряжения над нейтральной осью будет по существу той же формы, что и типичная кривая напряжения-деформации бетона.Напряжение растяжения стали fs равно пределу текучести стали fy. В конце концов, предельная мощность луча будет достигнута, и луч выйдет из строя.
Описанный выше реальный механизм разрушения железобетонной балки в целом достаточно сложен.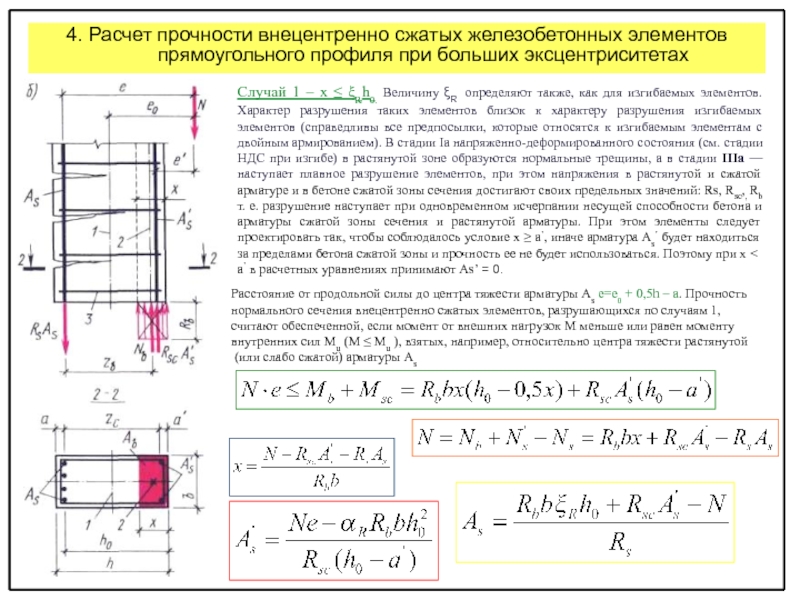 Именно поэтому разработка подхода к расчету прочности зависит от следующих основных допущений:
Именно поэтому разработка подхода к расчету прочности зависит от следующих основных допущений:- Напряжения в бетоне такие же, как и в арматурных стержнях на том же уровне, при условии, что связь между сталью и бетоном достаточна;
- Деформация бетона линейно пропорциональна расстоянию от нейтральной оси
- Плоские поперечные сечения остаются плоскими после изгиба
- Прочностью бетона на растяжение пренебрегают
- При отказе предполагается, что максимальная деформация в волокнах при предельном сжатии равна пределу, установленному нормами проектирования (0.003)
- Для расчетной прочности форма распределения напряжения сжатия бетона может быть упрощена.
Определение силы момента непросто из-за формы диаграммы нелинейного напряжения сжатия над нейтральной осью. В целях упрощения и практического применения Уитни предложил фиктивное, но эквивалентное прямоугольное распределение напряжений в бетоне, которое впоследствии было принято различными нормами проектирования, такими как ACI 318, EN 2, AS 3600 и другими. Что касается этого распределения эквивалентного напряжения, как показано ниже, средняя интенсивность напряжения принимается равной fc (при предельной нагрузке) и предполагается, что она действует в верхней части поперечного сечения балки, определяемой шириной b и глубиной а. В различных параметрах норм проектирования а определяется уменьшением с с коэффициентом. Прочность бетона fc также снижается. Например, в соответствии с кодом ACI 318 fc уменьшается на 0,85 и на коэффициент β1, который находится в диапазоне от 0.65 и 0,85.
Что касается этого распределения эквивалентного напряжения, как показано ниже, средняя интенсивность напряжения принимается равной fc (при предельной нагрузке) и предполагается, что она действует в верхней части поперечного сечения балки, определяемой шириной b и глубиной а. В различных параметрах норм проектирования а определяется уменьшением с с коэффициентом. Прочность бетона fc также снижается. Например, в соответствии с кодом ACI 318 fc уменьшается на 0,85 и на коэффициент β1, который находится в диапазоне от 0.65 и 0,85.
Для расчета сопротивления моменту железобетонного сечения необходимо правильно рассчитать глубину нейтральной оси c. SkyCiv использует итеративный процесс для расчета нейтральной оси на основе следующего:
Расчет мощности моментаНаконец, рассчитанные силы бетона и стали Fc, Fs, Fcs и их положение относительно нейтральной оси сечения a c , a s , a cs позволяют рассчитать сопротивление расчетному моменту из следующего уравнения:
M u = F c ∙ a c + F cs ∙ a cs + F s ∙ a 0 s Вся эта процедура полностью автоматизирована в ПО SkyCiv Reinforced Design Software, где инженер может легко определить железобетонную балку с действующими нагрузками и определить грузоподъемность секции. Этот и все другие расчеты проверки конструкции можно увидеть в подробном отчете о конструкции, который генерируется SkyCiv после анализа.
Этот и все другие расчеты проверки конструкции можно увидеть в подробном отчете о конструкции, который генерируется SkyCiv после анализа.
SkyCiv предлагает полнофункциональное программное обеспечение для проектирования железобетонных конструкций, которое позволяет проверять конструкции бетонных балок и бетонных колонн в соответствии со стандартами проектирования ACI 318, AS 3600 и EN2. Программное обеспечение простое в использовании и полностью облачное; не требует установки или загрузки, чтобы начать работу!
Программное обеспечение для железобетона
Влияние процента армирования ненапрягаемой арматурой на деформируемость предварительно напряженных железобетонных балок
Азизов Т.Н., Кочкарев Д.В., Галинская Т.А., 2019. Новые конструктивные решения для усиления неразрезных железобетонных балок. IOP Conference Series: Materials Science and Engineering, 708(1) Н., Селейдак Дж., 2020. Неравномерная коррозия стальной арматуры и ее влияние на надежность железобетонных элементов. Технологический архив, 26(2), 67-72 DOI: 10.30657/pea.2020.26.14.10.30657/pea.2020.26.14Search in Google Scholar
Технологический архив, 26(2), 67-72 DOI: 10.30657/pea.2020.26.14.10.30657/pea.2020.26.14Search in Google Scholar
Блихарский Ю., Вашкевич Р., Копийка Н., Бобало Т., Блихарский З., 2021. Расчет остаточной прочности железобетонных балок с повреждениями, возникшими при погрузке. IOP Conference Series: Materials Science and Engineering, 1021(1).10.1088/1757-899X/1021/1/012012Search in Google Scholar
Бобало Т., Блихарский Ю., Копийка Н., Волынец М., 2021. Влияние процента армирования на потери сжимающих усилий в предварительно напряженных железобетонных балках, усиленных пакетом стальных стержней.Конспект лекций по гражданскому строительству, 100, 182-191.10.1007/978-3-030-57340-9_7Поиск в Google Scholar
ДБН В.2.6-98. 2011. Конструкции будынкив и спор. Бетонни та зализобетонные конструкции. Основни положения. Киев: Минрехионстрой Украины, 72. [На укр.]. Поиск в Google Scholar
Дзюба С.Т., Ингальди М., Кадлубек М. 2018. Анализ качества стального проката на выбранном металлургическом предприятии. Металл 2018 — 27-я Международная конференция по металлургии и материалам, материалы конференции, 1893–1898 гг.Поиск в Google Scholar
Металл 2018 — 27-я Международная конференция по металлургии и материалам, материалы конференции, 1893–1898 гг.Поиск в Google Scholar
Карпюк В.В., Сомина Ю.В., Майстренко О.В., 2019. Инженерная методика расчета наклонных сечений балочных конструкций на основе модели усталостного разрушения. Lecture Notes in Civil Engineering, 47, 135-144, DOI: 10.1007/978-3-030-27011-7_17.10.1007/978-3-030-27011-7_17Поиск в Google Scholar
Хмиль Р.Ю., Титаренко Р.Ю., Блихарский Ю.З., Вегера П.И., 2021а. Совершенствование метода оценки вероятности безотказной работы железобетонных балок, усиленных под нагрузкой.IOP Conference Series: Materials Science and Engineering, 1021(1).10.1088/1757-899X/1021/1/012014Search in Google Scholar
Хмиль Р., Титаренко Р., Блихарский Ю., Вегера П., 2021б. Вероятностная расчетная модель железобетонных балок, усиленных железобетонным каркасом. Конспект лекций по гражданскому строительству, 100, 182-19110.1007/978-3-030-57340-9_23Search in Google Scholar
Кос Ж.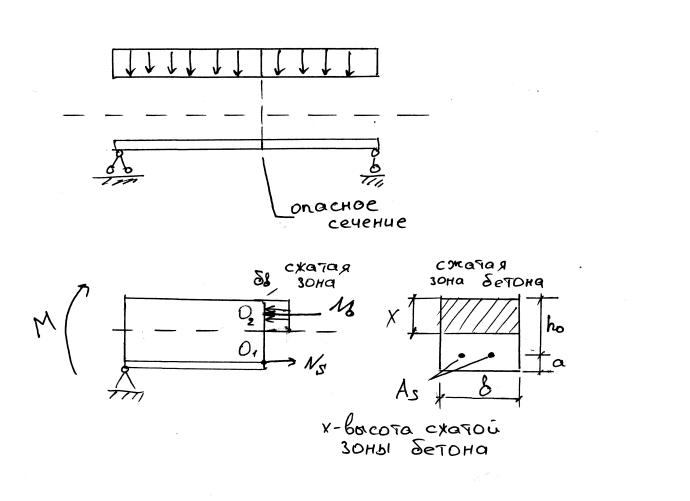 , Клименко Ю., 2019. Разработка модели прогнозирования силы разрушения поврежденных железобетонных конструкций. Бетонные стройные колонны.Tehnički vjesnik, 26(6), 1635-1641, DOI: 10.17559/TV-2018121
, Клименко Ю., 2019. Разработка модели прогнозирования силы разрушения поврежденных железобетонных конструкций. Бетонные стройные колонны.Tehnički vjesnik, 26(6), 1635-1641, DOI: 10.17559/TV-2018121
Котес П., Стриеска М., Броднан М., 2018 расчет скорости коррозии по стандартной методике. IOP Conference Series: Materials Science and Engineering, 385(1), 012031. , Вавруш, М., Йошт, Дж., Прокоп, Дж., 2020. Усиление бетонной колонны с использованием внешнего слоя фибробетона.Материалы, 12(23), 1-21. DOI: 10.3390/ma13235432.10.3390/ma13235432Search in Google Scholar
Ковальчук Б., Блихарский Ю., Селейдак Ю. Блихарский З., 2021. Прочность железобетонных балок, усиленных под нагрузкой дополнительным армированием разного уровня его предварительного натяжения. Конспект лекций по гражданскому строительству, 100, 182-191.10.1007/978-3-030-57340-9_28Поиск в Google Scholar
Крамарчук А., Ильницкий Б., Литвиняк О., Грабовский А.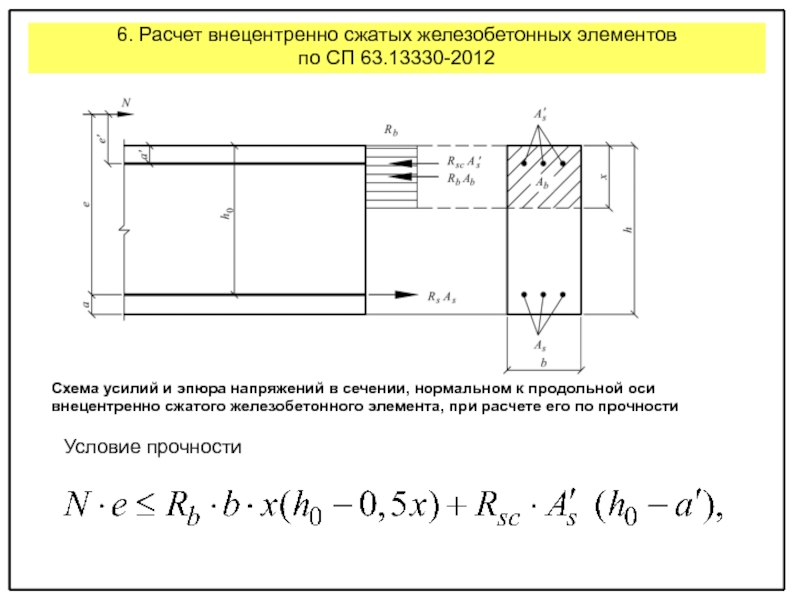 , 2019. Повышение сейсмостойкости существующих производственных зданий.Материалы конференции AIP, 2077. DOI: 10.1063/1.5091890.10.1063/1.5091890Search in Google Scholar
, 2019. Повышение сейсмостойкости существующих производственных зданий.Материалы конференции AIP, 2077. DOI: 10.1063/1.5091890.10.1063/1.5091890Search in Google Scholar
Lipiński T. 2017. Шероховатость стали 1.0721 после коррозионных испытаний в 20% NaCl. Архивы технологии производства, 15(15), 27-30 DOI: 10.30657/pea.2017.15.0710.30657/pea.2017.15.07Search in Google Scholar
Липинский Т., Улевич Р., 2021. Влияние пространств примесей на качество конструкционной стали, работающей при переменных нагрузках. Открытая инженерия, 11 (1), 233–238. ДОИ: 10.1515/eng-2021-0024.10.1515/eng-2021-0024Search in Google Scholar
Николич, Р.Р., Джокович, Дж.М., Хадзима, Б., Улевич, Р., 2020. Оценка срока службы точечной сварки на основе применения концепция межфазной трещины y. Материалы, 13(13), 1-11, DOI: 10.3390/ma13132976.10.3390/ma13132976Search in Google Scholar
Павликов А., Кочкарев Д., Харкава О., 2019. Расчет прочности железобетонных элементов по новым концепция. Материалы симпозиума fib 2019: Бетон — инновации в материалах, дизайне и конструкциях, 820–827.Поиск в Google Scholar
Материалы симпозиума fib 2019: Бетон — инновации в материалах, дизайне и конструкциях, 820–827.Поиск в Google Scholar
Турба Ю., Солодкий С., 2021. Трещиностойкость бетонов, армированных полипропиленовой фиброй. Lecture Notes in Civil Engineering, 100, 474-481, DOI: 10.1007/978-3-030-57340-9_58.10.1007/978-3-030-57340-9_58 Поиск в Google Scholar
Улевич Р., Улевич М. ., 2020. Проблемы реализации концепции бережливого производства в строительной отрасли. Lecture Notes in Civil Engineering, 47, 495-500, DOI: 10.1007/978-3-030-27011-7_63.10.1007/978-3-030-27011-7_63Поиск в Google Scholar
Ватулия Г., Лобиак А., Черногил В., Новикова М., 2019. Моделирование работы элементов CFST, содержащих трубы дифференцированного профиля, заполненные железобетоном. In Materials Science Forum Trans Tech Publications Ltd., 968, 281-287, DOI: 10.4028/www.scientific.net/MSF.968.281.10.4028/www.scientific.net/MSF.968.281Поиск в Google Scholar
Vatulia, G ., Резуненко М., Петренко Д. , Резуненко С., 2018. Оценка несущей способности прямоугольных железобетонных колонн. Гражданская и экологическая инженерия, 14 (1), 76–83.DOI: 10.2478/cee-2018-0010.10.2478/cee-2018-0010Search in Google Scholar
, Резуненко С., 2018. Оценка несущей способности прямоугольных железобетонных колонн. Гражданская и экологическая инженерия, 14 (1), 76–83.DOI: 10.2478/cee-2018-0010.10.2478/cee-2018-0010Search in Google Scholar
Вавруш М., Котеш П., 2019. Численное сравнение бетонных колонн, усиленных слоем фибробетона и железобетона. Transportation Research Procedia, 40, 920-926.10.1016/j.trpro.2019.07.129Поиск в Google Scholar
EC2: Минимальная и максимальная продольная арматура
7.3.2 Минимальные площади армирования
(1)P Если требуется контроль над трещинами, требуется минимальное количество связанной арматуры, чтобы контролировать растрескивание в областях, где ожидается растяжение.Величина может быть оценена по равновесию между растягивающей силой в бетоне непосредственно перед растрескиванием и растягивающей силой в арматуре при текучести или при более низком напряжении, если необходимо ограничить ширину трещины.
(2) Если более строгий расчет не показывает, что меньших площадей достаточно, требуемые минимальные площади армирования можно рассчитать следующим образом.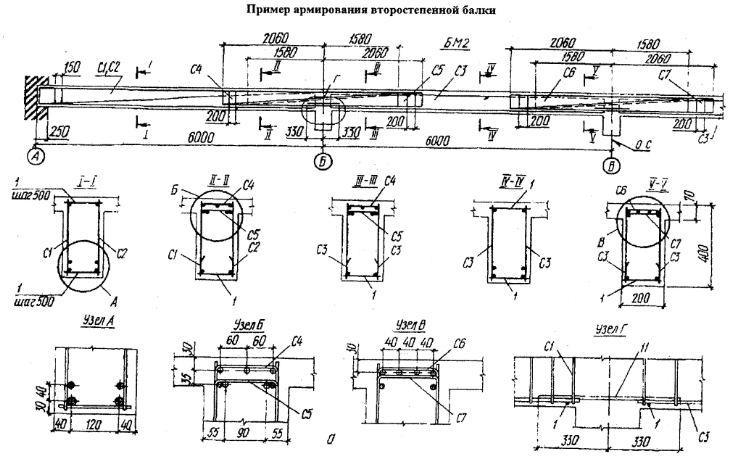 В профилированных поперечных сечениях, таких как тавровые балки и коробчатые фермы, минимальная арматура должна быть определена для отдельных частей сечения (стенки, полки).
В профилированных поперечных сечениях, таких как тавровые балки и коробчатые фермы, минимальная арматура должна быть определена для отдельных частей сечения (стенки, полки).
A s,min ·σ s = k c · k · f ct,eff · A ct
(7.1)
где:
9.2 Балки
9.2.1 Продольная арматура
9.2.1.1 Минимальная и максимальная площади армирования
(1) Площадь продольной растянутой арматуры следует принимать не менее A с,min .
Примечание 1: См. также 7.3 для площади продольной растянутой арматуры для предотвращения растрескивания.
Примечание 2. Значение A s,min для лучей, используемых в стране, можно найти в национальном приложении. Рекомендуемое значение приведено в следующем виде:
А с,мин = 0,26·f ctm /f yk ·b t ·d, но не менее 0,0013·b
(9,1 Н)
где:
- b t – средняя ширина зоны растяжения; для тавровой балки с сжатой полкой при расчете значения b t учитывается только ширина стенки
- f ctm следует определять по соответствующему классу прочности по таблице 3.
 1:
1:
f ctm = 0,30 × f ck (2/3) , f ck ≤ 50
f ctm = 2,12·Ln(1+(f см /10)), f ck > 50/60
с f см = f ck +8 (МПа)
(2) Секции, содержащие меньше арматуры, чем A s,min , следует считать неармированными.
(3) Площадь поперечного сечения растянутой или сжатой арматуры не должна превышать A с, макс. вне мест нахлеста.
Примечание. Значение A s,max для лучей, используемых в стране, можно найти в национальном приложении. Рекомендуемое значение 0,04·A c .
9.3 Сплошные плиты
(1) Этот раздел применяется к односторонним и двусторонним сплошным плитам, для которых b и l eff не менее 5h (элемент, для которого минимальный размер панели не менее чем в 5 раз превышает общую толщину плиты).
9.3.1 Армирование на изгиб
9. 3.1.1 Общие
3.1.1 Общие
(1) Для минимального и максимального процентного содержания стали в основном направлении применяются 9.2,1,1 (1) и (3).
(2) В однополосных плитах должна быть предусмотрена вторичная поперечная арматура в размере не менее 20% от основной арматуры. В зонах вблизи опор поперечное армирование основных верхних стержней не требуется, если отсутствует поперечный изгибающий момент.
(3) Расстояние между стержнями не должно превышать s max, плит .
Примечание; Значение s max,slabs для использования в стране можно найти в ее национальном приложении.Рекомендуемое значение:
. — для основной арматуры, 3·h ≤ 400 мм, где h — общая высота плиты;
— для вторичной арматуры, 3,5·h ≤ 450 мм
В зонах с сосредоточенными нагрузками или зонах с максимальным моментом эти положения становятся соответственно:
— для основной арматуры, 2·h ≤ 250 мм
— для вторичной арматуры 3·h ≤ 400 мм.
9,5 Столбцы
(1) Этот пункт касается столбцов, для которых больший размер h не превышает меньший размер b более чем в 4 раза.
9.5.1 Общие
9.5.2 Продольная арматура
(1) Продольные стержни должны иметь диаметр не менее Φ min .
Примечание. Значение ¢min для использования в стране можно найти в национальном приложении. Рекомендуемое значение 8 мм.
(2) Общее количество продольной арматуры должно быть не менее A s,min
Примечание. Значение A s,min для использования в стране можно найти в национальном приложении.Рекомендуемое значение определяется выражением (9.12N)
.A с, мин = макс.
где:
- f ярдов расчетный предел текучести арматуры
- N Ed — расчетная осевая сила сжатия
(3) Площадь продольной арматуры не должна превышать A s,max
Примечание. Значение A s,max для использования в стране можно найти в национальном приложении.Рекомендуемое значение составляет 0,04·A c за пределами точек нахлеста, если только не будет доказано, что целостность бетона не нарушена и что полная прочность достигается при ULS. Этот предел следует увеличить до 0,08·A c на кругах.
Этот предел следует увеличить до 0,08·A c на кругах.
(4) Для колонн с многоугольным поперечным сечением в каждом углу должно быть размещено не менее одного стержня. Количество продольных стержней в круглой колонне должно быть не менее четырех.
9.6 Стены
9.6.1 Общие
(1) Этот пункт относится к железобетонным стенам с отношением длины к толщине 4 или более, в которых армирование учитывается при расчете на прочность
9.6.2 Вертикальная арматура
(1) Площадь вертикальной арматуры должна лежать между A s,vmin и A s,vmax .
Примечание 1: Значение A s,vmin для использования в стране можно найти в ее национальном приложении.Рекомендуемое значение 0,002·A c .
Примечание 2. Значение A s,vmax для использования в стране можно найти в ее национальном приложении. Рекомендуемое значение составляет 0,04·Ac за пределами точек нахлеста, если только не будет доказано, что целостность бетона не нарушена и что полная прочность достигается при ULS.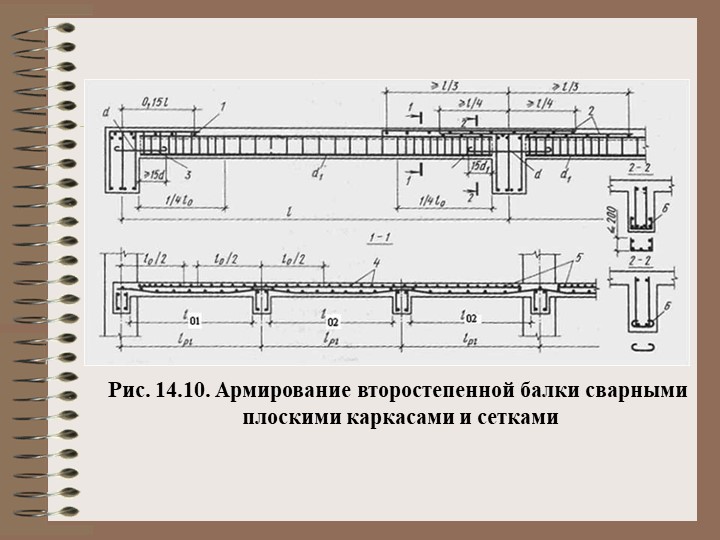 Этот лимит может быть удвоен на кругах.
Этот лимит может быть удвоен на кругах.
(2) Если минимальная площадь армирования, A s,vmin , является контрольной по конструкции, половина этой площади должна располагаться на каждой грани.
(3) Расстояние между двумя соседними вертикальными стержнями не должно превышать трехкратную толщину стены или 400 мм, в зависимости от того, что меньше.
9.6.3 Горизонтальная арматура
(1) На каждой поверхности должна быть предусмотрена горизонтальная арматура, идущая параллельно сторонам стены (и свободным краям). Оно должно быть не менее A s,hmin .
Примечание. Значение A s,hmin для использования в стране можно найти в национальном приложении.Рекомендуемое значение составляет либо 25% вертикальной арматуры, либо 0,001·A c , в зависимости от того, что больше.
(2) Расстояние между двумя соседними горизонтальными стержнями не должно превышать 400 мм.
9.8 Фундамент
9. 8.1 Фундаменты колонн и стен
8.1 Фундаменты колонн и стен
(1) Необходимо предусмотреть минимальный диаметр стержня Φ min
Примечание. Значение Φ min для использования в стране можно найти в национальном приложении.Рекомендуемое значение 8 мм.
График гибки стержней: как подготовить BBS
График гибки стержней или график гибки стержней представляет собой табличное представление арматурного стержня. Обычно он представлен для каждого типа работы RCC.
С помощью графика гибки стержней можно узнать потребность в различных длинах и размерах стержней, которые можно расположить и согнуть во время строительства.
График гибки стержней в целом описывает характеристики стержней, форму гибки с эскизами, а также общую длину и вес стержней вместе с их номерами.
График гибки стержней обычно составляется при оценке работы или конструкции из железобетона.
Преимущества BBS- Количество стальной арматуры разного диаметра и марки легко рассчитывается.

- Идеи различных размеров стержней, изгиба и длины стержней можно легко получить с помощью списка стержней.
- При проверке арматуры на строительной площадке очень полезен график гибки стержней.
- Кроме того, это помогает избежать путаницы на строительной площадке.
- Обеспечивает точное количество стали, необходимой для работы, благодаря чему можно провести оптимизацию армирования в случае перерасхода средств. График гибки стержней
- позволяет инженерам на стройплощадке легко проверять и проверять длину резки и изгиб стержня во время осмотра на месте.
- В конце всей работы с помощью этих графиков стержней можно легко создать строительные счета.
Читайте также: Изогнутая крыша: Конструкция, преимущества, недостатки
Читайте также: Типы значений в гражданском строительстве
Читайте также: Дистанционное зондирование: определение, классификация, методы
Как подготовить график гибки стержней
Общеармированные цементобетонные работы могут быть рассчитаны по 2 пунктам:
1. Бетонные работы, включая центровку и опалубку.
Бетонные работы, включая центровку и опалубку.
2. Стальная арматура вместе с ее гибкой, резкой, укладкой и т.д. в Квинталах или Тоннах.
Объем стали очень мал, поэтому для стали не производится вычет из объема бетона.
Стальная арматура рассчитывается в соответствии с фактическими требованиями, включая перекрытия, крюки, кривошипы и т. д., и определяется по детальному чертежу.
Обычно процент стальной арматуры зависит от конструкции конструкции. ню7
| Для перемычек, плит и т.д. | от 0,7 % до 1 % |
| Балка | от 1 % до 2 % |
| Столбец | от 1 % до 5 % |
| Фундамент | 0.от 5 % до 0,8 % |
1. Стандартный крюк (изгиб 180°):
- Дополнительная длина для 1 крючка = 9Φ
- Дополнительная длина для 2 крючков = 2 × 9Φ = 18Φ
2. Для изгиба 90°:
Для изгиба 90°:
- Изгиб 90°, как правило, предусмотрен для стержней HYSD (деформированных с высоким пределом текучести).
- Дополнительная длина для одного колена 90° = 6Φ
- Дополнительная длина для двух колен 90° = 2 × 6Φ = 12Φ
3.Изогнутые стержни:
- Дополнительная длина для одного наклона вверх =
- Дополнительная длина для двух изогнутых стержней = 2 × 0,42 d = 0,84 d
- d = D – (верхняя крышка + нижняя крышка)
4. Для двуногих стремян:
- Дополнительная длина крюка = 24Φ
- A = b – 2 (боковая крышка)
- B = D – (верхняя крышка + нижняя крышка)
- Общая длина хомутов = 2 (A + B) + 24Φ …… (Φ = диаметр стальной арматуры)
Вес стержней обычно рассчитывается в килограммах и рассчитывается на каждый метр длины.
Вес стержней в кг/м =
Здесь Φ = диаметр используемых стержней.
# Расчет количества баров:Количество баров =
Подготовка графика гибки стержней на простом примереПроблема: Свободно опертая железобетонная балка со стороной 300 мм × 650 мм усилена четырьмя стержнями диаметром 20 мм. В одном ряду предусмотрены основные стержни, а во втором — отогнутые стержни. Сверху предусмотрены два анкерных стержня диаметром 12 мм и хомуты диаметром 6 мм при 140 c/c.Пролет балки 5,6 м, а торцевая опора 30 см. Рассчитайте общее количество арматуры из мягкой стали и подготовьте для нее график изгиба стержней.
Решение: Теперь давайте проверим данные в задаче.
В первую очередь следует принять прозрачное покрытие со всех сторон балки = 25 мм .
Ширина (b) = 300 мм цел.
Общая глубина (D) = 650 мм
Глубина (d) = = 650 – (2 × 25 ) = 600 мм9 + 1
 ×
×
Шаг 1: Длина основных стержней:
Предусмотрены 4 стержня i.e 2 основных стержня и 2 изогнутых стержня.
а. Прямые стержни (2, 20Φ)
Длина прямого стержня = [TL – (2 × боковая крышка) + (2 × 9Φ)]
= 6200 – (2 × 25) + (2 × 9 × 20) 90 = 6510 мм / 6,51 м
б. Изогнутые стержни (2, 20Φ)
Длина изогнутого стержня = [TL – (2 × боковой крышки) + (2 × 0,42 d) + (2 × 9Φ)]
= 6200 – (2 × 25) + ( 2 × 0.42 × 600) + (2 × 9 × 20)
= 7014 мм/ 7,014 м
Шаг 2: Длина анкерных стержней (2, 12Φ):
L = [TL – (2 × боковая крышка) + (2 × 9Φ)] мм/ 6,366 м Этап 3: Длина хомутов (6 мм Φ): A = 300 – (2 × прозрачная крышка) B = 650 – (2 × прозрачная крышка) L = 2 (A + B) + 24Φ Количество стремян = = 45 №
= 6200 – (2 × 25) + (2 × 9 × 12)
= 300 – (2 × 25) = 250 мм
= 650 – (2 × 25) = 600 мм
= 2 (250 + 600) + (24 × 6)
= 1844 мм/1. 84 м
84 м
=





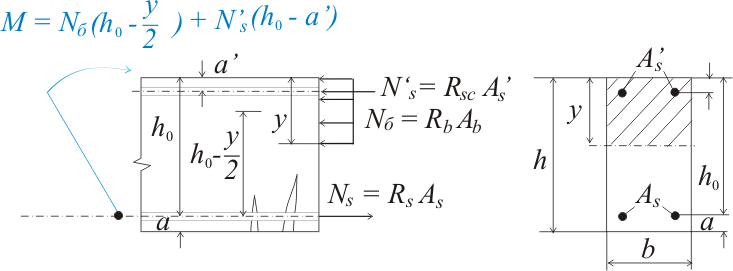 При плоскодеформированном сжатии трудно достичь изотермических условий.
При плоскодеформированном сжатии трудно достичь изотермических условий. 1:
1: