Пример расчета стропильной системы: Примеры расчета стропил и обрешетки
Как рассчитать стропильную систему: расчет элементов, формулы, калькулятор
- Как правильно рассчитать стропильную систему
- Нагрузки на стропила
- Расчет элементов
- Пример расчета при помощи программ
Возведение крыши собственными силами – задача вполне реальная. Конечно, для этого необходим определенный объем знаний, и в первую очередь это касается стропильной системы – основного элемента крыши, который воспринимает и противостоит всем типам нагрузок.
Стропильная система фактически обеспечивает жесткость конструкции кровли, поскольку распределяет нагрузку от обрешетки с уложенным материалом для кровли на внешние и внутренние опоры. Поэтому от того, как рассчитать стропильную систему, зависит надежность крыши, ее способность противостоять всем воздействиям.
Как правильно рассчитать стропильную систему ↑
Расчет элементов стропильной системы выполняют для того, чтобы определить оптимальные параметры конструкции, которые обеспечивают ее способность выдерживать воздействие от совокупного веса кровли, в том числе покрытия и теплоизоляции, в условиях максимального воздействия внешних нагрузок, ветровых и снеговых.
Как правило, расчетная схема, которую принимают при расчетах – «идеализированная». Считается, что крыша находится под воздействием равномерно распределенной нагрузки, т. е. испытывает одинаковую и ровную силу, которая равномерно воздействует на все скаты. На самом деле такая картина практически не встречается. Например, когда ветер наметает на какой-то скат снеговые мешки, то он одновременно сдувает его с другого. Сила воздействия на скатах, таким образом, оказывается неравномерной.
Нагрузки на стропила ↑
Стропила испытывают два вида воздействия – временные и постоянные. Ко вторым относится вес элементов крыши, включая кровлю, обрешетку, прогоны и стропила. Ко вторым – снег и ветер. К временным – относят также полезную, если таковая имеется.
Ко вторым – снег и ветер. К временным – относят также полезную, если таковая имеется.
Снеговая
Этот тип воздействия может представлять серьезную опасность для надежности конструкции, поскольку большие объемы скопившегося на крыше снега оказывают на нее существенное воздействие. Величина нагрузки снега определяется в горизонтальной проекции по формуле:
S=Sg * µ,
где
- Sg – масса снегового покрова, приходящейся на единицу площади горизонтальной плоскости. Этот параметр зависит от места расположения строения.
- µ – это коэффициент, выражающий зависимость от угла наклона кровли. К примеру, для плоских крыш до 25⁰ – 1,0, для скатных с уклоном более 25 ⁰< α < 60⁰ – 0,7. При крутом уклоне, свыше 60°, снеговая нагрузка не учитывается.
Ветровая
Для подсчета средней ветровой нагрузки на данной высоте применяют следующую формулу:
W=Woхk,
в которой
- Wo – нормативное значение, его подбирают по таблице, согласно ветровому району;
- k – коэффициент зависимости давления ветра от высоты, он отличается в зависимости от местности, где осуществляется строительство:
Поправка на ветер в расчет стропил вносится только при уклоне кровли более 30°.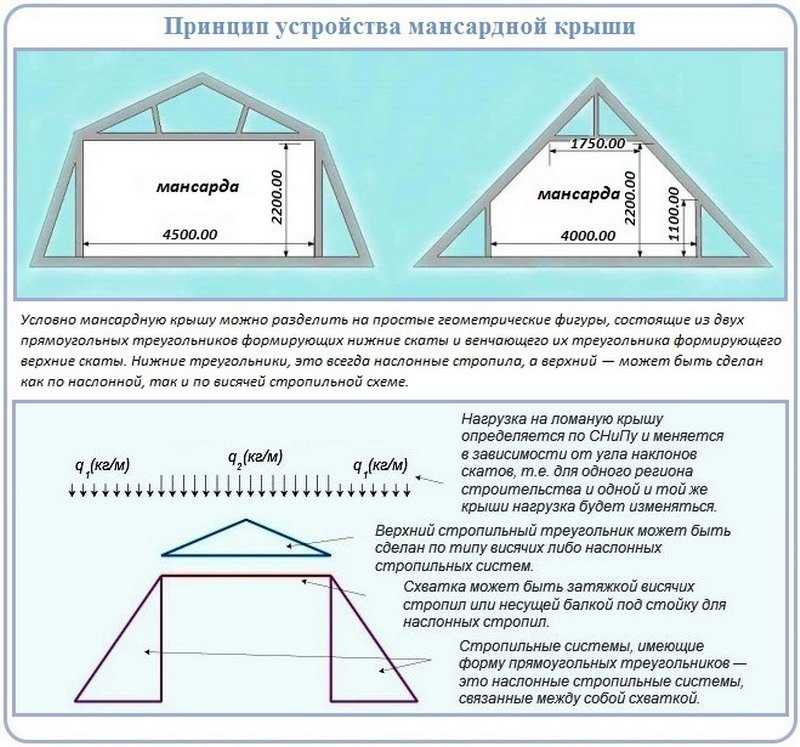
Выбор типа местности зависит от направления ветра, который применяют при расчете.
Как посчитать с учетом ветра и снега
Рассчитаем климатические нагрузки на примере Подмосковья, входящего в среднюю полосу РФ. Расчетные значения выбирают из СНиП 2.01.07-85*, а именно «Нагрузки и воздействия».
СНиП 2.01.07-85* «Нагрузки и воздействия» (1,1 MiB, 4 141 hits)
Допустим, уклон крыши составляет 22⁰. Это третий снеговой регион, для которого расчетная – 180 кг/м2, а µ=1,0, тогда 180 x 1,0 = 180 кг/м2. Для скатных кровель с коэффициентом µ=0,7 эта величина уменьшается до 126 кг/м2.
При образовании снегового мешка значение этого показателя может возрасти до 400-500 кг/м2.
Расчетная ветровая нагрузка для того же региона равна 32 кг/м2. Если предположить, что речь идет о 10-метровом доме, то величина воздействия ветра окажется равной 32 х 0,65 = 20,8 кг/м
Другие
- Нагрузку, создаваемую подкровельной конструкцией и самой кровлей рассчитывают согласно размерам сооружения и объему используемых материалов.

- Полезная учитывается для конструкций, «связанных» со стропильными фермами. К примеру, подвешенные к ним потолки, вентиляционные камеры или водяные баки, расположенные на фермах и т. д.
При проектировании крыши проводятся два типа расчетов:
- по прочности, который исключает повреждения стропильных ног;
- по деформации, который определяет максимальную степень прогиба такой балки. Так, расчет стропильной системы ломаной крыши должен учитывать, что прогиб стропил для такой конструкции не должен быть больше 0,004 длины участка, то есть, к примеру, максимальный прогиб 6-метровой балки достигает 2 см. На первый взгляд может показаться, что это не так уж и много, однако, если даже чуть превысить величину деформации, она станет зрительно заметна. А большие прогибы сделают крышу похожей на китайскую пагоду.
Расчет элементов ↑
Конструкцию системы определяют с учетом следующих параметров:
- наклон крыши,
- величина перекрываемого пролета,
- сечение стропил и обрешетин,
- совокупная нагрузка от кровельного покрытия, ветра и снега,
- расстояние между стропилами, его оптимальное значение определяют методом предела, то есть того значения, по достижении которого, можно ожидать частичного или полного разрушения.

Срез (сечение) стропил подбирают, исходя из их длины и величины испытываемых нагрузок.
Значения, приведенные в данной таблице, конечно, не являются результатом полноценного расчета, они всего лишь рекомендованы к применению при проведении стропильных работ для простых конструкций.
Полноценный расчет системы возможен при достаточном багаже теоретических знаний, определенных навыков черчения и рисования. К счастью, задача проектирования сегодня значительно облегчена, благодаря удобным компьютерным программам, предназначенным специально для разработки проектов всевозможных строительных элементов. Они подходят не только профессионалам, но и частным пользователям.
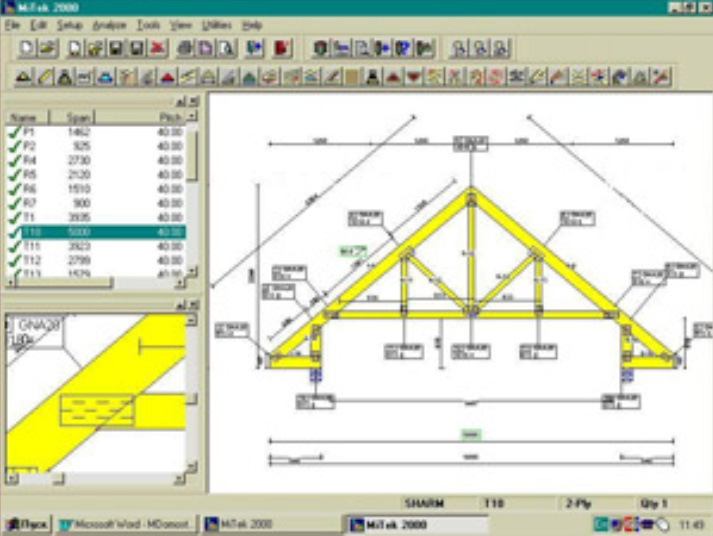
Пример расчета при помощи программ ↑
Шаг 1. Расчет нагрузок
На первом этапе в меню выбирают окно «Нагрузки» и вносят в ячейки таблиц голубого цвета необходимые изменения:
«Исходные данные»
- Изменяют уклон ската и шаг стропил на предполагаемые. Следующую строчку таблицы «Нагр.
 Кровли» заполняют данными из нижеприведенной таблицы.
Кровли» заполняют данными из нижеприведенной таблицы.
- В следующую ячейку заносят сумму предварительно рассчитанных нагрузок от ветра и снега. Далее идет «Утепление (манс.)» – ячейку оставляют без изменений для теплого чердака или вписывают 0 – для холодного.
- Корректируют также значения в таблице «Обрешетка».
Если заполненные данные корректны, в нижней части окна должно появиться сообщение «Несущая способность обрешетки обеспечена!». В противном случае потребуется изменить размеры обрешетки или расстояние между стропилами.
Шаг 2 Стропила с двумя опорами
На этом этапе работают с вкладкой «Строп. 1».
Начиная с этой вкладки, данные уже занесенные в таблицу будут подставляться программой в ячейки автоматически.
Какие правки выполняют на этом этапе?
- Вносят изменения в значение величины горизонтальной проекции стропила на схеме и приступают к заполнению таблицы «Расчет стропил».
- Значение толщины стропила, которое вносят в ячейку «В (заданное)» должно быть больше указанного« Втр (устойч.
 )».
)». - Ширина стропил, внесенная строчку «Принимаем Н», должна превышать значения, указанные в строчках «Нтр.,(прогиб)» и «Нтр.,(прочн.)». Если все значения подставлены верно, то программа под схемой «запишет»: «Условие выполнено».
Строчка «Н, (по сорт-ту)» заполняется самой программа, но следует знать что менять данные можно и самому.
Шаг 3 Стропила с тремя опорами
Такие стропила рассчитывают на вкладке «Строп.2» либо «Строп.3».
Какую выбрать зависит расположения промежуточной опоры. Вкладки отличаются по месту расположения средней стойки (опоры). В случае L/L1<2, иначе говоря, она находится правее середины стропила, пользуются «Строп.2», в противном случае – «Строп.3». Стойка может располагаться точно посередине, тогда не принципиально, какую из них выбрать – результат будет тот же. С этими вкладками работают аналогично «Строп. 1».
Шаг 4 Стойка
Величину изгибающего момента стойки и вертикального воздействия на нее вносят (в тоннах) соответственно в ячейки «М=» и «N=».
Шаг 5 Балка
Балки перекрытия в то же время испытывают распределенную и сосредоточенную нагрузки.
«Распределенная»
- В ней отмечают пролет и шаг балок. В качестве «Нагр.(норм.)» и «Нагр.(расч.)» выбирают соответственно 350 кг/м² и 450 кг/м². Согласно СНиП это усредненные значения с достаточным запасом прочности. В них включены эксплуатационные нагрузки и вес перекрытий.
- В строке «В, заданная» отмечают имеющуюся ширину сечения, в «Н, прогиб» и «Н, прочность» – наименьшие высоты сечения, обеспечивающие допустимый прогиб, при которым балка не сломается. Высоту сечения выбирают, равной большей из них.
- Если в конструкции нет стоек с опорой на балки перекрытия, расчет заканчивают. В противном случае заполняют следующие таблицы: «Распред.+сосредоточ.» и «Сосредоточенная нагрузка».
На практике работа с программой, как правило, затруднений не вызывает.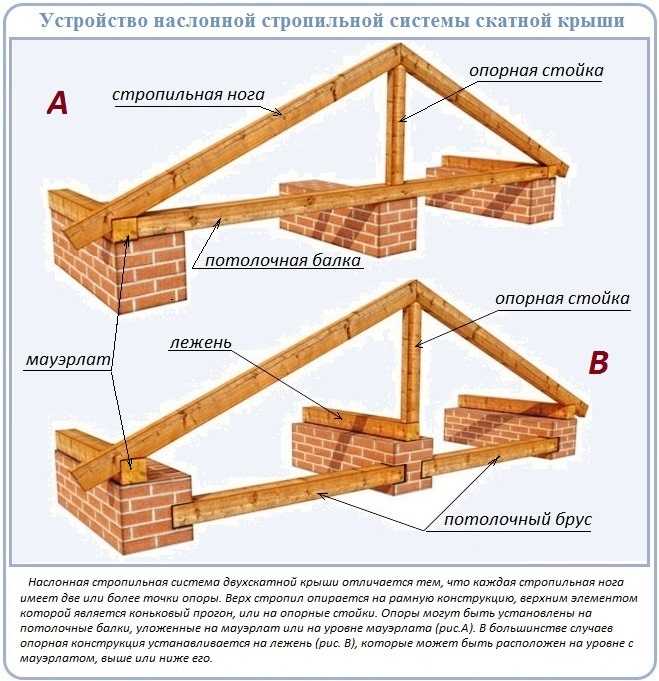
Для получения рекомендательных величин элементов конструкции можно использовать онлайн калькулятор стропильной системы, представленный ниже. Достаточно кликнуть по картинке, выбрать нужный раздел, и ввести данные крыши.
[js][/js]
© 2023 stylekrov.ru
правила и примеры. Как сделать расчет стропильной системы
Сентябрь 18 • Ремонтные и строительные работы • Просмотров 2866 • 1 комментарий к записи Расчет стропильной системы: правила и примеры
Крыша и коробка дома являются двумя взаимодополняющими конструкциями, которые отвечают за прочность, надежность и долговечность здания. Строительство крыши немыслимо без возведения стропильной системы – каркаса из досок и брусьев, на котором закреплены слои кровельного пирога. Чтобы построить прочную крышу, надо правильно рассчитать стропильную систему и подобрать подходящие для нее элементы.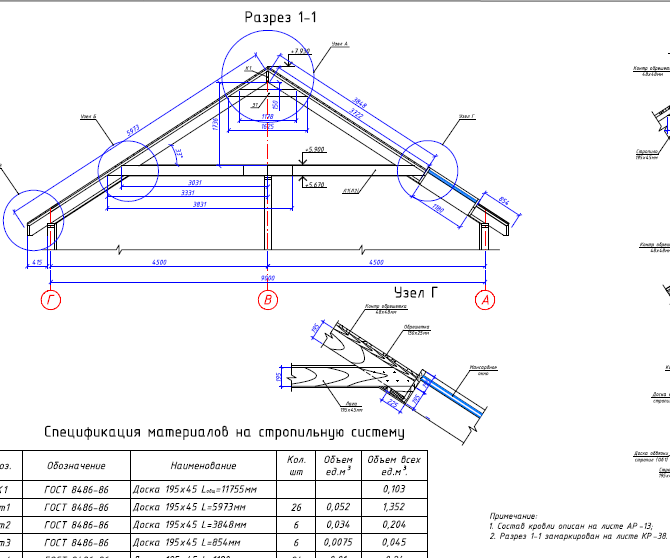 Именно это и вызывает большинство сложностей при возведении дома. В этой статье мы постарались затронуть все нюансы, связанные с этой задачей.
Именно это и вызывает большинство сложностей при возведении дома. В этой статье мы постарались затронуть все нюансы, связанные с этой задачей.
Содержание
- Виды нагрузок
- Нагрузка ветра и снега
- Нагрузка крыши
- Сечение стропил
- Расчет стропильной системы
- Односкатная крыша
- Расчет стропильной системы двухскатной крыши
- Четырехскатная крыша
- Стропильная система: фото
Виды нагрузок
Стропильный каркас отвечает за жесткость крыши и равномерно распределяет нагрузку пирога по внешним и внутренним опорам. От правильного расчета зависит прочность и надежность кровли, а также ее способность сопротивляться различным воздействиям. Воздействий этих довольно много, начиная от веса всех материалов, уложенных на стропила, заканчивая внешними факторами.
Для расчета стропильной системы крыши следует учитывать все нагрузки, оказываемые на конструкцию. Только после этого можно найти оптимальные параметры и подобрать элементы, способные выдерживать суммарные воздействия этих нагрузок.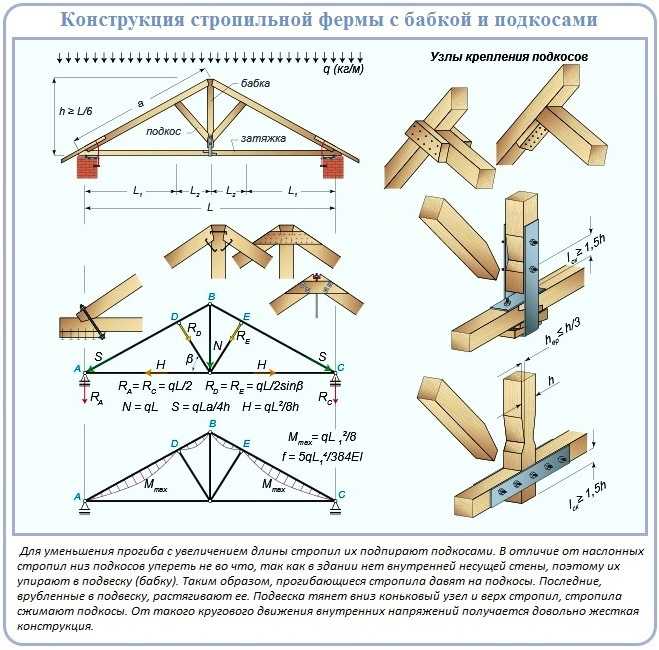 Но следует брать во внимание, что схема расчетов каждый раз получается «идеализированной». Это значит, что крыша испытывает равномерно распределенную нагрузку, а на самом деле все происходит совсем не так – где-то снега нападало больше, с какой-то стороны ветер дует сильнее и т.д.
Но следует брать во внимание, что схема расчетов каждый раз получается «идеализированной». Это значит, что крыша испытывает равномерно распределенную нагрузку, а на самом деле все происходит совсем не так – где-то снега нападало больше, с какой-то стороны ветер дует сильнее и т.д.
Нагрузки на стропильную систему:
- Переменные – снег, ветер, град и другие погодные явления.
- Регулярные – вес кровельных материалов и оборудования, установленного на крыше.
- Нетипичные (особые) – ураганные ветры, сейсмические толчки.
Все расчеты нагрузок описаны в соответствующих СНиП, поэтому в процессе работы следует постоянно сверяться с утвержденной документацией. То же самое касается определение оптимального угла наклона кровли, шага стропил и выбора материалов. После составления подробной схемы с учетом всех требуемых параметров можно сделать корректировку и приступать к монтажу.
Нагрузка ветра и снега
Ветровая нагрузка может серьезно навредить неправильно сконструированной крыше. То же самое касается большого количества снега, скопившегося на поверхности. Избежать неприятностей поможет верно подобранный угол наклона скатов.
То же самое касается большого количества снега, скопившегося на поверхности. Избежать неприятностей поможет верно подобранный угол наклона скатов.
Чтобы определить степень снеговой нагрузки в горизонтальной проекции, воспользуйтесь следующей формулой: S=Sg* µ.
Sg – вес снега на 1 м² площади, а µ — коэффициент зависимости от угла наклона. Так, для крыш с уклоном менее 25° он будет составлять 1,0, для крыш с уклоном от 25° до 60°коэффициент будет равен 0,7, а для очень крутых скатов больше 60° вообще можно не учитывать снеговую нагрузку – снег на такой поверхности просто не сможет удержаться.
Для нахождения ветровой нагрузки используйте другую формулу: W=Wₒ*k.
Wₒ здесь является нормативным значением, которое можно подобрать в зависимости от ветрового района (указано в СНиП), а k – это коэффициент, определяющий зависимость силы ветра от высоты дома и его месторасположения. Проследить эту зависимость можно по таблице ниже:
Если угол наклона кровли составляет больше 30°, в расчет стропильной системы следует внести поправку на ветер.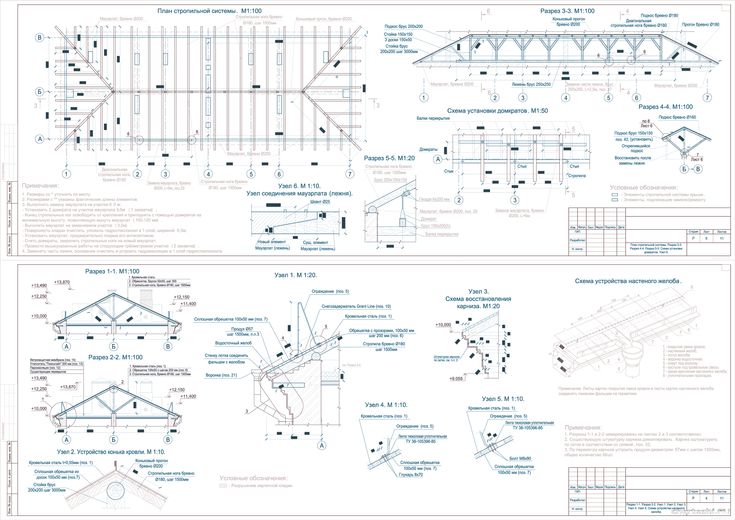 Также для расчета нужно знать постоянное направление ветра в местности, где строится дом.
Также для расчета нужно знать постоянное направление ветра в местности, где строится дом.
Ветер в зависимости от угла наклона крыши будет стремится либо приподнять ее, либо опрокинуть, так что в обоих случаях крепить стропила к опорному брусу следует очень прочно. Способы монтажа также будут отличаться в зависимости от воздействия ветра. Но что можно с уверенностью сказать, так чем крыша тяжелее, тем лучше – с тяжелой конструкцией ветер будет не в состоянии справиться.
Приведем пример расчета снеговой и ветровой нагрузки на крышу дома, строящегося в средней полосе России, скажем, в Подмосковье. Следовательно, чтобы посмотреть расчетные значения, понадобится СНиП 2.01.07-85 о «Нагрузках и воздействиях». Угол наклона скатов составляет 22°. Поскольку дом находится в третьем снеговом регионе, расчетная нагрузка для него будет составлять 180 кг/м², а коэффициент зависимости – 1,0. Умножаем друг на друга эти два значения и получаем снеговую нагрузку в 180 кг/м². Если коэффициент скатной кровли будет меньше, скажем, 0,7, то и нагрузка уменьшится до 126 кг/м².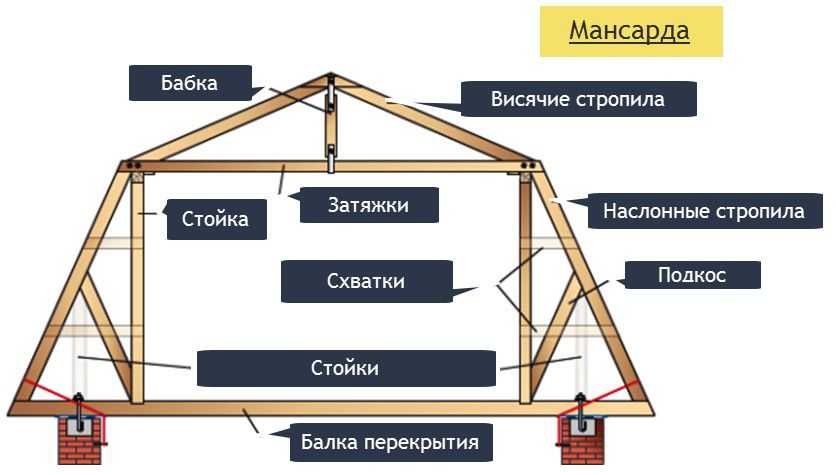
Важный момент: В случае образования снежного сугроба на крыше нагрузка увеличивается до 400-500 кг/м².
Что касается ветровой нагрузки для нашего дома в Подмосковье, то для этого региона она составляет 32 кг/м².Допустим, площадь дома 10 м², тогда вычислить степень воздействия ветра очень просто: 32*0,65=20,8 кг/м².
Нагрузка крыши
Рассчитывать стропильную систему крыши нужно с учетом всех материалов, которые вы будете укладывать на нее: гидроизоляцию, утеплитель, элементы вентиляционной системы, кровельный материал, оборудование и т.д. Выбор кровельного материала зависит от угла наклона скатов и напрямую влияет на требования к прочности составляющих стропильной системы.
Вес распространенных кровельных материалов на 1 м²:
- керамочерепица – 35-50 кг;
- цементная черепица – 40-50 кг;
- шифер – 10-15 кг;
- битумная черепица – 8-12 кг;
- битумный шифер – 4-6 кг;
- профнастил и металлочерепица – 4-5 кг.

Черновой настил для слоев кровельного пирога весит от 18 до 20 кг/ м², обрешетка – от 8 до 10 кг/ м², а вся стропильная система дает нагрузку от 15 до 20 кг/ м². Суммируйте все эти данные и вы поймете, что на стены дома и фундамент крыша оказывает нешуточное давление. К слову, если дом построен на облегченном фундаменте или имеет некрепкие стены, то о крыше, покрытой, например, керамической или цементной черепицей не может быть и речи.
Полезный совет: Многие продавцы кровельных материалов делают акцент на легкости изделий, дескать, это позволит сэкономить на стропильной системе, построив ее из более тонких и дешевых элементов. Но мы с вами уже знаем, что чем крыша тяжелее, тем сложнее ветру ее опрокинуть или оторвать, поэтому не стоит слепо верить подобным доводам.
Сечение стропил
Как вы уже поняли, выбирать сечение (толщину) стропил следует в зависимости от нагрузки на крышу, точнее, суммы всех перечисленных выше нагрузок.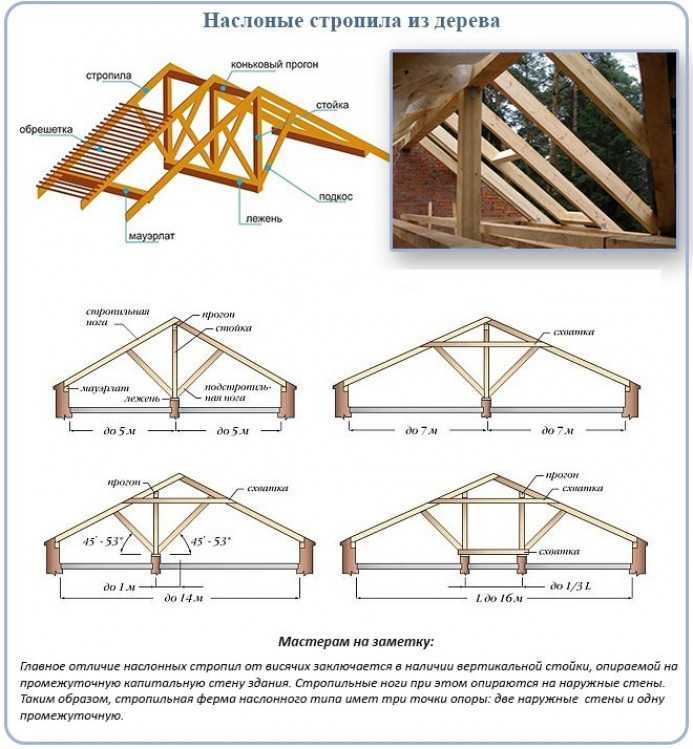 При строительстве двускатной или четырехскатной кровли используется множество различных элементов. Длина стандартных стропил может варьироваться от 4,5 до 6 м. При необходимости их можно укоротить или нарастить.
При строительстве двускатной или четырехскатной кровли используется множество различных элементов. Длина стандартных стропил может варьироваться от 4,5 до 6 м. При необходимости их можно укоротить или нарастить.
Прежде чем выбрать сечение бруса, нужно знать длину стропил, шаг их установки и нагрузку на них. В таблице ниже приведены необходимые данные для расчета кровельной системы. Однако эти значения подходят лишь для Московской области и учитывают климатические особенности именно этого региона.
Но «скелет» крыши состоит не только из стропил – в нем есть опорный брус (мауэрлат), подкосы, ригели и много других элементов. Ниже представлены рекомендуемые сечения для каждого из них:
- мауэрлат самый мощный элемент системы, поэтому для него нужно большое сечение в 100х100 мм, 100х150 мм или 150х150 мм;
- прогоны также выполняют поддерживающую функцию и должны быть прочными – 100х100 мм, 100х150 мм либо 100х200 мм;
- ендовы и диагональные стропильные ноги – 100х200 мм;
- подкосы и ригели – 100х150 мм или 150х150 мм;
- подшивочные доски – 25х100 мм;
- затяжки – 50х150 мм.

Когда выбрана длина, толщина и шаг расположения стропил, можно определить их количество. Делать это нужно, ориентируясь на длину дома. В процессе проектирования также надо делать расчет на прогиб, соотнося нагрузку на стропила и возможный прогиб деревянных элементов под ней. Для стропильной системы мансардной крыши прогиб не будет превышать 1/250 часть от длины сегмента, на который оказывается давление.
Иными словами, пятиметровые стропила прогнутся максимум на 2 см. При увеличении длины или нагрузки крыша может деформироваться.
Рекомендации для выбора брусьев на стропила:
- На 1 погонном метре материала не должно быть больше 3 сучков длиной до 3 см (если сучок больше, то стропило будет слабым).
- Допустимо присутствие несквозных трещин, но только если они не превышают половины длины всего бруса.
- Древесина должна быть хорошо просушенной. Допустимый уровень влажности брусьев составляет 18% и меньше. Если построить стропильную систему из сырых элементов, очень скоро она деформируется.

Полезный совет: Перед монтажом конструкции стропильной системы обязательно обработайте каждый деревянный элемент антисептическим и антипиренным средством. Делать это надо до установки, а не после.
Расчет стропильной системы
Расчет стропильной системы будет зависеть, в первую очередь, от конструктивных особенностей крыши и ее типа: односкатная, двускатная, вальмовая и т.д. В этой главе мы рассмотрим особенности расчета для самых распространенных видов крыш.
Односкатная крыша
Односкатная крыша очень проста в исполнении и сделать для нее расчет стропил не составит особого труда. Однако самым большим недостатком такой конструкции является ее сильная подверженность снеговым и ветровым нагрузкам. На большой пологой площади будет постоянно собираться много снега, поэтому стропильная система должна быть достаточно мощной. Особенно это касается тех случаев, если вы не сможете регулярно чистить крышу. Быть может, в подобной ситуации стоит задуматься о выборе другого вида крыши, например, самой простой двускатной.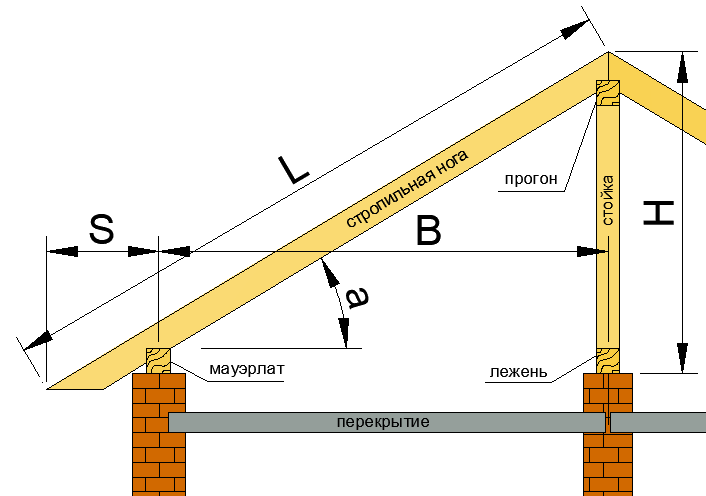 Небольшой угол наклона односкатной крыши требует не только мощного каркаса, но также использования усиленной гидроизоляции из-за высокого риска возникновения протечек.
Небольшой угол наклона односкатной крыши требует не только мощного каркаса, но также использования усиленной гидроизоляции из-за высокого риска возникновения протечек.
Чтобы сделать расчет стропильной системы односкатной крыши, сперва нужно задать угол наклона (от чего он зависит, мы уже выяснили в предыдущей главе). Для создания необходимого уклона следует организовать правильный перепад по высоте – расположить опоры соответствующей высоты.
Длина перекрываемого пролета определяет сложность стропильной системы:
- Для перекрытия небольшой длины можно использовать только стропильные ноги.
- При длине пролета от 4,5 до 6 м необходимо установить подкосы в нижней части ската.
- Чтобы закрыть пролет длиннее 6,5 м, понадобятся вертикальные стойки – они не дадут крыше прогнуться под нагрузками.
Приведем пример расчета каркаса односкатной крыши для гаража площадью 4х5 м с уклоном 25°. Сначала надо узнать высоту крыши, чтобы понять, настолько поднимать одну из несущих стен гаража. Для этого умножим тангенс уклона на длину боковой стены: tg25*5=2.35 м.
Для этого умножим тангенс уклона на длину боковой стены: tg25*5=2.35 м.
Чтобы найти длину стропильной ноги, делим высоту крыши на синус уклона и к полученному результату прибавляем двойную длину свеса: 2,35/sin25+2*0,5=6,6 м.
Расчет стропильной системы двухскатной крыши
Двускатная крыша пользуется популярностью на протяжении тысячелетий, и даже сегодня при обилии дизайнерских решений многие предпочитают этот классический вариант. Объяснить это можно не только эстетической привлекательностью, но также простотой возведения и практичностью конструкции.
Уклон стропильной системы двухскатной крыши может варьироваться от 5° до 90° в зависимости от климатической зоны и регулярных нагрузок. Конечно, дизайнерские предпочтения здесь также играют не последнюю роль. Если вы строите дом в благоприятной климатической зоне, где нет сильных ветров и снегопадов, но хотите украсить жилище остроконечной крышей, никто не может запретить вам это сделать. Самым распространенным вариантом являются крыши с уклоном от 35° до 45°.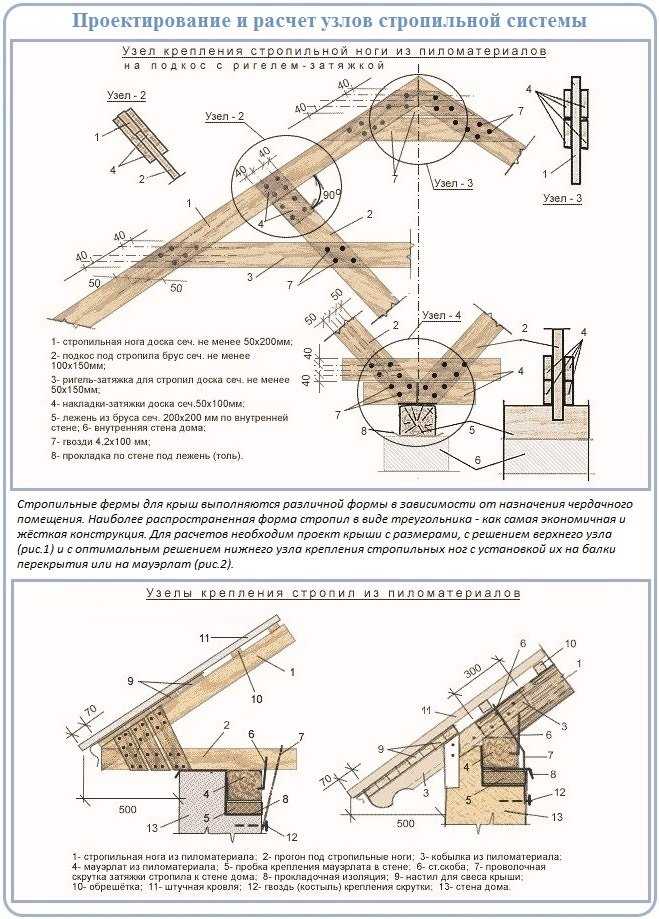 Они не загораживают обзор, лаконично вписывают дом в природный ландшафт и оставляют достаточно свободного пространства на чердаке.
Они не загораживают обзор, лаконично вписывают дом в природный ландшафт и оставляют достаточно свободного пространства на чердаке.
Устройство стропильной системы такой кровли отличается в плане использования опоры для стропил. Они могут быть висячими или наслонными. Первые используют в тех случаях, если расстояние между опорами не превышает 6-6,5 м. Наслонные элементы актуальны для сооружений, в которых есть несущая центральная стена или внутренние столбчатые опоры.
После определения суммированной нагрузки на 1 м² системы (ветер, снег, вес кровельного пирога и т.д.), можно определить сечение стропил. Чтобы облегчить задачу, разбейте крышу на несколько геометрических фигур, например, на 2 трапеции скатов. Вычислите нагрузку для каждого из них и сложите результаты. Тот же принцип можно использовать для расчета стропильной системы четырехскатной крыши.
Четырехскатная крыша
Конструкции четырехскатных крыш бывают нескольких видов, но самыми популярными являются шатровые и вальмовые. Шатровые крыши состоят из 4 треугольников, верхние углы которых сводятся в один коньковый узел. Кровли вальмового типа представляют собой 2 трапеции, соединенных коньковой балкой по верхним граням и 2 треугольника по бокам. Есть также ломаные кровли со сложным строением, но рассчитать для них стропильный каркас можно только при наличии большого опыта и квалификации.
Шатровые крыши состоят из 4 треугольников, верхние углы которых сводятся в один коньковый узел. Кровли вальмового типа представляют собой 2 трапеции, соединенных коньковой балкой по верхним граням и 2 треугольника по бокам. Есть также ломаные кровли со сложным строением, но рассчитать для них стропильный каркас можно только при наличии большого опыта и квалификации.
Вальмовая кровля лучше всего подходит для жилых домов, поскольку позволяет создать довольно просторное чердачное помещение. Его можно утеплить и превратить в жилую комнату: спальню, кабинет или мастерскую. Однако расчет вальмовой стропильной системы требует терпения и времени.
Специальные таблицы существенно облегчают задачу. Так, на изображении ниже показаны коэффициенты зависимости длины угловых и промежуточных стропил от угла наклона скатов.
При помощи таблиц зависимости сечения, ветровой нагрузки, массы кровельного материала можно довольно быстро собрать всю необходимую информацию для вашего проекта.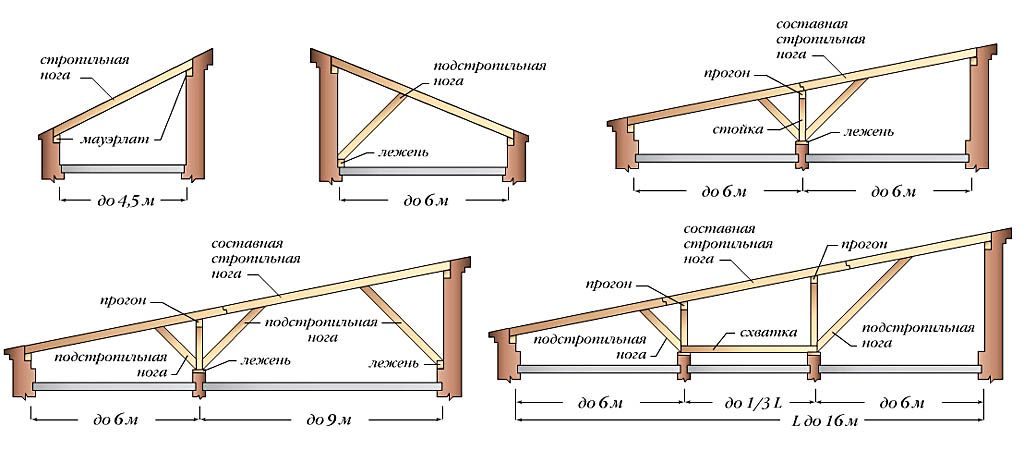 Геометрические параметры и площадь крыши измеряются квадратными метрами.
Геометрические параметры и площадь крыши измеряются квадратными метрами.
Если вы не имеете опыта или не уверены в своих математических способностях, лучше воспользоваться онлайн калькулятором или одной из специальных программ для расчета стропильной системы. В последнем случае вам надо лишь ввести нужные данные, а программа сделает все вычисления и сгенерирует результат. Ошибки таким образом сводятся к минимуму. Ниже вы найдете видео о расчете стропильной системы с помощью одной из таких программ:
Высота крыши (h) и дистанция между центром основания и ближайшим ее краем (b\2) соответствует тангенсу уклона (tg α). Так, зная угол наклона ската, можно найти высоту по формуле: h=(b*tg α)\2.
Зная косинус угла наклона, можно найти и длину боковых стропил (e): e=b\(2 cos α).
Для нахождения длины вальмовых стропил (d) пригодится теорема Пифагора:
Учитывайте, что диагональные стропила длиннее обычных и на них будут опираться более короткие элементы, поэтому важно обеспечить их прочность и жесткость.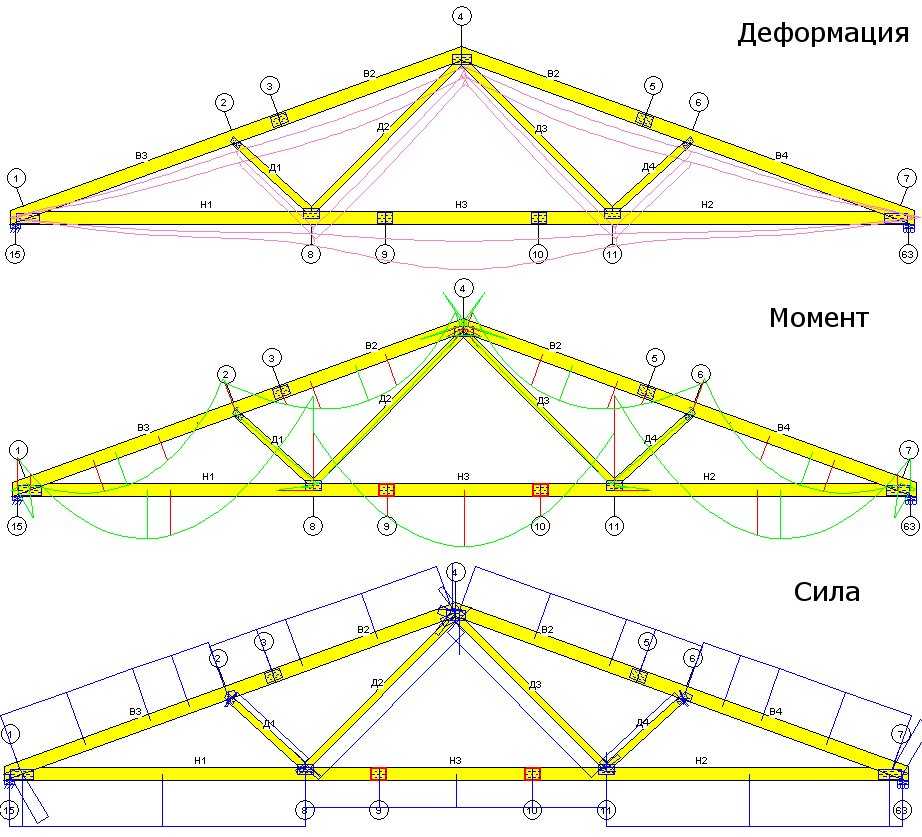 Это можно сделать, выбрав более твердую древесину и проведя правильное наращивание брусьев при необходимости.
Это можно сделать, выбрав более твердую древесину и проведя правильное наращивание брусьев при необходимости.
Расчеты и проектирование являются колоссально трудоемкой и ответственной задачей, будь то стропильная система двухскатной простой крыши, вальмовой или шатровой. Чтобы правильно выполнить задачу, необходимо четко понимать, для чего нужен каждый элемент и как «чувствует» себя крыша в процессе эксплуатации. Если вы сомневаетесь, что справитесь, лучше потренироваться на создании стропил для гаража или беседки, а потом переходить к жилому дому. Также можно воспользоваться услугами специалистов – экономить на строительстве можно, но только не за счет проектирования. Чтобы облегчить вам задачу, мы подготовили несколько схем стропильных систем.
Стропильная система: фото
« Как сделать лестницу в частном доме Профильный трубогиб своими руками »
Анализ ферм – методы обучения на примерах
🕑 Время чтения: 1 минута
Изучите методы анализа ферм на примерах. В статье разъясняется расчет ферм методами узлов и методами сечения.
Мы знаем основы равновесия тел; теперь мы обсудим фермы, которые используются при создании устойчивых несущих конструкций. Примерами этого являются стороны мостов или высокие телебашни или башни, по которым проходят электрические провода. Принципиальная схема конструкции со стороны моста изображена на рисунке 1. Структура, показанная на фиг.1, по существу является двумерной структурой. Это известно как плоская ферма. С другой стороны, микроволновая печь или вышка мобильной связи — это трехмерная структура. Таким образом, есть две категории ферм — плоские фермы, такие как по бокам моста, и пространственные фермы, такие как телебашни. В этом курсе мы сосредоточимся на плоских фермах, в которых базовые элементы склеены в плоскости.
Чтобы мотивировать конструкцию плоской фермы, позвольте мне взять тонкий стержень (12) между точками 1 и 2 и прикрепить его к неподвижному шарнирному соединению в точке 1 (см. рис. 2). Теперь я ставлю шпильку (pin2) в точку 2 на верхнем конце и вешаю на нее груз W.
В статье разъясняется расчет ферм методами узлов и методами сечения.
Мы знаем основы равновесия тел; теперь мы обсудим фермы, которые используются при создании устойчивых несущих конструкций. Примерами этого являются стороны мостов или высокие телебашни или башни, по которым проходят электрические провода. Принципиальная схема конструкции со стороны моста изображена на рисунке 1. Структура, показанная на фиг.1, по существу является двумерной структурой. Это известно как плоская ферма. С другой стороны, микроволновая печь или вышка мобильной связи — это трехмерная структура. Таким образом, есть две категории ферм — плоские фермы, такие как по бокам моста, и пространственные фермы, такие как телебашни. В этом курсе мы сосредоточимся на плоских фермах, в которых базовые элементы склеены в плоскости.
Чтобы мотивировать конструкцию плоской фермы, позвольте мне взять тонкий стержень (12) между точками 1 и 2 и прикрепить его к неподвижному шарнирному соединению в точке 1 (см. рис. 2). Теперь я ставлю шпильку (pin2) в точку 2 на верхнем конце и вешаю на нее груз W.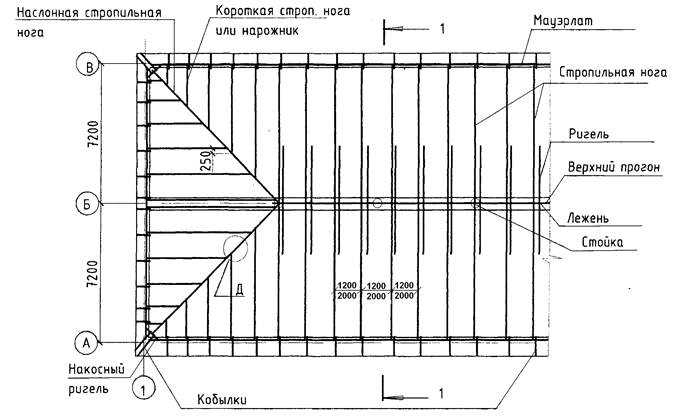 Вопрос в том, хотим ли мы удерживать вес в этой точке, какую еще минимальную поддержку мы должны обеспечить? Для стержней делаем только штифтовые соединения (предполагаем, что все находится в этой плоскости и конструкции не опрокидываются в стороны). Так как стержень (12) стремится повернуться по часовой стрелке, остановим движение точки 2 вправо, присоединив к ней стержень (23), а затем остановим движение точки 3 вправо, соединив ее с точкой 1 другим стержнем (13). Все соединения в этой конструкции шарнирные. Однако, несмотря на все это, вся конструкция все еще имеет тенденцию поворачиваться по часовой стрелке, потому что на нее действует крутящий момент из-за W. Чтобы противостоять этому, мы прикрепляем колесо к точке 3 и ставим его на землю. Это необходимый минимум, который нам требуется, чтобы удерживать вес на месте. Треугольник из стержней образует основу плоской фермы. Примечание: Здесь можно спросить, зачем нам горизонтальный стержень (13). Это потому, что в противном случае точка 3 будет продолжать двигаться вправо, делая всю конструкцию неустойчивой.
Вопрос в том, хотим ли мы удерживать вес в этой точке, какую еще минимальную поддержку мы должны обеспечить? Для стержней делаем только штифтовые соединения (предполагаем, что все находится в этой плоскости и конструкции не опрокидываются в стороны). Так как стержень (12) стремится повернуться по часовой стрелке, остановим движение точки 2 вправо, присоединив к ней стержень (23), а затем остановим движение точки 3 вправо, соединив ее с точкой 1 другим стержнем (13). Все соединения в этой конструкции шарнирные. Однако, несмотря на все это, вся конструкция все еще имеет тенденцию поворачиваться по часовой стрелке, потому что на нее действует крутящий момент из-за W. Чтобы противостоять этому, мы прикрепляем колесо к точке 3 и ставим его на землю. Это необходимый минимум, который нам требуется, чтобы удерживать вес на месте. Треугольник из стержней образует основу плоской фермы. Примечание: Здесь можно спросить, зачем нам горизонтальный стержень (13). Это потому, что в противном случае точка 3 будет продолжать двигаться вправо, делая всю конструкцию неустойчивой.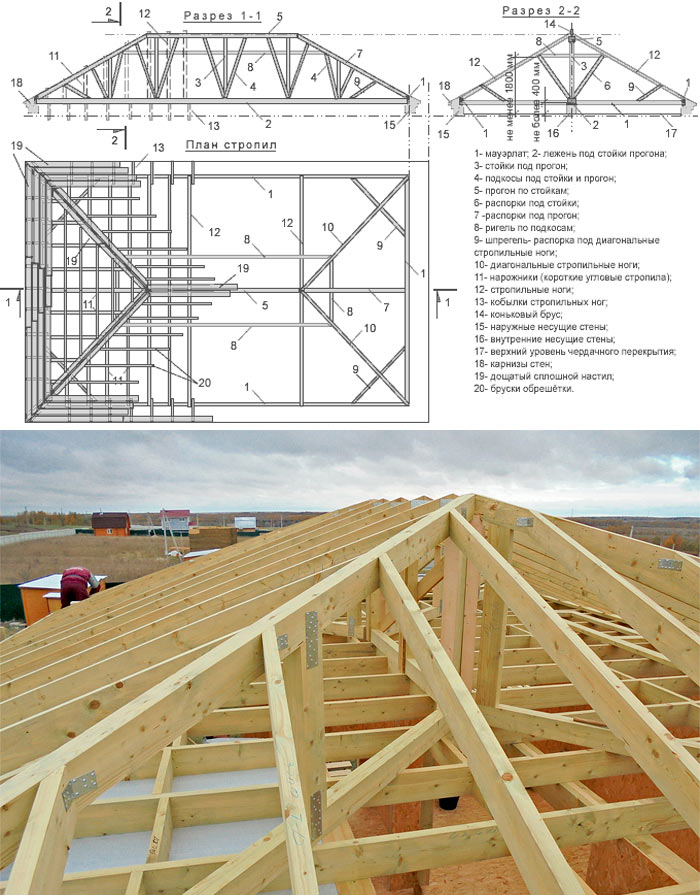 На стержень (13) действуют две силы: одна вертикальная сила от колеса, а другая на конце 2. Однако эти две силы не могут быть коллинеарными, поэтому без стержня (13) система не будет находиться в равновесии. Как правило, в ферме каждый шарнир должен быть соединен как минимум с тремя стержнями или двумя стержнями и одной внешней опорой.
Теперь проанализируем силы в только что образовавшейся структуре. Для простоты я беру длины всех стержней равными. Чтобы получить силы, я рассматриваю все силы, действующие на каждый штифт, и нахожу условия, при которых штифты находятся в равновесии. Первым делом отметим, что каждый стержень находится в равновесии под действием двух сил, приложенных штифтами на их концах. Как я уже говорил в предыдущей лекции, в этой ситуации силы должны быть коллинеарными и, следовательно, только вдоль стержней. Таким образом, каждый стержень находится под действием растягивающей или сжимающей силы. Таким образом, на стержни (12), (23) и (13) действуют силы, как показано на рисунке 3.
На стержень (13) действуют две силы: одна вертикальная сила от колеса, а другая на конце 2. Однако эти две силы не могут быть коллинеарными, поэтому без стержня (13) система не будет находиться в равновесии. Как правило, в ферме каждый шарнир должен быть соединен как минимум с тремя стержнями или двумя стержнями и одной внешней опорой.
Теперь проанализируем силы в только что образовавшейся структуре. Для простоты я беру длины всех стержней равными. Чтобы получить силы, я рассматриваю все силы, действующие на каждый штифт, и нахожу условия, при которых штифты находятся в равновесии. Первым делом отметим, что каждый стержень находится в равновесии под действием двух сил, приложенных штифтами на их концах. Как я уже говорил в предыдущей лекции, в этой ситуации силы должны быть коллинеарными и, следовательно, только вдоль стержней. Таким образом, каждый стержень находится под действием растягивающей или сжимающей силы. Таким образом, на стержни (12), (23) и (13) действуют силы, как показано на рисунке 3.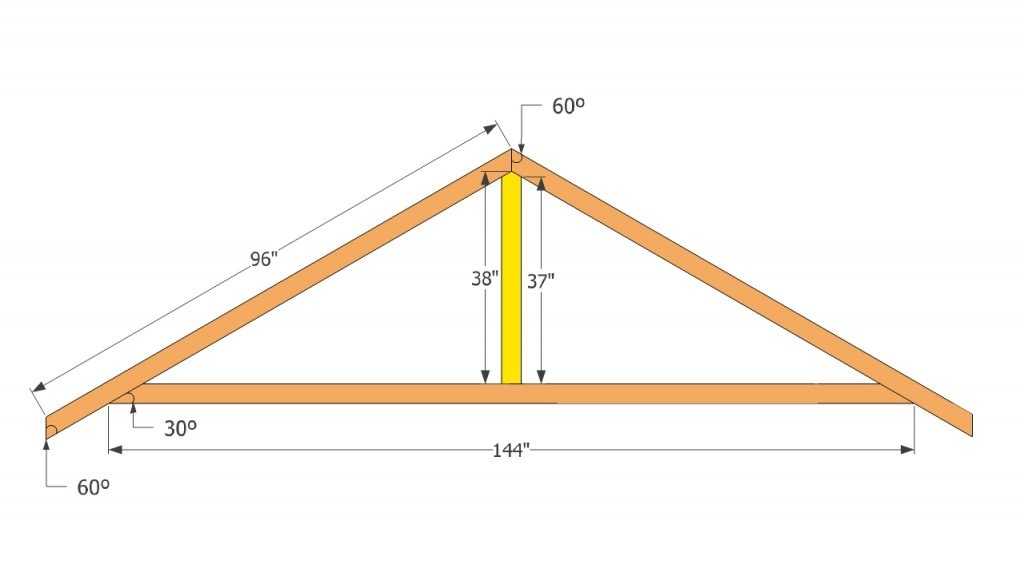 Обратите внимание, что мы приняли все силы за сжимающие. Если фактические силы являются растягивающими, ответ будет отрицательным. Теперь посмотрим на штифт 2. На штифт 2 действуют только силы F 12 за счет штока (12) и F 23 за счет штока (23). Далее он тянется вниз под действием веса W. Таким образом, силы, действующие на штифт 2, выглядят так, как показано на рис. 4. Применение условия равновесия к штифту (2) дает Теперь давайте посмотрим на контакт 3 (см. рис. 4). Он находится в равновесии под действием сил F 23 , нормальной реакции N и горизонтальной силы F 13 .
Применение условия равновесия дает Поскольку направление F 13 получается отрицательным, направление должно быть противоположным предполагаемому. Баланс сил в вертикальном направлении дает Таким образом, мы видим, что вес удерживается этими тремя стержнями. Структура является детерминированной и удерживает вес на месте.
Даже если мы заменим штифтовые соединения небольшой пластиной (известной как косынка) с двумя или тремя штифтами, анализ останется почти таким же, потому что штифты расположены так близко друг к другу, что едва ли создают какой-либо крутящий момент в соединениях.
Обратите внимание, что мы приняли все силы за сжимающие. Если фактические силы являются растягивающими, ответ будет отрицательным. Теперь посмотрим на штифт 2. На штифт 2 действуют только силы F 12 за счет штока (12) и F 23 за счет штока (23). Далее он тянется вниз под действием веса W. Таким образом, силы, действующие на штифт 2, выглядят так, как показано на рис. 4. Применение условия равновесия к штифту (2) дает Теперь давайте посмотрим на контакт 3 (см. рис. 4). Он находится в равновесии под действием сил F 23 , нормальной реакции N и горизонтальной силы F 13 .
Применение условия равновесия дает Поскольку направление F 13 получается отрицательным, направление должно быть противоположным предполагаемому. Баланс сил в вертикальном направлении дает Таким образом, мы видим, что вес удерживается этими тремя стержнями. Структура является детерминированной и удерживает вес на месте.
Даже если мы заменим штифтовые соединения небольшой пластиной (известной как косынка) с двумя или тремя штифтами, анализ останется почти таким же, потому что штифты расположены так близко друг к другу, что едва ли создают какой-либо крутящий момент в соединениях. Даже если стержни сварены друг с другом в местах соединений, с большой степенью точности большая часть усилия передается на стержни в продольном направлении, хотя некоторый очень небольшой (пренебрежимо малый) момент создается соединениями и может быть вызван возможным изгибом стержней. .
Теперь мы готовы построить ферму и проанализировать ее. Мы собираемся построить его, складывая все больше и больше треугольников вместе. Как видите, когда мы складываем эти треугольники, элемент суставов j и количество элементов (стержней) m связаны следующим образом:
Даже если стержни сварены друг с другом в местах соединений, с большой степенью точности большая часть усилия передается на стержни в продольном направлении, хотя некоторый очень небольшой (пренебрежимо малый) момент создается соединениями и может быть вызван возможным изгибом стержней. .
Теперь мы готовы построить ферму и проанализировать ее. Мы собираемся построить его, складывая все больше и больше треугольников вместе. Как видите, когда мы складываем эти треугольники, элемент суставов j и количество элементов (стержней) m связаны следующим образом:
м = 2j — 3
Это делает ферму статически определимой. Это легко понять следующим образом. Сначала рассмотрите всю ферму как одну систему. Если она должна быть статически определимой, то на нее должны действовать только три неизвестные силы, поскольку для сил на плоскости существуют три условия равновесия. Для этого достаточно зафиксировать один из его концов штифтовым соединением, а другой положить на ролик (ролик также дает дополнительное преимущество, заключающееся в том, что он может помочь в регулировке любого изменения длины элемента из-за деформаций).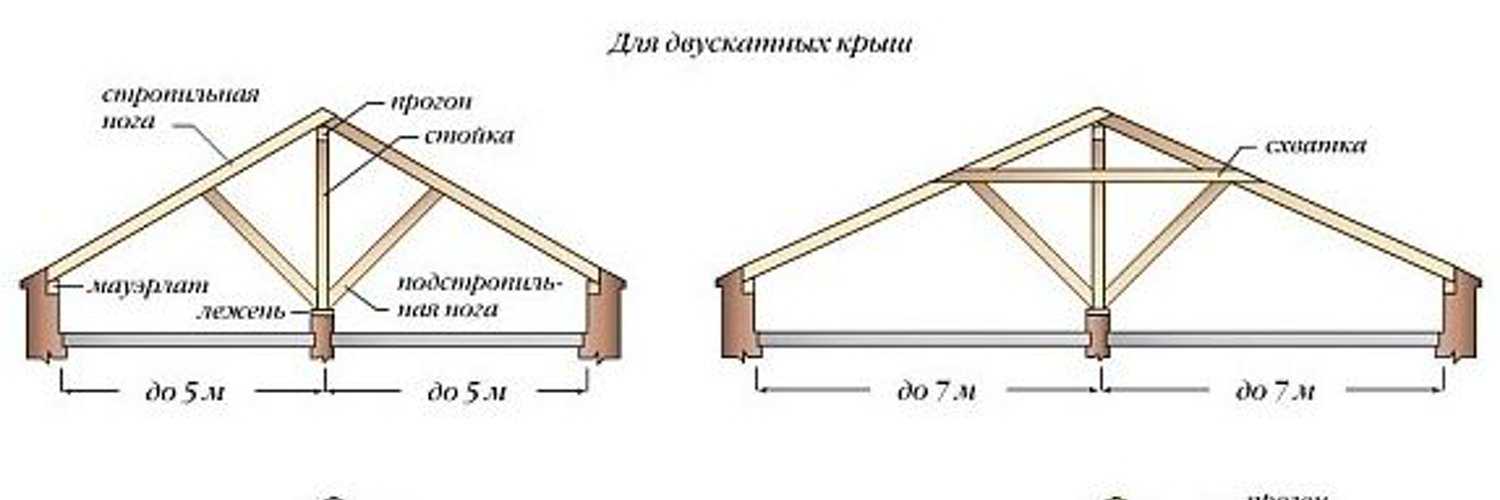 Если мы хотим определить эти внешние силы и силу в каждом элементе фермы, общее число неизвестных становится равным 9.0017 м + 3 . Мы находим эти неизвестные, записывая условия равновесия для каждой булавки; таких уравнений будет 2j . Для того чтобы система была детерминированной, мы должны иметь m + 3 = 2j , что является условием, приведенным выше. Если мы добавим еще членов, они станут излишними. С другой стороны, меньшее количество стержней сделает ферму неустойчивой, и она разрушится при нагрузке. Это произойдет потому, что ферма не сможет обеспечить необходимое количество усилий для выполнения всех условий равновесия. Статически определимые фермы известны как простые фермы. Упражнение 1: На рис. 5 показаны три часто используемые фермы по бокам мостов. Докажите, что все три из них являются простыми фермами. Вы можете спросить, почему мы ставим фермы на мосты. Как покажет наш дальнейший анализ, они распределяют нагрузку по всем элементам и тем самым делают мост прочнее.
Если мы хотим определить эти внешние силы и силу в каждом элементе фермы, общее число неизвестных становится равным 9.0017 м + 3 . Мы находим эти неизвестные, записывая условия равновесия для каждой булавки; таких уравнений будет 2j . Для того чтобы система была детерминированной, мы должны иметь m + 3 = 2j , что является условием, приведенным выше. Если мы добавим еще членов, они станут излишними. С другой стороны, меньшее количество стержней сделает ферму неустойчивой, и она разрушится при нагрузке. Это произойдет потому, что ферма не сможет обеспечить необходимое количество усилий для выполнения всех условий равновесия. Статически определимые фермы известны как простые фермы. Упражнение 1: На рис. 5 показаны три часто используемые фермы по бокам мостов. Докажите, что все три из них являются простыми фермами. Вы можете спросить, почему мы ставим фермы на мосты. Как покажет наш дальнейший анализ, они распределяют нагрузку по всем элементам и тем самым делают мост прочнее.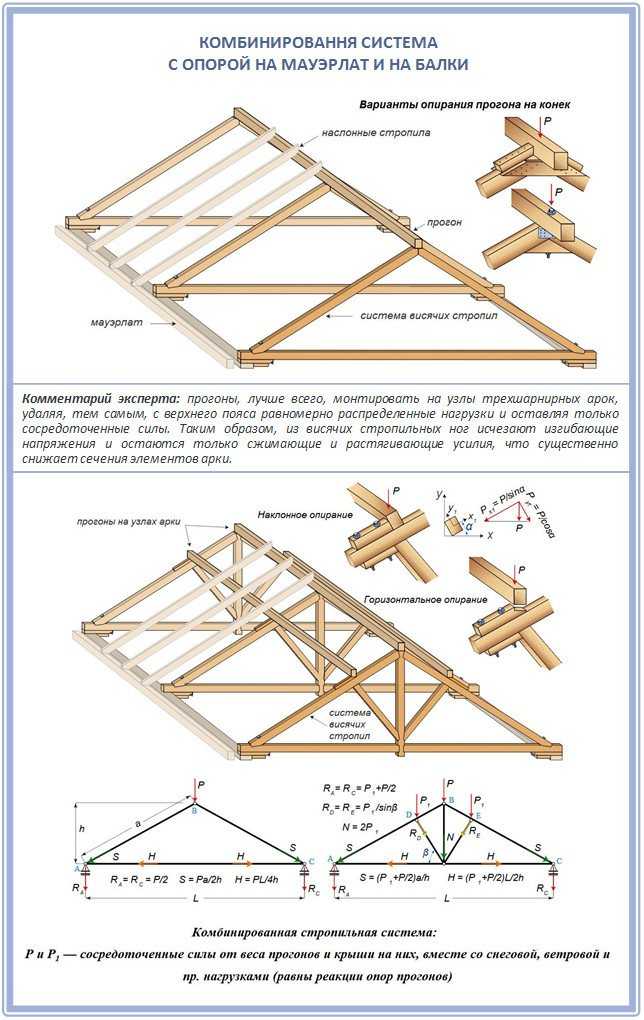 Теперь мы хотим получить силы, возникающие в различных плечах фермы, когда она нагружена извне. Это делается при следующих предположениях:
Теперь мы хотим получить силы, возникающие в различных плечах фермы, когда она нагружена извне. Это делается при следующих предположениях:
- Если средняя линия элементов фермы пересекается в какой-либо точке, то эта точка считается шарнирным соединением. Это очень правильное предположение, потому что, как мы видели ранее при введении фермы (треугольник с шарнирным соединением), нагрузка передается на другой элемент фермы, так что силы остаются по существу коллинеарными с элементом.
- Все внешние нагрузки действуют на штыревые соединения.
- Вес всех элементов поровну распределяется на соединительные штифты.
Существует два метода определения усилий в элементах фермы — метод соединений и метод сечений. Начнем с метода суставов:
Анализ фермы — метод соединений: В методе суставов мы смотрим на равновесие штифта в суставах. Поскольку силы на штифте действуют одновременно, уравнения моментов нет, а есть только два уравнения равновесия, а именно.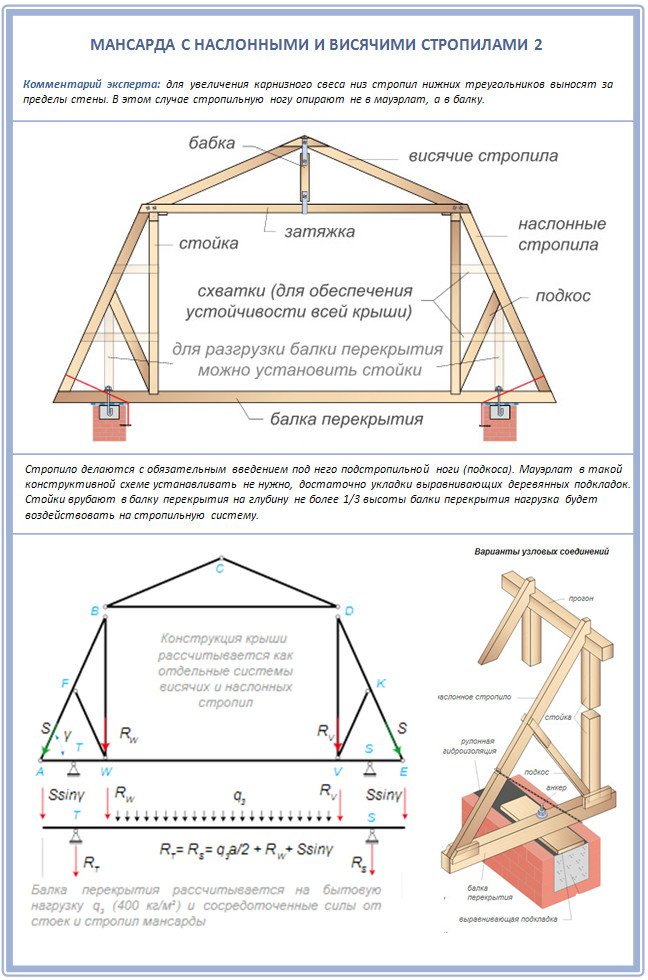 . Поэтому мы начинаем наш анализ с точки, где есть одна известная нагрузка и не более двух неизвестных сил. Вес каждого элемента делится на две половины и поддерживается каждым штифтом. В какой-то мере мы уже упоминали об этом методе, вводя фермы. Проиллюстрируем это двумя примерами. Пример 1: В качестве первого примера я беру ферму ABCDEF, как показано на рисунке 6, и нагружаю ее в точке E силой 5000 Н. Длина малых элементов фермы равна 4 м, диагональных — м. Теперь я найду силы в каждом элементе этой фермы, считая их невесомыми. Примем каждую точку за штифтовое соединение и начнем уравновешивать силы на каждом из штифтов. Поскольку контакт E имеет внешнюю нагрузку 5000 Н, можно начать с него. Однако в точке E действует более 2 неизвестных сил, поэтому мы не можем начать с E. Поэтому мы сначала рассматриваем ферму как единое целое и находим реакции грунта в точках A и D, потому что тогда в точках A и D останутся только две неизвестные силы. . Горизонтальная реакция Nx в точке A равно нулю, поскольку на систему не действует внешняя горизонтальная сила.
. Поэтому мы начинаем наш анализ с точки, где есть одна известная нагрузка и не более двух неизвестных сил. Вес каждого элемента делится на две половины и поддерживается каждым штифтом. В какой-то мере мы уже упоминали об этом методе, вводя фермы. Проиллюстрируем это двумя примерами. Пример 1: В качестве первого примера я беру ферму ABCDEF, как показано на рисунке 6, и нагружаю ее в точке E силой 5000 Н. Длина малых элементов фермы равна 4 м, диагональных — м. Теперь я найду силы в каждом элементе этой фермы, считая их невесомыми. Примем каждую точку за штифтовое соединение и начнем уравновешивать силы на каждом из штифтов. Поскольку контакт E имеет внешнюю нагрузку 5000 Н, можно начать с него. Однако в точке E действует более 2 неизвестных сил, поэтому мы не можем начать с E. Поэтому мы сначала рассматриваем ферму как единое целое и находим реакции грунта в точках A и D, потому что тогда в точках A и D останутся только две неизвестные силы. . Горизонтальная реакция Nx в точке A равно нулю, поскольку на систему не действует внешняя горизонтальная сила.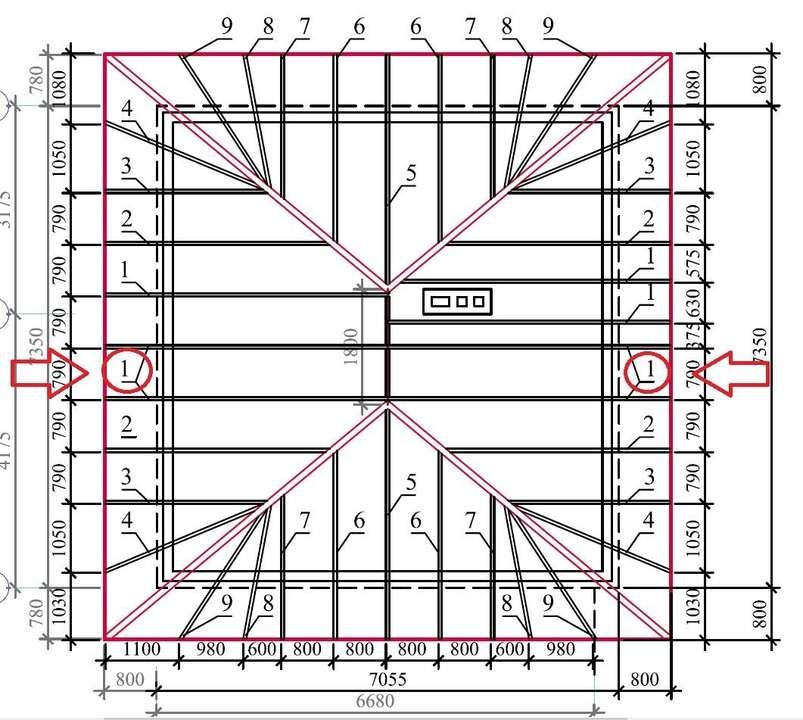 Чтобы найти N 2 Я использую момент A, чтобы получить что через уравнение дает В методе соединений давайте теперь начнем со штифта А и уравновешиваем различные силы. Мы уже предугадываем направление и показываем их примерно в точке А (рисунок 7). Все углы, образуемые диагоналями, равны 45°. Единственные уравнения, о которых мы сейчас беспокоимся, — это уравнения баланса сил. Имейте в виду, что сила, действующая на стержень AB и AF, будет противоположна силе, действующей на штифт (Ньютон III 9).0059-й Закон ). Следовательно, сила на стержне AB является сжимающей (отталкивает штифт A), тогда как сила на AF растягивающая (тянет A к себе).
Далее я рассматриваю соединение F, где сила AF известна, а две силы BF и FE неизвестны. Для пинты F Далее я иду в точку B, так как сейчас там только две неизвестные силы. В точке Б Отрицательный знак показывает, что хотя мы показали, что F BE сжимается, на самом деле он растягивается. Далее я рассматриваю точку C и уравновешиваю силы там.
Чтобы найти N 2 Я использую момент A, чтобы получить что через уравнение дает В методе соединений давайте теперь начнем со штифта А и уравновешиваем различные силы. Мы уже предугадываем направление и показываем их примерно в точке А (рисунок 7). Все углы, образуемые диагоналями, равны 45°. Единственные уравнения, о которых мы сейчас беспокоимся, — это уравнения баланса сил. Имейте в виду, что сила, действующая на стержень AB и AF, будет противоположна силе, действующей на штифт (Ньютон III 9).0059-й Закон ). Следовательно, сила на стержне AB является сжимающей (отталкивает штифт A), тогда как сила на AF растягивающая (тянет A к себе).
Далее я рассматриваю соединение F, где сила AF известна, а две силы BF и FE неизвестны. Для пинты F Далее я иду в точку B, так как сейчас там только две неизвестные силы. В точке Б Отрицательный знак показывает, что хотя мы показали, что F BE сжимается, на самом деле он растягивается. Далее я рассматриваю точку C и уравновешиваю силы там. Я уже предугадал направление сил и показал F CE на растяжение, тогда как F CD на сжатие Затем я иду к контакту D, где нормальная реакция равна N, и уравновешиваю силы там. Таким образом, были определены силы в различных элементах фермы. Они есть Вам может быть интересно, как мы получили все силы, не используя уравнения для всех суставов. Напомним, что именно так мы получили условие статической определенности. Нам не нужно было использовать все сочленения, потому что мы уже рассмотрели систему как единое целое и получили оттуда два уравнения. Таким образом, один косяк — в данном случае E — анализировать не нужно. Однако, учитывая, что ферма статически определима, все эти силы должны уравновешиваться в точке Е, где также была приложена нагрузка. Я оставлю это вам в качестве упражнения. Затем я спрашиваю, как изменилась бы ситуация, если бы каждый элемент фермы имел вес. Предположим, что каждый элемент весит 500 Н, тогда, если предположить, что нагрузка делится поровну между двумя штифтами, удерживающими элемент, нагрузка на ферму будет выглядеть, как показано на рисунке 8 (нагрузка из-за веса, как показано красным).
Я уже предугадал направление сил и показал F CE на растяжение, тогда как F CD на сжатие Затем я иду к контакту D, где нормальная реакция равна N, и уравновешиваю силы там. Таким образом, были определены силы в различных элементах фермы. Они есть Вам может быть интересно, как мы получили все силы, не используя уравнения для всех суставов. Напомним, что именно так мы получили условие статической определенности. Нам не нужно было использовать все сочленения, потому что мы уже рассмотрели систему как единое целое и получили оттуда два уравнения. Таким образом, один косяк — в данном случае E — анализировать не нужно. Однако, учитывая, что ферма статически определима, все эти силы должны уравновешиваться в точке Е, где также была приложена нагрузка. Я оставлю это вам в качестве упражнения. Затем я спрашиваю, как изменилась бы ситуация, если бы каждый элемент фермы имел вес. Предположим, что каждый элемент весит 500 Н, тогда, если предположить, что нагрузка делится поровну между двумя штифтами, удерживающими элемент, нагрузка на ферму будет выглядеть, как показано на рисунке 8 (нагрузка из-за веса, как показано красным). За исключением точек A и D нагрузка от веса составляет 750 Н; в точках A и D она равна 500 Н. Теперь внешняя реакция на каждом конце будет. Дополнительные 2000 Н можно рассчитать либо из уравнения момента, либо сразу, поняв, что новый добавленный вес совершенно симметричен относительно центра фермы и, следовательно, будет поровну разделен между двумя опорами. Для уравновешивания сил на других штифтах мы следуем той же процедуре, что и выше, с учетом того, что каждый штифт теперь имеет внешнюю нагрузку из-за веса каждого элемента. Я посчитаю силы в каком-нибудь члене фермы. Глядя на контакт А, мы получаем Далее переходим к точке F и видим, что силы Аналогичным образом можно решить и другие штифты в ферме, и я оставляю это вам в качестве упражнения.
Продемонстрировав вам метод соединений, теперь мы переходим к методу сечений, который непосредственно передает усилие на нужный элемент фермы.
За исключением точек A и D нагрузка от веса составляет 750 Н; в точках A и D она равна 500 Н. Теперь внешняя реакция на каждом конце будет. Дополнительные 2000 Н можно рассчитать либо из уравнения момента, либо сразу, поняв, что новый добавленный вес совершенно симметричен относительно центра фермы и, следовательно, будет поровну разделен между двумя опорами. Для уравновешивания сил на других штифтах мы следуем той же процедуре, что и выше, с учетом того, что каждый штифт теперь имеет внешнюю нагрузку из-за веса каждого элемента. Я посчитаю силы в каком-нибудь члене фермы. Глядя на контакт А, мы получаем Далее переходим к точке F и видим, что силы Аналогичным образом можно решить и другие штифты в ферме, и я оставляю это вам в качестве упражнения.
Продемонстрировав вам метод соединений, теперь мы переходим к методу сечений, который непосредственно передает усилие на нужный элемент фермы.
Как следует из названия, в методе сечений мы делаем сечения через ферму, а затем рассчитываем силу в элементах фермы, через которую выполняется разрез.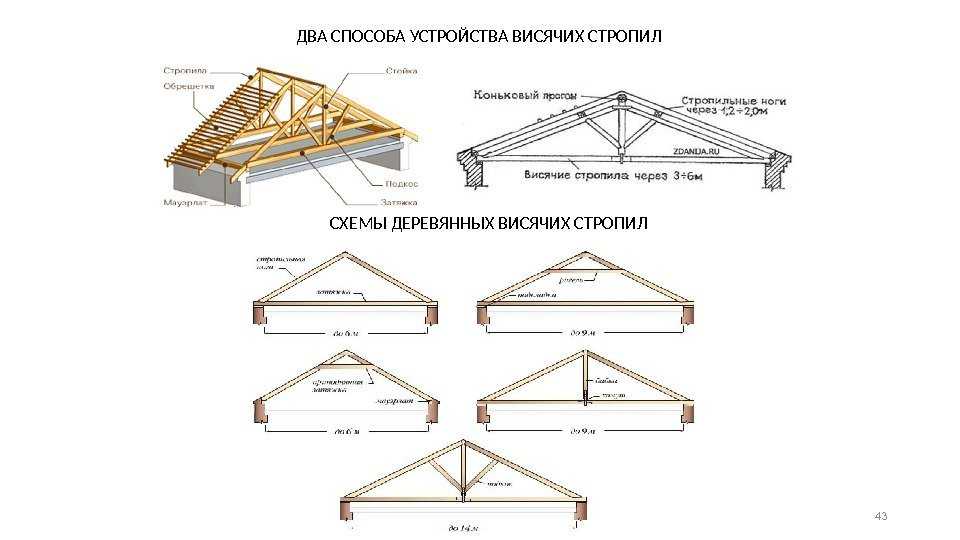 Например, если я возьму задачу, которую мы только что решили методом соединений, и сделаю сечение S 1 , S 2 (см. рис. 9), мы сможем определить силы в стержнях BC, BE и FE. путем рассмотрения равновесия части слева или справа от сечения. Позвольте мне теперь проиллюстрировать это. Как и в методе соединений, мы начинаем сначала с определения реакций на внешней опоре фермы, рассматривая ее как единое твердое тело. В данном конкретном случае это дает N в точке D и N в точке A. Теперь рассмотрим сечение фермы слева (см. рис. 10). Поскольку все это сечение находится в равновесии, . Обратите внимание, что теперь мы используем все три уравнения равновесия, поскольку силы в отдельных элементах не действуют одновременно. Направление силы в каждом члене можно в значительной степени угадать при осмотре. Таким образом, сила в сечении элементов BE должна быть направлена вниз, потому что нет другого элемента, который мог бы создать направленную вниз силу для уравновешивания 9.
Например, если я возьму задачу, которую мы только что решили методом соединений, и сделаю сечение S 1 , S 2 (см. рис. 9), мы сможем определить силы в стержнях BC, BE и FE. путем рассмотрения равновесия части слева или справа от сечения. Позвольте мне теперь проиллюстрировать это. Как и в методе соединений, мы начинаем сначала с определения реакций на внешней опоре фермы, рассматривая ее как единое твердое тело. В данном конкретном случае это дает N в точке D и N в точке A. Теперь рассмотрим сечение фермы слева (см. рис. 10). Поскольку все это сечение находится в равновесии, . Обратите внимание, что теперь мы используем все три уравнения равновесия, поскольку силы в отдельных элементах не действуют одновременно. Направление силы в каждом члене можно в значительной степени угадать при осмотре. Таким образом, сила в сечении элементов BE должна быть направлена вниз, потому что нет другого элемента, который мог бы создать направленную вниз силу для уравновешивания 9.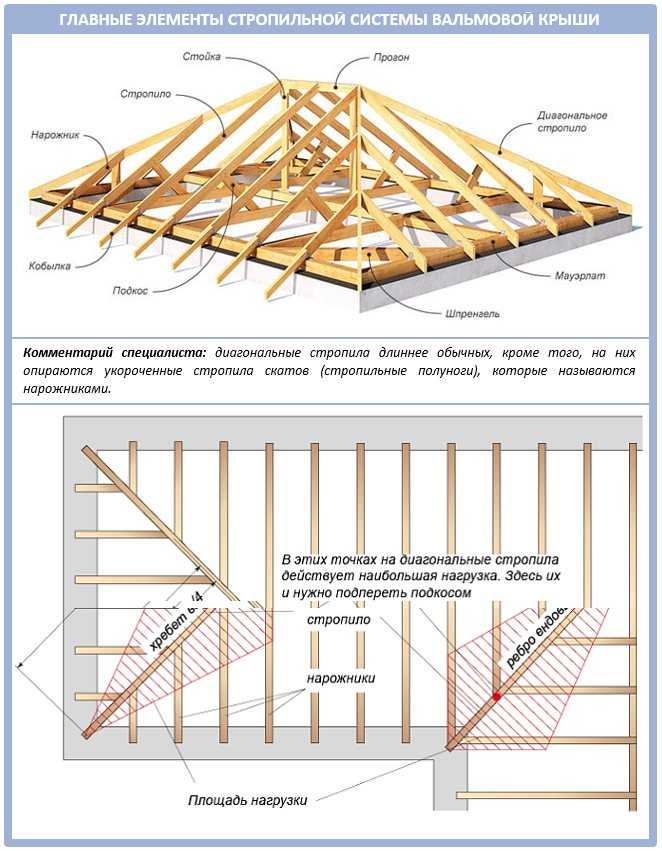 0017 N реакция в точке A. Это ясно говорит нам о том, что F BE является растяжимым. Точно так же, чтобы противодействовать крутящему моменту относительно B, создаваемому силой N в A, сила на FE также должна быть от F до E. Таким образом, эта сила также является растягивающей. Если мы далее рассмотрим баланс крутящего момента относительно A, N и F FE , то он не дает никакого крутящего момента относительно A. Таким образом, чтобы противодействовать крутящему моменту, создаваемому F BE , сила, действующая на BC, должна действовать в направлении B, тем самым делая силу сжимающей. .
Теперь вычислим отдельные силы. Ф FE вычислить проще всего. Для этого возьмем момент о B. Это дает
4 × = 4 × F КЭ
F КЭ = Н Далее вычисляем F BE . Для этого воспользуемся уравнением. Это дает Наконец, чтобы вычислить F BC , мы можем использовать либо уравнение относительно A, либо
Таким образом, мы определили силы в этих трех элементах напрямую, не вычисляя силы, идущие от одного сустава к другому, и при этом сэкономили много времени и усилий.
0017 N реакция в точке A. Это ясно говорит нам о том, что F BE является растяжимым. Точно так же, чтобы противодействовать крутящему моменту относительно B, создаваемому силой N в A, сила на FE также должна быть от F до E. Таким образом, эта сила также является растягивающей. Если мы далее рассмотрим баланс крутящего момента относительно A, N и F FE , то он не дает никакого крутящего момента относительно A. Таким образом, чтобы противодействовать крутящему моменту, создаваемому F BE , сила, действующая на BC, должна действовать в направлении B, тем самым делая силу сжимающей. .
Теперь вычислим отдельные силы. Ф FE вычислить проще всего. Для этого возьмем момент о B. Это дает
4 × = 4 × F КЭ
F КЭ = Н Далее вычисляем F BE . Для этого воспользуемся уравнением. Это дает Наконец, чтобы вычислить F BC , мы можем использовать либо уравнение относительно A, либо
Таким образом, мы определили силы в этих трех элементах напрямую, не вычисляя силы, идущие от одного сустава к другому, и при этом сэкономили много времени и усилий. Силы на правом сечении будут противоположны силам на левом сечении в точках, через которые разрезается сечение. Это можно использовать для проверки нашего ответа, и я оставлю это вам в качестве упражнения.
После этой иллюстрации позвольте мне записать шаги, которые предпринимаются для определения сил в элементах фермы методом сечений:
1. Сделайте разрез, чтобы разделить ферму на секции, пропустив разрез через элементы, где необходимо усилие.
2. Сделайте разрез через три члена фермы, потому что с тремя уравнениями равновесия, а именно. мы можем найти максимум три силы.
3. Примените условия равновесия и найдите нужные силы.
Применяя метод сечений, изобретательность заключается в том, чтобы сделать правильный. Метод после способа прямого расчета желаемой силы, минуя тяжелую работу, связанную с применением метода суставов, где нужно решать для каждого сустава.
Силы на правом сечении будут противоположны силам на левом сечении в точках, через которые разрезается сечение. Это можно использовать для проверки нашего ответа, и я оставлю это вам в качестве упражнения.
После этой иллюстрации позвольте мне записать шаги, которые предпринимаются для определения сил в элементах фермы методом сечений:
1. Сделайте разрез, чтобы разделить ферму на секции, пропустив разрез через элементы, где необходимо усилие.
2. Сделайте разрез через три члена фермы, потому что с тремя уравнениями равновесия, а именно. мы можем найти максимум три силы.
3. Примените условия равновесия и найдите нужные силы.
Применяя метод сечений, изобретательность заключается в том, чтобы сделать правильный. Метод после способа прямого расчета желаемой силы, минуя тяжелую работу, связанную с применением метода суставов, где нужно решать для каждого сустава.
5.6: Методы анализа ферм
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 42966
- Рене Альдерлистен
- Делфтский технологический университет через TU Delft Open
Существует несколько методов анализа ферм, но наиболее распространенными являются метод соединения и метод сечения (или момента).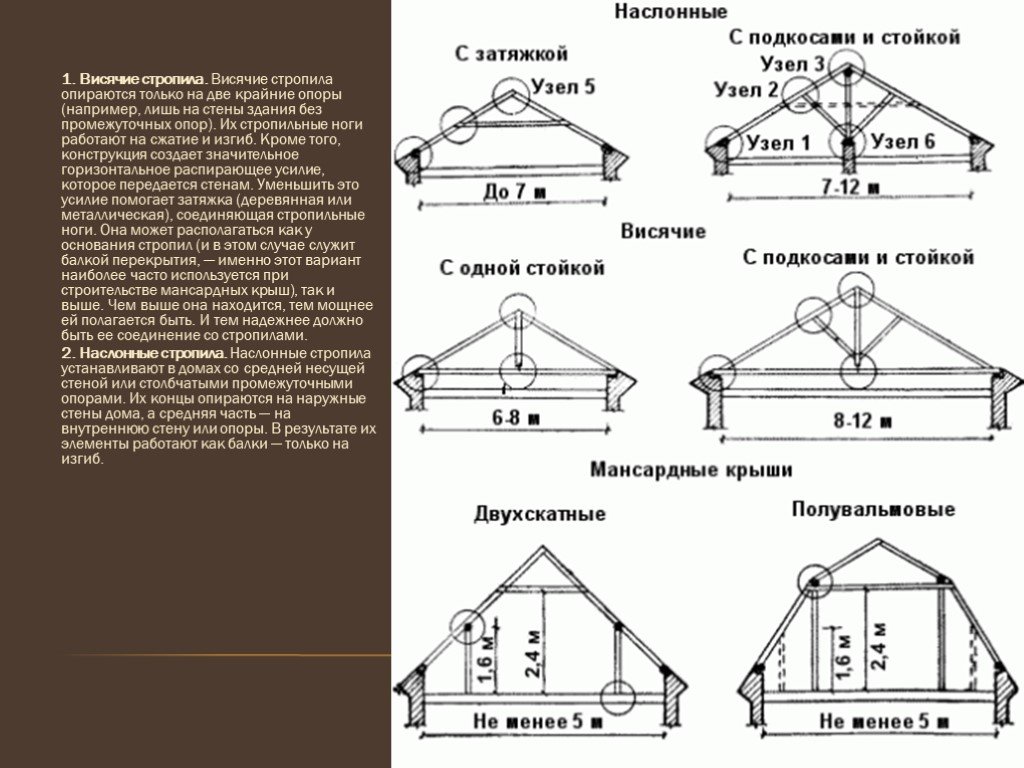
5.6.1 Соглашение о знаках
При расчете ферм отрицательная осевая сила на стержне означает, что элемент или соединения на обоих концах элемента испытывают сжатие, тогда как положительное значение осевой силы на стержне указывает на то, что элемент или соединения на обоих концах элемента находятся в состоянии растяжения.
5.6.2 Анализ ферм методом соединения
Этот метод основан на том принципе, что если структурная система представляет собой тело, находящееся в равновесии, то любое соединение в этой системе также находится в равновесии и, таким образом, может быть выделено из всей системы и проанализировано с использованием условий равновесия. Метод соединения включает в себя последовательную изоляцию каждого соединения в системе ферм и определение осевых усилий в элементах, встречающихся в соединении, с помощью уравнений равновесия. Подробная процедура анализа этим методом изложена ниже.
Процедура анализа
• Проверить устойчивость и определенность конструкции.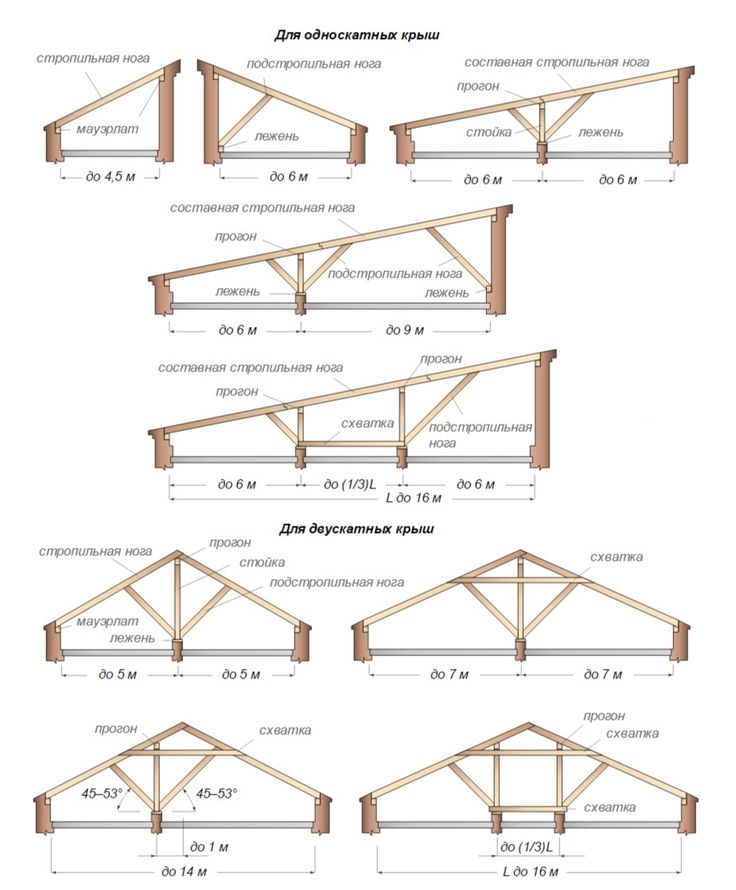 Если ферма устойчива и детерминирована, переходите к следующему шагу.
Если ферма устойчива и детерминирована, переходите к следующему шагу.
•Определить опорные реакции в ферме.
• Определить элементы нулевой силы в системе. Это неизмеримо сократит вычислительные усилия, связанные с анализом.
•Выберите соединение для анализа. Ни в коем случае в анализируемом соединении не должно быть более двух неизвестных сил стержня.
• Начертите изолированную диаграмму свободного тела выбранного соединения и обозначьте осевые силы во всех элементах, встречающихся в соединении, как растягивающие (т.е. отрывающие от соединения). Если это первоначальное допущение неверно, определенная осевая сила стержня при анализе будет отрицательной, что означает, что стержень находится в состоянии сжатия, а не растяжения.
• Примените два уравнения \(\Sigma F_{X}=0\) и \(\Sigma F_{Y}=0\) для определения осевых усилий стержня.
•Продолжить анализ, перейдя к следующему соединению с двумя или меньшим числом неизвестных сил-членов.
Пример 5. 2
2
Используя метод соединения, определите осевую силу в каждом элементе фермы, показанной на рис. 5.10а.
\(рис. 5.10\). Ферма.
Решение
Реакции поддержки. Применяя уравнения статического равновесия к диаграмме свободного тела, показанной на рис. 5.10б, опорные реакции можно определить следующим образом:
\(\begin{array}{ll}
+\curvearrowleft \sum M_{A} =0 \\
20(4)-12(3)+(8) C_{y}=0 \\
C_{y}=-5,5 \mathrm{кН} & C_{y}=5,5 \mathrm{кН } \стрелка вниз\\
+\стрелка вверх \сумма F_{y}=0 \\
A_{y}-5,5+20=0 \\
A_{y}=-14,5 \mathrm{кН} & A_{y}=14,5 \mathrm{ кН} \downarrow \\
+\rightarrow \sum F_{x}=0 \\
-A_{x}+12=0 \\
A_{x}=12 \mathrm{kN} & A_{x}= 12 \mathrm{кН} \leftarrow \\
\end{array}\)
Анализ соединений. Анализ начинается с выбора соединения, которое имеет две или меньше неизвестных сил стержня. Диаграмма свободного тела фермы покажет, что соединения \(A\) и \(B\) удовлетворяют этому требованию.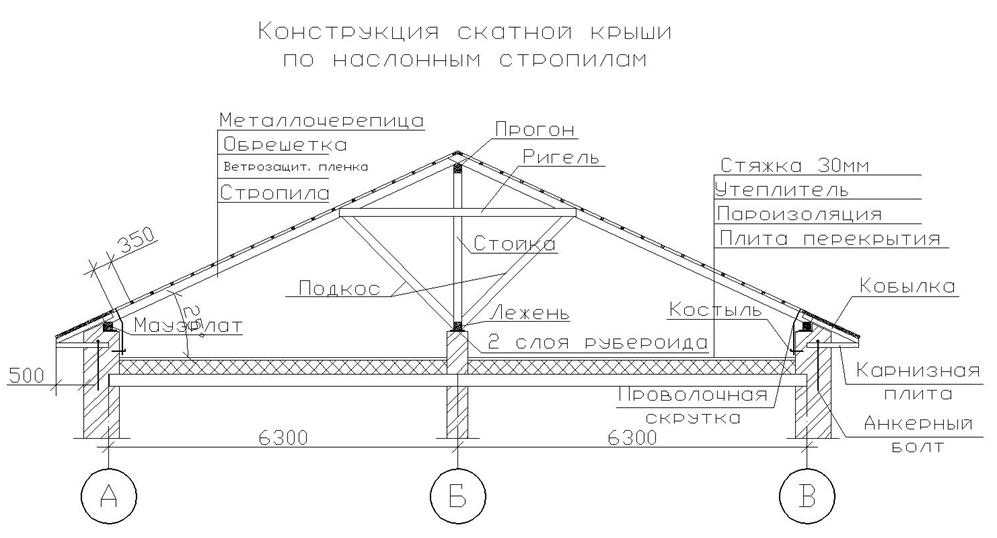 Чтобы определить осевые усилия в элементах, встречающихся в стыке \(A\), сначала изолируйте соединение от фермы и обозначьте осевые усилия элементов как \(F_{A B}\) и \(F_{A D}\) 9{\circ}=-7,34 \mathrm{kN}
Чтобы определить осевые усилия в элементах, встречающихся в стыке \(A\), сначала изолируйте соединение от фермы и обозначьте осевые усилия элементов как \(F_{A B}\) и \(F_{A D}\) 9{\circ}=-7,34 \mathrm{kN}
\end{array}\)
После завершения анализа соединения \(A\) , соединения \(B\) или \(D\) можно проанализировать, так как есть только две неизвестные силы.
Анализ соединения \(D\).
\(\begin{array}{l}
+\стрелка вверх \sum F_{y}=0 \\
F_{D B}=0 \\
+\стрелка вправо \sum F_{x}=0 \\
-F_{D A}+F_{D C}=0 \\
F_{D C}=F_{D A}=-7,34 \mathrm{кН}
\end{массив}\)
Анализ соединения \(B \).
\(\begin{array}{l}
+\rightarrow \sum F_{x}=0 \\
-F_{BA} \sin 53.13+F_{BC} \sin 53.13+15=0 \\
F_{B C} \sin 53.13=-15+24.17 \sin 53.13= \\
F_{BC}=5.42 \mathrm{кН}
\end{массив}\)
5.6.3 Члены Zero Force
Анализ сложной фермы можно значительно упростить, если сначала определить «элементы с нулевой силой».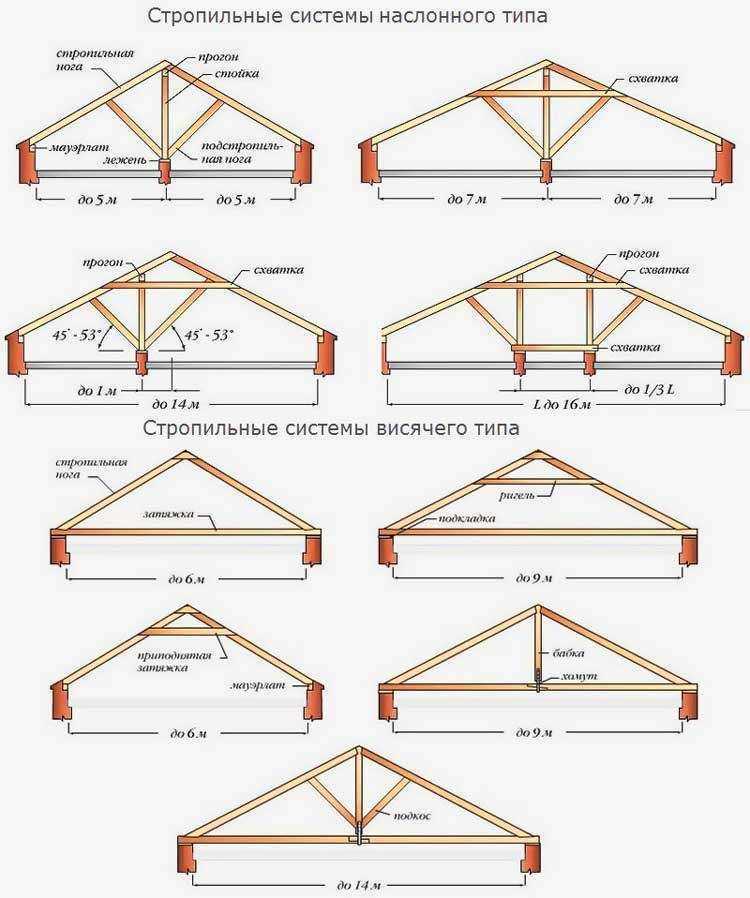 Элемент с нулевой силой — это элемент, который не подвергается какой-либо осевой нагрузке. Иногда такие элементы вводят в систему ферм, чтобы предотвратить коробление и вибрацию других элементов. Конструкции ферменных элементов, приводящие к элементам нулевой силы, перечислены ниже:
Элемент с нулевой силой — это элемент, который не подвергается какой-либо осевой нагрузке. Иногда такие элементы вводят в систему ферм, чтобы предотвратить коробление и вибрацию других элементов. Конструкции ферменных элементов, приводящие к элементам нулевой силы, перечислены ниже:
1. Если существует неколлинеарность между двумя элементами, встречающимися в стыке, на который не действует никакая внешняя сила, то эти два элемента являются элементами с нулевой силой (см. рис. 5.11а).
2. Если три элемента встречаются в стыке без внешней силы, а два из них коллинеарны, третий элемент является элементом с нулевой силой (см. рис. 5.11b).
3. Если два элемента встречаются в стыке, и сила, приложенная к стыку, параллельна одному элементу и перпендикулярна другому, то элемент, перпендикулярный приложенной силе, является элементом с нулевой силой (см. рис. 5.11c).
\(рис. 5.11\). Члены нулевой силы.
5.6.4 Анализ ферм методом раздела
Иногда определение осевой силы в конкретных элементах ферменной системы методом соединения может быть очень трудоемким и громоздким, особенно когда система состоит из нескольких элементов. В таких случаях использование метода сечения может сэкономить время и поэтому предпочтительнее. Этот метод включает в себя прохождение воображаемого сечения через ферму так, чтобы оно делило систему на две части и прорезало элементы, осевые усилия которых желательны. Осевые силы стержня затем определяются с использованием условий равновесия. Подробная процедура анализа этим методом представлена ниже.
В таких случаях использование метода сечения может сэкономить время и поэтому предпочтительнее. Этот метод включает в себя прохождение воображаемого сечения через ферму так, чтобы оно делило систему на две части и прорезало элементы, осевые усилия которых желательны. Осевые силы стержня затем определяются с использованием условий равновесия. Подробная процедура анализа этим методом представлена ниже.
Процедура анализа ферм методом раздела
•Проверьте устойчивость и определенность конструкции. Если ферма устойчива и детерминирована, переходите к следующему шагу.
•Определить опорные реакции в ферме.
• Сделайте воображаемый разрез в конструкции так, чтобы он включал в себя элементы, осевые усилия которых нужны. Воображаемый разрез делит ферму на две части.
• Прилагайте усилия к каждой части фермы, чтобы удерживать ее в равновесии.
• Выберите любую часть фермы для определения сил стержня.
• Применить условия равновесия для определения осевых усилий стержня.
Пример 5.3
Методом сечения определите осевые усилия в элементах \(CD\), \(CG\) и \(HG\) фермы, показанной на рис. 5.12а.
\(рис. 5.12\). Ферма.
Решение
Реакции поддержки. Применяя уравнения статического равновесия к диаграмме свободного тела на рис. 5.12b, опорные реакции можно определить следующим образом:
\(\begin{array}{l}
A_{y}=F_{y}=\frac{160}{2}=80 \mathrm{кН} \\
+\стрелка вправо \Sigma F_{x} =0 \quad A_{x}=0
\end{array}\)
Анализ методом сечения. Во-первых, воображаемое сечение проходит через ферму так, чтобы оно пересекало элементы \(CD\), \(CG\) и \(HG\) и делило ферму на две части, как показано на рис. 5.12c и рис. 5.12г. Все силы, воздействующие на стержень, обозначаются как силы растяжения (т. е. отрыв от соединения). Если это первоначальное предположение неверно, расчетные силы на стержнях будут отрицательными, что указывает на то, что они сжимаются. Любая из двух частей может быть использована для анализа. Левая часть будет использоваться для определения сил стержня в этом примере. Применяя уравнение равновесия к левому сегменту фермы, осевые силы в элементах можно определить следующим образом:
Левая часть будет использоваться для определения сил стержня в этом примере. Применяя уравнение равновесия к левому сегменту фермы, осевые силы в элементах можно определить следующим образом:
Осевая сила в стержне \(CD\). Чтобы определить осевую силу в стержне \(CD\) , , найдите момент относительно соединения в ферме, где только \(CD\) будет иметь момент относительно этого соединения, а все остальные разрезанные элементы не будут иметь момента. Внимательное рассмотрение покажет, что соединение, удовлетворяющее этому требованию, является соединением \(G\). Таким образом, взятие момента около \(G\) предполагает следующее:
\(\begin{array}{l}
+\curvearrowleft \sum M_{G}=0 \\
-80(6)+80( 3)-F_{C D}(3)=0 \\
F_{C D}=-80 \mathrm{кН} и 80 \mathrm{кН} (C)
\end{массив}\)
Осевая сила в стержне \(HG\).
\(\begin{array}{l}
+\curvearrowleft \sum M_{C}=0 \\
-80(3)+F_{H G}(3)=0 \\
F_{H G}= 80 \mathrm{kN} & 80 \mathrm{kN} (T)
\end{array}\)
Осевая сила в стержне \(CG\). Осевая сила в стержне \(CG\) определяется с учетом вертикального равновесия левой части. Таким образом,
Осевая сила в стержне \(CG\) определяется с учетом вертикального равновесия левой части. Таким образом,
\(\begin{array}{l}
+\uparrow \sum F_{y}=0 \\ 9{\circ}=0 \\
F_{C G}=0
\end{массив}\)
Краткое изложение главы
Внутренние силы в плоских фермах: Фермы представляют собой конструктивные системы, состоящие из прямых и гибких элементов, соединенных на концах. Допущения при расчете плоских ферм включают следующее:
1.Элементы ферм соединены на концах безфрикционными штифтами.
2. Стержни прямые и подвергаются осевым нагрузкам.
3. Деформации элементов малы и пренебрежимо малы.
4. Нагрузки в фермах действуют только на их соединения.
Элементы фермы могут подвергаться осевому сжатию или осевому растяжению. Осевое сжатие элементов всегда считается отрицательным, а осевое растяжение всегда считается положительным.
Фермы могут быть внешне или внутренне определенными или неопределенными.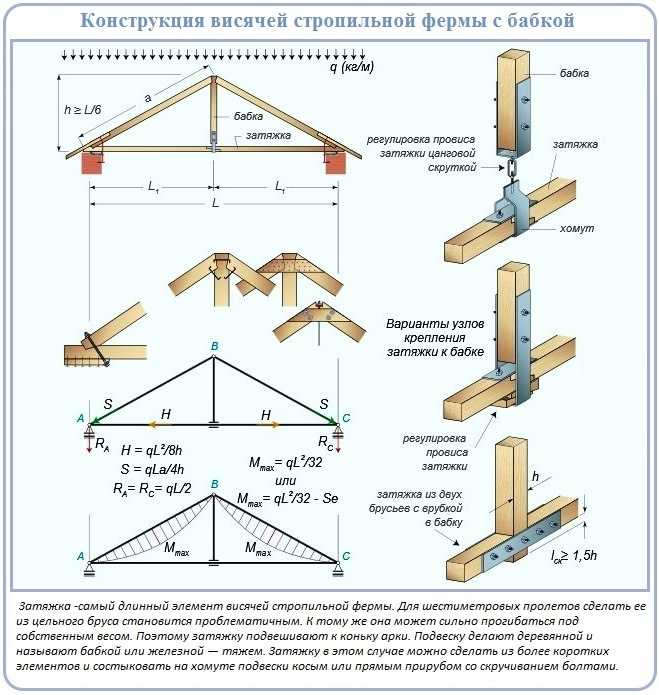 Внешне детерминированные фермы — это фермы, неизвестные внешние реакции которых можно определить, используя только уравнение статического равновесия. Внешне неопределенными называют фермы, внешняя неизвестная реакция которых не может быть полностью определена с помощью уравнений равновесия. Для определения числа неизвестных реакций, превышающих уравнение равновесия неопределенных ферм, необходимо составить дополнительные уравнения, исходя из совместимости частей системы. Внутренне определенные фермы — это фермы, элементы которых расположены таким образом, что образуется ровно столько треугольных ячеек, чтобы предотвратить геометрическую нестабильность системы.
Внешне детерминированные фермы — это фермы, неизвестные внешние реакции которых можно определить, используя только уравнение статического равновесия. Внешне неопределенными называют фермы, внешняя неизвестная реакция которых не может быть полностью определена с помощью уравнений равновесия. Для определения числа неизвестных реакций, превышающих уравнение равновесия неопределенных ферм, необходимо составить дополнительные уравнения, исходя из совместимости частей системы. Внутренне определенные фермы — это фермы, элементы которых расположены таким образом, что образуется ровно столько треугольных ячеек, чтобы предотвратить геометрическую нестабильность системы.
Формулировка устойчивости и определенности в фермах следующая:
\(\begin{array}{l}
м+r<2 j \quad \text { конструкция статически неустойчива } \\
m+r=2 j \quad \text { конструкция детерминирована } \\
м +r>2 j \quad \text { структура не определена }
\end{массив}\)
Методы анализа ферм: Двумя распространенными методами расчета ферм являются метод соединения и метод сечения (или момента).
Метод соединения : Этот метод включает изоляцию каждого соединения фермы и учет равновесия соединения при определении осевой силы элемента. Два уравнения, используемые для определения осевых сил стержня, это \(\Sigma F_{X}=0\) и \(\Sigma F_{y}=0\). Соединения изолируют последовательно для анализа, исходя из того принципа, что количество осевых сил неизвестного стержня никогда не должно быть больше двух в рассматриваемом соединении в плоском доверии.
Метод сечения: Этот метод предполагает прохождение воображаемого сечения через ферму, чтобы разделить ее на две части. Силы стержня определяются с учетом равновесия части фермы по обе стороны от сечения. Этот метод удобен, когда требуются осевые усилия в определенных элементах в ферме с несколькими элементами.
Практические задачи
5.1 Классифицируйте фермы, показанные на рис. P5.1a–рис. P5.1r.
\(Рис. П5.1\). Классификация ферм.
5.2 Определите усилие в каждом элементе ферм, показанных на рис. P5.2–рис. P5.12, используя метод соединения.
\(Рис. П5.2\). Ферма.
\(Рис. П5.3\). Ферма.
\(Рис. П5.4\). Ферма.
\(Рис. П5.5\). Ферма.
\(Рис. П5.6\). Ферма.
\(Рис. П5.7\). Ферма.
\(Рис. П5.8\). Ферма.
\(Рис. П5.9\). Ферма.
\(Рис. П5.10\). Ферма.
\(Рис. П5.11\). Ферма.
\(рис. 5.12\). Ферма.
5.3 Используя метод сечения, определите усилия в элементах, обозначенных X, ферм, показанных на рисунках с P5.13 по P5.19.
\(Рис. П5.13\). Ферма.
\(рис. П5.14\). Ферма.
\(рис. П5.15\). Ферма.
\(рис. П5.16\). Ферма.
\(Рис. П5.17\). Ферма.
\(рис. П5.18\). Ферма.
\(Рис.

 Кровли» заполняют данными из нижеприведенной таблицы.
Кровли» заполняют данными из нижеприведенной таблицы.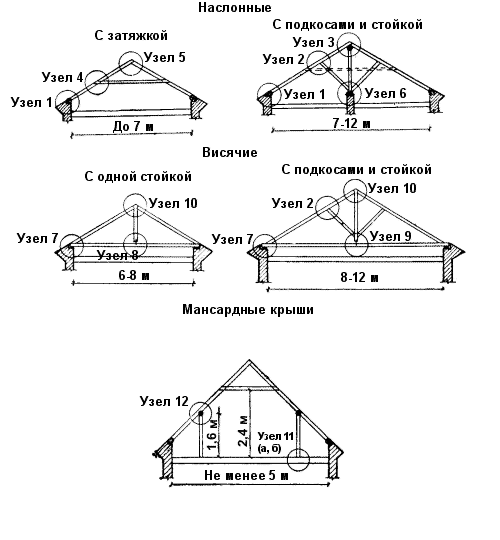 )».
)».