Подкосы стропильной системы: Стропила с подкосами — Все о ремонте и строительстве

Стропила с подкосами — Все о ремонте и строительстве

Для подбора сечения однопролетной деревянной балки (стропильной ноги на двух опорах) определяющим часто является прогиб при неполностью используемых напряжениях изгиба. Поэтому однопролетная балка с постоянным сечением обычно бывает не самой экономичной. Неразрезные двухпролетные балки позволяют использовать более экономичные поперечные сечения, чем однопролетные балки той же длины.

Эти системы наслонных стропил тоже можно делать по распорному и безраспорному варианту. Вся разница заключается только в устройстве концевых опор, не будем больше на этом останавливаться.

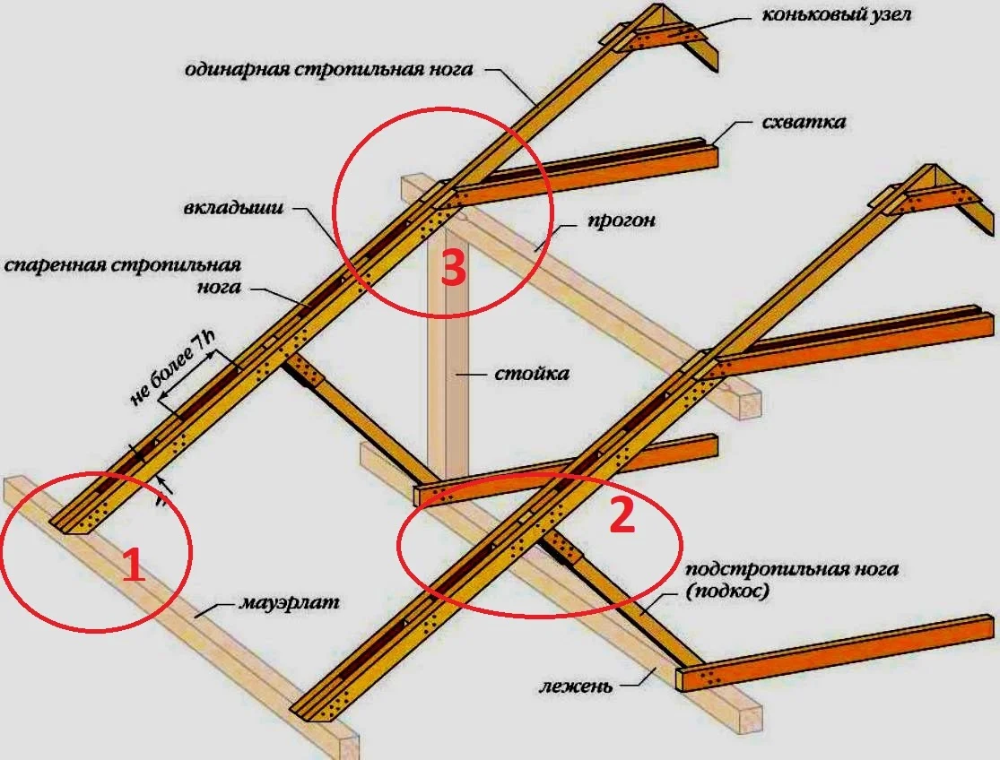
Третья опора стропильной ноги — подкос, другое название подстропильная нога (рис. 39), устанавливается под углом к горизонту не менее 45° и превращает стропило из однопролетной балки в двухпролетную неразрезную. Что позволяет уменьшить сечение стропильной ноги при той же нагрузке, а пролет, перекрываемый двускатной крышей, увеличить до 14 м.

В двухпролетной неразрезной балке максимальный изгибающий момент находится над средней опорой, его и принимают для расчета сечения стропильной ноги (рис 40). Простой пример, попробуйте перегнуть палку через колено, она сломается на колене. Здесь будет максимальный изгибающий момент, по которому и нужно определять сечение всего деревянного элемента. Прогиб неразрезной двухпролетной балки будет меньше, чем обычной балки на двух опорах той же длины. Мешает средняя опора, это очевидно. Однако если вспомнить, что наша реальная расчетная схема это все-таки не горизонтальная балка, а наклонная и подперта она наклонным подкосом, то очевидным становится и то, что прогнувшееся стропило сместит и узел соединения с подкосом. Поэтому прогиб стропильной ноги для упрощения считают по обычной формуле прогиба (2) однопролетной балки для наибольшего пролета. В данном случае, для крыш с уклонами скатов до 45°, прогиб считается для нижнего пролета — от узла соединения с мауэрлатом до узла соединения с подкосом.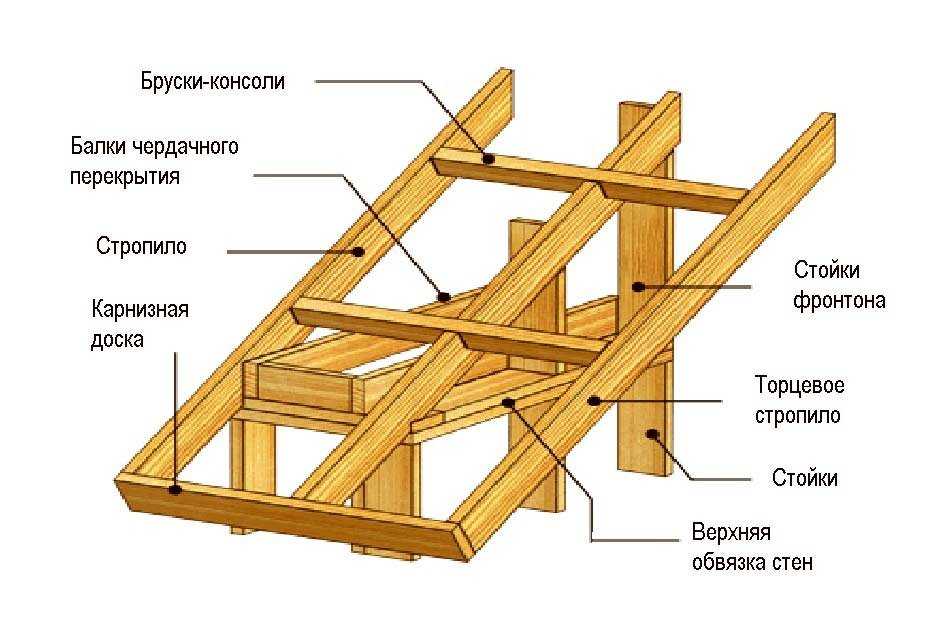

Узел крепления подкоса к стропильной ноге очень простой и не требует никакого расчета. Подкос просто заводят под стропильную ногу и фиксируют от смещения прибоинами: нижней и двумя боковыми. Расчет гвоздевого соединения не производится, оно здесь носит чисто конструктивный характер. Важно, чтобы торец подкоса был точно подпилен под угол наклона стропильной ноги так, чтобы у стропилины не было люфта на выбор зазора при приложении к ней нагрузки. Иными словами, точно подогнанный под низ стропила подкос не даст ему прогнуться в месте опирания. При полном расчете стропильной системы стропило в месте опирания подкоса проверяют на местное смятие древесины, но как правило, в таком расчете нет необходимости. Сечение подкоса определяют расчетом на сжатие и если получают слишком маленькое сечение, задают конструктивно, равным сечению стропильной ноги.

В верхней части рисунка 40 изображена распорная стропильная схема без схватки. Сжимающие усилия в ней принимают подкосы. Система, рассчитанная на распор воспринимаемый материалом стен, в схватке не нуждается. Здесь уже есть элементы, работающие на сжатие — подкосы. Схватка не снимает распор, значит в ней нет острой необходимости.

В нижней части рисунка 40 безраспорная схема стропил с затяжкой. Здесь все наоборот, затяжка необходимый элемент и она участвует в работе всей системы. Схватку нужно устанавливать ниже крепления подкосов. Иначе безраспорный узел опирания на мауэрлат — ползун при изменении нагрузок может действительно начать ползать по мауэрлату. Обычно рассчитывается только гвоздевое соединение схватки со стропильной ногой, из-за малых внутренних напряжений сечение схватки-затяжки подбирается конструктивно.

Стропила с подкосами

Для подбора сечения однопролетной деревянной балки (стропильной ноги на двух опорах) определяющим часто является прогиб при неполностью используемых напряжениях изгиба. Поэтому однопролетная балка с постоянным сечением обычно бывает не самой экономичной. Неразрезные двухпролетные балки позволяют использовать более экономичные поперечные сечения, чем однопролетные балки той же длины.

И эти системы наслонных стропил можно делать по распорному и безраспорному варианту. Вся разница заключается только в устройстве концевых опор, не будем больше на этом останавливаться.

рис. 1. Наслонные стропила с подкосами

Третья опора стропильной ноги — подкос, другое название подстропильная нога (рис. 1), устанавливается под углом к горизонту не менее 45° и превращает стропило из однопролетной балки в двухпролетную неразрезную. Что позволяет уменьшить сечение стропильной ноги при той же нагрузке, а пролет, перекрываемый двускатной крышей, увеличить до 14 м.

В двухпролетной неразрезной балке максимальный изгибающий момент находится над средней опорой, его и принимают для расчета сечения стропильной ноги (рис 2). Простой пример, попробуйте перегнуть палку через колено, она сломается на колене. Здесь будет максимальный изгибающий момент, по которому и нужно определять сечение всего деревянного элемента.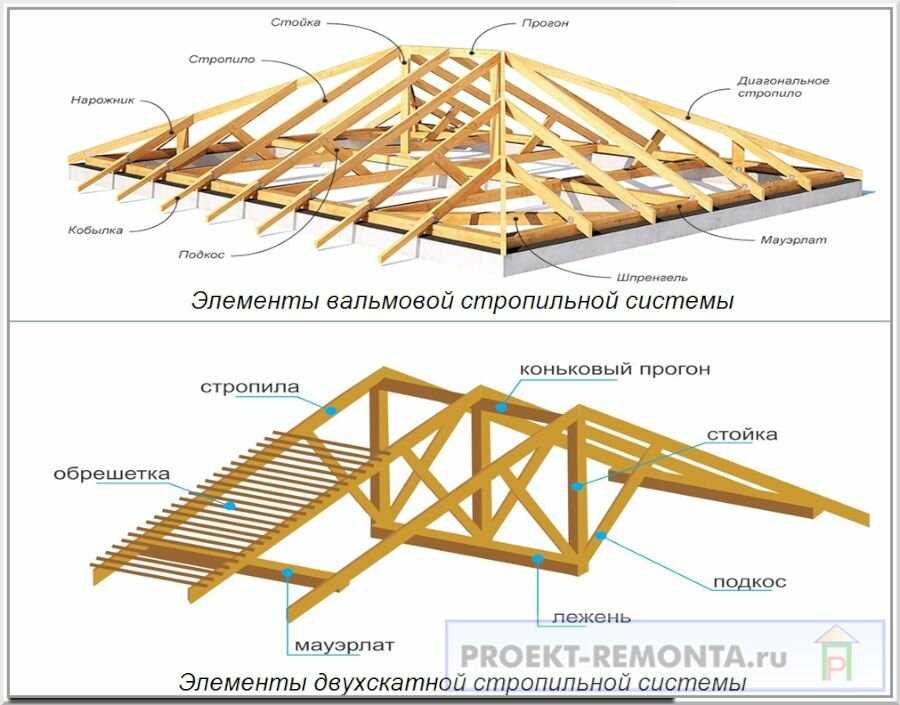 Прогиб неразрезной двухпролетной балки будет меньше, чем обычной балки на двух опорах той же длины. Мешает средняя опора, это очевидно. Однако если вспомнить, что наша реальная расчетная схема это все-таки не горизонтальная балка, а наклонная и подперта она наклонным подкосом, то очевидным становится и то, что прогнувшееся стропило сместит и узел соединения с подкосом. Поэтому прогиб стропильной ноги для упрощения считают по обычной формуле прогиба (2) однопролетной балки для наибольшего пролета. В данном случае, для крыш с уклонами скатов до 45°, прогиб считается для нижнего пролета — от узла соединения с мауэрлатом до узла соединения с подкосом.

Рис. 2. Конструктивные и расчетные схемы наслонных стропил с подкосами. Узел крепления подкоса

Узел крепления подкоса к стропильной ноге очень простой и не требует никакого расчета. Подкос просто заводят под стропильную ногу и фиксируют от смещения прибоинами: нижней и двумя боковыми. Расчет гвоздевого соединения не производится, оно здесь носит чисто конструктивный характер. Важно, чтобы торец подкоса был точно подпилен под угол наклона стропильной ноги так, чтобы у стропилины не было люфта на выбор зазора при приложении к ней нагрузки. Иными словами, точно подогнанный под низ стропила подкос не даст ему прогнуться в месте опирания. При полном расчете стропильной системы стропило в месте опирания подкоса проверяют на местное смятие древесины, но как правило, в таком расчете нет необходимости. Сечение подкоса определяют расчетом на сжатие и если получают слишком маленькое сечение, задают конструктивно, равным сечению стропильной ноги.

В верхней части рисунка 2 изображена распорная стропильная схема без схватки. Сжимающие усилия в ней принимают подкосы. Система, рассчитанная на распор воспринимаемый материалом стен, в схватке не нуждается. Здесь уже есть элементы, работающие на сжатие — подкосы. Схватка не снимает распор, значит в ней нет острой необходимости.

В нижней части рисунка 2 безраспорная схема стропил с затяжкой. Здесь все наоборот, затяжка необходимый элемент и она участвует в работе всей системы. Схватку нужно устанавливать ниже крепления подкосов. Иначе безраспорный узел опирания на мауэрлат — ползун при изменении нагрузок может действительно начать ползать по мауэрлату. Обычно рассчитывается только гвоздевое соединение схватки со стропильной ногой, из-за малых внутренних напряжений сечение схватки-затяжки подбирается конструктивно.

« назад           далее »

Источник:  «Конструкции крыш. Стропильные системы» Савельев А.А.

TBIL-LA Гражданское строительство: фермы и распорки

Подраздел A.1.1 Деятельность

Определение А.1.1.

В инженерии ферма представляет собой конструкцию, состоящую из нескольких балок материала, называемых стойками , которые собраны так, чтобы вести себя как единый объект.

Мероприятие А.1.2.

Рассмотрим изображение простой фермы, изображенное ниже. Все семь опор имеют одинаковую длину, прикреплены к двум анкерным точкам, прикладывая нормальную силу к узлам \(C\) и \(E\text{,}\) и с нагрузкой \(10000 Н\), приложенной к узел задан \(D\text{. }\)

Что из следующего должно выполняться, чтобы ферма была устойчивой?

1. Все стойки будут подвергаться сжатию.

2. Все стойки испытывают натяжение.

3. Некоторые стойки будут сжаты, а другие натянуты.

Мероприятие А.1.5.

Используя соглашения предыдущего замечания и где \(\vec L\) представляет вектор нагрузки на узел \(D\text{,}\), найдите еще четыре векторных уравнения, которые должны удовлетворяться для каждого из остальных четырех узлов. фермы.

\begin{equation*} А: \неизвестно \end{уравнение*}

\begin{уравнение*} Б: \неизвестно \end{уравнение*}

\begin{уравнение*} C: \vec F_{CA}+\vec F_{CD}+\vec N_C=\vec 0 \end{уравнение*}

\begin{уравнение*} Д:\неизвестно \end{уравнение*}

\begin{уравнение*} Э:\неизвестно \end{уравнение*}

Мероприятие А.1.8.

Сколько скалярных переменных потребуется для написания линейной системы, моделирующей рассматриваемую ферму с постоянной нагрузкой \(10000\) ньютонов?

• \(7\text{:}\) \(5\) от узлов, \(2\) от анкеров

• \(9\text{:}\) \(7\) от распорок, \(2\) от анкеров

• \(11\text{:}\) \(7\) от стоек, \(4\) от анкеров

• \(12\text{:}\) \(7\) от стоек, \(4\) от анкеров, \(1\) от груза

• \(13\text{:}\) \(5\) от узлов, \(7\) от стоек, \(1\) от нагрузки

Мероприятие А.1.12.

Разверните приведенное ниже векторное уравнение, используя синус и косинус соответствующих углов, затем вычислите каждый компонент (приблизительно \(\sqrt{3}/2\приблизительно 0,866\)).

\begin{equation*} D:\vec F_{DA}+\vec F_{DB}+\vec F_{DC}+\vec F_{DE}=-\vec L \end{уравнение*}

\begin{уравнение*} \влево x_3\begin{bmatrix}\cos(\unknown)\\\sin(\unknown)\end{bmatrix}+ x_4\begin{bmatrix}\cos(\unknown)\\\sin(\unknown)\end{bmatrix}+ x_6\begin{bmatrix}\cos(\unknown)\\\sin(\unknown)\end{bmatrix}+ x_7\begin{bmatrix}\cos(\unknown)\\\sin(\unknown)\end{bmatrix}= \begin{bmatrix}\unknown\\\unknown\end{bmatrix} \end{уравнение*}

\begin{уравнение*} \влево x_3\begin{bmatrix}\unknown\\\unknown\end{bmatrix}+ x_4\начало{bmatrix}\неизвестно\\\неизвестно\конец{bmatrix}+ x_6\begin{bmatrix}\unknown\\\unknown\end{bmatrix}+ x_7\begin{bmatrix}\unknown\\\unknown\end{bmatrix}= \begin{bmatrix}\unknown\\\unknown\end{bmatrix} \end{уравнение*}

Подраздел A.

Слайд-шоу с заданиями доступно по адресу https://teambasedinquirylearning.github.io/linear-алгебра/2022/truss.slides.html .

Вы предприняли попытку действий на этой странице.

Элементы с двумя и тремя элементами

Двух- и трехзвенные элементы

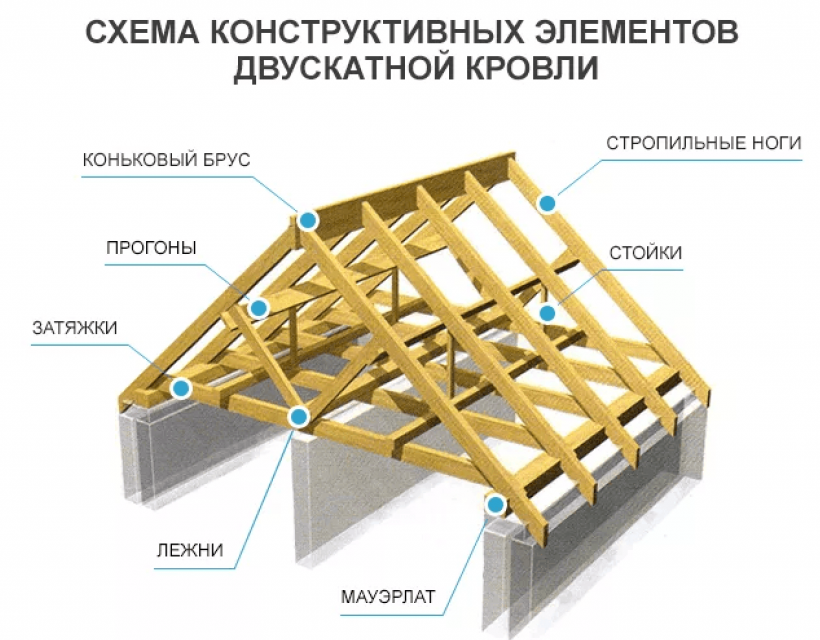
Одним из уникальных аспектов этих членов является тот факт, что линия действия равнодействующих сил, действующих на два конца элемент ДОЛЖЕН проходить вдоль осевой линии элемента конструкции. Если они не было бы, элемент не был бы в равновесии! Таким образом, даже если нагрузка существует на обоих концах и состоит только из одного из компонентов (т. е. F

Большинство, но не все члены двух отрядов натуралы. Прямые элементы обычно подвергаются либо растяжению, либо сжатию. Те члены другие геометрии будут иметь изгиб поперек (или внутри) своего сечения в дополнение на растяжение или сжатие, но принцип двух сил все еще применяется. Там НИКАКИХ ИСКЛЮЧЕНИЙ!!!

Некоторыми распространенными примерами двухсиловых элементов являются колонны, распорки, подвески, раскосы, шкворневые стропильные элементы, цепи и вантовые подвесные системы. Какие другие?

Рассмотрим простой показана система. Это упрощение указанной лампы. Нагрузка на точка F — подвесной светильник. Все соединения считаются заклепками. Если стержень BC изолирован, то видно, что на него действуют силы только при точки C и B. Это означает, что это двухсиловой член. Линия действия силы в точке С должны также проходить через точку В; аналогично, сила в точке B также должна проходить через точку C. Если бы сила в B не прошла через точку C (B’ на диаграмме), сила вызовет момент около точка С и равновесие невозможно. Поскольку две силы равные по величине, коллинеарные и противоположные по смыслу двухсиловые члены действуют только при чистом растяжении или чистом сжатии. Такие опоры, как кабели, хорошо работать как два члена отряда.

Если на тело, находящееся в равновесии, действуют три непараллельные силы, он известен как член с тремя силами .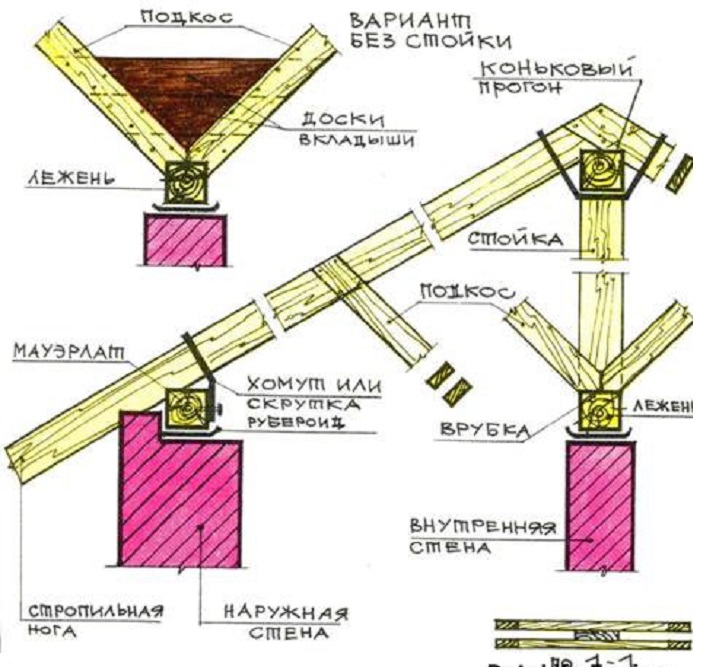 Три силы взаимодействуют с структурный элемент очень специфическим образом, чтобы поддерживать равновесие. Если элемент с тремя силами находится в равновесии и силы не параллельны, они должны быть одновременными. Следовательно, линии действия всех трех сил действующие на такой член должны пересекаться в общей точке; любая отдельная сила следовательно, уравновешивает две другие силы. Член с тремя силами часто является элементом, который имеет одну нагрузку и две реакции. Эти члены обычно имеют силы, которые вызывают изгиб, а иногда и дополнительное напряжение и сжатие. Наиболее распространенным примером члена с тремя силами является простой луч.

Пример лампы также имеет элемент с тремя усилиями как часть его конструкции. система.

Если изолировать элемент AF в штыревом соединении рамы с справа видно, что на него действуют силы в трех точках: А, С и F. Схему системы со свободным телом можно увидеть на диаграмме ниже. Величина и линия действия силы при F, 10 Кипс, известны.

Линии действия реакций в точках А и С имеют сейчас определился. Проблема установления их смысла и величины останки. Смысл этих сил может быть установлен интуитивно в этом например, но это не всегда так. Принцип трех сил , продемонстрировано шаг за шагом, покажет, как просто установить как смысл, так и величина реакций системы трех сил:

1. Нарисуйте вектор нагрузки в удобном масштабе.
   
2. Выберите любую из других сил и проведите линию, параллельную этой сила через начало вектора нагрузки.
   
3. Через хвост вектора нагрузки проведите линию, параллельную оставшейся сила. (Если эти линии простираются достаточно далеко в каждом направлении, они образуют замкнутый многоугольник).
6. Примените стрелки к векторам так, чтобы теперь они были соединены лоб в лоб. Силовой полигон завершен; стрелки показывают смысл и векторы можно масштабировать для определения величины.

Если бы предполагалось, что линия действия силы реакции, идущей через точку А взял направление, отличное от точки X, система не будет системой параллельных сил. Хотя это может быть в силовом равновесии, это не было бы моментным равновесием, потому что сумма моментов относительно ЛЮБОЙ точки больше не будет равно нулю. Это можно увидеть ниже.

Ниже приведен пример разрешения поддержки усилие для простой системы ламп.

Третий вектор силы проведен по линии действия проходит через вторую опору. Теперь смысл и направление известны. Если бы диаграмма была нарисована в масштабе, величина всех сил могла бы просто определить с помощью любого графического метода разрешения силы.

Три силы Члены

Вопросы для размышления

хммм.