От чего зависит модуль упругости: Модуль Юнга (модуль упругости): что это, таблица и формулы
Модуль Юнга (модуль упругости): что это, таблица и формулы
Модуль Юнга (модуль упругости) — это физическая величина, которая характеризует свойства какого-либо материала сгибаться или растягиваться под воздействием силы; по сути именно от этого зависит жёсткость тела.
Это свойство любого материала, и оно зависит от температуры и оказываемого давления.
В физике упругость — это свойство твёрдых материалов возвращаться в свою первоначальную форму и размер после устранения сил, которые применялись при деформации.
Другими словами: когда тело деформируется, то появляется сила, которая стремится восстановить первоначальную форму и размер тела. Сила упругости является этой проявляющейся силой. Также она представляет собой следствие электромагнитного взаимодействия между частицами.
Низкое значение модуля Юнга означает, что изучаемое твёрдое тело является эластичным.
Высокое значение модуля Юнга означает, что изучаемое твёрдое тело является

Примеры значений модуля Юнга (упругости) для:
- (т.е. для резины он в 5 раз меньше стали)
Таблица
Большинство материалов имеют значение E очень высокого порядка, поэтому они записываются при помощи «гигапаскалей» ([ГПа]; ).
| Материал | Модуль Юнга E, [ГПа] |
|---|---|
| Алмаз | 1220 |
| Алюминий | 69 |
| Дерево | 10 |
| Кадмий | 50 |
| Латунь | 97 |
| Медь | 110 |
| Никель | 207 |
| Резина | 0,9 (≈ 1 МПа, мегапаскаль) |
| Сталь | 200 |
| Титан | 107 |
Единица измерения и формулы
Единица измерения модуля Юнга в СИ — Ньютон на метр в квадрате (Н/м²), т.е. Паскаль (Па).
Формулы
Существует несколько формул, из которых можно вычислить модуль Юнга. Например, закон Гука.
Например, закон Гука.
Закон Гука
Можно вычислить модуль Юнга через эти формулы (мы это и сделаем на примере). Из-за этого закона существуют несколько интересных равенств, которые могут быть полезны для расчётов.
Закон Гука (этот описывает явления в теле, в дифференциальной форме):
Где:
- σ — механическое напряжение
- E — модуль Юнга (модуль упругости)
- ε — относительное удлинение
Закон Гука (этот описывает явления в теле)
Где:
- Fупр — сила упругости
- k × Δl — удлинение тела
Где:
- Fупр — сила упругости
- E — модуль Юнга (модуль упругости)
- S — площадь поперечного сечения
- l — первоначальная длина тела
- Δl — удлинение тела
Где:
- Fупр/S — механическое напряжение, обозначается как σ
- Δl/l — относительное удлинение, обозначается как ε
Следует заметить, что этот закон действует до той точки, когда материал необратимо деформируется и уже не возвращается в свою первоначальную форму.
Другие формулы вычисления модуля Юнга (модуля упругости)
Где:
- E — модуль Юнга (модуль упругости)
- k — жёсткость тела
- l — первоначальная длина стержня
- S — площадь поперечного сечения
Либо можно выразить k (жёсткость тела):
Где:
- k — жёсткость тела
- E — модуль Юнга (модуль упругости)
- S — площадь поперечного сечения
- l — первоначальная длина стержня/тела
Пример решения задачи (через закон Гука):
Проволока длиной 2,5 метра и площадью поперечного сечения 2,5 миллиметра² удлинилась на 1 миллиметр под действием силы 50 ньютонов. Определить модуль Юнга.
Дано:
- l = 2,5 м
- F = 50 H
- E = ?
Будем искать через закон Гука (σ = E × ε).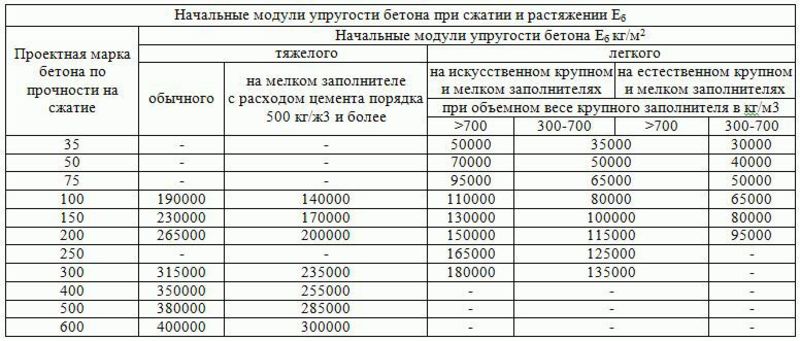
Помним из закона Гука:
σ = F / S (помните, что Fупр/S — механическое напряжение, обозначается как σ)
ε = Δl/l (а это относительное удлинение, обозначается как ε)
Подставляем в формулу (σ = E × ε):
Например, в нашей таблице такой модуль Юнга имеет кадмий.
Узнайте также про:
- Напряжённость электрического поля
- Законы Ньютона
- Закон сохранения энергии
Дата обновления 22/06/2021.
Другие значения и понятия, которые могут вас заинтересовать
- Закон сохранения энергии
- Напряженность электрического поля
- Сила Архимеда
- Сансара
- Гипербола в математике
- Законы Ньютона
- Ускорение свободного падения
- Теория относительности
- Уравнения Максвелла
- Теория вероятностей
Узнай Что Такое: узнайте значения, понятия и определения.
ПоследниеПопулярныеКонтактыПолитика КонфиденциальностиО нас
2018 — 2022 © 7Graus
Модуль упругости — что это такое? Определение модуля упругости для материалов
Модуль упругости — это физическая величина, которая характеризует упругое поведение материала при приложении к нему внешней силы в конкретном направлении. Под упругим поведением материала подразумевается его деформация в упругой области.
История исследования упругости материалов
Физическая теория упругих тел и их поведения при действии внешних сил была подробно рассмотрена и изучена английским ученым XIX века Томасом Юнгом. Однако сама концепция упругости была развита еще в 1727 году швейцарским математиком, физиком и философом Леонардом Эйлером, а первые эксперименты, связанные с модулем упругости, провел в 1782 году, то есть за 25 лет до работ Томаса Юнга, венецианский математик и философ Якопо Рикатти.
Заслуга Томаса Юнга заключается в том, что он придал теории упругости стройный современный вид, который впоследствии был оформлен в виде простого, а затем и обобщенного закона Гука.
Физическая природа упругости
Любое тело состоит из атомов, между которыми действуют силы притяжения и отталкивания. Равновесие этих сил обуславливает состояние и параметры вещества при данных условиях. Атомы твердого тела при приложении к ним незначительных внешних сил растяжения или сжатия начинают смещаться, создавая противоположную по направлению и равную по модулю силу, которая стремится вернуть атомы в начальное состояние.
В процессе такого смещения атомов энергия всей системы увеличивается. Эксперименты показывают, что при малых деформациях энергия пропорциональна квадрату величины этих деформаций. Это означает, что сила, будучи производной по энергии, оказывается пропорциональной первой степени величины деформации, то есть зависит от нее линейно. Отвечая на вопрос, что такое модуль упругости, можно сказать, что это коэффициент пропорциональности между силой, действующей на атом, и деформацией, которую эта сила вызывает. Размерность модуля Юнга совпадает с размерностью давления (Паскаль).
Предел упругости
Согласно определению, модуль упругости показывает, какое напряжение нужно приложить к твердому телу, чтобы его деформация составила 100 %. Однако все твердые тела обладают пределом упругости, который равен 1 % деформации. Это означает, что если приложить соответствующее усилие и деформировать тело на величину, меньшую 1 %, тогда после прекращения действия этого усилия тело точно восстанавливает свою первоначальную форму и размеры. При приложении слишком большого усилия, при котором величина деформации превышает 1 %, после прекращения действия внешней силы тело уже не восстановит первоначальные размеры. В последнем случае говорят о существовании остаточной деформации, которая является свидетельством превышения упругого предела данного материала.
Модуль Юнга в действии
Для определения модуля упругости, а также для понимания, как им пользоваться, можно привести простой пример с пружиной. Для этого необходимо взять металлическую пружину и измерить площадь круга, который образуют ее витки. Это делается по простой формуле S = πr², где п — число пи, равное 3,14, а r — радиус витка пружины.
Это делается по простой формуле S = πr², где п — число пи, равное 3,14, а r — радиус витка пружины.
Далее следует замерить длину пружины l0 без нагрузки. Если повесить какой-либо груз массой m1 на пружину, тогда она увеличит свою длину до некоторой величины l1. Модуль упругости E можно вычислить, исходя из знания закона Гука по формуле: E = m1gl0/(S(l1-l0)), где g — ускорение свободного падения. В данном случае отметим, что величина деформации пружины в упругой области может намного превышать 1 %.
Знание модуля Юнга позволяет предсказывать величину деформации при действии конкретного напряжения. В данном случае, если повесить на пружину другую массу m2, получим следующую величину относительной деформации: d = m2g/(SE), где d — относительная деформация в упругой области.
Изотропия и анизотропия
Модуль упругости является характеристикой материала, которая описывает силу связи между его атомами и молекулами, однако конкретный материал может иметь несколько различных модулей Юнга.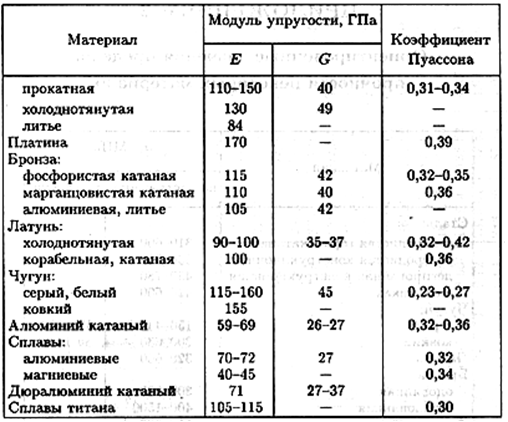
Дело в том, что свойства каждого твердого тела зависят от его внутренней структуры. Если свойства одинаковы во всех пространственных направлениях, то речь идет об изотропном материале. Такие вещества имеют однородное строение, поэтому действие внешней силы в различных направлениях на них вызывает одинаковую реакцию со стороны материала. Все аморфные материалы обладают изотропией, например, резина или стекло.
Анизотропия — явление, которое характеризуется зависимостью физических свойств твердого тела или жидкости от направления. Все металлы и сплавы на их основе обладают той или иной кристаллической решеткой, то есть упорядоченным, а не хаотичным расположением ионных остовов. Для таких материалов модуль упругости меняется в зависимости от оси действия внешнего напряжения. Например, металлы с кубической симметрией, к которым относятся алюминий, медь, серебро, тугоплавкие металлы и другие, обладают тремя различными модулями Юнга.
Модуль сдвига
Описание упругих свойств даже изотропного материала не обходится знанием одного модуля Юнга. Поскольку, помимо растяжения и сжатия, на материал можно подействовать сдвиговыми напряжениями или напряжениями кручения. В этом случае он будет реагировать на внешнее усилие иначе. Для описания упругой деформации сдвига вводят аналог модуля Юнга, модуль сдвига или модуль упругости второго рода.
Поскольку, помимо растяжения и сжатия, на материал можно подействовать сдвиговыми напряжениями или напряжениями кручения. В этом случае он будет реагировать на внешнее усилие иначе. Для описания упругой деформации сдвига вводят аналог модуля Юнга, модуль сдвига или модуль упругости второго рода.
Все материалы слабее сопротивляются сдвиговым напряжениям, чем растяжению или сжатию, поэтому значение модуля сдвига для них в 2-3 раза меньше, чем значения модуля Юнга. Так, для титана, модуль Юнга которого равен 107 ГПа, модуль сдвига составляет всего лишь 40 ГПа, для стали эти цифры имеют значения 210 ГПа и 80 ГПа, соответственно.
Модуль упругости дерева
Дерево относится к анизотропным материалам, поскольку древесные волокна ориентированы вдоль конкретного направления. Именно вдоль волокон измеряют модуль упругости древесины, поскольку поперек волокон он меньше на 1-2 порядка. Знание модуля Юнга для дерева играет важную роль и учитывается при проектировании конструкций из деревянных панелей.
Значения модуля упругости древесины для некоторых видов деревьев приведены в таблице ниже.
| Вид дерева | Модуль Юнга в ГПа |
| Лавровое дерево | 14 |
| Эвкалипт | 18 |
| Кедр | 8 |
| Ель | 11 |
| Сосна | 10 |
| Дуб | 12 |
Следует отметить, что приведенные значения могут отличаться на величину порядка 1 ГПа для конкретного дерева, поскольку на его модуль Юнга влияет плотность древесины и условия произрастания.
Модули сдвига для различных пород деревьев находятся в пределах 1-2 ГПа, например, для сосны это 1,21 ГПа, а для дуба 1,38 ГПа, то есть древесина практически не сопротивляется сдвиговым напряжениям. Данный факт должен учитываться при изготовлении деревянных несущих конструкций, которые проектируют так, чтобы они работали только на растяжение или сжатие.
Характеристики упругости металлов
Если сравнивать с модулем Юнга древесины, то средние значения этой величины для металлов и сплавов на порядок больше, что показано в следующей таблице.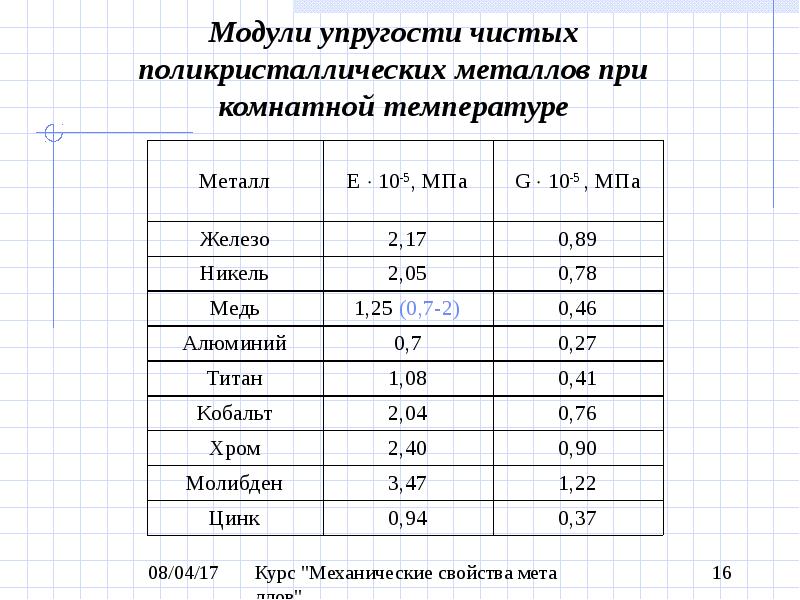
| Металл | Модуль Юнга в ГПа |
| Бронза | 120 |
| Медь | 110 |
| Сталь | 210 |
| Титан | 107 |
| Никель | 204 |
Упругие свойства металлов, которые имеют кубическую сингонию, описываются тремя упругими постоянными. К таким металлам относятся медь, никель, алюминий, железо. Если металл имеет гексагональную сингонию, тогда для описания его упругих характеристик уже необходимо шесть постоянных.
Для металлических систем модуль Юнга измеряют в пределах 0,2 % деформации, поскольку большие значения могут происходить уже в неупругой области.
Единицы модуля упругости (модуль Юнга)
Прежде чем углубиться в изучение различных типов и единиц модуля упругости (модуль Юнга), давайте сначала рассмотрим широкое определение этого очень важного механического свойства. .
Основное определение модуля упругости
Также известный как модуль упругости, модуль упругости представляет собой измеренное значение, которое представляет сопротивление материала упругой деформации, т. е. его «растяжимость». Это относится только к непостоянной деформации под действием напряжения.
е. его «растяжимость». Это относится только к непостоянной деформации под действием напряжения.
Модуль упругости определяется градиентом кривой напряжения-деформации в области, где она упруго деформируется (см. ниже – линейный участок перед «пределом текучести»). Менее эластичный (или более жесткий ) материал имеет сравнительно высокий модуль упругости, тогда как эластичный или упругий материал имеет более низкий модуль упругости.
Модуль упругости часто обозначается греческим символом лямбда, λ. Он принимает форму напряжения, деленного на деформацию, таким образом:
λ= напряжение/деформация- Напряжение определяется как сила, вызывающая деформацию, деленная на площадь воздействия.
- Деформация определяется как смещение частиц вещества относительно определенной длины.
Типы модуля упругости
Существует 3 основных типа модуля упругости:
- Модуль Юнга
- Модуль сдвига
- Объемный модуль
Это модули упругости, наиболее часто используемые в технике. Давайте рассмотрим каждый тип и то, как их можно использовать, прежде чем мы перейдем к единицам модуля упругости.
Давайте рассмотрим каждый тип и то, как их можно использовать, прежде чем мы перейдем к единицам модуля упругости.
Модуль Юнга
Именно его имеет в виду большинство людей, когда говорят «модуль упругости». Он описывает степень деформации материала вдоль заданной оси при приложении растягивающих усилий, также известную как эластичность при растяжении. Его можно описать простыми словами как меру жесткости.
Модуль Юнга можно упростить как тенденцию вещества становиться длиннее и тоньше.
Определяется как напряжение растяжения, деленное на деформацию растяжения (или отношение напряжения к деформации), и в расчетах обозначается буквой E.
Основным применением модуля Юнга является предсказание растяжения, которое может произойти при растяжении, или укорочения, которое может произойти при сжатии. Это полезно, например, при проектировании балок или колонн в строительстве.
- Подробнее о модуле Юнга
Модуль сдвига
Модуль сдвига материала является мерой его жесткости. Он используется, когда сила, параллельная данной оси, встречает противодействующую силу, например трение. Его можно упростить как тенденцию вещества изменяться от прямоугольной формы до параллелограмма.
Он используется, когда сила, параллельная данной оси, встречает противодействующую силу, например трение. Его можно упростить как тенденцию вещества изменяться от прямоугольной формы до параллелограмма.
Модуль сдвига определяется как отношение напряжения сдвига к деформации сдвига и обозначается символами G, S или µ.
Модуль сдвига чаще всего используется в расчетах, в которых участвуют два материала, находящихся в контакте и подверженных действию противоположных сил, т. е. трению друг о друга.
- Подробнее о модуле сдвига
Модуль объемного сжатия
Модуль объемного сжатия представляет собой термодинамическое свойство, определяющее устойчивость вещества к сжатию. Его можно упростить как тенденцию изменения объема вещества при неизменной форме.
Определяется как отношение увеличения давления к уменьшению относительного объема. Обозначается символами К или В.
Чаще всего используется при изучении свойств жидкостей при сжатии.
- Подробнее о модуле объемного сжатия
Как измеряется модуль упругости?
В этом разделе мы сосредоточимся на модуле Юнга, так как он чаще всего ассоциируется с эластичностью.
Наиболее распространенными методами измерения являются испытание на растяжение, испытание на изгиб или испытание на вибрацию собственной частоты. Методы испытаний на изгиб и растяжение основаны на применении закона Гука и называются статическими методами. Использование собственной частоты обеспечивает динамический модуль упругости, поскольку испытание проводится с использованием вибраций.
Статические методы осуществляются путем приложения измеримых параллельных или перпендикулярных сил и регистрации изменения длины или величины деформации. Используются точные устройства для измерения очень малых длин, известные как «экстензометры» или механические тензодатчики.
Единицы модуля упругости
Единицы модуля упругости – это единицы давления, поскольку он определяется как напряжение (единицы давления), деленное на деформацию (безразмерную). Чаще всего единицами измерения являются паскали (Па), которые являются единицей СИ, или фунты на квадратный дюйм (psi) в зависимости от отрасли или географического положения. В Европе наиболее распространена Па, в США более распространена единица измерения модуля упругости в фунтах на квадратный дюйм.
Чаще всего единицами измерения являются паскали (Па), которые являются единицей СИ, или фунты на квадратный дюйм (psi) в зависимости от отрасли или географического положения. В Европе наиболее распространена Па, в США более распространена единица измерения модуля упругости в фунтах на квадратный дюйм.
Ниже приведены некоторые примеры значений модуля упругости (модуля Юнга) материалов:
- Алмаз имеет высокий модуль Юнга 1050-1200 ГПа, поскольку он очень жесткий.
- Карбин имеет самый высокий из известных модулей Юнга 32 100 ГПа, что означает, что это наименее эластичный или самый жесткий материал, известный на данный момент.
Модуль упругости Единицы измерения и формула
Напряжение, деформация и модуль Юнга
Модуль Юнга (Е) определяется как отношение напряжения, приложенного к материалу вдоль продольной оси испытываемого образца, и деформации или деформации, измеренной по той же оси.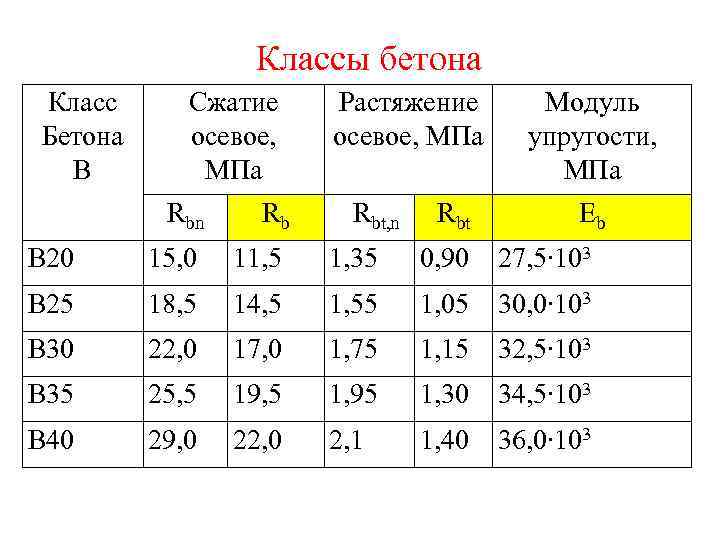 Модуль Юнга также известен как модуль упругости, модуль упругости или модуль упругости, а его единицей СИ является Паскаль (Па).
Модуль Юнга также известен как модуль упругости, модуль упругости или модуль упругости, а его единицей СИ является Паскаль (Па).
Когда к объекту прикладывается растягивающая сила (сила растяжения), он растягивается, и его поведение можно получить с помощью кривой напряжения-деформации в области упругой деформации (известной как закон Гука). Расширение, создаваемое силой, зависит не только от материала, но и от других факторов, таких как размеры объекта (например, длина, толщина и т. д.)
Напряжение определяется как усилие на единицу площади пластика и имеет единицы Нм -2 или Па.
σ (напряжение) = F/A
Где σ — напряжение (в ньютонах на квадратный метр или, что то же самое, в паскалях), F — сила (в ньютонах, обычно сокращенно обозначается Н), а A — площадь поперечного сечения образца.
Хотя, Штамм определяется как удлинение на единицу длины. И, поскольку это отношение длин, деформация не имеет единиц измерения.
ε (деформация) = ΔL/L 0 ; ΔL = L-L 0
где L 0 — первоначальная длина растягиваемого стержня, а L — его длина после растяжения. ΔL — удлинение стержня, разница между этими двумя длинами.
Используя измерения напряжения растяжения и деформации растяжения, жесткость различных материалов сравнивается с модулем Юнга, E . Е постоянна и не меняется для данного материала. Формула модуля упругости :
E = напряжение/деформация = σ/ε
Чем больше значение модуля Юнга, тем жестче материал
Единицы модуля упругости/модуля Юнга : Нм -2 или Па.
Практические единицы, используемые в пластмассах, — это мегапаскали (МПа или Н/мм 2 ) или гигапаскали (ГПа или кН/мм 2 ). В обычных единицах измерения в Соединенных Штатах это часто выражается в фунтах (сила) на квадратный дюйм (psi).
Посмотреть все полимеры и эластомеры с высокой прочностью на растяжение »
Области применения включают:
Модуль упругости является важным механическим свойством для выбора материалов, проектирования изделий и анализа характеристик в ряде инженерных, а также медицинских применений .
- Используется для выбора материалов для различных целей с учетом того, как они будут реагировать на различные виды сил
- В помощь процессу проектирования
- Чтобы снизить материальные затраты, определите качество партии и стабильность производства
Узнайте больше о модуле Юнга:
» Как рассчитать модуль Юнга пластика
» Факторы, влияющие на модуль упругости
» Значения модуля Юнга нескольких пластиков
Как рассчитать модуль упругости?
Как правило, «методы испытаний на растяжение» применяются для измерения модуля упругости материалов. Используемые общие методы:
Используемые общие методы:
- ASTM D638 — Стандартный метод испытаний свойств пластмасс на растяжение
- ISO 527-1:2012 — Определение свойств при растяжении. Общие принципы
Конечно, помимо перечисленных ниже, существует еще несколько методов, но они здесь не обсуждаются.
Методы испытаний ASTM D638 и ISO 527
Методы испытаний ASTM D638 и ISO 527 охватывают определение свойств при растяжении пластиков и пластиковых композитов в определенных условиях в форме стандартных испытательных образцов гантелевидной формы. Определенные условия могут варьироваться от предварительной обработки, температуры, влажности до скорости испытательной машины.
Методы используются для исследования поведения испытательных образцов при растяжении.
По результатам испытаний на растяжение можно сделать следующие расчеты:
Для ASTM D638 скорость испытания определяется спецификацией материала. Для ISO 527 скорость испытания обычно составляет 5 или 50 мм/мин для измерения прочности и удлинения и 1 мм/мин для измерения модуля.
Для ISO 527 скорость испытания обычно составляет 5 или 50 мм/мин для измерения прочности и удлинения и 1 мм/мин для измерения модуля.
Экстензометр используется для определения удлинения и модуля упругости.
Посмотрите интересное видео, показывающее метод проверки модуля упругости (Источник: ADMET Testing Systems)
Факторы, влияющие на модуль Юнга
Модуль тесно связан с энергиями связи атомов . Силы связи и, следовательно, модуль упругости обычно выше для материалов с высокой температурой плавления. Модуль Юнга действительно зависит от ориентации монокристаллического материала.
Силы связи и, следовательно, модуль упругости обычно выше для материалов с высокой температурой плавления. Модуль Юнга действительно зависит от ориентации монокристаллического материала.
Более высокая температура в материале увеличивает атомную вибрацию, что, в свою очередь, уменьшает энергию, необходимую для дальнейшего разделения атомов друг от друга (и, таким образом, обычно уменьшает напряжение, необходимое для создания данной деформации).
Наличие примесных атомов , легирующих атомов, неметаллических включений, частиц вторичной фазы, дислокаций (смещений или несоответствий в структуре решетки), дефектов (трещин, границ зерен и т.п.). Все эти вещи могут служить как для ослабления, так и для укрепления материала.
— Все, что препятствует движению дислокаций через решетку, будет иметь тенденцию к увеличению модуля и, следовательно, предела текучести.
— Все, что способствует движению дислокаций (например, повышение температуры) или создает локальные концентраторы напряжений (например, трещины, включения и т. д.), будет иметь тенденцию к снижению прочности (например, способствуя раннему началу разрушения).
д.), будет иметь тенденцию к снижению прочности (например, способствуя раннему началу разрушения).
Вдохновляйтесь: предотвратите выход из строя пластмассовых компонентов, выяснив 3 основные причины и предприняв корректирующие действия с самого начала.
Модуль упругости пластмасс намного меньше, чем у металлов или керамики и стекла. Например:
- Модуль упругости нейлона составляет 2,7 ГПа (0,4 x 10 6 фунтов на кв. дюйм)
- Модуль стекловолокна составляет 72 ГПа (10,5 x 10 6 фунтов на кв. дюйм)
- Модуль Юнга композитов, таких как композиты, армированные стекловолокном (GFRC) или композиты, армированные углеродным волокном (CFRC), находится между значениями для матричного полимера и волокнистой фазы (углеродных или стеклянных волокон) и зависит от их относительные объемные доли.
Марки полимеров с высокой прочностью на растяжение
Ознакомьтесь с широким ассортиментом полимеров с высокой прочностью на растяжение, проанализируйте технические характеристики каждого продукта, получите техническую поддержку или запросите образцы.
Значения модуля упругости некоторых пластиков
Нажмите, чтобы найти полимер, который вы ищете:
A-C |
Э-М |
ПА-ПК |
ПЭ-ПЛ |
ПМ-ПП |
PS-X

 00
00 12
12 10
10 10
10 20
20 00
00 20
20 50
50 30
30 00
00 00
00 00
00