От чего зависит модуль упругости: Модуль упругости (модуль Юнга)
Модуль Юнга (модуль упругости): что это, таблица и формулы
Модуль Юнга (модуль упругости) — это физическая величина, которая характеризует свойства какого-либо материала сгибаться или растягиваться под воздействием силы; по сути именно от этого зависит жёсткость тела.
Это свойство любого материала, и оно зависит от температуры и оказываемого давления.
В физике упругость — это свойство твёрдых материалов возвращаться в свою первоначальную форму и размер после устранения сил, которые применялись при деформации.
Другими словами: когда тело деформируется, то появляется сила, которая стремится восстановить первоначальную форму и размер тела. Сила упругости является этой проявляющейся силой. Также она представляет собой следствие электромагнитного взаимодействия между частицами.
Низкое значение модуля Юнга означает, что изучаемое твёрдое тело является эластичным.
Высокое значение модуля Юнга означает, что изучаемое твёрдое тело является 
Примеры значений модуля Юнга (упругости) для:
- (т.е. для резины он в 5 раз меньше стали)
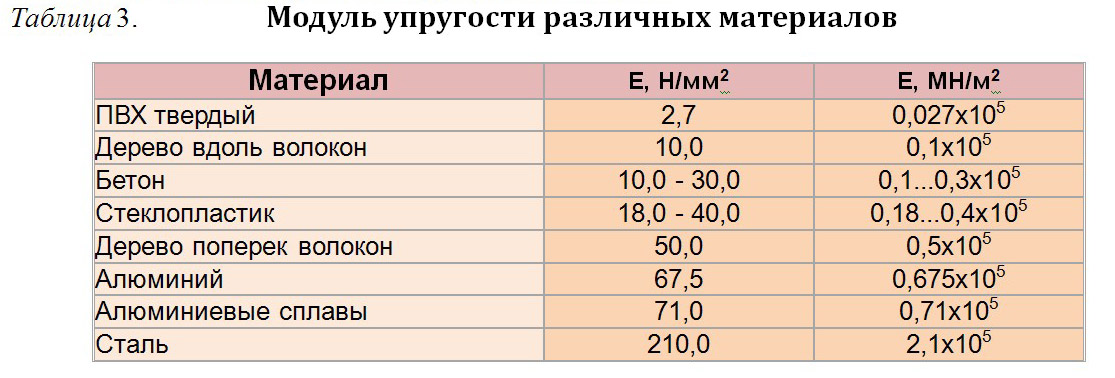
Таблица
Большинство материалов имеют значение E очень высокого порядка, поэтому они записываются при помощи «гигапаскалей» ([ГПа]; ).
| Материал | Модуль Юнга E, [ГПа] |
|---|---|
| Алмаз | 1220 |
| Алюминий | 69 |
| Дерево | 10 |
| Кадмий | 50 |
| Латунь | 97 |
| Медь | 110 |
| Никель | 207 |
| Резина | 0,9 (≈ 1 МПа, мегапаскаль) |
| Сталь | 200 |
| Титан | 107 |
Единица измерения и формулы
Единица измерения модуля Юнга в СИ — Ньютон на метр в квадрате (Н/м²), т.е. Паскаль (Па).
Формулы
Существует несколько формул, из которых можно вычислить модуль Юнга. Например, закон Гука.
Например, закон Гука.
Закон Гука
Можно вычислить модуль Юнга через эти формулы (мы это и сделаем на примере). Из-за этого закона существуют несколько интересных равенств, которые могут быть полезны для расчётов.
Закон Гука (этот описывает явления в теле, в дифференциальной форме):
Где:
- σ — механическое напряжение
- E — модуль Юнга (модуль упругости)
- ε — относительное удлинение
Закон Гука (этот описывает явления в теле)
Где:
- Fупр — сила упругости
- k × Δl — удлинение тела
Где:
- Fупр — сила упругости
- E — модуль Юнга (модуль упругости)
- S — площадь поперечного сечения
- l — первоначальная длина тела
- Δl — удлинение тела
Где:
- Fупр/S — механическое напряжение, обозначается как σ
- Δl/l — относительное удлинение, обозначается как ε
Следует заметить, что этот закон действует до той точки, когда материал необратимо деформируется и уже не возвращается в свою первоначальную форму.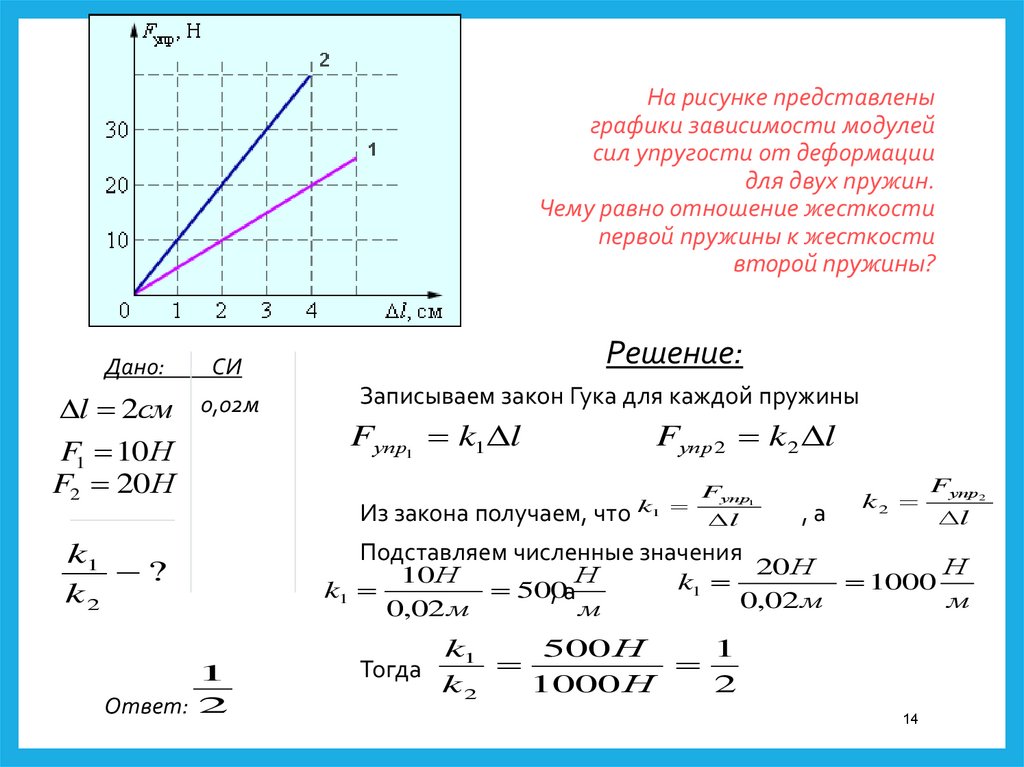
Другие формулы вычисления модуля Юнга (модуля упругости)
Где:
- E — модуль Юнга (модуль упругости)
- k — жёсткость тела
- l — первоначальная длина стержня
- S — площадь поперечного сечения
Либо можно выразить k (жёсткость тела):
Где:
- k — жёсткость тела
- E — модуль Юнга (модуль упругости)
- S — площадь поперечного сечения
- l — первоначальная длина стержня/тела
Пример решения задачи (через закон Гука):
Проволока длиной 2,5 метра и площадью поперечного сечения 2,5 миллиметра² удлинилась на 1 миллиметр под действием силы 50 ньютонов. Определить модуль Юнга.
Дано:
- l = 2,5 м
- F = 50 H
- E = ?
Будем искать через закон Гука (σ = E × ε).
Помним из закона Гука:
σ = F / S (помните, что Fупр/S — механическое напряжение, обозначается как σ)
ε = Δl/l (а это относительное удлинение, обозначается как ε)
Подставляем в формулу (σ = E × ε):
Например, в нашей таблице такой модуль Юнга имеет кадмий.
Узнайте также про:
- Напряжённость электрического поля
- Законы Ньютона
- Закон сохранения энергии
Дата обновления 22/06/2021.
Другие значения и понятия, которые могут вас заинтересовать
- Закон сохранения энергии
- Напряженность электрического поля
- Сила Архимеда
- Сансара
- Гипербола в математике
- Законы Ньютона
- Ускорение свободного падения
- Теория относительности
- Уравнения Максвелла
- Теория вероятностей
Узнай Что Такое: узнайте значения, понятия и определения.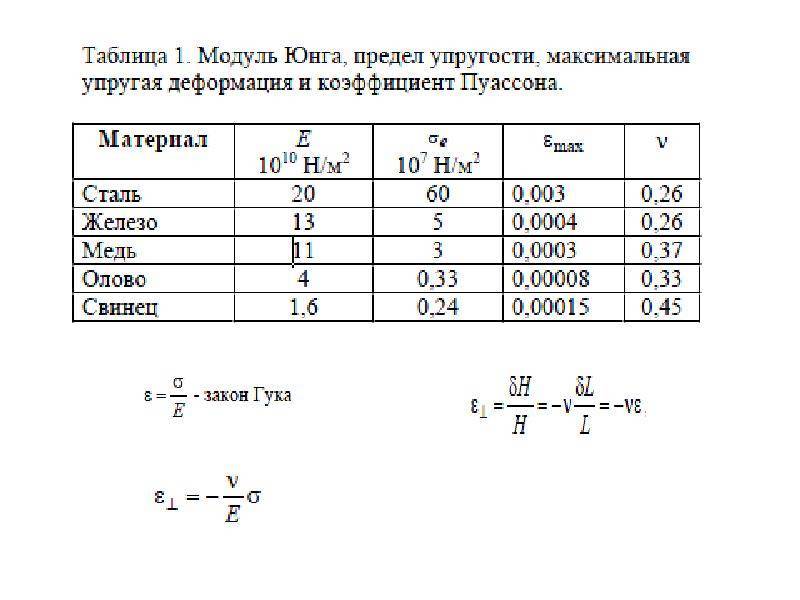
ПоследниеПопулярныеКонтактыПолитика КонфиденциальностиО нас
2018 — 2023 © 7Graus
Модуль упругости стали и формулы его расчета
О чем речь? Модуль упругости стали требуется при проектировании стальных изделий и элементов конструкций. Он показывает стойкость материала к разнонаправленным нагрузкам. Это одна из важнейших характеристик металла.
Как определять? Показатель рассчитывается по определенной формуле и зависит от вида стали и добавок в нее. Помимо этого, для расчетов используются специальные нормативы и практические испытания материала. Требуются точные вычисления, так как в противном случае изделию грозит деформация, способная привести к его разрушению.
Вопросы, рассмотренные в материале:
- Формула модуля упругости стали
- Типы модулей упругости стали
- Особенности модуля упругости стали
- Определение модуля упругости стали
- Другие коэффициенты для оценки свойств стали
Формула модуля упругости стали
Инженерное проектирование является направлением в сфере строительства, призванным решить целый ряд задач. Так, возведению любых объектов предшествует подготовка проекта. На данном этапе необходимо провести расчеты, чтобы подобрать оптимальное сечение профиля стальных конструкций и избежать разрушения готового здания.
Так, возведению любых объектов предшествует подготовка проекта. На данном этапе необходимо провести расчеты, чтобы подобрать оптимальное сечение профиля стальных конструкций и избежать разрушения готового здания.
Важным показателем, обеспечивающим прочность будущего объекта, считается модуль упругости стали. Его использование в расчетах позволяет защитить здание от преждевременных деформаций металлопроката. Сила упругости проявляется при деформации тела – она стремится восстановить его прежние размеры и форму и является следствием электромагнитного взаимодействия атомов и молекул.
Благодаря модулю упругости как физической величине (Е) описывают упругую сопротивляемость материала изделия приложенным нагрузкам. В случае с модулем упругости стали и других материалов нагрузки могут быть:
- продольные – растягивающие и сжимающие;
- объемные или скручивающие.

Данный показатель принято измерять в паскалях, мегапаскалях (МПа) и кгс/см2. От его значения напрямую зависит сопротивляемость материала нагрузкам, прочность предмета и предел разрушения. Так, у стали модуль упругости равен до 220 ГПа, у алюминия он находится на уровне в 70 ГПа, у чугуна – 120 ГПа, железа – 190 ГПа.
Для его вычисления используют формулу: E= σ / ε, где σ – напряжение, соответствующее силе, поделенной на площадь ее воздействия; ε – упругая деформация, определяемая как отношение удлинения образца с начала деформации к сжатию при завершении воздействия.
Рекомендуем статьи
- Титан и его сплавы: свойства, применение
- Сплавы черных металлов: классификация и особенности производства
- Плавление латуни в различных условиях
Коэффициент E иначе обозначают как модуль Юнга в честь Томаса Юнга, английского физика XIX века. Модуль Юнга определяется свойствами материала, тогда как размеры и форма объекта не оказывают на него влияния.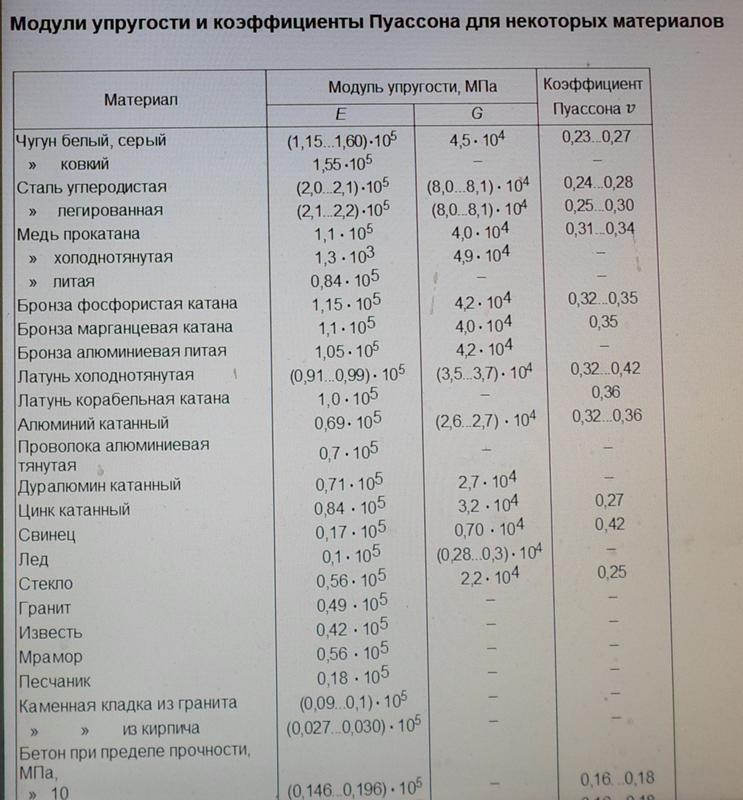 Показатель меняется в широких пределах в зависимости от конкретного материала. Допустим, у стали он равен ≈ 2·1011 Н/м2, а для резины он в пять раз меньше ≈ 2·106 Н/м2.
Показатель меняется в широких пределах в зависимости от конкретного материала. Допустим, у стали он равен ≈ 2·1011 Н/м2, а для резины он в пять раз меньше ≈ 2·106 Н/м2.
Напряжение измеряется в паскалях, а раз деформация считается безразмерной величиной, то Е принято указывать в паскалях.
Существует альтернативное определение, согласно которому модуль упругости представляет собой напряжение, которое достаточно, чтобы увеличить длину образца вдвое. Для подавляющего числа материалов эта формулировка является неточной. Дело в том, что данное значение значительно больше предела текучести материала или значения, когда удлинение делается нелинейным, но при этом оказывается более интуитивным.
Типы модулей упругости стали
Есть множество способов изменения напряжения и деформации, в том числе применение различных направлений действия силы. В связи с этим существует большое количество типов модулей упругости, среди которых основными считаются:
- Модуль Юнга, обозначаемый символом E.
 Является показателем сопротивления материала растяжению или сжатию при упругой деформации. Характеризует способность предмета деформироваться вдоль оси под действием силы, приложенной вдоль данной оси. Определяется как отношение напряжения к деформации сжатия или удлинения. Нередко данный модуль обозначают просто как модуль упругости.
Является показателем сопротивления материала растяжению или сжатию при упругой деформации. Характеризует способность предмета деформироваться вдоль оси под действием силы, приложенной вдоль данной оси. Определяется как отношение напряжения к деформации сжатия или удлинения. Нередко данный модуль обозначают просто как модуль упругости. - Модуль сдвига или модуль жесткости. Обозначается символом G и описывает способность материала сопротивляться изменению формы при сохранении объема. Вычисляется как отношение напряжения сдвига к деформации сдвига. Последнюю определяют как изменение прямого угла между плоскостями, по которым действуют касательные напряжения. Модуль сдвига входит в число составляющих вязкости.
- Модуль объемной упругости или объемного сжатия. Для его обозначения используют символ K. Показатель позволяет определить способность объекта изменять объем под воздействием всестороннего нормального напряжения (объемного), которое является одинаковым по всем направлениям.

Допустим, такое напряжение может появляться под действием гидростатического давления. Данный модуль вычисляется как отношение величины объемного напряжения к величине относительного объемного сжатия. K отличается от E и G тем, что для невязкой жидкости он не равен нулю, а для несжимаемой жидкости – бесконечен.
Это далеко не весь перечень модулей упругости, также существуют коэффициент Пуассона, параметры Ламе.
Описанная методика определения показателя применяется при вычислении Е для:
- стальных изделий;
- медных предметов;
- прочих упругих образцов.
Особенности модуля упругости стали
Сталь является прочным материалом с высоким модулем упругости. Самые высокие показатели устойчивости к воздействиям имеют стальные сплавы с измененной кристаллической решеткой. Они отличаются значительным пределом текучести, определяемым опытным путем.
Особенности упругого поведения стальных изделий зависят от того, насколько сложны связи в кристаллической решетке. Решетка формируется в соответствии с типом материала – легирующей сталью. Благодаря наличию углерода решетка становится более твердой, но избыточное количество данного компонента негативно сказывается на пластичности и пружинистых свойствах сплава, влияет на значение модуля упругости стали. Не допустить подобного эффекта удается за счет внесения легирующих добавок, к которым относятся:
Решетка формируется в соответствии с типом материала – легирующей сталью. Благодаря наличию углерода решетка становится более твердой, но избыточное количество данного компонента негативно сказывается на пластичности и пружинистых свойствах сплава, влияет на значение модуля упругости стали. Не допустить подобного эффекта удается за счет внесения легирующих добавок, к которым относятся:
- кремний;
- никель;
- вольфрам;
- марганец.
Хотя указанные элементы повышают упругость, не всегда с их помощью можно обеспечить требуемый результат. Тогда прибегают к термообработке, поскольку под влиянием температуры свойства стали меняются: пропадают слабые участки, выравнивается показатель текучести отдельных фрагментов.
На данный момент существует свыше нескольких сотен марок стали, каждая из которых имеет свои свойства. Далее приведены популярные марки стали и соответствующий им модуль упругости E:
Низкоуглеродистая
В пределах 180
Ст3
В пределах 189
Ст10
В пределах 192
Ст45
В пределах 223
Ст40Х
В пределах 260
65Г
В пределах 275
Х12МФ
В пределах 320
9ХС
В пределах 302
ХВГ
В пределах 302
4Х5МФС
В пределах 315
3Х3М3Ф
В пределах 310
Р6М5
В пределах 320
Р9
В пределах 330
Р18
В пределах 340
Р12МФ5
В пределах 310
У7
В пределах 315
У8
В пределах 315
У9
В пределах 330
У10
В пределах 330
У11
В пределах 340
У12
В пределах 315
У13
В пределах 315
Модуль упругости не относится к постоянным величинам, так как зависит от места воздействия нагрузки. Правда, для некоторых материалов, например, стали 3 или 10 первого и второго рода, алюминия, меди, показатель сохраняется при растяжении и сжатии. Для разных марок стали модуль упругости отличается незначительно. По этой причине в процессе подготовки проекта E округляют, а подобные погрешности не учитывают.
Правда, для некоторых материалов, например, стали 3 или 10 первого и второго рода, алюминия, меди, показатель сохраняется при растяжении и сжатии. Для разных марок стали модуль упругости отличается незначительно. По этой причине в процессе подготовки проекта E округляют, а подобные погрешности не учитывают.
Определение модуля упругости стали
Хотя твердые тела справляются с воздействием больших нагрузок, однако как только достигнуты определенные значения, они меняют форму и резко разрушаются. Чтобы определить момент, в который появятся трещины, разрыв, узнают модуль упругости стали посредством простых испытаний.
Госстандарты предлагают несколько возможных видов лабораторных исследований материала:
- нагружение в течение продолжительного периода времени;
- быстрые и длительные удары;
- воздействие на растягивание и сжатие;
- давление посредством гидравлики.
По модулю упругости стали удается понять, насколько жесткой и устойчивой будет оставаться конструкция, когда на нее будут воздействовать определенные нагрузки.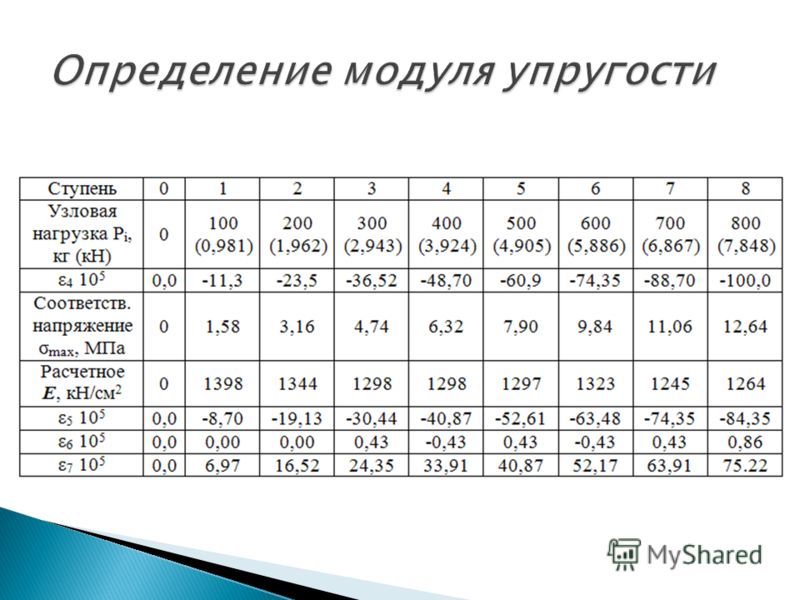
Чтобы узнать приблизительный показатель, прибегают к детальному изучению, выведению диаграммы напряжений. Для этого во время испытаний образец на специальных установках медленно растягивают до определенного предела. После этого результаты нормальных и относительных напряжений делят – итоговый показатель и является искомой величиной.
Модуль упругости ряда материалов содержится в нормативных документах. Так, определить его для конкретной марки стали можно, используя специальные таблицы, которые входят в состав нормативных документов в области строительства. Речь идет о строительных нормах и правилах (СНиП) и государственных стандартах (ГОСТ), указывающих искомые модули упругости стали.
Так, модуль упругости Юнга для белого и серого чугуна составляет 115–160 ГПа, а для ковкого находится на уровне 155. Модуль упругости углеродистой стали С245 может быть 200–210 ГПа. У легированной он немного выше: 210–220 ГПа. Для рядовых марок стали Ст. 3 и Ст.5 он равен 210 ГПа, а сталь Ст.45, 25Г2С и 30ХГС имеет показатель 200 ГПа.
3 и Ст.5 он равен 210 ГПа, а сталь Ст.45, 25Г2С и 30ХГС имеет показатель 200 ГПа.
Получается, у различных марок стали модуль упругости мало отличается, чего нельзя сказать о готовых изделиях. Рассмотрим в качестве примера аналогичный показатель для канатов:
- пряди и свивки проволоки, обладающие высокой прочностью – 200 ГПа;
- стальные тросы, имеющие металлический стержень – 150 ГПа;
- стальные канаты, в которых предусмотрен органический сердечник – 130 ГПа.
Модуль сдвига или жесткости (G) обычно имеет меньшие значения, которые указываются в тех же таблицах. Для прокатной стали этот модуль составляет 84 ГПа, для углеродистой и легированной 80-81 ГПа, а для типов стали Ст.3 и Ст.45 – 80 ГПа.
Значения параметра упругости отличаются, поскольку наблюдается одновременное действие сразу трех основных модулей – каждый из них вычисляют отдельным методом. При этом разница небольшая, а значит, можно считать, что достигается достаточно высокая точность определения упругости. Нет смысла концентрироваться только на вычислениях и формулах – разумнее принять за константу конкретную величину упругости.
Нет смысла концентрироваться только на вычислениях и формулах – разумнее принять за константу конкретную величину упругости.
Комплексный расчет вместо вычисления по отдельным модулям позволяет получить значение Е = 200 ГПа. Показатель будет отличаться в зависимости от присадок, использованных в стали, а также особенностей изделия, например, наличия элементов из других веществ. Однако разница окажется невелика. Модуль упругости стали зависит в первую очередь от доли углерода. Тогда как задействованный способ обработки, то есть горячий прокат либо холодная штамповка, мало воздействует на показатель.
Выбирая стальные изделия, важно опираться также на расчетное сопротивление растягивающим, сжимающим и изгибающим нагрузкам. Данный показатель регламентируется наравне с модулем упругости стали и других материалов таблицами ГОСТов и СНиПов. Он имеет аналогичную размерность, что и модуль упругости, но его значения на три порядка меньше.
Для показателя принимают во внимание расчетное и нормативное сопротивление. Первое необходимо для выполнения расчетов прочности конструкций. Например, для стали С255 при толщине проката 10–20 мм оно составляет 240 МПа, тогда как нормативное находится на уровне 245 МПа. Для проката 20–30 мм расчетное сопротивление равно 230 МПа.
Первое необходимо для выполнения расчетов прочности конструкций. Например, для стали С255 при толщине проката 10–20 мм оно составляет 240 МПа, тогда как нормативное находится на уровне 245 МПа. Для проката 20–30 мм расчетное сопротивление равно 230 МПа.
Другие коэффициенты для оценки свойств стали
Благодаря модулю упругости удается заранее понять, как различные типы стали и другие материалы будут вести себя в определенной ситуации. Однако с его помощью нельзя определить, как изменится вещество в иных обстоятельствах. Чтобы расчеты были более эффективны, прибегают к следующим показателям:
- Коэффициент жесткости – свидетельствует об уровне пластичности материала, исчисляется в килограмм-силах (кгс).
- Относительное продольное удлинение – измеряется в процентах. Формула для его вычисления предполагает учет длины образца и ее абсолютное изменение.
- Относительное поперечное удлинение – определяется по аналогии с предыдущим показателем с тем отличием, что для расчетов нужна не длина, а диаметр.

- Коэффициент Пуассона – представляет собой соотношение продольного относительного удлинения к поперечному. Позволяет определить, каким образом изменится форма заготовки в зависимости от разных значений силы и мест ее приложения.
- Модуль сдвига – свидетельствует о поведении упругих материалов, подвергаемых воздействию усилий по касательной. Показатель необходим, чтобы оценить воздействие ветра с перпендикулярным направлением и предельной величиной усилия.
- Модуль объемной упругости – демонстрирует изменение объема тела в случае равномерного, но при этом разностороннего приложения усилий.
Определить возможности применения стали позволяет предел упругости, исчисляемый в паскалях. По нему можно понять напряжение, которое вызовет разрушение, необратимую деформацию изделия.
При подготовке проекта конструкций важно использовать минимум два разных модуля упругости стали. Опираясь на коэффициент жесткости, проектировщик получает возможность перейти к другим видам сопротивления внешнему воздействию: упругости при изгибе и объемной упругости.
Строительство любого объекта предполагает использование набора конструкторских расчетов и грамотный подбор материалов в соответствии с их прочностью. Обеспечить безопасность зданий можно лишь при наличии у проектировщиков наиболее полных представлений о процессах, протекающих внутри материалов.
Модуль Юнга | Описание, пример и факты
Модуль Юнга
См. все СМИ
- Связанные темы:
- модуль упругости
См. все связанные материалы →
Модуль Юнга , числовая константа, названная в честь английского врача и физика 18-го века Томаса Юнга, которая описывает упругие свойства твердого тела, подвергающегося растяжению или сжатию только в одном направлении, как в случае металлический стержень, который после растяжения или сжатия в продольном направлении возвращается к своей первоначальной длине. Модуль Юнга — это мера способности материала выдерживать изменения длины при продольном растяжении или сжатии. Иногда его называют модулем упругости. Модуль Юнга равен продольному напряжению, деленному на деформацию. Напряжение и деформация могут быть описаны следующим образом в случае металлического стержня под напряжением.
Иногда его называют модулем упругости. Модуль Юнга равен продольному напряжению, деленному на деформацию. Напряжение и деформация могут быть описаны следующим образом в случае металлического стержня под напряжением.
Если металлический стержень с площадью поперечного сечения A тянуть с силой F за каждый конец, стержень растягивается от своей первоначальной длины L 0 до новой длины L n . (Одновременно уменьшается поперечное сечение.) Напряжение представляет собой отношение силы растяжения к площади поперечного сечения, или F / A . Деформация или относительная деформация – это изменение длины, L n − L 0 , деленное на исходную длину, или ( L n − L 0 0 1 ) 25 0
Модуль Юнга = напряжение/деформация = ( FL 0 )/ A ( L — 0 ).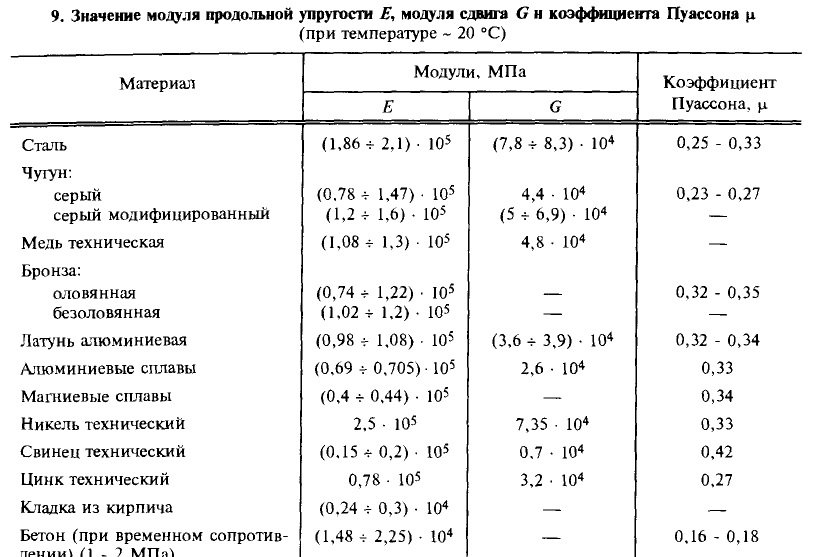
Это конкретная форма закона упругости Гука. Единицами модуля Юнга в английской системе являются фунты на квадратный дюйм (psi), а в метрической системе — ньютоны на квадратный метр (Н/м 2 ). Значение модуля Юнга для алюминия составляет около 1,0 × 10 7 фунтов на квадратный дюйм или 7,0 × 10 10 Н/м 2 . Значение для стали примерно в три раза больше, а это означает, что требуется в три раза больше силы, чтобы растянуть стальной стержень на ту же величину, что и алюминиевый стержень аналогичной формы.
Модуль Юнга имеет смысл только в диапазоне, в котором напряжение пропорционально деформации, и материал возвращается к своим первоначальным размерам при снятии внешней силы. По мере увеличения напряжений материал может либо течь, подвергаясь остаточной деформации, либо окончательно разрушаться.
Когда металлический стержень под напряжением удлиняется, его ширина немного уменьшается. Эта боковая усадка представляет собой поперечную деформацию, равную изменению ширины, деленному на первоначальную ширину. Отношение поперечной деформации к продольной называется коэффициентом Пуассона. Среднее значение коэффициента Пуассона для сталей равно 0,28, для алюминиевых сплавов — 0,33. Объем материалов с коэффициентом Пуассона менее 0,50 увеличивается при продольном растяжении и уменьшается при продольном сжатии.
Отношение поперечной деформации к продольной называется коэффициентом Пуассона. Среднее значение коэффициента Пуассона для сталей равно 0,28, для алюминиевых сплавов — 0,33. Объем материалов с коэффициентом Пуассона менее 0,50 увеличивается при продольном растяжении и уменьшается при продольном сжатии.
Оформите подписку Britannica Premium и получите доступ к эксклюзивному контенту. Подпишитесь сейчас
Редакция Британской энциклопедии Эта статья была недавно пересмотрена и обновлена Эриком Грегерсеном.
Физика — модуль Юнга — Бирмингемский университет
Одним из самых важных тестов в технике является знание того, когда объект или материал будет изгибаться или ломаться, и свойство, которое говорит нам об этом, — модуль Юнга. Это мера того, насколько легко материал растягивается и деформируется.
Введение | Видео | В фокусе | Заключение | Следующие шаги |
Согнется или сломается?
Провода подчиняются закону Гука, как и пружины.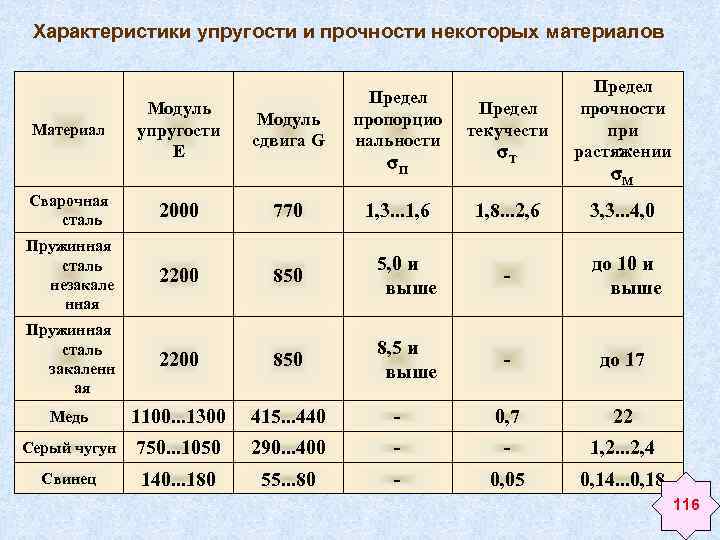 Когда приложена сила F , она удлинится на некоторое расстояние x , что можно просто описать уравнением F = kx
Когда приложена сила F , она удлинится на некоторое расстояние x , что можно просто описать уравнением F = kx
В то время как k для пружины — это жесткость пружины, степень удлинения проволоки зависит от ее площади поперечного сечения, длины и материала, из которого она изготовлена. Модуль Юнга ( E ) — это свойство материала, которое говорит нам, насколько легко он может растягиваться и деформироваться, и определяется как отношение растягивающего напряжения ( σ ) к деформации растяжения ( ε ). Где напряжение — это количество силы, приложенной к единице площади ( σ = F/A ), а деформация — удлинение на единицу длины ( ε = дл/л ).
Поскольку сила F = мг , мы можем получить модуль Юнга проволоки, измерив изменение длины ( dl ) при приложении гирь массой м (при условии, что г = 9,81 метра на секунда в квадрате).
Относится ли модуль Юнга к исследованиям?
Имеет ли модуль Юнга отношение к исследованиям?
Что важно знать?
Для разных типов материалов графики напряжения-деформации могут выглядеть очень по-разному. Хрупкие материалы, как правило, очень прочные, потому что они могут выдерживать большие нагрузки, они не сильно растягиваются и могут внезапно сломаться. Пластичные материалы имеют большую область упругости, где зависимость между напряжением и деформацией является линейной, но при первом обороте (предел упругости) линейность нарушается, и материал больше не может вернуться к своей первоначальной форме. Второй пик — это предел прочности при растяжении, и он говорит нам о максимальном напряжении, которое материал может выдержать до разрыва. Пластмассовые материалы не очень прочные, но выдерживают большую нагрузку. Модуль Юнга задается градиентом линии на графике напряжения-деформации.
В эксперименте, показанном на видео выше, мы измерили модуль Юнга медной проволоки, которая не сильно растягивается. Таким образом, можно использовать реперный маркер, например, ленту, чтобы определить исходную и увеличенную длину. Выполнение многократных измерений с различными массами увеличит количество точек на графике напряжения-деформации и сделает расчет модуля Юнга более надежным. Еще одна вещь, о которой нужно позаботиться, — это измерение площади поперечного сечения провода. Дефекты проволоки могут означать, что диаметр не является абсолютно постоянным по всей ее длине, поэтому может помочь среднее значение нескольких показаний микрометра.
Таким образом, можно использовать реперный маркер, например, ленту, чтобы определить исходную и увеличенную длину. Выполнение многократных измерений с различными массами увеличит количество точек на графике напряжения-деформации и сделает расчет модуля Юнга более надежным. Еще одна вещь, о которой нужно позаботиться, — это измерение площади поперечного сечения провода. Дефекты проволоки могут означать, что диаметр не является абсолютно постоянным по всей ее длине, поэтому может помочь среднее значение нескольких показаний микрометра.
Как это применимо ко мне?
Изучение механических свойств материалов важно, потому что оно помогает нам понять, как ведут себя материалы, и позволяет нам разрабатывать новые продукты и улучшать существующие. В качестве примера темы исследования в Бирмингеме рассматривалась разработка шестов для прыжков, используемых спортсменами, занимающимися прыжками в высоту, для достижения максимальной производительности. Эти шесты должны быть легкими, чтобы обеспечить быстрый разбег, но также должны сохранять энергию упругой деформации при изгибе шеста. Шест должен преобразовывать энергию упругости в кинетическую энергию по мере выпрямления шеста и быть в состоянии выдерживать нагрузку, вызванную весом прыгуна, а также выдерживать многократное использование спортсменом.
Шест должен преобразовывать энергию упругости в кинетическую энергию по мере выпрямления шеста и быть в состоянии выдерживать нагрузку, вызванную весом прыгуна, а также выдерживать многократное использование спортсменом.
В небольших масштабах существует множество продуктов, содержащих биологические (например, фармацевтические препараты, препараты для лечения бесплодия, тканевая инженерия) и небиологические микрочастицы (например, химикаты, сельское хозяйство, товары для дома). Благодаря пониманию их механических свойств мы можем прогнозировать их поведение при производстве и обработке, максимизировать их эксплуатационные возможности.
Модуль Юнга материала полезно знать, чтобы предсказать поведение материала под действием силы. Это важно практически для всего, что нас окружает, от зданий до мостов, транспортных средств и многого другого.
Следующие шаги
Эти ссылки предоставляются для удобства и только в информационных целях; они не являются подтверждением или одобрением Бирмингемским университетом какой-либо информации, содержащейся на внешнем веб-сайте.


 Является показателем сопротивления материала растяжению или сжатию при упругой деформации. Характеризует способность предмета деформироваться вдоль оси под действием силы, приложенной вдоль данной оси. Определяется как отношение напряжения к деформации сжатия или удлинения. Нередко данный модуль обозначают просто как модуль упругости.
Является показателем сопротивления материала растяжению или сжатию при упругой деформации. Характеризует способность предмета деформироваться вдоль оси под действием силы, приложенной вдоль данной оси. Определяется как отношение напряжения к деформации сжатия или удлинения. Нередко данный модуль обозначают просто как модуль упругости.