Онлайн расчет арматуры для ленточного фундамента: Калькулятор ленточного фундамента
Калькулятор ленточного фундамента, расчет онлайн монолита
Тип фундамента
Марка бетона
М100 (В7,5) М150 (В10)М200 (В15)М250 (В20)М300 (В22.5)М350 (В25)М400 (В30)М450 (В35)М500 (В40)М550 (В45)М600 (В50)М700 (В55)М800 (В60)
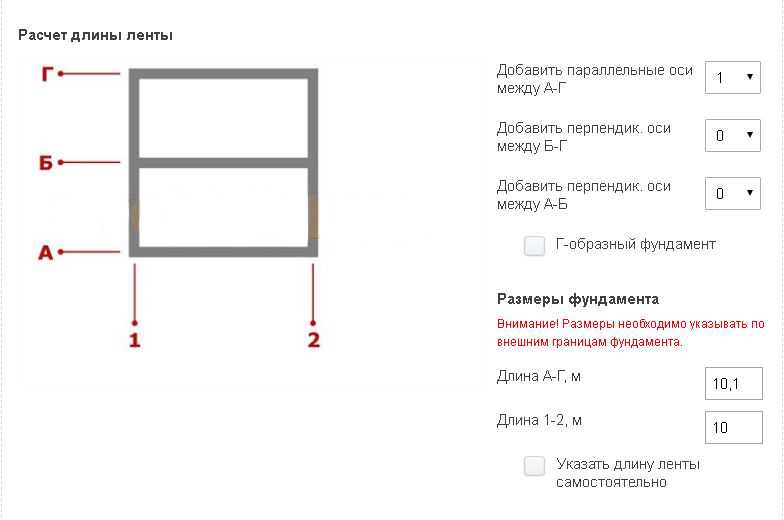
Длина А
Длина B
Длина C
Длина D
Высота E
Ширина F
Схема фундамента
Расчет арматуры
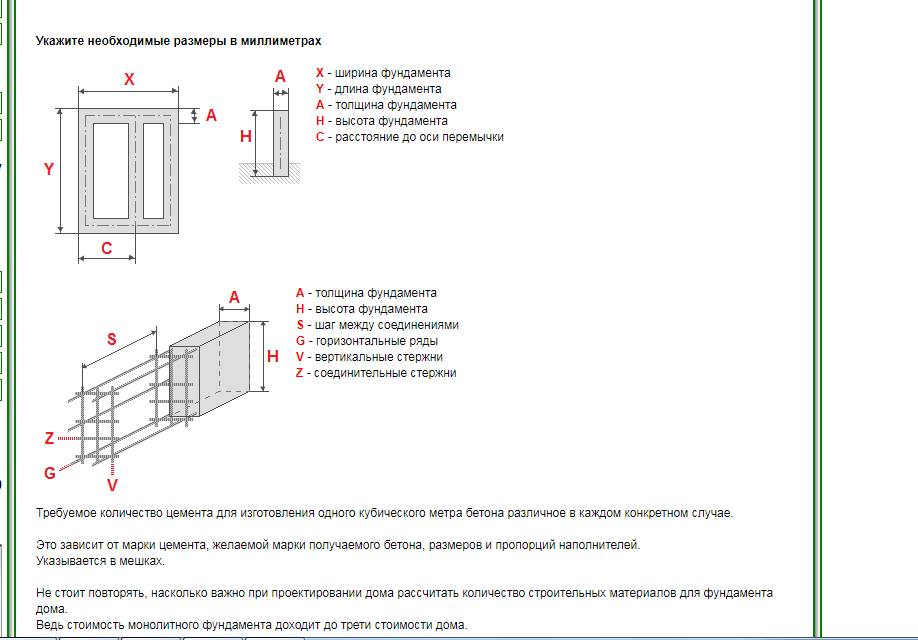
Бетонная подготовка
ДаНет
Длина стержня арматуры
Площадь сечения арматуры (μs min)
0. 050.10.150.20.250.30.350.4
%
050.10.150.20.250.30.350.4
%
Каркас арматуры
СварнойВязаный
[an error occurred while processing the directive]Расчет опалубки
Ширина доски
Длина доски
Толщина доски
Алгоритм расчета и конструирования ленточного фундамента построен на основе нормативных документов:
- СНиП 52-101-2003 «Бетонные и железобетонные конструкции»;
- СНиП 3.03.01-87 «Несущие и ограждающие конструкции»;
- ГОСТ Р 52086-2003 «Опалубка, термины и определения».
Формулы расчета ленточного фундамента и методика разработаны согласно «приложения рекомендаций по расчету железобетонных конструкций»
Данный калькулятор предназначен для базового расчета монолитной ленты, как мелкозаглубленной, так и классической и не подходит для расчета сборных и блочных фундаментов.
Онлайн калькулятор позволяет произвести предварительный расчет:
- Необходимого объема бетона для заливки фундамента;
- Конструкцию, размеры, требуемый метраж конструктивной и рабочей арматуры;
- Материал для опалубки и рекомендации по шагу установки опор.
Арматура ленточного фундамента (75) | Помощь пользователям Tekla
Арматура ленточного фундамента (75) создает арматуру для бетонного ленточного фундамента.
Бары созданы
Использовать для
Не использовать для
Фундаменты, имеющие:
Прежде чем начать
Порядок выбора
Выберите бетон ленточный фундамент.

Используйте Вкладка «Изображение» для определения толщины защитного слоя бетона и хомута компенсировать.
Толщина покрытия
| Описание | |
|---|---|
1 | Толщина покрытия (концы полосы) |
2 | Смещение хомута |
3 | Толщина покрытия (сверху и снизу) |
Используйте вкладку Основные стержни, чтобы определить свойства верхней,
нижняя, левая и правая полосы.
Длина соединения основных стержней
Длина связи определяет, насколько стержни проходят в соседние конструкции на концах ленточных фундаментов. Использовать Длина скрепления 1 коробка для первого конца фундамента (с желтой ручкой), и ящики Bond length 2 для второй конец основания (с пурпурной ручкой).
Длину связи можно определить отдельно для:
Используйте Вкладка «Хомуты» для определения свойств хомутов и расстояния между ними. тип.
Колено
Выберите расположение хомута нахлесты в ленточном фундаменте.
Размеры хомута
| Описание | |
|---|---|
1 | Толщина крышки (боковины) |
2 | Внешнее расстояние между основными стержнями и внешними боковыми стержнями |
3 | Длина перехлеста двойного хомута |
Длина нахлеста двойных U-образных стержней |
Направление изгиба
Опция | |
|---|---|
1 | |
2 | |
3 | |
4 |
Наконечник двойного хомута бары
Если вы выбрали двойное стремя
стержней, вы можете выбрать концевые формы для стержней из списка.
Опция | Примеры |
|---|---|
135 градусов По умолчанию | |
90 градусов | |
Перекрываются Если вы выберете
перекрываются, вы можете ввести длину перекрытия. |
Используйте Вкладка «Атрибуты» для определения свойств нумерации стержней и стремена.
Опция | Описание |
|---|---|
Префикс | Префикс для номера позиции детали. |
Стартовый номер | Начальный номер для номера позиции детали. |
Имя | Tekla Structures использует это имя на чертежах и в отчетах. |
Класс | Использовать Класс к групповому подкреплению. Например, вы можете отображать арматуру разных классов разными цветами. |
Реакция грунтового основания в гибких фундаментах
Введение
Когда фундамент не является жестким, распределение напряжений и модуль реакции грунтового основания зависят от его жесткость на изгиб .
Из-за гибкости фундамента осадки грунта неравномерны и достигают своего максимального значения в центре фундаментной плиты. Если фундамент очень гибкий, напряжения в его краях могут стать равными нулю.
Если фундамент очень гибкий, напряжения в его краях могут стать равными нулю.
Как правило, максимальный изгибающий момент, который испытывает гибкий фундамент, значительно ниже, чем у жесткого фундамента.
Рис. 1: Деформация (преувеличенно) и распределение реакции грунтового основания для гибкого основания, основанного на слое грунта. Реакцию грунтового основания можно определить с помощью:- Модель Winkler , в которой субстрат заменен системой конечных, дискретных, линейных упругих пружин. Эти пружины характеризуются жесткостью или модулем реакции грунтового основания k .
- Аналитические решения для балки бесконечной длины с использованием теории бесконечных балок на упругом основании .
Определение жесткости фундамента
Очень редко структурный фундамент бывает либо полностью жестким, либо гибким, а скорее существуют промежуточные условия, которые необходимо принимать во внимание. Согласно Хетеньи (1946), для количественной оценки жесткости фундамента с учетом свойств слоя грунта безразмерный параметр ( λ ) должен быть рассчитан как:
где: Модель Винклера (ее расчет будет представлен ниже)
 Для ленточного фундамента с определенной высотой H , I=BH 3 /12
Для ленточного фундамента с определенной высотой H , I=BH 3 /12 В зависимости от значения параметра 4 λ 9038 модель реакции грунтового основания может быть выбрана следующим образом:
- λ < π/4 → фундамент можно считать жестким; поэтому реакция грунтового основания рассчитывается с использованием решений для жестких фундаментов.
- π/4 < λ <π → Жесткость фундамента средняя. Его нельзя охарактеризовать ни как жесткое, ни как гибкое. Распределение напряжения определяется с использованием модели Винклера .
- λ > π → Фундамент гибкий. Реакцию грунтового основания можно определить либо с помощью модели Винклера, либо с помощью аналитических решений для ленточных фундаментов бесконечной длины.
Фундаменты средней жесткости
Для фундаментов средней жесткости модуль реакции грунтового основания сначала рассчитывается по следующей формуле (Vesic, 1961):
где:
- E : модуль упругости грунта
5 90 : коэффициент Пуассона грунта
Затем выводится параметр λ , чтобы определить, действительно ли фундамент имеет промежуточную жесткость ( Уравнение 1 ).
Если π/4, реакция грунтового основания оценивается с использованием метода Винклера с производным модулем k .
Расчет проводится путем решения дифференциального уравнения равновесия балки на основании Винклера: балка (м), E b – модуль упругости балки (МПа), I — момент инерции балки (m 4 ), y — деформация пружины в заданной точке (м).
Податливые фундаменты
При использовании податливых фундаментов методика остается прежней. Модуль реакции грунтового основания рассчитывается по уравнению 2 , а затем выводится параметр λ .
В этом случае λ > π , поэтому либо используется модель Винклера, представленная выше, либо можно предположить, что фундамент имеет бесконечную длину, и, таким образом, можно использовать аналитические решения с помощью теории «бесконечных балок» на эластичная основа.
Сосредоточенная точечная нагрузка на фундамент бесконечной длины
На основе аналитических решений осадки фундамента и силы его сечения выводятся как функция расстояния точки от сосредоточенной нагрузки P , как показано на рис. 2 .
2 .
где:
Сосредоточенный момент на бесконечно длинном основании
Тот же принцип применяется в случае сосредоточенного момента, действующего на определенную точку бесконечного основания . Осадки и силы сечения также получаются как функция расстояния точки от сосредоточенного момента Μ , как показано на рис. 3 .
Рисунок 3: Диаграммы осадки, изгибающего момента и поперечной силы, полученные с помощью аналитического решения для сосредоточенного момента M на бесконечно гибком основании.Результирующие осадка, изгибающий момент и поперечная сила в определенной точке x определяются с помощью следующих уравнений:
Сложные условия нагрузки на фундамент бесконечной длины
нагрузки (сосредоточенные нагрузки и моментные нагрузки), может использоваться принцип суперпозиции, и каждая нагрузка должна учитываться отдельно, как показано в примере ниже.
Пример расчета
Ленточная балка укладывается на слой грунта. В этом примере рассчитываются силы осадки и сечения, которые будут развиваться.
На основе характеристик фундамента и свойств грунта будет определена относительная жесткость фундамента и грунта, чтобы определить, какой метод будет использоваться.
Структурные свойства фундамента и упругие свойства грунта представлены в Таблица 1 и Таблица 2 соответственно.
Таблица 1: Структурно-геометрические характеристики ленточно-балочного фундамента
Таблица 2: Упругие свойства слоя грунта , как:
Параметры λ и λ’ затем выводятся с использованием уравнений 1 и 7 , as:
В результате фундамент можно считать гибким. Поэтому будут использоваться аналитические решения, вытекающие из теории бесконечных балок на упругом основании.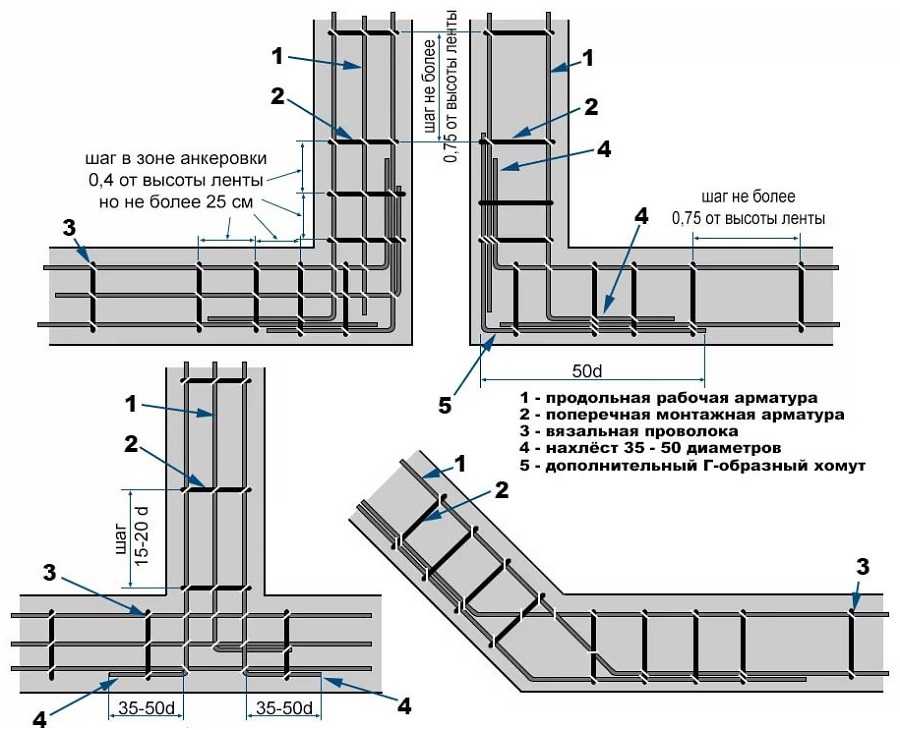
В этом примере расчета предполагается, что на фундамент действуют как вертикальная, так и моментная нагрузка ( рис. 4 ). Поэтому будет использован анализ комплексных нагрузок, действующих на определенную точку.
Рисунок 4: Вертикальная и изгибающая нагрузка, действующая на фундамент бесконечной длины. Приняты следующие значения нагрузки: подвергается множественным нагрузкам, используется принцип суперпозиции, и каждое условие нагрузки учитывается отдельно.В обоих случаях осадка, изгибающий момент и поперечная сила будут получены для центральной точки фундамента (x=0).
Сначала будет проанализировано влияние вертикальной нагрузки P . С помощью уравнений 4 — 6 определяются следующие значения: изгибающий момент и поперечная сила, определяется векторная сумма каждого расчетного значения. Особое внимание следует уделить центральной точке, поскольку знак (положительный или отрицательный) сил и моментов сечения изменяется, как показано в 9.