Объем колонны формула: Онлайн калькулятор: Объем геометрических фигур
Онлайн калькулятор: Объем геометрических фигур
Данная статья содержит калькуляторы для расчета объема различных геометрических фигур. Основной источник формул: Spiegel, Murray R. Mathematical Handbook of Formulas and Tables. Schaum’s Outline series in Mathematics. McGraw-Hill Book Co., 1968.
Объем куба
Размеры куба
Формула:
Объем куба
Длина ребра куба (H)
Точность вычисленияЗнаков после запятой: 5
save Сохранить extension Виджет
Объем прямоугольной призмы
Размеры прямоугольной призмы
Формула:
Объем прямоугольной призмы
Точность вычисленияЗнаков после запятой: 5
save Сохранить extension Виджет
Объем пирамиды
Размеры пирамиды
Формула:
Объем пирамиды
Площадь основания
Точность вычисленияЗнаков после запятой: 5
save Сохранить extension Виджет
Объем усеченной пирамиды
Размеры усеченной пирамиды
Формула:
Объем усеченной пирамиды
Точность вычисленияЗнаков после запятой: 5
пример решения задачи — OneKu
Содержание статьи:Объем является физической величиной, которая присуща телу с ненулевыми размерами вдоль каждого из трех направлений пространства (все реальные объекты). В статье в качестве примера формулы объема рассматривается соответствующее выражение для цилиндра.
Объем тел
Эта физическая величина показывает, какую часть пространства занимает то или иное тело. Например, объем Солнца намного больше этой величины для нашей планеты. Это означает, что принадлежащее Солнцу пространство, в котором находится вещество этой звезды (плазма), превышает земную пространственную область.
Вам будет интересно:Система — это… Значение слова «система»
Объем изменяется в кубических единицах длины, в СИ это метры в кубе (м3). На практике объемы жидких тел измеряют в литрах. Маленькие объемы могут выражать в кубических сантиметрах, миллилитрах и других единицах.
Для вычисления объема формула будет зависеть от геометрических особенностей рассматриваемого объекта. Например, для куба это тройное произведение длины его ребер. Ниже рассмотрим фигуру цилиндр и ответим на вопрос о том, как найти объем его.
Понятие о цилиндре
Фигура, о которой пойдет речь, является достаточно непростой. Согласно геометрическому определению, она представляет собой поверхность, образованную путем параллельного перемещения прямой (генератрисы) вдоль некоторой кривой (директрисы). Генератриса также называется образующей, а директриса — направляющей.
Если директриса — это окружность, а генератриса перпендикулярна ей, тогда полученный цилиндр называют круглым и прямым. О нем и пойдет дальше речь.
Цилиндр имеет два основания, которые параллельны друг другу и соединены цилиндрической поверхностью. Проходящая через центры двух оснований прямая называется осью круглого цилиндра. Все точки фигуры находятся на одинаковом расстоянии от этой прямой, которое равно радиусу основания.
Круглый прямой цилиндр однозначно определяется двумя параметрами: радиусом основания (R) и расстоянием между основаниями — высота H.
Формула объема цилиндра
Для расчета области пространства, которую занимает цилиндр, достаточно знать его высоту H и радиус основания R. Искомое равенство в этом случае имеет вид:
V = pi*R2*H, здесь pi = 3,1416
Понять эту формулу объема просто: поскольку высота перпендикулярна основаниям, то если ее умножить на площадь одного из них, получается нужная величина V.
Вычисление объема бочки
Для примера решим такую задачу: определим, сколько воды поместится в бочку, имеющую диаметр дна 50 см и высоту 1 метр.
Радиус бочки равен R=D/2=50/2=25 см. Подставляем данные в формулу, получаем:
V = pi*R2*H = 3,1416*252*100 = 196350 см3
Поскольку 1 л = 1 дм3 = 1000 см3, то получаем:
V = 196350/1000 = 196,35 литра.
То есть в бочку можно налить почти 200 литров воды.
Источник
Объем скважины формула: как рассчитать объем
Для заполнения паспорта изготовленной скважины используются расчетные данные источника. Например, определение объема скважины по формуле, учитывающей параметры насоса, дает возможность найти ее дебит. Эта величина, характеризующая производительность источника, позволяет узнать, способен ли он отдать на поверхность нужное количество воды.

Формула вычисления объема.
Расчет объема скважины и коммуникационного средства
Вычислить этот показатель можно по формуле:
V=πR²H,
где R — радиус внутреннего сечения обсадной трубы, а Н — высота столба воды. Поскольку эта величина для источника не является определяющей, пользуются значением дебита — главной характеристики скважин на воду.
Однако при добыче нефти и газа стволы имеют большие размеры и сложную конфигурацию. Глубина такого устройства достигает 3 км и больше. При подходе к нефтяному (газовому) горизонту для предотвращения выброса среды на поверхность скважину глушат с помощью растворов или пресной воды. Чтобы правильно рассчитать необходимое количество жидкости, нужно знать объем ствола устройства.
В связи с тем, что по высоте колонны ее диаметр неодинаков и уменьшается с глубиной, рассчитывают емкость каждого интервала изготовления шахты.
Если скважина имеет 3 участка с разными размерами, то общий объем будет равен:
Vскв=Va+Vb+Vc,
где Va, Vb, Vc — объемы соответствующих участков.

Еще одна формула вычисления объема.
Обсадные колонны, укрепляющие стенки колодца, уменьшают его емкость, что отражается на количестве жидкости необходимой для глушения.
Объем коммуникационного устройства определяется по формуле:
Vку=Vд-Vв,
где Vд — объем участка ствола, рассчитанный по диаметру долотом, а Vв — вычисленный по внутреннему диаметру обсадной колонны. Зная эти величины, можно рассчитать количество раствора для глушения на каждом интервале сверления.
Расчет объема технологических отходов бурения для скважины
Наиболее опасными видами отходов при изготовлении шахты скважины считаются отработанный промывочный раствор и буровой шлам или выбуренная порода. Они учитываются при расчете потерь промывочного раствора в процессе его очистки.
Величина технологических отходов на искомом интервале изготовления шахты вычисляется по формуле:
Vпр=0,785(αDв)²Lи,
где: Dв — внутренний диаметр обсадной трубы, опускаемой для крепления участка бурения; Lи — длина интервала бурения; α — коэффициент кавернозности породы в зоне бурения.
Данные рассчитываются для каждого участка ствола, пробуренного долотом своего диаметра. Среди значений емкости колонны на рассчитываемом интервале сверления выбирают большее. Эта величина используется для определения количества бурового раствора на каждом участке по формуле:
Vосв=kVскв,
где Vскв — максимальный объем участка бурения; k — коэффициент, учитывающий запас промывочной жидкости.
Эти величины нужны для расчета запаса технологического раствора, требуемого для безопасного проведения работ по освоению геологоразведочных либо ремонта действующих скважи.

Объем полого цилиндра
Объем полого цилиндра, формулы для вычисления объема и площадей правильного полого цилиндра.
Формула вычисления объема полого цилиндра часто применяются при расчете массы полой круглой трубы. Для вычисления массы трубы, необходимо вычисленный объем трубы (полого цилиндра) умножить на плотность материала из которого изготовлена труба (цилиндр).
Расчет площади поверхностей цилиндра, иногда необходим для определения расхода материала для нанесения защитного покрытия трубы (полого цилиндра).
Объем полого цилиндра, вычисленный через внутренний и наружный радиусы
r1 — внешний радиус
r2 — внутренний радиус
h — высота цилиндра
… вычисление …
Площадь основания… вычисление …
Площадь внутренней и внешней боковой поверхности… вычисление …
Общая площадь… вычисление …
Объем полого цилиндра по толщине стенки и наружному диаметру
D — внешний диаметр
δ — толщина стенки
h — высота цилиндра
… вычисление …
Площадь основания… вычисление …
Площадь внутренней и внешней боковой поверхности… вычисление …
Общая площадь поверностей… вычисление …
Объем полого цилиндра, вычисляемый по внутреннему диаметру и толщине стенки
d — внутренний диаметр
δ — толщина стенки
h — высота цилиндра
… вычисление …
Упрощение формулы:
Площадь основания… вычисление …
Упрощение формулы:
Общая площадь поверностей
… вычисление …
Различия между разными видами цилиндров, а также со свойствами правильного цилиндра, можно ознакомиться в статье «Объем цилиндра» в разделе« Теория».
Объем и площадь других видов цилиндров рассмотрен в статьях:
Объем цилиндра
Объем части цилиндра
Объем части полого цилиндра
Вы можете скачать формулы объема и площади поверхностей правильного полого цилиндра в виде картинки.
скачать скачать скачать скачать скачать скачатьГеометрические фигуры ℹ️ формулы вычисления объема всех фигур и многогранников, обозначения и единицы измерения величины
Объём — это аддитивная функция от множества (мера), характеризующая вместимость области пространства, которую оно занимает. Изначально возникло и применялось без строгого определения в отношении тел трёхмерного евклидова пространства. Первые точные определения были даны Пеано (1887) и Жорданом (1892). Впоследствии понятие было обобщено Лебегом на более широкий класс множеств.Для определения объёма существует несколько существенно различных подходов, которые дополняют друг друга и согласованы по конечному результату на «хороших множествах». Обычно под понятием объёма понимается мера Жордана, но иногда мера Лебега. Для римановых многообразий понятие объёма вводится аналогично понятию площади поверхности.
Все формулы объема геометрических тел
Объем куба
Объем куба равен кубу длины его грани.
Формула объема куба:
V = a 3
где:
V — объем куба,a — длина грани куба.
Объем призмы
Объем призмы равен произведению площади основания призмы, на высоту.
Формула объема призмы:
где:
V- объем призмы,
So — площадь основания призмы,
h — высота призмы.
Объем параллелепипеда
Объем параллелепипеда равен произведению площади основания на высоту.
Формула объема параллелепипеда:
где:
V- объем параллелепипеда,
So — площадь основания,
h — длина высоты.
Объем пирамиды
Объем пирамиды равен одной трети произведения площади основания S (ABCDE) на высоту h (OS).
Формула объема пирамиды:
где:
V — объем пирамиды,
So — площадь основания пирамиды,
h — длина высоты пирамиды.
Объем усеченной пирамиды
Объем усеченной пирамиды равен одной трети произведения высоты h (OS) на сумму площадей верхнего основания S1(abcde), нижнего основания усеченной пирамиды S2 (ABCDE) и средней пропорциональной между ними.
Формула объема усеченной пирамиды:
Где:
S1 — площадь верхнего основания усеченной пирамиды,
S2 — площадь нижнего основания усеченной пирамиды,
h — высота усеченной пирамиды.
Объем цилиндра
Объем цилиндра равен произведению площади его основания на высоту.
Формула объема цилиндра:
V= π R2 h
V= Sоh
Где:
V — объем цилиндра,
So — площадь основания цилиндра,
R — радиус цилиндра,
h — высота цилиндра,
π = 3.141592
Объем правильной треугольной пирамиды
Объем правильной треугольной пирамиды равен одной трети произведения площади правильного треугольника, являющегося основанием S (ABC) на высоту h (OS).Формула объема правильной треугольной пирамиды:
Где:
V — объем пирамиды;
h — высота пирамиды;
a — сторона основания пирамиды.
Объем конуса
Объем круглого конуса равен трети произведения площади основания S на высоту H.
Формула объема конуса:
Где:
V — объем конуса;
R — радиус основания;
H — высота конуса;
I — длина образующей;
S — площадь боковой поверхности конуса.
Объем усеченного конуса
Объем усеченного конуса равен разности объемов двух полных конусов.
Формула объема усеченного конуса:
Где:
V — объем усеченного конуса;
H — высота усеченного конуса;
R и R2 — радиусы нижнего и верхнего оснований.
Объем тетраэдра
Объем тетраэдра рассчитывается по классической формуле объема пирамиды. В нее нужно подставить высоту тетраэдра и площадь правильного (равностороннего) треугольника.Формула тетраэдра:
Где:
V — объем тетраэдра;
a — ребро тетраэдра.
Объем шара
Объем шара равен четырем третьим от его радиуса в кубе перемноженного на число пи.Формула объема шара:
Где:
V — объем шара;
R — радиус шара;
S — площадь сферы.
Объем шарового сегмента и сектора
Шаровый сегмент — это часть шара отсеченная плоскостью. В данном примере, плоскостью ABCD.
Формула объема шарового сегмента:
Где:
R — радиус шара
H — высота сегмента
π ≈ 3,14
Формула объема шарового сектора:
Где:
h — высота сегмента
R — радиус шара
π ≈ 3,14
Объем прямоугольного параллелепипеда
Объем прямоугольного параллелепипеда равен произведению его длины, ширины и высоты.
Формула объема прямоугольного параллелепипеда:
Где:
V — объем прямоугольного параллелепипеда,
a — длина,
b — ширина,
h — высота.
Объем части полусферы, отрезанной под углом
Калькулятор вычисляет объем части полусферы, полученной путем сечения полусферы плоскостью, проходящей на заданном расстоянии от центра полусферы под заданным углом.
Угол может быть в пределах (0..180) градусов.Расстояние h не должно превышать диаметра полусферы. Формулы вычисления можно найти сразу под калькулятором.
Объем полусферы, рассеченной плоскостью под заданным углом
Расстояние между центром основания полусферы и режущей плоскостью вдоль основания полусферы.
Угол в градусах между основанием полусферы и плоскостью разреза.
Точность вычисленияЗнаков после запятой: 5
save Сохранить extension Виджет
Формулы объема сечения полусферы плоскостью
Начинаем с простых случаев
Разрез проходит строго по центру полусферы, h=R
2)Центральный разрез полусферы, боковая проекция.Это самый простой случай, формула получается путем легкой модификации формулы объема полусферы:
Следующим образом:
, где a угол разреза в радианах.
Полусфера разрезана под углом 90 градусов
3)Прямой разрез полусферы. Боковая проекция.Если полусфера разрезана под прямым углом, мы попросту берем половину объема сечения сферы.
Полусфера разрезана ниже центра h > R
4)Разрез ниже середины полусферы. Боковая проекция.Если разрезать полусферу таким, образом, что центр полусферы окажется в части, для которой нужно вычислить объем мы получим самый сложный случай. Для такого случая мы вычисляем объем другой отрезанной части и вычитаем полученный объем из объема всей полусферы:
Vd вычисляется по формулам приведенным далее, с предварительным преобразованием угла
Сечение проходит выше центра полусферы h < R
5) Разрез полусферы под углом выше центраЭто наиболее общий случай, который решается интегрированием по объему.
Разместим полусферу на координатной плоскости таким образом, чтобы секущая плоскость была параллельна плоскости Z-O-Y, центр полусферы в начале координат. Секущая плоскость будет удаена от плоскости Z-O-Y на расстояние sin(α)*r0, где r0=R-h расстояние от пересечения основания полусферы и секущей плоскости до центра полусферы:
В линейной 3-мерной координатной системе секущая плоскость будет иметь уравнение .
В сферической системе координат (ISO): (1)
Далее будем решать интеграл в сферической системе координат:
(2)
Так как разрезанная полусфера расположена симметрично относительно плоскости X-O-Y мы будем интегрировать только половину возможного угла тета и домножим интеграл на 2.
Интервалы интегрирования
- Интервал угла φ постоянный:
Где a угол сечения к основанию полусферы в радианах
и согласно изображению (6) угол (3) - Интервал радиусов
Верхняя граница упрается в радиус полусферы — R. Плоскость сечения ограничивает интервал снизу, согласно формуле (1) имеем:
(4) - Интервалы угла θ
Так как мы интегрируем только верхнюю половину интервала θ то верхняя граница θ равна , а нижнюю можно выразить из формулы (1), принимая r=R. Таким образом:
(5)
Используя (3) мы можем сократить формулу так:
(6)
Формула объема
Для получения формулы объема сечения полусферы, решим интеграл (2) в интервалах (3),(4),(6):
Интегрируем по r
Результат:
Интегрируем по θ
Результат:- Интегрируем по φ
Получаем окончательную формулу:
Где:
,
.
Формулы объема
( пи = = 3,141592 …)Формулы объема
Примечание: «ab» означает «а» умножить на «б». «а 2 » означает «в квадрате», что то же самое, что «а» умножить на «а». «b 3 » означает «b в кубе», что то же самое как «b» умножить на «b» раз «б».
Будьте осторожны !! Количество единиц. Используйте одни и те же единицы для всех измерений.Примеры
куб = a 3
прямоугольная призма = abc
неправильная призма = b h
цилиндр = b h = pi r 2 h
пирамида = (1/3) b h
конус = (1/3) b h = 1/3 pi r 2 h
сфера = (4/3) pi r 3
эллипсоид = (4 / 3) pi r 1 r 2 r 3
Шт.
Объем измеряется в «кубических» единицах.Громкость фигуры — это количество кубиков, необходимых для ее полного заполнения, например блоки в коробке.
Объем куба = стороны, умноженные на стороны, умноженные на сторону. поскольку каждая сторона квадрата одинакова, это может быть просто длина одного сторона в кубе.
Если у квадрата одна сторона 4 дюйма, объем будет быть 4 дюйма на 4 дюйма на 4 дюйма, или 64 кубических дюйма.(Кубический дюймы также можно записать в 3 .)
Обязательно используйте одни и те же единицы для всех измерений. Нельзя умножить футы на дюймы на ярды, это не дает идеальное измерение в кубе.
Объем прямоугольной призмы равен длине на сторона, умноженная на ширину, умноженную на высоту. Если ширина составляет 4 дюйма, длина 1 фут и высота 3 фута, каков объем?
НЕ ПРАВИЛЬНО …. 4 раза 1 раз 3 = 12
ПРАВИЛЬНО …. 4 дюйма равны 1/3 фута. Объем: 1/3 фута умножить на 1 фут умножить на 3 фута = 1 кубический фут (или 1 куб. футов или 1 фут 3 ).
.Формулы объема
Здесь мы приводим формулы объема для некоторых распространенных трехмерных фигур, а также для эллипсоида и полого цилиндра, которые не так распространены.Куб:
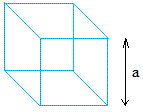 |
Цилиндр:
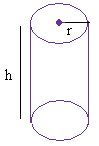 |
π = 3.14
h — высота
r — радиус
Прямоугольное тело или кубоид:
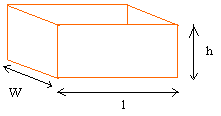 |
l — длина
w — ширина
h — высота
Сфера:
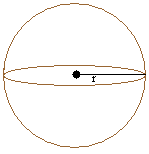 |
π = 3,14
r — радиус
Конус:
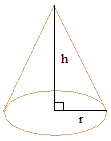 |
pi = 3.14
r — радиус
h — высота
Пирамида:
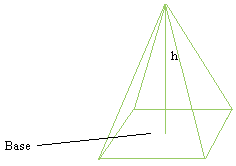 |
B — площадь основания
h — высота
Немного менее распространенные формулы объема
Эллипсоид:
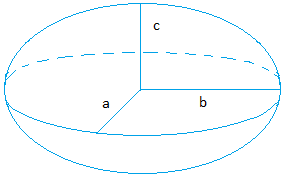 Объем = (4 × π × a × b × c) / 3
Объем = (4 × π × a × b × c) / 3Используйте π = 3,14
Полый цилиндр:
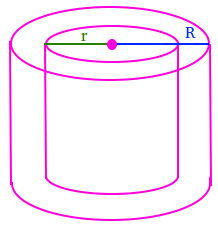 Объем = π × R 2 × h — π × r 2 × h
Объем = π × R 2 × h — π × r 2 × hОбъем = π × h (R 2 — r 2 )
Используйте π = 3.14.
Как использовать формулы объема для расчета объема.
Куб
Длина стороны = a = 2 см
Объем = (2 см) = 2 см × 2 см × 2 см = 8 см 3
Цилиндр
Высота 8 дюймов и радиус 2 дюйма.
Объем = π × r 2 × h = 3,14 × (2 дюйма) 2 × 8 дюймов = 3,14 × 4 × 8 дюймов = 3,14 × 4 × 8 дюймов 3
Объем = 3,14 × 32 дюймов 3 = 100,48 дюймов 3
Прямоугольный сплошной или прямоугольный
Длина 6 см, ширина 3 см и высота 5 см.
Объем = д × ш × в = 6 × 3 × 5 = 90 см 3
Сфера
Радиус = r = 20
Объем = (4 × π × r 3 ) / 3 = [4 × 3,14 × (20) 3 ] / 3 = 3,14 × (20) 3 × 4
Объем = 3,14 × 8000 × 4 = 3,14 × 32000 = 100480
Конус
Радиус равна 3, а высота равна 4.
Объем = (π × r 2 × h) / 3 = [3,14 × (3) 2 × 4] / 3 = 3.14 × 9 × 4
Объем = 3,14 × 36 = 113,04
Пирамида
Пирамида имеет высоту 6 футов. Если основание пирамиды представляет собой квадрат длиной 2 фута, найдите объем.
Объем = (B × h) / 3
B = площадь основания = 2 фута × 2 фута = 4 фута 2
Объем = (4 × 6) / 3 фута 3 = 24/3 фута 3 = 8 футов 3
Эллипсоид
Радиусы эллипсоида составляют 1 см, 2, см и 3 см.
Объем = (4 × π × a × b × c) / 3 = (4 × 3,14 × 1 × 2 × 3) / 3
Объем = (3,14 × 4 × 6) / 3 = (3,14 × 24) / 3 = 81,64 / 3 = 25,12 см 3
Полый цилиндр
Внешний радиус 8, внутренний радиус 6 и высота 10.
Объем = π × h (R 2 — r 2 ) = π × 10 (8 2 — 6 2 ) = π × 10 (64 — 36)
Объем = π × 10 (28) = π × 280 = 879,2
Новые уроки математики
Ваша электронная почта в безопасности.Мы будем использовать его только для информирования вас о новых уроках математики.
.Расчет формулы объема и площади в Excel
Программа Excel — лучший калькулятор. Мы привыкли использовать для расчетов традиционные бухгалтерские калькуляторы, хотя все их возможности поддерживаются программой Excel. Более того, у него есть неоспоримые преимущества.
В некоторых формулах можно выполнить только один математический расчет для расчета калькуляции. В таких случаях, если данные изменяются, вам нужно все изменить. Но если все данные распределены по ячейкам и формула будет относиться только к единицам, то при любых изменениях менять не нужно.Одна формула может использоваться много раз. Чтобы понять, как это работает, лучше привести несколько практических примеров.
Взаимодействие с другими людьмиКак рассчитать объем и площадь в Excel
В ячейку A1 записываем формулу для расчета объема параллелепипеда: a = 6 см; б = 8 см; c = 12 см.
В ячейку А2 записываем формулу расчета площади круга: r = 25 см.
В ячейке A3 формула содержит функцию без аргументов PI (), которая сама по себе содержит общее количество PI (а не 3.). Если мы пишем все в одну строчку, то надо соблюдать правила арифметической последовательности. Для этого нужно использовать круглые скобки.
Взаимодействие с другими людьмиФормула для расчета объема шара в Excel
Например, нам нужно регулярно рассчитывать объемы сфер разного радиуса.
Формула для вычисления объема шара выглядит так:
Предыдущие примеры плохо подходят для решения этой проблемы, так как они не используют значения переменных в формулах, а только константы.3 (A2 — ссылка на ячейку).
Примечание. Если вы используете несколько вычислений в Excel или формулы, которые содержат ссылки на ячейки в качестве значений переменных, вам всегда нужно подписывать каждую ячейку входящими данными и формулами. Это позволит избежать ошибок и легко прочитать значения или результаты расчета формул.
.Формула площади и объема для геометрических фигур
пи (π) = 3,1415926535 …
Формула периметра | ||
| Квадрат | 4 × сторона | |
| Прямоугольник | 2 × (длина + ширина) | |
| Параллелограмм | 2 × (сторона1 + сторона2) | сторона1 + сторона2 + сторона3 |
| Правильный n-многоугольник | n × сторона | |
| Трапеция | высота × (base1 + base2) / 2 | |
| Trapezoid | base1 + base2 + height × [ csc (theta1) + csc (theta2)] | |
| Окружность | 2 × pi × радиус | |
| Эллипс | 4 × radius1 × E (k, pi / 2) E (k, pi / 2) — полный эллиптический интеграл второго рода k = (1 / radius1) × sqrt (radius1 2 — radius2 2 ) | |
Формула площади | ||
| Квадрат | сторона 2 | |
| Прямоугольник | длина × ширина | |
| Параллелограмм | основание × высота | |
| Треугольник | основание × высота / 2 | |
| Трапеция | высота × (base1 + base2) / 2 | |
| Окружность | pi × радиус 2 | |
| Эллипс | пи × радиус1 × радиус2 | |
| Куб (поверхность) | 6 × сторона 2 | |
| Сфера (поверхность) | 4 × пи × радиус 2 | |
| Цилиндр ( вс сторона стороны) | периметр окружности × высота | |
| 2 × пи × радиус × высота | ||
| Цилиндр (вся поверхность) | Площади верхней и нижней окружностей + Площадь стороны | |
| 2 (пи × радиус 2 ) + 2 × пи × радиус × высота | ||
| Конус (поверхность) | пи × радиус × сторона | |
| Тор (поверхность) | пи 2 × (радиус2 2 — радиус1 2 ) | |
Формула объема | ||
| Куб | сторона 3 | |
| Прямоугольная призма | сторона1 × сторона2 × сторона3 | |
| Сфера | Сфера | 3) × пи × радиус 3 |
| Эллипсоид | (4/3) × пи × радиус1 × радиус2 × радиус3 | |
| Цилиндр | пи × радиус 2 × высота | Конус | (1/3) × пи × радиус 2 × высота |
| Пирамида | (1/3) × (площадь основания) × высота | |
| Тор | (1/4) × pi 2 × (r1 + r2) × (r1 — r2) 2 | |
Источник: Spiegel, Murray R.Математический справочник формул и таблиц.
Серия набросков Шаума по математике. McGraw-Hill Book Co., 1968.
