Модуль упругости это: Модуль упругости (Модуль Юнга): понятие, формулы, как определить
Модуль Юнга
Модуль Юнга (упругости I рода, продольной упругости) – механическая характеристика материалов, определяющая их способность сопротивляться продольным деформациям. Показывает степень жесткости материала.
Назван в честь английского ученого Томаса Юнга.
Обозначается латинской прописной буквой E
Единица измерения – Паскаль [Па].
В сопротивлении материалов модуль продольной упругости участвует в расчетах на жесткость при растяжении-сжатии и изгибе, а также в расчетах на устойчивость.
Учитывая то, что практически все конструкционные материалы имеют значение E высокого порядка (как правило 109 Па), его размерность часто записывают с помощью кратной приставки «гига» (гигапаскаль [ГПа])
Для всех материалов его величину можно определить в ходе эксперимента по определению модуля упругости I рода.
Приближенно значение модуля можно определить по диаграмме напряжений получаемой при испытаниях на растяжение.
Рис. 1 Начальный фрагмент диаграммы напряжений
В этом случае модуль Юнга равен отношению нормальных напряжений к соответствующим относительным деформациям, на участке диаграммы (рис. 1) до предела пропорциональности σпц (тангенсу угла α наклона участка пропорциональности к оси деформаций ε).
E=σ/ε=tgα
В таблице 1 приведены сравнительные значения модуля для некоторых наиболее часто используемых материалов
Таблица 1
Материал | Модуль Юнга |
Сталь | 200 |
Чугун | 120 |
Серый чугун | 110 |
Алюминий | 70 |
Дюралюминий | 74 |
Титан | 120 |
Бронза | 100 |
Латунь | 95 |
Медь | 110 |
Олово | 35 |
Хром | 300 |
Никель | 210 |
Кремний | 110 |
Свинец | 18 |
Бетон | 20 |
Дерево | 10 |
Стекло | 70 |
Модуль упругости I рода служит коэффициентом пропорциональности в формуле описывающей закон Гука:
σ=Eε
Связка модуля Юнга с геометрическими характеристиками поперечных сечений бруса показывает их жесткость:
EA – жесткость поперечного сечения при растяжении-сжатии,
где A – площадь поперечного сечения стержня;
EI – жесткость поперечного сечения при изгибе,
где I – осевой момент инерции сечения балки.
Модуль упругости II рода (модуль сдвига) >
Примеры решения задач >
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее
Здесь можно узнать стоимость и заказать решение
задач и выполнение учебных работ для студентов
Стоимость мы сообщим в течение 5 минут
на указанный вами адрес электронной почты.
Если стоимость устроит вы сможете оформить заказ.
НАБОР СТУДЕНТА ДЛЯ УЧЁБЫ
На нашем сайте можно бесплатно скачать:
— Рамки A4 для учебных работ
— Миллиметровки разного цвета
— Шрифты чертежные ГОСТ
— Листы в клетку и в линейку
Сохранить или поделиться с друзьями
Заказать решение
Поиск формул и решений задач
УПРУГОСТЬ, МОДУЛЬ УПРУГОСТИ, ЗАКОН ГУКА
УПРУГОСТЬ, МОДУЛЬ УПРУГОСТИ, ЗАКОН ГУКА. Упругость – свойство тела деформироваться под действием нагрузки и восстанавливать первоначальную форму и размеры после ее снятия. Проявление упругости лучше всего проследить, проведя простой опыт с пружинными весами – динамометром, схема которого показана на рис.1.
Упругость – свойство тела деформироваться под действием нагрузки и восстанавливать первоначальную форму и размеры после ее снятия. Проявление упругости лучше всего проследить, проведя простой опыт с пружинными весами – динамометром, схема которого показана на рис.1.
При нагрузке в 1 кг стрелка-индикатор сместится на 1 деление, при 2 кг – на два деления, и так далее. Если нагрузки последовательно снимать, процесс идет в обратную сторону. Пружина динамометра – упругое тело, ее удлинение Dl, во-первых, пропорционально нагрузке P и, во-вторых полностью исчезает при полном снятии нагрузки. Если построить график, отложить по вертикали оси величины нагрузки, а по горизонтальной – удлинение пружины, то получаются точки, лежащие на прямой, проходящей через начало координат, рис.2. Это справедливо как для точек, изображающих процесс нагружения так и для точек, соответствующих нагрузке.
Угол наклона прямой характеризует способность пружины сопротивляться действию нагрузки: ясно, что «слабая» пружина (рис.
Тангенс угла наклона характеристики называется жесткостью пружины С. Теперь можно записать уравнение деформирования пружины Dl = P / C
Жесткость пружины С имеет размерность кг / см\up122 и зависит от материала пружины (например, сталь или бронза) и ее размеров – длины пружины, диаметра ее витка и толщины проволоки, из которой она сделана.
В той или иной мере все тела, которые можно считать твердыми, обладают свойством упругости, но заметить это обстоятельство можно далеко не всегда: упругие деформации обычно очень малы и наблюдать их без специальных приборов удается практически только при деформировании пластинок, струн, пружин, гибких стержней.
Прямым следствием упругих деформаций являются упругие колебания конструкций и природных объектов. Можно легко обнаружить дрожание стального моста, по которому идет поезд;иногда можно услышать, как звенит посуда, когда на улице проезжает тяжелый грузовик; все струнные музыкальные инструменты так или иначе преобразуют упругие колебания струн в колебания частичек воздуха;в ударных инструментах тоже упругие колебания (например, мембраны барабана) преобразуются в звук.
При землетрясении происходят упругие колебания поверхности земной коры; при сильном землетрясении кроме упругих деформаций возникают пластические (которые остаются после катаклизма как изменения микрорельефа), а иногда появляются трещины. Эти явления не относятся к упругости: можно сказать, что в процессе деформирования твердого тела сначала всегда появляются упругие деформации, потом пластические, и, наконец, образуются микротрещины. Упругие деформации очень малы – не больше 1%, а пластические могут достигнуть 5–10% и более, поэтому обычное представление о деформациях относится к пластическим деформациям – например, пластилин или медная проволока. Однако, несмотря на свою малость, упругие деформации играют важнейшую роль в технике: расчет на прочность авиалайнеров, подводных лодок, танкеров, мостов, туннелей, космических ракет – это, в первую очередь, научный анализ малых упругих деформаций, возникающих в перечисленных объектах под действием эксплуатационных нагрузок.
Еще в неолите наши предки изобрели первое дальнобойное оружие – лук и стрелы, используя упругость изогнутой ветки дерева; потом катапульты и баллисты, построенные для метания больших камней, использовали упругость канатов, свитых из растительных волокон или даже из женских длинных волос.
Вероятно, в это время Гук уже понимал, что упругость – универсальное свойство твердых тел, но считал необходимым подтвердить свою уверенность экспериментально. В 1678 вышла книга Гука, посвященная упругости, где описывались опыты, из которых следует, что упругость есть свойство «металлов, дерева, каменных пород, кирпича, волос, рога, шелка, кости, мышцы, стекла и т. п.» Там же была расшифрована анаграмма. Исследования Роберта Гука привели не только к открытию фундаментального закона упругости, но и к изобретению пружинных хронометров (до того были только маятниковые). Изучая различные упругие тела (пружины, стержни, луки), Гук установил, что «коэффициент пропорциональности» (в частности, жесткость пружины) сильно зависит от формы и размеров упругого тела, хотя материал играет решающую роль.
п.» Там же была расшифрована анаграмма. Исследования Роберта Гука привели не только к открытию фундаментального закона упругости, но и к изобретению пружинных хронометров (до того были только маятниковые). Изучая различные упругие тела (пружины, стержни, луки), Гук установил, что «коэффициент пропорциональности» (в частности, жесткость пружины) сильно зависит от формы и размеров упругого тела, хотя материал играет решающую роль.
Прошло более ста лет, в течение которых опыты с упругими материалами проводили Бойль, Кулон, Навье и некоторые другие, менее известные физики. Одним из основных опытов стало растяжение пробного стержня из изучаемого материала. Для сравнения результатов, полученных в разных лабораториях, нужно было либо использовать всегда одинаковые образцы, либо научиться исключать слияние размеров образца. И в 1807 появилась книга Томаса Юнга, в которой был введен модуль упругости – величина, описывающая свойство упругости материала независимо от формы и размеров образца, который использовался в опыте. Для этого нужно силу P, приложенную к образцу, разделить на площадь сечения F, а произошедшее при этом удлинение Dl разделить на первоначальную длину образца l. Соответствующие отношения – это напряжение s и деформация e.
Для этого нужно силу P, приложенную к образцу, разделить на площадь сечения F, а произошедшее при этом удлинение Dl разделить на первоначальную длину образца l. Соответствующие отношения – это напряжение s и деформация e.
Теперь закон Гука о пропорциональности можно записать в виде:
s = Еe
Коэффициент пропорциональности Е называется модулем Юнга, имеет размерность, как у напряжения (МПа), а обозначение его есть первая буква латинского слова elasticitat – упругость.
Модуль упругости Е – это характеристика материала того же типа, как его плотность или теплопроводность.
В обычных условиях, чтобы продеформировать твердое тело, требуется значительная сила. Это означает, что модуль Е должен быть большой величиной – по сравнению с предельными напряжениями, после которых упругие деформации сменяются пластическими и форма тела заметно искажается.
Если измерять величину модуля Е в мегапаскалях (МПа), получатся такие средние значения:
| Сталь | 20·104 |
| Медь | 10·104 |
| Алюминий | 7·104 |
| Стекло | 7·104 |
| Кость | 3·104 |
| Дерево | 1·104 |
| Резина* | 0,001·104 |
Физическая природа упругости связана с электромагнитным взаимодействием (в том числе с силами Ван-дер-Ваальса в решетке кристалла). Можно считать, что упругие деформации связаны с изменением расстояния между атомами.
Можно считать, что упругие деформации связаны с изменением расстояния между атомами.
Упругий стержень имеет еще одно фундаментальное свойство – утоньшаться при растяжении. То, что канаты при растяжении становятся тоньше, было известно давно, но специально поставленные опыты показали, что при растяжении упругого стержня всегда имеет место закономерность: если измерить поперечную деформацию e’, т.е. уменьшение ширины стержня db , деленное на первоначальную ширину b, т.е.
и разделить ее на продольную деформацию e, то это отношение остается постоянным при всех значениях растягивающей силы P, то есть
(Полагают, что e’< 0 ; поэтому используется абсолютная величина). Константа v называется коэффициентом Пуассона (по имени французского математика и механика Симона Дени Пуассона) и зависит только от материала стержня, но не зависит от его размеров и формы сечения. Величина коэффициента Пуассона для разных материалов изменяется от 0 (у пробки) до 0,5 (у резины). В последнем случае объем образца в процессе растяжения не изменяется (такие материалы называются несжимаемыми). Для металлов значения различны, но близки к 0,3.
В последнем случае объем образца в процессе растяжения не изменяется (такие материалы называются несжимаемыми). Для металлов значения различны, но близки к 0,3.
Модуль упругости E и коэффициент Пуассона вместе образуют пару величин, которые полностью характеризуют упругие свойства любого конкретного материала (имеются в виду изотропные материалы, т.е. такие, у которых свойства не зависят от направления; пример древесины показывает, что это не всегда так – ее свойства вдоль волокон и поперек волокон сильно различаются. Это – анизотропный материал. Анизотропными материалами являются монокристаллы, многие композиционные материалы (композиты) типа стеклопластика. Такие материалы тоже в известных пределах обладают упругостью, но само явление оказывается значительно более сложным).
Если от рассмотрения растяжения стержня перейти к рассмотрению некоторого упругого тела, подверженного действию заданных сил, то следует выбрать некоторую точку M и перейти к рассмотрению ее малой окрестности в виде параллелепипеда с ребрами, параллельными координатным осям XYZ. Как известно (см. ДЕФОРМАЦИЯ), на гранях параллелепипеда действуют напряжения, которые задаются тензором s, что приводит к деформациям, которые задаются тензором e.
Как известно (см. ДЕФОРМАЦИЯ), на гранях параллелепипеда действуют напряжения, которые задаются тензором s, что приводит к деформациям, которые задаются тензором e.
В общем случае закон Гука устанавливает связь между компонентами этих тензоров, которую можно записать в виде:
,
,
,
, ,
В последние три уравнения входит величина G, которая называется модулем сдвига и выражается через E и v по формуле:
Модуль сдвига можно непосредственно определить из опыта на кручение круглого образца.
В физике для идеального газа вводится уравнение состояния (уравнение Клапейрона – Менделеева). Можно сказать, что закон Гука – это уравнение состояния для идеально упругого тела.
Владимир Кузнецов
Модуль упругости: определение, значения и примеры
Модуль упругости, также известный как модуль Юнга, является фундаментальным свойством материалов, которое измеряет их жесткость или сопротивление упругой деформации под нагрузкой. Это свойство имеет важное значение в технике и материаловедении, поскольку оно определяет способность материала выдерживать нагрузки и сохранять свою форму. Модуль упругости выражается как сила на единицу площади в паскалях (Па) или фунтах на квадратный дюйм (psi). Модуль упругости определяется путем расчета наклона упругой части кривой напряжения-деформации. Модуль упругости различен для разных материалов. Более жесткие материалы имеют более высокий модуль упругости.
Это свойство имеет важное значение в технике и материаловедении, поскольку оно определяет способность материала выдерживать нагрузки и сохранять свою форму. Модуль упругости выражается как сила на единицу площади в паскалях (Па) или фунтах на квадратный дюйм (psi). Модуль упругости определяется путем расчета наклона упругой части кривой напряжения-деформации. Модуль упругости различен для разных материалов. Более жесткие материалы имеют более высокий модуль упругости.
В этой статье представлен обзор модуля упругости, его измерения, единиц измерения и примеры материалов с различными значениями.
Что такое модуль упругости?
Модуль упругости можно определить как способность материала сопротивляться упругой деформации при воздействии на него напряжения. Это мера жесткости или жесткости материала. Модуль упругости в терминах кривой напряжение-деформация представляет собой наклон кривой напряжение-деформация в области упругости
, где напряжение линейно пропорционально деформации. Другие названия модуля упругости включают модуль Юнга, модуль упругости, модуль упругости при растяжении или модуль упругости. Для получения дополнительной информации см. наше руководство по модулю изгиба.
Другие названия модуля упругости включают модуль Юнга, модуль упругости, модуль упругости при растяжении или модуль упругости. Для получения дополнительной информации см. наше руководство по модулю изгиба.
На рис. 1 приведен пример графика модуля упругости Юнга (Y):
Что такое модуль упругости в системе СИ?
Модуль упругости измеряется в Паскалях (Па), в той же единице, что и для напряжения. МПа и ГПа обычно используются для выражения модуля упругости из-за большой величины типичных значений.
Что является примером модуля упругости?
Сталь широко используется в строительстве благодаря своей прочности и долговечности. Его высокий модуль упругости 200-210 ГПа означает, что он способен сопротивляться деформации и сохранять свою форму под нагрузкой, что делает его идеальным для использования в таких конструкциях, как здания и мосты. Это свойство позволяет стали выдерживать большие нагрузки, не изгибаясь и не ломаясь, обеспечивая безопасность и устойчивость конструкции. Кроме того, высокий модуль упругости стали делает ее отличным выбором для использования в деталях машин и инструментах, где важными факторами являются жесткость и сопротивление изгибу. Его жесткость позволяет машинам создавать точные детали, при этом его гибкость не участвует в изменчивости. Однако высокий модуль упругости стали также означает, что это относительно хрупкий материал, который при определенных условиях может растрескиваться. Рекомендуется учитывать конкретное применение и потенциальные нагрузки, которым будет подвергаться сталь, чтобы обеспечить ее безопасное и эффективное использование.
Кроме того, высокий модуль упругости стали делает ее отличным выбором для использования в деталях машин и инструментах, где важными факторами являются жесткость и сопротивление изгибу. Его жесткость позволяет машинам создавать точные детали, при этом его гибкость не участвует в изменчивости. Однако высокий модуль упругости стали также означает, что это относительно хрупкий материал, который при определенных условиях может растрескиваться. Рекомендуется учитывать конкретное применение и потенциальные нагрузки, которым будет подвергаться сталь, чтобы обеспечить ее безопасное и эффективное использование.
Каковы значения модуля упругости?
Модули упругости для некоторых распространенных материалов перечислены в таблице 1 ниже:
Как выражаются значения модуля упругости?
Значение модуля упругости обычно выражается в единицах давления или напряжения, таких как фунты на квадратный дюйм (psi) или паскали (Pa). Это мера жесткости материала или сопротивления упругой деформации под нагрузкой.
Существуют различные типы модуля упругости в зависимости от типа приложенного напряжения. Наиболее часто используемым модулем упругости является модуль Юнга. Модуль Юнга измеряет отношение напряжения к деформации, когда напряжение прикладывается перпендикулярно площади поперечного сечения материала.
Формула модуля Юнга:
Другие типы модуля упругости включают объемный модуль и модуль сдвига. Объемный модуль измеряет сопротивление сжатию, а модуль сдвига измеряет сопротивление деформации под действием напряжения сдвига.
Какой материал имеет самый высокий модуль упругости?
Алмаз имеет самый высокий из известных модулей упругости ~1220 ГПа, а также считается самым твердым из известных материалов. Это значительно выше, чем у всех видов пластмасс и металлов. Модуль упругости большинства пластиков обычно находится в диапазоне от 1 до 10 ГПа (гигапаскалей).
Напротив, модуль упругости металлов обычно намного выше, чем у пластмасс. Модуль упругости металлов может широко варьироваться в зависимости от конкретного материала и его состава.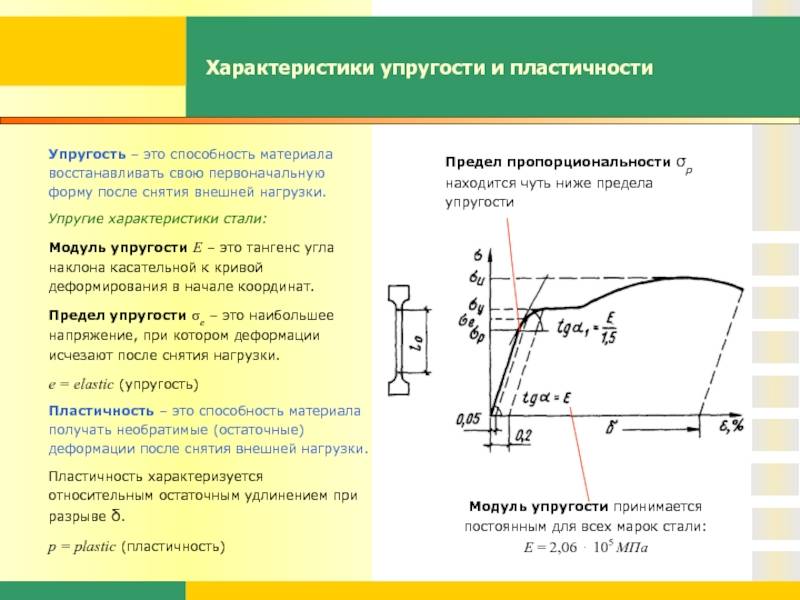 Большинство металлов имеют модули упругости в диапазоне от 50 до 400 ГПа. Важно отметить, что это общие диапазоны. Модуль упругости конкретного материала может варьироваться в зависимости от таких факторов, как температура, скорость деформации, наличие дефектов или примесей.
Большинство металлов имеют модули упругости в диапазоне от 50 до 400 ГПа. Важно отметить, что это общие диапазоны. Модуль упругости конкретного материала может варьироваться в зависимости от таких факторов, как температура, скорость деформации, наличие дефектов или примесей.
На что указывает большое значение модуля упругости?
Большой модуль упругости указывает на то, что материал очень жесткий. Расчет упругих прогибов включает использование модуля упругости, важнейшего параметра конструкции. Чем жестче материал или чем меньше упругая деформация, возникающая в результате приложения данного напряжения, тем больше модуль.
На что указывает малое значение модуля упругости?
Небольшой модуль упругости указывает на то, что не требуется большого усилия, чтобы вызвать значительную упругую деформацию в материале. Он гибкий, не жесткий. Он будет легко упруго деформироваться, если будет применено какое-либо напряжение сжатия или растяжения. Резина является примером такого материала с очень низким модулем упругости 0,05 ГПа.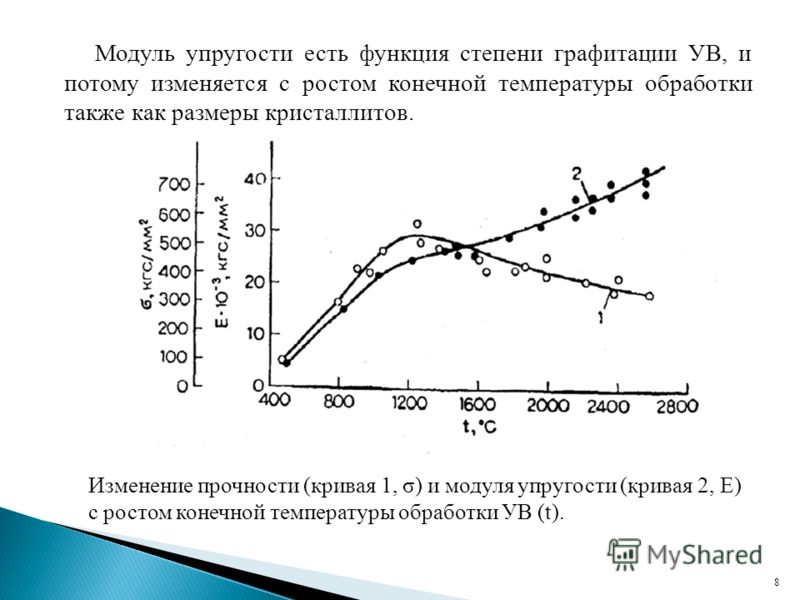
Что такое символ модуля упругости?
Модуль упругости обозначается символом E. Он равен напряжению, приложенному к материалу в области упругой деформации, деленному на деформацию, испытываемую этим материалом. Модуль упругости измеряется в Па или фунтах на квадратный дюйм.
Как определяется модуль упругости?
Модуль упругости материала определяется путем построения кривой напряжения-деформации для материала. Затем вычисляется наклон прямолинейной (линейно-упругой) части кривой. Во-первых, материал растягивается с помощью машины, которая измеряет приложенную силу и изменение длины, возникающее в результате этой силы, и наносит эти значения на кривую напряжения-деформации. Кривая напряжения-деформации будет иметь линейный участок в начале. Модуль упругости определяется путем расчета наклона этой части кривой.
Что такое уравнение модуля упругости?
Уравнение для модуля упругости:
Уравнение для модуля упругости представляет собой просто отношение напряжения, приложенного к материалу, к деформации, возникающей в результате этого напряжения.
В чем разница между модулем упругости и модулем сдвига?
Модуль упругости измеряет способность материала сопротивляться деформации при приложении к нему растягивающего напряжения, тогда как модуль сдвига измеряет способность материала сопротивляться деформации при приложении напряжения сдвига. Основное различие между двумя модулями заключается в типе напряжения, прикладываемого к испытательному образцу.
Резюме
В этой статье представлен модуль упругости, объяснено, что это такое, а также обсуждена его важность и способы его расчета. Чтобы узнать больше о модуле упругости, свяжитесь с представителем Xometry.
Xometry предоставляет широкий спектр производственных возможностей и других дополнительных услуг для всех ваших потребностей в прототипировании и производстве. Посетите наш веб-сайт, чтобы узнать больше или запросить бесплатное предложение без каких-либо обязательств.
Отказ от ответственности
Контент, отображаемый на этой веб-странице, предназначен только для информационных целей.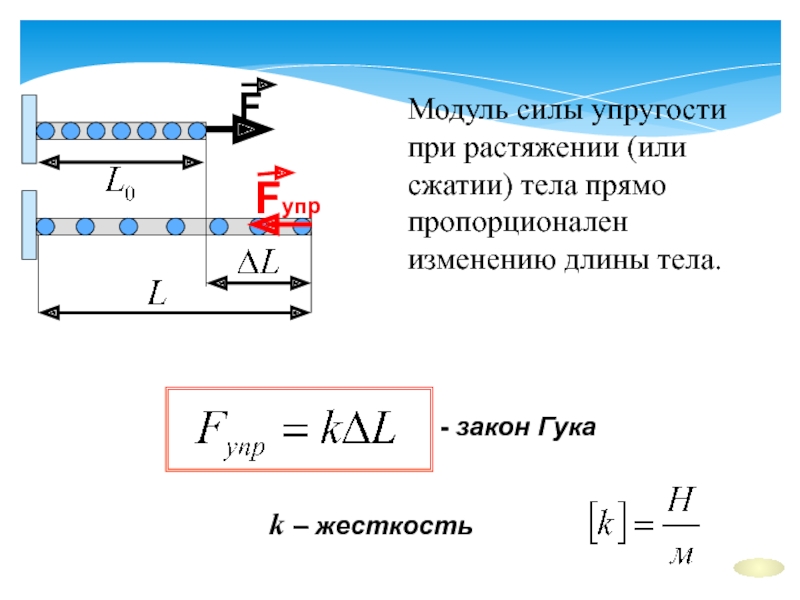 Xometry не делает никаких заявлений и не дает никаких гарантий, явных или подразумеваемых, в отношении точности, полноты или достоверности информации. Любые рабочие параметры, геометрические допуски, особенности конструкции, качество и типы материалов или процессов не должны рассматриваться как представляющие то, что будет поставляться сторонними поставщиками или производителями через сеть Xometry. Покупатели, которым нужны расценки на детали, несут ответственность за определение конкретных требований к этим частям. Пожалуйста, ознакомьтесь с нашими условиями для получения дополнительной информации.
Xometry не делает никаких заявлений и не дает никаких гарантий, явных или подразумеваемых, в отношении точности, полноты или достоверности информации. Любые рабочие параметры, геометрические допуски, особенности конструкции, качество и типы материалов или процессов не должны рассматриваться как представляющие то, что будет поставляться сторонними поставщиками или производителями через сеть Xometry. Покупатели, которым нужны расценки на детали, несут ответственность за определение конкретных требований к этим частям. Пожалуйста, ознакомьтесь с нашими условиями для получения дополнительной информации.
Team Xometry
Эта статья была написана различными участниками Xometry. Xometry — это ведущий ресурс по производству с помощью станков с ЧПУ, изготовления листового металла, 3D-печати, литья под давлением, литья уретана и многого другого.
Определение, единицы измерения, формулы [Примечания GATE]
Что такое модуль упругости?
В пределах предела пропорциональности модуля упругости отношение напряжения к деформации. пропорциональный предел. Он измеряет жесткость или жесткость материала. Если материал больше по модулю, материал будет более жестким или меньшим, чем упругая деформация, возникающая в результате приложения данного напряжения.
пропорциональный предел. Он измеряет жесткость или жесткость материала. Если материал больше по модулю, материал будет более жестким или меньшим, чем упругая деформация, возникающая в результате приложения данного напряжения.
Модуль упругости является важным расчетным параметром, используемым для расчета упругих прогибов. Модуль упругости называют модулем упругости. Модуль упругости также известен как модуль Юнга.
Типы модулей упругости
В зависимости от типа силы, приложенной к телу, и изменения деформации. Модуль упругости подразделяют на следующие виды.
- Модуль Юнга
- Модуль сдвига
- Объемный модуль упругости
Модуль Юнга
Модуль упругости объясняется только для одной оси вещества. Модуль Юнга материала является важным атрибутом для понимания того, как материал будет вести себя при приложении силы. Он представлен буквой E.
Размерная формула E: [M 1 L -1 T -2 ].
Модуль сдвига
Модуль сдвига материала представляет собой отношение напряжения сдвига к деформации сдвига в теле. Когда сила сдвига увеличивается, значение модуля сдвига также увеличивается. Обозначается G или C.
Размерная формула G: [M 1 L -1 T -2 ].
Объемный модуль упругости
Объемный модуль определяется при приложении к изменению объема равномерного давления со всех направлений. Объемный модуль упругости — это мера способности вещества изменяться в объеме при сжатии со всех сторон. Обозначается K.
Объемный модуль упругости,
K= — P/(ΔV/V)
Размеры K составляют [M 1 L -1 T -2 ].
Связь между модулем упругости
Различные типы модулей упругости могут быть связаны друг с другом с помощью следующих уравнений: +μ)
E = 9KG/(G+3K)
Где μ = коэффициент Пуассона
Анализ модуля упругости
Согласно закону Гука модуль упругости представляет собой наклон кривой напряжения-деформации до линейная пропорциональность напряжения деформации. На кривой напряжения-деформации стали площадь под кривой до точки текучести представляет собой модуль упругости, а от точки текучести до разрушения материала представляет собой модуль ударной вязкости.
На кривой напряжения-деформации стали площадь под кривой до точки текучести представляет собой модуль упругости, а от точки текучести до разрушения материала представляет собой модуль ударной вязкости.
E = напряжение/деформация = (P/A)/(ΔL/L)
E = модуль упругости или модуль Юнга в пределах пропорциональности.
Единица модуля Юнга
Модуль упругости — это свойство материала, определяющее его жесткость, и поэтому оно является одним из наиболее важных свойств твердых материалов. Это отношение напряжения к деформации, когда деформация является упругой в любом направлении.
- Единица СИ: Паскаль (или) Н/мм 2
- Единица СГС: Дин/см 2
- Единица MKS: кг/см 2
Различные материалы с их значением модуля Юнга в соответствии с упругостью в природе. Более высокое значение модуля Юнга относится к высокой эластичности в природе, когда к этому материалу прилагается нагрузка.
Материал | Модуль Юнга (ГПа) |
1000 | |
Мягкая сталь | 200 |
Медь | 120 90 210 |
Алюминий | 69 |
Бетон | 30 9 0003 |
Стекло | 65 |
Кость | 18 | 9021 7
Пластик | 3 |
Резина | 0,02 |
Дерево | 15 |
Примечание.
