Модуль деформации бетона: Модуль деформации бетона
Модуль деформации бетона
Главная » Статьи » Модуль деформации бетона
7. Модуль деформаций бетона
Начальный модуль упругости бетона при сжатии соответствует лишь упругим деформациям, возникающим при мгновенном загружении или при напряжениях . Он определяется в соответствии с законом Гука как тангенс угла наклона прямой упругих деформаций к оси абсцисс (рис. 1.11), т.е.
где р = 1 МПа — масштабно-размерный коэффициент.
Обычно определяется из специальных опытов на призмах при низком уровне напряжений (), когда бетон можно рассматривать как упругий материал.
При действии на бетон нагрузки, при которой , хотя бы в течение нескольких минут, в связи с развитием пластических деформаций (включая ползучесть) модуль полных деформаций бетона становится величиной переменной.
Для расчёта железобетонных конструкций пользуются средним модулем деформаций или модулем упругопластичности бетона, представляющим собой тангенс угла наклона секущей, проведённой через начало координат и точку на кривой с заданным напряжением, к оси абсцисс, т.
Начальный модуль упругости бетона при растяжении по абсолютной величине принимается равным , то есть , а
где vt = 0,15 — значение коэффициента упругопластичности бетона при растяжении в момент, предшествующий разрушению.
Значения модуля сдвига бетона G принимают по установленной в теории упругости зависимости
Подставив в неё начальный коэффициент поперечной деформации бетона ν=0,2, получим .
ЛЕКЦИЯ 3
Арматура для железобетонных конструкций
Назначение арматуры и требования к ней
2. Виды арматуры
3. Физико-механические свойства арматурных сталей
4. Классификация арматуры по основным характеристикам. Сортамент арматуры
5. Сварные арматурные изделия
6. Соединения арматуры
1. Назначение арматуры и требования к ней
Под арматурой понимают отдельные стержни или целые каркасы, которые располагаются в массе бетона в соответствии со статической схемой работы конструкции.
Арматура в железобетонных конструкциях используется преимущественно для восприятия растягивающих усилий.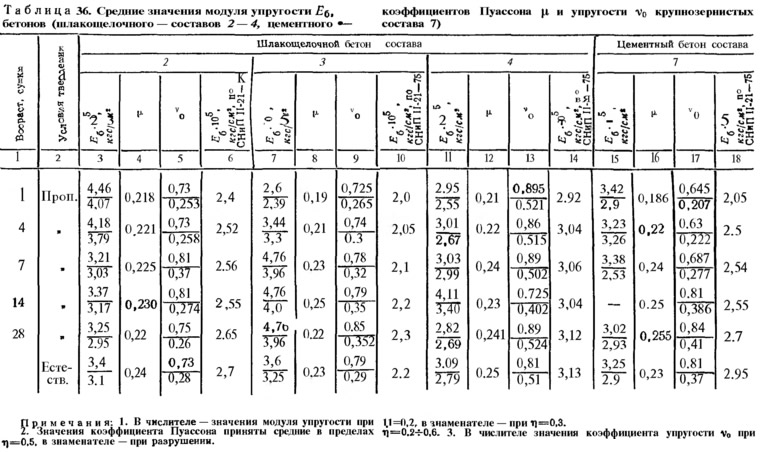 Но иногда арматуру применяют и для усиления сжатого бетона (например, в колоннах), а также для восприятия температурных и усадочных напряжений.
Но иногда арматуру применяют и для усиления сжатого бетона (например, в колоннах), а также для восприятия температурных и усадочных напряжений.
Арматура для железобетонных конструкций должна удовлетворять следующим требованиям:
2. Виды арматуры
Многообразие видов железобетонных конструкций определяет необходимость применения широкой номенклатуры арматурных сталей.
Для изготовления арматуры используют конструкционные стали обычно с содержанием углерода не более 0,65%, так как стали с более высоким содержанием углерода плохо свариваются.
Арматура классифицируется по функциональному назначению и способу изготовления по четырём признакам.
1. По технологии изготовления арматуру делят на: стержневую горячекатаную, термомеханически упрочненную и механически упрочненную в холодном состоянии (холоднодеформированную).
2. По форме наружной поверхности арматура бывает гладкая и периодического профиля.
3. По способу применения: арматура, которую укладывают в конструкцию без предварительного напряжения, называется ненапрягаемой, арматура, которую при изготовлении конструкции предварительно натягивают — напрягаемой.
4. Арматура, устанавливаемая в железобетонных конструкциях по расчёту, называется рабочей. Площадь её поперечного сечения определяется расчётом элементов конструкций на различные нагрузки и воздействия. Её главное назначение — восприятие растягивающих усилий в сечениях. Поэтому она располагается в растянутой зоне вдоль линии действия этих усилий, т. е. перпендикулярно к возможному направлению трещин.
Арматура, устанавливаемая по конструктивным или технологическим соображениям, называется монтажной или распределительной (в плитах). Она обеспечивает проектное положение рабочей арматуры в конструкции и более равномерно распределяет усилия между отдельными стержнями рабочей арматуры. Кроме того, монтажная арматура может воспринимать обычно не учитываемые расчётом усилия от усадки бетона, изменения температуры конструкции и т. п. Она может также выполнять роль рабочей при транспортировании и монтаже конструкции.
studfiles.net
1.1.7. Модуль деформаций бетона
Начальный модуль упругости бетона при сжатии () соответствует лишь упругим деформациям, возникающим при мгновенном загружении или при напряжениях . Он определяется, в соответствии с законом Гука, как тангенс угла наклона прямой упругих деформаций к оси абсцисс (рис. 16), т.е.:
Он определяется, в соответствии с законом Гука, как тангенс угла наклона прямой упругих деформаций к оси абсцисс (рис. 16), т.е.:
(1.18)
где ρ = 1 МПа – масштабно-размерный коэффициет.
Рис. 16. Схема для определения модуля деформаций бетона:
1 – упругие деформации; 2 – секущая; 3 – касательная; 4 – полные деформации
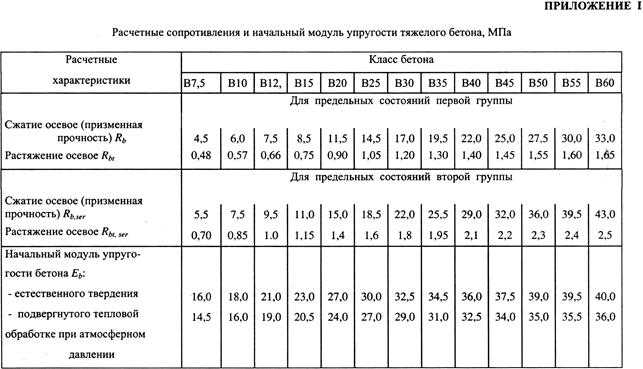
Обычно определяется из специальных опытов на призмах при низком уровне напряжений (), когда бетон можно рассматривать как упругий материал, или, если известна кубиковая прочность бетона, то по различным эмпирическим формулам. Так для тяжёлого бетона естественного твердения
. (1.19)
Значение при тепловой обработке бетона снижается на 10%, при автоклавной – на 25%.
При действии на бетон нагрузки, при которой , хотя бы в течение нескольких минут, в связи с развитием пластических деформаций (включая ползучесть) модуль полных деформаций бетона становится величиной переменной.
Для расчёта железобетонных конструкций пользуются средним модулем деформаций или модулем упругопластичности бетона, представляющим собой тангенс угла наклона секущей, проведённой через начало координат и точку на кривой с заданным напряжением, к оси абсцисс, т. е.
е.
(1.20)
Зависимость между и можно установить, если выразить по (1.18) и (1.20) одно и то же напряжение в бетоне через упругие деформации и полные деформации
(1.21)
где v = – коэффициент упругопластичности бетона. Значение v при сжатии изменяется от 1 (при упругой работе бетона) до 0,15 (в момент, предшествующий разрушению бетона при очень длительном загружении).
Начальный модуль упругости бетона при растяжении по абсолютной величине принимается равным , т.е. , а
(1.22)
где vt = 0,15 – значение коэффициента упругопластичности бетона при растяжении в момент, предшествующий разрушению.
Значения модуля сдвига бетона G принимают по установленной в теории упругости зависимости
Подставив в неё начальный коэффициент поперечной деформации бетона ν = 0,2, получим .
1.2. Арматура для железобетонных конструкций
1.2.1. Назначение арматуры и требования к ней
Под арматурой понимают отдельные стержни или целые каркасы, которые располагаются в массе бетона в соответствии со статической схемой работы конструкции.
Арматура в железобетонных конструкциях используется преимущественно для восприятия растягивающих усилий. Но иногда арматуру применяют и для усиления сжатого бетона (например, в колоннах), а также для восприятия температурных и усадочных напряжений.
Арматура для железобетонных конструкций должна удовлетворять следующим требованиям:
studfiles.net
8.5.3. Модуль упругости и деформации бетона при
КРАТКОВРЕМЕННОМ НАГРУЖЕНИИ
Деформации бетона при приложении нагрузки зависят от его состава, свойств составляющих материалов и вида напряженного состояния. Диаграмма сжатия бетона имеет криволинейное очертание, причем кривизна увеличивается с ростом напряжений (рис. 6.4).
С увеличением прочности бетона уменьшается его деформация и кривизна диаграммы . Низкопрочные бетоны имеют даже нисходящую ветвь диаграммы сжатия. Однако на этом участке сплошность материала уже нарушена, в нем возникают микроскопические трещины, отслоение отдельных частей. В железобетонных конструкциях арматура связывает отдельные части бетона в единое целое и для частных случаев расчета конструкций необходимо учитывать нисходящую ветвь диаграммы сжатия бетона.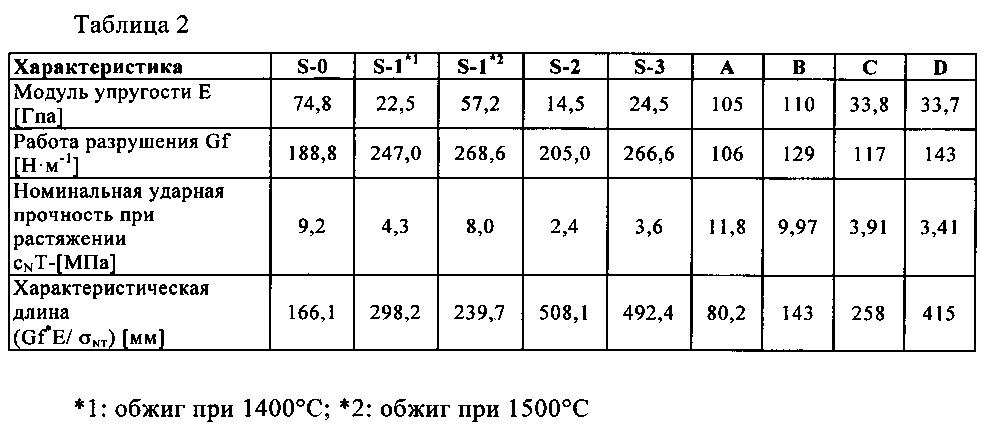
На характер нарастания деформаций под действием нагрузки влияют также скорость ее приложения, размеры образца, температурно-влажностное состояние бетона и окружающей среды и другие факторы. Деформация бетона включает упругую, пластическуюи псевдопластическуючасти (рис. 6.4):
Соотношение между ними зависит от состава бетона, использованных материалов и других факторов. Величина пластической и псевдопластической частей возрастает с увеличением длительности нагрузки, понижением прочности бетона, увеличением водоцементного отношения, при применении слабых заполнителей.
О деформативных свойствах бетона при приложении нагрузки судят по его модулю деформации, т. е. по отношению напряжения к относительной реформации, вызываемой его действием. Чем выше модуль деформации, тем менее деформативен материал. Поскольку диаграмма сжатия бетона криволинейна, то его модуль деформации зависит от значений относительных напряжений, постепенно понижаясь с их увеличением (рис.6.5), причем тем больше, чем ниже марка бетона. Обычно определяют либо начальный модуль деформации бетона Ео, когда преобладают упругие деформации, либо модуль деформации при определенном значении, например при= 0,5.
Обычно определяют либо начальный модуль деформации бетона Ео, когда преобладают упругие деформации, либо модуль деформации при определенном значении, например при= 0,5.
На практике используют эмпирические зависимости модуля деформации от различных факторов. Для расчета железобетонных конструкций важна зависимость модуля деформации при можно определить по формуле:
,
где R– прочность бетона.
В действительности модуль деформации может заметно отличаться от средних значений. В табл. 6.2 приведены значения модуля деформации при сжатии некоторых видов бетона, показывающие большое влияние на него технологических факторов.
Важное значение для расчета конструкций и оценки их поведения под нагрузкой имеют величины предельных деформаций, при которых начинается разрушение бетона, По опытным данным, предельная сжимаемость бетона изменяется в пределах 0.0015…0,003, увеличиваясь при повышении прочности бетона.
Предельную сжимаемость бетона можно также увеличивать, применяя более Деформативные компоненты и обеспечивая достаточно надежное сцепление между ними.
Предельная растяжимость бетона составляет 0,0001…0,0015, т.е. примерно в 15…20 раз меньше его предельной сжимаемости.
Предельная растяжимость повышается при введении в бетон пластифицирующих добавок, использовании белитовых цементов, уменьшении крупности заполнителей или при применении заполнителей с высокими деформативными свойствами и сцеплением с цементным камнем.
studfiles.net
6. Модуль деформации бетона и мера ползучести.
Начальный модуль упругости ЕВ бетона при сжатии – это величина, соответствующая мгновенному загружению.Геометрически – это тангенс угла наклона прямой упругих деформаций.
Модуль полных деформацийбетона при сжатиисоответствует полным деформациям, включая ползучесть. Это переменная величина. Геометрически – это тангенс угла наклона касательной к кривой в точке с заданным напряжением.
Для расчёта железобетонных конструкций используют модуль упругопластичности (секущий модуль).Это тангенс угла наклона секущей, проходящей через начало координат и любой точки, заданной на диаграмме.
Если мы выразим одно и то же напряжение через упругие деформациии полные деформации, то получим,
— коэффициент пластичности
–коэффициент упругопластичной деформации бетона
следовательно .
.
Для идеально упругого материала , для идеально пластического материала.
Зависимость между напряжениями и деформациями ползучести выражаются мерой ползучести .
где .
Мера ползучести зависит от класса бетона и его модуля упругости.
7. Реологические свойства бетона.
Усадка — уменьшение бетона в объеме при твердении в обычной среде.
Набухание — увеличение бетона в объеме при твердении вводе.
Ползучесть — свойство бетона, характеризующее нарастание неупругих деформаций с течением времени при постоянных напряжениях.
Релаксация — уменьшение с течением времени напряжений при постоянной начальной деформации.
Если испытываемый образец загрузить по этапам и замерять деформации на каждой ступени дважды (сразу после приложения нагрузки и через некоторое время), то получим ступенчатую линию. Деформации, измеренные сразу, являются упругими. При достаточно большом числе ступеней загружения зависимость σb – εbстановится плавной кривой.
Деформации, измеренные сразу, являются упругими. При достаточно большом числе ступеней загружения зависимость σb – εbстановится плавной кривой.
Опыты с бетонными призмами показывают, что независимо с какой скоростью Vбыло получено напряжениеσb1, конечные деформации ползучести, соответствующие этому напряжению, будут одинаковые.
С ростом напряжений ползучесть увеличивается.
Многократное повторение циклов загрузки — разгрузки приводит к постепенному накапливанию εpl. После достаточно большого числа циклов неупругие деформации, соответствующие данному уровню напряжений, выбираются, ползучесть достигает своего предельного значения, бетон начинает упруго работать ().
При больших напряжениях неупругие деформации неограниченно растут, и бетон разрушается.
8. Предельные деформации бетона.
Предельная сжимаемость
растяжимость
Cувеличением класса бетона предельные деформации падают, с увеличением длительности приложения нагрузки – возрастают.
studfiles.net
6. Модуль деформации бетона и мера ползучести.
Начальный модуль упругости ЕВ бетона при сжатии – это величина, соответствующая мгновенному загружению.Геометрически – это тангенс угла наклона прямой упругих деформаций.
Модуль
полных деформацийбетона при
сжатиисоответствует полным деформациям,
включая ползучесть.
Для расчёта железобетонных конструкций используют модуль упругопластичности (секущий модуль).Это тангенс угла наклона секущей, проходящей через начало координат и любой точки, заданной на диаграмме.
Если мы выразим одно и то же напряжение через упругие деформациии полные деформации, то получим,
— коэффициент пластичности
–коэффициент упругопластичной деформации бетона
следовательно .
.
Для идеально упругого материала , для идеально пластического материала.
Зависимость между напряжениями и деформациями ползучести выражаются
где .
Мера ползучести зависит от класса бетона и его модуля упругости.
7. Реологические свойства бетона.
Усадка — уменьшение бетона в объеме при твердении в обычной среде.
Набухание — увеличение бетона в объеме при
твердении вводе.
Ползучесть — свойство бетона, характеризующее нарастание неупругих деформаций с течением времени при постоянных напряжениях.
Релаксация — уменьшение с течением времени напряжений при постоянной начальной деформации.
Если испытываемый образец загрузить по этапам и замерять деформации на каждой ступени дважды (сразу после приложения нагрузки и через некоторое время), то получим ступенчатую линию. Деформации, измеренные сразу, являются упругими. При достаточно большом числе ступеней загружения зависимость σb– εbстановится плавной кривой.
Опыты с бетонными призмами показывают, что независимо с какой скоростью Vбыло получено напряжениеσb1, конечные деформации ползучести, соответствующие этому напряжению, будут одинаковые.
С ростом напряжений ползучесть увеличивается.
Многократное
повторение циклов загрузки — разгрузки
приводит к постепенному накапливанию
ε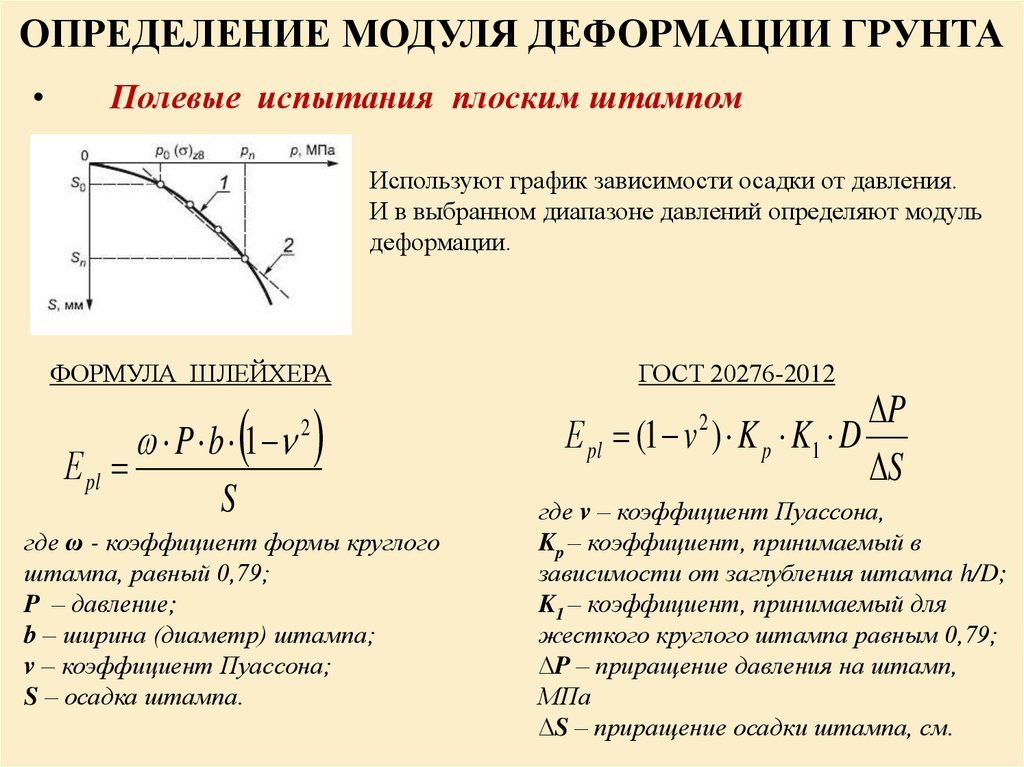 После достаточно большого числа
циклов неупругие деформации, соответствующие
данному уровню напряжений, выбираются,
ползучесть достигает своего предельного
значения, бетон начинает упруго работать
().
После достаточно большого числа
циклов неупругие деформации, соответствующие
данному уровню напряжений, выбираются,
ползучесть достигает своего предельного
значения, бетон начинает упруго работать
().
При больших напряжениях неупругие деформации неограниченно растут, и бетон разрушается.
8. Предельные деформации бетона.
Предельная сжимаемость
растяжимость
Cувеличением класса бетона предельные деформации падают, с увеличением длительности приложения нагрузки – возрастают.
14
Модуль упругости бетона? [3 различных стандарта]
Модуль упругости бетона? [3 разных стандарта]Инженер Мойд | 4 марта 2019 г. | Конкретные заметки | 1 комментарий
Содержание
- 1 Модуль упругости бетона
- 1.1 Упругость
- 1.2 Ед. Обладает высокой прочностью на сжатие и низкой прочностью на растяжение. Модуль упругости бетона различен для разных смесей.
 Бетон разрушается под действием растягивающих усилий. При низких напряжениях эластичность бетона постоянна, а при высоких напряжениях начинает развиваться трещинообразование.
Бетон разрушается под действием растягивающих усилий. При низких напряжениях эластичность бетона постоянна, а при высоких напряжениях начинает развиваться трещинообразование.Бетон имеет очень низкий коэффициент теплового расширения. Под действием растягивающих и усадочных напряжений все бетонные конструкции в той или иной степени трескаются. Как известно, бетон показывает разные свойства при разном водоцементном соотношении и имеет разнообразную бетонную смесь (
Определяется как отношение нормального напряжения к нормальной деформации ниже предела пропорциональности материала, называемого модулем упругости Ec .
Модуль упругости = единица напряжения/единица деформации
При испытании на прочность на сжатие образца бетона (цилиндр диаметром 15 см и длиной 30 см, объемом 15 см куб
В соответствии с нормами ACI модуль упругости бетона может быть измерен по формуле
. При нормальной плотности или весе бетона эти два соотношения можно упростить следующим образом:
При нормальной плотности или весе бетона эти два соотношения можно упростить следующим образом: #Где
Ec = модуль упругости бетона.
f’c = Прочность бетона на сжатие.
Модуль упругости бетона по
- ACI 318–08, (Бетон нормальной массы) Ec =4700 √f’c МПа и
- IS:456 модуль упругости бетона
Основными факторами, которые могут повлиять на определение значений модуля упругости, являются,
- Прочность бетона
- Состояние влажности бетона:
Эта таблица показала, что мы получаем различные эластичности в различных смесях,
#где
ГПА = Гигапаскаль
МПА = Мегапас. значение модуля упругости бетона может варьироваться и зависит от следующих факторов,
- Состав смеси.
- Свойства крупного заполнителя.
- Скорость загрузки.

- Условия отверждения.
- Добавки минеральные.
- Химические добавки.
Плотность бетона составляет около 150 фунтов/куб. футов или ( 2400 кг на кубический метр ).
Эластичность
Определяется как способность материала возвращаться в исходное положение (размер и форму) после снятия сил.
- Эластичность отличается для разных материалов.
- Под действием силы решетка материала меняет свою форму и размер и возвращается в исходное положение после прекращения действия силы.
- Делится на линейную или конечную эластичность .
Единицы
Единицы модуля упругости следующие:
- В единицах СИ МПа или Н/мм 2 или кН/м 2 .
- В единицах FPS psi или ksi или psf или ksf.
Связанная тема:
- блоки переоборудования для гражданского строительства
Поделитесь этой информацией со своими друзьями и распространяйте любовь
сообщите об этом объявлении
Модуль упругости бетона
 В последние годы в строительных спецификациях даже требуется соблюдение определенного модуля упругости бетона, в основном для ограничения чрезмерной деформации и раскачивания в высоких зданиях. Для Бурдж-Халифа (на данный момент самое высокое здание в мире) проектировщик указал минимум 43800 МПа для бетонных смесей 80 МПа для вертикальных элементов.
В последние годы в строительных спецификациях даже требуется соблюдение определенного модуля упругости бетона, в основном для ограничения чрезмерной деформации и раскачивания в высоких зданиях. Для Бурдж-Халифа (на данный момент самое высокое здание в мире) проектировщик указал минимум 43800 МПа для бетонных смесей 80 МПа для вертикальных элементов.Проще говоря, модуль упругости (MOE) измеряет жесткость материала и является хорошим общим показателем его прочности. Это отношение напряжения к деформации. Напряжение — это деформирующая сила, действующая на единицу площади (F/A), а деформация — деформация (изменение формы), вызванная напряжением (∆L/L).
Взаимосвязь стресс-деформация была впервые изучена Робертом Хуком, английским естествоиспытателем, архитектором и экспертом во многих различных областях знаний. В 1678 году он заявил, что «в пределах предела упругости напряжение прямо пропорционально деформации».
Напряжение α-деформация
т. е. напряжение/деформация = константа (эта константа называется модулем упругости)
Когда к телу прилагается напряжение, развивается деформация, и материал проходит различные стадии деформации, как показано на картинка ниже.

Эластичность – это свойство материи, благодаря которому материал восстанавливает свою первоначальную форму после прекращения действия деформирующей силы. Предел упругости (предел текучести) — это величина напряжения, которое может выдержать материал, прежде чем перейти от упругой деформации к пластической деформации. При пластической деформации материал не может восстановить свою первоначальную форму даже после прекращения действия деформирующей силы. Остается в деформированном виде. Пластическая деформация продолжается до предела прочности, а затем происходит разрыв. Эта точка напряжения, при которой материал разрушается с внезапным высвобождением накопленной упругой энергии, называется пределом прочности при растяжении (UTS).
В зависимости от типов напряжения (растяжение, сжатие или сдвиг) и деформации, включая направление, можно определить различные типы модуля упругости, как подробно описано ниже.
1. Модуль Юнга (E) – отношение линейного напряжения к линейной деформации,
2.
 Модуль сдвига (G или µ) – отношение напряжения сдвига к деформации сдвига и,
Модуль сдвига (G или µ) – отношение напряжения сдвига к деформации сдвига и,3. Модуль объемного сжатия (K) – отношение объемного напряжения к объемной деформации.
Модуль Юнга позволяет рассчитать изменение размеров бетонных элементов под действием растягивающих или сжимающих нагрузок. Например, он предсказывает, насколько бетонная колонна может укоротиться при сжатии. Другими словами, модуль упругости говорит нам, какое напряжение или сжатие требуется, чтобы сделать материал немного длиннее или короче.
Томас Янг (1773 – 1829) был английским ученым и экспертом во многих различных областях знаний. Его очень интересовали ранние эксперименты и исследования Леонарда Эйлера (1727 г.) и Джордано Рикатти (1782 г.) по модулям упругости материалов.
Модуль Юнга (E) = линейное напряжение/линейная деформация
Линейное напряжение = сила/площадь = F/A
Линейная деформация = изменение длины/исходная длина = ∆L/L
Следовательно, модуль Юнга (E) = (F/A)/ (∆L/L) = FL/ A∆L
Чем выше модуль упругости, тем бетон может выдерживать более высокие нагрузки, но бетон становится хрупким и быстрее появляются трещины.
 Низкий модуль упругости указывает на то, что он будет очень легко изгибаться и деформироваться. Высокий модуль упругости в раннем возрасте (7 дней или 14 дней) приводит к более высокому потенциалу растрескивания. Это происходит из-за высокого напряжения, возникающего из-за даже низкой деформации. Деформация может возникать по причинам, отличным от приложенного напряжения, например, усадки. Усадка и тепловая активность могут вызывать очень низкие напряжения, но из-за высокого модуля упругости соответствующие напряжения высоки. Поскольку предел прочности бетона на растяжение в этом раннем возрасте все еще низок, трещины будут развиваться.
Низкий модуль упругости указывает на то, что он будет очень легко изгибаться и деформироваться. Высокий модуль упругости в раннем возрасте (7 дней или 14 дней) приводит к более высокому потенциалу растрескивания. Это происходит из-за высокого напряжения, возникающего из-за даже низкой деформации. Деформация может возникать по причинам, отличным от приложенного напряжения, например, усадки. Усадка и тепловая активность могут вызывать очень низкие напряжения, но из-за высокого модуля упругости соответствующие напряжения высоки. Поскольку предел прочности бетона на растяжение в этом раннем возрасте все еще низок, трещины будут развиваться.Гидратированное цементное тесто имеет более низкий модуль упругости, чем заполнитель. Следовательно, объемное содержание заполнителя важно с точки зрения модуля упругости смеси. Модуль упругости затвердевшего цементного теста составляет от 10 до 30 ГПа, а заполнителя — от 45 до 85 ГПа. Бетон обычно имеет модуль упругости от 30 до 50 ГПа.
На модуль упругости бетона влияют следующие факторы:
1- Свойства крупного заполнителя, такие как модуль упругости заполнителя, тип заполнителя (дробленый или натуральный), петрология и минералогия, а также количество заполнителя.
 Чем выше объем заполнителя в смеси, тем выше модуль упругости.
Чем выше объем заполнителя в смеси, тем выше модуль упругости.2- Схема состава, включающая общее содержание вяжущего и водоцементное соотношение. Чем меньше пасты, тем выше модуль упругости.
3- Условия отверждения – образцы, отвержденные во влажном состоянии, показали лучшие результаты, чем образцы, отвержденные всухую, из-за усадки и связанных с ней трещин.
4- Скорость нагружения — высокая скорость нагружения приводит к более высокой прочности на сжатие и более высокому модулю упругости.
5- Химическая добавка – не оказывает большого влияния на модуль упругости. Но некоторые типы добавок могут привести к более высокой дисперсии цемента и, таким образом, привести к более высокой прочности на сжатие и более высокому модулю упругости.
6- Минеральные добавки – поскольку они влияют на прочность бетона, они также влияют на модуль упругости.
Наиболее важным фактором, влияющим на модуль упругости бетона, является используемый заполнитель.
 На него также влияет соотношение заполнителя и цемента и возраст бетона.
На него также влияет соотношение заполнителя и цемента и возраст бетона.В следующей таблице, взятой из Еврокода-2, приведены значения прочности на сжатие (на основе цилиндров и кубов), модуль упругости и прочность на растяжение для различных классов прочности бетона с нормальным весом, которые обычно используются для целей проектирования. 91,5 √fc —— в МПа
Где Ec — модуль упругости, Wc — вес бетона (фунты на фут или кг/м3), а fc — прочность цилиндра на сжатие через 28 дней (psi или МПа). ). Эти уравнения часто упрощаются на основе заполнителя нормальной плотности и нормального веса бетона следующим образом:
Ec = 57000 √fc —— в фунтах на квадратный дюйм или
Ec = 4700 √fc —— в МПа
BS 8110 Использование бетона в конструкциях Часть 2, пункт 7.2. Упругая деформация предлагает следующее уравнение для расчета ожидаемого значения модуля упругости на основе результатов кубической прочности за 28 дней.
Ec,28 = Ko + 0,2 fcu,28
Где Ko – постоянная, тесно связанная с модулем упругости заполнителя, часто принимаемым равным 20 кН/мм2 для заполнителя нормальной массы, а Fcu,28 – прочность на сжатие куба при 28 дней.

Если прогибы или деформации имеют большое значение, следует провести испытания бетона, изготовленного из заполнителя, который будет использоваться в конструкции. Но без предшествующих данных о заполнителе или с неизвестным заполнителем следует учитывать диапазон значений Ec, основанный на Ko = от 14 кН/мм2 до 26 кН/мм2. 90,5] ——- в МПа
Где ρ — плотность бетона в кг/м3, а fm — средняя прочность на сжатие в МПа через 28 дней.
Модуль упругости бетона испытывают с использованием цилиндрических образцов размером 150 мм X 300 мм в соответствии с:
1. ASTM C 469 – Статический модуль упругости и коэффициент Пуассона бетона при сжатии или
2. BS 1881 Часть 121- Определение статического модуля упругости при сжатии.
Модуль упругости определяется с помощью компрессометра, закрепленного на образце цилиндра (иногда также экстензометра для расчета коэффициента Пуассона, как показано на рисунке выше) и нагруженного при определенном уровне напряжения.
 Его можно оценить, используя уровни напряжения от 15 до 85% в диапазоне упругости. В ASTM уровень напряжения составляет 40 % прочности на сжатие сопутствующего цилиндра, а в BS — 33 % прочности сопутствующего цилиндра. В соответствии с методом испытаний ASTM результаты сообщаются с точностью до ближайших 200 МПа, а в соответствии с методом испытаний BS с точностью до ближайших 500 МПа.
Его можно оценить, используя уровни напряжения от 15 до 85% в диапазоне упругости. В ASTM уровень напряжения составляет 40 % прочности на сжатие сопутствующего цилиндра, а в BS — 33 % прочности сопутствующего цилиндра. В соответствии с методом испытаний ASTM результаты сообщаются с точностью до ближайших 200 МПа, а в соответствии с методом испытаний BS с точностью до ближайших 500 МПа.Доступны другие типы тензодатчиков (компрессометр и экстензометр). Электрический тензодатчик является наиболее подходящим методом для определения деформации бетона, который необходимо приклеить к образцу бетона, но который требует времени и внимания со стороны технических специалистов.
Эзеагу К.А. и Обаси К.С. (International Journal of Advanced Research) сообщили о своих исследованиях, что бетон, изготовленный с максимальным номинальным размером заполнителя 20 мм, показал более высокий модуль упругости, чем бетон с максимальным номинальным размером заполнителя 30 мм и 60 мм. Они рассчитали модуль упругости на основе различных уравнений и нашли различные значения модулей упругости.

Takafumi Noguchi и др. (ACI Structural Journal) сообщили, что, несмотря на то, что японские и американские кодовые правила предполагают удельный вес с показателем степени 1,5, их исследования показали, что существует прямая пропорциональная зависимость между модулем упругости бетона и его удельным весом. до 2.
К. Анбувелан и д-р К. Субраманиан (International Journal of Engineering and Technology) сообщили, что на основании их экспериментального исследования упругих свойств бетона, содержащего стальную фибру, IS 456 и EC-2 предсказывают более высокий модуль упругости. чем BS 8110, ACI 318 и NZS 3101.
Основываясь на результатах своего исследования, Валид Баалбаки и др. (Журнал материалов ACI) пришли к выводу, что точное предсказание модуля упругости высокопрочного бетона по его прочности на сжатие ненадежно.
В следующей таблице приведены прочность на сжатие и модуль упругости (результаты пробной смеси) бетонных смесей, используемых для вертикальных элементов Бурдж-Халифа – самой высокой башни в мире.
 Значения модуля упругости очень близки к уравнению ACI 318.
Значения модуля упругости очень близки к уравнению ACI 318.Прежде чем закончить эту статью, у автора есть вопрос к читателям. Всем известно, что модуль упругости указывает на жесткость материала. Другими словами, он представляет собой прочность материала. Прочность материала может быть шести следующих типов:
1- Хрупкий — материал очень легко ломается или превращается в порошок.
2- Податливый — материал можно растолочь в тонкие листы, как металл.
3- Пластичный — материал можно вытянуть в проволоку, как металл.
4- Сектильный — материал можно ровно разрезать ножом.
5- Пластика — материал деформируется под нагрузкой, но не может восстановить свою первоначальную форму при снятии силы.
6- Эластичный – материал деформируется под нагрузкой, но восстанавливает свою первоначальную форму при снятии силы.
По мере увеличения модуля упругости материал становится более жестким и хрупким. Но по сравнению со сталью бетон более хрупок, хотя модуль упругости стали составляет 200 ГПа, а бетона — от 25 до 50 ГПа.


 Бетон разрушается под действием растягивающих усилий. При низких напряжениях эластичность бетона постоянна, а при высоких напряжениях начинает развиваться трещинообразование.
Бетон разрушается под действием растягивающих усилий. При низких напряжениях эластичность бетона постоянна, а при высоких напряжениях начинает развиваться трещинообразование. При нормальной плотности или весе бетона эти два соотношения можно упростить следующим образом:
При нормальной плотности или весе бетона эти два соотношения можно упростить следующим образом: 
 В последние годы в строительных спецификациях даже требуется соблюдение определенного модуля упругости бетона, в основном для ограничения чрезмерной деформации и раскачивания в высоких зданиях. Для Бурдж-Халифа (на данный момент самое высокое здание в мире) проектировщик указал минимум 43800 МПа для бетонных смесей 80 МПа для вертикальных элементов.
В последние годы в строительных спецификациях даже требуется соблюдение определенного модуля упругости бетона, в основном для ограничения чрезмерной деформации и раскачивания в высоких зданиях. Для Бурдж-Халифа (на данный момент самое высокое здание в мире) проектировщик указал минимум 43800 МПа для бетонных смесей 80 МПа для вертикальных элементов.
 Модуль сдвига (G или µ) – отношение напряжения сдвига к деформации сдвига и,
Модуль сдвига (G или µ) – отношение напряжения сдвига к деформации сдвига и, Низкий модуль упругости указывает на то, что он будет очень легко изгибаться и деформироваться. Высокий модуль упругости в раннем возрасте (7 дней или 14 дней) приводит к более высокому потенциалу растрескивания. Это происходит из-за высокого напряжения, возникающего из-за даже низкой деформации. Деформация может возникать по причинам, отличным от приложенного напряжения, например, усадки. Усадка и тепловая активность могут вызывать очень низкие напряжения, но из-за высокого модуля упругости соответствующие напряжения высоки. Поскольку предел прочности бетона на растяжение в этом раннем возрасте все еще низок, трещины будут развиваться.
Низкий модуль упругости указывает на то, что он будет очень легко изгибаться и деформироваться. Высокий модуль упругости в раннем возрасте (7 дней или 14 дней) приводит к более высокому потенциалу растрескивания. Это происходит из-за высокого напряжения, возникающего из-за даже низкой деформации. Деформация может возникать по причинам, отличным от приложенного напряжения, например, усадки. Усадка и тепловая активность могут вызывать очень низкие напряжения, но из-за высокого модуля упругости соответствующие напряжения высоки. Поскольку предел прочности бетона на растяжение в этом раннем возрасте все еще низок, трещины будут развиваться. Чем выше объем заполнителя в смеси, тем выше модуль упругости.
Чем выше объем заполнителя в смеси, тем выше модуль упругости. На него также влияет соотношение заполнителя и цемента и возраст бетона.
На него также влияет соотношение заполнителя и цемента и возраст бетона.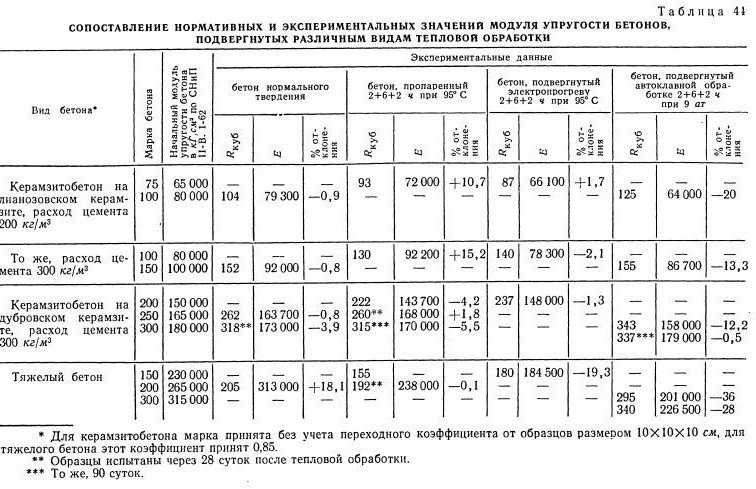
 Его можно оценить, используя уровни напряжения от 15 до 85% в диапазоне упругости. В ASTM уровень напряжения составляет 40 % прочности на сжатие сопутствующего цилиндра, а в BS — 33 % прочности сопутствующего цилиндра. В соответствии с методом испытаний ASTM результаты сообщаются с точностью до ближайших 200 МПа, а в соответствии с методом испытаний BS с точностью до ближайших 500 МПа.
Его можно оценить, используя уровни напряжения от 15 до 85% в диапазоне упругости. В ASTM уровень напряжения составляет 40 % прочности на сжатие сопутствующего цилиндра, а в BS — 33 % прочности сопутствующего цилиндра. В соответствии с методом испытаний ASTM результаты сообщаются с точностью до ближайших 200 МПа, а в соответствии с методом испытаний BS с точностью до ближайших 500 МПа.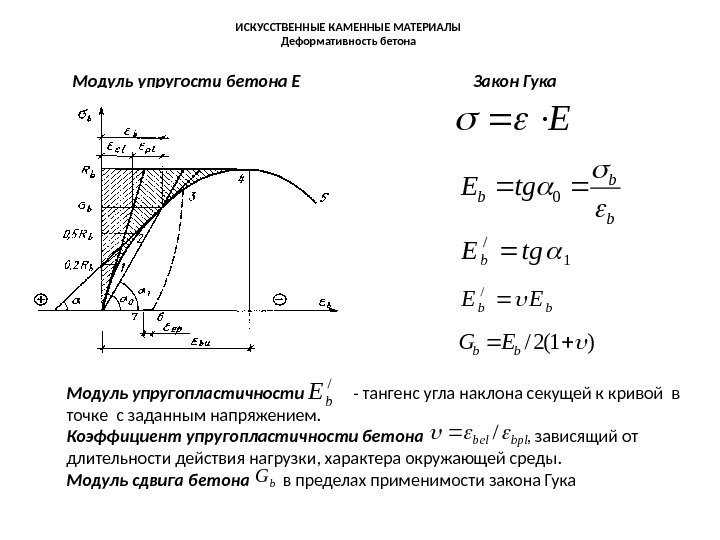
 Значения модуля упругости очень близки к уравнению ACI 318.
Значения модуля упругости очень близки к уравнению ACI 318.