Минимальный процент армирования железобетонных конструкций сп: конструируем.рф — электронный журнал
Как определить минимальный процент армирования конструкции?
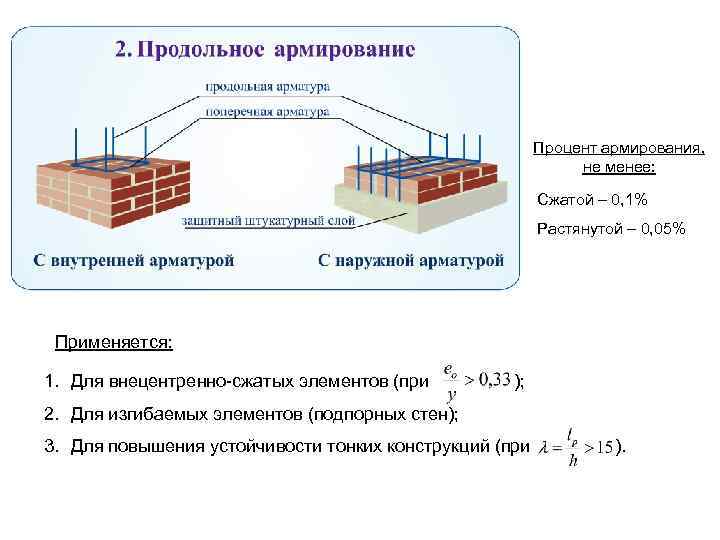
Нормы дают нам ограничение в армировании любых конструкций в виде минимального процента армирования – даже если по расчету у нас вышла очень маленькая площадь арматуры, мы должны сравнить ее с минимальным процентом армирования и установить арматуру, площадь которой не меньше того самого минимального процента армирования.
Где мы берем процент армирования? В «Руководстве по конструированию железобетонных конструкций», например, есть таблица 16, в которой приведены данные для всех типов элементов.
Но вот есть у нас на руках цифра 0,05%, а как же найти искомое минимальное армирование?
Во-первых, нужно понимать, что ищем мы обычно не площадь всей арматуры, попадающей в сечение, а именно площадь продольной рабочей арматуры. Иногда эта площадь расположена у одной грани плиты (в таблице она обозначена как А – площадь у растянутой грани, и А’ – площадь у сжатой грани), а иногда это вся площадь элемента.
На примерах, думаю, будет нагляднее.
Пример 1. Дана монолитная плита перекрытия толщиной 200 мм (рабочая высота сечения плиты h₀ до искомой арматуры 175 мм). Определить минимальное количество арматуры у нижней грани плиты.
1) Найдем площадь сечения бетона 1 погонного метра плиты:
1∙0,175 = 0,175 м² = 1750 см²
2) Найдем в таблице 16 руководства минимальный процент армирования для плиты (изгибаемого элемента):
0,05%
3) Составим известную со школы пропорцию:
1750 см² — 100%
Х – 0,05%
4) Из пропорции найдем искомую минимальную площадь арматуры:
Х = 0,05∙1750/100 = 0,88 см²
5) По сортаменту арматуры находим, что данная площадь соответствует 5 стержням диаметром 5 мм. То есть меньше этого мы устанавливать не имеем права.
Обратите внимание! Мы определяем площадь арматуры у одной грани плиты (а не площадь арматуры всего сечения плиты), именно она соответствует минимальному проценту армирования.
Пример 2. Дана плита перекрытия шириной 1,2 м, толщиной 220 мм (рабочая высота сечения плиты h₀ до искомой арматуры 200 мм), с круглыми пустотами диаметром 0,15м в количестве 5 шт. Определить минимальное количество арматуры в верхней зоне плиты.
Заглянув в примечание к таблице, мы увидим, что в случае с двутавровым сечением (а при расчете пустотных плит мы имеем дело с приведенным двутавровым сечением), мы должны определять площадь плиты так, как описано в п. 1:
1) Найдем ширину ребра приведенного двутаврового сечения плиты:
1,2 – 0,15∙5 = 0,45 м
2) Найдем площадь сечения плиты, требуемую условиями расчета:
0,45∙0,2 = 0,09 м² = 900 см²
3) Найдем в таблице 16 руководства минимальный процент армирования для плиты (изгибаемого элемента):
0,05%
4) Составим пропорцию:
900 см² — 100%
Х – 0,05%
5) Из пропорции найдем искомую минимальную площадь арматуры:
Х = 0,05∙900/100 = 0,45 см²
6) По сортаменту арматуры находим, что данная площадь соответствует 7 стержням диаметром 3 мм.
То есть меньше этого мы устанавливать не имеем права.
И снова обратите внимание! Мы определяем площадь арматуры у одной грани плиты (а не площадь арматуры всего сечения плиты), именно она соответствует минимальному проценту армирования.
Пример 3. Дан железобетонный фундамент под оборудование сечением 1500х1500 мм, армированная равномерно по всему периметру. Расчетная высота фундамента равна 4 м. Определить минимальный процент армирования.
1) Найдем площадь сечения фундамента:
1,5∙1,5 = 2,25 м² = 22500 см²
2) Найдем в таблице 16 руководства минимальный процент армирования для фундамента, предварительно определив l₀/h = 4/1.5 = 4,4 < 5 (для прямоугольного сечения):
0,05%
3) Из пункта 2 примечаний к таблице 16 (см. рисунок выше) определим, что мы должны удвоить процент армирования, чтобы найти минимальную площадь арматуры всего сечения фундамента (а не у одной его грани!), т.е. минимальный процент армирования у нас будет равен:
2∙0,05% = 0,1%
4) Составим пропорцию:
22500 см² — 100%
4) Из пропорции найдем искомую минимальную площадь арматуры:
Х = 0,1∙22500/100 = 22,5 см²
5) Принимаем шаг арматуры фундамента 200 мм, значит по периметру мы должны установить 28 стержней, а площадь одного стержня должна быть не меньше 22,5/28 = 0,8 см²
6) По сортаменту арматуры находим, что мы должны принять диаметр арматуры 12 мм.
То есть меньше этого мы устанавливать не имеем права.
И снова обратите внимание! В данном примере мы определяем площадь арматуры не у одной грани фундамента, а сразу для всего фундамента, т.к. он заармирован равномерно по всему периметру.
Пример 4. Дана железобетонная колонна сечением 500х1600 (рабочая высота сечения колонны в коротком направлении h₀= 460 мм). Расчетная высота колонны равна 8 м. Определить минимальный процент армирования у длинных граней колонны.
1) Найдем площадь сечения колонны:
0,46∙1,6 = 0,736 м² = 7360 см²
2) Найдем в таблице 16 руководства минимальный процент армирования для колонны (внецентренно-сжатого элемента с l₀/h = 8/0.5 = 16):
0,2%
3) Составим известную со школы пропорцию:
7360 см² — 100%
Х – 0,2%
4) Из пропорции найдем искомую минимальную площадь арматуры:
Х = 0,2∙7360/100 = 14,72 см²
5) Из руководства по проектированию находим, что максимальное расстояние между продольной арматурой в колонне не должно превышать 400 мм.
6) По сортаменту находим, что у каждой грани нам нужно установить 4 стержня диаметром 22 мм. Если считаем, что диаметр великоват, увеличиваем количество стержней, уменьшая тем самым диаметр каждого.
Обратите внимание! Мы определяем площадь арматуры
Пример 5. Дана стена и толщиной 200 мм (рабочая высота сечения плиты h₀ до искомой арматуры 175 мм), рабочая высота стены l₀ = 5 м. Определить минимальное количество арматуры у обеих граней стены.
1) Найдем площадь сечения бетона 1 погонного метра стены:
1∙0,175 = 0,175 м² = 1750 см²
2) Найдем в таблице 16 руководства минимальный процент армирования для стены, предварительно определив l₀/h = 5/0.
0,25%
3) Составим пропорцию:
1750 см² — 100%
Х – 0,25%
4) Из пропорции найдем искомую минимальную площадь арматуры:
Х = 0,25∙1750/100 = 4,38 см²
5) По сортаменту арматуры находим, что данная площадь соответствует 5 стержням диаметром 12 мм, которые нужно установить у каждой грани на каждом погонном метре стены.
Заметьте, если бы стена была толще, минимальный процент армирования резко бы упал. Например, при толщине стены 210 мм потребовалось бы уже 5 стержней диаметром 10 мм, а не 12.
Процент армирования железобетонных конструкций: минимальный, максимальный
С целью выполнения армированием своего прямого предназначения, необходим специальный расчет усиления бетона, что соответствует минимальному и максимальному проценту. Эта величина играет важную роль в проектных расчетах. Ее малый показатель не дает права считать изделие усиленным до ЖБИ, а больший приведет к существенному снижению технических характеристик ж/б материала.
Содержание
- Степень армирования
- Особенности расчетов
- Значение армирования
- Минимальный процент
- Максимальный коэффициент арматуры
- Сохранение прочности
- Защитный слой бетона
Степень армирования
Минимальная величина коэффициента армирования (0,05%) позволяет назвать изделие железобетонным.
Если металлические элементы поместить в бетон, но величина арматурной составляющей не будет соответствовать техническим требованиям ГОСТа, то это изделие относится к бетонным наименованиям с конструкционным укреплением и не допускается к эксплуатации. Для фундамента, колонн, несущих стен и балок степень армирования рассчитывается по формуле: К= (М1÷М2)x100; где
- М1 — вес стального каркаса;
- М2 — масса бетонного монолита.
Площадь сечения стержней обуславливает способность поддерживающего каркаса нести и распределять нагрузки.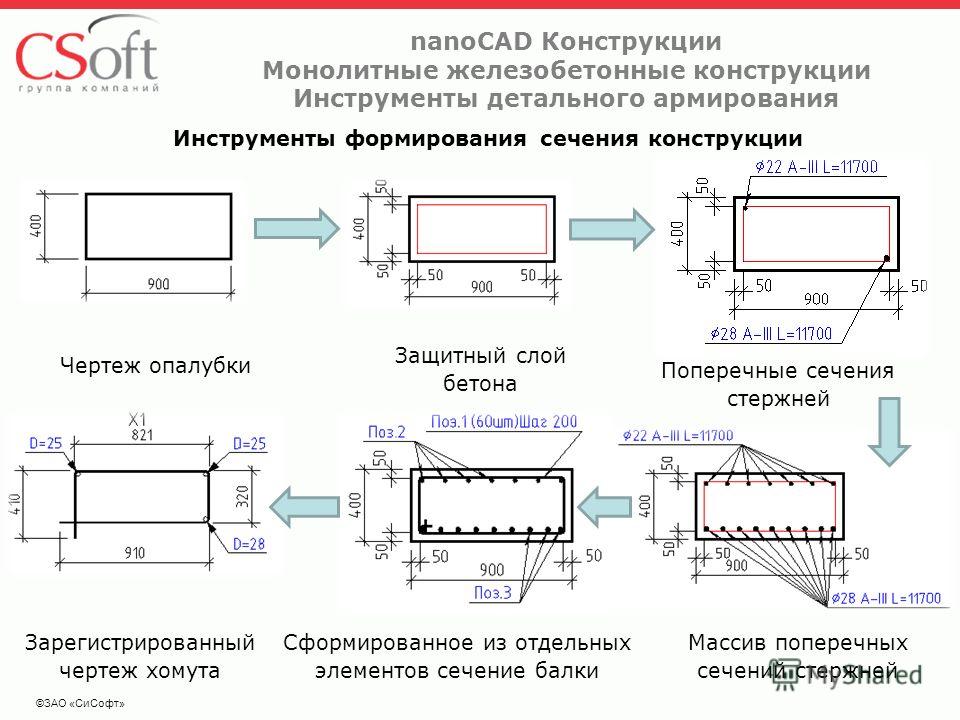
Чем больше диаметр прутьев, тем выше процент армирования и прочность сооружения. Обычно предпочитают стержни в 12—14 мм диаметром. Удельный показатель веса арматуры уменьшается с увеличением толщины бетонного слоя.
Особенности расчетов
В железобетоне используют только горячекатаную сталь высокого класса, так как она устойчива к коррозии и крепка. Чтобы сваренный металлический каркас, расположенный в бетоне, сделал свое дело, необходим точный расчет, позволяющий уточнить, сколько и какие материалы необходимы. Важность расчетов сложно переоценить. Они выполняются с привлечением технических формул, где учтены сопротивление используемых стройматериалов, соотношение предельно допустимых нагрузок к закладываемым и другие параметры. А также стандартные вычисления предусматривают тип фундамента, наличие дополнительных конструкционных элементов, марку бетона, несущие нагрузки. По окончании математической части все данные наносят на чертеж, где представлена схема армирования. Из проекта исполнители знают, сколько и какого вида стальных стержней нужно взять.
А также стоит учесть в каком порядке их расположить и связать.
Значение армирования
Минимальный процент
Наименьшая степень усиления бетона арматурой, что расположена продольно, вычисляется соответственно площади сечения железобетонного объекта и составляет 0,05%. Меньший показатель говорит лишь о локальном укреплении бетонного раствора. Такое сооружение ненадежное и опасное, поскольку возможно его разрушение. Минимальный процент армирования зависит от типа и локализации действующих нагрузок (сжатие, растяжение) вне пределов рабочего бетонного сечения, между прутьями каркаса, и колеблется в пределах от 0,5 до 0,25% для каждой конкретной конструкции.
Максимальный коэффициент арматуры
После заливки важно уплотнить бетон, чтобы не было воздуха возле решетки, который приводит к снижению прочности сооружения.Предельно допустимая доля стали для ж/б конструкций составляет 4% (в колоннах 5%). Тип стальных элементов и марка бетона влияния не имеют. Превышение максимальной величины приводит к снижению эксплуатационных характеристик изделия и возрастанию его веса, что усилит нагрузку вышерасположенных составляющих на нижние.
Укрепляя бетон, важно обеспечить плотное обволакивание всей металлической решетки раствором без образования воздушных карманов.
Сохранение прочности
Бетон создает защиту стали от влияния факторов внешней среды (влаги, химических веществ), поэтому металл должен быть полностью укрыт раствором. Любые манипуляции с железобетонным объектом типа алмазного бурения, резки, отделения частей, образования сквозных тоннелей в стене приводят к значительному уменьшению потенциала прочности.
Все работы, нарушающие монолитность железобетонной конструкции, должны проводиться с учетом схемы расположения и пространственной структуры каркаса.
Защитный слой бетона
В таблице представлена зависимость толщины бетонного слоя от типа строительного элемента:
| Наименование стройматериала | Ширина объекта, см | Слой бетона, см |
| Несущая стена | Более 10 | 1,5 |
| Стена | Менее 10 | 1 |
| Ребро | 25 | 2 |
| Балка | Менее 25 | 1,5 |
| Колонна | 3 | |
| Фундаментная балка | ||
Посмотреть «СНиП 2.
03.01-84» или cкачать в PDF (4.8 MB)
Особое внимание следует уделить фундаментам монолитной структуры. Наличие цементной подушки оправдывает слой бетонной защиты в 3,5 см, без нее — 7 см. Сборный фундамент потребует слоя шириной 3 сантиметра. Чем больше толщина искусственного камня, тем прочнее арматуру рекомендуют использовать. Технические выкладки взяты из свода требований к бетонным и железобетонным конструкциям СНиП 2.03.01—84.
Минимальное армирование в бетонных конструкциях и нестабильность материала/конструкции
Abdalla HM, Karihaloo BL (2003) Определение независимой от размера удельной энергии разрушения бетона по результатам испытаний на трехточечный изгиб и расщепление клиньев. Mag Concrete Res 55: 133–141
Артикул Google Scholar
Балух М.
Х., Азад А.К., Ашмави В. (1992) Применение механики разрушения к железобетонным элементам при изгибе. В: Карпинтери А. (ред.) Применение механики разрушения к железобетону. Elsevier, Лондон, стр. 413–436
Google Scholar
Bosco C, Carpinteri A (1992) Оценка механики разрушения минимальной арматуры в бетонных конструкциях. В: Карпинтери А. (ред.) Применение механики разрушения к железобетону. Elsevier, Лондон, стр. 347–377
Google Scholar
Bosco C, Carpinteri A (1992b) Размягчение и проламывание армированных элементов. J Eng Mech (ASCE) 118: 1564–1577
Артикул Google Scholar
Bosco C, Carpinteri A (1995) Прерывистая конститутивная реакция волокнистых композитов с хрупкой матрицей. J Mech Phys Solids 43: 261–274
Статья Google Scholar
Bosco C, Carpinteri A, Debernardi PG (1990) Минимальное армирование в высокопрочном бетоне.
Статья Google Scholar
Боско К., Карпинтери А., Дебернарди П.Г. (1992) Влияние масштаба на пластическую вращательную способность ж.д. лучи. В кн.: Бажан З.П.(ред.) Механика разрушения бетонных конструкций. Elsevier, Лондон, стр. 735–740
Google Scholar
Карпинтери А. (1981a) Модель механики разрушения железобетона. В: Труды I.A.B.S.E. коллоквиум по передовой механике железобетона. Делфт, стр. 17–30
Карпинтери А. (1981b) Статические и энергетические параметры разрушения горных пород и бетона. Материнская структура 14: 151–162
Google Scholar
Карпинтери А. (1984) Устойчивость процесса разрушения железобетонных балок. J Struct Eng (ASCE) 110: 544–558
Статья Google Scholar
Карпинтери А.
, Массабо Р. (1996) Мостовые и когезионные трещины в поведении композитов с хрупкой матрицей при изгибе. Int J Fract 81: 125–145
Артикул Google Scholar
Карпинтери А., Массабо Р. (1997a) Непрерывная и прерывистая модель перемычек трещин для армированных волокном материалов при изгибе. Int J Solids Struct 34: 2321–2338
Артикул Google Scholar
Карпинтери А., Массабо Р. (1997b) Обратное изменение масштаба разрушения волокнистых композитов. J Eng Mech (ASCE) 123: 107–114
Артикул Google Scholar
Карпинтери А., Ферро Г., Боско С., Элкатиб М. (1999) Масштабные эффекты и явления переходного разрушения железобетонных балок при изгибе. В: Карпинтери А. (ред.) Минимальное армирование в бетонных элементах, том 24. Публикации ESIS, Elsevier Science Ltd, стр. 1–30
Карпинтери А.
, Ферро Г., Вентура Г. (2003) Влияние размера на реакцию железобетона на изгиб элементы с нелинейной матрицей. Eng Fract Mech 70:995–1013
Артикул Google Scholar
Ferro G (2002) Модель многоуровневой мостиковой трещины для высокопрочных бетонов. Theor Appl Fract Mech 38: 177–190
Артикул КАС Google Scholar
Хокинс Н., Хьорсетет К. (1992) Минимальные требования к армированию бетонных изгибаемых элементов. В: Карпинтери А. (ред.) Применение механики разрушения к железобетону. Elsevier, Лондон, стр. 37–412
Google Scholar
Hillerborg A (1990) Концепции механики разрушения применительно к моменту и вращательной способности железобетонных балок. Eng Fract Mech 35: 233–240
Артикул Google Scholar
Хиллерборг А., Модер М., Петерссон П.
(1976) Анализ образования и роста трещин в бетоне с помощью механики разрушения и конечных элементов. Цемент Бетон Res 6: 773–782
Артикул Google Scholar
Дженк Ю.С., Шах С.П. (1986) Распространение трещин в фибробетоне. J Eng Mech (ASCE) 112: 19–34
Google Scholar
Карихалоо Б.Л. (1995) Механика разрушения и конструкционный бетон. Аддисон-Уэсли, Лонгман
Google Scholar
Karihaloo BL, Wang J (2000) Механика цементных композитов, армированных волокном. Вычислительная структура 76: 19–34
Артикул Google Scholar
Karihaloo BL, Abdalla HM, Imjai T (2003) Простой метод определения истинной удельной энергии разрушения бетона. Mag Concrete Res 55: 471–481
Артикул Google Scholar
Li VC, Wang Y, Backer S (1991) Микромеханическая модель размягчения при натяжении и упрочнения соединения коротких случайных волокон, армированных хрупкими матричными композитами.
J Mech Phys Solids 39: 607–625
Артикул Google Scholar
Ногабай К. (2000) Балки из фибробетона на сдвиг и изгиб: эксперимент и модель. J Struct Eng (ASCE) 126: 243–251
Статья Google Scholar
RILEM TC50 (1985) Определение энергии разрушения строительного раствора и бетона с помощью испытаний балок с надрезом на трехточечный изгиб. Материнская структура 18: 287–290
Google Scholar
RILEM TC89 (1990) Определение параметров разрушения простого бетона с помощью испытаний на трехточечный изгиб. Mater Struct 23:457–460
Google Scholar
Ruiz G (2001) Распространение когезионной трещины, пересекающей армирующий слой. Int J Fract 111: 265–282
Статья Google Scholar
Ruiz G, Elices M, Planas J (1998) Экспериментальное исследование разрушения железобетонных балок.
Mater Struct 31: 683–691
Артикул КАС Google Scholar
Свами Р.Н., Аль-Таан С.А. (1981) Деформация и предел прочности при изгибе армированных балок, изготовленных из сталефибробетона. ACI J Proc 5: 395–405
Google Scholar
Расчет железобетонных колонн в соответствии с ACI 318-14 в RFEM
При использовании элементов RF-CONCRETE возможен расчет бетонных колонн в соответствии с ACI 318-14. Точное проектирование сдвига бетонной колонны и продольного армирования важно для обеспечения безопасности. В следующей статье будет подтвержден расчет арматуры в элементах RF-CONCRETE с использованием пошаговых аналитических уравнений в соответствии со стандартом ACI 318-14, включая требуемую продольную стальную арматуру, общую площадь поперечного сечения и размер/расстояние связей.
Анализ бетонных колонн
Бетонная колонна с армированными квадратными анкерами предназначена для поддержки осевой статической и динамической нагрузки в 135 и 175 тысяч фунтов соответственно с использованием расчетных комбинаций нагрузки ULS и расчетных нагрузок LRFD в соответствии с ACI 318-14 [1], как показано на рисунке 01.
Бетонный материал имеет предел прочности при сжатии f’ c , равный 4 тысячам фунтов на квадратный дюйм, в то время как арматурная сталь имеет предел текучести f y , равный 60 тысячам фунтов на квадратный дюйм. Процент стальной арматуры изначально принимается равным 2%.
Pисунок 01 — Бетонная колонна — Вид фасада
Расчет размеров
Для начала необходимо рассчитать размеры поперечного сечения. Квадратная анкерная колонна предназначена для регулирования сжатия, поскольку все осевые нагрузки строго сжимаются. По таблице 21.2.2 [1] коэффициент снижения прочности Φ равен 0,65. При определении максимальной осевой прочности используется таблица 22.4.2.1 [1], в которой коэффициент альфа (α) установлен равным 0,80. Теперь можно рассчитать расчетную нагрузку P u .
Р у = 1,2 (135 тыс.) + 1,6 (175 тыс.)
На основании этих коэффициентов P u равно 442 тысячам фунтов. Далее, общее поперечное сечение A г может быть рассчитано с использованием уравнения.
22.4.2.2.
P U = (φ) (α) [0,85 F ‘ C (A G — A ST ) + F Y A ST ]
9 442K = 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0,65). ) [0,85 (4 тысячи фунтов) (A г — 0,02 A г ) + ((60 ksi) (0,02) A г )]Решение для A г получаем площадь 188 в 2 . Квадратный корень из A g берется и округляется в большую сторону, чтобы получить поперечное сечение колонны 14 x 14 дюймов.
Требуемая стальная арматура
st можно рассчитать по уравнению 22.4.2.2, подставив известное значение A г = 196 в 2 и решив
442k = (0,65) (0,80) [0,85 (4 тысяч фунтов) (193 в 2 — A st ) + ((60 ksi) (A st ))]
Решение для A st дает значение 3,24 в 2 . Отсюда можно найти количество брусков, необходимое для проектирования.
Согласно разд. 10.7.3.1 [1] квадратная соединительная колонна должна иметь не менее четырех стержней. На основании этих критериев и минимальной требуемой площади 3,24 по 2 (8) для стальной арматуры используются стержни № 6 из Приложения А [1]. Это обеспечивает зону армирования ниже.
A St = 3,52 дюйма 2
Выбор стяжки
Для определения минимального размера стяжки требуется разд. 25.7.2.2 [1]. В предыдущем разделе мы выбрали продольные стержни № 6, которые меньше, чем стержни № 10. Основываясь на этой информации и разделе, мы выбираем № 3 для галстуков.
Расстояние между стяжками
Для определения минимального расстояния между стяжками мы обращаемся к разд. 25.7.2.1 [1]. Стяжки, состоящие из деформированных стержней с замкнутой петлей, должны иметь расстояние, соответствующее пунктам (а) и (б) настоящего раздела.
(a) Расстояние в свету должно быть равно или больше (4/3) d agg . Для этого расчета мы примем совокупный диаметр (d agg ) равным 1,00 дюйма.
(b) Межцентровое расстояние не должно превышать минимум 16d b диаметра продольного стержня, 48d b поперечного сечения или наименьшего размера элемента.
с Макс. = Мин. (16d b , 48d b , 14 дюймов)
16d b = 16 (0,75 дюйма) = 12 дюймов
48d 9018 (48d 9018) = 18 дюймов
Рассчитанное минимальное расстояние между стяжками в чистоте равно 1,33 дюйма, а рассчитанное максимальное расстояние между стяжками равно 12 дюймам.
Проверка детализации
Теперь можно выполнить проверку детализации для проверки процента армирования. Требуемый процент стали должен составлять от 1% до 8% в соответствии с требованиями ACI 318-14 [1]. 92}\;=\;0,01795\;\cdot\;100\;\;=\;1,8\%$ ОК.
Расстояние между продольными стержнями
Максимальное расстояние между продольными стержнями можно рассчитать на основе расстояния между крышками и диаметра анкерных и продольных стержней.
Максимальный шаг продольных стержней:
$\frac{14\;\mathrm{дюйм}.\;-\;2\;(1,5\;\mathrm{дюйм}.)\;-\;2\;( 0,375\;\mathrm{дюйм}.)\;-\;3\;(0,75\;\mathrm{дюйм}.)}2\;=\;4,00\;\mathrm{дюйм}.$
4,00 дюйм … меньше 6 дюймов, что требуется в соответствии с 25.7.2.3 (a) [1]. ХОРОШО.
Минимальное расстояние между стержнями в продольном направлении можно рассчитать с помощью ссылки на 25.2.3 [1], в которой указано, что минимальное расстояние в продольном направлении для колонн должно быть как минимум наибольшим из значений от (a) до (c).
(a) 1,5 дюйма
(b) 1,5 d b = 1,5 (0,75 дюйма) = 1,125 дюйма
(c) (4/3) d b = (4/3) ( 1,00 дюйма) = 1,33 дюйма
Следовательно, минимальное расстояние между продольными стержнями равно 1,50 дюйма
Длина развертывания (L d ) также должна быть рассчитана со ссылкой на 25.4.9.2 [1]. Это будет равно наибольшему из (a) или (b), рассчитанному ниже.
(a) $ {\ mathrm L} _ {\ mathrm {dc}} \; = \; \ влево (\ frac {\ displaystyle {\ mathrm f} _ {\ mathrm y} \; \ cdot \; { \ mathrm \ psi} _ {\ mathrm r}} {\ displaystyle50 \; \ cdot \; \ mathrm \ lambda \; \ cdot \; \ sqrt {\ mathrm f’\; \ cdot \; \ mathrm c}} \ справа) \;\cdot\;{\mathrm d}_{\mathrm b}\;=\;\left(\frac{\displaystyle\left(60,000\;\mathrm{psi}\right)\;\cdot \;\left(1.
0\right)}{50\;\cdot\;\left(1.0\right)\;\cdot\;\sqrt{4000\;\mathrm{psi}}}\right)\;\ cdot\;\left(0.75\;\mathrm{in}.\right)\;=\;14.23\;\mathrm{in}.$
(б) $ {\ mathrm L} _ {\ mathrm {dc}} \; = \; 0,0003 \; \ cdot \; {\ mathrm f} _ {\ mathrm y} \; \ cdot \; {\ mathrm\psi}_{\mathrm r}\;\cdot\;{\mathrm d}_{\mathrm b}\;=\;0,0003\;\cdot\;(60000\;\mathrm{psi})\ ;\cdot\;(1.0)\;\cdot\;(0,75\;\mathrm{in}.)\;=\;13,5\;\mathrm{in}.$
В этом примере (a) равно большее значение, поэтому L dc = 14,23 дюйма
Ссылаясь на 25.4.10.1 [1], длина развертывания умножается на отношение требуемой стальной арматуры к имеющейся стальной арматуре. 92}\right)\;=\;0,65\;\mathrm{ft}$.
Усиленная квадратная анкерная колонна полностью спроектирована, ее поперечное сечение можно увидеть ниже на рис. 02.
Pисунок 02 — Железобетонная колонна — Расчет арматуры/размеры
Сравнение с RFEM
Альтернативой для расчета квадратной анкерной колонны вручную является использование дополнительного модуля RF-CONCRETE Members и выполнение расчета в соответствии с ACI 318-14 [1].
Модуль определит необходимое армирование, чтобы выдержать приложенные к колонне нагрузки. Кроме того, программа также спроектирует предоставленную арматуру на основе заданных осевых нагрузок на колонну с учетом требований стандарта к расстоянию. Пользователь может вносить небольшие коррективы в предоставленную компоновку армирования в таблице результатов.
На основе приложенных нагрузок для этого примера компания RF-CONCRETE Members определила требуемую площадь продольной арматуры 1,92 в 2 и предусмотренную площадь 3,53 в 2 . Длина разработки, рассчитанная в дополнительном модуле, равна 0,81 фута. Расхождение по сравнению с длиной разработки, рассчитанной выше по аналитическим уравнениям, связано с нелинейными расчетами программы, включая частный коэффициент γ. Коэффициент γ представляет собой отношение предельной и действующей внутренних сил, взятое из программы RFEM. Длина разработки в элементах RF-CONCRETE находится путем умножения обратного значения гаммы на длину, определенную из 25.