Куб блоков сколько штук: Сколько блоков в кубе таблица с рассчетами пеноблока и газосиликата на дом
сколько их в поддоне и кубе (в 1 м3)? Сколько штук в 1 м2? Расчет для кладки стен дома
Керамзитоблок – наряду со стандартным пено- или газоблоком – прочное, довольно лёгкое в использовании сырье, применимое в качестве опорного материала. Его возможностей хватит, чтобы несущие стены надёжно удерживали чердак и крышу строения.
Зачем нужно знать количество?
Керамзитобетонные блоки, как и иные разновидности строительных кирпичей и прямоугольных камней, получаемые из высокопористого и низкопористого материалов, рассчитываются в удельной величине, а именно: количество штук на кубометр в штабеле, число единиц на квадратный метр выкладываемой из них стены.
Учёт кубатуры используют компании, для которых важно не только количество блоков в кубометре, но и вес такого «куба». Благодаря знанию массы одного или нескольких штабелей компания-посредник, продающая данный стройматериал, вышлет грузовик (или несколько грузовиков) с нужной грузоподъёмностью, гружённый керамзитоблоками, по адресу клиента. В частности, фирма прикинет, на какой заправке – по маршруту следования – водитель зальёт в бак требуемое количество бензина, чтобы без отсрочки (в указанное время) доставить пеноблоки к клиенту на объект.
Конечному заказчику, в свою очередь, нецелесообразно закупать лишние керамзитоблоки.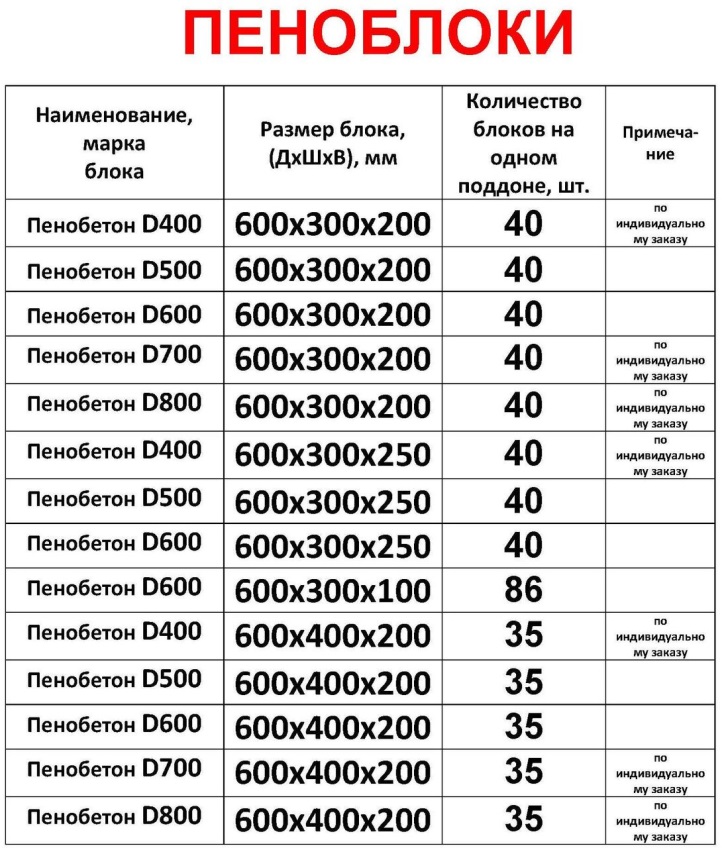 Даже с учётом небольшого процента возможного керамзитобоя потребитель просчитывает количество блоков, необходимых для укладки стен по проекту строящегося дома, не допуская лишних экземпляров.
Даже с учётом небольшого процента возможного керамзитобоя потребитель просчитывает количество блоков, необходимых для укладки стен по проекту строящегося дома, не допуская лишних экземпляров.
Сколько блоков в 1 м3 и 1 м2?
В качестве примера – блоки габаритами 20х20х40 см. В пачке (штабеле) их 63. Необходимо учитывать строительные блоки с округлением в большую сторону до ближайшего целого значения, т. к. пилить один из них ни один доставщик не станет.
Формула расчёта проста – умножаемые длину, ширину и высоту одного блока переводим в метрические величины.
Разделив кубометр на полученное дробное значение – также в кубометрах – получим искомую величину.
Зачастую блоки учитываются поштучно – для розничных клиентов, которым, к примеру, нужно небольшое количество, чтобы выложить маленькую лестницу при входе в постройку.
Стена толщиной в один блок, уложенный продольно (не поперечно), рассчитывается по квадратуре следующим способом: длину блока умножают на высоту – и квадратный метр делят на полученное значение. Так высчитывается количество блоков, идущих на квадратный метр. Несмотря на цементно-клеевой шов, которым обычно соединяют блоки (чтобы они не разлетелись от боковых нагрузок на стену), поправка вряд ли составит более 1… 2%. Так, для всё тех же керамзитоблоков размером 20*20*40 см квадратный метр стены потребует не более 13 экземпляров данного кладочного кирпича. С учётом скрепляющих швов данная численность легко уменьшится до 11–12, однако возможен вариант, когда один или несколько блоков пилятся под конкретный периметр (протяжённость в длину) возводимых в процессе стройки стен.
Сколько штук в поддоне?
В зависимости от конкретного поддона керамзитоблок укладывается штабельно – таким образом, чтобы паллет не прогнулся, не сломался под его тяжестью. Запас прочности в палете (евро- или FIN-поддоне) позволяет перенести тряску и вибрацию конкретного штабеля, когда грузовик проедет часть маршрута по дороге не самого лучшего качества покрытия.
Габариты, к примеру, европоддона выбираются такими, чтобы на одной такой подставке не перевозилось более 1 м3. Когда клиент указывает фирме-поставщику, к примеру, десяток поддонов, то считается, что водитель грузовика подвезёт именно 10 м3. Блок размером 39*19*19 см укладывается на поддон таким образом, чтобы в кубометр поместилось не более 72 шт.
Поддоны с блоками разрешено ставить друг на друга, но, как правило, в высоту – не более двух таких штабелей.
Поскольку твердосортная древесина, из которой изготовлен сам поддон, способна на большом ухабе пробить пеноблок, для уменьшения нагрузки от поддона вышележащего штабеля на верхний ярус в нижележащем дополнительно ставятся ограничивающие точечное давление проставки, к примеру, из необрезной доски любого сорта. Кроме нагрузок при транспортировке, поддон должен не рассыпаться под стройблоками при подъёме, переносе с платформы грузовика на стройплощадку при помощи автокрана.
Расчёт расхода на куб при кладке стен
Для оперативного и эффективного строительства, чтобы не допустить лишнего простоя при выполнении работ, применяются поправки на цементно-клеевые швы между блоками.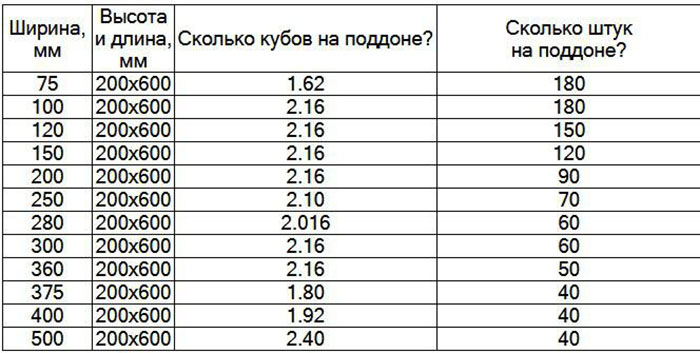
Заключение
Пересчитав реальное число стройблоков под определённую постройку, владелец будущего дома снизит возможные затраты на всё строительство.
Сколько пеноблоков в кубе? Сколько штук в поддоне размером 200х300х600, как рассчитать количество на дом
Пенобетон – очень популярный современный материал, его ценят частные и коммерческие застройщики в одинаковой степени. Но все достоинства изделий из него осложняются тяжелым подсчетом необходимого количества материала. Надо знать, как все сделать максимально быстро и без ошибок.
Размеры блоков
Строительные фирмы и производители рассчитывают количество пеноблоков в штуках.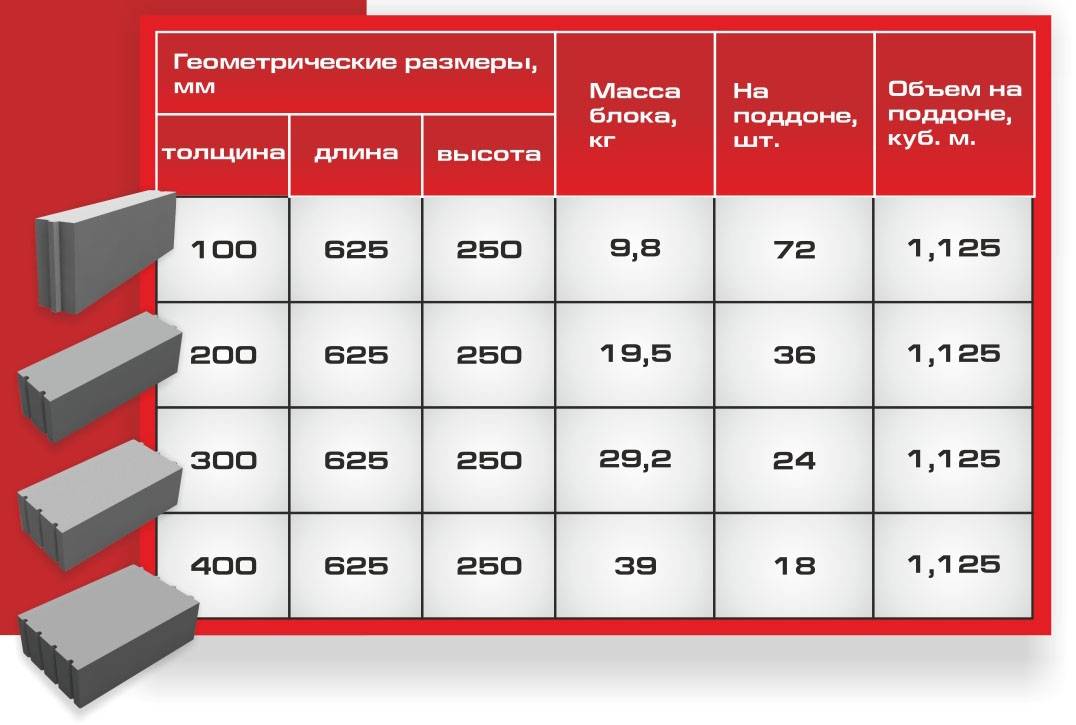 Но такой способ мало приемлем для частного заказчика, потому что он оставляет слишком большую вероятность ошибки. Самыми популярными габаритами блоков в России являются размеры 600х300х200 мм. Самый маленький серийно выпускаемый вариант – 600х250х250 мм. А наиболее крупный – 600х500х250 мм.
Но такой способ мало приемлем для частного заказчика, потому что он оставляет слишком большую вероятность ошибки. Самыми популярными габаритами блоков в России являются размеры 600х300х200 мм. Самый маленький серийно выпускаемый вариант – 600х250х250 мм. А наиболее крупный – 600х500х250 мм.
Еще иногда встречаются конструкции следующих размеров, мм:
- 250х300х600;
- 200х400х600;
- 300х300х600;
- 300х400х600.
Количество в поддоне
Чтобы рассчитать количество пенобетонных блоков в 1 поддоне, надо учесть только габариты самого материала и величину поддона. Перед покупкой обязательно нужно проверять сертификаты качества и соответствие продукции нормам государственного стандарта. Пусть имеется набор блоков величиной 200х300х600 мм, которые требуется положить в поддоны 1200х990 мм. Такой объем поддона указан не случайно – именно его чаще всего используют современные производители. Любой изготовитель для удобства подсчета всегда выкладывает на поддоны одно и то же число изделий.
Пусть имеется набор блоков величиной 200х300х600 мм, которые требуется положить в поддоны 1200х990 мм. Такой объем поддона указан не случайно – именно его чаще всего используют современные производители. Любой изготовитель для удобства подсчета всегда выкладывает на поддоны одно и то же число изделий.
Блоков 600х300х200 мм в одном поддоне вместимостью 1.8 м3 может разместиться ровно 50 штук. Если требуется рассчитывать вместимость поддона только в квадратных метрах, решение стандартное – умножение длины на ширину. Для все той же максимально популярной разновидности пенобетонных конструкций результат составит 0.18 м2. То есть на 1 кв. м площади поддона помещается 5 пенобетонных элементов.
Возвращаясь к объемному исчислению, надо указать на такие массовые разновидности поддонов, как:
При выкладке наиболее часто встречающейся группы пенобетонных изделий на них может поместиться соответственно 25, 40 и 50 штук. Масса изделия, плотность которого составляет 600 кг на куб. м, может достигать 23.4 кг. Но реальное строительство подразумевает нередко применение блоков нестандартной величины.
Масса изделия, плотность которого составляет 600 кг на куб. м, может достигать 23.4 кг. Но реальное строительство подразумевает нередко применение блоков нестандартной величины.
Раскладка по всем трем основным габаритам (0.9, 1.44 и 1.8 м3) поддонов составляет:
- для блоков 100х300х600 – 50, 80 и 100 штук;
- для блоков 240х300х625 – 20, 32, 40 единиц;
- для блоков 200х300х625 – 24, 38, 48 экземпляров.
Европаллет – поддон величиной 0.8х1.2 м. При его использовании советуют раскладку элементов по 2 шт. в длину и 4 шт. в ширину. На 1 подложке можно сделать 5 рядов. Если же применить поддон стандартного образца, его площадь будет больше, ведь размер составляет 1х1.2 м. На таком поддоне кладется 2 шт. пенобетонных изделий по длине и 5 шт. по ширине; используются все те же 5 рядов.
Сложности представляет собой расчет нестандартных блоков, которые надо раскладывать на нетипичные поддоны.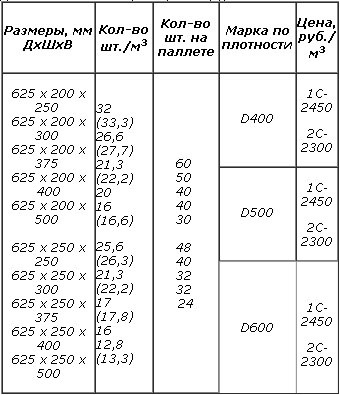 Допустим, при замере обнаружилось, что ширина пачки равна 1 м, а длина ее составит 0.8 м (при вышине 120 см). Простейший подсчет по школьным формулам покажет объем – 0.96 м3.
Допустим, при замере обнаружилось, что ширина пачки равна 1 м, а длина ее составит 0.8 м (при вышине 120 см). Простейший подсчет по школьным формулам покажет объем – 0.96 м3.
Замер отдельных изделий показывает, что они имеют стороны:
Объемный показатель вычисляется очень легко – 0.018 м3. Теперь точно ясно, каков объем пачки и насколько велик единственный блок. Дальнейшее исчисление не представляет особого труда. На пачку приходится ровно 53 детали. Ведь ни один поставщик не станет закладывать при отгрузке треть пенобетонного элемента.
Сколько в кубическом метре?
Количество штук пеноблоков в кубе определить довольно легко. Этот показатель позволит выяснить еще, сколько их будет в упаковке или в пачке заданной емкости. Для начала подсчитывают объем единичного блока. При использовании изделий величиной 100х300х600 мм объем каждого из них составит 0.018 м3. И на 1 куб. м будет приходиться соответственно 55 строительных элементов.
Для начала подсчитывают объем единичного блока. При использовании изделий величиной 100х300х600 мм объем каждого из них составит 0.018 м3. И на 1 куб. м будет приходиться соответственно 55 строительных элементов.
Бывает так, что габарит пеноблока составляет 240х300х600 мм. В таком случае объем единичного изделия будет равен 0.0432 м3. А в 1 куб. м будет 23 пенобетонных изделия. Из этой же цифры надо исходить и при учете перевозки материала различными видами транспорта.
Самый массовый вариант блоков (200х300х600 мм) позволяет уложить на 1 куб. м 27 изделий. Конструкции 100х300х600 мм нужны для формирования перегородок и внутренних стен. При вычислениях закономерно округляют полученный результат в меньшую сторону. Как показывают приведенные расчеты, определение количества материала, которое поможет выполнить ремонт или завершить строительство, довольно легко.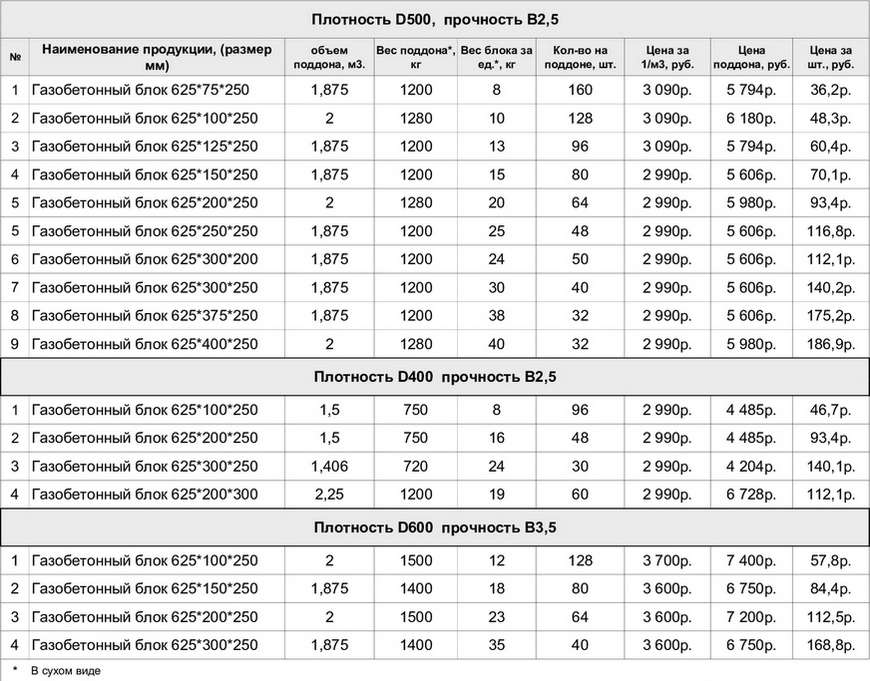 Потому проводить расчет желательно для контроля точности поставщиков.
Потому проводить расчет желательно для контроля точности поставщиков.
Пеноблок 200х200х400 мм имеет объем 0.016 м3. То есть на 1 куб. м приходится 62.5 экземпляра, а если использовать элементы 20х30х40 см, объем составит 0.024 куб. м, поэтому на 1 куб. м придется 41 штука пеноблоков. Если же применить конструкции 125х300х600 мм, каждая из них в объеме займет 0.023 м3, а на 1 м3 придется 43 единицы. Изредка на стройки отправляют пеноблок величиной 150х300х600 мм. Таких деталей в 1 м3 поместится 37 штук при единичном объеме – 0.027 м3.
Расчет на дом
В реальности, конечно, жилые дома и другие здания делают не из «кубометров», а из самого пенобетона в натуральном виде. Но все равно нужно проводить тщательный расчет потребности. Для начала еще раз повторим: при вычислении количества блоков, помещающихся в 1 куб. м, требуется округлять результат не в большую, а в меньшую сторону в любом случае. Математика, разумеется, строга, но такой прием позволяет точно разместить поставленные блоки в кузове автомобиля или в помещении склада. Если подсчет ведется в штуках, достаточно перемножить размеры всех элементов, после чего разделить результат на тысячу.
Математика, разумеется, строга, но такой прием позволяет точно разместить поставленные блоки в кузове автомобиля или в помещении склада. Если подсчет ведется в штуках, достаточно перемножить размеры всех элементов, после чего разделить результат на тысячу.
Чтобы рассчитать суммарную массу всех блоков, используемых для строительства дома, чаще всего ориентируются на стандартные размеры пеноблоков – 20х30х60 см. Типичная тяжесть такой конструкции составляет примерно 21-22 кг. Подобный расчет помогает выяснить, насколько сильно будет давление, оказываемое отдельной стеной на фундамент. Что касается количества изделий из пенобетона, расходуемых на постройку дома 6 на 8 м, сначала подсчитывается общий объем формируемых конструкций. Лишь затем отнимают размеры рам, дверей и иных вспомогательных, декоративных частей.
Лишь затем отнимают размеры рам, дверей и иных вспомогательных, декоративных частей.
Аналогичный подход практикуется и при строительстве зданий в виде квадратов 10х10 м. Подсчет кубатуры непременно проводится с учетом толщины основных стен. И тут решающее значение имеет метод кладки. Если положить пенобетонные фрагменты плашмя, расход будет больше по объему и по количеству.
Пусть периметр дома составляет 40 м, а высота сооружения – 300 см. При глубине стен 0.3 м общий объем будет равняться 36 куб. м. А потому нужное сооружение можно построить из 997 элементов стандартного габарита. Но бывает так, что блок монтируют малой гранью в стену. Тогда тот же периметр умножают на 20 см и на упомянутую высоту 300 см. В данном случае можно будет обойтись всего 664 блоками.
Очевидно, что это приносит колоссальную экономию любому заказчику. В южных, относительно теплых местностях укладка малой гранью наиболее рациональна. Расчет весовых характеристик пенобетона определяется целью его использования. Так, звукоизоляционный тип материала делают по особой технологии, подразумевающей вспенивание внутри.
Но даже возникновение большого числа пор не означает, что получится легкая стена. Совсем наоборот: на производстве используют цемент категории М500, поэтому получится конструкция втрое тяжелее обычного изделия. Однако это оправдывается увеличенной крепостью и плотностью. Подобные достоинства не омрачаются даже повышенной стоимостью.
Наиболее легкий пеноблок призван удержать тепло, потому что при производстве не только создают поры, но и стараются использовать облегченный цемент.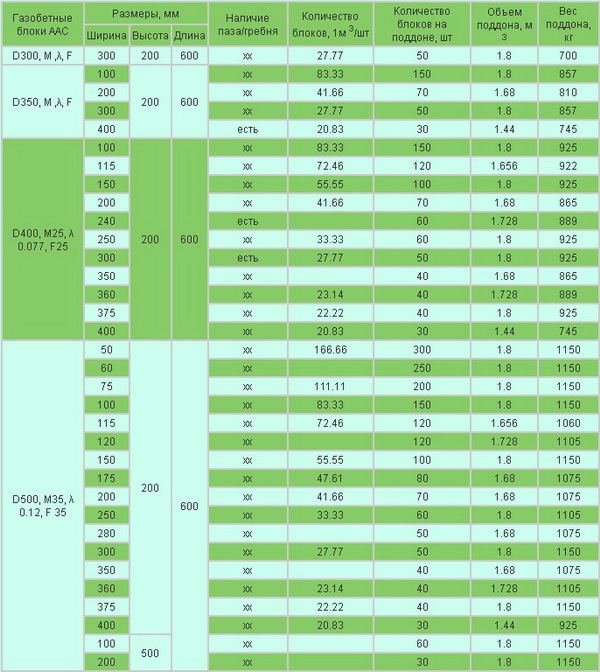 Максимально точные расчеты параметров производятся в специализированных организациях, однако для частного использования такие тонкости не нужны.
Максимально точные расчеты параметров производятся в специализированных организациях, однако для частного использования такие тонкости не нужны.
Приведем иной пример: дом длиной 6 и шириной 8 м, при стандартной высоте (все те же 3 м). Общий периметр составит 28 м, а площадь стен – 84 м2. Но останавливаться на этом этапе не следует, ведь не учтены еще проемы, которые вовсе не нужно делать из пенобетона. Пусть после вычета всех посторонних элементов формируемая площадь составит 70 кв. м. Если толщина будет равняться 20 см, то объем материала составит 14 куб. м, а при глубине постройки в 0.3 м он вырастет до 21 м3.
Самый часто используемый блок, как уже говорилось, имеет объем 0,036 м3. То есть потребуется 388 и 583 детали соответственно. Расчет для кладки плашмя и для узкой выкладки проводится по уже описанной схеме. Однако нередко оказывается, что вычисленного самым тщательным образом числа блоков на практике не хватает. Дело в том, что иногда на производстве допускают брак, и тогда пенные части мало пригодны для реальной работы.
Расчет для кладки плашмя и для узкой выкладки проводится по уже описанной схеме. Однако нередко оказывается, что вычисленного самым тщательным образом числа блоков на практике не хватает. Дело в том, что иногда на производстве допускают брак, и тогда пенные части мало пригодны для реальной работы.
Поэтому нужно покупать их исключительно у проверенных поставщиков. Но даже они изредка допускают ошибки. Не говоря уже о нарушениях при хранении и транспортировке, о повреждениях во время применения пенобетона. Компенсировать ошибки и трудности несложно. Надо лишь приготовить резерв в 5%, чтобы полностью исключить все неожиданности.
В определенных случаях практикуется индивидуальный заказ на пеноблоки. Тогда их размер совершенно нестандартный и в таблицах готовых цифр не найти. Пусть заказаны блоки 0.3х0.4х0.6 м. И пусть дом представляет собой тот же квадрат 10х10 м. Общий объем 1 детали составит 0.072 куб. м, то есть понадобится ровно 500 элементов.
Пусть заказаны блоки 0.3х0.4х0.6 м. И пусть дом представляет собой тот же квадрат 10х10 м. Общий объем 1 детали составит 0.072 куб. м, то есть понадобится ровно 500 элементов.
Если при строительстве дома используются окна и двери различных типоразмеров (а так чаще всего и бывает) простейшее вычисление оказывается куда сложнее. Однако есть еще один прием, который поможет самодеятельным застройщикам. Им понадобится только отыскать объемную совокупную характеристику. Линейные величины суммируются. Нет даже разницы, где окно, а где дверь – при просчете размеров это несущественно.
Подробности смотрите далее.
видео-инструкция по монтажу своими руками, фото
Прежде чем начинать возведение дома, необходимо подсчитать все расходы, связанные с приобретением строительных расходников. В некоторых случаях это довольно-таки проблематично, особенно если вы ни разу не сталкивались с данным процессом, к тому же, если не знаете габариты используемых материалов.
В некоторых случаях это довольно-таки проблематично, особенно если вы ни разу не сталкивались с данным процессом, к тому же, если не знаете габариты используемых материалов.
Чтобы помочь в этом нелегком деле, мы предлагаем вам ознакомиться с данной статьей, в которой описывается подробный процесс расчета пеноблоков и сколько их необходимо на дом.
Строительство дома из пенобетонных блоков начинается с расчета количества необходимых материалов для его возведения
Разновидности пеноблоков
Прежде чем узнать, сколько штук пеноблоков в кубе, необходимо понять какие виды данного строительного материала можно встретить:
На фото – несколько блоков, которые используются для строительства, но в различных областях
- Для несущих (внешних) стен используется блок, имеющий размеры 200х200х400 мм – такой вид называется классическим. Он более прочный и надежный, именно поэтому применяется только для лицевых стен. Вес одного изделия 11 кг.
- Для внутренних стен (межкомнатных перегородок) используется продукт, имеющий размеры 100х200х400 мм.
 Он более легкий, всего 5,5 кг, поэтому идеально подходит для установки внутри помещения.
Он более легкий, всего 5,5 кг, поэтому идеально подходит для установки внутри помещения. - Есть и еще один вид, который используется современными строителями, его размеры 200х300х600 мм, а вес около 25 кг. Такой продукт достаточно тяжелый для укладки своими руками, особенно для возведения двухэтажных домов. С другой стороны, его повышенная прочность и плотность позволяет экономить на теплоизоляционных материалах.
Примечание!
Есть и другие виды, которые различаются собой габаритами и весом, но они используются реже, чем вышеуказанные.
Важно также знать какое количество блоков помещается на одном поддоне – для экономии на транспортных услугах
Правила расчета
Чтобы определиться с тем, сколько штук пеноблоков в одном кубе, необходимо, в первую очередь, понять, что такое куб. Для тех, кто не знает, куб представляет собой квадрат, у которого все стороны равняются 1000 мм.
Классические изделия
- Для того чтобы выставить стену в 1000 мм вам потребуется 5 шт.
 с габаритом 200 мм, то есть на все уйдет 25 (5 шт. требуется с каждой стороны).
с габаритом 200 мм, то есть на все уйдет 25 (5 шт. требуется с каждой стороны). - Для возведения одного метра в высоту уйдет 2,5 пенобетонных изделия.
- Перемножаем общее (25) на количество в высоту (2,5) и получаем 62,5 штук.
Таким образом, число изделий, размером 200х200х400 мм, на 1 м3 составляет 62,5 шт.
Блоки для межкомнатных перегородок
А теперь давайте подсчитаем, сколько штук пеноблока в 1 кубе, имея за основу габариты изделия 100х200х400 мм:
- Для одной стороны у нас потребуется 5 блоков, а для другой 10.
К сведению!
Внимательно смотрите на размеры материалы, в некоторых производственных компаниях нарушают стандарты и допускают погрешность в +/- 1-2 см.
- Значит общее число вспененных изделий — 50, получилось путем перемножения одной стороны на другую.
- Количество изделий в высоту остается прежним – 2,5 шт.
- Конечный результат будет равен 125 штукам (50*2,5).

Укрепленные блоки
Давайте ответим на вопрос, сколько штук пеноблоков 200х300х600 в кубе?
- Обращая внимание на габариты, можно сказать, что по одной стороне куба потребуется 5 блоков, а по другой 3,3. Итого – 16,5 штук необходимо на один ряд кубического метра.
- В высоту необходимо 1,7 пенобетонных изделия, в результате перемножения 16,5 на 1,7 получается 28 шт.
Как видите, размеры очень сильно влияют на то, сколько будет приобретено материалов. При этом в большинстве случаев, цена более крупных изделий ниже (при разовой закупке необходимого количества изделий) стоимости малогабаритных.
Расчет расходников на дом
В данном разделе будет описана подробная инструкция подсчета строительных материалов не на 1 кубический метр, а конкретно – на определенную постройку.
Для начала, необходимо определиться с исходными данными, к ним относятся все размеры, связанные с домом: периметр, высота и толщина кладки пеноблоков, количество окон и дверей. Немаловажно заранее определиться с используемыми размерами изделий.
Немаловажно заранее определиться с используемыми размерами изделий.
Вычет оконных и дверных проемов не критичен, как минимум, небольшой запас строительных материалов необходим
Статьи по теме:
Для примера воспользуемся крупными блоками (200х300х600 мм), а габариты дома возьмем произвольные – он у нас будет одноэтажный и прямоугольный.
По одной стене длина будет равна 11 м (длина), по второй 7 м (ширина), от цоколя до кровли будет 3 м (высота).
- Первым делом подсчитываем периметр несущих стен здания, то есть складываем стороны, 11+11+7+7 = 36 погонных метров.
- Теперь необходимо полученный результат умножить на высоту, чтобы получить квадратные метры – 36*3 = 108 м2.
- Следующий расчет, переводим квадратные метры в кубические путем перемножения общей площади работ на толщину пеноблочной кладки – 108*0,3 = 32,4 м3.
Примечание!
Толщины в 300 мм достаточно для жилого дома с учетом того, что снаружи будет производиться утепление фасада, путем установки вентилируемой системы = пенополистирол + отделка.
А так как мы знаем, какое количество штук пеноблока в кубе(из раздела расчетов укрепленных материалов), то остается только перемножить полученные результаты. Итого: 32,4*28 = 907 штук (с небольшой погрешностью в +/- 5 шт.).
Блоки легко пилятся, поэтому не смущайтесь, если вам, например, требуется 22,4 изделия на один кубический метр
К сведению!
Аналогичным способом можно подсчитать и количество других расходников для возведения межкомнатных перегородок.
Помимо всего прочего, не лишним будет рассчитать массу клея для строительных материалов, которого в среднем используется около 30 кг на 1 м3. Согласно нашим данным (32 м3 * 30 кг) требуется 960 кг сухой или готовой смеси.
Вывод
Теперь вы знаете, как правильно рассчитать то, из чего строится ваш дом. По аналогии производятся расчеты кирпичной кладки, а также, сколько штук шлакоблока в кубе, на цокольные и подвальные помещения. Главное – взять за основу точные данные, чтобы случайно не переплатить за лишние материалы.
Главное – взять за основу точные данные, чтобы случайно не переплатить за лишние материалы.
Не забывайте, что внешне блоки могут отличаться не только габаритами, но и наличием пазо-гребневых сторон
В представленном видео в этой статье вы найдете дополнительную информацию по данной теме.
Сколько пеноблоков в 1м3 кубическом, таблица
Единицей измерения для ячеистобетонных и бетонных строительных блоков для размещения и установки являются кубические метры. Цена также указывается за 1 метр кубический или м3, а не поштучно или на вес. Данная сложившаяся ценовая политика измерения пенобетонных блоков выгодна тем, что зная размеры пеноблоков (они стандартны и приведены в справке ГОСТ, более распространен размер блока – 200 х 300 х 60 мм), будет легко рассчитать какое количество штук пеноблоков потребуется для возведения постройки, и сколько кубометров материала придется приобрести, для получения итоговой стоимости партии строительных блоков.
Расчеты
Сколько пеноблоков требуется на м3? — Необходимо поделить 1м3 на объем одного пеноблока. Один куб состоит из 27 блоков. После несложных расчетов получаем 27,7 штук. В данном случае округление приходится в меньшую сторону.
Ответ: В 1м3 = 27 штук пеноблоков
Еще один способ получения количества пеноблоков в кубе — делать расчеты в штуках. Выбранный способ выполняется он следующим образом: ширина, высота и длина одного блока перемножаются между собой, и получившийся итог делится на 1000. В итоге мы получим, сколько штук выбранного вида будет в одном кубе.
Расчет пенобетонных блоков
Справка: в 1 м3 – 27 единиц пеноблоков размером 200 х 300 х 600 мм. Проверить можно делением 1 м3 на объем одной стандартной единицы. Объем рассчитывается перемножением всех сторон блока.
Размерная линейка строительных блоков из разных материалов
В таблице приведены справочные данные соответствия размеров пеноблоков, количества в поддоне и пачке, а также объема и веса определенной тары и определенной марки:
| Длина L, см | Ширина B, см | Высота H, см | Сколько пеноблоков на поддоне | Объем 1 пеноблока дм3 | Объем 1 пачки дм3 | Марка и вес одного пеноблока | |
| D500, кг | D600, кг | ||||||
| 60,0 | 20,0 | 100 – 125 – 150 – 200 – 250 – 300 – 350 – 375 – 400 – 450 – 500 | |||||
| – | 25,0 | – | |||||
| – | 20,0 | 15,0 | 100,0 | 0,18 | 18 | 11,7 | 14 |
| – | – | 25,0 | 60,0 | 0,3 | 18 | 19,5 | 23,4 |
| – | – | 30,0 | 50,0 | 0,36 | 18 | 23,4 | 28 |
| – | – | 40,0 | 30,0 | 0,48 | 14,4 | 31,2 | 37,4 |
| – | 25,0 | 10,0 | 120,0 | 0,15 | 18 | 9,8 | 11,7 |
| – | – | 15,0 | 80,0 | 0,225 | 18 | 14,6 | 17,6 |
| – | – | 25,0 | 48,0 | 0,375 | 18 | 24,4 | 29,3 |
| – | – | 30,0 | 40,0 | 0,45 | 18 | 29,3 | 35,1 |
| – | – | 37,5 | 32,0 | 0,562 | 18 | 36,5 | 43,9 |
| – | – | 40,0 | 24,0 | 0,6 | 14,4 | 39 | 46,8 |
| – | – | 50,0 | 24,0 | 0,75 | 18 | 48,7 | 58,5 |
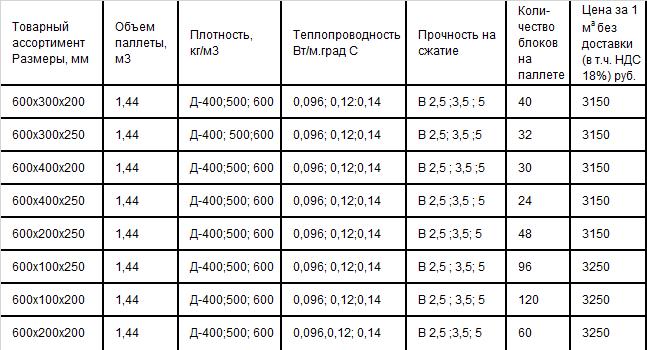
| Количество строительных блоков в одном кубическом метре | |||
| Марка Hebei, Masa Henke | Марка Ytong, AeroStooe | ||
| Параметры, см | Единиц в 1 м3 | Параметры, см | Единиц в 1 м3 |
| 5,0×20,0×60,0 | 166,7 | 5,0x200x625 | 160 |
| 7,5×20,0×60,0 | 111,1 | 7,5x200x625 | 106,7 |
| 10,0×20,0×60,0 | 83,3 | 10,0×20,0×62,50 | 80 |
| 12,5×20,0×60,0 | 66,7 | 12,5×20,0×62,50 | 64 |
| 15,0×20,0×60,0 | 55,6 | 15,0×20,0×62,50 | 53,3 |
| 17,5×20,0×60,0 | 47,6 | 17,5×20,0×62,50 | 45,7 |
| 25,0×20,0×60,0 | 33,3 | 25,0×20,0×62,50 | 32 |
| 30,0×20,0×60,0 | 27,8 | 30,0×20,0×62,50 | 26,7 |
| 37,5×20,0×60,0 | 22,2 | 37,5×20,0×62,50 | 21,3 |
| 40,0×20,0×60,0 | 20,8 | 40,0×20,0×62,50 | 20 |
| 50,0×20,0×60,0 | 16,7 | 50,0×20,0×62,50 | 16 |
| 5,0×25,0×60,0 | 133,3 | 5,0×25,0×62,50 | 128 |
| 7,5×25,0×60,0 | 88,9 | 7,5×25,0×62,50 | 85,3 |
| 10,0×25,0×60,0 | 66,7 | 10,0×25,0×62,50 | 64 |
| 12,5×25,0×60,0 | 53,3 | 12,5×25,0×62,50 | 51,2 |
| 15,0×25,0×60,0 | 44,4 | 15,0×25,0×62,50 | 42,7 |
| 17,5×25,0×60,0 | 38,1 | 17,5×25,0×62,50 | 36,6 |
| 20,0×25,0×60,0 | 33,3 | 20,0×25,0×62,50 | 32 |
| 30,0×25,0×60,0 | 22,2 | 30,0×25,0×62,50 | 21,3 |
| 37,5×25,0×60,0 | 17,8 | 37,5×25,0×62,50 | 17,1 |
| 40,0×25,0×60,0 | 16,7 | 40,0×25,0×62,50 | 16 |
| 50,0×25,0×60,0 | 13,3 | 50,0×25,0×62,50 | 12,8 |
Легче всего получится рассчитать сколько штук пеноблока в 1 кубе, получится делением одного кубического метра на объем одной строительной единицы (блока). Объем одной единицы равен перемноженным между собой размерам сторон блока – ширины, высоты и длины. Результат отображается в кубических метрах (м3) или кубических дециметрах, если небольшая партия (дм3).
Объем одной единицы равен перемноженным между собой размерам сторон блока – ширины, высоты и длины. Результат отображается в кубических метрах (м3) или кубических дециметрах, если небольшая партия (дм3).
Соотношение размеров и других параметров пеноблоков
Пример: объем стандартного пеноблока размером 200 х 300 х 60 мм будет равняться 200 * 300 * 60 = 0,36 дм3. Делим 1 м3 на 0,36 дм3, получаем результат 27,78, или ≈ 27-28 штук при массе одного пеноблока ≈ 21-22 кг. Эта простая формула подходит для любых существующих и заказных размеров блоков из тяжелого или ячеистого бетона, любых марок кирпича или ФБС небольших размеров.
Строительные пеноблоки проще отгружать с укладкой на поддоны. Сколько пеноблоков поместится в 1 поддоне? Их количество будет зависеть от размеров поддона, а поддоны изготавливают различных типов, но с таким расчетом, чтобы на них могло поместиться кратное число стандартных строительных блоков.
Поддоны для строительных блоков
Стандартные характеристики объема поддонов для укладки строительных блоков: 0,9 м3 (25 единиц на один поддон), 1,44 м3 (40 единиц) и 1,8 м3 (50 единиц). Соответственно остальные характеристики блоков: объем одной единицы – 0,36 дм3 или 0,036 м3, масса блока с плотностью 600 кг/мЗ – 23,4кг.
Составление проекта здания или другого строительного объекта включает в себя расчет требуемого количества строительных блоков, сделанных любого материала. Результаты расчетов должны отображаться в метрах кубических в любых сопроводительных документах.
Количество блоков в разных объемах
Нестандартные блоки других размеров, в том числе и заказных, можно рассчитать, применив те же самые методы. В качестве примера возьмем несколько изделий с различными размерами:
- Строительный блок с габаритами 100 х 300 х 600 мм и массой 11 кг: объем единицы равен 100 * 300 * 600 = 0,18 дм3или 0,018 м3.
 Количество штук в метре кубическом = 1 / 0,018 = 55 единиц;
Количество штук в метре кубическом = 1 / 0,018 = 55 единиц; - Строительный блок с габаритами 240 х 300 х 625 мм и массой 28 кг: объем единицы равен 240 * 300 * 625 = 0,45 дм3или 0,045 м3. Количество штук в метре кубическом = 1 / 0,045 = 22 единицы;
- Строительный блок с габаритами 200 х 300 х 625 мм и массой 25 кг: объем единицы равен 200 * 300 * 625 = 0,375 дм3или 0,0375 м3. Количество штук в метре кубическом = 1 / 0,0375 = 26 единиц.
В итоге можно рассчитать стоимость любого количества и объема строительных блоков для частного дома или другого строения.
В 1 кубе сколько пеноблоков: расчеты и инструкция
Любой стеновой материал измеряется в трех единицах: штуках, кубических и квадратных метрах.
При покупке пенобетонных блоков стоимость зачастую указывается за 1 куб. м, что не совсем понятно для обычного человека, который столкнулся с этим впервые.
м, что не совсем понятно для обычного человека, который столкнулся с этим впервые.
В результате возникает вопрос: как определить, сколько в 1 кубе пеноблоков?
Расчет достаточно простой, ведь для того чтобы узнать объем одного камня достаточно измерить его стороны: длину, высоту, ширину. Исходя из этих данных, можно будет получить необходимые результаты. Узнать что лучше: пеноблок или газоблок можно тут.
Как вычислить, сколько пеноблоков в 1 кубе?
Объем блока полностью зависит от собственных параметров, так как стеновой материал изготавливается в разных типоразмерах. Будет более понятным, если рассматривать на примерах:
- Пенобетон 600 х 300 х 200 мм весит 22 кг. Для того чтобы выполнить расчет необходимо миллиметры перевести в метры и все стороны перемножить: 0,6 х 0,3 х 0,2=0,036 куб. м в одном камне. Теперь можно узнать количество камня в кубическом метре: 1/0,036=27,78≈28 единиц.
- Стеновой материал 600 х 300 х 100 мм весит в два раза меньше 11 кг, это значит, его объем на половину меньше, а количество в 2 раза больше: 0,6 х 0,3 х 0,1=0,018 куб.
 м. или 1/0,018=55,56≈56 единиц.
м. или 1/0,018=55,56≈56 единиц.
- Камень размерами 600 х 300 х 240 мм весит 28 кг, имеет объем 0,0432 куб. м (0,6 х 0,3 х 0,24) и количество в 1 куб. м составляет 23 единицы (1/0,432).
- Пенобетон 600 х 400 х 200 мм имеет объем 0,048 куб. м и 21 единицу в 1 куб. м.
Зная, сколько в 1 кубе пеноблоков штук, проще будет определиться, какие размеры лучше всего подойдут для строительства дома, дачи, гаража. Количество материала зависит от высоты и толщины несущей стены. Какая плотность пенобетона и характеристики пенобетонных блоков смотрите в соответствующих статьях.
Что еще необходимо учитывать при расчете стенового материала?
Сделав предварительные подсчеты и узнав в 1 кубе, сколько пеноблоков, можно смело покупать стеновой материал в том количестве, которое получилось в конечном результате. Но, если учитывая то, что за один искусственный камень нужно будет заплатить немалую сумму, приходится задумываться о жесткой экономии.
Кладка камня осуществляется при помощи раствора, от выбора которого зависит толщина слоя:
- раствор цементно-песчаный – 1-2 см;
- клеевой состав – 2-3 мм.
Поэтому резонно произвести более тщательные расчеты, чтобы узнать, сколько в 1 кубе пеноблоков с раствором цементно-песчаным, так как применяя клеевой состав малая толщина слоя не сможет особо повлиять на количество стенового материала. Рекомендуем просмотреть статью и узнать что такое монолитный пенобетон.
Важно! Также при строительстве дома необходимо знать, сколько метров площади в 1 кубе пеноблоков.
Для того чтобы рассчитать площадь камня нужно высоту умножить на длину и получится цифра кв. м:
- Пенобетон размером 600 х 300 х 200 мм имеет площадь 0,18 кв.м.
- Если одна стена дома составляет 27 кв. м (3 х 9), тогда можно рассчитать количество камня, применив формулу: 27/0,18=150 единиц, соответственно в кубических метрах цифра будет 150х0,036=5,4 куб.
 м.
м.
Зная все варианты расчетов стенового материала, можно выбирать наиболее удобный способ или использовать несколько, чтобы удостовериться в правильности полученного результата. Важными показателями являются толщина стены и слоя раствора. Как перевезти ЖБИ читайте здесь.
Как посчитать газоблок
Сколько в кубе газобетонных блоков, как правильно посчитать? Такой вопрос возникает у многих, кто запланировал строительство. Ведь очень важно правильно рассчитать потребность в материалах, что будет гарантией отсутствия многих проблем. Недостаток нескольких блоков приводит к некоторым трудностям, поскольку поиск новых поставщиков занимает много времени и сил.
Блок: 1/6 | Кол-во символов: 364
Источник: https://SpecNavigator.ru/materialy/gazobeton/skolko-penoblokov-v-odnom-kube.html
Эксплуатационные характеристики газобетона
Газобетон считается идеальным материалом для индивидуального строительства. Это объясняется его отличными эксплуатационными характеристиками и оптимальной стоимостью. Основными преимуществами газоблоков называют:
Основными преимуществами газоблоков называют:
Преимущества газобетонных блоков
- простота обработки. Газобетонные блоки можно легко распиливать в любом направлении и придавать им нужную форму;
- низкая теплопроводность, что обеспечивает отличные теплосберегающие характеристики и позволяет сэкономить на утеплении;
- обеспечение высоких параметров шумоизоляции, что актуально в городских условиях;
- абсолютная безопасность для человека и окружающей среды;
- на газобетонных блоках не может завестись грибок и плесень, они не нуждаются в дополнительной антисептической обработке;
- газобетон довольно прочен. С его помощью разрешается возводить здания до двух этажей;
- высокая морозостойкость, способность выдерживать много циклов заморозки и размораживания без потери прочностных характеристик;
- небольшой вес блоков облегчает работу с ними и не требует применения спецтехники в процессе монтажа.

К недостаткам газобетона относят наличие у него пористой структуры. Это приводит к тому, что он отличается высоким уровнем поглощения влаги. Газобетонные блоки очень хрупкие. Их рекомендуется использовать совместно с фундаментами, которые отличаются минимальной усадкой. Такой недостаток приводит к тому, что на стену из газобетона довольно трудно закрепить массивные и тяжелые предметы.
Один из основных недостатков газобетона — хрупкость
Блок: 2/6 | Кол-во символов: 1534
Источник: https://SpecNavigator.ru/materialy/gazobeton/skolko-penoblokov-v-odnom-kube.html
Сколько газоблоков с размерами 20х30х60 в 1 кубометре?
Чтобы узнать, сколько газобетонных блоков в 1м3, следует знать габариты одного изделия. Распространенные размеры блоков:
- 250х300х600 мм;
- 600х400х250 мм;
- 600х300х300 мм;
- 625х200х250 мм.
кубов и кубовидных формул, примеры вопросов | Предыдущие статьи
1.
В кубе или кубоиде по шесть граней.
2. В кубе длина, ширина и высота одинаковы, а в кубе — разные.
3. В кубе количество единичных кубиков = и в кубоиде количество единичных кубов =
Пример куба и кубоида
Кубик с каждой стороной 4 см окрашен в черный, красный и зеленый цвета на парах противоположных граней.Затем его нарезают небольшими кубиками с каждой стороны по 1 см.
Затем найдите
1. Сколько там будет маленьких кубиков?
2. На скольких маленьких кубиках будут нарисованы три грани?
3. На скольких маленьких кубиках будут нарисованы только две грани?
4. На скольких маленьких кубиках будет нарисована только одна грань?
5. На скольких маленьких кубиках не будут нарисованы грани?
6. На скольких маленьких кубиках только две грани будут окрашены в черный и зеленый, а все остальные грани неокрашены?
7.Сколько маленьких кубиков будет иметь только две грани, окрашенные в зеленый и красный цвета.
8. Сколько маленьких кубиков будет иметь только две грани, окрашенные в черный и красный цвета?
9. Сколько маленьких кубиков будет только окрашено в черный цвет?
10. Сколько маленьких кубиков будет только покрашено в красный цвет?
11. Сколько маленьких кубиков будет только зеленой краской?
12. На скольких маленьких кубиках будет нарисована хотя бы одна грань?
13. На скольких маленьких кубиках будет нарисовано хотя бы две грани?
Решение каждого вопроса, приведенного выше, приводится ниже с пояснением.Здесь видны три лица.
Шагов:
(1) Здесь находится кубик каждой стороной 4 см.
(2) Нарезается небольшими кубиками каждой стороной по 1 см.
(3) Противоположные грани окрашены черной, красной и зеленой красками.
1. Итого кубиков — = 64.
2. Количество маленьких кубиков с тремя окрашенными гранями — Из рисунка видно, что маленький куб с тремя окрашенными гранями расположен в углах большого куба, потому что в этих углах встречаются только три грани большого куба. .Следовательно, необходимое количество таких кубиков всегда равно 8, потому что углов 8.
.Следовательно, необходимое количество таких кубиков всегда равно 8, потому что углов 8.
3. Количество маленьких кубиков, у которых только две окрашенные грани — Из рисунка видно, что к каждому краю большого куба присоединены 4 маленьких кубика, и два из них расположены по углам большого куба, который все три лица нарисованы. Таким образом, у каждого края остается по два маленьких кубика с двумя нарисованными гранями. В общем нет. ребер в кубе 12, следовательно, нет. маленьких кубиков с двумя гранями цвета
= = 24.
или
Количество маленьких кубиков с двумя цветными гранями
=
Где x =
4. Количество маленьких кубиков, у которых нарисована только одна грань. Кубики, нарисованные только на одной стороне, являются кубами в центре каждой грани большого куба. Так как в большом кубе 6 граней и каждая грань большого куба будет четыре таких маленьких куба. Следовательно, всего будет т.е.24 таких маленьких кубика.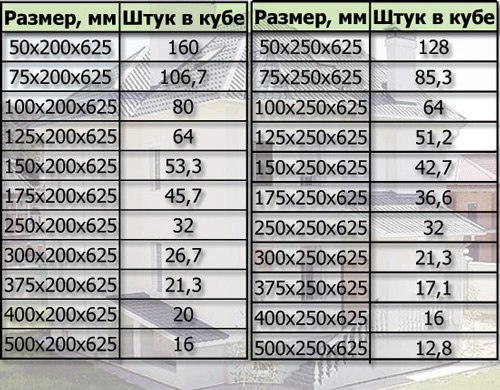
или
5. №маленьких кубиков без раскрашенной грани — Количество таких маленьких кубиков
=
=
6. Количество маленьких кубиков, у которых две грани окрашены в черный и зеленый цвета. В слое II есть 4 маленьких кубика, а в слое III — четыре маленьких кубика, две грани которых окрашены в зеленый и черный цвета.
Треб. нет. таких кубиков = 4 + 4 = 8.
7. Количество маленьких кубиков с двумя гранями, окрашенными в зеленый и красный цвета.
Треб. нет. таких кубиков = 4 + 4 = 8.
8. №маленьких кубиков с двумя сторонами, окрашенными в черный и красный цвет = 4 + 4 = 8.
9. Количество маленьких кубиков только черной краски. Будет 8 маленьких кубиков, окрашенных только черной краской. Четыре кубика будут с одной стороны и 4 с противоположной стороны.
10. Количество маленьких кубиков, окрашенных только красной краской
= 4 + 4 = 8
11. Количество маленьких кубиков, окрашенных только зеленой краской
Количество маленьких кубиков, окрашенных только зеленой краской
= 4 + 4 = 8
12. Количество маленьких кубиков, имеющих хотя бы одну окрашенную грань
= Нет.маленьких кубиков, у которых 1 окрашенная грань + 2 окрашенные грани + 3 окрашенные грани
= 24 + 24 +8 = 56
13. Количество маленьких кубиков, имеющих как минимум две окрашенные грани
= Количество маленьких кубиков, имеющих две окрашенные грани + 3 окрашенных грани
= 24 + 8 = 32
Куб и кубоид — вопросы прошлогодних экзаменов
0 из 14 вопросов завершено
Вопросы:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
Информация
Вы уже прошли тест раньше.Следовательно, вы не можете запустить его снова.
Вы должны войти в систему или зарегистрироваться, чтобы начать викторину.
Кубик Рубика — История кубика Рубика
В мире головоломок, головоломок и интеллектуальных игр кубик Рубика остается самым известным из всех. Куб, изобретенный в 1974 году венгерским профессором архитектуры Эрно Рубиком, когда-то был известен как волшебный куб. Хотя сейчас она широко известна как игра, изначально она предназначалась для науки. Эрно хотел создать куб, в котором все движущиеся части не разваливались.Получился кубик Рубика!
Однако, когда он был создан, Эрно заметил, что он также может действовать как головоломка. В первый раз, когда он поднял кубик, он подумал, что его невозможно решить. Однако через несколько месяцев Эрно, наконец, смог собрать первый кубик Рубика.
В форме куба с тремя рядами и столбцами, которые можно перемещать и поворачивать, каждая грань была покрыта девятью наклейками. Каждая грань куба содержала один из шести сплошных цветов: красный, синий, белый, оранжевый, желтый и зеленый.Цель игры заключалась в том, чтобы изменить цвета скремблированного куба так, чтобы каждая из шести граней содержала только один сплошной цвет. Это был чрезвычайно сложный подвиг, ведь существует более 40 000 способов расположить куб!
Это был чрезвычайно сложный подвиг, ведь существует более 40 000 способов расположить куб!
С 1980-х годов эта игра была огромным хитом: к январю 2009 года было продано более 350 миллионов кубиков. Этот подвиг принес кубику Рубика титул «Самой продаваемой головоломки в мире».
За 30 лет с момента его разработки энтузиасты кубика Рубика разработали стандартные протоколы для решения даже самых сложных перестановок куба.Сегодня эти протоколы неукоснительно соблюдаются участниками всемирных соревнований по кубику Рубика. Большинство из них позволяют собрать куб, используя менее 100 ходов.
Сегодня кубик Рубика остается невероятно популярной головоломкой во всем мире. Хотя многие до сих пор не могут собрать свой первый куб, конкуренция за кубирование скорости остается высокой: текущий рекорд установлен на 4,90 секунды. Другие усовершенствования кубика Рубика, включая массивный куб 17 x 17 x 17, были решены менее чем за 8 часов.Несмотря на эти, казалось бы, невозможные рекорды скорости, кубик Рубика остается забавным и интересным устройством, которое привлекает умы людей во всем мире.
Квадраты и кубики чисел
Вступительные действия
Эти упражнения знакомят с работой с квадратами и кубиками чисел в Elementary.
Описание материала:
Войлочный коврик, короткие цепочки
Метод:
Игра 1 — формы
Сформируйте цепочки с каждой короткой цепочкой, начиная с цепочки из трех, после формирования каждой фигуры попросите ребенка идентифицировать каждую фигуру, показывая их в ряд, позже вы можете попросить ребенка предсказать следующую фигуру
Игра 2 — концентрические формы
Сформируйте цепочки, каждая короткая цепочка на этот раз формируется затем концентрически, начиная с цепочки из трех, помещая вокруг нее квадрат, а затем пятиугольник.Скажем, «Треугольник вписан в квадрат, квадрат описывает треугольник и вписан в пятиугольник с описанием как квадрата, так и треугольника».
Цель:
Дети узнают что-то новое о цепочках, это число можно связать с геометрией.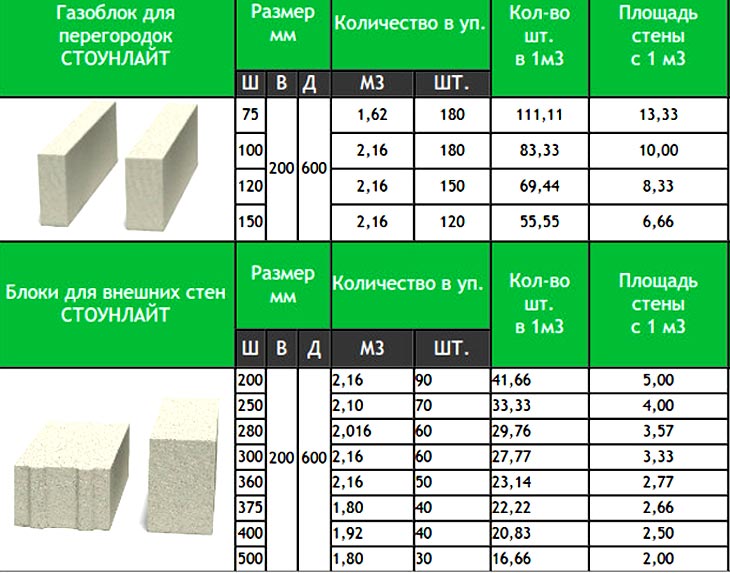
Примечания:
Это серия коротких игр
Когда проводить урок:
Это очень ранняя часть работы, которую нужно сделать в конце Casa или в начале Elementary
.Понятие и обозначения
Квадраты, разведка
Описание материала:
Билеты готовые с обозначением квадратов, пустые билеты, карандаш, короткие цепочки, квадрат каждой цепочки.
Метод:
«Вот короткая цепочка из пяти, не могли бы вы помочь мне сложить ее? Что мы сделали? (квадрат)
«Смотрите, вот у нас пятеро на базе». Удалите билет и напишите «5» . «Послушайте, у нас пять на стороне, я собираюсь написать билет и для этого», Удалите билет и напишите «5» .
«Вы помните, что мы сказали? Это похоже на квадрат, давайте сверимся с настоящим квадратом, когда мы хотим говорить о реальном квадрате, который мы говорим в квадрате». Наложите квадрат из пяти и поместите его рядом с цепочкой. « Да, они такие же».
Наложите квадрат из пяти и поместите его рядом с цепочкой. « Да, они такие же».
Теперь, когда мы говорим о «реальном квадрате», мы называем его пятью в квадрате, и именно так вы пишете его математически: сначала вы пишете «5» и небольшую цифру «2» в правом углу ». Удалить билет и напишите ‘5 2 ‘ .
«Теперь мы можем сделать математическое утверждение, пять раз, сколько раз (пять раз) дают мне 5 2’ .
Разложите билеты для чтения 5 x 5 = 5 2
Продолжайте использовать другие примеры.
Площади, систематическая разведка
Описание материала:
Готовые билеты с обозначением квадратов, пустые билеты, все короткие цепочки и их квадраты.
Метод:
- «Что у меня здесь?» укажите красную бусину, поместите ее, «Я брал одну однажды» , поместите красную бусину. «Я взял один раз, напиши билет« 1 × 1 ».
Что дает мне 1 2 , позволяет написать билет, Напишите и поместите билет «1 2». «Какова его стоимость?» (1) Напишите «1» на билете и поместите его.
- «Я взял два раза дважды» , сложите две цепочки, « Что дает мне 2 2 », поместите бусину в квадрат. Скажем, « Давайте напишем билет», напишем билет «2×2».
«Это двуквадратный». Напишите и поместите билет «2 2 », и, «Какое значение имеет значение 2 2 ? (4), Напишите билет для «4» и поместите его.
- «Я взял три раза трижды» , сложите цепочку из трех, «Что дает мне 3 2 » , поместите бусину в квадрат. Скажем, « Давайте напишем билет», напишите билет «3 × 3». ‘
Это три квадрата « напишите и поместите билет» 3 2 ‘и, «Какое значение 3 2 ?» (9), напишите билет » 9 ‘и поместите его.
- « Я взял четыре раза четыре», сложите четыре цепочки, «Что дает мне 4 2 » , поместите бусину в квадрат. Скажем, « Давайте напишем билет», напишем билет «4 × 4».
‘ Это квадрат’ напишите и поместите билет ‘4 2 ‘, и, ‘Какое значение 4 2 ?’ (16), напишите билет «16» и поместите его.
Продолжайте закреплять бортовые цепочки до 10 2 равно 100.
Кубики, разведка
Описание материала:
Готовые билеты с обозначением кубиков, заготовок, карандашей, длинных цепочек и соответствующего количества квадратов бус и кубиков бус.
Метод:
«Вот длинная цепочка из пяти, не могли бы вы помочь мне сложить ее? Выложите цепочку по прямой линии, загибая ее после пятой полоски бусинок, чтобы получилось пять квадратов.
Что мы сделали?… Похоже, у нас есть квадрат из пяти, взятый пять раз. Super: наложите квадрат из пяти один раз на каждый квадрат и выстроите пять квадратов в башню. Напишите два билета, во-первых, «5 x 5», поместите его под первым квадратом, а во-вторых, «5» поместите его под третьим квадратом.
Спросите, «Как это выглядит, как я сделал?» (куб) « Давайте посмотрим на настоящий куб, когда мы хотим поговорить о реальном кубе, который мы называем кубиком». Сравните их с кубом из пяти. Обозначая одну грань стопки квадратов, скажем: «Смотри, что у нас здесь?», «Пятерка в квадрате» (напишите листок с надписью «5 2 и поместите его балансирующим на одну грань куба). . Затем посмотрите на другую сторону стопки квадратов, скажем, «У нас пять лотов», напишите еще один билет «5» и поместите его напротив другой стороны стопки.
Обратитесь к кубу, скажем, «Я взял пять квадратов пять раз, и мы пишем это так: 5 и крошечная тройка в правом углу». Напишите билет с ‘5 3 ’и поместите его стоя вдоль стороны куба . « А что у нас здесь?» . Обозначая длинную цепочку, скажем, «5 × 5, выполнено 5 раз».
Теперь составьте математическое утверждение, формируя сначала квадрат, поскольку ребенок это знает, а затем задачу и результат.
«Теперь мы можем сделать математическое утверждение, мы взяли пять кубов, что равно пяти на пять, взятым пять раз, это то же самое, что 5 3’ . Переместите билеты, чтобы написать
5 2 x 5 = 5 x 5 x 5 = 5 3
Продолжайте делать другие примеры.
Кубики, систематическая разведка
Описание материала:
Готовые билеты с обозначением квадратов, пустые билеты, все короткие цепочки и их квадраты.
Метод:
- «Что у меня здесь?» укажите красную бусину, поместите ее, «Я взял один взятый квадрат, который дает мне один кубик» , поместите еще одну красную бусину.
Напишите и разместите билет ‘ 1 2 x 1 ’. Скажем, «Я знаю, что это то же самое, что и один раз», напишите билет «1x1x1», «Что дает мне 1 3 , давайте напишем билет» 1 3 ‘ Напишите и поместите билет: «1 3 », спросите, «Какова его стоимость?», (1) Напишите «1» на билете и поместите его.
- Поместите два квадрата из двух друг на друга, скажем, «Я взял два квадрата, взятых дважды» , , что дает мне 2 c ubed ‘, поместите кубик бусинки, скажем, ‘ См. , они одинаковые’.
Скажем: « Давайте напишем билет», напишем билет ’2 2 x 2’. Скажем, «Что я знаю, это то же самое, что два квадрата, взятые дважды, написать билет» 2x2x2 «, » Что дает мне 2 3 , позволяет написать билет. Напишите, ’2 3 ’ и поместите билет ’2 3’. «Сколько это стоит?» (8) Напишите «8» на билете и поместите его.
- Поместите три квадрата из трех друг на друга, скажем: « У меня есть три квадрата из трех , w , который дает мне 3 в кубе», поместите кубик бусинки, скажем, «Видите, они тем же’.
Скажем: « Давайте напишем билет», напишем билет ’3 2 x 3’.Скажем, ‘Что я знаю, это то же самое, что три квадрата, взятые три раза, напишите билет’ 3x3x3 ‘, ‘ Что дает мне 3 3 , давайте напишем билет , Напишите, ‘3 3 ‘ поместите билет ‘3 3′. «Какова его стоимость?» (27) Напишите «27» на билете и поместите его.
- Поместите четыре квадрата из четырех друг на друга, скажем: « У меня четыре квадрата из четырех , дает мне 4 в кубе», поместите кубик из бусинок, скажем, «Видите, они тем же’.
Скажем: « Давайте напишем билет», напишем билет »4 2 x 4’. Скажем, ‘Что я знаю, то же самое, что четыре квадрата, взятые четыре раза, напишите билет’ 4x4x4 ‘, ‘ Что дает мне 4 3 , давайте напишем билет , Напишите, ‘4 3 ‘ поместите билет ‘4 3′. «Сколько это стоит?» (64) Напишите «64» на билете и поместите его.
Продолжайте закреплять бортовые цепочки, пока 10 3 не станет 1000.
Примечания:
Эта работа усиливает таблицы умножения, а также квадраты и кубы первых десяти натуральных чисел.
Игры
Это игры, которые открыли сами дети
Игра 1 — Создание фигур с длинными цепями
Описание материала:
Любой набор из длинной цепочки, квадратов и кубиков
Метод:
Возьмите любую длинную цепочку и соедините стороны, чтобы сформировать большую копию формы, сделанной во введении.Затем разместите квадраты бусинок в каждом углу и куб в центре.
Дети могут продолжать работать с другими наборами
Игра 2 — Пирамида драгоценностей
Описание материала:
Все площади
Метод:
Начиная с 10-го квадрата, поместите все квадраты друг на друга, чтобы сформировать пирамиду.
«Давайте найдем значение пирамиды» , Запишите на бумаге значение каждого уровня.
10 2 = 100
9 2 = 81
8 2 = 64
7 2 = 49
6 2 = 36
5 2 = 25
4 2 = 16
3 2 = 9
2 2 = 4
1 2 = 1
385
Сложите их вместе, чтобы найти сумму квадратов десяти натуральных чисел
Игра 3 — Драгоценная башня
Описание материала:
Все кубики
Метод:
Начиная с квадрата 100, поместите все квадраты друг на друга, чтобы сформировать башню.
«Давай найдем значение башни», Запишите на бумаге значение каждого уровня.
10 3 = 1000
9 3 = 729
8 3 = 512
7 3 = 343
6 3 = 216
5 3 = 125
4 3 = 64
3 3 = 27
2 3 = 8
1 3 = 1
3 025
Сложите их вместе, чтобы найти сумму кубиков десяти натуральных чисел
Примечания:
Объем кубиков розовой башни 3025 см 3.
Игра 4 — Произнесение таблиц умножения по порядку с помощью бусинок
Описание материала:
Коробочка для бус 1-9, по одному квадрату на каждое число на лотке, бумага для записи
Метод:
Начните говорить: « я возьму один раз, будет один» возьму 1 единицу, «одна взятая дважды — это два », возьмем еще одну единицу и поместим ее ниже, «одна взятая трижды будет три» единица затем продолжайте до десяти.
«Теперь я возьму два раза, то есть два», поместите полоску из 2 рядом с первой единичной бусиной. ‘Теперь я беру два взятых, то есть четыре’, помещаю еще один столбик из двух, ‘ два взятых три раза равны шесть’, место другое, ‘два взятых четыре раза равно восемь’, взят еще один бар из двух продолжений до десяти.
Деканомиальные игры
Сенсорные исследования
Первоначальная разведка бисером
Описание материала:
55 полосок бусинок 1-10, дополнительная коробка для внесения изменений в скорректированный деканом
Метод:
Сенсорная деканомия
Скажите детям: «Я хочу разложить все столы от 1 до 10, я собираюсь поставить один бугорок вверху моей циновки, чтобы он был ориентиром.’ Поместите один бардовый стержень из 1–10 горизонтально поверх мата.
«Один взятый один раз — это один, и он у нас здесь», указывает на бусинку одного.
‘ Один взят дважды, один, два’, выложите два столбика из одного под ним, идя вертикально, ‘один взятый три раза’, один, два, три (3) Разложите три бусинки, скажем их имена, чтобы убедиться, что у вас есть нужная сумма, это действует как руководство при построении остальных. Вербализируйте таблицы, продолжая до 10, вовлекая детей и регулярно проверяя.
«Мы систематически переходим к каждой таблице» оставляя свободное пространство между каждой таблицей, заполняем каждый продукт. Продолжайте озвучивать таблицы: «Два взятых один раз здесь, два взятых дважды — четыре» Поместите два такта из двух, «Два взятых три раза», поместите три такта из двух.
Когда закончите, скажите детям: «Когда я смотрю на ковер из драгоценных камней, я вижу множество квадратов. Это квадрат единицы, я могу обменять его на квадрат , поменять его, поставить новую бусину под углом.« Это два, взятые дважды, это два в квадрате, я могу заменить его на квадрат два, три, взятые трижды, — это квадрат трех». Продолжайте систематически, если дети не предложат другие варианты истинных квадратов. Когда все они будут обменены, спросите детей: вы видите, где находятся квадраты? Они расположены по диагонали, как будто диагональ образует позвоночник ».
Примечания:
Это может начаться в позднем Каза и продолжено в начале Элементарного.
Это занятие в небольшой группе, 2-3 ребенка.
Формируем сенсорную схему таблицы умножения, которую мы называем ковром драгоценностей.
Множитель по горизонтали и множитель по вертикали
Скорректированный деканом
Описание материала:
Ковер из драгоценных камней с истинными квадратами по диагонали
Метод:
Присоединяйтесь к детям, которые установили это в другой день, меняя части, используя закон коммутативности, чтобы он стал скорректированным.Скажем, «Давайте посмотрим, сможем ли мы отрегулировать его так, чтобы все бусинки стали зелеными, начиная с прямого угла. Давайте посмотрим на двойки: если мы возьмем вертикальную полосу двух бусинок и заменим ее зеленым, все линии будут зелеными ». Обменять стержень на два. « Глядя на тройки, если мы возьмем вертикальную тройку и обменяем ее на розовую полосу трех». Заменим полосу трех. «Затем две полосы из трех и обменяйте их на две три розовых полосы, и леска вся розовая». Заменить оба слитка из трех.
Продолжайте заменять вертикальные валики, систематически работая по одному уровню за раз. Продолжайте словесно, например, скажем, ‘Мы используем закон коммутативности, который гласит, что не имеет значения, что вы берете первым, множимое или множитель, если вы возьмете два шесть раз, это то же самое, что если вы возьмете шесть дважды … И здесь у нас есть квадрат, так что шесть раз взяты шесть раз, не имеет значения, в каком порядке вы это делаете ».
Примечания:
Это может начаться в позднем Каза и продолжено в начале Элементарного.Предложите, «Давайте посмотрим на верхний левый угол и сделаем все бусинки зелеными».
Числовой деканом
Описание материала:
Это серия конвертов, содержащих фигуры, использованные для построения деканомиального квадрата.
- Один конверт с надписью «квадраты», содержащий кусочки желтого цвета для всех квадратов, с продуктом в центре и обозначениями 1 2 , 2 2 до 10 2 в верхнем левом углу.
Конверты от «1» до «9» (для продуктов от 2 до 10) имеют градуированное количество штук в каждом конверте, на них указано название продукта в центре, но нет обозначений квадратов;
- Конверт 1 содержит 18 прямоугольных кусков, отсортированных по размеру от 2 до 10, с двумя копиями каждого (один для горизонтального и один набор для вертикального)
- Конверты от 2 до 9 прямоугольных кусков, их становится все меньше, так как в них нет повторения коммутативного закона.
Метод:
С небольшой группой, за столом.
Попросите детей вынуть содержимое конверта с надписью «квадраты». Расположите их по вертикальной линии слева от таблицы, говоря: ‘ Один квадрат, то есть один, умноженный на один, то есть один, два в квадрате, то есть два, умноженные на два, что составляет четыре’ и т. Д. на, укажите товар, написанный в центре карточки.
Скажем, «Вы помните, когда мы делали ковер из драгоценных камней? Где были квадраты? (по диагонали) , так что давайте расположим эти квадраты по диагонали .Разложите квадраты от угла к углу, образуя диагональ.
Удалите содержимое конверта 1, разложите карточки слева или там, где вы работаете, от самого маленького до самого большого, в вертикальном и горизонтальном расположении, которое вы будете использовать позже. Скажем, «Содержимое этого конверта сформирует руки нашего квадрата».
Начните с горизонтальной поговорки: «два взятых один раз — один раз, два взятых один раз — два, три взятых один раз — три». раскладывает карты вверху.Затем разместите карты по вертикали, говоря: «Здесь снова две, но на этот раз одна взята дважды, то есть две, одна взятая трижды — три». , поместите карты так, как вы называете проблему.
«Итак, теперь мы построили наши руки, это поможет нам в умножении», достаньте содержимое конверта 2 и сгруппируйте его в соответствии с их ориентацией, на этот раз просто сгруппируйте их, а не размещайте их систематически. Возьмите одну карточку и скажите: «У меня есть произведение 16, что это такое, это два, умноженные на восемь, так что, по вашему мнению, оно должно быть? Поместите его, обращая внимание на порядок множимого и множителя и используя руки для помощи.Затем возьмите пару в соответствии с законом о замене и скажите: «Посмотрите, это еще 16, это означает 8, умноженное на 2, куда это денется?» Приведите еще несколько примеров, приведя ту же вербализацию.
Возьмите карточки из Конверта 3, содержимое конверта начинается после 3 2 , так что 6. Пусть дети переходят, они не могут решить складывать карточки Закона о замене. Оставайтесь с детьми для первых нескольких конвертов, поощряя их озвучивать их, а не механически складывать их в детали.
Убирая, начните с внешних рукавов, произнося столы, когда собираете их. Как вариант, начните с содержимого Конверта 1 и соберите кратные с тем же продуктом.
Цель:
Усиление квадратов деканома, дальнейшая работа с законами коммутативности и распределения, запоминание таблиц умножения и произведений в квадрат
Примечания:
Если материал сделан с квадратной карточкой, напишите только продукт.Если это делают дети, они могут написать задачу на одной стороне, а продукт — на номере. Материал должен показывать товар.
Работа детей с таблицами умножения является подготовкой к этому, теперь это случайное исследование умножения, показывающее формирование закона коммутативности.
Сначала построение магистрали, и тот факт, что каждый конверт начинается после магистрали, выделяет квадраты с числами 1-9.
Когда проводить урок:
После того, как сенсорные схемы были использованы, чтобы возродить интерес.
Им необходимо знать таблицу умножения и систему обозначений квадратов после 6 лет.
Доработка:
После того, как вы построите квадраты и руки, содержимое других конвертов можно смешать, и дети будут строить из них.
Дети могут нарисовать числовой десятичлен на бумаге
Дети могут построить квадрат задом наперед, начиная с квадрата десяти.
Дети могут собрать свой материал из миллиметровой бумаги.
Преобразования (от стержней до квадратов, кубиков и башни)
Описание материала:
Разместите деканомиал с полосками бисера, используя цветовой узор отрегулированного деканома, но без истинных квадратов. Дополнительная коробка для внесения изменений в настроенный деканом, все квадраты и кубы из шкафа для бус, большой коврик, большой лист прямоугольной бумаги
Метод:
После того, как дети поработают с Числовым деканомом, присоединитесь к детям, работающим с сенсорным деканомом, или разложите с ними бусинки для этой цели.Скажите детям: « Мы собираемся превратить ковер из драгоценных камней в башню из драгоценных камней, мы посмотрим, сможем ли мы превратить все эти бусинки в квадраты».
Проведите по квадрату одного и начните указывать вертикальные бусины из двух, скажем, «У меня есть один бусин из двух и еще один бусинный брусок из двух, что составляет квадрат из двух, поэтому я могу обменять их на два, « Сделай это, затем указав горизонтальные полосы, скажем, » У меня есть две другие бусинки из двух, так что я могу обменять их на квадрат из двух » Сделай это.
Затем укажите вертикальные полосы из трех, скажем, «У меня три полосы из трех, я могу обменять их на квадрат из трех», Сделайте это. Укажите вертикальные полосы, скажем, «У меня есть еще три полосы из трех», Укажите горизонтальные полосы, говоря: «Я могу заменить их на квадрат из трех». Сделайте так, «У меня есть еще три столбца из трех, я тоже могу заменить их на квадрат из трех». Сделай это.
Укажите вертикальные полосы четырех, скажем, «У меня четыре полосы из четырех, я могу составить квадрат.Я могу сделать еще один обменный столбик по горизонтали для квадрата из четырех ». Укажите горизонтальные столбцы и скажите: « У меня четыре столбца из четырех, я могу заменить его на квадрат », Сделайте это, затем скажите , затем сосчитайте остальные четыре слитка и поменяйте их местами. Для четных чисел квадрат будет отсутствовать.
Продолжайте для столбцов пятерок, вы можете начать считать столбцы, «один, два, три, четыре, пять», перед тем, как заменить их квадратом. После нескольких первых примеров вы можете работать так, как хотите, как хотите.
Скажем, ‘Теперь у нас есть деканом, состоящий полностью из квадратов, давайте соберем все квадраты по диагонали’ , пропустим один квадрат, который также является одним кубом, ничего не говоря. Затем укажите квадраты двух, сказав: «Теперь у нас есть два квадрата по два», складываем их вместе, когда вы считаете, «один, два» и спросите детей, «Что они такие же, как?» (2 3 ).Замените оба квадрата кубиком по диагонали. Затем укажите квадраты из трех, сосчитайте их в том же направлении, что и столбики, сложите их стопкой и скажите: «У нас есть три квадрата из трех, что это то же самое?» (3 3 ) теперь поменяйте местами квадраты для куба по диагонали.
Продолжайте до тех пор, пока квадраты из десяти не скажут: ‘У нас есть один, два, три, четыре, пять’ , укладывая их вдоль основания, а затем ‘шесть, семь, восемь, девять, десять’ , складывая их по диагонали, чтобы получился куб.Обменяйте их на настоящий куб.
Скажем: « Давайте построим башню» , поместим затем в куб на десятки и так далее, «Итак, ковер из драгоценных камней теперь стал башней».
После урока:
Предложите детям повернуть процесс в обратном порядке сразу же после обмена кубиков на квадраты, а также на столбики и отдельные бусинки.
Запись работы с Decanomial
Эти записи могут быть сделаны в любой момент работы с сенсорными исследованиями в период деканомии, позже Casa, в начальной школе, особенно для детей, которым необходимо работать со своими столами.
Описание материала:
Хороший выбор бумаги в квадрате, разных размеров и с разными размерами квадратов.
Метод:
Часть 1- с ковром
Присоединяйтесь к ребенку с завершенным деканомиальным ковром из драгоценных камней.Скажите: «Здесь один взят один раз и пишем (1 × 1 =), а там один взят дважды, пишем (1 × 2 =) и один взят три раза, пишем (1 × 3 =). Затем выполните таблицу умножения на два и продолжайте до десяти.
Ребенок может записывать продукты по порядку в любом направлении от 1 × 1 до 10 x 10. Он должен умещаться на одном листе бумаги.
Примечания:
Используйте только те символы, которые знакомы детям, используйте квадратные скобки, символы равенства зависят от уровня ребенка.
Ребенок может записывать в течение одного или нескольких дней.
Часть 2 — с ковром
Предложите ребенку записать стоимость ковра из драгоценных камней, спросите: « Что у нас на самом деле есть на циновке?» (квадрат)
У нас есть квадрат «один плюс два плюс три плюс четыре»,
Во время записи (1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10).
Когда у нас есть квадрат чего-то, это означает, что мы умножаем его на себя, помещаем показатель 2 за скобки, так что он читается как (1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10) 2
Скажем, «Мы можем это расширить», напишите;
(1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10) х (1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10)
Умножьте это на детей, «Я умножу все в первой скобке на единицу», поставьте галочку над «1» множимого и напишите,
(1 x 1) + (2 x 1) + (3 x 1) + (4 x 1) + (5 x 1) + (6 x 1) + (7 x 1) + (8 x 1) + ( 9 х 1) + (10 х 1)
Оставьте строку для дальнейших расчетов.Продолжайте умножать на 2, отметив двойку множимого галочкой, прежде чем позволить детям перейти к умноженному на десятки.
(1 x 2) + (2 x 2) + (3 x 2) + (4 x 2) + (5 x 2) + (6 x 2) + (7 x 2) + (8 x 2) + ( 9 х 2) + (10 х 2)
Вернитесь и заполните каждый частичный продукт в строке ниже, оставленную пустой.
Сложите частичные произведения в конце каждой строки, чтобы найти итоги каждого множимого.
Затем добавьте итоговое значение в столбце в конце каждой строки, что составляет 3025
.Примечания:
В зависимости от детей, может быть лучше сначала выполнить все расширения, а потом вычисления или произвести вычисления по ходу.
Дети постарше могут не захотеть записывать каждое умножение и могут записывать произведения напрямую.
Часть 3 — с башней
Присоединяйтесь к ребенку с завершенной деканомиальной башней.Скажем, ‘Здесь у нас есть один кубик плюс два куба, плюс три куба плюс четыре кубика’ и напишите 1 3 + 2 3 + 3 3 + 4 3 + 5 3 +6 3 = 7 3 + 8 3 = 9 3 = 10 3
Ниже напишите продукты 1 + 8 + 27 + 64 + 125 + 216 + 343 + 512 + 729 + 100
Сложите их, получив ответ 3 025.
Помогите ребенку найти связь между ценностью ковра и драгоценного камня.
Теперь они знают о квадрате Пифагора, он основан на его теореме, которая гласит, что «сумма первых десяти натуральных чисел в квадрате равна сумме кубов первых десяти натуральных чисел».
Когда проводить урок:
Для детей от 6 до 8 лет.
Часть 4 — добавочный номер
Присоединяйтесь к ребенку с настроенной деканомиальной раскладкой, обратите их внимание на то, что у нас
(1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10) 2
Выберите часть этого, например
(1 + 2 + 3 + 4) 2
Спросите, «Что это на самом деле означает, значит?»
(1 + 2 + 3 + 4) х (1 + 2 + 3 + 4)
Скажем, «Иногда мы можем использовать буквы алфавита, чтобы помочь нам в математике, поэтому сегодня утром мы будем использовать буквы, давайте напишем это снова, используя буквы» , напишите
1 =
2 = b
3 = с
4 = d
(а + б + в + г) х (а + б + в + г) 2
Мы начинаем с умножения всего в первой скобке на a, затем ставим галочку, чтобы показать, что это сделано.
Скажем, «Когда мы используем буквы, мы всегда придерживаемся их порядка, поэтому для второй половины мы меняем его», , т.е. ba = ab
a 2 + ab + ac + ad
ab + b 2 + bc + bd
ac + bc + c 2 + cd
ad + bd + cd + d 2
‘ Теперь мы собираем термины, мы складываем те же самые термины вместе»
a 2 = 2ab = 2ac + 2ad + b 2 + 2bc + 2bd + c 2 + 2cd + d 2
‘ Вот и все, потому что когда мы занимаемся алгеброй, нам не нужно писать термины”
Примечания:
Это еще один способ исследовать теоремы Пифагора
Деканомиальный квадрат — это исследование с первыми десятью натуральными числами.Существует формула для вычисления суммы любого набора чисел n 2 + n
2
Например, с набором (1, 2, 3, 4) возьмите наибольшее число 4 и возведите его в квадрат, 16, плюс это число 16 + 4, получите 20, а затем разделите все это на два, даст 10. 1 +2 +3+ 4 + 5 = 10.
С помощью набора (1, 2, 3, 4, 5) возьмите наибольшее число, например 5 и возводим его в квадрат, получаем 25 плюс это число 25 +5, получаем 30, а затем делим все на два, получаем 15. 1 + 2 + 3 + 4 + 5 = 15.
Продолжайте повторять умножение столбцов трех и продолжайте до девяти, дети помогают.
‘Теперь посмотрим, сможем ли мы обменять ряд одинаковых бусин на квадрат каждого числа,’ Один взятый один раз такой же, как квадрат одного, так что я могу его поменять ‘, отсчитайте один, удалите бусину и замените это для одного из их лотка, два взятых дважды дают мне два квадрата, так что я могу заменить их, сосчитать два столбика и удалить их и обменять на два квадрата из их лотка, три взятых три, это то же самое, что квадрат три, чтобы я мог его обменять ‘, сосчитайте три полоски, снимите бусину и обменяйте ее на квадрат из трех из их лотка, четыре взятых четыре дадут мне четыре в квадрате, так что я могу его заменить, сосчитать четыре бусинки, удалить бусинку и обменять его на квадрат из четырех штук.
У меня один квадрат и один взяты девять раз, посмотрите на девять квадратов, у меня девять квадратов и девять раз взяты один раз. У меня два в квадрате и два берут восемь раз, у меня восемь в квадрате, а у меня восемь дважды. У меня три в квадрате и три взяты семь раз, у меня семь в квадрате, а у меня семь раз в три раза.У меня четыре в квадрате и четыре взяты шесть раз, у меня шесть в квадрате, а у меня шесть в три четверти. У меня пять в квадрате и пять в пять раз.
Давай запишем;
10 = 1 2 + 9
20 = 2 2 +16
30 = 3 2 + 21
40 = 4 2 + 24
50 = 5 2 + 25
60 = 6 2 + 24
70 = 7 2 + 21
80 = 8 2 +16
90 = 9 2 + 9
Во время записи скажем, ‘на одного, что у меня есть? Один квадрат плюс девять , на двоих, что у меня есть? Два в квадрате плюс шестнадцать футов.
Вычтите каждое сложение из приведенного выше, например 16-7 = 2 и 21-16 = 5 и 24-21 = 3, продолжаем.
Если вычесть каждую разницу, получится «0»
Игра 5 — Квадраты чисел
Описание материала:
Бисер 1-9, бумага для записи
Метод:
Запишите квадраты чисел (например,грамм. 1 2 ), а затем значения каждого квадрата 1 2 равно 1, 2 2 равно 4)
Затем найдите разницу между каждым значением и продолжите вычитание.
Скажем, «Разница, когда я продолжаю вычитать, равна 2, так каков показатель степени?» (2)
Примечания:
См. Лист «Квадраты чисел»
«Показатель» относится к числу степени, показатель в квадрате равен 2, в кубе — 3
Игра 6 — Кубики чисел
Описание материала:
Бисер 1-9, бумага для записи
Метод:
Запишите кубики чисел (напр.грамм. 1 3 ), а затем значения каждого куба 1 3 равно 1, 2 3 равно 8)
Затем найдите разницу между каждым значением, продолжайте вычитание, пока различия не станут одинаковыми
Скажем, «Разница, когда я продолжаю вычитать, равна 2, так каков показатель степени?» (6)
Возможное открытие:
Дети могут обнаружить, что разность, умноженная на показатель степени, дает показатель степени следующей степени, т.е.грамм. показатель степени 2, умноженный на показатель степени 3, дает 6, разницу между кубиками. Следовательно, разность 6, умноженная на показатель степени четырех, дает 24, обычную разницу при использовании степени четырех.
Операции
Описание материала:
Квадрат из бумаги и бусинок
Метод:
Дополнение
Скажите детям: «Мы можем складывать числа из квадратов и кубиков, я хочу сложить четыре квадрата и три квадрата.Знаете ли вы, что четыре в квадрате (16) и три в квадрате (9) Итак, четыре в квадрате плюс три в квадрате равны ‘ (25).
При этом напишите
4 2 +3 2 = 25
16 + 9
25
Сделайте несколько примеров.
4 2 +4 2 = 32
16 +16
32
Вычитания
Из материала возьмите восьмерку в квадрате (не представляйте вычитаемое) и закройте один угол, эквивалент 5 2 , бумагой, считая пять горизонтальных и вертикальных бусинок вслух.Посчитайте, что осталось.
При этом напишите
8 2 -5 2 = 39
64–25 =
39
Умножение
Возьмите три лота по пять квадратов бус
При этом напишите
5 2 x 3 = 75
25 х 3
75
Примечание: задайте детям вопросы в аннотации, а затем сверьте их с квадратами.
Отдел
Возьмите пять кеглей и кубик из пяти. Спросите детей, как я могу разделить кубик, обменять его на пять квадратов из пяти и поделиться ими.
Ответ — доля одной кегли
При этом напишите
5 3 ÷ 5 = 25
1 ÷ 25 5
25
Операции со смешанными числами
Работа без материалов, продолжение исследования,
(5 3 + 2 2 ) — 8 2
(125 +4) — 64
129 — 64
65
Цель:
Повторение через разнообразие для интеллектуального развития
Magic Cube 4D
Magic Cube 4DMagicCube4D — это полнофункциональный четырехмерный аналог кубика Рубика плюс десятки красивых четырехмерных головоломок, помимо гиперкуба.На изображении выше показана головоломка 3 4 в решенном состоянии. или щелкните здесь правой кнопкой мыши и выберите «Сохранить ссылку как»Программа упакована в исполняемый файл jar, который должен работать в любой системе с установленной виртуальной машиной Java. Сохраните его на рабочем столе или в любом другом месте, если вы сможете найти его позже. Просто дважды щелкните по нему, чтобы запустить; установка не требуется. В Windows вы можете создать ярлык на рабочем столе, щелкнув правой кнопкой мыши и выбрав «Отправить на> Рабочий стол» из раскрывающегося списка.Пожалуйста, прочтите FAQ для более полного описания головоломки. Если он не запускается, вам может потребоваться установить текущую виртуальную машину Java. Щелкните здесь, чтобы увидеть последнюю версию.
Дон Хэтч и Мелинда Грин постоянно разрабатывала эту головоломку, начиная с 1988 года. Джей Беркенбильт и Позже к нам присоединилась Ройс Нельсон, которая внесла большой вклад. Дон и Джей первыми решили загадку, широко используя макросы.Ройс был первым, кто решил головоломку без использования макросов. Для своего решения он расширил 3D-модель Филипа Маршалла. «Окончательное решение кубика Рубика» в 4D. Вы можете изучите решение Ройса, если вам не хочется сначала решать его самостоятельно. (Польская версия здесь.) Дон даже написал программу, которая может решать кубики Рубика любого количества измерений. Наконец, специалист по математике на YouTube создал видео с решением, которое делает его довольно простым.
Мелинда 2x2x2x2
Наконец-то первая в мире настоящая физическая 4D извилистая головоломка! Это 3D-версия модели 2 4 .Посмотрите вступительное видео ниже и посетите домашнюю страницу проекта, чтобы узнать больше и получить один для себя.
Страницы проекта
- Список рассылки — для общего обсуждения. Открыт для всех. Примечание. Группы Yahoo прекращают свое существование и с декабря 2019 года больше не будут хранить архивы сообщений. Вы по-прежнему можете присоединяться и транслировать сообщения подписчикам, но для просмотра прошлых разговоров нам потребуется перенести наш расширенный архив сообщений на другую платформу.Мы загрузили эти данные в виде zip-файла размером 51 МБ здесь на случай, если вы захотите попробовать.
- Репозиторий исходного кода — это проект с открытым исходным кодом.
- Отслеживание проблем — пожалуйста, отправляйте отчеты об ошибках и запросы функций здесь.
- Project Wiki — корень всей документации.
- MagicCube4D Hall Of Fame — Список всех решателей 4D кубов и решений для записи.15
или в десятичной форме как 1756772880709135 843 168 526 079 081025 059 614 484 630 149 557 651 477 1560 21 733 236 798 970 168550 600 274 887 650 082 354 207 129 600 000 000 000 000Для для сравнения, обычный 3D Кубик Рубика имеет только 43 252003 274 489 856 000 уникальных позиций, что по-прежнему огромно. С другой стороны, у четырехмерного куба больше потенциальных позиций, чем общее количество атомов во Вселенной! Намного больше.Поговорим об игле в космическом стоге сена! Щелкните следующую ссылку, чтобы узнать, как вычислить перестановки 4D куба. Удивительно, но даже несмотря на то, что количество позиций четырехмерного куба пугающе велико, это не означает, что эту головоломку во много раз сложнее решить. Если вы уже можете собрать трехмерный куб, значит, вы более чем на полпути к решению этого. Здесь также применимы все техники, которые вы уже знаете.
Связанные пазлы
- MagicCube5D — Ройс написал потрясающую 5D версию этой головоломки, которую он и некоторые другие даже решили.После того, как вы попадете в Зал славы 4D, вы можете попробовать 5D зал безумия. Вот видео, показывающее мировой рекорд кратчайшее решение 5D от Андраса Эссеки. И если вас пугает 3 5 с его 810 наклейками, знайте, что Мэтью Ширин решил 7 5 с 24010 наклейками!
- Magic120Cell — автономный 4D аналог Roice Извилистая головоломка Megaminx. Этот монстр состоит из 120 гиперграней, каждая из которых представляет собой додекаэдр, выглядящий в точности как Мегаминкс.Он имеет в общей сложности 7 560 гипер-стикеров и поистине поразительные 2,3 x 10 8126 возможных позиций, только одна из которых является решенным состоянием. Прежде чем идти дальше, мы действительно должны остановиться и поразмышлять о том, насколько велико это число, потому что вы действительно не видите такие числа каждый день. Помните выше, как во Вселенной на 3 4 позиций больше, чем частиц? Представьте себе, что каждая частица во Вселенной на самом деле крошечная вселенная, в каждой из которых столько же частиц, сколько в нашей.Это намного больше, правда? А теперь представьте, что все этих частиц во всех этих вселенных также представляют собой целую вселенную, подобную нашей. Намного больше, правда? Представьте, что вы повторяете это упражнение на 100 уровней, и только тогда мы приближаемся к количеству позиций в этой головоломке. MagicCube4D теперь также поддерживает этого монстра, но версия Ройса лучше, если вы намерены серьезно попытаться решить эту проблему. Ноэль Чалмерс стал первым, кто разгадал это чудовище. Обязательно посмотрите покадровую видеозапись Решение Ноэля на YouTube.Поздравляю Ноэля!
- Ранняя реализация Джоном Бейли 2 4 в Javascript.
- В 2010 году Андрей Астрелин присоединился к нашему сообществу и сразу побил несколько наших самых заветных рекордов. Не удовлетворившись, он тогда написал и выпустил свою собственную семимерную версию !
MagicCube7D решает проблему визуализации такого многомерного объекта, начиная с нашей теперь уже знакомой 4D-проекции, а затем частично разворачивая последние три измерения, используя умный фрактальный дизайн.Не только одна головоломка, этот удивительный фрагмент кода поддерживает все 12 кубов от 3 4 до 5 7 . Ох, а затем он пошел и решил 3 7 . Молодец Андрей!
- Magic Cube 3D — Дэвид Вандершель написал трехмерный симулятор кубика Рубика, используя трехмерный эквивалент четырехмерной проекции и пользовательский интерфейс для четырехмерной головоломки. Может показаться странным создание трехмерного аналога четырехмерного аналога трехмерной головоломки, но в этом есть логика, поскольку это помогает прояснить смысл рабочего и пользовательского интерфейса головоломок более высоких измерений.
- MagicCube2D — Просто для удовольствия и чтобы посмотреть, как будет выглядеть эквивалентная 2D-головоломка.
- А Игра «4D строительные блоки» от Генрика Траппманна дает нам еще одно интересное занятие в 4-х измерениях.
- Magic Cube 4D для Android, мобильная версия.
- MagicTile от Roice позволяет вам разгадывать свои собственные 2D-гиперболические извилистые головоломки, включая удивительные Quartic Клейна, а также евклидово эллиптическое бесконечные правильные многогранники и даже четырехмерные косые многогранники! MagicTile — это красота.
- Magic Hyperbolic Tile {6,3,3} от Андрея — это трехмерная версия MagicTile Ройса, потому что она живет в гиперболическом трехмерном пространстве. Эта головоломка оказывается чертовски сложной, но при этом восхитительно красивой.
- Magic Puzzle Ultimate также от Андрея — его версия MagicCube4D. Пользовательский интерфейс совершенно другой, и некоторые опытные пользователи предпочитают его. Он включает в себя несколько уникальных и специальных головоломок, таких как желанные и очень сложные 24-элементные, 48-элементные, 600-элементные, а также глубоко усеченные, усеченные, исправленные и пренебрежительные версии многих из них, а также некоторые из них 5D и Пазлы 6D.
- 2D реализации
3D и
4D извилистые кубики от Alex.
- Отразить куб от Нан Ма дает нам трехмерный кубик Рубика с возможностью разрешать только отражающие движения и другие комбинации этой основной идеи.
- Light’s Out 3D Еще одна головоломка от Nan Ma поддерживает десятки симметричных многогранников. Нан действительно хорошо умеет собирать пазлы!
Ройс написал статью, в которой описал многие из вышеупомянутых головоломок и то, как они взрывались из оригинального кубика Рубика.Это было принято в качестве обложки в апрельский выпуск журнала Math Horizons за 2018 г.
Лицензия
Бесплатное ПО, требуется указание авторства, в идеале включая ссылки на эту страницу.
Другие реализации головоломки 4D-куб
Веб-страницы, ссылающиеся на эту
Вернуться на главную страницу Superliminal.Cube Escape Collection — Руководство по всем достижениям
Все достижения в игре.
Как получить все достижения
Введение
Это руководство включает краткое описание всех достижений в игре. Хотя некоторые из них могут показаться расплывчатыми или загадочными, они будут очень четкими во время игры. Достижения с пометкой Story нельзя пропустить. Достижения упорядочены так, как я их получил во время игры.
Времена года
Цветет
- Весна 1964 года. Щелкните женщину в окне (откройте шторы, увеличьте масштаб, если ее нет, уходите и возвращайтесь).
Харви- Весна 1964 года. Щелкните попугая примерно 10 раз.
Цветет- Рассказ. Полная весна 1964 года. Достижение откроется, когда вы вставите черный куб в отверстие
Озеро- Сюжет. Завершите «Лето 1971 года». Достижение появится, когда вы вставите черный куб в отверстие.
Молодая Лаура- Осень 1971. Используйте код 25641 на телевизоре. Код можно найти в Cube Escape: The Lake после открытия коробки с зеленым камнем.
Розовые цветы- Рассказ. Завершите осень 1971. Достижение откроется, когда вы вставите черный куб в отверстие
Чертеж- Сюжет. Завершите зиму 1981 года. Достижение появится, когда вы вставите синий куб в отверстие.
Найди меня в прошлом- После ремонта машины вернитесь в лето 1971 или осень 1971 года и нажмите на телефон.
Озеро
Apple
- История.Найдите яблоко. Это в мертвом теле.
EyeEye- История. Найди глаз. Он спрятан в стене рядом со шкафом. Чтобы его достать, понадобится лом.
Монета- Рассказ. Найдите монету. Это в шкафу.
Shell- Рассказ. Найдите ракушку. Используйте плесень в качестве приманки на рыбной дороге.
Голубая жемчужина- История. Найдите синий драгоценный камень. Он находится в первом зеленом сундуке.
Испорченная душа- В какой-то момент в окне появится черная фигура.Это случайно, вы можете уходить и возвращаться, пока он не появится. Щелкните его, чтобы получить достижение.
Hoarder- Полностью заполните свой инвентарь. Это довольно легко получить, учитывая, сколько предметов вы можете подобрать. У вас должно быть 12 предметов. Чтобы упростить задачу, когда у вас будет рыба, держите ее в своем инвентаре.
Пятиугольник- Это связано с альтернативным окончанием. Используйте зеленый камень вместо синего на дереве и завершите главу.
Arles
Мой любимый напиток!
- Рассказ. Приготовьте абсент.
Ура!
EarEar- Рассказ. Отрежьте Ван Гогу ухо.
Белый куб- Рассказ. Найдите белый куб. Увидев испорченную душу в зеркале, используйте на нее пистолет.
Черный куб- Сюжет. Найдите черный куб. Вы получите его после завершения покраски.
Déjà vu- Войдя в ухо и дойдя до двух дверей, щелкните левую (синюю), чтобы вернуться в свою комнату.
Греби, греби, греби лодкой ..- Откройте окно и нажмите на человека в лодке.
Rusty Lake Hotel- После входа в ухо и двух дверей введите код 1853. Откройте дверь, войдите в комнату, откройте окно и щелкните отель. Подсказка к коду появляется в «Cube Escape: Case 23» на фотографии на стене под названием «Спальня в Арле».
Harvey’s Box
Назад в коробке
- История. Он разблокируется, когда вы вернетесь в коробку после того, как наберете фрукт.
Эксперт по домино- Сюжет. Соберите домино.
Рыба копченая- Рассказ. Дайте рыбе сигару.
Peekaboo!- Рассказ. Используйте нож там, где голубь тыкает в ящик.
Ты умер!- Хотя технически это невозможно пропустить, это очень сложно пропустить.Чтобы получить его, нужно умереть. Когда вы подниметесь по веревке, появится испорченная душа и убьет вас, если вы не выпустите светлячков очень быстро. Пусть это тебя убьет.
Перо- Потяните за веревку несколько раз, пока перо не упадет. Щелкните по нему.
Знакомая мелодия- Сыграйте на гребне следующие ноты: C C D #D G E D #D C #A #G #G #G #G. Подсказка для этого достижения появляется в «Cube Escape: Theater» после получения достижения «Bad Egg Symphony».
Побег из коробки- Сюжет. Закончите главу.
Case 23
Вид на Арль
- Глава 1. Щелкните фотографию на стене и табличку с названием «Спальня в Арле». Щелкните окно на фотографии, чтобы открыть его и получить достижение. 1853 год — намек на достижение в «Cube Escape: Arles».
Принудительное кормление- Глава 1. Накормите рыбу в аквариуме тремя мухами.Это нужно сделать перед тем, как отправить муху на раковину.
Архив Расти-Лейк- Рассказ. Завершите главу 1. Она появляется, когда вы открываете улики из архива Расти-Лейк, найденные в сейфе.
Mugshot- Глава 2. Установите телевизор в офисе детектива на 171. Подсказка для этого достижения появляется в «Cube Escape: Theater» на зеркале, когда Боб идет в туалет.
Темные крылья- Глава 2. После завершения рассказа на машинке и получения цифр наберите «ворона».Намек на это достижение появляется в главе 1 в газете. Птица и часы, установленные на 3:25, которые появляются на бумаге, являются намеком на достижение «Старый ворона» в Cube Escape: «Мельница».
Вентилируемый- Рассказ. Завершите главу 2. Оно появляется, когда вы вставляете в телевизор черно-белые кубики.
Мистер Ворон- Рассказ. Завершите главу 3. Вы получите ее, как только мистер Ворон приблизится к вам.
Я сделал это- Рассказ.Завершите главу 4. Вы получите его, когда войдете в лифт.
Мельница
Чердак
- Рассказ. Попасть на чердак.
Изысканная кухня- Отдайте птицу, полученную от попугая, старухе.
Старый ворона- После телефонного разговора установите часы на 3:25 и вернитесь к попугаю. Он уйдет с вороной на его месте. Щелкните его, чтобы получить достижение.Подсказка для него появляется в «Cube Escape: Case 23» после получения достижения «Dark Wings»
The basement- Story. Доберитесь до подвала.
T-Pose- Рассказ. Глядя в телескоп, нажмите на тело Дейла.
Нежить корова- Когда корова мертва, щелкните ей по голове несколько раз.
Free Bird- Рассказ. Завершите игру.
Развлечение с Лаурой- Пока Лаура на цепи, нажимайте стрелки на устройстве в случайном порядке, пока не откроется достижение.
День рождения
Альтернативное решение
- На экране с дедом расставьте флажки в порядке 12 = 3×4
Мистер Кролик- Посмотрите в окно и нажмите на фигурку кролика.
Любимое оружие- Лопните пузырек жевательной резинки ножом.
Напиток в бареКоличество комбинаций — зона Рубика
Сколько комбинаций у кубика Рубика? Легко узнать, сколько у них 3x3x3, но когда я посмотрел, было очень мало страниц, которые показывали количество комбинаций для всех размеров от 2x2x2 до 7x7x7.Итак, я сделал эту страницу, перечислив количество комбинаций для кубиков разного размера. Также есть калькулятор javascript на тот случай, если вы хотите выяснить это для больших размеров.
- Кубик Рубика 2x2x2 (так называемый карманный куб ) имеет 3674160 комбинаций . Это управляемое число. Если вы возитесь с кубом 2x2x2 наугад, восемь часов в день непрерывно, вы решите его чисто случайно примерно два или три раза в год. Предположим, что ваш куб — или ваше запястье — пока что не ломается.Имейте в виду, что четыре месяца на сборку куба 2 × 2 несколько медленнее, чем мировой рекорд.
- Оригинальный кубик Рубика 3x3x3 содержит 43 252003 274 489 856 000 комбинаций , или 43 квинтиллиона. Опять же, как указано на главной странице этого веб-сайта, это легко вообразимое число. Например, это немного меньше, чем квадрат населения Земли.
- Кубик Рубика 4x4x4 (называемый Мастер Кубом или Месть Рубика — не уверен, за кого он мстил, должен сказать) имеет 7 401 196 841 564 901 869 874 093 974 498 574 336 000 000 000 комбинации (что есть, 7.4 quattuordecillion, если вы действительно хотели знать). Чтобы понять, насколько велико это число, представьте, что у вас есть столько чайных ложек сахара (скажем, вы планируете очень большое чаепитие , ). Сахар заполнил бы Солнечную систему примерно в 3,5 раза больше орбиты Плутона. Она также будет весить примерно в 70 раз больше, чем наша галактика, и мгновенно превратится в черную дыру со взрывом, который уничтожит Млечный путь, Магеллановы облака и, вероятно, разбудит некоторых сонных андромедианцев.Подумайте об этом в следующий раз, когда будете крутить 4 × 4.
- Как будто этого недостаточно, кубик Рубика 5x5x5 (называемый Кубиком профессора) имеет 282 870 942 277 741 856 536 180 333 107 150 328 293 127 731 985 672 134 721 536 000 000 000 000 000 комбинаций (он же 283 тревигинтиллион). Это неудобно приближается к количеству атомов в известной Вселенной.
- Недавно греческий инженер Панайотис Вердес придумал, как сделать кубики 6 × 6 и 7 × 7. V-Cube 6 (кубик Рубика 6x6x6) имеет 157 152 858 401 024 063 281013 95959 519 483 771 508 510 790 313 968 742 344 694 684829 502 629 887 168 573 442 107 637 760 000 000 000 000 000 000 000 000 комбинаций .Это, конечно, невероятно громадное число, но…
- Кубик Рубика 7x7x7 ( V-Cube 7 ) имеет 195551183731307 835 329 126 754019 748 794 904 992 64 567 152 132 912 323232706 135 469 180 065 278712 755 853 360 682 328 551 719 137 311 299 993 600 000 000 000 000 000 000 000 000 000 000 000 комбинации. Как я отмечаю в этом фильме, это больше комбинаций, чем восемь независимых кубов 3x3x3. Тем не менее, некоторые люди могут решить проблему 7x7x7 всего за несколько минут.Удивительный!
Никто не строил и не продавал куб большего размера, чем этот, хотя Панайотис Вердес обещает, что в разработке находятся несколько более крупных кубов. А пока существуют программы, которые позволят вам играть с кубом любого размера. Эти большие размеры решить не сложнее, чем 6 × 6 и 7 × 7, только более утомительно.
- Куб 8x8x8 будет иметь 35 173780 923 109 452 777 509 592 367 006 557 398 539 936 328 978 098 352 427 605 879 843 998 663 990 903 628 634 874024 098 344 287 402 504 043 608 4 016 679 717 941 937 308 041 012 307 368 528 117 622 006 727 311 360 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 комбинации.
- A 9x9x9 куб будет иметь 14 170 390 542 612 915 246 393916 889 970 75 2732 946 384 514 830 589 276833 655 387 444 667 609 821 068 034 079 045 039 617 216 635 075 219 765 012 56 942 990 302 517 903 971 787 699 783 519 265 329 288 048 603 083 134 861 573 075 5730
082 416 866 010 882 486 829 056 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 комбинации. - A 10x10x10 куб будет иметь 82983598 512 782 362 708769 381 780 036 344745 129 162094677 382 883 567 691 311 764 021 348095 163 778 336 143 207 042 993 152556079 271 030 423741 1108 732 457 008 486 832 096 777 758 106 509 177 169 197 894 747 758 859 723 340 177 608764 906 985 646 389 382047 319 811 227 549 112 086 753524 742 719 830 990 076 8054244 479 380 054 016 000 00000000000000000000000000000000000000000000000000000000000000000000000000000000000 комбинации.Ты!
Если вы хотите узнать количество комбинаций для куба большего размера, вы можете сделать это, используя форму ниже. Я должен вас предупредить, что если вы наберете смехотворный размер для куба (скажем, больше 30), он уволит ваш компьютер , а не мой.
Примечание. Из-за ошибок в Internet Explorer вам может потребоваться использовать Google Chrome или Mozilla Firefox, чтобы исправить эту форму — пока я не найду способ обойти ошибки. В любом случае, Chrome и Firefox намного лучше IE, поэтому было бы ошибкой получить их , а не .
Наслаждайтесь!
.

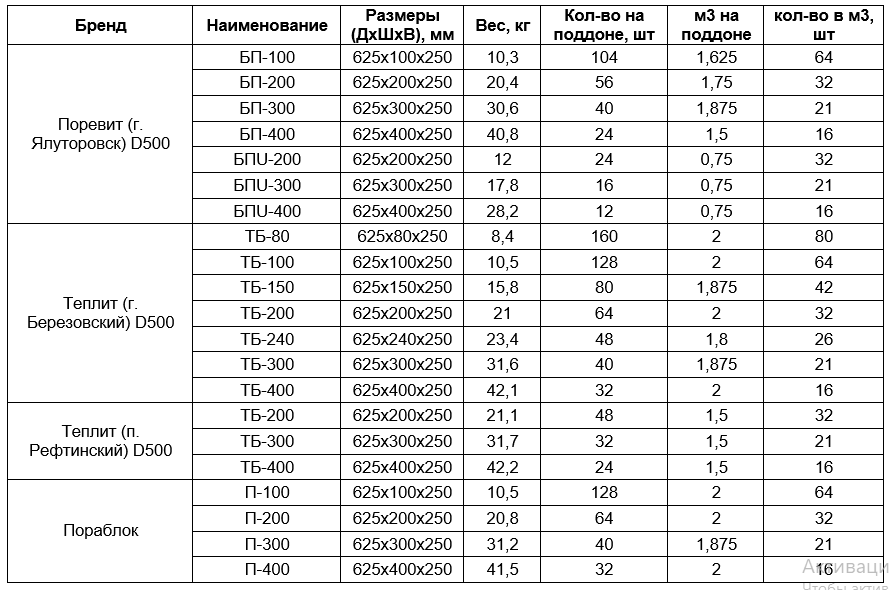 Разделив кубометр на полученное дробное значение – также в кубометрах – получим искомую величину.
Разделив кубометр на полученное дробное значение – также в кубометрах – получим искомую величину.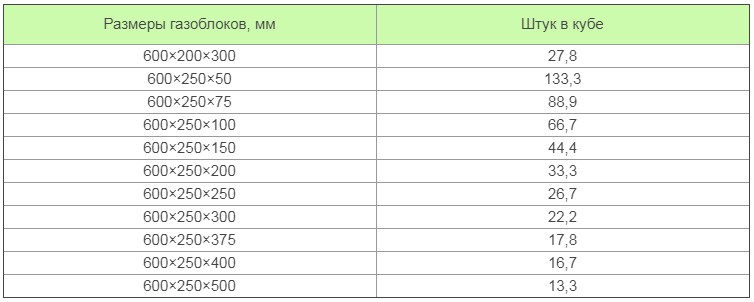
 Он более легкий, всего 5,5 кг, поэтому идеально подходит для установки внутри помещения.
Он более легкий, всего 5,5 кг, поэтому идеально подходит для установки внутри помещения. с габаритом 200 мм, то есть на все уйдет 25 (5 шт. требуется с каждой стороны).
с габаритом 200 мм, то есть на все уйдет 25 (5 шт. требуется с каждой стороны).

 Количество штук в метре кубическом = 1 / 0,018 = 55 единиц;
Количество штук в метре кубическом = 1 / 0,018 = 55 единиц; м. или 1/0,018=55,56≈56 единиц.
м. или 1/0,018=55,56≈56 единиц. м.
м.