Коэффициент перекрытия: Коэффициент перекрытия косозубых передач — Лекции и примеры решения задач технической механики

Коэффициент перекрытия прямозубой передачи

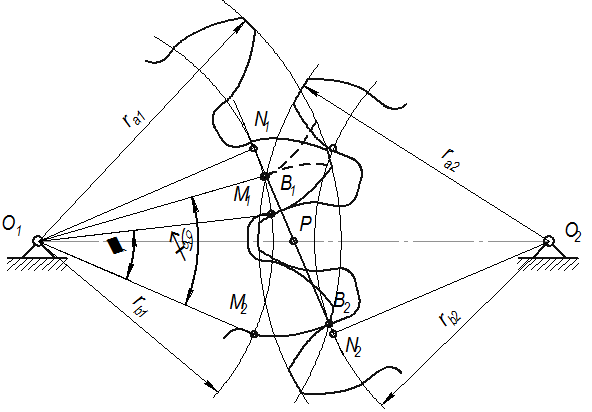
Начало контактов зубьев колес (рис.5.8), образующих зубчатую пару, происходит в момент, когда точка В₁ зуба ведомого колеса, лежащая на окружности вершин, оказывается на линии зацеплени. Далее профиль ведущего зуба будет давить на профиль ведомого и скользить по нему до тех пор, пока зубья не выйдут из зацепления. Последняя точка В₂ контакта зубьев располагается на пересечении линии зацепления с окружностью вершин ведущего колеса.

Отрезок линии зацепления В₁В₂, внутри которого происходит контакт сопряженных профилей зубьев, называется активным участком линии зацепления. Соответственно часть профиля зуба, точки которого последовательно контактируют с парным колесом, называется активным профилем. Он располагается между окружностью вершин и вспомогательной окружностью, проведенной из центра колеса через крайнюю точку активного участка линии зацепления.

Угол поворота колеса от положения, соответствующего входу зуба в зацепление, до положения, соответствующего выходу зуба из зацепления, называется углом перекрытия . Для прямозубых передач полный угол перекрытия равен углу торцового перекрытия , т.е. углу перекрытия в любом сечении, перпендикулярном оси колеса.

При работе зубчатых колес необходимо, чтобы в любой момент времени колеса находились в зацеплении.

Для этого требуется, чтобы угол перекрытия был больше углового шага, т.е. > . В противном случае пара зубьев выйдет из зацепления раньше, чем в

зацепление войдет следующая пара; причем это зацепление произойдет с ударом.

Отношение угла перекрытия к угловому шагу называется коэффициентом перекрытия:

.

Для прямозубых передач полный коэффициент перекрытия равен коэффициенту торцового перекрытия, т.е. коэффициенту перекрытия в торцовом сечении:

= В₁В₂ /(pm cosa) .

Коэффициент перекрытия характеризует плавность работы передачи. Чем больше этот коэффициент, тем плавнее, спокойнее работает передача; меньше шум, динамические нагрузки. Недопустимо, чтобы величина коэффициента перекрытия была меньше единицы.

При прочих равных условиях коэффициент перекрытия возрастает с увеличением числа зубьев колес (отрезок В₁В₂ увеличивается) и уменьшается с увеличением коэффициента суммы смещения колес (в этом случае активный участок В₁В₂ линии зацепления уменьшается).

Наибольший коэффициент торцового перекрытия соответствует фиктивному случаю зацепления двух реек: ( при

Читайте также:

Расчёт цилиндрического эвольвентного зубчатого зацепления (внешнего и внутреннего), оптимальный расчёт коэффициентов смещения — Kompas — блог

Расчёт цилиндрического эвольвентного зубчатого зацепления (внешнего и внутреннего), оптимальный расчёт коэффициентов смещения для прямозубого внешнего зацепления и расчёт профиля зуба.

Автором разработана программа позволяющая, производить указанные выше, вычисления. Она предназначена заменить, существующую на данный момент, программу для расчёта прямозубого зацепления (внешнего и внутреннего) http://www.chipmaker…les/file/12127/.

Программа и процесс по устранению ошибок и доводке её до нужных параметров, оказались очень даже не простыми, при возникновении сложных вопросов, я обращался за консультациями к Евгению (tmpr), я ему очень благодарен за оказанную помощь. Поэтому можно сказать, что получилась почти профессиональная программа, которая гарантирует высокую точность вычислений.

Для расчёта геометрии прямозубого внешнего зацепления, автор впервые ввёл понятие оптимального расчёта коэффициентов смещения.

Как известно, для расчёта шестерён с количеством зубьев более десяти и менее 16, без коэффициентов смещения никак не обойтись.

К расчёту эвольвентного зацепления предъявляется очень большое количество противоречивых требований:

1. Не должно быть подрезания ножки зуба;

2. Не должно быть интерференции зубьев;

3. Не должно быть заострения зубьев, т.е., толщина зуба на поверхности вершин не должна быть – Sa1, Sa2 < 0.3m;

4. Коэффициент перекрытия – Ea >1.0 , в литературе рекомендуется, чтобы коэффициент перекрытия был > 1.2.

5. Коэффициенты удельного скольжения должны быть близки друг к другу, а в лучшем случае равны, тогда износ зубьев будет относительно равномерным.

Всё это заложено в построении блокирующих контуров: см. ГОСТ- 16532-70 и ГОСТ – 19274-73, но, к сожалению, там приведены не все возможные случаи сочетания количества зубьев шестерён и колёс.

Автор попытался решить эту проблему с помощью компьютера, создать программу, которая позволяет производить оптимальный расчёт, с учётом указанных требований для прямозубого внешнего зацепления. Вручную эту работу сделать – невозможно.

Компьютеру приходится производить колоссальное количество вычислений при расчёте коэффициентов смещения X1 и X2.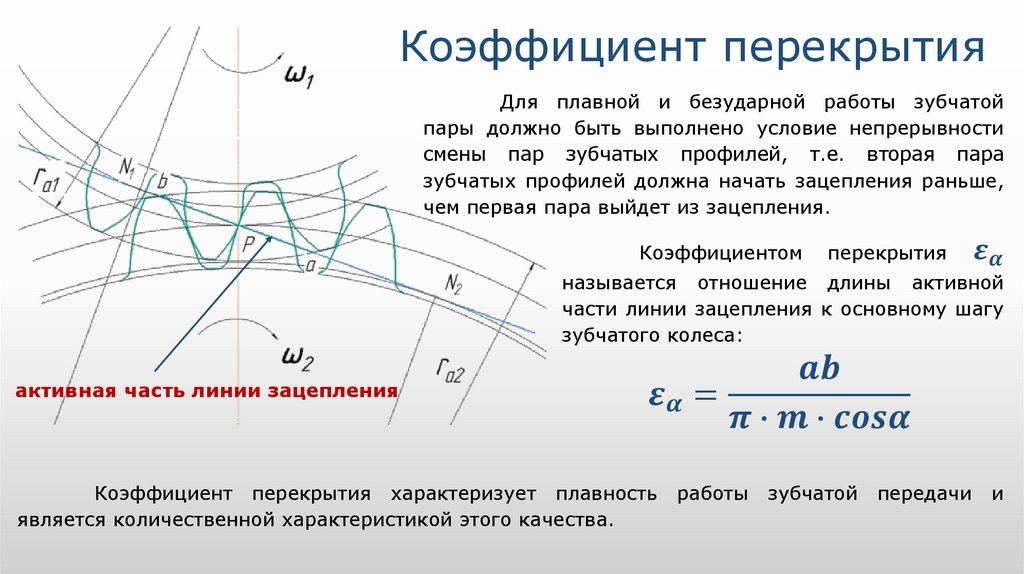

Например: при вычислении только одного угла зацепления, для достижения необходимой точности, требуется 5000 циклов, и все эти вычисления происходит до тех пор, пока все приведённые выше параметры не уложатся в заданный промежуток, удовлетворяющий всем требованиям к данному зубчатому зацеплению. На рисунке ниже, показан « оптимальный» расчёт внешнего эвольвентного зубчатого зацепления со смещением. Как видите, все выше перечисленные требования к зацеплению, выполняются.

А, вот тот же самый расчёт, выполненный программой, согласно ГОСТ-16532-70.

Коэффициент торцового перекрытия, в данном случае, уже не достигает оптимального Ea=1.2.

Разработанная программа позволяет рассчитать все данные для построения профиля зуба. Формулы для расчёта взяты из ГОСТ – 16532-70. Это позволило произвести построение профиля зубьев с высокой степенью точности. Ниже на рисунке показано построение зуба шестерни, эвольвентного зацепления, когда: Z1=11, Z2=25, m=5, x1=0.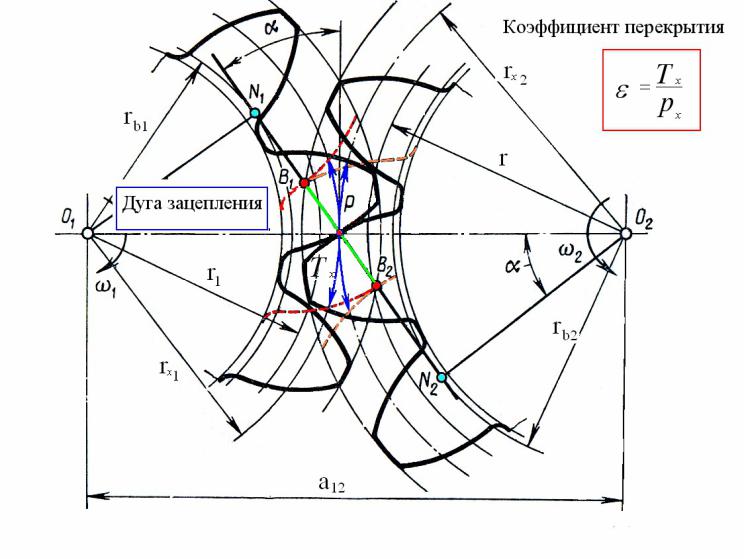 5, x2=0.5.

Метод построения профиля зуба по формулам с помощью программы, обеспечивает более точное его построение и как факт построение всего чертежа зацепления, чем графическое вычерчивание зубьев зацепления, как показано здесь:

Расчёт радиуса дуги переходной кривой равной 0,38m, программа рассчитывает для случаев, когда радиус основной окружности rb1 и rb2 больше радиуса впадин rf1 и rf2, для случая когда rf1 или rf2 > rb1 или rb2, автор не сумел составить и решить уравнения для расчёта переходной кривой, но если кто то сумеет решить эту задачу, я буду очень благодарен и внесу изменения в программу. На данный момент программа выдаёт результат «нет решения» и поэтому в данном случае конструктору придётся решать эту задачу графически, а не аналитически с помощью программы.

Точность построения чертежа подтверждается снятием размеров непосредственно с чертежа: количество зубьев в общей нормали шестерни и колеса, а также длина общей нормали, соответствуют расчётным.

Программа расположена по адресу:

Коэффициент торцового перекрытия — fiziku5.ru

(84)

(85)

Расстояние между центрами колёс называется межцентровым расстоянием

(86)

Расстояние между одноименными точками двух соседних зубьев измеренное по делительной окружности, называется шагом зубчатого колеса по делительной окружности

. (87)

Толщина зуба s и ширина впадины e по делительной окружности равны

(88)

Диаметр основной окружности колеса

(89)

шаг по основной окружности

(90)

Диаметр начальной окружности колеса dw, нарезанного без смещения инструментальной рейки равен диаметру делительной окружности d.

В случае зацепления двух колёс, нарезанных со смещениями x1 и x2 инструментальной рейки, угол зацепления определяется по формуле

(91)

В этом случае диаметр начальной окружности определяют по формуле

(92)

а начальное межосевое расстояние – по формуле

(93)

6. 7. Коэффициент торцового перекрытия

Коэффициент торцового перекрытия учитывает непрерывность и плавность зацепления в передаче. Эти качества передачи обеспечиваются перекрытием работы одной пары зубьев работой другой пары. Для этого каждая последующая пара зубьев должна войти в зацепление ещё до того, как предшествующая пара выйдет из зацепления. О величине перекрытия судят по

(94)

здесь τ1=2π/z1 – угловой шаг шестерни, а τ2=2π/z2 – колеса.

Коэффициент торцового перекрытия для прямозубой цилиндрической передачи можно определять по следующей формуле:

(95)

Знак плюс в (92) соответствует внешнему зацеплению, а знак минус – внутреннему.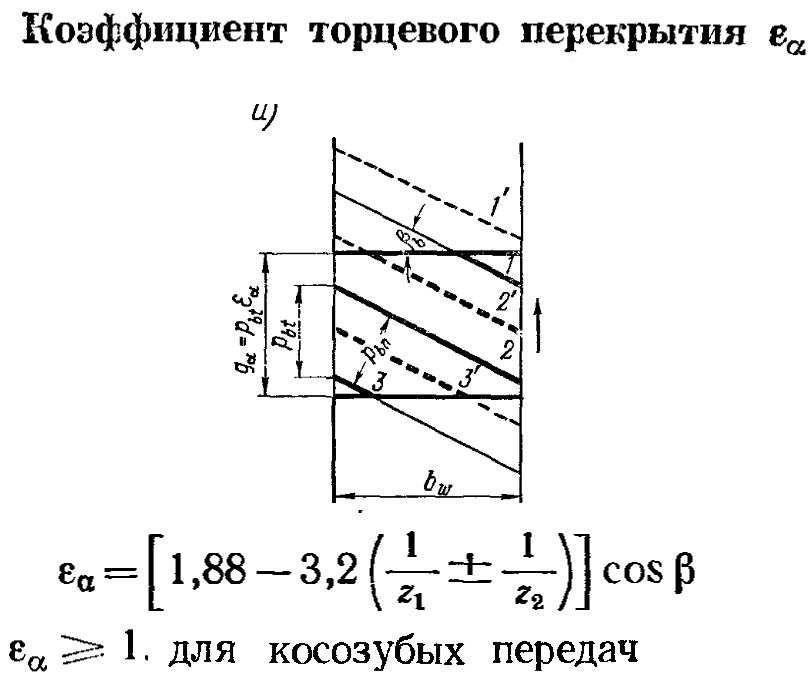

Для обеспечения непрерывности вращения рекомендуется εα >1,2. Обычно в прямозубых цилиндрических передачах εα=1,2…1,8.

Начальное межосевое расстояние аw, угол зацепления αw, передаточное число i и коэффициент торцового перекрытия εα являются основными параметрами зацепления.

6.8. Материалы зубчатых колёс

Определяющими факторами при выборе материала зубчатых колёс являются:

– режим работы передачи: степень нагруженности, окружная скорость;-

– габаритные и массовые требования;

– экономические соображения.

Наиболее распространёнными материалами зубчатых колёс силовых передач являются углеродистые стали.

Для цилиндрических и конических колёс, работающих с небольшими окружными скоростями (до 3 м/с), обычно применяют качественные конструкционные стали 20…35, при повышенных скоростях – стали 45. 50 и легированные стали 20Х, 40Х, 12ХН3А. Повышение долговечности зубчатых передач может быть достигнуто, если зубья малого колеса (шестерни), нагружаемые чаще, выполнить с более высокой твёрдостью рабочих поверхностей по сравнению со вторым колесом. С этой целью для изготовления шестерни выбирают более качественный материал или предусматривают упрочнение зубьев.

В малонагруженных мелкомодульных передачах прочность зубьев не является определяющим фактором и почти всегда обеспечена с большим запасом. В таких передачах материалы колёс выбирают исходя из минимального износа зубьев. Из этих соображений шестерни изготовляют из углеродистых сталей (35, 45, 50, У8А, У10А) или легированных сталей (40Х, 12ХН3А и др.), а колёса – из цветных металлов и сплавов (бронза БрОЦС6-6-3, БрАЖ9-4), латуни (ЛС59-1) и др.

Вопросы для самопроверки  

1. Для чего применяют передаточные механизмы? Виды передаточных механизмов, их основные внешние характеристики.

2. Зубчатые механизмы (передачи), область применения, достоинства и недостатки.

3. Как классифицируются зубчатые передачи по геометрическим и функциональным особенностям?

4. Назовите основные, на Ваш взгляд, пять основных требований, которые должны быть предъявлены к зубчатым передачам.

5. Сформулируйте основной закон зацепления. Какие кривые называют сопряжёнными?

6. Эвольвента окружности и её свойства. Уравнения эвольвенты в полярных координатах.

7. Покажите, что передаточное отношение зубчатой передачи с эвольвентным профилем зубьев величина постоянна. Что такое полюс зацепления, линия зацепления и угол зацепления?

8. Геометрические параметры эвольвентных прямозубых передач.

Заключение

При изучении данного курса студенты при необходимости смогут производить не сложные предварительные прочностные расчёты различных соединений (сварных, заклёпочных резьбовых, шпоночных, шлицевых и др.) деталей; сделать статический расчёт вала (оси) на прочность и жёсткость, производить необходимые расчёты и конструктивные разработки для улучшения производственных процессов. В первую очередь, это касается модернизации швейного оборудования, разработки средств механизации и автоматизации. Полученные знания позволят правильно оценивать действительные возможности машин, грамотно их эксплуатировать и совместно с другими специалистами создавать новую технику с целью повышения производительности труда.

Библиографический список

1. Тарг, С. М. Краткий курс теоретической механики; М.: Высшая школа, 1995, − 416 с.

2. Теория механизмов и машин:Учеб. для втузов /под ред. К. В.Фролова.- М.: Высш. шк., 1987. — 496 с.: ил.

3. Семин, М. И. Основы сопротивления материалов : учеб. пособие для студентов вузов / М. И. Семин. – М. : Гуманитар. изд. центр ВЛАДОС, 2004. – 255 с.

5 Прикладная механика,: учебник для вузов / В. В. Джамай, Ю. Н. Дроздов, Е. А. Самойлов и др. ; под общ. ред. В. В. Джамая. – М. : Дрофа, 2004. – 414 с.

6. Иванов, С. Г. Теория механизмов и машин. Пособие к курсу и контрольной работе Омск, ОГИСа, 2003. — 54с.

7. Девятов С. А. Теоретическая механика : учебное пособие. – Омск ; ОГИС, 2008. – 116 с

8. Иванов, С. Г. Детали машин и основы конструирования : Учебное пособие. — Омск : ОГИС, 2006. 149 с.

9. Иванов, С. Г. Основы функционирования систем сервиса (раздел «Сопротивление материалов»): Учебное пособие. — Омск : ОГИС, 2010. — 95 с.

СОДЕРЖАНИЕ

Коэффициент перекрытия

Коэффициентом перекрытия называется отношение длины активной линии зацепления к основному шагу зубчатого колеса, он обозначается и определяется отношением

.

Передача движения в зубчатом зацеплении происходит таким образом, что, прежде чем предыдущая пара зубьев выйдет из зацепления (из контакта), последующая должна войти в зацепление (в контакт). Чем раньше она вступит в зацепление, тем более плавно работает передача. Количественной характеристикой этого качества и является коэффициент перекрытия, т.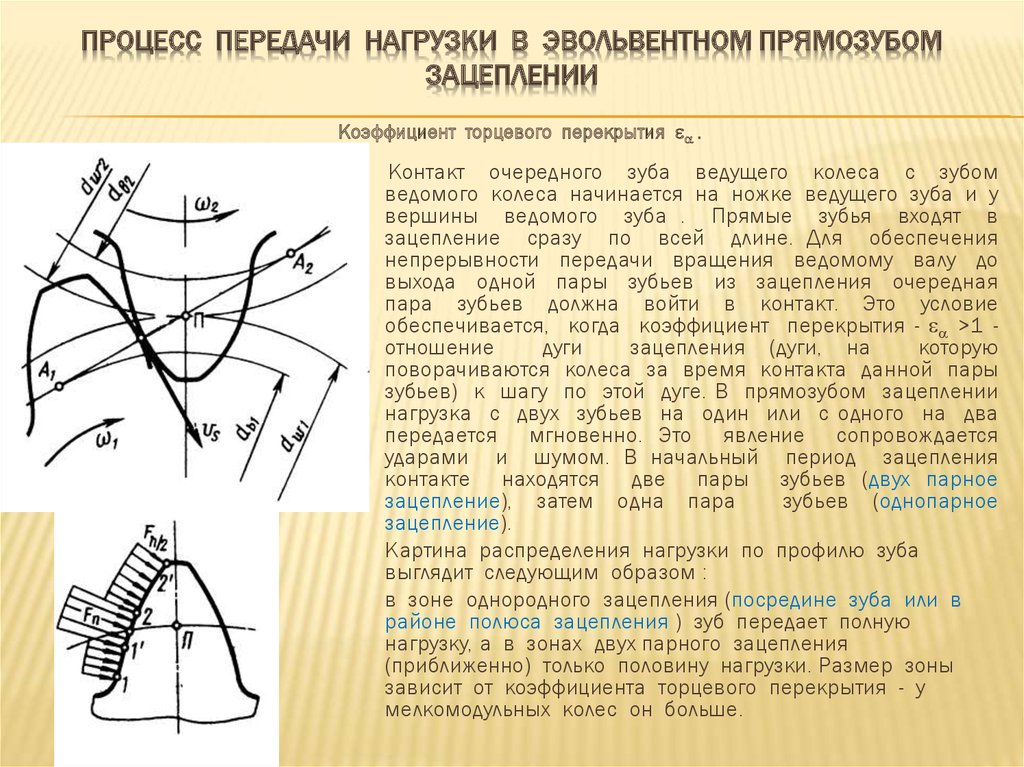 е. он, по существу, характеризует плавность работы зубчатой передачи. Обычно величина коэффициента перекрытия заключена между 1 и 2, при этом минимальное значение не должно быть меньше 1,1. Схематически соотношение между длиной активной лини зацепления и основным шагом показано на рис. 3.12. Точка контакта профилей зубьев перемещается вдоль активной линии зацепления от точки H₁ к точке H₂. Основной шаг короче активной линии зацепления, поэтому в пределах этой линии работают то одна, то две пары зубьев. Если отложить, как показано на рис. 3.12, основной шаг p_b от точек H₁ и H₂, то отрезок H₁H₂ будет разделён на три части. Две крайние части соответствуют зонам двухпарного зацепления зубьев, а средняя – зоне однопарного зацепления. Чем короче средняя зона, тем плавнее работает зубчатая передача, так как суммарная длина двух крайних участков становится длиннее.

Дата добавления: 2015-07-08; просмотров: 209 | Нарушение авторских прав

Волнистость шлифовального круга ( шаг резьбы ) определяется через коэффициент перекрытия Ud Коэффициент перекрытия рассчитывается на основ

Каталоги комплексных поставщиков для предприятий и служб сервиса / Catalogues of one-stop shop suppliers HOFFMANN GROUP | Справочник HOFFMANN GROUP 2012 Обработка резанием Garant (Всего 1091 стр.)
1060 Справочник HOFFMANN GROUP 2012 Обработка материалов резанием Garant ToolScout Стр.1036
Волнистость шлифовального круга ( шаг резьбы ) определяется через коэффициент перекрытия Ud. Коэффициент перекрытия рассчитывается на основе количества оборотом шлифовального круга во время смещения правящего инструмента (подача при правке fad) на его рабочую ширину bd. При увеличении коэффициента перекрытия волнистость поверхности шлифовального круга уменьшается и шлифовальный круг становится более гладким, что, в свою очередь, ведет к уменьшению эффективной высоты микронеровностей Rth. Ud Коэффициент перекрытия (уравн. 11.48) bd Рабочая ширина мм fad Осевая подача мм nsd Частота вращения шлифовального круга при правке об/мин Vfad Скорость осевой подачи мм/мин и f = fad nsd bd fad Коэффициент перекрытия Ud Грубое шлифование (черновая обработка) 2-3 Нормальное шлифование (обработка средней чистоты) 4-6 Тонкое шлифование (чистовая обработка) > 7 Таблица 11.15 Ориентировочные значения для коэффициента перекрытия при правке Рис. 11.28 Зависимость между коэффициентом перекрытия и волнистостью шлифовального круга Коэфф. перекрытия Волнистость Поверх. шлиф. круга Производит. резания Поверхность детали Опасность прижога и трещин на теплочувствительных деталях высокая слабая гладкая низкая чистая повышенная низкий сильная шероховатая высокая грубая низкая Таблица 11.16 Зависимости при структурировании поверхностей шлифовальных кругов 1036 Коэффициент перекрытия Ud
См. также / See also :
Соотношение твердостей Таблица / Hardness equivalent table			Аналоги марок стали / Workpiece material conversion table
Отклонение размера детали / Fit tolerance table			Перевод оборотов в скорость / Surface speed to RPM conversion
Диаметр под резьбу / Tap drill sizes			Виды резьбы в машиностроении / Thread types and applications
Дюймы в мм Таблица / Inches to mm Conversion table			Современные инструментальные материалы / Cutting tool materials
Справочник HOFFMANN GROUP 2012 Обработка резанием Garant (Всего 1091 стр. )
1057 Выбор и рекомендации по использованию неподвижного правящего инструмента Выбор однокристальных правящих инструментов и алмазно-металлическ	1058	1059	1061	1062	1063
Справочники по резанию и каталоги инструмента HOFFMANN GROUP
Каталог HOFFMANN GROUP 2020 Режущий и вспомогательный инструмент для станков (1098 страниц)	Каталог HOFFMANN GROUP 2020 Измерительный и ручной инструмент Инвентарь (1194 страницы)	Каталог HOFFMANN GROUP 2020 Промышленная мебель и складское оборудование (666 страниц)	Каталог HOFFMANN GROUP 2020 Средства индивидуальной защиты (англ.яз / ENG) (442 страницы)	Каталог HOFFMANN GROUP 2018 Инструмент вспомогательный и режущий (1034 страницы)	Каталог HOFFMANN GROUP 2018 Инструмент Приборы Инвентарь (1162 страницы)
Каталог HOFFMANN GROUP 2017 Вспомогательный и режущий инструмент (998 страниц)	Каталог HOFFMANN GROUP 2017 Ручной и измерительный инструмент (1126 страниц)	Каталог HOFFMANN GROUP 2017 Производственная мебель и системы хранения (624 страницы)	Каталог HOFFMANN GROUP 2016 Станочный режущий инструмент и оснастка (англ. яз / ENG) (934 страницы)	Каталог HOFFMANN GROUP 2016 Слесарно- монтажный и мерительный инструмент (англ.яз / ENG) (1094 страницы)	Каталог HOFFMANN GROUP 2016 Производственная мебель (англ.яз / ENG) (562 страницы)
Каталог HOFFMANN GROUP 2016 Режущий инструмент и оснастка (нем.яз / DEU) (932 страницы)	Каталог HOFFMANN GROUP 2016 Ручной и измерительный инструмент (нем.яз / DEU) (1094 страницы)	Справочник HOFFMANN GROUP 2016 Режимы резания для режущего инструмента (EN DE ES IT FR) (904 страницы)	Каталог HOFFMANN GROUP 2015 Инструмент Оборудование Инвентарь (1643 страницы)	Каталог HOFFMANN GROUP 2015 Производственная мебель (459 страниц)	Справочник HOFFMANN GROUP 2012 Обработка резанием Garant (1091 страница)
Каталоги комплексных поставщиков для предприятий и служб сервиса / Catalogues of one-stop shop suppliers
— —

коэффициент перекрытия зуба 🎓 ⚗ перевод с английского на русский

Все языкиАбхазскийАдыгейскийАзербайджанскийАймараАйнский языкАканАлбанскийАлтайскийАнглийскийАрабскийАрагонскийАрмянскийАрумынскийАстурийскийАфрикаансБагобоБаскскийБашкирскийБелорусскийБолгарскийБретонскийБурятскийВаллийскийВарайскийВенгерскийВепсскийВерхнелужицкийВьетнамскийГаитянскийГреческийГрузинскийГуараниГэльскийДатскийДолганскийДревнерусский языкИвритИдишИнгушскийИндонезийскийИнупиакИрландскийИсландскийИспанскийИтальянскийЙорубаКазахскийКарачаевскийКаталанскийКвеньяКечуаКиргизскийКитайскийКлингонскийКомиКорейскийКриКрымскотатарскийКумыкскийКурдскийКхмерскийЛатинскийЛатышскийЛингалаЛитовскийЛожбанЛюксембургскийМайяМакедонскийМалайскийМаньчжурскийМаориМарийскийМикенскийМокшанскийМонгольскийНауатльНемецкийНидерландскийНогайскийНорвежскийОрокскийОсетинскийОсманскийПалиПапьяментоПенджабскийПерсидскийПольскийПортугальскийРумынский, МолдавскийРусскийСанскритСеверносаамскийСербскийСефардскийСилезскийСловацкийСловенскийСуахилиТагальскийТаджикскийТайскийТатарскийТвиТибетскийТофаларскийТувинскийТурецкийТуркменскийУдмурдскийУзбекскийУйгурскийУкраинскийУрдуУрумскийФарерскийФинскийФранцузскийХиндиХорватскийЦерковнославянский (Старославянский)ЧеркесскийЧерокиЧеченскийЧешскийЧувашскийШайенскогоШведскийШорскийШумерскийЭвенкийскийЭльзасскийЭрзянскийЭсперантоЭстонскийЮпийскийЯкутскийЯпонский

Все языкиАзербайджанскийАлбанскийАрабскийАрмянскийАфрикаансБаскскийБолгарскийВенгерскийВьетнамскийГаитянскийГреческийГрузинскийДатскийДревнерусский языкИвритИндонезийскийИрландскийИсландскийИспанскийИтальянскийЙорубаКазахскийКаталанскийКвеньяКитайскийКлингонскийКорейскийКурдскийЛатинскийЛатышскийЛитовскийМакедонскийМалайскийМальтийскийМаориМарийскийМокшанскийМонгольскийНемецкийНидерландскийПалиПапьяментоПерсидскийПольскийПортугальскийРумынский, МолдавскийРусскийСербскийСловацкийСловенскийСуахилиТагальскийТайскийТамильскийТатарскийТурецкийУдмурдскийУйгурскийУкраинскийУрдуФарерскийФинскийФранцузскийХиндиХорватскийЦерковнославянский (Старославянский)ЧаморроЧерокиЧешскийЧувашскийШведскийЭрзянскийЭстонскийЯпонский

tool. overlap function | R Документация

Вычислить перекрытия между группами указанных элементов

tool.overlap проверяет каждую пару блоков, находит количество общих items и получает значения значимости разделения для пар блоков.

Использование

  
 tool.overlap (items, groups, nbackground = NULL) 
  

Аргументы

предметы

массив идентификаторов товаров

группы

массив групповых идентификаторов для товаров

n фон

общее количество позиций

Значение

A

название группы

B

название группы

POSa

ранг названия группы

POSb

ранг названия группы

Na

размер группы A

Nb

размер группы B

Nab

общие элементы

R

коэффициент перекрытия

F

кратное изменение до нулевого ожидания

P

перекрытие P-значение (тест Фишера)

Псевдонимы

Примеры

  ## в качестве примера прочтите файл модуля coexpr:
moddata <- инструмент. читать (system.file ("extdata",
"modules.mousecoexpr.liver.human.txt", package = "Mergeomics"))
## найдем коэффициент перекрытия двух модулей:
## выбираем первый и последний модули:
mod.names <- unique (moddata $ MODULE) [c (1, length (unique (moddata $ MODULE)))]
if (length (mod.names)> 0) {
modA.members <- moddata [which (moddata $ MODULE == mod.names [1]),]
modB.members <- moddata [which (moddata $ MODULE == mod.names [2]),]
}
mod.pool <- rbind (modA.members, modB.members)
overlap.stats <- tool.overlap (мод.бассейн [, 2], mod.pool [, 1])
  

Примеры сообщества

Похоже, примеров пока нет.

определение, формула, нормы и ограничения

Коэффициент текущей ликвидности Определение

Коэффициент текущей ликвидности указывает на способность компании выполнять краткосрочные долговые обязательства. Коэффициент текущей ликвидности определяет, достаточно ли у фирмы ресурсов для выплаты своих долгов в течение следующих 12 месяцев. Потенциальные кредиторы используют этот коэффициент при принятии решения о выдаче краткосрочных ссуд. Коэффициент текущей ликвидности также может дать представление об эффективности операционного цикла компании или ее способности превращать свой продукт в наличные. Коэффициент текущей ликвидности также известен как коэффициент оборотного капитала .

Расчет (формула)

Коэффициент текущей ликвидности рассчитывается путем деления оборотных активов на краткосрочные обязательства:

Коэффициент текущей ликвидности = оборотные активы / текущие обязательства.

Обе переменные показаны в балансе (отчете о финансовом положении).

Нормы и ограничения

Чем выше коэффициент, тем более ликвидна компания.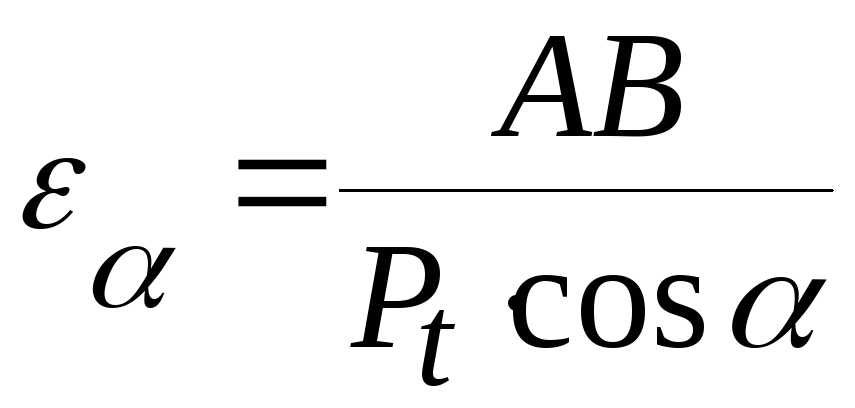 Обычно приемлемый коэффициент текущей ликвидности - 2; это удобное финансовое положение для большинства предприятий.Приемлемые текущие коэффициенты варьируются от отрасли к отрасли. Для большинства промышленных компаний коэффициент текущей ликвидности 1,5 может быть приемлемым.

Низкие значения коэффициента текущей ликвидности (значения менее 1) указывают на то, что у фирмы могут возникнуть трудности с выполнением текущих обязательств. Однако инвестор также должен учитывать операционный денежный поток компании, чтобы лучше понять ее ликвидность. Низкий коэффициент текущей ликвидности часто может поддерживаться сильным операционным денежным потоком.

Если коэффициент текущей ликвидности слишком высок (намного больше 2), значит, компания может неэффективно использовать свои оборотные активы или средства краткосрочного финансирования.Это также может указывать на проблемы в управлении оборотным капиталом.

При прочих равных условиях кредиторы считают, что высокий коэффициент текущей ликвидности лучше, чем низкий коэффициент текущей ликвидности, потому что высокий коэффициент текущей ликвидности означает, что компания с большей вероятностью выполнит свои обязательства, которые подлежат погашению в течение следующих 12 месяцев.

Точная формула в аналитическом программном обеспечении ReadyRatios

Коэффициент текущей ликвидности = F1 [CurrentAssets] / F1 [CurrentLiabilities]

F1 - Отчет о финансовом положении (МСФО).

Коэффициент текущей ликвидности Отраслевой эталон

Средние значения коэффициента вы можете найти в нашем справочнике по отраслевому сравнительному анализу - Коэффициент текущей ликвидности.

и шкала соотношения: в чем разница?

Шкала интервалов и шкала отношений представляют собой шкалы переменных измерений. Они предлагают количественное определение переменных атрибутов.

Разница между шкалами интервалов и соотношений связана с их способностью опускаться ниже нуля.Шкалы интервалов не содержат истинного нуля и могут представлять значения ниже нуля. Например, вы можете измерить температуру ниже 0 градусов Цельсия, например -10 градусов.

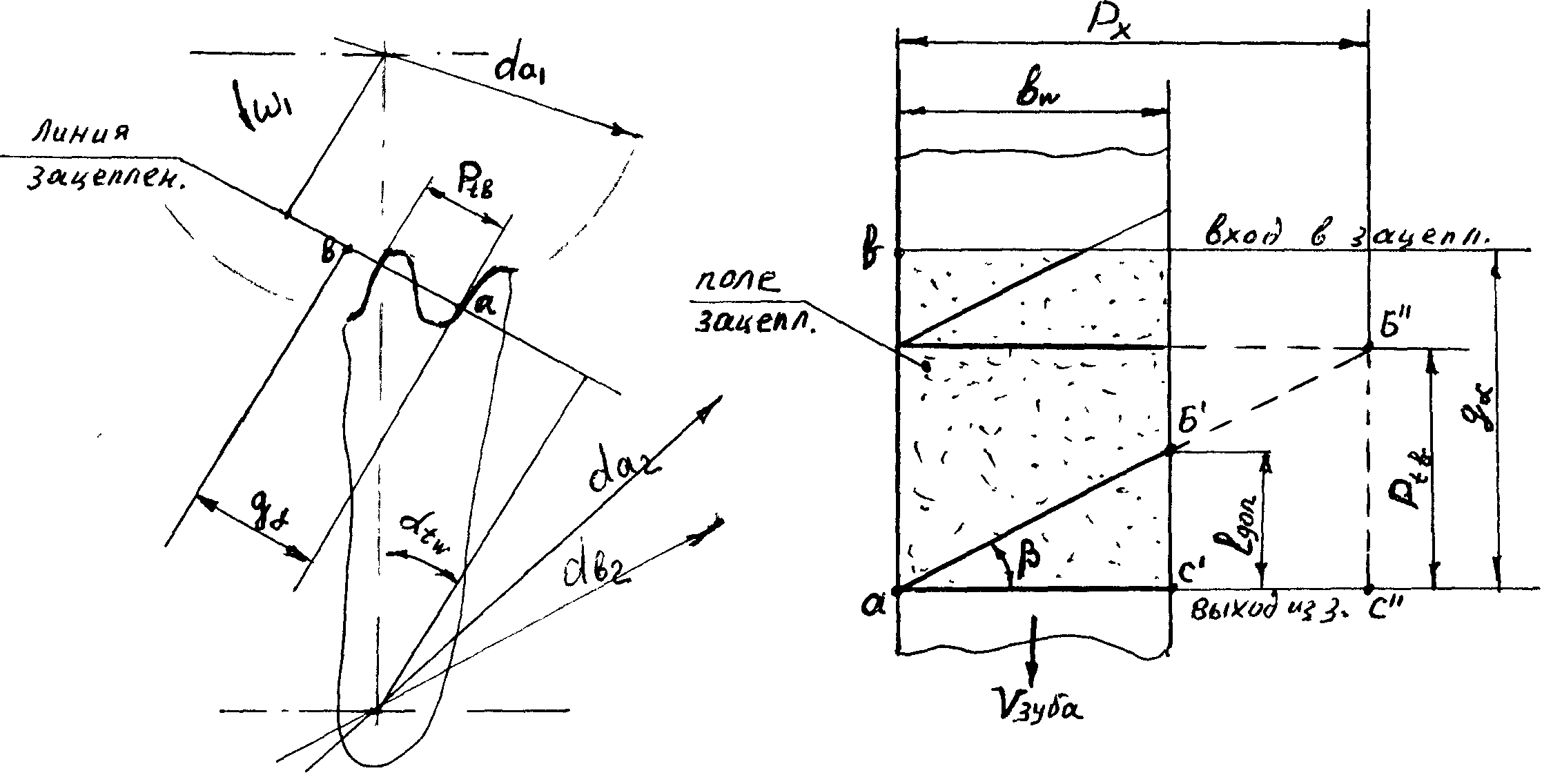никогда не опускаются ниже нуля. Рост и вес измеряются от 0 и выше, но никогда не опускаются ниже него.

Интервальная шкала позволяет измерять все количественные атрибуты. Любое измерение шкалы интервалов может быть ранжировано, подсчитано, вычтено или добавлено, и равные интервалы разделяют каждое число на шкале.Однако эти измерения не дают никакого представления о соотношении между собой.

Шкала отношений имеет те же свойства, что и шкалы интервалов. Вы можете использовать его для сложения, вычитания или подсчета измерений. Шкалы отношения различаются наличием символа происхождения, который является начальной или нулевой точкой шкалы.

Соотношение интервалов Сравнение масштабов

Измерение температуры - отличный пример интервальных шкал. Температура в помещении с кондиционером составляет 16 градусов по Цельсию, а температура за пределами помещения - 32 градуса по Цельсию.Можно сделать вывод, что температура на улице на 16 градусов выше, чем внутри помещения.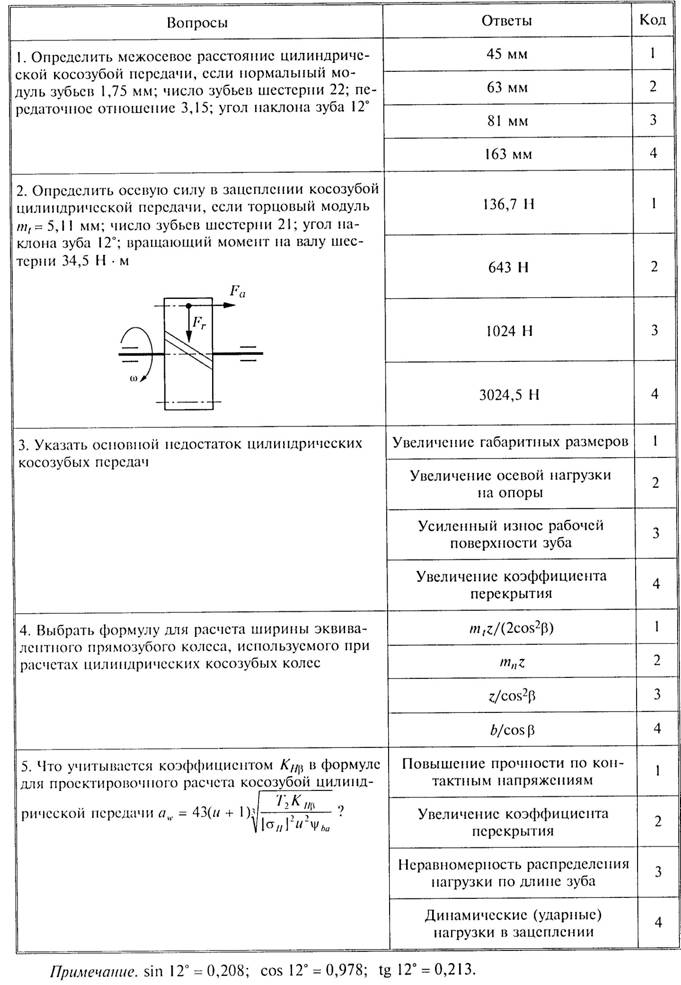

Но если бы вы сказали: «На улице в два раза жарче, чем внутри», вы ошиблись бы. Указав, что температура снаружи вдвое выше, чем внутри, вы используете 0 градусов в качестве точки отсчета для сравнения двух температур. Поскольку можно измерить температуру ниже 0 градусов, вы не можете использовать ее в качестве ориентира для сравнения. Вместо этого вы должны использовать фактическое число (например, 16 градусов).

Интервальные переменные обычно называются масштабируемыми переменными.Они часто выражаются в виде единиц, например, градусов. В статистике среднее значение, режим и медиана также могут определять интервальные переменные.

Масштаб отношения отображает порядок и количество объектов между значениями шкалы. Ноль - это вариант. Эта шкала позволяет исследователю применять статистические методы, такие как геометрическое и гармоническое среднее.

Если вы не можете подразумевать, что температура на улице вдвое теплее, потому что это интервальная шкала, вы можете сказать, что вы вдвое старше другого, потому что это переменная отношения.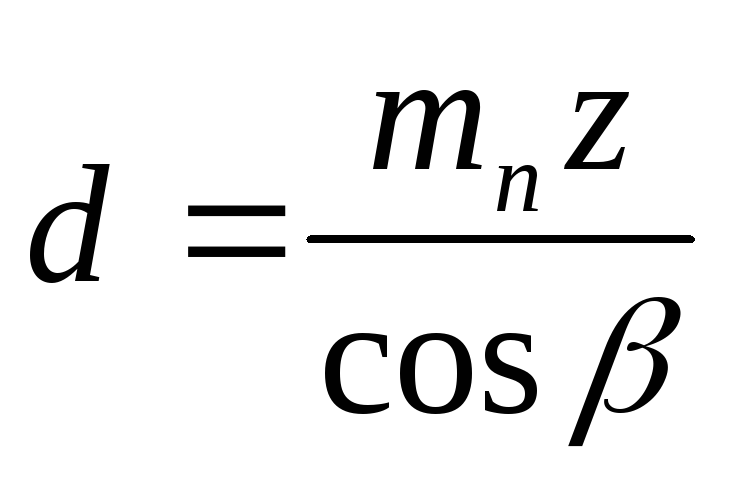

Возраст, деньги и вес являются общими переменными шкалы отношения. Например, если вам 50 лет, а вашему ребенку 25 лет, вы можете точно указать, что вы вдвое старше его.

Соотношение интервалов Масштаб измерений

Понимание различных шкал измерения позволяет вам видеть различные типы данных, которые вы можете собрать. Эти различия помогут вам определить тип статистического анализа, необходимый для вашего исследования.

Вот краткое описание разницы в интервале и уровнях отношения измерения:

Интервальный уровень измерения классифицирует и упорядочивает измерение.Он определяет расстояние между каждым интервалом эквивалентной шкалы, от нижнего интервала до верхнего интервала. Например, разница между 90 градусами по Фаренгейту и 100 градусами по Фаренгейту такая же, как 110 градусов по Фаренгейту и 120 градусов по Фаренгейту.

В дополнение к тому же качеству, что и уровни интервалов, уровни отношения могут иметь нулевое значение.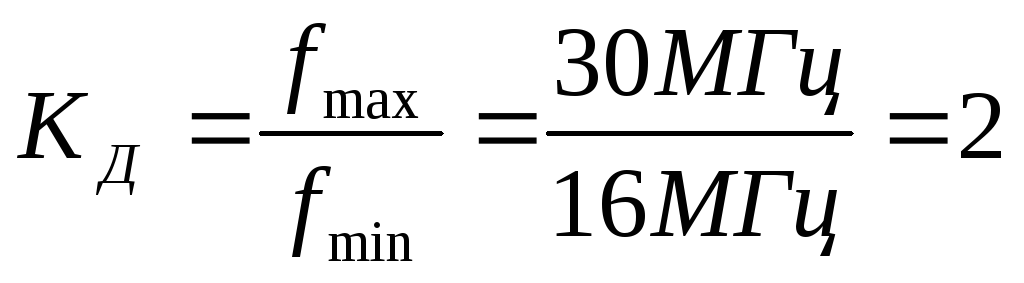 Разница в стоимости между двумя парами обуви, которые составляют 10 и 20 долларов соответственно, такая же, как между двумя парами, которые составляют 20 и 30 долларов.Однако вы не найдете туфли дешевле 0 долларов.

Шкала интервалов по шкале соотношений: точки различия

Характеристики	Интервальная шкала	Масштаб отношения
Переменное свойство	Все переменные, измеренные в интервальной шкале, можно складывать, вычитать и умножать. Вы не можете рассчитать соотношение между ними.	Масштаб отношения имеет все характеристики интервальной шкалы, кроме того, он позволяет вычислять отношения. То есть вы можете использовать цифры на шкале против 0.
Абсолютная нулевая точка	Нулевая точка на интервальной шкале произвольна. Например, температура может быть ниже 0 градусов по Цельсию и иметь отрицательные значения.	Шкала отношения имеет абсолютный ноль или знак происхождения. Рост и вес не могут быть нулевыми или ниже нуля.
Расчет	Статистически в интервальной шкале вычисляется среднее арифметическое.	Статистически в шкале соотношений вычисляется среднее геометрическое или гармоническое.
Измерение	Интервальная шкала может измерять размер и величину как несколько коэффициентов определенной единицы.	Шкала отношения может измерять размер и величину как коэффициент одной определенной единицы по отношению к другой.
Пример	Классическим примером интервальной шкалы является температура в градусах Цельсия.Разница в температуре между 50 и 60 градусами составляет 10 градусов; это такая же разница между 70 градусами и 80 градусами.	Классическими примерами шкалы соотношений являются любые переменные, которые обладают характеристиками абсолютного нуля, такими как возраст, вес, рост или показатели продаж.

Создать бесплатный счет

Доверительный интервал Отношение рисков Отношение шансов Отношение ставок

Рабочий пример II

В нашем втором примере используются результаты поперечного исследования распространенности дистоции у кошек.Ранее мы рассматривали эту работу в отношении доверительных интервалов, связанных с оценками распространенности. Мы рассчитаем как отношение шансов (используемое авторами), так и отношение рисков с соответствующими интервалами.

Распространенность дистоции у кошек по сравнению с породой Порода Число положительных Нет отрицательных % положительных Отношение шансов OR Отношение рисков RR Манкс 1 17 5. 55 15,686 14,87 Колония 3 800 0,37 (1,00) (1,00)

В этом случае один из размеров выборки мал, а одна из пропорций мала. Следовательно, вычисленный ниже интервал Вальда может быть ненадежным, поэтому нам лучше также вычислить условный точный интервал, используя функцию отношения шансов эпитулов для R:

Для отношения шансов в R мы получаем то же самое для интервала Вальда (OR = 15,69, 95% CI от 1,55 до 158,60), но условный точный интервал перекрывает 1 (OR = 15.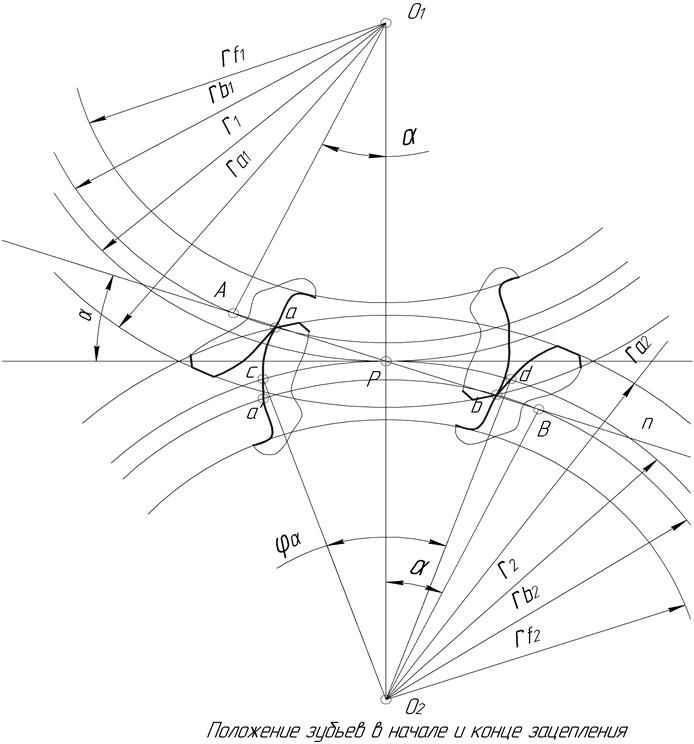 48, 95% ДИ от 0,28 до 204,67), как и (более надежный) средний интервал P (OR = 16,77, 95% ДИ от 0,56 до 153,09). Следовательно, сейчас очень сомнительно, действительно ли мы продемонстрировали, что существует какая-либо разница между породами.

Для отношения рисков мы получили отношение рисков 14,87 с интервалом Вальда от 1,62 до 136,2, то же самое, что дает функция riskratio пакета epitool для доверительного интервала нормального приближения (Вальда). Используя ту же R-функцию, нормальное приближение Вальда с небольшой поправкой на выборку дало коэффициент риска 11.17 с интервалом от 1,22 до 102,25. Однако точное среднее значение P было 0,0876, что несколько выше обычного уровня 0,05.

Использование

Набор инструментов для анализа данных всего генома

1. Введение 2. Основная информация 3. Скачать и общие примечания 4. Справочная таблица команд 5. Базовое использование / форматы данных 6. Управление данными 7. Сводная статистика 8. Пороги включения 9. Стратификация населения 10. Оценка IBS / IBD 11.Ассоциация 12. Семейные ассоциации 13. Процедуры перестановки 14. Расчеты LD 15. Мультимаркерные тесты. 16. Условные тесты гаплотипов. 17. Прокси-ассоциация 18. Вменение (бета) 19. Данные по дозировке 20. Мета-анализ 21. Аннотация 22. Объединение результатов на основе LD 23. Генный отчет 24. Эпистаз. 25. Редкие CNV 26. Общие CNP 27. R-плагины 28. Поиск аннотаций в Интернете. 29. Инструменты моделирования. 30. Оценка профиля 31. ID помощник 32. Ресурсы 33. Блок-схема 34. Разное 35. Часто задаваемые вопросы и подсказки 36. gPLINK

Базовый ассоциативный тест предназначен для признака болезни и основан на сравнение частот аллелей между случаями и контролем (асимптотический и эмпирические p-значения доступны).Также реализованы Тест трендов Кокрана-Армитиджа, точный тест Фишера, различные генетические модели (доминантный, рецессивный и общий), тесты для стратифицированных выборок (например, Cochran-Mantel-Haenszel, Breslow-Day tests), тест для количественной черта; тест на различия в частоте пропущенных генотипов между случаями и элементы управления; мультилокусные тесты с использованием статистики Хотеллинга T (2) или Суммарно-статистический подход (оцениваемый перестановкой), а также тесты гаплотипов. Базовый тесты могут выполняться с перестановкой, описанной в в следующем разделе представлены эмпирические p-значения и учитывают различные конструкции (например,грамм. за счет использования структурированных, внутрикластерная перестановка). Семейные тесты описаны в следующий раздел HINT Основные команды ассоциации (--assoc, --model, --fisher, --linear и --logistic) будет проверить только один фенотип. Если ваш файл альтернативного фенотипа содержит более одного фенотипа, затем добавление флага --all-pheno сделает цикл PLINK для каждого фенотип, например вместо одного выходного файла plink.assoc, если есть 100 фенотипов, теперь PLINK покажет Плинк.P1.assoc plink.P2.assoc ... plink.P100.assoc Естественно, это займет в 100 раз больше времени ... Если вы тестируете очень большое количество фенотипов, возможно, стоит также указать --pfilter, чтобы уменьшить количество суммы (например, вывод только тестов, значимых при p = 1e-4, если --pfilter 1e-4).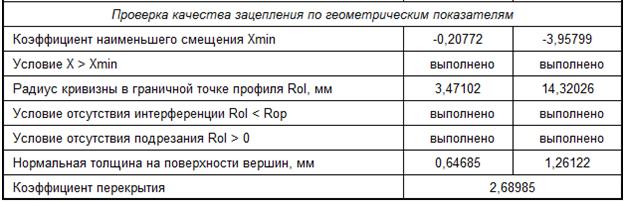 Базовый тест ассоциации случай / контроль Чтобы выполнить стандартный анализ ассоциации случай / контроль, используйте опцию: plink --file mydata --assoc который генерирует файл Плинк.ассоциированный который содержит поля: Хромосома CHR SNP ID SNP BP Физическое положение (пара оснований) Название минорного аллеля A1 (на основе всей выборки) F_A Частота данного аллеля в случаях F_U Частота данного аллеля в контроле Название основного аллеля A2 CHISQ Базовый аллельный тест хи-квадрат (1df) P Асимптотическое p-значение для этого теста ИЛИ Расчетное отношение шансов (для A1, т.е. A2 является справочным) Подсказка Кроме того, если необязательная команда --ci X (где X - желаемое покрытие для доверительный интервал, e.грамм. 0.95 или 0.99), затем два дополнительных к этому выводу добавляются поля: L95 Нижняя граница 95% доверительного интервала для отношения шансов U95 Верхняя граница 95% доверительного интервала для отношения шансов (где 95 изменится, если использовать другое значение с --ci вариант, естественно). Добавление опции --счетов с --assoc будет указывать количество аллелей в отчетах PLINK, а не частоты в случаях и элементах управления. См. Следующий раздел о перестановке, чтобы узнать, как для генерации эмпирических p-значений и использования других аспектов основанных на перестановках тестирование.См. Раздел о многомаркерных тестах, чтобы узнать, как выполнять тесты на основе гаплотипов. тесты ассоциации. Этот анализ должен автоматически обрабатывать SNP X / Y хромосомы. Точный тест Фишера (аллельная ассоциация) Чтобы выполнить стандартный анализ ассоциации случай / контроль, используя Для получения значимости используйте точный критерий Фишера: plink --file mydata --fisher который генерирует файл plink.fisher который содержит поля: Хромосома CHR SNP ID SNP BP Физическое положение (пара оснований) Название минорного аллеля A1 (на основе всей выборки) F_A Частота данного аллеля в случаях F_U Частота данного аллеля в контроле Название основного аллеля A2 P Точное значение p для этого теста ИЛИ Расчетное отношение шансов (для A1) Как описано ниже, если --fisher также указан с --model, PLINK выполнит генотипические тесты с использованием точного теста Фишера. Примечание Вы также можете использовать перестановку для генерации точных, эмпирические значения значимости, которые также будут действительны для небольших выборок, и т.п. Альтернативные / полные тесты ассоциации моделей Можно провести тесты ассоциации между заболеванием и вариантом, отличным от базовый аллельный тест (который сравнивает частоты аллелей в случаях по сравнению с контролем), используя параметр --model. Предлагаемые здесь тесты (в дополнение к основному аллельному тесту): Трендовый тест Кокрана-Армитиджа Генотипический (2 df) тест Тест на действие доминантного гена (1df) Тест на рецессивное действие гена (1df) Одним из преимуществ теста Кокрана-Армитиджа является то, что он не предполагает равновесия Харди-Вайнберга, поскольку единицей анализа является индивид, а не аллель (хотя эмпирические p-значения из базового аллельного теста также обладают этим свойством).Важно помнить, что SNP демонстрация серьезных отклонений от Харди-Вайнберга часто может быть плохой Однако SNP или отражают стратификацию в выборке, и поэтому, вероятно, во многих случаях лучше всего исключить. Генотипический тест представляет собой общий тест на ассоциацию в таблице 2 на 3 для распределения болезней по генотипам. В Доминантная и рецессивная модели - это тесты на минорный аллель (который является минорный аллель можно найти в выходных данных --assoc или команды --freq. То есть, если D младший аллель (а d - основной аллель): Аллельный: D против d Доминант: (DD, Dd) по сравнению с dd Рецессивный: DD против (Dd, dd) Генотип: DD против Dd против dd Как упоминалось выше, эти тесты создаются с опцией: plink --file mydata --model который генерирует файл Плинк.модель который содержит следующие поля: CHR Номер хромосомы SNP Идентификатор SNP ТЕСТ Тип теста AFF Генотипы / аллели в случаях UNAFF Генотипы / аллели в контроле Статистика CHISQ Хи-квадрат DF Степени свободы для теста P Асимптотическое p-значение Каждый SNP будет представлен в пяти строках вывода, что соответствует применено пять тестов. Столбец ТЕСТ относится к либо АЛЛИК, ТРЕНД, ГЕНО, DOM или REC, относящиеся к различным типам тестов упомянутое выше.Генотипический или аллельный подсчет дан для случаев и контролирует отдельно. Для рецессивных и доминантных тестов представляют собой генотипы с двумя объединенными классами. Эти тесты рассматривают только диплоидные генотипы: то есть для X хромосомные самцы будут исключены даже из теста АЛЛЛИК. Сюда те же данные используются для пяти представленных здесь тестов. Обратите внимание, что, напротив, основные команды ассоциации (--assoc и --linear и т. д.) включают одиночные мужские X-хромосомы, и поэтому результаты могут отличаться.Генотипические и доминантные / рецессивные тесты будут проводиться только в том случае, если минимальное количество наблюдений на ячейку в 2х3 таблица: по умолчанию, если хотя бы одна из ячеек имеет частоту меньше чем 5, то пропускаем альтернативные тесты (NA записывается на файл результатов). Тесты Кокрана-Армитажа и аллельные тесты выполняется во всех случаях.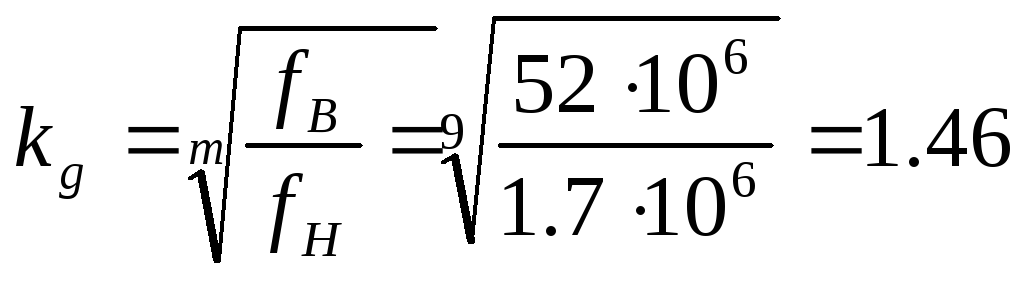 Этот порог можно изменить с помощью Опция --cell: plink --file mydata --model --cell 20 Если перестановка (с параметрами --mperm или --perm) указан, опция -model по умолчанию выполнит перестановочный тест на основе наиболее значимого результата моделей ALLELIC, DOM и REC.То есть, для каждого SNP лучший исходный результат будет сравниваться с лучший из этих трех тестов для этого SNP для каждой реплики. В макс. (Т) режим перестановки, это также будет сравниваться с лучшим результатом из всех SNP для поля EMP2. Эта процедура контролирует тот факт, что мы выбрали лучшее из трех коррелированных тестов для каждого SNP. Вывод будет создан в файле plink.model.best.perm или plink.model.best.mperm в зависимости от того, использовалась ли перестановка адаптивная или max (T).Поведение команды --model можно изменить, добавив --model-gen, --model-trend, --model-dom или --model-rec, чтобы перестановка использовала генотипический, тест тенденции Кокрэма-Армитиджа, доминантный тест или вместо этого рецессивный тест как основа для перестановки. В этом случае один из следующих файлов будут созданы: plink.model.gen.perm plink.model.gen.mperm plink.model.trend.perm plink.model.trend.mperm plink.model.dom.perm plink.model.dom.mperm plink.model.rec.perm plink.model.rec.mperm Также можно добавить флаг --fisher для получения точных p-значений: ./plink --bfile mydata --model --fisher , в этом случае поле CHISQ не отображается. Заметка что генотипические, аллельные, доминантные и рецессивные модели используют Точный Фишера; тренд-тест не дает и даст то же значение p, что и без флаг --fisher. Также по умолчанию при добавлении --fisher Поле --cell установлено в 0, т.е.е. включить все SNP. Стратифицированный анализ Когда переменная кластера была указана, указав файл содержащий эту информацию, с помощью команды --within, можно выполнить ряд тестов на связь случай / контроль которые принимают во внимание эту кластеризацию или явно проверяют однородность эффекта между кластерами. Примечание Во многих случаях процедуры перестановки также могут использоваться для учета кластеров в данные. См. Более подробную информацию в следующем разделе.Представленные ниже тесты применимы только для данных случая / контроля, поэтому перестановка может быть полезна для количественных результатов по признаку, и т.п. Есть два основных класса тестов: Тестирование общей ассоциации заболевания / гена, контроль кластеров Тестирование на неоднородность ассоциации заболевания / гена между различными кластерами Тип кластерной структуры будет варьироваться в зависимости от количества кластеров. есть в образце, а сколько люди принадлежат к каждому кластеру.С одной стороны, у нас может быть два только 2 кластеры в выборке, каждый с большое количество корпусов и элементов управления. С другой стороны, мы могли бы иметь очень большое количество кластеров, так что в каждом кластере есть только 2 человека. Эти факторы будут влияют на выбор стратифицированных анализ. Предлагаемые тесты: Тест Кохрана-Мантеля-Хензеля для стратифицированных таблиц 2x2xK Тест Кохрана-Мантеля-Хензеля для стратифицированных таблиц IxJxK Тест Бреслоу-Дея на однородность отношения шансов Разделение общей ассоциации хи-квадрат для выполнения между кластером и внутри кластера ассоциация, и тест на однородность эффекта Тесты Кохрана-Мантеля-Хензеля (CMH) действительны как с большим количество маленьких кластеров и небольшой количество крупных кластеров.Эти тесты представляют собой тест, основанный на "среднее" отношение шансов, которое учитывает потенциальное вмешательство из-за переменная кластера. Тест Бреслоу-Дэй спрашивает, имеют ли разные кластеры разные Отношение шансов болезнь / ген: этот тест предполагает средний размер выборки в каждом кластере. Разбиение тест общей ассоциации, который концептуально подобен тесту Бреслоу-Дея, также делает то же самое предположение. Как упоминалось выше, тест CMH бывает двух видов: 2x2xK и IxJxK. В настоящее время тест 2x2xK представляет {болезнь x SNP | cluster} test.Обобщенная форма, IxJxK, представляет собой тест {кластера x SNP | болезнь}, т.е. меняется ли SNP между кластерами, с контролем любого возможного истинного SNP / заболевания ассоциация. Последний тест может быть полезен при интерпретации значимые ассоциации в стратифицированных выборках. Обычно первые Однако форма теста будет более интересной. Эти два теста запускаются с использованием параметров: plink --file mydata --mh --within mycluster.dat для основного теста CMH, или plink --file mydata --mh3 - внутри mycluster.Дат для теста IxJxK. Параметр --mh создает файл plink.cmh который содержит поля CHR Номер хромосомы SNP Идентификатор SNP Код минорного аллеля A1 Код основного аллеля A2 BP Физическое положение (пара оснований) Статистика CHISQ Cochran-Mantel-Haenszel (1df) P Асимптотическое значение p для теста CMH ИЛИ отношение шансов CMH L95 Нижняя граница доверительного интервала для отношения шансов CMH U95 Верхняя граница доверительного интервала для отношения шансов CMH Диапазон доверительного интервала с параметром --mh может быть изменено опцией --ci: plink --file mydata --mh - внутри mycluster. dat --ci 0.99 Параметр --mh3 создает файл plink.cmh3 который содержит поля: Хромосома CHR SNP Идентификатор SNP CHISQ_CMh3 Тест Кохрана-Мантеля-Хензеля для таблиц IxJxK P_CMh3 Асимптотическое значение p для этого теста Невозможно получить доверительные интервалы или отношения шансов для тестов --mh3. Подсказка Уловка для анализа фенотипов с более чем двумя категории (но только с номинальными, а не порядковыми результатами) заключается в использовании --mh3 вариант с фенотип в файле кластера и фенотип в файле PED устанавливают все к единственному значению. Тестирование гетерогенной ассоциации Как упоминалось в предыдущем разделе, для тестирования предоставляются два метода. для межкластерных различий в ассоциации при использовании случая / контроля дизайн. Тест Бреслоу-Дей задается с опцией: plink --file mydata --bd --within myclst.txt который запускает и генерирует те же файлы, что и --mh вариант, описанный выше, но с добавленными двумя дополнительными полями: CHISQ_BD Тест Бреслоу-Дея P_BD Асимптотическое p-значение где значимое значение указывает на межкластерную гетерогенность в отношении шансов ассоциации заболевания / SNP. Аналогичный тест на однородность тестов отношения шансов на основе разделение статистики хи-квадрат определяется следующим образом: plink --file mydata --homog - внутри myclst.txt который генерирует файл plink.homog который содержит поля CHR Номер хромосомы SNP Идентификатор SNP Код минорного аллеля A1 Код основного аллеля A2 F_A Частота аллеля случая F_U Частота контрольного аллеля Число аллелей N_A случая N_U Количество контрольных аллелей ТЕСТ Тип теста Статистика ассоциации CHISQ Хи-квадрат DF Степени свободы P Асимптотическое p-значение ИЛИ отношение шансов Тип ТЕСТ: ИТОГО Всего SNP и ассоциация страт Ассоциация ASSOC SNP контролирует страты HOMOG Тест межпластовой неоднородности X_1 Ассоциация в первом слое X_2 Ассоциация во втором слое ... Тест на мультилокусную ассоциацию T (2) Хотеллинга ВАЖНО Эта команда временно отключена PLINK обеспечивает поддержку болезненных черт мультилокусный, генотипический тест с использованием Т2 Хотеллинга (Т-квадрат) статистика. Параметр --set следует использовать для указания какие SNP должны быть сгруппированы следующим образом: plink --file data --set mydata.set --T2 где mydata.set определяет, какие SNP в каком наборе (см. этот раздел для получения дополнительной информации о определяющие множества).Эта команда сгенерирует файл plink.T2 который содержит поля SET Установить имя РАЗМЕР Количество SNP в этом наборе F F-статистика из теста Хотеллинга DF1 Степени свободы 1 DF2 Степени свободы 2 P_HOTEL Асимптотическое p-значение СОВЕТ Используйте перестановку --genedrop для выполнить семейное приложение теста Т2 Хотеллинга. Эта команда может использоваться со всеми методами перестановки (замена меток или гено-сбрасывающий, адаптивный или макс (Т)).Фактически, проверка перестановки основан на 1-p, чтобы сделать сравнение между наборами для max (T) более значимой (поскольку наборы разного размера будут иметь F-статистика с разными степенями свободы иначе). С помощью перестановка создаст один из следующих файлов: plink.T2.perm которые содержат поля SET Установить имя РАЗМЕР Количество SNP в этом наборе EMP1 Эмпирическое значение p NR Количество повторов перестановки или, если использовался --mperm, Плинк.T2.mperm которые содержат поля SET Установить имя РАЗМЕР Количество SNP в этом наборе EMP1 Эмпирическое значение p EMP2 max (T) эмпирическое значение p Обратите внимание, что этот тест использует простой подход к отсутствующим данным: скорее, чем удаление по регистру (удаление человека, если у него есть хотя бы одно пропущенное наблюдение) мы приписываем среднее значение аллеля. Несмотря на то что это сохраняет власть в большинстве сценариев, это также может вызвать некоторую предвзятость когда много недостающих точек данных.Использование перестановки - это хороший способ обойти эту проблему. Ассоциация количественных признаков Количественные признаки также можно проверить на ассоциацию, используя либо асимптотический (тест отношения правдоподобия и тест Вальда) или эмпирический значения значимости. Если фенотип (столбец 6 файла PED или фенотип, указанный с параметром --pheno) количественный (т.е. содержит значения, отличные от 1, 2, 0 или отсутствующие) тогда PLINK автоматически обработает анализ как количественный анализ признаков.То есть та же команда, что и для ассоциация болезнь-признак: plink --file mydata --assoc сгенерирует файл plink.qassoc со следующими полями: CHR Номер хромосомы SNP Идентификатор SNP BP Физическое положение (пара оснований) NMISS Количество не пропущенных генотипов БЕТА Коэффициент регрессии SE Стандартная ошибка R2 Регрессия r-квадрат Тест Т-Вальда (на основе t-распределения) Асимптотическое p-значение критерия Вальда Если также были запрошены перестановки, то дополнительный файл, либо Плинк.Assoc.perm или plink.assoc.mperm будет сгенерирован, в зависимости от того, адаптивная или max (T) перестановка использовался (подробнее см. следующий раздел Детали). Эмпирические p-значения основаны на статистике Вальда. Средние значения генотипа количественных признаков Добавление флага --qt-means вместе с --assoc команда, при запуске с количественным признаком, даст дополнительный файл со списком средних и стандартных отклонений стратифицированный по генотипу, называется Плинк.qassoc.means и формат Код хромосомы CHR SNP Идентификатор SNP ЗНАЧЕНИЕ Описание следующих трех полей G11 Значение для первого генотипа G12 Значение для второго генотипа G22 Значение для третьего генотипа где VALUE - одно из GENO, COUNTS, FREQ, MEAN или SD (стандартное отклонение). Например: CHR ЗНАЧЕНИЕ SNP G11 G12 G22 5 hCV26311749 GENO 2/2 2/1 1/1 5 hCV26311749 СЧИТАЕТ 1 60 597 5 hCV26311749 ЧАСТОТА 0.00152 0,09119 0,9073 5 hCV26311749 СРЕДНЕЕ 0,9367 0,4955 0,5074 5 hCV26311749 SD 0 0,273 0,2902 5 hCV918000 GENO 2/2 2/1 1/1 5 hCV918000 СЧИТАЕТ 47 237 359 5 hCV918000 ЧАСТОТА 0,07309 0,3686 0,5583 5 hCV918000 СРЕДНЕЕ 0,505 0,5091 0,5074 5 hCV918000 SD 0,2867 0,3064 0,2797 т. е. каждый SNP занимает 5 строк. Взаимодействие количественных признаков (GxE) PLINK позволяет проверить разницу в связь с количественным признаком между двумя средами (или более как правило, две группы).Этот тест просто основан на сравнении разница между двумя коэффициентами регрессии. Чтобы выполнить этот тест: plink --file mydata --gxe --covar mycov.dat где mycovar.txt - файл, содержащий следующие поля: Семейный ID Индивидуальный идентификатор Ковариатное значение См. Примечания к файлам ковариаций для получения дополнительной информации. Детали. Эта опция создаст файл plink.qassoc.gxe который содержит поля: CHR Номер хромосомы SNP Идентификатор SNP NMISS1 Количество не пропавших генотипов в первой группе (1) BETA1 Коэффициент регрессии в первой группе SE1 Стандартная ошибка коэффициента в первой группе NMISS2 Как указано выше, вторая группа BETA2 Как и выше, вторая группа SE2 Как и выше, вторая группа Z_GXE Z score, тест на взаимодействие P_GXE Асимптотическое значение p для этого теста ВАЖНО! Ковариата должна быть закодирована как привязанность переменная состояния, т. е.е. 1 или 2 представляют первую или вторую группу. Значения 0 или -9 могут использоваться для обозначения отсутствующих значений ковариант в в этом случае этот человек будет исключен из анализа. Линейные и логистические модели Эти две функции позволяют использовать несколько ковариат при тестировании обоих количественный признак и ассоциация SNP признака болезни, и для взаимодействия с этими ковариатами. Ковариаты могут либо быть непрерывным или бинарным (т.е.для категориальных ковариат, вы должны сначала создать набор двоичных фиктивных переменных). ВНИМАНИЕ! Эти команды в некотором смысле более гибкие, чем стандартная команда --assoc, но за это приходится платить: они работают медленнее ... В этом разделе мы рассматриваем: Basic uasge Ковариата и взаимодействия Гибкое определение точной модели Гибкое определение совместных тестов Основное использование Для количественных признаков используйте plink --bfile mydata --linear Для признаков заболевания укажите логистическую регрессию с помощью plink --bfile mydaya --логистика вместо. Все остальные команды в этом разделе одинаково применимы к обеим этим моделям. Эти команды либо сгенерируют выходной файл plink.assoc.linear или plink.assoc.logistic в зависимости от используемого фенотипа / команды. Базовый формат: Хромосома CHR SNP Идентификатор SNP BP Физическое положение (пара оснований) A1 Протестированный аллель (минорный аллель по умолчанию) ТЕСТ Код для теста (см. Ниже) NMISS Количество не пропавших без вести лиц, включенных в анализ БЕТА / ИЛИ Коэффициент регрессии (- линейный) или отношение шансов (--логистический) STAT Коэффициент t-статистика P Асимптотическое p-значение для t-статистики Для аддитивных эффектов SNP направление регрессии коэффициент представляет собой эффект каждого лишнего минорного аллеля (я.е. положительный коэффициент регрессии означает, что минорный аллель увеличивает средний риск / фенотип). Если команда --beta добавляется вместе с --logistic, затем коэффициенты регрессии вместо отношения шансов будет возвращено. ПРИМЕЧАНИЕ В других местах данной документации термин Ссылочный аллель иногда используется для обозначения A1, то есть команда --reference-allele может использоваться для указания какой аллель - A1. Обратите внимание, что в ассоциативном тестировании отношения шансов, и т. д. обычно рассчитываются с использованием A2 как фактического референсного аллеля (я.е. положительное ИЛИ означает, что A1 увеличивает риск по сравнению с A2). СОВЕТ Добавление --ci 0.95, например, вариант предоставит 95% доверительный интервал для предполагаемого параметров в дополнительных полях L95 и U95 в выходные файлы. Сама по себе команда --linear даст идентичные результаты для команды Тест Вальда из команды --assoc применительно к количественному черты. Команда --logistic может немного отличаться результаты команды --assoc для признаков болезни, но это потому что применяется другой тест / модель (т.е. логистическая регрессия а не подсчет аллелей). Разница может быть особенно большой для очень редкие аллели (т. е. если SNP мономорфен в случаях или в контроле, то модель логистической регрессии не является четко определенной и асимптотической результаты могут не соответствовать базовому тесту). При использовании --linear добавляется опция - стандартная бета сначала будет стандартизировать фенотип (среднее значение 0, единичная дисперсия), поэтому результирующие коэффициенты будут стандартизированы. Столбец TEST по умолчанию ADD означает добавку. эффекты дозировки аллелей.Добавление опции --генотипный создаст файл, в котором будет два дополнительных теста для каждого SNP, соответствующие до двух дополнительных строк: DOMDEV и GENO_2DF, которые представляют отдельный тест на компонент доминирования или совместный тест 2 df обоих аддитивная и доминирующая (т.е. соответствующая общему, генотипическому модель в команде --model). В отличие от модели доминирования --model, DOMDEV относится к переменной с кодом 0,1,0 для трех генотипов AA, Aa, aa, т.е. представляющих отклонение доминирования от аддитивности, скорее указывая, что конкретный аллель является доминантным или рецессивным. То есть ДОМДЕВ термин подбирается вместе с членом ADD в одной модели. ПРИМЕЧАНИЕ! Кодировка, которую PLINK использует с 2 df - генотипическая модель включает две переменные, представляющие аддитивный эффект и отклонение доминирования; А Д AA 0 0 AB 1 1 BB 2 0 Хотя тест 2df будет идентичным, вы должны будете , а не ожидайте увидеть аналогичные значения p и т. д. для двух отдельных терминов, если вместо этого вы использовали другую версию «генотипического» кодирования, например.грамм. в другой пакет анализа, например использование фиктивных переменных для представления генотипы: G1 G2 AA 0 0 AB 1 0 BB 0 1 То есть, хотя в принципе то же самое, с точки зрения теста 2df, толкование двух отдельных терминов различно в этих два случая. Чтобы добиться этого в PLINK (начиная с версии 1.02), добавьте флаг --hethom, а также --genotypic. В соответствующей заметке вы не всегда ожидаете, что ADD p-значение должно быть таким же при вводе условия доминирования, как оно есть без этого; если вы сомневаетесь, советуем вам просто интерпретировать тест 2 df при использовании параметра --genotypic. Чтобы указать модель, предполагающую полное доминирование (или рецессивное) для минорный аллель (то есть вместо упомянутой выше модели 2 df), вы можно указать либо - доминирующий или --рецессивный Ковариаты и взаимодействия Если также указан файл ковариат, то все ковариаты в этом файл будет включен в регрессионную модель с пометкой COV1, COV2 и т. д. Это отличается от других команд, которые принимают только одну ковариату (возможно, работает вместе с параметром --mcovar). ПРИМЕЧАНИЕ Можно использовать команды --covar-name или --covar-number. для выбора подмножества всех ковариат в файле, описанном здесь. Например, если файл ковариат сделан как описан здесь и содержит 2 коварирует тогда команду plink --bfile mydata --linear --genotypic --covar mycov.txt добавит два дополнительных теста на SNP, COV1 и COV2. Значение p для термина или терминов SNP. в модели будут корректироваться ковариаты; то есть, к данным подходит одна модель (которая также включает термин доминирования, так как также был установлен флаг --genotypic): Y = b0 + b1.ДОБАВИТЬ + b2.DOMDEV + b3.COV1 + b4.COV2 + e (Обратите внимание, что при использовании этого обозначения генотипический тест имеет вид b1 = b2 = 0.) Вывод для каждого SNP может выглядеть примерно так: CHR SNP BP A1 TEST NMISS OR STAT P 5 rs000001 10001 A ADD 664 0,7806 -1,942 0,05216 5 rs000001 10001 A DOMDEV 664 0,9395 -0,3562 0,7217 5 rs000001 10001 A COV1 664 0,9723 -0,7894 0,4299 5 rs000001 10001 A COV2 664 1.159 0,5132 0,6078 5 rs000001 10001 A GENO_2DF 664 NA 5,059 0,0797 То есть это представляет коэффициенты из четырех членов в кратном регресс болезни на СДВ, DOMDEV, COV1 и COV2 совместно. Финал test - это тест 2df, который проверяет коэффициенты для ADD и ДОМДЕВ вместе. Важно отметить, что p-значения для каждой строки отражать эффект объекта в столбце ТЕСТ, а не SNP, контролируя эту конкретную ковариату. (То есть p = 0.0797 - это 2df-тест SNP с одновременным контролем COV1 и COV2.) СОВЕТ Чтобы подавить множественные строки вывода для каждая ковариата (которая часто сама по себе не представляет интереса) добавляет flag --hide-covar, т.е. приведенное выше будет выглядеть следующим образом для этого SNP: CHR SNP BP A1 TEST NMISS OR STAT P 5 rs000001 10001 A ADD 664 0,7806 -1,942 0,05216 5 rs000001 10001 A GENO_2DF 664 NA 5.059 0,0797 СОВЕТ Чтобы обусловить анализ определенным SNP при использовании --linear или --logistic, используйте параметр --condition, например plink --bfile mydata --linear --condition rs123456 проверит все SNP, но добавит аллельную дозу для rs123456 в качестве ковариаты. Этот можно использовать вместе с --covar и другими параметрами, перечисленными здесь. Чтобы использовать несколько SNP, используйте, например, plink --bfile mydata --linear --condition-list snps.txt , где snps.txt - это простой текстовый файл содержат список SNP, которые должны быть включены как ковариаты. Теперь вывод будет включать термины, соответствующие к SNP, перечисленным в файле snps.txt. Обусловливающие SNP вводятся в модель просто как ковариаты, с использованием простого кодирования дозировки 0, 1, 2 аллелей. То есть для двух кондиционирующих SNP, rs1001 и rs1002 говорят, а также стандартную ковариату, модель будет Y = b0 + b1.ADD + b2.rs1001 + b3.rs1002 + b4.COV1 + e Если коэффициент b1 для тестового SNP все еще значим после ввода этих ковариат, это может означать, что это действительно имеет эффект, независимый от rs1001, rs1002 и другая ковариата.(Другие коэффициенты все еще могут быть очень значимыми, но они отражают влияние обусловливающие SNP и ковариаты, а не тестовый SNP.) Если добавлен флаг --sex, то пол будет введен как ковариант в модели (кодируется 1 для мужчин, 0 для женщин), например plink --bfile mydata --logistic --sex Если добавлена ​​опция --interaction, то будут введены условия которые соответствуют ковариатным взаимодействиям SNP x (с DOMDEV а также ADD, если указано --genotypic).в случай двух ковариат без --genotypic, например, команда plink --bfile mydata --linear --covar tmp.cov --interaction результаты в модели Y = b0 + b1.ADD + b2.COV1 + b3.COV2 + b4.ADDxCOV1 + b5.ADDxCOV2 + e ПРИМЕЧАНИЕ Помните, что при взаимодействии условия включены в модель, значимость основных эффектов не может быть обязательно интерпретируются прямо (т.е. они будут зависеть от о произвольном кодировании переменных).Другими словами, когда включая флаг --interaction, вам, вероятно, следует интерпретировать р-значение взаимодействия. См. Любой стандартный текст регрессионные модели, если вам это неясно. Наконец, опция --test-all удаляет все термины в модели. в тесте на множественную степень свободы. Гибкое определение модели Используйте такие команды, как --covar и --interaction автоматически введите все ковариаты и возможные взаимодействия ковариант SNP x. Если не хочешь проверить все это, а затем использовать флаг --parameters, чтобы извлечь только интерес.Например, чтобы взять пример выше: Y = b0 + b1.ADD + b2.COV1 + b3.COV2 + b4.ADDxCOV1 + b5.ADDxCOV2 + e Если нужно только ADD, две ковариаты и ADDxCOV2 но , а не , взаимодействие ADDxCOV1, то из приведенного выше примера вы могли бы использовать plink --bfile mydata --linear --covar tmp.cov --interaction --parameters 1,2,3,5 То есть --parameters принимает список целых чисел, разделенных запятыми, начиная с 1, которые представляют термины в модели (в том порядке, в котором они появляются, если команда была запущена без флага --parameters).В этом случае: ДОБАВИТЬ [1] COV1 [2] COV2 [3] ДОБАВИТЬ x COV1 [4] Гибкое определение совместных тестов Чтобы выполнить определяемый пользователем совместный тест более чем одного параметра, используйте - вариант тестирования. Для этого требуется набор параметров, разделенных запятыми. числа, например: если модель ДОБАВИТЬ [1] COV1 [2] COV2 [3] ADDxCOV1 [4] ADDxCOV2 [5] тогда plink --bfile mydate --linear --covar file.cov --interaction --tests 1,4,5 представляет собой тест ADD с тремя степенями свободы и два взаимодействия. Обратите внимание: если это используется вместе с параметром --parameters вариант, то кодировка здесь относится к сокращенной модели - например, команда plink --bfile mydate --linear --covar file.cov --interaction - параметры 1,2,3,5 - тесты 1,4 выполняет совместный тест ADD и ADDxCOV2 (тест 2df) контролируя основные эффекты COV1 и COV2, то есть мы не используем --tests 1,5, так как сейчас их всего 4 термины в модели: - параметры 1,2,3,5 - тесты 1,4 ДОБАВИТЬ [1] [1] ТЕСТ COV1 [2] [2] COV2 [3] [3] ADDxCOV1 [4] н / д ADDxCOV2 [5] [4] ТЕСТ Другими словами, мы подбираем модель Y = b0 + b1.ADD + b2.COV1 + b3.COV2 + b4.ADDxCOV2 + e и совместно проверяем гипотезу H0: b1 = b4 = 0 Как упоминалось выше, используйте --test-all, чтобы удалить все термины в модели. в одиночном совместном тесте. Мультиколлинеарность Распространенной проблемой множественной регрессии является мультиколлинеарность: когда переменные-предикторы слишком сильно коррелированы друг с другом, оценки параметров станут нестабильными. PLINK пытается обнаружит это, и отобразит NA для статистики теста и p-значение для всех членов модели, если есть доказательства мультиколлинеарность.Один из распространенных случаев, когда это может произойти, будет если один из них включает параметр --genotypic, но в SNP есть только два три возможных класса генотипов: в данном случае ADD и DOM будет идеально коррелирован, а PLINK - отображать NA для обоих тестов; это в основном говорит вам, что вы должны перезапустить без опции --genotypic для этого конкретный SNP. Аналогичные принципы применяются к включению ковариат и условия взаимодействия: чем больше терминов вы включите, тем больше вероятность, что вы иметь проблемы.Опция --vif может использоваться для указания дисперсии коэффициент инфляции (VIF), использованный в первоначальном тесте для мультиколлинеарность. Значение по умолчанию - 10 - меньшие значения представляют более строгие тесты. СОВЕТ Если у вас есть количественный признак, вам нужна только аддитивная модель и иметь только одну двоичную ковариату, используйте параметр --gxe (описанный выше) вместо --linear: он будет работать намного быстрее (на основе более простого тест на разницу двух наклонов регрессии; это не обязательно даст численно идентичные результаты для подхода множественной регрессии, но асимптотически оба тесты должны быть похожи). Тесты на основе набора Эти тесты на основе наборов особенно подходят для крупных кандидатов. исследования генов в отличие от исследований ассоциации всего генома, поскольку они используйте permutaiton. ПРИМЕЧАНИЕ Основа теста на основе наборов была изменена в версии 1.04 и выше. Этот анализ работает следующим образом: Для каждого набора для каждого SNP определить, какие другие SNP находятся в LD, выше определенного порога R Выполните стандартный анализ одиночного SNP (который может быть основным ассоциация случай / контроль, семейная TDT или количественный признак анализ). Для каждого набора выберите до N «независимых» SNP (как определено на шаге 1) со значениями p ниже P . Лучший SNP - это выбран первым; последующие SNP выбираются в порядке уменьшения статистическая значимость после удаления SNP в LD с ранее выбранные SNP. Из этих подмножеств SNP вычисляется статистика для каждого набора. как среднее значение этой статистики одного SNP Переставляйте набор данных много раз, сохраняя LD между Константа SNP (т.е.е. перестановочные метки фенотипа) Для каждого переставленного набора данных повторите шаги 2–4 выше. Эмпирическое значение p для набора (EMP1) - это количество раз переставленная статистика множества превышает исходную для этого набора. Обратите внимание, что эмпирические p-значения скорректированы для нескольких SNP. в наборе (с учетом LD между этими SNP). Они есть не исправлено для многократного тестирования, если имеется более одного набора, однако (т.е. не существует эквивалента EMP2 (см. стр. о перестановке).Критические параметры, описанные выше, R , N и P, все могут быть изменены пользователем, как описано ниже. Для выполнения теста на основе наборов критически важными ключевыми словами являются --set-test --set my.set --мперм 10000 которые заявляют, что мы выполняем основанный на наборах тест, который устанавливает файл на использовать и сколько перестановок выполнить (последняя команда необходимо). Как упоминалось выше, команда --assoc может быть заменяется на --tdt или --logistic и т. д.Установленный файл my.set имеет форму SET1 rs1234 rs28384 rs29334 КОНЕЦ SET2 rs4774 rs662662 rs77262 КОНЕЦ ... Например, plink --file mydata --set-test --set my.set --mperm 10000 --assoc отобразит в файле журнала следующие критические параметры с их значения по умолчанию Проведен тест набора на основе LD с параметрами: r-квадрат (--set-r2) = 0,5 p-значение (--set-p) = 0.05 максимальное количество SNP (--set-max) = 5 Вывод записывается в файл с расширением .set.mperm, например plink.assoc.set.mperm с полями SET Установить имя NSNP Количество SNP в наборе NSIG Общее количество SNP ниже порогового значения p ISIG Количество значимых SNP, также прошедших LD-критерий STAT Средняя статистика теста на основе ISIG SNP EMP1 Эмпирическое значение p на основе набора SNPS Список SNP в комплекте Например, вот результат набора данных случай / контроль с SNP для пять родственных генов (строки усечены) УСТАНОВИТЬ NSNP NSIG ISIG STAT EMP1 SNPS GABRB2 45 0 0 0 1 NA ГАБРА6 6 4 3 5.199 0,09489 rs3811991 | rs2197414 | ... ГАБРА1 22 11 5 5,951 0,09459 rs4254937 | rs4260711 | ... GABRG2 24 0 0 0 1 NA ГАБРП 17 2 1 7,64 0,0269 rs7736504 Здесь первый ген, GABRB2 , имеет 45 SNP, но ни один из них значимы при p = 0,05, поэтому эмпирическое значение p обязательно 1.00. Следующий ген имеет 6 SNP, 4 из которых значимы, но только 3 из которых независимо значимы на основе порога r-квадрата из 0.5. STAT 5,199 - это среднее значение хи-квадрат. статистика по этим трем SNP. Это не должно толковаться в сам по себе - скорее, вы должны учитывать значение EMP1 значение, основанное на нем. В этом случае P = 0,095. Финал ген GABRP здесь номинально значим, P = 0,027, но это конечно, не корректирует 5 протестированных генов. Естественно, разные пороги будут давать разные полученные результаты. В зависимости от неизвестной генетической архитектуры они могут различаться. существенно и содержательно так.В общем, если набор представляет собой очень большой путь (десятки генов), который вы можете захотеть увеличить --set-max. Наверное, нет жестких правил относительно того, как установить --set-p и --set-r2, за исключением того, что работает под большим количеством настроек и выбирать наиболее важные - не лучшая идея. Бег с более строгим набором ценностей --set-r2 0,1 --set-p 0,01 --set-max 2 мы видим в целом похожую картину результатов; естественно, пороговое значение p-значения означает, что GABRA6 перестает показывать какой-то сигнал, чтобы вообще никакого сигнала. УСТАНОВИТЬ NSNP NSIG ISIG STAT EMP1 SNPS GABRB2 45 0 0 0 1 NA ГАБРА6 6 0 0 0 1 Н / Д ГАБРА1 22 2 2 7,464 0,05949 rs4254937 | rs4260711 GABRG2 24 0 0 0 1 NA ГАБРП 17 1 1 7,64 0,06309 rs7736504 В качестве альтернативы более инклюзивная настройка может быть чем-то вроде --сет-r2 0.8 --set-p 1 --сет-макс 10 что в данном конкретном случае дает немного более сильные сигналы для ГАБРА6 и ГАБРА1 но слабее для GABRp (строки усечены) УСТАНОВИТЬ NSNP NSIG ISIG STAT EMP1 SNPS GABRB2 45 12 10 1,749 0,7162 hCV26311691 | ... ГАБРА6 6 6 6 3,998 0,0184 rs3811991 | ... ГАБРА1 22 13 10 5,277 0,0182 rs4254937 |... GABRG2 24 11 10 0,6976 0,9099 hCV3167705 | ... ГАБРП 17 10 10 2,753 0,1225 rs7736504 | ... СОВЕТ Две крайности - выполнение теста на основе а) наилучшего результата одиночного SNP для набора: --set-max 1 --set-p 1 или использовать все SNP в наборе: --сет-макс 99999 --set-p 1 --set-r2 1 Регулировка для многократного тестирования: Bonferroni, Sidak, FDR и т. Д. Для создания файла скорректированных значений значимости, корректирующих все выполненные тесты и другие показатели, используйте опцию: plink --file mydata --assoc --adjust который генерирует файл Плинк.отрегулировать который содержит поля CHR Номер хромосомы SNP Идентификатор SNP UNADJ Не скорректированное значение p Скорректированные p-значения GC Genomic-control BONF Bonferroni с пошаговой регулировкой p-значений HOLM Holm (1979) понижение скорректированных p-значений SIDAK_SS Сидак скорректированные за один шаг p-значения SIDAK_SD Понижение скорректированных значений p Сидака FDR_BH Benjamini & Hochberg (1995) повышающий контроль FDR FDR_BY Benjamini & Yekutieli (2001) усиление контроля FDR Этот файл отсортирован по значимости, а не по местоположению в геноме. наиболее значимые результаты находятся наверху. ПРЕДУПРЕЖДЕНИЕ В настоящее время эти процедуры только реализовано для асимптотических значений значимости для стандартной TDT и ассоциация (признак заболевания и количественный trait, --assoc, --linear, --logistic) тесты и тест 2x2xK Кокрана-Мантеля-Хензеля. Будущие версии будут разрешить эти результаты для эмпирических значений значимости и для других тесты (например, эпистаз и т. д.).

Коэффициенты | Purplemath

Purplemath

Пропорции строятся из соотношений.«Отношение» - это просто сравнение или соотношение двух разных вещей. Например, кто-то может посмотреть на группу людей, сосчитать носы и сослаться на «соотношение мужчин и женщин» в группе. Предположим, есть тридцать пять человек, пятнадцать из которых - мужчины. Остальные - женщины, итак:

... в группе двадцать женщин. Выражение «отношение (этого) к (этому)» означает, что (это) стоит перед (этим) в сравнении. Итак, если бы можно было выразить «соотношение мужчин и женщин», то соотношение, выражаясь английскими словами, было бы «15 мужчин к 20 женщинам» (или просто «15 к 20»).

MathHelp.com

Порядок элементов в соотношении очень важен и должен соблюдаться; какое бы слово ни было первым в соотношении (если оно выражено словами), его номер должен стоять первым в соотношении.Если бы выражение было «соотношение женщин и мужчин», то словесным выражением было бы «20 женщин к 15 мужчинам» (или просто «20 к 15»).

Соотношение мужчин и женщин выражается как «15 к 20», что выражается словами. Есть два других обозначения этого отношения "15 к 20":

обозначение шансов: 15: 20

дробное представление:

Вы должны уметь распознать все три обозначения; вы, вероятно, должны будете знать их и как конвертировать между ними на следующем тесте.Например:

• В определенном парке живут 16 уток и 9 гусей. Выразите соотношение уток и гусей через двоеточие, через дробь (не уменьшать) и прописью.

Они хотят «соотношение уток и гусей», поэтому число уток идет первым (или, в дробной форме, сверху). Итак, мой ответ:

• Рассмотрим вышеупомянутый парк с 16 утками и 9 гусями.Выразите соотношение гусей и уток во всех трех форматах.

На этот раз они хотят, чтобы я дал им «соотношение гусей и уток». Я буду использовать те же самые числа, но в этом случае количество гусей идет первым (или, для дробной формы, сверху). Итак, мой ответ:

Числа были одинаковыми в каждом из двух упражнений, описанных выше, но порядок , , в котором они были перечислены, различается в зависимости от порядка, в котором были выражены элементы соотношения.В соотношениях очень важен порядок.

Давайте вернемся к 15 мужчинам и 20 женщинам в нашей первоначальной группе. Я выразил это отношение дробью, а именно:

Это указывает на одну важную вещь о соотношениях: числа, используемые в соотношении, могут не быть абсолютными измеренными значениями.Соотношение «15 к 20» относится к абсолютным числам мужчин и женщин, соответственно, в группе из тридцати пяти человек. Упрощенное или сокращенное соотношение «3 к 4» говорит нам только о том, что на каждых трех мужчин приходится четыре женщины. Упрощенное соотношение также говорит нам, что в любой репрезентативной выборке из семи человек (3 + 4 = 7) из этой группы трое будут мужчинами. Другими словами, мужчины составляют