Каркас плоский и пространственный: Арматурные каркасы. Плоские и пространственные

Арматурные каркасы. Плоские и пространственные

Арматурные каркасы. Основные виды арматурных каркасов: плоские и пространственные, почему сегодня без них не обходится ни одно строительство.

Общеизвестно,что армирование бетона резко повышает прочность и устойчивость строений. В современном строительстве широко применяются специальные изделия, предназначенные для армирования − арматурные каркасы. Без них сегодня вряд ли обходиться хоть бы одно сколько нибудь крупное строительство.

Арматурный каркас − это изделие из металлических прутов. Он может быть либо сварным, либо вязанным. Разделяют два вида армокаркасов − объёмные и плоские. Давайте немного поговорим о особенностях применения и изготовления арматурных каркасов каждого из них.

Пространственные арматурные каркасы

Пространственные арматурные каркасы (по другому их называют пространственные каркасы) чаще всего представляют собой соединённые специальными арматурными стержнями несколько плоских арматурных решёток. Соединение арматурных решёток осуществляется в перпендекулярной плоскости. Назначение пространственных арматурных каркасов весьма различно. Бывают специальные каркасы для свай. Они могут быть круглыми или квадратными.

Производство каркасов для свай осуществляется на специальных автоматизированных поточных линиях. Также к пространственным каркасам относятся и большие объёмные конструкции клеточного типа. Они, как правило, применяются при строительстве промышленных объектов, крупных объектов социальной и спортивной инфраструктуры, больших жилых зданий. Производство таких каркасов осуществляется индивидуально, с учётом размеров фундамента.

Плоские арматурные каркасы

Плоские арматурные каркасы представляют собой конструкции, которые состоят из арматурных стержней. Стержни расположены в параллельных плоскостях, под разными углами друг к другу. Как правило, они соединяются при помощи контактной сварки. По другому такие каркасы называют арматурными сетками. Область применения данного вида арматурных каркасов также довольно широка.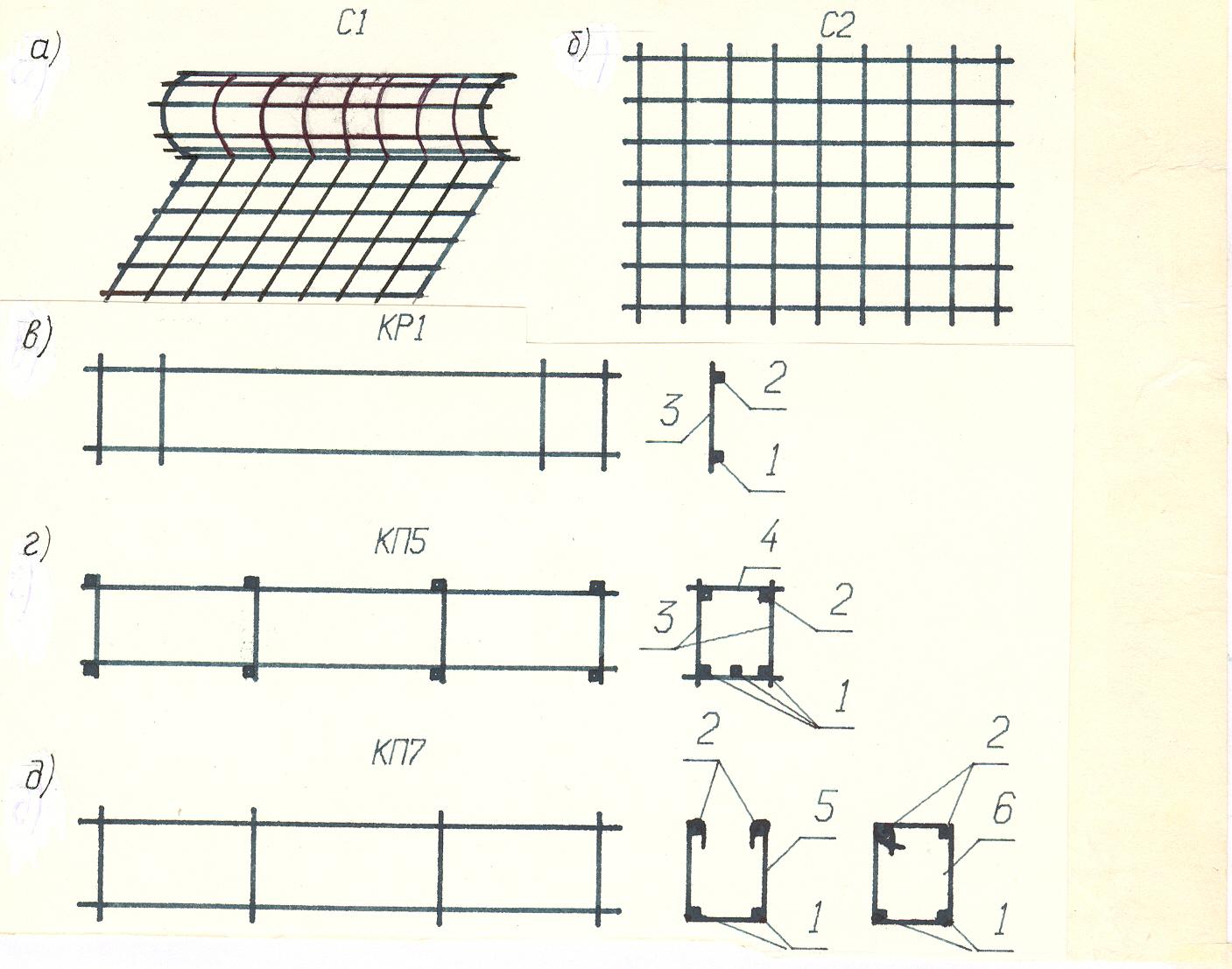 Они используются при заливке фундамента для его армирования и при производстве железобетонных изделий. Как правило, данные каркасы сегодня изготавливаются в заводских условиях. Но на строительстве небольших объектов и сейчас можно встретить изготовление плоских арматурных каркасов вручную, которые собираются на месте.

Тем самым, без армокаркасов сегодня не обходится ни одна крупная стройка. И с проблемой изготовления арматурных каркасов, а также их применения сталкивается сегодня практически каждый заказчик и застройщик.

Читайте также: Пластиковая (стекловолоконная) арматура, гибкие связи, стекломагнитовый лист

Читайте также

По данным аналитики агентства «Метриум», число предложений от застройщиков в секторе квартир без отделки в …

Плоские и пространственные армокаркасы

ПРИМЕНЕНИЕ АРМАТУРНЫХ КАРКАСОВ

Монолитное строительство

Представляет собой технологию постройки, при которой здание возводят из железобетона, основные составляющие которого бетон и арматурный каркас. Данный метод позволяет сократить расход стали и бетона, расширить горизонт архитектурных решений.
Одним из основных преимуществ монолитного строительства, перед остальными, является высокая жесткость каркаса всего сооружения, его сейсмостойкость. Именно поэтому данная технология постройки позволяет возводить высотные здания. Вес монолитного здания в среднем на 15 % меньше такого же кирпичного, но при этом монолитное строительство требует больших трудозатрат на строительной площадке.

предельная прочность соединений

580 Н/мм2

плоского арматурного каркаса на разрыв

Метро

С каждым годом строительство в крупных городах становится все плотнее, работать приходится во все более стесненных условиях, именно поэтому технология застройки «стена в грунте» становится все популярнее.

Арматурные каркасы данного типа дают возможность сделать долговечные ограждающие системы с наименьшими расходами времени и ресурсов. Особенно данная технология актуальна в метростроении для ограждения вестибюлей станций и вентиляционных камер, при строительстве многоуровневых паркингов, супермаркетов и т.д.

максимальная длина сегмента

20 метров

арматурного каркаса для стены в грунте

Опоры мостов

Применение буронабивных свай в строительстве за последние годы получает всё большее распространение. В условиях плотной городской застройки строители всё чаще прибегают к устройству фундаментов посредством использования данной технологии.
Устройство буронабивных свай обеспечивает надежность высотного строения, несущая способность таких свай выше, чем забивных.

Буронабивные сваи незаменимы в местах, где не допускается сильная вибрационная и динамическая нагрузка на близлежащие грунты. Они находят свое применение при строительстве жилых домов, объектов промышленности и инфраструктуры, усиления основания в ходе реконструкционных работ, ограждения котлованов, устройства фундаментов сооружений, устройства подпорных стен, устройства шумозащитных экранов (автодорожное строительство), строительство мостов и эстакад.

Возможные диаметры

200 — 3000 мм

арматурного каркаса

Почему стоит выбрать Армикон

Высокое качество продукции

Мы используем только самое передовое современное европейское оборудование и высококвалифицированную рабочую силу. Продукция проходит жесткий контроль качества на всех этапах производства, а также обязательную сертификацию.

Минимальные сроки изготовления

Мы обладаем большим запасом производственной мощности, имеем возможность оперативной переналадки и оптимизации производственного процесса под Ваш заказ.

Доставка готовой продукции 24/7

Наличие собственного автопарка позволяет нам минимизировать Ваши транспортные расходы, и оперативно осуществлять доставку по всей территории России и за ее пределами.

Выгодные условия

Мы не только производим продукцию с самым лучшим соотношением цены и качества на рынке, но и всегда готовы искать компромиссы! Наши специалисты всегда предложат максимально эффективное и выгодное решение при расчете стоимости Вашего заказа!

Нам доверяют

Надежным партнером на всех этап строительства выступила наша компания «Завод «АРМИКОН».

Для пассажиров в 2021 году планируют открыть станцию «Стромынка» северо-восточного участка Большой кольцевой линии (БКЛ) метро. «Стромынка» расположится у главного входа в парк «Сокольники» – на Сокольнической площади, между улицами Русаковская и Сокольнический Вал. Сотрудничество с правительством Москвы дало нам возможность принять участие в спец.проекте по улучшению транспортного сообщение в городе Москве. Строительство Большой кольцевой линии позволит быстрее добираться из центра (кольцевая линия метро) до любой станции радиальной ветки. Благодаря нашей продуктивной работе откроют свои двери такие станции метро как «Стромынка» (запуск станции назначен на 2022 год) и «улица Новаторов» (запуск станции назначен на 2021 год).

Являясь важным промышленным объектом для страны ПО «Маяк» доверяет только самым надежным поставщикам

Нам очень приятно, что именно мы являемся надежными партнерами для такой крупной международной компании, как ООО “Эста Констракшен”.

Можно ли полностью описать общую теорию относительности как поле в плоском пространстве?

**** (В конце добавлено длинное разъяснение о работе Дезера и других, как упоминалось в других ответах, которые могут показаться противоречащими этому) **.

ДОПОЛНЕНИЕ: в статье Straumann, N. — Размышления о гравитации (Семинар ESA-CERN по фундаментальной физике в космосе и смежным темам, Европейское космическое агентство, 5-7 апреля 2000 г. (2001 г.), SP- 469,55) , показано (аналогично классической работе Дезера, но в более наглядном стиле), что теория поля со спином 2 на плоском 4-многообразии Минковки оказывается полностью эквивалентной эйнштейновскому искривленному пространству-времени, где абстинент Минковского метрика в конечном итоге становится ненаблюдаемой, тогда как наблюдаемая и физическая метрика является динамической, поддерживая реляционное значение, отстаиваемое в остальной части этого ответа, в котором подчеркивается идея о том, что пространство, время и причинная структура являются реляционными понятиями между динамическими объектами, а НЕ абсолютной статической стадией (будь то Ньютона или Минвкоски), где живут вещи, включая гравитацию.

Вывод из длинного отступления ниже : да, вы можете сформулировать гравитацию как поле в плоском многообразии (например, поле Дезера, Дорана-Галла-Лазенби, телепараллелизм…), но нет, это многообразие (и его дополнительная структура) не является плоским пространством-временем.

В любой эквивалентной формулировке общей теории относительности вы не можете избежать связи между физической метрикой пространства-времени и причинной структурой с остальными степенями свободы (материей, силами…). Следовательно, в любой формулировке существуют поля, живущие друг над другом, а пространство-время сводится к относительным совпадениям между ними. Лежащее в основе многообразие служит необходимым индексирующим устройством для степеней свободы полей, но не имеет физического наблюдаемого смысла. Если ситуация такова, что интересующая область может быть координирована физическими наблюдаемыми (например, полями материи, воплощающими наблюдателей в этой области), то мы можем использовать их как индекс совпадений полей; если, кроме того, связью этих наблюдаемых с гравитацией можно пренебречь, то они описывают физическое пространство-время Минковского в этой области. (Но плоское пространство-время Минковского не является решением уравнений поля Эйнштейна, когда существует ненулевая космологическая постоянная! Поэтому допущение физической реальности к глобальному плоскому «пространству-времени» бессмысленно в любой эквивалентной формулировке).

Для прекрасного обсуждения и развития всех этих концептуальных вопросов вам следует прочитать Карло Ровелли ‘s — Quantum Gravity , глава 2 (в частности 2.2, 2.3 и 2.4).

Общая теория относительности Эйнштейна — это теория динамики пространства-времени; точнее, это осознание того, что гравитационное поле «есть» пространство-время, и что нерелятивистские (ньютоновские и минковские) пространство и время являются частным решением, полезным в качестве фона в режимах почти пренебрежимых гравитационных эффектов по сравнению с другими явлениями. интересов. Как заметил Эйнштейн в своей оригинальной статье,

«… требование общей ковариантности лишает пространство и время последний остаток физической объективности…»

A. Einstein, Grundlage der allgemeinen Relativitätstheorie, Ann. дер физ. 49 (1916) 769-822.

Принцип эквивалентности, наряду с общей ковариантностью и детерминизмом классической теории, требует, чтобы теория была инвариантна к диффеоморфизму, т. \mu$ многообразия оказываются равными быть калибровочным артефактом. Эти «общие координаты многообразия» не следует путать с надлежащими физическими наблюдаемыми. Фиксация калибровки подобна выбору подходящей многообразной системы координат, где координаты могут соответствовать или не соответствовать физическим наблюдаемым, и только после этого мы вычисляем расстояния и время, используя гравитационное поле (метрическое или тетрадное) между событиями, как указано пространственно-временными совпадениями полей. .

Таким образом, вопрос об общей теории относительности, описываемой как поле в плоском пространстве (на самом деле пространстве-времени), упускает большую часть концептуального революционного содержания самой теории. Тем не менее, вы можете выбрать конкретное решение, такое как плоское пространство-время Минковского, и расширить гравитационное поле как возмущение поверх этого. Тогда вы получите эффективную теорию поля возмущения спина 2 в ненаблюдаемом плоском пространстве-времени с неперенормируемыми трудностями. Такой подход является оригинальным подходом сообщества физиков элементарных частиц с помощью теории пертурбативных струн. В этом нет ничего плохого, но тогда нужно быть метафизически осторожным с тем, что называть пространством-временем и гравитационным полем. Каноническая/петлевая квантовая гравитация также сталкивается с серьезными трудностями, хотя она не зависит от фона, поэтому следует быть непредвзятым в отношении того, какой урок следует извлечь из общей теории относительности, поскольку у нас все еще нет квантовой теории гравитации.

Подводя итог, с моей личной точки зрения и без лучшей экспериментально успешной теории гравитации, чем общая теория относительности, мы должны принять «факт», что, по крайней мере, на макроскопическом, классическом уровне, измеримые пространство и время являются относительными. концепции, полученные путем соединения полей материи с гравитационным полем, где лежащее в основе многообразие служит индексирующим датчиком, не имеющим никакого физического смысла. В этом смысле вы можете сказать, что общая теория относительности уже является теорией поля, но в классе эквивалентности диффеоморфизмов «базового пространства-времени», где поля определены, но вы не можете говорить о «плоскостности», таким образом, никакой геометрии, только дифференциальная топология (и размерность и подпись), потому что то, что обычно определяется как плоское в геометрии физического пространства (и времени), — это особые свойства физических траекторий и реляционная геометрия среди полей, соответствующих евклидовым/минковским свойствам.

—

ДОПОЛНЕНИЕ : Физическое содержание диффеоморфизм-инвариантности состоит в следующем. Общая ковариация позволяет выражать физику в любой системе отсчета (любой пространственно-временной криволинейной системе координат), что полезно для решения задач выбора наиболее подходящих координат. Когда у вас есть решение уравнений поля, у вас есть ваше гравитационное поле (метрика или тетрада) и уравнения движения других полей, на которые влияет эта метрика. Теперь решения можно перевести в любую другую общую систему координат, что может усложнить выражения из-за использования лучших координат для получения решения. И вот тут начинается магия: по аргументу дырки любой диффеоморфизм решения должен быть другим решением, то есть наше исходное решение в новой системе координат само должно быть новым решением в нашей исходной системе координат!! Это связано с тем, что активные диффеоморфизмы (плавное изменение лежащих в их основе многообразий с соответствующим преобразованием полей) и пассивные диффеоморфизмы (изменения координат) не могут быть различимы фоновой независимостью! Дело в том, что координаты, которые вы выбираете в течение всего процесса, могут не иметь прямого физического смысла (подумайте о сложных изменениях координат, чтобы упростить метрическую форму, чтобы легче получить решения Шварцшильда или Фридмана). В частности, физические расстояния и собственные времена — это не те причудливые координаты, в которых легко решается ваша задача, а вообще должны быть выражены в терминах метрики, т. е. гравитационного поля. Таким образом, учитывая координаты, вы можете говорить о двух точках (событиях), их координатное расстояние не обязательно должно быть их пространственно-временным интервалом, поскольку последний всегда подразумевает метрику, и только в плоском случае Минковского вы можете идентифицировать обе точки повсюду. В общем релятивистском контексте с неисчезающей гравитацией не существует глобальных плоских (= инерциальных) систем координат, кривизна Римана является как раз мерой этого препятствия. Поэтому, как я понимаю вопрос, я не вижу, как построить базовое многообразие с той же физической геометрией в случае неплоского пространства-времени.

ДОПОЛНЕНИЕ+ : относительно вашего второго комментария. Пространство-время нашей Вселенной НЕ является плоским, поскольку оно расширяется с ускорением. Плоское пространство-время Минковского НЕ является решением уравнений поля Эйнштейна, когда существует ненулевая космологическая постоянная, поэтому блочная Вселенная не может быть глобально плоской. То, что приблизительно плоско в космологических масштабах, — это трехмерные КОСМИЧЕСКИЕ сечения, индуцированное физическое расстояние которых расширяется, как видно из сопутствующей системы отсчета, определенной только в больших масштабах, как вы хотите. Но даже в этом решении измеренные пространственные расстояния не являются координатными расстояниями, поскольку они связаны масштабным коэффициентом FRW, который меняется в зависимости от космологического времени в этой системе отсчета. Итак, не путайте пространственноподобную 3-кривизну (которая может быть плоской) слоения пространства-времени с глобальным решением пространства-времени. Часто сбивающий с толку вопрос относительности заключается в том, что абсолютной одновременности не существует. Даже такое космологическое решение, как FRW, говорит о «пространствах, которые развиваются в глобальном времени», но это только из-за удобства сопутствующей системы отсчета, которая всегда является приближением для больших масштабов. Каждый реальный наблюдатель локален и не движется вместе с космологической сопутствующей системой отсчета. Важно помнить то, что подчеркивал Эйнштейн: наблюдаемое пространство и время — это реляционные понятия, определяемые операционально посредством измерения линеек и часов. Называть лежащее в основе многообразие «пространством-временем» вводит в заблуждение. Гравитоны и (квантовая) теория поля, какими мы их знаем, являются приблизительными теориями мира, поддающимися определению и применимыми только в областях пространства-времени (не только пространства!) приблизительно плоских для наших целей и точности. Поля, частицы как их кванты, энергия и подобные понятия требуют определения группы симметрии Пуанкаре, чего нет в общем релятивистском случае. Вот почему каноническая/петлевая/спиновая квантовая гравитация не определяется в этих терминах, в отличие от теории струн. Повседневные концепции квантовой теории поля, живущие в общем пространстве-времени, вводят в заблуждение и являются лишь полуклассическими; хотя классическая теория поля может быть разработана, короткодействующие силы, такие как слабые и сильные ядерные взаимодействия, являются только квантово-механическими. Таким образом, хотя общая теория относительности также является приближенной макроскопической теорией, ее эмпирическая адекватность и успех учат нас тому, что классическая или квантовая теория поля в плоском пространстве-времени также является приближенной макро/микроскопической моделью. Пока говорят о гравитационном поле во взаимодействии с другими полями, обе концепции не полностью совместимы, и это проблема квантовой гравитации.

ДОПОЛНЕНИЕ О РАБОТЕ ДЕЗЕРА ИЛИ ДОРАНА-ГАЛЛА-ЛАСЕНБИ: , в других ответах ниже и в комментарии к этому говорится, что работа Дезера или других «показывает», что общая теория относительности может быть, например, описана как поле со спином 2 в плоском пространстве-времени Минковского, и что этот факт опровергает мой ответ и вводит читателя в заблуждение, что ответ на заданный вопрос — «нет». Я хотел бы прояснить, почему оба ответа не только совместимы и эквивалентно правильны, но, кроме того, доказывают, что путаница в отношении смысла общей теории относительности вводит в заблуждение изучающих теорию из-за категорической ошибки в онтологии: пространство-время Минковского специальной теории относительности представляет собой набор и причинную структуру физических событий, измеряемых наблюдателями в приближении пренебрежимо малой связи между гравитацией и динамикой наблюдателя . С другой стороны, «Многообразие Минковского», используемое в работе Дезера и других, является нефизическим , потому что оно ненаблюдаемо; ТАКИМ ОБРАЗОМ, то, что вводит в заблуждение и сбивает с толку, — это называть «пространство-время» ингредиентом эквивалентной математической формулировки, которая операционально не коррелирует с предполагаемым физическим значением. Более того, работа Дезера снова показывает, что наблюдаемые пространственные и временные свойства событий являются корреляциями между совпадениями полей гравитационного поля со спином 2 и остальными, тем самым подкрепляя открытие Эйнштейна о том, что наблюдаемое пространство-время является чисто относительным, тогда как лежащая в основе многообразная структура является просто калибровочный артефакт, необходимый для индексации степеней свободы этих полей. Категорическая ошибка сводится к приданию онтологического веса частям формализма, не относящимся к исходным сущностям. Физическая теория состоит из 3 элементов: эмпирических фактов, математического формализма и интерпретации (последняя является оперативной связью между первыми двумя). Ньютоновское пространство-время и пространство-время Минковского формализуются соответственно как евклидово вещественное аффинное пространство и лоренцево плоское 4-многообразие; их интерпретация представляет собой оперативную связь между физическими событиями и фактами и их координатами по отношению к физическим наблюдателям (в частности, к инерциальным наблюдателям, представляющим собой меньший набор физических эталонных тел, состояние движения которых оставляет неизменной структуру евклидовых и минковских многообразий). Это ясно позволяет нам понять смысл механики в необщековариантной ситуации: наблюдатели измеряют расстояния и время, и в этих точках они измеряют локальные значения полей (таких как электромагнитное поле и распределение материи/заряда), затем уравнения движения Ньютона-Лагранжа-Гамильтона позволяют предсказывать будущие корреляции между значениями поля в согласованных точках физического пространства-времени. Отличие от общей теории относительности состоит в том, что в общей ситуации существует связь между степенями свободы любого тела отсчета (то есть любого наблюдателя) и гравитацией, поэтому нельзя пренебрегать влиянием динамики на наблюдателя, а это означает, что динамика материи и силовых полей влияет на длину, время и причинную структуру. Ньютоновское и минковское пространство-время предполагается фиксированным и нединамическим, но принцип эквивалентности приписывает метрическую и причинную структуру эффектам гравитации, тем самым делая любое физическое пространство-время подверженным динамике. Тогда можно сформулировать общековариантную теорию, в которой это понимание фиксируется либо старой псевдоримановой метрикой на «основном многообразии», либо $SO(1,3)$-связностью и тетрадой лоренцевских реперов, либо любым другим мантематически эквивалентная структура. Например, в телепараллельной гравитации общая теория относительности описывается чисто плоской «основной геометрией», но где степени свободы захвачены кручением. В формулировке Дезера гравитация описывается через поле со спином 2. НО путаница заключается в том, что мы думаем, что основная многообразная структура, необходимая для формулирования теории, соответствует/может быть интерпретирована как физическая структура! Это историческая случайность, что координаты многообразия $x^\mu$ имеют те же символы, что и в предобщековариантных теориях: «основное многообразие» $x^\mu$ не относится к возможным измерениям наблюдателя, как в ньютоновских и минковских теориях. фиксированное пространство-время, а поскольку теория (Эйнштейна или Дезера) полностью диффеоморфно инвариантна, то физические события, формирующие наблюдаемое пространство-время, являются относительными совпадениями полей, живущих друг над другом. Это ясно подчеркивает упомянутая формулировка Дорана-Галла-Ласенби в их реферате: «Таким образом из физики удаляются все свойства фонового пространства-времени, и остается набор внутренних отношений между физическими полями» .

В частности, любое расщепление гравитации а-ля $g_{\mu\nu}=\eta_{\mu\nu}+h_{\mu\nu}$, где $\eta_{\mu\nu}$ любое решение уравнений поля (пространство Минковского в обычном случае), разделяет степени свободы гравитации , если сохранить физический смысл, на $\eta_{\mu\nu}$ , потому что в этом случае описывается поле $h_ {\mu\nu}$, живущий за счет конкретного решения гравитации, следовательно, физического пространства-времени, но ограниченного метрической и причинной структурой, заданной именно этим решением; если, как в работе Дезера, кто-то хочет захватить все степени свободы в поле со спином 2, то метрическая и причинная структура лежащего в основе многообразия больше не сохраняет физического смысла. Следует понимать, что в то время как физическая теория может быть недоопределена математически, ее онтологические обязательства относительно того, что сущности реальны даже в принципе, могут быть оспорены только после уточнения теории из-за необходимости новой эмпирической адекватности. Все эквивалентные формулировки теории не должны вводить нас в заблуждение о том, что существуют разные интерпретации: интерпретация формулировки Дезера (спин-2) получается как перефразирование обычной через ее эквивалентность обычной (метрической/тетрадной) формулировке; общая теория относительности была обнаружена путем тщательного анализа предыдущих физических принципов, операционного значения наблюдаемости и математической непротиворечивости:

«Теорема» ван Кампена : Если вы наделяете математические символы большим значением, чем они имеют на практике, вы сами несете ответственность за последствия, и вы не должны винить исходную теорию, когда попадаете в отчаянное положение…

Эйнштейн Относительно просто — локальная плоскостность или локальные инерциальные системы отсчета и кривизна пространства-времени

До сих пор мы видели, как свободные частицы перемещаются в пространстве-времени, и это привело нас к понятию геодезических. Но нам предстоит более детально разобраться в том, как связаны эти два понятия.

Напомним, что геодезическое уравнение для частицы с массой имеет вид

Поскольку мы знаем, что в общей теории относительности гравитация эквивалентна искривлению пространства-времени, можем ли мы утверждать, что если все символы Кристоффеля равны нулю, то пространство-время плоское, как мы убедились в нашей статье Геодезические упражнения часть I: расчет для двумерного евклидова пространства для двумерного евклидова пространства — в каких геодезических являются прямые?

2-поверхностная гауссова кривизна

Фактически, то, что мы ищем, является обобщением для четырехмерного пространства-времени двумерной гауссовой кривизны, например, способ определения внутренней меры кривизны , в зависимости только от расстояний, измеренных на поверхности, а не от того, как он встроен в какое-либо пространство.

Если вы возьмете плоский лист бумаги и аккуратно согнете его, он согнется только в одном направлении за раз . В любой точке листа можно найти хотя бы одно направление, через которое проходит прямая на поверхности . Вы можете согнуть его в цилиндр или в конус, но вы никогда не сможете согнуть его без смятия или искажения, чтобы получить часть поверхности сферы.

В терминах Гаусса кривизна цилиндра, определяемая как произведение K ₁ K ₂ двух главных кривизн, равна нулю, потому что одна из этих главных кривизн — вдоль оси цилиндра — равна нулю .

В этой статье мы хотим найти тест, похожий на сгибание листа бумаги в двух измерениях.

В четырехмерном пространстве-времени тест будет состоять в том, чтобы попытаться преобразовать общую метрику g _μν в форму Минковского η _μν с помощью подходящего преобразования координат x ^μ -> x’ ^мк

Из нашей предыдущей статьи Обобщение метрического тензора в псевдоримановом многообразии мы знаем, что метрика g _µν имеет 10 независимых компонент (16 — 6, так как тензор симметричен.

Также относительно преобразования координат функция что связывает x’ ^α с (x ⁰ , x ¹ , x ² и x ³ ) для каждого значения 0,1,2 и 3 α.

Итак, мы имеем 90 005 4 градуса свободы заполнения 10 условий , что вообще невозможно: как и ожидалось, вообще невозможно свести метрику, описывающую искривленное пространство-время, к метрике плоского пространства-времени с помощью преобразования координат.0003

Локальная плоскостность или локальная инерциальная система отсчета (LIF)

 Похоже, мы должны быть менее амбициозными и попытаться найти систему координат со штрихом только локально, т.е. вокруг события P в пространстве-времени

• — может привести метрику g’ _μν в P к метрике плоского пространства-времени Минковского η _μν
• — и для которого все первые производные метрики g’ _µν равны нулю

Если мы возьмем аналогию с искривленной поверхностью земли, мы должны выделить множество маленьких квадратных участков, каждый из которых будет почти плоским.