Калькулятор бревен: Онлайн калькулятор расчета оцилиндрованного бревна на дом
Расчет кубатуры бревна — калькулятор онлайн объема и стоимости материала
Для расчета кубатуры бревна введите в левой части таблицы свои данные.
Строительный онлайн конструктор поможет рассчитать материалы для строительства деревянного дома или бани из оцилиндрованного бревна.
Результат расчета программы содержит данные как по отдельности для стен, фронтонов и перегородок, так и их сумму.
Калькулятор поможет рассчитать периметр сруба, количество венцов, площади и объемы стен и перегородок, количество бревен и их общую длину.
Программа посчитает общий вес сруба и ориентировочную стоимость всего дома. Не забудьте учесть цену работы по сборке и монтажу, стоимость транспортировки.
Площади наружных стен и перегородок будут полезны для расчета количества пропитки и покраски.
Общая длина бревен поможет рассчитать утеплитель между венцами.
Проемы, окна и двери не учитываются. На стоимость материалов они не влияют.
Чтобы узнать стоимость, укажите цену 1 кубического метра оцилиндрованного бревна в вашем регионе.
масштаб чертежа: 1
0.51234
Укажите габариты стен (в метрах):
A — Длина стены по фасаду.
B — Длина боковой стены.
Эти размеры можно указывать по внешним габаритам сруба или по осям стен. Вариант 1 или 2.
H — Высота фасада до конька фронтона. Если сруб без фронтона, то установите значение = 0.
G — Высота боковой стены до конька фронтона. Если сруб без бокового фронтона, то установите значение = 0.
U — Высота стены по углу.
Если высоты стен будут не кратны шагу венца, то программа изменит эти высоты. В этом случае около результата появится сообщение (увеличена)
T — Длина лапы.
Длина стены фасада A: м.
Длина боковой стены B: м.
Размеры по: осямгабаритам
Высота фасада H: м.
Высота боковой стены G: м.
Высота стены сруба U: м.
Длина лапы T: см.
Укажите размеры перегородок (в метрах):
Укажите общую длину для всех перегородок первого этажа L1 и второго этажа L2.
Укажите высоту перегородок первого этажа P1 и второго этажа P2.
Если высоты перегородок будут не кратны шагу венца, то программа изменит эти высоты. В этом случае около результата появится сообщение (увеличена)
Если расчет перегородок сруба не требуется, то установите значения = 0
Длина перегородок 1-го этажа L1: м.
Высота перегородок 1-го этажа P1: м.
Длина перегородок 2-го этажа L2: м.
Высота перегородок 2-го этажа P2: м.
Укажите размеры бревна (в сантиметрах):
D — Диаметр бревна.
C — Полезная высота бревна, шаг одного венца. Размер должен быть обязательно меньше диаметра бревна.
Диаметр бревна D: см.
Высота C: см.
Размеры указываются в метрах.
Укажите дополнительные данные:
N — Расстояние между нагелями.
Количество нагелей (деревянных гвоздей) расчитывается приблизительно.
V — Вес одного кубического метра оцилиндрованного бревна.
S — Ориентировочная стоимость одного кубического метра оцилиндрованного бревна.
Чтобы узнать стоимость, укажите цену 1 кубического метра бревна в вашем регионе.
Расстояние между нагелями N: м.
Вес 1 кубического метра V:
кг.
Стоимость 1 кубического метра. S:
Фасад | Боковая стена |
Размеры в плане | Размеры бревна (масштаб 1:0.25) |
Основной сруб:
Высота стены: 3.2 м.
Количество венцов: 16
Длина бревна фасада: 6.5 м.
Длина бревна боковой стены: 5.5 м.
Периметр: 24 м.
Общая длина бревен: 384 м.
Площадь стен (внутренних и внешних): 70.4 м2. x 2 = 140.8 м2.
Объем: 17.372 м3.
Вес: 9.381 т.
Стоимость: 8685.88
Фронтоны:
Высота: 4 м. (увеличена)
Количество венцов: 20
Площадь стен (внутренних и внешних): 24 м2.
Общая длина бревен: 130 м.
Объем: 5.881 м3.
Вес: 3.176 т.
Стоимость: 2940.53
Боковые фронтоны:
Высота: 2.8 м.
Количество венцов: 14
Площадь стен (внутренних и внешних): 14 м2. x 2 = 28 м2.
Общая длина бревен: 77 м.
Объем: 3.483 м3.
Вес: 1.881 т.
Стоимость: 1741.7
Объем стен основного сруба и фронтонов: 26.736 м3.
Площадь стен основного сруба и фронтонов: 216.8 м2.
Общая длина бревен основного сруба и фронтонов: 591 м.
Перегородки 1-го этажа:
Длина: 8.5 м.
Высота: 2.8000000000000003 м. (увеличена)
Количество венцов: 14
Общая длина бревен: 119 м.
Площадь стен (с двух сторон): 23.8 м2. x 2 = 47.6 м2.
Объем: 5.383 м3.
Вес: 2.907 т.
Стоимость: 2691.72
Перегородки 2-го этажа:
Длина: 6 м.
Высота: 2.6 м. (увеличена)
Количество венцов: 13
Общая длина бревен: 78 м.
Площадь стен (с двух сторон): 15.6 м2. x 2 = 31.2 м2.
Объем: 3.529 м3.
Вес: 1.905 т.
Стоимость: 1764.32
Общий объем перегородок: 8.912 м.
Общая площадь перегородок: 78.8 м.
Общая длина брёвен перегородок: 197 м.
Вся конструкция:
Объем: 35.648 м3.
Площадь: 295.6 м2.
Длина брёвен: 788 м.
Кол-во нагелей: 525
Вес: 19.2501 т.
Стоимость: 17824.14
Калькулятор: расчет количества материалов для сруба из бруса и бревен
РЕЗУЛЬТАТЫ ПОДСЧЕТОВ ПО ЗАДАННЫМ РАЗМЕРАМ
«; document.getElementById(‘raschet’).innerHTML += «Объем для строительства сруба со всеми стенами составляет: «+all_info.toFixed(2)+» куб. м.
«;
document.getElementById(‘raschet’).innerHTML += «Для строительства сруба со всеми стенами требуется «+obj_dlina.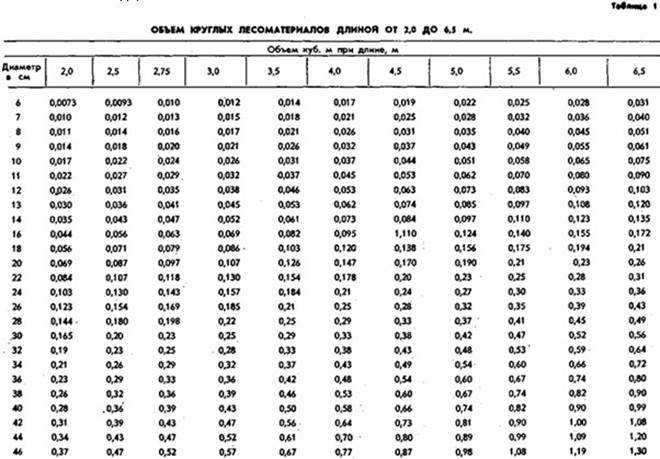
«; //******************************************************************* }
Как рассчитать, сколько потребуется бруса или бревен для строительства сруба? Очень просто — введите требуемые параметры: длину, ширину, высоту сруба, а также данные о внутренних стенах и после заполнения всех нужных полей нажмите кнопку «Рассчитать» в конце калькулятора.
Вниманние! Калькулятор ТОЛЬКО ПРИМЕРНО подсчитывает объем материалов, необходимых для строительства дома. Не учитывается количество окон, дверей и т.п.
| —Сруб дома по вашим размерам— | ||
| Длина, м | 3 м. 3.5 м. 4 м. 4.5 м. 5 м. 5.5 м. 6 м. 6.5 м. 7 м. 7.5 м. 8 м. 8.5 м. 9 м. 9.5 м. 10 м. 10. 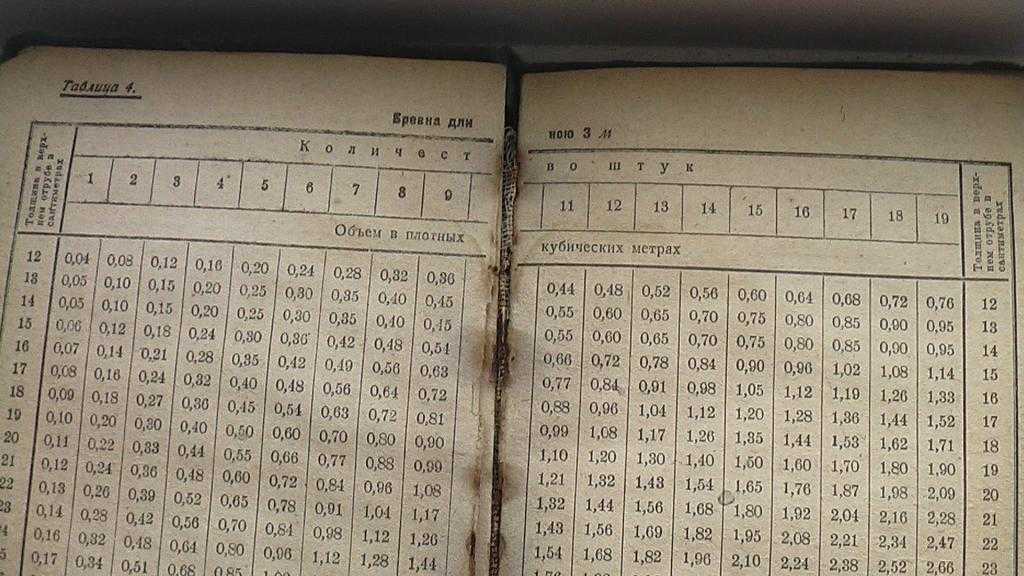 5 м. 5 м.11 м. 11.5 м. 12 м. 12.5 м. 13 м. 13.5 м. 14 м. 14.5 м. 15 м. 15.5 м. 16 м. 16.5 м. 17 м. 17.5 м. | |
| Ширина, м | 3 м. 3.5 м. 4 м. 4.5 м. 5 м. 5.5 м. 6.5 м. 7 м. 7.5 м. 8 м. 8.5 м. 9 м. 9.5 м. 10 м. 10.5 м. 11 м. 11.5 м. 12 м. 12.5 м. 13 м. 13.5 м. 14 м. 14.5 м. 15 м. 15.5 м. 16 м. 16.5 м. 17 м. 17.5 м. | |
| Высота, м | 1.5 м. 1.6 м. 1.7 м. 1.8 м. 1.9 м. 2 м. 2.1 м. 2.2 м. 2.3 м. 2.4 м. 2.5 м. 2.6 м. 2.7 м. 2.8 м. 2.9 м. 3 м. 3.1 м. 3.2 м. 3.3 м. 3.4 м. | |
| ——Наличие межкомнатных стен и их размеры—— | ||
| Длина 1-ой стены, м | нет стены 3 м. 3.5 м. 4 м. 4.5 м. 5 м. 5.  6 м. 6.5 м. 7 м. 7.5 м. 8 м. 8.5 м. 9 м. 9.5 м. 10 м. 10.5 м. 11 м. 11.5 м. 12 м. 12.5 м. 13 м. 13.5 м. 14 м. 14.5 м. 15 м. 15.5 м. 16 м. 16.5 м. 17 м. 17.5 м. | |
| Длина 2-ой стены, м | нет стены 3 м. 3.5 м. 4 м. 4.5 м. 5 м. 5.5 м. 6 м. 6.5 м. 7 м. 7.5 м. 8 м. 8.5 м. 9 м. 9.5 м. 10 м. 10.5 м. 11 м. 11.5 м. 12 м. 12.5 м. 13 м. 13.5 м. 14 м. 14.5 м. 15 м. 15.5 м. 16 м. 16.5 м. 17.5 м. | |
| Длина 3-ей стены, м | нет стены 3 м. 3.5 м. 4 м. 4.5 м. 5 м. 5.5 м. 6 м. 6.5 м. 7 м. 7.5 м. 8 м. 8.5 м. 9 м. 9.5 м. 10 м. 10.5 м. 11 м. 11.5 м. 12 м. 12.5 м. 13 м. 13.5 м. 14 м. 14.5 м. 15 м. 15.5 м. 16 м.  16.5 м. 17 м. 17.5 м. | |
| Длина 4-ой стены, м | нет стены 3 м. 3.5 м. 4 м. 4.5 м. 5 м. 5.5 м. 6 м. 6.5 м. 7 м. 7.5 м. 8 м. 8.5 м. 9 м. 9.5 м. 10 м. 10.5 м. 11 м. 11.5 м. 12 м. 12.5 м. 13 м. 13.5 м. 14 м. 14.5 м. 15 м. 15.5 м. 16 м. 16.5 м. 17 м. 17.5 м. | |
| ——Используемое бревно/брус при строительстве—— | ||
| Бревно/брус,мм | 160 мм. 180 мм. 200 мм. 220 мм. 240 мм. 260 мм. | |
Заказать строительство дома под ключ или отдельный этап работ можно по тел. (8-909) 155-88-38 или через почтовую форму
См. также:
- Все строительные калькуляторы
- Онлайн-проектирование сруба
- Посчитать количество блоков на дом
- Строительство дома под ключ
- Рассчитать количество сайдинга на дом

Roman Chernyshov
Калькулятор логарифмов log(x)
Калькулятор логарифмов находит результат логарифмической функции (может называться показателем степени) по заданному основанию и действительному числу.
Калькулятор журнала журналлогарифм б (х) = у
b: логарифмический базовый номер, b>0 и b≠1/ x: действительное число, x>0
log b (x) = y и x = log b (b x )
log б (х) = у и х = б у
Логарифм считается одним из основных понятий в математике. Существует множество определений, начиная от очень сложных и заканчивая довольно простыми. Чтобы ответить на вопрос, что такое логарифм, давайте взглянем на таблицу ниже:
| 2 1 | 2 2 | 2 3 | 2 4 | 2 5 | 2 6 |
| 2 | 4 | 8 | 16 | 32 | 64 |
Это таблица, в которой мы можем видеть два, итак, в квадрате два и в кубе. Это операция в математике, известная как возведение в степень .
Если мы посмотрим на числа в нижней строке, то можем попытаться найти значение степени, в которое нужно возвести 2, чтобы получить это число.
Например, чтобы получить 16, надо два возвести в четвертую степень.
А чтобы получить 64, нужно возвести два в шестую степень.
Это операция в математике, известная как возведение в степень .
Если мы посмотрим на числа в нижней строке, то можем попытаться найти значение степени, в которое нужно возвести 2, чтобы получить это число.
Например, чтобы получить 16, надо два возвести в четвертую степень.
А чтобы получить 64, нужно возвести два в шестую степень.
Следовательно, логарифм — это показатель степени, в которую необходимо возвести фиксированное число (которое называется основанием), чтобы получить число у. Другими словами, логарифм можно представить следующим образом:
журнал б х = у
, где b — основание, x — действительное число, а y — показатель степени.
Например, 2 3 = 8 ⇒ log 2 8 = 3 (логарифм 8 по основанию 2 равен 3, потому что 2 3 = 8).
Аналогично, log 2 64 = 6, потому что 2 6 = 64.
Таким образом, очевидно, что логарифмирование является обратной операцией возведения в степень .
| 2 1 | 2 2 | 2 3 | 2 4 | 2 5 | 2 6 |
| 2 | 4 | 8 | 16 | 32 | 64 |
| журнал 2 2 = 1 | журнал 2 4 = 2 | журнал 2 8 = 3 | журнал 2 16 = 4 | журнал 2 32 = 5 | журнал 2 64 = 6 |
К сожалению, не все логарифмы можно вычислить так просто. Например, найти журнал 2 5 вряд ли возможно, просто используя наши простые вычислительные способности. После использования калькулятора логарифмов мы можем узнать, что
журнал 2 5 = 2,32192809
Существует несколько конкретных типов логарифмов.
Например, логарифм по основанию 2 известен как двоичный логарифм,
и он широко используется в информатике и языках программирования. Логарифм по основанию 10 обычно называют десятичным логарифмом, т.
и имеет огромное количество применений в технике, научных исследованиях, технике и т.д.
Наконец, так называемый натуральный логарифм использует в качестве основания число e (приблизительно равное 2,71828).
и этот вид логарифма имеет большое значение в математике, физике,
и другие точные науки.
Логарифм по основанию 10 обычно называют десятичным логарифмом, т.
и имеет огромное количество применений в технике, научных исследованиях, технике и т.д.
Наконец, так называемый натуральный логарифм использует в качестве основания число e (приблизительно равное 2,71828).
и этот вид логарифма имеет большое значение в математике, физике,
и другие точные науки.
Логарифм log b (x) = y читается как log основание b числа x равно y .
Обратите внимание, что основание номера журнала b должно быть больше 0 и не должно быть равно 1.
И число (x), которое мы вычисляем log по основанию (b), должно быть положительным действительным числом.
Например, журнал 2 из 8 равен 3.
log 2 (8) = 3 (логарифмическая база 2 из 8) Экспонента 2 3 = 8
Общие значения для базы журналов
| BOG BASE | Имя журнала | Обозначение | Пример log |
|---|---|---|---|
| 2 | BINAR LOGARITHM | FB (X) | 611111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111Р1н (X). 4 = 16 4 = 16 |
| 10 | Общий логарифм | LG (x) | Log 10 (1000) = LG (1000) = 3 => 3 = 1000 |
| натуральный логарифм | ln(x) | log e (8) = ln(8) = 2,0794 => e 2,0794 = 8 |
Логарифмические тождества
Список логарифмических тождеств, формул и примеров логарифмов в логарифмической форме.
Логарифм произведения
log b (x·y) = log b (x) + log b (y) log 2 (5·7) = log 2 (5) + log 2 (7)
Логарифм частного
log b (x/y) = log b (x) - log b (y) журнал 2 (5/7) = журнал 2 (5) - журнал 2 (7)
Логарифм степени
log b (x y ) = y·log b (x) log 2 (5 7 ) = 7 · log 2 (5)
Изменение базы
log b (x) = (log k (x)) / (log 1 k (б))
Натуральный логарифм Примеры
- ln(2) = log e (2) = 0,6931
- ln(3) = log e (3) = 1,0986
- ln(4) = log e (4) = 1,3862
- ln(5) = log e (5) = 1,609
- ln(6) = log e (6) = 1,7917
- ln(10) = log e (10) = 2,3025
Таблицы логарифмических значений
Список таблиц значений логарифмических функций в общих базовых числах.
| лог 2 (х) | Обозначение | Value | |
|---|---|---|---|
| log 2 (1) | lb(1) | 0 | |
| log 2 (2) | lb(2) | 1 | |
| log 2 (3) | lb(3) | 1.584963 | |
| log 2 (4) | lb(4) | 2 | |
| log 2 (5) | lb(5) | 2.321928 | |
| бревно 2 (6) | lb(6) | 2.584963 | |
| log 2 (7) | lb(7) | 2.807355 | |
| log 2 (8) | lb(8) | 3 | |
| log 2 (9) | lb(9) | 3.169925 | |
| log 2 (10) | lb(10) | 3.321928 | |
| log 2 (11) | фунтов(11) | 3,459432 | |
| log 2 (12) | lb(12) | 3. 584963 584963 | |
| log 2 (13) | lb(13) | 3.70044 | |
| log 2 (14) | lb(14) | 3.807355 | |
| log 2 (15) | lb(15) | 3. | 1 |
| log 2 (16) | lb(16) | 4 | |
| бревно 2 (17) | фунтов(17) | 4.087463 | |
| log 2 (18) | lb(18) | 4.169925 | |
| log 2 (19) | lb(19) | 4.247928 | |
| log 2 (20) | lb(20) | 4.321928 | |
| log 2 (21) | lb(21) | 4.392317 | |
| log 2 (22) | lb(22) | 4.459432 | |
| log 2 (23) | lb(23) | 4.523562 | |
| log 2 (24) | lb(24) | 4. 584963 584963 |
| log 10 ( x) | Notation | Value |
|---|---|---|
| log 10 (1) | log(1) | 0 |
| log 10 (2) | log(2) | 0.30103 |
| бревно 10 (3) | log(3) | 0.477121 |
| log 10 (4) | log(4) | 0.60206 |
| log 10 (5) | log(5) | 0.69897 |
| log 10 (6) | log(6) | 0.778151 |
| log 10 (7) | log(7) | 0.845098 |
| log 10 (8) | журнал(8) | 0, |
| log 10 (9) | log(9) | 0.954243 |
| log 10 (10) | log(10) | 1 |
| log 10 (11) | log(11) | 1. 041393 041393 |
| log 10 (12) | log(12) | 1.079181 |
| log 10 (13) | log(13) | 1.113943 |
| бревно 10 (14) | log(14) | 1.146128 |
| log 10 (15) | log(15) | 1.176091 |
| log 10 (16) | log(16) | 1.20412 |
| log 10 (17) | log(17) | 1.230449 |
| log 10 (18) | log(18) | 1.255273 |
| log 10 (19) | бревно(19) | 1,278754 |
| log 10 (20) | log(20) | 1.30103 |
| log 10 (21) | log(21) | 1.322219 |
| log 10 (22 ) | log(22) | 1.342423 |
| log 10 (23) | log(23) | 1. 361728 361728 |
| log 10 (24) | log(24) | 1.380211 |
| log e (x) | Notation | Value |
|---|---|---|
| log e (1) | ln(1) | 0 |
| log e (2) | ln (2) | 0.693147 |
| log e (3) | ln(3) | 1.098612 |
| log e (4) | ln(4) | 1.386294 |
| журнал e (5) | In(5) | 1,609438 |
| Log E (6) | LN (6) | 1,791759 |
| E (7) | ||
| E (7) | ||
| E (7) | ||
| ln(8) | 2.079442 | |
| log e (9) | ln(9) | 2.197225 |
| log e (10) | ln(10) | 2. 302585 302585 |
| журнал e (11) | ln(11) | 2.397895 |
| log e (12) | ln(12) | 2.484907 |
| log e (13) | ln( 13) | 2.564949 |
| log e (14) | ln(14) | 2.639057 |
| log e (15) | ln(15) | 2.70805 |
| log и (16) | лн(16) | 2.772589 |
| log e (17) | ln(17) | 2.833213 |
| log e (18) | ln(18) | 2.8 |
| log e (19) | ln(19) | 2.944439 |
| log e (20) | ln(20) | 2.995732 |
| log e (21) | ln(21) | 3.044522 |
| журнал e (22) | ln(22) | 3. 0 0 |
| log e (23) | ln(23) | 3.135494 |
| log e (24) | ln( 24) | 3.178054 |
Связанные калькуляторы базы журналов
- Калькулятор натурального логарифма ln(x)
- Калькулятор Common Log base 10
- Калькулятор основания логарифма 2
Калькулятор изменения базовой формулы
Скажите, что конец семестра все ближе и ближе, и это может означать только одно — тест по математике , который обобщает все, что вы узнали за последние несколько месяцев.
Будучи хорошим учеником, вы решили начать учиться рано и систематически . Первая рассматриваемая тема касается логарифмов . Излишне говорить, что это не самая простая вещь в математике. Но и они не кажутся слишком уж плохими. Тем не менее, если это будет на тесте, кажется хорошей идеей уделить несколько минут этому предмету, особенно изменение базового правила . Вы выбираете два примера, чтобы попрактиковаться в запоминании: замените log 27 (9) на основание
Вы выбираете два примера, чтобы попрактиковаться в запоминании: замените log 27 (9) на основание 3 и замените log 5 (1000) на основание 10 .
Во-первых, давайте посмотрим, как легко решается задача, когда у нас под рукой есть калькулятор изменения базовой формулы . Там у нас есть три переменных поля: x , a и b . По приведенной выше формуле определяем, что x обозначает число внутри нашего логарифма , a — его основание , а b — это новое основание , которое мы хотели бы получить.
Следовательно, для первого случая, т. е. когда мы хотим заменить log 27 (9) на основание 3 , мы должны ввести в калькулятор:
x = 9 , a = 27 , б = 3 .
Аналогично, когда мы меняем log 5 (1000) в основание 10 , тогда имеем:
x = 1000 , a = 5 , b = 10 .
Обратите внимание, что когда мы вводим первые два значения, калькулятор изменения основной формулы уже дает нам значение нашего логарифма. Как только мы вводим третье, оно дополнительно дает пошаговое применение изменения базового правила . Вот так просто мы получили ответ!
Давайте теперь посмотрим как изменить базу лога самостоятельно, используя все, что мы узнали в этой статье . Начнем с преобразования log 27 (9) в выражение с основанием 3 .
В соответствии с логарифмическим изменением основания из приведенного выше раздела, мы должны переписать нашу функцию как дробь двух других, обе с основанием 3 вместо 27 , которое у нас есть. Номинатор — это логарифм аргумента (большое число, то, что в скобках). А знаменатель равен исходному основанию . Итак:
Номинатор — это логарифм аргумента (большое число, то, что в скобках). А знаменатель равен исходному основанию . Итак:
лог. 27 (9) = лог. 3 (9) / лог. 3 (27) .
Теперь заметим, что 3² = 9 и 3³ = 27 , поэтому:
log 27 (9) = log 3 /7 = 90 3 (21 3 3
.
Ну, это было не так уж и плохо, не так ли? Воодушевленный, давайте рассмотрим второй пример: изменение log 5 (1000) на основание 10 . Снова воспользуемся формулой и получим:
лог 5 (1000) = лог 10 (1000) / лог 10 (5) .
Немного поразмыслив, мы видим, что 10³ = 1000 , поэтому
log 5 (1000) = log 10 (1000) / log 3 (110 5)900 10 (5) .
