Как высчитать объем в кубах: Как посчитать объем
объем куба — Формула и как найти
, написанный
Малкольм МакКинси
Проверка по фактам
Пол Маззола
Объем куба
. cube – это объем пространства, который занимает куб в трех измерениях. Объем куба всегда измеряется в кубических единицах, полученных из линейной единицы, заданной или используемой для измерения длины стороны.
Вы можете найти объем любого куба с одним заданным измерением, используя объем куба формула :
Что такое куб?
Куб представляет собой трехмерное тело с шестью конгруэнтными квадратными гранями, сходящимися под прямым углом, восемью вершинами и двенадцатью сторонами одинаковой длины. Куб является одним из пяти Платоновых тел и также называется шестигранником.
Каковы размеры куба?
Куб — это трехмерный объект, поэтому куб имеет три измерения:
Длина — обычно понимается как большее из «плоских» измерений.
Ширина – обычно понимается как более короткий из «плоских» размеров.
Высота или глубина — измерение, которое привносит форму в наш трехмерный мир
Обратите внимание, что у нас есть два способа описать третье измерение:
Высота — используйте этот термин, когда объект возвышается перед вами, как высокое здание.
Глубина — Используйте этот термин, если объект падает под вами, как дыра в земле.
Нам нужна информация хотя бы об одном из этих трех измерений, чтобы измерить объем куба.
Формула объема куба
Формула объема это объем, равный длине, умноженной на ширину, на высоту.
Формула объемаЭто уравнение объема не работает для каждого твердого тела, но оно работает для кубов, прямоугольных призм и параллелепипедов.
Поскольку все три значения ( l , w и 9{3} м3 (метры в кубе).
Как найти объем куба
Чтобы найти объем куба, достаточно знать длину любого ребра.
Если вам известна длина одной стороны, вы можете найти объем куба, подставив его в одну из формул объема куба:
Измерение пространства, занимаемого кубом, зависит от знания длины любого одно ребро, потому что все длины сторон куба равны по длине.
Как найти длину, ширину и высоту из тома
Что, если вам дан объем куба и вас попросят найти его размеры?
Если вам дан объем куба и вас попросят найти длину ребра, все, что вам нужно сделать, это извлечь кубический корень из объема:
Ваш ответ больше не будет в кубических единицах; это будет в линейных единицах.
Как найти длину, ширину и высоту по формуле объемаЧто если у нас есть куб, и нам говорят, что его объем равен 729 кубических метров . Чтобы найти длину ребра куба:
Как рассчитать объем, используя площадь
Вот еще одна задача. Что если вам скажут площадь одной грани куба? Можете ли вы использовать эту информацию, чтобы найти объем?
Да, площадь одного лица равна произведению длины лица на ширину.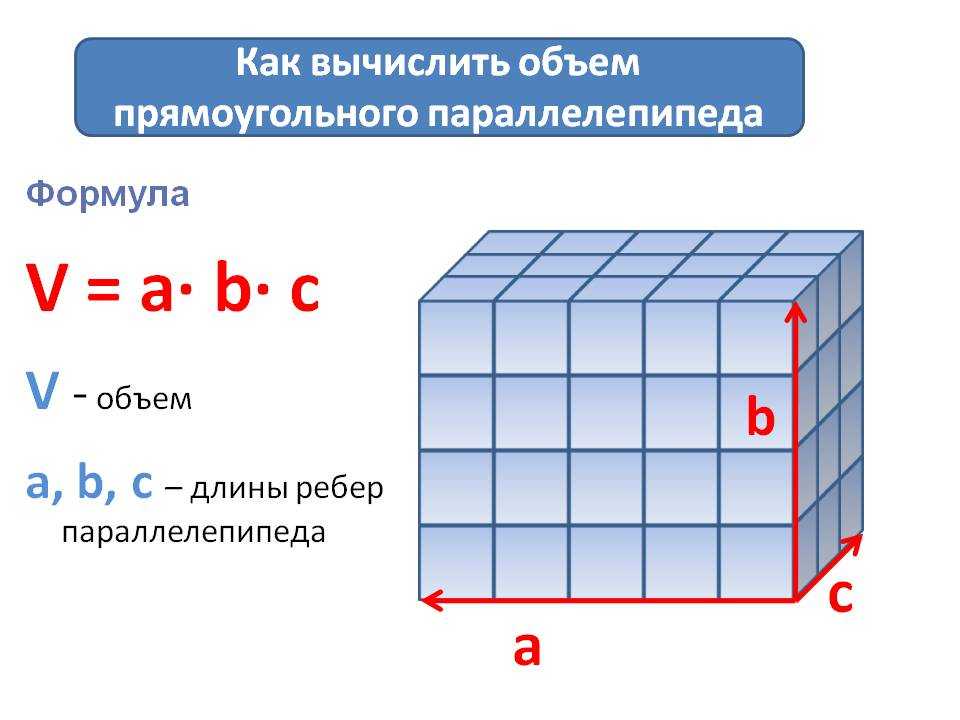
Как только вы найдете ширину или длину, вы можете применить формулу объема:
Найдите квадратный корень из заданного измерения площади; это даст вам длину любой стороны, с 9{3}V=s3, чтобы найти площадь.
Как вычислить площадь поверхности куба, используя объем
Если вам известен объем куба, вы можете преобразовать его в длину одной стороны. Затем вы можете использовать длину стороны для расчета общей площади поверхности.
Используйте длину ребра, чтобы вычислить площадь поверхности одной стороны, затем умножьте эту площадь на 6 . Это дает вам общую площадь поверхности куба с использованием объема.
Что если вам сообщат общую площадь поверхности всего куба? Сможете ли вы найти объем?
Да, общая площадь поверхности включает площади всех шести конгруэнтных граней. Найдите площадь одной грани, а затем выполните шаги, описанные выше, чтобы найти объем:
Разделите заданную общую площадь поверхности на шесть, чтобы получить площадь одной грани
Найдите квадратный корень из площади одной грани, чтобы получить длину любой стороны, 9{3}V=s3
Примеры объема куба
Если у вас есть трехмерное тело с шестью гранями, а стороны помечены 4′ , 6′ и 8′ .
Это куб? Нет, это прямоугольная призма, потому что метки, опережающие рисунок, показывают разную длину!
Что, если бы стороны нашего тела были 4′ , 4′ и 4′ ; Является ли этим кубом? Да, это куб, потому что на этикетках указано, что ширина, длина и высота одинаковы. 9{3}V=64 фута3?
Давайте посмотрим на другой пример куба с длиной стороны 12 ярдов . Каков его объем?
Как насчет куба с одной гранью площадью 25 см . Каков объем куба?
Во-первых, какова длина любого ребра или стороны куба?
Подумайте: чему равен квадратный корень из 25 ? Ответ 5 , поэтому:
Теперь, когда у вас есть длина стороны, вы можете вычислить объем:
Теперь попробуем найти объем, зная площадь поверхности. Общая площадь поверхности куба составляет 7776 квадратных дюймов . Каков объем куба? Помните, что общая площадь поверхности — это площадь всех шести квадратных граней. Разделите общую площадь поверхности на 6 , извлеките из нее квадратный корень, затем используйте формулу объема:
Теперь мы можем вычислить объем куба:
Что такое объем куба? Значение, формула, вывод, примеры
Что такое объем куба?
Куб — это трехмерное твердое тело с шестью квадратными гранями одинаковой длины.
Вся площадь, занимаемая кубом, называется его объемом. Если у нас есть куб, и мы наполняем его водой, то количество воды, которое помещается внутри куба, называется его объемом.
Связанные игры
Примеры объема куба из повседневной жизни
- Если мы заполним картонную коробку шариками конфетти, количество шариков конфетти, которые поместятся в картонную коробку, покажет ее объем.
- Если мы наполним кубический аквариум водой, количество воды, залитой внутрь, будет его объемом.
Связанные рабочие листы
Каков объем куба?
Точно так же, как площадь — это количество пространства, занимаемое двухмерным объектом, объем определяется как пространство, занимаемое трехмерным объектом.
Рассмотрим квадратный лист бумаги со стороной s. Его площадь будет s²; теперь, если мы сложим их друг над другом до высоты s, то объем куба можно будет найти, умножив площадь основания (s²) на высоту (s).
Таким образом, объем куба = s² ✕ s = s³
Объем куба также можно найти по количеству кубических единиц, необходимых для полного заполнения куба.
У единичного куба все стороны имеют длину 1 единицу.
Итак, объем единичного куба = 1 единица ✕ 1 единица ✕ 1 единица = 1 кубическая единица.
Теперь найдем объем куба со стороной = 4 единицы.
Объем куба будет равен количеству единичных кубов, составляющих куб.
В каждом ряду по 16 кубиков.
Куб со стороной 4 единицы состоит из 64 единичных кубов. Следовательно, его объем составляет 64 кубических единицы.
Объем куба ФормулаЧтобы найти объем куба, нам нужно знать длину любого ребра куба. Длину нужно умножить на себя трижды, чтобы получить объем.
Объем измеряется в кубических единицах. Например, кубические метры (м 3 ), кубические сантиметры (см 3 ) и т. д.
Например, если известно, что длина ребра равна 6 см, то объем куба будет 6 × 6 × 6 = 216, а единицей измерения будет см 3 ; здесь объем куба равен 216 см 3 .
Где мы используем объем куба в повседневной жизни?
Мы можем видеть много примеров объема куба в повседневной жизни.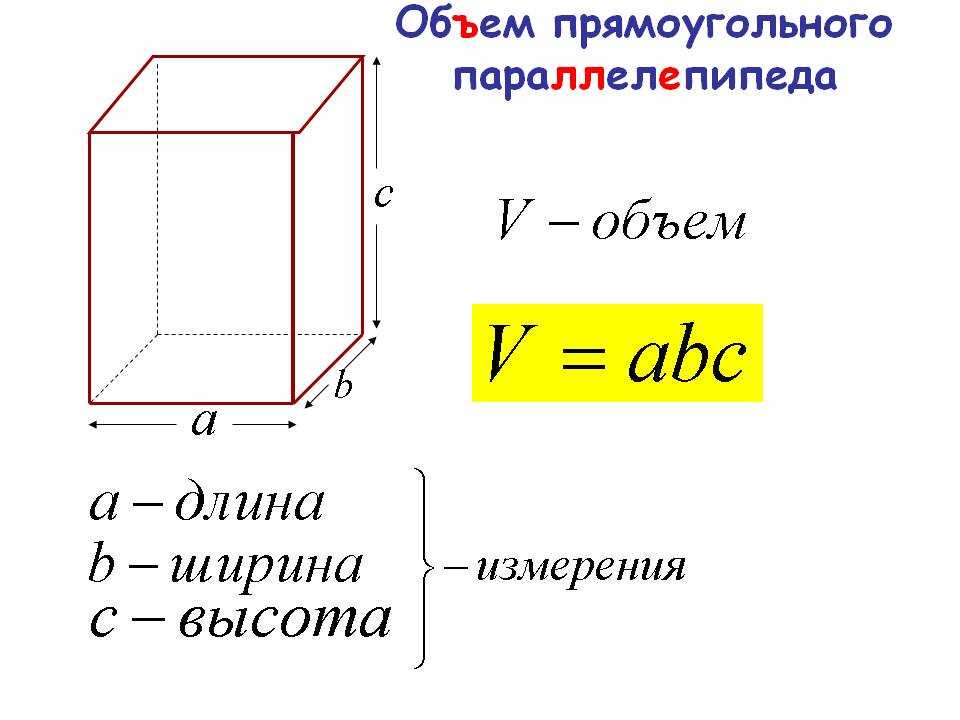
- Резервуар для воды в форме куба может хранить воду, равную объему куба.
- Объем воздуха, занимаемый кубической комнатой.
- Объем древесины, необходимый для постройки прочного кубического блока.
- Объем конфет в форме кубиков необходимо измерить перед тем, как упаковать их в коробки для сладостей, чтобы точно знать, сколько места они займут.
Заключение
Объем куба является мерой пространства, занимаемого воздухом внутри него. Используется во многих сферах повседневной жизни. Комната здания или дома может иметь форму куба. Пространство внутри него, где мы живем и работаем, является его объемом. Если вас интересуют более простые и краткие ресурсы по кубам или другим математическим темам, например, что такое куб?, что такое единичный куб? и т. д., вы можете загрузить приложение Splashlearn.
Чтобы получить дополнительные материалы по математике для учителей, бесплатно зарегистрируйтесь на Splashlearn.
com.
Решенные примеры
- Каков объем куба, если его ребро равно 2 см?
Решение:
Учитывая, что S = 2 см
Том A Cube = S × S × S
SO, SO, DADES 2 ×
SO, SO DADES 2 ×
, SO DADES 2 ×
. 2 = 8 см 3
Таким образом, общий объем куба с ребром 2 см равен 8 см 3 .
- Объем куб.контейнера 343 м 3 . Найдите длину стороны контейнера.
Решение:
Том куба = S × S × S
343 = S × S. S S S S S S S S S S S S S S . 343}$ = s
$\sqrt[3]{7 × 7 × 7}$ = s
Итак, длина стороны контейнера равна 7 м.
- Найдите объем кубика сахара со стороной 5 см.
Решение:
Учитывая, что с = 5 см
Объем куба = с × с × с
х 5 объем данного куба, см 3 . Таким образом, общий объем куба с ребром 5 см равен 125 см 3 .Практические задачи
1
Каков объем куба, длина ребра которого равна 10 см? 9{3}}{9}$
Связан ли объем куба с объемом конуса?
Нет, объем конуса не связан с объемом куба. Вместо этого он связан с объемом прямоугольного параллелепипеда. Объем кубоида = длина × ширина × высота . В кубе длина = ширина = высота
Можем ли мы найти объем квадрата?
Нет. Квадрат — это двумерная фигура. У него нет объема. И наоборот, куб представляет собой трехмерную форму и имеет объем.