Как высчитать объем: Калькулятор расчета объема резервуара и перевод литров в кубы в ООО ЗРК

Калькулятор расчета объема резервуара и перевод литров в кубы в ООО ЗРК

Перевод литров в кубы

Выберете среду: ВодаБензинМолокоДиз. топливоМаслоНефтьСпирт

Введите объем в литрах:

Единица измерения объема – это кубический метр. Данный факт относится к числу общепринятых аксиом. Сторона этого куба равна одному метру. Этот показатель принято использовать, если необходимо определить объем бака, резервуара, либо цистерны. Определенные трудности вызывает расчет в связи с тем, что жидкости принято мерить в литрах. Пытаясь рассчитать величину актуального для хранения и сохранения жидкой субстанции резервуара либо цистерны, нужно учесть еще и вес вещества. Он не соответствует количеству литров.

Расчет объема резервуара

Выберите форму: ПрямоугольнаяЦилиндрическая

Длина в метрах:

Ширина в метрах:

Высота в метрах:

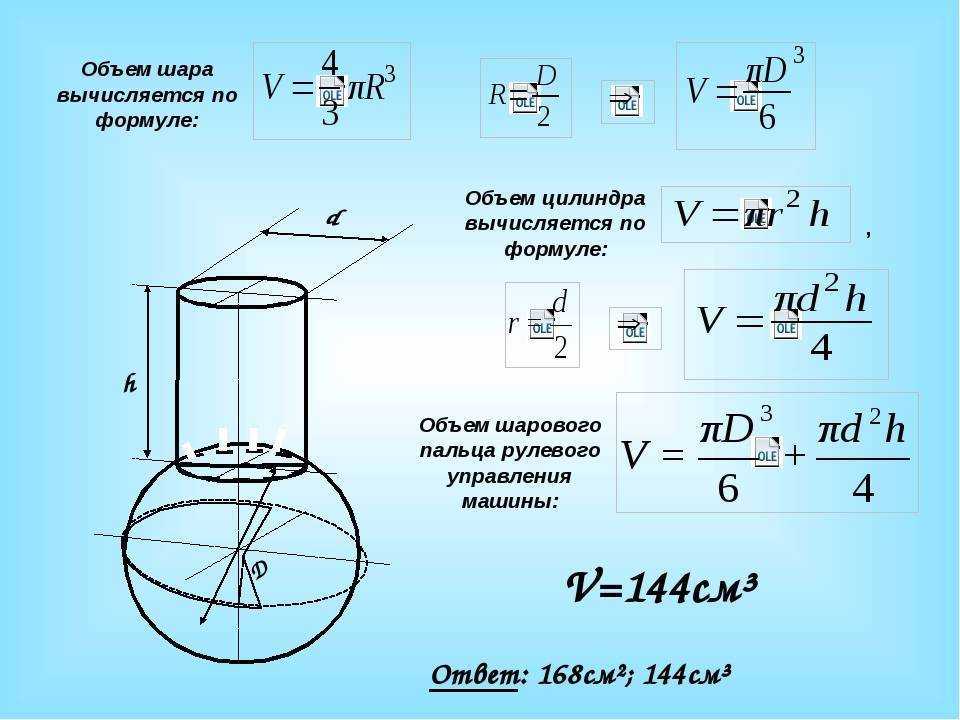
Всем, кто прилежно изучал школьный курс физики, известно, что минимальной площадью поверхности при максимальном объеме обладает сосуд в форме шара. Но шарообразные емкости сложны в изготовлении и непрактичны, поэтому производители изготавливают емкости в форме цилиндра или куба (прямоугольника).

ЦИЛИНДРИЧЕСКИЕ ЕМКОСТИ

Могут располагаться горизонтально или вертикально. Объем рассчитывается по формуле V=πr2h. То есть умножаем число π (3,14159) на радиус в квадрате и на высоту h цилиндра.

Пример: есть вертикальный цилиндрический резервуар диаметром 3 метра и высотой 5 метров. Рассчитываем объем: Радиус – 1,5 метра, в квадрате будет 2,25. Умножаем: 3,14159 ×2.25 ×5 (высота) = 35,34 м3. Итого, рабочий объем нашего резервуара будет равен 35 кубическим метрам, или 35 000 литрам (в 1 кубе – 1000 литров).

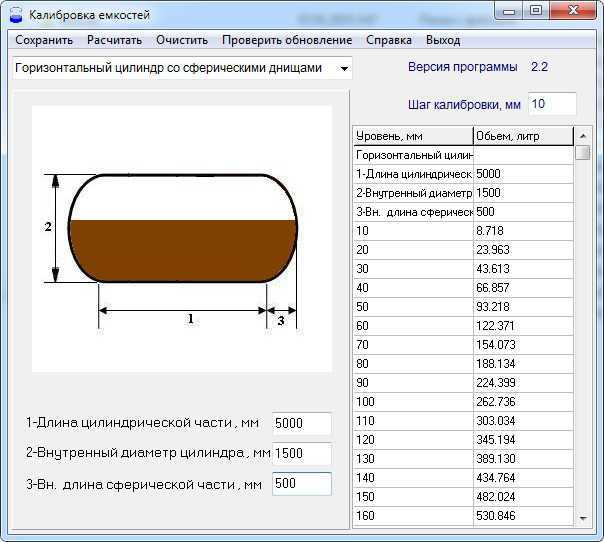
На практике конкретные размеры резервуара рассчитываются с учетом его функциональности. Например, горизонтальный резервуар диаметром 1 метр и длиной 10 метров будет просто неудобен в использовании. Его объем составит 7,8 куба. Если нам нужен резервуар такого объема, уместнее увеличить его диаметр и уменьшить длину – например, сделать диаметр 2 метра при длине 3 метра.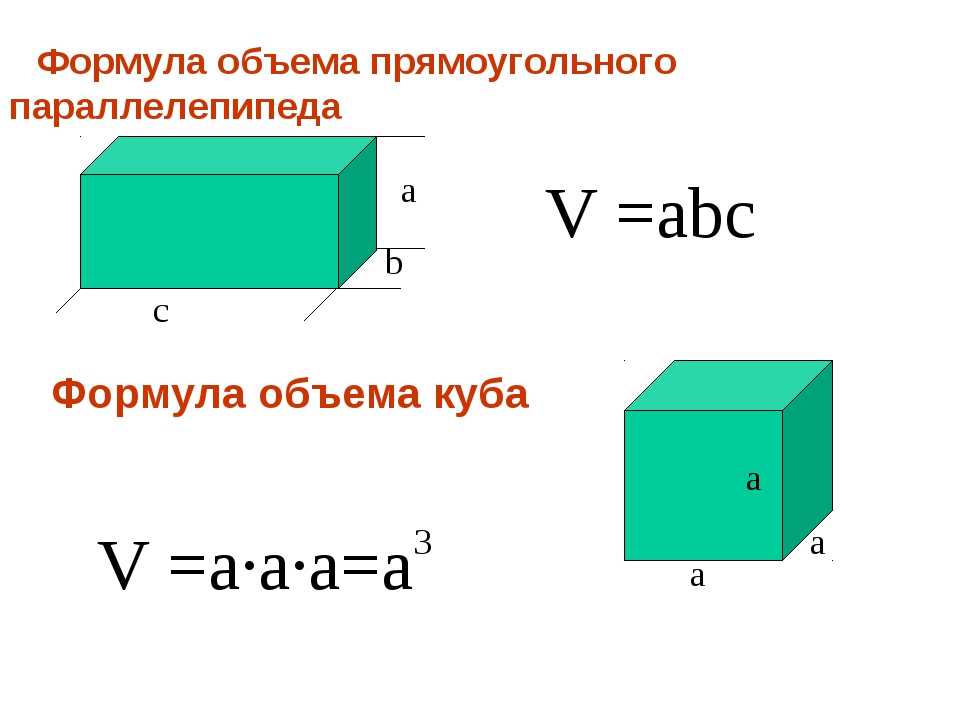

ПРЯМОУГОЛЬНЫЕ ЕМКОСТИ

Здесь все еще проще. Чтобы узнать полный объем, достаточно длину емкости умножить на ее ширину и высоту. Например, кубический резервуар со стороной 1 метр будет вмещать 1 куб жидкости. Емкость размером 3000 мм × 2000 мм × 2500 мм будет иметь объем 15 кубометров.

Почему большинство резервуаров имеют не квадратную или прямоугольную, а цилиндрическую форму? Потому что конструктивно такие емкости являются более прочными. Чтобы сварить куб, нужны 6 листов стали и 12 сварных швов. Цилиндрическая емкость имеет всего 3 поверхности: два круглых дна и цилиндрический корпус.

Корпус может быть сварен из одного листа металла, свернутого в цилиндр, для этого нужен всего 1 сварной шов. Плюс еще два круговых шва, чтобы приварить днища. Итого, в идеальном варианте всего 3 сварных шва – вместо 12 у куба.

Зачем тогда делают прямоугольные емкости? У них есть свои сферы использования.

В нашей компании вы можете заказать резервуар практически любого типа, формы и назначения. Мы предлагаем как типовые варианты, так и изготавливаем продукцию на заказ. Зная основные принципы расчета размеров и объема резервуаров, вы можете оценить, какой вариант для вас окажется наиболее подходящим.

Выбрать подходящую ёмкомсть в каталоге, производство металлических ёмкостей для разных задач.

Калькулятор расчета объема груза — Avrora Logistic

• На главную
• Расписание
  движения
• КАЛЬКУЛЯТОР
  ТАМОЖЕННЫХ
  ПЛАТЕЖЕЙ
• КАЛЬКУЛЯТОР
  СБОРНЫХ
  ГРУЗОВ
• КАЛЬКУЛЯТОР
  ЦЕЛЫХ
  КОНТЕЙНЕРОВ
• РАСЧЕТ ОБЪЕМА
  ГРУЗА

Рассчитайте объем вашего груза

РАСЧЕТ ОБЪЕМА ГРУЗА

ШИРИНА (W) *

ДИАМЕТР (D) *

РАСЧЕТ ОБЪЕМА КоробкиЦилиндр

ВЫСОТА (H) * ЕДИНИЦА ИЗМЕРЕНИЯ * ммсмм

ДЛИНА (L) *

КОЛИЧЕСТВО КОРОБОК *

КОЛИЧЕСТВО ЦИЛИНДРОВ *

ИТОГО:

ИСПОЛЬЗУЙТЕ ПОЛУЧЕННЫЕ РАСЧЕТЫ
ДЛЯ ОФОРМЛЕНИЯ ЗАЯВКИ

Далее

• На главную
• Расписание
  движения
• РАСЧЕТ ОБЪЕМА
  ГРУЗА
• КАЛЬКУЛЯТОР
  ТАМОЖЕННЫХ
  ПЛАТЕЖЕЙ
• КАЛЬКУЛЯТОР
  СБОРНЫХ
  ГРУЗОВ
• КАЛЬКУЛЯТОР
  ЦЕЛЫХ
  КОНТЕЙНЕРОВ

Возникли вопросы?

Я согласен на обработку персональных данных в порядке и на условиях, указанных по ссылке

Прикрепить файл (максимальный размер 20 Мб)

Расчет объема | SkillsYouNeed

На этой странице объясняется, как рассчитать объем твердых предметов, т. е. сколько вы могли бы вместить в предмет, если, например, вы наполнили его жидкостью.

Площадь — это мера того, сколько места находится внутри двухмерного объекта (дополнительную информацию см. на нашей странице: Расчет площади).

Объем — это мера пространства внутри трехмерного объекта. Наша страница о трехмерных фигурах объясняет основы таких фигур.

В реальном мире вычисление объема, вероятно, не будет использоваться так часто, как вычисление площади.

Тем не менее, это может быть важно. Возможность рассчитать объем позволит вам, например, определить, сколько места у вас есть для упаковки при переезде, сколько офисного пространства вам нужно или сколько варенья вы можете поместить в банку.

Это также может быть полезно для понимания того, что имеют в виду СМИ, когда говорят о мощности плотины или расходе реки.

Примечание по единицам измерения

Площадь выражается в квадратных единицах ( ² ), поскольку она измеряется в двух измерениях (например, длина × ширина).

Объем выражается в кубических единицах ( ³ ), поскольку он измеряется в трех измерениях (например, длина × ширина × глубина). Кубические единицы включают см3, м3 и кубические футы. Кубические единицы включают ³ см, ³ м и кубические футы.

ВНИМАНИЕ!

Объем также может быть выражен как емкость по жидкости.

Метрическая система

В метрической системе вместимость жидкости измеряется в литрах, что напрямую сравнимо с кубическим измерением, поскольку 1 мл = 1 см ³ . 1 литр = 1000 мл = 1000 см ³ .

Имперская/английская система

В имперской/английской системе эквивалентными единицами измерения являются жидкие унции, пинты, кварты и галлоны, которые нелегко перевести в кубические футы. Поэтому лучше всего придерживаться либо жидких, либо твердых единиц объема.

Для получения дополнительной информации см. нашу страницу о системах измерения.

Основные формулы для вычисления объема

Объем тел на основе прямоугольников

В то время как основная формула площади прямоугольной формы представляет собой длину × ширину, основная формула объема — длина × ширина × высота.

То, как вы ссылаетесь на различные измерения, не меняет расчет: вы можете, например, использовать «глубину» вместо «высоты». Важно то, что три измерения умножаются вместе. Вы можете умножать в любом порядке, поскольку это не изменит ответ (см. нашу страницу на умножить на для большего).

Объем коробки шириной 15 см, длиной 25 см и высотой 5 см:
15 × 25 × 5 = 1875 см ³

Объем призм и цилиндров

для покрытия объема цилиндров и призм тоже. Вместо прямоугольного конца у вас просто другая форма: круг для цилиндров, треугольник, шестиугольник или любой другой многоугольник для призмы.

Фактически, для цилиндров и призм объем равен площади одной стороны, умноженной на глубину или высоту формы.

Таким образом, основная формула для объема призм и цилиндров:

Площадь торца × высота/глубина призмы/цилиндра.

Остерегайтесь несовместимых единиц!

Прямой отрезок круглой трубы имеет внутренний диаметр 2 см и длину 1,7 м. Рассчитайте объем воды в трубе.

В этом примере вам нужно рассчитать объем очень длинного тонкого цилиндра, образующего внутреннюю часть трубы. Площадь одного конца можно рассчитать по формуле площади круга πr ² . Диаметр 2см, значит радиус 1см. Таким образом, площадь равна π × 1 ² , что составляет 3,14 см ² .

Длина трубы 1,7 м, поэтому вам нужно умножить площадь конца на длину, чтобы найти объем.

Остерегайтесь несовместимых юнитов! Площадь в сантиметрах, а длина в метрах. Сначала преобразуйте длину в см 1,7 × 1000 = 1700 см.

Таким образом, объем равен 3,14 × 1700 = 5338 см ³ . Это эквивалентно 5,338 литра или 0,0053 м ³ .

Объем конусов и пирамид

Тот же принцип, что и выше (ширина × длина × высота), применяется для расчета объема конуса или пирамиды, за исключением того, что, поскольку они сходятся в точке, объем составляет лишь долю сумма, которая была бы, если бы они продолжали иметь ту же форму (поперечное сечение) насквозь.

Объем конуса или пирамиды составляет ровно одну треть объема коробки или цилиндра с таким же основанием.

Таким образом, формула выглядит следующим образом:

Площадь основания или торца × высота конуса/пирамиды × ¹ / ₃

Вернитесь к нашей странице 05

Расчет площади 900 не может вспомнить, как вычислить площадь круга или треугольника.

Например, чтобы вычислить объем конуса с радиусом 5 см и высотой 10 см:

Площадь внутри круга = πr ² (где π (пи) приблизительно равно 3,14, а r – радиус круг).

В этом примере площадь основания (круга) = πr ² = 3,14 × 5 × 5 = 78,5 см ² .

78,5 × 10 = 785

785 × 1/3 = 261,6667см ³

Объем сферы

Формула 4/3 × π × радиус ³ .

Вам может быть интересно, как можно вычислить радиус мяча. Если не считать протыкания вязальной спицы (эффективно, но смертельно для мяча!), есть более простой способ.

Расстояние вокруг самой широкой точки сферы можно измерить напрямую, например, рулеткой. Этот круг является окружностью и имеет тот же радиус, что и сама сфера.

Длина окружности рассчитывается как 2 x π x радиус.

Чтобы вычислить радиус по длине окружности:

Разделите длину окружности на (2 x π) .

Примеры работы: Расчет объема

Расчет объема неправильных тел

Точно так же, как вы можете рассчитать площадь неправильных двумерных фигур, разбив их на правильные, вы можете сделать то же самое для расчета объема неправильных тел. Просто разделите тело на более мелкие части, пока не получите только многогранники, с которыми вам будет легко работать.

Дальнейшее чтение из книги «Навыки, которые вам нужны»

Понимание геометрии
Часть руководства «Навыки, которые вам необходимы для счета»

Эта электронная книга охватывает основы геометрии и рассматривает свойства форм, линий и твердых тел. Эти концепции построены в книге, с примерами работы и возможностями для вас, чтобы попрактиковаться в ваших новых навыках.

Если вы хотите освежить свои знания или помочь своим детям в обучении, эта книга для вас.

В заключение…

Используя эти принципы, если необходимо, теперь вы сможете рассчитать объем почти всего в вашей жизни, будь то упаковочный ящик, комната или водяной цилиндр.

Объем куба. Формула и как его найти0229

Проверено

Полом Маццолой

Объем куба

Объем куба  – это объем пространства, который куб занимает в трех измерениях.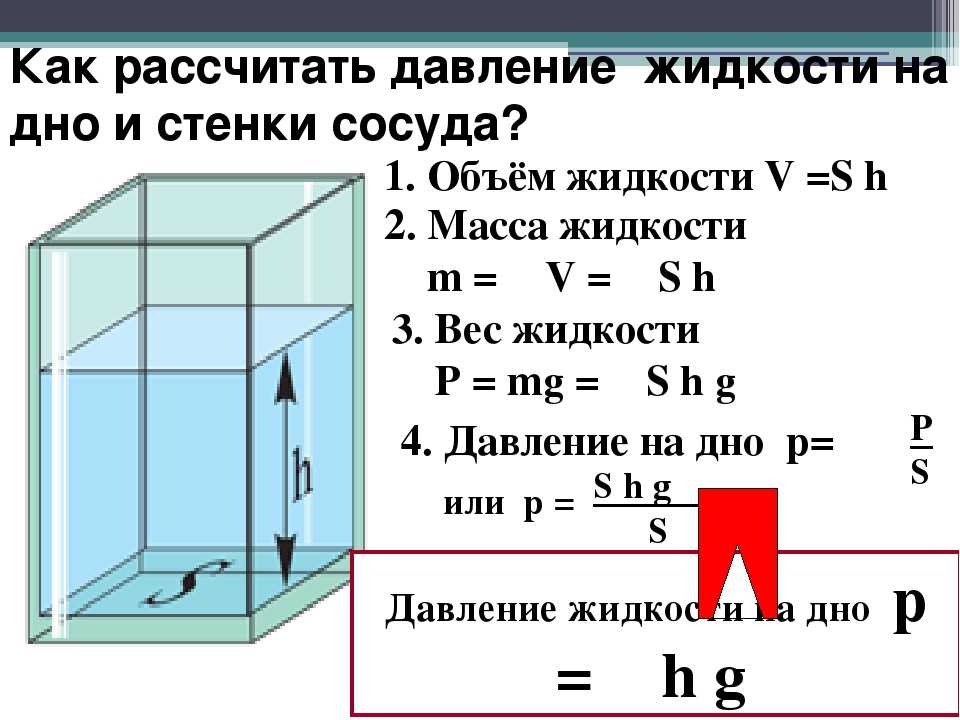 Объем куба всегда измеряется в кубических единицах, полученных из линейной единицы, заданной или используемой для измерения длины стороны.

Вы можете найти объем любого куба с одним заданным измерением, используя формулу объема куба :

Что такое куб?

А куб  – трехмерное тело с шестью конгруэнтными квадратными гранями, сходящимися под прямым углом, восемью вершинами и двенадцатью сторонами одинаковой длины. Куб является одним из пяти Платоновых тел и также называется шестигранником.

Каковы размеры куба?

Куб — это трехмерный объект, поэтому куб имеет три измерения:

• Длина — обычно понимается как большее из «плоских» измерений.

• Ширина – обычно понимается как более короткий из «плоских» размеров.

• Высота или Глубина – Измерение, которое привносит форму в наш трехмерный мир

Обратите внимание, что у нас есть два способа описать третье измерение:

1. Высота – Используйте этот термин, когда объект возвышается перед вами, как высокое здание.

2. Глубина — используйте этот термин, если объект падает под вами, как дыра в земле.

Нам нужна информация хотя бы об одном из этих трех измерений, чтобы измерить объем куба.

Формула объема куба

Формула объема  равна объему, равному произведению длины на ширину и на высоту.

Это уравнение объема не работает для каждого твердого тела, но оно работает для кубов, прямоугольных призм и параллелепипедов.

Поскольку все три значения ( l , w и h) одинаковы в кубе, простейший объем формулы куба:

В этом объеме уравнения куба s 9{3} м3 (метры в кубе).

Как найти объем куба

Чтобы найти объем куба, достаточно знать длину любого ребра.

Если вам известна длина одной стороны, вы можете найти объем куба, подставив его в одну из формул объема куба:

Измерение пространства, занимаемого кубом, зависит от знания длины любого одно ребро, потому что все длины сторон куба равны по длине.

Как найти длину, ширину и высоту из тома

Что, если вам дан объем куба и вас попросят найти его размеры?

Если вам дан объем куба и вас попросят найти длину ребра, все, что вам нужно сделать, это извлечь кубический корень из объема:

Ваш ответ больше не будет в кубических единицах; это будет в линейных единицах.