Как высчитать объем: Как посчитать объем
Как рассчитать объём — онлайн калькулятор объёма воды
Как рассчитать объём ёмкости, воды или другой жидкости … несколько онлайн калькуляторов для расчёта объёма, формулы, а также конвертер единиц объёма.
1. Как рассчитать объём любой прямоугольной емкости, в том числе куба — онлайн калькулятор расчёта объема воды в аквариуме, баке …
2. Как рассчитать объём цилиндра — онлайн калькулятор расчёта объёма воды в трубе, бочке, круглом бассейне …
3. Единицы измерения объёма
3.1. Соотношение единиц объёма
4. Конвертер единиц объёма
5. Заключение
6. Как рассчитать объём — калькулятор объёма куба, прямоугольной ёмкости, объёма цилиндра, объёма воды в трубе …
Как рассчитать объём любой прямоугольной емкости, в том числе куба — онлайн калькулятор расчёта объема воды в аквариуме, баке …
Как рассчитать объём по формуле — формула расчёта объёма прямоугольной ёмкости
V = X * Y * Z, где V — объём, а X, Y, и Z это длины сторон ёмкости (длина, ширина, высота).
При этом мы помним, что у куба все стороны равны — X=Y=Z . Соответственно формула объёма куба имеет такой вид — V = X3 , где X — длина стороны куба.
Внимание! При расчёте объёма жидкости в ёмкости необходимо учитывать реальную заполненность ёмкости и привязывать величины непосредственно к самой жидкости.
Для конвертации единиц объёма вы можете воспользоваться нашим ОНЛАЙН КОНВЕРТЕРОМ ЕДИНИЦ ОБЪЁМА →
Как рассчитать объём цилиндра — онлайн калькулятор расчёта объёма воды в трубе, бочке, круглом бассейне …
Для конвертации единиц объёма вы можете воспользоваться нашим ОНЛАЙН КОНВЕРТЕРОМ ЕДИНИЦ ОБЪЁМА →
Как рассчитать объём по формуле — формулы расчёта объёма цилиндра
Объём воды в цилиндре и других ёмкостях, имеющих цилиндрическую форму, рассчитывается таким образом.
Вначале рассчитываем площадь основания (площадь внутреннего сечения) по формуле — S = π * R2
Где, R — радиус трубы, π — число ПИ равное 3,1415926535 .
Затем вычисляем объём — V = S * L
Где, L — длина (высота) цилиндра (трубы, бочки, бассейна).
Внимание! При расчёте объёма жидкости в ёмкости необходимо учитывать заполненность ёмкости и привязывать величины непосредственно к самой жидкости.
Единицы измерения объёма
Вначале кратко ознакомимся с единицами измерения объёма как таковыми.
Официальной единицей измерения объема в системе СИ является м3 — метр кубической. Объём так же может быть выражен и в других единицах. Наиболее популярными из них являются — дм3 — кубические дециметры, см3 — кубические сантиметры, литры …
Отметим, что такая популярная единица измерения объёма жидкостей как литр не входит в Международную систему измерений (СИ). Тем не менее, поскольку литр является весьма популярной мерой жидкостей, он считается официальной внесистемной единицей.
Один литр — это объём куба стороны которого равны 10 см. Полезно также знать, что 1 литр воды вести приблизительно 1 кг при температуре + 4 °C
Соотношение единиц объёма
1 м3 = 1000 дм3 = 1 000 000 см3 = 1 000 000 000 мм3 = 1000 литров
1 литр = 0,001 м3 = 1 дм3 = 1 000 см3 = 1 000 000 мм3
Конвертер единиц объёма
Конвертация кубических метров ( м
3 ) в кубические сантиметры ( см3 ) и литрыКонвертация литров в метры кубические ( м
3 ) и кубические сантиметры ( см3 )Конвертация кубических сантиметров ( см
3 ) в кубические метры ( м3 ) и литрыЗаключение
Практически каждый человек рано или поздно сталкивается с необходимостью рассчитать объём того или другого объекта.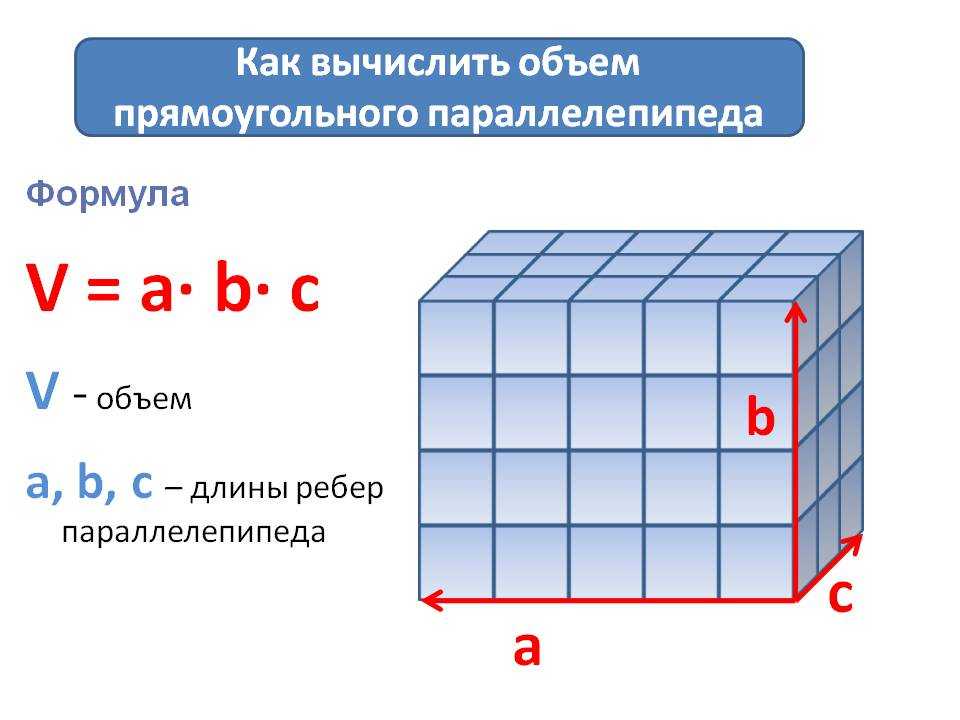
Для удобства и экономии времени предлагаем Вам воспользоваться нашими онлайн калькуляторами.
Поделись с друзьями 🙂
Как рассчитать объём — калькулятор объёма куба, прямоугольной ёмкости, объёма цилиндра, объёма воды в трубе …
Статья опубликована: 2021-06-07 Автор: Waterman
Онлайн калькулятор: Объем геометрических фигур
УчебаМатематикаГеометрия
Рассчитывает объем геометрических фигур (куб, призма, пирамида, усеченная пирамида, конус, цилиндр, сфера, эллипсоид, тороид).
Данная статья содержит калькуляторы для расчета объема различных геометрических фигур. Основной источник формул: Spiegel, Murray R. Mathematical Handbook of Formulas and Tables. Schaum’s Outline series in Mathematics. McGraw-Hill Book Co., 1968.
Объем куба
Размеры куба
Формула:
Объем куба
Сторона (H)
Длина ребра куба (H)
Точность вычисления
Знаков после запятой: 5
Объем
Объем прямоугольной призмы
Размеры прямоугольной призмы
Формула:
Объем прямоугольной призмы
Ширина (W)
Высота (H)
Высота (H)
Длина (L)
Точность вычисления
Знаков после запятой: 5
Объем
Объем пирамиды
Размеры пирамиды
Формула:
Объем пирамиды
Площадь основания (Sb)
Площадь основания
Высота (H)
Высота (H)
Точность вычисления
Знаков после запятой: 5
Объем
Объем усеченной пирамиды
Размеры усеченной пирамиды
Формула:
Объем усеченной пирамиды
Площадь первого основания (Sb1)
Площадь второго основания (Sb2)
Высота (H)
Высота (H)
Точность вычисления
Знаков после запятой: 5
Объем
Объем конуса
Размеры конуса
Формула:
Объем конуса
Радиус (R)
Высота (H)
Высота (H)
Точность вычисления
Знаков после запятой: 5
Объем
Объем цилиндра
Размеры цилиндра
Formula:
Объем цилиндра
Высота (H)
Высота (H)
Радиус (R)
Точность вычисления
Знаков после запятой: 5
Объем
Объем сферы
Размеры сферы
Формула:
Объем сферы
Радиус (R)
Точность вычисления
Знаков после запятой: 5
Объем
Объем эллипсоида
Размеры эллипсоида
Формула:
Объем эллипсоида
Радиус 1 (R1)
Радиус 2 (R2)
Радиус (R3)
Точность вычисления
Знаков после запятой: 5
Объем
Объем тороида
Размеры тороида
Формула:
Объем тора
Радиус 1 (R1)
Радиус 2 (R2)
Точность вычисления
Знаков после запятой: 5
Объем
Ссылка скопирована в буфер обмена
Похожие калькуляторы
- • Куб
- • Конус
- • Тор
- • Объем сегмента цилиндра
- • Объем жидкости в прямоугольном баке под наклоном
- • Раздел: Геометрия ( 94 калькуляторов )
#геометрия #объем Геометрия Инженерные конус куб Математика объем пирамида прямоугольная призма сфера тор тороид усеченная пирамида цилиндр эллипсоид
PLANETCALC, Объем геометрических фигур
Anton2020-11-03 14:19:26
Расчет объема | SkillsYouNeed
На этой странице объясняется, как рассчитать объем твердых предметов, т.
е. сколько вы могли бы вместить в предмет, если, например, вы наполнили его жидкостью.
Площадь — это мера того, сколько места находится внутри двухмерного объекта (дополнительную информацию см. на нашей странице: Расчет площади).
Объем — это мера пространства внутри трехмерного объекта. Наша страница о трехмерных фигурах объясняет основы таких фигур.
В реальном мире вычисление объема, вероятно, не будет использоваться так часто, как вычисление площади.
Тем не менее, это может быть важно. Возможность рассчитать объем позволит вам, например, определить, сколько места у вас есть для упаковки при переезде, сколько офисного пространства вам нужно или сколько варенья вы можете поместить в банку.
Это также может быть полезно для понимания того, что имеют в виду СМИ, когда говорят о мощности плотины или расходе реки.
Примечание по единицам измерения
Площадь выражается в квадратных единицах ( 2 ), поскольку она измеряется в двух измерениях (например, длина × ширина).
Объем выражается в кубических единицах ( 3 ), поскольку он измеряется в трех измерениях (например, длина × ширина × глубина). Кубические единицы включают см3, м3 и кубические футы. Кубические единицы включают 3 см, 3 м и кубические футы.
ВНИМАНИЕ!
Объем также может быть выражен как емкость по жидкости.
Метрическая система
В метрической системе вместимость жидкости измеряется в литрах, что напрямую сравнимо с кубическим измерением, поскольку 1 мл = 1 см 3 . 1 литр = 1000 мл = 1000 см 3 .
Имперская/английская система
В имперской/английской системе эквивалентными единицами измерения являются жидкие унции, пинты, кварты и галлоны, которые нелегко перевести в кубические футы. Поэтому лучше всего придерживаться либо жидких, либо твердых единиц объема.
Для получения дополнительной информации см. нашу страницу о системах измерения.
Основные формулы для вычисления объема
Объем тел, основанных на прямоугольниках
В то время как основная формула площади прямоугольной формы равна длине × ширине, основная формула для объема равна длине × ширине6 ×
высота.
То, как вы ссылаетесь на различные измерения, не влияет на расчет: вы можете, например, использовать «глубину» вместо «высоты». Важно то, что три измерения умножаются вместе. Вы можете умножать в любом порядке, поскольку это не изменит ответ (см. нашу страницу на умножить на для большего).
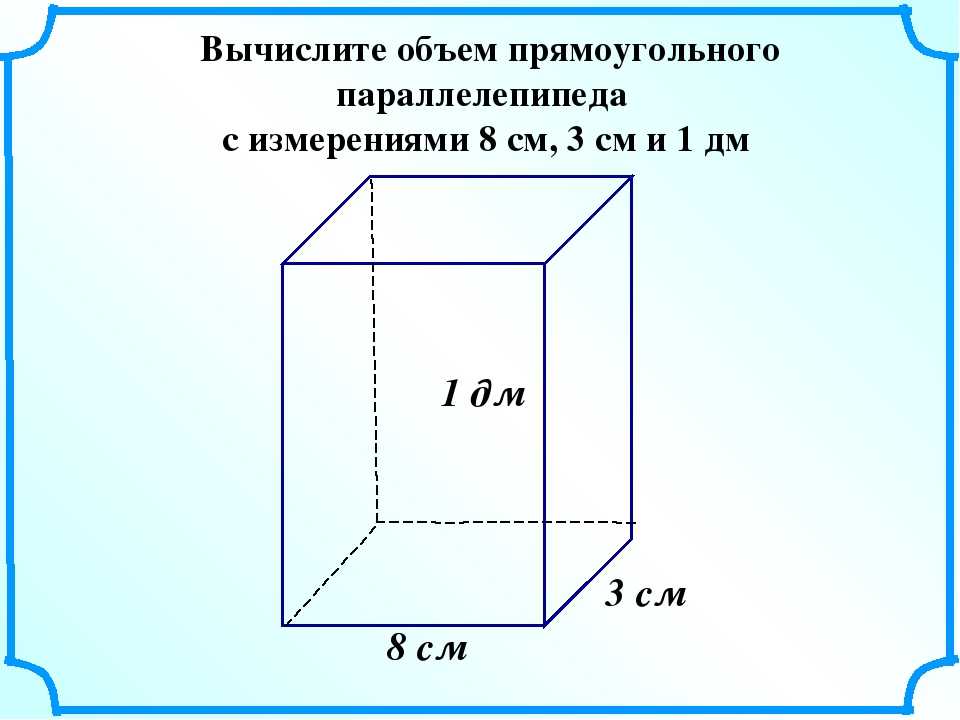
Коробка с размерами 15 см в ширину, 25 см в длину и 5 см в высоту имеет объем:
15 × 25 × 5 = 1875 см для покрытия объема цилиндров и призм тоже. Вместо прямоугольного конца у вас просто другая форма: круг для цилиндров, треугольник, шестиугольник или любой другой многоугольник для призмы.Фактически, для цилиндров и призм объем равен площади одной стороны, умноженной на глубину или высоту формы.
Таким образом, основная формула для объема призм и цилиндров:
Площадь торца × высота/глубина призмы/цилиндра.
Остерегайтесь несовместимых единиц!
Прямой отрезок круглой трубы имеет внутренний диаметр 2 см и длину 1,7 м. Рассчитайте объем воды в трубе.
В этом примере вам нужно рассчитать объем очень длинного тонкого цилиндра, образующего внутреннюю часть трубы. Площадь одного конца можно рассчитать по формуле площади круга πr 2 . Диаметр 2см, значит радиус 1см. Таким образом, площадь равна π × 1 2 , что составляет 3,14 см 2 .
Длина трубы 1,7 м, поэтому вам нужно умножить площадь конца на длину, чтобы найти объем.
Остерегайтесь несовместимых юнитов! Площадь в сантиметрах, а длина в метрах. Сначала преобразуйте длину в см 1,7 × 1000 = 1700 см.
Таким образом, объем равен 3,14 × 1700 = 5338 см 3 . Это эквивалентно 5,338 литра или 0,0053 м 3 .
Объем конусов и пирамид
Тот же принцип, что и выше (ширина × длина × высота), применяется для расчета объема конуса или пирамиды, за исключением того, что, поскольку они сходятся в точке, объем составляет лишь долю сумма, которая была бы, если бы они продолжали иметь ту же форму (поперечное сечение) насквозь.
Объем конуса или пирамиды составляет ровно одну треть объема коробки или цилиндра с таким же основанием.
Таким образом, формула выглядит следующим образом:
Площадь основания или торца × высота конуса/пирамиды × 1 / 3
Если не можете, вернитесь на нашу страницу
0 0 Расчет площади помните, как вычислить площадь круга или треугольника.Например, чтобы вычислить объем конуса с радиусом 5 см и высотой 10 см:Площадь внутри круга = πr 2 (где π (пи) приблизительно равно 3,14, а r — радиус круг).
В этом примере площадь основания (круга) = πr 2 = 3,14 × 5 × 5 = 78,5 см
2 . 78,5 × 10 = 785
785 × 1/3 = 261,6667 см 3
Объем сферы
Как и в случае с кругом, для вычисления объема сферы требуется π (пи).
Формула 4/3 × π × радиус 3 .
Вам может быть интересно, как можно вычислить радиус мяча. Если не считать протыкания вязальной спицы (эффективно, но смертельно для мяча!), есть более простой способ.
Расстояние вокруг самой широкой точки сферы можно измерить напрямую, например, рулеткой. Этот круг является окружностью и имеет тот же радиус, что и сама сфера.
Длина окружности рассчитывается как 2 x π x радиус.
Чтобы вычислить радиус по длине окружности:
Разделите длину окружности на (2 x π) .
Примеры работы: Расчет объема
Расчет объема неправильных тел
Точно так же, как вы можете рассчитать площадь неправильных двумерных фигур, разбив их на правильные, вы можете сделать то же самое, чтобы вычислить объем неправильных тел.
Просто разделите тело на более мелкие части, пока не получите только многогранники, с которыми вам будет легко работать.
Дальнейшее чтение из книги «Навыки, которые вам нужны»
Понимание геометрии
Часть руководства «Навыки, которые вам необходимы для счета»В этой электронной книге рассматриваются основы геометрии и рассматриваются свойства форм, линий и твердых тел. Эти концепции построены в книге, с примерами работы и возможностями для вас, чтобы попрактиковаться в ваших новых навыках.
Если вы хотите освежить свои знания или помочь своим детям в обучении, эта книга для вас.
В заключение…
Используя эти принципы, если необходимо, теперь вы сможете рассчитать объем почти всего в вашей жизни, будь то упаковочный ящик, комната или цилиндр с водой.
Расчет объема
Расчет объема
Просто разделите тело на более мелкие части, пока не получите только многогранники, с которыми вам будет легко работать.
1417
x R x D 