Как высчитать кубы: Как рассчитать куб доски — интернет-магазин Корпорация Снабжения
ЛесОрск — Калькулятор пиломатериалов
Расчет кубатуры производимого пиломатериала: бруса, доски обрезной, доски необрезной, рейки, бруска, вагонки и доски позволит рассчитать сколько досок в 1 м3. (кубатурник).
| Брус | 100х100х6 | 1 штука — 0.06 куба | 16.67 штук в кубе |
| Брус | 100х150х6 | 1 штука — 0.09 куба | 11.11 штук в кубе |
| Брус | 150х150х6 | 1 штука — 0.135 куба | 7.41 штук в кубе |
| Брус | 100х200х6 | 1 штука — 0.12 куба | 8.33 штук в кубе |
| Брус | 150х200х6 | 1 штука — 0.18 куба | 5.56 штук в кубе |
| Брус | 200х200х6 | 1 штука — 0.24 куба | 4.17 штук в кубе |
| Брус | 100х100х7 | 1 штука — 0.07 куба | 14, 28 штук в кубе |
| Брус | 100х150х7 | 1 штука — 0.105 куба | 9.52 штук в кубе |
| Брус | 150х150х7 | 1 штука — 0. 1575 куба 1575 куба | 6.35 штук в кубе |
| Брус | 100х200х7 | 1 штука — 0.14 куба | 7.14 штук в кубе |
| Брус | 150х200х7 | 1 штука — 0.21 куба | 4.76 штук в кубе |
| Брус | 200х200х7 | 1 штука — 0.28 куба | 3.57 штук в кубе |
| Доска обрезная | 22х100х6 | 1 штука — 0.0132 куба | 45.46 м.кв. в кубе |
| Доска обрезная | 22х150х6 | 1 штука — 0. 0198 куба | 45.46 м.кв. в кубе |
| Доска обрезная | 22х200х6 | 1 штука — 0.0264 куба | 45.46 м.кв. в кубе |
| Доска обрезная | 25х100х6 | 1 штука — 0.015 куба | 40 м.кв в кубе |
| Доска обрезная | 25х150х6 | 1 штука — 0.0225 куба | 40 м.кв в кубе |
| Доска обрезная | 25х200х6 | 1 штука — 0.03 куба | 40 м. кв в кубе кв в кубе |
| Доска обрезная | 40х100х6 | 1 штука — 0.024 куба | 25 м.кв в кубе |
| Доска обрезная | 40х150х6 | 1 штука — 0.036 куба | 25 м.кв в кубе |
| Доска обрезная | 40х200х6 | 1 штука — 0.048 куба | 25 м.кв в кубе |
| Доска обрезная | 50х100х6 | 1 штука — 0.03 куба | 20 м.кв в кубе |
| Доска обрезная | 50х150х6 | 1 штука — 0.045 куба | 20 м.кв в кубе |
| Доска обрезная | 50х200х6 | 1 штука — 0.06 куба | 20 м.кв в кубе |
| Доска обрезная | 32х100х6 | 1 штука — 0.0192 куба | 31.25 м.кв в кубе |
| Доска обрезная | 32х150х6 | 1 штука — 0.0288 куба | 31.25 м.кв в кубе |
| Доска обрезная | 32х200х6 | 1 штука — 0.0384 куба | |
| Доска обрезная | 25х100х2 | 1 штука — 0. 005 куба 005 куба | 40 м.кв в кубе |
| Доска обрезная | 25х100х7 | 1 штука — 0.0175 куба | 40 м.кв в кубе |
| Доска обрезная | 25х150х7 | 1 штука — 0.02625 куба | 40 м.кв в кубе |
| Доска обрезная | 25х200х7 | 1 штука — 0.035 куба | 40 м.кв в кубе |
| Доска необрезная | 50х6 | 1 штука — 0.071 куба | |
| Доска необрезная | 40х6 | 1 шутка — 0.05 куба | |
| Доска необрезная | 25х6 | 1 штука — 0.0294 куба | |
| Рейка | 22х50х3 | 1 штука — 0.0033 куба | 909 м.п. в кубе |
| Рейка | 25х50х3 | 1 штука — 0.00375 куба | 800 м.п. в кубе |
| Рейка | 22х50х2 | 1 штука — 0.0022 куба | 909 м.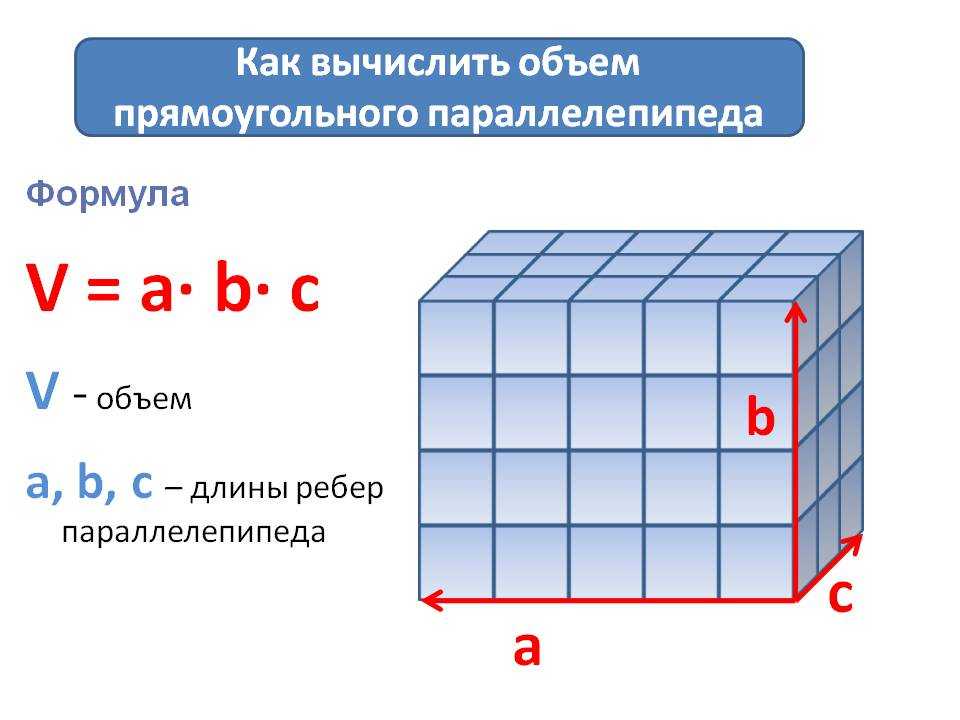 п. в кубе п. в кубе |
| Рейка | 25х50х2 | 1 штука — 0.0025 куба | 800 м.п. в кубе |
| Брусок | 40х40х3 | 1 штука — 0.0048 куба | 624.99 м.п. в кубе |
| Брусок | 50х50х3 | 1 штука — 0.006 куба | 500.01 м.п. в кубе |
| Брусок | 40х80х3 | 1 штука — 0.0096 куба | 312.51 м.п. в кубе |
| Брусок | 50х50х3 | 1 штука — 0.0075 куба | 399.99 м.п. в кубе |
| Доска пола | 36х106х6 | 1 штука — 0.0229 куба | 27.77 м.кв. в кубе |
| Доска пола | 36х136х6 | 1 штука — 0.0294 куба | 27.77 м.кв. в кубе |
| Доска пола | 45х136х6 | 1 штука — 0.0375 куба | 21.74 м.кв. в кубе |
| Вагонка | 16х88х6 | 1 штука — 0.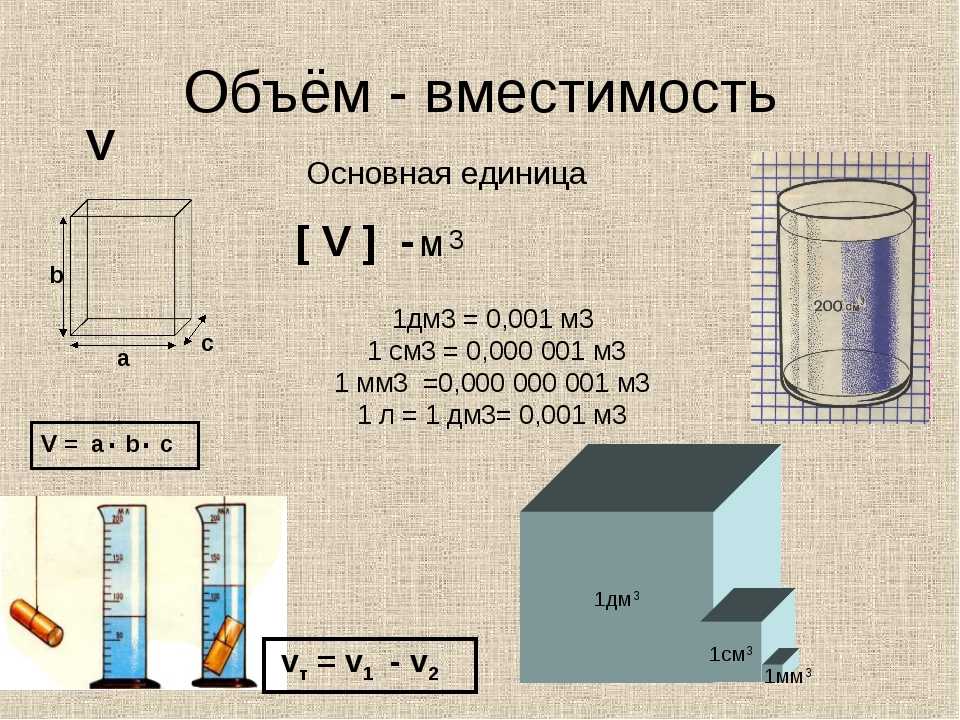 0084 куба 0084 куба | 62.5 м.кв. в кубе |
| Вагонка | 16х88х3 | 1 штука — 0.0042 куба | 62.5 м.кв. в кубе |
| Вагонка | 12.5х90х3 | 1 штука — 0.0034 | 80 м.кв. в кубе |
Кубический метр древесины – объем, полученный замером каждого отдельного сортимента (пиломатериала, фанера, бревна) исключающий объем пустот между бревнами и объем коры.
Складочный кубический метр – единица измерения объема древесины уложенной в штабеля с пустотами объемом 1 кубический метр. В складских кубических метрах учитываются короткомерные сортименты, дрова, включая объем пустот между бревнами и объем коры.
Перевод из складочных кубических метров в кубические метры плотной древесины производится путем умножения коэффициента полнодревесности штабеля на их величину.
Как посчитать сколько досок в кубометре. Например, вы подсчитали что вам нужно 20 шестиметровых досок толщиной 40 мм и шириной 150 мм.
Соответсвенно так же нетрудно узнать сколько будет досок в кубометре, для этого надо 1 куб. метр разделить на объем доски — для нашей сороковки шириной 150 мм и длиной 6 метров подсчеты будут такими — 1/0,04/0,15/6=27,777, значит в 1 кубометре 27,777 нужных нам доски.
Как рассчитать кубатуру бруса на дом?
Расчёт количества строительных материалов — важный этап, который проводится перед началом любого ремонта или строительства дома. Грамотное и продуманное выполнение этого мероприятия станет гарантией того, что работа будет завершена в запланированные сроки и без дополнительных издержек. Кроме того, перед началом работ нужно хотя бы приблизительно определиться с бюджетом и просчитать ориентировочные расходы на материал. Знание как рассчитать, сколько нужно бруса на дом, пригодится в любом случае.
Как рассчитать кубатуру бруса на дом (первый способ)
Брусовые дома имеют ряд преимуществ в сравнении с прочими деревянными домами (бревно, каркас). Одно из основных — простой подсчёт количества используемого материала. Поскольку брус отличается геометрически правильной формой, не придётся ломать голову над тем, как рассчитать объем бруса на дом, ведь делается это довольно легко.

Как рассчитать количество бруса на дом (второй способ)
Есть задача — надо приобрести 20 заготовок с размерами: 145 мм×90 мм×2 м. Аналогично с предыдущим примером, делаем перевод всех единиц измерения в метры с последующим перемножением. Итого получается: 0,145 м × 0,009 м × 2 м. Полученный объём 1 изделия — 0,026 м³. Общая кубатура 20 заготовок — 0,026 м³ × 20 = 0,52 м³. Как узнать, сколько штук бруса будет в одном м³? Для этого нужно произвести деление. То есть один м³ разделить на объем одной заготовки. Поскольку в частном строительстве практически всегда применяется брус нескольких основных размеров, для того чтобы узнать количество бруса в одном кубометре материала и облегчить себе дальнейшие расчёты, можно воспользоваться данными следующей таблицы (длина бруса стандартная — 6 м):
|
Сечение (мм) |
Количество штук |
Объём (м³) |
|
200×200 |
4,1 |
0,24 м³ |
|
150×150 |
7,4 |
0,135 м³ |
|
100×150 |
11,1 |
0,09 м³ |
|
100×100 |
16,6 |
0,06 м³ |
Расчёт бруса — о чём нужно помнить
Рассчитывая количество материала, нужно сразу уяснить тот факт, что уложиться тютелька в тютельку не получится. Потери будут в любом случае, ведь иногда случается так, что даже идеальный на вид брус при распиливании может выявлять тот или иной дефект. По этой причине покупать нужно с запасом. Умеренные цены на древесину позволяют это.
Потери будут в любом случае, ведь иногда случается так, что даже идеальный на вид брус при распиливании может выявлять тот или иной дефект. По этой причине покупать нужно с запасом. Умеренные цены на древесину позволяют это.
Брусовые дома от компании «ЭКОДОМ-13»
Уже более 10 лет команда высококлассных специалистов компании «ЭКОДОМ-13» занимается профессиональным строительством жилых домов, гостиниц, бань и садовых построек. Мы имеем собственную производственную базу и способны реализовать для наших клиентов любые архитектурные формы. Будь то обычный коттедж, баня или элементы приусадебного декора — всё может быть изготовлено как по типовым проектам, так и с полным перепланированием под ваши пожелания.
Строительство доступно в различной комплектации (под усадку, дачная, зимняя, зимняя+), которые отличаются по стоимости и делают нашу ценовую политику очень гибкой. Если вы ищете высокое качество строительства, хорошую рыночную цену, экологически чистые материалы, комплексный подход к работе и полную ответственность за результат — звоните нам и заказывайте новый качественный дом без посредников, переплат и лишней волокиты. Наш телефон
Наш телефон
, звонок бесплатный.
Назад к списку статей
Площадь поверхности куба: Формула и примеры
Давайте узнаем, как определить площадь поверхности куба .
Что такое куб?Единственный правильный шестигранник, куб представляет собой трехмерный объект с шестью квадратными поверхностями или сторонами одинакового размера, 12 ребрами и 8 вершинами. Учитывая, что его квадратные стороны равны, отсюда следует, что длина, ширина и высота куба также равны. Примерами объектов в форме куба являются игральные кости, шкатулки для драгоценностей, кубики льда, кубики сахара и кубики Рубика.
Вот иллюстрация куба. Обратите внимание, как в развернутом виде он образует 6 равных квадратных поверхностей или сторон. Получающаяся двумерная форма, когда куб разворачивается, называется сетью куба .
Как найти площадь поверхности куба : Напомним, что площадь поверхности трехмерной фигуры относится к общей площади, занимаемой поверхностью фигуры. Чтобы лучше понять площадь поверхности, посмотрите на сеть или плоскую компоновку куба на иллюстрации ниже.
Чтобы лучше понять площадь поверхности, посмотрите на сеть или плоскую компоновку куба на иллюстрации ниже.
Площадь поверхности куба , равная , равна сумме площадей всех его шести квадратных сторон. Напомним, что площадь квадрата вычисляется путем умножения длины каждой стороны ( на ) на себя: на или на ². Просто умножьте площадь стороны квадрата на 6, и вы получите площадь поверхности куба.
Используйте эту формулу, чтобы найти общую площадь поверхности куба: SA = 6 a ²
, где a = длина одной стороны куба и a ² = площадь одной квадратной стороны куба.
Примечание: Не забывайте, что площади поверхности измеряются в квадратных единицах, таких как см 2 , м 2 , км 2 и 2 .
Краткое руководство по нахождению площади поверхности куба : Шаг 1. Запишите данные числа. Вам понадобится длина стороны куба, чтобы найти площадь поверхности. Убедитесь, что все единицы измерения одинаковы. Если нет, преобразуйте любой из них, чтобы он соответствовал другому.
Запишите данные числа. Вам понадобится длина стороны куба, чтобы найти площадь поверхности. Убедитесь, что все единицы измерения одинаковы. Если нет, преобразуйте любой из них, чтобы он соответствовал другому.
Шаг 2. Подставьте цифры в формулу.
Шаг 3. Выполните операции. Не забудьте указать квадратную единицу площади поверхности.
Пример #1:
Найдите площади поверхности куба ниже.
Решение для примера №1:
Шаг 1. Запишите данное измерение, a = 8 м .
Шаг 2. Подставьте 8m вместо a в формуле для площадь поверхности .
SA = 6 a ²
SA = 6(8m)²
Шаг 3. Упростите и решите уравнение.
SA = 6(64 м²)
SA = 384 м²
Таким образом, площадь равна 384 м² .
Хотите узнать, как найти объем этого куба?
Связанные материалы: Объем куба – формула и примеры
Найдите площади поверхности куба длиной 4 метра.
Шаг 1. Запишите данное измерение, a = 4м .
Шаг 2. Замените 4 м на a в формуле для площади поверхности .
SA = 6 a ²
SA = 6(4m)²
Шаг 3. Упростите и решите уравнение.
SA = 6(16м²)
SA = 96 м²
Следовательно, площадь поверхности равна 96 м² .
Спасибо, что прочитали. Мы надеемся, что это эффективно! Всегда не стесняйтесь возвращаться на эту страницу, если у вас возникнут вопросы о площади поверхности куба .
Ознакомьтесь с некоторыми другими сообщениями в нашем блоге или инвестируйте в свое будущее с помощью одного из наших курсов самообучения!
Нажмите здесь, чтобы ознакомиться с руководством по подготовке к экзамену AP Calculus AB 2021 !Нажмите здесь, чтобы ознакомиться с руководством по подготовке к экзамену AP Calculus BC 2021 !Вычисление объема и вместимости кубов и прямоугольных параллелепипедов | Хацуди
В математике мы часто думаем о фигурах в терминах трехмерных объектов, а не двухмерных объектов. На самом деле все вокруг нас трехмерно.
На самом деле все вокруг нас трехмерно.
Итак, давайте удостоверимся, что мы можем вычислить размер трехмерных объектов. В начальной школе геометрии мы изучаем формулы для вычисления размеров трехмерных фигур. Также размер трехмерной фигуры называется объемом. Используя формулу, вы сможете рассчитать объем.
Итак, давайте сначала вычислим объем куба и прямоугольного параллелепипеда. Тогда мы сможем понять вместимость сосуда. В этом разделе мы объясним, как рассчитать объем и вместимость кубов и прямоугольных параллелепипедов.
Содержание
- 1 Что такое кубы и прямоугольные параллелепипеды?
- 1.1 Как рассчитать объем куба и параллелепипеда
- 2 Расчет вместимости сосуда: объем воды, заполненный трехмерным объектом
- 2.1 Случаи, когда объем и вместимость различаются
- 3 Почему мы можем рассчитать объем и емкость?
- 3.1 Расчет длин сторон по объему
- 4 Узнайте, как рассчитать объем и вместимость
Что такое кубы и прямоугольные параллелепипеды?
Во-первых, давайте разберемся, что такое куб и прямоугольный параллелепипед. Куб — это объект, окруженный шестью квадратами. Кроме того, прямоугольный параллелепипед — это объект, окруженный шестью прямоугольниками.
Куб — это объект, окруженный шестью квадратами. Кроме того, прямоугольный параллелепипед — это объект, окруженный шестью прямоугольниками.
Ниже приведены куб и прямоугольный параллелепипед.
Вы должны уметь вычислять размер таких цифр.
Как рассчитать объем куба и параллелепипеда
Поймите, что объем — это размер трехмерного объекта. Вы будете вычислять размер объекта, который имеет высоту, а также длину и ширину.
При расчете объема куба или параллелепипеда используйте следующую формулу.
- Объем трехмерного объекта = длина × ширина × высота
Например, каков объем следующего куба и параллелепипеда?
В случае куба все стороны имеют одинаковую длину. Итак, давайте умножим одно и то же число три раза. Так как длина стороны 3 см, объем куба следующий.
- $3×3×3=27$
Таким образом, ответ равен 27 см 3 . В площади длина стороны умножается в два раза, поэтому единица измерения равна см 2 . С другой стороны, при вычислении объема длина стороны умножается на три раза, поэтому единицей измерения является см 3 .
С другой стороны, при вычислении объема длина стороны умножается на три раза, поэтому единицей измерения является см 3 .
Далее вычислим объем прямоугольного параллелепипеда, длины сторон которого различны. Итак, давайте умножим длину, ширину и высоту соответственно. Результат следующий.
- $4×3×2=24$
Таким образом, мы видим, что объем прямоугольного параллелепипеда равен 24 см 3 .
Расчет вместимости сосуда: объем воды, заполненный трехмерным объектом
После понимания объема давайте узнаем о вместимости сосуда. Когда жидкость (например, воду) наливают в сосуд, емкость показывает, сколько жидкости можно налить в этот сосуд. Объем и вместимость сосуда — это одни и те же понятия, и формула используется одна и та же.
При вычислении объема мы умножали длину, ширину и высоту соответственно. При расчете вместимости сосуда умножьте длину, ширину и высоту сосуда соответственно.
В этом случае вместимость судна следующая.
- 15×8×10=1200$
Таким образом, мы можем рассчитать, что этот сосуд может быть наполнен до 1200 см 3 воды. 1 л равен 1000 см 3 , поэтому мы также можем видеть, что этот сосуд может вместить 1,2 л воды.
Случаи, когда объем и вместимость различаются
Как упоминалось ранее, формула для расчета объема и вместимости судна одинакова. Однако в реальности объем и емкость могут отличаться. Это связано с толщиной контейнера.
Например, каковы объем и вместимость следующего контейнера?
Объем равен размеру всего контейнера. Итак, давайте умножим на внешнюю длину контейнера. Так как длина 8 см, ширина 6 см и высота 5 см, объем следующий.
- $8×6×5=240$
С другой стороны, как рассчитать вместимость судна? В емкости важно знать, сколько воды можно залить. Только внутренняя часть контейнера может удерживать воду. Итак, давайте умножим внутреннюю длину контейнера. Так как длина 6 см, ширина 4 см и высота 4 см, объем следующий.
- $6×4×4=96$
Таким образом, мы можем рассчитать объем и вместимость сосуда. Поймите, что если емкость имеет толщину, то объем и вместимость будут другими.
Почему мы можем рассчитать объем и емкость?
Почему можно рассчитать объем и вместимость сосуда путем умножения длины, ширины и высоты? Давайте выясним, почему.
Прежде всего, каков объем куба со стороной 1 см?
Поскольку все стороны имеют длину 1 см, объем этого куба равен 1 см 3 . Тогда каков объем этого куба, если он устроен следующим образом?
Всего кубиков 12. Следовательно, мы знаем, что это 12 см 3 . Однако подсчет количества кубиков по одному затруднителен. Итак, посчитаем объем.
В отличие от куба, все стороны которого имеют длину 1 см, кубоид на приведенном выше рисунке имеет высоту 1 см, но его вертикальная и горизонтальная длины различны. Итак, давайте умножим длину на ширину так же, как вычисляем площадь.
- $3×4×1=12$
Высота 1 см. Однако умножение на единицу не меняет ответ. Следовательно, в этом прямоугольном параллелепипеде вычисление площади такое же, как вычисление объема.
Далее рассмотрим прямоугольный параллелепипед высотой 3 см вместо 1 см. Результат следующий.
В этом прямоугольном параллелепипеде есть три параллелепипеда $3×4×1$, поставленные друг на друга. Поскольку блоки имеют высоту 3 см, мы вычисляем высоту в 3 см вместо 1 см следующим образом.
- $3×4×3=36$
Когда вы думаете об этом таким образом, вы можете понять, почему умножение на длину, ширину и высоту позволит вам вычислить объем.
Расчет длин сторон по объему
Если объем известен, в некоторых случаях можно вычислить длины сторон. Например, если объем следующего прямоугольного параллелепипеда равен 16 см3, какова длина $a$?
Мы уже знаем объем. Кроме того, мы знаем длину и высоту. Итак, если мы установим ширину как $□$, мы можем составить следующее уравнение.
- $16=4×2×□$
Теперь давайте посчитаем стоимость $□$. Измените его на следующее уравнение.
- $□=16÷4÷2$
Вычислив это выражение, мы видим, что ширина равна 2 см. В математике вы можете вычислить длину стороны по ее объему.
Узнайте, как рассчитать объем и емкость
Объекты вокруг нас не плоские, а трехмерные. Следовательно, мы должны уметь вычислять размеры трехмерных фигур. В частности, много кубических и прямоугольных объектов. Если вы осмотрите свой дом, вы обнаружите, что в нем много кубических и прямоугольных предметов.
Размер куба равен объему. При расчете объема мы можем использовать формулу.
Другим понятием, аналогичным объему, является вместимость судна. Когда жидкость наливается в контейнер и контейнер полон, вместимость определяется тем, сколько жидкости может вместить контейнер. Если вы можете рассчитать объем, вы можете рассчитать вместимость сосуда.
Когда вы узнаете о кубах и прямоугольных параллелепипедах, вы сможете вычислить объем.
