Как вычислить кубатуру фундамента: сколько бетона нужно на фундамент
Как рассчитать кубатуру фундамента
22 января 2014
4451
Оглавление: [скрыть]
- Расчет плитного основания
- Расчеты ленточного фундамента
- Расчет столбчатого основания
В строительной сфере очень широко используются монолитные конструкции из железобетона.
Они популярны как в массовом строительстве, так и при индивидуальных постройках. Прежде чем приступать к работе, необходимо узнать, как рассчитать кубатуру фундамента. Если эти данные будут отсутствовать, то спланировать затраты на строительство и процесс работы будет невозможно.
Схема «пирога» фундамента.
К основным объектам монолитных сооружений из железобетона можно отнести стены, перекрытия и фундамент. Последнее — это основа любого сооружения, поэтому нужно обратить внимание на качество используемых для его строительства материалов.
С типом основания, которое нужно будет построить для сооружения здания, следует определиться изначально. И только после того, как выбор будет сделан, можно будет подумать над тем, как рассчитать кубатуру фундамента.
Фундаменты бывают, ленточные, столбчатые, плиточные.
Специалисты выделяют следующие основные типы фундамента:
- Ленточный.
- Столбчатый.
- Плиточный.
Конечный результат работы зависит от того, насколько правильно произведен расчет. Необходимо тщательнейшим образом измерить все нужные параметры.
Расчет плитного основания
Каждый тип основания имеет свои конкретные особенности при составлении расчета. Плиточный фундамент можно назвать одним из самых легких вариантов. Чтобы посчитать необходимое количество кубов бетона, которое понадобится для фундамента из монолитной плиты, нужно просто перемножить между собой три величины: толщину, ширину и длину.
Вернуться к оглавлению
Расчеты ленточного фундамента
Для расчета ленточного фундамента нужно периметр умножить на длину и ширину.
Выбирая этот вид, нужно в первую очередь определить сечение основания. Если сечение одинаковое, то периметр территории нужно умножить на длину и толщину. Нужно помнить о том, что на некоторых участках сечение ленты может немного отличаться. Этот фактор можно объяснить тем, что нагрузка неровно распределена по основанию, поэтому подбираются разные типы сечения лент. Но даже так рассчитать объем не будет сложно. Для этого нужно просто сделать расчет для каждого участка отдельно, а после сложить все вместе.
Специалисты советуют при монтаже основания ленточного типа использовать готовый фундаментный блок стен (ФБС). Сегодня ФБС очень активно используют в строительстве. Эти блоки изготавливают на заводах в больших объемах, поэтому купить ФБС не составит совершенно никакого труда. В его основе лежит пескобетон. Данные блоки обладают также очень высоким уровнем прочности.
Чтобы вычислить, сколько блоков стен понадобится для постройки конструкции, нужно посчитанную кубатуру поделить на объем блока. Сумма, которая получится, покажет, сколько блоков потребуется для постройки основания.
Вернуться к оглавлению
Расчет столбчатого основания
Что бы узнать кубатуру столба фундамента надо ширину умножить на длину.
Основание столбчатого типа — это конструкция, которая состоит из столбиков прямоугольного или круглого сечения. Столбики между собой могут быть связаны при помощи ростверка. Вначале нужно сделать расчет кубатуры одного бетонного столба. Это делается при помощи умножения ширины на длину.
Если столбики имеют круглое сечение, то следует постоянный коэффициент «Пи» умножить на произведение квадрата радиуса. Результат, который получится, нужно будет умножить на высоту столба. Полученный результат умножается на количество столбиков, которые размещаются на территории. Полученная в итоге цифра и будет объемом.
Если столбики соединены при помощи ростверка, то нужно использовать формулу параллелепипеда, чтобы определить его кубатуру.
После того как расчет кубатуры будет выполнен, нужно выбрать марку бетона. Хочется сразу отметить, что данный процесс весьма сложный и трудоемкий. Прежде чем сделать выбор, нужно произвести следующие расчеты:
- Посчитать проектную и нормативную нагрузку на объект.
- Вычислить вес самой конструкции.
Опираясь на полученные данные и строительные правила и нормы, можно сделать вывод, какая из марок бетона будет более подходящей для конкретного сооружения.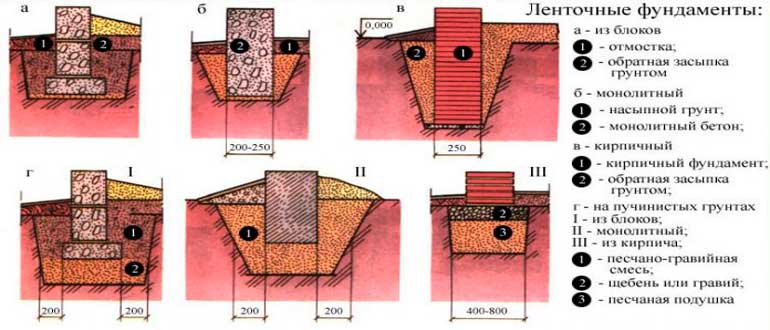
При выборе марки бетона лучше проконсультироваться со специалистом. Человек, который знает толк в этом деле, сможет подобрать именно тот материал, который будет идеален для конкретного основания. Ведь нужно помнить о том, что от правильно подобранного материала зависит и прочность основания. А от прочности основания напрямую зависит и срок его эксплуатации
Узнаем как рассчитать объем бетона для заливки фундамента
Прочность и долговечность любого сооружения напрямую зависят от качества фундамента. А в любом деле для достижения успеха нельзя игнорировать подготовительный этап. Правильность расчётов экономит не только время, нервы, но и ресурсы. О том, как рассчитать объём бетона для заливки фундамента правильно и какие нюансы необходимо учесть, чтобы не попасть впросак, пойдёт речь в данной статье.
Классификация фундаментных оснований и конструктивных особенностей зданий
Необходимо сразу сказать несколько слов о типах фундамента и зданий, так как от этого напрямую зависят расчёты. Если речь идёт о фундаменте, то в первую очередь рассматривается его функциональность. Подобные конструкции бывают несущие или комбинированные. Уровень закладки — глубокий или неглубокий. Кроме этого, важно учитывать регион, тип почвы и глубину залегания грунтовых вод. Прежде чем подходить вплотную к вопросу о том, как правильно посчитать кубатуру бетона, рассматриваются конструкции здания, материалы, из которых оно будет впоследствии построено, планировка и этажность. Различают 3 основных типа фундамента: ленточный, плитный и столбчатый.
Узнаем как посчитать объем — формулы расчета
В статье речь идет о способах определения объема различных тел, прикладных задачах, связанных с…
При каких условиях применение различных типов фундамента наиболее эффективно
Ленточный фундамент – это сплошная непрерывная лента под несущими стенами.
Такой тип используется для того, чтобы нагрузка распределялась равномерно по всей площади основания. Следовательно, перекос здания из-за вспучивания почвы не предвидится. Однако следует понимать, что заилованный, торфяной или болотистый грунт не подойдут для такого основания. В этих случаях применяются сваи. Поэтому определение грунта и его особенностей – важная задача, и решить её могут специалисты. При нормальной почве ленточный фундамент одинаково хорошо подойдёт для возведения как частных коттеджей, так и монолитных зданий.
Следующий тип бетонного основания – плитный. По всей площади будущего строения заливается одна сплошная монолитная плита. Данный фундамент прекрасно зарекомендовал себя на проблемных почвах. Он не только равномерно распределит нагрузку при промерзании грунта, но даже при вспучивании основа приподнимется, чтобы потом снова вернуться в прежнее положение под собственным весом. Дополнительные преимущества – долговечность и надёжность.
Узнаем как много в миксере кубов бетона? Стандарт,.
..
Сколько в миксере кубов бетона: вместимость разных автомобилей, загрузка, транспортировка….
Столбчатый фундамент – это ряд опор, которые обычно располагаются по углам и местам, куда будет распределена наибольшая нагрузка. Главный минус – обустроить подвал не получится. Его применяют для зданий и сооружений с невысоким весом.
При решении вопроса «сколько кубов бетона на фундамент различных типов может понадобиться» необходимо также учитывать климатические особенности местности, в которой будет производится строительство.
Оптимальная глубина заложения фундамента
Промерзание грунта в различных регионах России и странах СНГ имеет свои индивидуальные особенности. Для наиболее точных расчётов лучше всего воспользоваться данными о глубине промерзания грунта и закладывать фундамент ниже. В Воркуте, Сургуте, где зимы более суровы, грунт промерзает не меньше чем на 250 см, а в Москве эта величина будет равняться всего 140 см. В Минске, Киеве и Ростове и того меньше – в среднем это 90-100 см.
Но тут важную роль также играет и тип почвы. Для примера возьмем скальный или полускальный грунт. Закладывать фундамент под 2-этажный коттедж в данном случае можно, в принципе, на любое расстояние. Глубина залегания грунтовых вод в период промерзания земли тоже роли играть не будет. А вот если имеем дело с глиной или суглинком, то углубляться ниже расчётных данных промерзания грунта для данного региона не рекомендуется – если работы ведутся, скажем, в Минске или Киеве, то рыть траншеи под фундамент следует не ниже 100 см. И так далее по аналогии. При рассмотрении вопроса о том, как правильно рассчитать необходимый объём бетона, нелишним будет остановиться на таком важном моменте, как марки бетона.
Сколько весит дом: специфические особенности расчета
Что взять во внимание при расчете веса дома. Удельный вес кровельного покрытия. Расчет площади и…
Специфика применения различных марок бетона
На выбор той или иной марки бетона влияют характеристики прочности.
При подготовительных работах (например, черновая стяжка полов) используется марка 100 или 150. Для небольших хозяйственных построек с ленточным фундаментом и бетонирования дорожек подойдут 200 и 250 марки. 300 и 350 – для фундаментов домов. 400 и 500 применяются, когда есть необходимость в особой прочности. Как рассчитать объём бетона применительно к ленточному, плитному и столбчатому типам фундамента? Об этом пойдёт разговор ниже.
Расчёт объёма бетона для ленточного типа фундамента
Как рассчитать объем бетона с минимальными погрешностями? На самом деле задача сложности особой не представляет. Для расчета по формуле нужны данные о ширине основы (n), высоте фундамента (k), длине по наружной стороне фундамента (a) и длине по внутренней стороне (b). Вставив значения в формулу, можно получить нужный объем бетона (S):
S = 2nk × (a + b).
Расчёт плитного фундамента
Как рассчитать объём для заливки фундамента данного типа? Здесь опять помогут несложные вычисления, заимствованные из школьного курса по геометрии.
Для того чтобы получить объём, необходимо перемножить между собой значения разных сторон – так получается необходимое значение площади, которая, в свою очередь, умножается на высоту будущего фундамента. И все: теперь известен необходимый объём бетона.
Можно, конечно, использовать обычные монолитные плиты, но на практике такое происходит редко из-за дороговизны последних. Хотя плитный фундамент — просто находка в условиях неустойчивых почв, да и при близком залегании грунтовых вод тоже зарекомендовал себя превосходно. И долговечность его выше всяких похвал.
Столбчатый фундамент и его расчёты
Самый экономичный вариант для зданий с небольшим весом и в то же время неприемлемый для всех тех, кто желал бы иметь подвальное помещение. Как рассчитать объём бетона для данного фундамента? Это не составляет труда. Снова геометрия нам в помощь. Для точного расчета объема используемого бетона требуется знать количество столбов в основании здания и расход бетона на единицу.
Вычисления проводятся по формуле, учитывающей длину одной опоры (g) и ее сечение (k):
V = (3,14 × k2 / 4) х g.
Допустим, нужно рассчитать количество бетона на столбчатый фундамент с параметрами сваи g=1,5, k=0,28 и количеством столбов 15 штук. Решение будет выглядеть следующим образом:
(3,14 × 0,28 × 2 / 4) х 1,5 = 0,09 кубометра бетона (расход на одну сваю).
Чтобы вычислить общую массу, умножаем результат на количество свай в основании:
0,09 х 15 = 1,35 кубометра.
Калькулятор бетона на фундамент
Для облегчения расчётов можно воспользоваться программой – калькулятором фундаментов, благо их полно на различных сайтах. Там уже заданы рекомендованные параметры – учитывается не только сам материал древесины, из которого можно изготовить опалубку, но и толщина доски. Также туда можно внести такие параметры: толщина, глубина и высота фундамента над землёй, его периметр (сумма длин всех стен).
Для того чтобы рассчитать нужное количество бетона при помощи онлайн-программы, не обязательно знать формулу объёма.
Калькулятор самостоятельно выполнит необходимые операции. Даже количество необходимого цемента можно вычислить без труда, но с этим поможет уже другой онлайн-калькулятор.
Устроить самопроверку можно, ознакомившись с информацией из таблиц расхода цемента разных марок для изготовления бетона нужной крепости. Чтобы приготовить марку бетона М400 при помощи цемента марки 500, потребуется 440 кг на м3. Понятно, что в любых расчётах может присутствовать погрешность. Обычно она составляет от 3 до 10 процентов. Факторов может быть несколько. Это и неточности при проведении земляных работ, и разгрузка бетона (могут быть потери), и усадка грунта. В любом случае эти, на первый взгляд, мелочи могут легко привести к негативным последствиям. Не хватило бетона — и это уже аврал, потому что нельзя нарушать монолитность. Довезти недостающий материал, учитывая транспортные расходы, обойдётся в 2,5 раза дороже.
Так что лучше наперед все рассчитать и приобрести немного больше материала, чем нужно.
Вы уже знаете, как посчитать, сколько потребуется бетона на фундамент. С калькулятором произвести необходимые вычисления не составит труда, работать с ним удобно, но даже в случае наличия такого помощника помните: расчёты и подготовительные работы в столь важном деле, как строительство, не терпят суеты и спешки.
Заключение
Есть ещё один нюанс при расчёте необходимого количества бетона. Работайте всегда с крупными и проверенными организациями. К сожалению, отпуская свою продукцию, некоторые не очень чистоплотные производители выдают меньшее количество стройматериалов.
$$ \тег{2} C _ {j} знак равно я ( {\ mathcal L} _ {j}), \ \ j = 1 \точки \mu . $$
Существование интегралов (2) равносильно существованию моментов весовой функции, $ p _ {i} = I ( \phi _ {i} ) $,
$ i = 1 \точки \mu $.
Здесь и далее предполагается, что искомые моменты $ p ( x) $
существовать. Кубатурная формула (1), имеющая $ N = \mu $
узлов, не содержащихся ни в одной алгебраической гиперповерхности степени $ m $
и с коэффициентами, определяемыми формулой (2), называется интерполяционной кубатурной формулой. Формула (1) обладает $ m $-свойством, если она является точным равенством, когда $ f ( x) $
является полиномом степени не выше $m$;
интерполяционная кубатурная формула обладает $m$-свойством.
Естественно требовать, чтобы количество неизвестных совпадало с количеством уравнений: $N ( n + 1) = \mu $.
Это уравнение дает предварительную оценку количества узлов. Если $ N = \mu /( n + 1) $
не является целым числом, полагается $ N = [ \mu /( n + 1)] + 1 $,
где $ [ \mu / ( n + 1)] $
обозначает целую часть $ \mu /( n + 1) $.
Кубатурная формула с таким количеством узлов не всегда должна существовать. Если он существует, то количество его узлов равно $ 1/( n + 1) $
умноженное на количество узлов интерполяционной кубатурной формулы. Однако в этом случае сами узлы и коэффициенты определяются нелинейной системой уравнений (3). В методе неопределенных параметров кубатурную формулу строят, пытаясь придать ей вид, упрощающий систему (3). Это можно сделать, когда $ \Omega $
и $ р ( х) $
иметь симметрии.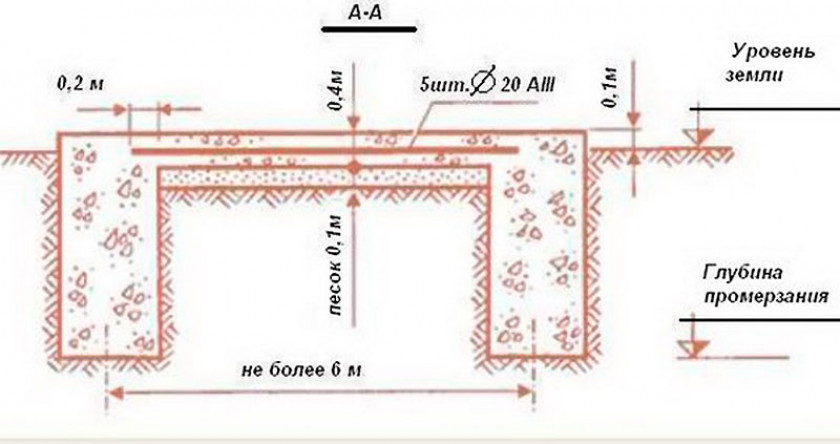
Пример. Пусть $ \Omega = K _ {2} = \{ — 1 \leq x _ {1} , x _ {2} \leq 1 \} $,
$ р ( х _ {1} , х _ {2} ) = 1 $.
Одного просят построить кубатурную формулу со свойством $7$; $n = 2$,
$ \mu = M ( 2, 7) = 36 $,
и 12 узлов. Узлы расположены следующим образом. Первая группа узлов состоит из точек пересечения окружности радиуса $a$,
с центром в начале координат, с осями координат. Вторая группа состоит из точек пересечения окружности радиуса $b$,
также с центром в начале координат с прямыми линиями $ x _ {1} = \pm x _ {2} $.
Аналогично строится и третья группа, радиус которой обозначается $c$.
Коэффициенты, приписываемые узлам одной группы, одинаковы и обозначаются $A, B, C$
для узлов первой, второй и третьей группы соответственно.
Теорема 1) Кубатурная формула, инвариантная относительно $ G $ обладает $m$-свойством тогда и только тогда, когда оно точно для всех многочленов степени не выше $m$ которые инвариантны относительно $G$ (см. [5]). Метод неопределенных коэффициентов можно определить как метод построения инвариантных кубатурных формул, обладающих $m$-свойством. В приведенном примере роль группы $G$ может играть группа симметрии квадрата. Теорема 1 имеет существенное значение при построении инвариантных кубатурных формул.
Для простых областей интегрирования, таких как куб, симплекс, шар или сфера, и для веса $ p (x) = 1 $, можно построить кубатурные формулы, многократно используя квадратурные формулы. Например, когда $ \Omega = K _ {n} = \{ {- 1 \leq x _ {i} \leq 1 } : {i = 1 \dots n } \} $ является кубом, можно использовать квадратурную формулу Гаусса с $ k $ узлы $ t _ {i} $ и коэффициенты $A_{i}$ чтобы получить кубатурную формулу
$$
\int\limits _ {K _ {n} }
f ( x) dx \ cong \
\ сумма _ {я _ {1} \ точки я _ {п} = 1 } ^ {к}
А _ {я _ {1} } \ точки А _ {я _ {п} }
е ( т _ {я _ {1} } \ точки т _ {я _ {п} } )
$$
9\альфа $
такое, что $ 0 \leq \alpha _ {i} \leq 2k — 1 $,
$ i = 1 \ точек n $,
и, в частности, для всех многочленов степени не выше $2k — 1$.
Количество узлов таких кубатурных формул быстро увеличивается, что ограничивает их применимость.
В дальнейшем предполагается, что весовая функция имеет фиксированный знак, скажем
$$ \тег{4} р ( х) \geq 0 \ \ \mathop{\rm in} \Omega \ \ \textrm{ и } \ \ р _ {1} > 0. $$
Тот факт, что коэффициенты кубатурной формулы с такой весовой функцией положительны, является ценным свойством формулы.
Теорема 2) Если область интегрирования $ \Omega $ замкнут и $ p ( x) $ удовлетворяет (4), существует интерполяционная кубатурная формула (1), обладающая $ m $-свойством, $ N \leq \mu $, с положительными коэффициентами и с узлами в $\Omega$. Вопрос о реальном построении такой формулы пока открыт.
Теорема 3) Если кубатурная формула с весом, удовлетворяющим (4), имеет вещественные узлы и коэффициенты и обладает $m$-свойством, то не менее $\lambda = M(n,l)$
ее коэффициентов положительны, где $ l = [ m/2] $
— целая часть $ m/2 $.
В условиях теоремы 3 число $ \lambda $
является нижней границей количества узлов:
9{(к)} $
и $C_{j}$
реальны.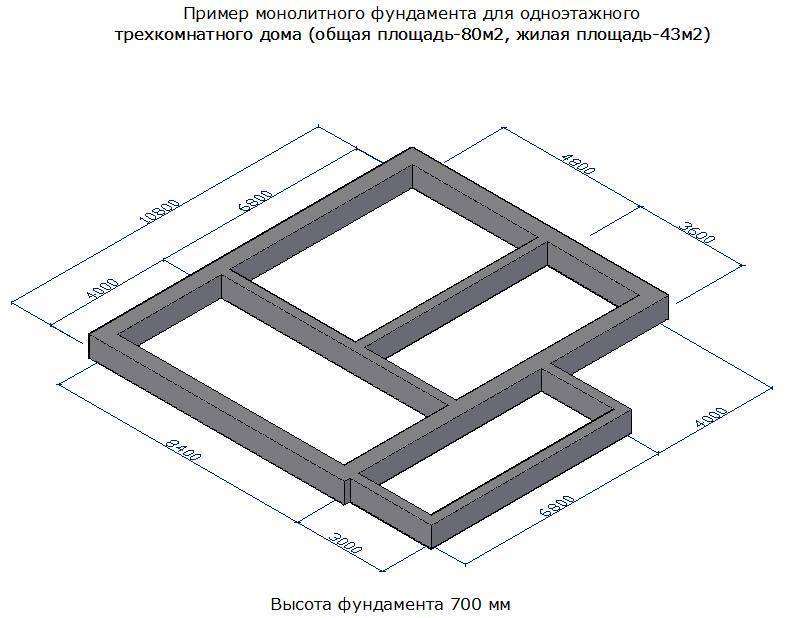
Что касается кубатурных формул со свойством $ m $, то особенно интересны те, которые имеют минимальное количество узлов. При $ м = 1, 2 $ такие формулы легко найти для любых $n$, произвольный $\Omega$ и $ p ( x) \geq 0 $; минимальное количество узлов — это как раз нижняя граница $\lambda$: В первом случае он равен 1, а в $n+1$ В секунду. Когда $ m \geq 3 $, минимальное количество узлов зависит от домена и веса. Например, если $m = 3$, область центрально-симметрична, и если $p(x)=1$, количество узлов $2n$; для симплекса и $p(x)=1$, это $n+2$.
В силу (4),
$$ \тег{5} ( \ фи , \ фунтов на квадратный дюйм ) = \ I ( \phi \overline \psi \; ) $$
— скалярное произведение в пространстве многочленов. Пусть $ {\ mathcal P} _ {k} $
– векторное пространство многочленов степени $k$
которые ортогональны в смысле (5) всем полиномам степени не выше $k — 1$.
Это пространство имеет размерность $ M (n — 1, k) $—
количество мономов степени $k$.
Многочлены от $ {\ mathcal P} _ {k} $
называются ортогональными многочленами для $ \Omega $
и $p(x)$.
{n} ) $,
где $m > n/2$,
и в этом случае искомая кубатурная формула считается точной для всех многочленов степени не выше $m — 1$.
{(j)}$).
В. Бойков, В. А. Есафьева, П. В. Айкашев, «О построении квадратурных и кубатурных формул для вычисления гиперсингулярных интегралов”, Известия вузов. Поволжский регион. Физико-математические науки, 2018, № 1, с. 1, 94–105
org/10.21685/2072-3040-2018-1-8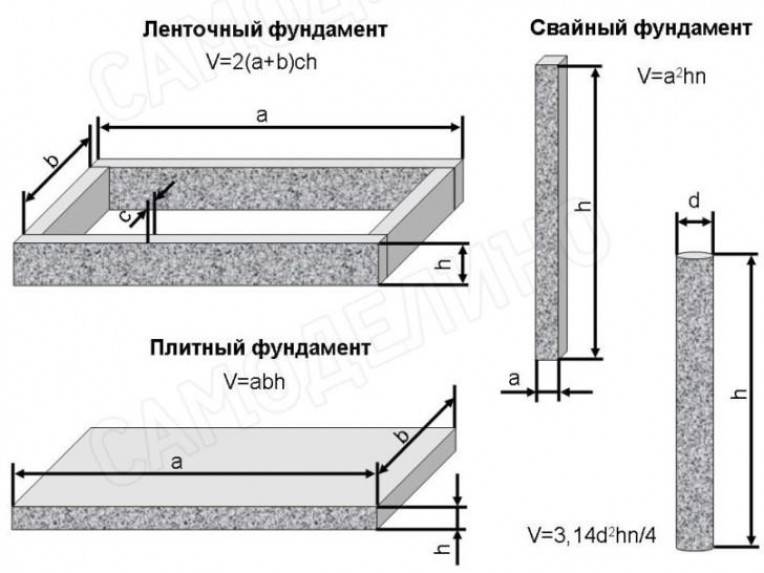
Мы рассматриваем гиперсингулярные и полигиперсингулярные интегралы с периодическими ядрами и на классах периодических функций. Выводы. В работе предложены оптимальные по точности методы вычисления гиперсингулярных и полигиперсингулярных интегралов, которые могут быть использованы для решения задач физики, инженерной и вычислительной математики.