Как рассчитать объем в м3 фундамента: Ничего не найдено для Fundament Obem Fundamenta Kak Poschitat Obem Fundamenta V M3 Kalkulyator %23Kak Poschitat Kubaturu Fundamenta Pod Dom
Как правильно рассчитать объем фундамента?
Бетонная смесь является универсальным строительным материалом, без которого невозможно возвести дом или другое строение. Данный материал обладает многими полезными свойствами, поэтому его успешно используют при любой влажности и в широких температурных диапазонах. Для определения необходимого количества данного материала и точного планирования времени выполнения строительных работ нужно правильно провести все расчеты и выявить требуемый объем фундамента (V).
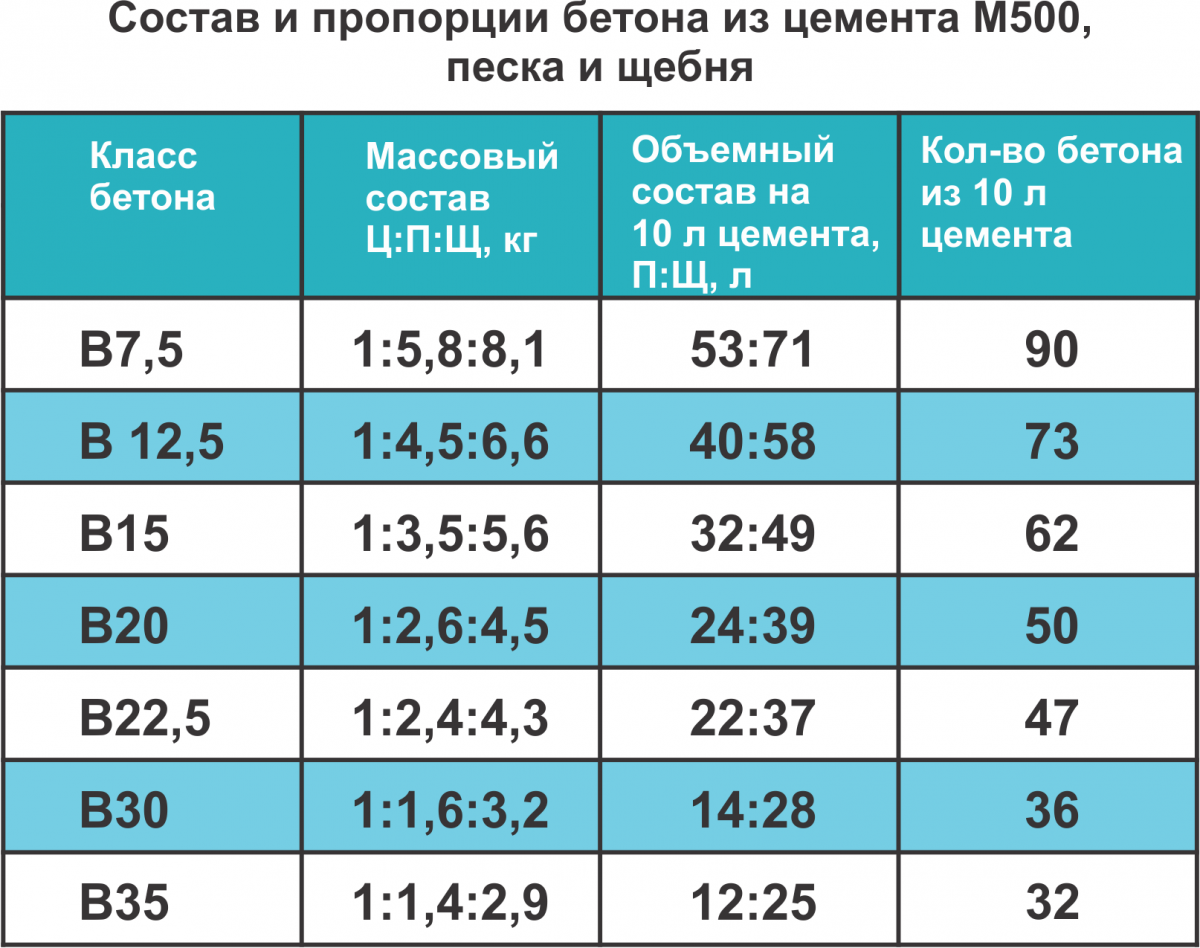
Рисунок 1. Таблица состава и пропорций бетонной смеси.
В связи с тем что большинство бетонных оснований представляют собой сложную геометрическую форму, расчет объема можно несколько облегчить, используя разбивку фундамента на простые участки.
При применении арматуры, площадь которых обычно составляет около 5-10% общего объема основания, данную погрешность можно не учитывать, отнеся ее к строительным потерям.
Вернуться к оглавлению
Как вычислить объем столбчатого фундамента?
Чертеж столбчатого фундамента.
Столбчатый фундамент представляет собой сваи, погруженные в грунт, или заливку армирующей бетонной смеси в пробуренные скважины. Использование столбчатого основания целесообразно при глубоком залегании твердого (несущего) слоя земли или для конструирования легких строений на вспучивающей почве. Благодаря большой экономии строительных материалов и простоте строительства, свайный фундамент является популярной конструкцией.
При круглом сечении элементов столбчатого фундамента расчет проводится исходя из их площади поперечного сечения: S = 3.14*R2, где R – радиус сваи. Полученный результат следует умножить на высоту столбика и количество таких элементов.
Например, если радиус 1-го элемента столбчатого основания составляет 0,15 м, а высота столбика – 2,0 м, то для одной сваи потребуется такое количество бетонной смеси: 3,14*0,15*0,15*2 = 0,1413 м
Вернуться к оглавлению
Как рассчитать объем ленточного фундамента?
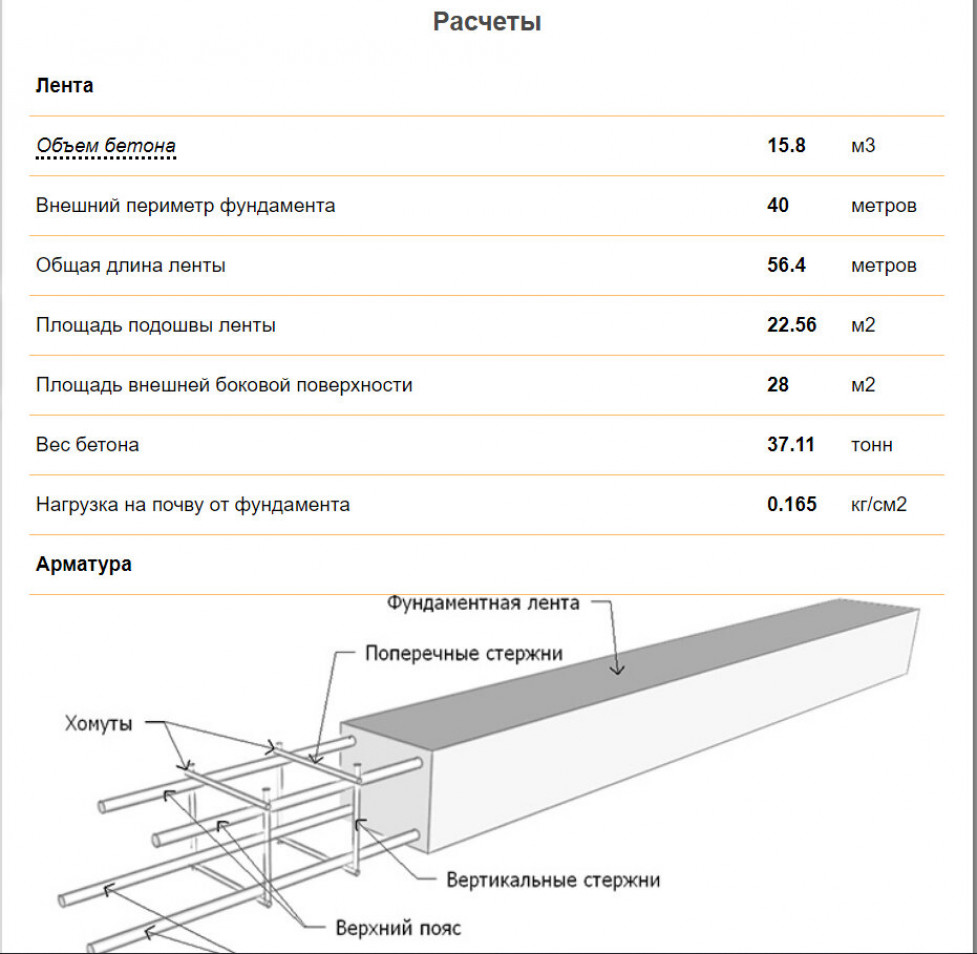
Данное основание широко применяется при малоэтажном частном строительстве, потому что оно обладает отличными эксплуатационными характеристиками и легкостью монтирования. Объем ленточного фундамента можно посчитать, зная высоту и ширину ленты. Поскольку такой элемент является прямоугольной формы, то для определения его площади необходимо перемножить высоту на ширину. Чтобы определить полный объем ленточного фундамента, нужно площадь умножить на его длину.
Объем ленточного фундамента можно посчитать, зная высоту и ширину ленты. Поскольку такой элемент является прямоугольной формы, то для определения его площади необходимо перемножить высоту на ширину. Чтобы определить полный объем ленточного фундамента, нужно площадь умножить на его длину.
Схема ленточного фундамента.
Стоит отметить, что высота ленты включает в себя высоту надземной части и глубину закладки. При этом высота фундамента ленточного вида должна быть минимум в 2 раза больше его ширины. Под общей длиной ленты подразумевается не только внешний периметр, но и длина всех перегородок, под которыми будет улаживаться фундамент. Нужно помнить, что такие перегородки не всегда являются несущими, поэтому под них в большинстве случаев монтируется более легкий вид фундамента, который также имеет другие габариты. Этот факт также необходимо учесть при подсчете объема бетона.
Общий V основания состоит из объемов его отдельных частей, имеющих разную геометрическую структуру, каждая из которых рассчитывается по формуле: V = L*S, где L – длина ленты основания, а S – площадь поперечного сечения.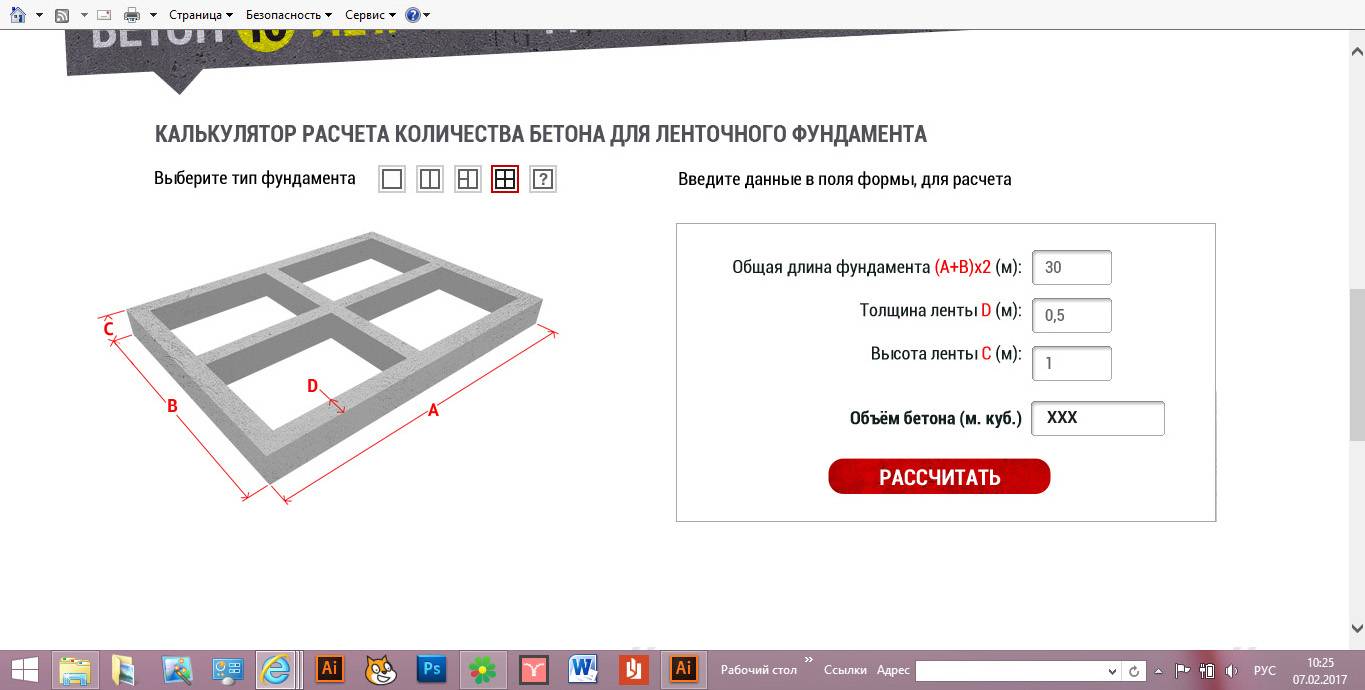 Например, ленточный фундамент одинаковой геометрической структуры имеет размеры: длина – 30 м, площадь поперечного сечения – 0,2 м2. В этом случае объем основания составит: V = 30*0,2 = 6 м3.
Например, ленточный фундамент одинаковой геометрической структуры имеет размеры: длина – 30 м, площадь поперечного сечения – 0,2 м2. В этом случае объем основания составит: V = 30*0,2 = 6 м3.
Вернуться к оглавлению
Как рассчитать объем плиточного фундамента?
- при отсутствии в строительном проекте подвального помещения;
- на плавающих грунтах;
- при использовании монолитной плиты в качестве основы для пола.
Схема плитного фундамента.
Такое основание оказывает достаточно маленькое давление на почву (порядка 0,1 кг/см2) и обладает большей жесткостью, с помощью которой он легко переносить разнонаправленные нагрузки без образования трещин и других разрушений. В большинстве случаев при конструировании плиточного фундамента применяют ребра жесткости, которые нужно учитывать при подсчете количества бетонной смеси.
V плиточного основания можно посчитать по формуле: V = S*H, где S – площадь плиты, а H – ее толщина. Например, если плита имеет размеры: ширина – 6 м, длина – 10 м, высота – 0,2 м, то в результате мы получим такое значение: V = 6*10*0,2 = 12 м3. При использовании ребер жесткости необходимо отдельно рассчитать их объем. Например, используется 4 таких элемента с объемом каждого ребра: V1 = 0,11; V2 = 0,12; V3 = 0,14; V4 = 0,15 м3. Общий объем ребер жесткости будет: Vсумм = 0,11+0,12+0,14+0,15 = 0,52 м
Чтобы получить V бетона, который нужно будет приготовить для фундамента, необходимо из объема плиты вычесть объем ребер жесткости, то есть: 12-0,52 = 11,48 м3.
Вернуться к оглавлению
Расчет объема компонентов бетона
При проведении строительных работ необходимо знать не только общий объем бетонной смеси, но и количество всех ее составляющих по отдельности. Если вы покупаете уже готовый бетон, то такие расчеты вам ни к чему. Если же вы изготавливаете бетонную смесь своими руками, то очень важно посчитать количество всех компонентов.
Если же вы изготавливаете бетонную смесь своими руками, то очень важно посчитать количество всех компонентов.
В состав бетонной смеси входит цемент, песок, вода, щебень или другой наполнитель, поэтому правильный подбор этих составляющих позволит получить качественный материал, из которого получится надежный и долговечный фундамент. Чтобы бетонная смесь соответствовала всем нормам и требованиям, нужно провести расчет точного количества всех компонентов на 1 м
Расчет состава следует начинать с подсчета основного компонента – бетона. Например, если нужно приготовить легкий бетон марки М100, то следует брать цемент М400. Для изготовления такого бетона потребуется 230 кг цемента на 1 м3. Нужно знать, что состав бетонной смеси во многом определяется водоцементным соотношением, то есть количеством воды на единицу объема материала. Для разных марок бетона этот показатель будет разным:
- для марки М100 и цемента М300 – 0,80;
- для М150 и М300 – 0,66;
- для М200 и М300 – 0,64.

Определив количество цемента и воды, можно рассчитать необходимый объем остальных составляющих. Для этого требуется из единицы объема отнять количество цемента и воды. Также необходимо учесть, что используемые песок и щебень отличается по крупности. Поэтому можно утверждать, что объем песка и щебня будет равен произведению количества готового материала на процентное соотношение, которое разделено на 100. Зная эти величины, можно произвести вычисления для нескольких кубов бетона. На рис. 1 приведен пример состава и пропорций бетонной смеси из цемента М400 и М500.
Правильно рассчитав состав бетонной смеси и ее количество, вы сможете не только сконструировать надежное основание, но и сэкономить денежные средства, так как в этом случае у вас не будет лишнего материала или его недостачи.
Объем полуцилиндра – формула, примеры, определение
Объем полуцилиндра определяется как количество пространства, занимаемого фигурой в трехмерной плоскости. Объем полуцилиндра измеряется в кубических единицах, таких как кубические сантиметры (см 3 ), кубические дюймы (в 3 ), кубические футы (футы 3 ), кубические метры (м  Полуцилиндр в математике — это объемная объемная фигура, которая получается при продольном усечении цилиндра. Когда горизонтальный цилиндр разрезается на две равные части, параллельные длине цилиндра, полученные таким образом формы называются полуцилиндрами. Давайте подробно разберем формулу для расчета объема полуцилиндра и частичного цилиндра в следующих разделах.
Полуцилиндр в математике — это объемная объемная фигура, которая получается при продольном усечении цилиндра. Когда горизонтальный цилиндр разрезается на две равные части, параллельные длине цилиндра, полученные таким образом формы называются полуцилиндрами. Давайте подробно разберем формулу для расчета объема полуцилиндра и частичного цилиндра в следующих разделах.
| 1. | Формула объема полуцилиндра |
| 2. | Как найти объем неполного цилиндра? |
| 3. | Формула площади поверхности полуцилиндра |
| 4. | Часто задаваемые вопросы об объеме полуцилиндра |
Формула объема полуцилиндра
Полуцилиндр в математике относится к трехмерной объемной фигуре, представляющей собой продольно усеченный цилиндр. Объем полуцилиндра равен половине всего объема цилиндра. Объем полуцилиндра определяется как объем пространства, занимаемый полуцилиндром. Объем полуцилиндра измеряется в кубических единицах, таких как кубические сантиметры, кубические дюймы, кубические футы, кубические метры и т. д.
Объем полуцилиндра измеряется в кубических единицах, таких как кубические сантиметры, кубические дюймы, кубические футы, кубические метры и т. д.
Формула для расчета объема полуцилиндра может быть получена как,
Мы знаем, объем цилиндра = площадь основания × высота
⇒ Объем цилиндра = πr 2 × h
где
- r = радиус
- ч = Высота
Поскольку объем полуцилиндра = (1/2) × объем цилиндра
⇒ Объем полуцилиндра = (1/2) × πr 2 h
Также диаметр, d = 2 × r
или r = d/2
Таким образом, объем полуцилиндра в единицах диаметра может быть выражен как 92})\)
где,
- r = радиус цилиндра.
- ч = высота воды.
- l = длина цилиндра.
Примечание: Функция cos -1 выражается в радианах.
Объем неполного цилиндра будет в кубических единицах. Например, кубические дюймы, кубические футы и кубические метры. Теперь, когда мы научились вычислять объем полуцилиндра, давайте быстро посмотрим, как вычислить площадь его поверхности в следующем разделе.
Теперь, когда мы научились вычислять объем полуцилиндра, давайте быстро посмотрим, как вычислить площадь его поверхности в следующем разделе.
Формула площади поверхности полуцилиндра
Мы можем рассчитать площадь поверхности полуцилиндра, сложив половину площади криволинейной поверхности цилиндра с площадью двух полукругов и площадью нижнего прямоугольного сечения. Формула площади поверхности полуцилиндра может быть представлена следующим образом:
Общая площадь поверхности полуцилиндра = (1/2) × площадь изогнутой поверхности цилиндра + 2 × площадь полукруга + площадь нижнего прямоугольника.
Общая площадь поверхности полуцилиндра = (1/2) × 2πrh + 2 × (1/2)πr 2 + 2rh
Общая площадь поверхности полуцилиндра = πrh + πr 2 + 2rh
Давайте лучше поймем объем полуцилиндра на нескольких решенных примерах.
Решенные примеры для объема полуцилиндра
Пример 1: Найдите количество кофе, которое может поместиться в чашке, имеющей форму полуцилиндра.
 Радиус чашки равен 2 дюймам, а высота — 4 дюймам (используйте π = 3,14)
Радиус чашки равен 2 дюймам, а высота — 4 дюймам (используйте π = 3,14)Решение:
Дано:
Радиус (r) = 2 в
Высота (h) = 4 вМы воспользуемся формулой объема полуцилиндра, чтобы найти количество кофе, которое может вместить кружка.
Объем полуцилиндра = (1/2)πr 2 ч кубических единицПодставляя значения в приведенную выше формулу,
Объем полуцилиндра = (1/2) × 3,14 × (2) 2 × (4)Ответ: Объем кофе равен 25,12 в 3 .
Пример 2: У Сэма есть цилиндрическая свеча диаметром 4 дюйма и высотой 10 дюймов. Он хочет разрезать его на два полуцилиндра. Каков будет объем половины свечи? рассчитать объем по формуле полуцилиндра. (Используйте π = 3,14)
Решение:
Дано:
Радиус свечи (r) = 2 в
Высота свечи (h) = 10 вИспользуем формулу объема полуцилиндра,
Объем полуцилиндра = (1/2)πr 2 ч кубических единицПодставляя значения в приведенную выше формулу,
Объем полуцилиндрической свечи, V = (1/2) × 3,14 × (2) 2 × 10Ответ: Объем полуцилиндрической свечи равен 62,8 в 3 .

перейти к слайдуперейти к слайду
Разбивайте сложные концепции с помощью простых визуальных средств.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.
Записаться на бесплатный пробный урок
Практические вопросы по объему полуцилиндра
перейти к слайдуперейти к слайду
Часто задаваемые вопросы об объеме полуцилиндра
Каков объем полуцилиндра?
Объем полуцилиндра определяется как общее пространство, занимаемое полуцилиндром в трехмерной плоскости. Объем полуцилиндра равен половине объема цилиндра.
Как найти объем полуцилиндра?
Объем полуцилиндра можно рассчитать, разделив общий объем цилиндра на 2. Зная радиус и высоту полуцилиндра, мы можем рассчитать его объем по формуле Объем цилиндра = (1 /2)πr 2 ч
где
- r — радиус
- h высота цилиндра
Как найти радиус полуцилиндра, используя объем?
Радиус полуцилиндра можно рассчитать, если известны объем и высота. Чтобы найти радиус в этом случае, мы можем применить формулу объема полуцилиндра, V = (1/2)πr 2 h, где «r» — радиус, а «h» — высота цилиндра, и подставьте известные значения для решения «r».
Чтобы найти радиус в этом случае, мы можем применить формулу объема полуцилиндра, V = (1/2)πr 2 h, где «r» — радиус, а «h» — высота цилиндра, и подставьте известные значения для решения «r».
Как найти высоту полуцилиндра, используя объем
Высота полуцилиндра с использованием объема и радиуса может быть рассчитана по формуле Объем полуцилиндра = (1/2)πr 2 h, где «r» — радиус, а «h » — высота цилиндра. Подставьте данные значения и решите найти недостающее значение высоты полуцилиндра.
Как изменится объем полуцилиндра при увеличении радиуса вдвое?
Объем полуцилиндра пропорционален квадрату радиуса полуцилиндра. Следовательно, объем полуцилиндра увеличивается в четыре раза при увеличении радиуса вдвое.
Какие единицы измерения объема полуцилиндра?
Единицей измерения объема цилиндра являются кубические единицы. Это может быть выражено в таких единицах, как см 3 , в 3 , фут 3 , м 3 и т. д.
д.
Какова формула площади поверхности полуцилиндра?
Общая формула для общей площади поверхности полуцилиндра имеет следующий вид: Общая площадь поверхности полуцилиндра = πrh + πr 2 + 2rh, где «r» — радиус, а «h» — высота цилиндра.
Скачать БЕСПЛАТНЫЕ учебные материалы
Объем цилиндра. Рабочие листы
Как рассчитать объем прямоугольной призмы?
В геометрии призма представляет собой объект трехмерной формы, который состоит из двух одинаковых многоугольников, обращенных друг к другу и соединенных по бокам прямоугольными или параллелограммными гранями. Эти одинаковые многоугольники называются основаниями призмы и могут иметь любую форму, например треугольники, квадраты, прямоугольники или любой n-сторонний многоугольник. Призма является важным членом семейства многогранников. В зависимости от типа многоугольного основания призмы делятся на два типа: правильные и неправильные призмы. И в зависимости от выравнивания оснований существует два типа призм: прямые призмы и наклонные призмы.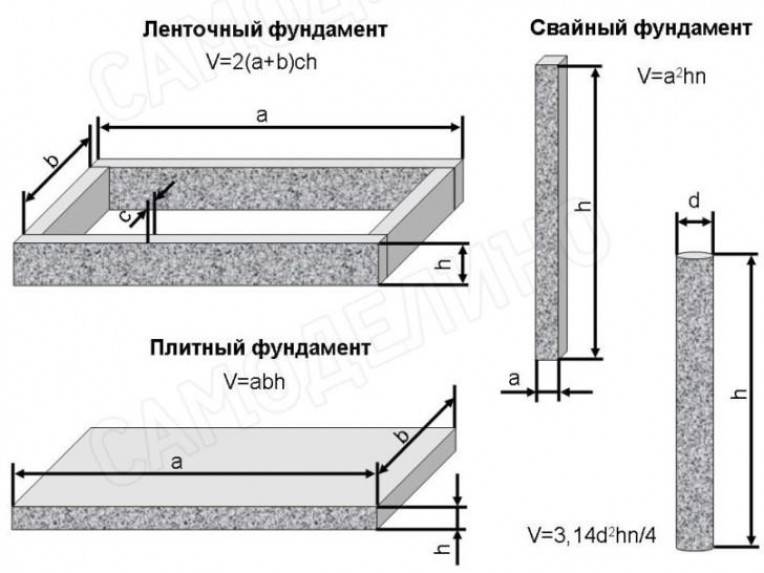 Кроме того, в зависимости от формы многоугольного основания призмы подразделяются на различные типы: треугольные призмы, прямоугольные призмы, квадратные призмы, пятиугольные призмы, шестиугольные призмы и т. д.
Кроме того, в зависимости от формы многоугольного основания призмы подразделяются на различные типы: треугольные призмы, прямоугольные призмы, квадратные призмы, пятиугольные призмы, шестиугольные призмы и т. д.
Прямоугольная призма
Прямоугольная призма представляет собой трехмерную фигуру, состоящую из шести прямоугольных плоских граней. Это призма с двумя прямоугольными основаниями и четырьмя боковыми прямоугольными гранями, двенадцатью сторонами и восемью вершинами. Согласно математическим исследованиям, прямоугольным параллелепипедом называется любой многогранник, напоминающий прямоугольную призму. В прямоугольной призме каждый угол прямой. Он также известен как прямоугольный шестигранник, правильная прямоугольная призма и прямоугольный параллелепипед.
Объем прямоугольной призмы
Объем прямоугольной призмы — это полное пространство, заключенное внутри прямоугольной призмы. Она обычно обозначается буквой «V» и измеряется в см 3 , м 3 , в 3 и т. д. Объем прямоугольной призмы определяется путем умножения площади ее основания на ее высоту.
д. Объем прямоугольной призмы определяется путем умножения площади ее основания на ее высоту.
Формула объема прямоугольной призмы дается следующим образом:
Объем прямоугольной призмы = площадь основания × высота призмы
Поскольку основанием призмы является прямоугольник, ее площадь равна произведению длины и ширины. Пусть «h» — высота призмы, «l» — длина основания, а «b» — ширина основания.
Теперь формула для объема прямоугольной призмы дается следующим образом:
Объем прямоугольной призмы = l × w × h кубических единиц
Решаемые примеры на основе
Объем прямоугольной призмыЗадача 1. Найдите высоту прямоугольной призмы, если ее объем равен 90 кубических дюймов, а его базовая площадь равна 15 квадратных дюймов.
Решение:
Приведены данные,
Объем прямоугольной призмы = 90 куб.
в
Площадь основания = 15 кв. в
Мы знаем, что,
Формула объема прямоугольной призмы = Площадь основания × Высота призмы
⇒ 90 = 15 × h
⇒ h = 90/15 = 6 дюймы.
Следовательно, высота данной призмы равна 6 дюймам.
Задача 2: Определить объем прямоугольной призмы, если длина ее основания 10 см, ширина основания 6 см, а высота призмы 15 см.
Решение:
Приведенные данные,
Высота прямоугольной призмы (h) = 15 см
Длина основания (l) = 10 см см
Мы знать, что,
Объем прямоугольной призмы формула (V) = площадь основания × высота призмы
площадь основания = l × w
= 10 × 6 = 60 кв.см.
В = 60 × 15 = 900 куб. см
Отсюда объем прямоугольной призмы 900 куб. см.
Задача 3: Какова ширина основания прямоугольной призмы, если ее объем 2100 куб. см, а его высота и длина основания равны 25 см и 12 см соответственно?
Решение:
Приведены данные,
Объем прямоугольной призмы = 2100 куб.
см
Высота прямоугольной призмы (h) = 25 см
Длина основания (l) = 12 см
Мы знаем, что,
Формула объема прямоугольной призмы (V) = площадь основания × высота призмы
Площадь основания = длина × ширина
⇒ V = длина × ширина × высота
⇒ 2100= 12 × ширина × 25
⇒ 300w = 2100
⇒ w = 2100/ 300 = 7 см
Следовательно, ширина основания прямоугольной призмы 7 см.
Задача 4. Каков объем прямоугольной призмы высотой 20 единиц и площадью основания 120 квадратных единиц?
Решение:
Приведены данные,
Высота прямоугольной призмы (h) = 20 единиц
Площадь основания = 120 квадратных единиц
Мы знаем, что
Объем прямоугольной призмы по формуле (V) = Площадь основания × Высота призмы
V = 120 × 20 = 2400 кубических единиц.
Следовательно, объем прямоугольной призмы равен 2400 кубических единиц.
Задача 5. Какова длина основания прямоугольной призмы, если ее объем 150 куб. см, а его высота и ширина основания равны 10 см и 3 см соответственно?
Решение:
Приведены данные,
Объем прямоугольной призмы = 150 куб. см
Высота прямоугольной призмы (h) = 10 см
Ширина основания (w) = 3 см
Мы знаем, что,
Формула объема прямоугольной призмы (V) = площадь основания × высота призмы
Площадь основания = длина × ширина
⇒ V = длина × ширина × высота
⇒ 150 = длина × 3 × 10
⇒ 30l = 150 5 см
Следовательно, длина основания прямоугольной призмы равна 5 см.
Задача 6. Каков объем прямоугольной призмы, высота которой равна 20 единицам, а длина и ширина основания равны 15 единицам и 12 единицам соответственно?
Решение:
Приведенные данные,
Высота прямоугольной призмы (h) = 20 единиц
Длина основания (l) = 15 единиц
Ширина основания (w) = 12 шт.
Мы знать, что,
Объем прямоугольной призмы = l × w × h кубических единиц
V = 15 × 12 × 20 = 3600 кубических единиц.
Следовательно, объем прямоугольной призмы равен 3600 кубических единиц.
Задача 7. Определить объем прямоугольной призмы, если ее высота равна 10 см, а длина и ширина основания равны 8 см и 6 см соответственно.
Решение:
Приведенные данные,
Высота прямоугольной призмы (h) = 10 см
Длина основания (l) = 8 см
Ширина основания (w) = 6 см
Мы знаем, что,
Объем прямоугольной призмы = l × w × h кубических единиц
V = 8 × 6 × 10 = 480 куб. см
Значит, объем прямоугольной призмы равен 480 куб. см.
Часто задаваемые вопросы на основе прямоугольной призмы
Вопрос 1: Каков объем прямоугольной призмы?
Ответ:
Объем прямоугольной призмы — это количество вещества, которое она может удержать, или это пространство, занимаемое ею в трехмерном пространстве.
Итак, объем прямоугольной призмы рассчитывается путем умножения площади ее основания на ее высоту. Формула для нахождения объема прямоугольной призмы:
Объем (V) = высота призмы × площадь основания.
Рассчитывается в кубических единицах, таких как см 3 , м 3 , ин 3 и т. д.
Вопрос 2: Какие изменения происходят с объемом прямоугольного см, если его высота удвоится ?
Ответ:
Объем прямоугольной призмы является произведением ее трех измерений, т. е.
объем = длина × ширина × высота.
Если высоту прямоугольной призмы увеличить вдвое, то ее объем будет V 2 = l × w × (2h) = 2 × lwh = 2 × V 1 . Таким образом, можно с уверенностью сказать, что объем прямоугольной призмы удваивается, когда ее высота увеличивается вдвое.
Вопрос 3: Что произойдет с объемом прямоугольной призмы, если ее высоту уменьшить вдвое?
Ответ:
Объем прямоугольной призмы равен произведению ее трех измерений, т.


 Радиус чашки равен 2 дюймам, а высота — 4 дюймам (используйте π = 3,14)
Радиус чашки равен 2 дюймам, а высота — 4 дюймам (используйте π = 3,14)
 в
в см
см

 Итак, объем прямоугольной призмы рассчитывается путем умножения площади ее основания на ее высоту. Формула для нахождения объема прямоугольной призмы:
Итак, объем прямоугольной призмы рассчитывается путем умножения площади ее основания на ее высоту. Формула для нахождения объема прямоугольной призмы: