Как рассчитать кубы: Как рассчитать куб доски — интернет-магазин Корпорация Снабжения

Как рассчитать объём ламината: простые способы

«Мясо лучше в магазине покупать». Так говорил Шарик из мультфильма нашего детства «Лето в Простоквашино». И глубокомысленно добавлял: «Там костей больше». А вот ламинат лучше покупать в интернет-магазине. Здесь больше выбор брендов, коллекций и расцветок. Существует только одна проблема — доставка. Иногда для определения её стоимости надо знать не только количество ламината, но и его объём. Например, его требуют указывать транспортные компании, которые доставляют наш ламинат в регионы и за пределы Москвы. В этой статье мы расскажем, как рассчитать объём ламината для доставки.

Как рассчитать объём коробки ламината

Современный ламинат поставляется в коробках, в которые упаковано сразу несколько досок. Обратите внимание на описание товара на нашем сайте. Внизу обязательно указано, сколько досок ламината в каждой коробке и какова её масса. Есть и третий параметр — площадь, которую можно покрыть материалом из одной коробки. Он нужен вам для расчета количества коробок для пола в вашей комнате.

Доски ламината в коробке уложены в стопку. Зная их количество в коробке и высоту одной доски, мы легко посчитаем высоту упаковки. А ширина и длина коробки будут совпадать с аналогичными показателями отдельной доски. Перемножив эти три цифры, мы получим объём в кубических мм, мм³. Чтобы перевести в привычные для транспортной компании кубические метры, нужно просто переставить десятичную точку на 9 цифр левее и отбросить лишние знаки. Если математика не являлась вашим любимым предметом в школе, то сразу можете перейти к следующему пункту. А здесь мы приводим пример такого расчёта.

Например, возьмём ламинат Holzmeister Original. Одна доска этого надёжного и красивого материала имеет толщину 12 мм. В каждой коробке находится 8 штук. Значит высота коробки составляет 12×8 = 96 мм. Длина доски — 1 212 мм, а ширина — 142 мм. Таким образом, объём коробки равен 1 212×142×96 = 16 521 984 мм³. Теперь ставим десятичную точку. Отсчитываем справа 9 знаков и при необходимости добавляем нули слева. При расчете на калькуляторе просто поделите результат на 1 000 000 000. Получается примерно 0,0165 м³. Такая точность транспортной компании ни к чему. Так что округляем до 0,017 м³. Последний знак округляем в большую сторону, так как картон и полиэтилен тоже немного увеличивают объём коробки.

Как рассчитать объём ламината: простые способы

1. Посчитайте на калькуляторе

Просто перемножьте высоту, длину и ширину одной доски, выраженную в мм, которые указаны на нашем сайте. А потом умножьте на количество штук в упаковке и поделите на 1 000 000 000 для получения объёма в м³.

2. Перемножьте размеры в метрах

При желании можно и не перемножать размеры в мм, а сразу перевести их в метры и умножить на количество досок в коробке. Получится 8×1,2×0,14×0,012 = 0,0161 м³ ≈ 0,017 м³≈ 0,02 м³. Обратите внимание, что мы сразу округлили цифры. И особого значения эти округления на результат не оказали.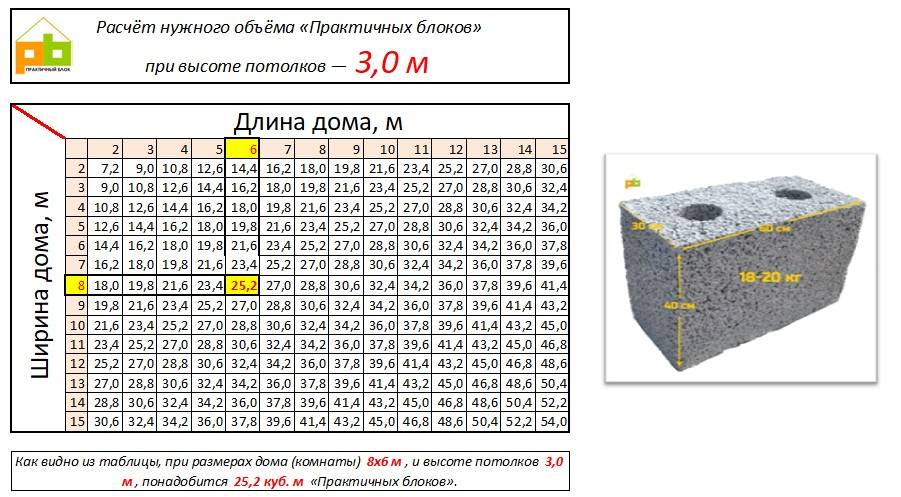 Поэтому при расчете объёма коробки ламината перемножьте округлённые до одного-двух знаков после запятой размеры доски и умножьте на их количество в одной упаковке.

3. Воспользуйтесь мастером на сайте транспортной компании

Ну и самый простой способ определить объём ламината — использовать мастер расчета тарифа на сайте выбранной вами транспортной компании. Как примерно это выглядит, показано на рисунке.

Итак, определить объём и вес коробки ламината для транспортной компании для вас не составит труда, если вы просто перемножите выраженные в метрах до второго знака высоту, ширину и длину доски, которая есть на нашем сайте. Затем умножьте полученное число на число досок в коробке и получите объём упаковки. Но самый простой способ — использовать калькулятор стоимости доставки на сайте транспортной компании, если он там предусмотрен.

Калькулятор кубов бруса — сколько штук в кубе + таблица

Содержание

• 1 Сколько штук бруса в кубе: онлайн калькулятор
• 2 Брус длинною 6 метров: сколько штук в кубе. Таблица с расчетами
• 3 Количество бруса в кубе — как рассчитать количество бруса?
  • 3.1 Как перевести погонные метры в кубические?

Сколько штук бруса в кубе: онлайн калькулятор

калькулятор количества бруса в кубе

В строительстве любого каркасного дома требуется закупка бруса, так как этот материал используется при сборке венцов сруба и возведении крыши. Кроме того, брус применяется в изготовлении многих других деревянных конструкций. Чтобы избежать ошибок, важно научиться определять количество бруса в кубометре.

Данная операция отличается очень простой математической схемой. Объем любого предмета прямоугольной формы вычисляется путем умножения его ширины и высоты на длину. При покупке большого количества бруса, имеющего разную длину и сечение, могут возникать различные сложности. В результате сумма переплаты может оказаться достаточно большой.

Эта статься посвящена нюансам подсчета количества бруса в одном кубе. Мы предлагаем познакомиться с калькулятором и удобными в использовании таблицами «шпаргалками». Это поможет легко перевести погонные метры бруса в кубы.

Брус длинною 6 метров: сколько штук в кубе. Таблица с расчетами

Таблица — количества 6 метрового бруса в кубе

Количество бруса в кубе — как рассчитать количество бруса?

Для расчета кубатуры на дом и определения точного количества брусьев необходимо произвести простые расчеты. Для этого нужные некоторые сведения: объем пиломатериалов и объем штучного изделия. Это необходимо для деления одной величины на другую. В приведенной ниже таблице представлены самые распространенные размеры сечений. При этом длина материала составляет 6 метров.

Формула расчета количества штук бруса в кубе 150 * 150 * 6000:
0,15 (м) * 0,15 (м) * 6 (м) = 0,135 куб.м
1 м³ / 0,135 м³ = 7 штук в кубе.

Как перевести погонные метры в кубические?

Расчет количества бруса в одном кубе продаваемого материала может рассчитать даже обычный школьник. В качестве примера для расчета количества бруса размером 150*150 в одном кубе древесины необходимо произвести следующие действия. Размер грани балки бруса, который указывается в миллиметрах, возводится в квадрат. Затем 100000 нужно разделить на то значение, которое получилось. В результате выясняется, что в одном кубе содержится 44,4 погонных метров материала. Количество шестиметровых балок в кубе будет равно 7,4 штук. Четырехметровых балок в нем будет 11 штук.

Производители и продавцы пиломатериалов не всегда бывают честными по отношению к покупателям. Сечение бруса нередко занижается по сравнению с заявленным. Часто получается, что продаваемый брус размером 150 × 200 по факту имеет сечение 140 × 190. Прежде, чем покупать брус, нужно проверить реальные параметры материала. Также важно узнать у продавца о формировании цены за куб материала.

1. 5
2. 4
3. 3
4. 2
5. 1

(22 голоса, в среднем: 3. 3 из 5)

Объем куба | Формула и как найти (видео)

Объем куба

Объем куба — это то, сколько места куб занимает в трех измерениях. Вы можете найти объем любого куба с одним заданным измерением, используя формулу объема куба :

V = s3

Объем куба всегда измеряется в кубических единицах, полученных из линейной единицы, заданной или используемой для измерения длина стороны.

Содержание

1. Объем куба
2. Что такое куб?
   • Каковы размеры куба?
3. Объем куба Формула
4. Как найти объем куба
   • Как найти длину, ширину и высоту по объему
   • Как рассчитать объем, используя площадь
   • Как рассчитать площадь поверхности куба, используя объем
5. Объем куба Примеры

Что такое куб?

А куб представляет собой трехмерное тело с шестью конгруэнтными квадратными гранями, встречающимися под прямым углом, восемью вершинами и двенадцатью сторонами одинаковой длины. Куб является одним из пяти Платоновых тел и также называется шестигранником.

Каковы размеры куба?

Куб — это трехмерный объект, поэтому куб имеет три измерения:

• Длина — обычно понимается как большее из «плоских» измерений.
• Ширина – обычно понимается как более короткий из «плоских» размеров.
• Высота или глубина — Измерение, которое привносит форму в наш трехмерный мир

Обратите внимание, у нас есть два способа описать третье измерение:

1. Высота — Используйте этот термин, когда объект возвышается перед вами, как высокое здание.
2. Глубина — используйте этот термин, если объект падает под вами, как дыра в земле.

Нам нужна информация хотя бы об одном из этих трех измерений, чтобы измерить объем куба.

Объем формулы куба

Объем формулы куба равен объему, равному произведению длины на ширину и на высоту.

V = l × w × h

Это уравнение объема не работает для каждого твердого тела, но оно работает для кубов, прямоугольных призм и параллелепипедов.

Поскольку все три значения — l, w и h — одинаковы в кубе, простейший объем формулы куба:

V = s3

В этом объеме уравнения куба s = длина любой край.

Объем всегда измеряется в кубических единицах на основе предоставленных вам линейных единиц. Если вам говорят, что сторона куба имеет длину 3 м, объем измеряется в кубических метрах или м3 (метры в кубе).

Как найти объем куба

Чтобы найти объем куба, вам нужно знать только длину любого ребра.

Если вам дана длина одной стороны, вы можете найти объем куба, подставив его в одну из формул объема для куба:

• В = l × w × h
• В = с3

Чтобы измерить пространство, занимаемое кубом, нужно знать длину любого ребра, потому что длины всех сторон куба равны.

Как найти длину, ширину и высоту по объему

Что, если вам дан объем куба и вас попросят найти его размеры?

Если вам дан объем куба и вас просят найти длину ребра, все, что вам нужно сделать, это извлечь кубический корень из объема:

с = V3

Ваш ответ больше не будет в кубических единицах; это будет в линейных единицах.

Что, если у нас есть куб, и нам говорят, что его объем составляет 729 кубических метров. Чтобы найти длину ребра куба:

с = 729 м33

с = 9 метров

Как рассчитать объем, используя площадь

Вот еще одна задача. Что если вам скажут площадь одной грани куба? Можете ли вы использовать эту информацию, чтобы найти объем?

Да, площадь одного лица равна произведению длины лица на ширину. Как только вы найдете ширину или длину, вы можете применить формулу объема:

1. Найдите квадратный корень из заданного измерения площади; это даст вам длину любой стороны, s.
2. Используйте формулу объема, V = s3, чтобы найти площадь

Как вычислить площадь поверхности куба, используя объем

Если вам известен объем куба, вы можете преобразовать его в длину одной стороны. Затем вы можете использовать длину стороны для расчета общей площади поверхности.

Используйте длину ребра, чтобы вычислить площадь поверхности одной стороны, затем умножьте эту площадь на 6. Это даст вам общую площадь поверхности куба с использованием объема.

Что если вам скажут общую площадь поверхности всего куба? Сможете ли вы найти объем?

Да, общая площадь поверхности включает площади всех шести конгруэнтных граней. Найдите площадь одной грани, а затем выполните действия, описанные выше, чтобы найти объем:

1. Разделите заданную общую площадь поверхности на шесть, чтобы получить площадь одной грани
2. Найдите квадратный корень из площади одной грани, чтобы получить длину любой стороны, с
3. Используйте формулу объема, V = s3

Объем куба Примеры

Если у вас есть трехмерное тело с шестью гранями, а стороны помечены 4′, 6′ и 8′. Это куб?

Нет, это прямоугольная призма, потому что метки, опережающие рисунок, имеют разную длину!

Что, если стороны нашего твердого тела равны 4 футам, 4 футам и 4 футам; это куб?

Это куб, потому что на этикетках указано, что ширина, длина и высота одинаковы.

Каков объем куба выше?

Вы записали V = 43?

Вы вычислили V = 64 кубических фута или фут3?

Давайте рассмотрим еще один пример куба со стороной 12 ярдов. Каков его объем?

V = s3

V = 123

V = 1728 кубических ярдов (ярд3)

Что насчет куба с одной гранью площадью 25 см? Каков объем куба?

Во-первых, какова длина любого ребра или стороны куба?

Подумайте: чему равен квадратный корень из 25? Ответ равен 5, поэтому:

s = 25 см

s = 5 см

Теперь, когда у вас есть длина стороны, вы можете вычислить объем:

V = s3

V = 53

V = 125 кубических сантиметров, или см3 

Общая площадь поверхности куба составляет 7 776 квадратных дюймов (дюйм2). Каков объем куба?

Помните, что общая площадь поверхности равна площади всех шести квадратных граней. Разделите общую площадь поверхности на 6, извлеките из нее квадратный корень, затем используйте формулу объема:

7 776 IN26 = 1 296 в 2

1,296 IN2 = 36 в

Теперь мы можем рассчитать объем куба:

V = 363

V = 46,656. Кубические дюймы или IN3

Следующий урок:

. Что на поверхности. Площадь

Калькулятор объема куба

Создано Альваро Диесом

Отредактировано Домиником Черниа, доктором философии, и Джеком Боуотером

Последнее обновление: 10 октября 2022 г.

• Что такое куб?
• Каков объем куба?
• Как рассчитать объем куба (вручную)?
• Как использовать калькулятор объема куба Omni?
• Расширенные возможности калькулятора Omni: найдите объем куба, не зная стороны.
• Почему формула объема куба такая простая?
• Кубики в мире от Ice Cube до IceCube и далее

Добро пожаловать в Omni объем калькулятора кубов .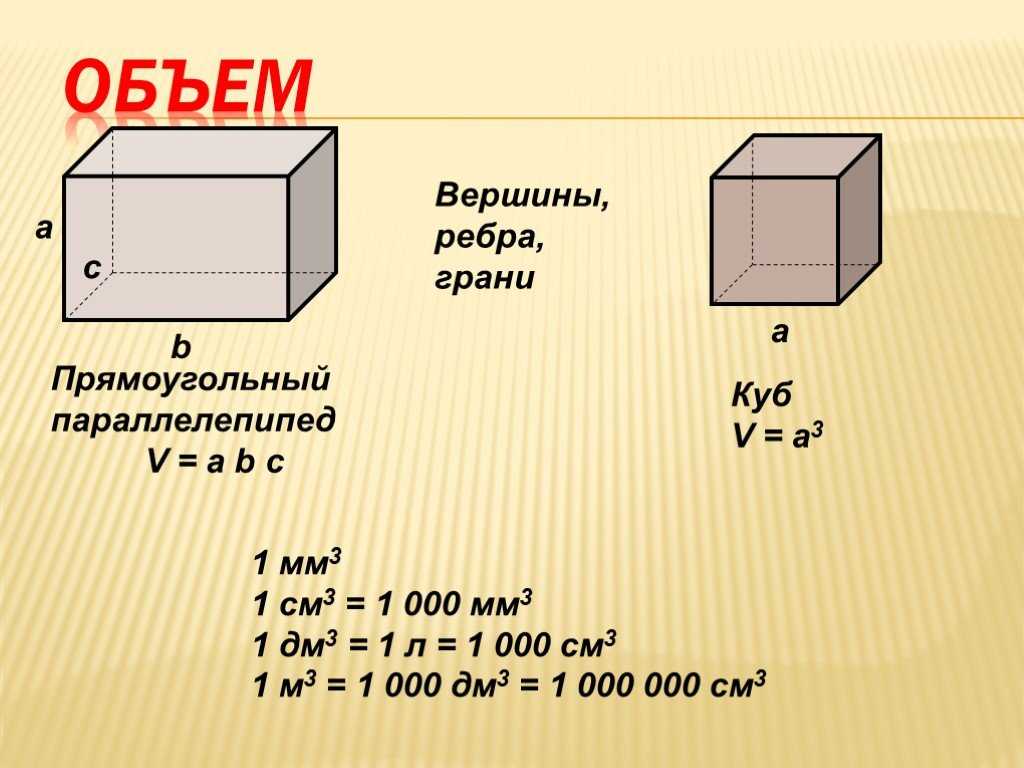 Вы когда-нибудь задумывались каков объем куба или почему формула для объема куба так проста? Да, мы это сделали, и у нас есть ответы. Здесь мы объясним, как рассчитать объем куба, а также посмотрим, что делает куб такой популярной формой.

🔎 С помощью нашего калькулятора объема вы можете найти объем многих других трехмерных фигур.

Что такое куб?

Начнем с самого начала. Куб — это 3D-объект , состоящий из 6 граней, каждая из которых представляет собой квадратов одинакового размера . Если вы хотите спуститься в эту конкретную кроличью нору, мы можем сказать, что квадраты также являются обычными объектами, на этот раз в 2D-пространстве, состоящими из 4 сегментов одинаковой длины, встречающихся в 9углы 0 градусов.

Куб является одним из основных трехмерных объектов, наряду с тетраэдром (правильная треугольная пирамида) и сферой. Вы уже должны быть знакомы с его формой; если вы когда-нибудь видели кубик Рубика (подсказка в названии, верно?), кубик льда (не рэпер) или игральные кости, вы видели кубик.

Из этого раздела следует, что куб — ​​это трехмерный объект; следовательно, имеет объем . Он также очень регулярен, что означает, что найти объем куба несложно.

Каков объем куба?

Объем — это мера трехмерного пространства, занимаемого объектом. Но если вас не интересуют абстрактные понятия и вы просто хотите узнать объем куба, есть простой ответ на вопрос Каков объем куба?

объем = л³

где л длина сторон куба. Это просто еще один способ сказать, что вам нужно умножить длину каждой стороны l на себя три раза: l × l × l = l³ , или, другими словами, возведение в третью степень (узнайте больше о степени в калькуляторе степени)

Предыдущая формула исходит из того, что объем куба (в 3D) равен аналогично площади квадрата (в 2D). Подобно тому, как вы вычисляете площадь квадрата, умножая длины каждой стороны на , вы можете умножать три стороны куба, поскольку все они одинаковы.

Если все это звучит для вас очень просто, просто знайте, что есть еще формулы объема куба на случай, если вы не знаете длины сторон . Это сложнее и, вероятно, сделает вас счастливее. Если вас устраивает текущий уровень сложности, давайте двигаться дальше.

Теперь, когда мы увидели и поняли формулу объема куба, мы перейдем к объяснению того, как вычислить объем куба. Сначала мы вычислим объем куба вручную, а позже воспользуемся омни-калькулятором , чтобы найти объем куба, вообще не имея дело с формулой.

Как вычислить объем куба (вручную)?

В настоящем стиле папы , мы научим вас делать вещи старомодным способом , прежде чем вы отправитесь в будущее. Для этого есть веская причина; это поможет вам лучше понять, как вычислить объем куба. Вернемся к формуле и используем ее на простом примере : объем = л³ . Предположим, у нас есть куб со стороной l = 5 см .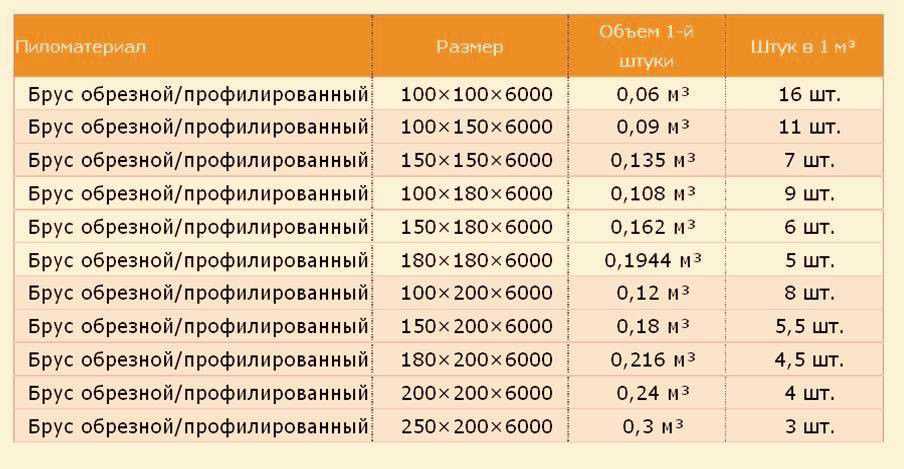 Единицы на самом деле не имеют значения, но мы сохраним их, чтобы отслеживать размеры.

Возьмите лист бумаги и начните атаковать формулу объема куба, умножив сначала l × l = 5cm × 5cm = 25cm² . Мы вычислили площадь квадратов, составляющих каждую из шести сторон нашего куба. Мы в одном измерении (т. е. в одном умножении) от нахождения объема куба , так что просто снова возьмите ручку и давайте сделаем это!

объем = л³ = л² × л = 25 см² × 5 см = 125 см³ . И с этим у нас получилось — мы вычислили объем куба и ушли целыми и невредимыми. Поздравляем!

Теперь позвольте нам рассказать вам секрет об инструменте , который живет слева от этого текста и позволяет вам вычислить объем куба за один простой шаг. Что ты говоришь? Вы хотите знать больше? Конечно!

Как пользоваться калькулятором объема куба Omni?

Вы пришли сюда за этим. Калькулятор для решения всех ваших задач по объему куба: Калькулятор объема куба Omni . Здесь, в Omni, мы подготовили простой калькулятор, который использует формулу объема куба для автоматического вычисления объема без каких-либо усилий с вашей стороны.

Все, что вам нужно сделать, это ввести длину стороны в поле с именем Сторона , и он автоматически рассчитает объем куба. Никогда еще не было так просто ответить на вопрос: Каков объем куба? Кроме того, вы также можете вычислить длину стороны куба, если вы уже знаете его объем. Просто введите громкость в соответствующее поле и наблюдайте, как происходит волшебство (на самом деле это математика, но магия звучит круче).

Калькулятор также выполняет обратное вычисление почти так же, как это сделали бы вы сами. Возьмите формулу объема куба и переверните ее: объем = l³ => l = ³√объем , где ³√ — кубический корень.

Расширенные возможности калькулятора Omni: найдите объем куба, не зная стороны.

Если вы не заметили, этот калькулятор Omni имеет «Расширенный режим». Он расширяет функциональные возможности калькулятора, позволяя вычислять объем куба по чему-то другому, кроме длины его сторон. Вы можете ввести площадь поверхности, диагональ грани или диагональ куба.

Разница между диагональю грани и диагональю куба может быть не совсем ясна, поэтому давайте объясним это немного подробнее. Диагональ куба — это трехмерное расстояние между любыми двумя противоположными углами. Это наибольшее расстояние между любыми двумя углами куба. Говоря о диагонали грани, мы имеем в виду двумерное расстояние между двумя самыми дальними углами любого из квадратов, составляющих шесть граней куба. Все диагонали грани имеют одинаковую длину.

Почему формула объема куба такая простая?

Как и было обещано, теперь мы рассмотрим, почему формула для объема куба такая простая и почему состоит всего из двух переменных и двух математических символов. Основная причина, на которую мы могли бы указать, — это простота куба. Куб очень правильный и, самое главное, его очень легко определить. Если подумать, сфера или тетраэдр даже правильнее куба, но вычислить их объем или площадь намного сложнее. Отчасти это можно объяснить тем, что сложно математически смоделировать поверхность сферы при использовании типичных декартовых координат.

Куб, однако, следует именно этому образцу. Стороны куба всегда выровнены с единичными векторами, которые создают трехмерное декартово пространство. Это делает вычисление объема таким же простым, как вычисление перекрестного произведения трех унитарных декартовых векторов (векторное произведение), каждый из которых умножается на длину сторон куба .

Проверив математические формулы, вы можете увидеть, что квадратные формы предпочтительнее округлых. Если не верите, взгляните на калькулятор формы прямоугольной призмы и калькулятор объема цилиндра и скажите мне 9. 0005 какой из них вы бы предпочли вычислить вручную.

Кубики в мире от Ice Cube до IceCube и далее

Предпочтение кубическим формам, вероятно, связано с их простотой конструкции и, что более важно, с упаковочными свойствами. Как и квадраты и шестиугольники в двумерном пространстве, кубы могут

Преимущество? Эффективность. Если вы сделаете контейнеров в форме кубов (прямоугольные призмы также подойдут), вы можете быть уверены, что используете все доступное пространство, и между ними не останется мертвого пространства. Только это свойство определяет формы контейнеров, ящиков и шкафов.

По этой причине кубиков льда являются кубиками