Как рассчитать кубатуру фундамента: сколько бетона нужно на фундамент

Как рассчитать кубатуру фундамента: правила и справочные таблицы

При возведении основания любой конструкции важным этапом является решение вопроса, каким образом рассчитать кубатуру фундамента. Представленная процедура не требует выполнения сложных математических расчетов и выполняется в считанные минуты при знании некоторых индивидуальных показателей.

Содержание

• 1 Общие особенности подсчета и возможные пути решения
• 2 Проведение расчетов кубатуры в зависимости от вида фундамента
  • 2.1 Подсчет объема монолита
  • 2.2 Подсчет объема ленты
  • 2.3 Подсчет объема столбчатого фундамента
  • 2.4 Подсчет объема буронабивного фундамента с цельной ростверковой частью
• 3 Заключение

Общие особенности подсчета и возможные пути решения

По общему правилу, расчет кубатуры фундамента устанавливается по объему возведенной опалубочной системы. Простыми словами, какая вместимость внутренней полости опалубки, такое количество бетона потребуется для возведения основания.

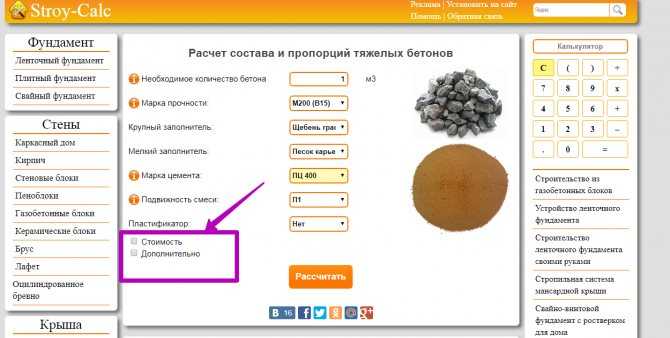
Наряду с описанными выше способами определения объема, с развитием современных информационных технологий застройщики получили возможность проведения расчета при помощи специальных программных средств, доступных в информационной сети «Интернет».

Вбив необходимые значения, практически моментально можно получить не только искомое значение, но и советы специалистов по рациональному приготовлению смеси и рекомендуемым пропорциям составляющих компонентов.

Проведение расчетов кубатуры в зависимости от вида фундамента

Из курса школьной алгебры объем любого тела можно посчитать путем нахождения произведения его высоты, длины и ширины. Однако расчет кубатуры распространенных видов основания дома предопределяет учет их индивидуальных особенностей.

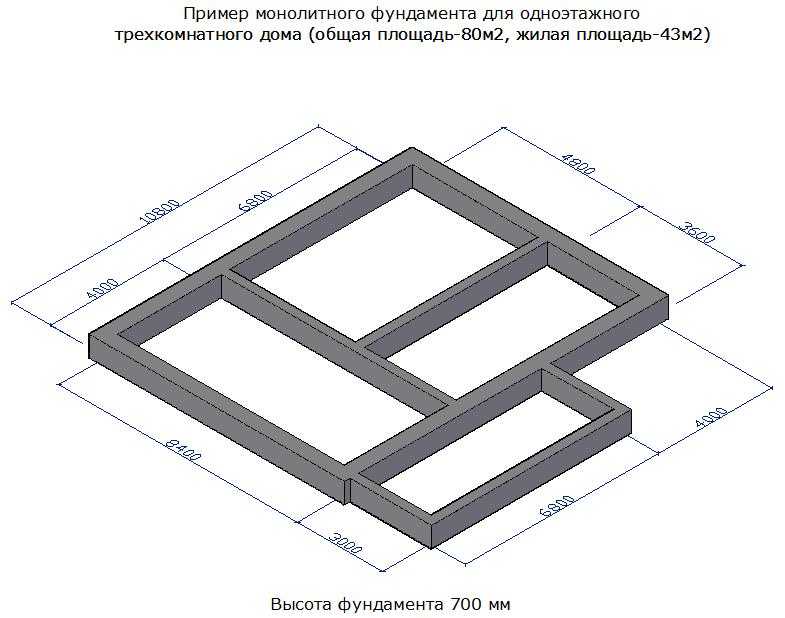
Подсчет объема монолита

Основание данного типа имеет форму прямоугольного параллелепипеда, грани которого можно найти путем сличения с эскиза на этапе планирования или посредством фактического замера возведенной опалубки.

Замеряя высоту опалубки, стоит учитывать, что на ней выполняются отметки необходимого уровня бетона, и она возводится с запасом в 10-15 см.

Посмотрите видео, в котором эксперт рассказывает, как правильно сделать расчет монолитной плиты.

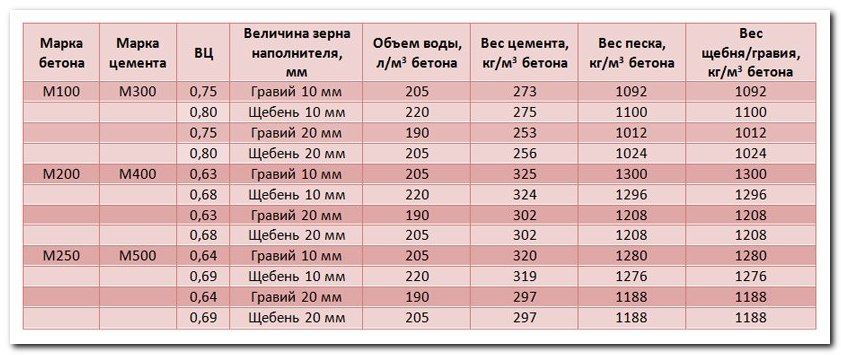
Объем представленного основания вычисляется по общей формуле: Н х А х В, где Н – высота, А – длина, В – ширина. Для наглядности стоит привести пример. Так, при глубине фундамента 0,8 м, длине 10 м и ширине 10 м кубатура необходимого бетона равняется 0,8 х 10 х 10 = 80 м3.

Для выполнения более точных расчетов следует учитывать и объем армированной сетки, укладываемой во внутреннее пространство возведенной опалубки. Однако сильно повлиять на общие показатели арматура не сможет по причине ее несущественных, в данном случае, габаритов.

Подсчет объема ленты

Расчет кубатуры ленточного фундамента дома также сводится к вычислению объема прямоугольного параллелепипеда за вычетом внутренних пустотелых областей. Несмотря на видимую сложность, данный показатель легко вычисляется на практике.

Для расчета необходимо по составленному чертежу подсчитать объемы внешнего и внутреннего параллелепипеда, найти их разницу, а затем к полученному результату прибавить кубатуру внутренних ленточных элементов.

Рекомендуем посмотреть видео о проведении расчета монолитной ленты основания.

Так, при габаритах фундамента 12 х 15 м и шириной ленты в 0,5 м, углубленных в почву на 1,5 м, с внутренней добавочной лентой шириной в 0,6 м кубатуру основания вычисляют следующим образом:

1. Устанавливаем кубатуру внешнего параллелепипеда: 12 х 15 х 1,5 = 270 м3.
2. Определяем аналогичный показатель для внутренней фигуры: (12 – 0,5 – 0,5) х (15 – 0,5 – 0,5) х 1,5 = 231 м3.
3. Находим разницу полученных значений: 270 – 231 = 39 м3.
4. Вычисляем кубатуру внутренней ленты: (12 – 0,5 – 0,5) х 0,6 х 1,5 = 9,9 м3.
5. Итоговый объем заливки ленточного фундамента: 39 + 9,9 = 48,8 м3.

Подсчет объема столбчатого фундамента

Объем оснований столбчатого типа вычисляется как сумма объемов двух геометрических тел – параллелепипедов столба и его подошвы, умноженная на общее количество опорных элементов.

В цифровом выражении для расчета столбчатого фундамента под сооружение 8х8 м с общим количеством столбов с 2 м шагом в 16 экземплярах (4 угловых и 12 вспомогательных), подошвы которых имеют размеры в 0,6 х 0,6 х 0,3 м, а тело столбовых опор 0,4 х 0,4 х 1, вычисляется по следующему принципу:

1. Итоговый объем подошвы: 16 х 0,6 х 0,6 х 0,3 = 1,73 м3.
2. Итоговая кубатура столбовых опор: 16 х 0,4 х 0,4 х 1 = 2,56 м3.
3. Итоговый объем необходимого бетона: 1,73 + 2,56 = 4,29 м3.

Посмотрите видео, как правильно осуществить расчет столбчатого основания своими руками.

Подсчет объема буронабивного фундамента с цельной ростверковой частью

Общая кубатура представленного вида оснований дома устанавливается как сумма объемов буронабивных столбовых опор (цилиндров) и монолитной плиты ростверковой части (классический параллелепипед). Так же, как и при расчете кубатур представленных выше оснований, для вычисления общего объема бетона потребуется разбить фигуру на составные элементы, установить объем каждой из них и полученные значения просуммировать.

В данном случае необходимо помнить, что объем колонны или любого строительного элемента цилиндрической формы вычисляется как произведение площади основания на высоту.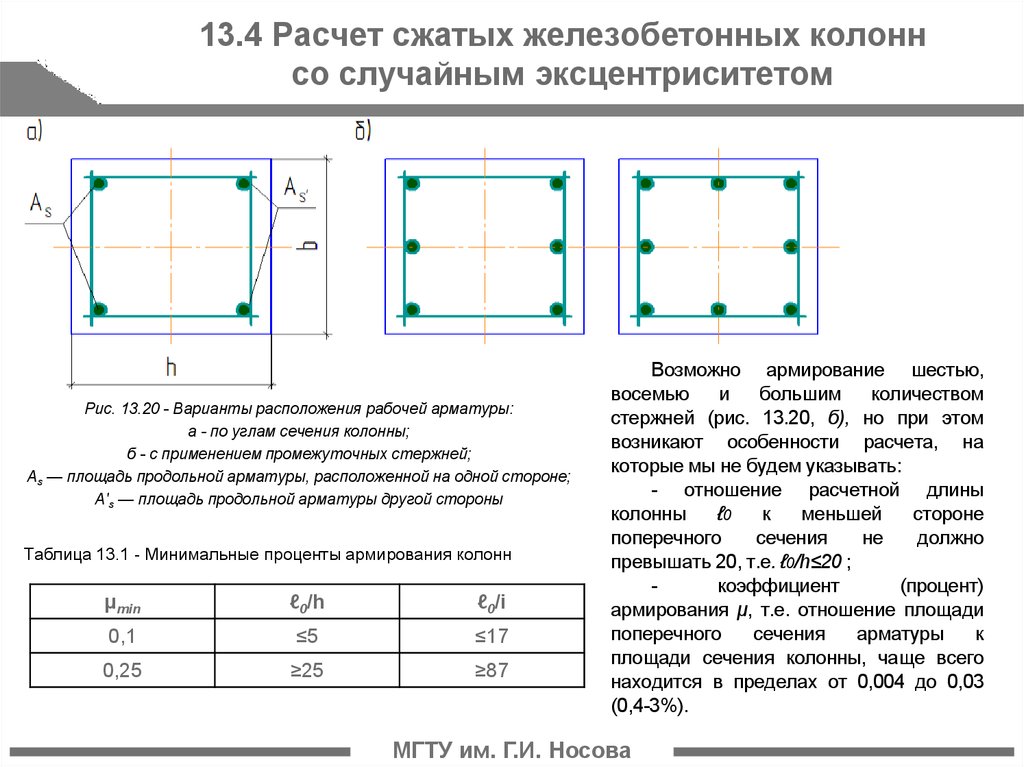

где π – математическая константа (3,1415…), D – диаметр круга (подошвы).

Для наглядности приведем пример, общий объем основания на 20 опорах диаметров 0,5 м и глубиной залегания в почве в 2 м, поддерживающих ростверковую часть с размерами 10 х 15 х 0,5 м, устанавливается по следующему принципу:

Кубатура столбов: 20 х (3,14 х 0,5 х 0,5 / 4) = 7,85 м3.

1. Кубатура ростверковой части: 10 х 15 х 0,5 = 75 м3.
2. Итоговый объем: 7,85 + 75 = 82,85 м3.

Заключение

Правильно посчитав искомый показатель, любой заказчик без труда сможет заранее спрогнозировать свой бюджет и рассчитать необходимое количество смеси, что существенно сэкономит время.

Как рассчитать кубатуру фундамента для частного дома

Чтобы строительный процесс шел в оптимальном направлении, и вы не понесли ненужных финансовых затрат, связанных с чрезмерным расходом материалов, должен производиться подробный расчет. Надо четко представлять себе, как рассчитать кубатуру фундамента и избежать всевозможных задержек. Если у вас будет в наличии точный план с расчетами, ваш проект будет реализован с минимальными затратами.

Перед возведением строительного объекта, есть возможность рассчитывать расход материалов, пользуясь специальными калькуляторами, в которые нужно заложить исходные параметрические данные. Вся информация относительно параметров объекта должна находиться в проекте и в его техническом описании. Существуют разные виды фундаментов, применяемых в строительстве:

• столбчатый,
• плитный,
• ленточное основание.

Расчет фундамента для частного домовладения

Давайте разберемся, как рассчитать кубатуру фундамента — бетонной конструкции с минимальной толщиной. Используется формула:

V = A×B×C, где итоговое значение является объемом, а остальные длиной, шириной и высотой. Таким образом, получить кубатуру данного типа фундамента просто и быстро, нужно только знать исходные данные.

Эта конструкция фундамента числится самой прочной и устойчивой, потому что на ней нет стыков, которые несколько нарушают целостность.

Но экономически выгодный — опорный фундамент, для сооружения которого применяются бетонные столбы определенного сечения. Нужно сложить объем бетонного столба и объём его подошвы, а затем умножить на число опор, участвующих в формировании фундамента.

Например, здание имеет площадь 10 × 10 метров и в конструкции будет задействовано 20 опор с квадратным сечением. Расположение столбов будет происходить следующим образом:

• 4 в углах,
• 16 на остальной площади по периметру объекта.

Бетонный столб имеет сечение 300 × 300 мм и высоту 2 метра, подошва имеет сечение 500 × 500 мм и толщиной 20 сантиметров. Кубатура подошвы бетонных столбов получается 20 × 0,5 × 0,5 × 0,2 = 1. А объем опор: 20 × 0,3 × 0,3 × 2 = 3,6. И если сложить результаты расчетов, то получится, что 4,6 кубических метров фундамента требуется для данного строительного объекта. Для круглых столбов применяется формула:

• V = π × r2 × h, где задействованы высота опоры и ее диаметр. Когда объем одного столба с круглым сечением будет определен, нужно выполнить умножение на количество опор.

Объем ленточного фундамента

Также важно знать, как рассчитать кубатуру фундамента ленточного типа, потому что эта конструкция является наиболее распространенной при строительстве небольших загородных домов. Конструкция такого основания получается полой, но наружная часть должна быть настолько прочной, чтобы выдерживать предполагаемые нагрузки.

Все равно в полом пространстве ленточного фундамента могут быть элементы, к которым привязываются стены объекта. Если грамотно подойти к расчету, его можно выполнить быстро и точно. За основу расчетов берется объем всего ленточного фундамента, из него просто вычитаются стенки внутренние.

Когда будет получен итог, к нему нужно прибавить данные межкомнатных элементов основания. Например:

• размер дома 10×8 м,
• ширина ленточного фундамента 400 мм,
• глубина фундамента 2 м,
• внутренняя перегородка миллиметров 500 шириной.

Общий объем ленточного фундамента вычисляется следующим образом:

10 × 8 × 2 = 160. Внутренняя часть: (10 – (0,4 × 2)) × (8 – (0,4 × 2)) × 2 = 132,5. Теперь от общего объема ленточного основания отнимается внутренняя часть:

160 – 132,5 = 27,5. Вычисляются для сооружения стен элементы и их объемы, занимаемые в фундаменте: (10 – (0,4× 2)) × 0,5 × 2 = 9,2.

Остается сложить все результаты и получить 36,7 кубических метров. Таким образом, зная как посчитать кубатуру фундамента, вы более рационально подойдете к закупке расходных материалов.

Калькуляция фундамента

Если ответственно подойти к вычислению объемов расходных материалов, то есть шанс снизить свои текущие расходы и сделать строительство менее затратным на всех уровнях. Тем более что имеются упрощенные варианты расчетов, доступные гражданам, которые никогда не сталкивались со строительной инженерией.

Домовладелец способен самостоятельно произвести все необходимые расчеты, влияющие на итоговые суммы, которые будут использоваться для закупки строительных материалов и для проведения работ. Калькуляция расходов позволяет грамотно расставить акценты в строительном процессе и построить надежное домовладение.

Квадратный корень Кубатурный фильтр Калмана-алгоритм фильтра Калмана для интеллектуальной оценки положения транспортного средства Академическая исследовательская статья по «Гражданскому строительству»

CrossMark

Доступно на сайте www.sciencedirect.com

Procedía Engineering

www.elsevier.com/locate/procedia

GITSS2015

Кубатурный фильтр Калмана с квадратным корнем — алгоритм фильтра Калмана для интеллектуальной оценки положения автомобиля

Jianmin Duan, Hui Shi*, Dan Liu, Hongxiao Yu

Пекинская ключевая лаборатория организации дорожного движения, Пекинский технологический университет, Пекин 100124, Китай

Abstract

Новый алгоритм фильтрации, адаптивная кубатура квадратного корня Фильтр Калмана-Калмана Фильтр (SRCKF-KF) предлагается для уменьшения проблем, связанных с объемом вычислений, сложным преобразованием формулы, низкой точностью, плохой сходимостью или даже расхождением. Метод использует кубатурный фильтр Калмана (CKF) для оценки нелинейных состояний модели, в то время как ее линейные состояния оцениваются фильтром Калмана (KF). Результаты моделирования и практического эксперимента показывают, что по сравнению с расширенным фильтром Калмана (EKF) и фильтром Калмана без запаха (UKF) модифицированный фильтр не только повышает численную устойчивость, гарантирует положительную определенность ковариации состояния, но и увеличивает точность, что имеет высокую практичность. © 2016 г. Опубликовано Elsevier Ltd. Это статья в открытом доступе по лицензии CC BY-NC-ND (http://creativecommons.Org/licenses/by-nc-nd/4.0/).

Рецензирование под руководством Департамента транспортного машиностроения Пекинского технологического института Ключевые слова: фильтр Калмана с кубатурой квадратного корня; фильтр Калмана; встроенный фильтр; интеллектуальное транспортное средство

1. Введение

Исследования показали, что основные причины возникновения дорожно-транспортных происшествий кроются в субъективной оценке водителя, около 90% дорожно-транспортных происшествий вызваны ошибкой водителя (например, Fachinger et al. [1]). В целях повышения безопасности дорожного движения и эффективности транспорта интеллектуальные транспортные средства получили широкое признание во многих развитых странах, что привело к их быстрому развитию. Предпосылкой безопасности вождения является предоставление точной навигационной информации для интеллектуального транспортного средства (например, Nobe et al. [2]). Короче говоря, исследование навигационной системы автомобиля очень важно. Навигацию транспортного средства часто называют нелинейной задачей оценки состояния. Расширенный фильтр Калмана (EKF) играет ключевую роль в оценке нелинейного состояния на протяжении десятилетий (например, Nobe et al. [2]). Однако одно из ограничений

* Автор, ответственный за переписку. Тел.: +8613261217744; Эл. -nc-nd/4.0/).

Рецензирование под ответственность Департамента транспортного машиностроения Пекинского технологического института doi:10.1016/j.proeng.2016.01.258

EKF — это расчет матриц Якоби [3], которые являются аппроксимацией первого порядка нелинейной модели процессов и измерений. Кроме того, ЭКФ имеет ошибки усечения, он хорошо работает только в том случае, когда справедливо линейное приближение нелинейной динамической системы и модели наблюдения, что сужает область применения ЭКФ в практических нелинейных системах [4]. В последние годы несколько исследователей сосредоточились на передовых алгоритмах нелинейной оценки состояния; например, сигма-точечные фильтры, такие как неароматизированный фильтр Калмана (UKF) у Джулиера и Ульмана и кубатурный фильтр Калмана (CKF) у Арасаратнама и Хайкина и т. д. [2]. UKF привлек наибольшее внимание в этой области, в которой используется подход детерминированной выборки для получения среднего значения и ковариации [3]. Показано, что UKF работает намного лучше, чем EKF, но время его выполнения значительно больше [5] из-за того, что UKF использует детерминированные сигма-точки для захвата среднего значения и ковариации, формирующих временных задержек [6]. Кроме того, UKF нуждается в дополнительном масштабирующем параметре, так как при отрицательных значениях, когда количество состояний больше 3, UKF может прекратить свою работу [5]. В то же время, параметры должны быть точной настройки, это неудобно для эксплуатации с практической точки зрения. Хотя CKF также использует детерминированные сигма-точки, CKF требует только 2n кубатурных точек [6]. Теоретически CKF имеет лучшую вычислительную скорость. Поэтому предлагаемый алгоритм слияния кадров в CKF

Во время реализации KF в реальном времени ковариационные матрицы распространения ошибок могут стать плохо обусловленными. Эти типы плохо обусловленных ковариационных матриц могут вызвать численную нестабильность во время реализации в режиме реального времени, даже привести к расходимости фильтрации [7]. Чтобы справиться с этими трудностями, можно использовать фильтры квадратного корня, которые распространяют и обновляют квадратный корень из ковариации ошибки с выполнением разложения Холецкого на каждом шаге, и они обеспечивают положительную полуопределенность матрицы ковариации оценки состояния [8]. Некоторыми из ключевых свойств фильтров квадратного корня являются положительно определенная ковариация ошибок и повышенная числовая точность и т. д. [9].].

2. Фильтр Калмана с кубатурой квадратного корня — фильтр Калмана

В этом подразделе выводится производная кубатура фильтра Калмана с квадратным корнем — фильтр Калмана для нелинейных систем. Это означает, что предлагаемый алгоритм получен из CKF и KF с квадратным корнем, CKF с квадратным корнем используется для завершения нелинейной оценки состояния, а фильтр KF может иметь дело с линейной оценкой состояния. Фильтр Калмана кубатуры квадратного корня имеет сильную стабильность и высокую точность. Рассмотрим следующие модели процесса и наблюдения [8].

xk = f (xk-i) + wk-i (j) zk = h( xk ) + vk-i

где xk и zk представляют состояние системы и измерения в момент времени k соответственно. f (•) и h(-) — известные векторные отображения, wt ~N(0,Qk) и vk ~N(0,Rk) — белый шум состояния и измерения соответственно и взаимно независимы. Кубатурное правило для аппроксимации n-мерного взвешенного интеграла Гаусса:

I(f) = jRn f (x) exp(-xTx)dx. (2)

, где f (x) — произвольная функция. Rn — область интегрирования. xT является преобразованием x . Интегральное уравнение трудно решить в общем условии. Аппроксимация для набора точек с весом ) следующим образом 9— i-я кубатурная точка, расположенная на пересечении единичной сферы и ее осей, ®> — соответствующий вес кубатурной точке. Таким образом, можно видеть, что CKF использует 2n точек, которые с равной вероятностью могут быть вычислены путем прямого интегрирования Гаусса.

Затем кубатурный фильтр Калмана с квадратным корнем — фильтр Калмана для задачи оценки состояния содержит следующие разделы.

COi =-

i = i,2,…,2n

2.1. Initialization

Инициализация фильтра с состоянием инициализации и квадратным корнем ковариационной матрицы 9Генерация весов

2.2. Актуализация времени

Оценка кубатурных точек

*,k-i = Sk_& + xk „i = i,2,…,2n (7)

Распространение кубатурных точек

Kk = f (x,k-i) (8)

Прогнозируемое состояние

xk = fa. k] (17) 9Zi,(k,k-1) Zk,k-1 ) (Zi,(k,k-1) Zk,k-1 )

«k — коэффициент адаптивного замирания, который может сбалансировать вес уравнения состояния , прогностическая информация и измерительная информация. По сути, это уменьшит воздействие помех. Коэффициент усиления фильтра SRCKF-KF

Wk = (Pz,k\kV SZ,k)/Szz,k (21)

Обновленное состояние на основе нового измерения

xk = *;+ Wk (Zk — zk) ( 22)

Коэффициент квадратного корня ковариации ошибки

Sk = tria([n — Wklk WkSRt ]) (23)

3. Моделирование

Чтобы показать эффективность предложенного алгоритма, важно, чтобы все фильтры имели одинаковую инициализацию и включали два сценария. Первый сценарий имеет дело с оценкой состояния класса нелинейных систем, а второй — с нелинейной интегрированной навигационной системой высокого порядка.

Для количественной оценки производительности фильтрации мы определяем среднеквадратичную ошибку (RMSE) в позиции как

RMSE =

\xi — xa

, где Xat и — фактическое и расчетное положения при прогоне методом Монте-Карло соответственно. Подобно среднеквадратичному отклонению положения, мы можем легко записать среднеквадратичное отклонение скорости и ускорения. Меньшее значение RMSE означает более высокую точность алгоритма фильтрации.

3.1. Класс нелинейной системы

Рассмотрим нелинейную негауссову систему с одномерным состоянием, которую можно смоделировать уравнениями (25) [7]

xk+i = °-5xt +

+ 8cos[1,2(/ -1)] + wk

, где wk и vk — белый шум с нулевым средним и невырожденной ковариацией. Значения дисперсии wk и vk равны 10 и 0,001. На рис. 1 показаны истинное значение (зеленая линия) и оценка EKF (красная линия), UKF (синяя линия) и SRCKF-KF (черная линия).

10 20 30 40 Время/с

Рис. 1. истинное значение и оценка.

Как упоминалось ранее, SRCKF-KF (черная линия) превосходит EKF (красная линия) и UKF (синяя линия), из-за ограничения по координате, отличия от рис. 1 не существенны, только в первые десять секунд синяя линия (UKF) отчетливо отклоняется от зеленой линии (истинное значение), а примерно через 13 секунд как красная линия (EKF), так и синяя линия (UKF) отклоняются больше, чем в другое время. В целом, черная линия (SRCKF-KF) является ближайшей линией к зеленой линии (истинное значение).

Для количественного анализа различий различных алгоритмов мы делаем 100 независимых прогонов Монте-Карло (МК) и вычисляем СКО в положении, показанном на рис. 2, и после ряда 100 прогонов МК СКО и расчетные стоимость временного шага (всего 100 временных шагов) приведены в табл.1

Рис. 2. СКО нескольких методов в примере 1.

Таблица 1. Сравнение производительности в примере 1. )

ЭКФ 2,8501 0,0057

UKF 2,2405 0,0253

SRCKF-KF 1,9350 0,0152

На рис. 1 оценочное значение SRCKF-KF наиболее близко к истинному значению. На рис. 2 RMSE с использованием фильтра SRCKF-KF меньше, чем EKF или UKF. Точность количественной оценки и вычислительная сложность алгоритма приведены в таблице 1. Очевидно, результат показал, что SRCKF-KF имеет лучшие характеристики по точности оценки по сравнению с UKF, относительное улучшение средней точности SRCKF-KF составляет почти 10,8. %. Но по сравнению с откликом фильтров, EKF имеет лучшие характеристики по простоте вычислений. Как UKF, так и SRCKF-KF требуют больших вычислительных ресурсов, поскольку они представляют собой детерминированный фильтр выборки, затраты времени выше, но для SRCKF-KF требуется меньше точек выборки, чем для UKF. Хотя разница в моделировании не очевидна, по мере увеличения точки выборки UKF будет по крайней мере на один порядок медленнее, чем SRCKF-KF, и эта разница окажет значительное негативное влияние на реальный инжиниринг.

3.2. Интегрированная навигационная система

В этом подразделе для обеспечения достоверного и разумного сравнения производительности различных алгоритмов фильтрации будет рассмотрена оценка состояния GPS/INS. Транспортное средство аппроксимируется здесь как двумерная точечная масса, движущаяся с ограниченной скоростью и скоростью поворота. И он был расположен по относительному местоположению. Для удобного преобразования в этой системе используются координаты UTM (универсальная поперечная проекция Меркатора) для отображения информации о положении транспортного средства, систематическое уравнение

X+i = Fk+i xk + uk + W (26)

где uk — известные входные управляющие векторы, uk = I в моделировании, а I — единичная матрица; wk — белый гауссовский шум, а переменные состояния предлагаются в следующем виде [10]:

= [Se, sn, Ve, vn, a, an]T к положению, скорости и ускорению двух направлений на восток и север соответственно. Единицы: м, м, м/с, м/с, м/с2, м/с2; Матрица перехода:

1 0 T 0 T2/2 0 9пер = [1,0,0;0,1,0] .

Модель инициализируется при X0 = [237 68 0 0 0 0]T, а шумы процесса и измерения равны

Qk = Tal*rTal* e

T2 /2 0 T 0 10 0 T2 /2 0 T 0 1

T = 0,1

, где t — шаг расчета, vgP1 предполагается как белое гауссово распределение с нулевым средним значением. Соответствующие результаты оценки различных алгоритмов фильтрации показаны на рис. 3, где красная пунктирная линия соответствует оценочному значению EKF, аналогичным образом зеленая пунктирная линия соответствует оценочному значению UKF, черная пунктирная линия соответствует SPCKF-KF и синяя линия означает реальную траекторию. Должно быть понятно, что черными пунктирными линиями (SPCKF-KF) получаются самые близкие точки сближения. Другими словами, результаты моделирования доказывают, что предложенный алгоритм демонстрирует отличные характеристики, особенно с точки зрения отслеживания полосы движения при повороте. Хотя зеленая пунктирная линия (UKF) в моделировании показывает очевидные проблемы UKF с временной задержкой. Кроме того, мы используем RMSE для визуализации ошибок каждого алгоритма фильтрации. СКО независимой составляющей востока с использованием фильтров EKF, UKF и SRCKF-KF показаны на рисунках 4 и 5. Из-за ограничения длины независимая составляющая севера не указывается. Результат моделирования показывает, что SRCKF-KF имеет более высокую точность и более высокую скорость сходимости, чем существующий метод.

■*■….. EKF —

……… UKF

-Реальная траектория —

—■— SPCKF-KE

150 X(m)

Fk+1 =

Рис. 3. Реальная траектория и оценка.

Рис. 4(a) показывает, что четкие различия в оценке ошибки в положении между тремя типами алгоритмов, RMSE EKF даже более 10 м, в то время как RMSE SRCKF-KF менее 5 м в целом и даже более точный . В аспекте оценки скорости, который показан на рис. 4(b), нет большой разницы между тремя алгоритмами, однако мы все же можем отделить SRCKF-KF от других, потому что оценка SRCKF-KF генерирует только одно большое значение ошибки. более 0,25 м/с, EKF имеет два значения погрешности более 0,25 м/с и UKF больше. На рис. 4(в) показаны преимущества предложенного алгоритма, как EKF, так и UKF дают довольно большую ошибку в первые 100 9

100 200 300 400

___ I ____ ¡.____]-SRCKF-KF

200 300 ВРЕМЯ /S

400 500

/M / /E U.5R

I | Время/с

100 200 300 400

100 200 300 400

-SRCKF-KF

100 200 300 400 Время/с

Рис. (b) среднеквадратическая ошибка скорости; (c) RMSE при ускорении.

4. Эксперименты

Для проверки работоспособности предложенных алгоритмов в данном разделе представлена ​​проверка метода, которая проводится путем серьезных испытаний транспортных средств.

Возьмите интеллектуальный автомобиль Пекинского технологического университета (BJUT-IV) в качестве экспериментальной платформы для проверки осуществимости и превосходства нового алгоритма. На рис. 5 показана платформа интеллектуального автомобиля (БЮТ-IV с несколькими датчиками, отмеченными на рисунке). «БЮТ-IV» представляет собой электрический кастомизированный автомобиль, переоборудованный из электрических гольф-каров с усовершенствованиями. БЮТ-IV движется с постоянной скоростью или постоянным ускорением, равномерное движение поворота аппроксимируем равномерным движением без влияния на точность контроля.

Рис. 5. Пекинский технологический университет – интеллектуальное транспортное средство (БЮТ-IV).

Информация об азимуте транспортного средства, полученная с помощью GPS/INS, используется для оценки расстояния, скорости и другой информации о движении транспортного средства посредством нелинейной фильтрации. БЮТ-IV оборудован системой измерения фазы несущей GPS. Это оборудование состояло из приемника GPS серии FlexPak-G2, антенны серии GPS-702-GG и радиовещательной станции передачи данных серии PDL4535. На рис. 5 показано оборудование, использовавшееся в БЖУТ-IV.

БЮТ-IV использует встроенную навигацию (GPS/INS) в качестве навигационной системы. Для точной навигации координаты UTM использовались для преобразования системы географических координат в двухмерную прямоугольную систему координат. Сбросить N39.8719°, E116.4789° как начало координат, отмеченное как N8.

Мы разработали программную платформу для тестирования и проверки работоспособности различных алгоритмов фильтрации. Экспериментальная платформа была создана комбинацией VC++6.0, MapX, Matlab и Matcom. Платформа реализует слияние и визуализацию мультисенсорных данных.

Для обработки экспериментальных данных использовались фильтры KF (зеленая линия), EKF (желтая линия) и UKF (синяя линия), SRCKF-KF (красная линия) соответственно. Оранжевая линия обозначает фактическую дорогу движения автомобиля. При условии выбора координаты Восток-Север-Вверх в качестве навигационной координаты положение, скорость и ускорение БЮТ-IV принимаются в виде матрицы переменных состояния в прямоугольной системе координат, которая описывается следующим образом:

X = [x y x y x y]T (32 )

где матричные элементы представляют собой положение, компоненты скорости и ускорения востока и севера соответственно. На рис. 6 показано предполагаемое положение по разным фильтрам и увеличенный рисунок углов.

Стадион

Nio College of Softwar

Архитектурный колледж Building Building

Рис. 6. Фактическое и расчетное состояния.

Очевидно, из скриншотов эксперимента видно, что при оценке положения автомобиля лучшие результаты были достигнуты с помощью предложенного алгоритма фильтра (красная линия), положение, оцененное SRCKF-KF, имеет более пологую кривую отклика, особенно для поворота дороги. В отличие от предложенного алгоритма, производительность KF (зеленая линия), EKF (желтая линия) и UKF (синяя линия) была меньше, чем у SRCKF-KF. С одной стороны, расчетная траектория как EKF, так и KF (зеленая линия) нестабильна, поскольку EKF представляет собой простую нелинейную фильтрацию, а KF — просто линейную фильтрацию, ни EKF, ни KF не могут адаптироваться к интегрированной навигационной системе, особенно при поворот, отмеченный как N10, с другой стороны, синяя линия (оценочное значение UKF) представляет очевидный гистерезисный характер, поскольку точки выборки UKF больше, чем у SRCKF-KF, этот экспериментальный результат согласуется с теоретическим анализом. Основываясь на приведенном выше анализе, предложенный алгоритм доказал свою надежность и точность при тестировании автомобилей на практике.

5. Выводы

В этой статье кубатурный фильтр квадратного корня с фильтром Калмана разработан для нелинейных систем. Предлагаемый фильтр получен из расширенного кубатурного фильтра квадратного корня, объединенного с фильтром Калмана, который использует кубатурный фильтр Калмана (CKF) для оценки нелинейных состояний модели, в то время как ее линейные состояния оцениваются фильтром Калмана. Преимущества предложенного алгоритма следующие:

• Он не требует вычисления якобианов для нелинейного оценивания состояния, что имеет низкую вычислительную сложность. Во многих инженерных приложениях, чувствительных ко времени, он может дать быстрые, но хорошие приближения к гораздо более сложным вычислениям.

• В процессе фильтрации непосредственно с помощью квадратного корня из ковариационной матрицы. Это гарантирует положительную определенность ковариации состояния, сохраняя при этом высокую точность и избегая расхождения

• Он использует нелинейное состояние оценки CKF и линейное состояние оценки KF, что является более логичным и гибким для интеллектуальной интегрированной навигационной системы транспортного средства.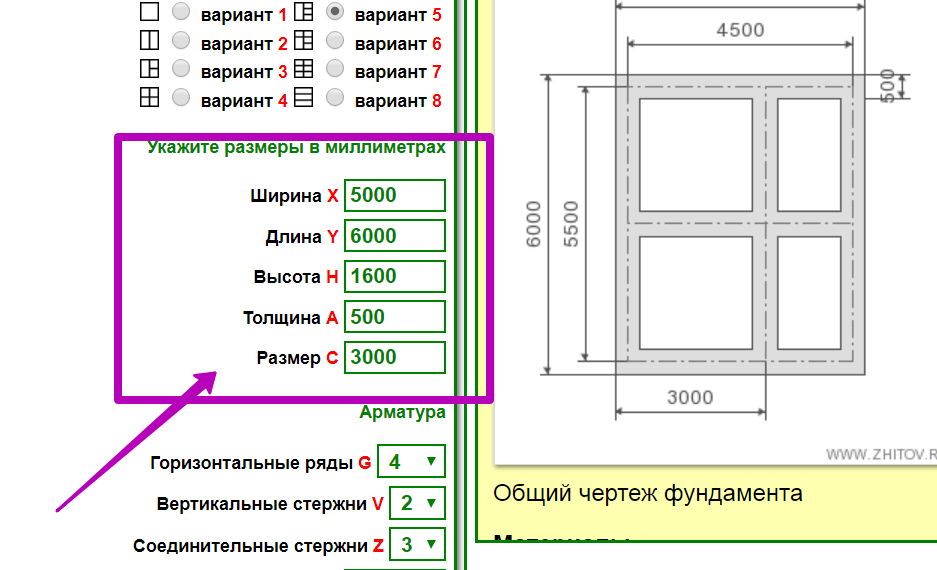

• Отличные характеристики при практических испытаниях. Благодаря адаптивному коэффициенту затухания SRCKF-KF отличается высокой скоростью отклика и высокой надежностью, что имеет определенное значение для решения практических инженерных задач.

Следующие этапы исследования включают введение коэффициента затухания для улучшения адаптивности, затем усиление алгоритма оценкой статистики шума для решения проблемы снижения точности алгоритма и дальнейшего расхождения, когда априорная статистика шума неизвестна и изменяется во времени.

Благодарности

Эта работа поддерживается Пекинским муниципальным фондом естественных наук Китая (JJ0027

802) и Проектом финансирования развития академических кадров в высших учебных заведениях под юрисдикцией Пекинского муниципалитета (038000543115025). Авторы хотели бы поблагодарить Ян Чена, Ли Лунцзе и Чжан Юйчен за их большую помощь во время экспериментов.

Ссылки

[1] Fachinger, J., 2006. Поведение топливных элементов HTR в водных фазах вмещающих горных пород хранилища. Ядерная инженерия и проектирование 236, 54.

[2] Nobe S A, WANG Fei-yue. Обзор последних разработок в области автоматизированного поперечного и продольного управления транспортными средствами. Международная конференция IEEE по SMC. Тусон, Аризона, 2001. 3447-3452.

[3] Песонен, Х.; Пише, Р., «Кубатурные фильтры Калмана для позиционирования», «Навигация и связь с позиционированием» (WPNC), 7-й семинар, 2010 г., том, №, стр. 45,49., 11-12 марта 2010 г.

[4] Джулиер С.Дж., Ульманн Дж.К., Даррант-Уайт Х.Ф. Новый метод нелинейного преобразования средних и ковариаций в фильтрах и оценщиках. Транзакции IEEE на автоматическом управлении. 2000

[5] Мерве Р.В., Ван Э.А. Сигма-точечные фильтры Калмана для интегрированной навигации. Материалы 60-го ежегодного собрания Института навигации. Дейтон: Институт навигации, 2004: 641-654.

[6] Гарридо С., Ахдеррахим М., Хименес А. и др. Противораскачивающий входной контроль автоматического строительного крана. IEEE Transactions on Automa-tion Science and Engineering, 2008, 5 (3): 549. -557.

[7] Иенкаран Арасаратнам, Саймон Хайкин. Кубический фильтр Калмана. IEEE Transactions on Automatic Control, 2009, 54 (6): 1254-1269.

[8] Сунь Фэн Тан Лицзюнь. Кубатурный фильтр Калмана Алгоритм фильтрации Калмана Сунь Фенг. Контроль и решение, 2012, потеря объема (10): 1561-1565

[9] Чандра, К.П.Б.; Да-вэй Гу; Постлетуэйт, И., Кубатурный информационный фильтр квадратного корня. Sensors Journal, IEEE, том 13, № 2, стр. 750,758, февраль 2013 г.

[10] Ван дер Мерве Р., Ван Э. А. Фильтр Калмана без запаха с квадратным корнем для оценки состояния и параметров. проц. Международная конференция IEEE по ICASSP, 2001:3461-3464

Кубатурный фильтр Калмана при минимальной энтропии ошибки с опорными точками для интеграции INS/GPS

[1]	Б. Паркинсон, Дж. Спилкер, П. Аксельрад и П. Энге, Глобальная система позиционирования: теория и приложения . Норвуд, Массачусетс, США: Artech House, 2008. .
[2]	Л. Чанг, Дж. Ли и К. Ли, «Выравнивание на основе оптимизации для бесплатформенной инерциальной навигационной системы: сравнение и расширение», IEEE Trans. Аэросп. Электрон. Сист. , том. 52, нет. 4, стр. 1697–1713, август 2016 г. doi: 10.1109/TAES.2016.130824
[3]	Д. Титтертон и Дж. Уэстон, Бесплатформенная инерциальная навигационная технология . Лондон, Великобритания: Инженерно-технологический институт, 2004 г. .
[4]	П. Д. Гроувс, Принципы работы ГНСС, инерциальных и мультисенсорных интегрированных навигационных систем . Вашингтон, США: Американский институт аэронавтики и астронавтики, 1996. .
[5]	М. Гревал, Л. Вейл и А. Эндрюс, Системы глобального позиционирования, инерциальная навигация и интеграция . Хобокен, Нью-Джерси: John Wiley & Sons, 2007. .
[6]	Ф. Чжао, К. Чен, В. Хе и С. Сэм Ге, «Подход к фильтрации на основе MMAE для интегрированной навигационной системы БИНС/ЦНС», IEEE/CAA Journal of Automatica Sinica , vol. 5, нет. 6, стр. 1113–1120, ноябрь 2018 г. doi: 10.1109/JAS.2017.7510445
[7]	Ю. Хуанг, Ю. Чжан и Л. Чан, «Новый быстрый метод грубой настройки в движении для недорогих БИНС с помощью GPS», IEEE/ASME Trans. Мехатроника , вып. 23, нет. 3, pp. 1303–1313, May 2018. doi: 10.1109/TMECH.2018.2835486
[8]	С. Б. Медейрос и М. М. Вандерли, «Многомодельный линейный фильтр Калмана для непредсказуемых сигналов», IEEE Sensors J. , vol. 14, нет. 4, стр. 979–991, апрель 2014 г. doi: 10.1109/JSEN.2013.2291683
[9]	А. Сингх, «Основные разработки в области фильтрации Гаусса после использования фильтра Калмана без запаха», IEEE/CAA Journal of Automatica Sinica , vol. 7, нет. 5, стр. 1308–1325, сентябрь 2020 г.
[10]	С. Джулиер и Дж. Ульманн, «Новое расширение фильтра Калмана для нелинейных систем», в Proc. 11-й междунар. Симп. Аэрокосмическая/оборонная служба, Simul. Элементы управления , 1997, стр. 182–193.
[11]	К. Х. Ким, Дж. Г. Ли и К. Г. Парк, «Адаптивный двухэтапный расширенный фильтр Калмана для отказоустойчивой слабосвязанной системы INS/GPS», IEEE Trans. Аэросп. Электрон. Сист. , том. 45, нет. 1, стр. 125–137, январь 2009 г. doi: 10.1109/TAES.2009.4805268
[12]	Д. Сан, М. Г. Петовелло и М. Э. Кэннон, «Сверхплотная интеграция GPS/упрощенного IMU для навигации наземных транспортных средств», IEEE Trans. Аэросп. Электрон. Сист. , том. 49, нет. 3, стр. 1781–1791, июль 2013 г. doi: 10.1109/TAES.2013.6558019
[13]	Дж. Вендель, Дж. Мецгер, Р. Моэникес, А. Майер и Г. Ф. Троммер, «Сравнение производительности тесно связанных систем навигации GPS/ИНС на основе расширенных и сигма-точечных фильтров Калмана», Навигация , том. 53, нет. 1, стр. 21–31, август 2014 г.
[14]	J. Zhou, Y. Yang, J. Zhang, E. Edwan и O. Loffeld, «Сильная связь INS/GPS с использованием фильтра Калмана без запаха на основе кватернионов», в Proc. AIAA Guid., Navigat., Control Conf. , Портленд, штат Орегон, США, 2011 г., стр. 1–14.
[15]	Л. Чанг, К. Ли и Б. Ху, «Надежный фильтр погрешности процесса на основе оценки M компании Huber для интегрированной INS/GPS», IEEE Sensors J. , vol. 15, нет. 6, стр. 3367–3374, июнь 2015 г. doi: 10.1109/JSEN.2014.2384492
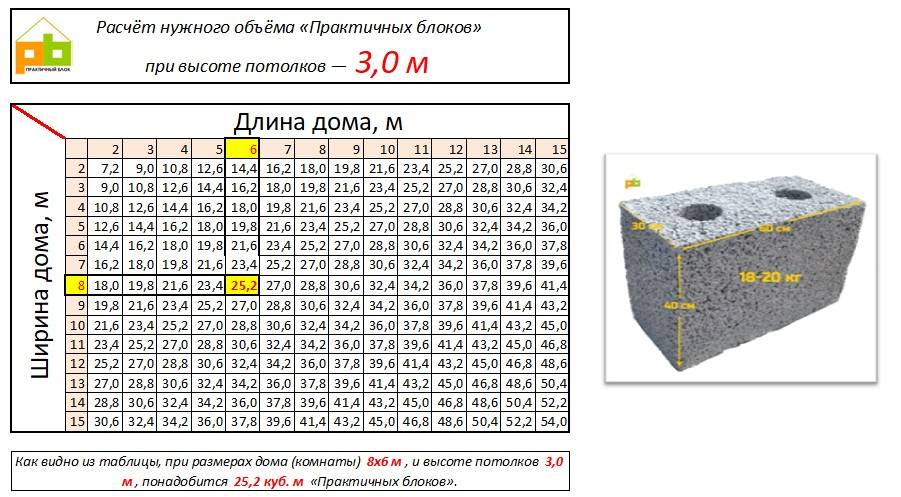[16]	И. Арасаратнам и С. Хайкин, «Кубатурные фильтры Калмана», IEEE Trans. автомат. Контроль , том. 54, стр. 1254–1269, июнь 2009 г. doi: 10.1109/TAC.2009.2019800
[17]	B. Cui, X. Chen и X. Tang, «Улучшенный кубатурный фильтр Калмана для GNSS/INS на основе преобразования апостериорной ошибки сигма-точек», IEEE Trans. Сигнальный процесс. , том. 65, нет. 11, стр. 2975–2987, март 2017 г. doi: 10.1109/TSP.2017.2679685
[18]	Ю. Чжао, «Оценка эффективности кубатурного фильтра Калмана в тесно связанной навигационной системе GPS/IMU», Сигнальный процесс. , том. 119, стр. 67–79, февраль 2016 г. doi: 10.1016/j.sigpro.2015.07.014
[19]	B. Cui, X. Chen, Y. Xu, H. Huang и X. Liu, «Анализ производительности улучшенного повторяющегося кубатурного фильтра Калмана и его применение к GNSS/INS», ISA Trans. , том. 66, стр. 460–468, январь 2017 г. doi: 10.1016/j.isatra.2016.09. 010
[20]	М. Д. Фам, К. С. Лоу, С. Т. Гох и С. С. Чен, «Расширенный фильтр Калмана с планированием усиления для системы определения ориентации наноспутников», IEEE Trans. Аэросп. Электрон. Сист. , том. 51, нет. 2015. Т. 2. С. 1017–1028. doi: 10.1109/TAES.2014.130204
[21]	С. В. Бордонаро, П. В., Ю. Бар-Шалом и Т. Лугинбул, «Сигма-точечный фильтр Калмана с преобразованными измерениями для бистатического гидролокатора и радиолокационного слежения», IEEE Trans. Аэросп. Электрон. Сист. , том. 55, нет. 1, стр. 147–159, февраль 2019 г. doi: 10.1109/TAES.2018.2849179
[22]	K. Feng, J. Li, X. Zhang, X. Zhang, C. Shen, H. Cao, Y. Yang и J. Liu, «Улучшенный кубатурный фильтр Калмана с сильным отслеживанием для интегрированных навигационных систем GPS/INS, Датчики , об. 18, нет. 6, статья № 1919, июнь 2018 г. doi: 10.3390/s18061919
[23]	X. Chen, C. Shen, WB Zhang, M. Tomizuka, Y. Xu и KL Chiu, «Новый гибрид сильного фильтра Калмана и вейвлетной нейронной сети для GPS/INS во время сбоев GPS», Measurement , vol. 46, нет. 10, стр. 3847–3854, декабрь 2013 г. doi: 10.1016/j.measurement.2013.07.016
[24]	Арулампалам М. С., Маскелл С., Гордон Н. и Клапп Т., «Учебное пособие по фильтрам частиц для онлайн-нелинейного/негауссовского байесовского отслеживания», IEEE Trans. Сигнальный процесс. , том. 50, нет. 2, стр. 174–188, февраль 2002 г. doi: 10.1109/78.978374
[25]	X. Liu, H. Qu, J. Zhao и P. Yue, «Кубатурный фильтр Калмана с квадратным корнем максимальной коррентропии с применением к интегрированным системам SINS/GPS», ISA Trans. , том. 80, стр. 195–202, май 2018 г. doi: 10.1016/j.isatra.2018.05. 001
[26]	JC Príncipe, Информационно-теоретическое обучение: энтропия Реньи и перспективы ядра , Нью-Йорк, штат Нью-Йорк, США: Springer, 2010.
[27]	Д. Л. Алспах и Х. Соренсон, «Нелинейная байесовская оценка с использованием приближений суммы Гаусса», IEEE Trans. автомат. Контроль , том. 17, нет. 4, стр. 439–448, август 1972 г. doi: 10.1109/TAC.1972.1100034
[28]	Y. Huang и Y. Zhang, «Новый устойчивый к неопределенности процесса фильтр Калмана на основе t Стьюдента для интеграции SINS/GPS», IEEE Access , vol. 5, стр. 14391–14404, июль 2017 г. doi: 10.1109/ACCESS.2017.2726519
[29]	О. Страка и Й. Дуник, «Стохастическая интеграция Студенческая − t filter», в Proc. 20-й междунар. конф. Инф. Fusion , стр. 1–8, июль 2017 г.
[30]	Ю. Хуанг и Ю. Чжан, «Надежный стохастический кубатурный фильтр Стьюдента на основе t для нелинейных систем с шумами процессов и измерений с тяжелыми хвостами», IEEE Access , vol. 5, нет. 5, стр. 7964–7974, май 2017 г.
[31]	F. Sun и L. Tang, «Кубатурный фильтр частиц», Syst. англ. Электрон. , том. 33, нет. 11, стр. 2554–2557, ноябрь 2011 г.
[32]	B. Cui, X. Chen, X. Tang, H. Huang и X. Liu, «Надежный кубатурный фильтр Калмана для GNSS/INS с отсутствующими наблюдениями и цветным шумом измерений», ISA Trans. , том. 72, стр. 138–146, январь 2018 г. doi: 10.1016/j.isatra.2017.09.019
[33]	Мили Л., Стино Г., Добрака Ф. и Френч Д. Надежный метод оценки для выявления топологических ошибок // IEEE Trans. Система питания , том. 14, нет. 4, стр. 1469–1476, ноябрь 1999 г. doi: 10.1109/59.801932
[34]	Л. Мили и К. В. Коукли, «Надежная оценка в структурированной линейной регрессии», Энн. Статист. , том. 24, нет. 6, стр. 2593–2607, декабрь 1996 г.
[35]	Ю. С. Шмалий, «Итеративный алгоритм типа Калмана, игнорирующий шум и начальные условия», IEEE Trans. Сигнальный процесс. , том. 59, нет. 6, стр. 2465–2473, июнь 2011 г. doi: 10.1109/TSP.2011.2129516
[36]	Т. Чиен-Хао, С. Ф. Лин и Дж. Дах-Цзин, «Надежный кубатурный фильтр Калмана на основе Губера для обработки GPS-навигации», J. Navigat , vol. 229, нет. 7, том. 70, стр. 527–546, Otc. 2016.
[37]	К. Ли, Б. Ху, Л. Чанг и Ю. Ли, «Надежный квадрат — кубатурный корневой фильтр Калмана на основе методологии оценки Хубера», Proc. Инст. мех. англ. Г-Дж. воздух , том. 229, нет. 7, стр. 1236–1245, июнь 2015 г. doi: 10.1177/0954410014548698
[38]	А. Сингх и Дж. К. Принсипи, «Использование коррентропии как функции стоимости в линейных адаптивных фильтрах», в Proc. Междунар. Совместная конф. Нейронная сеть (IJCNN) , июль 2009 г., стр. 2950–2955.
[39]	Б. Чен, Дж. Ван, Х. Чжао, Н. Чжэн и Дж. К. Принсипи, «Сходимость алгоритма с фиксированной точкой по критерию максимальной коррентропии», IEEE Signal Process. лат. , том. 22, нет. 10, стр. 1723–1727, Otc. 2015. doi: 10.1109/LSP.2015.2428713
[40]	B. Chen, X. Liu, H. Zhao, JC Príncipe, «Максимальный корретропный фильтр Калмана», Automatica , vol. 76, стр. 70–77, февраль 2017 г. doi: 10.1016/j.automatica.2016.10.004
[41]	H. Wang, H. Li, J. Zuo, W. Zhang, and H. Wang, «Надежный фильтр Калмана без производной максимальной коррентропии и сглаживатель», Доступ IEEE , том. 6, стр. 70794–70807, ноябрь 2018 г. doi: 10.1109/ACCESS.2018.2880618
[42]	С. Ван, С. Инь, Г. Цянь, Ю. Фенг, С. Кай и Л. Ван, «Кубатурный фильтр Калмана с максимальной корретропией, основанный на статистической линейной регрессии», C.N. Патент, 106487358 A, 8 марта 2017 г. [Онлайн]. Доступно: https://ieeexplore.ieee.org/document/9546666.
[43]	Б. Чен, Л. Син, Б. Сюй, Х. Чжао и Дж. К. Принсипи, «Понимание надежности оценки энтропии с минимальной ошибкой», IEEE Trans. Нейронная сеть. Учиться. Сист. , том. 29, нет. 3, стр. 731–737, март 2018 г. doi: 10.1109/TNNLS.2016.2636160
[44]	Д. Эрдогмус и Дж. К. Принсипе., «Минимизация энтропии ошибки для контролируемого обучения нелинейных адаптивных систем», IEEE Trans. Сигнальный процесс. , том. 50, нет. 7, стр. 1780–1786, июль 2002 г. doi: 10.1109/TSP.2002.1011217
[45]	Y. Zhang, B. Chen, X. Liu, Z. Yuan и JC Príncipe, «Сходимость алгоритма энтропии минимальной ошибки с фиксированной точкой», Entropy , vol. 17, нет. 8, стр. 5549–5560, август 2015 г.
[46]	Б. Чен, Л. Данг, Ю. Гу, Н. Чжэн и Дж. К. Принцип, «Энтропийный фильтр Калмана с минимальной ошибкой», IEEE Trans. Сист. , Человек , Киберн. , Сист. , том. 51, нет. 9, стр. 5819–5829, сентябрь 2021 г.
[47]	Лю В., Покхарел П. П. и Принсипи Дж. К., «Энтропия ошибок, коррентропия и М-оценка», в Proc. 16-й семинар IEEE по машинному обучению. Сигнальный процесс ., 2006, стр. 179–184.
[48]	Дж. Чжао и Л. Мили, «Надежный фильтр Калмана с обобщенным максимальным правдоподобием для оценки динамического состояния энергосистемы», IEEE J. Sel. Темы Сигнальный процесс. , том. 12, нет. 4, стр. 578–592, август 2018 г. doi: 10.1109/JSTSP.2018.2827261
[49]	К. Андреу и В. Каратанасси, «Оценка количества конечных элементов с использованием надежного метода обнаружения выбросов», IEEE J. Сел. Темы Наблюдение за Землей. Дистанционный датчик , том. 7, нет. 1, стр. 247–256, январь 2014 г. doi: 10.1109/JSTARS.2013.2260135
[50]	B. Chen, X. Wang, Y. Li, and JC Príncipe, «Критерий максимальной корретропии с переменным центром», IEEE Signal Process. лат. , том. 26, нет. 8, стр. 1212–1216, август 2019 г. doi: 10.1109/LSP.2019.2925692
[51]	Б. Чен, С. Ван, З. Юань, П. Рен и Дж. Цинь, «Многоядерная корретропия для надежного обучения», [онлайн]. Доступно: https://ieeexplore.ieee.org/document/9546666. Дата обращения: 15 октября 2021 г.
[52]	Б. LEAVE A REPLY Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Рубрики Газобетон Дом Разное Своими руками Советы Строительство Схема