Как рассчитать куб: Как рассчитать куб доски — интернет-магазин Корпорация Снабжения
Как рассчитать объём — онлайн калькулятор объёма воды
Онлайн калькуляторы / 1 комментарий
Как рассчитать объём ёмкости, воды или другой жидкости … несколько онлайн калькуляторов для расчёта объёма, формулы, а также конвертер единиц объёма.
1. Как рассчитать объём любой прямоугольной емкости, в том числе куба — онлайн калькулятор расчёта объема воды в аквариуме, баке …
2. Как рассчитать объём цилиндра — онлайн калькулятор расчёта объёма воды в трубе, бочке, круглом бассейне …
3. Единицы измерения объёма
3.1. Соотношение единиц объёма
4. Конвертер единиц объёма
5. Заключение
6. Как рассчитать объём — калькулятор объёма куба, прямоугольной ёмкости, объёма цилиндра, объёма воды в трубе …
Как рассчитать объём любой прямоугольной емкости, в том числе куба — онлайн калькулятор расчёта объема воды в аквариуме, баке …
Как рассчитать объём по формуле — формула расчёта объёма прямоугольной ёмкости
V = X * Y * Z, где V — объём, а X, Y, и Z это длины сторон ёмкости (длина, ширина, высота).
При этом мы помним, что у куба все стороны равны — X=Y=Z . Соответственно формула объёма куба имеет такой вид — V = X3 , где X — длина стороны куба.
Внимание! При расчёте объёма жидкости в ёмкости необходимо учитывать реальную заполненность ёмкости и привязывать величины непосредственно к самой жидкости.
Для конвертации единиц объёма вы можете воспользоваться нашим ОНЛАЙН КОНВЕРТЕРОМ ЕДИНИЦ ОБЪЁМА →
Как рассчитать объём цилиндра — онлайн калькулятор расчёта объёма воды в трубе, бочке, круглом бассейне …
Для конвертации единиц объёма вы можете воспользоваться нашим ОНЛАЙН КОНВЕРТЕРОМ ЕДИНИЦ ОБЪЁМА →
Как рассчитать объём по формуле — формулы расчёта объёма цилиндра
Объём воды в цилиндре и других ёмкостях, имеющих цилиндрическую форму, рассчитывается таким образом.
Вначале рассчитываем площадь основания (площадь внутреннего сечения) по формуле — S = π * R2
Где, R — радиус трубы, π — число ПИ равное 3,1415926535 .
Затем вычисляем объём — V = S * L
Где, L — длина (высота) цилиндра (трубы, бочки, бассейна).
Внимание! При расчёте объёма жидкости в ёмкости необходимо учитывать заполненность ёмкости и привязывать величины непосредственно к самой жидкости.
Единицы измерения объёма
Вначале кратко ознакомимся с единицами измерения объёма как таковыми.
Официальной единицей измерения объема в системе СИ является м3 — метр кубической. Объём так же может быть выражен и в других единицах. Наиболее популярными из них являются — дм3 — кубические дециметры, см3 — кубические сантиметры, литры …
Отметим, что такая популярная единица измерения объёма жидкостей как литр не входит в Международную систему измерений (СИ). Тем не менее, поскольку литр является весьма популярной мерой жидкостей, он считается официальной внесистемной единицей.
Один литр — это объём куба стороны которого равны 10 см. Полезно также знать, что 1 литр воды вести приблизительно 1 кг при температуре + 4 °C
Соотношение единиц объёма
1 м3 = 1000 дм3 = 1 000 000 см3 = 1 000 000 000 мм3 = 1000 литров
1 литр = 0,001 м3 = 1 дм3 = 1 000 см3 = 1 000 000 мм3
Конвертер единиц объёма
Конвертация кубических метров ( м
3 ) в кубические сантиметры ( см3 ) и литрыКонвертация литров в метры кубические ( м
3 ) и кубические сантиметры ( см3 )Конвертация кубических сантиметров ( см
3 ) в кубические метры ( м3 ) и литрыЗаключение
Практически каждый человек рано или поздно сталкивается с необходимостью рассчитать объём того или другого объекта.
Для удобства и экономии времени предлагаем Вам воспользоваться нашими онлайн калькуляторами.
Поделись с друзьями 🙂
Как рассчитать объём — калькулятор объёма куба, прямоугольной ёмкости, объёма цилиндра, объёма воды в трубе …
Статья опубликована: 2021-06-07 Автор: Waterman
Расчет объема и стоимости бака для воды
Калькулятор стоимости и объема бака по индивидуальным размерам Просто вводим цифры в поля ↓Прямоугольный бак
Затем определяем стоимость по таблице ↓
Купить бак для воды из нержавейки → | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Что такое число в кубе? (Примеры и рабочие листы)
org/BreadcrumbList»>Когда вы умножаете целое число (не дробь) само на себя, а затем еще раз само на себя, результатом будет число в кубе . Например, 3 x 3 x 3 = 27.
Простой способ записать 3 в кубе: 3 3 . Это означает, что три умножить само на себя три раза.
Самый простой способ выполнить это вычисление — выполнить первое умножение (3×3), а затем умножить ответ на то же число, с которого вы начали; 3 х 3 х 3 = 9x 3 = 27.
Кубические числа могут быть немного более запутанными, чем числа в квадрате, просто из-за дополнительного умножения. По сути, вы вычисляете трехмерную форму, а не плоскую.
Вот плоский (или двумерный) квадрат 4 x 4:
Вот трехмерный куб 4 x 4:
Чтобы вычислить количество блоков (число в кубе), на этот раз мы должны умножить 4 x 4 x 4 или 4 3 , что равно 64.
В KS2 вам не нужно изучать куб цифры наизусть, но вы должны иметь общее представление о том, что они собой представляют и как их вычислить. Часто детям дается образец чисел, например, числа нижнего конца куба, и может быть предложено попытаться разобраться в этом образце.
Вот список чисел в кубе до 12×12:
| 0 Кубический | = | 0 3 | = | 0 × 0 × 0 | = | 0 |
| 1 куб | = | 1 3 | = | 1 х 1 х 1 | = | 1 |
| 2 куба | = | 2 3 | = | 2 × 2 × 2 | = | 8 |
| 3 куба | = | 3 3 | = | 3 х 3 х 3 | = | 27 |
| 4 куба | 4 3 | = | 4 х 4 х 4 | = | 64 | |
| 5 Куб | = | 5 3 | = | 5 х 5 х 5 | = | 125 |
| 6 кубов | = | 6 3 | = | 6 х 6 х 6 | = | 216 |
| 7 Куб | = | 7 3 | = | 7 х 7 х 7 | = | 343 |
| 8 кубов | = | 8 3 | = | 8 х 8 х 8 | = | 512 |
| 9 Кубический | = | 9 3 | = | 9 × 9 × 9 | = | 729 |
| 10 кубов | = | 10 3 | = | 10 х 10 х 10 | = | 1000 |
| 11 Куб | = | 11 3 | = | 11 х 11 х 11 | = | 1 331 |
| 12 кубов | = | 12 3 | = | 12 х 12 х 12 | = | 1 728 |
Куб отрицательного числа всегда будет отрицательным, точно так же, как куб положительного числа всегда будет положительным.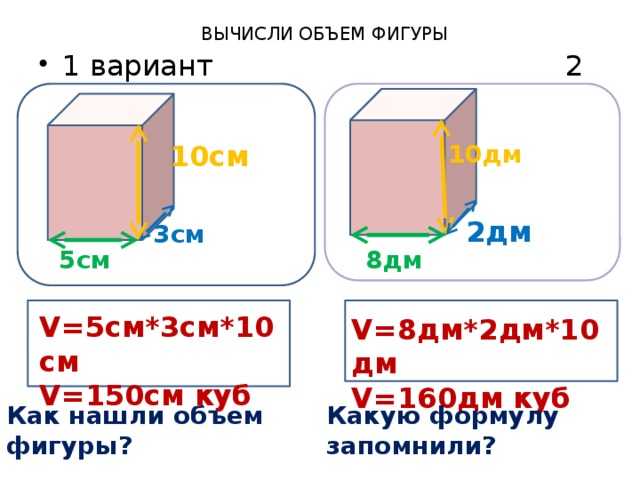
Например; -5 3 = -5 х -5 х- -5 = (25 х -5) = -125.
Так же, как и целые числа (целые числа), десятичное число также легко возвести в куб. Не волнуйтесь, вам не нужно запоминать их на ключевом этапе 2 (или, возможно, даже отрабатывать)!
| 1,23 Кубический | = | 1,23 3 | = | 1,23 × 1,23 × 1,23 | = | 1.860867 | |
| 2,56 Кубический | = | 2,56 3 | = | 2,56 × 2,56 × 2,56 | = | 16.777216 |
Вот несколько рабочих листов, предназначенных специально для того, чтобы разобраться с числами в кубе и отработать свои навыки.
6-й класс – Рисование точек на кубиках
8-й класс – Знай свои квадраты и кубики
8-й класс – Кубические числа и кубические корни Если вам нравятся кубические числа и головоломки, и вы действительно хотите бросить себе вызов, почему бы не заглянуть на веб-сайт BBC Bitesize или не попробовать некоторые из головоломок и задач, поставленных командой NRich из Кембриджского университета?
https://nrich.
maths.org/public/leg.php?code=-308
http://www.bbc.co.uk/guides/z2ndsrd
АВТОР, МС ЭЛИСОН – УЧИТЕЛЬ МАТЕМАТИКИ.
НАПИСАНО: Шарлотта Поттер
Кубический корень числа
Кубический корень числа можно найти очень простым методом, который является методом простой факторизации. Кубический корень обозначается символом «∛». Пример: ∛8 = ∛(2 × 2 × 2) = 2. Поскольку 8 — совершенное кубическое число, легко найти кубический корень числа.
Нахождение кубического корня из несовершенного кубического числа — немного сложный процесс, но его легко освоить. Чтобы найти кубический корень из любого числа, нам нужно найти число, которое при трехкратном умножении само на себя дает исходное число.
Здесь мы научимся находить кубический корень, используя метод простой факторизации и решенные примеры. Кроме того, найдите кубы и кубические корни чисел от 1 до 15 здесь, в приведенной таблице.
Содержание:
- Определение
- Нахождение кубического корня
- Кубический корень из 2
- Кубический корень из 4
- Корневые списки куба
- Кубический корень с помощью простой факторизации
- Кубический корень из 64
- Кубический корень из 216
- Кубический корень из 343
- Кубический корень из 512
- Кубический корень из 729
- Примеры вопросов
- Видео урок
- Часто задаваемые вопросы
Определение
Кубический корень любого числа, скажем, «а», — это число «b», которое удовлетворяет приведенному ниже уравнению:
б 3 = а
Это может быть представлено как:
а = ∛b
Как найти кубический корень числа
Кубический корень — это процесс, обратный вычислению куба числа. Обозначается символом ‘ ∛’.
Давайте посмотрим некоторые примеры здесь сейчас.
Чтобы найти кубический корень из числа 27, нам нужно число, которое при троекратном умножении само на себя даст 27. Мы можем написать,
27 = 3 × 3 × 3 = 3 3
Извлечение кубического корня с обеих сторон;
или ∛27 = ∛3 3
Следовательно, кубический корень из 27 равен 3.
Обратите внимание, что мы будем рассматривать только положительные значения кубических корней натуральных чисел.
Кубический корень из 2
Давайте рассмотрим другой пример числа 2. Так как 2 не является совершенным кубическим числом . Найти кубический корень из 2 непросто. С помощью метода деления в длину можно найти кубические корни несовершенных кубических чисел. Приблизительное значение ∛2 равно 1,260.
Мы можем оценить ∛2, используя здесь прием.
Так как 2 = 1 х 1 х 2
Кубический корень из 2 примерно равен (1 + 1+2)/3 = 4/3 = 1,333.
.
Кубический корень из 4
Опять же, 4 — это число, которое не является совершенным кубом. Если мы разложим его на множители, то получим:
4 = 2 x 2 x 1
Следовательно, как мы видим, мы не можем найти здесь кубический корень простой факторизацией.
Опять же, если мы воспользуемся упрощенным методом, мы получим:
∛4 равно (2+2+1)/3 = 1,67·
Фактическое значение ∛4 равно 1,587, что приблизительно равно 1,67.
Кубы и кубические корни Список от 1 до 15
| Номер | Куб ( 3 ) | Кубический корень ∛a |
|---|---|---|
| 1 | 1 | 1.000 |
| 2 | 8 | 1,260 |
| 3 | 27 | 1,442 |
| 4 | 64 | 1,587 |
| 5 | 125 | 1.710 |
| 6 | 216 | 1,817 |
| 7 | 343 | 1,913 |
| 8 | 512 | 2. 000 |
| 9 | 729 | 2,080 |
| 10 | 1000 | 2,154 |
| 11 | 1331 | 2,224 |
| 12 | 1728 | 2,289 |
| 13 | 2197 | 2,351 |
| 14 | 2744 | 2.410 |
| 15 | 3375 | 2,466 |
Также читайте:
Кубический корень методом простой факторизации
Мы можем найти кубический корень числа методом простой факторизации. Рассмотрим следующий пример для ясного понимания:
2744 = 2 × 2 × 2 × 7 × 7 × 7 = (2 × 7) 3
Следовательно, кубический корень из 2744 = ∛2744 = 2 × 7 = 14
Нахождение кубического корня методом деления
Для нахождения кубического корня с помощью метода деления аналогично использованию метода деления в длину или ручного метода возведения в квадрат.
Составьте пару трехзначных чисел сзади наперед. Следующий шаг — найти число, кубический корень которого меньше или равен заданному числу. Теперь вычтите полученное число из заданного числа и запишите второе число. После этого шага необходимо найти коэффициент умножения для дальнейшего процесса в методе длинного деления, который происходит путем умножения первого полученного числа. Точно так же продолжайте описанный выше процесс, чтобы найти кубический корень числа. Этот долгий процесс деления используется, когда заданное число не является числом в идеальном кубе. Нахождение кубического корня числа с помощью этого процесса занимает много времени.
Кубический корень из 64
Так как 64 является совершенным кубом числа 4, его кубический корень легко найти методом простой факторизации.
64 = 2 x 2 x 2 x 2 x 2 x 2
∛64 = ∛(2 x 2 x 2 x 2 x 2 x 2)
= 2 x 2
= 4
Кубический корень из 216
Так как 216 — это совершенный куб из 6, следовательно, мы можем найти кубический корень из 216 с помощью факторизации.
216 = 2 x 2 x 2 x 3 x 3 x 3
∛216 = ∛(2 x 2 x 2 x 3 x 3 x 3)
∛216 = 2 x 3
∛216 = 6
Кубический корень из 343
Найдем кубический корень из 343 с помощью метода простой факторизации.
Делим 343 на наименьший простой множитель, пока не получим в остатке 1. Выполните следующие шаги;
Кубический корень из 343
Следовательно, 343 = 7 × 7 × 7
А, ∛343 = 7
Кубический корень из 512
Чтобы найти кубический корень из 512, мы должны сначала разложить его на множители.
Разложение числа 512 на простые множители может быть записано как:
512 = 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2
Извлекая кубические корни с обеих сторон, получаем;
∛512 = ∛(2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2)
∛512 = 2 x 2 x 2
∛512 = 8
Кубический корень из 729
Теперь найдем кубический корень из 729.
Кубический корень из 729
729 = 3 × 3 × 3 × 3 × 3 × 3 = 9 × 9 × 9
Следовательно, кубический корень из 729, т.
е. ∛729 = 9
Вопросы о кубическом корне
Вопрос 1: Решите: ∛24389
Решение:
Простые множители = 29×29×29 = 293·
Следовательно, ∛24389= 29,
Вопрос 2: Найдите ∛46656 методом простой факторизации.
Решение:
Сначала найдем простые множители:
Кубический корень чисел
∛46656 = 2×2×2×2×2×2×2×3×3×3×3×3×3 = 23×2 3 ×3 3 ×3 3 = (2×2× 3 × 3) 3
Следовательно, ∛46656= 36.
Видео урок
Часто задаваемые вопросы
Что такое кубический корень числа?
Кубический корень числа определяется как число, результатом которого является исходное число при возведении в куб. Например, для числа 8 кубический корень будет равен 2, поскольку 2×2×2 = 8.
Какой самый простой способ найти кубический корень числа?
Кубический корень из идеальных кубов можно легко найти, используя метод простой факторизации, как описано в этом уроке.