Как посчитать объем в м3 формула фундамента: Онлайн калькулятор расчета бетона для ленточного фундамента

26.02.2023

0 Comment

Содержание

как посчитать в м3, калькулятор

В этой статье мы расскажем о том, как рассчитать объем бетона в соответствии с типом сооружения. Тема статьи неслучайна, так как фундамент, плиты перекрытия и каркас при индивидуальном строительстве являются самыми массивными конструкциями, изготовленными с применением строительных растворов.

Заливка раствора в опалубку

Необходимость проведения точных расчетов

На фото — крупномасштабное бетонирование в промышленном строительстве

Почему так важно правильно знать объем необходимого раствора, ведь, если материала не хватит, можно будет сделать еще? На самом деле максимальная прочность и долговечность монолитных конструкций обеспечивается только в том случае, если раствор подаётся в опалубку для бетонных изделий без длительных простоев.

Избежать простоев, которые могут привести к расслоению бетона, можно зная точное количество смеси, которая потребуется для проведения тех или иных строительных работ.

Актуальные формулы расчета

На фото — установка для приготовления строительных растворов в ограниченных количествах

На данный момент есть немало способов проведение расчетов, например можно применить калькулятор объема бетона. Но онлайн калькулятор в самый ответственный момент может быть недоступен, а потому рассмотрим те формулы, реализовать которые на практике можно в любое время и при любых обстоятельствах.

Не секрет, что есть несколько разновидностей оснований, закладываемых на ту или иную глубину до начала основных строительных работ. В зависимости от конфигурации этих сооружений различается их размер и, как следствие, объем раствора, который потребуется.

Важно: При проведении расчетов потребуется учесть ряд различных факторов, включая выбранную конфигурацию сооружения, условия при которых будет проводиться строительство, температурные и влажностные характеристики воздуха и почвы, глубину залегания грунтовых вод и т.д.

Формула для оснований столбчатого типа

На фото — опалубка для столбчатого (свайного) фундамента

Итак, как посчитать объем бетона? Для этого нужно замерить высоту сооружения узнать площадь и перемножить эти показатели. Но подход к подсчетам в соответствии с формулой V=S*H актуален только к простым сооружениям, тогда как для расчета объёма применительно к сложным конструкциям потребуется иной подход.

Способ расчёта для оснований столбчатого типа с круглыми сваями следующий:

Вычисляем площадь основания каждого столба, делаем это по формуле S = 3,14*r², где r – это радиус каждой отдельно взятой сваи;
Дальше умножаем параметры площади на предполагаемую высоту сваи и получаем объем;
Затем полученный объём умножаем на количество свай, которые будут применены согласно проекту.

Важно: независимо от того насколько правильно проведены расчеты, заказывать раствор нужно на 5-10% больше посчитанной суммы.

Расчеты для оснований плитного типа

На фото — опалубка плитного основания

Теперь рассмотрим то, как посчитать объем в м3 бетона для плитного фундамента.

Инструкция в данном случае проста, так как такое основание представляется собой цельную конструкцию.

Для начала разбиваем запланированный периметр фундамента на прямоугольники. Это нужно сделать, если форма основания сложная. Если конфигурация простая и представляет собой прямоугольник или квадрат, площадь узнаем, умножив длину на ширину.
Дальше определяемся с глубиной закладки и умножаем это число на полученную площадь .

Важно: Как и в случае со столбчатым основанием, заказывать бетон нужно с небольшим запасом.
Дело в том, что по проекту глубина закладки одинакова по всей площади, но на практике эта величина может быть разной.

Расчет объема материала для ленточного фундамента

На фото — опалубка ленточного основания

Ленточный бетонный фундамент на сегодняшний день является наиболее популярной разновидностью оснований, так как характеризуется достаточной прочностью и долговечностью. Кроме того, выбирая такой тип основания можно экономить раствор, так как он будет заливаться не по всему периметру объекта, а только под несущими стенами и перегородками.

Расчет объема бетона в данном случае не представляет собой ничего сложного и выполняется следующим образом:

Замеряем предполагаемую ширину и общую протяженность ленты. Полученные параметры перемножаем и получаем площадь основания.
Затем определяем то, насколько будет заглублен фундамент, и умножаем это число на площадь и получаем номинальный объем раствора, который необходим для заливки в опалубку.

Важно: Если глубина основания под несущие стены и под перегородки предполагается разная, то площадь стен и перегородок нужно считать отдельно и по-отдельности перемножать на соответствующую величину заглубления.

Считаем количество материала для плит перекрытия

Каркас стен и плиты перекрытия

Попробуем рассчитать объем бетона для устройства плит перекрытия. В отличие от плит заводского типа, конструкции, изготовленные своими руками, не имеют сквозных полостей, а представляют собой сплошное сооружение. Поэтому используем формулу V=S*H, согласно которой площадь необходимо умножить на высоту конструкции.

Так как в отличие от заводских аналогов, самостоятельно изготовленные плиты не имеют полостей, их вес может быть внушительным, а потому необходимо позаботиться о своевременном облегчении бетона.

На объектах с малой нагрузкой на перекрытие можно применить пористые или ячеистые бетоны. Отличным решением для обустройства малоэтажных объектов жилищного назначения стал керамзитобетон, который в разы легче тяжёлых плотных растворов.

Расчет материалов для строительства стен

Цена строительства по большему счету определяется стоимостью применённых материалов и именно поэтому так важно заранее знать, сколько чего пойдет для устройства стен.

Как правило, стены целиком из бетона не отливаются, а делается монолитный каркас в виде колон по углам и горизонтальных перекладин. В полости каркаса укладываются стеновые блоки, кирпичи или другие кладочные материалы.

Вывод

Итак, вам известна инструкция расчёта количества строительного раствора для устройства различных конструкционных элементов в составе жилого дома. Полученные навыки вы сможете применить на практике и таким образом избежать перерасхода недешевого бетона.

Больше полезной информации вы сможете найти, посмотрев видео в этой статье.

Добавить в избранное Версия для печати

Поделитесь:

Статьи по теме

Все материалы по теме

Определить строительный объем здания, сооружения, площадь застройки

Расчет объемов работ в строительстве играет важную роль. В проектной документации указывают разные величины, например, отапливаемый объем, общую площадь, жилую площадь и так далее. Как найти строительный объем здания, что это такое и зачем нужен показатель:

Общий строительный объем здания — что это такое

Правила подсчета показателя прописаны в СНиП 31-06-2009 года, а точнее — в их актуализированной редакции, СП 118.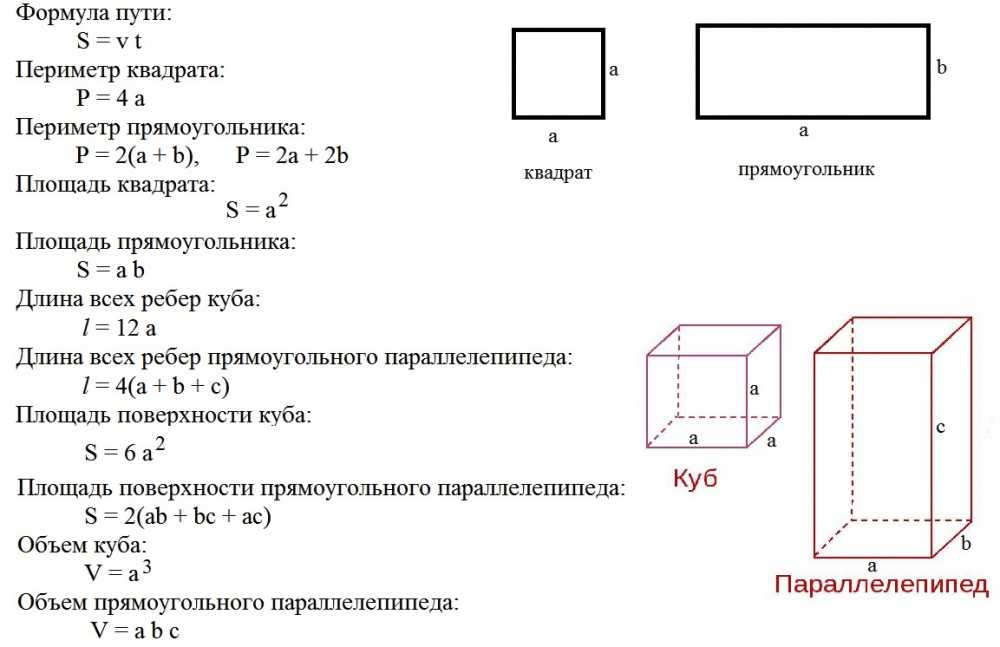 13330.2012 . В документе указано, что строительный объем здания определяется как сумма строительного объема выше отметки 0.00 — надземная часть — и ниже этой отметки — подземная часть. То есть величина — объем подземной и надземной части вместе. При этом учитываются все помещения — как жилые, так и нежилые, а фундамент не входит в формулы.

Строительный объем зданий указывают в кубических метрах. При подсчете полученные значения округляют до 1 м3. Например, если в результате получится цифра 4200,13 м3, то в проектной документации будет отражено значение 4200 м3.

Зачем нужен строительный объем жилого дома и других зданий

Чтобы предварительно определить стоимость строительства или проверить работу подрядчиков — например, узнать, нет ли в смете серьезных ошибок.

Определить стоимость восстановительного ремонта жилого объекта.

Рассчитать затраты на обустройство систем кондиционирования, вентиляции и других.

Также строительный объем можно использовать в других сферах.

Например, в качестве приблизительного значения его могут применять при обустройстве системы отопления для расчета необходимой мощности.

Какие показатели используют при расчете

Высота здания. Расстояние от проектной отметки земли до наивысшей точки отметки конструктивного элемента здания — например, конька или фронтона для скатных крыш.

Длина здания. Расстояние от одного торца здания до другого с учетом внешней отделки стен. В ряде случаев нужна внутренняя длина стен — ее измеряют от одного угла внешней стены до другого, без учета толщины внешних стен и отделки.

Общая площадь. Сумма площадей всех этажей, а также галерей, антресолей, веранд и других помещений, конструкций. Также в значение включают площадь открытых неотапливаемых планировочных элементов — например, наружных тамбуров или открытых лоджий.

Площадь застройки. Площадь горизонтального сечения по внешнему обводу здания по цоколю с учетом разных выступающих элементов, например, ступеней. Проезды под домом, площадь под ним, если здание расположено на столбах, выступающие элементы на уровне менее 4,5 м тоже включаются в площадь застройки. Если часть здания консольно выступает за пределы стены на высоте более 4,5 м, ее не учитывают.

Как считается строительный объем здания: основные правила

Если здание состоит из надземной и подземной части, то сначала считают объем каждой части отдельно, а потом их суммируют.

В расчетах можно использовать как и площадь застройки, так и общую площадь, но формулы для двух способов подсчета отличаются.

Предусмотрены разные формулы расчета для зданий с чердачным перекрытием и без него.

Надземной частью считается часть от пола первого этажа до верха крыши или чердачного перекрытия. Все, что ниже — подземная часть.

Если в доме нет подвала или других помещений подземной части, высоту здания измеряют от уровня пола первого этажа.

В строительный объем не входят объемы балконов, проездов и портиков, но включены объемы мансард, тамбуров, веранд и световых фонарей.

Длина здания измеряется с учетом толщины облицовки и штукатурки.

Если точных данных нет, можно посчитать объем по приблизительным с учетом поправочных коэффициентов.

Как посчитать строительный объем здания — примеры, инструкции, советы

Самый простой способ

Самый простой способ узнать ориентировочный строительный объем — это умножить площадь застройки на высоту здания. Точное значение площади застройки можно посмотреть в технических документах, проектной декларации. Если ее нет, можно использовать простую формулу: длину дома умножить на его ширину.

Например, есть рулетка для измерения длины, ширины и высоты здания. В результате измерений получились следующие данные:

высота — 3,4 м;
длина — 13 м;
ширина — 8 м.

Сначала перемножаем длину и ширину, получаем площадь — 104 м3. Полученное значение умножаем на высоту: 3,4 м. Получаем 353,6 м3, округляем значение до 1 м3 и получаем строительный объем 353 м3.

Полученное значение далеко от реального результата, потому что не учитывает подземную часть, толщину перекрытий, толщину стен, индивидуальные особенности проектировки. Метод подсчета не соответствует требованиям к определению строительного объема, поэтому его нельзя использовать в проектной документации.

Более точный расчет строительного объема

Посчитать строительный объем дома точнее без специальных знаний и навыков помогут поправочные коэффициенты. В этом случае формула будет выглядеть так:

X = S1 x (h + 0,2) x 1,2,

где 0,2 и 1,2 — поправочные коэффициенты, S1 — общая площадь, а h — высота здания.

Как считать общую площадь здания, если она не указана в технической документации? Нужно найти площадь отдельно для каждого помещения, а потом сложить значения. Например, в доме есть 5 комнат площадью 10, 15, 10, 25 и 5 м2. Суммарная площадь составит 65 м2.

После того, как нашли площадь, нужно измерить или посмотреть высоту — допустим, она составляет 4,5 м. Добавляем к полученному значению 0,2 — примерную толщину перекрытий, получаем 4,7 м.

Теперь нужно перемножить полученные значения и умножить их на 1,2 — коэффициент перехода внутренней площади здания к внешней.

65 м2 x 4,7 м x 1,2 = 306,7 или 307 м3.

Этот способ расчета более достоверный по сравнению с первым, но тоже не дает точных результатов. Он не учитывает индивидуальные конструктивные особенности здания: толщину перекрытий и стен. Зато позволяет быстро посчитать строительный объем для зданий необычной формы — например, многоугольной.

Дома с подземной частью

Если в доме есть подвал, технический этаж или другие помещения под землей, нужно отдельно посчитать строительный объем подземной части здания и наземной, а потом сложить полученные значения.

Для определения объема подземной части нужно знать площадь застройки или площадь горизонтального сечения подвала. Например, для подвала правильной прямоугольной формы площадь горизонтального сечения можно легко найти: нужно умножить длину на ширину.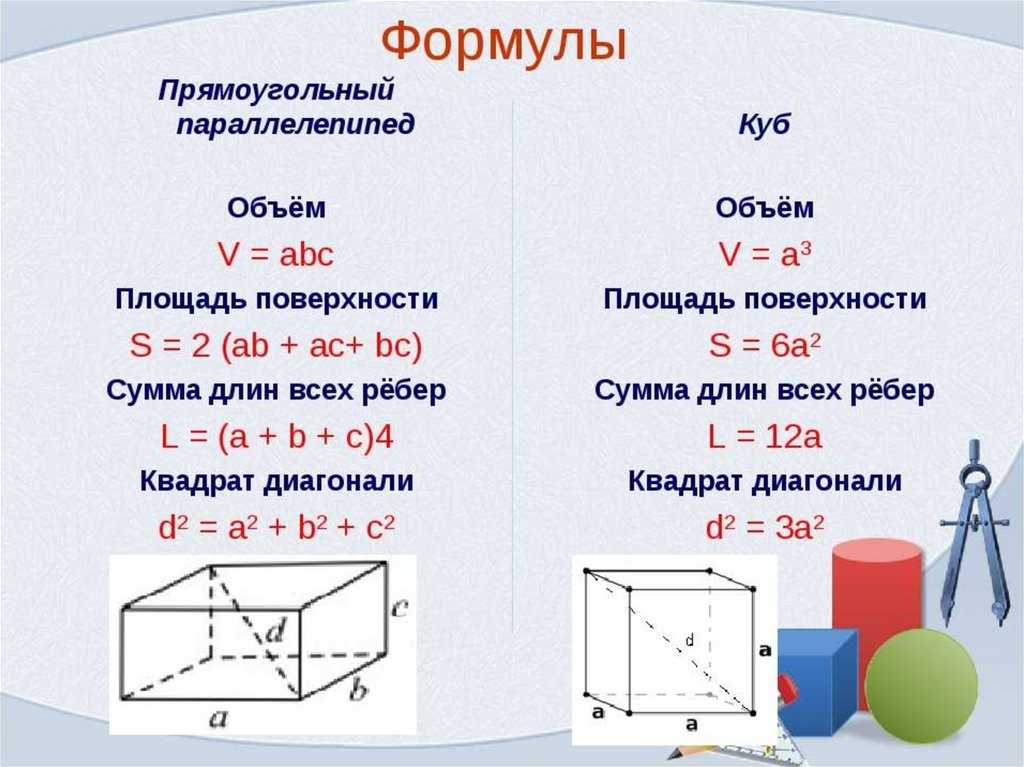 Например, длина составляет 23 м, ширина — 10 м. Площадь застройки или сечения дальне нужно умножить на высоту — ее измеряют от уровня пола подвала до пола первого этажа. Например, она составляет 3 м. Перемножаем площадь 230 м? на высоту 3 м и получаем объем 690 м?.

Чтобы определить объем надземной части, тоже нужно выяснить площадь горизонтального сечения и высоту. Сечение измеряем по внешней части здания. Например, длина составляет 23,6 м, ширина — 10,3 м. Высоту измеряем от пола первого этажа до начала теплоизоляционного слоя чердачного помещения, а если крыша плоская — до середины чердака. Допустим, она составила 13 м. Точно также находим площадь — она составила 243,08 м2 — и умножаем ее на высоту. Получаем 3160,04 м3, или округленные 3160 м3.

Полученные значения складываем: прибавляем 690 м3 к 3160 м3 и получаем общий строительный объем: 3850 м3.

Здания без подвала

Если в доме нет подземной части, то строительный объем считается только по надземной части. Посчитать его можно по предыдущей формуле: находим сначала площадь горизонтального сечения, а затем умножаем ее на высоту.

Чтобы определить площадь поперечного сечения, тоже нужно проводить измерение по внешней части здания, с учетом штукатурки и облицовки. Если форма здания сложная, можно условно поделить его на отдельные геометрические фигуры. Например, если два параллельно расположенных здания соединены переходом в форме буквы «Н», можно рассчитать площадь отдельно каждого прямоугольника, а затем суммировать их и умножить на высоту.

Например, длина двух параллельных зданий — 30 м, их ширина — 15 м. Размеры перехода — 2,5 на 6 м. Значит, сначала нужно найти площадь одинаковых зданий: умножаем 15 на 30, получаем 450 м2. Площадь перехода — 15 м2. Складываем три площади: 450 + 450 + 15, получается 915 м2. Если высота здания составляет 3 м, то строительный объем будет 2745 м3.

Здания с чердачными перекрытиями

Если в здании есть чердачное перекрытие, то строительный объем надземной части считают по особой формуле:

X = S1 x h.

В этом случае под S1 понимают площадь горизонтального сечения здания. Ее измеряют на уровне первого этажа выше цоколя, по внешнему обводу здания. Чтобы найти площадь, нужно также умножить ширину на длину здания, как и в расчетах по другим формулам.

Высоту h измеряют от верха чистого пола на первом этаже до верха засыпки чердачного перекрытия.

Допустим, площадь горизонтального сечения здания на уровне первого этажа составляет 420 м2. Высота составляет 25 м. В этом случае строительный объем будет равен 10500 м3.

Если у здания есть поздемная часть, ее объем считают так же, как и в предыдущих случаях, а затем оба значения складывают.

Дома без чердачного перекрытия

Строительный объем надземной части зданий без чердачных перекрытий считают по другой формуле:

X = S2 x L

S2 — тоже площадь поперечного сечения, но не горизонтального, а вертикального. Ее измеряют по наружным стенам, тоже с учетом слоя штукатурки и облицовки. В этом случае для определения площади нужна высота здания и его ширина.

L — это длина здания, перпендикулярная прямая относительно вертикального поперечного сечения. Ее измеряют от одного торца здания к другому, тоже с учетом штукатурки и облицовки, на уровне первого этажа либо цоколя.

Например, нужно рассчитать объем здания высотой 6 м, длиной 23 м и шириной 4 м. Площадь вертикального поперечного сечения в этом случае составит 24 м2, а строительный объем — 552 м3.

Если у здания есть подземная часть, ее также считают отдельно, а потом полученные значения суммируют.

Если известна общая площадь

Детальные данные, например, длину, высоту до определенных перекрытий и другие, не всегда указывают в технической документации. Поэтому строительный объем можно посчитать по другим формулам.

Если известна общая площадь, можно использовать формулу:

X = S x H x К

В этом случае S — сумма площадей всех этажей, или общая площадь. Ее измеряют по внутренней обводке наружных стен, то есть не учитывается их толщина. Кроме того, замеряют также площадь подвала, поэтому отдельных расчетов для подземной части не нужно.

H в формуле — высота здания изнутри без учета перекрытий, так называемая высота в свету.

К — поправочный коэффициент, который учитывает толщину стен. Для жилых зданий он составляет 0,8.

То есть для расчета нужно знать всего два точных значения: общую площадь и высоту в свету. Допустим, площадь составляет 2 000 м2, а высота в свету — 15 м. В этом случае показатель составит 24000 м3 с учетом поправочного коэффициента.

Если известна площадь застройки

Если известна площадь застройки, можно использовать другую формулу. В ней больше переменных, и выглядит она так:

X = S1 x h2 + S2 x h3

S1 в этом случае — площадь общей застройки. Ее можно найти, представив здание в виде геометрической фигуры или нескольких таких фигур, если постройка сложной формы. h2 — высота дома, в которой можно не учитывать выступающие части крыши.

S2 и h3 — площадь и высота подвала соответственно. Площадь замеряют по внутренней обводке стен. Высоту — от верхней точки пола подвала до пола первого этажа.

Дома с мансардами

Мансарда — этаж в чердачном пространстве, фасад которого частично либо полностью образован поверхностями наклонной крыши. Обязательное условие — линия пересечения плоскости крыши и фасада должна находиться не больше, чем на высоте 1,5 м от уровня пола в мансарде. Согласно нормативам, строительный объем мансарды считается отдельно.

Чтобы найти строительный объем мансарды, нужно умножить площадь ее поперечного вертикального сечения на длину дома.

Ширину и высоту нужно измерять по внешнему обводу, вертикаль — до начала перекрытий. Все эти данные понадобятся для того, чтобы найти площадь вертикального сечения. Она равна половине произведения ширины, то есть основания, на высоту. Например, высота мансарды — 1,5 м, ширина, то есть основание — 6 м. Тогда площадь составит 9 м2.

Полученное значение нужно умножить на длину дома. Например, она составляет 12 м. В этом случае строительный объем мансарды составит 108 м3.

Оставшуюся надземную часть нужно считать по предыдущим формулам, но высоту измерять до начала основания мансарды, то есть до верхнего перекрытия. Объемы мансарды, надземной и подземной частей нужно просто сложить.

Если здание имеет сложную форму

Расчет строительного объема для зданий сложной формы — например, с мезонинами, башенками и различными пристроями — намного сложнее. В этом случае нужно сначала найти строительный объем каждого конструктивного элемента, а потом сложить полученные значения.

Полная формула расчета строительного объема зависит от исходных данных — есть ли подвал, предусмотрены ли чердачные перекрытия, построена ли мансарда. Чтобы получить точное значение, нужно провести тщательные замеры и использовать сложные схемы подсчета.

Страница не найдена — Фонд Наффилда

Страница, которую вы ищете, не может быть найдена. Пожалуйста, попробуйте использовать либо главное меню, либо поиск по сайту.

Поиск проектов, новостей, воздействия, событий

Поиск

Образование 643 Когнитивные и некогнитивные навыки 32Curriculum и субъект. 30 лет.Образование и навыки после 16 лет 94Начальное образование 130Q-Step 26Эффективность школы 45Среднее образование 154Специальные образовательные потребности и инвалидность 54Проблемы системного образования 97Правосудие 231Доступ к правосудию 36Административное правосудие 23Гражданское правосудие 21Судебный опыт и доказательства 18Уголовное право 22Домашнее насилие 5Равенство и права человека 2Семейное правосудие и 130Частный сектор закон о социальном обеспечении 9Молодежное правосудие 22Благополучие 761Искусственный интеллект 3Помощь при смерти 1Дополненная реальность 0Преимущества 52Обязанности по уходу 27Сообщества и социальная сплоченность 63Страна рождения 24COVID-19327Прогнозирование преступности 2Данные для общественного блага 27Цифровой вред и дезинформация 33Цифровая интеграция и исключение 14Цифровые навыки 16Цифровое общество 47Инвалидность 14Экономика, государственные расходы и услуги 178Этническая принадлежность 48Семья и семейная динамика 115Гендер 42Глобальное неравенство в отношении здоровья и нуждающиеся дети 73Психическое здоровье 91Заболевания опорно-двигательного аппарата 11Пенсии 16Физическое здоровье 43Бедность и уровень жизни 108Производительность и инновации 7Общественное здравоохранение 150Социальные сети 2Социоэкономика старения 24Социоэкономика раннего взросления 40Спортивная наука 1Злоупотребление психоактивными веществами 11Налоги 47Доверие к демократии 65Оценка данных 5

ProjectsNewsEventsImpactOpinionPublicationsSeriesReportsEducation 643Cognitive and non-cognitive skills 32Curriculum and subject choice 30Early years 161Education workforce 75Educational assessment 28Higher education 92Language and literacy 78Lifelong learning 14Nuffield Research Placements 23Numeracy 83Parenting 73Pedagogy 19Post-16 education and skills 94Primary education 130Q-Step 26School effectiveness 45Secondary education 154Special educational needs и инвалидность 54Системные проблемы образования 97justice 231 к правосудию 36 Административное правосудие 23Civil юстиции 21 Корт. Опыт и доказательства 18 КРИМИНАЛЬНОЕ ПРАВДОВОСТИ 22DOMESTIC ЗАПОЛНЕНИЕ 5 ИСПРАВЛЕНИЕ И ПРАВО ПРАВА 16 СВЯЗАНСКОЕ ПРЕДОСТАВЛЕНИЕ 130 ПРИВАТ И ПРОМЕМОЙ ПРАВО 2 Социальное правовое право. 19 327Прогнозирование преступности 2Данные для общественного блага 27Цифровой вред и дезинформация 33Цифровая интеграция и исключение 14Цифровые навыки 16Цифровое общество 47Инвалидность 14Экономика, государственные расходы и услуги 178Этническая принадлежность 48Семья и семейная динамика 115Гендер 42Глобальное неравенство в отношении здоровья дети и нуждающиеся дети 73Психическое здоровье 91Заболевания опорно-двигательного аппарата 11Пенсии 16Физическое здоровье 43Бедность и уровень жизни 108Производительность и инновации 7Общественное здравоохранение 150Социальные сети 2Социоэкономика старения 24Социоэкономика раннего взросления 40Спортивная наука 1Злоупотребление психоактивными веществами 11Налоги 47Доверие к демократии 65Оценка данных 5

Ознакомьтесь с нашими проектами

В процессе

Образование | 2023 – 2025

Помогают ли субтитры на одном языке детям научиться читать?

Посмотреть проект

Новый

Благосостояние | 2023 – 2025

Региональный индекс регенерации для отслеживания социально-экономического «повышения уровня»

Посмотреть проект

В процессе

Образование | 2022 – 2024

Посмотреть проект

Увидеть все

Последние

Как рассчитать объем прямоугольной призмы?

В геометрии призма представляет собой объект трехмерной формы, который состоит из двух одинаковых многоугольников, обращенных друг к другу и соединенных по бокам прямоугольными или параллелограммными гранями. Эти одинаковые многоугольники называются основаниями призмы и могут иметь любую форму, например треугольники, квадраты, прямоугольники или любой n-сторонний многоугольник. Призма является важным членом семейства многогранников. В зависимости от типа многоугольного основания призмы делятся на два типа: правильные и неправильные призмы. И в зависимости от выравнивания оснований существует два типа призм: прямые призмы и наклонные призмы. Кроме того, в зависимости от формы многоугольного основания призмы подразделяются на различные типы: треугольные призмы, прямоугольные призмы, квадратные призмы, пятиугольные призмы, шестиугольные призмы и т. д.

Прямоугольная призма

Прямоугольная призма представляет собой трехмерную фигуру, состоящую из шести прямоугольных плоских граней. Это призма с двумя прямоугольными основаниями и четырьмя боковыми прямоугольными гранями, двенадцатью сторонами и восемью вершинами. Согласно математическим исследованиям, прямоугольным параллелепипедом называется любой многогранник, напоминающий прямоугольную призму. В прямоугольной призме каждый угол прямой. Он также известен как прямоугольный шестигранник, правильная прямоугольная призма и прямоугольный параллелепипед.

Объем прямоугольной призмы

Объем прямоугольной призмы — это полное пространство, заключенное внутри прямоугольной призмы. Она обычно обозначается буквой «V» и измеряется в см ³ , м ³ , в ³ и т. д. Объем прямоугольной призмы определяется путем умножения площади ее основания на ее высоту.

Формула объема прямоугольной призмы дается следующим образом:

Объем прямоугольной призмы = площадь основания × высота призмы

Поскольку основанием призмы является прямоугольник, ее площадь равна произведению длины и ширины. Пусть «h» — высота призмы, «l» — длина основания, а «b» — ширина основания.

Теперь формула для объема прямоугольной призмы дается следующим образом:

Объем прямоугольной призмы = l × w × h кубических единиц

Решаемые примеры на основе

Объем прямоугольной призмы

Задача 1. Найдите высоту прямоугольной призмы, если ее объем равен 90 кубических дюймов, а его базовая площадь равна 15 квадратных дюймов.

Решение:

Приведены данные,
Объем прямоугольной призмы = 90 куб. в
Площадь основания = 15 кв. в
Мы знаем, что,
Объем прямоугольной призмы формула = Площадь основания × Высота призмы
⇒ 90 = 15 × h
⇒ h = 90/15 = 6 дюймы.
Следовательно, высота данной призмы равна 6 дюймам.

Задача 2: Определить объем прямоугольной призмы, если длина ее основания 10 см, ширина основания 6 см, а высота призмы 15 см. 9

Высота основания (h) = 15 см знать, что,

Объем прямоугольной призмы формула (V) = площадь основания × высота призмы

площадь основания = l × w

= 10 × 6 = 60 кв.см.

В = 60 × 15 = 900 куб. см

Отсюда объем прямоугольной призмы 900 куб. см.

Задача 3.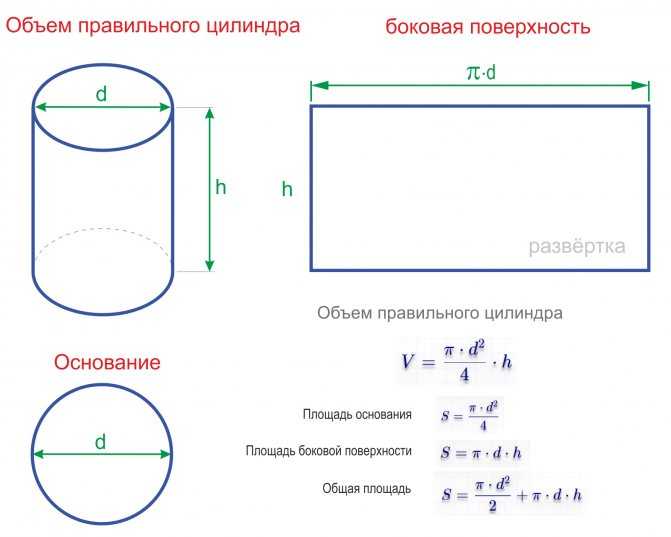 Какова ширина основания прямоугольной призмы, если ее объем 2100 куб. см, а его высота и длина основания равны 25 см и 12 см соответственно?

Решение:

Приведены данные,
Объем прямоугольной призмы = 2100 куб. см
Высота прямоугольной призмы (h) = 25 см
Длина основания (l) = 12 см
Мы знаем, что,
Объем прямоугольной призмы формула (V) = площадь основания × высота призмы
Площадь основания = l × w
⇒ V = l × w × h
⇒ 2100= 12 × w × 25
⇒ 300w = 2100
⇒ w = 2100/390 см ширина основания прямоугольной призмы 7 см.

Задача 4. Каков объем прямоугольной призмы высотой 20 единиц и площадью основания 120 квадратных единиц?

Решение:

Приведены данные,
Высота прямоугольной призмы (h) = 20 единиц
Площадь основания = 120 квадратных единиц
Мы знаем, что
Объем прямоугольной призмы по формуле (V) = Площадь основания × Высота призмы
V = 120 × 20 = 2400 кубических единиц.
Следовательно, объем прямоугольной призмы равен 2400 кубических единиц.

Задача 5. Какова длина основания прямоугольной призмы, если ее объем 150 куб. см, а его высота и ширина основания равны 10 см и 3 см соответственно?

Решение:

Приведенные данные,
Объем прямоугольной призмы = 150 куб. см
Высота прямоугольной призмы (h) = 10 см
Ширина основания (w) = 3 см
Мы знаем, что,
Формула объема прямоугольной призмы (V) = площадь основания × высота призмы
Площадь основания = l × w
⇒ V = l × w × h
⇒ 150 = l × 3 × 10
⇒ 30l = 150 длина основания прямоугольной призмы равна 5 см.

Задача 6. Каков объем прямоугольной призмы, высота которой равна 20 единицам, а длина и ширина основания равны 15 единицам и 12 единицам соответственно?

Решение:

Приведенные данные,
Высота прямоугольной призмы (h) = 20 ед.
Длина основания (l) = 15 ед. знать, что,
Объем прямоугольной призмы = l × w × h кубических единиц
V = 15 × 12 × 20 = 3600 кубических единиц.
Следовательно, объем прямоугольной призмы равен 3600 кубических единиц.

Задача 7. Определить объем прямоугольной призмы, если ее высота равна 10 см, а длина и ширина основания равны 8 см и 6 см соответственно.

Решение:

Приведенные данные,
Высота прямоугольной призмы (h) = 10 см
Длина основания (l) = 8 см
Ширина основания (w) = 6 3 см
0002 Мы знаем, что,
Объем прямоугольной призмы = l × w × h кубических единиц
V = 8 × 6 × 10 = 480 куб. см
Значит, объем прямоугольной призмы равен 480 куб. см.

Часто задаваемые вопросы на основе прямоугольной призмы

Вопрос 1: Каков объем прямоугольной призмы?

Ответ:

Объем прямоугольной призмы — это количество вещества, которое она может удержать, или это пространство, занимаемое ею в трехмерном пространстве. Итак, объем прямоугольной призмы рассчитывается путем умножения площади ее основания на ее высоту. Формула для нахождения объема прямоугольной призмы:
Объем (V) = высота призмы × площадь основания.
Он рассчитывается в кубических единицах, таких как см ³ , м ³ , ³ и т. д.

Вопрос 2: Какие изменения происходят с объемом прямоугольной призмы, если ее высота удвоена ?

Ответ:

Объем прямоугольной призмы является произведением ее трех измерений, т. е.
объем = длина × ширина × высота.
Если высоту прямоугольной призмы увеличить вдвое, то ее объем будет V ₂ = l × w × (2h) = 2 × lwh = 2 × V ₁ . Таким образом, можно с уверенностью сказать, что объем прямоугольной призмы удваивается, когда ее высота увеличивается вдвое.

Вопрос 3. Что произойдет с объемом прямоугольной призмы, если ее высоту уменьшить вдвое?

Ответ:

Объем прямоугольной призмы есть произведение ее трех измерений, т.