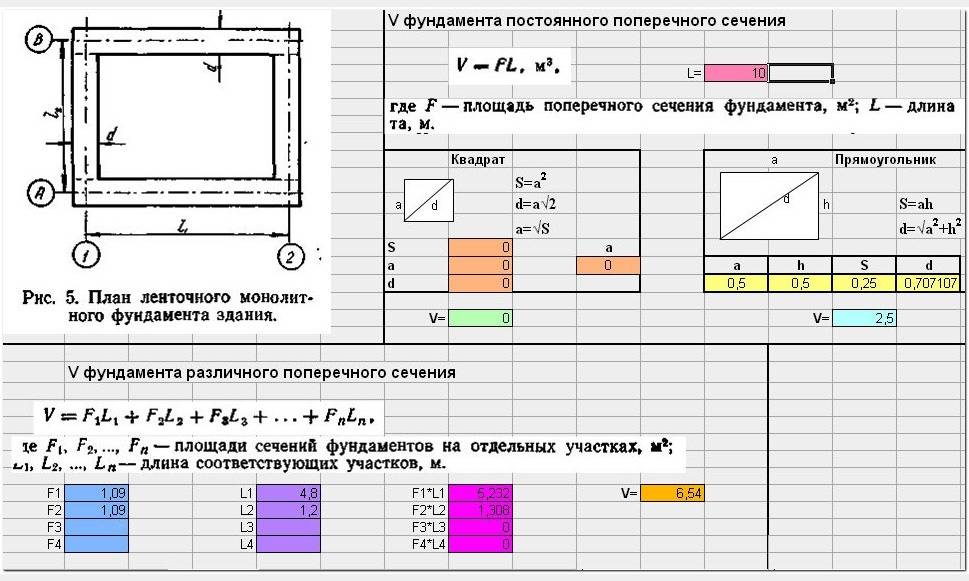
Как посчитать объем в м3 формула фундамента: Ничего не найдено для Fundament Obem Fundamenta Kak Poschitat Obem Fundamenta V M3 Kalkulyator %23Kak Poschitat Kubaturu Fundamenta Pod Dom
Определить строительный объем здания, сооружения, площадь застройки
Расчет объемов работ в строительстве играет важную роль. В проектной документации указывают разные величины, например, отапливаемый объем, общую площадь, жилую площадь и так далее. Как найти строительный объем здания, что это такое и зачем нужен показатель:
Общий строительный объем здания — что это такоеПравила подсчета показателя прописаны в СНиП 31-06-2009 года, а точнее — в их актуализированной редакции, СП 118.13330.2012 . В документе указано, что строительный объем здания определяется как сумма строительного объема выше отметки 0.00 — надземная часть — и ниже этой отметки — подземная часть. То есть величина — объем подземной и надземной части вместе. При этом учитываются все помещения — как жилые, так и нежилые, а фундамент не входит в формулы.
Строительный объем зданий указывают в кубических метрах. При подсчете полученные значения округляют до 1 м3. Например, если в результате получится цифра 4200,13 м3, то в проектной документации будет отражено значение 4200 м3.
Высота здания. Расстояние от проектной отметки земли до наивысшей точки отметки конструктивного элемента здания — например, конька или фронтона для скатных крыш.
Длина здания. Расстояние от одного торца здания до другого с учетом внешней отделки стен. В ряде случаев нужна внутренняя длина стен — ее измеряют от одного угла внешней стены до другого, без учета толщины внешних стен и отделки.
Общая площадь. Сумма площадей всех этажей, а также галерей, антресолей, веранд и других помещений, конструкций. Также в значение включают площадь открытых неотапливаемых планировочных элементов — например, наружных тамбуров или открытых лоджий.
Площадь застройки. Площадь горизонтального сечения по внешнему обводу здания по цоколю с учетом разных выступающих элементов, например, ступеней. Проезды под домом, площадь под ним, если здание расположено на столбах, выступающие элементы на уровне менее 4,5 м тоже включаются в площадь застройки. Если часть здания консольно выступает за пределы стены на высоте более 4,5 м, ее не учитывают.
Как считается строительный объем здания: основные правила
Самый простой способ узнать ориентировочный строительный объем — это умножить площадь застройки на высоту здания. Точное значение площади застройки можно посмотреть в технических документах, проектной декларации. Если ее нет, можно использовать простую формулу: длину дома умножить на его ширину.
Если ее нет, можно использовать простую формулу: длину дома умножить на его ширину.
Например, есть рулетка для измерения длины, ширины и высоты здания. В результате измерений получились следующие данные:
- высота — 3,4 м;
- длина — 13 м;
- ширина — 8 м.
Сначала перемножаем длину и ширину, получаем площадь — 104 м3. Полученное значение умножаем на высоту: 3,4 м. Получаем 353,6 м3, округляем значение до 1 м3 и получаем строительный объем 353 м3.
Полученное значение далеко от реального результата, потому что не учитывает подземную часть, толщину перекрытий, толщину стен, индивидуальные особенности проектировки. Метод подсчета не соответствует требованиям к определению строительного объема, поэтому его нельзя использовать в проектной документации.
Посчитать строительный объем дома точнее без специальных знаний и навыков помогут поправочные коэффициенты. В этом случае формула будет выглядеть так:
X = S1 x (h + 0,2) x 1,2,
где 0,2 и 1,2 — поправочные коэффициенты, S1 — общая площадь, а h — высота здания.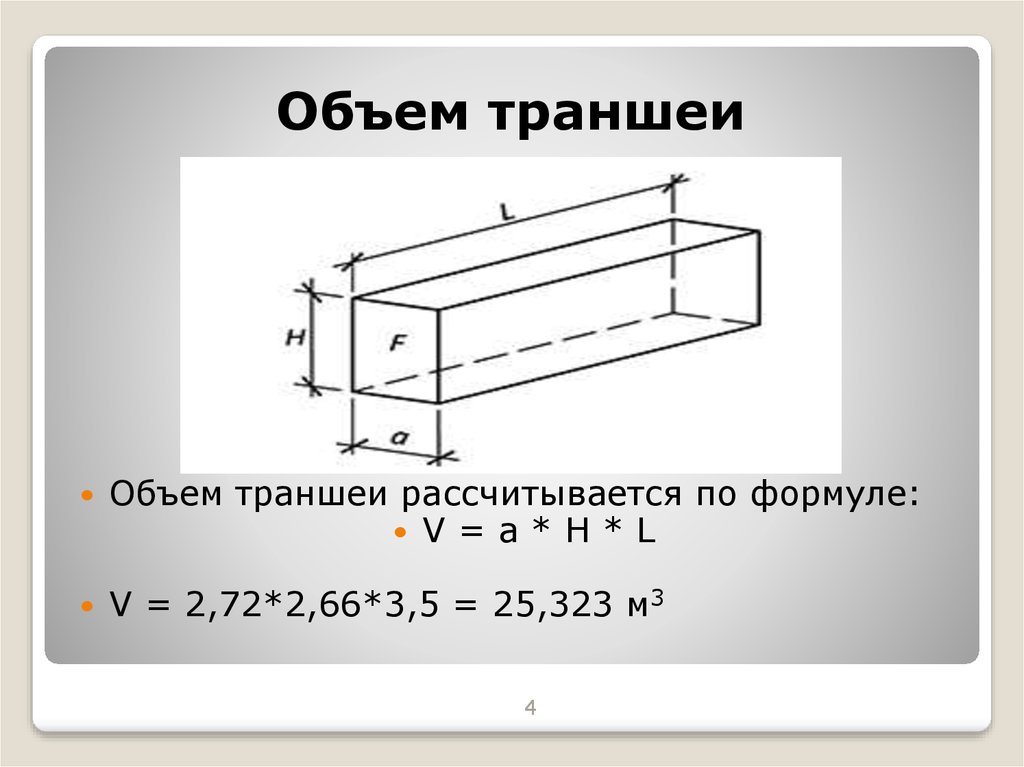
Как считать общую площадь здания, если она не указана в технической документации? Нужно найти площадь отдельно для каждого помещения, а потом сложить значения. Например, в доме есть 5 комнат площадью 10, 15, 10, 25 и 5 м2. Суммарная площадь составит 65 м2.
После того, как нашли площадь, нужно измерить или посмотреть высоту — допустим, она составляет 4,5 м. Добавляем к полученному значению 0,2 — примерную толщину перекрытий, получаем 4,7 м.
Теперь нужно перемножить полученные значения и умножить их на 1,2 — коэффициент перехода внутренней площади здания к внешней.
65 м2 x 4,7 м x 1,2 = 306,7 или 307 м3.
Этот способ расчета более достоверный по сравнению с первым, но тоже не дает точных результатов. Он не учитывает индивидуальные конструктивные особенности здания: толщину перекрытий и стен. Зато позволяет быстро посчитать строительный объем для зданий необычной формы — например, многоугольной.
Дома с подземной частью
Если в доме есть подвал, технический этаж или другие помещения под землей, нужно отдельно посчитать строительный объем подземной части здания и наземной, а потом сложить полученные значения.
Для определения объема подземной части нужно знать площадь застройки или площадь горизонтального сечения подвала. Например, для подвала правильной прямоугольной формы площадь горизонтального сечения можно легко найти: нужно умножить длину на ширину. Например, длина составляет 23 м, ширина — 10 м. Площадь застройки или сечения дальне нужно умножить на высоту — ее измеряют от уровня пола подвала до пола первого этажа. Например, она составляет 3 м. Перемножаем площадь 230 м? на высоту 3 м и получаем объем 690 м?.
Чтобы определить объем надземной части, тоже нужно выяснить площадь горизонтального сечения и высоту. Сечение измеряем по внешней части здания. Например, длина составляет 23,6 м, ширина — 10,3 м. Высоту измеряем от пола первого этажа до начала теплоизоляционного слоя чердачного помещения, а если крыша плоская — до середины чердака. Допустим, она составила 13 м. Точно также находим площадь — она составила 243,08 м2 — и умножаем ее на высоту. Получаем 3160,04 м3, или округленные 3160 м3.
Полученные значения складываем: прибавляем 690 м3 к 3160 м3 и получаем общий строительный объем: 3850 м3.
Здания без подвала
Если в доме нет подземной части, то строительный объем считается только по надземной части. Посчитать его можно по предыдущей формуле: находим сначала площадь горизонтального сечения, а затем умножаем ее на высоту.
Чтобы определить площадь поперечного сечения, тоже нужно проводить измерение по внешней части здания, с учетом штукатурки и облицовки. Если форма здания сложная, можно условно поделить его на отдельные геометрические фигуры. Например, если два параллельно расположенных здания соединены переходом в форме буквы «Н», можно рассчитать площадь отдельно каждого прямоугольника, а затем суммировать их и умножить на высоту.
Например, длина двух параллельных зданий — 30 м, их ширина — 15 м. Размеры перехода — 2,5 на 6 м. Значит, сначала нужно найти площадь одинаковых зданий: умножаем 15 на 30, получаем 450 м2. Площадь перехода — 15 м2. Складываем три площади: 450 + 450 + 15, получается 915 м2. Если высота здания составляет 3 м, то строительный объем будет 2745 м3.
Складываем три площади: 450 + 450 + 15, получается 915 м2. Если высота здания составляет 3 м, то строительный объем будет 2745 м3.
Здания с чердачными перекрытиями
Если в здании есть чердачное перекрытие, то строительный объем надземной части считают по особой формуле:
X = S1 x h.
В этом случае под S1 понимают площадь горизонтального сечения здания. Ее измеряют на уровне первого этажа выше цоколя, по внешнему обводу здания. Чтобы найти площадь, нужно также умножить ширину на длину здания, как и в расчетах по другим формулам.
Высоту h измеряют от верха чистого пола на первом этаже до верха засыпки чердачного перекрытия.
Допустим, площадь горизонтального сечения здания на уровне первого этажа составляет 420 м2. Высота составляет 25 м. В этом случае строительный объем будет равен 10500 м3.
Если у здания есть поздемная часть, ее объем считают так же, как и в предыдущих случаях, а затем оба значения складывают.
Дома без чердачного перекрытия
Строительный объем надземной части зданий без чердачных перекрытий считают по другой формуле:
X = S2 x L
S2 — тоже площадь поперечного сечения, но не горизонтального, а вертикального.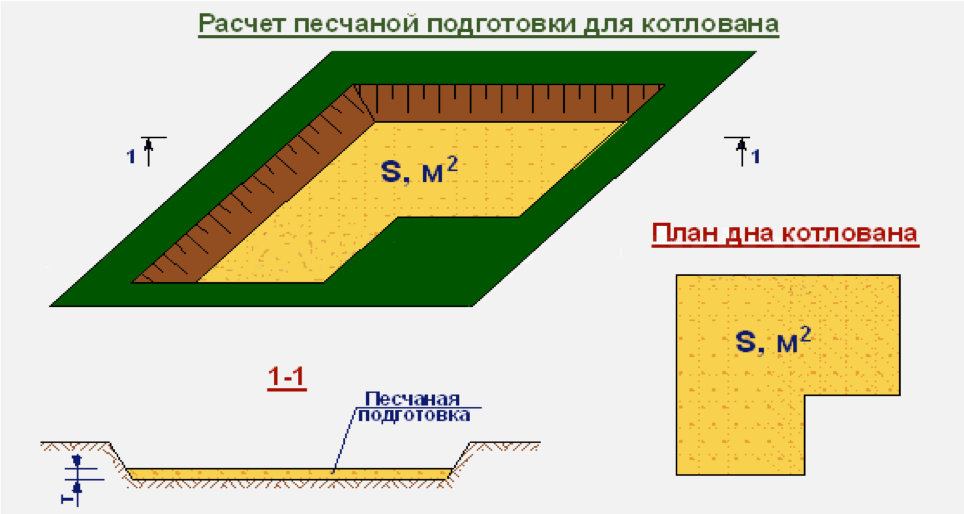 Ее измеряют по наружным стенам, тоже с учетом слоя штукатурки и облицовки. В этом случае для определения площади нужна высота здания и его ширина.
Ее измеряют по наружным стенам, тоже с учетом слоя штукатурки и облицовки. В этом случае для определения площади нужна высота здания и его ширина.
L — это длина здания, перпендикулярная прямая относительно вертикального поперечного сечения. Ее измеряют от одного торца здания к другому, тоже с учетом штукатурки и облицовки, на уровне первого этажа либо цоколя.
Например, нужно рассчитать объем здания высотой 6 м, длиной 23 м и шириной 4 м. Площадь вертикального поперечного сечения в этом случае составит 24 м2, а строительный объем — 552 м3.
Если у здания есть подземная часть, ее также считают отдельно, а потом полученные значения суммируют.
Если известна общая площадь
Детальные данные, например, длину, высоту до определенных перекрытий и другие, не всегда указывают в технической документации. Поэтому строительный объем можно посчитать по другим формулам.
Если известна общая площадь, можно использовать формулу:
X = S x H x К
В этом случае S — сумма площадей всех этажей, или общая площадь. Ее измеряют по внутренней обводке наружных стен, то есть не учитывается их толщина. Кроме того, замеряют также площадь подвала, поэтому отдельных расчетов для подземной части не нужно.
Ее измеряют по внутренней обводке наружных стен, то есть не учитывается их толщина. Кроме того, замеряют также площадь подвала, поэтому отдельных расчетов для подземной части не нужно.
H в формуле — высота здания изнутри без учета перекрытий, так называемая высота в свету.
К — поправочный коэффициент, который учитывает толщину стен. Для жилых зданий он составляет 0,8.
То есть для расчета нужно знать всего два точных значения: общую площадь и высоту в свету. Допустим, площадь составляет 2 000 м2, а высота в свету — 15 м. В этом случае показатель составит 24000 м3 с учетом поправочного коэффициента.
Если известна площадь застройки
Если известна площадь застройки, можно использовать другую формулу. В ней больше переменных, и выглядит она так:
X = S1 x h2 + S2 x h3
S1 в этом случае — площадь общей застройки. Ее можно найти, представив здание в виде геометрической фигуры или нескольких таких фигур, если постройка сложной формы. h2 — высота дома, в которой можно не учитывать выступающие части крыши.
S2 и h3 — площадь и высота подвала соответственно. Площадь замеряют по внутренней обводке стен. Высоту — от верхней точки пола подвала до пола первого этажа.
Дома с мансардамиМансарда — этаж в чердачном пространстве, фасад которого частично либо полностью образован поверхностями наклонной крыши. Обязательное условие — линия пересечения плоскости крыши и фасада должна находиться не больше, чем на высоте 1,5 м от уровня пола в мансарде. Согласно нормативам, строительный объем мансарды считается отдельно.
Чтобы найти строительный объем мансарды, нужно умножить площадь ее поперечного вертикального сечения на длину дома.
Ширину и высоту нужно измерять по внешнему обводу, вертикаль — до начала перекрытий. Все эти данные понадобятся для того, чтобы найти площадь вертикального сечения. Она равна половине произведения ширины, то есть основания, на высоту. Например, высота мансарды — 1,5 м, ширина, то есть основание — 6 м. Тогда площадь составит 9 м2.
Полученное значение нужно умножить на длину дома. Например, она составляет 12 м. В этом случае строительный объем мансарды составит 108 м3.
Например, она составляет 12 м. В этом случае строительный объем мансарды составит 108 м3.
Оставшуюся надземную часть нужно считать по предыдущим формулам, но высоту измерять до начала основания мансарды, то есть до верхнего перекрытия. Объемы мансарды, надземной и подземной частей нужно просто сложить.
Если здание имеет сложную форму
Расчет строительного объема для зданий сложной формы — например, с мезонинами, башенками и различными пристроями — намного сложнее. В этом случае нужно сначала найти строительный объем каждого конструктивного элемента, а потом сложить полученные значения.
Полная формула расчета строительного объема зависит от исходных данных — есть ли подвал, предусмотрены ли чердачные перекрытия, построена ли мансарда. Чтобы получить точное значение, нужно провести тщательные замеры и использовать сложные схемы подсчета.
Расчет объемов земляных работ
- Главная
- Калькуляторы
- Расчет объемов земляных работ
- Траншея с вертикальными стенками на спланированной местности
- Траншея с вертикальными стенками, с перепадом высот
- Траншея с откосами на спланированной местности
- Траншея с откосами, с перепадом высот
- Котлован с вертикальными стенками на спланированной местности
- Котлован с вертикальными стенками, с разными отметками вершин
- Котлован с откосами на спланированной местности
- Описание
 Высота траншеи (H), м.
Длина траншеи (L), м.
Ширина траншеи (a), м.
Высота траншеи в начале (h2), м.
Высота траншеи в начале (h3), м.
Длина траншеи (L), м.
Высота траншеи (H), м.
Длина траншеи (L), м.
Ширина траншеи (a), м.
Высота траншеи в начале (h2), м.
Высота траншеи в начале (h3), м.
Длина траншеи (L), м.Насыпной неуплотненныйПесчаный и гравийныйСупесьСуглинокГлинаЛессы и лессовидныеРасчет по размеру a2
Ширина основания траншеи (a1), м. Ширина верха траншеи (a2), м. Высота траншеи (H), м. Длина траншеи (L), м. Укажите вид грунта
Насыпной неуплотненныйПесчаный и гравийныйСупесьСуглинокГлинаЛессы и лессовидныеРасчет по размеру a
 Ширина верха траншеи (a2), м.
Высота траншеи (h2), м.
Высота траншеи (h3), м.
Длина траншеи (L), м.
Ширина котлована (L1), м.
Длина котлована (L2), м.
Высота котлована (H), м.
Ширина верха траншеи (a2), м.
Высота траншеи (h2), м.
Высота траншеи (h3), м.
Длина траншеи (L), м.
Ширина котлована (L1), м.
Длина котлована (L2), м.
Высота котлована (H), м.Насыпной неуплотненныйПесчаный и гравийныйСупесьСуглинокГлинаЛессы и лессовидные
Ширина основания котлована (L1), м.
Траншея — это открытая выемка в земле, предназначенная для устройства ленточного фундамента, прокладки коммуникаций (водопровод, канализация, силовые кабеля, сети связи).
При устройстве ленточного фундамента ширину траншеи рекомендуется принимать на 600 мм больше ширины основания фундамента bф (для возможности выполнения монтажных работ, проход людей).
Траншея с вертикальными стенками на спланированной местности — самая простая форма выемки. В основном применяется при низкой высоте траншеи и при производстве работ в зимних условиях, когда откосы траншеи заморожены, и нет опасности обвала грунта, так же применяется при устройстве механических креплений стен выемки (распорных; консольных; консольно-распорных).
Крутизна откосов в зависимости от вида грунта и глубины выемки
| Наименование грунтов | Крутизна откосов (отношение его высоты к заложению — 1:m) при глубине выемки, м, не более | ||
| 1.5 | 3 | 5 | |
| Насыпной неуплотненный | 1:0,67 | 1:1 | 1:1,25 |
| Песчаный и гравийный | 1:0,5 | 1:1 | 1:1 |
| Супесь | 1:0,25 | 1:0,67 | 1:0,85 |
| Суглинок | 1:0 | 1:0,5 | 1:0,75 |
| Глина | 1:0 | 1:0,25 | 1:0,5 |
| Лессы и лессовидные | 1:0 | 1:0,5 | 1:0,5 |
Объем выемки траншеи можно опрделить как произведение площади поперечного сечения на длинну.
Объем обратной засыпки определяется как разность между объемом выемки и монтируемых конструкций (фундаментных блоков, труб).
Котлован — выемка в грунте, предназначенная для устройства оснований и фундаментов зданий и других инженерных сооружений.
Расчет бетонной смеси | Рассчитать объем бетона
Эта статья по строительству проливает свет на следующие темы: —
Как рассчитать объем бетона для плит, балок, колонн, фундаментов и элементов конструкции здания.
Для расчета количества цемента, песка, заполнителя и воды, необходимого для любого объема бетона; сначала требуется рассчитать объем бетона, а затем количества отдельных компонентов.
Определение объема: —
Выберите коробку длиной (1 м), шириной (1 м) и глубиной (1 м) и залейте ее бетоном.
Объем бетона рассчитывается как длина x ширина x глубина = 1 м x 1 м x 1 м = 1 м 3
Чтобы заполнить 1 м3 коробки, необходимо 25 кН бетона. [1KN = 1000 кг].
Плотность бетона = 25 кН/м 3
Объем вычисляется в трех измерениях, что означает, что три измерения умножаются.
Основное определение объема = произведение трех измерений = Д x Ш x Г
Формула изменена в зависимости от формы, но процедура остается идентичной для расчета объема любой формы, т. е. необходимо умножить три измерения. Например, выберите цилиндр, который не содержит длины и ширины. Чтобы определить объем цилиндра, вычисляют площадь круга, а затем умножают ее на высоту цилиндра. (данный ниже, упомянутый круглый столбец для примера цилиндра).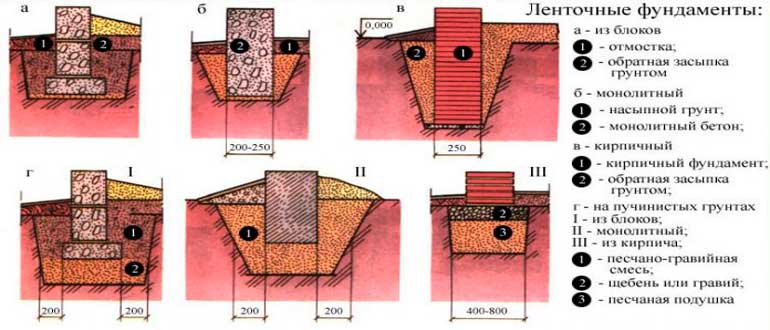
Чтобы избежать путаницы, примените следующую формулу для расчета объема бетона.
Формулы для расчета объема бетона: —
Объем бетона = Площадь поверхности x Глубина
Расчет объема бетона для плит:
Плита имеет форму прямоугольника. Чтобы измерить объем бетона, необходимого для плиты, определите площадь поверхности плиты, а затем умножьте ее на глубину/толщину плиты.
Предположим, длина = 6 м, ширина = 5 м и толщина/глубина плиты = 0,15 м
Объем бетона = площадь прямоугольника x глубина
Площадь прямоугольника = длина x ширина
Объем бетона = длина x ширина x глубина = 6x5x0,15=4,5 м 3
Следовательно, 4,5 м3 бетона необходимо для возведения вышеуказанной плиты.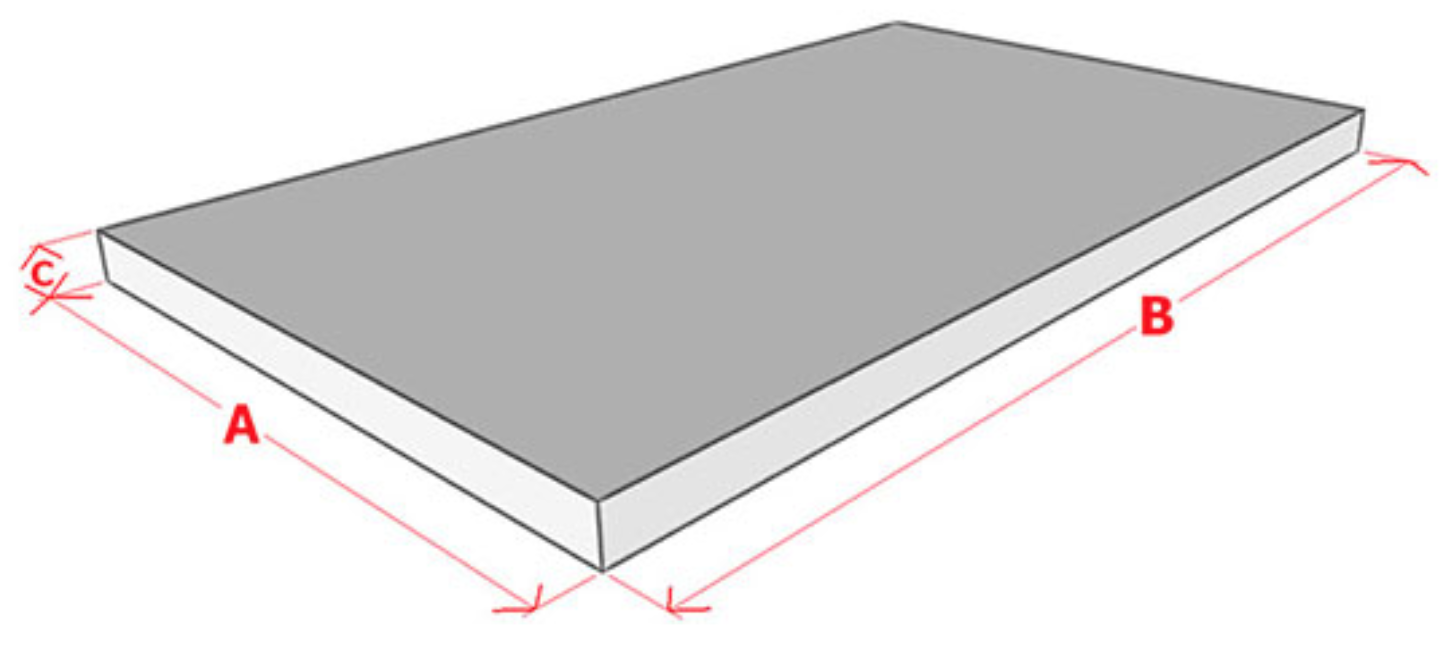
Имейте в виду, что все значения должны быть рассчитаны в миллиметрах.
Расчет объема бетона для колонны:
Колонна доступна в различных формах, таких как прямоугольная, круглая, шестиугольная и т. д.
Объем бетона = площадь поверхности x глубина
Прямоугольная колонна:
Предположим, длина = 0,6 м, ширина = 0,4 м, высота колонны = 3 м
Рассчитайте площадь верхней поверхности и умножьте ее на глубину или высоту колонны.
Объем бетона = 0,6×0,4×3= 0,72 м 3
Круговой столбец:
Предположим, радиус окружности = 0,25 м.
Объем бетона для круглой колонны = площадь поверхности круга x высота колонны.
Объем круглой колонны = πr2 x 3 = 3,14 x 0,252 x3 = 0,58 м 3
Как рассчитать объем бетона для балок: —
Балки обычно имеют прямоугольную форму. Чтобы рассчитать объем необходимого бетона для балок, определите площадь верхней или нижней поверхности балки и умножьте ее на глубину балок.
Объем бетона для прямоугольной балки = Площадь поверхности x Глубина = Длина x Ширина x Глубина = 4×0,5×0,4=0,8 м 3
Для получения дополнительной информации перейдите по следующей ссылке https://civilread.com/concrete-volume-calculator/
Объем сферы, формула, примеры и приложения
Объем сферыОбъем сферы — это количество места, которое она занимает внутри себя. Сфера представляет собой трехмерную круглую твердую форму, все точки на поверхности которой расположены на равном расстоянии от ее центра. Фиксированное расстояние известно как радиус сферы, а фиксированная точка известна как центр сферы.
Когда мы повернем круг, мы заметим изменение формы. Трехмерная форма сферы получается путем вращения двумерного объекта, известного как круг.
Вы заметили, почему мяч для крикета кажется тяжелее, чем мяч для тенниса? Или почему крошечный шарик трудно разбить? Ответ кроется в их объемах. Хотя они сделаны из разных материалов, их объемы играют важную роль в определении их веса.
Хотя они сделаны из разных материалов, их объемы играют важную роль в определении их веса.
Объем — это пространство внутри трехмерного объекта или формы. Двумерные объекты не будут иметь объема. Объем сферы означает емкость, которую она может вместить. Что это значит или какова его формула? Давай выясним!
Объем сферы Уравнение
Как упоминалось выше, объем сферы — это емкость, которую она может вместить. Если шар разрезать на две части, то внутреннее пространство или наполнитель внутри него будет его объемом. Если внутри есть пространство, то сфера полая. В то время как если материал наполнителя находится внутри, сфера будет твердой.
Объем сферы определяется тремя координатами x, y и z. Почему? Потому что трехмерный объект будет лежать по всем трем осям. Объем измеряется в кубических метрах, кубических футах, кубических дюймах и подобных единицах. Обозначается символами см 3 ,m 3 ,in 3 и т.д.
Тогда как найти объем шара? Ну, это зависит от диаметра сферы. Если площадь поверхности умножить на диаметр, то получится объем, в котором каждая точка его поверхности равноудалена от его центра. Математически для расчета объема сферы используется следующая формула:
Если площадь поверхности умножить на диаметр, то получится объем, в котором каждая точка его поверхности равноудалена от его центра. Математически для расчета объема сферы используется следующая формула:
Объем сферы = 4/3 𝜋 r³, где r — радиус сферы.
Объем является фиксированной величиной и может быть найден по закону Архимеда. Согласно Архимеду, если бросить твердый шар в сосуд, наполненный водой, то объем вытесненной воды будет равен объему шара. Объем изменится, когда изменятся значения диаметра или радиуса сферы. В противном случае формула объема сферы останется прежней.
Всегда ли этот метод подходит для измерения объема? Должны ли мы каждый раз держать ванну с водой, чтобы измерить объем? Теперь, подойдя к тому, как это происходит? Откуда взялась эта формула объема? Для этого пришло время пойти элементарным методом и изучить некоторые другие 3D-формы.
Откуда взялся Объем Сферы?
Уравнение для объема сферы может быть получено из метода интегрирования и объемов конуса и цилиндра.
Метод 1: Метод интегрирования
Рассмотрим сферу с множеством тонких сферических дисков, расположенных над другим, как показано на рисунке. Поскольку сфера состоит из тонких круглых дисков, расположенных коллинеарно, их диаметры будут различаться по всей длине сферы. В результате объем будет меняться и по всему диаметру сферы.
Теперь рассмотрим тонкий диск радиусом r и толщиной dy, расположенный на расстоянии y от оси x. Также объем сферы будет произведением площади круга на его толщину. Мы можем представить радиус кругового диска r через y, используя теорему Пифагора.
Формула Пифагора.
Таким образом, dV = r 2 dy можно использовать для расчета объема элемента диска.
(R 2 – y 2 ) dy = dV
Путем интегрирования приведенного выше уравнения общий объем сферы будет равен:
900 03
Таким образом, окончательная формула объема сферы определяется выражением V = 4/3 𝜋 r³.
Метод 2: Из объемов конуса и цилиндра
Знаете ли вы, что сфера, цилиндр и конус имеют связь? Именно, их объемы имеют связь! Объем цилиндра равен сумме объема конуса и объема шара. Математически
Vконус + Vсфера = Vцилиндр
В результате мы можем рассчитать объем сферы по формуле Vсфера = Vцилиндр – Vконус.
Vcone равно r 2 h, где h — наклонная высота конуса.
Vцилиндр равен 13 р 2 h, где h — высота цилиндра.
Vсфера равна 13 r 2 ч – r 2 ч, что равно 2/3 r 2 ч.
Если мы посмотрим на сферу, мы увидим, что высота равна диаметру сферы. Следовательно, h = 2r.
Подставляя значение h в окончательное уравнение, получаем
V сфера = ⅔ 𝜋r 2 (2r) = 4/3 𝜋 r 3 , что является объемом сферы.
Объем полой сферы
Более того, объем полой сферы связан с объемом сферы. В полой сфере внешний радиус обозначается буквой R, а внутренний радиус — буквой r.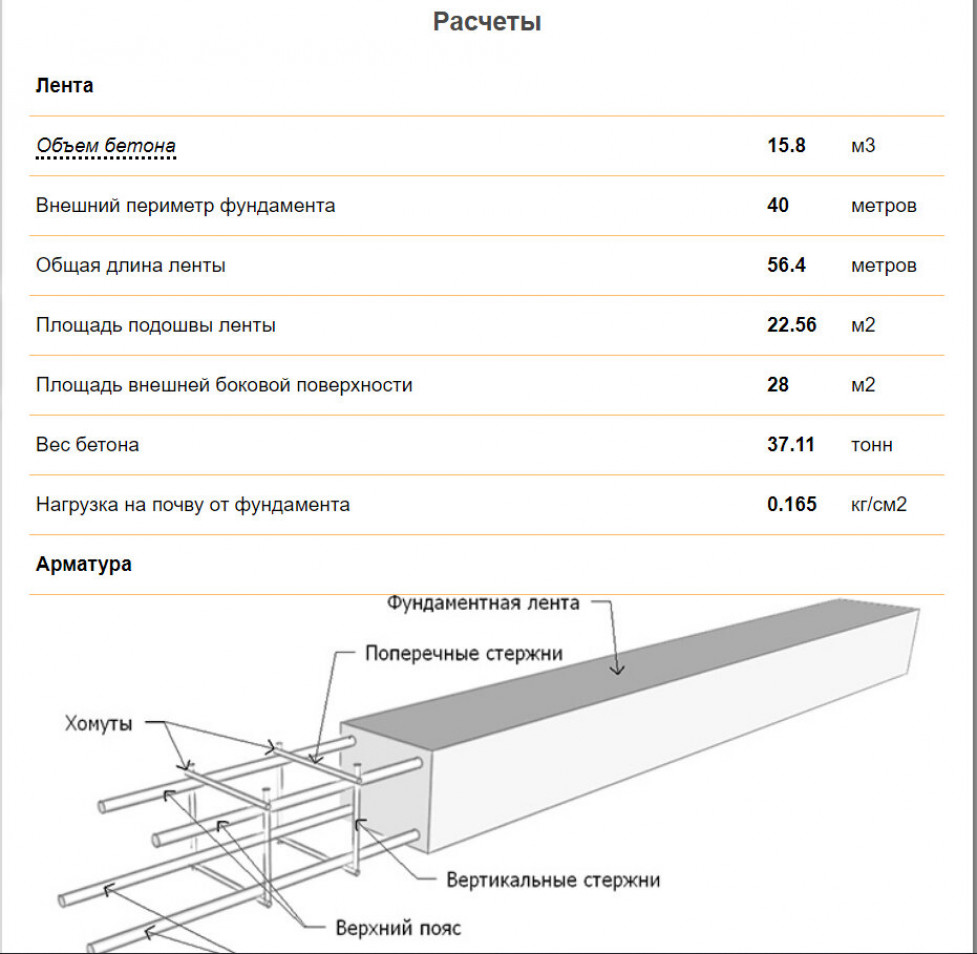 Тогда объем полого шара определяется как
Тогда объем полого шара определяется как
V полый = 4/3 𝜋 R 3 – 4/3 𝜋 r 3
Его также можно записать как V полый = 4/3 𝜋 ( 3 – 3 ). Единицей объема полого шара являются кубические метры.
Как найти объем шара?
После того, как мы узнали объем сферы, все, что нам нужно сделать, это найти объем! Любой может найти объем сферы, не используя калькулятор объема сферы. Выполните следующие действия и найдите том:
Шаг 1: Внимательно просмотрите данные, указанные в вопросе.
Шаг 2: Проверьте, какое значение задано; радиус, диаметр, площадь поверхности или окружность.
Шаг 3: Найдите радиус сферы. Если диаметр дан, разделите его на 2, чтобы найти радиус. Если площадь поверхности дана, найдите значение радиуса из площади поверхности сферы по формуле 4𝜋r. Если дана длина окружности, найдите радиус по формуле 2𝜋r.
Шаг 4: Внимательно просмотрите блоки. Преобразуйте все единицы, эквивалентные друг другу, в одну единую форму.
Преобразуйте все единицы, эквивалентные друг другу, в одну единую форму.
Шаг 5: Получите куб радиуса, т.е. r³.
Шаг 6: Умножьте значение r³ на 𝜋.
Шаг 7: Умножьте значение, найденное в шаге 6, на 4/3.
Шаг 8: Окончательное значение будет требуемым объемом сферы.
Применение объема сферы
В реальном мире объем сферы используется несколькими способами. Если мы знаем его формулу, нам не нужен калькулятор объема сферы, чтобы вычислять его каждый раз. Вот несколько приложений, в которых часто используется формула объема:
- Формула объема используется во многих отраслях промышленности при производстве таких предметов, как шары, шары, подшипники, пузырьки и т. д.
- Полезно рассчитать количество воздуха, необходимое для предотвращения утечек в воздушном шаре.
- Расчет объема необходим при перевозке любого вредного химического вещества в сферическом контейнере.

- Объем полой сферы используется для определения количества любого материала, содержащегося в чаше или полусферической оболочке.
Объем сферы Примеры
Пример 1. Найдите объем сферы, длина окружности которой составляет 144 единицы.
Решение: Учитывая, что длина окружности сферы составляет 144 единицы.
Мы знаем, что длина окружности равна 2𝜋r, где r — радиус.
Следовательно, C = 2𝜋r = 144
Решив это, мы получим r = 22,9 единиц.
Формула дает объем шара, V = 4/3 𝜋 r 3
Подставляя значение r, получаем V = 4/3 𝜋 (22,92) 3
V = 50453,197 единиц³.
Пример 2: Полая сфера сконструирована компанией таким образом, что ее толщина составляет 10 см, а внутренний диаметр — 6 м. Каков будет объем сферы, спроектированной компанией?
Решение: Учитывая, что внутренний диаметр равен 6 м, а толщина 10 см, равна 0,1 м.
Следовательно, внешний диаметр будет равен 6 + 0,1 м = 6,1 м.
Объем полой сферы обозначается: Объем = 4/3 𝜋R 3 – 4/3 𝜋r 3 , где R — радиус внешней сферы, а r — радиус внутренней сферы.
Установка значений в вышеуказанное уравнение, мы получаем,
V = 4/3 𝜋 (3,05 3 — 3 3 ) = 4/3 𝜋 (1,37)
Следовательно, V = 5,735 м 3 .
Пример 3. Найдите объем шара, если площадь его поверхности 100 квадратных метров.
Решение: Мы знаем, что площадь поверхности сферы равна S = 4𝜋r, где r — радиус сферы.
Следовательно, S = 4𝜋r = 100
Найдя значение r, получим, r = 7,96 м
Объем шара равен V = 4/3 𝜋 r 3
Подставив значение r, получим ,
В = 4/3 𝜋 (7,96) 3 = 2111,58 м 3 .
Решение: Радиус, r = см, как указано
Объем сферы равен (4/3)πr 3 кубических единиц.