Как определить куб: Как рассчитать куб доски — интернет-магазин Корпорация Снабжения

Что такое куб: определение, свойства, формулы

Sign in

Password recovery

Восстановите свой пароль

Ваш адрес электронной почты

MicroExcel.ru Математика Геометрия Что такое куб: определение, свойства, формулы

В публикации мы рассмотрим определение и основные свойства куба, а также формулы, касающиеся данной геометрической фигуры (расчет площади поверхности, периметра ребер, объема, радиуса описанного/вписанного шара и т.д.).

• Определение куба
• Свойства куба
  • Свойство 1
  • Свойство 2
  • Свойство 3
• Формулы для куба
  • Диагональ
  • Диагональ грани
  • Площадь полной поверхности
  • Периметр ребер
  • Объем
  • Радиус описанного вокруг шара
  • Радиус вписанного шара

Определение куба

Куб – это правильный многогранник, все грани которого являются квадратами.

• Вершины куба – это точки, являющиеся вершинами его граней.
  Всего их 8: A, B, C, D, A₁, B₁, C₁ и D₁.
• Ребра куба – это стороны его граней.
  Всего их 12: AB, BC, CD, AD, AA₁, BB₁, CC₁, DD
  1, A₁B₁, B₁C₁, C₁D₁ и A₁D₁.
• Грани куба – это квадраты, из которого состоит фигура.
  Всего их 6: ABCD, A₁B₁C₁D₁, AA₁B₁B, BB₁C₁C, CC₁D₁D и AA₁D₁D.

Примечание: куб является частным случаем параллелепипеда или призмы.

Свойства куба

Свойство 1

Как следует из определения, все ребра и грани куба равны. Также противоположные грани фигуры попарно параллельны, т.

• ABCD || A₁B₁C₁D₁
• AA₁B₁B || CC₁D₁D
• BB₁C₁C || AA₁D₁D

Свойство 2

Диагонали куба (их всего 4) равны и в точке пересечения делятся пополам.

• AC₁ = BD₁ = A₁C = B₁D (диагонали куба).
• О – точка пересечения диагоналей:
  AO = OC₁ = BO = OD₁ = A₁O = OC = B₁O = OD.

Свойство 3

Все двугранные углы куба (углы между двумя гранями) равны 90°, т.е. являются прямыми.

Например, на рисунке выше угол между гранями ABCD и AA₁B₁B является прямым.

Формулы для куба

• a – ребро куба;
• d – диагональ куба или его грани.

Диагональ

Длина диагонали куба равняется длине его ребра, умноженной на квадратный корень из трех.

Диагональ грани

Диагональ грани куба равна его ребру, умноженному на квадратный корень из двух.

Площадь полной поверхности

Площадь полной поверхности куба равняется шести площадям его грани. В формуле может использоваться длина ребра или диагонали.

Периметр ребер

Периметр куба равен длине его ребра, умноженной на 12. Также может рассчитываться через диагональ.

Объем

Объем куба равен длине его ребра, возведенной в куб.

Радиус описанного вокруг шара

Радиус шара, описанного около куба, равняется половине его диагонали.

Радиус вписанного шара

Радиус вписанного в куб шара равен половине длины его ребра.

ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ

Таблица знаков зодиака

Нахождение площади трапеции: формула и примеры

Нахождение длины окружности: формула и задачи

Римские цифры: таблицы

Таблица синусов

Тригонометрическая функция: Тангенс угла (tg)

Нахождение площади ромба: формула и примеры

Нахождение объема цилиндра: формула и задачи

Тригонометрическая функция: Синус угла (sin)

Геометрическая фигура: треугольник

Нахождение объема шара: формула и задачи

Тригонометрическая функция: Косинус угла (cos)

Нахождение объема конуса: формула и задачи

Таблица сложения чисел

Нахождение площади квадрата: формула и примеры

Что такое тетраэдр: определение, виды, формулы площади и объема

Нахождение объема пирамиды: формула и задачи

Признаки подобия треугольников

Нахождение периметра прямоугольника: формула и задачи

Формула Герона для треугольника

Что такое средняя линия треугольника

Нахождение площади треугольника: формула и примеры

Нахождение площади поверхности конуса: формула и задачи

Что такое прямоугольник: определение, свойства, признаки, формулы

Разность кубов: формула и примеры

Степени натуральных чисел

Нахождение площади правильного шестиугольника: формула и примеры

Тригонометрические значения углов: sin, cos, tg, ctg

Нахождение периметра квадрата: формула и задачи

Теорема Фалеса: формулировка и пример решения задачи

Сумма кубов: формула и примеры

Нахождение объема куба: формула и задачи

Куб разности: формула и примеры

Нахождение площади шарового сегмента

Что такое окружность: определение, свойства, формулы

Расчет объема куба

Куб это геометрическое тело, ограниченное шестью квадратами, которое ещё можно назвать правильный шестигранник, а так же правильный многогранник. Слово «куб» образовано от греческого слова «kybos».

Определение объема куба

Расчет объема куба можно произвести с помощью следующей формулы:

V = a3

a – сторона куба

V – объем куба

Куб представляет собой правильный многогранник, каждая из граней которого является квадратом. Это геометрическое тело является частным случаем других (а именно – параллелепипеда и призмы) и в повседневной жизни встречается достаточно часто. Инженерам и архитекторам при разработке проектов различных машин и зданий нередко приходится производить расчет объема куба, причем ввиду относительной его простоты решение этой задачи обычно не представляет большой сложности.

На практике с кубами и параллелепипедами чаще всего приходится встречаться в архитектуре. Их форму имеют многие современные здания и сооружения, причем она считается одной из наиболее практичных: такие сооружения проще и быстрее как проектировать, так и возводить. При этом формула объема куба используется преимущественно для точного определения размеров внутренних пространств, что особенно важно для таких зданий, как склады, цеха промышленных предприятий, объекты социально-культурного назначения.

Форму куба нередко имеют различные предметы корпусной мебели, и при их разработке конструкторам требуется определять, в том числе, и такую величину, как объем, для того, чтобы достичь наиболее рациональной компоновки этих элементов. Вычислить объем куба часто бывает необходимо и тем инженерам, которые занимаются созданием проектов контейнеров, железнодорожных вагонов, а также стеллажных систем, использующихся в складском хозяйстве.

Одним из наиболее ярких примеров кубов является знаменитый «магический куб» – оригинальная головоломка, созданная талантливым венгерским преподавателем архитектуры и скульптором Эрне Рубиком и впоследствии названная в его честь. Каждая из граней этого кубика состоит из нескольких квадратов, окрашенных в один цвет.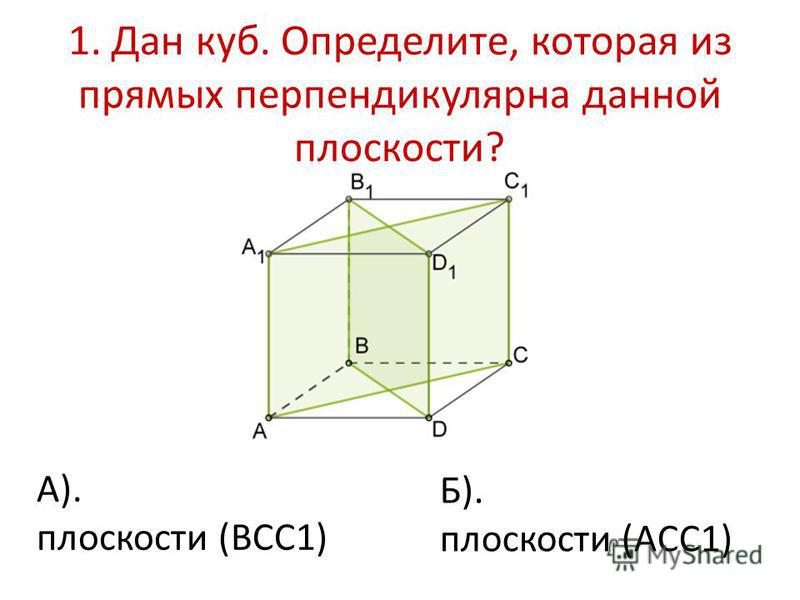 С помощью поворотов их можно комбинировать в различных вариантах, а задача игрока состоит в том, чтобы «разобранную» конструкцию (то есть такую, грани которой содержат квадратики разных цветов) привести в изначальное состояние. Согласно статистике, «Кубик Рубика» за все время своего существования (с 1974 года) был продан в количестве около 350 000 000 экземпляров, и на сегодняшний день является одной из признанных в мире головоломок. Изначально каждая из его граней состояла из девяти квадратов, но впоследствии появились и более сложные варианты (например, содержащие по двадцать пять элементов). В различных странах проводятся соревнования по сборке этой головоломки на время, а также чемпионаты Европы и мира, организатором которого является организация «World Cube Association» («Всемирная ассоциация кубика»).

Форму куба имеют не только рукотворные, но и некоторые природные сущности, например, кристаллические решетки такого минерала, как флюорит, а также обычной поваренной соли. Наконец, следует заметить, что с этими геометрическими телами все мы знакомы еще с детства, поскольку одними из самых любимых игрушек для многих из нас были именно кубики.

Что такое куб? Определение, формула, форма, свойства, примеры

Что такое куб?

Куб представляет собой твердое тело с шестью квадратными гранями. Каждая квадратная грань имеет одинаковую длину стороны и, следовательно, все грани имеют одинаковый размер.

Куб имеет 12 ребер и 8 вершин. Каждая вершина относится к углу, где встречаются три ребра куба.

Мы можем наблюдать несколько примеров формы куба в нашей повседневной жизни. Объекты в форме куба включают в себя кубики сахара, игральные кости, кубики льда и всемирно известный кубик Рубика!

Давайте изучим свойства и роль куба в математике и в реальной жизни.

Родственные игры

Свойства куба

• Это трехмерная фигура квадратной формы
• Имеет 6 граней, 12 ребер и 8 вершин
• Все грани имеют форму квадрата
• Все стороны имеют одинаковую длину
• Каждая вершина встречается с тремя гранями и тремя ребрами 
• Ребра идут параллельно тем, которые параллельны ему
• Все углы куба прямые

Связанные листы

Площадь поверхности куба

Общая площадь поверхности куба определяется как площадь его внешней поверхности.

Поскольку у куба шесть квадратных граней и все квадратные грани имеют одинаковый размер, общая площадь поверхности куба = 6 ✕ площади одной грани.

Допустим, длина каждого ребра равна «а».

Площадь одной квадратной грани = край ✕ край = a ✕ a = a ²

Следовательно, общая площадь поверхности куба = 6a ²

Общая площадь поверхности куба будет равна сумме всех шести граней куба.

Площадь боковой поверхности куба

Представьте, что вы сидите в комнате в форме куба. Затем вы можете увидеть четыре стены вокруг вас. Это обозначает площадь боковой поверхности этой комнаты. То есть площадь боковой поверхности комнаты в форме куба равна площади ее четырех стен, исключая потолок и пол.

Площадь боковой поверхности куба равна сумме площадей его квадратных граней, исключая площади верхней и нижней граней.

Таким образом, площадь боковой поверхности куба = сумма площадей 4 граней = 4a²

Объем куба

Объем трехмерного объекта можно определить как его емкость или количество жидкости, которое он мог бы вместить, если бы он был полым изнутри.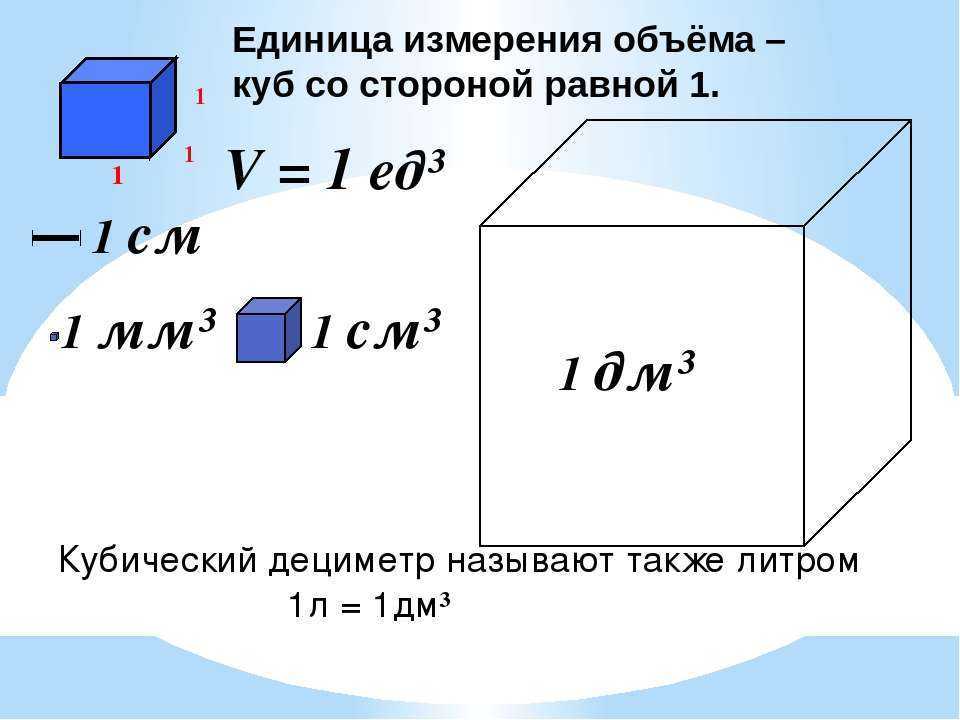

Объем рассчитывается путем умножения длины, ширины и высоты объекта. В случае форма куба , длина, ширина и высота имеют одинаковую длину. Обозначим его буквой «а».

Следовательно, объем куба равен a ✕ a ✕ a = a³  

Решенные примеры

Пример 1 : Каждая сторона куба равна 20 см. Какова площадь поверхности куба?

Решение : Воспользуемся формулой для расчета площади поверхности, где значение каждой стороны равно a.

Площадь поверхности куба = 6 а² = 6 ✕ 400 = 2400 см²

Пример 2 : Каждая сторона куба равна 10 см. Каков объем куба?

Решение : Воспользуемся формулой для вычисления объема куба, где каждая сторона равна а.

Объем куба = a³ = 10 × 10 × 10 = 1000 см³

Пример 3: Кубический контейнер со стороной 2 м подлежит окраске. Какова общая площадь окрашиваемой поверхности?

Решение : Поскольку каждая сторона равна 2 м, воспользуемся формулой  6 ✕ (Сторона)² Следовательно, общая площадь окрашиваемой поверхности = 6 ✕ 4 ​​= 24 м²

Практические задачи

Каков объем кубического стеклянного аквариума длиной 6 дюймов?

216 дюйм

36 дюйм

220 дюйм

360 дюйма

Правильный ответ: 216 дюйм
Длина каждого края кубического аквариума = 6 дюймов.
Формула объема куба = а³, где а — длина каждого ребра куба.
Следовательно, объем данного куба = 6 ✕ 6 ✕ 6 = 216 дюймов³

Какова общая площадь поверхности куба, если длина его ребра равна 30 см?

7200 см²

5400 см²

900 см²

1100 см²

Правильный ответ: 5400 см²
Длина каждого края кубического аквариума = 30 см 9012 7 Формула площади поверхности одной квадратной грани = ребро ✕ ребро = axa = 900
Следовательно, общая площадь поверхности куба = 6a² = 5400 см²

Какова площадь боковой поверхности куба, длина стороны которого равна 6 дюймов?

36 см²

144 см²

148 см²

196 см²

Правильный ответ: 144 см²
Площадь боковой поверхности куба равна сумме площадей его квадратных граней без учета площади верхняя и нижняя грань.
Таким образом, площадь боковой поверхности куба = сумма площадей 4 граней = 4a²
Площадь поверхности одной квадратной грани = a² = 36
Площадь боковой поверхности равна сумме площадей 4 граней = 4a² = 144 см²

Часто задаваемые вопросы

В чем разница между кубом и квадратом?

Ключевое отличие состоит в том, что квадрат — это двумерный объект, а куб — ​​трехмерный. Следовательно, у куба есть дополнительное измерение, которым является его высота.

Какими свойствами обладает куб?

Вот некоторые свойства куба:

1. Куб имеет шесть граней в форме квадратов с одинаковыми размерами.

2. Каждая диагональ грани образует два прямых угла.

3. Каждая вершина встречается с тремя гранями и тремя ребрами.

Как рассчитать объем куба?

Все стороны куба имеют одинаковую длину. Следовательно, объем куба является произведением его длины, ширины и высоты, которые равны по размерности.

Следовательно, объем куба равен e³ кубических единиц, где «e» — длина каждой стороны.

Куб (определение, форма, свойства, объем и площадь поверхности, примеры)

В математике или геометрии Куб — это твердая трехмерная фигура, которая имеет 6 квадратных граней, 8 вершин и 12 ребер. Также говорят, что это правильный шестигранник. Вы, должно быть, видели кубик Рубика 3 × 3 , который является наиболее распространенным примером в реальной жизни и помогает повысить мощность мозга. Точно так же вы столкнетесь со многими примерами из реальной жизни, такими как шестигранные игральные кости и т. д. Твердотельная геометрия — это все о трехмерных формах и фигурах, у которых есть площади поверхности и объемы. Другими твердыми формами являются куб, цилиндр, конус, сфера. Здесь мы обсудим его определение, свойства и важность в математике. Кроме того, выучите формулу площади поверхности куба вместе с формулой его объема.

Содержание:

• Определение
• Форма
• Площадь и объем
• Свойства
• Разница между квадратом и кубом
• Как сделать куб
• Примеры
• Практические задачи
• Часто задаваемые вопросы

Определение куба

Как обсуждалось ранее, куб является трехмерным

твердая форма, которая имеет 6 граней. Куб — одна из простейших фигур в трехмерном пространстве. Все шесть граней куба — квадраты, двумерная форма.

Форма куба

Иногда форму куба считают кубической. Можно также сказать, что куб рассматривается как блок, у которого все длины, ширины и высоты одинаковы. При этом у него 8 вершин и 12 ребер, так что 3 ребра сходятся в одной вершине. Проверьте данное изображение ниже, определяя его грани, ребра и вершины. Он также известен как квадратный параллелепипед, равносторонний кубоид и правильный ромбоэдр. Куб является одним из платоновых тел и рассматривается как выпуклый многогранник, у которого все грани квадратные. Можно сказать, что куб имеет октаэдрическую или кубическую симметрию. Куб — это частный случай квадратной призмы.

На приведенном выше рисунке вы можете видеть ребро, грань и вершину куба. Здесь L обозначает длину, B обозначает ширину, а H обозначает высоту. Мы можем видеть длину, ширину и высоту куба, которые представляют ребра куба, соединенные в одной точке, которая является вершиной.

Формула площади поверхности и объема для куба

Площадь поверхности и объем куба обсуждаются ниже:

Площадь поверхности куба

Мы знаем, что для любой формы площадь определяется как область, занимаемая ею на плоскости. Куб — это трехмерный объект, поэтому занимаемая им площадь будет находиться в трехмерной плоскости. Поскольку у куба шесть граней, следовательно, нам нужно вычислить площадь поверхности куба, покрытую каждой гранью. Формулу для нахождения площади поверхности можно найти, как указано ниже.

Пусть a будет ребром куба.

Площадь одной грани = Площадь квадрата = a ²

Мы знаем, что у куба 6 квадратных граней.

Площадь боковой поверхности (исключая верхнюю и нижнюю грани) = 4 × площадь одной грани

ЛСА = 4a ²

Общая площадь поверхности = LSA + Площадь верхней и нижней граней

TSA = 4a ²  + a ²  + a ²

ВСТ = 6а ²

Объем куба

Объем куба — это заключенное в нем пространство. Допустим, если предмет имеет кубическую форму и нам нужно погрузить в него какой-либо материал, скажем, воду, то мера воды в литрах, которая должна храниться в предмете, рассчитывается по его объему. Формула объема:

Для получения дополнительной информации об объемах кубов и параллелепипедов посмотрите видео ниже:

Длина диагонали куба

Если а — длина стороны, то

• Длина диагонали грани куба = √2 a
• Длина диагонали куба = √3 a

См. также:

Свойства куба

Ниже перечислены важные свойства куба:

1. У него все грани квадратной формы.
2. Все грани или стороны имеют одинаковые размеры.
3. Плоские углы куба прямые.
4. Каждая из граней встречается с четырьмя другими гранями.
5. Каждая из вершин встречается с тремя гранями и тремя ребрами.
6. Ребра, противоположные друг другу, параллельны.

Разница между квадратом и кубом

Основное различие между квадратом и кубом заключается в том, что квадрат является двумерной фигурой и имеет только два измерения, такие как длина и ширина, тогда как куб является трехмерной фигурой и его три измерения — длина, ширина и высота. Куб получается из формы квадрата.

Как сделать куб?

Куб можно сформировать, сложив сетку из шести квадратов, соединенных друг с другом, как показано на рисунке ниже:

Примеры кубов

Пример 1:

Если сторона куба равна 10 см, то найдите площадь его поверхности и объем.

Решение:

Дано, сторона, а = 10 см

Следовательно, по формуле площади поверхности и объема куба мы можем написать;

Площадь поверхности = 6a ² = 6 × 10 ² = 6 × 100 ^. = 600 см ²

Объем = а ³ = 10 ³ = 1000 см ³

Пример 2:

Найдите длину стороны куба, объем которого равен 512 см ³ .

Решение:

Дано: Объем куба, v = 512 см ²

Мы знаем, что формула объема куба представляет собой ³ кубических единиц.

Следовательно, 512 = a ³

512 можно записать как 8 ³

8 ³ = а ³

Следовательно, а= 8

Следовательно, длина стороны куба а = 8 см.

Практические задачи

Решите следующие проблемы, указанные ниже:

1. Длина стороны куба 6 см. Найдите площадь его поверхности.
2. Определите объем куба, длина стороны которого равна 4 см.
3. Найдите объем куба, площадь поверхности которого равна 24 см ² .
4. Найдите длину диагонали куба, когда a = 9см.