Газоблок характеристики теплопроводность: технические характеристики газобетона Xella YTONG

26.08.1975

0 Comment

Содержание

технические характеристики газобетона Xella YTONG

Газобетон – конструкционно-теплоизоляционный строительный материал. Он прочный, с хорошей несущей способностью. И вместе с тем он сохраняет в помещении тепло в холодный период года и прохладу летом. Поэтому стены из газобетона могут одновременно быть несущими (воспринимать нагрузку от конструкций здания), и выполнять роль теплозащиты. То есть из газобетона можно строить однослойные стеновые конструкции, которые обладают достаточным сопротивлением теплопередаче и не требуют утепления в средней полосе России.

Всё дело в пористой структуре газобетона: в закрытых порах находится воздух в неподвижном состоянии, который, как известно, является лучшим теплоизолятором. Причём, газобетонные блоки имеют однородную структуру, поэтому их теплозащитные свойства одинаково высокие во всех направлениях.

Чем меньше марка по плотности газобетона, тем он «теплее». Величина, которая показывает, насколько хорошо материал проводит тепло, называется коэффициентом теплопроводности (λ).

Чем меньше эта величина, тем эффективнее материал. При проектировании обычно принимают во внимание коэффициент теплопроводности в условиях эксплуатации с влажностью Б (λБ, это и есть показатель теплопроводности в реальных условиях эксплуатации газобетонной кладки).

У газобетона YTONG любой плотности показатели λБ – одни из лучших на рынке:

· Блоки YTONG A++ (D300), λБ=0,088 Вт/м°С
· Блоки YTONG D400 λБ=0,117 Вт/м°С
· Блоки YTONG D500 λБ=0,147 Вт/м°С

Ещё одна важная величина – сопротивление теплопередаче (R). Она демонстрирует, насколько хорошо строительная конструкция сопротивляется прохождению тепла. Чем выше эта величина, тем меньше потери тепла через наружную стену. Так, у стены из газобетонных блоков D400, толщиной 375 мм, сопротивление теплопередаче – 3,36 (м²•°С)/Вт, и это выше, чем требуется по теплотехнике для однослойной стены в средней полосе России (согласно СП 50.13330.2012 «Тепловая защита зданий»). Иными словами, из блоков YTONG D400 можно строить наружные стены без дополнительного утепления.

У менее плотных блоков D300 (YTONG A++) сопротивление теплопередаче ещё выше, что позволяет выбрать один из двух вариантов их использования:

· Строить из блоков меньшей толщины, 300 мм, тем самым увеличивая полезную площадь здания, а также экономя на газобетоне, кладочном клее и их доставке.
· Строить из блоков стандартной толщины, 375 мм, получая энергоэффективный дом, который можно бюджетно отапливать даже электричеством.

Сохранению тепла способствует и то, что газобетон укладывают не на обычный цементный раствор, а на специальный клей, благодаря которому толщина кладочного шва – всего 1-3 мм. Чем тоньше шов, тем меньше тепла теряется из дома в холодное время года.

Теплопроводность газобетона, технические характеристики, способы определения

Низкий коэффициент теплопроводности считается главным преимуществом газобетона наряду с легкостью, хорошей морозостойкостью и прочностью на сжатие. Его обеспечивает высокая (до 85 %) пористость структуры и закрытость ячеек, благодаря этому свойству материал успешно совмещает конструкционные и утепляющие функции и является оптимальным при строительстве энергосберегающих домов.

Факторы влияния и методы определения

Теплопроводность газоблока отражает его способность к передаче тепла от более нагретых частей к холодным в ходе движения молекул. В численном выражении данная характеристика измеряется в Вт/м·°C. Низкое значение у автоклавных газо- и пенобетона (не более 0,12-0,14 у востребованных марок D500 и D600) свидетельствует о хороших энергосберегающих свойствах, что позволяет сократить затраты на обогрев зданий в зимнее время и на кондиционирование – в летнее.

Все изготавливаемые изделия проходят обязательный контроль, подтверждающий данный коэффициент опытным путем, соответствующая информация указывается в сертификате продукции и является ориентиром при расчете толщины стен и перекрытий.

Метод проверки теплопроводности регламентирован требованиями ГОСТ 7076, его суть заключается в подаче стационарного теплового потока через блоки в перпендикулярном направлении и последующем измерении его плотности и температуры лицевой поверхности и граней образца.

Результаты сертификации продукции принято разделять на 2 группы, отражающих значения в сухом состоянии и при определенной влажности. Также теплопроводность напрямую зависит от состава и плотности. Ориентировочные показатели для самых востребованных в частном строительстве марок приведены ниже:

Коэффициент, Вт/м·°C	Марка газоблоков
Коэффициент, Вт/м·°C	D300	D400	D500	D600
В сухом состоянии	0,072	0,096	0,12	0,14
При влажности 4 %	0,084	0,113	0,141	0,16

Теплопроводность снижается при поглощениях ячейками влаги, материал нуждается в защите от внутреннего пара и конденсатов и внешних осадков. У изделий, изготовленных на золе, при равной прочности она на несколько единиц меньше, чем у чисто песчаных (0,1 Вт/м·°C у марки D500, 0,13 у D600), но в первую очередь способность к удерживанию тепла зависит от их плотности и условий эксплуатации.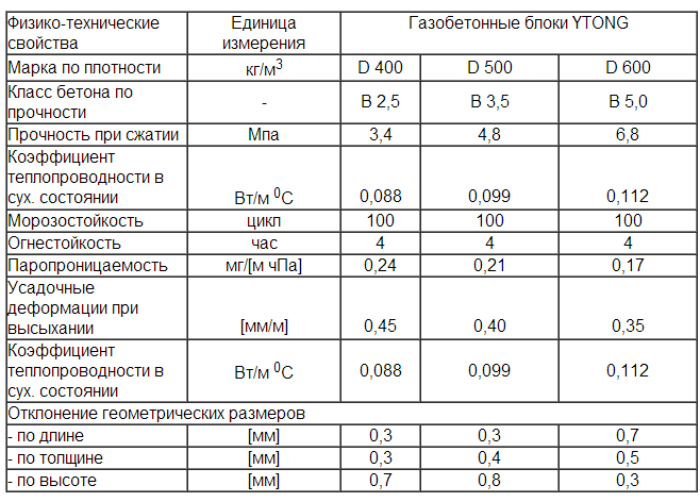 Для сравнения – у незащищенных газобетонных стен, подвергаемым стандартным влажностным нагрузкам в пределах 60%, коэффициент повышается почти в два раза. По этой же причине помимо данной характеристики (отклонения не должны отходить на ± 20 %) в ходе выпуска блоков контролируется показатель отпускной влажности, допустимый нормами максимум не превышает 25-30 %.

Сравнение теплопроводности

В строительстве этот коэффициент учитывают прежде при выборе кладочных материалов для возведения стен, потребность в утеплителе. Ориентировочные значения для самых востребованных из них приведены в таблице:

Наименование	Диапазон плотности, кг/м3	Теплопроводность, Вт/м·°C
Автоклавные газоблоки	280-1000	0,07-0,21
Пенобетон	300-1250	0,12-0,35
Плотный красный кирпич	1700-2100	0,67
Дерево (на примере соснового бруса)	500	0,18
То же, пористый	1500	0,44
Клинкер	1800-2000	0,8-1,6
Облицовочные марки	1800	0,93
Кирпич строительный	800-1500	0,23-0,3
Силикатный сплошной	1000-2200	0,5-1,3
То же, с тех. пустотами		0,7
Силикатный щелевой		0,4

На практике на теплопроводность стен оказывает влияние не только тип газоблоков, но и наличие и вид используемого соединительного раствора. Результаты сравнения для разных кладок приведены ниже:

Вид стены	Диапазон плотности, кг/м3	Теплопроводность, Вт/м·°C
Газобетонные блоки, монтируемые на клей	630-820	0,26-0,34
То же, при использовании газосиликатных теплоизоляционных плит	540	0,24
Керамический сплошной кирпич на цементно-перлитовом растворе	1600	0,47
То же, на ЦПС	1800	0,56
То же, на цементно-шлаковом составе	1700	0,52
Керамический пустотный кирпич на ЦПР	1000-1400	0,35-0,47
Малоразмерные кладочные изделия	1730	0,8
Пустотелые стеновые	1220-1460	0,5-0,65
Силикатный 11-ти пустотный кирпич на ЦПС	1500	0,64
То же, 14-ти пустотный	1400	0,52

Результаты сравнения выявляют однозначное преимущество пористых материалов перед плотными и сплошными в плане способностей к энергосбережению.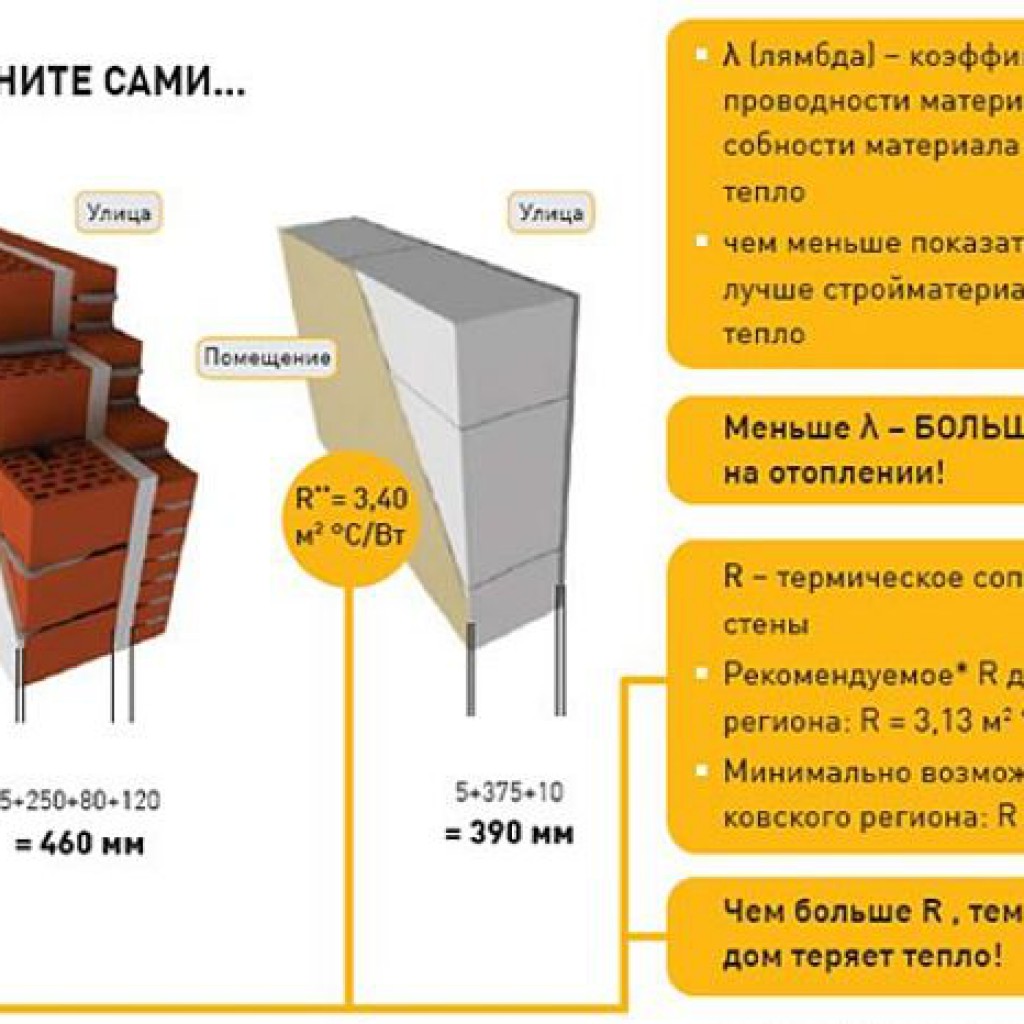

По этой причине и автоклавные газоблоки, и прошедший обычную сушку пенобетон выигрывают у кирпича при условии кладки их на тонкий шов облегченного раствора с близким показателями теплопроводности. Монтаж на ЦПС нивелирует это преимущество и приводит к образованию в стенах мостиков холода, то есть к потребности в наружном утеплении. Пенобетон в сравнении с газобетоном уступает в равномерности структуры (и как следствие – чуть хуже держит тепло), но при равной плотности их коэффициенты теплопередачи практически не отличаются.

<center><ins class="lazy lazy-hidden adsbygoogle" style="display:block; text-align:center;" data-ad-layout="in-article" data-ad-format="fluid" data-ad-client="ca-pub-1812626643144578" data-ad-slot="4491286225"></ins> <script>(adsbygoogle=window.adsbygoogle||[]).push({});</script></center>

Плотность газоблока (газобетона), d300, d400, d500 что это

От чего зависит плотность газоблоков

Газоблоки, производят в процессе соединения бетона, воды, кремнеземистого материала, извести и алюминиевой пудры. На выходе получают фрагменты с воздушными вкраплениями диаметром 1 – 3 мм. От размеров и количества пузырьков зависит теплопроводность материала, прочность и вес.
Основной технической характеристикой газобетона является плотность. Материал маркируется в зависимости от этого показателя и обозначается буквой D.

На Украине наиболее часто используются газобетонные блоки плотностью D300, D400, D500.


ВАЖНО: AEROC (АЕРОК) производит газобетон-D300, D400, D500. UDK (УДК) только D400. ХСМ (ХЕТТЕН) только D500.

При производстве происходит химическая реакция между алюминиевой пудрой и известью. В результате взаимодействия компонентов выделяется водород. При
сушке блоки застывают, в их структуре сохраняются пузырьки неправильной формы, при этом равномерно распределенные в каждом фрагменте. На выходе получается пористый материал с малым весом и низкой теплопроводностью.
От соотношения ингредиентов, закладываемых при производстве газобетона, зависит количество и размеры пузырьков, то есть пористость. Это же является основным моментом, влияющим на плотность газобетона(пенобетона). Чем больше в составе газобетона цемента и песка, тем выше прочность и способность удерживать большую нагрузку. Добавляя или снижая количество этих ингредиентов, корректируют их свойства.

Пузырьки в газобетонных блоках нужны для задержки теплого воздуха в стене и снижения веса газосиликатных блоков. Попадая в ячейки, воздух нагревается медленнее, чем в бетоне, препятствуя потере тепла. Чем больше пузырьков образовывается, тем теплее газоблок, но прочность его снижается. То есть газоблок плотностью d300 теплее газоблока d400 и d500.

На характеристики газобетона влияет влажность. Он гигроскопичен и легко поглощает воду, после чего его плотность и изоляционные качества ухудшаются. Наружные стены постройки из газобетонных блоков сразу штукатурят, чтобы избежать утраты плотности. Если газоблок( пеноблок) хранится под открытым небом, его обязательно накрывают.
В маркировке газобетона указывается плотность в сухом состоянии, либо при определенной влажности. Выбирая блоки, учитывайте влажность воздуха и особенности климата.
Цена 1 м3 газоблока зависит от производителя и плотности газобетона.


Совет: При выборе газобетона обращайте внимание не только на его плотность, но и на его прочность !

Газоблок d300 (Д300)

Преимущество газоблоков плотностью d300 (Д300) в низкой теплопроводности и малом весе. Здание из газоблока этой марки оказывает на фундамент и грунт нагрузку в 3 – 4 раза меньшую, чем кирпич. При этом удерживает тепло в помещении в 2 – 3 раза лучше. Такие теплоизоляционные блоки хрупкие, при работе с ними соблюдают осторожность. Газобетон с малым весом и плотностью хорошо удерживает тепло, стены из такого материала не нуждаются в дополнительном утеплении, но такой газоблок имеет более низкие показатели в прочности.

Газобетонные блоки с маркировкой д300 используются при возведении двух и трехэтажных зданий. Но достаточно часто люди комбинируют плотность газоблока в разных этажах здания и D300 используют для строительства второго этажа.

Производители Украины газобетона D300 (д300)- Aeroc (Аерок) Киев
Нормируемая объемная плотность- 300 кг/м3
Класс прочности на сжатие- В1,5-В2
Коэффициент теплопроводности-0,08 Вт/(мК)
Вес 1 паллеты (поддона) газоблока d300 (д300) — 800 кг


Рекомендации: Если Вы строите гараж, сарай или иную хозяйственную постройку своими руками рекомендуем выбрать газоблок d500 (д500). Цена такого газоблока ниже, а прочность выше

Газоблок d400 (Д400)

Такой газобетон используют в строительстве одно и двухэтажных зданий. Это наиболее популярная плотность газобетона. Он хорошо удерживает тепло благодаря низкой теплопроводности и при этом обладает большей прочностью, чем газобетон д300, но меньшей прочностью, чем d500. Прекрасно подходит для строительства жилого дома.

Производители Украины газобетона D400 (д400)- AEROC (аерок), UDK (ЮДК) Днепр
Нормируемая объемная плотность- 400 кг/м3
Класс прочности на сжатие- В2-В2,5
Коэффициент теплопроводности-0,10 Вт/(мК)
Вес 1 паллеты (поддона) газоблока d400 (д400) — 1000 кг


Рекомендации: При строительстве жилого дома - рекомендуем выбрать газобетон d400 (д400), стоимость его выше, но он теплее и имеет среднюю прочность.

Газоблок d500 (Д500)

Газоблок d500 (Д500) изготовляется в Харькове производителем ХСМ (ХЕТТЕН) и Киеве производителем AEROC (АЕРОК). Прочность блоков марки D500 (д500) – 2 – 3 МПа, теплопроводность – 0,12 – 0,13 Вт/(мК). Такие блоки прочные, легко справляются с высокой нагрузкой на 1 м3. Но этот газобетон уступает в теплопроводности маркам д300 и д400, но превосходит их про прочности, так как хорошо справляется с нагрузкой. Блоки с плотностью 500 используют для строительства гаражей, сараев, летних кухонь и других хоз построек и домов не выше 3 этажей.

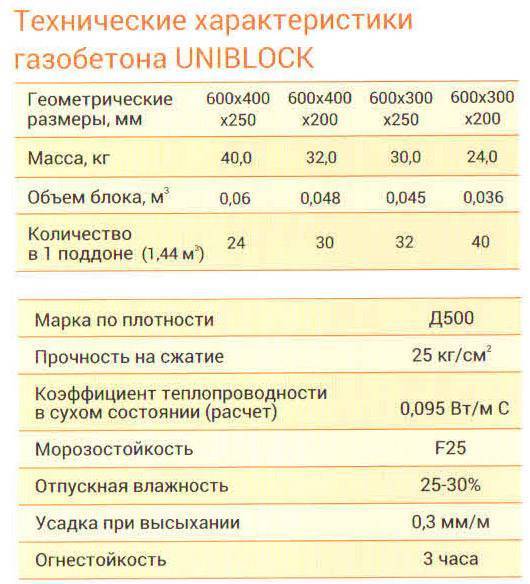
Технические характеристики газобетона YTONG

Наибольшее количества тепла покидает дом через наружную стену. Потерю можно предотвратить, используя при возведении стен дома блоки YTONG®. Благодаря наличию воздуха в порах газобетон YTONG® имеет превосходные теплоизоляционные характеристики.

Среди множества доступных на рынке стеновых материалов газобетон YTONG® характеризуется самой низкой теплопроводностью: коэффициент составляет 0,088- 0.11 Вт/м°C Помимо этого, стоит отметить, что в отличие от других материалов теплопроводность газобетона YTONG® одинакова низка во всех направлениях. Показатель теплоизоляции такой оштукатуренной конструкции внешней стены R= 3,65 м²*°С/Вт

Благодаря идеальной геометрии блоков, монтаж газобетонных блоков осуществляется на клеевой раствор для ячеистых бетонов. Клеевой шов при этом имеет ширину не более 2 мм, что сводит к нулю теплопотери через так называемые «мостики холода». Метод тонкошовной кладки позволяет нам сделать стену из блоков единым монолитом и добиться высокой энергоэффективности дома.

В отличии от классических теплоизоляционных материалов, так называемых эффективных утеплителей: минеральной ваты, пенополистирола, — срок службы блоков YTONG® практически неограничен. Долгий срок службы исключает необходимость периодической реставрации и обновления, обеспечивая дополнительную экономию средств. Благодаря пористой структуре материала YTONG® и беспрепятственному воздухообмену, одновременно с теплосберегающим эффектом достигается и требуемый уровень вентиляции помещений, необходимый для поддержания благоприятного микроклимата зданий. Показатели теплопроводности YTONG® (0,088-0,11) позволяют также в несколько раз сократить ширину стен и, соответственно, снизить трудозатраты при их возведении. Более того, отличные термоизоляционные свойства ячеистых блоков обеспечивают низкие эксплуатационные расходы по содержанию помещений, как благодаря экономии на отоплении зимой, так и с помощью сохранения прохлады в помещениях летом.

Газовая теплопроводность — обзор

8.6.3 Наноизоляционные материалы

Переход от VIP к наноизоляционным материалам (NIM) показан на рис. 8.10. В NIM размер пор в материале уменьшается ниже определенного уровня (т. е. 40 нм или ниже для воздуха), чтобы достичь общей теплопроводности менее 4 мВт/(мК) в первозданном состоянии. То есть NIM представляет собой в основном однородный материал с закрытой или открытой структурой малых нанопор с общей теплопроводностью менее 4 мВт/(мК) в первозданном состоянии.

Рисунок 8.10. Переход от вакуумной изоляционной панели к наноизоляционному материалу (Jelle et al. , 2010a).

Сетчатая структура в НИМ не требует, в отличие от ВИМ и ГИМ, предотвращения проникновения воздуха и влаги в их пористую структуру при сроке службы не менее 100 лет. NIM достигают своей низкой теплопроводности без создания вакуума в порах за счет использования эффекта Кнудсена. Теплопроводность газа λ _газа , также включая взаимодействие газа и стенки поры, с учетом эффекта Кнудсена может быть упрощенно записана как (Baetens et al., 2010а; Букерель и др., 2012; Желле, 2011а; Джелле и др., 2010a; Каганер, 1969):

[8.2]λгаз=λгаз,01+2βKn=λгаз,01+2βkBTπd2pδ

где

[8.3]Kn=σmeanδ=kBT2πd2pδ

где λ

в газе поры, в том числе с учетом взаимодействия газа и стенки поры (Вт/(мК)), λ _газ,0 – теплопроводность газа в порах при стандартной температуре и давлении (Вт/(мК)), β – коэффициент, характеризующий (в)эффективность переноса энергии столкновения молекулы со стенкой (между 1.5 и 2.0), k _B – постоянная Больцмана ≈1,38 · 10 ⁻²³ Дж/К, T – температура (К), d – диаметр столкновения молекул газа (м),0 p – давление газа в порах (Па), δ – характерный диаметр пор (м), а σ _{означает} – длина свободного пробега молекул газа (м).

При уменьшении размера пор в материале ниже определенного уровня (т. е. диаметра пор порядка 40 нм или меньше для воздуха) теплопроводность газа и, следовательно, общая теплопроводность становятся очень низкими (<4 мВт/(мК) с адекватной твердотельной структурой с низкой проводимостью) даже с заполненными воздухом порами.Это вызвано эффектом Кнудсена, когда длина свободного пробега молекул газа больше, чем диаметр пор. То есть молекула газа, находящаяся внутри поры, ударится о стенку поры, а не о другую молекулу газа, где взаимодействие твердого тела и газа определяется коэффициентом β в уравнении. [8.2]. Следовательно, результирующая теплопроводность газа λ _газа , также учитывающая взаимодействие газа и стенок пор, в зависимости от диаметра пор и давления газа в порах, может быть рассчитана в этой упрощенной модели и изображена, как на рис.8.11. Для получения дополнительной информации см. работу Baetens et al. (2010a) и Jelle et al. (2010а).

Рисунок 8. 11. Теплопроводность газа и (вверху) 2D-график, изображающий влияние диаметра пор для воздуха, аргона, криптона и ксенона, и (внизу) 3D-график, изображающий влияние диаметра пор и давления газа в порах для воздуха (Jelle et al. др., 2010а).

Соотношение Стефана-Больцмана можно применить, чтобы показать, что радиационная теплопроводность уменьшается линейно с уменьшением диаметра поры, где коэффициент излучения внутренних стенок поры определяет наклон снижения.То есть чем меньше поры и чем ниже коэффициент излучения, тем ниже будет радиационная теплопроводность. Однако в различных работах (например, Joulain et al., 2005; Mulet et al., 2002; Zhang, 2007) описывается значительное увеличение теплового излучения по мере того, как диаметр пор уменьшается ниже длины волны теплового (инфракрасного) излучения (например, , 10 мкм), где туннелирование затухающих волн может играть важную роль (эффекты излучения ближнего поля). Работа Mulet et al. (2002) и Joulain et al.(2005) указывают на то, что сильное тепловое излучение сосредоточено только вокруг определенной длины волны (или нескольких). То есть это может означать, что суммарное тепловое излучение, интегрированное по всем длинам волн, не так уж велико. Какой вклад это на самом деле вносит в общую (общую) теплопроводность, на данный момент до конца не известно, хотя предполагается, что он, по крайней мере, довольно умеренный. Тем не менее, эти темы в настоящее время рассматриваются в рамках продолжающейся исследовательской деятельности. Исследование Jelle et al.(2010a) более подробно останавливается на этих проблемах теплового излучения.

Проводимость решетки в твердом состоянии в NIM должна поддерживаться на как можно более низком уровне, чтобы получить как можно более низкую общую теплопроводность. Если решетка твердого тела с низкой проводимостью и низкая теплопроводность газа будут достигнуты и по-прежнему будут доминировать в теплопереносе (т.е. больше, чем часть теплового излучения), то NIM могут стать высокоэффективным теплоизоляционным материалом будущего.

Произошла ошибка при настройке пользовательского файла cookie

Этот сайт использует файлы cookie для повышения производительности. Если ваш браузер не принимает файлы cookie, вы не можете просматривать этот сайт.

Настройка браузера на прием файлов cookie

Существует множество причин, по которым файл cookie не может быть установлен правильно. Ниже приведены наиболее распространенные причины:

В вашем браузере отключены файлы cookie. Вам необходимо сбросить настройки браузера, чтобы принять файлы cookie, или спросить вас, хотите ли вы принимать файлы cookie.
Ваш браузер спрашивает, хотите ли вы принимать файлы cookie, и вы отказались.Чтобы принять файлы cookie с этого сайта, нажмите кнопку «Назад» и примите файл cookie.
Ваш браузер не поддерживает файлы cookie. Попробуйте другой браузер, если вы подозреваете это.
Дата на вашем компьютере в прошлом. Если часы вашего компьютера показывают дату до 1 января 1970 г., браузер автоматически забудет файл cookie. Чтобы это исправить, установите правильное время и дату на своем компьютере.
Вы установили приложение, которое отслеживает или блокирует установку файлов cookie.Вы должны отключить приложение при входе в систему или проконсультироваться с системным администратором.

Почему этому сайту требуются файлы cookie?

Этот сайт использует файлы cookie для повышения производительности, запоминая, что вы вошли в систему, когда переходите со страницы на страницу. Предоставить доступ без файлов cookie потребует от сайта создания нового сеанса для каждой посещаемой вами страницы, что замедляет работу системы до неприемлемого уровня.

Что сохраняется в файле cookie?

Этот сайт не хранит ничего, кроме автоматически сгенерированного идентификатора сеанса в файле cookie; никакая другая информация не фиксируется.

Как правило, в файле cookie может храниться только информация, которую вы предоставляете, или выбор, который вы делаете при посещении веб-сайта.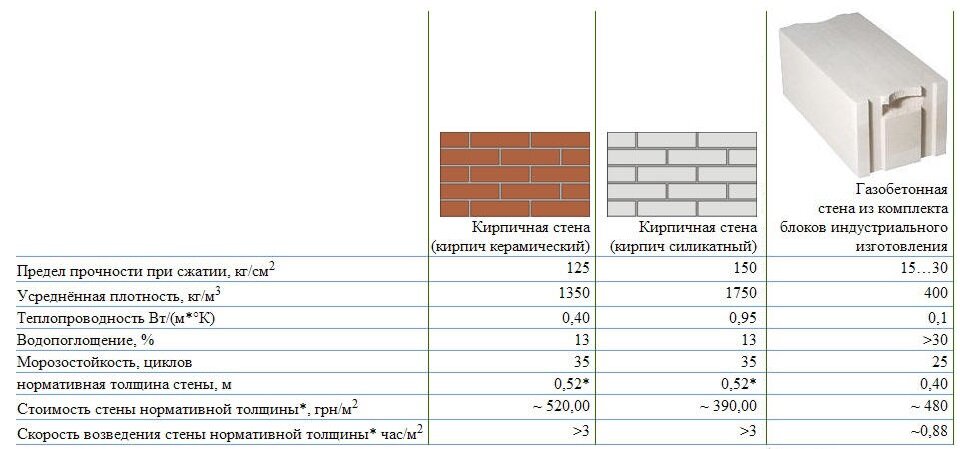 2}\left( L_{22}-\frac{L_{12}L_{21}}{L_{11}} \справа)\) ²⁹ .2}\справа) . \end{выровнено}$$

(3)

Здесь корреляционные функции ток-ток $\overleftrightarrow {L}_{ij}({\mathbf{q}},\Omega )$ могут быть получены преобразованием Фурье запаздывающих корреляционных функций $\overleftrightarrow {L} _ {ij} ({\ mathbf {q}}, t) = \ mathrm {i} \ Theta (t) \ langle [{\ mathbf {j}} _i ({\ mathbf {q}}, t ),{\mathbf{j}}_j(-{\mathbf{q}},0)]\rangle$, где ступенчатая функция $\Theta (t)$ обеспечивает причинно-следственную связь, а $\langle \ cdots \rangle$ обозначает термодинамическое среднее.\dag (0)]\rangle\) (Подробнее можно увидеть в дополнительной информации).

В кроссовере BCS-BEC наиболее часто используемыми микроскопическими подходами для получения функций Грина, которые включают парные флуктуации, являются многочастичные t -матричные теории ¹ . Существует по крайней мере пять видов альтернативных t -матричных подходов, которые могут быть численно приняты выше $T_c$ ²⁴ .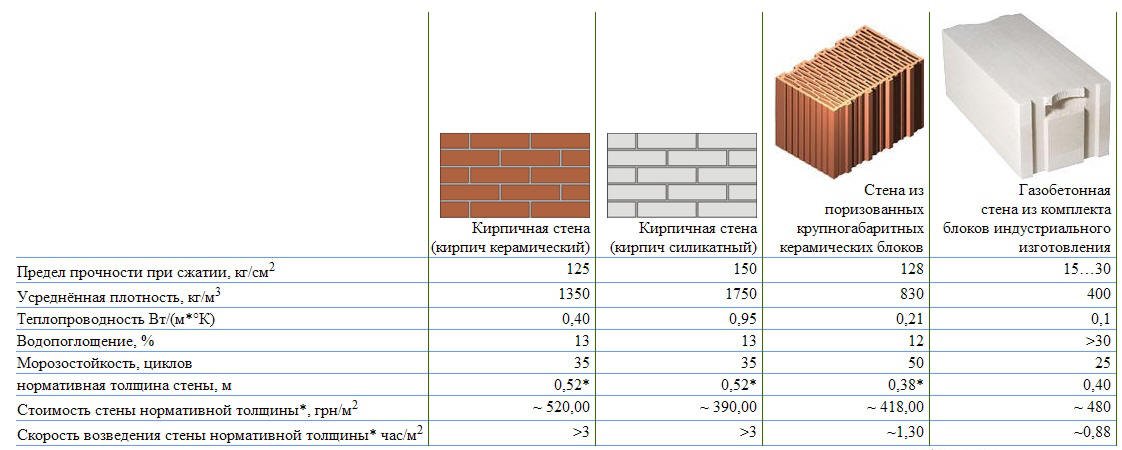 2\).{-1}\) и спектральные функции $A({\mathbf{k}},\epsilon )\!=\!-2\mathrm{Im}G({\mathbf{k}},\epsilon ) $ и $B_{sc(pg)}({\mathbf{k}},\epsilon )\!=\!-2\mathrm{Im}F_{sc(pg)}({\mathbf{k} },\эпсилон)$. Подробный вывод приведенных выше выражений и явный вид обобщенных нормальных и аномальных функций Грина $G({\mathbf{k}},\omega )$ и $F_{sc(pg)}({\mathbf {k}},\omega )$ можно увидеть в дополнительной информации. Мы также оцениваем зависящий от температуры и взаимодействия член затухания, связанный с эффектами конечного времени жизни термически возбужденных носителей (время релаксации $\tau$) в СИ.*\), при котором действительно имеют место эффекты псевдощели.

При температурах, близких к нулю, $\каппа$ уменьшаются до нуля для всех $\nu$ из-за экспоненциального роста конденсированных пар, не передающих тепло. По сравнению с кинетическими результатами, основанными на тепловом переносе сверхтекучих фононов ^21,23 , наши результаты значительно выше. Вблизи $T_c$ расчетные кривые имеют точки перегиба, которые обусловлены наибольшим вкладом парных флуктуаций вокруг точек фазового перехода, а также отражают различные микроскопические свойства сверхтекучего и псевдощелевого состояний. {-1}\) обычно рассматривается как энергетическая граница для оценки бесстолкновительной и гидродинамической областей мод возбуждения. Здесь мы находим, что она меньше характерных масштабов энергии, таких как $\mu \sim 0,4E_F$ и $\Delta \sim 0,6E_F$ ³⁰ , особенно при низких температурах ниже $T_c$. Следовательно, система находится в области слабой диссипации в сверхтекучей фазе, что также согласуется с исследованиями сдвиговой вязкости ^11,21,22 . Совсем недавно в эксперименте со звуковыми волнами изучалось подобное обстоятельство ¹⁶ .Он наблюдает моды возбуждения на частоте $\omega _0\sim (0,35-0,5)E_F$, лежащие в бесстолкновительном режиме в сверхтекучей фазе и переходе между гидродинамическим и бесстолкновительным режимом выше $T_c$. Для этих режимов возбуждения с частотами, немного отклоняющимися от низкочастотного предела, мы считаем, что гидродинамические выражения все еще приблизительно верны. Таким образом, мы можем сравнить скорость затухания $\Gamma$ с экспериментальными данными, которые могут быть непосредственно измерены по отклику плотности и включают вклады сдвиговой вязкости $\eta$ и теплопроводности $\kappa$ при единичных, как ³³

$$\begin{align} \Gamma =\left( \frac{4\eta }{3mn}+\frac{4\kappa T}{15\mathscr {P}}\right) q ^ 2.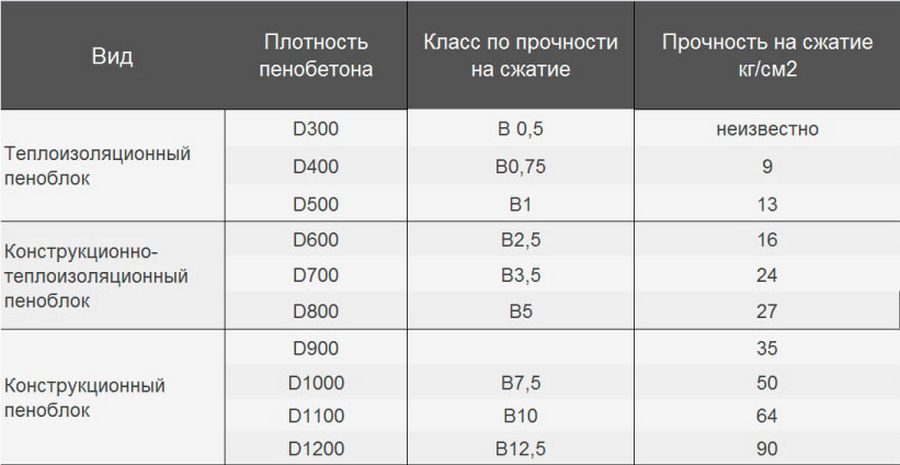 \end{выровнено}$$

(5)

Обратите внимание, что в рамках псевдощелевой теории дисперсия голдстоуновских бозонов является квадратичной в сверхтекучей фазе. Здесь мы используем тот же волновой вектор $q=0.5k_F$, что и измерение. Для $\eta$ мы используем наши предыдущие расчеты, которые хорошо согласуются с экспериментами и другими теориями ¹¹ , а для давления $\mathscr {P}$ мы используем экспериментальные данные Массачусетского технологического института ³⁰ . На рис. 2 наши результаты $\Gamma$ как функции $T/T_c$ хорошо согласуются с экспериментальными данными вблизи и ниже $T_c$.Расчет приближения случайной фазы квазичастиц (QRPA), основанный на столкновениях между фермионами, также согласуется с нашими результатами ниже $T_c$, что подтверждает, что фермионные квазичастицы являются доминирующими тепловыми возбуждениями ниже $T_c$, которые также могут быть сопоставлены с аналогичными случаями слабой диссипации. Между тем, поскольку теория псевдощели утверждает, что бозонные степени свободы дают вклад примерно в околонулевой области импульса и энергии ³ , взаимодействиями между парами можно пренебречь в бесстолкновительном режиме с волновым вектором при $q\sim 0 .5k_F$. Таким образом, наша трактовка игнорирования члена взаимодействия в операторе теплового тока в этом случае разумна. Можно заключить, что в слабодиссипативном и бесстолкновительном режимах в тепловом переносе преобладают фермионные квазичастицы.

Наши расчеты несколько отклоняются от экспериментальных данных при более высоких температурах выше $T_c$, когда система уже не может быть описана как бесстолкновительная и имеет относительно сильную диссипацию. В этот момент все большую роль играют бозонные возбуждения с большим импульсом, что делает теорию псевдощели менее надежной.*\) на каждой из этих кривых выше показанного диапазона температур. Вставка: $\kappa$ по сравнению с $\nu$ для разных $T/T_F$.

Со стороны БЭК наши расчеты дают относительно небольшие значения $\каппа$, детали показаны на рис. 3. Мы видим, что кривые пересекаются с разной силой взаимодействия при $T\gtrsim 0,3T_F$ ($T_c\simeq 0.25T_F$, см. черные треугольники). Это означает, что как функция $\nu$, $\kappa$ имеет минимум при $\nu \simeq 0,3$ над сверхтекучей фазой, как показано на вставке к рис.3. Обнаружен аномальный минимум при измерении $\eta$ выше $T_c$ при $\nu \simeq 0,25$ ³⁴ , который должен был иметь место на унитарном пределе ¹² . Этот минимальный сдвиг в $\eta$ можно понять с помощью модификаций более высокого порядка в кинетической теории ³⁵ . Поскольку скорость затухания $\Gamma$ включает оба вклада $\eta$ и $\kappa$, мы можем предсказать, что может быть минимум скорости затухания $\Gamma$ на волне вектор $q\sim 0.5k_F$, при силе взаимодействия $\nu \sim (0.2-0.3)$ на стороне БЭК.

Поскольку наши расчеты построены на существенной многочастичной фермионной природе, лучше не охватывать границу $\nu \приблизительно 0,5$, где химический потенциал при нулевой температуре $\mu$ меняет знак, что сигнализирует исчезновение подстилающей поверхности Ферми и статистики Ферми.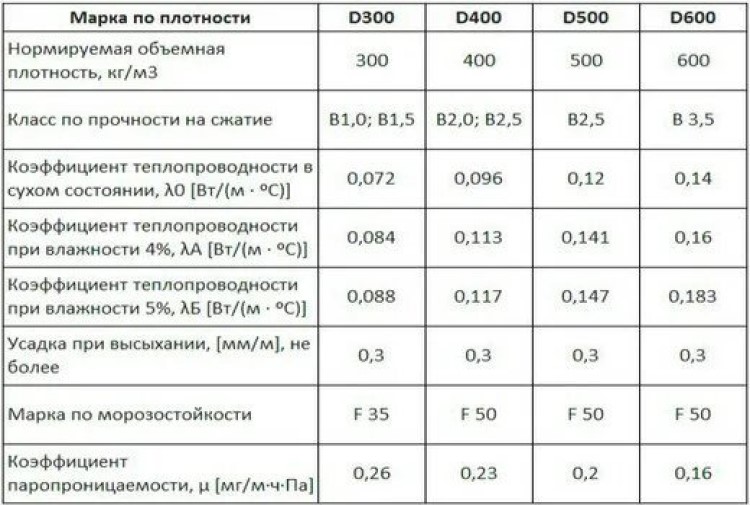 После этого система переходит в двухчастичный молекулярный режим, где доминирующим механизмом демпфирования становятся бозонные возбуждения, а теплопроводности ожидаются почти как бозе-результаты ^26,36 .

Общие свойства газа для подключенного контура

Матрица значений плотности газа, для двумерного табличного поиска в зависимости от давления и температуры. Размер матрицы должен соответствовать размеры векторов давления и температуры. Строки таблицы соответствуют значениям вектора температуры , и столбцы соответствуют вектору давления ценности.

По умолчанию [0,232389928446798, 0,465063671432694, 1.16479567270147, 2.33676613945539, 4.70263894299404, 11.983516436453, 24. 7878864888476, 53.4753944012435, 188.202476404452, 488.088746553617; 0,217841319668304, 0,435

028115, 1,024660849, 2,18825141646267, 4.39865940277095, 11.1676860192343, 22.9408518273177, 48.6188318442922, 151.41140977555, 397.086323615566; 0.20500_{95605, 0.410186693889784, 1.026732943, 2.05770371150129, 4.132493848, 10.4620818492884, 21.3797637857971, 44.7465382224065, 130.788260466556, 323.533424670971; 0,193606079729805, 0,38734394286521, 0,969349656759853, 1,9420081}962438, 3.16140997822029, 6.311456322, 12.5766989218007, 31.0826018729834, 60.72079736; 0,05805995729, 0,116115694052286, 0,2544054221, 0,580409375636267, 1.1603953396719, 2.89780177016166, 5.784603688, 11.5265728971708, 28.4843351052556, 55.829341571381; 0.0535937940886494, 0.107183660899874, 0.2679296_{126, 0,535761125401431, 1,07112886747126, 2,67486471725533, 5.339826312, 10.63973457213, 26.2952097273985, 51.5589206387574; 0,0497656797149008, 0,0995277403610491, 0,248792203124892, 0,497493882078744, 0,99462543314985, 2.48384153794703, 4.95858078750581, 9.88055926765067, 24. 4240170579045, 47.69639003; 0,0464479959361466, 0,0928926705710533, 0,232206763597689, 0,464330464081941, 0,928328524958611, 2,31832536465517, 4,62831259866885, 9.22315228584034, 22.8051678288226, 44.7645110499732; 0,0435450312171066, 0,0870870188301226, 0,217694718092182, 0,435313326650428, 0,870322119623417, 2,17351945401494, 4.33940803061583, 8.64821978531377, 21.3}8076149, 42.0123332867245; 0,0409835963547538, 0,0819644033075145, 0,2048547796, 0,409710426055867, 0,8105232369, 2.04576053_{4, 4.084534353, 8.14108047721294, 20.14231739, 39.5856012611331; 0,0387067675798369, 0,077410976131965, 0,193508246917561, 0,386952511151441, 0. 77364}61575, 1.93220226835442, 3.85799954128176, 7,65147706, 19,0335137737723, 37,4287645642868; 0,0366696057813522, 0,073336860231159, 0,183324515224783, 0,3665538238, 0,732945322059316, 1,8305992514921, 3,65531662685461, 7,28709889581498, 18,0413651664581, 35.4984330382504; 0,0348361601073285, 0,0696701556937661, 0.174159155188816, 0,348264195999875, 0,696311928298658, 1,73915624407237, 3,472_{125895, 6,92415359223964, 17.1482850565279, 33.7601783509398; 0,0232242994681783, 0,0464475414045395, 0,11611092226157, 0,232195408621678, 0.464285085702862, 1.15991997307222, 2.31719916466188, 4.62384864786652, 11.4808038114339, 22.7013239671071; 0. 3 .} границ | Улучшенные чувствительные свойства датчиков газа CO2 теплопроводного типа путем загрузки многослойных углеродных нанотрубок в порошки нано-Al2O3 Введение Большое количество выбросов парниковых газов CO ₂ усугубляет глобальное потепление. Кислотные дожди, мгла и другие непогоды нанесли огромный экономический ущерб и серьезный ущерб окружающей среде (Hansen and Sato, 2004). Контроль за выбросами CO ₂ является основным способом борьбы с потеплением климата, как это в целом признано международным сообществом (Zhang et al., 2008). В промышленном производстве, особенно в угольных шахтах, CO ₂ часто является продуктом выбросов, что также является источником опасности в производственном процессе (в истории добычи угля было много аварий с выбросами углекислого газа). Поэтому необходимо обнаруживать и контролировать выбросы CO ₂ распределенно, в режиме реального времени и точно (Ghosh et al. , 2013; Zaitsev et al., 2017). Датчик теплопроводности — это датчик теплового эффекта, который может измерять концентрацию газа в соответствии с разницей теплопроводности различных газов и воздуха (Gardner et al., 2020). Обычно разность теплопроводностей преобразуют в изменение сопротивления с помощью схемы Уитстона. Режим теплопроводности обычно включает конвекцию, теплопроводность и излучение, которые работают при температуре около 300°С. Его механизм срабатывания определяет, что он имеет преимущества большой дальности обнаружения, хорошей рабочей стабильности и высокой надежности. Однако он также демонстрирует проблемы, связанные с медленным временем отклика и низкой точностью обнаружения (Wei-Yong et al., 2006). Для достижения высокой точности и быстрого срабатывания обнаружения в опасной среде необходимо улучшить теплопроводность и чувствительность срабатывания датчика. В последние годы углеродные нанотрубки (УНТ) постепенно стали использоваться при разработке теплопроводных датчиков газа из-за их лучших тепловых свойств и пористой структуры по сравнению с обычными керамическими носителями (Huang et al. , 2019). Исследователи в стране и за рубежом изучали газовые сенсоры, модифицированные углеродными нанотрубками (Zhang, 2012). Датчик газа, изготовленный Guo et al. (2006) был покрыт небольшим количеством МУНТ между встречно-штыревыми золотыми электродами на основе Al ₂ O ₃ и имеет хороший газочувствительный отклик на толуол при комнатной температуре.Танг и др. (2020) использовали одностенные углеродные нанотрубки (SWNT) для изготовления датчиков NH ₃, получив превосходную чувствительность 2,44% ΔR/R на ppm _v NH ₃ , что более чем в 60 раз выше, чем собственные SWNT. датчики на основе. Бин Шен (Shen et al., 2018) и другие изучили технологию порообразования МУНТ, закрепленных на ориентированных нанотрубках, и спроектировали и изготовили своего рода датчик теплопроводности керамического порошка с покрытием из горячей проволоки для обнаружения метана со временем восстановления отклика 8 с и 16 с (Xibo et al., 2013). В этой статье МУНТ используются для улучшения несущей структуры глухих отверстий традиционных шариков, таких как датчик теплопроводности, открытия большего количества каналов передачи газа и эффективного улучшения проницаемости чувствительного материала «керамического шарика» (Wu and Lin, 2006; Торрес-Торрес и др. , 2013). Представлены метод изготовления и ключевая технология такого рода датчиков. Измеряется производительность датчика и обсуждается возможный механизм. Результаты показывают, что время отклика и восстановления сенсора при загрузке модификации МУНТ в порошки нано-Al ₂ O ₃ было значительно сокращено.Исследование оказало важное влияние на совершенствование технологии обнаружения в режиме реального времени высокой концентрации CO ₂ в угольных шахтах (Qin et al., 2011). Экспериментальная секция Структура датчика и конструкция взрывозащищенного корпуса Газовый датчик теплопроводности состоит из детектирующего и компенсирующего элементов, представляющих собой пару рабочих компонентов (рис. 1А), состоящих из платинового терморезистора и держателя (рис. 1Б). Эти два компонента отдельно собраны в две стандартные трубы.Один из них представляет собой негерметичную упаковку (рис. 1С), а другой представляет собой герметичную упаковку, которая используется для защиты от влаги и компенсации температуры окружающей среды чувствительного компонента. Затем изготавливается датчик теплопроводности путем сборки двух компонентов в корпусе из порошковой металлургии (рис. 1D) для реализации взрывозащищенной конструкции. Рис. 1. Комплект датчика в сборе. На этикетке (a) показаны рабочие компоненты, на этикетке (b) показан несущий шар, на этикетке (c) показана форма упаковки, на этикетке (d) показан корпус из порошковой металлургии. Процесс изготовления датчика Методы изготовления чувствительного элемента и компенсационного элемента датчика теплопроводности аналогичны, но форма упаковки отличается, что играет роль дифференциальной компенсации (Xue et al., 2013). Ключевыми факторами, ограничивающими работоспособность сенсора, являются в основном состав носителя сенсора, микроструктура, типы и формы распределения катализаторов. Основной производственный процесс датчика состоит из 10 этапов, таких как изготовление носителя, модификация носителя (загрузка смешанных углеродных нанотрубок и катализатора), намотка катушки элемента, покрытие носителя на катушке, спекание элемента, чернение элемента, согласование элемента и упаковка элемента, старение датчика и тестирование производительности и так далее. Конкретный процесс показан на рисунке 2. Рис. 2. Процесс изготовления датчика. Разработка ключевых процессов Конструкция из композитного несущего материала γ-Al ₂ O ₃ Преимущество наночастиц заключается в более высокой удельной поверхности. После смешивания с МУНТ образуется большое количество микронанопор (Zhang et al., 2018). Некоторые из сквозных отверстий подходят для производства чувствительных блоков для датчиков теплопроводности (Wu et al., 2013). В этой статье наноразмерные γ-Al ₂ O ₃ керамические ультратонкие порошкообразные материалы-носители были приготовлены методом химического осаждения (Saha et al., 2005). Под непрерывным воздействием ультразвуковой волны раствор, состоящий из 0,02 моль муравьиной кислоты, 5,4 г воды и 7 мл изопропанола, медленно прикапывали в смесь 20,4 г изопропилалюминия и 200 мл толуола. После завершения операции включают механическую мешалку и нагревают раствор до 50-60°С. Затем реакцию поддерживают в течение 1 ч, после чего получают полупрозрачный гель. Продукты фильтровали, сушили при 60°С в течение 12 ч и повторно сушили при 120°С в течение 1 ч. Затем получали рыхлый сухой гель-порошок. Порошок нано-Al ₂ O ₃ можно получить прокаливанием порошка ксерогеля в течение 2 ч при 700-800°С. Следует отметить, что режим добавления микрокапель под действием ультразвуковой волны и температуры прокаливания являются ключевыми для формирования наноразмерного порошка γ-Al ₂ O ₃. Поскольку МУНТ трудно растворяются в воде, в эксперименте были выбраны гидроксилированные МУНТ (SSA > 490m ² /г, чистота > 95 вес. %, Chengdu Organic Chemicals Co. Ltd). СЭМ-характеристика показала, что МУНТ имеют внешний диаметр 8 нм и длину 5–30 мкм. Для повышения равномерности диспергирования МУНТ в порошке Al ₂ O ₃ необходимо приготовить МУНТ в водном растворе путем добавления определенного количества диспергатора под действием ультразвуковой волны. Для улучшения термической стабильности носителя целевой композитный носитель также необходимо модифицировать путем добавления 5% по массе порошка Nano-CeO ₂ (30~50 нм, чистота 99,99%, Маклин). Наконец, материал был добавлен в порошок γ-Al ₂ O ₃ /CeO ₂ в соотношении 5% по массе с образованием нано-γ-Al ₂ O ₃ /CeO _{2 Композитный носитель катализатора} /МУНТ. Чернение чувствительных и компенсационных компонентов Благодаря высокой удельной поверхности и поверхностной активности нано-γ-Al ₂ O ₃ носитель, изготовленный из него, обладает сильной адсорбцией на полярных молекулах (включая молекулы воды в воздухе) (Liu et al., 2011), но эффект десорбции становится слабым. В то же время серая шкала керамики, обожженной носителем γ-Al ₂ O ₃ /CeO ₂ /МУНТ, низкая, что приводит к усугублению эффекта теплового излучения, что влияет на обнаружение тепловой конвекции. эффект. В данной работе частицы Pd и Pt образуются при пропитке раствором чистой хлорированной палладиевой кислоты (H ₂ PtCl ₆ ⋅6H ₂ O и H ₂ PdCl _{2 901 ⋅16H чисто аналитический , Синофарм Кемикал Реагент Ко., Ltd), которые, следовательно, электротермически разлагают частицы Pd и Pt, вызывая изменение цвета носителя с серого на черный. Эффективность рассеивания тепла носителя может быть эффективно снижена, когда датчик работает. Для уменьшения каталитического действия наночастиц Pd/Pt раствор нитрата свинца пропитывали поверхность черных частиц Pd/Pt и разлагали при высокой температуре с образованием десенсибилизированного монооксида свинца. В итоге были сформированы чувствительный и компенсационный элементы датчика теплопроводности без каталитического эффекта.} Сопротивление спеканию и термическому разложению Необходимо выполнить три ключевых шага, чтобы решить проблему легкого горения углеродных нанотрубок при высоких температурах. Первым этапом электрифицированного спекания является спекание размера порошка носителя при высокой температуре для объединения зерен и создания микро/наноотверстий, чтобы носитель имел определенную механическую прочность и стабильную высокую удельную поверхность. Чувствительную катушку носителя с покрытием нагружали постоянным напряжением под защитой азота высокой чистоты и при температуре около 550°С, а ток спекания 150 мА поддерживали в течение 60 мин. Во-вторых, под защитой азота высокой чистоты пропускают ток спекания 140 мА при температуре около 500°C и поддерживают этот ток в течение 30 мин для термического разложения раствора хлорида палладия, импрегнированного в носителе. Поэтому чувствительные компоненты и компоненты компенсации станут черными. Третий этап заключается в защите азотом высокой чистоты и при 550°C, при токе спекания 150 мА, разложении погружения раствора нитрата свинца в черный носитель 30 мин, за счет термического разложения раствора нитрата свинца с образованием МБТ и PbO, устранит носитель катализатора Pt и Pd. В результате чувствительный компонент будет иметь только эффект теплопроводности во время работы. Создание тестовой системы и метод тестирования производительности Система динамических испытаний, показанная на рис. 3, состоит из устройств ввода и вывода (включая компьютер, стабилизированный источник питания постоянного тока и коллектор данных), чистого газообразного диоксида углерода, трехходового клапана, камеры для динамических испытаний (датчик и основание датчика), измерительного схема, интерфейс и шина. Среди них динамическая испытательная камера является основной частью всей системы, и ее объем можно регулировать с помощью внешнего поршня (аналогично поршню игольчатого цилиндра).Концентрацию целевого газа контролируют, регулируя объем испытательной камеры и объемное соотношение вводимого углекислого газа. Основание датчика закреплено снаружи испытательной камеры, и датчик можно быстро переключать между целевым газом и воздухом с помощью поршня. Эта конструкция устраняет недостаток медленного воздухообмена в традиционной тестовой камере датчика и устраняет влияние диффузии газа на время отклика датчика. Рис. 3. Тест-система. Модуль датчика представляет собой типичный мост Уитстона для преобразования концентрации газа в выходное напряжение, как показано на рисунке 4. Постоянные резисторы R ₁ и R ₂ (200 Ом) подключены к плечу моста на одном конце, а чувствительный элемент и компенсационный элемент (C, D) соединены на другом конце. Два плеча соединены друг с другом с помощью источника постоянного напряжения 3,0 В (Vin). Схема обнаружения может выводить значения в милливольтах в соответствии с изменением концентрации целевого газа.R ₃ — скользящий реостат, используемый для регулировки нулевого выходного значения датчика, которое составляет 2000 Ом. Рис. 4. Схема обнаружения моста Уитстона. Результаты и обсуждение Микроскопическая характеристика углеродных нанотрубок, модифицированных Nano-Al ₂ O ₃ Носитель Сканирующий электронный микроскоп Zeiss Supra 55 использовался для наблюдения и измерения морфологии многостенных углеродных нанотрубок (МУНТ) и их композитных материалов-носителей при рабочем напряжении 15000 В. Микроразмер приготовленного носителя Al ₂ O ₃ составляет 20–50 нм, как показано на рис. 5. Углеродные нанотрубки в носителе Al ₂ O ₃ переплетаются, образуя канал внутри носителя, т.к. показано на рисунке 6. Образование углеродных нанотрубок в основном представляет собой смесь sp2-гибридизированных и sp3-гибридизированных нанотрубок. Под влиянием квантовой физики он может создавать особые электрические свойства в зависимости от структуры и диаметра сети. В то же время углеродные нанотрубки также синтезируются с двойными углерод-углеродными связями, полыми клетками и закрытыми топологиями, поэтому они обладают превосходными термическими и механическими свойствами (Dongmei et al., 2014). Рис. 5. СЭМ-изображение размера частиц носителя Al ₂ O ₃. Рис. 6. СЭМ-изображение МУНТ Al ₂ O ₃, адаптированных к носителю. На рис. 7 показано, что носитель в основном состоит из углеродных нанотрубок Al ₂ O ₃ и CeO ₂ . Ожидаемые компоненты углеродных нанотрубок и CeO ₂ были модифицированы. Массовое соотношение Pt и Pd составляет 2:1, как показано в результатах картографической характеристики (таблица 1), тогда как углеродные нанотрубки достигают 4.14%. Рис. 7. Энергетический спектр носителя датчика. Таблица 1. Результаты характеристики картирования. Тест производительности датчика Характеристики рабочего напряжения датчика На рис. 8 показаны значения чувствительности при различных рабочих напряжениях от 1,5 до 3,0 В с 10% CO ₂ . Очевидно, что зависимость между чувствительностью и рабочим напряжением не является линейной. При повышенном рабочем напряжении чувствительность сначала имеет тенденцию к росту, а затем снижается по сравнению с установленной чувствительностью. Чувствительность достигает своего максимума при 2,7 В, поэтому в последующих тестах используется рабочее напряжение 2,7 В. Это показывает, что датчик, модифицированный МУНТ, может работать при более низком напряжении и имеет меньшее энергопотребление, чем коммерческий датчик, работающий при напряжении 3,0 В. Рис. 8. Кривая подбора чувствительности для 10% CO ₂ при различных рабочих напряжениях. Линейные характеристики реакции датчика Кривая восстановления отклика концентрации СО ₂ определяется от 0 до 100 % путем контроля концентрации СО ₂ в тест-системе при температуре окружающей среды 25°С и влажности 45 % с интервалом концентрации 10 % и рабочее напряжение 2.7 В в три раза. Линейная аппроксимация среднего выходного напряжения датчика и концентрации CO ₂ показана на рисунке 9, из которого видно, что датчик имеет хорошую линейную зависимость (y = 0,464 + 0,754X, R ² = 0,9986) с средняя чувствительность около 0,00754 В/10% CO ₂ . Чувствительность CO ₂ при концентрации менее 40% несколько выше, чем при концентрации более 40%. Рис. 9. Входная и выходная характеристики датчика. Характеристики согласованности отклика датчика Одной из проблем при применении газовых сенсоров теплопроводности является согласованность отклика целевых газов с различной концентрацией, на которую влияют как условия испытаний, так и характеристики сенсора. В этом тесте динамическая газовая камера со шкалой объема используется для быстрого переключения между воздухом и измеряемым газом. Тогда достигается идеальный результат. На рисунке 10 показано, что датчик имеет хорошие характеристики отклика и восстановления для различных концентраций CO ₂ с одинаковыми характеристиками отклика и восстановления при десяти различных концентрациях.Результаты испытаний трехкратного времени отклика и восстановления показаны на рисунке 11, время отклика T ₉₀ разработанного датчика составляет 9 с, а время восстановления T ₉₀ составляет 13 с. Рис. 10. Кривая отклика и восстановления при непрерывном измерении. Рис. 11. Время отклика и время восстановления при различных концентрациях. Влияние легирования углеродных нанотрубок на характеристики отклика датчика Время отклика является важным показателем датчика газа.Как правило, время, необходимое для того, чтобы выходное значение датчика газа достигло 90% стабильного значения после контакта с целевым газом, определяется как время отклика датчика, которое выражается как T ₉₀ . Чем меньше значение, тем выше скорость отклика. Время отклика датчика делится на диффузию газа CO ₂ в оболочку из порошковой металлургии и время прямого отклика датчика на газ CO ₂. На время диффузии газа будет влиять размер этого наложения порошковой металлургии.Определено, что спецификация 400 меш является лучшим выбором для газовых испытаний. В условиях концентрации 30% CO ₂ рабочее напряжение датчика было установлено равным 2,7 В, а кривые отклика и восстановления трех типов датчиков теплопроводности: модифицированных без МУНТ, модифицированных МУНТ и MD62, которые произвели компании Winsen (Китай) (Winsen, 2018) с чувствительностью 0,0061 В/10% CO ₂, как показано на рис. 12. Чувствительность модифицированных МУНТ намного выше по сравнению с датчиком до модификации и MD62.Время отклика T ₉₀ модифицированного датчика, не содержащего МУНТ, составляет 11 с, а время восстановления T ₉₀ составляет 17 с. Время отклика T ₉₀ датчика MD62 составляет 10 с, а время восстановления T ₉₀ — 18 с. Результаты показывают, что разработанный датчик с временем отклика T ₉₀ 9 с и временем восстановления T ₉₀ 13 с имеет лучшие характеристики. Кроме того, модифицированные углеродные нанотрубки могут значительно улучшить характеристики восстановления отклика датчика теплопроводности. Рисунок 12. Кривые отклика для 30% CO ₂ по сравнению с датчиком, не модифицированным МУНТ, и коммерческим датчиком MD62. Обсуждение механизма быстрого срабатывания датчика теплопроводности При изменении целевого окружающего газа быстрое достижение нового баланса компонентов измерения датчика является ключом к повышению производительности датчика газа с теплопроводностью. Из механизма срабатывания датчика теплопроводности способность чувствительного элемента к тепловому балансу является ключом к влиянию на реакцию датчика, которая зависит от теплопроводности и микроструктуры самого датчика.Традиционный способ заключается в уменьшении размера носителя из оксида алюминия и увеличении удельной поверхности. Когда порошок оксида алюминия уменьшается до наноразмеров (< 50 нм) благодаря механизму образования носителя, во внутренней части носителя из оксида алюминия наблюдается большое количество отверстий. Однако большая часть этих отверстий является глухими, непроницаемость которых приведет к возникновению газопроницаемого барьера, что приведет к недостаточному воздухообмену и, как следствие, к снижению скорости отклика датчика и легкому снижению производительности. Электрические свойства носителя датчика могут быть улучшены за счет улучшения углеродных нанотрубок. Во-первых, углеродные нанотрубки улучшают транспортную эффективность измеряемого газа за счет улучшения микроканала носителя, как показано на рисунке 13. Внутренний диаметр МУНТ составляет 2–5 нм, что позволяет газу CO ₂ диффундировать и транспортироваться в МУНТ. МУНТ и порошок оксида алюминия сцементированы вместе, что играет роль образования вторичных пор и обеспечивает множество каналов для носителя, так что первоначальный теплообмен при поверхностном расширении может быть распространен на внутренний обмен.Во-вторых, текущая длина углеродных нанотрубок составляет 5–30 мкм, а их теплопроводность может достигать 1000 Вт/м⋅K, что в 100 раз больше, чем у Al ₂ O ₃ , что эффективно улучшает теплопроводность композитный материал-носитель (Shanni et al., 2020). Кроме того, из-за большой площади углеродных нанотрубок он также может повысить эффективность теплообмена измеряемого газа на чувствительном носителе, что значительно улучшает время отклика и стабильность датчика. Рис. 13. Принципиальная схема легирования микроканала МУНТ. Заключение (1) Материал-носитель γ-Al ₂ O ₃ /CeO ₂, модифицированный углеродными нанотрубками, имеет решающее значение для чувствительности датчика теплопроводности. Термическая обработка может изменить его кристаллическую форму, сделать его более активным и сохранить хорошие физические и химические свойства, предотвратить агломерацию носителя и улучшить стабильность датчика.В условиях воздуха испытание CO ₂ показало, что средняя чувствительность датчика составляет 0,0075 В/10% CO ₂ и демонстрирует хорошую линейность. (2) Для разных концентраций CO ₂ датчик продемонстрировал хорошие характеристики отклика и восстановления, которые одинаковы при разных концентрациях. Время отклика T ₉₀ и время восстановления T ₉₀ датчика составляют 9 с и 13 с соответственно, что лучше по сравнению с датчиком без МУНТ и коммерческим датчиком того же типа. (3) Многослойные углеродные нанотрубки обладают теплопроводностью. Модифицированный композитный носитель способствует полной теплопередаче измеряемого газа в отверстии и повышает эффективность теплопередачи измеряемого газа на носителе, что может значительно улучшить теплопроводность носителя и позволить датчику демонстрировать быстрый отклик. характеристики. Заявление о доступности данных Оригинальные материалы, представленные в исследовании, включены в статью/дополнительный материал, дальнейшие запросы можно направлять соответствующему автору. Вклад авторов BS: концептуализация, исследование, написание обзора, управление проектом и получение финансирования. XWL: методология и руководство. ФЗ и XLL: программное обеспечение. БС и ЖЖ: валидация. XQ: ресурсы. FZ и XS: обработка данных. BS и XLL: написание – подготовка и редактирование исходного проекта. Все авторы внесли свой вклад в статью и одобрили представленную версию. Финансирование Эта работа была поддержана Национальной ключевой программой исследований и разработок Китая (2018YFC0810500), Национальным фондом естественных наук Китая (52074111), Фондом естественных наук провинции Хэйлунцзян (YQ2020E034) и проектом Университетской программы обучения молодых инновационных талантов провинции Хэйлунцзян. (UNPYSCT-2018095). Конфликт интересов Авторы заявляют, что исследование проводилось при отсутствии каких-либо коммерческих или финансовых отношений, которые могли бы быть истолкованы как потенциальный конфликт интересов. Благодарности Авторы хотели бы поблагодарить Хунцюань Чжана и его команду из Харбинского инженерного университета за их долгосрочное предоставление всех видов газа и техническое руководство. Они также хотели бы поблагодарить рецензентов за их проницательные и конструктивные комментарии. Каталожные номера Дунмей, З., Чжэньвэй, Л., Линди, Л., Яньхун, З., Декай, Р., и Цзянь, Л. (2014). Ход получения и применения композиционных материалов графен/углеродные нанотрубки. Акта Чими. Грех. 72, 185–200. дои: 10.6023/A13080857 Полнотекстовая перекрестная ссылка | Академия Google Гарднер, Э.Л.В., Лука, А.Д., Винсент, Т., Джонс, Р.Г., Гарднер, Дж.В., и Удреа, Ф. (2020). Датчик теплопроводности с изолирующими мембранными отверстиями. 2019 ДАТЧИКИ IEEE. Нью-Йорк, штат Нью-Йорк: IEEE. Академия Google Гош Р., Мидья А., Сантра С., Рэй С. К. и Гуха П. К. (2013). Химически восстановленный оксид графена для обнаружения аммиака при комнатной температуре. Приложение ACS Матер. Интерфейсы 5, 7599–7603. дои: 10.1021/am4019109 Реферат PubMed | Полный текст перекрестной ссылки | Академия Google Го М., Пан М., Чен Дж., Ми Ю. и Чен Ю. (2006). Многослойные углеродные нанотрубки, модифицированные палладием, для обнаружения бензола при комнатной температуре. Подбородок. Дж. Анал. хим. 34, 1755–1758. дои: 10.1016/S1872-2040(07)60020-6 Полнотекстовая перекрестная ссылка | Академия Google Хуанг, Дж. Р., Ян, X. X., Хер, С. К., и Лян, Ю. М. (2019). Гибридная пленка углеродных нанотрубок/графеновых нанопластинок в качестве гибкого многофункционального датчика. Датчики 19:317. doi: 10.3390/s1 17 Реферат PubMed | Полный текст перекрестной ссылки | Академия Google Лю Ф. , Абед М. Р. М. и Ли К. (2011). Получение и характеристика ультрафильтрационных мембран на основе поли(винилиденфторида) (ПВДФ) с использованием нано γ-al2o3. Дж. Член. науч. 366, 97–103. doi: 10.1016/j.memsci.2010.09.044 Полнотекстовая перекрестная ссылка | Академия Google Цинь, X., Фу, М., и Шен, Б. (2011). «Беспроводная система мониторинга угольных шахтных газов на основе WSN [C]», в материалах Proceedings of the Second International Conference on Digital Manufacturing & Automation 2011 (Zhangjiajie: IEEE), 309–312. doi: 10.1109/ICDMA.2011.82 Полнотекстовая перекрестная ссылка | Академия Google Саха Д., Мистри К.К., Гири Р., Гуха А. и Сенгупта К. (2005). Зависимость свойства влагопоглощения от золь-гель процесса прозрачной наноструктурированной керамики γ-al2o3. Сенсорные приводы B Chem. 109, 363–366. doi: 10.1016/j.snb.2005.01.002 Полнотекстовая перекрестная ссылка | Академия Google Шанни В.У. , Юань З., Хун Дж., Фэн В. и Чуньронг Х. (2020). Создание функциональных наномультислоев w/al2o3 с низкой теплопроводностью и превосходными механическими свойствами. Матер.Респ. 34, 2023–2028 гг. Академия Google Шэнь Б., Чжан Х., Лю Х., Цао С. и Ян П. (2018). Изготовление и характеристика каталитического датчика метана на основе технологии микроэлектромеханических систем. Дж. Наноэлектрон. Оптоэлектрон. 13, 1816–1822 гг. doi: 10.1166/jno.2018.2435 Полнотекстовая перекрестная ссылка | Академия Google Тан С., Чен В., Чжан Х., Сун З. и Ван Ю. (2020). Сенсор газа из функционализированных однослойных углеродных нанотрубок с наночастицами pd для обнаружения водорода в высоковольтных трансформаторах. Перед. хим. 8:174. doi: 10.3389/fchem.2020.00174 Реферат PubMed | Полный текст перекрестной ссылки | Академия Google Торрес-Торрес, К., Переа-Лопес, Н., Мартинес-Гутьеррес, Х., Трехо-Вальдес, М., Ортис-Лопес, Дж. , и Терронес, М. (2013). Оптоэлектронная модуляция многослойными углеродными нанотрубками. Нанотехнологии 24:045201. дои: 10.1088/0957-4484/24/4/045201 Полнотекстовая перекрестная ссылка | Академия Google Вэй-Юн, Х., Мин-Мин, Т., и Цзы-Хуэй, Р.(2006). Новый метод определения концентрации газа с помощью датчика теплопроводности. Подбородок. Приводы J. Sens. 19, 973–975. дои: 10.1016/S1005-8885(07)60041-7 Полнотекстовая перекрестная ссылка | Академия Google Ву, Т. М., и Лин, Ю. В. (2006). Легированные композиты полианилин/многослойные углеродные нанотрубки: получение, характеристика и свойства. Полимер 47, 3576–3582. doi: 10.1016/j.polymer.2006.03.060 Полнотекстовая перекрестная ссылка | Академия Google Сибо, Д., Xiaoyan, G., Yuechao, C., Xue, S., and Zhaoxia, L. (2013). Исследование метода определения постоянной температуры датчика метана по теплопроводности. Телкомника 11:725. doi: 10. 12928/ТЕЛКОМНИКА.v11i4.1168 Полнотекстовая перекрестная ссылка | Академия Google Сюэ, С., Сибо, Д., Юечао, К., Ген, Х., и Лонг, Б. (2013). «Температурный дрейф и методы компенсации для газового датчика теплопроводности», в Трудах 8-го Международного форума по стратегическим технологиям (IFOST) 2013 г. (Нью-Йорк, штат Нью-Йорк: IEEE). Академия Google Ву, Ю., Ма, Дж., Ли, М., и Ху, Ф. (2013). Синтез гамма-al2o3 с большой площадью поверхности и большим объемом пор; метод обратного осаждения-азеотропной перегонки. Хим. Рез. Подбородок. ун-т 29, 206–209. doi: 10.1007/s40242-013-2207-7 Полнотекстовая перекрестная ссылка | Академия Google Зайцев Б.Д., Теплых А.А., Бородина И.А., Кузнецова И.Е., Верона Е. (2017). Датчик бензина на основе пьезоэлектрического резонатора, возбуждаемого боковым электрическим полем. Ультразвук 80:96–100. doi: 10.1016/j.ultras.2017.05.003 Реферат PubMed | Полный текст перекрестной ссылки | Академия Google Чжан Х. , Шен Б., Ху В. и Лю Х. (2018). Исследование быстродействующего датчика теплопроводности на основе модификации углеродных нанотрубок. Датчики 18, 2191–2120. doi: 10.3390/s18072191 Реферат PubMed | Полный текст перекрестной ссылки | Академия Google Чжан, К. (2012). Спасение Земли: правовые подходы к адаптации к изменению климата: защита интересов жертв. Шанхай: Издательство Шанхайской академии социальных наук. Академия Google Чжан, Т., Мубин, С., Мьюнг, Н.В., и Дешуссес, М.А. (2008). Недавний прогресс в сенсорах газа на основе углеродных нанотрубок. Нанотехнологии 19:332001. дои: 10.1088/0957-4484/19/33/332001 Полнотекстовая перекрестная ссылка | Академия Google Измерение теплопроводности газов переходным методом с горячей проволокой на JSTOR Абстрактный Описана конструкция и работа прибора для измерения теплопроводности газов и газовых смесей методом нестационарной горячей проволоки. Описание поставлено в контексте развития этого метода за последние 12 лет в ряде центров и дана библиография результатов, полученных за этот период. Подробно обсуждаются источники ошибок и последствия как для ограничений экспериментальных условий, так и для применяемых поправок. Описанные экспериментальные и теоретические процедуры отражают текущее состояние этой развивающейся методики. Приведены результаты для гелия и корреляционные уравнения для данных для других газов и газовых смесей.Они показывают точность 0,1% и абсолютную точность 0,5% для описанного аппарата при температурах от 300 до 470 К и давлениях от 1 до 25 МПа. Информация об издателе Королевское общество является самоуправляемым объединением многих самых выдающихся ученых мира, представляющих все области науки, техники и медицины, и является старейшей непрерывно существующей научной академией. Фундаментальная цель Общества, отраженная в его учредительных Уставах 1660-х годов, состоит в том, чтобы признавать, продвигать и поддерживать превосходство в науке, а также поощрять развитие и использование науки на благо человечества. Общество сыграло роль в некоторых из самых фундаментальных, значительных и судьбоносных открытий в истории науки, и ученые Королевского общества продолжают вносить выдающийся вклад в науку во многих областях исследований. Права и использование Этот предмет является частью коллекции JSTOR. Условия использования см. в наших Условиях использования Философские труды Лондонского королевского общества.Серия А, Математические и физические науки © 1988 Королевское общество Запросить разрешения Модель теплопроводности порошкообразных материалов в вакууме на основе экспериментальных исследований: AIP Advances: Vol 7, No 1 В этом разделе мы представляем теоретическую модель теплопроводности порошкообразных материалов в вакууме, основанную на приведенных выше экспериментальных результатах. При моделировании были приняты следующие допущения: (1) частицы имеют сферическую форму и одинаковый размер; (2) внутри слоя частиц возникает одномерный поток тепла в направлении силы тяжести; и (3) кондуктивный и радиационный теплообмен происходят параллельно, так что эффективная теплопроводность выражается как сумма твердотельной и лучистой теплопроводности. Мы моделировали твердотельную и лучистую проводимости отдельно. A. Модель твердотельной проводимости . Рассмотрим шарики одинакового размера, однородно упакованные в кубический контейнер с единичной длиной и единичной площадью поперечного сечения, как показано на фиг.9. Одномерный поток тепла происходит снизу вверх по слою сферы. В этой конфигурации твердотельная проводимость эквивалентна объемной теплопроводности слоя. Объемная теплопроводность может быть сформулирована как параллельные и последовательные соединения теплопроводности в элементарной ячейке. Предположим, что N _A — это количество сфер на единицу площади перпендикулярно направлению теплового потока, а N _L — это количество сфер на единицу длины вдоль него. N _A и N _L отражают параллельное и последовательное соединения соответственно. Тогда твердотельная проводимость определяется выражением, где 90 108 H 90 109 — теплопроводность элементарной ячейки. В этом уравнении член Н _А Н представляет собой эффективную теплопроводность отдельных горизонтальных слоев высотой 1/ Н _L . H можно также сформулировать как последовательное соединение общей проводимости контактов на контактах, H _{c, всего} , и теплопроводности внутри каждой сферы, H _s , как, кроме того, H _{c, всего} представлено как C /2 параллельных соединения теплопроводности на каждом контакте H _c , при этом C среднее координационное число.15, 3.89732426996839, 9.84460606064557, 20.0372743829505, 41.551685035359, 116.744404785154, 273.404057887341; 0.183405807765996, 0,36691546510227, 0,918068262208759, 1,83874006288175, 3,68793116346732, 9,2989642809239, 18,8669316601087, 38. 8510263281099, 106.248040134752, 239.063674783047; 0,174227353976232, 0,348537012803259, 0.871960127107058, 1.74598097193374, 3.50022045445381, 8.81280884432948, 17.8353318467781, 36.5262009931833, 97.9572133071041, 214.144269454883; 0,139362218300841, 0,278750918818379, 0,697075681624698, 1,39481110010495, 2,79224958681861, 7.00009934436889, 14.0635945083875, 28.3693859898697, 72.4958995959279, 148.0611083; 0,1161277516, 0,232262711724454, 0,580710652868886, 1,16159962682988, 2.323_{733333, 5.81485119489922, 11.6454651017326, 23.345179818482, 58.6036404676478, 116.933272564178; 0,0995348730218713, 0,1927735142, 0,497672062326111, 0,995337472158662, 1,939855983, 4,97624478331013, 9. 95052507838832, 19.8877675359538, 49.5222664696343, 97,8281817865855; 0,08701079571, 0,174179875730153, 0,435425837514054, 0,870771682736456, 1,74121977223468, 4.35055112014231, 8.6923131825558, 17.3462098741118, 43.0204270425471, 84.5862815012905; 0,0774139632775453, 0,154823661826077, 0,387027124125729, 0,773947181340524, 1.54746386958083, 3.86538722275345, 7.71958432856407, 15.3924298760864, 38.0966874262009, 74.7409240194489; 0,0696722132563204, 0,139339881699215, 0,3483155 498, 0,696517280056477, 1,3925775726502, 3,47798929739441, 6.94428820700405, 13.840595299045, 34.2211656015534, 67.0763619510542; 0,0633382100675146, 0,126671957763271, 0.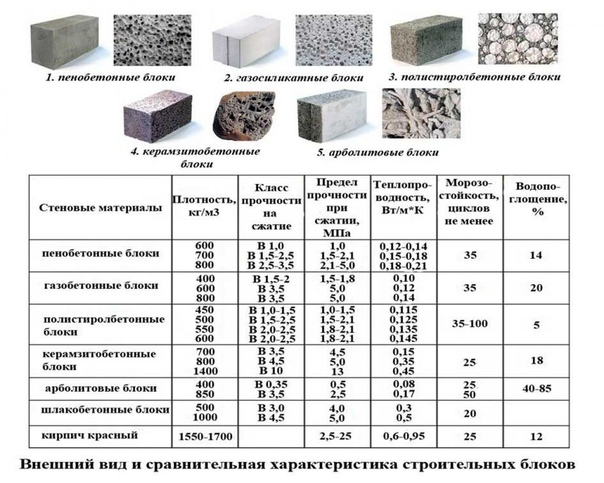 316646408860559, 0.633181081307499, 1.265} Hc, всего=C22πHc=CπHc. (8) Поскольку поверхности контакта между частицами наклонены против вертикального направления (чистого теплового потока), количество теплопроводности через контакт в направлении чистого теплового потока должно быть скорректировано в сторону уменьшения. Предполагая случайные углы наклона контактных поверхностей, средний поправочный коэффициент определяется как (∫−π/2π/2cosθdθ)/(∫−π/2π/2dθ)=2/π, где θ — угол между перпендикулярной линией поверхности контакта и чистого направления теплового потока (РИС.9). Следовательно, в уравнении появляется множитель 2/π. (8). N _A и N _L в уравнении. (6) можно выразить через радиус частицы R _p и объемную пористость ϕ. Число сфер в единице объема, N , может быть записано как: Для трехмерного случайного условия простые выражения N _L и N _A будут равны N ^{1 /3} и N ^2/3 соответственно.Однако высота горизонтальных слоев 1/ N _L должна быть меньше диаметра частиц, чтобы обеспечить контакт верхнего и нижнего слоев, если частицы оседают в гравитационном поле. Если мы возьмем N _L = N ^1/3 , 1/ N _L станет больше, чем 2 R _p, когда 7 ϕ>0. 4. Чтобы избежать этой проблемы, мы принимаем N _L в качестве константы, не зависящей от пористости для гранецентрированной кубической структуры как, Тогда влияние пористости на число частиц накладывается на N _A как NA=NNL=6(1−ϕ)2πRp2. (11) Когда пористость увеличивается, как N _A, так и C уменьшаются, и результирующая проводимость твердого тела уменьшается. Применимость этого выражения будет проверена путем сравнения его с экспериментальными данными в разделе . Контактная проводимость H _c может быть оценена путем аппроксимации двух контактирующих сфер как двух круговых цилиндров, соединенных с поперечным сечением π rc2, где r _c — радиус контактной площадки.Когда тепловой поток дан перпендикулярно поверхности контакта и если R _p достаточно больше, чем r _c , проводимость контакта H _c пропорциональна радиусу контакта, согласно H _c = 2 k _m r _c , где k _m – теплопроводность контактирующего материала. ²¹ 21. М. Г. Купер, Б. Б. Микич и М.Йованович М. Теплопроводность контакта // Межд. J. Heat Mass Transfer 12 , 279–300 (1969). https://doi.org/10.1016/0017-9310(69)_{-8 Применимость этой формулы к контакту сфер-сфер продемонстрировали Чан и Тиен. ⁶ 6. C.K.Chan и C.L.Tien, «Проводимость упакованных сфер в вакууме», J. Heat Transfer 95 , 302-308 (1973). https://doi.org/10.1115/1.3450056 Как следует из наших экспериментов (см. раздел и рис. 6), теплопроводность также зависит от микроскопической шероховатости поверхности частицы.При соприкосновении двух частиц с шероховатой поверхностью в области макроскопического контакта образуется множество микроскопических контактов. Это уменьшает реальную площадь поперечного сечения, через которое течет тепло, и, следовательно, теплопроводность на контактах становится меньше, чем у соответствующих частиц с идеально гладкой поверхностью. В этом исследовании влияние шероховатости поверхности на контактную теплопроводность просто добавляется к ξ в модели контактной теплопроводности, поскольку значение ξ меньше 1 для шероховатых частиц и равно 1, когда частица поверхность идеально гладкая.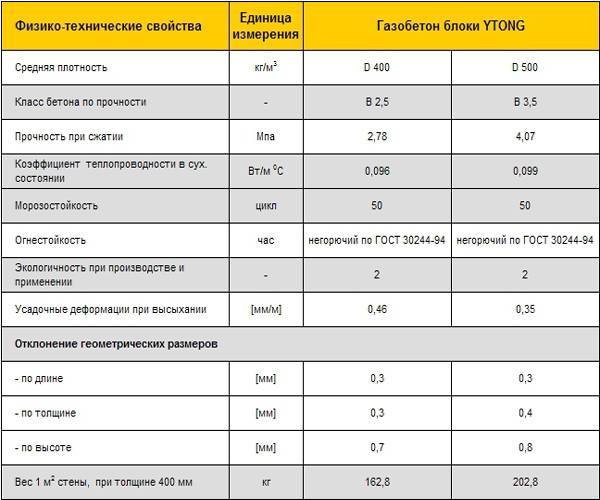 Обратите внимание, что r _c в приведенном выше уравнении — радиус контакта идеальных сфер без шероховатости поверхности. Параметр ξ имеет значение, аналогичное отношению реальной площади контакта к кажущейся, используемой при изучении трения и теплопроводности между твердыми материалами. ^22–24 22. Б. Н. Дж. Перссон, Трение скольжения — физические принципы и приложения , 2-е изд. (Спрингер, Нью-Йорк, 2000 г.).23. Дж. Дитрих и Б. Д. Килгор, «Отображение контактов на поверхности: распределение контактов по степенному закону и контактные напряжения в кварце, кальците, стекле и акриловом пластике», Tectonophysics 256 , 219–239 (1996).https://doi.org/10.1016/0040-1951(95)00165-424. CV Madhusudana, Тепловая контактная проводимость , 2-е изд. (Springer, New York, 2014). Координационное число C зависит от пористости. Здесь мы используем модель Судзуки и др., ²⁵ 25. Судзуки М., Макино К., Ямада М., Иноя К. Исследование координационного числа в случайно упакованной системе одноразмерных сферических частиц (в японский)», Kagaku Kogaku Ronbunshu 6 , 59–64 (1980). https://doi.org/10.1252/kakoronbunshu.6.59, который предсказывает, что C уменьшается с пористостью ϕ as, ²⁶ 26. H. Masuda, K. Higashitani, and H. Yoshida, Справочник по технологии порошков , 3rd ed. (CRC Press, Лондон, 2006 г.). C=2,812(1−ϕ)−1/3f2(1+f2), (13) , где сфере, H _s , мы аппроксимируем сферу кубом с объемом, эквивалентным объему сферы.В этом случае для неконсолидированных частиц вклад H _s в проводимость H пренебрежимо мал по сравнению с H _c,total , поскольку Hc,total ≪Hs. Радиус контакта между двумя сферами, r _c в уравнении. (12) моделируется следующим образом. Когда два шара приходят в соприкосновение внешней нормальной силой F , радиус контактной площадки соответствует теории Герца, ²⁷ 27. С.П. Тимошенко и Ю.Н.Goodier, Theory of Elasticity (McGraw-Hill Book Company, Inc. , Нью-Йорк, 1951). где радиус контакта r _c записывается как — модуль Юнга. Помимо внешней силы F между частицами может действовать сила сцепления, которая также создает конечную площадь контакта. Джонсон и др. ²⁸ 28.Джонсон К.Л., Кендалл К., Робертс А.Д. Поверхностная энергия и контакт упругих твердых тел // Proc. Р. Соц. Лонд. А. Мет. физ. науч. 324 , 301–313 (1971). https://doi.org/10.1098/rspa.1971.0141 расширил теорию Герца, включив эффект силы сцепления как Rp]1/3, (16) где γ — поверхностная энергия твердого материала. Эта модель называется теорией JKR (Джонсона, Кендалла и Робертса).Когда γ=0, уравнение (16) становится эквивалентным теории Герца, представленной уравнением. (15). Внешняя сила F , действующая на частицу, рассчитывается через напряжение сжатия σ как F=σNA=2πRp26(1−ϕ)σ. (17) Коэффициент 1/ N _A соответствует средней площади поперечного сечения частицы, включая окружающее пустотное пространство. Когда сжимающее напряжение σ в порошкообразных средах вызвано собственным весом частиц, оно может быть представлено гидростатическим давлением как где ρm — истинная плотность твердой частицы, г — ускорение свободного падения, z – глубина захоронения материалов под поверхностью.Таким образом, пренебрегая H _s в уравнении. (7), наш расчет для твердой проводимости: (13) и r _c по уравнению. (16). Это уравнение означает, что проводимость твердого тела пропорциональна отношению радиуса контакта r _c к радиусу частицы R _p . Когда поверхностная энергия равна нулю, радиус контакта пропорционален радиусу частицы (см.15 и 17), поэтому проводимость твердого тела не зависит от размера частиц. Напротив, проводимость твердого тела уменьшается с увеличением размера частиц, когда γ>0, потому что сила сцепления оказывает большее влияние на более мелкие частицы. B. Модель радиационной проводимости Радиационная теплопередача через пустоты в порошкообразных средах моделируется одномерным тепловым излучением между множеством бесконечно тонких параллельных плоскостей, как показано на фиг. 10. Как и в модели твердотельной проводимости, радиационная проводимость эквивалентна полной теплопроводности этой многослойной среды в пределах единичного куба.Предполагается, что две соседние плоскости имеют разность температур ΔT и плоскости или частицы непрозрачны для теплового излучения. Теплопроводность между двумя плоскостями по тепловому излучению, H _r , может быть рассчитана как, где ε — коэффициент излучения, σSB (= 5,67×10−8 Вт · м ⁻² K ⁻⁴ ) — постоянная Стефана-Больцмана, а T — температура более холодной плоскости.Поскольку L _r — это расстояние между двумя соседними плоскостями, количество слоев на единицу длины равно 1/ L _r . Тогда радиационная проводимость многослойных сред может быть выражена как 1/ L _r последовательных соединений лучистой проводимости H _r as, крад=LrHr=4ε2−εσSBLrT3. (21) где L _r представляет собой эффективное расстояние для теплопередачи излучением.Это можно масштабировать по характерной длине пустот в порошкообразных средах. В однородно упакованных сферах одинакового размера объем пустот на частицу рассчитывается по радиусу частицы R _p и пористости ϕ as, V=ϕN=43πRp3ϕ1−ϕ, (22) , где N — количество сфер в единице объема, определяемое уравнением (9). Аппроксимируя этот типичный объем пустот как объем сферы диаметром D _v, геометрическая длина пустоты может быть сформулирована на основе Пике и Кристенсена, ¹⁷ 17.S. Piqueux и P.R. Christensen, «Модель теплопроводности планетарных почв: 1. теория рыхлых почв», J. Geophys. Рез. 114 (2009). https://doi.org/10.1029/2008JE003308 Мы вводим коэффициент ζ для масштабирования средней геометрической длины пустоты D _v к эффективному расстоянию для теплопередачи излучением L _r . Lr=ζDv=2ζ(ϕ1−ϕ)1/3Rp. (24) Повышение радиационной проводимости, вызванное агрегацией, как следует из наших экспериментов с использованием стеклянных шариков EMB, представлено значением ζ больше единицы.Подставляя уравнение (24) в уравнение. (21) радиационная проводимость может быть получена из крад=8ε2−εσSBζ(ϕ1−ϕ)1/3RpT3. (25) C. Сравнение модели с экспериментальными данными Полученные выше модели твердотельной и радиационной проводимости можно непосредственно сравнить с экспериментальными данными, представленными в разделе . Физические параметры образцов ФГБ и ЭМБ, использованных для модельных расчетов, приведены в табл. IV. К сожалению, поверхностная энергия используемых нами стеклянных шариков неизвестна.Наши экспериментальные результаты показали, что стеклянные шарики EMB обладают высокой адгезией, а стеклянные шарики FGB — нет (см. Раздел ). Поэтому поверхностная энергия 0,02 Дж·м ⁻² принята для стеклянных шариков EMB в качестве типичного значения для SiO ₂ (ссылка 1313. B. Gundlach and J. Blum, система — II: перенос тепла в сухих, пористых поверхностных слоях пыли», Icarus 219 , 618–629 (2012). https://doi.org/10.1016/j.icarus.2012.03.013 и ссылки в нем), и поверхностная энергия стеклянных шариков FGB была установлена на ноль, так что радиус контакта был представлен законом Герца (уравнение).(15). Для обоих типов стеклянных шариков использовали модуль Юнга 55,1 ГПа и коэффициент Пуассона 0,22. ⁶ 6. C.K.Chan и C.L.Tien, «Проводимость упакованных сфер в вакууме», J. Heat Transfer 95 , 302-308 (1973). https://doi.org/10.1115/1.3450056 Коэффициент излучения 0,9 был измерен устройством измерения коэффициента излучения (A&D AERD, Kyoto Electronics Manufacturing Co. Ltd., Токио, Япония). ТАБЛИЦА IV. Параметры модели для стеклянных шариков ФГБ и ЭМБ. 9151 EMB диаметр частиц 2 R _P Переменная (53-1000 мкм) 5 мкм Пористость ϕ 0. 40 Переменная (0.495-0.862) ρm ρm 2480 кг м ^-3 2600 кг м ^-3 глубина Z 1 см 1 см Материал проводимости K _{M 0} 0.855 W M ^-1 K ^-1 1.406 W M ^-1 K ^-1 д к _м/д Т 8.50 × 10 ^-4 W M ^-1 K ^-1 K ^-1 K ^-1 K ^-2 5. 10 × 10 ^-4 W M ^-1 K ^-2 K ^-2 K ^-2 γ 0.0 J M ^-2 ^-2 0,02 J ^-2 Young Modulus 55.1 GPA 55.1 GPA 55.1 GPA ν 0.22 0.22 0.22 Коэффициент излучения ε 0.9 0,9 РИС. 11(a) показаны модельные оценки проводимости твердого тела при 300 K с использованием параметров стеклянных шариков FGB, где ξ установлено на 1,0, 0,5 и 0,2. Для сравнения также показана средняя проводимость четырех измерений, полученных с использованием контейнеров с одним и тремя датчиками, где вертикальные планки погрешностей представляют собой максимальное и минимальное значения четырех измерений (такие же, как заштрихованный диапазон на фиг. 5). Как обсуждалось в разделе , проводимость твердого тела не зависит от размера частиц, если сила сцепления не принимается во внимание.Оно оценивается в 0,00341 Вт·м ⁻¹ K ⁻¹, если ξ = 1,0, что означает сферы с гладкой поверхностью. Эта оценка по модели выше, чем любое измерение стеклянных шариков ФГБ. Разумное объяснение этой более высокой проводимости твердого тела, полученной с помощью модели, состоит в том, что поверхность стеклянных шариков ФГБ была шероховатой и не чистой, поэтому значение ξ было меньше единицы. Предпочтительные значения ξ для стеклянных шариков FGB находятся в диапазоне от 0,29 до 0.83 (см. Таблицу V). ТАБЛИЦА V. Сводка значений ξ и ζ, применимых к нашим образцам стеклянных шариков. Отметим, что для стеклянных шариков ФГБ было принято γ=0 Дж·м ^–2·, а для стеклянных шариков ЭМБ γ=0,02 Дж·м ^–2. Образец ξ ζ ФГБ-20 0,34 — 0,83 0.7 — 1.2 ФГБ-40 0,30 — 0,65 1,1 — 1.9 FGB-80 0.36 — 0.46 1.2 — 1.7 FGB-180 0,36 — 0,44 1,8 — 2. 6 FGB-300 0,29 — 0.33 2.5 — 4,0 EMB ~1 ~15 На фиг. 12(а) электропроводность твердого тела, рассчитанная с использованием параметров стеклянных шариков EMB, показана как функция пористости наряду с экспериментальными данными.Модель с ξ = 1,0 согласуется с экспериментальными данными. Например, при пористости 0,862 предсказана твердотельная проводимость 0,00062 Вт·м ^-1 К ^-1, что согласуется с экспериментальными данными. Поскольку стеклянные шарики ЭМП имели гладкую поверхность, соответствие между значениями, предсказанными моделью с ξ = 1,0, и экспериментальными данными является разумным и свидетельствует о применимости нашей твердотельной модели проводимости в этом случае. Кроме того, зависимость проводимости твердого тела от пористости зависела от N _L и N _A . Мы предварительно установили N _L равным значению гранецентрированной кубической решетки, независимой от пористости, и влияние пористости было принудительно установлено на N _A (уравнения 10 и 11). Согласованность между моделью и экспериментальными данными, показанная на фиг. 12(а) подразумевает, что это допущение применимо на практике. На фиг. 11(b) показана радиационная проводимость, предсказанная нашей моделью при температуре 300 K для стеклянных шариков FGB, наряду с экспериментальными данными. Наша модель предсказывает, что радиационная проводимость изменяется линейно с размером частиц.При ζ = 1,0 расчетная радиационная проводимость при 300 К составляет 0,00429 Вт м ^-1 К ^-1 при диаметре частиц 1000 мкм м, что согласуется с экспериментальным результатом для самых крупных стеклянных шариков. Меньшие по размеру стеклянные шарики имели относительно более высокую радиационную проводимость, чем оцененная моделью.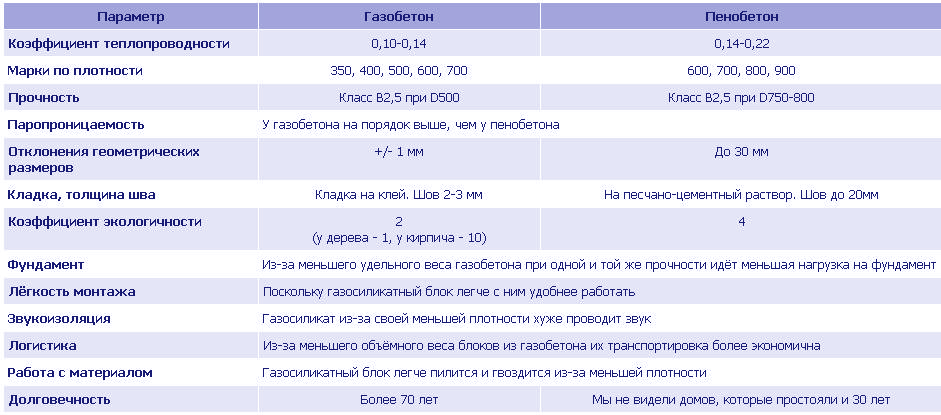 Другими словами, значение ζ , которое является мерой отклонения длины свободного пробега фотонов от типичного размера пустоты, увеличивается с уменьшением размера частиц.Одно из возможных объяснений этой тенденции состоит в том, что более мелкие частицы не были непрозрачны для теплового излучения. При температурах около 300 К тепловое излучение черного тела имеет спектральный пик на длинах волн около λmax ≈ 10 μ м. Когда λmax≪Dp, частицы можно аппроксимировать непрозрачными для теплового излучения. Этого не происходит, когда λmax≈Dp, при котором рассеяние вперед является обычным согласно теории рассеяния Ми. ²⁹ 29. М. Ф. Модест, Радиационная теплопередача , 3-е изд.(Академическая пресса, Нью-Йорк, 2013). Следовательно, более эффективное прямое рассеяние теплового излучения более мелкими частицами может способствовать увеличению расстояния лучистой теплопередачи по сравнению с типичным размером пустот. Влияние пористости на радиационную проводимость рассмотрено на фиг. 12(b) с использованием параметров стеклянных шариков EMB. На графике представлены экспериментальные данные для стеклянных шариков EMB, за исключением данных для EMB-49.5 и EMB-58.5, которые имели большую неопределенность в их радиационной проводимости (см. раздел ).Лучевая проводимость стеклянных шариков ЭМЗ с ζ=1 оказалась на порядок выше расчетной по модели. Как показано на фиг. 8, стеклянные шарики ЭМБ образовывали агрегаты крупнее размера зерен благодаря подготовке образцов с использованием сит. ЭМБ-86.2, ЭМБ-77.9 и ЭМБ-69.5 имели агрегаты размером около 50 мк м, а ЭМБ-75.3 имели агрегаты размером 500 мк м и менее. Эти образцы имели большие пустоты между агрегатами, а не между отдельными частицами.Через эти большие пустоты лучистое тепло может передаваться более эффективно. ¹³ 13. Б. Гундлах и Дж. Блюм, «Выделение газа из ледяных тел в Солнечной системе — II: перенос тепла в сухих, пористых поверхностных слоях пыли», Icarus 219 , 618–629 (2012).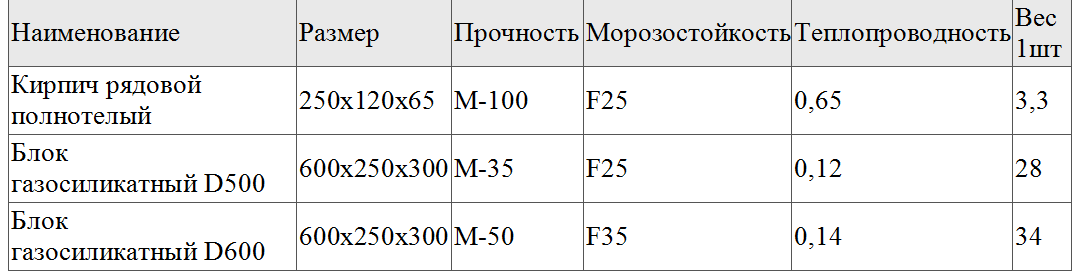 https://doi.org/10.1016/j.icarus.2012.03.013 Принимая постоянное значение ζ = 15, модель может быть хорошо приспособлена к экспериментальным данным для стеклянных шариков EMB. Поскольку образцы, просеянные с сеткой 53 90 108 μ 90 109 мкм, имели агрегаты примерно в 10 раз больше по размеру, чем отдельные частицы, это подогнанное значение 90 108 ζ 90 109 является разумным.Кроме того, зависимость проводимости твердого тела от напряжения сжатия была проверена путем сравнения значений, предсказанных моделью, с нашими ранее опубликованными экспериментальными данными. ¹⁵ 15. Н. Сакатани, К. Огава, Ю. Иидзима, М. Аракава и С. Танака, «Влияние напряжения сжатия на теплопроводность порошкообразных материалов: измерения и их влияние на лунный реголит», Icarus 267 , 1–11 (2016). https://doi.org/10.1016/j.icarus.2015.12.012 Мы измерили теплопроводность стеклянных шариков ФГБ-20 и ФГБ-180 в зависимости от напряжения сжатия.ИНЖИР. 13 показана модель твердотельной проводимости для стеклянных шариков FGB в терминах внешнего напряжения сжатия σ . Подобно результатам этого исследования, показанным на фиг. 11(а), модель с ξ=1 предсказывает более высокую проводимость твердого тела, чем по экспериментальным данным. Наиболее подходящие значения ξ составляют 0,69 и 0,42 для ФГБ-20 и ФГБ-180 соответственно. Они согласуются со значениями 90×108×90×109 для каждого образца, определенными по результатам, показанным на фиг. 11(а), где образцы не подвергались внешнему сжатию.В таблице V приведены значения ξ и ζ для исследованных стеклянных шариков. ξ колеблется от 0,29 до 1, а ζ — от 0,7 до 15. Для более точного применения модели следует тщательно подбирать значения ξ и ζ в зависимости от природы частиц и условий упаковки. . Хотя ξ и ζ рассматриваются как подгоночные параметры в данных обстоятельствах, мы считаем, что можно рассчитать эти параметры с точки зрения шероховатости частиц, радиационного рассеяния и агрегации.Это выходит за рамки данной статьи, но должно быть рассмотрено в будущих исследованиях.}

			EMB
диаметр частиц	2 R _P	Переменная (53-1000 мкм)	5 мкм
Пористость	ϕ	0. 40	Переменная (0.495-0.862)
ρm	ρm	2480 кг м ^-3	2600 кг м ^-3
глубина		Z	1 см	1 см
Материал проводимости	K _{M 0}	0.855 W M ^-1 K ^-1	1.406 W M ^-1 K ^-1
	д к _м/д Т	8.50 × 10 ^-4 W M ^-1 K ^-1 K ^-1 K ^-1 K ^-2	5. 10 × 10 ^-4 W M ^-1 K ^-2 K ^-2 K ^-2		γ	0.0 J M ^-2 ^-2	0,02 J ^-2
Young Modulus		55.1 GPA	55.1 GPA	55.1 GPA
			ν	0.22	0.22	0.22
Коэффициент излучения	ε	0.9	0,9

Образец	ξ	ζ
ФГБ-20	0,34 — 0,83	0.7 — 1.2
ФГБ-40	0,30 — 0,65	1,1 — 1.9
FGB-80	0.36 — 0.46	1.2 — 1.7
FGB-180	0,36 — 0,44		1,8 — 2. 6
FGB-300	0,29 — 0.33	2.5 — 4,0
EMB	~1	~15