Газоблок характеристики теплопроводность: Сравнительная характеристика теплопроводности газобетона. Выбор толщины блока.
Сравнительная характеристика теплопроводности газобетона. Выбор толщины блока.
Технические характеристики газобетонных блоков
Отопительный сезон зачастую сопряжён с потерей тепла, которое крадут «холодные» стены не из газобетона UDK :-). А потому целесообразно строить или утеплять частный коттедж с использованием пористого материала. Газобетон различают по его плотности, которая измеряется в кг/м3. В зависимости от марки блока, его используют в различных целях: теплоизоляционных — в роли утеплителя, для постройки не высоких зданий, для строительства несущих конструкций высотных зданий.
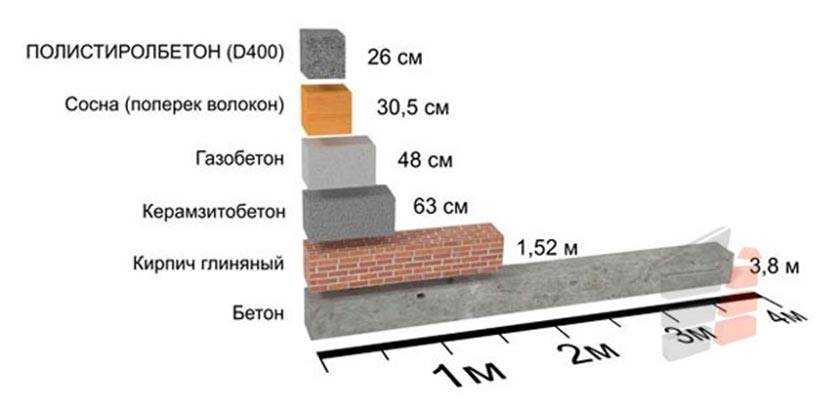
Маркировка D400 обозначает, что в 1м3 пористого материала находится 400 кг. твёрдых частиц, занимающих 1/3 всей массы блока. Воздушные массы в ячейках являются естественной теплоизоляцией, не позволяющей внутреннему теплу из помещения проникать сквозь них. А потому, чем менее плотный монолит, тем лучше он сохранит тепло. В отличие от других стройматериалов, газобетонные блоки обладают более низкими показаниями теплопроводности. В этом можно убедиться взглянув на данную сравнительную таблицу и наглядные графики.
В этом можно убедиться взглянув на данную сравнительную таблицу и наглядные графики.
| с Материал | Теплопроводность, Вт/м °C | |
| Показатели плотности, кг/м3 | ||
| D400 | D500 | |
| Газобетон при уровне влажности 0% | 0,096 | 0,112 |
| 5% | 0,117 | 0,147 |
| Пенобетон при уровне влажности 0% | 0,102 | 0,131 |
| 5% | 0,131 | 0,161 |
| Древесина, при уровне влажности 0% | 0,116 | 0,146 |
| 5% | 0,181 | 0,187 |
Структура пеноблоков похожа на газобетон, но при этом в пеноблоках замкнутые ячейки и высокие показатели плотности. Геометрия пеноблоков не точна и не совершенна, а потому в роли теплоизоляционного материала намного выгоднее использовать именно газобетон.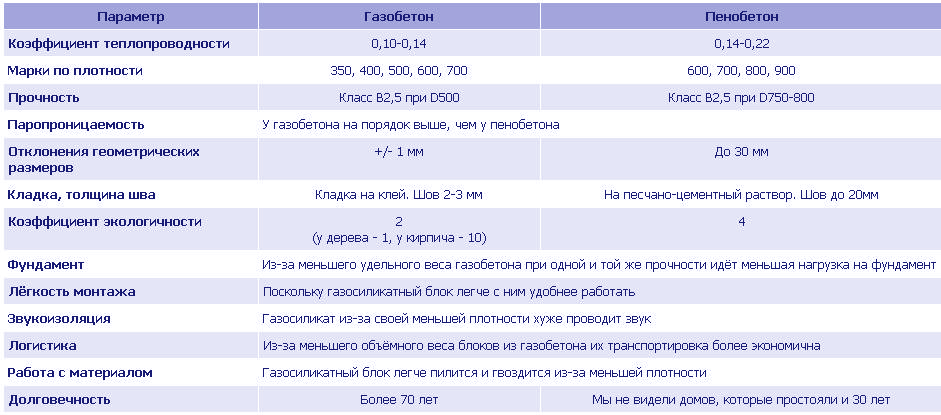
Древесина, хоть и является экологически чистым материалом, но когда речь заходит о её качественных теплоизоляционных свойствах, то она значительно проигрывает газобетону, так как не способна в должной мере сохранить тепло.
Однако отметим, что ячеистый блок – дышащий, огнеупорный материал, который отлично справляется со всеми поставленными перед ним задачами. Используя его в строительстве, важно сделать ограждение фундамента и цоколя здания от влаги. Потому как пористая структура может её тянуть в себя. С этой целью применяется рубероид и битум.
Характеристики теплопроводности кирпича и газобетонных блоков
Кирпич — классический вариант стройматериала, используемый для строительства дачных домиков и частных коттеджей. Он морозоустойчив, долговечен и обладает высокой плотностью. Но в отличие от газобетонных блоков, кирпичная стена возводится многослойной. Для того, чтобы дополнительно проложить утепляющие материалы между наружными и внутренними кладками.
| Материал | Показатели средней теплопроводности, Вт/м ° C |
| Газоблок | 0,08-0,14 |
| Керамические кирпичи | 0,36-0,42 |
| Красные глиняные кирпичи | 0,57 |
| Силикатные кирпичи | 0,71 |
Выбор толщины блока
Толщина стен влияет на их теплоизоляционные свойства. Чем они толще, тем дольше будет сохранятся комфортная атмосфера внутри жилища.В процессе проектирования ширины ограждений, необходимо учитывать «мостики холода» (толщина цемента для укладки). Блоки монтируют при помощи пазового замка и клеевого раствора. Данный способ гарантирует сохранность тепла, сводя его потери до минимальных значений. Чтобы не платить больше, важно знать некоторые показатели, которыми обладают сборные конструкции стандартной толщины.
Чем они толще, тем дольше будет сохранятся комфортная атмосфера внутри жилища.В процессе проектирования ширины ограждений, необходимо учитывать «мостики холода» (толщина цемента для укладки). Блоки монтируют при помощи пазового замка и клеевого раствора. Данный способ гарантирует сохранность тепла, сводя его потери до минимальных значений. Чтобы не платить больше, важно знать некоторые показатели, которыми обладают сборные конструкции стандартной толщины.
| Материал | Показатели толщины наружных стен, см | ||||
| 12 см | 20 см | 24 см | 30 см | 40 см | |
| Показатели теплопроводности, Вт/м ° C | |||||
| Белые кирпичи | 7,51 | 4,52 | 3,75 | 3,12 | 2,25 |
| Красные кирпичи | 6,75 | 4,05 | 3,37 | 2,71 | 2,02 |
| Газобетонный блок D400 | 0,82 | 0,51 | 0,41 | 0,32 | 0,25 |
Наилучшими качественными характеристиками на сегодняшний день обладают газобетон ЮДК которые производятся в городе Днепр (Украина). Шесть лет назад (в 2012 г.) завод UDK создал газобетон D400 с показателем прочности — 35 кг/см2. Данные свойства стройматериала позволили значительно сократить глубину наружных стен, что в свою очередь повлияло на себестоимость стройки.
Шесть лет назад (в 2012 г.) завод UDK создал газобетон D400 с показателем прочности — 35 кг/см2. Данные свойства стройматериала позволили значительно сократить глубину наружных стен, что в свою очередь повлияло на себестоимость стройки.
За счёт того, что геометрия блоков ЮДК чёткая и точная, их можно класть на ультратонкий слой клея UDK TBM, благодаря чему в итоге не образуется «мостиков холода». К тому же, за счёт низкого коэффициента теплопотери, наружным стенам не потребуется дополнительное утепление. А высокий уровень прочности газобетона позволяет возводить здания до 5 этажей. При этом не используя монолитный каркас. Срок службы газоблока ЮДК около 100 лет.
Выбор толщины стены из газобетонных блоков ЮДК
| Стена | Размер блока |
| Наружная стена: | D400, D500; В2,5-В2,0; 25-35 кг/см2; 400-500 мм. |
| Несущая | |
| Не несущая | |
| Жилой дом до 4 этажей, где проживают круглый год | |
| Перегородка: | D400, D500; В2,5-В2,0; 25-35 кг/см2; 200-500 мм.  |
| Несущая при условии устройства монолитного пояса | |
| Перегородка: | D500; В2,5; |
| Не несущая |
Выбор толщины стен необходимо делать с учётом вида постройки. Для постройки жилого дома у застройщиков пользуется популярностью толщина стены в один слой — 300-400 мм (иногда 500 мм). Ведь однослойные стены – всегда на порядок дешевле, нежели «сэндвичи». Классический стандартный газоблок имеет такие параметры: плотность — D300, D400; прочность В2,0,В2,5. Такой блок подходит для строительства одно- и двухэтажных зданий.
Для загородного дачного домика, куда хозяин наведывается лишь в тёплое время года, а зимой не требуется поддержание в помещении тепла, блока глубиной в 200 мм более чем достаточно. Такие стены прогреются очень быстро, а значит потребуется меньше энергоресурсов.
Для хозяйственных построек, а также гаража, толщину стен необходимо выбирать с учётом частоты нахождения в них.
Определится с толщиной стены из газобетонных блоков, инвестор может исходя из нескольких нюансов. Во-первых, это стоимость газобетона. А она очень выгодная с учётом всех требований. Во-вторых, это типовой проект. Обычно в него закладывают средний показатель толщины стены с указанием температурной зоны и требования к коэффициенту сопротивления теплопередачи, как указано на рисунке ниже.
Для южной части Украины стена может быть более тонкой, нежели в северном регионе страны. Чем тоньше стена – тем большая жилая площадь выйдет в итоге. Естественно, толстые стены крадут жилые метры. Но, при злоупотреблении правилами грамотной стройки, можно существенно потерять на отоплении в зимний период и охлаждении в летний сезон. Ведь сквозь «холодные» стены тепло будет утекать с большой скоростью, а летом наоборот станет невыносимо жарко. К тому же, суммы за отопление и охлаждение помещения дополнительными средствами, увеличатся в разы.
Решение строить здание с толстыми стенами, это опять же не выгодно, ведь необходимо будет потратиться на дополнительный фундамент. Альтернативный и разумный выбор – стены из газобетона. Удовлетворяющие как потребителя, так и застройщика тем, что не дорого стоят и надёжно сохраняют тепло, при этом не мешая помещению «дышать».
На сегодняшний день газобетон ЮДК является оптимальным выбором стройматериала. Долговечный (70-100 лет), надёжный, обладающий низкой теплопроводностью и безупречной геометрией блоков – он находится на пике своей популярности. Благодаря его не высокому объёмному весу идёт меньшая нагрузка на фундамент. Лучше ложатся отделочные материалы и не требуется больших трудозатрат. А разнообразный выбор газобетонных блоков, отличающихся по толщине, прочности и назначению — способен удовлетворить требования большинства застройщиков.
Теплопроводность газобетона и газобетонных блоков
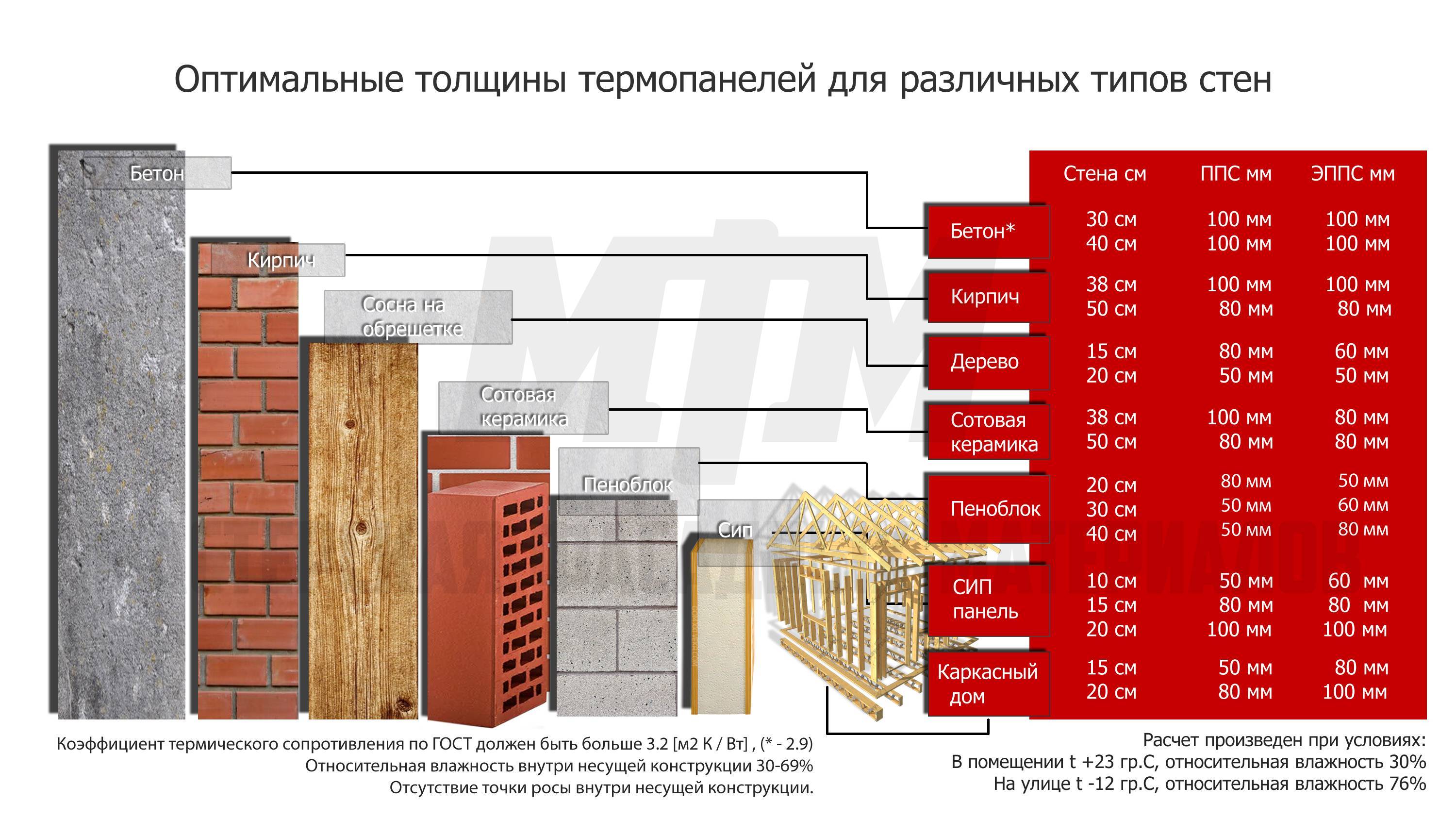 Современный рынок предлагает ряд альтернативных материалов, среди которых ячеистые бетоны, обладающие большим количеством преимуществ. Одним из важных плюсов газобетона является теплопроводность, которая подразумевает способность материала сохранять тепло внутри помещения.
Современный рынок предлагает ряд альтернативных материалов, среди которых ячеистые бетоны, обладающие большим количеством преимуществ. Одним из важных плюсов газобетона является теплопроводность, которая подразумевает способность материала сохранять тепло внутри помещения.
Способность строительного материала к удержанию тепла зависит от многих факторов, среди которых плотность, характеристика взаимодействия с влагой, расположенность к теплоусвоению и паропроходимость.
Теплопроводность газобетона обусловлена его структурой. Любой ячеистый бетон на 85% состоит из пузырьков воздуха, который создает своеобразную прослойку при взведении стен здания и оказывается отличным утеплителем. В сравнении с пенобетоном газоблок оказывается более подвержен воздействию влаги, что сказывается на его теплопроводности. Поэтому при проведении строительных работ необходимо осуществить гидроизоляцию используемых изделий и будущей постройки.
От чего зависит теплопроводность газобетонных блоков?
На теплопроводность газобетона влияет влажность воздуха. В сухом климате его показатели будут более располагающими, но в иных условиях способность ячеистых бетонов к пропусканию тепла практически схожи с теми, которые демонстрирует кирпич. Каждый регион имеет индивидуальные климатические и погодные особенности, которые предполагают использование тех или иных материалов. В случае с областями, где наблюдается высокая влажность воздуха, прибегают к эксплуатации изделий с большей толщиной, а любое строительство требует проведения предварительных расчетов для того, чтобы полученная в финале теплопроводность газобетона не сказалась на пригодности дома к эксплуатации и комфорте проживания в нем.
В сухом климате его показатели будут более располагающими, но в иных условиях способность ячеистых бетонов к пропусканию тепла практически схожи с теми, которые демонстрирует кирпич. Каждый регион имеет индивидуальные климатические и погодные особенности, которые предполагают использование тех или иных материалов. В случае с областями, где наблюдается высокая влажность воздуха, прибегают к эксплуатации изделий с большей толщиной, а любое строительство требует проведения предварительных расчетов для того, чтобы полученная в финале теплопроводность газобетона не сказалась на пригодности дома к эксплуатации и комфорте проживания в нем.
Осуществление расчетов предполагает учет толщины газоблоков, возможность их эффективного утепления и обустройство потенциальной системы отопления.
Теплопроводность газобетона, используемого при возведении стен, может зависеть от качества клеевого раствора, так как места смыкания блоков являются возможными причинами проникания холода. Также сказывается и наличие армопоясов. Использование обычного бетона приведет к тому, что дом будет сильно промерзать, поэтому строители используют железобетонные армированные пояса для увеличения теплопроводности газобетонных блоков. Необходимость использования этих деталей сказывается на финансовых затратах на строительство.
Также сказывается и наличие армопоясов. Использование обычного бетона приведет к тому, что дом будет сильно промерзать, поэтому строители используют железобетонные армированные пояса для увеличения теплопроводности газобетонных блоков. Необходимость использования этих деталей сказывается на финансовых затратах на строительство.
Зависимость теплопроводности от плотности
Коэффициент теплопроводности газобетона напрямую зависит от плотности материала. Чем плотнее его структура, тем выше способность к удержанию тепла. При этом наблюдается специфичная зависимость теплоизоляции от прочности материала: чем менее прочен газобетон, тем лучше он удерживает тепло. Выбирая марку материала, стоит ориентироваться и на эту особенность, и при строительстве дома выбирать газобетон марки D500- D600.
Преимущества теплопроводности газобетона
Низкий коэффициент теплопроводности материала позволяет серьезно сэкономить на системе отопления и электроэнергии, затрачиваемой на поддержание комфортной температуре в помещении.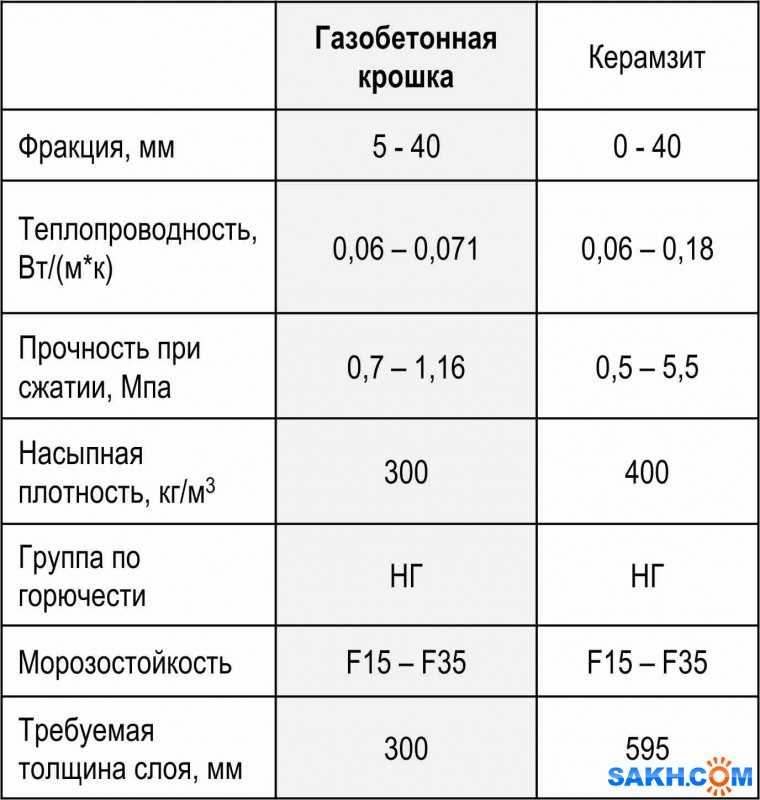 Стены дома из газобетона помогают поддерживать приятный микроклимат, сохраняя тепло зимой, а жарким летом создавая приятную прохладу благодаря тому, что они не пропускают тепло извне.
Стены дома из газобетона помогают поддерживать приятный микроклимат, сохраняя тепло зимой, а жарким летом создавая приятную прохладу благодаря тому, что они не пропускают тепло извне.
Экономичность в использовании газобетона заключается еще в том, что нет необходимости в затратах на дополнительную теплоизоляцию. В случае необходимости повышения теплоизоляции можно облицевать фасады здания кирпичом, сделав более привлекательным его внешний вид и увеличив его способность к сохранению тепла.
Купить газобетонные блоки высокого качества и по выгодным ценам можно на сайте компании «УниверсалСнаб».
Теплопроводность упорядоченных пористых структур, взаимодействующих с газовой и твердой фазами: исследование молекулярной динамики
- Список журналов
- Материалы (Базель)
- PMC8123498
Материалы (Базель). 2021 май; 14(9): 2221.
2021 май; 14(9): 2221.
Опубликовано в сети 26 апреля 2021 г. doi: 10.3390/ma14092221
Доминик Бейлис, академический редактор
Информация об авторе Примечания к статье Информация об авторских правах и лицензии Отказ от ответственности
- Заявление о доступности данных важный процесс для многих промышленных применений. Оптимизация конструкции теплоизоляционного материала очень важна во многих областях, таких как изоляция труб, тепловая защита космических кораблей и изоляция зданий. Понимание микромеханизма эффекта взаимодействия твердого тела с газом необходимо для разработки изоляционного материала. Прогнозирование теплопроводности для некоторых видов пористых материалов затруднено из-за взаимодействия твердого тела и газа. В этом исследовании метод Grand Canonical Monte Carlo (GCMC) и моделирование молекулярной динамики (MD) используются для исследования теплопроводности упорядоченных пористых структур пересекающихся квадратных стержней.
 Выявлено влияние концентрации газа (давления) и взаимодействия твердого тела с газом на теплопроводность. Результаты моделирования показывают, что для различных структур каркаса влияние давления на теплопроводность представляет собой непоследовательный режим, который отличается от предыдущих исследований. При одном и том же давлении теплопроводность практически не меняется при различных взаимодействиях газовой и твердой фаз. Это исследование обеспечивает возможность прямого расчета теплопроводности для пористых структур, связывающих газовую и твердую фазы, с использованием моделирования молекулярной динамики. Теплопередачу в пористых структурах, содержащих газ, можно понять на фундаментальном уровне.
Выявлено влияние концентрации газа (давления) и взаимодействия твердого тела с газом на теплопроводность. Результаты моделирования показывают, что для различных структур каркаса влияние давления на теплопроводность представляет собой непоследовательный режим, который отличается от предыдущих исследований. При одном и том же давлении теплопроводность практически не меняется при различных взаимодействиях газовой и твердой фаз. Это исследование обеспечивает возможность прямого расчета теплопроводности для пористых структур, связывающих газовую и твердую фазы, с использованием моделирования молекулярной динамики. Теплопередачу в пористых структурах, содержащих газ, можно понять на фундаментальном уровне.Ключевые слова: теплопроводность, пористые структуры, молекулярно-динамическое моделирование, метод Грина-Кубо
Пористые материалы широко используются во многих областях, таких как изоляция зданий, хранение и разделение газа, аэрокосмическая промышленность и т.
 д. Теплоперенос в пористых материалах, содержащих газовую фазу, является важным процессом, который невозможно полностью понять на фундаментальном уровне, особенно для нанопористых материалов. Точное предсказание теплопроводности нанопористых материалов крайне необходимо для применения.
д. Теплоперенос в пористых материалах, содержащих газовую фазу, является важным процессом, который невозможно полностью понять на фундаментальном уровне, особенно для нанопористых материалов. Точное предсказание теплопроводности нанопористых материалов крайне необходимо для применения.Большое количество теоретических моделей теплопроводности было разработано в предыдущих исследованиях [1, 2, 3, 4, 5, 6] с учетом влияния газа, твердого тела и излучения в непористом материале, в котором существуют некоторые отклонения по сравнению с с экспериментальным значением в некоторой степени. Из-за чрезвычайно сложных структур и эффекта взаимодействия твердого тела с газом в теоретической модели необходимо много эмпирических параметров, которые трудно определить. Численное моделирование является возможным выбором для непосредственного получения свойств нанопористых материалов. Решеточный метод Больцмана применялся для исследования фононного теплообмена в сферическом сегменте зерен аэрогеля нанокремнезема [7].
 Результаты моделирования показали, что распределение температуры в зерне кремнеземного аэрогеля сильно зависит от размера, а рассеяние фононов на граничных поверхностях становится более заметным при уменьшении размера зерен. Ли и др. В работе [8] разработана модифицированная модель для прогнозирования газовой теплопроводности в нанопористых материалах на основе метода прямого моделирования Монте-Карло (DSMC). Результаты показали, что модифицированная модель имеет более высокую точность без сложных расчетов и допущений. Влияние размера на теплопроводность газа изучалось методом ПСМ [9].]. На границе существует очевидный скачок температуры, и теплопроводность имеет тенденцию к уменьшению при увеличении числа Кнудсена от 0,01 до 0,1. Чжао и др. В работе [10] получена газовая теплопроводность азота с использованием трехмерного метода DSMC с переменной моделью столкновения мягких сфер. Результаты согласуются с экспериментальными данными, но намного выше, чем по соотношению Эйкена, особенно при высокой температуре.
Результаты моделирования показали, что распределение температуры в зерне кремнеземного аэрогеля сильно зависит от размера, а рассеяние фононов на граничных поверхностях становится более заметным при уменьшении размера зерен. Ли и др. В работе [8] разработана модифицированная модель для прогнозирования газовой теплопроводности в нанопористых материалах на основе метода прямого моделирования Монте-Карло (DSMC). Результаты показали, что модифицированная модель имеет более высокую точность без сложных расчетов и допущений. Влияние размера на теплопроводность газа изучалось методом ПСМ [9].]. На границе существует очевидный скачок температуры, и теплопроводность имеет тенденцию к уменьшению при увеличении числа Кнудсена от 0,01 до 0,1. Чжао и др. В работе [10] получена газовая теплопроводность азота с использованием трехмерного метода DSMC с переменной моделью столкновения мягких сфер. Результаты согласуются с экспериментальными данными, но намного выше, чем по соотношению Эйкена, особенно при высокой температуре. Нанопористые аэрогели были реконструированы с помощью усовершенствованного метода трехмерной кластерно-кластерной агрегации с ограничением диффузии (DLCA), в котором количественно определялся вклад теплопередачи твердого тела-газа в теплопроводность, обусловленную газом [11]. Для прогнозирования эффективной теплопроводности нанопористых аэрогелевых материалов был разработан модифицированный решеточный метод Больцмана [12], который ввел дополнительный коэффициент для регулирования разницы теплопроводности между твердой и газовой фазами и гарантировал конвергентное решение. Фанг и др. В работе [13] решеточный метод Больцмана использовался для решения уравнения проводимости-излучения для предсказания эффективной теплопроводности. Результаты моделирования показали, что эффективная теплопроводность чистого нанопористого аэрогеля быстро увеличивается с температурой и сильно снижается при легировании добавками. Теплопроводность нанопористой пленки и нанокомпозита численно исследовалась путем решения фононного уравнения переноса Больцмана с частотно-зависимой моделью [14].
Нанопористые аэрогели были реконструированы с помощью усовершенствованного метода трехмерной кластерно-кластерной агрегации с ограничением диффузии (DLCA), в котором количественно определялся вклад теплопередачи твердого тела-газа в теплопроводность, обусловленную газом [11]. Для прогнозирования эффективной теплопроводности нанопористых аэрогелевых материалов был разработан модифицированный решеточный метод Больцмана [12], который ввел дополнительный коэффициент для регулирования разницы теплопроводности между твердой и газовой фазами и гарантировал конвергентное решение. Фанг и др. В работе [13] решеточный метод Больцмана использовался для решения уравнения проводимости-излучения для предсказания эффективной теплопроводности. Результаты моделирования показали, что эффективная теплопроводность чистого нанопористого аэрогеля быстро увеличивается с температурой и сильно снижается при легировании добавками. Теплопроводность нанопористой пленки и нанокомпозита численно исследовалась путем решения фононного уравнения переноса Больцмана с частотно-зависимой моделью [14]. Был введен локальный угол между тепловыми потоками и локальным тепловым потоком, и все результаты показали, что наноструктурный материал с большим средним углом будет иметь меньшую теплопроводность. Танг и др. [15] исследовали теплопроводность тонкой пленки нанопористого кремния с использованием метода дискретных ординат (DOM). Учитывались эффекты толщины, пористости и пористой структуры. Численные результаты показали, что нанопоры способны резко снижать теплопроводность тонкой пленки кремния за счет граничного рассеяния фононов.
Был введен локальный угол между тепловыми потоками и локальным тепловым потоком, и все результаты показали, что наноструктурный материал с большим средним углом будет иметь меньшую теплопроводность. Танг и др. [15] исследовали теплопроводность тонкой пленки нанопористого кремния с использованием метода дискретных ординат (DOM). Учитывались эффекты толщины, пористости и пористой структуры. Численные результаты показали, что нанопоры способны резко снижать теплопроводность тонкой пленки кремния за счет граничного рассеяния фононов.Молекулярно-динамическое моделирование также является эффективным методом решения наноразмерных задач переноса тепла газами и твердыми телами. Кокил и др. [16] впервые применили моделирование неравновесной молекулярной динамики для предсказания теплопроводности аморфного нанопористого кремнезема. Результаты моделирования показали, что теплопроводность нанопористого кремнезема при комнатной температуре не зависит от размера пор и зависит только от пористости.
 Нг и др. В работе [17] исследована теплопроводность образцов нанопористого аэрогеля различной плотности путем разрыва плотных образцов кремнезема отрицательным давлением. Результаты показали, что степенная зависимость теплопроводности изменяется почти линейно с плотностью, при этом уменьшение плотности и увеличение пористости приведет к линейному уменьшению теплопроводности. Теплоперенос в цепочке вторичных частиц аэрогеля нанопористого кремнезема изучался с помощью молекулярно-динамического моделирования [18]. Перенос тепла подавлялся, когда длина контакта или концентрация дефектов увеличивались, а ограничивающий эффект был гораздо более очевидным, когда доля длины контакта находилась в небольшом диапазоне. Характеристики теплопередачи наноразмерного газа исследовались методом молекулярно-динамического моделирования [19].]. Рассмотрено влияние силового поля стенки, жесткости стенки и потенциальной напряженности взаимодействия стенка-газ на эффективную теплопроводность. Babaei и Wilmer [20] исследовали механизмы переноса тепла в системе пористый кристалл-газовая смесь с помощью молекулярно-динамического моделирования.
Нг и др. В работе [17] исследована теплопроводность образцов нанопористого аэрогеля различной плотности путем разрыва плотных образцов кремнезема отрицательным давлением. Результаты показали, что степенная зависимость теплопроводности изменяется почти линейно с плотностью, при этом уменьшение плотности и увеличение пористости приведет к линейному уменьшению теплопроводности. Теплоперенос в цепочке вторичных частиц аэрогеля нанопористого кремнезема изучался с помощью молекулярно-динамического моделирования [18]. Перенос тепла подавлялся, когда длина контакта или концентрация дефектов увеличивались, а ограничивающий эффект был гораздо более очевидным, когда доля длины контакта находилась в небольшом диапазоне. Характеристики теплопередачи наноразмерного газа исследовались методом молекулярно-динамического моделирования [19].]. Рассмотрено влияние силового поля стенки, жесткости стенки и потенциальной напряженности взаимодействия стенка-газ на эффективную теплопроводность. Babaei и Wilmer [20] исследовали механизмы переноса тепла в системе пористый кристалл-газовая смесь с помощью молекулярно-динамического моделирования. Исследование показало, что в теплопроводности системы преобладает кристалл, который снижается по мере увеличения концентрации газа в порах. Пониженная проводимость, связанная с увеличением концентрации газа, связана с рассеянием фононов кристаллом, вызванным взаимодействием с молекулами газа.
Исследование показало, что в теплопроводности системы преобладает кристалл, который снижается по мере увеличения концентрации газа в порах. Пониженная проводимость, связанная с увеличением концентрации газа, связана с рассеянием фононов кристаллом, вызванным взаимодействием с молекулами газа.Несмотря на то, что было выполнено большое количество работ по теплопроводности нанопористых материалов, теоретическую модель особенно трудно использовать для непосредственного описания подробного взаимодействия газа и твердого тела, и большинство работ по моделированию сосредоточено только на одном компоненте. , твердое тело или газы. В этой работе мы проводим моделирование равновесной молекулярной динамики для изучения теплопроводности упорядоченных пористых структур, связывающих газовую и твердую фазы. Рассмотрено влияние давления и взаимодействия газа с твердым телом на теплопроводность.
Молекулярно-динамическое моделирование в данной работе выполнено с использованием пакета LAMMPS [21].
 Ячейка моделирования, включающая газ и твердое тело, получается из упорядоченных пористых структур пересекающихся квадратных стержней, как показано на рис. Периодическое граничное условие используется во всех направлениях. В качестве твердой фазы упорядоченных пористых структур, заполненных газом гелия при 20 К, выбран аргон. Твердый аргон представляет собой гранецентрированный кубический кристалл с периодом решетки S = 5,4 Å. Потенциал Леннарда-Джонса 12–6, E = 4 ε [( σ / r ) 12 − ( σ / r ) 6 ] 14 Å. Подробные параметры, используемые в нашем моделировании, перечислены как в . Ансамбль NVT, который поддерживает постоянным число атомов, объем и температуру, используется с термостатом Нозе-Гувера при 20 K с временным шагом 5 фс.
Ячейка моделирования, включающая газ и твердое тело, получается из упорядоченных пористых структур пересекающихся квадратных стержней, как показано на рис. Периодическое граничное условие используется во всех направлениях. В качестве твердой фазы упорядоченных пористых структур, заполненных газом гелия при 20 К, выбран аргон. Твердый аргон представляет собой гранецентрированный кубический кристалл с периодом решетки S = 5,4 Å. Потенциал Леннарда-Джонса 12–6, E = 4 ε [( σ / r ) 12 − ( σ / r ) 6 ] 14 Å. Подробные параметры, используемые в нашем моделировании, перечислены как в . Ансамбль NVT, который поддерживает постоянным число атомов, объем и температуру, используется с термостатом Нозе-Гувера при 20 K с временным шагом 5 фс.Открыть в отдельном окне
Настройка системы моделирования.
Таблица 1
Параметры, используемые при моделировании.
Material ε (kcal/mol) σ (Å) l ( S ) L ( S ) Аргон 0,39 3,35 4, 5, 6, 7, 8 8, 12, 16, 20, 24 Гелий 0,25 6,70 0095 Аргон-Гелий 0,16 10,05 Открыть в отдельном окне
Теплопроводность нанопористой системы рассчитана по формуле Грин-Кубо
λ=VkbT2∫0∞〈j(0)j(t)〉dt
(1)
где k b — постоянная Больцмана, V — объем ячейки моделирования, а угловые скобки обозначают среднее значение по времени.
 Микроскопический тепловой поток j получается из следующего уравнения
Микроскопический тепловой поток j получается из следующего уравненияj(t)=1V(∑iviεi+12∑i∑j,j≠irij(vi·Fij))
(2)
где v i — скорость атома i и F ij — сила, действующая на атом i со стороны атома j . ε i в первом члене уравнения (2) представляет собой энергию на атом, включая потенциальную и кинетическую энергию.
Для исследования теплопроводности нанопористой системы при различных давлениях все расчеты выполняются в два этапа. На первом этапе для определения газосодержания при различных давлениях используется симуляция Grand Canonical Monte Carlo. Алгоритм создает большой канонический ансамбль, в котором атомы газа могут быть перемещены, удалены или созданы в окне моделирования. На этом этапе на каждом шаге осуществляется большое количество попыток вставки и удаления атомов газа. Вставка или удаление атомов газа равновероятны в любом месте, если судить по обычным критериям Большого канонического алгоритма Монте-Карло.
 Газ гелия рассматривается как идеальный газ и химический потенциал μ можно определить, используя давление P , заданное формулой μ = k b T ln( Pφ / k b T ), где Количество атомов газа усредняется за последние 400 000 шагов как содержание газа для различных давлений. На втором этапе ячейка моделирования, включающая твердое тело и газ, сначала достигает равновесного состояния в ансамбле НВТ при 20 К. Затем по формуле Грина-Кубо рассчитывается теплопроводность нанопористой системы. Вектор теплового потока регистрируется каждые 5 временных шагов в ансамбле NVE для 5 × 10 7 временных шагов. Время корреляции составляет 10 000 временных шагов. Для всех случаев мы выполнили 5 независимых симуляций с разными случайными затравками для распределения атомов по скоростям. Усредненное значение 5 симуляций используется для прогнозов теплопроводности.
Газ гелия рассматривается как идеальный газ и химический потенциал μ можно определить, используя давление P , заданное формулой μ = k b T ln( Pφ / k b T ), где Количество атомов газа усредняется за последние 400 000 шагов как содержание газа для различных давлений. На втором этапе ячейка моделирования, включающая твердое тело и газ, сначала достигает равновесного состояния в ансамбле НВТ при 20 К. Затем по формуле Грина-Кубо рассчитывается теплопроводность нанопористой системы. Вектор теплового потока регистрируется каждые 5 временных шагов в ансамбле NVE для 5 × 10 7 временных шагов. Время корреляции составляет 10 000 временных шагов. Для всех случаев мы выполнили 5 независимых симуляций с разными случайными затравками для распределения атомов по скоростям. Усредненное значение 5 симуляций используется для прогнозов теплопроводности.показывает автокорреляционные функции теплового потока (HFACF), отвечающие уравнению (1) для нанопористой системы.
 Мы можем обнаружить, что HFACF постепенно приближается к нулю примерно через 10 пс, что также доказывает, что время корреляции 50 пс, используемое в нашем моделировании, достаточно велико для получения стабильной теплопроводности. Текущая теплопроводность получена на основе HFACF, которая стабилизируется на уровне около 0,14 Вт м 9 .0047 −1 K −1 после 20 пс.
Мы можем обнаружить, что HFACF постепенно приближается к нулю примерно через 10 пс, что также доказывает, что время корреляции 50 пс, используемое в нашем моделировании, достаточно велико для получения стабильной теплопроводности. Текущая теплопроводность получена на основе HFACF, которая стабилизируется на уровне около 0,14 Вт м 9 .0047 −1 K −1 после 20 пс.Открыть в отдельном окне
ВТАКФ и погонная теплопроводность.
3.1. The Pressure Effect
и показывает распределение атомов газа в нанопористой системе ( L = 12 S , l = 4 S и L = 12 S 7 09 l , 9003 ). Мы используем постоянную решетки S в качестве радиуса отсечки для проведения кластерного анализа для системы газ-твердое тело. Атомы газа вблизи твердой фазы рассматриваются как адсорбированное состояние, а остальные рассматриваются как свободные атомы. Общее количество атомов газа в нанопористых системах увеличивается с давлением.
 Однако для системы L = 12 S , l = 8 S , атомы свободного газа не зависят от давления из-за ограниченного пространства. Теплопроводность нанопористой системы ( л = 12 с , л = 4 с и л = 12 с , л = 8 с) как функция давления Показано в . Суммарная теплопроводность л = 8 С выше, чем у системы л = 4 S в диапазоне от 0 до 4 атм из-за высокой теплопроводности твердой фазы (давление = 0). Для нанопористой системы l = 4 S общая теплопроводность увеличивается с более высоким давлением или газовой нагрузкой, что связано с увеличением количества свободных атомов газа, что соответствует лучшей способности к теплопередаче. Полученная теплопроводность для л = 8 С практически не изменяется при изменении давления. Это связано с тем, что в нанопористой системе практически отсутствуют свободные атомы газа, а в общей теплопроводности преобладает твердая фаза.
Однако для системы L = 12 S , l = 8 S , атомы свободного газа не зависят от давления из-за ограниченного пространства. Теплопроводность нанопористой системы ( л = 12 с , л = 4 с и л = 12 с , л = 8 с) как функция давления Показано в . Суммарная теплопроводность л = 8 С выше, чем у системы л = 4 S в диапазоне от 0 до 4 атм из-за высокой теплопроводности твердой фазы (давление = 0). Для нанопористой системы l = 4 S общая теплопроводность увеличивается с более высоким давлением или газовой нагрузкой, что связано с увеличением количества свободных атомов газа, что соответствует лучшей способности к теплопередаче. Полученная теплопроводность для л = 8 С практически не изменяется при изменении давления. Это связано с тем, что в нанопористой системе практически отсутствуют свободные атомы газа, а в общей теплопроводности преобладает твердая фаза.
Открыть в отдельном окне
Распределение атомов газа в нанопористых системах.
Открыть в отдельном окне
Общее и количество свободных атомов газа в нанопористых системах.
Открыть в отдельном окне
Зависимость теплопроводности от давления.
3.2. Эффект структуры
На практике нанопористые материалы имеют различные структурные особенности в зависимости от метода и условий получения. Между тем структура также оказывает существенное влияние на общую теплопроводность нанопористой системы. Теплопроводность имитационной единицы, принимающей различные конструктивные параметры при одном и том же давлении, получается, как показано на и . Когда длина ( L ) блока моделирования теплопроводность системы сначала уменьшится и достигнет минимума около 10 S , а затем увеличится. Первоначальное снижение теплопроводности связано с увеличением пористости, при которой твердая фаза является основным фактором, определяющим общую теплопроводность.
 По мере того, как длина ( L ) модуля моделирования продолжает увеличиваться, количество атомов газа и теплопроводность соответствующего газа будут увеличиваться. Для той же длины ( L ) модуля моделирования увеличение ширины твердого каркаса приведет к быстрому увеличению общей теплопроводности, что в основном связано с увеличением теплопроводности твердой фазы. Хотя атомы газа в этой ситуации уменьшаются, влияние твердой фазы более очевидно и приводит к увеличению общей теплопроводности, как показано на рис.
По мере того, как длина ( L ) модуля моделирования продолжает увеличиваться, количество атомов газа и теплопроводность соответствующего газа будут увеличиваться. Для той же длины ( L ) модуля моделирования увеличение ширины твердого каркаса приведет к быстрому увеличению общей теплопроводности, что в основном связано с увеличением теплопроводности твердой фазы. Хотя атомы газа в этой ситуации уменьшаются, влияние твердой фазы более очевидно и приводит к увеличению общей теплопроводности, как показано на рис.Открыть в отдельном окне
Коэффициент теплопроводности для различных единиц длины ( л ).
Открыть в отдельном окне
Теплопроводность для разной ширины ( л ).
3.3. Взаимодействие газ-твердое тело
Чтобы соответствовать условиям применения, нанопористые материалы могут потребовать модификации поверхности, при которой изменяется взаимодействие газ-твердое тело. До сих пор неясно, как зависит теплопроводность нанопористой системы от взаимодействия газ-твердое тело.
 В нашем моделировании энергетический параметр ε , используемый в потенциале Леннарда-Джонса 12-6, может быть скорректирован, чтобы представить этот вид модификации поверхности как упрощение. ε / ε газ-твердое тело в диапазоне от 0,3 до 1 используется при моделировании при том же давлении и газовой нагрузке. и показать результаты распределения атомов газа и общей теплопроводности для различных ε при одном и том же давлении. Атомы газа в нанопористой системе увеличиваются из-за сильного взаимодействия газ-твердое тело и демонстрируют хорошие адсорбционные характеристики с увеличенным ε . Однако, как показано в , теплопроводность нанопористой системы стабилизируется на уровне около 0,24 Вт м -1 К -1 . Взаимодействие атомов твердого тела и газа мало влияет на теплопроводность при том же давлении. Это связано с тем, что, хотя общее количество атомов газа увеличивается из-за сильного взаимодействия газ-твердое тело, увеличенное количество атомов газа находится в адсорбированном состоянии, которое вносит небольшой вклад в теплообмен в нанопористой системе.
В нашем моделировании энергетический параметр ε , используемый в потенциале Леннарда-Джонса 12-6, может быть скорректирован, чтобы представить этот вид модификации поверхности как упрощение. ε / ε газ-твердое тело в диапазоне от 0,3 до 1 используется при моделировании при том же давлении и газовой нагрузке. и показать результаты распределения атомов газа и общей теплопроводности для различных ε при одном и том же давлении. Атомы газа в нанопористой системе увеличиваются из-за сильного взаимодействия газ-твердое тело и демонстрируют хорошие адсорбционные характеристики с увеличенным ε . Однако, как показано в , теплопроводность нанопористой системы стабилизируется на уровне около 0,24 Вт м -1 К -1 . Взаимодействие атомов твердого тела и газа мало влияет на теплопроводность при том же давлении. Это связано с тем, что, хотя общее количество атомов газа увеличивается из-за сильного взаимодействия газ-твердое тело, увеличенное количество атомов газа находится в адсорбированном состоянии, которое вносит небольшой вклад в теплообмен в нанопористой системе. Однако, согласно уравнению состояния идеального газа, свободные атомы газа, участвующие в процессе теплопроводности, практически одинаковы при одном и том же давлении. Следовательно, теплопроводность нанопористой системы стабильна и не зависит от взаимодействия газ-твердое тело при одном и том же давлении.
Однако, согласно уравнению состояния идеального газа, свободные атомы газа, участвующие в процессе теплопроводности, практически одинаковы при одном и том же давлении. Следовательно, теплопроводность нанопористой системы стабильна и не зависит от взаимодействия газ-твердое тело при одном и том же давлении.Открыть в отдельном окне
Распределение атомов газа для разных ε при давлении 2 атм.
Открыть в отдельном окне
Число атомов газа и теплопроводность для разных ε при давлении 2 атм.
В предыдущей работе [20] изучался теплообмен в пористых кристаллах, содержащих адсорбированные газы. Результаты показали, что в теплопроводности системы преобладает теплопроводность кристалла и снижается по мере увеличения концентрации газа в порах. Уменьшение проводимости при увеличении концентрации газа связано с фононным рассеянием кристалла, вызванным взаимодействием с атомами газа. В нашем моделировании аналогичные результаты не получены для пористой кристаллической системы.
 Следовательно, в таких системах общая теплопроводность является результатом множества факторов, включая концентрацию газа, коэффициент диффузии, свойства материала, структурные параметры и так далее. Влияние давления на общую теплопроводность представляет различные характеристики для нанопористой системы.
Следовательно, в таких системах общая теплопроводность является результатом множества факторов, включая концентрацию газа, коэффициент диффузии, свойства материала, структурные параметры и так далее. Влияние давления на общую теплопроводность представляет различные характеристики для нанопористой системы.Чтобы дополнительно проиллюстрировать влияние взаимодействия газа и твердого тела на общую теплопроводность, случай постоянных атомов газа для различных взаимодействий газа и твердого тела исследуется, как показано на и . В системе L = 16 S , l = 4 S , мы можем найти, что атомы газа для ε / ε газ-твердое = 0,3, что означает нижнюю поверхность энергии, может поддерживать свободное состояние. Однако для случая ε / ε газ-твердое = 1, большинство атомов газа ограничены на поверхности и сохраняют поглощенное состояние, что не может способствовать теплообмену в пористых структурах, связывающих газовую и твердую фазы.
 Таким образом, общая теплопроводность резко уменьшается с 0,37 Вт·м·–1··K·–1· до 0,11 Вт·м·–1··K·–1· из-за различных состояний атомов газа. Влияние адсорбции на общую теплопроводность при постоянных атомах газа заметно, а свободные атомы газа необходимы для переноса тепла в пористых структурах, связывающих газовую и твердую фазы.
Таким образом, общая теплопроводность резко уменьшается с 0,37 Вт·м·–1··K·–1· до 0,11 Вт·м·–1··K·–1· из-за различных состояний атомов газа. Влияние адсорбции на общую теплопроводность при постоянных атомах газа заметно, а свободные атомы газа необходимы для переноса тепла в пористых структурах, связывающих газовую и твердую фазы.Открыть в отдельном окне
Распределение атомов газа для различных ε при постоянном числе атомов газа.
Открыть в отдельном окне
Поглощенные атомы и теплопроводность для постоянных атомов газа.
В данной работе мы исследовали теплопроводность упорядоченных пористых структур с использованием Большого канонического метода Монте-Карло (GCMC) и моделирования молекулярной динамики (МД). Выявлено влияние концентрации газа, пористой структуры и взаимодействия газа с твердым телом на теплопроводность.
Результаты моделирования показывают, что для различных конструкций влияние давления на теплопроводность проявляется непостоянно.
 При одном и том же давлении теплопроводность практически не меняется при различных взаимодействиях газовой и твердой фаз. Кроме того, существенное влияние на теплопроводность нанопористой системы оказывает состояние атомов газа, поглощенных или свободных. Из этого исследования теплопередача в пористых структурах, связывающих газовую и твердую фазы, может быть понята на фундаментальном уровне.
При одном и том же давлении теплопроводность практически не меняется при различных взаимодействиях газовой и твердой фаз. Кроме того, существенное влияние на теплопроводность нанопористой системы оказывает состояние атомов газа, поглощенных или свободных. Из этого исследования теплопередача в пористых структурах, связывающих газовую и твердую фазы, может быть понята на фундаментальном уровне.Концептуализация, Х.Г. и Д.Н.; методика, Д.Н.; программное обеспечение, Д.Н.; валидация, HG и DN; формальный анализ, Д.Н.; расследование, Д.Н.; ресурсы, Д.Н.; курирование данных, Д.Н.; написание – черновая подготовка, Д.Н.; написание-обзор и редактирование, Д.Н.; визуализация, Д.Н.; надзор, Х.Г.; администрация проекта, Х.Г.; приобретение финансирования, Х.Г. и Д.Н. Все авторы прочитали и согласились с опубликованной версией рукописи.
Эта работа была поддержана Китайским фондом постдокторских наук (№ 2020M670725), Фондом ключевой лаборатории терможидкостной науки и техники (Сианьский университет Цзяотун), Министерством образования (KLTFSE2020KFJJ01), Фондами фундаментальных исследований для центральных университетов.
 (№3132019305).
(№3132019305).Неприменимо.
Неприменимо.
Данные, представленные в этом исследовании, доступны по запросу у соответствующего автора.
Авторы заявляют об отсутствии конфликта интересов.
Примечание издателя: MDPI сохраняет нейтралитет в отношении юрисдикционных претензий в опубликованных картах и институциональной принадлежности.
1. Райхенауэр Г., Хайнеманн У., Эберт Х.П. Связь между размером пор и зависимостью газовой теплопроводности от давления газа. Коллоидный прибой. А-Физикохим. англ. Асп. 2007; 300: 204–210. doi: 10.1016/j.colsurfa.2007.01.020. [Перекрестная ссылка] [Академия Google]
2. Чжао Дж.Дж., Дуань Ю.Ю., Ван X.Д., Ван Б.Х. Влияние взаимодействия твердого тела с газом, а также микроструктуры пор и частиц на эффективную газовую теплопроводность в аэрогелях. Дж. Нанопарт. Рез. 2012; 14:1–15. doi: 10.1007/s11051-012-1024-0. [CrossRef] [Google Scholar]
3. Bi C., Tang G.H., Hu Z.J., Yang H.
 L., Li J.N. Модель связи теплообмена между твердой и газовой фазами в аэрогеле и экспериментальное исследование. Междунар. J. Тепломассообмен. 2014;79:126–136. doi: 10.1016/j.ijheatmasstransfer.2014.07.098. [CrossRef] [Google Scholar]
L., Li J.N. Модель связи теплообмена между твердой и газовой фазами в аэрогеле и экспериментальное исследование. Междунар. J. Тепломассообмен. 2014;79:126–136. doi: 10.1016/j.ijheatmasstransfer.2014.07.098. [CrossRef] [Google Scholar]4. Hümmer E., Lu X., Rettelbach T., Fricke J. Теплопередача в непрозрачных порошках аэрогеля. J. Некристалл. Твердые вещества. 1992; 145: 211–216. doi: 10.1016/S0022-3093(05)80458-2. [CrossRef] [Google Scholar]
5. Hemberger F., Weis S., Reichenauer G., Ebert H.P. Теплотранспортные свойства функционально градиентных углеродных аэрогелей. Междунар. Дж. Термофиз. 2009;30:1357–1371. doi: 10.1007/s10765-009-0616-0. [CrossRef] [Google Scholar]
6. Хаясе Г., Кугимия К., Огава М., Кодера Ю., Канамори К., Наканиши К. Теплопроводность полиметилсилсесквиоксановых аэрогелей и ксерогелей с различными размерами пор для практического применения в качестве тепловые суперизоляторы. Дж. Матер. хим. А. 2014;2:6525–6531. дои: 10.1039/C3TA15094A. [CrossRef] [Google Scholar]
7.
 Хан Ю.Ф., Ся С.Л., Тан Х.П., Лю Х.Д. Моделирование фононного теплообмена в сферическом сегменте зерен кремнеземного аэрогеля. физ. Б. 2013; 420:58–63. doi: 10.1016/j.physb.2013.03.015. [CrossRef] [Google Scholar]
Хан Ю.Ф., Ся С.Л., Тан Х.П., Лю Х.Д. Моделирование фононного теплообмена в сферическом сегменте зерен кремнеземного аэрогеля. физ. Б. 2013; 420:58–63. doi: 10.1016/j.physb.2013.03.015. [CrossRef] [Google Scholar]8. Li Z.Y., Zhu C.Y., Zhao X.P. Теоретическое и численное исследование газовой теплопроводности в аэрогеле. Междунар. J. Тепломассообмен. 2017; 108:1982–1990. doi: 10.1016/j.ijheatmasstransfer.2017.01.051. [Перекрестная ссылка] [Академия Google]
9. Чжу С.Ю., Ли З.Ю., Тао В.К. Теоретические и DSMC исследования теплопроводности газа, заключенного в кубовидную нанопору. Дж. Теплопередача. 2017;139:052405. doi: 10.1115/1.4035854. [CrossRef] [Google Scholar]
10. Чжао С.П., Ли З.Ю., Лю Х., Тао В.К. Расчет теплопроводности методом трехмерного прямого моделирования Монте-Карло. Дж. Наноски. нанотехнологии. 2015;15:3299–3304. doi: 10.1166/jnn.2015.9679. [PubMed] [CrossRef] [Google Scholar]
11. Zhu C.Y., Li Z.Y., Pang H.Q., Pan N. Численное моделирование газовой теплопроводности аэрогелей.
 Междунар. J. Тепломассообмен. 2019;131:217–225. doi: 10.1016/j.ijheatmasstransfer.2018.11.052. [CrossRef] [Google Scholar]
Междунар. J. Тепломассообмен. 2019;131:217–225. doi: 10.1016/j.ijheatmasstransfer.2018.11.052. [CrossRef] [Google Scholar]12. Цюй З.Г., Фу Ю.Д., Лю Ю., Чжоу Л. Подход к прогнозированию эффективной теплопроводности аэрогелевых материалов с помощью модифицированного метода Больцмана на решетке. заявл. Терм. англ. 2018; 132:730–739. doi: 10.1016/j.applthermaleng.2018.01.013. [CrossRef] [Google Scholar]
13. Фанг В.З., Чжан Х., Чен Л., Тао В.К. Численные прогнозы теплопроводности кремнеземного аэрогеля и его композитов. заявл. Терм. англ. 2017; 115:1277–1286. doi: 10.1016/j.applthermaleng.2016.10.184. [Перекрестная ссылка] [Академия Google]
14. Тан Г.Х., Би С., Фу Б. Теплопроводность в тонкой пленке нанопористого кремния. Дж. Заявл. физ. 2013;114:184302. doi: 10.1063/1.4829913. [CrossRef] [Google Scholar]
15. Fu B., Tang G.H., Bi C. Теплопроводность в наноструктурированных материалах и анализ локального угла между тепловыми потоками. Дж. Заявл. физ. 2014;116:124310.
 doi: 10.1063/1.4896551. [CrossRef] [Google Scholar]
doi: 10.1063/1.4896551. [CrossRef] [Google Scholar]16. Coquil T., Fang J., Pilon L. Молекулярно-динамическое исследование теплопроводности аморфного нанопористого кремнезема. Междунар. J. Тепломассообмен. 2011;54:4540–4548. doi: 10.1016/j.ijheatmasstransfer.2011.06.024. [Перекрестная ссылка] [Академия Google]
17. Нг Т.Ю., Йео Дж.Дж., Лю З.С. Молекулярно-динамическое исследование теплопроводности аэрогеля нанопористого кремнезема, полученного разрывом при отрицательном давлении. J. Некристалл. Твердые вещества. 2012; 358:1350–1355. doi: 10.1016/j.jnoncrysol.2012.03.007. [CrossRef] [Google Scholar]
18. Liu M., Qiu L., Zheng X.H., Zhu J., Tang D.W. Исследование термического сопротивления в цепочке вторичных частиц кремнеземного аэрогеля методом молекулярной динамики. Дж. Заявл. физ. 2014;116:093503. дои: 10.1063/1.4894511. [CrossRef] [Google Scholar]
19. Рабани Р., Хейдаринеджад Г., Хартинг Дж., Ширани Э. Влияние жесткости стенки, массы и потенциальной силы взаимодействия на характеристики теплопередачи газа в наноразмерах.
 Междунар. J. Тепломассообмен. 2020;147:118929. doi: 10.1016/j.ijheatmasstransfer.2019.118929. [CrossRef] [Google Scholar]
Междунар. J. Тепломассообмен. 2020;147:118929. doi: 10.1016/j.ijheatmasstransfer.2019.118929. [CrossRef] [Google Scholar]20. Babaei H., Wilmer C.E. Механизмы теплопередачи в пористых кристаллах, содержащих адсорбированные газы: приложения к металлоорганическим каркасам. физ. Преподобный Летт. 2016;116:025902. doi: 10.1103/PhysRevLett.116.025902. [PubMed] [CrossRef] [Google Scholar]
21. Плимптон С. Быстрые параллельные алгоритмы для молекулярной динамики ближнего действия. Дж. Вычисл. физ. 1995; 117:1–19. doi: 10.1006/jcph.1995.1039. [CrossRef] [Google Scholar]
Статьи из материалов предоставлены здесь Многопрофильный институт цифровых публикаций (MDPI)
Материалы | Бесплатный полнотекстовый | Теплопроводность упорядоченных пористых структур, взаимодействующих с газовой и твердой фазами: исследование молекулярной динамики
1. Введение
Пористые материалы широко используются во многих областях, таких как изоляция зданий, хранение и разделение газа, аэрокосмическая промышленность и т.
 д. Теплоперенос в пористых материалах, содержащих газовую фазу, является важным процессом, который невозможно полностью понять на фундаментальном уровне, особенно для нанопористых материалов. Точное предсказание теплопроводности нанопористых материалов крайне необходимо для применения.
д. Теплоперенос в пористых материалах, содержащих газовую фазу, является важным процессом, который невозможно полностью понять на фундаментальном уровне, особенно для нанопористых материалов. Точное предсказание теплопроводности нанопористых материалов крайне необходимо для применения.Большое количество теоретических моделей теплопроводности было разработано в предыдущих исследованиях [1, 2, 3, 4, 5, 6] с учетом влияния газа, твердого тела и излучения в непористом материале, в котором существуют некоторые отклонения по сравнению с с экспериментальным значением в некоторой степени. Из-за чрезвычайно сложных структур и эффекта взаимодействия твердого тела с газом в теоретической модели необходимо много эмпирических параметров, которые трудно определить. Численное моделирование является возможным выбором для непосредственного получения свойств нанопористых материалов. Решеточный метод Больцмана применялся для исследования фононного теплообмена в сферическом сегменте зерен аэрогеля нанокремнезема [7].
 Результаты моделирования показали, что распределение температуры в зерне кремнеземного аэрогеля сильно зависит от размера, а рассеяние фононов на граничных поверхностях становится более заметным при уменьшении размера зерен. Ли и др. В работе [8] разработана модифицированная модель для прогнозирования газовой теплопроводности в нанопористых материалах на основе метода прямого моделирования Монте-Карло (DSMC). Результаты показали, что модифицированная модель имеет более высокую точность без сложных расчетов и допущений. Влияние размера на теплопроводность газа изучалось методом ПСМ [9].]. На границе существует очевидный скачок температуры, и теплопроводность имеет тенденцию к уменьшению при увеличении числа Кнудсена от 0,01 до 0,1. Чжао и др. В работе [10] получена газовая теплопроводность азота с использованием трехмерного метода DSMC с переменной моделью столкновения мягких сфер. Результаты согласуются с экспериментальными данными, но намного выше, чем по соотношению Эйкена, особенно при высокой температуре.
Результаты моделирования показали, что распределение температуры в зерне кремнеземного аэрогеля сильно зависит от размера, а рассеяние фононов на граничных поверхностях становится более заметным при уменьшении размера зерен. Ли и др. В работе [8] разработана модифицированная модель для прогнозирования газовой теплопроводности в нанопористых материалах на основе метода прямого моделирования Монте-Карло (DSMC). Результаты показали, что модифицированная модель имеет более высокую точность без сложных расчетов и допущений. Влияние размера на теплопроводность газа изучалось методом ПСМ [9].]. На границе существует очевидный скачок температуры, и теплопроводность имеет тенденцию к уменьшению при увеличении числа Кнудсена от 0,01 до 0,1. Чжао и др. В работе [10] получена газовая теплопроводность азота с использованием трехмерного метода DSMC с переменной моделью столкновения мягких сфер. Результаты согласуются с экспериментальными данными, но намного выше, чем по соотношению Эйкена, особенно при высокой температуре. Нанопористые аэрогели были реконструированы с помощью усовершенствованного метода трехмерной кластерно-кластерной агрегации с ограничением диффузии (DLCA), в котором количественно определялся вклад теплопередачи твердого тела-газа в теплопроводность, обусловленную газом [11]. Для прогнозирования эффективной теплопроводности нанопористых аэрогелевых материалов был разработан модифицированный решеточный метод Больцмана [12], который ввел дополнительный коэффициент для регулирования разницы теплопроводности между твердой и газовой фазами и гарантировал конвергентное решение. Фанг и др. В работе [13] решеточный метод Больцмана использовался для решения уравнения проводимости-излучения для предсказания эффективной теплопроводности. Результаты моделирования показали, что эффективная теплопроводность чистого нанопористого аэрогеля быстро увеличивается с температурой и сильно снижается при легировании добавками. Теплопроводность нанопористой пленки и нанокомпозита численно исследовалась путем решения фононного уравнения переноса Больцмана с частотно-зависимой моделью [14].
Нанопористые аэрогели были реконструированы с помощью усовершенствованного метода трехмерной кластерно-кластерной агрегации с ограничением диффузии (DLCA), в котором количественно определялся вклад теплопередачи твердого тела-газа в теплопроводность, обусловленную газом [11]. Для прогнозирования эффективной теплопроводности нанопористых аэрогелевых материалов был разработан модифицированный решеточный метод Больцмана [12], который ввел дополнительный коэффициент для регулирования разницы теплопроводности между твердой и газовой фазами и гарантировал конвергентное решение. Фанг и др. В работе [13] решеточный метод Больцмана использовался для решения уравнения проводимости-излучения для предсказания эффективной теплопроводности. Результаты моделирования показали, что эффективная теплопроводность чистого нанопористого аэрогеля быстро увеличивается с температурой и сильно снижается при легировании добавками. Теплопроводность нанопористой пленки и нанокомпозита численно исследовалась путем решения фононного уравнения переноса Больцмана с частотно-зависимой моделью [14]. Был введен локальный угол между тепловыми потоками и локальным тепловым потоком, и все результаты показали, что наноструктурный материал с большим средним углом будет иметь меньшую теплопроводность. Танг и др. [15] исследовали теплопроводность тонкой пленки нанопористого кремния с использованием метода дискретных ординат (DOM). Учитывались эффекты толщины, пористости и пористой структуры. Численные результаты показали, что нанопоры способны резко снижать теплопроводность тонкой пленки кремния за счет граничного рассеяния фононов.
Был введен локальный угол между тепловыми потоками и локальным тепловым потоком, и все результаты показали, что наноструктурный материал с большим средним углом будет иметь меньшую теплопроводность. Танг и др. [15] исследовали теплопроводность тонкой пленки нанопористого кремния с использованием метода дискретных ординат (DOM). Учитывались эффекты толщины, пористости и пористой структуры. Численные результаты показали, что нанопоры способны резко снижать теплопроводность тонкой пленки кремния за счет граничного рассеяния фононов.Молекулярно-динамическое моделирование также является эффективным методом решения наноразмерных задач переноса тепла газами и твердыми телами. Кокил и др. [16] впервые применили моделирование неравновесной молекулярной динамики для предсказания теплопроводности аморфного нанопористого кремнезема. Результаты моделирования показали, что теплопроводность нанопористого кремнезема при комнатной температуре не зависит от размера пор и зависит только от пористости.
 Нг и др. В работе [17] исследована теплопроводность образцов нанопористого аэрогеля различной плотности путем разрыва плотных образцов кремнезема отрицательным давлением. Результаты показали, что степенная зависимость теплопроводности изменяется почти линейно с плотностью, при этом уменьшение плотности и увеличение пористости приведет к линейному уменьшению теплопроводности. Теплоперенос в цепочке вторичных частиц аэрогеля нанопористого кремнезема изучался с помощью молекулярно-динамического моделирования [18]. Перенос тепла подавлялся, когда длина контакта или концентрация дефектов увеличивались, а ограничивающий эффект был гораздо более очевидным, когда доля длины контакта находилась в небольшом диапазоне. Характеристики теплопередачи наноразмерного газа исследовались методом молекулярно-динамического моделирования [19].]. Рассмотрено влияние силового поля стенки, жесткости стенки и потенциальной напряженности взаимодействия стенка-газ на эффективную теплопроводность. Babaei и Wilmer [20] исследовали механизмы переноса тепла в системе пористый кристалл-газовая смесь с помощью молекулярно-динамического моделирования.
Нг и др. В работе [17] исследована теплопроводность образцов нанопористого аэрогеля различной плотности путем разрыва плотных образцов кремнезема отрицательным давлением. Результаты показали, что степенная зависимость теплопроводности изменяется почти линейно с плотностью, при этом уменьшение плотности и увеличение пористости приведет к линейному уменьшению теплопроводности. Теплоперенос в цепочке вторичных частиц аэрогеля нанопористого кремнезема изучался с помощью молекулярно-динамического моделирования [18]. Перенос тепла подавлялся, когда длина контакта или концентрация дефектов увеличивались, а ограничивающий эффект был гораздо более очевидным, когда доля длины контакта находилась в небольшом диапазоне. Характеристики теплопередачи наноразмерного газа исследовались методом молекулярно-динамического моделирования [19].]. Рассмотрено влияние силового поля стенки, жесткости стенки и потенциальной напряженности взаимодействия стенка-газ на эффективную теплопроводность. Babaei и Wilmer [20] исследовали механизмы переноса тепла в системе пористый кристалл-газовая смесь с помощью молекулярно-динамического моделирования. Исследование показало, что в теплопроводности системы преобладает кристалл, который снижается по мере увеличения концентрации газа в порах. Пониженная проводимость, связанная с увеличением концентрации газа, связана с рассеянием фононов кристаллом, вызванным взаимодействием с молекулами газа.
Исследование показало, что в теплопроводности системы преобладает кристалл, который снижается по мере увеличения концентрации газа в порах. Пониженная проводимость, связанная с увеличением концентрации газа, связана с рассеянием фононов кристаллом, вызванным взаимодействием с молекулами газа.Несмотря на то, что было выполнено большое количество работ по теплопроводности нанопористых материалов, теоретическую модель особенно трудно использовать для непосредственного описания подробного взаимодействия газа и твердого тела, и большинство работ по моделированию сосредоточено только на одном компоненте. , твердое тело или газы. В этой работе мы проводим моделирование равновесной молекулярной динамики для изучения теплопроводности упорядоченных пористых структур, связывающих газовую и твердую фазы. Рассмотрено влияние давления и взаимодействия газа с твердым телом на теплопроводность.
2. Материалы и методы
Молекулярно-динамическое моделирование в данной работе выполнено с использованием пакета LAMMPS [21].
 Ячейка моделирования, включающая газ и твердое тело, получается из упорядоченных пористых структур пересекающихся квадратных стержней, как показано на рисунке 1. Периодическое граничное условие используется во всех направлениях. В качестве твердой фазы упорядоченных пористых структур, заполненных газом гелия при 20 К, выбран аргон. Твердый аргон представляет собой гранецентрированный кубический кристалл с периодом решетки S = 5,4 Å. Потенциал Леннарда-Джонса 12–6, E = 4ε[(σ/r) 12 — (σ/r) 6 ], используется для описания взаимодействия между атомами и усекается по радиусу отсечки 14 Å. Подробные параметры, использованные в нашем моделировании, перечислены в таблице 1. Ансамбль NVT, который поддерживает количество атомов, объем и температуру постоянными, используется с термостатом Нозе-Гувера при 20 K с временным шагом 5 фс.
Ячейка моделирования, включающая газ и твердое тело, получается из упорядоченных пористых структур пересекающихся квадратных стержней, как показано на рисунке 1. Периодическое граничное условие используется во всех направлениях. В качестве твердой фазы упорядоченных пористых структур, заполненных газом гелия при 20 К, выбран аргон. Твердый аргон представляет собой гранецентрированный кубический кристалл с периодом решетки S = 5,4 Å. Потенциал Леннарда-Джонса 12–6, E = 4ε[(σ/r) 12 — (σ/r) 6 ], используется для описания взаимодействия между атомами и усекается по радиусу отсечки 14 Å. Подробные параметры, использованные в нашем моделировании, перечислены в таблице 1. Ансамбль NVT, который поддерживает количество атомов, объем и температуру постоянными, используется с термостатом Нозе-Гувера при 20 K с временным шагом 5 фс.Теплопроводность нанопористой системы рассчитывается по формуле Грина-Кубо
где k b — постоянная Больцмана, V — объем ячейки моделирования, а угловые скобки обозначают среднее значение по времени.
 Микроскопический тепловой поток j получается из следующего уравнения
Микроскопический тепловой поток j получается из следующего уравнениягде v i — скорость атома i, а F ij — сила, действующая на атом i со стороны атома j. ε i в первом члене уравнения (2) представляет собой энергию на атом, включая потенциальную и кинетическую энергию.
Для исследования теплопроводности нанопористой системы при различных давлениях все расчеты выполняются в два этапа. На первом этапе для определения газосодержания при различных давлениях используется симуляция Grand Canonical Monte Carlo. Алгоритм создает большой канонический ансамбль, в котором атомы газа могут быть перемещены, удалены или созданы в окне моделирования. На этом этапе на каждом шаге осуществляется большое количество попыток вставки и удаления атомов газа. Вставка или удаление атомов газа равновероятны в любом месте, если судить по обычным критериям Большого канонического алгоритма Монте-Карло. Газ гелия рассматривается как идеальный газ, и химический потенциал μ можно определить, используя давление P, определяемое выражением μ = k b Tln(Pφ/k b T), где φ — коэффициент летучести.
 Количество атомов газа усредняется за последние 400 000 шагов как содержание газа для различных давлений. На втором этапе ячейка моделирования, включающая твердое тело и газ, сначала достигает равновесного состояния в ансамбле НВТ при 20 К. Затем по формуле Грина-Кубо рассчитывается теплопроводность нанопористой системы. Вектор теплового потока регистрируется каждые 5 временных шагов в ансамбле NVE для 5 × 10 7 временных шагов. Время корреляции составляет 10 000 временных шагов. Для всех случаев мы выполнили 5 независимых симуляций с разными случайными затравками для распределения атомов по скоростям. Усредненное значение 5 симуляций используется для прогнозов теплопроводности.
Количество атомов газа усредняется за последние 400 000 шагов как содержание газа для различных давлений. На втором этапе ячейка моделирования, включающая твердое тело и газ, сначала достигает равновесного состояния в ансамбле НВТ при 20 К. Затем по формуле Грина-Кубо рассчитывается теплопроводность нанопористой системы. Вектор теплового потока регистрируется каждые 5 временных шагов в ансамбле NVE для 5 × 10 7 временных шагов. Время корреляции составляет 10 000 временных шагов. Для всех случаев мы выполнили 5 независимых симуляций с разными случайными затравками для распределения атомов по скоростям. Усредненное значение 5 симуляций используется для прогнозов теплопроводности.На рис. 2 показаны автокорреляционные функции теплового потока (HFACF), отвечающие уравнению (1) для нанопористой системы. Мы можем обнаружить, что HFACF постепенно приближается к нулю примерно через 10 пс, что также доказывает, что время корреляции 50 пс, используемое в нашем моделировании, достаточно велико для получения стабильной теплопроводности.
 Текущая теплопроводность получена на основе HFACF, которая стабилизируется на уровне около 0,14 Вт м 9 .0047 −1 K −1 после 20 пс.
Текущая теплопроводность получена на основе HFACF, которая стабилизируется на уровне около 0,14 Вт м 9 .0047 −1 K −1 после 20 пс.3. Результаты
3.1. Эффект давления
На рис. 3 и 4 показано распределение атомов газа в нанопористой системе (L = 12S, l = 4S и L = 12S, l = 8S). Мы используем постоянную решетки S в качестве радиуса отсечки для проведения кластерного анализа для системы газ-твердое тело. Атомы газа вблизи твердой фазы рассматриваются как адсорбированное состояние, а остальные рассматриваются как свободные атомы. Общее количество атомов газа в нанопористых системах увеличивается с давлением. Однако для системы L = 12S, l = 8S свободные атомы газа не зависят от давления из-за ограниченности пространства. Зависимость теплопроводности нанопористой системы (L = 12S, l = 4S и L = 12S, l = 8S) от давления показана на рис. 5. Суммарная теплопроводность системы l = 8S выше, чем у системы l = 4S в диапазоне от 0 до 4 атм из-за высокой теплопроводности твердой фазы (давление = 0).
 Для нанопористой системы с l = 4S общая теплопроводность увеличивается с более высоким давлением или газовой нагрузкой, что связано с увеличением количества свободных атомов газа, что соответствует лучшей способности к теплопередаче. Полученная теплопроводность для l = 8S практически не изменяется при изменении давления. Это связано с тем, что в нанопористой системе практически отсутствуют свободные атомы газа, а в общей теплопроводности преобладает твердая фаза.
Для нанопористой системы с l = 4S общая теплопроводность увеличивается с более высоким давлением или газовой нагрузкой, что связано с увеличением количества свободных атомов газа, что соответствует лучшей способности к теплопередаче. Полученная теплопроводность для l = 8S практически не изменяется при изменении давления. Это связано с тем, что в нанопористой системе практически отсутствуют свободные атомы газа, а в общей теплопроводности преобладает твердая фаза.3.2. Структурный эффект
На практике нанопористые материалы имеют различные структурные особенности в зависимости от метода и условий приготовления. Между тем структура также оказывает существенное влияние на общую теплопроводность нанопористой системы. Теплопроводность имитационной единицы, использующей различные конструктивные параметры при одном и том же давлении, получается, как показано на Рисунке 6 и Рисунке 7. Когда длина (L) имитирующей единицы увеличивается, теплопроводность системы сначала уменьшается, а затем уменьшается.
 достигают минимума примерно через 10 с, затем увеличиваются. Первоначальное снижение теплопроводности связано с увеличением пористости, при которой твердая фаза является основным фактором, определяющим общую теплопроводность. По мере того, как длина (L) модуля моделирования продолжает увеличиваться, количество атомов газа и теплопроводность соответствующего газа будут увеличиваться. Для той же длины (L) модуля моделирования увеличение ширины твердого каркаса приведет к быстрому увеличению общей теплопроводности, что в основном связано с увеличением теплопроводности твердой фазы. Хотя атомы газа в этой ситуации уменьшаются, влияние твердой фазы более очевидно и приводит к увеличению общей теплопроводности, как показано на рис. 7.9.0011
достигают минимума примерно через 10 с, затем увеличиваются. Первоначальное снижение теплопроводности связано с увеличением пористости, при которой твердая фаза является основным фактором, определяющим общую теплопроводность. По мере того, как длина (L) модуля моделирования продолжает увеличиваться, количество атомов газа и теплопроводность соответствующего газа будут увеличиваться. Для той же длины (L) модуля моделирования увеличение ширины твердого каркаса приведет к быстрому увеличению общей теплопроводности, что в основном связано с увеличением теплопроводности твердой фазы. Хотя атомы газа в этой ситуации уменьшаются, влияние твердой фазы более очевидно и приводит к увеличению общей теплопроводности, как показано на рис. 7.9.00113.3. Взаимодействие газ-твердое тело
Чтобы соответствовать условиям применения, нанопористые материалы могут потребовать модификации поверхности, при которой изменяется взаимодействие газ-твердое тело. До сих пор неясно, как зависит теплопроводность нанопористой системы от взаимодействия газ-твердое тело.
 В нашем моделировании параметр энергии ε, используемый в потенциале Леннарда-Джонса 12-6, может быть скорректирован, чтобы представить этот вид модификации поверхности как упрощение. ε/ε газ-твердое вещество в диапазоне от 0,3 до 1 используется при моделировании при том же давлении и газовой нагрузке. На рис. 8 и рис. 9 показаны результаты распределения атомов газа и общей теплопроводности для разных значений ε при одном и том же давлении. Атомы газа в нанопористой системе увеличиваются из-за сильного взаимодействия газ-твердое тело и демонстрируют хорошие адсорбционные характеристики с увеличением ε. Однако, как показано на рис. 9, теплопроводность нанопористой системы стабилизируется на уровне около 0,24 Вт·м 9 .0047 -1 К -1 . Взаимодействие атомов твердого тела и газа мало влияет на теплопроводность при том же давлении. Это связано с тем, что, хотя общее количество атомов газа увеличивается из-за сильного взаимодействия газ-твердое тело, увеличенное количество атомов газа находится в адсорбированном состоянии, которое вносит небольшой вклад в теплообмен в нанопористой системе.
В нашем моделировании параметр энергии ε, используемый в потенциале Леннарда-Джонса 12-6, может быть скорректирован, чтобы представить этот вид модификации поверхности как упрощение. ε/ε газ-твердое вещество в диапазоне от 0,3 до 1 используется при моделировании при том же давлении и газовой нагрузке. На рис. 8 и рис. 9 показаны результаты распределения атомов газа и общей теплопроводности для разных значений ε при одном и том же давлении. Атомы газа в нанопористой системе увеличиваются из-за сильного взаимодействия газ-твердое тело и демонстрируют хорошие адсорбционные характеристики с увеличением ε. Однако, как показано на рис. 9, теплопроводность нанопористой системы стабилизируется на уровне около 0,24 Вт·м 9 .0047 -1 К -1 . Взаимодействие атомов твердого тела и газа мало влияет на теплопроводность при том же давлении. Это связано с тем, что, хотя общее количество атомов газа увеличивается из-за сильного взаимодействия газ-твердое тело, увеличенное количество атомов газа находится в адсорбированном состоянии, которое вносит небольшой вклад в теплообмен в нанопористой системе. Однако, согласно уравнению состояния идеального газа, свободные атомы газа, участвующие в процессе теплопроводности, практически одинаковы при одном и том же давлении. Следовательно, теплопроводность нанопористой системы стабильна и не зависит от взаимодействия газ-твердое тело при одном и том же давлении.
Однако, согласно уравнению состояния идеального газа, свободные атомы газа, участвующие в процессе теплопроводности, практически одинаковы при одном и том же давлении. Следовательно, теплопроводность нанопористой системы стабильна и не зависит от взаимодействия газ-твердое тело при одном и том же давлении.4. Обсуждение
В предыдущей работе [20] изучался теплообмен в пористых кристаллах, содержащих адсорбированные газы. Результаты показали, что в теплопроводности системы преобладает теплопроводность кристалла и снижается по мере увеличения концентрации газа в порах. Уменьшение проводимости при увеличении концентрации газа связано с фононным рассеянием кристалла, вызванным взаимодействием с атомами газа. В нашем моделировании аналогичные результаты не получены для пористой кристаллической системы. Следовательно, в таких системах общая теплопроводность является результатом множества факторов, включая концентрацию газа, коэффициент диффузии, свойства материала, структурные параметры и так далее.
 Влияние давления на общую теплопроводность представляет различные характеристики для нанопористой системы.
Влияние давления на общую теплопроводность представляет различные характеристики для нанопористой системы.Чтобы дополнительно проиллюстрировать влияние взаимодействия газа с твердым телом на общую теплопроводность, случай постоянных атомов газа для различных взаимодействий газа с твердым телом исследуется, как показано на рис. 10 и рис. 11. В системе L = 16S, l = 4S, мы можем найти, что атомы газа при ε/ε газ-твердое тело = 0,3, что означает более низкую поверхностную энергию, могли сохранять свободное состояние. Однако для случая ε/ε газ-твердое = 1 большинство атомов газа ограничены на поверхности и сохраняют поглощенное состояние, что не может способствовать теплообмену в пористых структурах, связывающих газовую и твердую фазы. Таким образом, общая теплопроводность резко снижается с 0,37 Вт м -1 К -1 до 0,11 Вт м -1 К -1 из-за различных состояний атомов газа. Влияние адсорбции на общую теплопроводность при постоянных атомах газа заметно, а свободные атомы газа необходимы для переноса тепла в пористых структурах, связывающих газовую и твердую фазы.

5. Выводы
В данной работе мы исследовали теплопроводность упорядоченных пористых структур с использованием Большого канонического метода Монте-Карло (GCMC) и молекулярно-динамического моделирования (МД). Выявлено влияние концентрации газа, пористой структуры и взаимодействия газа с твердым телом на теплопроводность.
Результаты моделирования показывают, что для различных конструкций влияние давления на теплопроводность проявляется непостоянно. При одном и том же давлении теплопроводность практически не меняется при различных взаимодействиях газовой и твердой фаз. Кроме того, существенное влияние на теплопроводность нанопористой системы оказывает состояние атомов газа, поглощенных или свободных. Из этого исследования теплопередача в пористых структурах, связывающих газовую и твердую фазы, может быть понята на фундаментальном уровне.
Вклад авторов
Концептуализация, Х.Г. и Д.Н.; методика, Д.Н.; программное обеспечение, Д.Н.; валидация, HG и DN; формальный анализ, Д.
 Н.; расследование, Д.Н.; ресурсы, Д.Н.; курирование данных, Д.Н.; написание – черновая подготовка, Д.Н.; написание-обзор и редактирование, Д.Н.; визуализация, Д.Н.; надзор, Х.Г.; администрация проекта, Х.Г.; приобретение финансирования, Х.Г. и Д.Н. Все авторы прочитали и согласились с опубликованной версией рукописи.
Н.; расследование, Д.Н.; ресурсы, Д.Н.; курирование данных, Д.Н.; написание – черновая подготовка, Д.Н.; написание-обзор и редактирование, Д.Н.; визуализация, Д.Н.; надзор, Х.Г.; администрация проекта, Х.Г.; приобретение финансирования, Х.Г. и Д.Н. Все авторы прочитали и согласились с опубликованной версией рукописи.Финансирование
Эта работа была поддержана Китайским фондом постдокторских наук (№ 2020M670725), Фондом ключевой лаборатории терможидкостной науки и техники (Сианьский университет Цзяотун), Министерством образования (KLTFSE2020KFJJ01), Фондами фундаментальных исследований для центральных университетов. (№3132019305).
Заявление Институционального контрольного совета
Неприменимо.
Заявление об информированном согласии
Неприменимо.
Заявление о доступности данных
Данные, представленные в этом исследовании, доступны по запросу у соответствующего автора.
Конфликт интересов
Авторы заявляют об отсутствии конфликта интересов.

Ссылки
- Reichenauer, G.; Хайнеманн, У .; Эберт, Х.П. Связь между размером пор и зависимостью газовой теплопроводности от давления газа. Коллоидный прибой. А-Физикохим. англ. Асп. 2007 , 300, 204–210. [Google Scholar] [CrossRef]
- Чжао, Дж. Дж.; Дуань, Ю.Ю.; Ван, XD; Ван, Б.Х. Влияние взаимодействия твердого тела с газом, а также микроструктуры пор и частиц на эффективную газовую теплопроводность в аэрогелях. Дж. Нанопарт. Рез. 2012 , 14, 1–15. [Google Scholar] [CrossRef]
- Bi, C.; Тан, GH; Ху, ZJ; Ян, HL; Ли, Дж.Н. Модель связи теплообмена между твердой и газовой фазами в аэрогеле и экспериментальное исследование. Междунар. J. Тепломассообмен. 2014 , 79, 126–136. [Google Scholar] [CrossRef]
- Хюммер, Э.; Лу, Х .; Реттельбах, Т .; Фрике, Дж. Теплопередача в непрозрачных порошках аэрогеля. J. Некристалл. Твердые вещества 1992 , 145, 211–216.
 [Академия Google] [CrossRef]
[Академия Google] [CrossRef] - Хембергер, Ф.; Вайс, С.; Райхенауэр, Г.; Эберт, Х.П. Теплотранспортные свойства функционально градиентных углеродных аэрогелей. Междунар. Дж. Термофиз. 2009 , 30, 1357–1371. [Google Scholar] [CrossRef][Зеленая версия]
- Хаясе, Г.; Кугимия, К .; Огава, М .; Кодера, Ю.; Канамори, К .; Наканиши, К. Теплопроводность полиметилсилсесквиоксановых аэрогелей и ксерогелей с порами различного размера для практического применения в качестве теплоизоляционных материалов. Дж. Матер. хим. А 2014 , 2, 6525–6531. [Google Scholar] [CrossRef]
- Хан, Ю.Ф.; Ся, XL; Тан, HP; Лю, Х.Д. Моделирование фононного теплообмена в сферическом сегменте зерен кремнеземного аэрогеля. физ. Б 2013 , 420, 58–63. [Google Scholar] [CrossRef]
- Li, Z.Y.; Чжу, CY; Чжао, Х.П. Теоретическое и численное исследование газовой теплопроводности в аэрогеле. Междунар. J. Тепломассообмен.
 2017 , 108, 1982–1990. [Google Scholar] [CrossRef]
2017 , 108, 1982–1990. [Google Scholar] [CrossRef] - Zhu, CY; Ли, З.Ю.; Тао, В.К. Теоретические и DSMC исследования теплопроводности газа, заключенного в кубовидную нанопору. Дж. Теплопередача. 2017 , 139, 052405. [Google Scholar] [CrossRef]
- Zhao, X.P.; Ли, З.Ю.; Лю, Х .; Тао, В.К. Расчет теплопроводности методом трехмерного прямого моделирования Монте-Карло. Дж. Наноски. нанотехнологии. 2015 , 15, 3299–3304. [Google Scholar] [CrossRef]
- Zhu, CY; Ли, З.Ю.; Панг, штаб-квартира; Пан, Н. Численное моделирование газовой теплопроводности аэрогелей. Междунар. J. Тепломассообмен. 2019 , 131, 217–225. [Академия Google] [CrossRef]
- Цюй З.Г.; Фу, Ю.Д.; Лю, Ю.; Чжоу, Л. Подход к прогнозированию эффективной теплопроводности аэрогелевых материалов с помощью модифицированного метода решетки Больцмана. заявл. Терм. англ. 2018 , 132, 730–739. [Google Scholar] [CrossRef] «> Fang, WZ; Чжан, Х .; Чен, Л.; Тао, В.К. Численные прогнозы теплопроводности кремнеземного аэрогеля и его композитов. заявл. Терм. англ. 2017 , 115, 1277–1286. [Google Scholar] [CrossRef]
- Tang, GH; Би, К.; Фу, Б. Теплопроводность в тонкой пленке нанопористого кремния. Дж. Заявл. физ. 2013 , 114, 184302. [Google Scholar] [CrossRef]
- Fu, B.; Тан, GH; Bi, C. Теплопроводность в наноструктурированных материалах и анализ локального угла между тепловыми потоками. Дж. Заявл. физ. 2014 , 116, 124310. [Google Scholar] [CrossRef]
- Coquil, T.; Фанг, Дж.; Пилон, Л. Молекулярно-динамическое исследование теплопроводности аморфного нанопористого кремнезема. Междунар. J. Тепломассообмен. 2011 , 54, 4540–4548. [Google Scholar] [CrossRef]
- Ng, TY; Йео, Джей Джей; Лю, З.С. Молекулярно-динамическое исследование теплопроводности аэрогеля нанопористого кремнезема, полученного разрывом при отрицательном давлении.
 J. Некристалл. Твердые вещества 2012 , 358, 1350–1355. [Google Scholar] [CrossRef]
J. Некристалл. Твердые вещества 2012 , 358, 1350–1355. [Google Scholar] [CrossRef] - Лю М.; Цю, Л.; Чжэн, XH; Чжу, Дж.; Тан, Д.В. Исследование термического сопротивления в цепочке вторичных частиц кремнеземного аэрогеля методом молекулярной динамики. Дж. Заявл. физ. 2014 , 116, 093503. [Google Scholar] [CrossRef]
- Рабани Р.; Хейдаринежад, Г.; Хартинг, Дж.; Ширани, Э. Влияние жесткости стенки, массы и потенциальной силы взаимодействия на характеристики теплопередачи наноразмерного газа. Междунар. J. Тепломассообмен. 2020 , 147, 118929. [Google Scholar] [CrossRef]
- Babaei, H.; Уилмер, К.Э. Механизмы теплопередачи в пористых кристаллах, содержащих адсорбированные газы: приложения к металлоорганическим каркасам. физ. Преподобный Летт. 2016 , 116, 025902. [Google Scholar] [CrossRef]
- Плимптон, С. Быстрые параллельные алгоритмы для молекулярной динамики ближнего действия.
 Дж. Вычисл. физ. 1995 , 117, 1–19. [Google Scholar] [CrossRef][Green Version]
Дж. Вычисл. физ. 1995 , 117, 1–19. [Google Scholar] [CrossRef][Green Version]
Рисунок 1. Настройка системы моделирования.
Рис. 1. Настройка системы моделирования.
Рисунок 2. HFACF и бегущая теплопроводность.
Рис. 2. HFACF и бегущая теплопроводность.
Рисунок 3. Распределение атомов газа в нанопористых системах.
Рис. 3. Распределение атомов газа в нанопористых системах.
Рисунок 4. Общее и количество свободных атомов газа в нанопористых системах.
Рис. 4. Общее и количество свободных атомов газа в нанопористых системах.
Рисунок 5. Теплопроводность как функция давления.
Рис. 5. Теплопроводность как функция давления.
Рисунок 6. Теплопроводность для разных единиц длины (L).
Рис. 6. Теплопроводность для разных единиц длины (L).
Рис. 7. Теплопроводность для разной ширины (l).

Рис. 7. Теплопроводность для разной ширины (l).
Рис. 8. Распределение атомов газа для разных ε при давлении 2 атм.
Рис. 8. Распределение атомов газа для разных ε при давлении 2 атм.
Рис. 9. Число атомов газа и теплопроводность для различных ε при давлении 2 атм.
Рис. 9. Число атомов газа и теплопроводность для различных ε при давлении 2 атм.
Рисунок 10. Распределение атомов газа для различных ε при постоянном числе атомов газа.
Рис. 10. Распределение атомов газа для различных ε при постоянном числе атомов газа.
Рисунок 11. Поглощенные атомы и теплопроводность для постоянных атомов газа.
Рис. 11. Поглощенные атомы и теплопроводность для постоянных атомов газа.
Таблица 1. Параметры, используемые в моделировании.
Таблица 1. Параметры, используемые в моделировании.
Material ε (kcal/mol) σ (Å) l (S) L (S) Argon 0. 

 Выявлено влияние концентрации газа (давления) и взаимодействия твердого тела с газом на теплопроводность. Результаты моделирования показывают, что для различных структур каркаса влияние давления на теплопроводность представляет собой непоследовательный режим, который отличается от предыдущих исследований. При одном и том же давлении теплопроводность практически не меняется при различных взаимодействиях газовой и твердой фаз. Это исследование обеспечивает возможность прямого расчета теплопроводности для пористых структур, связывающих газовую и твердую фазы, с использованием моделирования молекулярной динамики. Теплопередачу в пористых структурах, содержащих газ, можно понять на фундаментальном уровне.
Выявлено влияние концентрации газа (давления) и взаимодействия твердого тела с газом на теплопроводность. Результаты моделирования показывают, что для различных структур каркаса влияние давления на теплопроводность представляет собой непоследовательный режим, который отличается от предыдущих исследований. При одном и том же давлении теплопроводность практически не меняется при различных взаимодействиях газовой и твердой фаз. Это исследование обеспечивает возможность прямого расчета теплопроводности для пористых структур, связывающих газовую и твердую фазы, с использованием моделирования молекулярной динамики. Теплопередачу в пористых структурах, содержащих газ, можно понять на фундаментальном уровне.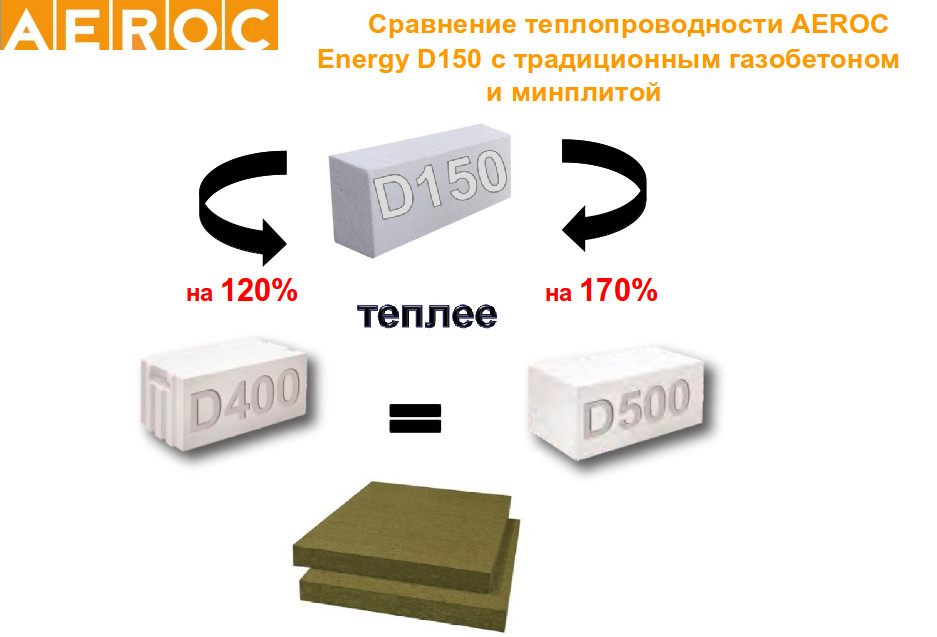 д. Теплоперенос в пористых материалах, содержащих газовую фазу, является важным процессом, который невозможно полностью понять на фундаментальном уровне, особенно для нанопористых материалов. Точное предсказание теплопроводности нанопористых материалов крайне необходимо для применения.
д. Теплоперенос в пористых материалах, содержащих газовую фазу, является важным процессом, который невозможно полностью понять на фундаментальном уровне, особенно для нанопористых материалов. Точное предсказание теплопроводности нанопористых материалов крайне необходимо для применения. Результаты моделирования показали, что распределение температуры в зерне кремнеземного аэрогеля сильно зависит от размера, а рассеяние фононов на граничных поверхностях становится более заметным при уменьшении размера зерен. Ли и др. В работе [8] разработана модифицированная модель для прогнозирования газовой теплопроводности в нанопористых материалах на основе метода прямого моделирования Монте-Карло (DSMC). Результаты показали, что модифицированная модель имеет более высокую точность без сложных расчетов и допущений. Влияние размера на теплопроводность газа изучалось методом ПСМ [9].]. На границе существует очевидный скачок температуры, и теплопроводность имеет тенденцию к уменьшению при увеличении числа Кнудсена от 0,01 до 0,1. Чжао и др. В работе [10] получена газовая теплопроводность азота с использованием трехмерного метода DSMC с переменной моделью столкновения мягких сфер. Результаты согласуются с экспериментальными данными, но намного выше, чем по соотношению Эйкена, особенно при высокой температуре.
Результаты моделирования показали, что распределение температуры в зерне кремнеземного аэрогеля сильно зависит от размера, а рассеяние фононов на граничных поверхностях становится более заметным при уменьшении размера зерен. Ли и др. В работе [8] разработана модифицированная модель для прогнозирования газовой теплопроводности в нанопористых материалах на основе метода прямого моделирования Монте-Карло (DSMC). Результаты показали, что модифицированная модель имеет более высокую точность без сложных расчетов и допущений. Влияние размера на теплопроводность газа изучалось методом ПСМ [9].]. На границе существует очевидный скачок температуры, и теплопроводность имеет тенденцию к уменьшению при увеличении числа Кнудсена от 0,01 до 0,1. Чжао и др. В работе [10] получена газовая теплопроводность азота с использованием трехмерного метода DSMC с переменной моделью столкновения мягких сфер. Результаты согласуются с экспериментальными данными, но намного выше, чем по соотношению Эйкена, особенно при высокой температуре. Нанопористые аэрогели были реконструированы с помощью усовершенствованного метода трехмерной кластерно-кластерной агрегации с ограничением диффузии (DLCA), в котором количественно определялся вклад теплопередачи твердого тела-газа в теплопроводность, обусловленную газом [11]. Для прогнозирования эффективной теплопроводности нанопористых аэрогелевых материалов был разработан модифицированный решеточный метод Больцмана [12], который ввел дополнительный коэффициент для регулирования разницы теплопроводности между твердой и газовой фазами и гарантировал конвергентное решение. Фанг и др. В работе [13] решеточный метод Больцмана использовался для решения уравнения проводимости-излучения для предсказания эффективной теплопроводности. Результаты моделирования показали, что эффективная теплопроводность чистого нанопористого аэрогеля быстро увеличивается с температурой и сильно снижается при легировании добавками. Теплопроводность нанопористой пленки и нанокомпозита численно исследовалась путем решения фононного уравнения переноса Больцмана с частотно-зависимой моделью [14].
Нанопористые аэрогели были реконструированы с помощью усовершенствованного метода трехмерной кластерно-кластерной агрегации с ограничением диффузии (DLCA), в котором количественно определялся вклад теплопередачи твердого тела-газа в теплопроводность, обусловленную газом [11]. Для прогнозирования эффективной теплопроводности нанопористых аэрогелевых материалов был разработан модифицированный решеточный метод Больцмана [12], который ввел дополнительный коэффициент для регулирования разницы теплопроводности между твердой и газовой фазами и гарантировал конвергентное решение. Фанг и др. В работе [13] решеточный метод Больцмана использовался для решения уравнения проводимости-излучения для предсказания эффективной теплопроводности. Результаты моделирования показали, что эффективная теплопроводность чистого нанопористого аэрогеля быстро увеличивается с температурой и сильно снижается при легировании добавками. Теплопроводность нанопористой пленки и нанокомпозита численно исследовалась путем решения фононного уравнения переноса Больцмана с частотно-зависимой моделью [14]. Был введен локальный угол между тепловыми потоками и локальным тепловым потоком, и все результаты показали, что наноструктурный материал с большим средним углом будет иметь меньшую теплопроводность. Танг и др. [15] исследовали теплопроводность тонкой пленки нанопористого кремния с использованием метода дискретных ординат (DOM). Учитывались эффекты толщины, пористости и пористой структуры. Численные результаты показали, что нанопоры способны резко снижать теплопроводность тонкой пленки кремния за счет граничного рассеяния фононов.
Был введен локальный угол между тепловыми потоками и локальным тепловым потоком, и все результаты показали, что наноструктурный материал с большим средним углом будет иметь меньшую теплопроводность. Танг и др. [15] исследовали теплопроводность тонкой пленки нанопористого кремния с использованием метода дискретных ординат (DOM). Учитывались эффекты толщины, пористости и пористой структуры. Численные результаты показали, что нанопоры способны резко снижать теплопроводность тонкой пленки кремния за счет граничного рассеяния фононов.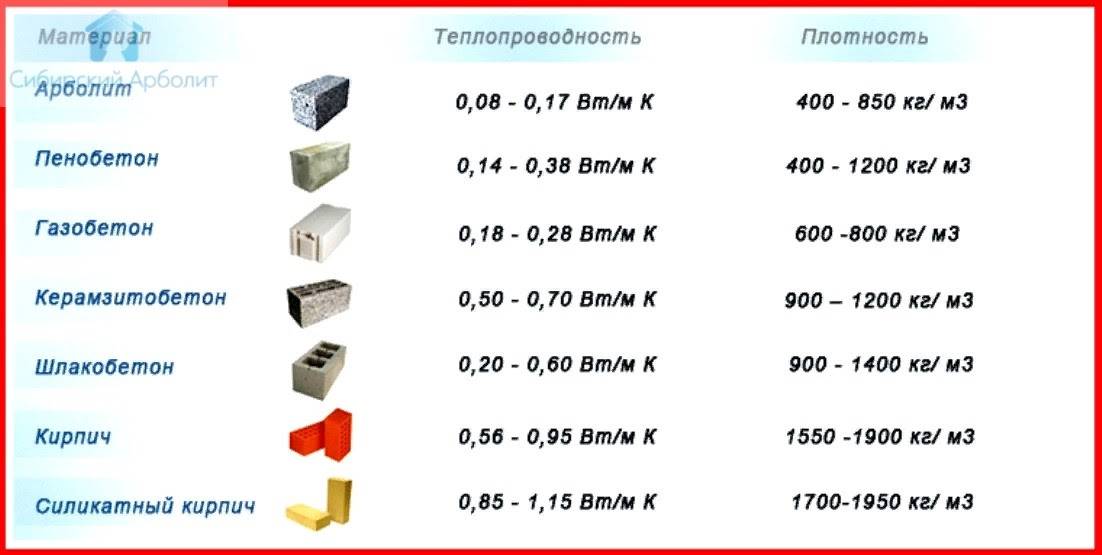 Нг и др. В работе [17] исследована теплопроводность образцов нанопористого аэрогеля различной плотности путем разрыва плотных образцов кремнезема отрицательным давлением. Результаты показали, что степенная зависимость теплопроводности изменяется почти линейно с плотностью, при этом уменьшение плотности и увеличение пористости приведет к линейному уменьшению теплопроводности. Теплоперенос в цепочке вторичных частиц аэрогеля нанопористого кремнезема изучался с помощью молекулярно-динамического моделирования [18]. Перенос тепла подавлялся, когда длина контакта или концентрация дефектов увеличивались, а ограничивающий эффект был гораздо более очевидным, когда доля длины контакта находилась в небольшом диапазоне. Характеристики теплопередачи наноразмерного газа исследовались методом молекулярно-динамического моделирования [19].]. Рассмотрено влияние силового поля стенки, жесткости стенки и потенциальной напряженности взаимодействия стенка-газ на эффективную теплопроводность. Babaei и Wilmer [20] исследовали механизмы переноса тепла в системе пористый кристалл-газовая смесь с помощью молекулярно-динамического моделирования.
Нг и др. В работе [17] исследована теплопроводность образцов нанопористого аэрогеля различной плотности путем разрыва плотных образцов кремнезема отрицательным давлением. Результаты показали, что степенная зависимость теплопроводности изменяется почти линейно с плотностью, при этом уменьшение плотности и увеличение пористости приведет к линейному уменьшению теплопроводности. Теплоперенос в цепочке вторичных частиц аэрогеля нанопористого кремнезема изучался с помощью молекулярно-динамического моделирования [18]. Перенос тепла подавлялся, когда длина контакта или концентрация дефектов увеличивались, а ограничивающий эффект был гораздо более очевидным, когда доля длины контакта находилась в небольшом диапазоне. Характеристики теплопередачи наноразмерного газа исследовались методом молекулярно-динамического моделирования [19].]. Рассмотрено влияние силового поля стенки, жесткости стенки и потенциальной напряженности взаимодействия стенка-газ на эффективную теплопроводность. Babaei и Wilmer [20] исследовали механизмы переноса тепла в системе пористый кристалл-газовая смесь с помощью молекулярно-динамического моделирования. Исследование показало, что в теплопроводности системы преобладает кристалл, который снижается по мере увеличения концентрации газа в порах. Пониженная проводимость, связанная с увеличением концентрации газа, связана с рассеянием фононов кристаллом, вызванным взаимодействием с молекулами газа.
Исследование показало, что в теплопроводности системы преобладает кристалл, который снижается по мере увеличения концентрации газа в порах. Пониженная проводимость, связанная с увеличением концентрации газа, связана с рассеянием фононов кристаллом, вызванным взаимодействием с молекулами газа. Ячейка моделирования, включающая газ и твердое тело, получается из упорядоченных пористых структур пересекающихся квадратных стержней, как показано на рис. Периодическое граничное условие используется во всех направлениях. В качестве твердой фазы упорядоченных пористых структур, заполненных газом гелия при 20 К, выбран аргон. Твердый аргон представляет собой гранецентрированный кубический кристалл с периодом решетки S = 5,4 Å. Потенциал Леннарда-Джонса 12–6, E = 4 ε [( σ / r ) 12 − ( σ / r ) 6 ] 14 Å. Подробные параметры, используемые в нашем моделировании, перечислены как в . Ансамбль NVT, который поддерживает постоянным число атомов, объем и температуру, используется с термостатом Нозе-Гувера при 20 K с временным шагом 5 фс.
Ячейка моделирования, включающая газ и твердое тело, получается из упорядоченных пористых структур пересекающихся квадратных стержней, как показано на рис. Периодическое граничное условие используется во всех направлениях. В качестве твердой фазы упорядоченных пористых структур, заполненных газом гелия при 20 К, выбран аргон. Твердый аргон представляет собой гранецентрированный кубический кристалл с периодом решетки S = 5,4 Å. Потенциал Леннарда-Джонса 12–6, E = 4 ε [( σ / r ) 12 − ( σ / r ) 6 ] 14 Å. Подробные параметры, используемые в нашем моделировании, перечислены как в . Ансамбль NVT, который поддерживает постоянным число атомов, объем и температуру, используется с термостатом Нозе-Гувера при 20 K с временным шагом 5 фс.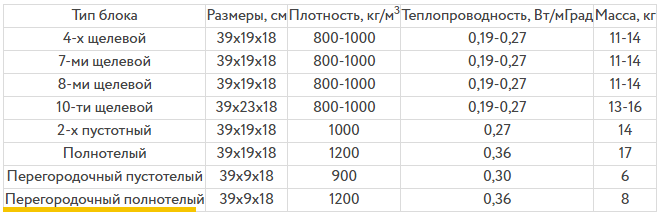 Микроскопический тепловой поток j получается из следующего уравнения
Микроскопический тепловой поток j получается из следующего уравнения Газ гелия рассматривается как идеальный газ и химический потенциал μ можно определить, используя давление P , заданное формулой μ = k b T ln( Pφ / k b T ), где Количество атомов газа усредняется за последние 400 000 шагов как содержание газа для различных давлений. На втором этапе ячейка моделирования, включающая твердое тело и газ, сначала достигает равновесного состояния в ансамбле НВТ при 20 К. Затем по формуле Грина-Кубо рассчитывается теплопроводность нанопористой системы. Вектор теплового потока регистрируется каждые 5 временных шагов в ансамбле NVE для 5 × 10 7 временных шагов. Время корреляции составляет 10 000 временных шагов. Для всех случаев мы выполнили 5 независимых симуляций с разными случайными затравками для распределения атомов по скоростям. Усредненное значение 5 симуляций используется для прогнозов теплопроводности.
Газ гелия рассматривается как идеальный газ и химический потенциал μ можно определить, используя давление P , заданное формулой μ = k b T ln( Pφ / k b T ), где Количество атомов газа усредняется за последние 400 000 шагов как содержание газа для различных давлений. На втором этапе ячейка моделирования, включающая твердое тело и газ, сначала достигает равновесного состояния в ансамбле НВТ при 20 К. Затем по формуле Грина-Кубо рассчитывается теплопроводность нанопористой системы. Вектор теплового потока регистрируется каждые 5 временных шагов в ансамбле NVE для 5 × 10 7 временных шагов. Время корреляции составляет 10 000 временных шагов. Для всех случаев мы выполнили 5 независимых симуляций с разными случайными затравками для распределения атомов по скоростям. Усредненное значение 5 симуляций используется для прогнозов теплопроводности. Мы можем обнаружить, что HFACF постепенно приближается к нулю примерно через 10 пс, что также доказывает, что время корреляции 50 пс, используемое в нашем моделировании, достаточно велико для получения стабильной теплопроводности. Текущая теплопроводность получена на основе HFACF, которая стабилизируется на уровне около 0,14 Вт м 9 .0047 −1 K −1 после 20 пс.
Мы можем обнаружить, что HFACF постепенно приближается к нулю примерно через 10 пс, что также доказывает, что время корреляции 50 пс, используемое в нашем моделировании, достаточно велико для получения стабильной теплопроводности. Текущая теплопроводность получена на основе HFACF, которая стабилизируется на уровне около 0,14 Вт м 9 .0047 −1 K −1 после 20 пс. Однако для системы L = 12 S , l = 8 S , атомы свободного газа не зависят от давления из-за ограниченного пространства. Теплопроводность нанопористой системы ( л = 12 с , л = 4 с и л = 12 с , л = 8 с) как функция давления Показано в . Суммарная теплопроводность л = 8 С выше, чем у системы л = 4 S в диапазоне от 0 до 4 атм из-за высокой теплопроводности твердой фазы (давление = 0). Для нанопористой системы l = 4 S общая теплопроводность увеличивается с более высоким давлением или газовой нагрузкой, что связано с увеличением количества свободных атомов газа, что соответствует лучшей способности к теплопередаче. Полученная теплопроводность для л = 8 С практически не изменяется при изменении давления. Это связано с тем, что в нанопористой системе практически отсутствуют свободные атомы газа, а в общей теплопроводности преобладает твердая фаза.
Однако для системы L = 12 S , l = 8 S , атомы свободного газа не зависят от давления из-за ограниченного пространства. Теплопроводность нанопористой системы ( л = 12 с , л = 4 с и л = 12 с , л = 8 с) как функция давления Показано в . Суммарная теплопроводность л = 8 С выше, чем у системы л = 4 S в диапазоне от 0 до 4 атм из-за высокой теплопроводности твердой фазы (давление = 0). Для нанопористой системы l = 4 S общая теплопроводность увеличивается с более высоким давлением или газовой нагрузкой, что связано с увеличением количества свободных атомов газа, что соответствует лучшей способности к теплопередаче. Полученная теплопроводность для л = 8 С практически не изменяется при изменении давления. Это связано с тем, что в нанопористой системе практически отсутствуют свободные атомы газа, а в общей теплопроводности преобладает твердая фаза.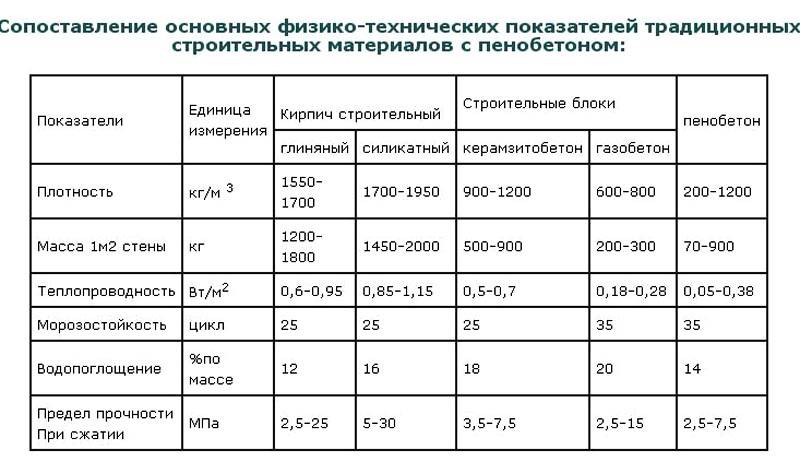
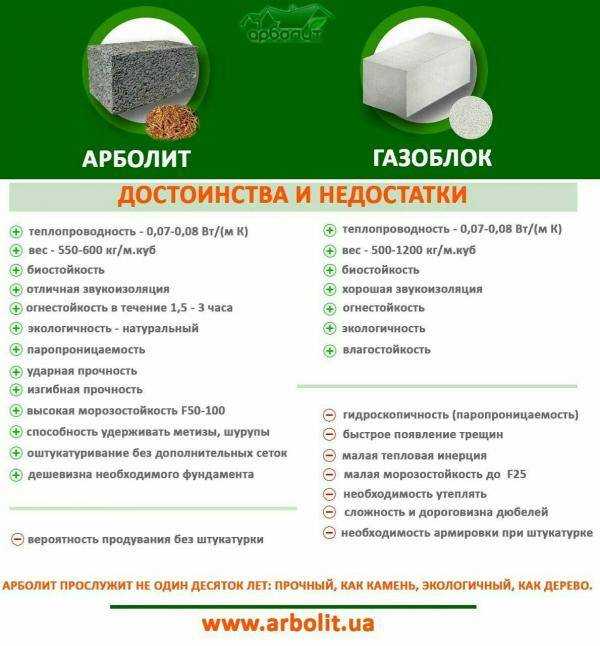 По мере того, как длина ( L ) модуля моделирования продолжает увеличиваться, количество атомов газа и теплопроводность соответствующего газа будут увеличиваться. Для той же длины ( L ) модуля моделирования увеличение ширины твердого каркаса приведет к быстрому увеличению общей теплопроводности, что в основном связано с увеличением теплопроводности твердой фазы. Хотя атомы газа в этой ситуации уменьшаются, влияние твердой фазы более очевидно и приводит к увеличению общей теплопроводности, как показано на рис.
По мере того, как длина ( L ) модуля моделирования продолжает увеличиваться, количество атомов газа и теплопроводность соответствующего газа будут увеличиваться. Для той же длины ( L ) модуля моделирования увеличение ширины твердого каркаса приведет к быстрому увеличению общей теплопроводности, что в основном связано с увеличением теплопроводности твердой фазы. Хотя атомы газа в этой ситуации уменьшаются, влияние твердой фазы более очевидно и приводит к увеличению общей теплопроводности, как показано на рис. В нашем моделировании энергетический параметр ε , используемый в потенциале Леннарда-Джонса 12-6, может быть скорректирован, чтобы представить этот вид модификации поверхности как упрощение. ε / ε газ-твердое тело в диапазоне от 0,3 до 1 используется при моделировании при том же давлении и газовой нагрузке. и показать результаты распределения атомов газа и общей теплопроводности для различных ε при одном и том же давлении. Атомы газа в нанопористой системе увеличиваются из-за сильного взаимодействия газ-твердое тело и демонстрируют хорошие адсорбционные характеристики с увеличенным ε . Однако, как показано в , теплопроводность нанопористой системы стабилизируется на уровне около 0,24 Вт м -1 К -1 . Взаимодействие атомов твердого тела и газа мало влияет на теплопроводность при том же давлении. Это связано с тем, что, хотя общее количество атомов газа увеличивается из-за сильного взаимодействия газ-твердое тело, увеличенное количество атомов газа находится в адсорбированном состоянии, которое вносит небольшой вклад в теплообмен в нанопористой системе.
В нашем моделировании энергетический параметр ε , используемый в потенциале Леннарда-Джонса 12-6, может быть скорректирован, чтобы представить этот вид модификации поверхности как упрощение. ε / ε газ-твердое тело в диапазоне от 0,3 до 1 используется при моделировании при том же давлении и газовой нагрузке. и показать результаты распределения атомов газа и общей теплопроводности для различных ε при одном и том же давлении. Атомы газа в нанопористой системе увеличиваются из-за сильного взаимодействия газ-твердое тело и демонстрируют хорошие адсорбционные характеристики с увеличенным ε . Однако, как показано в , теплопроводность нанопористой системы стабилизируется на уровне около 0,24 Вт м -1 К -1 . Взаимодействие атомов твердого тела и газа мало влияет на теплопроводность при том же давлении. Это связано с тем, что, хотя общее количество атомов газа увеличивается из-за сильного взаимодействия газ-твердое тело, увеличенное количество атомов газа находится в адсорбированном состоянии, которое вносит небольшой вклад в теплообмен в нанопористой системе. Однако, согласно уравнению состояния идеального газа, свободные атомы газа, участвующие в процессе теплопроводности, практически одинаковы при одном и том же давлении. Следовательно, теплопроводность нанопористой системы стабильна и не зависит от взаимодействия газ-твердое тело при одном и том же давлении.
Однако, согласно уравнению состояния идеального газа, свободные атомы газа, участвующие в процессе теплопроводности, практически одинаковы при одном и том же давлении. Следовательно, теплопроводность нанопористой системы стабильна и не зависит от взаимодействия газ-твердое тело при одном и том же давлении. Следовательно, в таких системах общая теплопроводность является результатом множества факторов, включая концентрацию газа, коэффициент диффузии, свойства материала, структурные параметры и так далее. Влияние давления на общую теплопроводность представляет различные характеристики для нанопористой системы.
Следовательно, в таких системах общая теплопроводность является результатом множества факторов, включая концентрацию газа, коэффициент диффузии, свойства материала, структурные параметры и так далее. Влияние давления на общую теплопроводность представляет различные характеристики для нанопористой системы. Таким образом, общая теплопроводность резко уменьшается с 0,37 Вт·м·–1··K·–1· до 0,11 Вт·м·–1··K·–1· из-за различных состояний атомов газа. Влияние адсорбции на общую теплопроводность при постоянных атомах газа заметно, а свободные атомы газа необходимы для переноса тепла в пористых структурах, связывающих газовую и твердую фазы.
Таким образом, общая теплопроводность резко уменьшается с 0,37 Вт·м·–1··K·–1· до 0,11 Вт·м·–1··K·–1· из-за различных состояний атомов газа. Влияние адсорбции на общую теплопроводность при постоянных атомах газа заметно, а свободные атомы газа необходимы для переноса тепла в пористых структурах, связывающих газовую и твердую фазы. При одном и том же давлении теплопроводность практически не меняется при различных взаимодействиях газовой и твердой фаз. Кроме того, существенное влияние на теплопроводность нанопористой системы оказывает состояние атомов газа, поглощенных или свободных. Из этого исследования теплопередача в пористых структурах, связывающих газовую и твердую фазы, может быть понята на фундаментальном уровне.
При одном и том же давлении теплопроводность практически не меняется при различных взаимодействиях газовой и твердой фаз. Кроме того, существенное влияние на теплопроводность нанопористой системы оказывает состояние атомов газа, поглощенных или свободных. Из этого исследования теплопередача в пористых структурах, связывающих газовую и твердую фазы, может быть понята на фундаментальном уровне.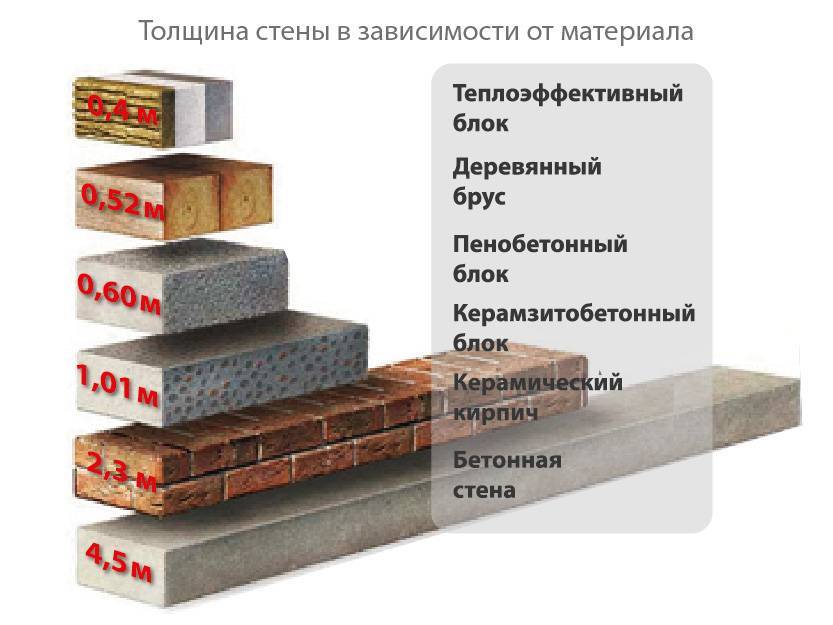 (№3132019305).
(№3132019305). L., Li J.N. Модель связи теплообмена между твердой и газовой фазами в аэрогеле и экспериментальное исследование. Междунар. J. Тепломассообмен. 2014;79:126–136. doi: 10.1016/j.ijheatmasstransfer.2014.07.098. [CrossRef] [Google Scholar]
L., Li J.N. Модель связи теплообмена между твердой и газовой фазами в аэрогеле и экспериментальное исследование. Междунар. J. Тепломассообмен. 2014;79:126–136. doi: 10.1016/j.ijheatmasstransfer.2014.07.098. [CrossRef] [Google Scholar] Хан Ю.Ф., Ся С.Л., Тан Х.П., Лю Х.Д. Моделирование фононного теплообмена в сферическом сегменте зерен кремнеземного аэрогеля. физ. Б. 2013; 420:58–63. doi: 10.1016/j.physb.2013.03.015. [CrossRef] [Google Scholar]
Хан Ю.Ф., Ся С.Л., Тан Х.П., Лю Х.Д. Моделирование фононного теплообмена в сферическом сегменте зерен кремнеземного аэрогеля. физ. Б. 2013; 420:58–63. doi: 10.1016/j.physb.2013.03.015. [CrossRef] [Google Scholar] Междунар. J. Тепломассообмен. 2019;131:217–225. doi: 10.1016/j.ijheatmasstransfer.2018.11.052. [CrossRef] [Google Scholar]
Междунар. J. Тепломассообмен. 2019;131:217–225. doi: 10.1016/j.ijheatmasstransfer.2018.11.052. [CrossRef] [Google Scholar]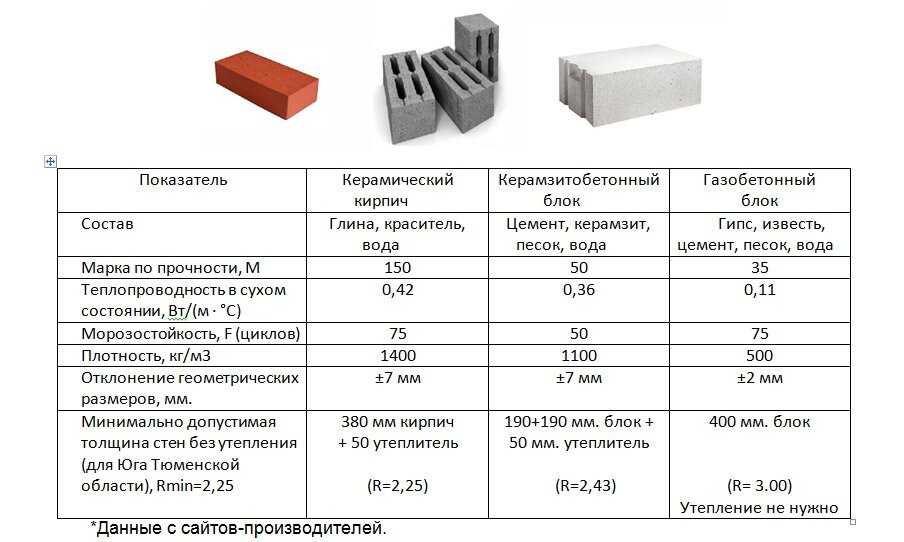 doi: 10.1063/1.4896551. [CrossRef] [Google Scholar]
doi: 10.1063/1.4896551. [CrossRef] [Google Scholar] Междунар. J. Тепломассообмен. 2020;147:118929. doi: 10.1016/j.ijheatmasstransfer.2019.118929. [CrossRef] [Google Scholar]
Междунар. J. Тепломассообмен. 2020;147:118929. doi: 10.1016/j.ijheatmasstransfer.2019.118929. [CrossRef] [Google Scholar] д. Теплоперенос в пористых материалах, содержащих газовую фазу, является важным процессом, который невозможно полностью понять на фундаментальном уровне, особенно для нанопористых материалов. Точное предсказание теплопроводности нанопористых материалов крайне необходимо для применения.
д. Теплоперенос в пористых материалах, содержащих газовую фазу, является важным процессом, который невозможно полностью понять на фундаментальном уровне, особенно для нанопористых материалов. Точное предсказание теплопроводности нанопористых материалов крайне необходимо для применения.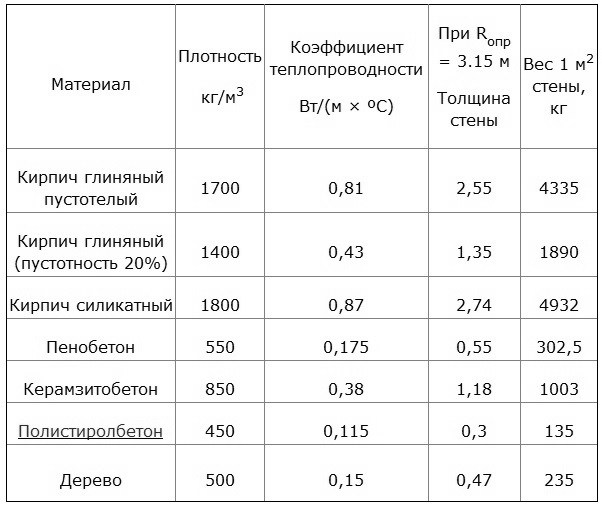 Результаты моделирования показали, что распределение температуры в зерне кремнеземного аэрогеля сильно зависит от размера, а рассеяние фононов на граничных поверхностях становится более заметным при уменьшении размера зерен. Ли и др. В работе [8] разработана модифицированная модель для прогнозирования газовой теплопроводности в нанопористых материалах на основе метода прямого моделирования Монте-Карло (DSMC). Результаты показали, что модифицированная модель имеет более высокую точность без сложных расчетов и допущений. Влияние размера на теплопроводность газа изучалось методом ПСМ [9].]. На границе существует очевидный скачок температуры, и теплопроводность имеет тенденцию к уменьшению при увеличении числа Кнудсена от 0,01 до 0,1. Чжао и др. В работе [10] получена газовая теплопроводность азота с использованием трехмерного метода DSMC с переменной моделью столкновения мягких сфер. Результаты согласуются с экспериментальными данными, но намного выше, чем по соотношению Эйкена, особенно при высокой температуре.
Результаты моделирования показали, что распределение температуры в зерне кремнеземного аэрогеля сильно зависит от размера, а рассеяние фононов на граничных поверхностях становится более заметным при уменьшении размера зерен. Ли и др. В работе [8] разработана модифицированная модель для прогнозирования газовой теплопроводности в нанопористых материалах на основе метода прямого моделирования Монте-Карло (DSMC). Результаты показали, что модифицированная модель имеет более высокую точность без сложных расчетов и допущений. Влияние размера на теплопроводность газа изучалось методом ПСМ [9].]. На границе существует очевидный скачок температуры, и теплопроводность имеет тенденцию к уменьшению при увеличении числа Кнудсена от 0,01 до 0,1. Чжао и др. В работе [10] получена газовая теплопроводность азота с использованием трехмерного метода DSMC с переменной моделью столкновения мягких сфер. Результаты согласуются с экспериментальными данными, но намного выше, чем по соотношению Эйкена, особенно при высокой температуре. Нанопористые аэрогели были реконструированы с помощью усовершенствованного метода трехмерной кластерно-кластерной агрегации с ограничением диффузии (DLCA), в котором количественно определялся вклад теплопередачи твердого тела-газа в теплопроводность, обусловленную газом [11]. Для прогнозирования эффективной теплопроводности нанопористых аэрогелевых материалов был разработан модифицированный решеточный метод Больцмана [12], который ввел дополнительный коэффициент для регулирования разницы теплопроводности между твердой и газовой фазами и гарантировал конвергентное решение. Фанг и др. В работе [13] решеточный метод Больцмана использовался для решения уравнения проводимости-излучения для предсказания эффективной теплопроводности. Результаты моделирования показали, что эффективная теплопроводность чистого нанопористого аэрогеля быстро увеличивается с температурой и сильно снижается при легировании добавками. Теплопроводность нанопористой пленки и нанокомпозита численно исследовалась путем решения фононного уравнения переноса Больцмана с частотно-зависимой моделью [14].
Нанопористые аэрогели были реконструированы с помощью усовершенствованного метода трехмерной кластерно-кластерной агрегации с ограничением диффузии (DLCA), в котором количественно определялся вклад теплопередачи твердого тела-газа в теплопроводность, обусловленную газом [11]. Для прогнозирования эффективной теплопроводности нанопористых аэрогелевых материалов был разработан модифицированный решеточный метод Больцмана [12], который ввел дополнительный коэффициент для регулирования разницы теплопроводности между твердой и газовой фазами и гарантировал конвергентное решение. Фанг и др. В работе [13] решеточный метод Больцмана использовался для решения уравнения проводимости-излучения для предсказания эффективной теплопроводности. Результаты моделирования показали, что эффективная теплопроводность чистого нанопористого аэрогеля быстро увеличивается с температурой и сильно снижается при легировании добавками. Теплопроводность нанопористой пленки и нанокомпозита численно исследовалась путем решения фононного уравнения переноса Больцмана с частотно-зависимой моделью [14]. Был введен локальный угол между тепловыми потоками и локальным тепловым потоком, и все результаты показали, что наноструктурный материал с большим средним углом будет иметь меньшую теплопроводность. Танг и др. [15] исследовали теплопроводность тонкой пленки нанопористого кремния с использованием метода дискретных ординат (DOM). Учитывались эффекты толщины, пористости и пористой структуры. Численные результаты показали, что нанопоры способны резко снижать теплопроводность тонкой пленки кремния за счет граничного рассеяния фононов.
Был введен локальный угол между тепловыми потоками и локальным тепловым потоком, и все результаты показали, что наноструктурный материал с большим средним углом будет иметь меньшую теплопроводность. Танг и др. [15] исследовали теплопроводность тонкой пленки нанопористого кремния с использованием метода дискретных ординат (DOM). Учитывались эффекты толщины, пористости и пористой структуры. Численные результаты показали, что нанопоры способны резко снижать теплопроводность тонкой пленки кремния за счет граничного рассеяния фононов. Нг и др. В работе [17] исследована теплопроводность образцов нанопористого аэрогеля различной плотности путем разрыва плотных образцов кремнезема отрицательным давлением. Результаты показали, что степенная зависимость теплопроводности изменяется почти линейно с плотностью, при этом уменьшение плотности и увеличение пористости приведет к линейному уменьшению теплопроводности. Теплоперенос в цепочке вторичных частиц аэрогеля нанопористого кремнезема изучался с помощью молекулярно-динамического моделирования [18]. Перенос тепла подавлялся, когда длина контакта или концентрация дефектов увеличивались, а ограничивающий эффект был гораздо более очевидным, когда доля длины контакта находилась в небольшом диапазоне. Характеристики теплопередачи наноразмерного газа исследовались методом молекулярно-динамического моделирования [19].]. Рассмотрено влияние силового поля стенки, жесткости стенки и потенциальной напряженности взаимодействия стенка-газ на эффективную теплопроводность. Babaei и Wilmer [20] исследовали механизмы переноса тепла в системе пористый кристалл-газовая смесь с помощью молекулярно-динамического моделирования.
Нг и др. В работе [17] исследована теплопроводность образцов нанопористого аэрогеля различной плотности путем разрыва плотных образцов кремнезема отрицательным давлением. Результаты показали, что степенная зависимость теплопроводности изменяется почти линейно с плотностью, при этом уменьшение плотности и увеличение пористости приведет к линейному уменьшению теплопроводности. Теплоперенос в цепочке вторичных частиц аэрогеля нанопористого кремнезема изучался с помощью молекулярно-динамического моделирования [18]. Перенос тепла подавлялся, когда длина контакта или концентрация дефектов увеличивались, а ограничивающий эффект был гораздо более очевидным, когда доля длины контакта находилась в небольшом диапазоне. Характеристики теплопередачи наноразмерного газа исследовались методом молекулярно-динамического моделирования [19].]. Рассмотрено влияние силового поля стенки, жесткости стенки и потенциальной напряженности взаимодействия стенка-газ на эффективную теплопроводность. Babaei и Wilmer [20] исследовали механизмы переноса тепла в системе пористый кристалл-газовая смесь с помощью молекулярно-динамического моделирования.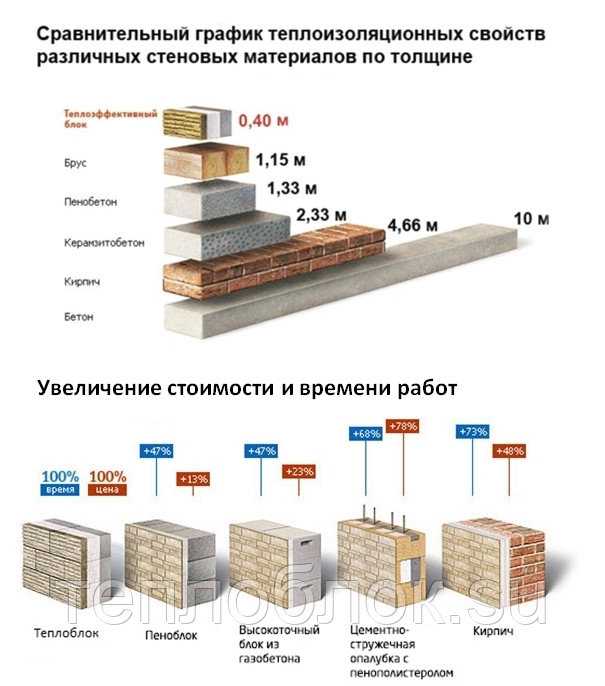 Исследование показало, что в теплопроводности системы преобладает кристалл, который снижается по мере увеличения концентрации газа в порах. Пониженная проводимость, связанная с увеличением концентрации газа, связана с рассеянием фононов кристаллом, вызванным взаимодействием с молекулами газа.
Исследование показало, что в теплопроводности системы преобладает кристалл, который снижается по мере увеличения концентрации газа в порах. Пониженная проводимость, связанная с увеличением концентрации газа, связана с рассеянием фононов кристаллом, вызванным взаимодействием с молекулами газа.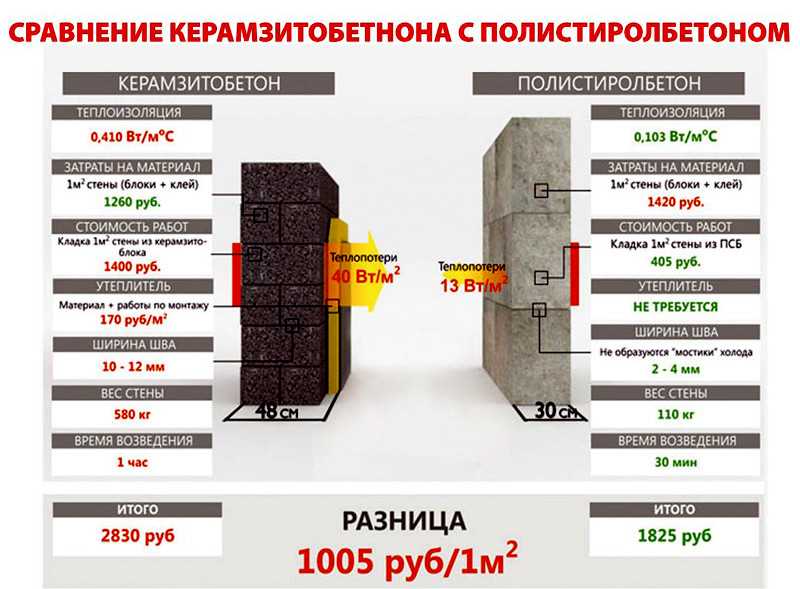 Ячейка моделирования, включающая газ и твердое тело, получается из упорядоченных пористых структур пересекающихся квадратных стержней, как показано на рисунке 1. Периодическое граничное условие используется во всех направлениях. В качестве твердой фазы упорядоченных пористых структур, заполненных газом гелия при 20 К, выбран аргон. Твердый аргон представляет собой гранецентрированный кубический кристалл с периодом решетки S = 5,4 Å. Потенциал Леннарда-Джонса 12–6, E = 4ε[(σ/r) 12 — (σ/r) 6 ], используется для описания взаимодействия между атомами и усекается по радиусу отсечки 14 Å. Подробные параметры, использованные в нашем моделировании, перечислены в таблице 1. Ансамбль NVT, который поддерживает количество атомов, объем и температуру постоянными, используется с термостатом Нозе-Гувера при 20 K с временным шагом 5 фс.
Ячейка моделирования, включающая газ и твердое тело, получается из упорядоченных пористых структур пересекающихся квадратных стержней, как показано на рисунке 1. Периодическое граничное условие используется во всех направлениях. В качестве твердой фазы упорядоченных пористых структур, заполненных газом гелия при 20 К, выбран аргон. Твердый аргон представляет собой гранецентрированный кубический кристалл с периодом решетки S = 5,4 Å. Потенциал Леннарда-Джонса 12–6, E = 4ε[(σ/r) 12 — (σ/r) 6 ], используется для описания взаимодействия между атомами и усекается по радиусу отсечки 14 Å. Подробные параметры, использованные в нашем моделировании, перечислены в таблице 1. Ансамбль NVT, который поддерживает количество атомов, объем и температуру постоянными, используется с термостатом Нозе-Гувера при 20 K с временным шагом 5 фс. Микроскопический тепловой поток j получается из следующего уравнения
Микроскопический тепловой поток j получается из следующего уравнения Количество атомов газа усредняется за последние 400 000 шагов как содержание газа для различных давлений. На втором этапе ячейка моделирования, включающая твердое тело и газ, сначала достигает равновесного состояния в ансамбле НВТ при 20 К. Затем по формуле Грина-Кубо рассчитывается теплопроводность нанопористой системы. Вектор теплового потока регистрируется каждые 5 временных шагов в ансамбле NVE для 5 × 10 7 временных шагов. Время корреляции составляет 10 000 временных шагов. Для всех случаев мы выполнили 5 независимых симуляций с разными случайными затравками для распределения атомов по скоростям. Усредненное значение 5 симуляций используется для прогнозов теплопроводности.
Количество атомов газа усредняется за последние 400 000 шагов как содержание газа для различных давлений. На втором этапе ячейка моделирования, включающая твердое тело и газ, сначала достигает равновесного состояния в ансамбле НВТ при 20 К. Затем по формуле Грина-Кубо рассчитывается теплопроводность нанопористой системы. Вектор теплового потока регистрируется каждые 5 временных шагов в ансамбле NVE для 5 × 10 7 временных шагов. Время корреляции составляет 10 000 временных шагов. Для всех случаев мы выполнили 5 независимых симуляций с разными случайными затравками для распределения атомов по скоростям. Усредненное значение 5 симуляций используется для прогнозов теплопроводности. Текущая теплопроводность получена на основе HFACF, которая стабилизируется на уровне около 0,14 Вт м 9 .0047 −1 K −1 после 20 пс.
Текущая теплопроводность получена на основе HFACF, которая стабилизируется на уровне около 0,14 Вт м 9 .0047 −1 K −1 после 20 пс. Для нанопористой системы с l = 4S общая теплопроводность увеличивается с более высоким давлением или газовой нагрузкой, что связано с увеличением количества свободных атомов газа, что соответствует лучшей способности к теплопередаче. Полученная теплопроводность для l = 8S практически не изменяется при изменении давления. Это связано с тем, что в нанопористой системе практически отсутствуют свободные атомы газа, а в общей теплопроводности преобладает твердая фаза.
Для нанопористой системы с l = 4S общая теплопроводность увеличивается с более высоким давлением или газовой нагрузкой, что связано с увеличением количества свободных атомов газа, что соответствует лучшей способности к теплопередаче. Полученная теплопроводность для l = 8S практически не изменяется при изменении давления. Это связано с тем, что в нанопористой системе практически отсутствуют свободные атомы газа, а в общей теплопроводности преобладает твердая фаза.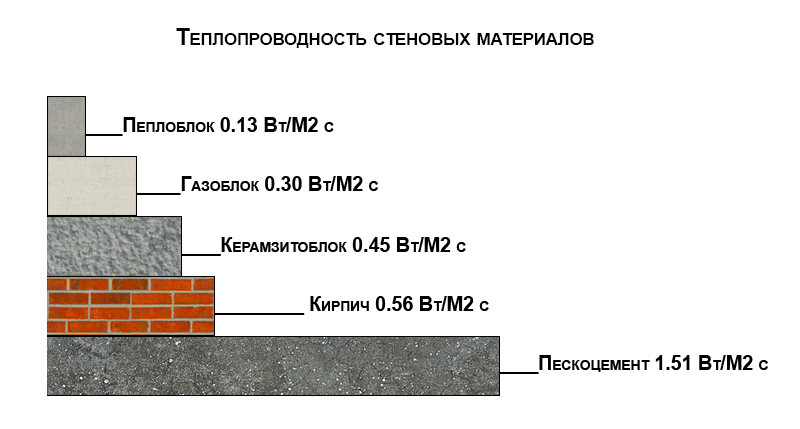 достигают минимума примерно через 10 с, затем увеличиваются. Первоначальное снижение теплопроводности связано с увеличением пористости, при которой твердая фаза является основным фактором, определяющим общую теплопроводность. По мере того, как длина (L) модуля моделирования продолжает увеличиваться, количество атомов газа и теплопроводность соответствующего газа будут увеличиваться. Для той же длины (L) модуля моделирования увеличение ширины твердого каркаса приведет к быстрому увеличению общей теплопроводности, что в основном связано с увеличением теплопроводности твердой фазы. Хотя атомы газа в этой ситуации уменьшаются, влияние твердой фазы более очевидно и приводит к увеличению общей теплопроводности, как показано на рис. 7.9.0011
достигают минимума примерно через 10 с, затем увеличиваются. Первоначальное снижение теплопроводности связано с увеличением пористости, при которой твердая фаза является основным фактором, определяющим общую теплопроводность. По мере того, как длина (L) модуля моделирования продолжает увеличиваться, количество атомов газа и теплопроводность соответствующего газа будут увеличиваться. Для той же длины (L) модуля моделирования увеличение ширины твердого каркаса приведет к быстрому увеличению общей теплопроводности, что в основном связано с увеличением теплопроводности твердой фазы. Хотя атомы газа в этой ситуации уменьшаются, влияние твердой фазы более очевидно и приводит к увеличению общей теплопроводности, как показано на рис. 7.9.0011 В нашем моделировании параметр энергии ε, используемый в потенциале Леннарда-Джонса 12-6, может быть скорректирован, чтобы представить этот вид модификации поверхности как упрощение. ε/ε газ-твердое вещество в диапазоне от 0,3 до 1 используется при моделировании при том же давлении и газовой нагрузке. На рис. 8 и рис. 9 показаны результаты распределения атомов газа и общей теплопроводности для разных значений ε при одном и том же давлении. Атомы газа в нанопористой системе увеличиваются из-за сильного взаимодействия газ-твердое тело и демонстрируют хорошие адсорбционные характеристики с увеличением ε. Однако, как показано на рис. 9, теплопроводность нанопористой системы стабилизируется на уровне около 0,24 Вт·м 9 .0047 -1 К -1 . Взаимодействие атомов твердого тела и газа мало влияет на теплопроводность при том же давлении. Это связано с тем, что, хотя общее количество атомов газа увеличивается из-за сильного взаимодействия газ-твердое тело, увеличенное количество атомов газа находится в адсорбированном состоянии, которое вносит небольшой вклад в теплообмен в нанопористой системе.
В нашем моделировании параметр энергии ε, используемый в потенциале Леннарда-Джонса 12-6, может быть скорректирован, чтобы представить этот вид модификации поверхности как упрощение. ε/ε газ-твердое вещество в диапазоне от 0,3 до 1 используется при моделировании при том же давлении и газовой нагрузке. На рис. 8 и рис. 9 показаны результаты распределения атомов газа и общей теплопроводности для разных значений ε при одном и том же давлении. Атомы газа в нанопористой системе увеличиваются из-за сильного взаимодействия газ-твердое тело и демонстрируют хорошие адсорбционные характеристики с увеличением ε. Однако, как показано на рис. 9, теплопроводность нанопористой системы стабилизируется на уровне около 0,24 Вт·м 9 .0047 -1 К -1 . Взаимодействие атомов твердого тела и газа мало влияет на теплопроводность при том же давлении. Это связано с тем, что, хотя общее количество атомов газа увеличивается из-за сильного взаимодействия газ-твердое тело, увеличенное количество атомов газа находится в адсорбированном состоянии, которое вносит небольшой вклад в теплообмен в нанопористой системе.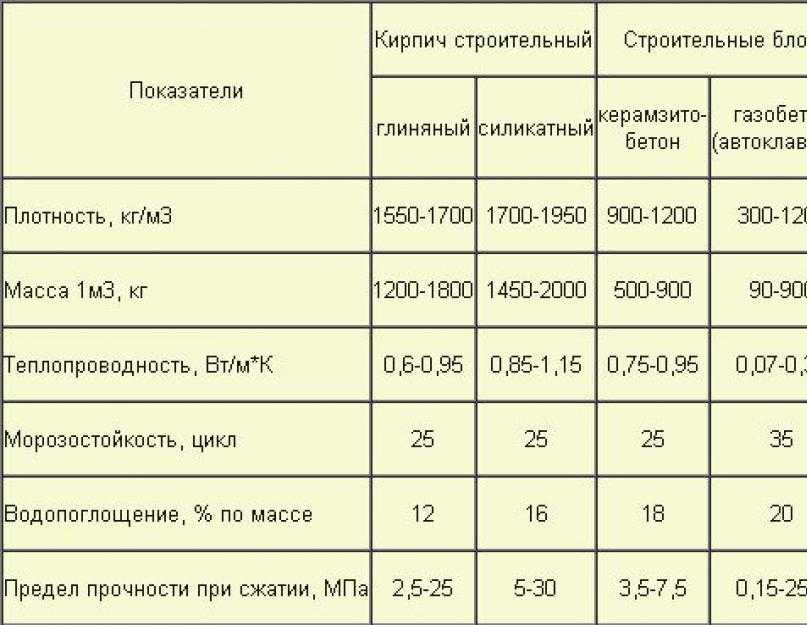 Однако, согласно уравнению состояния идеального газа, свободные атомы газа, участвующие в процессе теплопроводности, практически одинаковы при одном и том же давлении. Следовательно, теплопроводность нанопористой системы стабильна и не зависит от взаимодействия газ-твердое тело при одном и том же давлении.
Однако, согласно уравнению состояния идеального газа, свободные атомы газа, участвующие в процессе теплопроводности, практически одинаковы при одном и том же давлении. Следовательно, теплопроводность нанопористой системы стабильна и не зависит от взаимодействия газ-твердое тело при одном и том же давлении.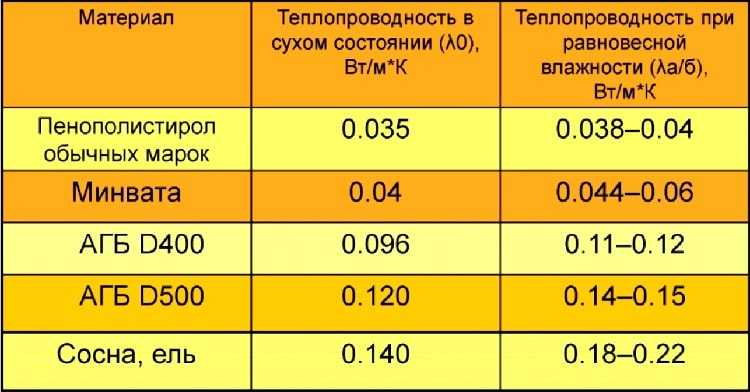 Влияние давления на общую теплопроводность представляет различные характеристики для нанопористой системы.
Влияние давления на общую теплопроводность представляет различные характеристики для нанопористой системы.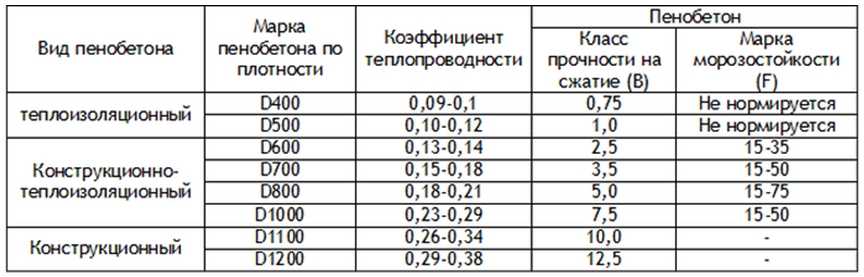
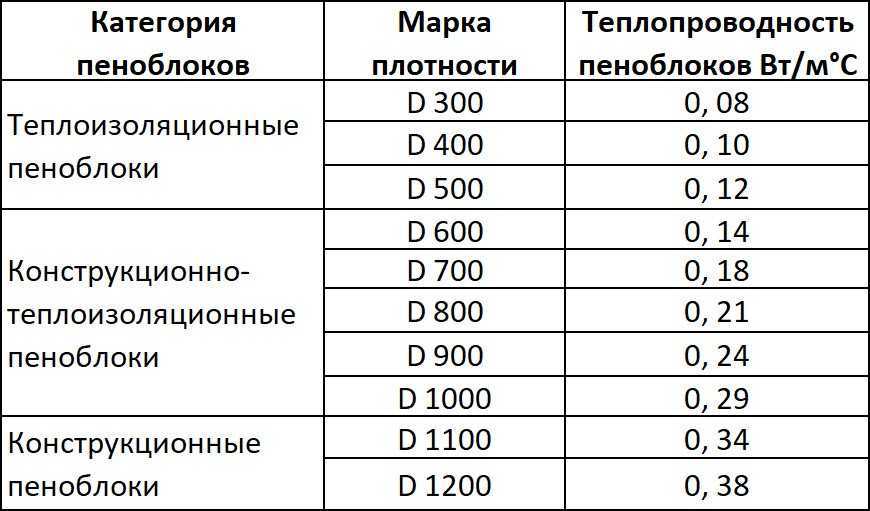 Н.; расследование, Д.Н.; ресурсы, Д.Н.; курирование данных, Д.Н.; написание – черновая подготовка, Д.Н.; написание-обзор и редактирование, Д.Н.; визуализация, Д.Н.; надзор, Х.Г.; администрация проекта, Х.Г.; приобретение финансирования, Х.Г. и Д.Н. Все авторы прочитали и согласились с опубликованной версией рукописи.
Н.; расследование, Д.Н.; ресурсы, Д.Н.; курирование данных, Д.Н.; написание – черновая подготовка, Д.Н.; написание-обзор и редактирование, Д.Н.; визуализация, Д.Н.; надзор, Х.Г.; администрация проекта, Х.Г.; приобретение финансирования, Х.Г. и Д.Н. Все авторы прочитали и согласились с опубликованной версией рукописи.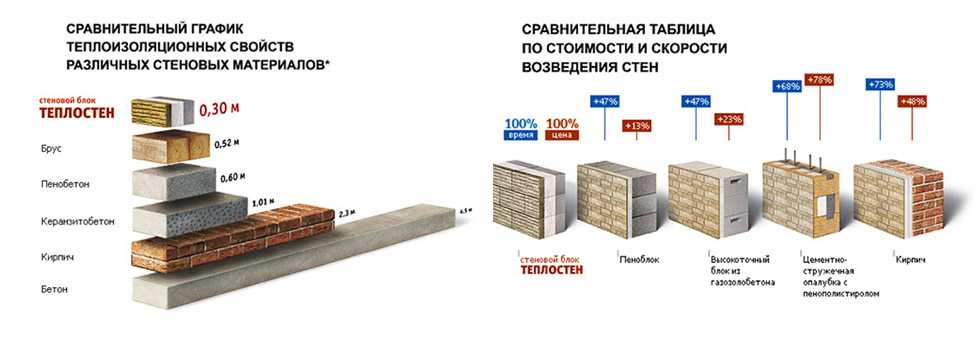
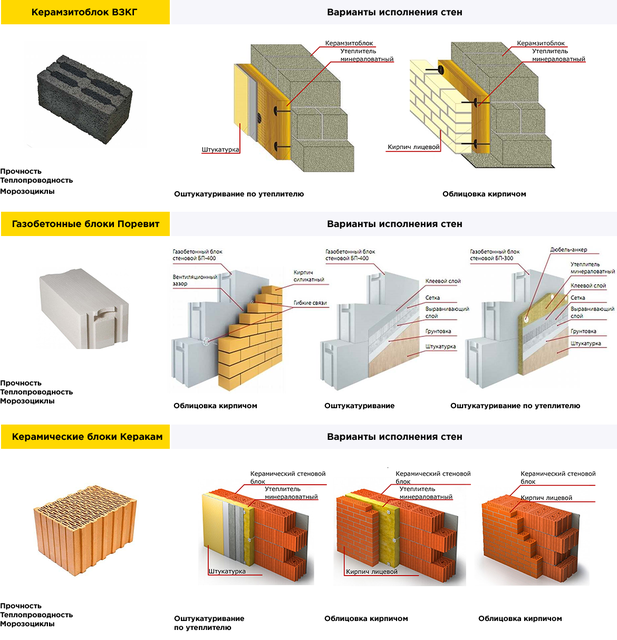 [Академия Google] [CrossRef]
[Академия Google] [CrossRef] 2017 , 108, 1982–1990. [Google Scholar] [CrossRef]
2017 , 108, 1982–1990. [Google Scholar] [CrossRef]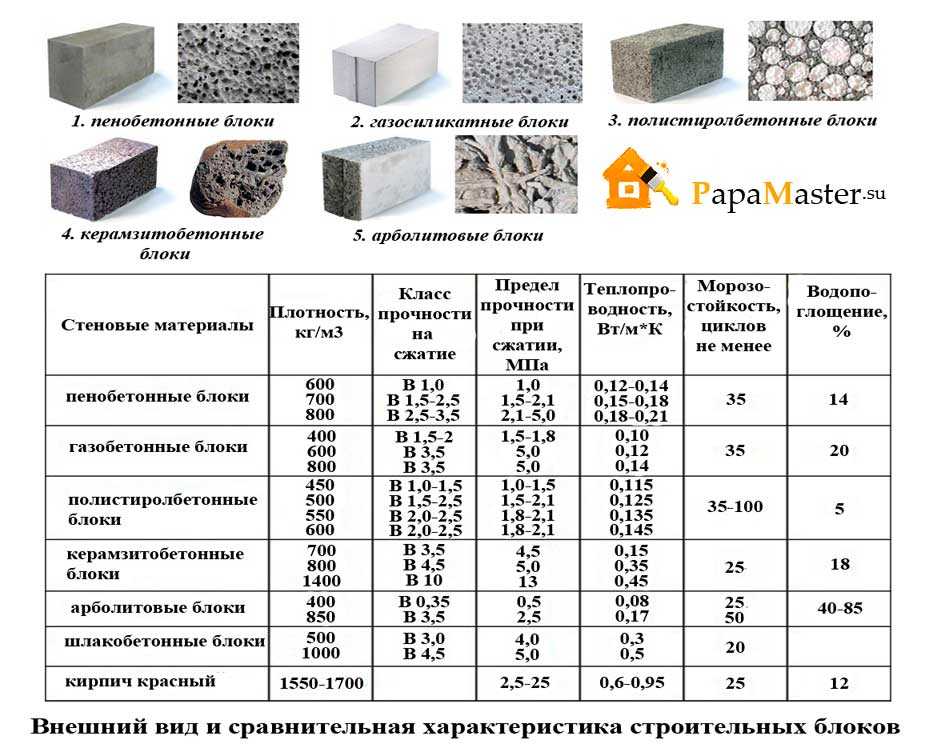 J. Некристалл. Твердые вещества 2012 , 358, 1350–1355. [Google Scholar] [CrossRef]
J. Некристалл. Твердые вещества 2012 , 358, 1350–1355. [Google Scholar] [CrossRef] Дж. Вычисл. физ. 1995 , 117, 1–19. [Google Scholar] [CrossRef][Green Version]
Дж. Вычисл. физ. 1995 , 117, 1–19. [Google Scholar] [CrossRef][Green Version]