Формула расчета фундамента ленточного: Как рассчитать ленточный фундамент? Методика, СНиП, особенности и факторы влияния на устройство ленточного фундамента, видео
Как рассчитать ленточный фундамент? Методика, СНиП, особенности и факторы влияния на устройство ленточного фундамента, видео
Наиболее распространенным видом основания под здание, будь то бревенчатый сруб, каменный или кирпичный коттедж, каркасный домик или строение из СИП-панелей, считается ленточный фундамент. Он может быть сделан из составных элементов или залит из бетона и армирован прутьями; основные достоинства такого основания – устойчивость, возможность обустройства подпола или погреба, небольшой объем работы на подготовительном этапе и сравнительно невысокая цена устройства.
Один из вопросов, который считается наиболее важным на этапе планирования дома, связан с расчетом параметров ленты. Чтобы основание для дома было крепким и простояло много десятков лет, нужно понимать, как рассчитать ленточный фундамент правильно. Если делать основание без расчетов, то можно либо занизить объем материалов и построить неустойчивый фундамент, либо, наоборот, закупить слишком много, так что после создания ленты будет слишком много остатков.
Расчет ленточного фундамента: факторы влияния
На такие параметры основания, как глубина залегания, ширина и толщина, влияет несколько факторов, которые следует принять во внимание при вычислениях:
- Структурные особенности грунта. Различные его виды имеют разную несущую способность, промерзают на разную глубину, имеют свои характеристики твердости, влажности, сыпучести и устойчивости. Именно поэтому перед тем, как сделать план и расчет ленточного фундамента, потребуется провести геодезические исследования, узнав состав и характерные особенности почвы. Так, на слабых и пучинистых грунтах лучше устанавливать ленту с большой степенью заглубленности и правильно обустроенной системой дренажа.
Важно! На глинистом грунте фундамент заглублен на 80 и более см, на песчаном и суглинке – на 45 и более см, на каменистом грунте – на 45-55 см.

- Конструктивные особенности здания, его предполагаемый вес. Для того, чтобы это выяснить, в расчет берется ряд аспектов. К ним относится материал, из которого будут сделаны стены и крыша, количество этажей здания, его размеры. Также необходимо учесть особенности внутренней планировки, число несущих стен, наличие пристроек. Кроме того, требуется определиться с назначением здания, которое может быть частным домом, производственным строением, второстепенной пристройкой или коммерческим предприятием, отчего общий вес может существенно меняться.
- Расположение грунтовых вод. Если они находятся достаточно глубоко, то фундамент может быть заглубленным, и на нем можно устанавливать многоэтажные крупные здания, которые имеют большой вес. Если же грунтовые воды находятся близко к поверхности, то необходимо устраивать мелкозаглубленную ленту: ее высота составит около 50 см.
Методика расчета ленточного фундамента в различных аспектах
Для того, чтобы правильно вычислить параметры ленточного основания и количество материалов, которые уйдут на его создание, нужно начать с вычисления глубины.
После того, как это будет сделано, нужно взять в расчет длину и ширину дома, а затем высчитать толщину самой ленты. Подошва основания должна быть устойчивой и прочной, поэтому лучше округлять полученные значения в большую сторону. Расчет ширины ленточного фундамента делается с учетом нагрузок, которые ложатся на него: их степень должна быть не более 70% от несущих способностей того грунта, на котором будет вестись строительство здания. Обычно минимальной по ширине считается лента в 30 см, а в среднем она составляет порядка 40-45 см.
Если расчеты произвести точно не удается, лучше сделать ширину больше, чтобы в процессе усадки лента не растрескалась и не лопнула; то же самое касается и глубины.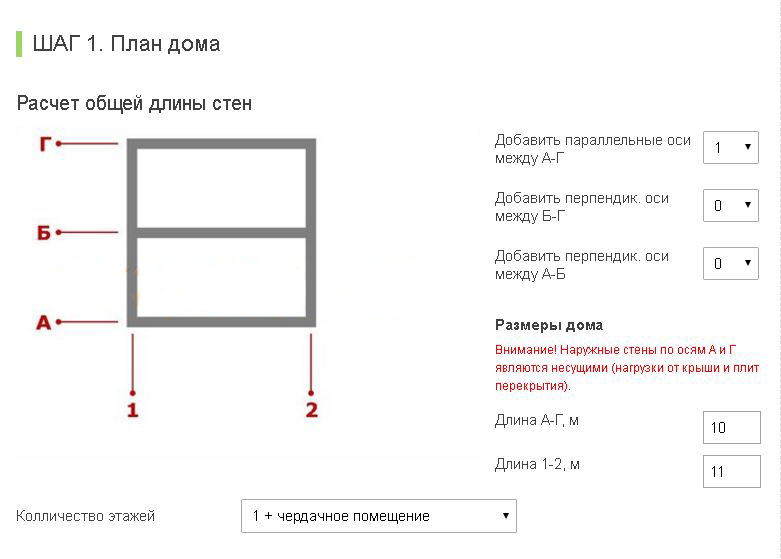 Расчет подошвы ленточного фундамента производится с учетом ширины основания, нагрузок, планируемой надежности и сопротивляемости грунта.
Расчет подошвы ленточного фундамента производится с учетом ширины основания, нагрузок, планируемой надежности и сопротивляемости грунта.
Затем следует вычислить нагрузку строения. Для этого складываются такие параметры, как мертвый вес, примерную массу предметов, которые будут установлены в доме, а также вес, возлагаемый на кровлю в виде влияния ветра или осадков. Полученный показатель перемножают на постоянное число 1,3.
Важно! Все значения следует округлять в большую сторону, чтобы быть уверенным в устойчивости и высокой несущей способности готового основания. Расчет нагрузки ленточного фундамента напрямую связан с весом здания и типом грунта, поэтому данным вычислениям нужно уделить особое внимание.
После этого необходимо установить, какой высоты будет основание. Для вычислений используется два метода. Согласно первому, высота ленты будет равна глубине ее подземной части, а по второму необходимо умножить параметр ширины на постоянное число 4, и результат будет обозначать предел высоты надземной части.
Как произвести расчет бетона на ленточный фундамент?
После того, как глубина, высота, ширина и нагрузка на ленту будут установлены, нужно определить, сколько материала понадобится для обустройства фундамента. Чтобы понять, какой объем бетона, арматуры, песка и щебня понадобится для создания основания, необходимо учесть параметры фундамента по высоте, ширине, глубине и периметру, а также то, какую марку бетона предстоит использовать. Для определения толщины подушки из песка и щебня нужно обратить внимание на характеристики грунта и расположение грунтовых вод, а вычисление количества арматуры производится с учетом конструктивных особенностей дома и размеров основания.
Чтобы осуществить расчет, можно воспользоваться формулами или обратиться к помощи онлайн-калькуляторов, которые широко представлены на строительных порталах и сайтах строительных подрядчиков. Как показывает соответствующий СНиП, расчет ленточного фундамента осуществляется при условиях определения предельных нагрузок на разных почвах, и установленные значения перечислены в нем в табличном виде.
Как показывает соответствующий СНиП, расчет ленточного фундамента осуществляется при условиях определения предельных нагрузок на разных почвах, и установленные значения перечислены в нем в табличном виде.
Выводы
При создании дома важнейшую роль играет планировка основания, которое должно отвечать всем требованиям безопасности и устойчивости в каждом конкретном случае. При этом потребуется рассчитывать не только габариты ленты, но и объем материалов, которые уйдут на ее создание: правильно произведенные вычисления позволят построить долговечное и крепкое основание без ненужных затрат.
Расчет ленточных фундаментов можно произвести самостоятельно, при помощи формул или онлайн-программ наподобие калькуляторов на определение глубины залегания ленты и затрат по материалам, или обратиться к специалистам. При этом все получаемые значения желательно превысить на практике: лучше, если на основание уйдет больше материала, нежели оно окажется слишком непрочным и начнет деформироваться уже в процессе усадки.
Расчет ленточного фундамента: пример проведения
Разновидности ленточной конструкцииВ самостоятельном строительстве дома важно получить действительно прочное основание, и одним из вариантов выполнения расчета ленточного фундамента послужит пример здания периметром 6 × 8 м из газобетона с мансардным 2 этажом без подвальных (цокольных) помещений. Такой тип опоры является наиболее универсальным решением в большинстве случаев индивидуального строительства капитального жилого дома. Тщательно проведенный расчет на стадии проектирования станет одним из условий долговременной эксплуатации постройки.
Порядок расчетных операций
Последовательность расчета ленточного монолитного фундамента будет состоять из 2 главных этапов, которые определят исходные данные для определения размеров конструкции. Для каждого конкретного участка строительства нужно:
- определить действующие нагрузки;
- узнать несущую способность залегающего грунта.
Соотношение действующей весовой нагрузки всех элементов здания, включая фундамент, к величине несущей способности грунтовой основы позволит узнать оптимальное значение ширины ленточной опоры.
Определяющее значение имеет площадь опирающейся подошвы. Ширина самой ленты может меняться в зависимости от суммарных размеров несущих стен (блок + утеплитель + облицовка). показаны на чертежах:
У ленточной конструкции прямоугольного сечения значения ширины по всей вертикали равны. Выбор Т-образной формы, у которой площадь подошвы фундамента больше, чем цоколь, происходит в случае строительства массивного здания (2 и более этажей) из керамзитобетонных блоков или кирпича. Для каркасных домов, построек из бруса, срубов обычно будет достаточно прямоугольного сечения.
Расчеты площади подошвы опорной части для монолитных и сборных видов фундамента ничем не отличаются.
Подробно все требования к определению расчетных величин и принимаемых коэффициентов изложены в таких нормативных документах:
- СНиП 2.02.01-83*. Основания зданий и сооружений. Госстрой СССР, 1995 г.
- СНиП 2.03.01-84*. Бетонные и железобетонные конструкции. Госстрой СССР, 1989 г.

- СНиП 23-01-99*. Строительная климатология. Госстрой России, 2003 г.
- СНиП 2.01.07-85. Нагрузки и воздействия. Госстрой СССР, 1986 г.
Рациональность выбора определенного типа конструкции основания прямо зависит от инженерно-геологических условий данного участка, условий работы в комплексе всех элементов здания в реальных условиях.
Ошибки проектирования, нарушения технологии закладки фундамента, не оправданная вычислениями экономия на работах и материалах могут привести к необходимости принятия дополнительных мер, себестоимость которых в несколько раз превысит первоначальные затраты на устройство основания.
Сбор нагрузок
Проектирование основания начинают после того, как определены параметры устанавливаемого на него здания.
Для этого нужно сделать следующие операции:
- вычертить в масштабе план дома с разметкой каждого простенка;
- задать высоту цокольного возвышения, назначить используемые для него материалы;
- определить виды и толщину материалов, используемых для теплоизоляции, гидроизоляции, ветровой защиты, отделки горизонтальных и вертикальных поверхностей внутри и снаружи помещений.

Найти в справочных таблицах удельный вес каждой составляющей. Пример такой таблицы:
В рассматриваемый пример расчета фундамента нужно выбрать:
- стены 1 этажа из газоблока толщиной 0, 4 м, высотой 3 м, периметром 28 м – 20160 кг;
- стены мансарды 1, 2 м высота, толщина 0,25 м, длина та же, бревенчатые – 5150 кг;
- перегородки каркасные, длиной 17 м при высоте 2,7 м, 16 м – 1,2 м, всего весят 19530 кг;
- перекрытие дощатое по деревянным балкам с плотностью утеплителя 200 кг/м³ – 14400 кг (полы 1 и 2 этажа), с коэффициентом 1,2 = 17280 кг;
- крыша из ондулина двускатная площадью 58 м² – 1740 кг, с коэфф. 1,1 = 1914 кг;
- полезная нагрузка составляет 200 кг/м², (коэффициент надежности 1,2) – 11520 кг.
Всего вес основных надземных конструкций получим 75554 кг.
Если частный дом не имеет малой площади основания при значительной высоте, то влиянием ветровой нагрузки именно на фундамент можно пренебречь.
Снеговую нагрузку лучше взять по максимальному значению для данной зоны (100 кг/м²). С коэффициентом надежности 1,4 на крышу придется 8120 кг.
Всего расчетный вес дома без фундамента составит 83674 кг
Для небольших частных зданий обычно пренебрегают разделением нагрузок и просто суммируют их без применения в расчете понижающих коэффициентов сочетания.
Высота фундамента
При назначении проектного задания необходимо определить значениями габаритов ленточного основания. Для определения нагрузки от фундамента нужно задать глубину его заложения.
Сезонные показатели приводятся на картах:
Для более подробного расчета это значение берут из таблицы:
Нормативное требование к расположению подошвы заглубленного основания на 0,2-0,3 м ниже отметки промерзания в данной климатической зоне.
Согласно СНиП 2.02.01-83 рекомендуется соблюдать такие отметки заложения при УГВ:
- ниже глубины промерзания для глины и суглинка отметку берут равной 0,5 ГП, для остальных типов грунта зависимости нет;
- выше ГП – не ниже ГП (кроме гравелистых, скалистых песков).

Для легких зданий (деревянных, пенобетонных, малых кирпичных) на слабопучинистых грунтах она составит 0,5 – 0,7 м. В проектном расчете применяют коэффициент 1,1. Соответственно, для строящегося в примере дома следует выбрать глубину 0,6 м и высоту цоколя 0,4 м.
Вес ленты
К рассчитанной нагрузке дома нужно добавить собственный вес опоры. Можно строить из фундаментных блоков и взять значения из таблицы:
При укладке ФБС 24.4.6 в 1 ряд до уровня земли вес без надстройки цоколя кирпичом составит 15167 кг. Цоколь из полнотелого кирпича 0,4 × 0,4 м будет весить 8064 кг. Всего вес такого фундамента будет 23231 кг при площади опоры 0,4 м × 28 м = 11,2 м². Теперь следует посчитать легкий наливной фундамент с уширением подошвы.
Для этого надо посчитать нагрузку от вертикального подъема стены, расширяющейся подошвы, и добавить вес грунта, который ляжет обратной засыпкой на поверхность расширения сверху.
Высота подземной части ленты из монолитного бетона составит 0,6 м, цоколя 0,4 м, толщина равна стене из блоков 0,4 м. Неармированный бетон имеет объемный вес 2400 кг/м³, коэффициент надежности по нагрузке = 1,1. Тогда нагрузка будет: 1 м × 0,4 м × 2400 кг/м³ × 1,1 = 1056 кг/м.
Неармированный бетон имеет объемный вес 2400 кг/м³, коэффициент надежности по нагрузке = 1,1. Тогда нагрузка будет: 1 м × 0,4 м × 2400 кг/м³ × 1,1 = 1056 кг/м.
Ширину фундаментной подошвы надлежит взять 0,6 м. Если из нее вычесть учтенный ранее размер ленты 0,4 м, то можно получить суммарные выступы 0,2 м.
Вес армированного бетона подошвы при 0,3 м составляет 2500 кг/м³, в нашем случае получится 0,3 м × 0,6 м × 2500 кг/м³ × 1,1 = 495 кг/м.
Грунт для обратной засыпки с плотностью 1650 кг/м³, коэффициент 1,15. В результате получится 0,2м × 1650кг/м³ × 0,3 м × 1,15 = 113,85 кг/м.
Складываем полученные значения нагрузок 1664,85 кг/м или 46615,8 кг. Площадь подошвы для этого варианта 0,6 м × 28 м = 16,8 м²
Выполняем аналогичный расчет для бетонного монолита прямоугольной формы шириной 0,3 м (с западающим цоколем): 1 м × 0,3 м × 2400 кг/м³ × 1,1 = 792 кг/м. Масса всей ленты составит 22176 кг, площадь опоры – 8,4 м².
Несущая способность основы
Для проведения точного расчёта несущей способности залегающего на участке грунта потребуются его физико – механические характеристики, полученные в результате инженерно-геологических изысканий. Затраты на заказ ИГЭ отчёта в перспективе могут окупиться сторицей, если площадка располагается в сложных неблагоприятных условиях.
Затраты на заказ ИГЭ отчёта в перспективе могут окупиться сторицей, если площадка располагается в сложных неблагоприятных условиях.
Упрощенно можно воспользоваться справочными таблицами, которые содержат приведенные значения этого показателя для типичных видов грунта, например, такой таблицей:
Важным условием является однородность подстилающего слоя без образования так называемых «линз». Для уточнения всех особенностей и нужны практические исследования геологии участка и выполнение камеральных расчетов на основании максимально точных данных.
Соотношение несущих показателей
Создавать выбранный вариант фундамента можно, если общая нагрузка от постройки будет меньше (в крайнем случае, равна) несущей способности грунта. Считаем полученные варианты ленточного основания:
- Блоки ФБС 24.4.6 с кирпичным цоколем (83674 кг + 23231 кг)/11,2 м² = 9545 кг/м² или 1 кг/см².
- Монолитный бетон с расширенной подошвой (83674 кг + 46615,8 кг)/16,8 м² = 7754 кг/м² или 0,8 кг/см².

- Ленточный монолит шириной 0,3 м будет иметь такое значение: (83674 кг + 22176 кг)/8,4 м² = 12601 кг/м² или 1,3 кг/см².
Из сравнения видно, что с минимальными затратами построить здание весом 106 т можно на ленточном наливном фундаменте шириной 0,3 м.
Советы специалиста, как самостоятельно рассчитать опорную площадь фундаментов при строительстве собственного дома, представлены на этом видео:
Продвинутые строители всегда могут воспользоваться бесплатными программами для расчета, которые можно скачать (или работать онлайн) в Интернете.
Пример такой программы показан на фото:
Однако существуют сомнения в точности расчетов сложных случаев на этих калькуляторах, так как работа их формул наглядно не контролируется пользователем (применяемые округления и полнота расчета).
Уверенный результат получают по методикам, приведенным в строительных нормах и специальной справочной литературе. Программы – калькуляторы целесообразно применять для более простого подсчета нужного количества расходных материалов.
Программы – калькуляторы целесообразно применять для более простого подсчета нужного количества расходных материалов.
Расчет ленточного фундамента: как рассчитать, пример
- Монтаж фундамента
- Выбор типа
- Из блоков
- Ленточный
- Плитный
- Свайный
- Столбчатый
- Устройство
- Армирование
- Гидроизоляция
- После установки
- Ремонт
- Смеси и материалы
- Устройство
- Устройство опалубки
- Утепление
- Цоколь
- Какой выбрать
- Отделка
- Устройство
- Сваи
- Виды
- Инструмент
- Работы
- Устройство
- Расчет
Поиск
Фундаменты от А до Я.
- Монтаж фундамента
- ВсеВыбор типаИз блоковЛенточныйПлитныйСвайныйСтолбчатый
Фундамент под металлообрабатывающий станок
Устройство фундамента из блоков ФБС
Заливка фундамента под дом
Характеристики ленточного фундамента
- ВсеВыбор типаИз блоковЛенточныйПлитныйСвайныйСтолбчатый
- Устройство
Как рассчитать фундамент ленточный правильно?
Для домов с плитными перекрытиями и тяжелыми стенами лучше всего рассматривать именно ленточный вариант фундамента. Хотя этот вид фундамента требует больших затрат трудов и материала, он не теряет своей высокой популярности в сфере индивидуального строительства. Связано это с тем, что ленточный фундамент прост в возведении и имеет отличные эксплуатационные качества. Если такой фундамент сделан правильно, он прослужит много десятилетий.
Хотя этот вид фундамента требует больших затрат трудов и материала, он не теряет своей высокой популярности в сфере индивидуального строительства. Связано это с тем, что ленточный фундамент прост в возведении и имеет отличные эксплуатационные качества. Если такой фундамент сделан правильно, он прослужит много десятилетий.
Схема монтажа ленточного мелкозаглубленного фундамента.
Как рассчитать фундамент ленточный правильно? Главное при этом – соблюдать все технологии строительства и сделать точный расчет. Для этого понадобится рассчитать следующие параметры:
- Глубину укладки.
- Ширину.
- Высоту.
- Объем.
- Количество сопутствующих материалов.
Как рассчитать глубину укладки
В первую очередь глубина закладки определяется исходя из типа грунта, его влажности и глубины промерзания. Зависит глубина и от того, присутствует ли в проекте подвальное помещение.
Если нужно рассчитать строительство небольшого дома без подвала, следует использовать малозаглубленный ленточный фундамент, что позволит сократить расходы почти втрое. Этот вид применим и на пучинистых грунтах, если предварительно будет проведен комплекс мелиоративных работ и утепление основания.
Этот вид применим и на пучинистых грунтах, если предварительно будет проведен комплекс мелиоративных работ и утепление основания.
Для того чтобы рассчитать и правильно построить долговечное здание, грунт должен быть соответствующей несущей способности и не должен задерживать воду.
Хорошо, если грунт на участке под строительство именно такой. В противном случае эти свойства придется придавать ему самостоятельно. Это легко достижимо при помощи дренажной системы. Можно подсыпать и такой материал, как щебень, галька или крупнозернистый песок. Такая подготовка грунта устраняет его склонность к пучинистости и придаст строению большую устойчивость. Подвижки грунта всегда связаны с содержащейся в нем излишней влагой.
Бытует мнение, что ленточный фундамент более 2,5 метров глубиной не оправдывает себя экономически.
Именно эта максимальная глубина чаще всего используется в домах с подвальными помещениями. Если при расчетах свойства грунта требуют закладывать ленточный фундамент на большую глубину, стоит рассмотреть другие типы.
Правильно рассчитанный ленточный фундамент допустим следующей минимальной глубины:
- глинистые грунты – не менее 75 см;
- песчаные и суглинистые грунты – от 45 см;
- каменистый и скальный грунт, искусственно подготовленный в том числе – до 45 см.
Вернуться к оглавлению
Как правильно рассчитать фундамент по ширине
Разметка фундамента.
Главное требование, предъявляемое к тому, насколько широким будет фундамент, – это обеспечение на грунт допустимого давления. И зависит это не от того, какой выбран материал, а от типа грунта.
Чем меньше несущая способность грунта, тем фундамент, особенно его нижняя часть, шире. Минимальная величина, на которую строится ленточный фундамент, – 30 см.
Рассчитать ширину нужно с учетом того, что нагрузка подошвы не должна превышать 70% от номинальной несущей способности каждого вида грунта.
Затем рассчитывается нагрузка дома. Для того чтобы рассчитать все правильно, нужно суммировать мертвый вес строения, нагрузки снеговую и ветровую, а также примерный вес мебели и оборудования для дома.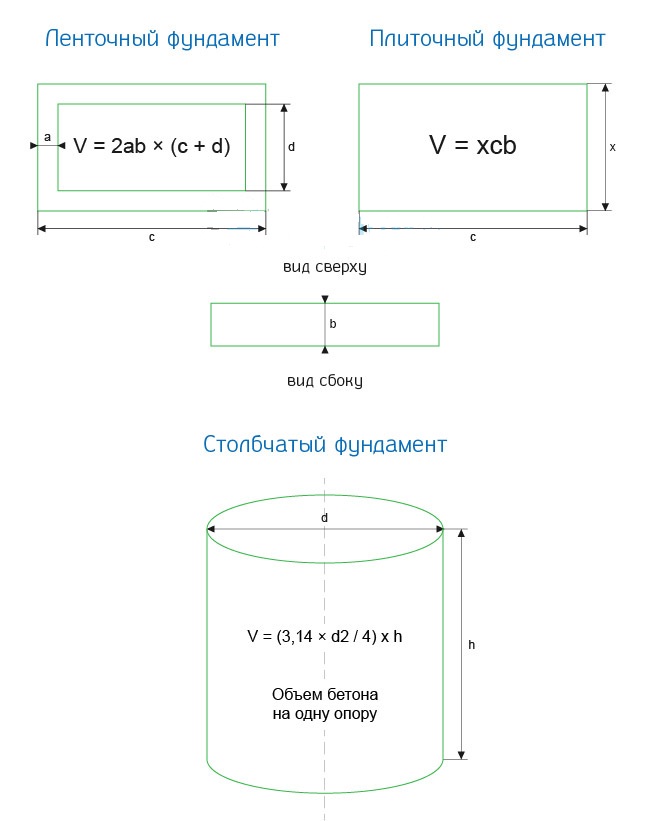 Затем полученную величину умножают на коэффициент 1,3.
Затем полученную величину умножают на коэффициент 1,3.
Мертвый вес здания напрямую зависит от того, какой выбран материал, так как они сильно различаются по весу.
Затем рассчитывается нагрузка перекрытий. К примеру, 1 м³ цокольного или межэтажного перекрытия оказывает нагрузку величиной 500 кгс/м³. Эта цифра должна быть умножена на суммарную площадь всех домовых перекрытий. Также рассчитывается и величина нагрузки чердачного перекрытия.
Принято брать вес мебели и другого внутридомового оборудования по нормам СНиП, эта величина равняется 195 кг/м³. Все эти величины суммируются и умножаются на 1,3, чтобы получить расчетную нагрузку.
После этого вычисляется общая длина ленты и число это переводят в см. Ширина, которой должен обладать ленточный фундамент, вычисляется по формуле: расчетная нагрузка делится на длину фундамента в см и на величину несущей способности грунта.
Вернуться к оглавлению
Способы расчета высоты
Высота, на которую возводится ленточный фундамент, рассчитывается двумя способами.
Самый простой способ – 1:1, или английский. Расчет здесь таков, что глубина фундамента равна его высоте. Если фундамент глубиной 1 м, высота его может быть до 1 м.
При применении второго способа ширину подошвы фундамента умножают на 4, полученное число и является максимально допустимой высотой.
Вернуться к оглавлению
Расчет объема внутренней части
Виды ленточных фундаментов.
Тип фундамента, материал для заливки которого будет рассчитываться, можно использовать для небольших построек: подсобки, душа, туалета. Рассчитывать материал для больших зданий сложнее из-за объема погрешностей.
Данный фундамент имеет форму прямоугольника. Ширина фундамента не может быть уже стен здания. Для примера берутся следующие цифры: 3,5 – ширина, 10 – длина, 0,2 – высота отливки и 0,18 – высота пояса отливки.
Чтобы рассчитать материал, нужно знать полный объем отливки (V), представляющий из себя прямоугольный параллелепипед. Для этого вычисляют периметр и полученное значение умножают на ширину и высоту отливки. Таким образом можно получить значение объема самой отливки ленточного фундамента.
Таким образом можно получить значение объема самой отливки ленточного фундамента.
Далее необходимо вычислить объем. находящийся внутри. Этого можно достичь, перемножив длину, ширину и высоту. Из получившегося числа необходимо вычесть предыдущее полученное V отливки. Таким образом получается число, равное внутренней части под материал.
Необходимо помнить, что под суммарной длиной ленты подразумевается не один только внешний периметр, но и длина всех межкомнатных перегородок.
В заливке ленточного фундамента используется такой материал, как арматура. Количество ее тоже лучше просчитать заранее. Для примера можно использовать стержни диаметром 12 мм, два из которых будут расположены горизонтально по всему периметру, а также вертикально, каждые полметра по 1 стержню.
Значение периметра умножается на материал, сначала на количество расположенной горизонтально арматуры (на 2). Затем значение периметра умножают на получившееся количество вертикальных стержней.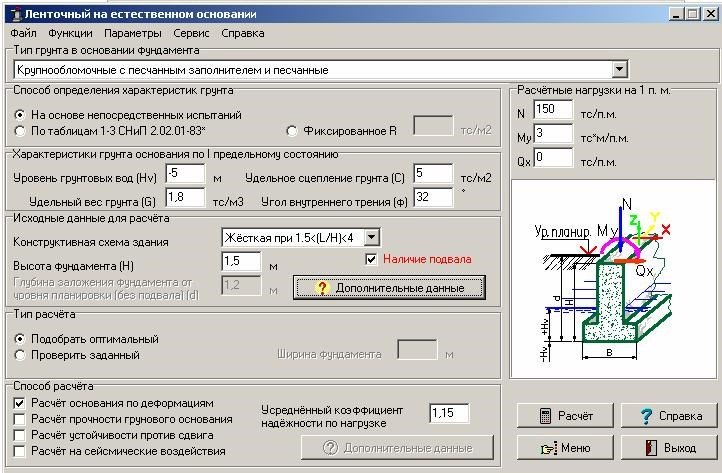 При этом прибавляют дополнительно по стержню в каждый из имеющихся углов. Количество стержней умножается на высоту фундамента, равную в этом случае их высоте.
При этом прибавляют дополнительно по стержню в каждый из имеющихся углов. Количество стержней умножается на высоту фундамента, равную в этом случае их высоте.
После этого необходимо произвести расчет опалубки. Для этого производят расчет боковой поверхности, умножая значение периметра на высоту отливки. Полученное число умножается на 2, чтобы рассчитать с запасом, невзирая на то, что внутренний периметр меньше.
Количество брусков для соединения можно подсчитать самостоятельно, так как оно зависит от вида соединения.
его типы, использование и расчет
Ленточный фундамент – это одна из наиболее распространенных разновидностей фундаментов, используемых при возведении различных строений. Их долговечность определяется правильным подбором типа фундамента, его технически верным исполнением и, конечно, грамотным расчетом. Именно этому вопросу мы и намерены посвятить нашу сегодняшнюю статью.
Содержание статьи
Однако подробную информацию о расчетах мы хотим предварить некоторыми общими сведениями, которые позволят вам не совершить ошибку, сделав выбор в пользу фундамента ленточного типа.
Ленточный фундамент и его разновидности
Ленточный фундамент – это лентовидное основание, уложенное под все несущие, а иногда и ненесущие стены дома. Исходя из характера материалов, используемых для их обустройства, фундаменты могут быть:
- бутовыми;
- бутобетонными;
- бетонными;
- железобетонными;
- кирпичными.
В конструктивном отношении, различают ленточные фундаменты сборного типа и монолитные. Сборные фундаменты изготавливаются из отдельных готовых блоков и отличаются большой быстротой возведения, тогда как монолитные должны некоторое время выдерживаться для того, чтобы бетон смог набрать прочность. Важный недостаток сборных конструкций состоит в их меньшей прочности в сравнении с литой бетонной лентой.
Несмотря на быстроту возведения сборных конструкций, монолитные ленточные фундаменты относятся к значительно более распространенным. По материалу изготовления они могут быть бутового состава или, что случается значительно чаще, быть железо- или просто бетонными.
Для каких строений подходят ленточные фундаменты и их достоинства
Если расчет ленточного фундамента выполнен правильно, он может являться надежным основанием для:
- кирпичных и газобетонных домов;
- домов из камня;
- железобетонных строений средней тяжести;
- бревенчатых домов.
Кроме того, данный тип фундамента может успешно использоваться для бань и гаражей, заборов и пристроек и т.д.
К достоинствам ленточных фундаментов следует отнести:
- обеспечение возможности по обустройству подвалов;
- способность выдерживать существенные нагрузки;
- возможность обустройства перекрытий с использованием бетонных плит;
- простота возведения и возможность выполнения работ своими силами.
Недостаток фундамента данного типа состоит в его относительно дороговизне. Однако он с лихвой перекрывается той надежностью, которую в состоянии обеспечить эта конструкция.
Заглубленность фундаментов ленточного типа
По степени заглубленности ленточные конструкции могут быть:
- мелкозаглубленными;
- заглубленными.

Мелкозаглубленные фундаменты
Как правило, мелкозаглубленные фундаменты укладываются на глубину 60 см и менее. Основанием для их укладки могут быть щебеночные и непучинистые песчаные и каменистые грунты.
Мелкозаглубленные фундаменты подходят там, где зеркало грунтовых вод находится ниже обычной глубины промерзания. Их не рекомендуется использовать на неровных участках, а также для тяжелых каменных строений.
Эти конструкции могут являться прекрасным основанием для легких каркасных построек, деревянных домов и пристроек к ним, гаражей и заборов.
Заглубленные фундаменты
Заглубленные фундаменты обустраиваются на любых надежных грунтах и закладываются ниже той глубины, на которую промерзает грунт в конкретной местности.
Фундаменты данного типа не рекомендуются в следующих условиях:
- если грунтовые воды проходят очень высоко, что чревато промерзанием и разрушением конструкции;
- при наличии больших перепадов высот;
- в случае заболоченности почвы или сыпучести грунта;
- при очень глубоком промерзании почвы, что делает закладку такого фундамента экономически неприемлемой.

Заглубленные фундаменты ленточного типа являются отличной и надежной основой для любых тяжелых каменных построек.
А теперь мы можем рассказать вам и о том, как производится расчетных ленточных фундаментов. Причем делать это будем на основе личного опыта, полученного в ходе возведения бани.
Порядок расчета ленточного фундамента
Наиболее сложная стадия строительства бани – безусловно, создание нулевого уровня. С одной лишь сметы уходит на его больше 20%, и не меньшая часть времени и сил. С одной стороны, хорошо, если занимаются фундаментом нанятые строители, которых наняли вообще для всех этапов строительства – с другой стороны, наиболее серьёзные проблемы уже спустя 1-2 года начинаются у доверившихся им. Самое безобидное из возможных зол — это когда рабочие заместо бетона заливают неизвестного происхождения смесь либо «забывают» устроить гидроизоляцию.
Правильно просчитанный и спроектированный фундамент
Поэтому знание, как рассчитывать правильно стройматериалы для ленточного фундамента и как грамотно его строить, крайне полезным окажется для тех, кто делает всё своими руками, и для тех, кто только наблюдает за нанятой бригадой. Разумеется, на 100% точный расчёт выполнить не сумеет даже опытный архитектор либо прораб, однако достоверные примерные данные можно получить. Ведь основное – это верный расчёт ленточного фундамента относительно нагрузки на будущий фундамент, кубатура его, объём, геометрические размеры.
Разумеется, на 100% точный расчёт выполнить не сумеет даже опытный архитектор либо прораб, однако достоверные примерные данные можно получить. Ведь основное – это верный расчёт ленточного фундамента относительно нагрузки на будущий фундамент, кубатура его, объём, геометрические размеры.
По стандарту во внимание берутся во время строительства 2 важные позиции – это расчёт деформации грунта и расчёт несущей способности его. В целом всё делиться на такие этапы:
I этап. Определение типа грунта
Чтоб определить тип грунта, присутствующий на участке, ныне есть больше 10 надёжных способов, это и «дедовские», и предполагающие привлечение современной техники. Простейший из них таков – делаются несколько глубоких ям на всём участке и рассматривается так называемый срез почвы. При этом буквально в 2 метрах земля может быть уже иной – это нормально. По таким результатам надо сложить геологическую картину для себя, она и будет определять глубину закладывания фундамента и вид последнего.
Любой сухой грунт, будь он глинистый либо песчаный, обладает стандартной несущей способностью от 2кг/см2. На данную цифру и надо ориентироваться, делая расчёт ленточного фундамента. Тогда нагрузка и в случае бревенчатой, и в случае кирпичной бани останется всё же в пределах нормы, даже с некоторым запасом.
Если у вас выходит, что масса бани явно превышает данное значение, и вы не уверены, что фундамент выдержит нагрузку, необходимо простое увеличение ширины его ленты, это всё, поскольку надо будет учесть ещё с годами расчёт осадки ленточного фундамента. Лишь после этого снова следует пересчитать нагрузку на грунт – масса фундамента в таком случае изменится, общее значение станет иным.
К слову, тяжёлыми называют грунты, которые тяжело копаются, их ещё называют и «плотными», т.е. имеющими низкую пористость и неэластичность. А те, которые копаются легко, являются среднеплотными грунтами, которые могут также называться текучими, пористыми и пластичными.
Немаловажное значение имеет принадлежит глубине промерзания почвы. Ведь земля, находящаяся ниже данной точки, уже и так уплотнена, причём «дальше некуда» — в таком состоянии она пребывает сотни лет. А грунт, который выше данной точки, всегда насыщен влагой, он при сезонном размораживании увеличивает свой объём, т.е. пучится. Причём минимум на 10% — это для фундамента достаточно ощутимо, для стен бани также. Отсюда и возникло понятие максимальной деформации стройматериала, и поэтому столь важно вычисление характеристики почвы и её возможного пучения к весне, на основе этого делают расчёт ленточного монолитного фундамента – надёжный и точный.
Ведь земля, находящаяся ниже данной точки, уже и так уплотнена, причём «дальше некуда» — в таком состоянии она пребывает сотни лет. А грунт, который выше данной точки, всегда насыщен влагой, он при сезонном размораживании увеличивает свой объём, т.е. пучится. Причём минимум на 10% — это для фундамента достаточно ощутимо, для стен бани также. Отсюда и возникло понятие максимальной деформации стройматериала, и поэтому столь важно вычисление характеристики почвы и её возможного пучения к весне, на основе этого делают расчёт ленточного монолитного фундамента – надёжный и точный.
II этап. Определение приблизительного веса постройки
Сюда непременно надо вписать вес мебели и прочих предметов, которые будут в бане, а ещё снег, который осядет на её крыше, — он может весить даже тонну (так наз. снеговая нагрузка).
Проверка выбранного типа фундамента проходит по 3-м параметрам:
- Несущая способность грунта превышает удельную нагрузку.
Что представляет собою несущая способность грунтов? Данная характеристика выбранного участка показывает, какая именно нагрузка «под силу» единице площади грунта, а также какой должна быть суммарная площадь фундамента бани – оказывается, чем хуже грунт способен выдержать давление, тем больше нужна площадь нулевого уровня. Как определяется несущая способность грунта? На способность грунта «держать» фундамент влияет одновременно целый комплекс факторов. Это тип грунта основания, его плотность, сезонная влажность, близость подземных вод. И это лишь пример расчёта ленточного фундамента, поскольку для каждого участка необходим учёт природных и техногенных факторов.
Как определяется несущая способность грунта? На способность грунта «держать» фундамент влияет одновременно целый комплекс факторов. Это тип грунта основания, его плотность, сезонная влажность, близость подземных вод. И это лишь пример расчёта ленточного фундамента, поскольку для каждого участка необходим учёт природных и техногенных факторов.
- Деформация морозного пучения грунта намного меньше, чем предельно допустимая для данного фундамента и данной конструкции бани.
- Возможные напряжения на фундамент не превышают напряжений, при которых утрата упругости в арматуре фундамента рискует стать необратимой.
Так, наиболее хрупки и наиболее склонны к трещинам блоки без армирования и кирпич. Показатель деформации для них не может быть выше 0,0005. Таким образом, в случае длины фундамента 15 м выгиб стены может быть не больше 7,5 мм, в зависимости от этого и делают расчёт арматуры для ленточного фундамента.
III этап. Коррекция размеров фундамента
Итак, остался лишь расчёт бетона на ленточный фундамент – объём его будет равняться кубатуре самого фундамента. Как вычислить её? Всё просто – ширина ленты умножается на общую длину и на высоту. Ширина ленты обычно не выше 40 см, а длина составляет суммарную длину всех стен бани, являющихся несущими, высота – это сумма надземной и подземной части.
Как вычислить её? Всё просто – ширина ленты умножается на общую длину и на высоту. Ширина ленты обычно не выше 40 см, а длина составляет суммарную длину всех стен бани, являющихся несущими, высота – это сумма надземной и подземной части.
Конструктивно для железобетонной балки минимальная допустимая ширина — 15 см, для ленточного фундамента (представляющего собою, в сущности, свободно лежащие на упругом основании балки) рекомендуемая ширина — минимум 25 см для садовой лёгкой постройки, и минимум 30 см для дачного дома. Ширина мелкозаглубленного ленточного фундамента не должна превышать ширину стены, опираемой на неё.
Но, помимо конструкционных ограничений имеются также требования, которые задаются несущими способностями грунтов, подлежащих под фундаментами. Удельная нагрузка от здания, рассчитываемая на единицу площади, должна не превышать 70% несущей способности грунта. Величину нагрузки регулировать возможно при помощи площади опоры фундамента на почву. Чем эта площадь опоры больше, тем удельная нагрузка, которая передаётся на грунт, меньше.
Методика определения наименьшей достаточной ширины ленточного мелкозаглубленного фундамента основывается на представлении про то, что удельная нагрузка на единицу площади грунта, лежащего под фундаментом, должна быть меньше, чем несущая способность (т.е. расчётное сопротивление основания) грунта, лежащего под фундаментом. Разница между несущей способностью грунта и нагрузкой от дома должна быть минимум на 30% больше в сторону несущей способности грунтов (это коэффициент запаса прочности бетонных конструкций, которые отливаются на стройплощадках с удельном весом меньше 1600 кг/м3).
На этом всё: подготовка к созданию нулевого уровня бани, бесспорно, всегда кропотлива, отнимает немало времени, много сил, однако минимум 3 поколения будут париться в добротной парной со спокойной душою.
Пример расчета ленточного фундамента по несущей способности грунта для каркасного дома
Вводные данные.
Дом с мансардой, деревянной каркасной конструкции на ленточном монолитном железобетонном фундаменте.
Каркасный дом
Состав помещений: 1 комната — 9,47 м2, 2 комната — 6,30 м2, 3 кухня — 6,30 м2, 4 веранда — 9,47 м2, 5 мансарда — 12,15 м2. Высота до потолка 2,65 м. Площадь крыши 55 м2. Окна деревянные, двойные. Двери наружные металлические, внутренние деревянные.
Строительство дома предполагается на суглинистых грунтах с глубиной промерзания до 1,0 м. Расстояние от планировочной отметки до уровня грунтовых вод, в период промерзания грунта, менее расчетной глубины промерзания. Место строительства — Харьковская обл.
Задаем предварительные параметры фундамента исходя из имеющихся геологических условий и принятой схеме его планировки.
Схема фундамента (6,0 м х 6,0 м).
Исходя из наших условий. принимаем предварительные геометрические размеры фундамента: ширина – 0,4 м; высота – 1,1 м. Общая площадь подошвы фундамента: длина 30 м х ширина 0,4 м = 12 м2.
Элементы конструкции и применяемые материалы:
- фундамент – ЖБ ленточный, монолитный;
- цоколь – кирпич;
- стены — деревянные каркасные с наружной обшивкой из вагонки;
- двери:
- наружные — металлические,
- внутренние – деревянные;
- пол – брус, половая доска;
- перегородки – каркасные;
- внутренняя обшивка стен и перегородок – вагонка;
- крыша – двухскатная (угол наклона 45 градусов), брус, доска, горбыль;
- обшивка потолока – ДВП;
- кровля — профнастил;
- лестница – брус, доска;
- утеплитель — пенопласт;
- гидроизоляция – Акваизол, GEOFOL;
- гвозди, шурупы, скобы – металл, сталь.

Расход строительных материалов и их вес(а):
- бетон марки М 150 для ЖБ ленточного монолитного фундамента. Объем фундамента (предварительный) определяем расчетом: длина 30 м х ширина 0,4 м х высота 1,1 м = 13,2 м3 (предварительно принятые геометрические размеры фундамента). Удельный вес железобетона – 2500 кг/м3 (по данным СНиП II-3-79). Считаем вес фундамента: объем 13,2 м3 х 2500 кг/м3 = 33000 кг или 33,0 т.
- металл, сталь на металлические двери и крепежные материалы. Двери металлические высотой 2,0 м и шириной 0,8 м с металлической коробкой. По сертификату производителя вес составляет 85 кг. Вес гвоздей, шурупов, скоб, металлических закладных деталей — 105 кг. Всего металла — 190 кг, или 0,19 т;
- кирпич полнотелый одинарный М 150 для возведения цоколя. По расчету при укладке цоколя высотой в 40,0 см (0,4 м), шириной в два ряда необходимо 2400 штук полнотелого кирпича из расчета — для 1 м2 кладки шириной в 2 кирпича, при одинарном кирпиче, с учетом растворных швов необходимо 204 штук.
 Вес одного полнотелого кирпича 3,4 кг. Тогда вес цоколя по кирпичу составит 2400 шт. х 3,4 кг =8160 кг или 8,6 т;
Вес одного полнотелого кирпича 3,4 кг. Тогда вес цоколя по кирпичу составит 2400 шт. х 3,4 кг =8160 кг или 8,6 т; - лесоматериалы (хвойных пород) для сооружения деревянных каркасных стен с наружной обшивкой из вагонки, внутренних деревянных дверей, пола из бруса и половой доски, внутренних каркасных перегородок, внутренней обшивки стен вагонкой, стропил крыши из бруса, доски, горбыля, лестницы из бруса и доски, фронтона мансарды из досок. Обмер всех составных элементов этих конструкций (по выполненным эскизам) составил объем в сумме 23,1 м3. Удельный вес хвойных пород древесины – 500 кг/м3 (по данным СНиП II-3-79). Определяем вес всего использованного лесоматериала — 23,1 м3 х 500 кг/м3 = 11550 кг или 11,550 т;
- профнастил для покрытия крыши. Площадь крыши составляет 55 м2. Применяем оцинкованный профнастил ТУ 1122-002-42831956-02. При весе 1 погонного метра профнастила марки НС18 — 4,35 кг, шириной 1 м, нам необходимо 62 м2 (с учетом перекрытия листов профнастила) или 62 мп (при ширине 1,0 м), что составит 62,0 мп х 4,35 кг = 270 кг или 0,27 т;
- ДВП (древесно-волокнистая плита) для потолка.
 Площадь потолка 6,0 м х 6,0 м = 36 м2. Размер примененных плит 1,0 м х 1,2 м = 1,2 м2. Всего необходимо плит — 36 м2 : 1,2 м2 = 30 плит. По плотности материала планируется применить полутвердые плиты с удельным весом 400 кг/м3. Вес одной плиты, при толщине 5 см, составит: 1,2 м2 х 0,05 м х 400 кг/м3 = 24 кг. Общий вес облицовки потолка 24 кг х 30 плит = 720 кг или 0,72 т;
Площадь потолка 6,0 м х 6,0 м = 36 м2. Размер примененных плит 1,0 м х 1,2 м = 1,2 м2. Всего необходимо плит — 36 м2 : 1,2 м2 = 30 плит. По плотности материала планируется применить полутвердые плиты с удельным весом 400 кг/м3. Вес одной плиты, при толщине 5 см, составит: 1,2 м2 х 0,05 м х 400 кг/м3 = 24 кг. Общий вес облицовки потолка 24 кг х 30 плит = 720 кг или 0,72 т;
Справка. ДВП по плотности материала делятся на: сверхтвёрдые (плотность 950 кг/м3), твёрдые (850 кг/м3), полутвёрдые (400 кг/м3), изоляционно-отделочные (250-350 кг/м3) и изоляционные (до 250 кг/м3). Промышленностью выпускаются ДВП с размерами (мм): длина 1200-5500; ширина 1000-2140; толщина 2,5-12. По материалам нормативных документов: ГОСТ 4598-86 (2000) «Плиты древесноволокнистые. Технические условия»; Технические условия»; ТУ 5536-0257438-009-99 «Плиты древесноволокнистые средней плотности».
- утеплитель для стен, пола, потолка и крыши. Общая площадь утепления: стен 6 м+6 м+6 м+6 м=24 м х 2,65 м (высота до потолка) = 63,6 м2; потолка 6 м х 6 м =36 м2; пола 6 м х 6 м = 36 м2; крыши 55 м2. Всего 63,6 м2 + 36,0 м2 + 36 м2 + 55 м2 = 190,6 м2. В качестве утеплителя используем пенопласт листовой ПСБ-С 25 по ГОСТ 15588-86, толщиной 0,15 м, плотностью 25 кг/м3. При этом объем утеплителя составит 190,6 м2 х 0,15 м = 28,59 м3, а вес 28,59 м3 х 25 кг/м3 = 714,75 кг или 0,715 т.
- гидроизоляция для фундамента и крыши. Для фундамента применяем в качестве гидроизоляции материал «Акваизол СБС» по ТУ 30510965-001, в два слоя. Удельный вес материала — 2,5 кг/м2. Длина фундамента 30 м. При укладки «Акваизола» в один слой шириной 0,5 м нам необходимо 30 м х 0,5 м = 15 м2 материала, а при двух слоях 15 м2 х 2 = 30 м2.
 Вес гидроизоляции составит 30 м2 х 2,5 кг/м2 = 75 кг. Для крыши используем гидроизоляционный материал мембрана толщиной 0,6 мм, плотностью 0,94 г/см3 или 940 кг/м3 (1 г/см3 =1000 кг/м3). Площадь для гидроизоляции крыши – 55 м2. Объем пленки 55 м2 х 0,0006 м = 0,033 м3. Вес 0,033 м3 х 940 кг/м3 = 31 кг.
Вес гидроизоляции составит 30 м2 х 2,5 кг/м2 = 75 кг. Для крыши используем гидроизоляционный материал мембрана толщиной 0,6 мм, плотностью 0,94 г/см3 или 940 кг/м3 (1 г/см3 =1000 кг/м3). Площадь для гидроизоляции крыши – 55 м2. Объем пленки 55 м2 х 0,0006 м = 0,033 м3. Вес 0,033 м3 х 940 кг/м3 = 31 кг.
Общий вес гидроизоляции будет 75 кг + 31 кг = 106 кг или 0,106 т.
- цементно-песчаный раствор для кладки кирпича цоколя. Исходим из существующих норм — на 1 м3 сплошной стенки одинарного кирпича шириной в два кирпича необходимо 0,240 м3 раствора. Объем нашего цоколя составляет: ширина 0,51 м х длина 30 м х высота 0,4 м = 6,1 м3. Тогда объем необходимого количества раствора для 6,1 м3 кирпичной кладки составит 6,1 х 0,240 = 1,4 м3.
 Удельный вес раствора составляет 1800 кг/м3 (по данным СНиП II-3-79). Вес раствора составит 1,4 м3 х 1800 кг/м3=2574 кг или 2,574 т.
Удельный вес раствора составляет 1800 кг/м3 (по данным СНиП II-3-79). Вес раствора составит 1,4 м3 х 1800 кг/м3=2574 кг или 2,574 т.
Общий вес дома, действующий на грунт.
- Определяем вес конструкции дома, включая все его элементы.
Эта величина состоит из суммы веса материалов используемых для строительства (а):
33,0+0,19+8,6+11,55+0,27+0,72+0,715+0,106+2,574= 57,725 т.
- Определяем снеговую нагрузку на дом.
Расчет проводим в соответствии с требованием ДБН В.1.2-2:2006 «Нагрузки и воздействия» раздел 8.
Площадь крыши 55 м2х160 кг/м2 = 8800 кг. Где 160 кг/м2 величина снеговой нагрузки в районе строительства дома. Определить снеговую нагрузку можно из пункта «снеговая нагрузка» статьи Фундамент дома. Расчет ленточного фундамента для дома.
С учетом угла наклона ската крыши (45 градусов) применяем поправочный коэффициент М = 0,56. 8800 кг х 0,56 = 4930 кг или 4,93 т.
8800 кг х 0,56 = 4930 кг или 4,93 т.
- Определяем полезную нагрузку от мебели, оборудования, количества людей и т. д., все, что будет находиться в доме.
Эта величина (с запасом) принимается равной общей площади дома умноженной на 180 кг/м2. 180 кг/м2 является принятой величиной удельной полезной нагрузки при расчетах. В нашем случае принимаем 36 м2 х 180 кг/м2 = 6480 кг или 6,48 т.
Суммарный вес дома со всеми нагрузками воспринимаемыми фундаментом составит сумму трех слагаемых, т.е. 57,725+4,93+6,48=69,135 т.
Таким образом на грунт действует стационарная сила 69,135 тонны.
Удельное давление, действующее на один м2 грунта.
Проводим проверку выбранных размеров нашего фундамента на работоспособность. Проверка проводится по упрощенной методике (см. Фундамент дома. Расчет ленточного фундамента для дома) на соответствие фундамента требованиям ДБН В. 2.1.-10-2009 «Основания и фундаменты сооружений». (Приложение Е).
2.1.-10-2009 «Основания и фундаменты сооружений». (Приложение Е).
Целью расчета является определение соотношения величин удельного давления на грунт под подошвой фундамента от веса дома со всеми нагрузками — Р т/м2 и расчетного сопротивления грунта — R т/м2. Расчетное сопротивление грунта характеризует его способность воспринимать нагрузку от здания без осадки. Величина Р определяется расчетом, а R регламентируется ДБН.
Главным требованием для надежной работы фундамента является соблюдение условий, при которых величина P должна быть меньше величины R.
Определяем удельное давление на грунт под подошвой фундамента Р т/м2.
Для этого общий вес дома с нагрузками 69,135 т делим на площадь подошвы фундамента 12 м2 получаем Р = 5,76 т/м2.
По таблице Е.3 ДБН находим что R для суглинков составляет 10,0 т/м2. При определении R, поскольку не проводились геологические исследования грунта, из таблицы выбираем самый минимальный показатель этой величины (принимая во внимание самые неблагоприятные показатели пористости и текучести грунта).
При определении R, поскольку не проводились геологические исследования грунта, из таблицы выбираем самый минимальный показатель этой величины (принимая во внимание самые неблагоприятные показатели пористости и текучести грунта).
Как мы видим R значительно больше Р, что соответствует главному условию надежной работы фундамента.
Для создания запаса прочности фундамента, перекрывающего неточности в выборе исходных данных, необходимо чтобы величина R была на 15-20% больше чем Р. У нас, при 20% запасе достаточно чтобы величина Р = 8,0 т/м2(контрольная величина).
Проверка и корректировка размеров фундамента.
Исходя из полученных расчетных данных, для экономии средств, целесообразно уменьшить размеры фундамента. Будем поэтапно искать оптимальный вариант.
Уменьшаем ширину фундамента на 10 см (т.е. принимаем ширину 30 см), при этом площадь подошвы фундамента будет 9 м2.
Определяем Р, которое будет составлять: 69,135 т : 9,0 м2 = 7,68 т/м2, что не превышает допустимое Р=8,0 т/м2.
Проведем уточненную проверку Р, т.к. уменьшился вес самого фундамента. Вес фундамента при его ширине 30 см составит 0,3 м х 1,1 м х 30 м х 2500 кг/м2=20455 кг или 20,46 т. При этом вес конструкций дома составит: 57,725-33+20,46=45,185 т, а суммарный вес дома 45,185+4,93+6,48 = 56,59 т. Определяем Р — 56,59 т : 9,0 м2=6,29 т/м2. Эта величина значительно меньше контрольной — 8,0 т/м2.
Уменьшаем ширину фундамента еще на 5 см (т.е. принимаем ширину фундамента 25 см), при этом площадь подошвы фундамента составит 7,5 м2.
Определяем Р — 56,59 т : 7,5 м2=7,54 т/м2. Полученное значение Р достаточно близко к контрольной величине Р = 8,0 т/м2. Очевидно, что дальнейшая корректировка параметров фундамента не целесообразна, поэтому полученные результаты расчета могут считаться окончательными.
Очевидно, что дальнейшая корректировка параметров фундамента не целесообразна, поэтому полученные результаты расчета могут считаться окончательными.
формул вычисляемого поля | Документы Microsoft
- 15 минут на чтение
В этой статье
Применимо к: SharePoint Foundation 2010
В следующих таблицах представлена информация о различных типах формул, которые можно реализовать в вычисляемом поле с помощью формулы класса Microsoft.SharePoint.SPFieldCalculated.
Важные примечания
Примечание
Формулы Microsoft SharePoint Foundation для вычисляемых полей основаны на функциях и синтаксисе Microsoft Excel. Однако Microsoft поддерживает только те функции, которые упомянуты на этой странице, для использования в вычисляемых полях SharePoint Foundation. Например, функция Excel MID не поддерживается.
Однако Microsoft поддерживает только те функции, которые упомянуты на этой странице, для использования в вычисляемых полях SharePoint Foundation. Например, функция Excel MID не поддерживается.
Важно
Во всех примерах формул в этом разделе в качестве символа-разделителя параметра используются запятые «,». В некоторых странах запятая зарезервирована для использования в качестве десятичного знака.В таких странах пользователи, создающие вычисляемое поле, должны использовать точку с запятой «;» как символ-разделитель. Независимо от того, какой символ используется при создании поля, формула работает со списками на веб-сайтах SharePoint в любой точке мира. SharePoint автоматически меняет символ-разделитель на тот, который соответствует языку / культуре текущей страницы. Например, предположим, что следующая формула создана на веб-сайте, региональные параметры которого — fr-fr (Франция): = IF (Number1> Number2; 5; 10).Если культура веб-сайта затем изменится на en-us (США), формула автоматически изменится на: = IF (Number1> Number2,5,10).
Условные формулы
Вы можете использовать следующие формулы для проверки условия оператора и возврата значения Да или Нет, для проверки альтернативного значения, такого как ОК или Не ОК, или для возврата пробела или дефиса для представления нулевого значения.
Определить, больше или меньше одно число другого числа
Используйте функцию ЕСЛИ для выполнения этого сравнения.
Столбец 1 | Колонка 2 | Формула | Описание (возможный результат) |
|---|---|---|---|
15000 | 9000 | = [Столбец1]> [Столбец2] | Столбец1 больше, чем Столбец2? (Да) |
15000 | 9000 | = ЕСЛИ ([Столбец1] <= [Столбец2], "ОК", "Неверно") | Столбец1 меньше или равен столбцу2? (Не в порядке) |
Вернуть логическое значение после сравнения содержимого столбца
Для получения результата, который является логическим значением (Да или Нет), используйте функции И, ИЛИ и НЕ.
Столбец 1 | Колонка 2 | Столбец 3 | Формула | Описание (возможный результат) |
|---|---|---|---|---|
15 | 9 | 8 | = И ([Столбец1]> [Столбец2], [Столбец1] <[Столбец3]) | 15 больше 9 и меньше 8? (Нет) |
15 | 9 | 8 | = ИЛИ ([Столбец1]> [Столбец2], [Столбец1] <[Столбец3]) | 15 больше 9 или меньше 8? (Да) |
15 | 9 | 8 | = НЕ ([Столбец1] + [Столбец2] = 24) | 15 плюс 9 не равно 24? (Нет) |
Для результата, который представляет собой другое вычисление или любое другое значение, кроме Да или Нет, используйте функции ЕСЛИ, И и ИЛИ.
Столбец 1 | Колонка 2 | Столбец 3 | Формула | Описание (возможный результат) |
|---|---|---|---|---|
15 | 9 | 8 | = ЕСЛИ ([Column1] = 15, «ОК», «Не в порядке») | Если значение в столбце 1 равно 15, вернуть «ОК».(ОК) |
15 | 9 | 8 | = ЕСЛИ (И ([Столбец1]> [Столбец2], [Столбец1] <[Столбец3]), «ОК», «Неверно») | Если 15 больше 9 и меньше 8, вернуть «ОК». (Не в порядке) |
15 | 9 | 8 | = ЕСЛИ (ИЛИ ([Столбец1]> [Столбец2], [Столбец1] <[Столбец3]), «ОК», «Неверно») | Если 15 больше 9 или меньше 8, вернуть «ОК».(ОК) |
Отображать нули как пробелы или дефисы
Чтобы отобразить ноль, выполните простое вычисление.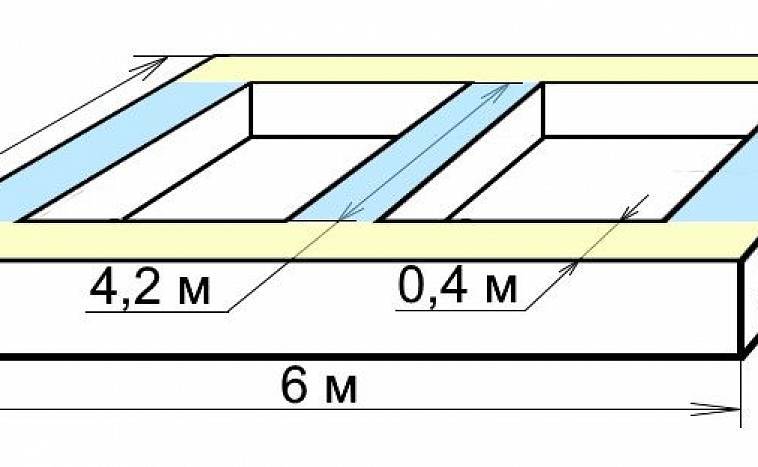 Чтобы отобразить пробел или тире, используйте функцию ЕСЛИ.
Чтобы отобразить пробел или тире, используйте функцию ЕСЛИ.
Столбец 1 | Колонка 2 | Формула | Описание (возможный результат) |
|---|---|---|---|
10 | 10 | = [Столбец1] — [Столбец2] | Второе число, вычитаемое из первого.(0) |
15 | 9 | = ЕСЛИ ([Столбец1] — [Столбец2], [Столбец1] — [Столбец2], «-») | Возвращает прочерк, если значение равно нулю. (-) |
Скрыть значения ошибок в столбцах
Чтобы отобразить тире, # N / A или NA вместо значения ошибки, используйте функцию ISERROR.
Столбец 1 | Колонка 2 | Формула | Описание (возможный результат) |
|---|---|---|---|
10 | 0 | = [Столбец1] / [Столбец2] | Результатов с ошибкой (# DIV / 0) |
10 | 0 | = ЕСЛИ (ЕСТЬ ОШИБКА ([Столбец1] / [Столбец2]), «НЕТ», [Столбец1] / [Столбец2]) | Возвращает NA, если значение является ошибкой |
10 | 0 | = ЕСЛИ (ЕСТЬ ОШИБКА ([Столбец1] / [Столбец2]), «-», [Столбец1] / [Столбец2]) | Возвращает тире, если значение является ошибкой |
Формулы даты и времени
Вы можете использовать следующие формулы для выполнения вычислений, основанных на датах и времени, таких как добавление числа дней, месяцев или лет к дате, вычисление разницы между двумя датами и преобразование времени в десятичное значение.
Добавить даты
Чтобы добавить количество дней к дате, используйте оператор сложения (+).
Примечание
Когда вы манипулируете датами, тип возвращаемого значения вычисляемого столбца должен быть установлен на Дата и время.
Столбец 1 | Колонка 2 | Формула | Описание (возможный результат) |
|---|---|---|---|
09.06.2007 | 3 | = [Столбец1] + [Столбец2] | Добавляет 3 дня к 09.06.2007 (12.06.2007) |
10.12.2008 | 54 | = [Столбец1] + [Столбец2] | Добавляет 54 дня к 10.12.2008 (02.02.2009) |
Чтобы добавить количество месяцев к дате, используйте функции ДАТА, ГОД, МЕСЯЦ и ДЕНЬ.
Столбец 1 | Колонка 2 | Формула | Описание (возможный результат) |
|---|---|---|---|
09. | 3 | = ДАТА (ГОД ([Столбец1]), МЕСЯЦ ([Столбец1]) + [Столбец2], ДЕНЬ ([Столбец1])) | Добавляет 3 месяца к 09.06.2007 (09.09.2007) |
10.12.2008 | 25 | = ДАТА (ГОД ([Столбец1]), МЕСЯЦ ([Столбец1]) + [Столбец2], ДЕНЬ ([Столбец1])) | Добавляет 25 месяцев к 10.12.2008 (01.10.2011) |
Чтобы добавить количество лет к дате, используйте функции ДАТА, ГОД, МЕСЯЦ и ДЕНЬ.
Столбец 1 | Колонка 2 | Формула | Описание (возможный результат) |
|---|---|---|---|
09.06.2007 | 3 | = ДАТА (ГОД ([Столбец1]) + [Столбец2], МЕСЯЦ ([Столбец1]), ДЕНЬ ([Столбец1])) | Добавляет 3 года к 09.06.2007 (09.06. |
10.12.2008 | 25 | = ДАТА (ГОД ([Столбец1]) + [Столбец2], МЕСЯЦ ([Столбец1]), ДЕНЬ ([Столбец1])) | Добавляет 25 лет к 10.12.2008 (10.12.2033) |
Чтобы добавить к дате комбинацию дней, месяцев и лет, используйте функции ДАТА, ГОД, МЕСЯЦ и ДЕНЬ.
Столбец 1 | Формула | Описание (возможный результат) |
|---|---|---|
09.06.2007 | = ДАТА (ГОД ([Столбец1]) + 3, МЕСЯЦ ([Столбец1]) + 1, ДЕНЬ ([Столбец1]) + 5) | Добавляет 3 года, 1 месяц и 5 дней к 9.06.2007 (14.07.2010) |
10.12.2008 | = ДАТА (ГОД ([Столбец1]) + 1, МЕСЯЦ ([Столбец1]) + 7, ДЕНЬ ([Столбец1]) + 5) | Добавляет 1 год, 7 месяцев и 5 дней к 10.12.2008 (15.07. |
Вычислить разницу между двумя датами
Используйте функцию РАЗНДАТ, чтобы выполнить это вычисление.
Столбец 1 | Колонка 2 | Формула | Описание (возможный результат) |
|---|---|---|---|
01 января 1995 г. | 15 июня 1999 г. | = РАЗНДАТ ([Столбец1], [Столбец2], «г») | Возвращает количество дней между двумя датами (1626) |
01 января 1995 г. | 15 июня 1999 г. | = РАЗНДАТ ([Столбец1], [Столбец2], «гм») | Возвращает количество месяцев между датами, игнорируя часть года (5) |
01 января 1995 | 15 июня 1999 г. | = РАЗНДАТ ([Столбец1], [Столбец2], «ярд») | Возвращает количество дней между датами, игнорируя часть года (165) |
Вычислить разницу между двумя значениями
Чтобы представить результат в стандартном формате времени (часы: минуты: секунды), используйте оператор вычитания (-) и функцию ТЕКСТ.Чтобы этот метод работал, часы не должны превышать 24, а минуты и секунды не должны превышать 60.
Столбец 1 | Колонка 2 | Формула | Описание (возможный результат) |
|---|---|---|---|
09.06.2007 10:35 | 09.06.2007 15:30 | = ТЕКСТ ([Столбец2] — [Столбец1], «h») | Число часов между двумя точками (4) |
09.06.2007 10:35 | 09.06.2007 15:30 | = ТЕКСТ ([Столбец2] — [Столбец1], «ч: мм») | Часы и минуты между двумя точками (4:55) |
09.06.2007 10:35 | 09.06.2007 15:30 | = ТЕКСТ ([Столбец2] — [Столбец1], «ч: мм: сс») | Часы, минуты и секунды между двумя значениями (4:55:00) |
Чтобы представить результат в виде суммы, основанной на одной единице времени, используйте функцию ЦЕЛОЕ или функцию ЧАС, МИНУТА или СЕКУНДА.
Столбец 1 | Колонка 2 | Формула | Описание (возможный результат) |
|---|---|---|---|
09.06.2007 10:35 | 10.06.2007 15:30 | = INT (([Столбец2] — [Столбец1]) * 24) | Общее количество часов между двумя периодами (28) |
09.06.2007 10:35 | 10.06.2007 15:30 | = ЦЕЛОЕ (([Столбец2] — [Столбец1]) * 1440) | Всего минут между двумя значениями (1735) |
09.06.2007 10:35 | 10.06.2007 15:30 | = ЦЕЛОЕ (([Столбец2] — [Столбец1]) * 86400) | Всего секунд между двумя значениями (104100) |
09.06.2007 10:35 | 10.06.2007 15:30 | = ЧАС ([Столбец2] — [Столбец1]) | Часы между двумя моментами времени, когда разница не превышает 24 (4) |
09.06.2007 10:35 | 10.06.2007 15:30 | = МИНУТА ([Столбец2] — [Столбец1]) | Минуты между двумя моментами времени, когда разница не превышает 60 (55) |
09.06.2007 10:35 | 10.06.2007 15:30 | = ВТОРОЙ ([Столбец2] — [Столбец1]) | Секунды между двумя моментами времени, когда разница не превышает 60 (0) |
Конвертировать раз
Чтобы преобразовать часы из стандартного формата времени в десятичное число, используйте функцию INT.
Столбец 1 | Формула | Описание (возможный результат) |
|---|---|---|
10:35 утра | = ([Столбец1] -INT ([Столбец1])) * 24 | Количество часов с 00:00 (10,583333) |
12:15 | = ([Столбец1] -INT ([Столбец1])) * 24 | Количество часов с 00:00 (12.25) |
Чтобы преобразовать часы из десятичного числа в стандартный формат времени (часы: минуты: секунды), используйте оператор деления и функцию ТЕКСТ.
Столбец 1 | Формула | Описание (возможный результат) |
|---|---|---|
23:58 | = ТЕКСТ (Столбец 1/24, «чч: мм: сс») | Часы, минуты и секунды с 00:00 (00:59:55) |
2:06 | = ТЕКСТ (Столбец 1/24, «ч: мм») | Часы и минуты с 00:00 (0:05) |
Вставить юлианские даты
Юлианская дата относится к формату даты, который представляет собой комбинацию текущего года и количества дней с начала года.Например, 1 января 2007 года представлено как 2007001, а 31 декабря 2007 года представлено как 2007365. Этот формат не основан на юлианском календаре.
Чтобы преобразовать дату в юлианскую дату, используйте функции ТЕКСТ и ДАТАЗНАЧ.
Столбец 1 | Формула | Описание (возможный результат) |
|---|---|---|
23.06.2007 | = ТЕКСТ ([Column1], «yy») & TEXT (([Column1] -DATEVALUE («1/1 /» & TEXT ([Column1], «yy»)) + 1), «000») | Дата в юлианском формате с двузначным годом (07174) |
23.06.2007 | = ТЕКСТ ([Column1], «yyyy») & TEXT (([Column1] -DATEVALUE («1/1 /» & TEXT ([Column1], «yy»)) + 1), «000») | Дата в юлианском формате с четырехзначным годом (2007174) |
Чтобы преобразовать дату в юлианскую дату, которая используется в астрономии, используйте константу 2415018.50. Эта формула работает только для дат после 01.03.1901, и если вы используете систему дат 1900 года.
Столбец 1 | Формула | Описание (возможный результат) |
|---|---|---|
23.06.2007 | = [Столбец1] +2415018,50 | Дата в юлианском формате, используется в астрономии (2454274.50) |
Показывать даты как день недели
Чтобы преобразовать даты в текст дня недели, используйте функции ТЕКСТ и ДЕНЬ НЕДЕЛИ.
Столбец 1 | Формула | Описание (возможный результат) |
|---|---|---|
19 февраля 2007 г. | = ТЕКСТ (ДЕНЬ НЕДЕЛИ ([Столбец1]), «дддд») | Вычисляет день недели для даты и возвращает полное название дня (понедельник) |
3 января 2008 г. | = ТЕКСТ (ДЕНЬ НЕДЕЛИ ([Столбец1]), «ддд») | Вычисляет день недели для даты и возвращает сокращенное название дня (чт) |
Математические формулы
Вы можете использовать следующие формулы для выполнения различных математических вычислений, таких как сложение, вычитание, умножение и деление чисел; вычисление среднего или медианы чисел; округление числа; и подсчет значений.
Сложите числа
Чтобы сложить числа в двух или более столбцах подряд, используйте оператор сложения (+) или функцию СУММ.
Столбец 1 | Колонка 2 | Столбец 3 | Формула | Описание (возможный результат) |
|---|---|---|---|---|
6 | 5 | 4 | = [Столбец1] + [Столбец2] + [Столбец3] | Складывает значения в первых трех столбцах (15) |
6 | 5 | 4 | = СУММ ([Столбец1], [Столбец2], [Столбец3]) | Складывает значения в первых трех столбцах (15) |
6 | 5 | 4 | = СУММ (ЕСЛИ ([Столбец1]> [Столбец2], [Столбец1] — [Столбец2], 10), [Столбец3]) | Если Column1 больше, чем Column2, складывается разница и Column3.Иначе добавьте 10 и столбец 3 (5) |
Вычесть числа
Чтобы вычесть числа в двух или более столбцах в строке, используйте оператор вычитания (-) или функцию СУММ с отрицательными числами.
Столбец 1 | Колонка 2 | Столбец 3 | Формула | Описание (возможный результат) |
|---|---|---|---|---|
15000 | 9000 | -8000 | = [Столбец1] — [Столбец2] | Вычитает 9000 из 15000 (6000) |
15000 | 9000 | -8000 | = СУММ ([Столбец1], [Столбец2], [Столбец3]) | Суммирует числа в первых трех столбцах, включая отрицательные значения (16000) |
Вычислить разницу между двумя числами в процентах
Используйте операторы вычитания (-) и деления (/), а также функцию ABS.
Столбец 1 | Колонка 2 | Формула | Описание (возможный результат) |
|---|---|---|---|
2342 | 2500 | = ([Столбец2] — [Столбец1]) / ABS ([Столбец1]) | Изменение в процентах (6,75% или 0,06746) |
Умножение чисел
Чтобы умножить числа в двух или более столбцах в строке, используйте оператор умножения (*) или функцию ПРОИЗВОД.
Столбец 1 | Колонка 2 | Формула | Описание (возможный результат) |
|---|---|---|---|
5 | 2 | = [Столбец1] * [Столбец2] | Умножает числа в первых двух столбцах (10) |
5 | 2 | = ПРОДУКТ ([Столбец1], [Столбец2]) | Умножает числа в первых двух столбцах (10) |
5 | 2 | = ПРОДУКТ ([Столбец1], [Столбец2], 2) | Умножает числа в первых двух столбцах и число 2 (20) |
Делить числа
Чтобы разделить числа на два или более столбца подряд, используйте оператор деления (/).
Столбец 1 | Колонка 2 | Формула | Описание (возможный результат) |
|---|---|---|---|
15000 | 12 | = [Столбец1] / [Столбец2] | Делит 15000 на 12 (1250) |
15000 | 12 | = ([Столбец1] +10000) / [Столбец2] | Складывает 15000 и 10000, а затем делит сумму на 12 (2083) |
Вычислить среднее значение
Среднее значение также называют средним.Чтобы вычислить среднее значение чисел в двух или более столбцах подряд, используйте функцию СРЕДНЕЕ.
Столбец 1 | Колонка 2 | Столбец 3 | Формула | Описание (возможный результат) |
|---|---|---|---|---|
6 | 5 | 4 | = СРЕДНЕЕ ([Столбец1], [Столбец2], [Столбец3]) | Среднее значение чисел в первых трех столбцах (5) |
6 | 5 | 4 | = СРЕДНЕЕ (ЕСЛИ ([Столбец1]> [Столбец2], [Столбец1] — [Столбец2], 10), [Столбец3]) | Если Column1 больше, чем Column2, вычислить среднее значение разницы и Column3.В противном случае вычислите среднее значение 10 и Столбец 3 (2,5) |
Вычислить медиану чисел
Медиана — это значение в центре упорядоченного диапазона чисел. Используйте функцию МЕДИАНА, чтобы вычислить медиану группы чисел.
A | В | С | D | E | Ф | Формула | Описание (результат) |
|---|---|---|---|---|---|---|---|
10 | 7 | 9 | 27 | 0 | 4 | = СРЕДНИЙ (A, B, C, D, E, F) | Медиана чисел в первых 6 столбцах (8) |
Вычислить наименьшее или наибольшее число в диапазоне
Чтобы вычислить наименьшее или наибольшее число в двух или более столбцах в строке, используйте функции MIN и MAX.
Столбец 1 | Колонка 2 | Столбец 3 | Формула | Описание (возможный результат) |
|---|---|---|---|---|
10 | 7 | 9 | = МИН ([Столбец1], [Столбец2], [Столбец3]) | Наименьшее число (7) |
10 | 7 | 9 | = МАКС ([Столбец1], [Столбец2], [Столбец3]) | Наибольшее число (10) |
Значения счета
Для подсчета числовых значений используйте функцию СЧЁТ.
Столбец 1 | Колонка 2 | Столбец 3 | Формула | Описание (возможный результат) |
|---|---|---|---|---|
Яблоко | 12.12.2007 | = СЧЁТ ([Столбец1], [Столбец2], [Столбец3]) | Подсчитывает количество столбцов, содержащих числовые значения.Исключает дату и время, текст и пустые значения (0) | |
$ 12 | # DIV / 0! | 1.01 | = СЧЁТ ([Столбец1], [Столбец2], [Столбец3]) | Подсчитывает количество столбцов, содержащих числовые значения, но исключает ошибки и логические значения (2) |
Увеличение или уменьшение числа на процент
Используйте оператор процента (%) для выполнения этого вычисления.
Столбец 1 | Колонка 2 | Формула | Описание (возможный результат) | |
|---|---|---|---|---|
23 | 3% | = [Столбец1] * (1 + 5%) | Увеличивает число в столбце 1 на 5% (24,15) | |
23 | 3% | = [Столбец1] * (1+ [Столбец2]) | Увеличивает число в столбце 1 на процентное значение в столбце 2: 3% (23.[Column2] | Вычисляет пять в квадрате (25) |
5 | 3 | = МОЩНОСТЬ ([Столбец1], [Столбец2]) | Вычисляет пять кубов (125) |
Округлить число
Чтобы округлить число, используйте функцию ОКРУГЛВВЕРХ, НЕЧЕТНО или ЧЕТНО.
Столбец 1 | Формула | Описание (возможный результат) |
|---|---|---|
20.3 | = ОКРУГЛ ВВЕРХ ([Столбец1], 0) | Округляет 20,3 до ближайшего целого числа (21) |
-5,9 | = ОКРУГЛ ВВЕРХ ([Столбец1], 0) | Округляет -5,9 до ближайшего целого числа (-5) |
12,5493 | = ОКРУГЛ ВВЕРХ ([Столбец1], 2) | Округляет 12,5493 до ближайшей сотой, до двух десятичных знаков (12,55) |
20.3 | = ЧЕТНЫЙ ([Столбец1]) | Округляет 20,3 до ближайшего четного числа (22) |
20,3 | = НЕЧЕТ ([Столбец1]) | Округляет 20,3 до ближайшего нечетного числа (21) |
Чтобы округлить число, используйте функцию ROUNDDOWN.
Столбец 1 | Формула | Описание (возможный результат) |
|---|---|---|
20.3 | = ОКРУГЛ ВНИЗ ([Столбец1], 0) | Округляет 20,3 до ближайшего целого числа (20) |
-5,9 | = ОКРУГЛ ВНИЗ ([Столбец1], 0) | Округляет -5,9 до ближайшего целого числа (-6) |
12,5493 | = ОКРУГЛ ВНИЗ ([Столбец1], 2) | Округляет 12,5493 до ближайшей сотой и двух десятичных знаков (12.54) |
Чтобы округлить число до ближайшего числа или дроби, используйте функцию ОКРУГЛ.
Столбец 1 | Формула | Описание (возможный результат) |
|---|---|---|
20,3 | = ОКРУГЛ ([Столбец1], 0) | Округляет 20,3 вниз, так как дробная часть меньше 0,5 (20) |
5.9 | = ОКРУГЛ ([Столбец1], 0) | Округляет 5,9 в большую сторону, поскольку дробная часть больше 0,5 (6) |
-5,9 | = ОКРУГЛ ([Столбец1], 0) | Округляет -5,9 в меньшую сторону, поскольку дробная часть меньше -,5 (-6) |
1,25 | = ОКРУГЛ ([Столбец1], 1) | Округляет число до ближайшей десятой (один десятичный знак).Поскольку округляемая часть составляет 0,05 или больше, число округляется в большую сторону (результат: 1,3) |
30,452 | = ОКРУГЛ ([Столбец1], 2) | Округляет число до ближайшей сотой (два десятичных знака). Поскольку округляемая часть, 0,002, меньше 0,005, число округляется в меньшую сторону (результат: 30,45) |
Чтобы округлить число до значащей цифры выше 0, используйте функции ROUND, ROUNDUP, ROUNDDOWN, INT и LEN.
Столбец 1 | Формула | Описание (возможный результат) |
|---|---|---|
54 | = ОКРУГЛ ([Column1], 3-LEN (INT ([Column1]))) | Округляет число до 3 значащих цифр (54 ) |
22230 | = ОКРУГЛ ВНИЗ ([Column1], 3-LEN (INT ([Column1]))) | Округляет нижнее число до трех значащих цифр (22200) |
54 | = ОКРУГЛВВЕРХ ([Столбец1], 5-LEN (ЦЕЛОЕ ([Столбец1]))) | Округляет верхнее число до 5 значащих цифр (54 |
Текстовые формулы
Вы можете использовать следующие формулы для управления текстом, например для объединения или конкатенации значений из нескольких столбцов, сравнения содержимого столбцов, удаления символов или пробелов и повторения символов.
Изменить регистр текста
Чтобы изменить регистр текста, используйте функцию ВЕРХНИЙ, НИЖНИЙ или ПРАВИЛЬНЫЙ.
Столбец 1 | Формула | Описание (возможный результат) |
|---|---|---|
Нина Вьетцен | = ВЕРХНИЙ ([Столбец1]) | Переводит текст в верхний регистр (NINA VIETZEN) |
Нина Вьетцен | = НИЖНИЙ ([Столбец1]) | Переводит текст в нижний регистр (Нина Витцен) |
Нина Вьетцен | = ПРАВИЛЬНО ([Столбец1]) | Заменяет текст на регистр (Нина Вьетзен) |
Объединить имя и фамилию
Чтобы объединить имя и фамилию, используйте оператор амперсанда (&) или функцию СЦЕПИТЬ.
Столбец 1 | Колонка 2 | Формула | Описание (возможный результат) |
|---|---|---|---|
Карлос | Карвалло | = [Столбец1] и [Столбец2] | Сочетает две струны (Карлос Карвалло) |
Карлос | Карвалло | = [Столбец1] & «» & [Столбец2] | Объединяет две строки, разделенные пробелом (Карлос Карвалло) |
Карлос | Карвалло | = [Столбец2] & «,» & [Столбец1] | Объединяет две строки, разделенные запятой и пробелом (Карвалло, Карлос) |
Карлос | Карвалло | = СЦЕПИТЬ ([Столбец2], «,», [Столбец1]) | Объединяет две строки, разделенные запятой (Карвалло, Карлос) |
Объединение текста и чисел из разных столбцов
Для объединения текста и чисел используйте функцию СЦЕПИТЬ, оператор амперсанда (&) или функцию ТЕКСТ и оператор амперсанда.
Столбец 1 | Колонка 2 | Формула | Описание (возможный результат) |
|---|---|---|---|
Ян | 28 | = [Столбец1] & «продано» & [Столбец2] & «единиц.» | Объединяет приведенное выше содержание во фразу (Ян продал 28 шт.) |
Dubois | 40% | = [Столбец1] & «продано» & ТЕКСТ ([Столбец2], «0%») & «от общего объема продаж.» | Объединяет приведенное выше содержание во фразу (Дюбуа продал 40% от общего объема продаж.) Примечание Функция ТЕКСТ добавляет форматированное значение столбца 2 вместо базового значения, равного 0,4. |
Ян | 28 | = СЦЕПИТЬ ([Столбец1], «продано», [Столбец2], «единиц.») | Объединяет приведенное выше содержание во фразу (Ян продал 28 шт.) |
Объединить текст с датой или временем
Чтобы объединить текст с датой или временем, используйте функцию ТЕКСТ и оператор амперсанда (&).
Столбец 1 | Колонка 2 | Формула | Описание (возможный результат) |
|---|---|---|---|
Дата выставления счета | 5 июня 2007 г. | = «Дата выписки:» & ТЕКСТ ([Столбец2], «д-ммм-гггг») | Объединяет текст с датой (Дата выписки: 5 июня 2007 г.) |
Дата выставления счета | 5 июня 2007 г. | = [Столбец1] & «» & ТЕКСТ ([Столбец2], «ммм-дд-гггг») | Объединяет текст и дату из разных столбцов в один столбец (Дата выставления счета 05 июня 2007 г.) |
Сравнить содержимое столбца
Чтобы сравнить один столбец с другим столбцом или списком значений, используйте функции ТОЧНО и ИЛИ.
Столбец 1 | Колонка 2 | Формула | Описание (возможный результат) |
|---|---|---|---|
BD122 | BD123 | = ТОЧНЫЙ ([Столбец1], [Столбец2]) | Сравнивает содержимое первых двух столбцов (№) |
BD122 | BD123 | = ТОЧНЫЙ ([Столбец1], «BD122») | Сравнивает содержимое столбца Column1 и строки «BD122» (Да) |
Определите, соответствует ли значение столбца или его часть определенному тексту
Чтобы определить, соответствует ли значение столбца или его часть определенному тексту, используйте функции ЕСЛИ, НАЙТИ, ПОИСК и ЕЧИСЛО.
Столбец 1 | Формула | Описание (возможный результат) |
|---|---|---|
Vietzen | = ЕСЛИ ([Column1] = «Vietzen», «OK», «Not OK») | Определяет, является ли Column1 Vietzen (OK) |
Vietzen | = ЕСЛИ (ISNUMBER (FIND («v», [Column1])), «OK», «Not OK») | Определяет, содержит ли Column1 букву v (ОК) |
BD123 | = ЕЧИСЛО (НАЙТИ («BD»; [Столбец1])) | Определяет, содержит ли столбец 1 BD (Да) |
Подсчитать непустые столбцы
Чтобы подсчитать непустые столбцы, используйте функцию СЧЁТ.
Столбец 1 | Колонка 2 | Столбец 3 | Формула | Описание (возможный результат) |
|---|---|---|---|---|
Продажи | 19 | = СЧЁТ ([Столбец1], [Столбец2]) | Подсчитывает количество непустых столбцов (2) | |
Продажи | 19 | = СЧЁТ ([Столбец1], [Столбец2], [Столбец3]) | Подсчитывает количество непустых столбцов (2) |
Удалить символы из текста
Чтобы удалить символы из текста, используйте функции LEN, LEFT и RIGHT.
Столбец 1 | Формула | Описание (возможный результат) |
|---|---|---|
Витамин А | = ЛЕВЫЙ ([Столбец1], LEN ([Столбец1]) — 2) | Возвращает 7 (9-2) символов, начиная слева (Витамин) |
Витамин B1 | = ПРАВО ([Столбец1], LEN ([Столбец1]) — 8) | Возвращает 2 (10-8) символа, начиная справа (B1) |
Удалить пробелы в начале и конце столбца
Чтобы удалить пробелы из столбца, используйте функцию ОБРЕЗАТЬ.
Столбец 1 | Формула | Описание (возможный результат) |
|---|---|---|
Всем привет! | = ОБРЕЗАТЬ ([Столбец1]) | Удаляет пробелы в начале и в конце (Привет!) |
Повторение символа в столбце
Чтобы повторить символ в столбце, используйте функцию ПОВТОР.
Формула | Описание (возможный результат) |
|---|---|
= ПОВТОР («.», 3) | Повторяет период 3 раза (…) |
= ПОВТОР («-«, 10) | Повторяет тире 10 раз (———-) |
См. Также
Номер ссылки
SPFieldCalculated
Формулы для расчета напряжения в точке
- Образование
- Наука
- Формулы для расчета напряжения в точке
Джеймс Х.Allen, III
Раздел «Механика материалов для манекенов» Шпаргалка
При работе с механикой материалов выбор правильной формулы для расчета напряжения в заданной точке может быть затруднительным. Нормальные напряжения и напряжения сдвига используются в самых разных областях, причем каждое приложение напряжения имеет свою формулу расчета. Наиболее распространенные типы напряжений, с которыми вы имеете дело в базовой механике материалов, делятся на несколько основных категорий:
Осевое натяжение: A NET равно общей площади поперечного сечения за вычетом любых отверстий, которые могут существовать.
Тонкостенные Сосуды под давлением: Существуют два напряжения: осевое напряжение вдоль оси элемента и кольцевое (или радиальное) напряжение, возникающее по касательной к радиусу поперечного сечения. Эти напряжения основаны на избыточном давлении p внутри сосуда высокого давления.
Для цилиндрических сосудов под давлением используйте эту пару формул:
Для сферических сосудов под давлением используйте следующую формулу:
Напряжения изгиба: Для симметричных поперечных сечений в плоскости XY используйте эту формулу:
(момент около оси x ) (момент около оси y )
Напряжения сдвига при изгибе: Вот формула для расчета напряжения сдвига при изгибе:
Напряжение сдвига при кручении: Используйте эту формулу, чтобы найти напряжение сдвига при кручении:
Об авторе книги
Джеймс Х.Аллен III , PE, PhD, доцент кафедры гражданского строительства и зарегистрированный профессиональный инженер. Его области специализации включают проектирование конструкций, численный анализ и контроль ошибок, а также проектирование стали. Он также является автором книги Statics For Dummies .формул Excel: функции
закрыть поиск поиск менюТемы
печать- Английский expand_more expand_less
- Español
- Português
Функции
Вернуться к учебнику закрыть- Я хочу…
- Начать работу с компьютерами
- Изучите Microsoft Office
- Устроиться на работу
- Улучшить свои рабочие навыки
- Создавайте красивые документы
- Больше…
- Microsoft
- Офис 2019 | 2016 | 2013
- слово
- Excel
- Силовая установка
- Доступ
- Формулы Excel
- Больше…
- Основные навыки
- Компьютеры
- Смартфоны и планшеты
- Учебник по вводу текста
- Windows
- Больше…
- Интернет-навыки
- Интернет
- Безопасность в Интернете
- Социальные медиа
- Электронное письмо
- Поиск лучше
- Больше…
- Google
- Gmail
- Гугл документы
- Google Таблицы
- Больше…
- Работа и карьера
- Планирование карьеры
- Написание резюме
- Сопроводительные письма
- Поиск работы и работа в сети
- Деловое общение
- Больше…
- Навыки на сегодня
- Адаптация к изменениям
- 3D печать
- Носимые
- Внештатную работу
- Личные финансы
- Совместная экономика
- Принятие решений
- Больше…
- Творчество и дизайн
- Графический дизайн
- Творческий подход
- Фотография
- Редактирование изображений
- Фотошоп
- Больше…
- Основные навыки
- Математика
- Чтение
- Грамматика
- Изучение языка
- Больше…
- Для преподавателей
- Переводы
- Выбор персонала
- Все темы
Формулы стандартного отклонения
Отклонение просто означает, насколько далеко от нормы
Стандартное отклонение
Стандартное отклонение — это мера степени распространения наши номера .
Возможно, вам сначала захочется прочитать эту более простую страницу о стандартном отклонении.
Но здесь мы объясняем формулы .
Обозначение стандартного отклонения — σ (греческая буква сигма).
Это формула для стандартного отклонения:
Сказать что? Объясните, пожалуйста!
ОК. Давайте объясним это шаг за шагом.
Допустим, у нас есть набор чисел, например 9, 2, 5, 4, 12, 7, 8, 11.
Чтобы вычислить стандартное отклонение этих чисел:
- 1. Определите среднее (простое среднее номеров)
- 2. Затем для каждого числа: вычтите Среднее и возведите результат в квадрат
- 3. Затем вычислите среднее значение этих квадратов разностей.
- 4. Извлеките из этого квадратный корень и готово!
На самом деле все это сказано в формуле, и я покажу вам, как это сделать.
Объяснение формулы
Во-первых, давайте поработаем несколько примеров значений:
Пример: У Сэма 20 кустов роз.
Количество цветков на каждом кусте
9, 2, 5, 4, 12, 7, 8, 11, 9, 3, 7, 4, 12, 5, 4, 10, 9, 6, 9, 4
Определите стандартное отклонение.
Шаг 1. Определите среднее значение
В приведенной выше формуле μ (греческая буква «мю») — это среднее всех наших значений …
Пример: 9, 2, 5, 4, 12, 7, 8, 11, 9, 3, 7, 4, 12, 5, 4, 10, 9, 6, 9, 4
Среднее значение:
9 + 2 + 5 + 4 + 12 + 7 + 8 + 11 + 9 + 3 + 7 + 4 + 12 + 5 + 4 + 10 + 9 + 6 + 9 + 4 20
= 140 20 = 7
Итак:
мк = 7
Шаг 2.Затем для каждого числа: вычтите Среднее и возведите результат в квадрат
Это часть формулы, которая гласит:
Так что же такое x i ? Это отдельные значения x 9, 2, 5, 4, 12, 7 и т. Д.
Другими словами x 1 = 9, x 2 = 2, x 3 = 5 и т. Д.
Итак, он говорит: «для каждого значения вычтите среднее и возведите результат в квадрат», как это
Пример (продолжение):
(9-7) 2 = (2) 2 = 4
(2-7) 2 = (-5) 2 = 25
(5-7) 2 = (-2) 2 = 4
(4-7) 2 = (-3) 2 = 9
(12-7) 2 = (5) 2 = 25
(7-7) 2 = (0) 2 = 0
(8-7) 2 = (1) 2 = 1
… и т.д …
И получаем такие результаты:
4, 25, 4, 9, 25, 0, 1, 16, 4, 16, 0, 9, 25, 4, 9, 9, 4, 1, 4, 9
Шаг 3. Затем вычислите среднее значение квадратов разностей.
Чтобы вычислить среднее значение, сложите все значения , затем разделите на сколько .
Сначала сложите все значения из предыдущего шага.
Но как сказать в математике «сложить все»? Используем «Сигма»: Σ
Удобная сигма-нотация позволяет суммировать столько терминов, сколько мы хотим:
Сигма-нотация
Мы хотим сложить все значения от 1 до N, где N = 20 в нашем случае, потому что есть 20 значений:
Пример (продолжение):
Это означает: суммировать все значения от (x 1 -7) 2 до (x N -7) 2
Мы уже рассчитали
Стандартное отклонение | Пошаговое руководство с формулами
Стандартное отклонение — это средняя величина изменчивости в вашем наборе данных.Он сообщает вам, в среднем, насколько далеко каждое значение от среднего.
Высокое стандартное отклонение означает, что значения обычно далеки от среднего, в то время как низкое стандартное отклонение указывает, что значения сгруппированы близко к среднему.
Что вам говорит стандартное отклонение?
Стандартное отклонение — полезная мера разброса для нормальных распределений .
В нормальном распределении данные распределяются симметрично без перекоса. Большинство значений группируются вокруг центральной области, причем значения сужаются по мере удаления от центра.Стандартное отклонение показывает, насколько в среднем разбросаны ваши данные от центра распределения.
Многие научные переменные подчиняются нормальному распределению, включая рост, результаты стандартизированных тестов или оценки удовлетворенности работой. Когда у вас есть стандартные отклонения различных выборок, вы можете сравнить их распределения с помощью статистических тестов, чтобы сделать выводы о более крупных популяциях, из которых они произошли.
Пример: сравнение различных стандартных отклонений. Вы собираете данные об оценках удовлетворенности работой трех групп сотрудников, используя простую случайную выборку.Средние оценки ( M ) одинаковы для каждой группы — это значение на оси x, когда кривая находится на пике. Однако их стандартные отклонения ( SD ) отличаются друг от друга.
Стандартное отклонение отражает дисперсию распределения. Кривая с наименьшим стандартным отклонением имеет высокий пик и небольшой разброс, тогда как кривая с наибольшим стандартным отклонением более пологая и широко распространенная.
Эмпирическое правило
Стандартное отклонение и среднее значение вместе могут сказать вам, где находится большая часть значений в вашем распределении, если они соответствуют нормальному распределению.
Эмпирическое правило , или правило 68-95-99.7, говорит вам, в чем заключаются ваши ценности:
- Около 68% оценок находятся в пределах 2 стандартных отклонений от среднего,
- Около 95% оценок находятся в пределах 4 стандартных отклонений от среднего значения,
- Около 99,7% оценок находятся в пределах 6 стандартных отклонений от среднего.
Следуя эмпирическому правилу:
- Около 68% оценок находятся в диапазоне от 40 до 60.
- Около 95% оценок находятся в диапазоне от 30 до 70.
- Около 99,7% оценок находятся в диапазоне от 20 до 80.
Эмпирическое правило — это быстрый способ получить обзор ваших данных и проверить любые выбросы или экстремальные значения, которые не соответствуют этому шаблону.
Для ненормальных распределений стандартное отклонение является менее надежным показателем изменчивости и должно использоваться в сочетании с другими показателями, такими как размах или межквартильный размах.
Формулы стандартного отклонения для популяций и выборок
Для расчета стандартных отклонений используются разные формулы в зависимости от того, есть ли у вас данные от всей генеральной совокупности или от выборки.
Стандартное отклонение совокупности
Когда вы собрали данные по каждому члену населения, которое вас интересует, вы можете получить точное значение стандартного отклонения населения.
Формула стандартного отклонения населения выглядит так:
| Формула | Пояснение |
|---|---|
|
Стандартное отклонение выборки
Когда вы собираете данные из выборки, стандартное отклонение выборки используется для оценок или выводов о стандартном отклонении генеральной совокупности.
Формула стандартного отклонения выборки выглядит следующим образом:
| Формула | Пояснение |
|---|---|
|
Для выборок мы используем в формуле n — 1, потому что использование n даст нам смещенную оценку, которая последовательно занижает изменчивость.Стандартное отклонение выборки будет, как правило, ниже, чем реальное стандартное отклонение генеральной совокупности.
Уменьшение выборки n до n -1 делает стандартное отклонение искусственно большим, давая вам консервативную оценку изменчивости.
Хотя это не беспристрастная оценка, это менее предвзятая оценка стандартного отклонения: лучше переоценить, чем недооценить изменчивость в выборках.
Этапы расчета стандартного отклонения
Стандартное отклонение обычно рассчитывается автоматически любым программным обеспечением, которое вы используете для статистического анализа.Но вы также можете рассчитать его вручную, чтобы лучше понять, как работает формула.
Есть шесть основных шагов для определения стандартного отклонения вручную. Мы будем использовать небольшой набор данных из 6 оценок, чтобы пройти через шаги.
| Набор данных | |||||
|---|---|---|---|---|---|
| 46 | 69 | 32 | 60 | 52 | 41 |
Шаг 1 : Найдите среднее значение
Чтобы найти среднее значение, сложите все баллы, затем разделите их на количество баллов.
| Среднее (x̅) |
|---|
| x̅ = (46 + 69 + 32 + 60 + 52 + 41) ÷ 6 = 50 |
Шаг 2 : Найдите отклонение каждой оценки от среднего
Вычтите среднее значение из каждой оценки, чтобы получить отклонения от среднего.
Поскольку x̅ = 50, мы убираем 50 из каждого результата.
| Оценка | Отклонение от среднего |
|---|---|
| 46 | 46-50 = -4 |
| 69 | 69-50 = 19 |
| 32 | 32-50 = -18 |
| 60 | 60-50 = 10 |
| 52 | 52-50 = 2 |
| 41 | 41-50 = -9 |
Шаг 3 : Возвести в квадрат каждое отклонение от среднего
Умножьте каждое отклонение от среднего на само себя.Это приведет к положительным числам.
| Квадратные отклонения от среднего |
|---|
| (-4) 2 = 4 × 4 = 16 |
| 19 2 = 19 × 19 = 361 |
| (-18) 2 = -18 × -18 = 324 |
| 10 2 = 10 × 10 = 100 |
| 2 2 = 2 × 2 = 4 |
| (-9) 2 = -9 × -9 = 81 |
Шаг 4 : Найдите сумму квадратов
Сложите все квадраты отклонений.Это называется суммой квадратов.
| Сумма квадратов |
|---|
| 16 + 361 + 324 + 100 + 4 + 81 = 886 |
Шаг 5: Найдите отклонение
Разделите сумму квадратов на n — 1 (для выборки) или N (для генеральной совокупности) — это дисперсия.
Поскольку мы работаем с размером выборки 6, мы будем использовать n — 1, где n = 6.
| Разница |
|---|
| 886 ÷ (6 — 1) = 886 ÷ 5 = 177,2 |
Шаг 6 : Найдите квадратный корень из дисперсии
Чтобы найти стандартное отклонение, мы извлекаем квадратный корень из дисперсии.
| Стандартное отклонение |
|---|
| √177,2 = 13,31 |
Исходя из того, что SD = 13.31, можно сказать, что каждая оценка отклоняется от среднего значения в среднем на 13,31 балла.
Почему стандартное отклонение является полезным показателем изменчивости?
Хотя существуют более простые способы расчета вариабельности, формула стандартного отклонения позволяет взвешивать неравномерно распределенные образцы больше, чем равномерно распределенные. Более высокое стандартное отклонение говорит о том, что распределение не только более равномерно, но и более неравномерно.
Это означает, что он дает вам лучшее представление об изменчивости ваших данных, чем более простые меры, такие как среднее абсолютное отклонение (MAD).
MAD похож на стандартное отклонение, но его легче вычислить. Сначала вы выражаете каждое отклонение от среднего в абсолютных значениях, преобразуя их в положительные числа (например, -3 становится 3). Затем вы вычисляете среднее значение этих абсолютных отклонений.
В отличие от стандартного отклонения, вам не нужно вычислять квадраты или квадратные корни чисел для MAD. Однако по этой причине он дает менее точную меру изменчивости.
Давайте возьмем две выборки с одной и той же центральной тенденцией, но с разной степенью изменчивости.Образец B более изменчив, чем образец A.
| Значения | Среднее значение | Среднее абсолютное отклонение | Стандартное отклонение | |
|---|---|---|---|---|
| Образец А | 66, 30, 38, 64 | 50 | 15 | 17,5 |
| Образец B | 51, 21, 79, 49 | 50 | 15 | 21,1 |
Для выборок с одинаковыми средними отклонениями от среднего MAD не может различать уровни разброса.Стандартное отклонение более точное: оно выше для выборки с большим разбросом отклонений от среднего.
Возводя в квадрат разности от среднего, стандартное отклонение более точно отражает неравномерную дисперсию. Эта ступень более взвешивает крайние отклонения, чем небольшие отклонения.
Однако это также делает стандартное отклонение чувствительным к выбросам.
Часто задаваемые вопросы о стандартном отклонении
- Что вам говорит стандартное отклонение?
Стандартное отклонение — это средняя величина изменчивости в вашем наборе данных.Он сообщает вам, в среднем, насколько далеко каждая оценка отличается от среднего значения.
В нормальных распределениях высокое стандартное отклонение означает, что значения обычно далеки от среднего, в то время как низкое стандартное отклонение указывает, что значения сгруппированы близко к среднему.
- Что такое эмпирическое правило?
Эмпирическое правило, или 68-95-99.Правило 7 говорит вам, где большинство значений лежит в нормальном распределении:
- Около 68% значений находятся в пределах 2 стандартных отклонений от среднего.
- Около 95% значений находятся в пределах 4 стандартных отклонений от среднего.
- Около 99,7% значений находятся в пределах 6 стандартных отклонений от среднего.
Эмпирическое правило — это быстрый способ получить обзор ваших данных и проверить любые выбросы или экстремальные значения, которые не соответствуют этому шаблону.
Расчет среднего и стандартного отклонения с помощью Excel
В поисках среднего
Введите результаты в один из столбцов электронной таблицы Excel (см. Пример ниже).После того, как данные были введены, поместите курсор в то место, где должно появиться среднее (среднее), и щелкните кнопкой мыши. Выберите Insert Function ( f x ) на вкладке FORMULAS . Появится диалоговое окно. Выберите СРЕДНИЙ из категории Статистический и нажмите ОК . (Примечание: если вам нужна медиана, выберите МЕДИАНА . Если вам нужен режим, выберите MODE.SNGL . Excel предоставляет только один режим.Если бы в наборе данных было несколько режимов, Excel отобразил бы только один из них.)
Введите диапазон ячеек для вашего списка чисел в поле Число 1 . Например, если бы ваши данные находились в столбце A в строках с 1 по 13, вы должны ввести A1: A13. Вместо того, чтобы вводить диапазон, вы также можете переместить курсор в начало набора партитур, который вы хотите использовать, и щелкнуть и перетащить курсор по ним. После того, как вы ввели диапазон для своего списка, нажмите OK внизу диалогового окна.Среднее (среднее) значение для списка появится в выбранной вами ячейке.
Определение стандартного отклонения
Поместите курсор в то место, где должно появиться стандартное отклонение, и щелкните кнопкой мыши. Выберите Insert Function (f x ) на вкладке FORMULAS . Появится диалоговое окно. Выберите STDEV.S (для выборки) из категории Statistical .

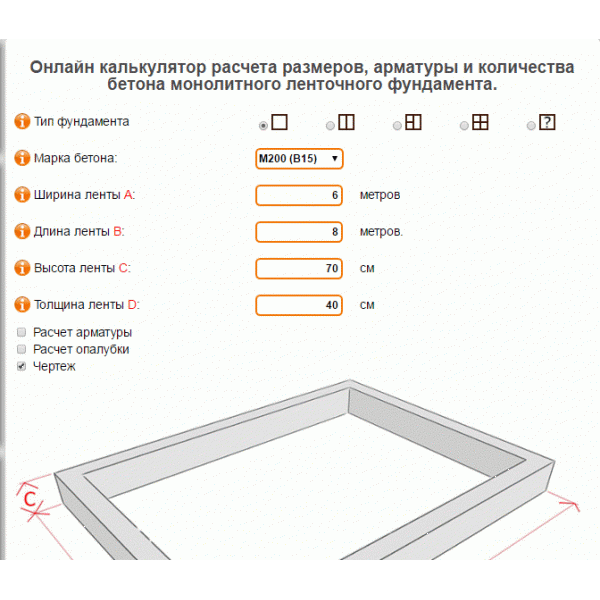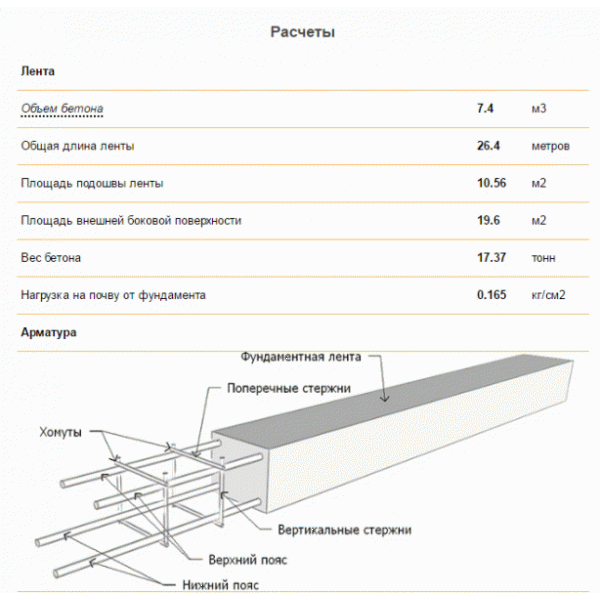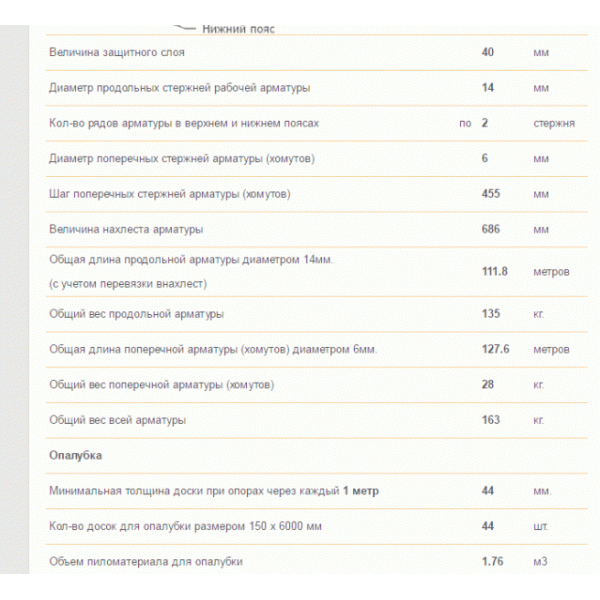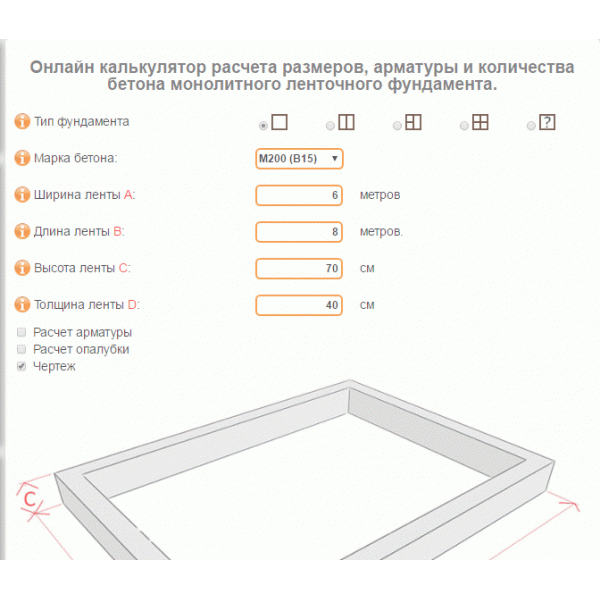

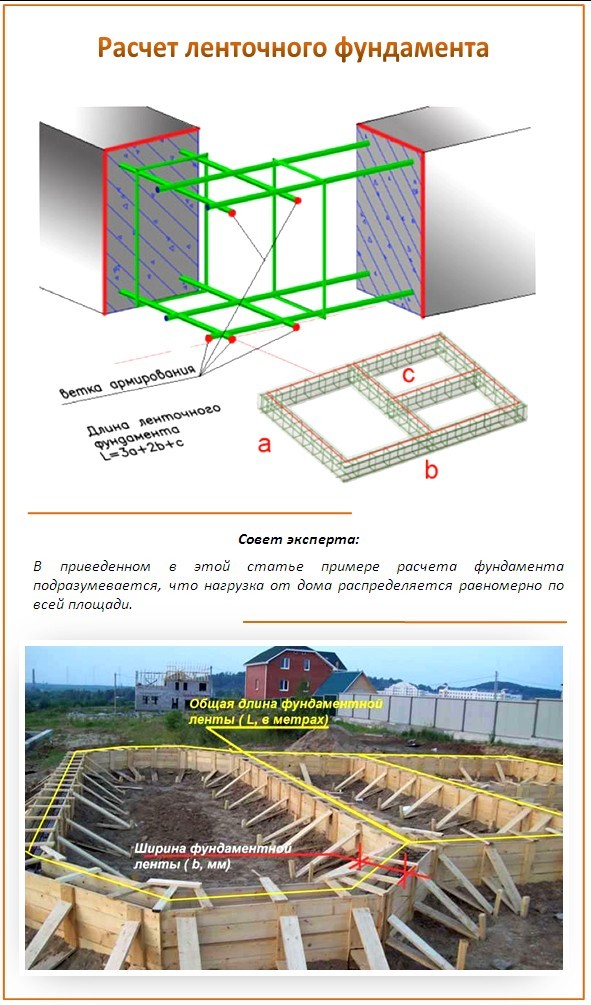

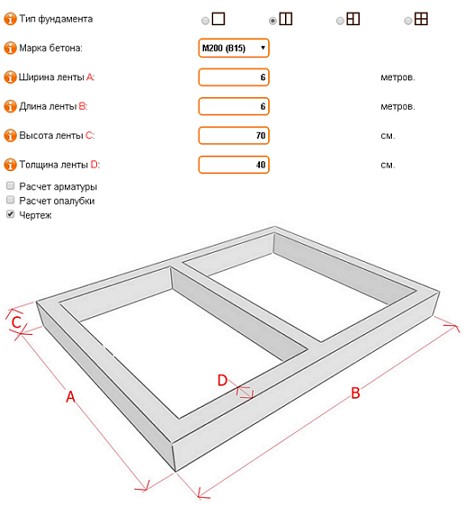



 Вес одного полнотелого кирпича 3,4 кг. Тогда вес цоколя по кирпичу составит 2400 шт. х 3,4 кг =8160 кг или 8,6 т;
Вес одного полнотелого кирпича 3,4 кг. Тогда вес цоколя по кирпичу составит 2400 шт. х 3,4 кг =8160 кг или 8,6 т; Площадь потолка 6,0 м х 6,0 м = 36 м2. Размер примененных плит 1,0 м х 1,2 м = 1,2 м2. Всего необходимо плит — 36 м2 : 1,2 м2 = 30 плит. По плотности материала планируется применить полутвердые плиты с удельным весом 400 кг/м3. Вес одной плиты, при толщине 5 см, составит: 1,2 м2 х 0,05 м х 400 кг/м3 = 24 кг. Общий вес облицовки потолка 24 кг х 30 плит = 720 кг или 0,72 т;
Площадь потолка 6,0 м х 6,0 м = 36 м2. Размер примененных плит 1,0 м х 1,2 м = 1,2 м2. Всего необходимо плит — 36 м2 : 1,2 м2 = 30 плит. По плотности материала планируется применить полутвердые плиты с удельным весом 400 кг/м3. Вес одной плиты, при толщине 5 см, составит: 1,2 м2 х 0,05 м х 400 кг/м3 = 24 кг. Общий вес облицовки потолка 24 кг х 30 плит = 720 кг или 0,72 т;  Вес гидроизоляции составит 30 м2 х 2,5 кг/м2 = 75 кг. Для крыши используем гидроизоляционный материал мембрана толщиной 0,6 мм, плотностью 0,94 г/см3 или 940 кг/м3 (1 г/см3 =1000 кг/м3). Площадь для гидроизоляции крыши – 55 м2. Объем пленки 55 м2 х 0,0006 м = 0,033 м3. Вес 0,033 м3 х 940 кг/м3 = 31 кг.
Вес гидроизоляции составит 30 м2 х 2,5 кг/м2 = 75 кг. Для крыши используем гидроизоляционный материал мембрана толщиной 0,6 мм, плотностью 0,94 г/см3 или 940 кг/м3 (1 г/см3 =1000 кг/м3). Площадь для гидроизоляции крыши – 55 м2. Объем пленки 55 м2 х 0,0006 м = 0,033 м3. Вес 0,033 м3 х 940 кг/м3 = 31 кг.  Удельный вес раствора составляет 1800 кг/м3 (по данным СНиП II-3-79). Вес раствора составит 1,4 м3 х 1800 кг/м3=2574 кг или 2,574 т.
Удельный вес раствора составляет 1800 кг/м3 (по данным СНиП II-3-79). Вес раствора составит 1,4 м3 х 1800 кг/м3=2574 кг или 2,574 т. 06.2007
06.2007 2010)
2010) 2010)
2010)