Формула процент армирования: Минимальный процент армирования железобетонных конструкций
Минимальный процент армирования железобетонных конструкций
В строительной отрасли широко применяются конструкции из железобетона, надежность и долговечность которых обеспечивает металлический каркас. Он способен воспринимать значительную нагрузку, если правильно подобрать сечение рифленого прута арматуры, а также выдержать расстояние между арматурой и поверхностью бетона в стенах, колоннах, фундаментах и балках. Зная процент армирования, для вычисления которого выполняются специальные расчеты, несложно определить минимальное количество арматуры. Проектируя каркас, важно уметь определять армирующий показатель.
Формула процента армирования железобетонных конструкций – соотношение бетона
В процессе длительной эксплуатации строительные конструкции подвергаются воздействию сжимающих и изгибающих нагрузок, а также крутящих моментов. Для усиления выносливости железобетона и расширения сферы его использования выполняется усиление бетона арматурой. В зависимости от массы каркаса, диаметра прутков в поперечном сечении и пропорции бетона изменяется коэффициент армирования железобетонных конструкций.
Разберемся, как вычисляется данный показатель согласно требованиям стандарта.
 Для того, чтобы армирование выполняло свое назначение, необходимо расчитать усиление бетона, соответствующий минимальному проценту
Для того, чтобы армирование выполняло свое назначение, необходимо расчитать усиление бетона, соответствующий минимальному процентуПроцент армирования колонны, балки, фундаментной основы или капитальных стен определяется следующим образом:
- масса металлического каркаса делится на вес бетонного монолита;
- полученное в результате деления значение умножается на 100.
Коэффициент армирования бетона – важный показатель, применяемый при выполнении различных видов прочностных расчетов. Удельный вес арматуры изменяется:
- при увеличении слоя бетона показатель армирования снижается;
- при использовании арматуры большого диаметра коэффициент возрастает.
Для определения армирующего показателя на подготовительном этапе выполняются прочностные расчеты, разрабатывается документация и делается чертеж армирования. При этом учитывается толщина бетонного массива, конструкция металлического каркаса и размер сечения прутков. Данная площадь определяет нагрузочную способность силовой решетки. При увеличении сортамента арматуры возрастает степень армирования и, соответственно, прочность бетонных конструкций. Целесообразно отдать предпочтение стержням диаметром 12–14 мм, обладающим повышенным запасом прочности.
Показатель армирования имеет предельные значения:
- минимальное, составляющее 0,05%. При удельном весе арматуры ниже указанного значения эксплуатация бетонных конструкций не допускается;
- максимальное, равное 5%. Превышение указанного показателя ведет к ухудшению эксплуатационных показателей железобетонного массива.
Соблюдение требований строительных норм и стандартов по степени армирования гарантирует надежность конструкций из железобетона. Остановимся более детально на предельной величине армирующего процента.
 Чтобы гарантировать надежность конструкций из железобетона, необходимо соблюдать требования строительных норм
Чтобы гарантировать надежность конструкций из железобетона, необходимо соблюдать требования строительных нормМинимальный процент армирования в конструкциях из железобетона
Рассмотрим, что выражает минимальный процент армирования. Это предельно допустимое значение, ниже которого резко повышается вероятность разрушения строительных конструкций. При показателе ниже 0,05% изделия и конструкции нельзя называть железобетонными. Меньшее значение свидетельствует о локальном усилении бетона с помощью металлической арматуры.
В зависимости от особенностей приложения нагрузки минимальный показатель изменяется в следующих пределах:
- при величине коэффициента 0,05 конструкция способна воспринимать растяжение и сжатие при воздействии нагрузки за пределами рабочего сечения;
- минимальная степень армирования возрастает до 0,06% при воздействии нагрузок на слой бетона, расположенный между элементами арматурного каркаса;
- для строительных конструкций, подверженных внецентренному сжатию, минимальная концентрация стальной арматуры достигает 0,25%.
При выполнении усиления в продольной плоскости по контуру рабочего сечения коэффициент армирования вдвое превышает указанные значения.
Коэффициент армирования – предельное значение для монолитных фундаментов
Желая обеспечить повышенный запас прочности конструкций из железобетона, нецелесообразно превышать максимальный процент армирования.
 Нецелесообразно превышать максимальный процент армирования, чтобы обеспечить повышенный запас прочности конструкций
Нецелесообразно превышать максимальный процент армирования, чтобы обеспечить повышенный запас прочности конструкцийЭто приведет к негативным последствиям:
- ухудшению рабочих показателей конструкции;
- существенному увеличению веса изделий из железобетона.
Государственный стандарт регламентирует предельную величину уровня армирования, составляющую пять процентов. При изготовлении усиленных конструкций из бетона важно обеспечить проникновение бетона в глубь арматурного каркаса и не допустить появления воздушных полостей внутри бетона. Для армирования следует использовать горячекатаный пруток, обладающий повышенной прочностью.
Какова величина защитного слоя бетона
Для предотвращения коррозионного разрушения силового каркаса следует выдерживать фиксированное расстояние от стальной решетки до поверхности бетонного массива. Этот интервал называется защитным слоем.
Его величина для несущих стен и железобетонных панелей составляет:
- 1,5 см – для плит толщиной более 10 см;
- 1 см – при толщине бетонных стен менее 10 см.
Размер защитного слоя для ребер усиления и ригелей немного выше:
- 2 см – при толщине бетонного массива более 25 см;
- 1,5 см – при толщине бетона меньше указанного значения.
Важно соблюдать защитный слой для опорных колонн на уровне 2 см и выше, а также выдерживать фиксированный интервал от арматуры до поверхности бетона для фундаментных балок на уровне 3 см и более.
- 3 см – для сборных фундаментных конструкций из сборного железобетона;
- 3,5 см – для монолитных основ, выполненных без цементной подушки;
- 7 см – для цельных фундаментов, не имеющих демпфирующей подушки.
Строительные нормы и правила регламентируют величину защитного слоя для различных видов строительных конструкций.
Заключение
Усиление бетонных конструкций с помощью арматурных каркасов позволяет повысить их долговечность и увеличить прочностные свойства. На расчетном этапе важно правильно определить показатель армирования. При выполнении работ необходимо соблюдать требования строительных норм и правил, а также руководствоваться положениями действующих стандартов.
Как определить минимальный процент армирования конструкции?
Нормы дают нам ограничение в армировании любых конструкций в виде минимального процента армирования – даже если по расчету у нас вышла очень маленькая площадь арматуры, мы должны сравнить ее с минимальным процентом армирования и установить арматуру, площадь которой не меньше того самого минимального процента армирования.
Где мы берем процент армирования? В «Руководстве по конструированию железобетонных конструкций», например, есть таблица 16, в которой приведены данные для всех типов элементов.
Но вот есть у нас на руках цифра 0,05%, а как же найти искомое минимальное армирование?
Во-первых, нужно понимать, что ищем мы обычно не площадь всей арматуры, попадающей в сечение, а именно площадь продольной рабочей арматуры. Иногда эта площадь расположена у одной грани плиты (в таблице она обозначена как А – площадь у растянутой грани, и А’ – площадь у сжатой грани), а иногда это вся площадь элемента. Каждый случай нужно рассматривать отдельно.
На примерах, думаю, будет нагляднее.
Пример 1. Дана монолитная плита перекрытия толщиной 200 мм (рабочая высота сечения плиты h₀ до искомой арматуры 175 мм). Определить минимальное количество арматуры у нижней грани плиты.
1) Найдем площадь сечения бетона 1 погонного метра плиты:
1∙0,175 = 0,175 м² = 1750 см²
2) Найдем в таблице 16 руководства минимальный процент армирования для плиты (изгибаемого элемента):
0,05%
3) Составим известную со школы пропорцию:
1750 см² — 100%
Х – 0,05%
4) Из пропорции найдем искомую минимальную площадь арматуры:
Х = 0,05∙1750/100 = 0,88 см²
5) По сортаменту арматуры находим, что данная площадь соответствует 5 стержням диаметром 5 мм. То есть меньше этого мы устанавливать не имеем права.
Обратите внимание! Мы определяем площадь арматуры у одной грани плиты (а не площадь арматуры всего сечения плиты), именно она соответствует минимальному проценту армирования.
Пример 2. Дана плита перекрытия шириной 1,2 м, толщиной 220 мм (рабочая высота сечения плиты h₀ до искомой арматуры 200 мм), с круглыми пустотами диаметром 0,15м в количестве 5 шт. Определить минимальное количество арматуры в верхней зоне плиты.
Заглянув в примечание к таблице, мы увидим, что в случае с двутавровым сечением (а при расчете пустотных плит мы имеем дело с приведенным двутавровым сечением), мы должны определять площадь плиты так, как описано в п. 1:
1) Найдем ширину ребра приведенного двутаврового сечения плиты:
1,2 – 0,15∙5 = 0,45 м
2) Найдем площадь сечения плиты, требуемую условиями расчета:
0,45∙0,2 = 0,09 м² = 900 см²
3) Найдем в таблице 16 руководства минимальный процент армирования для плиты (изгибаемого элемента):
0,05%
4) Составим пропорцию:
900 см² — 100%
Х – 0,05%
5) Из пропорции найдем искомую минимальную площадь арматуры:
Х = 0,05∙900/100 = 0,45 см²
6) По сортаменту арматуры находим, что данная площадь соответствует 7 стержням диаметром 3 мм. То есть меньше этого мы устанавливать не имеем права.
И снова обратите внимание! Мы определяем площадь арматуры у одной грани плиты (а не площадь арматуры всего сечения плиты), именно она соответствует минимальному проценту армирования.
Пример 3. Дан железобетонный фундамент под оборудование сечением 1500х1500 мм, армированная равномерно по всему периметру. Расчетная высота фундамента равна 4 м. Определить минимальный процент армирования.
1) Найдем площадь сечения фундамента:
1,5∙1,5 = 2,25 м² = 22500 см²
2) Найдем в таблице 16 руководства минимальный процент армирования для фундамента, предварительно определив l₀/h = 4/1.5 = 4,4 < 5 (для прямоугольного сечения):
0,05%
3) Из пункта 2 примечаний к таблице 16 (см. рисунок выше) определим, что мы должны удвоить процент армирования, чтобы найти минимальную площадь арматуры всего сечения фундамента (а не у одной его грани!), т.е. минимальный процент армирования у нас будет равен:
2∙0,05% = 0,1%
4) Составим пропорцию:
22500 см² — 100%
Х – 0,1%
4) Из пропорции найдем искомую минимальную площадь арматуры:
Х = 0,1∙22500/100 = 22,5 см²
5) Принимаем шаг арматуры фундамента 200 мм, значит по периметру мы должны установить 28 стержней, а площадь одного стержня должна быть не меньше 22,5/28 = 0,8 см²
6) По сортаменту арматуры находим, что мы должны принять диаметр арматуры 12 мм. То есть меньше этого мы устанавливать не имеем права.
И снова обратите внимание! В данном примере мы определяем площадь арматуры не у одной грани фундамента, а сразу для всего фундамента, т.к. он заармирован равномерно по всему периметру.
Пример 4. Дана железобетонная колонна сечением 500х1600 (рабочая высота сечения колонны в коротком направлении h₀= 460 мм). Расчетная высота колонны равна 8 м. Определить минимальный процент армирования у длинных граней колонны.
1) Найдем площадь сечения колонны:
0,46∙1,6 = 0,736 м² = 7360 см²
2) Найдем в таблице 16 руководства минимальный процент армирования для колонны (внецентренно-сжатого элемента с l₀/h = 8/0.5 = 16):
0,2%
3) Составим известную со школы пропорцию:
7360 см² — 100%
Х – 0,2%
4) Из пропорции найдем искомую минимальную площадь арматуры:
Х = 0,2∙7360/100 = 14,72 см²
5) Из руководства по проектированию находим, что максимальное расстояние между продольной арматурой в колонне не должно превышать 400 мм. Значит, у каждой грани мы можем установить по 4 стержня (между угловой арматурой колонны, которая является рабочей, и ее площадь определялась расчетом), площадь каждого из стержней равна 14,72/4 = 3,68 см²
6) По сортаменту находим, что у каждой грани нам нужно установить 4 стержня диаметром 22 мм. Если считаем, что диаметр великоват, увеличиваем количество стержней, уменьшая тем самым диаметр каждого.
Обратите внимание! Мы определяем площадь арматуры у каждой из двух граней колонны, именно она соответствует минимальному проценту армирования в данном случае.
Пример 5. Дана стена и толщиной 200 мм (рабочая высота сечения плиты h₀ до искомой арматуры 175 мм), рабочая высота стены l₀ = 5 м. Определить минимальное количество арматуры у обеих граней стены.
1) Найдем площадь сечения бетона 1 погонного метра стены:
1∙0,175 = 0,175 м² = 1750 см²
2) Найдем в таблице 16 руководства минимальный процент армирования для стены, предварительно определив l₀/h = 5/0.2 = 25 > 24:
0,25%
3) Составим пропорцию:
1750 см² — 100%
Х – 0,25%
4) Из пропорции найдем искомую минимальную площадь арматуры:
Х = 0,25∙1750/100 = 4,38 см²
5) По сортаменту арматуры находим, что данная площадь соответствует 5 стержням диаметром 12 мм, которые нужно установить у каждой грани на каждом погонном метре стены.
Заметьте, если бы стена была толще, минимальный процент армирования резко бы упал. Например, при толщине стены 210 мм потребовалось бы уже 5 стержней диаметром 10 мм, а не 12.
class=»eliadunit»> Добавить комментарий
Процент армирования железобетонных конструкций: минимальный и максимальный
Арматурный каркас является необходимой частью в железобетонных конструкциях. Цель его использования — усиление и повышение прочности бетонных изделий. Арматурный каркас изготавливается из стальных прутьев или готовой металлической сетки. Необходимое количество усиления рассчитывается с учетом возможных нагрузок и воздействий на изделие. Расчетная арматура называется рабочей. При укреплении в конструктивных или технологических целях производится монтажное армирование. Чаще используются оба типа для обеспечения более равномерного распределения усилий между отдельными элементами арматурного каркаса. Арматура выдерживает нагрузку от усадки, колебаний температур и прочих воздействий.
Армирование бетона
Прочность на излом, повышенная надежность являются основными характеристиками, которым наделяется железобетонная конструкция при армировании. Стальной каркас многократно усиливает выносливость материала, расширяя область его применения. Горячекатаная сталь используется для армирования в железобетоне. Она наделена максимальной стойкостью к негативным воздействиям и коррозии.
Сваренный скелет из арматуры размещается внутри бетона. Однако недостаточно просто поместить его туда. Чтобы армирование выполняло свое назначение, требуются специальный расчет усиления бетона, соответствующий минимальному и максимальному проценту.
Вернуться к оглавлениюМинимальный армирующий процент
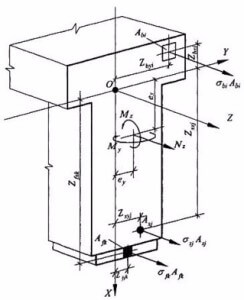 Расчетная схема нормального сечения железобетонного элемента с внешним армированием.
Расчетная схема нормального сечения железобетонного элемента с внешним армированием.Под предельно минимальным армирующим процентом принято понимать степень преобразования бетона в железобетон. Недостаточная величина этого параметра не дает права считать изделие усиленным до ЖБИ. Это будет простым упрочнением конструкционного типа. Площади сечения бетонного изделия учитываются в минимальном проценте усиления при использовании продольного армирования в обязательном порядке:
- Усиление прутьями будет соответствовать 0,05 процентам от площади разреза изделия из бетона. Это актуально для объектов с внецентренно изгибаемыми и растянутыми нагрузками, когда оказывается продольное давление за пределами действительной высоты.
- Армирование прутьями равно не менее 0,06 процентам, когда давление во внецентренно растянутых изделиях осуществляется на пространство между армирующими прутьями.
- Упрочнение будет составлять 0,1—0,25 процента, если железобетонные материалы усиливаются во внецентренно сжатых частях, то есть между арматурами.
При расположении продольного усиления по периметру сечения, то есть равномерно, степень армирования должна равняться величинам, вдвое большим указанных для всех перечисленных выше случаев. Это правило аналогично и для усиления центрально-растянутых изделий.
Вернуться к оглавлениюМаксимальный армирующий процент
При армировании нельзя укреплять бетонную конструкцию слишком большим количеством прутьев. Это приведет к существенному ухудшению технических показателей железобетонного материала. ГОСТ предлагает определенные нормативы максимального процента армирования.
Максимально допустимая величина усиления, вне зависимости от марки бетона и типа арматуры, не должна превышать пяти процентов. Речь идет о расположении в разрез сечения изделия с колоннами. Для других изделий допускается максимально четыре процента. При заливке арматурного каркаса, бетонный раствор должен проходить сквозь каждый отдельный конструкционный элемент.
Вернуться к оглавлениюЗащитный слой бетона
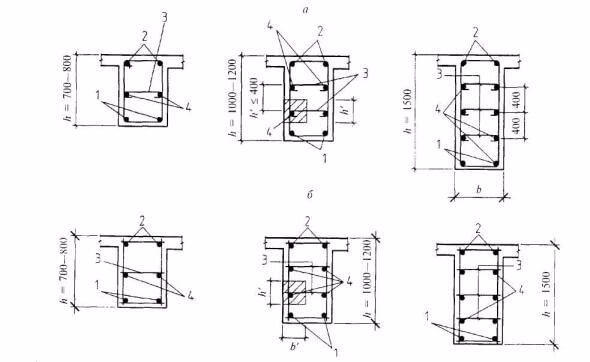 Армирование элементов монолитных железобетонных зданий.
Армирование элементов монолитных железобетонных зданий.Для защиты арматуры от коррозии, влаги и прочих неблагоприятных внешний воздействий, бетон должен полностью покрывать стальной каркас. Толщина бетонного пласта над металлическим скелетом в монолитных стенах более 10 см должна составлять максимально 1,5 см. Для плит толщиной до 10 см величина слоя составляет 1 см. Если речь идет о 25-сантиметровых ребрах, слой бетона должен достигать 2 см. При армировании балок до 25 см пласт цементного раствора равен 1,5 см, но для балок в фундаментах — 3 см. Для колонн стандартных размеров следует заливать бетон слоем более 2 см.
Что касается фундаментов, то для монолитных конструкций с прослойкой из цемента требуемая толщина слоя над арматурным каркасом составляет 3,5 см. При обустройстве сборных основ — 3 см. Монолитные базы без подушки требуют 7-сантиметровый слой бетона над скелетом из арматуры. При использовании толстых защитных слоев бетона рекомендуется проводить дополнительное усиление. Для этого используется стальная проволока, вязанная в виде сетки.
При дальнейшей обработке железобетонных конструкций алмазными кругами важно учитывать расположение каждого армирующего элемента и структуру его скелета. Это особенно касается процессов сверления отверстий в железобетоне и его резки. Такая обработка материалов может снизить потенциальную прочность изделия. Когда железобетон демонтируется полностью, учет перечисленных выше требований не производится.
Вернуться к оглавлениюЗаключение
Индивидуальное строительство немыслимо без использования бетонных растворов. Для повышения надежности и прочности возводимых конструкций армирование является важным условием.
При наличии базовых знаний и опытных помощников усиление бетонных объектов не составит труда. В этом деле важно выполнять требования и следовать правилам расположения арматуры. Только так можно получить гарантированно долговечные и надежные железобетонные конструкции.
Процент армирования железобетонных конструкций – минимальный и максимальный
Архив рассылки «Непрошеные советы» для начинающих проектировщиков. Выпуск № 14.
Здравствуйте!
В очередном выпуске непрошенных советов я хочу поговорить о проценте армирования в железобетонных конструкциях.
Обычно, чтобы не попасть впросак, начинающие проектировщики стараются свериться с данными по допустимому проценту армирования железобетона. С минимальным процентом все просто: есть таблица 47 (38) в Пособии по проектированию бетонных и железобетонных конструкций из тяжелого бетона плюс важные примечания под этой таблицей – этих данных достаточно, чтобы недоармирования не произошло.
Но что же делать с переармированием? Ведь нигде не пишется, какой максимум арматуры может быть в бетоне. Разобраться с этим вопросом поможет здравый смысл и требования по конструированию, с них мы и начнем.
Чтобы конструкция была надежной не только на бумаге, нужно расположить арматуру так, чтобы бетонирование было качественным. Для этого нужно всегда соблюдать требования по минимальному расстоянию между стержнями арматуры (см. п.п. 5.38 – 5.41 того же пособия). Только тогда бетон надежно заполнит пространство между стержнями, сцепление с арматурой будет надежным, а конструкция – прочной. Также нужно обращать особое внимание на расположение стержней в местах нахлестки, т.к. арматуры там в два раза больше, и ее нужно расположить так, чтобы выполнялось требование по минимальному расстоянию в свету между стержнями (50 мм – для монолитных колонн, например). Не лишним также будет обращать внимание на реальный диаметр стержней периодической арматуры (с учетом выступов и ребер), особенно в стесненных условиях. Выполняя эти конструктивные требования, вы сделаете первый шаг к тому, чтобы не переармировать конструкцию.
Второй шаг – это учет расположения арматуры в расчете. На первый взгляд, можно разогнаться и уложить арматуру в несколько рядов – сечение по расчету проходит, почему бы не попробовать? Этот соблазн особенно для тех, кто считает в программах и не чувствует зависимости результатов расчета от расположения арматуры в сечении. Да, в балках руководство по конструированию допускает расположение арматуры в несколько рядов (см. рисунок 84), в колоннах – не рекомендуется.
Из рисунка мы видим, что процент армирования в балке можно значительно увеличить. Но при этом, как всегда, всплывает одно «но»: рабочая высота сечения h0, которая имеет большое значение при определении итогового армирования для каждого последующего ряда арматуры значительно уменьшается. И это оказывает прямое влияние на искомую площадь арматуры, т.к. она пропорциональна рабочей высоте сечения: As=(ξbh0Rb)/Rs+As’ (формула 25 Пособия по проектированию бетонных и железобетонных конструкций к СНиП 2.03.01-84).
Поэтому всегда советую обращать внимание при расчете балок на то, в сколько рядов в итоге будет уложена арматура. Если в начале предполагался один ряд и h0 была соответствующей, а в итоге арматуры получилось столько, что в один ряд она не поместится, то нужно обязательно пересчитать армирование с уточнением рабочей высоты сечения – очень часто это дает увеличение площади арматуры.
Еще из рисунка видны четкие требования к расстоянию в свету между стержнями арматуры. Это обусловлено тем, что заполнитель в бетоне – щебень разных фракций, и густо расположенная арматура не должна помешать качественному бетонированию. Всегда нужно обращать внимание на это требование, чтобы не попасть впросак.
В итоге, по балкам мы имеем как минимум два ограничивающих процент армирования требования: расстояние между стержнями и рабочая высота сечения арматуры (т.е. ограничения в самом расчете). И если соблюдать эти требования, переармировать конструкцию будет не возможно.
В Руководстве по конструированию, на которое я уже не раз ссылалась, Вы найдете конструктивные требования к расположению арматуры в любых типах железобетонных конструкций. Если их тщательно соблюдать, Ваши конструкции всегда будут заармированы, как следует, и о проценте армирования беспокоиться будет не нужно.
Удачного Вам освоения нашей непростой профессии!
С уважением, Ирина.
class=»eliadunit»> Добавить комментарий60. Каковы особенности расчета переармированных сечений? Чем определяется максимальный и минимальный процент армирования?
Предельный процент армирования изгибаемых элементов с одиночной арматурой (расположенной только в растянутой зоне) определяют из уравнения равновесия предельных усилий RbbxR -RsAsp =0 при высоте сжатой зоны, равной граничной. При этом для прямоугольного сечения RbbxR-RsAsp=0. Отсюда µ=100ξR(Rb/Rs)
Предельный процент армирования с учетом значения ξrпо формуле для предварительно напряженных элементов
µ=100ωRb/[(1+(σsr/σscu)(1-ω/1.1)Rs] для элементов без предварительного напряжения при σsr=σscu=Rs :
µ=100ωRb/[2(1-ω/1.1)Rs]
Предельный процент армирования с повышением класса арматуры уменьшается. Сечения изгибаемых элементов, имеющие процент армирования, превышающий предельный, называют переармированными.
Нижний предел процента армирования установлен в нормах из конструктивных соображений для восприятия не учитываемых расчетом различных усилий (усадочных, температурных и т. п.). Для изгибаемых и внецентренно растянутых прямоугольных сечений шириной b, высотой h минимальный процент армирования продольной растянутой арматурой µ1 =0,05 %; для внецентренно растянутых элементов в случае
В тавровых сечениях с полкой в сжатой зоне минимальный процент армирования относится к площади сечения ребра, равной b*h.
61. Выведите формулы для расчета прямоугольных сечений изгибаемых элементов с двойной арматурой. Какие условия обеспечивают прочность изгибаемых элементов прямоугольного профиля с двойной арматурой (рассмотрите 2 типа задач)?
Элементы с двойной арматурой – это такие элементы, у которых арматуру по расчету устанавливают в растянутой и сжатой зонах.
Сжатую арматуру устанавливают по расчету, когда прочность бетона сжатой зоны недостаточна, т.е. когда x£xR.
Элементы с двойной арматурой требуют повышенного расхода стали, поэтому их применение должно быть обосновано. Двойную арматуру приходиться принимать, когда сечение элемента ограничено и невозможно увеличение класса бетона. Сжатую арматуру устанавливают также при воздействии на элемент изгибающих моментов двух знаков (неразрезные конструкции и т.д.), а также для уменьшения эксцентриситета предварительного обжатия в преднапряженных элементах.
Формулы для расчета нормальных сечений элементов с двойной арматурой получены из тех же условий, что и для элементов с одиночной.(рис)
Прочность сечения будет обеспечена, если расчетный момент от внешней нагрузки не превысит расчетного момента внутренних усилий, или, иначе, SМ = 0.
Уравнение равенства моментов относительно центра тяжести растянутой арматуры:
M £ Nb × (h0 — x/2) + Ns’ × (h0 – a’) или M £ Rb × b × x × (h0 — x/2) + Rsc × As’ × (h0 – a’)
и уравнение равенства моментов относительно центра тяжести сжатой зоны бетона:
M £ Ns × (h0 — x/2) + Ns’ × (x/2 — a’) или M £ ss × As × (h0 — x/2) + Rsc × As’ × (x/2 — a’)
где а’ – расстояние от сжатой грани сечения до центра тяжести сжатой арматуры;
As’ – площадь сечения сжатой арматуры.
Составляется также вспомогательное уравнение равенства нулю суммы проекций усилий на продольную ось элемента:
Nb × b × x + Ns’ × As’ – Ns × As = 0 или ss × As = Rb × b × x + Rsc × As’ .
Исследования показали, что сечение будет наиболее экономичным, когда на бетон передается максимально возможное сжимающее усилие. Это будет иметь место при x=xR. В этом случае площади сжатойAs’ и растянутойAsарматуры определяют приведенных уравнений, принимаяx=xR=xR×h0. Таким образом:
Rsc×As’×(h0–a’) =M-Rb×b×xR×(h0-xR/2)
Rs × As = Rb × b × xR + Rsc × As’
Задача типа 1. Заданы размеры b и h. Требуется определить площадь сечения арматуры As и As’.
As’= [M — Rb × b × xR × (h0 — xR/2)]/[ Rsc-(h0 – a’)]
As= [Rb × b × xR + Rsc × As’]/Rs
Задача 2 типа. Заданы размеры сечения b и h и площадь сечения сжатой арматуры As’. Определить площадь сечения арматуры As
αm = (M-Rsc·A’S·zs)/(b·h20·Rb) по таблице находим ξ, проверяя условие ξ< ξR.
AS=M/(ξ·h0·RS)=[As’·Rsc +ξ·b·h0·Rb]/Rs
Если αm> αR, заданного количества арматуры по площади сечения As’ недостаточно.
Пример расчета непрерывно армированного покрытия — Студопедия
Требуется запроектировать конструкцию дорожной одежды с непрерывно армированным покрытием.
6.1. Исходные данные
Местность по условию увлажнения относится к I типу, проходит в нулевых отметках. Грунт земляного полотна — суглинок тяжелый — Егр = 35 МПа.
Расчетный срок службы покрытия — 35 лет. Суммарный размер движения за срок службы — 20 млн (приведенных к группе А) автомобилей. Суточные перепады температуры на поверхности покрытия (Dtп) в течение года даны в табл. 1.
Дорожная одежда включает:
подстилающий слой из среднезернистого песка — Еп = 120 МПа;
верхний слой основания из песка, стабилизированного цементом М75, с модулем упругости Епц = 600 МПа;
непрерывно армированное покрытие из бетона В30,0 и арматуры класса A-III.
Величина сил сцепления бетона с арматурой составляет 7,0 МПа. Сцепление покрытия с основанием равно 0,7 МПа.
Таблица 1*
| Перепад температуры на поверхности покрытия, °С | ||||||
| Повторяемость дней в году с данным перепадом |
* Табл. 1 составляется по СНиП, в зависимости от суточного перепада температуры воздуха, или по опытным данным.
6.2. Проектирование дорожной одежды
6.2.1. Общая толщина дорожной одежды и толщина песчаного подстилающего слоя определяется общепринятыми методами (см.ОДН 218.046-01) по условию морозоустойчивости и осушения дорожной одежды. Для принятых данных они составляют, соответственно, 75 и 25 см.
6.2.2. Толщина покрытия предварительно назначается равной 24 см, толщина слоя стабилизированного песка — 14 см.
Для получения общей толщины дорожной одежды Н = 75 см толщина песчаного слоя должна составлять не менее 37 см. Принимаем округленно hп = 40 см.
6.2.3. Процент армирования покрытия в продольном направлении определяется по формулам (3) и (4):
6.2.4. Раскрытие трещин определяется по формуле (5). При диаметре арматуры 14 мм раскрытие трещин составляет
где q = 44/15,4 = 2,86.
При диаметрах арматуры 12, 10, 8 и 6 мм раскрытие трещин, соответственно, уменьшается до 0,31, 0,26, 0,21 и 0,15 мм.
Из условия минимального раскрытия трещин выбираем арматуру диаметром 6 мм.
6.2.5. Эквивалентный модуль упругости основания определяется последовательным решением по номограмме двухслойной системы на упругом основании (см. ОДН 218.046-01). Принятая конструкция имеет эквивалентный модуль упругости основания (Еэкв), равный 90,0 МПа.
6.2.6. В предварительном расчете дорожной одежды на автомобильную нагрузку покрытие считается как бетонное без учета арматуры.
По формуле (10) определяется радиус жесткости покрытия:
6.2.7. Изгибающий момент в покрытии определяется по формуле (7):
Мн = 6,0(0,0592 — 0,09284×ln(18,25/94)) = 1,20 тм.
Влияние соседних колес учитывается по формуле (8). Приведенные ординаты ближайшего колеса равны: h = 160/94 = 1,70; x = 0.
Суммарный нормативный изгибающий момент равен 1,35 тм.
6.2.8. Проверка бетонного сечения на выносливость проводится по формуле (20):
1,35×105 кг×см = 45×0,7×0,43×9600 = 1,35×105 кг×см.
Таким образом, покрытие обладает достаточной несущей способностью по выносливости.
6.2.9. Толщина покрытия армированного непрерывной арматурой в верхней зоне плиты уменьшается на величину Dh по формуле (21), где Fa = m×Fб:
Dh = 0,0059×24×(100/100)×17 = 2,5.
Принимаем Dh = 3 см и толщину покрытия — 21 см.
При расположении арматуры на нейтральной оси покрытия или ниже толщины плиты может быть уменьшена на 2Dh (до 18 см) с последующей проверкой расчетом. Принимаем толщину покрытия h = 18 см с расположением арматуры на нейтральной оси покрытия.
6.2.10. Расчет железобетонного покрытия на автомобильную нагрузку производится в следующем порядке:
а) задаем процент армирования покрытия в продольном и поперечном направлениях.
Процент армирования в продольном направлении принимаем по расчету на объемные изменения материала равным 0,59 %. Процент армирования в поперечном направлении принимаем равным 0,15 %, из стали А-III диаметром 6 мм с расположением арматуры на расстоянии 9,6 см от поверхности покрытия;
б) определяем геометрические характеристики сечения.
По формуле (14) находим высоту сжатой зоны бетона (Хс) в продольном и поперечном направлениях:
в продольном направлении Хс = 2,9 см;
в поперечном направлении Хс = 1,7 см.
По формуле (12) определяем жесткость сечения:
в продольном направлении
В = 2,0×106×11,0×(9,0 — 2,9/3)(9,0 — 2,9) = 1,17×109 кг×см2;
в поперечном направлении
В = 2,0×106×2,7×(9,6 — 1,7/3)(9,6 — 1,7) = 0,41×109 кг×см2.
Погонная жесткость, соответственно, равна:
в продольном направлении Вп = 1,17×107 кг×см;
в поперечном направлении Вп = 0,41×107 кг×см;
в) определяем радиус жесткости покрытия по формуле (11):
в продольном направлении
в поперечном направлении
г) по формуле (7) находим изгибающий момент:
в продольном направлении
М = 6,0(0,0592 — 0,09284×ln(18,25/30)) = 0,63 тм;
в поперечном направлении М = 6,0(0,0592 — 0,09284×ln(18,25/21)) = 0,43 тм;
д) проверку железобетонного сечения на выносливость производим по формулам (22) и (23):
в продольном направлении
для бетона
0,63×105 кг×см < 305×100×2,9×(9,0 — 2,9/3)×0,7×0,43 = 2,13×105 кг×см;
для арматуры
0,63×105 кг×см < 4000×11,0×(9,0 — 2,9/3)×0,85×0,52 = 1,55×105 кг×см;
в поперечном направлении
для бетона
0,43×105 кг×см < 305×100×1,7(9,6 — 1,7/3)×0,7×0,43 = 1,4×105 кг×см;
для арматуры
0,43×105 кг×см < 4000×2,7×(9,6 — 1,7/3)×0,85×0,52 = 0,43×105 кг×см.
Непрерывно армированное покрытие обладает несущей способностью по выносливости.
Определение эффективных параметров армирования железобетонных конструкций
Леонид Скорук
К.т.н., доцент, старший научный сотрудник НП ООО «СКАД Софт» (г. Киев).
В настоящее время монолитный железобетон (обеспечивающий произвольную форму изделий, свободу планировочных решений и многое другое) получил большее распространение и применение по сравнению со сборным железобетоном (ограниченная номенклатура сборных изделий и пролет). В то же время сборные изделия прошли проверку временем по надежности и долговечности, а их армирование является оптимальным с точки зрения некоего условного соотношения «материал/стоимость конструкции». В монолитных же конструкциях величина арматуры в большинстве случаев является переменной и зависит от многих исходных факторов: геологии, типа фундамента, нагрузки, геометрии здания и т.д.
Это нужно понимать при проектировании монолитных конструкций и не идти на поводу у заказчиков, далеких от инженерного дела и желающих в первую очередь оптимизировать свои расходы на строительство.
Как известно, чтобы обеспечить необходимую прочность и устойчивость здания или сооружения, следует провести соответствующие расчеты и подобрать необходимое количество арматуры для восприятия действующих нагрузок. При этом в конструкциях должны быть соблюдены требования как по 1й (прочность, устойчивость), так и по 2й группе (прогибы, ширина раскрытия трещин) предельных состояний.
В практике проектирования сформировался определенный условный параметр, по которому можно оценить затраты металла в конструкции: содержание арматуры в бетоне (как правило, берут вес всей арматуры в конструкции — продольной и поперечной — и делят на объем ее бетона, получая параметр в килограммах на кубический метр (кг/м3)).
При этом в действующих строительных нормах [13] такой параметр напрочь отсутствует и никоим образом не регламентируется. В нормативах указывается только необходимость обеспечить в сечении элемента минимальный процент арматуры от площади бетона (min 0,050,25%) и опосредованно рекомендован оптимальный процент армирования в конструкциях на уровне примерно 3% (это опять же отклик оптимизации для сборных конструкций).
До какойто степени величина содержания арматуры в конструкциях отражена в некоторых сметных нормативах [4, 5]. Там величина арматуры в бетоне находится в пределах 190200 кг/м3 — опять же без привязки к различным изменчивым исходным данным.
Для оценки величины содержания арматуры в бетоне монолитных конструкций проведем небольшой численный эксперимент. Возьмем для примера фрагмент плиты размерами в плане 1,0×1,0 м с двумя арматурными сетками у каждой грани, имеющими шаг стержней 100×100 мм, и проследим изменение содержания арматуры в бетоне в зависимости от изменения некоторых исходных параметров: толщины плиты и диаметра арматуры (рис. 1).
Рис. 1. Содержание арматуры в бетоне (кг/м3) для монолитного фрагмента площадью 1 м2 при различных исходных данных: а — при разных диаметрах арматуры; б — при разных толщинах плит
Рис. 2. Интерфейс программы SCAD++. Постпроцессор «Железобетон», режим «Экспертиза железобетона»
Как видно из приведенных данных, даже при «идеальных» условиях проектирования (отсутствие поперечной арматуры, дополнительного армирования, различных элементов локального усиления и т.п.) величина содержания арматуры, например, для элемента толщиной 200 мм с размещенной в нем арматурой из двух сеток диаметром 10 мм составляет 123,2 кг/м3. При наличии же различных дополнительных факторов суммарное содержание арматуры в бетоне будет резко расти.
Таблица 1. Факторы, которые влияют на расход бетона и арматуры
Фактор |
Следствие |
Инженерногеологические условия строительной площадки |
Тип фундамента (свайный, плитный, ленточный) |
Шаг сетки несущих вертикальных элементов |
Пролет плит, их толщина (жесткость) |
Размеры сечения колонн/пилонов/стен |
Удельный вес арматуры в бетоне |
Класс бетона и арматуры |
Расход арматуры в сечении |
Довольно трудоемкую и рутинную работу по определению содержания арматуры в бетоне для некоторых отдельных элементов и всего сооружения в целом на начальном этапе проектирования (еще до начала разработки чертежей стадии КЖ/КЖИ) с довольно высокой точностью можно выполнить в программе SCAD++. В режиме «Экспертиза железобетона» постпроцессора «Железобетон», используя операцию Вес заданной арматуры (рис. 2), можно в реальном времени не только определить расход арматуры, но заодно (что очень важно) и проверить, насколько заданная арматура удовлетворяет необходимым критериям прочности конструкции согласно выбранным нормам проектирования.
При этом нужно помнить, что программа считает расход:
- арматуры без учета ее нахлеста и загибов, которые могут добавлять в реальный расход арматуры около 1520%;
- бетона с учетом пересечения элементов, поскольку стыковка элементов происходит по оси стержневых и срединной плоскости плитных элементов (увеличение около 510%).
Суммарный расход арматуры и бетона в любом здании зависит от многих факторов, которые можно в некоторой степени скорректировать на начальной стадии расчета и проектирования. Основные факторы, которые влияют на расход бетона и арматуры в конструкциях и зданиях, приведены в табл. 1.
Таблица 2. Содержание арматуры в бетоне для разных типов зданий
Тип здания |
Элемент здания |
Расход, кг/м3 |
а) 22этажное здание на сваях |
Сваи |
64 |
Фундаментная плита |
392 |
|
Вертикальные несущие элементы |
263 |
|
Плиты перекрытия |
193 |
|
Всего по зданию |
212 |
|
б) 10этажное здание на сваях |
Сваи |
70 |
Фундаментная плита |
223 |
|
Вертикальные несущие элементы |
148 |
|
Плиты перекрытия |
129 |
|
Всего по зданию |
148 |
|
в) 8, 9этажное здание на плите |
Фундаментная плита |
238 |
Вертикальные несущие элементы |
126 |
|
Плиты перекрытия |
150 |
|
Всего по зданию |
175 |
|
г) 2этажное здание на сваях |
Сваи |
83 |
Фундаментная плита |
179 |
|
Вертикальные несущие элементы |
118 |
|
Плиты перекрытия |
170 |
|
Всего по зданию |
147 |
В табл. 2 на различных типах реальных зданий и сооружений показано, насколько изменчивой может быть величина содержания арматуры в бетоне и как она зависит от различных исходных данных — типа фундамента, шага несущих вертикальных элементов, толщины элементов, этажности здания, величины нагрузки и т.д.
Более точно содержание арматуры в бетоне можно определить по формуле:
, где
Са — содержание арматуры в бетоне для всего здания, кг/м3;
Сэ — содержание арматуры в бетоне для отдельных конструктивных элементов (фундаментная плита, плиты перекрытия и т.д.), кг/м3;
Υ э — удельный вес бетона отдельных конструктивных элементов в общем объеме бетона здания, %;
n — общее количество конструктивных элементов здания.
Выводы
Всё вышесказанное дает основания утверждать, что содержание арматуры в бетоне (кг/м3)
для монолитных конструкций не является величиной постоянной и в большой степени зависит от меняющихся выходных данных — типа фундамента, шага несущих вертикальных элементов, толщины элементов, этажности здания, величины нагрузки и многих других факторов.
Величина содержания арматуры в бетоне конструкций является сугубо индивидуальной характеристикой каждой конкретной конструкции и должна базироваться на соответствующих прочностных расчетах, быть следствием этих расчетов, а также отвечать конструктивным требованиям, предъявляемым к данному типу конструкции.
С помощью новых функций, реализованных в 21й версии программы SCAD++, появилась возможность на начальном этапе проектирования (стадия расчетной схемы) оперативно получить данные о расходе бетона и арматуры как для отдельного элемента, так и для всего здания в целом. На основании полученных данных проектировщик при необходимости принимает решение об изменении конструктивной схемы здания и оценивает, насколько эти изменения влияют на содержание арматуры в бетоне. В предыдущих версиях ПК SCAD такая задача тоже решалась, но гораздо более трудоемко, и при этом она требовала от проектировщика очень много времени на выполнение большого количества рутинных операций.
Литература:
- СП 63.13330.2012. Бетонные и железобетонные конструкции. Основные положения (Актуализированная редакция СНиП 52012003).
- СП 521012003. Бетонные и железобетонные конструкции без предварительного напряжения арматуры.
- Пособие по проектированию бетонных и железобетонных конструкций и тяжелого бетона без предварительного напряжения арматуры (к СП 521012003).
- ГЭСН 8102062001.
- ФЕР 060100117.
Как рассчитать процент в Excel — примеры процентных формул
В этом руководстве вы познакомитесь с быстрым способом расчета процентов в Excel, найдете базовую формулу процента и еще несколько формул для расчета увеличения в процентах, процента от общего числа и т. Д.
Расчет процентов полезен во многих сферах жизни, будь то чаевые в ресторане, комиссия реселлера, ваш подоходный налог или процентная ставка. Допустим, вам посчастливилось получить скидку 25% на новый плазменный телевизор.Это хорошая сделка? И сколько в итоге придется заплатить?
В этом руководстве мы собираемся изучить несколько методов, которые помогут вам эффективно вычислять процент в Excel, и выучить базовые процентные формулы, которые избавят вас от догадок при расчетах.
Базовый процент
Термин «процент» образован от латинского per centum , что означает «на сотню». Как вы, вероятно, помните из школьного урока математики, процент — это дробная часть от 100, которая вычисляется путем деления числителя на знаменатель и умножения результата на 100.
Основная процентная формула выглядит следующим образом:
(Часть / Целое) * 100 = Процент
Например, если у вас было 20 яблок и вы дали 5 своим друзьям, сколько вы дали в процентном отношении? Выполнив несложный расчет = 5/20 * 100 вы получите ответ — 25%.
Так обычно вычисляются проценты в школе и в повседневной жизни. Вычислить процент в Microsoft Excel еще проще, поскольку Excel выполняет некоторые операции за вас автоматически в фоновом режиме.
К сожалению, не существует универсальной формулы Excel для расчета процентов, которая охватывала бы все возможные сценарии. Если вы спросите кого-нибудь: «Какую формулу процентов я использую, чтобы получить желаемый результат?», Скорее всего, вы получите ответ типа «Ну, это зависит от того, какого именно результата вы хотите достичь».
Итак, позвольте мне показать вам несколько простых формул для вычисления процентов в Excel, таких как формула процентного увеличения, формула для получения процентов от общего количества и многое другое.
Базовая процентная формула Excel
Основная формула для расчета процента в Excel:
Часть / Итого = Процент
Если вы сравните ее с основной математической формулой для процента, вы заметите, что в формуле для процента в Excel отсутствует часть * 100.При вычислении процента в Excel вам не нужно умножать полученную дробь на 100, поскольку Excel делает это автоматически, когда процентный формат применяется к ячейке.
А теперь давайте посмотрим, как можно использовать процентную формулу Excel для реальных данных. Предположим, у вас есть количество « Заказанных товаров » в столбце B и « Доставленных товаров » в столбце C. Чтобы узнать процент доставленных товаров, выполните следующие действия:
- Введите формулу
= C2 / B2в ячейку D2 и скопируйте ее в нужное количество строк. - Нажмите кнопку Percent Style (вкладка Home > Number group), чтобы отобразить полученные десятичные дроби в виде процентов.
- Не забудьте при необходимости увеличить количество десятичных знаков, как описано в разделе «Советы по процентному соотношению».
- Готово! 🙂
Та же последовательность шагов должна быть выполнена при использовании любой другой процентной формулы в Excel.
В следующем примере в столбце D отображается округленный процент доставленных товаров без десятичных знаков.

Расчет процента от суммы в Excel
Фактически, приведенный выше пример является частным случаем вычисления процентов от общей суммы. Теперь давайте рассмотрим еще несколько примеров, которые помогут вам быстро вычислить процент от общей суммы в Excel для различных наборов данных.
Пример 1. Итог находится в конце таблицы в определенной ячейке
Очень распространенный сценарий — сумма в одной ячейке в конце таблицы.В этом случае процентная формула будет аналогична той, которую мы только что обсудили, с той лишь разницей, что ссылка на ячейку в знаменателе является абсолютной ссылкой (с $). Знак доллара фиксирует ссылку на данную ячейку, поэтому что он никогда не меняется, где бы ни копировалась формула.
Например, если у вас есть несколько значений в столбце B и их сумма в ячейке B10, вы должны использовать следующую формулу для вычисления процентов от общей суммы: = B2 / $ B $ 10
Вы используете относительную ссылку на ячейку B2, потому что хотите, чтобы она изменялась при копировании формулы в другие ячейки столбца B.Но вы вводите $ B $ 10 в качестве абсолютной ссылки на ячейку, потому что хотите оставить знаменатель фиксированным на B10 при автоматическом заполнении формулы до строки 9.
Наконечник. Чтобы сделать знаменатель абсолютной ссылкой, введите вручную знак доллара ($) или щелкните ссылку на ячейку в строке формул и нажмите F4.
На снимке экрана ниже показаны результаты, возвращаемые формулой, столбец процентов от общего отформатирован как процент с отображением 2 десятичных знаков.

Пример 2. Части итога находятся в нескольких строках
В приведенном выше примере предположим, что у вас есть несколько строк для одного и того же продукта, и вы хотите знать, какая часть общей суммы приходится на все заказы этого конкретного продукта.
В этом случае вы можете использовать функцию СУММЕСЛИ, чтобы сначала сложить все числа, относящиеся к данному продукту, а затем разделить это число на сумму, например:
= СУММЕСЛИ (диапазон, критерий, сумма_диапазон) / всего
Учитывая, что столбец A содержит все названия продуктов, столбец B перечисляет соответствующие количества, ячейка E1 представляет собой название продукта, который вас интересует, а итоговая сумма находится в ячейке B10, ваша реальная формула может выглядеть примерно так:
= СУММЕСЛИ (A2: A9, E1, B2: B9) / $ B $ 10

Естественно, вы можете указать название продукта прямо в формуле, например:
= СУММЕСЛИ (A2: A9, «вишня», B2: B9) / $ B $ 10
Если вы хотите узнать, какую часть общей суммы составляют несколько различных продуктов, сложите результаты, возвращаемые несколькими функциями СУММЕСЛИ, а затем разделите это число на общую сумму.Например, по следующей формуле рассчитывается процент вишни и яблок:
= (СУММЕСЛИ (A2: A9, «вишня», B2: B9) + СУММЕСЛИ (A2: A9, «яблоки», B2: B9)) / $ B $ 10
Для получения дополнительной информации о функции СУММ, пожалуйста, ознакомьтесь со следующими руководствами:
Как рассчитать процентное изменение в Excel
Из всех формул для расчета процента в Excel формула процентного изменения, вероятно, является той, которую вы будете использовать чаще всего.
Формула Excel для процентного изменения (процентное увеличение / уменьшение)
Чтобы вычислить процентное изменение между значениями A и B, используйте следующую формулу:
Процентное изменение = (B — A) / A
При применении этой формулы к реальным данным важно правильно определить, какое значение — A, а какое — B.Например, вчера у вас было 80 яблок и сколько у вас 100, что означает, что теперь у вас на 20 яблок больше, чем раньше, что на 25% больше. Если у вас было 100 яблок, а теперь у вас 80, ваше количество яблок уменьшилось на 20, то есть на 20%.
Учитывая вышеизложенное, наша формула Excel для процентного изменения принимает следующую форму:
(новое значение — старое значение) / старое значение
А теперь давайте посмотрим, как вы можете использовать эту формулу процентного изменения (также известную как формула процентного увеличения Excel) в ваших таблицах.
Пример 1. Расчет процентного изменения между 2 столбцами
Предположим, что у вас есть цены за последний месяц в столбце B и цены за этот месяц в столбце C. Затем вы можете ввести следующую формулу в ячейку D2, чтобы рассчитать процентное изменение в таблице Excel:
= (C2-B2) / B2
Эта формула процентного изменения вычисляет процентное увеличение / уменьшение в этом месяце (столбец C) по сравнению с прошлым месяцем (столбец B).
После копирования формулы в другие строки не забудьте нажать кнопку Percent Style на ленте, чтобы отобразить десятичные дроби в процентах, и вы получите результат, аналогичный тому, что вы видите на снимке экрана ниже.В этом примере положительные проценты, показывающие процентное увеличение, отформатированы обычным черным цветом, а отрицательные проценты (процентное уменьшение) отформатированы красным цветом с использованием техники, описанной в этом совете.

Пример 2. Расчет процентного изменения между строками
Если у вас есть один числовой столбец, например столбец C, в котором указаны еженедельные или ежемесячные продажи, вы можете рассчитать процентное изменение, используя следующую формулу:
= (C3-C2) / C2
Где C2 — это 1 st , а C3 — 2 -я ячейка с данными.
Примечание. Обратите внимание, что вы должны пропустить первую строку с данными и поместить свою процентную формулу Excel в ячейку 2 и , которой в данном примере является D3.
После применения процентного формата к столбцу с формулой процентного изменения вы получите следующий результат:

Если вы хотите рассчитать процентное изменение по сравнению с определенной ячейкой, вам необходимо исправить ссылку на эту ячейку, используя абсолютную ссылку на ячейку со знаком $, e.г. $ C $ 2.
Например, вот формула процентного изменения Excel, которая вычисляет процентное увеличение / уменьшение для каждого месяца по сравнению с январем (C2):
= (C3- 2 канадских доллара) / 2 канадских доллара
Когда вы перетаскиваете формулу вниз, чтобы скопировать ее в другие ячейки, абсолютная ссылка ($ C $ 2) останется прежней, а относительная ссылка (C3) изменится на C4, C5 и так далее.

Расчет суммы и итога в процентах
Как вы только что видели, вычислять проценты в Excel легко, как и вычислять суммы и итоги, если вы знаете проценты.
Пример 1. Рассчитать сумму по итогу и в процентах
Предположим, вы покупаете новый ноутбук за 950 долларов, и они взимают НДС в размере 11% с этой покупки. Вопрос в том, сколько вы должны заплатить сверх чистой цены? Другими словами, что составляет 11% от 950 долларов?
Поможет следующая формула:
Итого * Процент = Сумма
Предполагая, что общее значение находится в ячейке A2, а процентное значение — в B2, приведенная выше формула превращается в простую форму = A2 * B2 и возвращает 104.50

Помните, когда вы вводите число, за которым следует знак процента (%) в Excel, число интерпретируется как сотая часть его значения. Например, 11% фактически сохраняется как 0,11, и Excel использует это базовое значение во всех формулах и расчетах.
Другими словами, формула = A2 * 11% эквивалентна = A2 * 0,11 . Естественно, вы можете использовать десятичное число, соответствующее процентному соотношению, непосредственно в формуле, если это лучше подходит для ваших рабочих листов.
Пример 2. Подсчет итога по сумме и процентам
Например, ваш друг предложил вам свой старый компьютер за 400 долларов, что на 30% ниже первоначальной цены. Вы хотите знать, какова была первоначальная цена.
Поскольку 30% — это скидка, вы сначала вычитаете ее из 100%, чтобы узнать, какой процент вы действительно должны заплатить (100% — 30% = 70%). Теперь вам нужна формула для расчета исходной цены, т.е. найти число, 70% которого равно 400.
Формула выглядит следующим образом:
Сумма / Процент = Итого
Применительно к реальным данным он может принимать любую из следующих форм:
= A2 / B2 или = A2 / 0.7 или = A2 / 70%

Как увеличить / уменьшить число на процент
Сезон отпусков приближается, и это указывает на изменение ваших обычных еженедельных расходов. Вы можете рассмотреть различные варианты, чтобы определить оптимальное еженедельное пособие.
Чтобы увеличить сумму на процент, используйте эту формулу:
= Сумма * (1 +%)
Например, формула = A1 * (1 + 20%) увеличивает значение в ячейке A1 на 20%.
до уменьшить сумма на процент:
= Сумма * (1 -%)
Например, формула = A1 * (1-20%) уменьшает значение в ячейке A1 на 20%.
В нашем примере, если A2 — ваши текущие расходы, а B2 — процент, на который вы хотите увеличить или уменьшить эту сумму, вот формулы, которые вы должны ввести в ячейку C2:
Увеличение на процент: = A2 * (1 + B2)
Уменьшить на процент: = A2 * (1-B2)

Как увеличить / уменьшить весь столбец на процент
Предположим, у вас есть столбец чисел, который вы хотите увеличить или уменьшить на определенный процент, и вы хотите, чтобы обновленные числа были в том же столбце, а не добавляли новый столбец с формулой.
Вот 5 быстрых шагов для решения этой задачи:
- Введите все числа, которые вы хотите увеличить или уменьшить в каком-либо столбце, столбец B в этом примере.
- В пустой ячейке введите одну из следующих формул:
Увеличение в процентах:
= 1 + 20%Уменьшить на процент:
= 1-20%
Естественно, вы можете заменить 20% в приведенных выше формулах на желаемый процент.
- Выделите ячейку с формулой (в нашем случае C2) и скопируйте ее, нажав Ctrl + C.
- Выберите диапазон ячеек, который вы хотите изменить, щелкните выделение правой кнопкой мыши и выберите Специальная вставка…

- В диалоговом окне Специальная вставка выберите Значения в разделе Вставить , Умножить в разделе Операция и нажмите ОК .

И вот результат — все числа в столбце B увеличены на 20%:

Таким же образом можно умножить или разделить столбец чисел на определенный процент.Просто введите желаемый процент в пустую ячейку и следуйте инструкциям выше.
Вот как вы рассчитываете процент в Excel. И даже если работа с процентами никогда не была вашим любимым видом математики, с помощью этих основных процентных формул вы можете заставить Excel делать эту работу за вас. На сегодня все, спасибо, что прочитали!
Вас также может заинтересовать
.Формула для процента
Формула для процента является следующей, и ее будет легко использовать, если вы будете следовать простым данным инструкциям. Прежде чем рассматривать примеры, внимательно изучите приведенную ниже формулу. 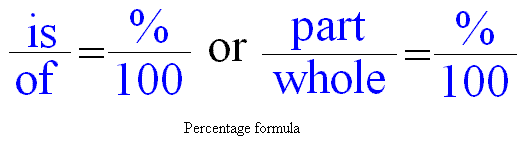 |
Для иллюстрации рассмотрим несколько примеров. Начнем с формулы слева.
Важно помнить о перекрестном умножении после того, как вы определили различные части формулы.
Перекрестное умножение означает умножение числителя одной дроби на знаменатель другой дроби.
25% от 200 составляет ____
В этой задаче из = 200, это =? И % = 25
Мы получаем:
это /200 = 25/100
Так как — это в неизвестном, вы можете заменить его на y, чтобы проблема была более знакомой.
y / 200 = 25/100
Перемножьте крестиком, чтобы получить y × 100 = 200 × 25
y × 100 = 5000
Разделите 5000 на 100, чтобы получить y
Так как 5000/100 = 50, y = 50
Итак, 25% от 200 составляет 50
Пример № 2:
Какое число составляет 2% от 50?
Это просто еще один способ сказать, что 2% от 50 — это ___
Итак, настройте пропорцию как пример # 1:
это /50 = 2/100
Заменить на y и перемножить, чтобы получить :
y × 100 = 50 × 2
y × 100 = 100
Так как 1 × 100 = 100, y = 1
Следовательно, 1 составляет 2% от 50
Пример # 3:
24 % от ___ равно 36
На этот раз обратите внимание, что — это = 36, но из отсутствует
После настройки формулы вы получите:
36/ из = 24/100
Заменить из на y и умножаем крест-накрест, чтобы получить:
36 / y = 24/100
y × 24 = 36 × 100
y × 24 = 3600
Разделите 3600 на 24, чтобы получить y
3600/24 = 150 , y = 150
Следовательно, 24% от 150 равно 36
Как использовать другую формулу для процента справа.
Теперь мы рассмотрим примеры, чтобы проиллюстрировать, как использовать формулу для процента справа
Пример № 4:
Чтобы использовать другую формулу, которая говорит часть и целое, просто запомните следующее:
- Число после из всегда целиком.
- Номер после — всегда является частью.
Ваша пропорция будет такой:
60/ целое = 25/100
После перекрестного умножения мы получить:
целиком × 25 = 60 × 100
целиком × 25 = 6000
Разделите 6000 на 25, чтобы получить целое
6000/25 = 240, итого целое = 240
Следовательно, 25% от 240 — это 60
Пример # 5:
___% от 45 равно 9
Здесь целое = 45 и часть = 9, но % отсутствует
Получаем:
9/45 = % / 100
Замена% на x и перекрестное умножение дает:
9 × 100 = 45 × x
900 = 45 × x
Разделите 900 на 45, чтобы получить x
900/45 = 20, поэтому x = 20
Поехали! Надеюсь, формула процентного соотношения была полезной.
Классные математические хитрости
7 окт, 20 13:37

Хотите произвести впечатление на своих друзей? Ознакомьтесь с этими классными математическими приемами, которые помогут вам без особых усилий решать сложные базовые математические задачи.
Подробнее
Новые уроки математики
Ваша электронная почта в безопасности. Мы будем использовать его только для информирования вас о новых уроках математики.
.Изменение в процентах — увеличение и уменьшение в процентах
Объяснение и повседневные примеры использования процентов обычно можно найти на нашей странице Проценты: Введение . Для более общих расчетов процентов см. Нашу страницу Калькуляторы процентов .
Для расчета увеличения в процентах:
Первый: вычислите разницу (увеличение) между двумя числами, которые вы сравниваете.
Увеличение = новый номер — исходный номер
Затем: разделите увеличение на исходное число и умножьте ответ на 100.
Увеличение % = Увеличение ÷ Исходное число × 100 .
Если ваш ответ отрицательный, то это процентное уменьшение.
Для расчета уменьшения в процентах:
Первый: вычислите разницу (уменьшение) между двумя числами, которые вы сравниваете.
Уменьшение = исходный номер — новый номер
Затем: разделите уменьшение на исходное число и умножьте ответ на 100.
% Уменьшение = Уменьшение ÷ Исходное число × 100
Если ваш ответ отрицательный, то это процентное увеличение.
Если вы хотите рассчитать процентное увеличение или уменьшение нескольких чисел, мы рекомендуем использовать первую формулу. Положительные значения указывают на процентное увеличение, тогда как отрицательные значения указывают на процентное уменьшение.

Калькулятор процентного изменения
Используйте этот калькулятор для вычисления процентного изменения двух чисел.
Подробнее: Калькуляторы процентов
Примеры — увеличение и уменьшение в процентах
В январе Дилан проработал 35 часов, в феврале — 45.5 часов — на сколько процентов увеличилось рабочее время Дилана в феврале?
Чтобы решить эту проблему, сначала мы вычисляем разницу в часах между новым и старым числами. 45,5 — 35 часов = 10,5 часов. Мы видим, что Дилан в феврале проработал на 10,5 часов больше, чем в январе — это его прирост . Чтобы рассчитать увеличение в процентах, теперь необходимо разделить увеличение на исходное (январское) число:
10,5 ÷ 35 = 0.3 (См. Инструкции и примеры деления на странице , раздел .)
Наконец, чтобы получить процентное значение, мы умножаем ответ на 100. Это просто означает перемещение десятичной точки на два столбца вправо.
0,3 × 100 = 30
Таким образом, Дилан отработал в феврале на 30% больше часов, чем в январе.
В марте Дилан снова проработал 35 часов — столько же, сколько он работал в январе (или 100% его январских часов). Какова процентная разница между февральскими часами Дилана (45.5) и его мартовские часы (35)?
Сначала рассчитайте уменьшение количества часов, то есть: 45,5 — 35 = 10,5
Затем разделите уменьшение на исходное число (февральские часы) так:
10,5 ÷ 45,5 = 0,23 (с точностью до двух десятичных знаков).
Наконец, умножьте 0,23 на 100, чтобы получить 23%. Часы Дилана в марте были на 23% меньше, чем в феврале.
Вы могли подумать, что, поскольку между часами работы Дилана в январе (35) и февралем (45.5) часов, что между его часами февраля и мартом также будет 30% сокращение. Как видите, это предположение неверно.
Причина в том, что наше исходное число в каждом случае разное (35 в первом примере и 45,5 во втором). Это подчеркивает, насколько важно убедиться, что вы рассчитываете процент от правильной начальной точки.
Иногда проще показать процентное уменьшение как отрицательное число — для этого следуйте приведенной выше формуле, чтобы вычислить процентное увеличение — ваш ответ будет отрицательным числом, если было уменьшение.В случае Дилана увеличение на часов в период с февраля по март составляет -10,5 (отрицательно, потому что это уменьшение). Следовательно, -10,5 ÷ 45,5 = -0,23. -0,23 × 100 = -23%.
Часы Дилана могут отображаться в таблице данных как:
| Месяц | часов отработано | Процент Изменение |
| январь | 35 | |
| Февраль | 45,5 | 30% |
| Март | 35 | -23% |
Расчет значений на основе процентного изменения
Иногда полезно иметь возможность рассчитать фактические значения на основе процентного увеличения или уменьшения.В СМИ часто можно увидеть примеры того, когда это может быть полезно.
Вы можете увидеть заголовки вроде:
Осадки в Великобритании этим летом были на 23% выше среднего.
Уровень безработицы снизился на 2%.
Банкиры ’бонусы сократились на 45%.
Эти заголовки дают представление о тенденции — когда что-то увеличивается или уменьшается, но часто нет реальных данных.
Без данных цифры процентного изменения могут вводить в заблуждение.
Кередигион, графство в Западном Уэльсе, имеет очень низкий уровень насильственных преступлений.
Полицейские отчеты Кередигиона за 2011 год показали 100% -ный рост насильственных преступлений. Это поразительное число, особенно для тех, кто живет или думает о переезде в Кередигион.
Однако, когда исследуются основные данные, выясняется, что в 2010 году в Кередигионе было зарегистрировано одно насильственное преступление. Таким образом, увеличение на 100% в 2011 году означало, что было зарегистрировано два насильственных преступления.
Если взглянуть на реальные цифры, восприятие количества насильственных преступлений в Ceredigion значительно изменится.
Чтобы определить, насколько что-то увеличилось или уменьшилось в реальном выражении, нам нужны реальные данные.
Возьмем, к примеру, « осадков в Великобритании этим летом было на 23% выше среднего » — мы можем сразу сказать, что в Великобритании за лето выпало почти на четверть (25%) осадков больше, чем в среднем. Однако, не зная, каков средний уровень осадков или сколько осадков выпало за рассматриваемый период, мы не можем определить, сколько осадков выпало на самом деле.
Расчет фактического количества осадков за период, если известно среднее количество осадков.
Если мы знаем, что среднее количество осадков составляет 250 мм, мы можем рассчитать количество осадков за период, вычислив 250 + 23%.
Первая тренировка 1% от 250, 250 ÷ 100 = 2,5. Затем умножьте ответ на 23, потому что количество осадков увеличилось на 23%.
2,5 × 23 = 57,5.
Таким образом, общее количество осадков за рассматриваемый период составило 250 + 57,5 = 307,5 мм.
Расчет среднего количества осадков, если известно фактическое количество.
Если в новостном сообщении говорится о новом измерении и процентном увеличении, « Великобритании количество осадков было на 23% выше среднего… Выпало 320мм дождя… ».
В этом примере мы знаем, что общее количество осадков составило 320 мм. Мы также знаем, что это на 23% выше среднего. Другими словами, 320 мм соответствует 123% (или 1,23 раза) от среднего количества осадков. Чтобы вычислить среднее значение, мы разделим общую сумму (320) на 1,23.
320 ÷ 1,23 = 260,1626. Округленное до одного десятичного знака, среднее количество осадков 260,2 мм .
Теперь можно рассчитать разницу между средним и фактическим количеством осадков:
320 — 260.2 = 59,8 мм .
Мы можем заключить, что 59,8 мм составляет 23% от среднего количества осадков (260,2 мм), и что в реальном выражении выпало на 59,8 мм больше осадков, чем в среднем.
Мы надеемся, что эта страница оказалась для вас полезной — почему бы не посетить наши другие страницы, посвященные навыкам счета? Или дайте нам знать о предмете, который вы хотели бы увидеть на SkillsYouNeed — Свяжитесь с нами .
.Как рассчитать процент отклонения в Excel
Понятие процента отклонения означает разницу между двумя числовыми значениями в процентах. Приведем конкретный пример: например, сегодня со склада было продано 120 планшетных компьютеров, а на следующий день — 150. Разница в объемах продаж очевидна: на следующий день продано еще 30 штук планшетов. При вычитании из 150-го числа 120 получаем отклонение, равное числу +30. Возникает вопрос: какое отклонение в процентах?
Взаимодействие с другими людьмиКак рассчитать отклонение в процентах в Excel
Процент отклонения рассчитывается путем вычитания старого значения из нового и последующего деления результата на старое.Результат вычисления этой формулы в Excel должен отображаться в процентном формате ячейки. В этом примере формула расчета выглядит следующим образом (150-120) / 120 = 25%. Формулу проверить несложно: 120 + 25% = 150.
Оплачивайте внимание! Если поменять местами старые и новые числа, то у нас есть формула для расчета наценки.
Ниже на картинке вы можете увидеть пример, как вышеуказанный расчет может быть представлен в виде формулы Excel. Формула в ячейке D2 вычисляет процент отклонения между значениями продаж за текущий и прошлый год: = (C2-B2) / B2
Важно обратить внимание на наличие круглых скобок в этой формуле.По умолчанию в Excel операция деления всегда имеет наивысший приоритет по отношению к операции вычитания. Следовательно, если мы не ставим круглые скобки, первое значение будет разделено, а затем из него будет вычтено другое значение. Такой расчет (без скобок) будет ошибочным. Закрытие первой части вычислений в формуле скобок автоматически повышает приоритет операции вычитания, указанной выше, по отношению к операции деления.
Вам нужно правильно ввести формулу в ячейку D2 с квадратными скобками, а затем просто скопировать ее в другие пустые ячейки диапазона D2: D5.Чтобы скопировать формулу самым быстрым способом, вам нужно просто переместить курсор мыши к курсору курсора клавиатуры (в нижний правый угол), чтобы курсор мыши сменился со стрелки на черный крестик. После этого достаточно сделать двойной щелчок левой кнопкой мыши и Excel автоматически заполнит пустые ячейки формулой и определит диапазон D2: D5, который необходимо заполнить до ячейки D5 и не более. Это очень удобный лайфхак в Excel.
Взаимодействие с другими людьмиАльтернативная формула для расчета процента отклонения в Excel
В альтернативной формуле, которая вычисляет относительное отклонение значений продаж от текущего года, оно сразу делится на значения продаж предыдущего года, и только тогда единица удаляется из результата: = C2 / B2-1
Как видно на рисунке, результат вычисления альтернативной формулы такой же, как и в предыдущей, а значит, правильный.Но альтернативную формулу проще записать, хотя кто-то может прочитать больше, чтобы понять принцип ее действия. Или сложнее понять, какое значение дает эта формула, если она не подписана.
Единственным недостатком этой альтернативной формулы является то, что невозможно вычислить процентное отклонение при отрицательных числах в числителе или в заместителе. Даже если мы используем функцию ABS в формуле, формула вернет результат ошибки с отрицательным числом в замене.
Поскольку в Excel по умолчанию приоритет операции деления выше, чем операции вычитания в этой формуле, нет необходимости применять круглые скобки.
.



