Формула глубины: Как измерить глубину? Вопросы и ответы по физике :: Класс!ная физика

Вы делаете это неправильно: расчет глубины / Хабр

Приветствую вас, глубокоуважаемые!

Что если я скажу, что глубина, что бы вы под ней не подразумевали, является одной из самых сложных для точного измерения величин? На какой глубине плывет подводная лодка? Какая глубина марианской впадины? На какой глубине лежит Титаник? Если вам не повезет с параметрами, то на первом километре глубины, вы можете ошибиться примерно на 30-40 метров и на 200-300 метров на 6-ом километре, используя датчик давления. Если вы предпочитаете эхолот, то при неудачном стечении обстоятельств, которые вы не учли, ошибка на первом километре составит метров 100, а на 6-ом — целый километр. Конечно, можно еще использовать длинную веревку… Но там, как известно, свои подводные камни.

Как такое могло случиться и как делать правильно я расскажу под катом. В довесок к статье есть Open-source библиотека на C#/C/Rust/Matlab/Octave/JavaScript и пара онлайн-калькуляторов для демонстрации.

Статья будет полезна разработчикам подводной техники, число которых за последние лет пять выросло в разы.

• и расстояние по вертикали от поверхности воды до точки, где эту глубину измеряют,
• и расстояние по вертикали от поверхности воды до дна.

В первом случае — это глубина погружения, а во втором — глубина места.

Есть ровно два с половиной фундаментальных способа изменения этих величин, как я уже упомянул:

• по гидростатическому давлению столба жидкости, т.е. при помощи датчика давления;
• по времени распространения звука — эхолотом
• по длине выпущенной за борт веревки =)

С веревкой все понятно, а с остальными двумя давайте разберемся. Сегодня разберем:

Способ 1 — По давлению столба жидкости

Все мы знаем из школьного курса физики формулу гидростатического давления столба жидкости:

Из нее легко посчитать высоту столба жидкости (т. 2.

Давайте абстрагируемся от точности конкретных приборов, пусть даже они у нас суперточные.
Проблема в том, что никакой член формулы не является константой. Даже атмосферное давление может меняться в течение часа.

Как влияет атмосферное давление?

Давление у поверхности моря может варьироваться в пределах 641-816 мм. рт. ст., или, тоже самое в миллибарах: от 855 до 1087. Если просто взять за стандартное значение в 1013.25 мБар, то в зависимости от погоды уже можно получить ошибку в 40-50 сантиметров, причем, как в «плюс», так и в «минус».

Что с ускорением свободного падения?

Боюсь показаться Кэпом, но все же напомню, что земля у нас

вращается, и за счет центробежной силы притягивает на экваторе слабее, чем на полюсах.

Если не крохоборничать и не учитывать гравитационные аномалии из-за разной плотности земных пород, гор, впадин, изменения скорости вращения земли от сброшенной земными деревьями листвы и перемещениями соков по их стволам, то нас вполне устроит стандартная зависимость ускорения свободного падения от георафической широты.

Согласно этой формуле, ускорение свободного падения меняется от 9.7803 м/с2 на экваторе (0° градусов широты) до 9.8322 м/с2 на полюсах (90/-90° широты).

Допустим, мы возьмем стандартное значение ускорения свободного падения 9.80665 м/с2, на сколько мы ошибемся в худшем случае?

Это иллюстрируетя картинкой ниже. На ней синий график показывает ошибку определения глубины на экваторе, если мы будем использовать стандартное значение , а оранжевый график — такую же ошибку на полюсах.

То есть, если мы подставим в формулу стандартное значение и пойдем погружаться где-то ближе к экватору, то на 100 метрах ошибемся всего на 20-30 сантиметров, на километре — на 2,5-3 метра, а на 9-10 километрах (Бездна Челленжера, кстати, находится на 11° северной широты) ошибка будет уже 25-30 метров. Т.е. реальная глубина будет больше, чем та, которую мы измерим.

А как влияет плотность воды?

Самым нехорошим образом.

Дело в том, что плотность воды в упрощенном случае есть функция температуры, давления и солености.

То есть мало измерять давление, атмосферное давление, учитывать географическую широту места. Нужно еще знать температуру и соленость воды.

Для определения плотности морской воды в (разумном) диапазоне условий на практике наиболее широко применяется формула из работы Чена и Миллеро (Да, ЮНЕСКО занимается еще и этим!)

Допустим, мы измерили и температуру и соленость, но остается сжимаемость воды — изменение плотности с давлением (т.е. с глубиной), и чтобы определить высоту столба жидкости нужно просуммировать высоты элементарных столбиков, на которых давление изменяется на какую-то малую величину . В целом это конечно интеграл, но чтобы сразу привнести некое практическое значение, запишем его так:

N — это число интервалов разбиения давления от до измеренного .

Плотность зависит от давления практически линейно, и считать такую сумму из-за учета одной лишь сжимаемости смысла нет, но я привел здесь эту формулу не просто так.

Сам факт, что плотность зависит от трех параметров — это еще пол беды. Сложность кроется в том, что все эти параметры могут сильно меняться с глубиной. В этом случае принято говорить о профиле температуры и солености. Вот так, к примеру, выглядит профиль из Арктики:

Вот так с северной части тихого океана:

А вот так, для сравнения — с юга атлантики:

Например, если представить, что мы погружается в северной части тихого океана (39°СШ,152°ВД) учитываем атмосферное давление и географическую широту места и сжимаемость воды, а наш датчик давления показывает 100 Бар (~1000 м), а температуру и соленость мы берем в точке измерения, но не учитываем профиль, мы ошибемся с глубиной на 2 метра.

Я специально запилил онлайн-калькулятор и добавил три тестовых профиля (их можно переключать кнопками), чтобы каждый мог сам попробовать.

Если теперь просто переключить профиль на «южноатлантический» и попробовать пересчитать, то мы увидим, что разница выросла до 6-и метров. Напомню: все, даже сжимаемость воды мы уже учли! Ошибка связана только с наличием профиля — слоев разной температуры и солености в толще воды.

Естественно, все меняется и со сменой времен года и со сменой времени суток. Летом (в северном полушарии, зимой — в южном) верхний слой прогревается, а зимой — остывает. Шторма перемешивают воду, дожди смывают грязь с суши и реками уносят в моря, таят снега и ледники.

Это я к тому, что нельзя один раз перемерить и выбить в граните все профили температуры и солености для всех морей и океанов — все течет, все меняется. И если вдруг вы собрались погружаться на ощутимые глубины и у вас нет температурного профиля — я не поверю в ваш рекорд )

Матчасть

Как я упомянул в начале статьи, все необходимое для расчета глубины я собрал в библиотеку и положил на GitHub.

Она в том числе переведена на JavaScript, а в качестве интерактивного примера ее использования привожу онлайн-калькулятор.

P.S.

Благодарю за внимание, буду искренне благодарен за конструктивную критику, сообщения об ошибках, пожелания и предложения.

В следующей статье разберу второй способ определения глубины — по эхолокации.

Определение глубины сезонного промерзания грунта по разумным ценам в Москве и области

Для возможности проектирования фундаментной опоры здания необходимо предварительно определить характеристики грунта, в частности, глубину промерзания.

На выбор типа фундамента влияет и пучинистость, то есть грунт, который содержит большое количество воды и способен к расширению и вспучиванию при замерзании, что может привести к сдвигу и разрушению основания строения, появлению трещин на стенах, разрушению всего сооружения.

Определение глубины сезонного промерзания грунта

Заказать

Глубина промерзания грунта для конкретных регионов России

Глубина промерзания грунта в Подмосковье

Как определить реальную глубину сезонного промерзания почвы?

Нормативные и настоящие показатели глубины промерзания грунта всегда отличаются, так как каждый год толщина снежного и ледяного покрова на заданной местности различная.

Чтобы точно определить глубину промерзания почвы, используется мерзлотомер – обсадная трубка с внутренним элементом — шлангом с водой и ограничителями, предупреждающими миграцию льда. На шланге имеется сантиметровая шкала. При выполнении измерений прибор погружается в почву на глубину ниже номинального промерзания. В местах, где с мерзлотомером контактирует мерзлая почва, вода в шланге превращается в лед. Через 10-12 часов шланг вынимается из трубки и по шкале определяется реальный уровень промерзания грунта.

Для расчета уровня промерзания грунта используется следующая формула:

d1 = d0 √M, где d1 – глубина промерзания согласно нормативам, d0 – отдельный параметр для каждого типа грунта, M – сумма абсолютных сезонных среднемесячных температур в данном регионе.

Показатели d0 – для песчаной и супесей – 0,28, глинистой почвы и суглинка – 0,23, крупнозернистого песка – 0,3, крупнообломочного грунта – 0,34. Показатели минусовых температур указаны в метеорологических справочниках либо СНиП, описывающих климатические условия конкретной местности.

Тип грунта определяет фирма, занимающаяся геологическими исследованиями.

Комплекс работ включает

• изучение геологического строения района;
• выезд бригады специалистов на участок для бурения скважин, взятия проб грунта;
• лабораторное исследование образцов для определения слоев земли;
• составление технического отчета с рекомендациями по строительству – выбору материала для стен и типа фундамента.

На стоимость геологических изысканий оказывают влияние количество скважин, погонных метров бурения и взятых образцов.

Компания «GeoCompani» выполняет работы по геодезии любой сложности для клиентов из Москвы и Московской области. Мы гарантируем выгодные цены и сжатые сроки исполнения заказа. Получить консультации специалистов и заказать услуги можно по телефону +7-495-777-65-35 или WhatsApp.

Почему с нами выгодно сотрудничать?

• Рассчитываем глубину сезонного промерзания именно для Вашего участка и грунтов.
• Выпускаем отчет за 10 дней.
• Все образцы сдаются в лабораторию.
• Собственный камеральный отдел.

Читайте также:

1. Испытания грунтов
2. Нужно ли Вам выполнять геологические изыскания?
3. Поиск грунтовых вод на участке
4. Как используется геодезия в прикладных задачах?
5. Как используется на практике специальная инженерная геология?

11.4 Изменение давления в зависимости от глубины в жидкости – Колледж физики, главы 1-17

11 Статистика жидкости

Резюме

• Определить давление по весу.
• Объясните изменение давления в жидкости с глубиной.
• Расчет плотности по давлению и высоте.

Если у вас когда-либо лопало ухо во время полета на самолете или болело во время глубокого погружения в бассейн, вы испытали влияние глубины на давление в жидкости. На поверхности Земли давление воздуха, оказываемое на вас, является результатом веса воздуха над вами. Это давление уменьшается по мере того, как вы поднимаетесь на высоту, и вес воздуха над вами уменьшается. Под водой давление, оказываемое на вас, увеличивается с увеличением глубины. В этом случае давление, оказываемое на вас, является результатом веса воды над вами и — это атмосфера над вами. Вы можете заметить изменение давления воздуха во время поездки на лифте, который перенесет вас во многие истории, но вам нужно всего лишь нырнуть на метр или около того под поверхность бассейна, чтобы почувствовать увеличение давления. Разница в том, что вода намного плотнее воздуха, примерно в 775 раз плотнее.

Рассмотрим контейнер на рис. 1. Его дно поддерживает вес жидкости в нем. Рассчитаем давление, оказываемое на дно весом жидкости. Это давление — это вес жидкости[латекс]\boldsymbol{мг}[/латекс], деленный на площадь[латекс]\жирныйсимвол{А}[/латекс], поддерживающую его (площадь дна сосуда):

[латекс]\boldsymbol{P\:=}[/латекс][латекс]\boldsymbol{\frac{mg}{A}}. [/latex]

Мы можем найти массу жидкости по ее объему и плотности:

[латекс]\boldsymbol{m\:=\rho{V}}.[/латекс]

Объем жидкости[латекс]\boldsymbol{V}[/латекс]относится к размерам контейнера. это

[латекс]\boldsymbol{V=Ah},[/латекс]

, где [латекс]\boldsymbol{A}[/латекс]– площадь поперечного сечения, а [латекс]\boldsymbol{h}[/латекс]– глубина. Объединение последних двух уравнений дает

[латекс]\boldsymbol{m=\rho{Ah}}.[/latex]

Если мы подставим это в выражение для давления, то получим

[латекс]\boldsymbol{P\:=}[/латекс][латекс]\boldsymbol{\frac{(\rho{Ah})g}{A}}.[/latex]

Область отменяется, и перестановка переменных дает

[латекс]\boldsymbol{P=h\rho{g}.}[/латекс]

Это значение представляет собой давление из-за веса жидкости . Уравнение имеет общую справедливость вне особых условий, при которых оно здесь выведено. Даже если бы контейнера не было, окружающая жидкость все равно оказывала бы это давление, удерживая жидкость в статике. Таким образом, уравнение[латекс]\boldsymbol{P=h\rho{g}}[/latex] представляет собой давление, обусловленное весом любой жидкости со средней плотностью [латекс]\boldsymbol{\rho}[/latex] на любой глубине[латекс]\boldsymbol{h}[/латекс]ниже его поверхности. Для жидкостей, почти несжимаемых, это уравнение выполняется до больших глубин. Для газов, которые достаточно сжимаемы, это уравнение можно применять, пока изменения плотности малы на рассматриваемой глубине. Пример 2 иллюстрирует эту ситуацию.

Пример 1: Расчет среднего давления и приложенной силы: какую силу должна выдерживать плотина?

В главе 11.2 Пример 1 мы рассчитали массу воды в большом резервуаре. Теперь рассмотрим давление и силу, действующие на удерживающую воду плотину.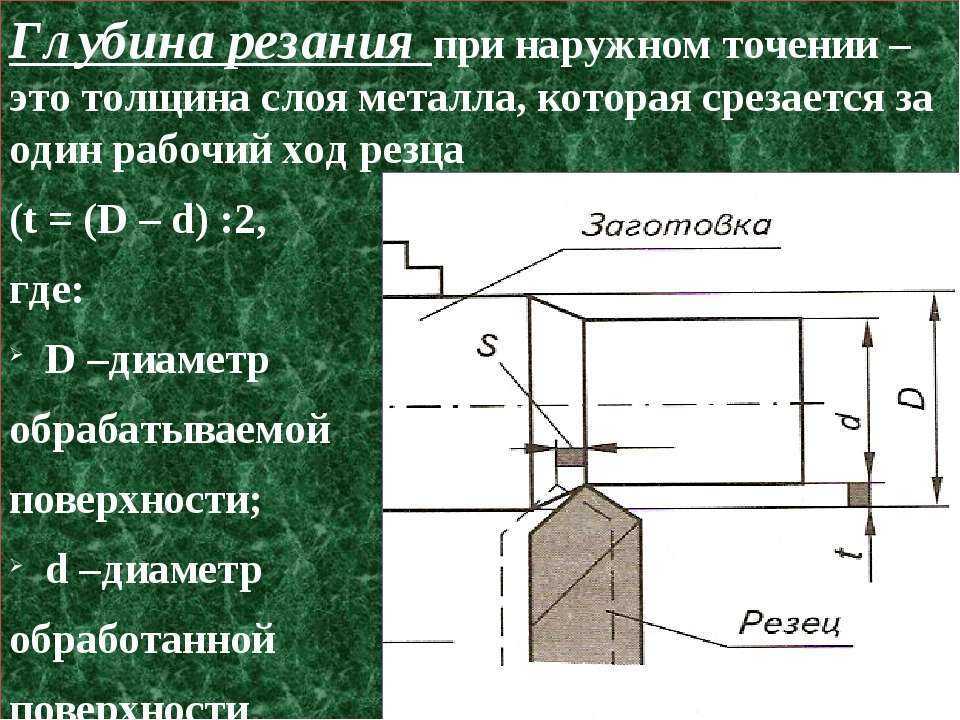 (См. рис. 2.) Плотина имеет ширину 500 м, а глубина воды у плотины составляет 80,0 м. а) Каково среднее давление воды на плотину? (b) Рассчитайте силу, действующую на плотину, и сравните ее с весом воды в плотине (ранее было установлено, что это [латекс]\boldsymbol{1.9{13}\textbf{ N}}[/latex]).

Стратегия для (a)

Среднее давление[латекс]\boldsymbol{\bar{P}}[/latex]из-за веса воды – это давление на средней глубине[латекс]\boldsymbol{ \bar{h}}[/latex] 40,0 м, так как давление увеличивается линейно с глубиной.

Решение для (a)

Среднее давление из-за веса жидкости равно

[латекс]\boldsymbol{\bar{P}=\bar{h}\rho{g}}.[/ латекс]

Вводя плотность воды из таблицы 1 и принимая [латекс]\жирныйсимвол{\бар{ч}}[/латекс]в качестве средней глубины 40,0 м, получаем 9{13}\textbf{ N}}[/latex]масса воды в резервуаре — на самом деле это всего лишь[latex]\boldsymbol{0,0800\%}[/latex]веса. Обратите внимание, что давление, найденное в части (а), совершенно не зависит от ширины и длины озера — оно зависит только от его средней глубины у плотины. Таким образом, сила зависит только от средней глубины воды и размеров плотины, , а не от горизонтальной протяженности водохранилища. На диаграмме толщина плотины увеличивается с глубиной, чтобы уравновесить возрастающую силу из-за увеличивающегося давления.

Атмосферное давление — еще один пример давления из-за веса жидкости, в данном случае из-за веса воздуха над заданной высотой. Атмосферное давление у поверхности Земли меняется незначительно из-за масштабного течения атмосферы, вызванного вращением Земли (это создает погодные «максимумы» и «понижения»). Однако среднее давление на уровне моря дается 95\textbf{N}},[/latex]эквивалентно[latex]\boldsymbol{1\textbf{atm}}.[/latex](см. рис. 3.)

Пример 2. Расчет средней плотности: насколько плотен воздух?

Рассчитайте среднюю плотность атмосферы, учитывая, что она простирается до высоты 120 км. Сравните эту плотность с плотностью воздуха, указанной в таблице 1.

Стратегия

Если мы решим [латекс]\boldsymbol{P=h\rho{g}}[/latex]для плотности, мы увидим, что

[латекс]\boldsymbol{\bar{\rho}\ :=}[/latex][latex]\boldsymbol{\frac{P}{hg}}.[/latex]

Затем мы принимаем [latex]\boldsymbol{P}[/latex] за атмосферное давление,[ латекс]\boldsymbol{h}[/latex]дан, а [латекс]\boldsymbol{g}[/латекс]известен, поэтому мы можем использовать это для вычисления[латекс]\boldsymbol{\bar{\rho} }.[/latex]

Solution

Ввод известных значений в выражение для [latex]\boldsymbol{\bar{\rho}}[/latex] дает 93}[/latex] — примерно в 15 раз больше среднего значения. Поскольку воздух настолько сжимаем, его плотность имеет наибольшее значение у поверхности Земли и быстро уменьшается с высотой.

Пример 3: расчет глубины под поверхностью воды: какая глубина воды создает такое же давление, как и вся атмосфера?

Рассчитайте глубину под поверхностью воды, на которой давление от веса воды равно 1,00 атм.

Стратегия

Начнем с решения уравнения [латекс]\boldsymbol{P=h\rho{g}}[/latex]для глубины[латекс]\boldsymbol{h}:[/latex] 92)}}[/latex][latex]\boldsymbol{=\:10.3\textbf{ м.}}[/latex]

Обсуждение

Всего 10,3 м воды создают такое же давление, как 120 км воздуха . Поскольку вода почти несжимаема, мы можем пренебречь изменением ее плотности на этой глубине.

Как вы думаете, какое общее давление на глубине 10,3 м в бассейне? Влияет ли атмосферное давление на поверхность воды на давление под ней? Ответ положительный. Это кажется вполне логичным, поскольку необходимо поддерживать как вес воды, так и вес атмосферы. Итак, общее давление на глубине 10,3 м составляет 2 атм — половина из воды наверху и половина из воздуха наверху. В главе 11.5 «Принцип Паскаля» мы увидим, что давления жидкости всегда складываются таким образом.

• Давление – это вес жидкости[латекс]\boldsymbol{мг}[/латекс], деленный на площадь[латекс]\boldsymbol{A}[/латекс], поддерживающую ее (площадь дна сосуда):

  [латекс]\boldsymbol{P\:=}[/латекс][латекс]\boldsymbol{\frac{mg}{A}}.[/latex]

• Давление от веса жидкости определяется выражением

  [латекс]\boldsymbol{P=h\rho{g}},[/латекс]

  где[латекс]\жирныйсимвол{Р}[/латекс]это давление,[латекс]\жирныйсимвол{ч}[/латекс]это высота жидкости,[латекс]\жирныйсимвол{\ро}[/латекс] — плотность жидкости, а[latex]\boldsymbol{g}[/latex] — ускорение свободного падения.

давление

вес жидкости, деленный на площадь, поддерживающую его

DoF – упрощенная формула для понимания DoF

Обычный фотограф знает, что глубина резкости зависит от диафрагмы, фокусного расстояния и расстояния до объекта. Но какой из параметров является доминирующим? И насколько сильно влияние каждого параметра? В этой статье используется уравнение глубины резкости и показано, что когда глубина резкости короткая, она изменяется пропорционально диафрагме, а также квадрату фокусного расстояния и расстояния до объекта.

Некоторые люди говорят, что картинка стоит тысячи слов, но для других формула стоит тысячи слов. Понимание упрощенной формулы глубины резкости избавит вас от чтения многих других статей по этой теме.

Начнем с точной формулы глубины резкости, предоставленной Википедией, с первого взгляда ее сложно понять, но мы ее упростим. (Если вам не нравится математика, вы можете сразу перейти к следующему абзацу).

 - А номер диафрагмы
- с - круг нерезкости
- f - фокусное расстояние
- s - расстояние до объекта
- DoF - это глубина резкости:
 

Это станет немного более читабельным, если мы выразим DoF как функцию гиперфокального расстояния «H»:

Но это все еще сложно, поэтому давайте предположим 2 условия, чтобы упростить его:
– s>> f, что верно, если только мы не снимаем макро.
– s<

Итак, вот единственная формула, которую вам нужно знать, когда вы имеете дело с короткой глубиной резкости, но не с макросъемкой:

- A - номер диафрагмы
- с - круг нерезкости
- f - фокусное расстояние
- s - расстояние до объекта
- H - гиперфокальное расстояние
- DoF — это глубина резкости 

В предположении, что s>>f и s>>H, DoF пропорциональна числу апертуры и квадратична с (s/f), что является обратной величиной увеличения объекта. Вот некоторое практическое применение упрощенной формулы в этой ситуации:

• Уменьшение диафрагмы с f/4,0 до f/8,0 удваивает глубину резкости.
• Увеличение с 50 мм до 100 мм без изменения положения уменьшает глубину резкости в 4 раза.
• Двукратное приближение к объекту без изменения фокусного расстояния с уменьшением глубины резкости в 4 раза.
• Двукратное приближение к объекту при уменьшении масштаба со 100 мм до 50 мм обеспечивает ту же глубину резкости и такое же увеличение объекта. (см. статью, посвященную ГРИП и увеличению предмета)

Можно усомниться в точности этой упрощенной формулы. На приведенном ниже графике рядом друг с другом показаны точная и упрощенная формулы с полнокадровым сенсором с диафрагмой f8,0 и фокусным расстоянием 50 мм. В этой ситуации гиперфокальное расстояние равно 11 м. Как и ожидалось, упрощенная формула больше не является точной вблизи гиперфокального расстояния.