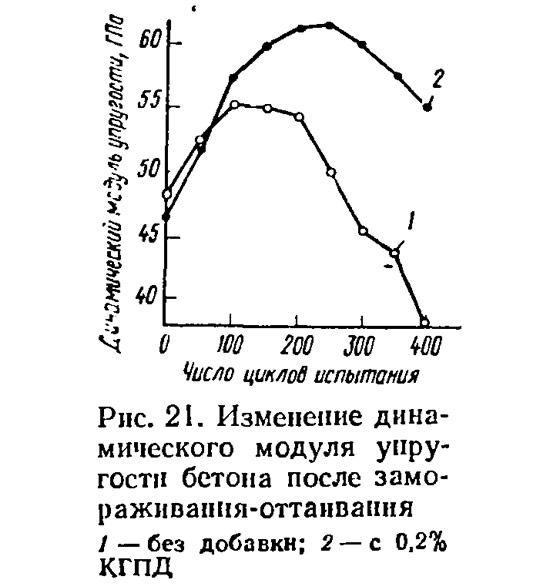
Динамический модуль упругости бетона: Определение динамического и статического модуля упругости бетона — Студопедия

Модуль упругости бетона

Одной из важнейших характеристик бетона является модуль его упругости. Под упругостью понимают способность материала к обратимой деформации после воздействия на него механических сил. Именно такие деформации и называют модулем упругости бетона. В отличие от ряда других материалов, упругость бетона является достаточно сложной функцией. Реакция материала на деформирующие нагрузки или кратковременные напряжения напоминает реакцию пружины. Модуль упругости возрастает пропорционально с увеличением прочности бетона. Так же он зависит и от пористости материла – чем она выше, тем ниже данный показатель. Так, разница модуля упругости у тяжелых бетонов и у ячеистых будет отличаться примерно в 2-2,5 раза. Таким образом, модуль упругости бетона напрямую зависит от его структуры. Следствием данного вывода является тот факт, что значение модуля упругости связано не только с качеством исходных материалов, но и с технологией его производства.

Модуль упругости бетона рассчитывается в двух конфигурациях – как динамический и статический. Динамический модуль упругости определяется в процессе колебания опытного образца и его значение является более высоким, чем у статического. Статический модуль упругости позволяет дополнительно определить и ползучесть бетона, которая характеризует динамику появления деформация при постоянных нагрузках.

При проведении исследований исходят из посылки тождества модулей упругости бетона на растяжение и на сжатие. Однако в тех случаях, когда напряжение превышает 0,2 предела прочности бетона, начинают наблюдаться остаточные деформации. Тогда в местах сцепления заполнителей с цементом начинают образовываться микротрещины, которые с течением времени увеличиваются и приводят к искрашиванию или разрушению цементного камня.

Суть испытания заключается в подвергании образца постоянной непрерывно возрастающей нагрузке до окончательного его разрушения. Для этого применяются нагружающие установки. После этого составляется диаграмма, которая раскрывает зависимость между показателями нагрузки и деформации. По окончании работы со всеми образцами модуль упругости рассчитывается как среднее арифметическое показателей всех образцов, задействованных в ходе эксперимента.

Еще статьи из этой рубрики:

Марки бетона по прочности

Одной из технических характеристик бетона является его прочность, под которой понимают его способность сопротивляться действию деструктивных внешних и внутренних сил. Так как бетон изначально является неоднородным материалом, то …

Класс морозостойкости бетона

Одной из важнейших характеристик бетона является его морозостойкость, под которой понимают способность самого материала, структура которого насыщенна влагой, многократно выдерживать попеременные циклы замораживания и оттаивания без потери свойств и нарушения …

Коэффициент расширения бетона

Определение коэффициента расширения бетона относится к разряду реологических исследований – то есть направления, посвященного деформации и текучести веществ.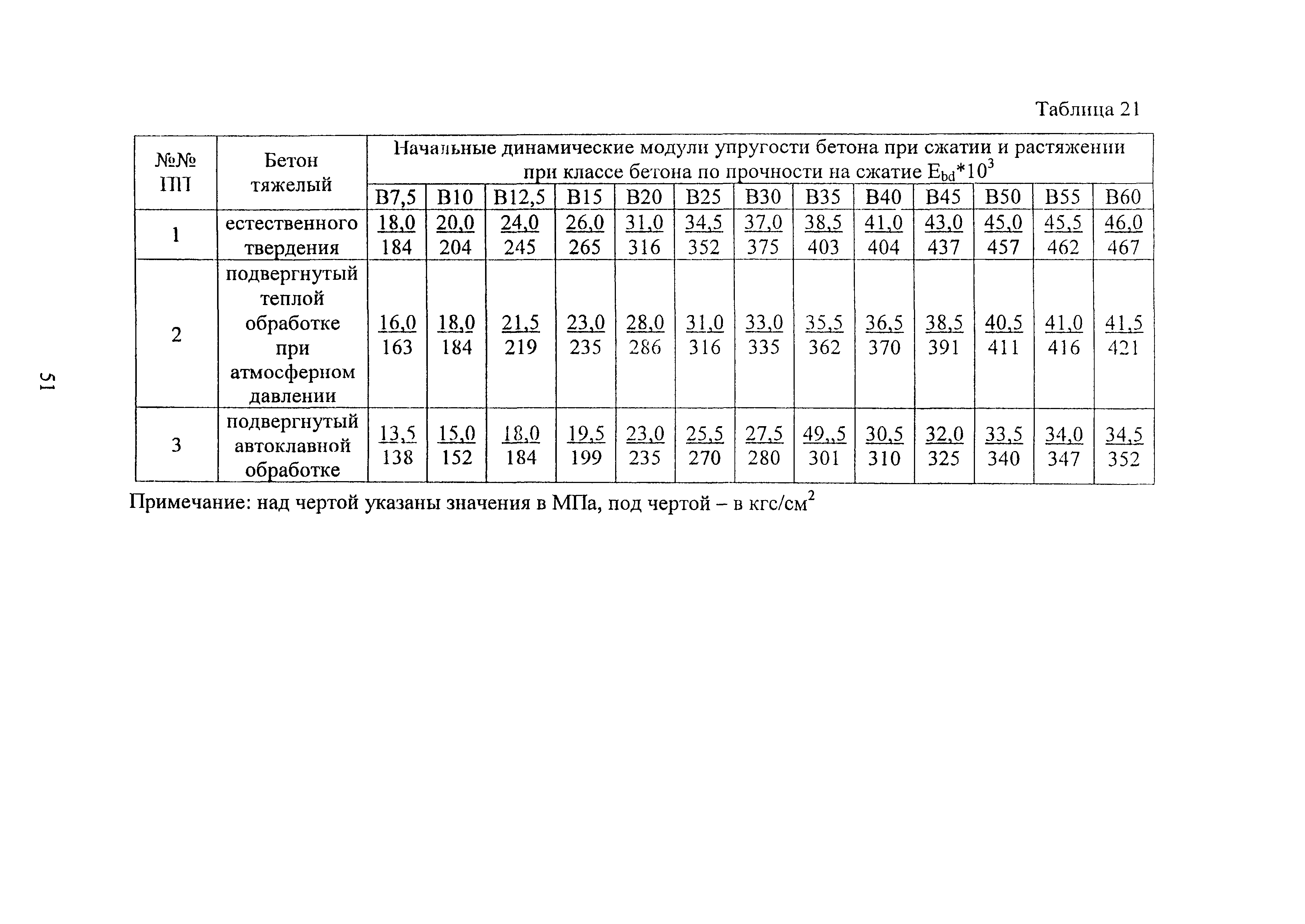 Коэффициент температурного или теплового расширения является величиной, показывающей изменение объема и линейных …

Модуль (коэффициент) упругости бетона: формула для расчета

Определение упругости и единицы измерения

Изделия и конструкции из бетона подвергаются большим нагрузкам, причем этот процесс происходит постоянно. Технологи нашли возможность придать бетону упругость, т. е. способность упруго деформироваться при воздействии давления и силы, направленной на сжатие и расширение. Величина, которая характеризует этот показатель, называется модулем упругости бетона и по определению вычисляется с помощью формулы соотношения напряжения и упругой деформации образца: данные занесены в специальную таблицу.

Нормативные сведения также включают данные о:

• классе материала,
• его видах (тяжелый, мелкозернистый, легкий, пористый бетон и т. д:.),
• технологии производства, в частности способах твердения (естественное, автоклавная или тепловая обработка).

В связи с этим модуль упругости бетона В30 может быть различным и определяться исходя из других характеристик. Если взять в качестве примера тяжелые и ячеистые бетоны одного и того же класса прочности, их модули будут иметь абсолютно разные значения. Таблица утверждена СНиП и составлена на основе результатов опытных исследований.

Таблица начальных модулей упругости E (МПа*10^-3) при сжатии и растяжении бетонов с различными эксплуатационными характеристиками

От чего зависит упругость бетона

1. Состав

Бетон с более высоким модулем упругости подвергается меньшей относительной деформации.

Значительную роль в этом играет качество цементного камня и наполнителя – двух компонентов, из которых и состоит бетон. И раствор, и заполнитель берут на себя всю нагрузку. При анализе зависимости модуля упругости бетона от модуля упругости его составляющих, исследователи выяснили, что прочность заполнителя не всегда задействуется для улучшения характеристик готового материала, а вот показатель упругости оказывает значительное влияние.

2. Класс

Начальный модуль упругости бетона при сжатии и расширении зависит от класса изделия по прочности на сжатие.

Эта зависимость устанавливается путем применения эмпирических формул, поэтому для практических целей проще всего получать информацию из готовой таблицы. Даже без сложных математических расчетов можно заметить, что модуль упругости увеличивается пропорционально прочности материала. Другими словами, чем выше класс, тем больше модуль упругости бетона, т. е. материал класса В25 является более устойчивым к относительным деформациям по сравнению с В20.

Расчет модуля упругости в лабораторных условиях

Когда речь идет о модуле упругости, принимают во внимание оба его варианта – динамический и статический. У первого значение выше и определяется в ходе вибрации образца. Статический модуль, помимо основной информации, предоставляет данные о такой характеристике, как ползучесть бетона – динамика образования деформаций при постоянной нагрузке.

При расчетах учитывают тождество модулей упругости материала как на растяжение, так и на сжатие. Замечено, что если напряжение составляет 0,2 и более максимальной прочности бетона, происходят остаточные деформации. Это приводит к тому, что при сцеплении раствора и наполнителей возникают микротрещины, а это становится причиной крошения и в конечном итоге разрушения.

Во время эксперимента образец подвергают непрерывной нагрузке, имеющей тенденцию к возрастанию, до полного разрушения. Для этого используют особое оборудование – нагружающие установки. В диаграмму вносят данные, показывающие влияние нагрузок на степень деформаций. На завершающем этапе производится расчет среднего модуля упругости всех образцов.

Модуль упругости бетона

Вообще бетон является упруго-пластическим телом.

При приложении нагрузки мгновенно проявляются упругие деформации. При повышенных напряжениях (больше 30% прочности) к ним добавляются развивающиеся в течение некоторого времени пластические деформации.

Кроме обычного (или статического), используется также динамический модуль упругости. Он определяется неразрушающими методами (например резонансным) и применяется при изучении изменений структуры бетона при испытаниях на морозостойкость или коррозионных воздействиях. Динамический модуль упругости примерно на 10% больше статического.

Важное значение для эксплуатационного поведения бетона имеют и его предельные деформации. Они достаточно низки, особенно предельная растяжимость.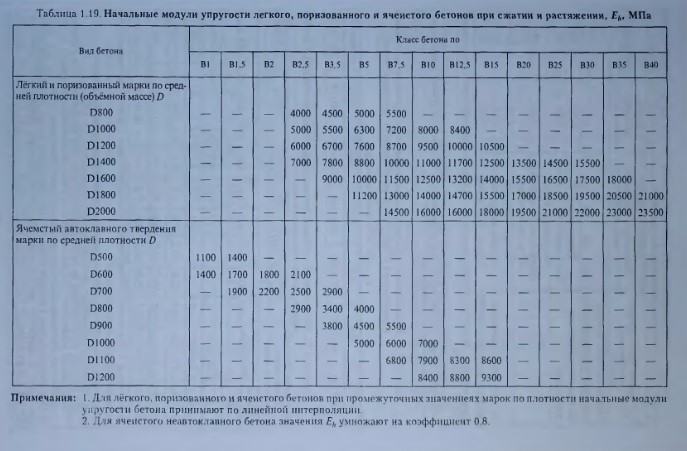 Предельная сжимаемость бетона составляет 0,15—0,3%, предельная растяжимость 0,01— 0,015%. Эти величины позволяют отнести бетон к хрупким материалам (т. е. разрушающимся уже при небольших деформациях).

Ползучесть бетона

Пластические деформации загруженного бетона затухают в течение короткого времени (менее 1 ч.). Но при существенном увеличении длительности наблюдений (до многих дней) можно установить, что они все же продолжаются, хотя с гораздо меньшей интенсивностью. Эти медленно развивающиеся во времени деформации под нагрузкой называются ползучестью. Они также затухают, но для этого уже требуются месяцы, а иногда и годы.

Бетон «ползет» в направлении приложенной нагрузки (сжатые конструкции укорачиваются, растянутые конструкции или их зоны удлиняются). Если упругие деформации под нагрузкой претерпевают оба компонента бетона, как цементный камень, так и заполнители), то причины ползучести, как и усадки, заключены в цементном камне. А еще точнее — в цементном геле: частицы гидросиликатов, окруженные водными оболочками, под нагрузкой смещаются одна относительно другой. Но так как вода находится в сильно адсорбированном («остеклованном») состоянии, эти перемещения протекают крайне медленно. Кроме того, заполнители сдерживают деформации ползучести цементного камня.

Ползучесть оказывает противоречивое влияние на свойства бетона и конструкций. Негативные аспекты: увеличивается прогиб изгибаемых конструкций, снижается напряжение в предварительно напряженной арматуре.

Модуль упругости бетона: таблица, как определить

Выбор стройматериала является важнейшей задачей строителя перед началом выполнения работ. Модуль упругости бетона — один из главных критериев, влияющих на эксплуатационные характеристики. Параметр определяет возможность стеснения и расширения материала, зависит от многих факторов, которые важно учитывать.

Что за величина?

Модуль упругости бетона — это возможность конструкции противостоять изменениям под воздействиями внешних факторов. Это важный критерий выбора марки материала для определенной работы, так как затвердевший материал в процессе эксплуатации сжимается и растягивается. Поэтому на этапе проектирования нужно правильно рассчитать допустимые значения для той или иной конструкции. Для расчетов пользуются таблицами определения модуля упругости, что представлены в нормативах для строительных работ.

Разновидности бетона и их показатель упругости

Бетонный камень в окончательном виде — твердый материал, что под влиянием внешней среды способен деформироваться. При постоянных механических нагрузках, даже модуль упругости железобетона может быть недостаточно высоким. Для определения вида прочности учитывается 2 критерия — растяжение и сжатие, что влияют на сопротивление нагрузкам.

Различают следующие виды материала:

Материал может производиться в нескольких разновидностях.

• тяжелые;
• легкие;
• мелкозернистые;
• поризованные;
• автоклавного твердения.

Таблица, содержащая классы и соответствующие модули упругости

Классификация в таблице производится согласно СП 52—101—2003:

Класс бетона	Модуль упругости
19,0	В10
24,0	В15
27,5	В20
30,0	В25
32,5	В30
34,5	В35
36,0	В40
37,0	В45
38,0	В50
39,0	В55
39,5	В60

От чего зависит величина?

На величину данного показателя значительно влияет наполнитель в материала.

Упругость раствора зависит от множества факторов. Первое, на что обращают внимание — наполнитель. Коэффициент напрямую связан с упругостью раствора. Так, высокими показателями являются тяжелые бетоны, наполнителями в которых являются гравий и щебень. Допустимые нагрузки на постройки из такого материала самые высокие, поэтому важно выбирать правильные заполнители. Учитывают не только интенсивность нагрузок, но и частоту.

Возраст и время укладки материала играют немаловажную роль в показателях модуля упругости. Крепость материала возрастает на протяжении 50 лет с момента заливки, вне зависимости от внешних температур (до 230 ⁰C). Кроме того, характеристики завися от процесса затвердевания (автоклавный, естественный). Чтобы узнать продолжительность предполагаемых нагрузок, нужно начальный показатель перемножать с показателем: 0,7 для поризованных бетонов, 0,85 — для тяжелых легких и мелкозернистых.

Возраст залитого материала находится в прямопропорциональной зависимости с данным показателем.

Классы бетонного раствора в частной стройке варьируют в пределах В7,5—30 (марки М100—400), но таких прочностных и других характеристик хватает вне зависимости от требований и сложностей конструкций. Показатели модуля увеличивает арматура, так как характеристики арматуры повышают показатели общей конструкции. Методика укладки арматуры в бетон определяется ГОСТом 24452—80.

Посмотреть «ГОСТ 24452-80» или cкачать в PDF (0 KB)

Как определить?

СП 52 101 2003 — стандарт определения параметров применения бетона. Здесь указаны значения всех необходимых коэффициентов для расчета параметров, а подтверждение проводится путем эксперимента на изготовленных образцах. Суть испытания заключается в постепенной нагрузке на образцы (цилиндры или призмы из бетонной смеси) путем осевого сжимающего нагружения до разрушения. Параллельно измеряется степень деформации.

Посмотреть «СП 52-101-2003» или cкачать в PDF (0 KB)

Результаты можно обозначить следующим образом:

• Показатель соответствует расчетам, образец поддался пластической деформации без растрескивания.
• Предварительные подсчеты неверные: при предполагаемом нагружении образец подвергается сильным разрушениям.

Расчетным способом определяют запас прочности не только обычных зданий, но и арочных сооружений, перекрытий, мостов и дорог. Модуль упругости асфальтобетона при использовании — проблемная задача проектирования, так как подход, разрешающий провести точные расчеты еще не выведен. Не удается определить взаимосвязь между статическим и динамическим модулями в процессе использования дорог.

Модуль поверхности бетона (бетонной конструкции)

Один из параметров, который оказывает существенное влияние на результат постройки — это модуль поверхности бетонной конструкции. Если рассчитать эту величину и учесть при возведении сооружения, то результат проявится в виде крепости и долговечности конструкции.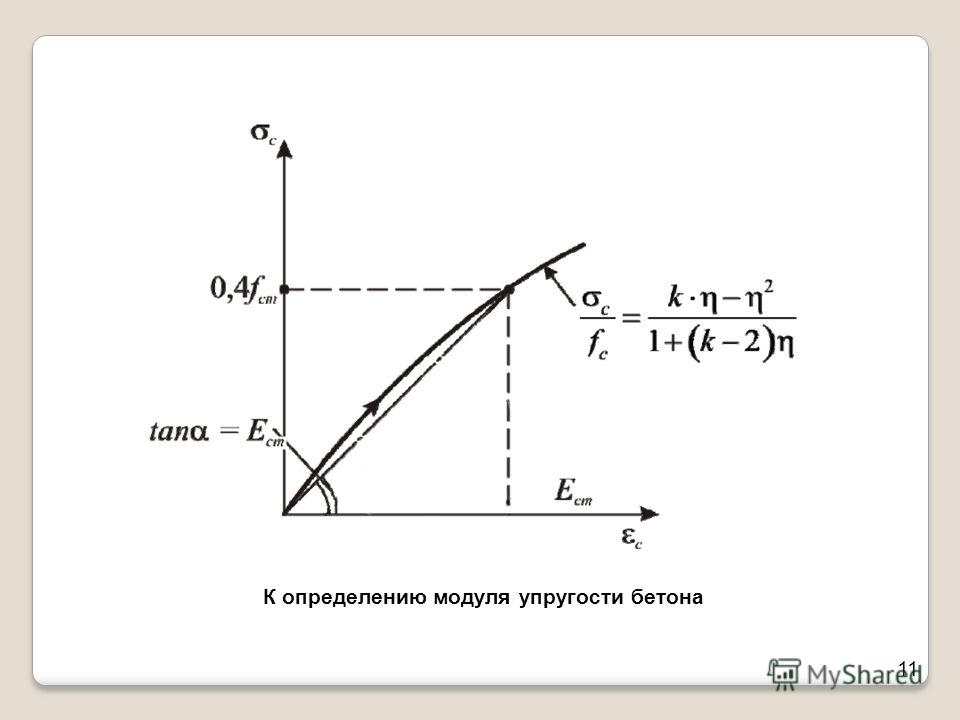

Что это такое

Основной сезон ведения строительных работ — лето. В этот период погодные условия в максимальной степени располагают к заготовке растворов, установке опор, и т.д. Но поставленной цели не всегда удается добиться в срок, поэтому процесс возведения сооружений может затянуться до поздней осени или даже зимы.

Из-за снижения температуры воздуха процессы работы с цементным раствором усложняются. Необходимо рассчитать время, за которое жидкость в смеси начнет замерзать, и создать условия, чтобы бетон оформился и приобрел крепость быстрее, чем вода в нем замерзнет. С этой целью была введена рассматриваемая величина.

Модуль поверхности бетона — это величина, выраженная через частное площади поверхности конструкции, имеющей контакт с воздухом, и объема смеси.

Определение

Площадь и объем смеси вычисляются с применением формул сферы:

1. S = AB.
2. S общ. = S1+S2+S3+S4+S5+S6.
3. V = ABH.

Здесь приведены формулы для вычисления величин прямоугольного параллелепипеда, т.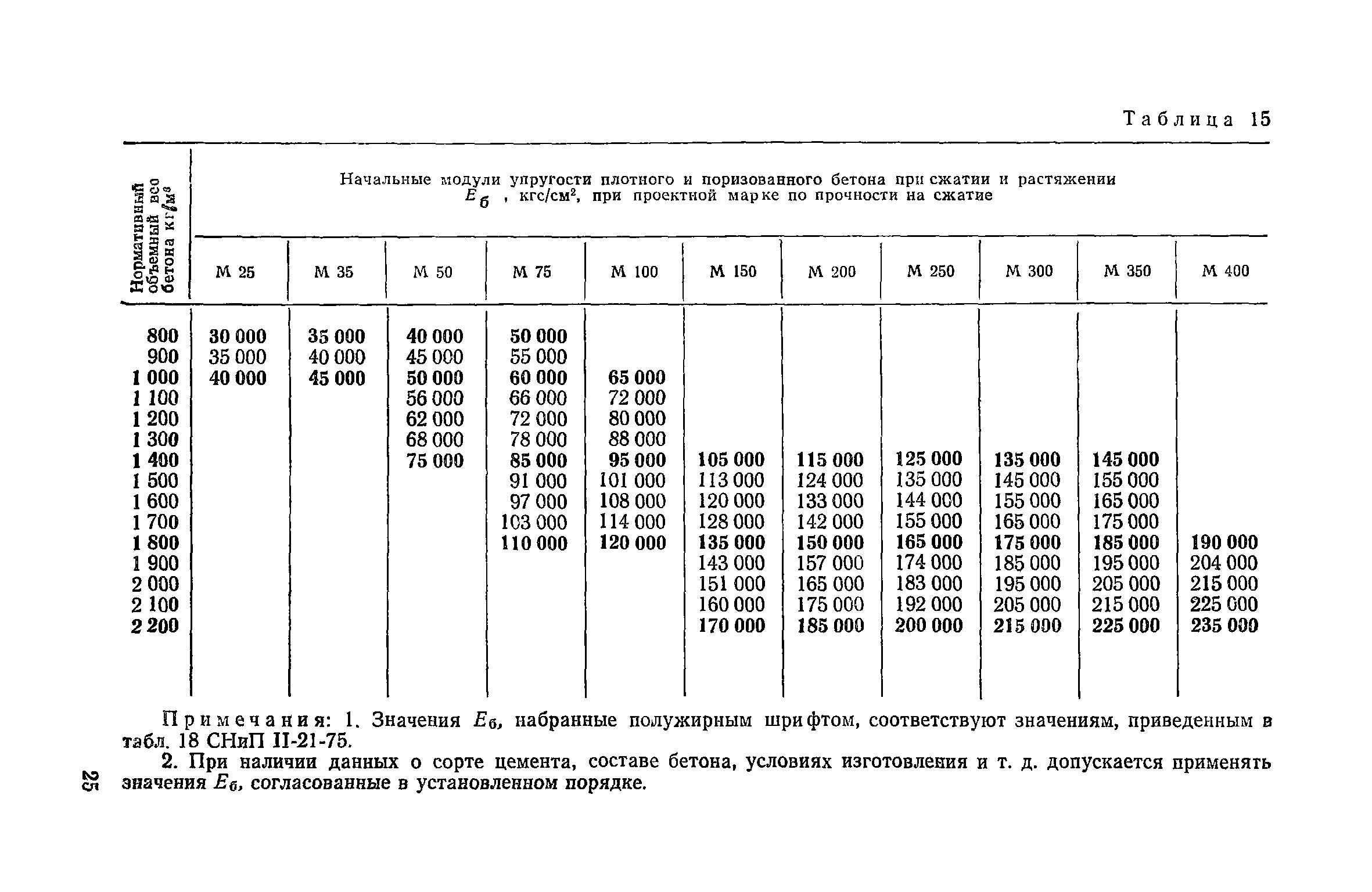 к. в большинстве случаев раствор закладывают в такую форму. Идеальный вариант с точки зрения времени остывания — сфера, но ее использование не оправдано другими обстоятельствами.

Единицы измерения, полученные в результате вычислений, представляют собой м-1 или 1/м. Происходит это по той причине, что площадь измеряется в м², а объем — в м³. Путем деления первого на второе получается, что единица измерения модуля поверхности бетона = м2/м3 = м2-3 = м-1 = 1/м.

В условиях реальности невозможно представить метр, выраженный в минус первой степени. Это значение изменяется в последующих вычислениях в более понятные единицы измерения согласно законами физики. Практического применения величина не имеет, но при ведении записей отчетов принято записывать все вычисления в полной форме.

Примеры расчета

Для лучшего понимания того, как работает формула модуля поверхности бетона, необходимо увидеть ее в действии. В качестве примера можно взять плитный фундамент с длиной 12 м, шириной 8 м и толщиной 20 см.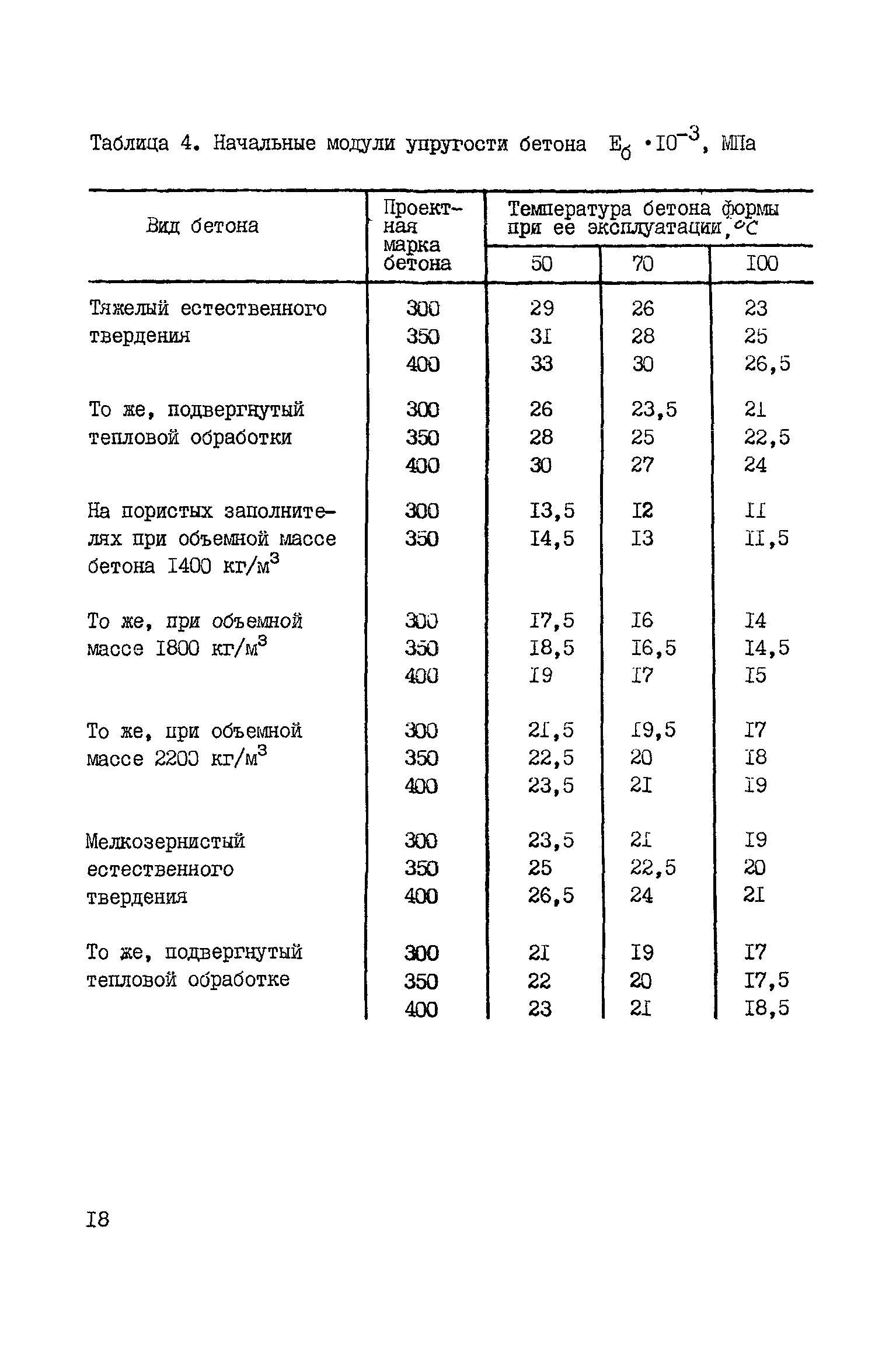 Единицы измерения лучше сразу подогнать под один стандарт, превратив 20 см в 0,2 м.

Охлаждению подвержены в данной ситуации все поверхности фундамента кроме нижней, т.к. она соприкасается с основанием, обладающим достаточно высокой температурой для того, чтобы не брать эту сторону в расчет.

Вычисления бетонных элементов:

1. Вычислить площадь каждой из сторон:
   • 8х0,2х2 = 3,2;
   • 12х0,2х2 = 4,8;
   • 12х8 = 96;
2. Найти сумму площадей: 96+3,2+4,8 = 104.
3. Вычислить объем поверхности: 8х12х0,2 = 19,2.
4. Вычислить значение модуля: 104/19,2 = 5,41(6).

Если речь идет о сложных элементах конструкции, то для вычисления значений их модулей существуют упрощенные формулы.

Некоторые из них представлены ниже:

1. Прямоугольные блоки и колонны = 2/A + 2/B.
2. Квадратные балки = 4/A.
3. Куб = 6/A.
4. Цилиндр = 2/R+2/H.

Что с этим делать

После того как необходимая величина вычислена, нужно правильно ее применить. От верного использования зависит, получится ли в результате строительства крепкое надежное здание.

Скорость нагрева и охлаждения

Чем меньше полученная величина, тем большим количеством трещин будет покрыт бетон, если вовремя не принять меры, которые заключаются в поддержании температуры на едином уровне и постепенном охлаждении.

Допустимая скорость охлаждения в зависимости от величины модуля:

• меньше 4 м-1 — до 5°C в час;
• от 5 до 10 м-1 — до 10°C в час;
• более 10 м-1 — до 15°C в час включительно.

Для реализации условий постепенного снижения температуры достаточно использовать тепловые пушки или греющие кабели, которые оснащены функцией постепенного снижения силы нагрева. Пушка подойдет для любых значений модуля.

Выбор способа поддержания температуры

Существует несколько способов обеспечения постепенного охлаждения без использования электрических приборов. Уровень их эффективности зависит от значения модуля поверхности.

Если значение модуля не поднялось выше 6, то в качестве меры хватит простой плотной теплоизоляции. Достаточное количество тепла будет выделяться изнутри, во время застывания смеси. Такое значение позволит сэкономить на электричестве и общем времени работы.

Если модуль равен 6 или превышает это значение, то помогут справиться с недостатком теплоты несколько вариантов событий:

1. Разогревать раствор непосредственно перед укладкой в форму. Если смесь будет обладать высокой температурой, то получившийся бетон будет гораздо крепче, чем при стандартных условиях. Структура успеет устояться прежде, чем все остынет.
2. Вводить в раствор помимо основных компонентов специальные катализаторы, которые ускоряют процесс затвердевания бетона. Использование дополнительных средств повысит крепость конструкции и количество тепла, выделяемого внутренними процессами.
3. Другой вариант добавок, связанный со снижением уровня кристаллизации жидкости в застывающем растворе. Уровень теплоты не повышается, но бетон будет продолжать набирать крепость при температуре ниже 0°C.

Распалубка

Процесс снятия поддерживающих конструкций после приобретения бетоном начального уровня крепости в условиях низкой температуры отличается от стандартного. При снятии опалубки и теплоизоляции те поверхности, что были под прикрытием, сталкиваются с холодным воздухом, что может сказаться в дальнейшем на уровне их крепости.

Значение в данном случае имеет не только величина модуля, но и коэффициент армирования. Это значение определяет количество арматуры относительно массы бетона. Для определения достаточно сложить сечение каждого прута и разделить сумму на площадь верхней части бетонной плиты. Значение выражается в виде процентов.

Допустимы следующие перепады температур в разных условиях:

1. Если модуль не превышает значения 5 м-1, коэффициент армирования меньше 1%, то снимать опалубку стоит лишь при разнице в температуре бетона и воздуха менее 20°C.
2. При модуле меньше 5 м-1, но коэффициенте 1-3% допустимая разница повышается на 10°C.
3. Если арматуры много, коэффициент выше 3%, то ощутимых повреждений не будет, при снятии опалубки с разницей температур воздуха и раствора в 40°C.
4. При модуле поверхности выше 5 м-1 используются те же значения, но на 10°C выше:
   • меньше 1% — 30°C;
   • от 1% до 3% — 40°C;
   • больше 3% — 50°C.

Обработка зимнего бетона

Работа с бетонной поверхностью, не достигшей полной крепости, в зимнее время имеет отличия от обработки летом или весной. Использование перфораторов и отбойных молотков в данной ситуации недопустимо, т.к. локальные воздействия вызовут трещины и нарушение структуры формирующегося бетона.

Создавать арки, выемки и подобные изменения формы следует заранее при помощи опалубки и дополнительных приспособлений. Тонкая обработка, создание мелких отверстий становится возможным при помощи алмазного бура, который не обеспечивает ударные действия.

Если есть необходимость в создании круглого отверстия, то в опалубку достаточно поместить пластиковую трубку, диаметр которой совпадает со значениями желаемой дыры.

Смежное понятие

Помимо уже введенных ранее понятий существует еще одна существенная величина, которая перекликается с модулем бетона, — модуль упругости (деформации). Установить значение можно путем проведения экспериментов с точными измерительными приборами.

Модуль может оказать влияние на крупные здания (с большим количеством этажей и малой площадью основания) и скорее играет ознакомительную роль, чем практическую. Величина упругости показывает, насколько сильно деформируется опора при воздействии на все здание механизмов или сильного ветра.

Заключение

При работе с бетоном в неподходящих условиях вводятся дополнительные величины, призванные учесть особенности новых факторов, оказывающих влияние на результат работы. Модуль поверхности бетона — одна из таких величин.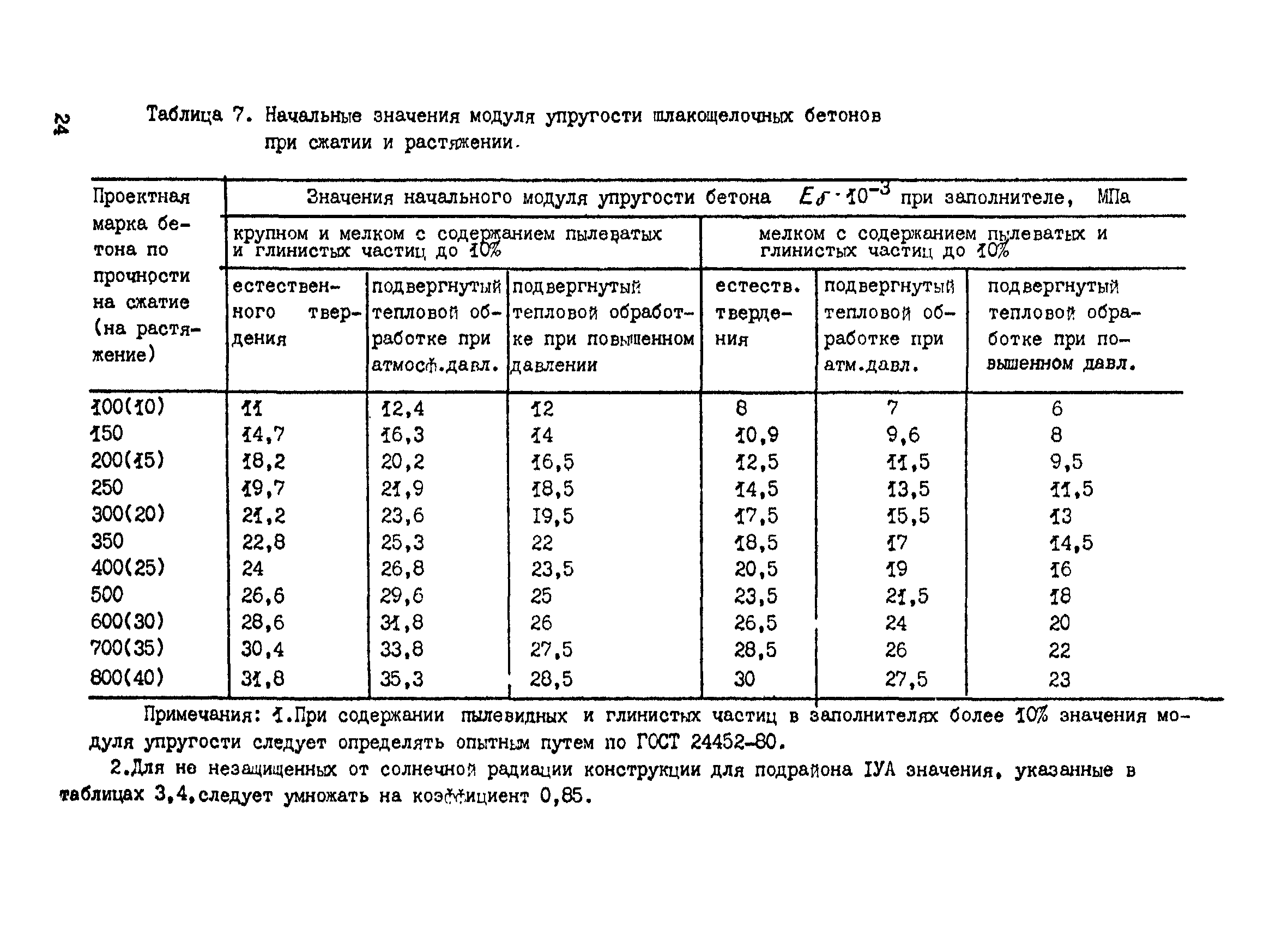

Модуль упругости |

Модуль упругости

Строго говоря, термин «модуль упругости» (модуль Юнга) относится непосредственно только к прямолинейному участку диаграммы напряжение— деформация или, в случае отсутствия такого участка, к касательной к кривой, проходящей через начало координат. Этот начальный модуль имеет небольшое практическое значение. Можно определять модуль упругости по касательным, проходящим через любую точку графика напряжение — деформация, однако этот модуль применим только при очень малых отклонениях нагрузки выше или ниже того уровня, при котором этот модуль определяется.

Величина наблюдаемых деформаций и ход кривой напряжение—деформация зависят, по крайней мере частично, от скорости приложения нагрузки. Когда нагрузка прилагается чрезвычайно быстро, например менее чем за 0,01 сек, деформации резко снижаются и кривизна зависимости напряжение—деформация становится чрезвычайно малой. Увеличение времени нагружения с 5 сек до 2 мин может изменить деформацию на 15%, но в пределах интервала от 2 до 10 мин (и даже до 20), т. е. за время, обычно применяемое при испытаниях образцов на стандартном испытательном оборудовании, увеличение деформаций ничтожно мало.

Увеличение деформации под нагрузкой или часть такого увеличения обусловлено ползучестью бетона, однако разделение упругой и пластической части деформации затруднительно из-за зависимости мгновенной деформации от скорости загружения. Для практических целей разделение деформаций производят следующим образом: деформация за время нагружения считается упругой, дальнейшее увеличение деформации протекает за счет ползучести бетона. Модуль упругости, удовлетворяющий этому условию, показан на рис. 6.1 как модуль деформации. Стандартных методов определения модуля деформации в настоящее время нет; в некоторых лабораториях он определяется при уровнях напряжений в интервалах от 28 до 140 кгс/см2, в других— при напряжениях, достигающих 15, 25, 33 или 50% разрушающей нагрузки. Поскольку модуль деформации уменьшается с увеличением напряжения, то напряжение, при котором он определяется, всегда должно быть установлено.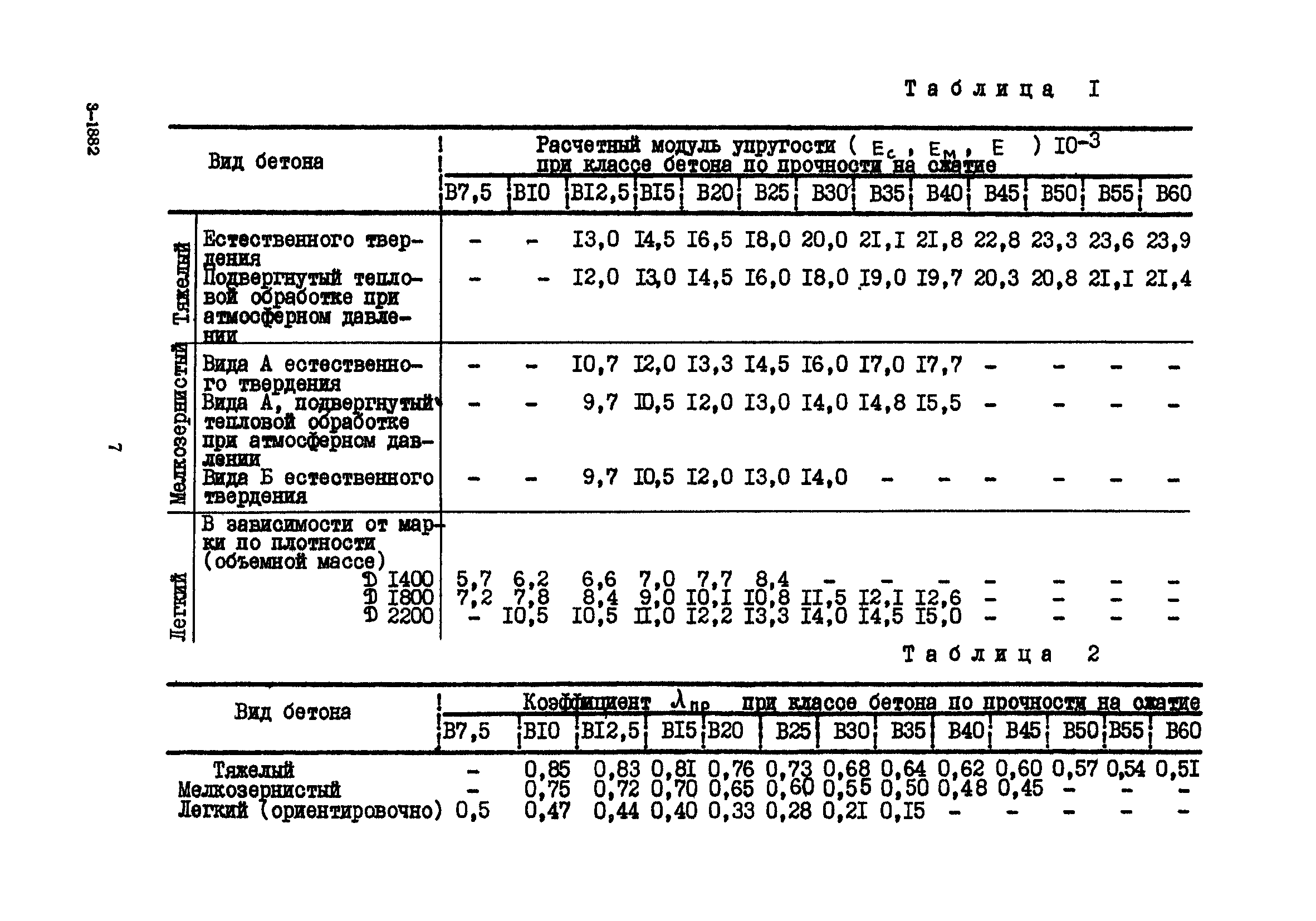 Этот модуль является статическим модулем упругости, так как определяется он из отношения напряжения к деформации, которое в противоположность динамическому модулю устанавливается на уровне 280 кгс/см2.

Определение начального модуля упругости связано со значительными трудностями, однако его приблизительная величина может быть определена косвенным путем: секущая к кривой напряжение—деформация на ветви разгрузки часто, хотя и не во всех случаях, параллельна касательной, проходящей через начало координат (рис. 6.1). Повторная нагрузка и разгрузка уменьшает ползучесть, поэтому диаграмма напряжение—деформация, полученная после трех или четырех нагружений, характеризуется весьма малой кривизной.

Влияние ползучести на величину общей деформации значительно уменьшается при измерениях деформаций в малом диапазоне изменения напряжений, однако в этом случае точный замер деформации представляет большие трудности.

На рис. 6.2 представлен график деформаций бетона различной прочности в зависимости от отношения действующих напряжений к прочности бетона. Под нагрузкой, составляющей половину конечной прочности, более высокой величиной деформации характеризуется бетон большей прочности. При этом для любых двух бетонов отношение их деформаций значительно меньше, чем отношение их прочностей, т. е. бетон большей прочности характеризуется большей величиной модуля упругости (табл. 6.1).

Модуль упругости бетона увеличивается пропорционально корню квадратному из его прочности. Эта зависимость справедлива только для основной части графика и зависит от условий испытания образцов: водонасы-щенные образцы характеризуются более высоким модулем упругости, чем сухие (рис. 6.3), в то время как прочности их находятся на одном уровне. Свойства заполнителя также влияют на модуль упругости бетона; с увеличением модуля упругости крупного заполнителя увеличивается модуль упругости бетона. Форма поверхности крупного заполнителя и характеристика его поверхности могут также влиять на величину модуля упругости бетона и на вид графической зависимости напряжение — деформация (рис.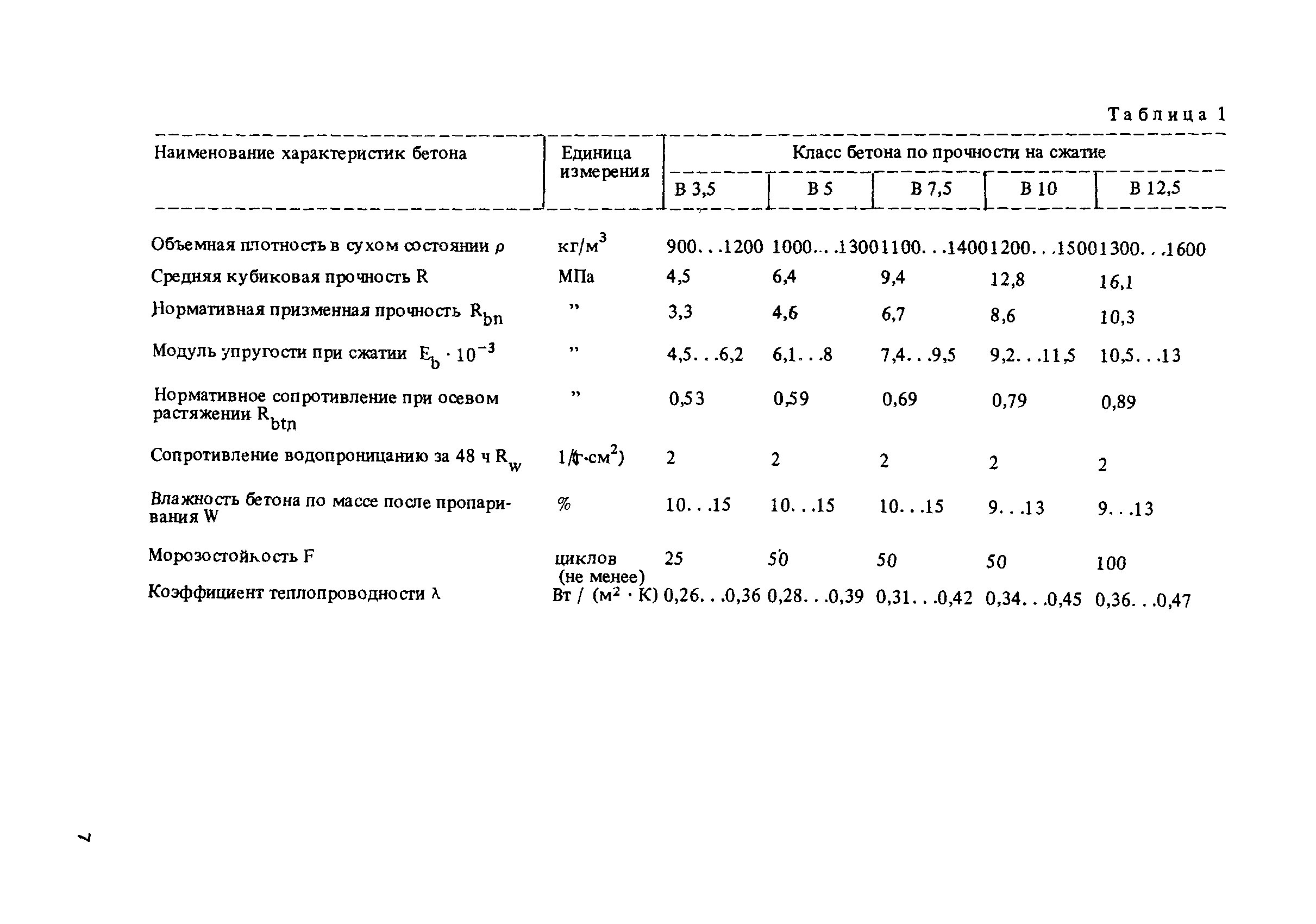 6.4).

Ниже приведен модуль упругости бетона различной прочности, определенный в соответствии с руководством СР 2007—1960 по проектированию предварительно напряженного бетона.

Соотношение между модулем упругости и прочностью бетона зависит также от количественного соотношения компонентов в смеси (модуль упругости заполнителей обычно выше, чем модуль упругости цементного камня) и от возраста образцов: с увеличением возраста бетона модуль упругости его растет быстрее, чем прочность.

Эту зависимость можно четко проследить на рис. 6.5, где также приводятся результаты испытаний бетона на керамзите. Модуль упругости бетона на легком заполнителе обычно составляет от 40 до 80% модуля упругости тяжелого бетона той же прочности, при этом модуль упругости легкого бетона не зависит от модуля упругости цементного камня и соотношения компонентов в составе бетона.

Соотношение между модулем упругости и прочностью бетона остается неизменным при действии повышенных (до 230° С) температур, поскольку в этом температурном интервале и модуль упругости и прочность бетона изменяется с повышением температуры по одному закону.

Выше были рассмотрены вопросы, связанные с модулем упругости при сжатии, однако для ряда бетонов модуль упругости при растяжении имеет те же значения, что и модуль упругости при сжатии. Модуль упругости при растяжении может быть определен по результатам испытаний образцов на изгиб, при этом, в случае необходимости, производится корректировка результатов на влияние среза.

При испытаниях на изгиб на графической зависимости напряжение— деформация имеется нисходящая ветвь кривой при нагрузках, близких к разрушающим, т. е. имеет место уменьшение напряжений, сопровождающееся увеличением деформаций бетона (рис. 6.6). Такое же явление наблюдается и при испытаниях на сжатие при условии, что образец загружается при постоянной величине деформации.

Модуль упругости при срезе прямыми экспериментами не определяется.

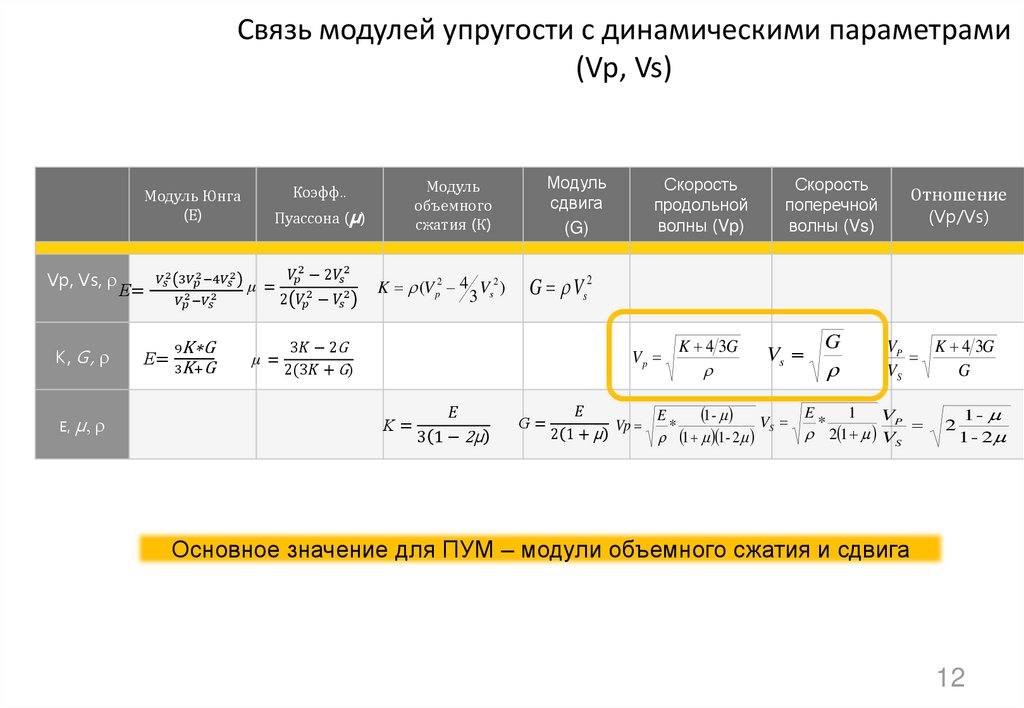
Оценка динамического модуля упругости бетона с использованием измерений скорости поперечной волны

Цели данного исследования — изучить взаимосвязь между статическими и динамическими модулями упругости, определенными с помощью измерений скорости поперечной волны, и продемонстрировать практический потенциал поперечной волны. скоростной метод для оценки динамического модуля на месте. Были изготовлены 300 бетонных цилиндров размером 150 на 300 мм из трех различных смесей с целевой прочностью на сжатие 30, 35 и 40 МПа.Статические и динамические испытания проводились через 4, 7, 14 и 28 дней для оценки прочности на сжатие, а также статических и динамических модулей цилиндров. Результаты, полученные из измерений скорости поперечной волны, сравнивали с динамическими модулями, полученными с помощью стандартных методов испытаний (измерения скорости продольной волны в соответствии с ASTM C597 / C597M-16 и фундаментальные испытания на продольный и поперечный резонанс в соответствии с ASTM C215-14). Скорость поперечной волны, измеренная с помощью цилиндров, показала отличную повторяемость с коэффициентом вариации (COV) менее 1%, что не хуже, чем у стандартных методов испытаний.Установлена ​​взаимосвязь между динамическим модулем упругости на основе скорости поперечной волны и хордовым модулем упругости в соответствии с ASTM C469 / C469M.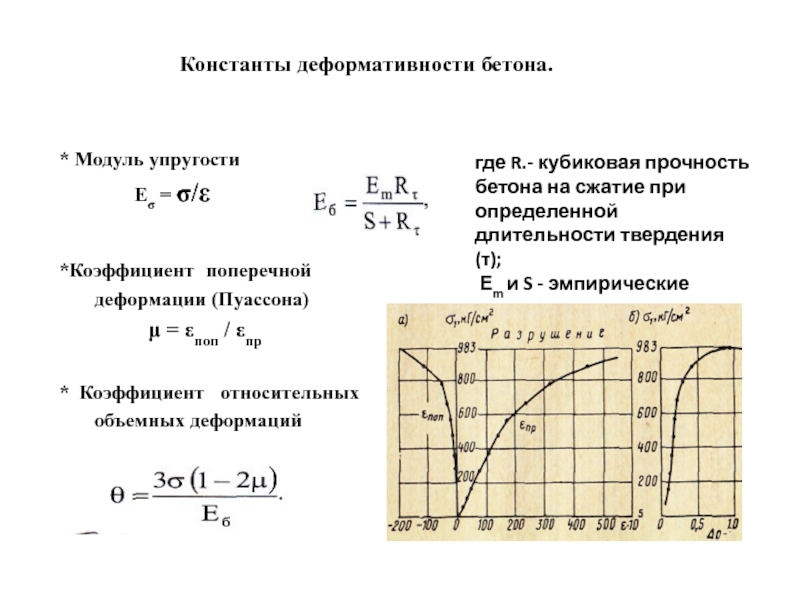 Кроме того, было продемонстрировано, что наиболее подходящая линия для скорости поперечной волны эффективна для оценки прочности на сжатие с использованием эмпирической зависимости между прочностью на сжатие и статическим модулем упругости.

1. Введение

При проектировании конструкций модуль упругости бетона () является основным параметром при оценке деформации элемента конструкции в условиях эксплуатации.На практике она оценивается по прочности на сжатие на основе правил проектирования, а не на основании прямых измерений. Эта практика может недооценивать и требовать более высокой прочности на сжатие для достижения желаемого, чем фактически требуется при проектировании конструкций [1]. Кроме того, было продемонстрировано, что это эффективный параметр для оценки состояния бетона в существующих конструкциях [2, 3]. Разрушающие испытания, такие как извлечение керна, широко используются для получения точной информации об упругих свойствах бетона.Однако они трудозатратны и требуют много времени и не могут применяться повсеместно по всей площади конструкции.

Существует несколько методов неразрушающей оценки (NDE) для оценки упругих свойств бетона, включая измерения скорости ультразвуковых импульсов в соответствии с ASTM C597 / C597M-16 [4] и испытания на резонансной частоте в соответствии с ASTM C215-14 [5]. Модуль упругости, определяемый методами неразрушающего контроля, обычно называется динамическим модулем упругости, который обычно превышает статический модуль упругости, измеренный в соответствии с ASTM C469 / C469M-14 [6].Предполагается, что динамический модуль является начальным касательным модулем при нулевом напряжении, определенным в стандартном испытании, потому что во время измерений скорости ультразвуковых импульсов (UPV) и испытаний резонансной частоты прикладывается лишь незначительное напряжение [7]. Филлео [8] также объяснил, что разница между динамическими и статическими модулями основана на том факте, что неоднородные характеристики бетона по-разному влияют на эти два модуля. Более того, разница между двумя модулями уменьшается по мере увеличения прочности бетона: динамический модуль упругости обычно на 20, 30 и 40% выше, чем статический модуль упругости для бетона высокой, средней и низкой прочности соответственно [2] . Лидон и Балендран [9] предложили эмпирическую взаимосвязь следующим образом: Британский стандарт испытаний BS8100, часть 2 [10] предоставляет другое эмпирическое уравнение следующим образом: Примечательно, что это уравнение не применяется к бетону, содержащему более 500 кг цемента на кубический метр. метр бетона или до бетона из легких заполнителей [7]. Более общее соотношение было предложено Поповиксом [11] как для легкого бетона, так и для бетона нормальной плотности, учитывающее влияние плотности бетона следующим образом: где — плотность затвердевшего бетона в единицах кг / м ³ .

Два стандартных метода неразрушающего контроля для оценки динамического модуля упругости имеют преимущества и ограничения. Метод скорости продольных волн удобен в использовании и имеет явные преимущества перед резонансным методом, так как испытания не ограничиваются лабораторными образцами правильной формы, а результаты нечувствительны к неупругому эффекту [8]. P-волны перемещают частицы параллельно направлению распространения и могут распространяться через среду с достаточной поперечной жесткостью: таким образом, они могут распространяться в твердой, жидкой и газовой средах.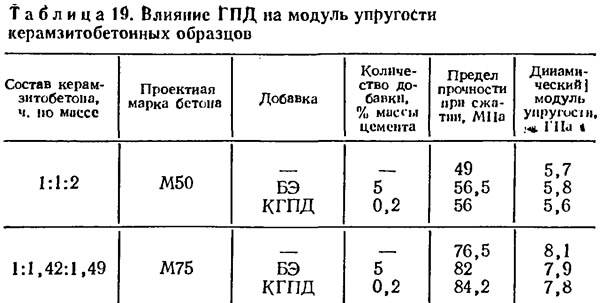 Следовательно, на скорость продольных волн в пористых материалах влияют свойства трех разностных фаз в среде. Известно, что динамический модуль упругости, определяемый измерениями скорости продольной волны, обладает характеристиками бетона, неоднородного и пористого материала, такими как тип заполнителя, содержание воды, воздушные пустоты и пористость по сравнению со статическим модулем упругости. Кроме того, значения скорости продольных волн зависят от условий удержания в твердых средах: скорости продольных волн в неограниченных твердых средах (), тонких пластинах () и тонких стержнях () называются скоростями стесненных, частично стесненных и неограниченных сжимающих волн. , соответственно, и выражаются в виде следующих уравнений [12]: На рис. 1 показаны вариации продольных волн с коэффициентом Пуассона для упругих однородных и изотропных сред.Учитывая коэффициент Пуассона, скорость продольной волны находится в диапазоне между неограниченной и ограниченной скоростями [13]. Скорость продольной волны увеличивается с увеличением степени удержания, а эффект удержания увеличивается с увеличением коэффициента Пуассона. Однако в полевой практике иногда бывает непросто оценить точные динамические модули упругости по измерениям скорости продольной волны из-за трудностей в оценке эффекта удержания в полевых условиях и отсутствия теоретической или практической формулы, связывающей скорость продольной волны и динамику. модуль упругости, учитывающий эффект удержания.В этом смысле некоторые из предыдущих исследователей утверждают, что метод скорости продольной волны ненадежен и не рекомендуется для оценки динамического модуля упругости бетона [1, 7, 14]. Напротив, испытание на резонансной частоте широко используется для оценки динамического модуля упругости бетона, который менее чувствителен, чем скорость продольной волны. Однако для испытания на резонансной частоте обязательно нужны бетонные образцы правильной формы; Таким образом, применение этого метода на месте является трудоемким и требует много времени и не подходит для общего применения по всей площади конструкции.

Существуют некоторые теоретические и экспериментальные данные, демонстрирующие, что измерение поперечной волны потенциально может быть эффективным методом неразрушающего контроля на месте для оценки твердости различных вяжущих материалов (например, цементного теста, строительного раствора и бетона). Теоретически поперечные волны перемещают частицы перпендикулярно направлению распространения и, таким образом, могут распространяться через твердые среды с достаточной жесткостью на сдвиг. Следовательно, распространение S-волн менее чувствительно к жидкостям или газам в пористых материалах.Предыдущие исследователи продемонстрировали экспериментами в лаборатории, что поперечные волны менее чувствительны к содержанию воды и / или воздуха и являются эффективным параметром для оценки увеличения жесткости (или прочности) цементных материалов раннего возраста. Voigt et al. [15] показали, что отражение S-волны тесно связано со степенью связи между частицами независимо от содержания воды в цементном тесте. Zhu et al. [16] экспериментально продемонстрировали, что на скорость поперечных волн не влияет содержание воздуха в диапазоне 0.От 2% до 5,2% в цементном тесте, в то время как скорость продольной волны слишком чувствительна к содержанию воздуха. Лю и др. [17] успешно контролировали процессы схватывания и твердения раствора и бетона с помощью ультразвуковой скорости поперечной волны в лаборатории и подтвердили, что скорость поперечной волны хорошо коррелирует с сопротивлением проникновению в строительный раствор независимо от испытательной установки и водоцементного отношения.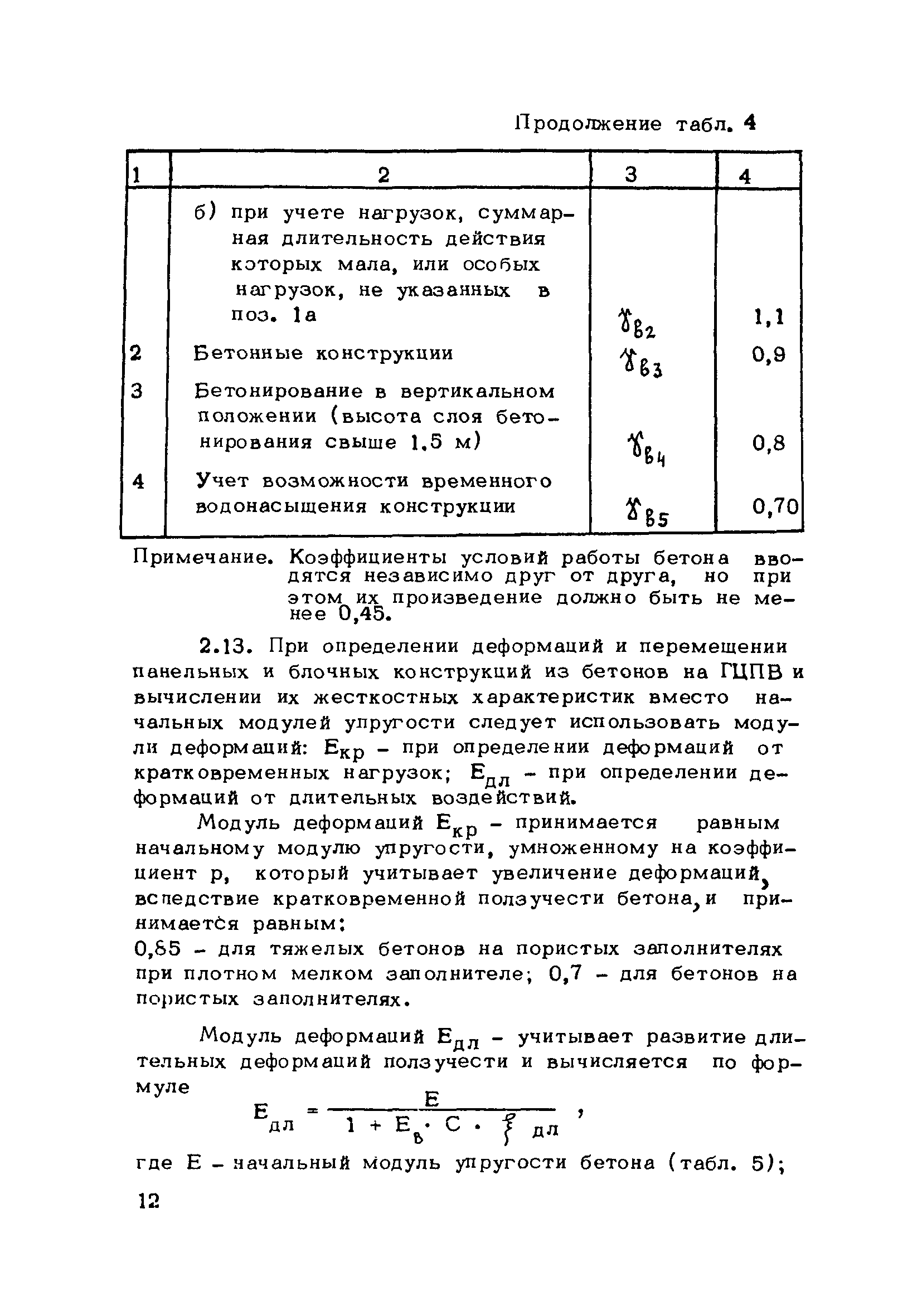 Каретт и Стаке [18] заметили, что скорость поперечной волны более чувствительна к процессу схватывания материалов на основе цемента, чем скорость продольной волны.Кроме того, в отличие от продольных волн, поперечные волны теоретически нечувствительны к условиям удержания в бетоне [12]. В однородной и изотропной среде скорость поперечной волны выражается следующим уравнением без учета условий удержания [12]: Кроме того, некоторые исследователи отметили, что скорость поперечной волны является более стабильным параметром для оценки прочности на сжатие затвердевшего материала. конкретнее, чем в скорости продольной волны. An et al. [19]. наблюдал, что скорость S-волны тесно коррелирует с прочностью на сжатие безотносительно типов заполнителя, возраста и условий отверждения.Чианцио и Хелински [20] продемонстрировали, что измерение скорости поперечной волны эффективно при оценке прочности на сжатие торкретбетона, армированного волокном, в полевых испытаниях из-за его пониженной чувствительности к присутствию поровой воды. Кроме того, Lencis et al. [21] заметил, что скорость поперечной волны менее чувствительна к арматурной стали в бетоне, чем скорость продольной волны. В ходе исследования было продемонстрировано, что влияние арматурных сталей несущественно для измерений скорости поперечной волны в методе непрямого распространения, когда бетонное покрытие составляет не менее 40 мм, что справедливо для большинства бетонных конструкций в полевой практике.Самокрутов и др. [22] продемонстрировали, что использование S-волн по сравнению с P-волнами снижает количество обратного рассеяния и ослабление сигнала в направлении, параллельном распространяющейся волне в затвердевшем бетоне. Недавно Ли и О [23] измерили скорости поперечных волн с помощью оборудования MIRA, которое генерирует томографию поперечных волн [24], и продемонстрировали эффективность измерений поперечных волн для оценки состояния железобетонных и предварительно напряженных бетонных плит. В исследовании было продемонстрировано, что скорость S-волны статистически более стабильна, чем скорость P-волны, из-за меньшего затухания энергии и меньшей чувствительности к эффектам ограничения.Таким образом, метод определения скорости поперечной волны имеет потенциал в качестве метода неразрушающего контроля на месте для оценки модуля упругости и прочности бетона на сжатие. Однако сделать общий вывод по-прежнему сложно из-за недостатка экспериментальных исследований по оценке динамического модуля упругости с измерением скорости поперечной волны.

Цели этого исследования — изучить взаимосвязь между статическими и динамическими модулями упругости, определенными с помощью измерений скорости поперечной волны, и продемонстрировать практический потенциал метода скорости поперечной волны для оценки динамического модуля упругости на месте.В этом исследовании было приготовлено триста бетонных цилиндров размером 150 на 300 мм из трех различных смесей с заданной прочностью на сжатие 30, 35 и 40 МПа. Статические и динамические испытания проводились через 4, 7, 14 и 28 дней для оценки прочности на сжатие, а также статических и динамических модулей цилиндров. Результаты, полученные при измерениях скорости поперечной волны, сравнивали с динамическими модулями, полученными с помощью стандартных методов испытаний (измерения скорости продольной волны в ASTM C597 / C597M-16 и фундаментальные тесты продольного и поперечного резонанса в ASTM C215-14).

2. Экспериментальная программа

2.1. Материалы и подготовка образцов

Бетон в этом исследовании состоит из портландцемента типа I, речного песка, гранитного щебня с максимальным размером 25 мм и дополнительных вяжущих материалов (летучая зола и шлаковый цемент). Были использованы три различных отношения воды к связующему (W / B): 0,3, 0,35 и 0,45, что привело к целевым значениям прочности на сжатие 40, 35 и 30 МПа соответственно. Три разные бетонные смеси (далее именуемые смесью 1, смесь 2 и смесь 3) были приготовлены из товарного бетона, и пропорции приведены в таблице 1.

ID Тип цемента W / B S / A Количество единиц (кг / м 3 ) W C S G SCMs Химическая добавка FA SC AE (связующее%) SP (связующее%) Смесь 1 Тип I 0.45 0,46 259 121 777 934 58 69 0,9 — Смесь 2 0,35 0,47 308 166 761 886 81 85 — 1 Смешивание 3 0,3 0,46 357 165 714 868 94 99 — 1

Примечание .SCM: дополнительные вяжущие материалы, W: вода, C: цемент, S: песок, G: гравий, FA: летучая зола, SC: шлаковый цемент, AE: воздухововлекающий агент и SP: суперпластификатор.

Триста бетонных цилиндров были отлиты в пластиковые формы размером 150 на 300 мм в соответствии со стандартом ASTM C31 / C31M [25]. На следующий день цилиндры были отверждены водой после того, как были демонтированы. Была проведена серия испытаний на статический и динамический модуль упругости для 25 цилиндров в разном возрасте: 4, 7, 14 и 28 дней.

2.2. Статические испытания на прочность при сжатии и модуль упругости

Цилиндры шлифовали с обоих концов перед испытанием, чтобы удалить любые неровности поверхности, а также убедиться, что концы перпендикулярны сторонам образца. Статический модуль упругости и прочность на сжатие цилиндров были измерены на универсальной испытательной машине (UTM) мощностью 1000 кН в соответствии с ASTM C469 / C469M-14 [6] и ASTM C39 / C39M-14 [26] соответственно. Испытания проводились при скорости нагружения примерно 0.28 МПа / с. Деформации были измерены с помощью трех наборов линейных дифференциальных преобразователей напряжения, прикрепленных к двум неподвижным кольцам (рис. 2). Аппарат состоял из двух алюминиевых колец с винтами для крепления к образцу. Расстояние между винтами на верхнем и нижнем кольцах составляло 150 мм. Он служил эталонной длиной для расчета осевой деформации по измеренным деформациям. Статический модуль упругости бетона определяется как модуль хорды на кривой зависимости напряжения от деформации, с первой точкой на уровне деформации 0.00005 () и вторая точка при 40% максимального напряжения () следующим образом:

Модуль упругости бетона

Модуль упругости является фундаментальным параметром при проектировании бетонных конструкций. В последние годы строительные спецификации даже требовали соблюдения определенного модуля упругости бетона, в основном для ограничения чрезмерной деформации и раскачивания в высотных зданиях. Для Бурдж-Халифа (в настоящее время самое высокое здание в мире) проектировщик указал минимум 43800 МПа для бетонных смесей 80 МПа для вертикальных элементов.

Проще говоря, модуль упругости (MOE) измеряет жесткость материала и является хорошим общим показателем его прочности. Это отношение напряжения к деформации. Напряжение — это деформирующая сила, действующая на единицу площади (F / A), а деформация — это деформация (изменение формы), вызванная напряжением (∆L / L).

Взаимосвязь напряжения и деформации впервые была изучена Робертом Хуком, английским естествоиспытателем, архитектором и экспертом во многих различных областях знаний.В 1678 году он заявил, что «в пределах упругости напряжение прямо пропорционально деформации».

Напряжение α деформация

т.е. напряжение / деформация = константа (эта константа называется модулем упругости)

Когда к телу прикладывается напряжение, возникает деформация, и материал проходит различные стадии деформации, как показано на рисунке ниже.

Эластичность — это свойство материала, благодаря которому материал восстанавливает свою первоначальную форму, когда деформирующая сила прекращается.Предел упругости (предел текучести) — это величина напряжения, которому может подвергнуться материал перед переходом от упругой деформации к пластической деформации. При пластической деформации материал не может вернуть свою первоначальную форму даже после снятия деформирующего усилия. Остается в деформированном виде. Пластическая деформация продолжается до точки разрыва, а затем происходит разрыв. Эта точка напряжения, при которой материал разрывается, с внезапным высвобождением накопленной упругой энергии, называется пределом прочности при растяжении (UTS).

На основе типов напряжения (растяжение, сжатие или сдвиг) и деформации, включая направление, можно определить различные типы модуля упругости, как подробно описано ниже.

1. Модуль Юнга (E) — отношение линейного напряжения к линейной деформации,

2. Модуль сдвига (G или µ) — отношение напряжения сдвига к деформации сдвига и,

3. Модуль объемной упругости (K) — отношение объемного напряжения к объемной деформации.

Модуль Юнга

позволяет рассчитать изменение размеров бетонных элементов под действием растягивающих или сжимающих нагрузок.Например, он предсказывает, насколько бетонная колонна может укоротиться при сжатии. Другими словами, модуль упругости говорит нам, какое растяжение или сжатие требуется, чтобы материал стал немного длиннее или короче.

Томас Янг (1773–1829) был английским ученым и специалистом во многих различных областях знаний. Он очень интересовался ранними экспериментами и исследованиями Леонарда Эйлера (1727) и Джордано Рикатти (1782) по модулям упругости материалов.

Модуль Юнга (E) = линейное напряжение / линейная деформация

Линейное напряжение = Сила / площадь = F / A

Линейная деформация = Изменение длины / исходная длина = ∆L / L

Следовательно, модуль Юнга (E) = (F / A) / (∆L / L) = FL / A∆L

Более высокий модуль упругости означает, что бетон может выдерживать более высокие нагрузки, но бетон станет хрупким и быстрее появятся трещины.Низкий модуль упругости означает, что он очень легко изгибается и деформируется. Высокий модуль упругости в раннем возрасте (7 или 14 дней) приведет к более высокому потенциалу растрескивания. Это происходит из-за высокого напряжения, возникающего даже из-за низкого напряжения. Деформация может возникать не только из-за приложенного напряжения, например, усадки. Усадка и термическая активность могут вызывать очень низкое напряжение, но из-за высокого модуля упругости соответствующее напряжение велико. Поскольку прочность бетона на растяжение в таком раннем возрасте все еще низкая, будут развиваться трещины.

Гидратированная цементная паста имеет более низкий модуль упругости, чем заполнитель. Следовательно, объемное содержание заполнителя важно, поскольку рассматривается модуль упругости смеси. Модуль упругости затвердевшего цементного теста составляет от 10 до 30 ГПа, а заполнителя — от 45 до 85 ГПа. Бетон обычно имеет модуль упругости от 30 до 50 ГПа.

Факторы, влияющие на модуль упругости бетона:

1- Свойства крупного заполнителя — такие как модуль упругости заполнителя, тип заполнителя (дробленый или натуральный), петрология и минералогия, а также количество заполнителя.Чем больше объем заполнителя в смеси, тем выше модуль упругости.

2- Состав смеси, который включает общее содержание цемента и соотношение воды и газа. Чем меньше пасты, тем выше модуль упругости.

3- Условия отверждения — образец, отвержденный влажным способом, показал лучшие результаты, чем образец сухого отверждения, из-за усадки и связанных с этим трещин.

4- Скорость нагружения — высокая скорость нагружения приведет к более высокой прочности на сжатие и более высокому модулю упругости.

5- Химическая примесь — не оказывает большого влияния на модуль упругости.Но некоторые типы добавок могут привести к более высокой дисперсности цемента и, таким образом, к более высокой прочности на сжатие и модулю упругости.

6- Минеральные добавки — поскольку они влияют на прочность бетона, они также влияют на модуль упругости.

Наиболее важным фактором, влияющим на модуль упругости бетона, является используемый заполнитель. На это также влияют соотношение заполнитель / цемент и возраст бетона.

В следующей таблице, взятой из Еврокода-2, приведены значения прочности на сжатие (по цилиндрам и кубам), модуль упругости и предел прочности на разрыв для различных классов прочности бетона с нормальным весом, которые обычно используются для целей проектирования.1,5 √fc —— в МПа

где Ec — модуль упругости, Wc — вес бетона (фунты на фут или кг / м3), а fc — прочность цилиндра на сжатие через 28 дней (фунт / кв. Дюйм или МПа). Эти уравнения часто упрощаются на основе заполнителя нормальной плотности и бетона с нормальной массой следующим образом:

Ec = 57000 √fc —— в фунтах на квадратный дюйм или

Ec = 4700 √fc —— в МПа

BS 8110 Использование бетона в конструкциях, Часть 2, пункт 7.2. Упругая деформация предлагает следующее уравнение для расчета ожидаемого значения модуля упругости на основе результатов 28-дневной кубической прочности.

Ec, 28 = Ko + 0,2 fcu, 28

Где Ko — константа, тесно связанная с модулем упругости заполнителя, который часто принимается равным 20 кН / мм2 для заполнителя нормального веса, а Fcu, 28 — прочность куба на сжатие через 28 дней.

Если прогиб или деформации имеют большое значение, испытания должны проводиться на бетоне, изготовленном с использованием заполнителя, который будет использоваться в конструкции. 1.0,5] ——- в МПа

Где ρ — плотность бетона в кг / м3, а fm — средняя прочность на сжатие в МПа за 28 дней.

Модуль упругости бетона испытывают с использованием цилиндрических образцов размером 150 мм X 300 мм в соответствии с:

1. ASTM C 469 — Статический модуль упругости и коэффициент Пуассона бетона при сжатии или

2. BS 1881 Часть 121 — Определение статического модуля упругости при сжатии.

Модуль упругости определяется с помощью компрессометра, закрепленного на образце цилиндра (иногда экстензометра также для вычисления коэффициента Пуассона, как показано на рисунке выше) и нагруженного при определенном уровне напряжения.Его можно оценить, используя уровни напряжения от 15 до 85% в диапазоне упругости. В ASTM уровень напряжения составляет 40% от прочности на сжатие сопутствующего цилиндра, а по BS 33% от прочности сопутствующего цилиндра. Согласно методу испытаний ASTM, результаты сообщаются с точностью до ближайших 200 МПа, а по методу испытаний BS — с точностью до ближайших 500 МПа.

Доступны и другие типы тензометров (компрессометр и экстензометр). Электрический тензодатчик — это наиболее подходящий метод для определения деформации бетона, который должен быть приклеен к бетонному образцу, но требует времени и внимания со стороны технических специалистов.

Ezeagu C.A. и Обаси К. (International Journal of Advanced Research) сообщили в своих исследованиях, что бетон, изготовленный из заполнителя с максимальным номинальным размером 20 мм, показал более высокий модуль упругости, чем бетон с 30 мм и 60 мм. Они рассчитали модуль упругости на основе разных уравнений и нашли разные значения модулей упругости.

Такафуми Ногучи и др. (ACI Structural Journal) сообщили, что даже несмотря на то, что японские и американские правила кодов предлагают вес единицы с показателем 1.5, их исследования показали, что существует прямая зависимость между модулем упругости бетона и его удельной массой 2.

К. Анбувелан и д-р К. Субраманиан (Международный журнал инженерии и технологий) сообщили на основании своего экспериментального исследования упругих свойств бетона, содержащего стальную фибру, что IS 456 и EC-2 предсказывают более высокий модуль упругости, чем BS 8110, ACI 318 и NZS 3101.

Основываясь на результатах своего исследования, Валид Баалбаки и др. (ACI Materials Journal) пришли к выводу, что невозможно точно предсказать модуль упругости высокопрочного бетона по его прочности на сжатие.

В следующей таблице приведены значения прочности на сжатие и модуля упругости (результаты пробной смеси) бетонных смесей, используемых для изготовления вертикальных элементов Бурдж-Халифа — самой высокой башни в мире. Значения модуля упругости очень близки к уравнению ACI 318.

Перед тем, как завершить эту статью, у автора есть вопрос к читателям. Всем известно, что модуль упругости указывает на жесткость материала. Другими словами, он представляет собой прочность материала.Прочность материала может быть шести следующих типов:

1- Хрупкость — Материал очень легко ломается или превращается в порошок.

2- Податливый — материал можно измельчать на тонкие листы, например металл.

3- Дуктильный — материал можно растянуть в проволоку, как металл.

4- Sectile — Материал можно легко разрезать ножом.

5- Пластик — материал деформируется под воздействием напряжения, но не может восстановить свою первоначальную форму при снятии усилия.

6- Эластичность — Материал деформируется под действием напряжения, но восстанавливает свою первоначальную форму при снятии усилия.

По мере увеличения модуля упругости материал становится более жестким и хрупким. Но по сравнению со сталью бетон более хрупкий, несмотря на то, что модуль упругости стали составляет 200 ГПа, а бетон — от 25 до 50 ГПа. Почему это так?

Алмаз имеет модуль упругости 1220 ГПа и очень хрупкий.

_____________________

Спасибо.

Модуль упругости Юнга для металлов и сплавов

Эластичность материала удобно выражать с помощью отношения напряжения к деформации, параметра, также называемого модулем упругости при растяжении или модулем Юнга материала — обычно с символом — Е .

• Модуль Юнга можно использовать для прогнозирования удлинения или сжатия объекта.

Модуль упругости для некоторых распространенных металлов при различных температурах в соответствии с ASME B31.1-1995:

• 1 фунт / дюйм (фунт / дюйм ² ) = 1 фунт / дюйм (фунт / дюйм ² ) = 144 фунт / дюйм (фунт _f / фут ² ) = 6 894,8 Па (Н / м ² ) = 6,895×10 ^-3 Н / мм ²
• T ( ^o C) = 5/9 [T ( ^o F) — 32]

Для полный стол с более высокими температурами — поверните экран!

9037 -129 N04400)

Модуль упругости Юнга — E — (10 6 psi)
Металл	Температура ( o C)
	-73	21	93	149	204	260	316	371	427	482	593		593 9034 o F)
-325	-200	-100	70	200	300	400	500	600	700	800	700	800	1100	1200
Чугун
Серый чугун				13 .4	13,2	12,9	12,6	12,2	11,7	11,0	10,2
Сталь
Углеродистая сталь C <= 0,3%	31,4		30,2	29,5	28,8	28,3	27,7	27,3	26,7	25,5	24,2	22,4	20.4	18,0
Углеродистая сталь C => 0,3%	31,2	30,6	30,0	29,3	28,6	28,1	27,5	27,1	26,5	25,3	24,0	22,2	20,2	17,9	15,4
Углерод-молибденовые стали	31,1	30,5	29,9	29,2	28.5	28,0	27,4	27,0	26,4	25,3	23,9	22,2	20,1	17,8	15,3
Никелевые стали Ni 2% — 9%	29,6	29,1	28,5	27,8	27,1	26,7	26,1	25,7	25,2	24,6	23,0
Cr-Mo стали Cr-Mo 1/2% — 2%	31.6	31,0	30,4	29,7	29,0	28,5	27,9	27,5	26,9	26,3	25,5	24,8	23,9	23,0	21,8
Cr-Mo стали Cr 2 1/4% — 3%	32,6	32,0	31,4	30,6	29,8	29,4	28,8	28,3	27,7	27.1	26,3	25,6	24,6	23,7	22,5
Cr-Mo стали Cr 5% — 9%	32,9	32,3	31,7	30,9	30,1	29,7	29,0	28,6	28,0	27,3	26,1	24,7	22,7	20,4	18,2
Хромистые стали Cr 12%, 17%, 27%	31.2	30,7	30,1	29,2	28,5	27,9	27,3	26,7	26,1	25,6	24,7	23,2	21,5	19,1	16,6
Сталь Austenit TP304, 310, 316, 321, 347)	30,3	29,7	29,1	28,3	27,6	27,0	26,5	25,8	25.3	24,8	24,1	23,5	22,8	22,1	21,2
Медь и медные сплавы
Сравн. и свинцово-Sn бронза (C83600, C)	14,8	14,6	14,4	14,0	13,7	13,4	13,2	12,9	12,5	12,0					900 латунь Si & Al бронза (C46400, C65500, C95200, C95400)	15.9	15,6	15,4	15,0	14,6	14,4	14,1	13,8	13,4	12,8
Медь (16,6000)	16,9	16,6000)	16,9		16,0	15,6	15,4	15,0	14,7	14,2	13,7
Медь красная латунь Al-бронза (C10200, C12000, C12200, C14500, C142006, C142006, C142006 )	18.0	17,7	17,5	17,0	16,6	16,3	16,0	15,6	15,1	14,5
Никель и никелевые сплавы
27,8	27,3	26,8	26,0	25,4	25,0	24,7	24,3	24,1	23.7	23,1	22,6	22,1	21,7	21,2
Титан
Нелегированный титан марок 1, 2, 3 и 7				15,5	15,0		14,0	13,3	12,6	11,9	11,2
Алюминий и алюминиевые сплавы
Марки 443, 1060, 1100, 3003, 3004, 6063	11.1	10,8	10,5	10,0	9,6	9,2	8,7

• 1 фунт / кв. Дюйм (фунт / дюйм ^{2 ) = 6 фунт / дюйм 2} (Па)
• T ( ^o C) = 5/9 [T ( ^o F) — 32]

Примечание! Вы можете использовать конвертер единиц давления для переключения между единицами модуля упругости.

Модуль упругости — определение модуля упругости по The Free Dictionary

[1] Использование этого материала очень популярно, потому что он имеет несколько преимуществ, таких как легкий, биосовместимый, эстетичный, относительно дешевый, низкое водопоглощение, простой в использовании, полировке и ремонте, [1,2,4,5] но это Материал еще не является идеальным для удовлетворения механических требований к основе зубного протеза, поскольку он имеет относительно низкую ударную вязкость, поперечную прочность и модуль упругости, что делает его более подверженным разрушению во время клинического использования.Теперь они могут производить бетонные конструкции с высоким модулем упругости в диапазоне 4000–7000 тыс. Фунтов на квадратный дюйм », — говорит Вильямс. Пиломатериалы из южной сосны: Часть А, модуль упругости. Научные исследования по древесному волокну. Николсон и Биенявски, разработанные на основе RMR в качестве входного параметра Сонмез разработал эмпирическую модель с использованием модуля упругости Юнга и RMR в качестве входных параметров, Бейки и др., Где: J (t, [tau]) = 1 / [E.sub.c] ([tau]) + C (t, [ tau]) — податливость к ползучести, возникающая в результате удельного напряжения бетона, E ([tau]) — это модуль упругости и удельная ползучесть бетона в возрасте [tau], [t.sub.s] = [t.sub.0] — это время, когда начинает развиваться автогенная деформация усадки. В таблице 4 показаны результаты, полученные в ходе предыдущих испытаний для определения модуля упругости, параллельного волокну для изгиба и сжатие. где, когда [[сигма]. Sub.d] [стрелка вправо] 0, 1 / a относится к наклону касательной, когда кривая проходит начало координат и физически относится к начальному динамическому модулю упругости замороженной глины [ E.sub.d max], и 1 / b относится к асимптоте кривой и физически относится к максимальному осевому динамическому напряжению [[сигма].sub.d max]. Как и в случае предела текучести, включение фотоселекторных добавок в рецептуры снизило модуль упругости пленок по сравнению с эталонной пленкой из ЛПЭНП 3304. Влияние типа агрегата на модуль упругости t-критерий Стьюдента был использован для сравнения средних значений модуля упругости и растяжения при разрыве между GI x G2, G3 x G4 и G5 x G6. Было обнаружено, что содержание наполнителя не влияет на прочность на разрыв EOC / WF, но на удлинение при разрыве, модуль эластичности EOC / WF и EOC / FS и прочности на разрыв EOC / FS значительно зависят от содержания наполнителя.Ключевые слова: кукуруза, напряжение изгиба, модуль упругости, напряжение сдвига, удельная энергия сдвига.

Статический модуль упругости бетона

[1] П. Хунка, Дж. Колиско, М. Вокач, С. Рехачек, 2013 г., Испытания и технологические воздействия на модуль упругости бетона — Резюме, Разработка процедур, Том.65, стр 266-272.

DOI: 10.1016 / j.proeng.2013.09.041

[2] Ф.Фогель, Р. Совьяк, О. Хольчапек, Л. Маржик, Й. Шах, 2015 г., Экспериментальное исследование бетона тоннелей для первичной футеровки после тридцати лет эксплуатации, Прикладная механика и материалы, Vol. 732, стр 403-406.

DOI: 10.4028 / www.scientific.net / amm.732.403

[3] Т.Влах, Л. Лайблова, А. Чира, М. Новотна, К. Фиала, М. Женишек, П. Хаек, 2014 г., Сравнение различных методов определения модуля упругости композитной арматуры, полученной из ровинга, Advanced Materials Research, Vol. . 1054, стр 104-109.

DOI: 10.4028 / www.scientific.net / amr.1054.104

[4] Б.Craeye, P. Van Itterbeeck, P. Desnerck, V. Boel, G. De Schutter, Модуль упругости и предел прочности при растяжении самоуплотняющегося бетона: Обзор экспериментальных данных и конструктивных норм, Цемент и бетонные композиты 54 (2014) 53 -61.

DOI: 10.1016 / j.cemconcomp.2014.03.011

[5] Т.Плахи, П. Падевет, М. Полак, М .: Сравнение статического и динамического модулей упругости бетона, в: Б. Марвалова, И. Петрикова, Л. Чапек (ред.), Труды ЭКСПЕРИМЕНТАЛЬНОГО АНАЛИЗА НАПЕТИ 2009 / ЭКСПЕРИМЕНТАЛЬНЫЙ АНАЛИЗ НАПРЯЖЕНИЙ, Страницы: 201-206, Опубликовано: (2009).

[6] А.Бейчиоглу, Х.Ю. Aruntas, Технологичность и механические свойства самоуплотняющихся бетонов, содержащих LLFA, GBFS и MC, Строительные материалы 73 (2014) 626-635.

DOI: 10.1016 / j.conbuildmat.2014.09.071

[7] ЧАС.С. Абдельгадер, А.С. Эльбаден, отредактированный: Diouri, A; Хачани, Н; Талби, М.А., Метод бетонирования, обеспечивающий высокий модуль упругости, МЕЖДУНАРОДНЫЙ КОНГРЕСС ПО МАТЕРИАЛАМ И СТРУКТУРНОЙ УСТОЙЧИВОСТИ, Серия книг: MATEC Web of Conferences, Vol. 11, (2014).

DOI: 10.1051 / matecconf / 20141103012

[8] Л.Беднарский, Р. Сиенко, Т. Ховяцки, Оценка значения и изменчивости модуля упругости бетона в существующей конструкции на основе непрерывных измерений на месте, Цемент Wapno Beton 19 (6) (2014) 396.

[9] О.Хольчапек, Ф. Фогель, Т. Вавржиник, М. Кепперт, 2014, Прогресс прочности на сжатие высокопрочного бетона, Прикладная механика и материалы, Vol. 486, стр 167-172.

DOI: 10.4028 / www.scientific.net / amm.486.167

[10] Поповиц, С., Прочность и связанные с ней свойства бетона, Издано John Wiley & Sons, Inc, Нью-Йорк, (1997).

Глава 2 (продолжение) — Руководство пользователя для бетонного материала LS-DYNA, модель 159, май 2007 г.

PDF-файлы можно просматривать с помощью Acrobat® Reader® Глава 2.Теоретическое руководство Модуль объема и сдвига Модуль Юнга бетона зависит от прочности бетона, как показано в таблице 1. Эти измерения взяты из уравнения в CEB, как показано на рисунке 74: Рисунок 74. Уравнение. Модуль Юнга по умолчанию E . Здесь E — это модуль Юнга, а E C = 18,275 МПа (2651 фунт / кв. Дюйм) (что является значением модуля Юнга при f ‘ c = 10 МПа (1450 фунт / кв. Дюйм)).Это значение E C предназначено для моделирования, которое моделируется линейно по отношению к пику (без предварительного пикового упрочнения). Коэффициент Пуассона обычно составляет от 0,1 до 0,2. Здесь выбрано значение η = 0,15, и предполагается, что оно остается постоянным с учетом прочности бетона. Основываясь на этой информации, модули объема и сдвига по умолчанию ( K и G ) в таблице 1 получены из классических соотношений между константами жесткости, как показано на рисунке 75: Рисунок 75.Уравнение. Модули сдвига и объема, G и K . Уравнения на рисунках 74 и 75 реализованы в процедурах инициализации бетонной модели для установки модулей бетона по умолчанию в зависимости от прочности бетона на сжатие. В качестве альтернативы Комитет 318 ACI предлагает формулу, показанную на Рисунке 76 для модуля упругости: Рисунок 76. Уравнение. Модуль упругости ACI, E c . , где w c — плотность бетона в килограммах на кубический метр (кг / м 3 ). Для бетона нормального веса с w c = 2286 кг / м 3 (5040 фунтов на кубический фут (фунт / фут 3 )) эта формула сводится к уравнению, показанному на рисунке 77: Рисунок 77. Уравнение. Приведенный модуль Юнга по ACI, E c . Эта формула дает модули Юнга, которые находятся в пределах ± 9 процентов от значений, представленных на рисунке 74, как показано в таблице 2. Таблица 1. Данные модули объемной массы и сдвига бетона по умолчанию получены из формулы для модуля Юнга, приведенной в CEB. Предел прочности при неограниченном сжатии МПа (фунт / кв. Дюйм) Модуль Юнга, ГПа (тыс. Фунтов на квадратный дюйм) Коэффициент Пуассона Модуль объемной упругости, ГПа (тыс. Фунтов на квадратный дюйм) Модуль сдвига, ГПа (тыс. Фунтов на квадратный дюйм) 20 (2,901) 23,0 (3 336) 0.15 11,0 (1 595) 10,0 (1450) 28 (4061) 25,8 (3 742) 0,15 12,3 (1784) 11,2 (1 624) 38 (5,511) 28,5 (4 134) 0,15 13,6 (1973) 12,4 (1798) 48 (6962) 30,8 (4 467) 0.15 14,7 (2132) 13,4 (1 944) 58 (8,412) 32,8 (4 757) 0,15 15,6 (2263) 14,3 (2074) ГПа = гигапаскали МПа = мегапаскалей тысяч фунтов / кв. Дюйм = тысячи фунтов на квадратный дюйм psi = фунтов на квадратный дюйм Таблица 2. Эти объемные модули и модули сдвига для бетона выводятся из формулы для модуля Юнга, предложенной Комитетом Кодекса ACI. Предел прочности при неограниченном сжатии МПа (фунт / кв. Дюйм) Модуль Юнга, ГПа (тыс. Фунтов на квадратный дюйм) Коэффициент Пуассона Модуль объемной упругости, ГПа (тыс. Фунтов на квадратный дюйм) Модуль сдвига, ГПа (тыс. Фунтов на квадратный дюйм) 20 (2,901) 21,0 (3046) 0,15 10,0 (1450) 9,1 (1320) 28 (4061) 24.9 (3 611) 0,15 11,9 (1726) 10,8 (1566) 38 (5,511) 28,9 (4 192) 0,15 13,8 (2 002) 12,6 (1827) 48 (6962) 32,6 (4728) 0,15 15,5 (2248) 14,2 (2060) 58 (8,412) 35.8 (5,192) 0,15 17,0 (2 466) 15,6 (2263) Поверхность трехосного сжатия Уравнение поверхности текучести TXC подходит для четырех измерений прочности. С точки зрения безопасности на дорогах режимы, представляющие интерес, прежде всего, представляют собой режимы растяжения и низкого ограничивающего давления. Следовательно, первое и наиболее распространенное измерение — это неограниченное сжатие, при котором давление составляет одну треть от силы.Второе измерение — это одноосное растяжение, которое часто называют прямым растяжением. Третье измерение — трехосное натяжение (равное натяжение в трех направлениях), которое определяет вершину поверхности текучести TXC. Четвертое измерение — TXC при заданном давлении. Выбранное давление составляет 70 МПа (10 153 фунтов на кв. Дюйм). Подгонка к этому измерению фиксирует поверхность текучести при давлении от низкого до среднего. Измерения прочности приведены в таблице 3. Измерения одноосного сжатия и растяжения взяты из таблиц и информации, представленной в CEB.Измерение трехосного натяжения равно измерению одноосного натяжения. Этот выбор, наряду с соответствующим выбором трехинвариантных масштабных коэффициентов, будет моделировать прочность на двухосное растяжение, приблизительно равную прочности на одноосное растяжение. Это рекомендация CEB. Измерение TXC (разность главных напряжений) взято из анализа данных испытаний. Например: Измерения, проведенные для трех одинаковых бетонов с f ‘c = 45 МПа (6527 фунтов на кв. Дюйм), показывают среднюю трехосную прочность около 120 МПа (17 405 фунтов на квадратный дюйм) (разница главных напряжений) при давлении 69 МПа (10 008 фунтов на квадратный дюйм). ). (25) Измерения, указанные в справочном материале 28 для бетона нормальной прочности с f ‘ C = 25 МПа (3626 фунтов на квадратный дюйм), указывают на разность главных напряжений 69 МПа (10 008 фунтов на квадратный дюйм) при давлении 37 МПа (5366 фунтов на квадратный дюйм). ). Таблица 3. Приблизительные измерения прочности, используемые для установки параметров поверхности текучести TXE по умолчанию. Тип измерения Набор сильных сторон 1 Набор сильных сторон 2 Набор сильных сторон 3 Набор сильных сторон 4 Набор сильных сторон 5 Одноосное сжатие f ‘ C МПа (psi) 20 (2 901) 28 (4061) 38 (5 511) 48 (6962) 58 (8 412) Одноосное растяжение f ‘ T МПа (фунт / кв. Дюйм) 1.6 (232) 2,2 (319,1) 2,9 (421) 3,5 (508) 4,1 (595) Трехосное натяжение МПа (фунт / кв. Дюйм) 1,6 (232) 2,2 (319,1) 2,9 (421) 3,5 (508) 4,1 (595) Трехосное сжатие 2,75 f ‘ C при P = 1,5 f’ C МПа (фунт / кв. Дюйм) 55 (7 977) 77 (11 168) 105 (15 229) 132 (19 145) 160 (23 206) Уравнение поверхности текучести TXC связывает прочность с давлением через четыре параметра, как показано на рисунке 78: Рисунок 78.Уравнение. TXC Strength. При каждом значении прочности на неограниченное сжатие четыре параметра прочности ( α, λ, β, θ ) одновременно соответствуют четырем значениям прочности с помощью итерационной процедуры. Соответствующие значения для пяти сильных сторон приведены в таблице 4. Очевидно, пользователь может пожелать проанализировать бетон с прочностью, отличной от пяти перечисленных. Для этого квадратные уравнения в зависимости от прочности на неограниченное сжатие подходят для каждого параметра, P , как показано на рисунке 79: Рисунок 79.Уравнение. Параметр интерполяции P . Для поверхности текучести TXC параметр P представляет α, λ, β, или q . Подгоняемые значения A P , B P и C P приведены в таблице 5. Подходящие значения A P , B P и C P для всех остальных входных параметров конкретной модели (TOR и TXE поверхности текучести, крышка, повреждение, параметры скоростных эффектов) приведены в последующих разделах. Таблица 4. Входные параметры поверхности текучести ТХС в зависимости от прочности на неограниченное сжатие. Неограниченный Компрессия Прочность МПа (фунт / кв. Дюйм) α МПа (фунт / кв. Дюйм) λ МПа (фунт / кв. Дюйм) β МПа -1 (фунт / кв. Дюйм -1 ) θ 20 (2,901) 12.8 (1856) 10,5 (1523) 1.929E-02 0,266 28 (4061) 14,2 (2060) 10,5 (1523) 1.929E-02 0,290 38 (5,511) 15,4 (2234) 10,5 (1523) 1.929E-02 0,323 46 (6 672) 15,9 (2 306) 10.5 (1 523) 1.929E-02 0,350 58 (8,412) 15,9 (2 306) 10,5 (1523) 1.929E-02 0,395 МПа -1 = 0,006895 фунт / кв. Дюйм -1 Таблица 5. Коэффициенты квадратного уравнения, которые устанавливают параметры поверхности текучести TXE, TOR и TXE по умолчанию в зависимости от прочности на неограниченное сжатие. Входной параметр P A P B P С П TXC Поверхность α (МПа) -0,003 (МПа -1 ) 0,3169747 7,7047 (МПа) λ (МПа) 0 (МПа -1 ) 0 10.5 (МПа) β (МПа -1 ) 0 (МПа -3 ) 0 (МПа -2 ) 1.929E-02 (МПа -1 ) θ 1,3216E-05 (МПа -2 ) 2.3548E-03 (МПа -1 ) 0,2140058 Поверхность TOR α λ 0 (МПа -2 ) 0 (МПа -1 ) 0.74735 λ λ 0 (МПа -2 ) 0 (МПа -1 ) 0,17 β λ (МПа -1 ) -1.9972e-05 (МПа -3 ) 2.2655e-04 (МПа -2 ) 8.1748e-02 (МПа -1 ) θ λ (МПа -1 ) -3.8859e-07 (МПа -3 ) -3.9317e-04 (МПа -2 ) 1,5820e-03 (МПа -1 ) Поверхность TXE α 2 0 (МПа -2 ) 0 (МПа -1 ) 0,66 λ 2 0 (МПа -2 ) 0 (МПа -1 ) 0.16 (МПа) β 2 (МПа -1 ) -1.9972e-05 (МПа -3 ) 2.2655e-04 (МПа -2 ) 8.2748e-02 (МПа -1 ) θ 2 (МПа -1 ) -4,8697e-07 (МПа -3 ) -1,8883e-06 (МПа -2 ) 1.8822e-03 (МПа -1 ) фунт / кв. Дюйм = 145,05 МПа МПа -1 = 0,006895 фунт / кв. Дюйм -1 МПа -2 = 0,000047538 фунтов на кв. Дюйм -2 МПа -3 = 0,000000328 фунт / кв. Дюйм -3 Поверхности для трехосного удлинения и кручения Масштабные функции Рубина определяют прочность бетона при любом напряженном состоянии относительно прочности TXC. (17) Коэффициенты прочности показаны на рисунке 80: Рисунок 80.Уравнение. Наиболее общая форма для Q 1 , Q 2 . , где Q 1 — это соотношение сил TOR / TXE, а Q 2 — соотношение сил TXE / TXE. Каждое соотношение может оставаться постоянным или изменяться в зависимости от давления. Подгонки этих уравнений к данным по умолчанию приведены в таблицах 6 и 7 и основаны на следующих данных и предположениях: Форма поверхности текучести в девиаторной плоскости треугольная, когда давление растягивающее.Это означает, что Q 1 = 0,5774 и Q 2 = 0,5. В этом случае Q 1 и Q 2 устанавливаются внутренне, а значения α λ , λ λ , β λ , θ λ и α 2 , λ 2 , β 2 , θ 2 не используются. Они соответствуют модельным значениям прочности на двухосное растяжение, которые находятся в пределах 1 процента от пределов одноосного растяжения, как указано в CEB. Форма поверхности текучести в девиаторной плоскости переходит от треугольника при P = 0 к неправильному шестиугольнику при P > 0. В этом случае Q 2 задается для получения прочности на двухосное сжатие. это примерно на 15 процентов больше, чем прочность на одноосное сжатие ( f ‘ BC = 1,15 f ‘ C ), как указано в CEB. Эта спецификация CEB согласуется с данными ссылки 16.Эта ссылка предлагает двухосную прочность на сжатие, которая примерно на 16 процентов выше, чем прочность на неограниченное сжатие. Посадки при растяжении и сжатии будут плавно пересекаться при значениях Q 1 = 0,5774 и Q 2 = 0,5 при чистом сдвиге ( P = 0). Таблица 6. Входные параметры поверхности текучести TOR в зависимости от прочности на неограниченное сжатие. Неограниченный Компрессия Прочность МПа (фунт / кв. Дюйм) α 1 λ 1 β 1 МПа -1 (фунт / кв. Дюйм -1 ) θ 1 МПа -1 (фунт / кв. Дюйм -1 ) 20 (2,901) 0.74735 0,170 0,07829 1,372E-03 28 (4061) 0,74735 0,170 0,07252 1.204E-03 38 (5,511) 0,74735 0,170 0,06135 9.247e-04 46 (6 672) 0,74735 0.170 0,05004 6.382E-04 58 (8,412) 0,74735 0,170 0,02757 1.147E-04 МПа -1 = 0,006895 фунт / кв. Дюйм -1 Таблица 7. Входные параметры поверхности текучести TXE в зависимости от прочности на неограниченное сжатие. Предел прочности на сжатие МПа (фунт / кв. Дюйм) α 2 λ 2 β 2 МПа -1 (фунт / кв. Дюйм -1 ) θ 2 МПа -1 (фунт / кв. Дюйм -1 ) 20 (2,901) 0.66 0,16 0,07829 1.649E-03 28 (4061) 0,66 0,16 0,07252 1.450E-03 38 (5,511) 0,66 0,16 0,06135 1.102e-03 46 (6 672) 0,66 0,16 0.05004 7.687e-04 58 (8,412) 0,66 0,16 0,02757 1,310E-04 МПа -1 = 0,006895 фунт / кв. Дюйм -1 Опять же, поскольку пользователи могут захотеть проанализировать бетон с прочностью, отличной от пяти перечисленных, квадратные уравнения как функция прочности на неограниченное сжатие подходят для каждого набора значений параметров для поверхностей TOR и TXE.Коэффициенты квадратного уравнения ранее были приведены в таблице 5. Расположение, форма и параметры заглушки Параметры крышки выбираются путем подбора кривых зависимости давления от объемной деформации, измеренных при испытаниях на гидростатическое сжатие и одноосную деформацию. Посадки по умолчанию, приведенные в таблице 8, основаны на следующих данных и предположениях: Начальное положение крышки — инвариант давления, при котором гидростатическая Кривая давление-объемная деформация становится нелинейной.Нелинейность возникает при более низких давлениях для бетона с более низкой прочностью. Следовательно, первоначальное расположение крышки уменьшается с уменьшением прочности бетона. Форма крышки в сочетании с первоначальным положением крышки задает давление, при котором кривая одноосной деформации давление-объемная деформация становится нелинейной. Параметр формы крышки 5 является типичным и обычно используется разработчиком для подгонки бетона с f ‘c = 45 МПа (6 527 фунтов на кв. Дюйм). Максимальное изменение пластического объема устанавливает диапазон объемной деформации, в котором кривая давления-объемной деформации является нелинейной (от начала до фиксации).Обычно максимальное пластическое изменение объема примерно равно пористости воздушных пустот. Значение 0,05 указывает на пористость воздушных пустот 5 процентов. Не ожидается, что поры в приложениях для обеспечения безопасности на дорогах будут полностью уплотнены. Таким образом, этот параметр установлен так, чтобы обеспечить разумную форму кривой давление-объемная деформация в режиме от низкого до среднего давления, применимого к испытаниям безопасности на дорогах. Параметр линейного упрочнения крышки задает форму кривой объемной деформации давления, хотя он производит внезапный переход в начале нелинейности.Параметр квадратичной закалки шапки сглаживает этот переход. Пример кривой зависимости давления от объемной деформации из моделирования изотропного сжатия приведен на рисунке 81. Этот рисунок демонстрирует, как каждый параметр влияет на форму кривой. Исходное положение крышки зависит от прочности на сжатие. Квадратное уравнение используется для определения положения крышки при прочности на сжатие, отличной от пяти указанных в таблице. Коэффициенты квадратного уравнения: A P = 8.769178e-03 МПа -1 , B P = -7,3302306e-02 и C P = 84,85 МПа (12306 фунтов на кв. Дюйм) . Таблица 8. Форма, расположение и параметры твердения крышки в зависимости от прочности на неограниченное сжатие. Предел прочности на сжатие МПа (фунт / кв. Дюйм) Форма крышки R Расположение крышки X o МПа (фунт / кв. Дюйм) Максимальное изменение объема пластика Вт Линейное упрочнение D 1 МПа (psi) Квадратичное упрочнение D 2 МПа 2 (psi 2 ) 20 (2,901) 5 87 (12 618) 0.05 2,50e-04 3,49e-07 28 (4061) 5 90 (13 053) 0,05 2,50e-04 3,49e-07 38 (5,511) 5 95 (13 779) 0,05 2,50e-04 3,49e-07 48 (6962) 5 102 (14 794) 0.05 2,50e-04 3,49e-07 58 (8,412) 5 110 (15 954) 0,05 2,50e-04 3,49e-07 фунт / кв. Дюйм = 145,05 МПа фунт / кв. Дюйм = 145,05 МПа Рисунок 81. График. Это моделирование изотропного сжатия демонстрирует, как параметры крышки задают форму кривой объемной деформации давления. Параметры повреждений Бетон размягчается в режимах растяжения и низкого ограничивающего давления. Для целей моделирования энергия разрушения определяется как площадь под участком разупрочнения кривой «напряжение-смещение» от пикового напряжения до полного разупрочнения. Одно уравнение в CEB связывает измеренную энергию разрушения при растяжении с прочностью на неограниченное сжатие и максимальным размером заполнителя, как показано на Рисунке 82: . Рисунок 82.Уравнение. Энергия разрушения по умолчанию G F . Таблица 9. Коэффициенты для уравнения энергии разрушения. Максимальный размер заполнителя, мм (дюймы) G F0 КПа-см (фунт / дюйм2) 8 (0,31 дюйма) 2,5 16 (0,62 дюйма) 3,0 32 (1.26 дюймов) 3,8 КПа-см = килопаскаль-сантиметр 1 КПа-см = 0,05710 фунтов на квадратный дюйм Здесь G F0 — энергия разрушения при f ¢ c = 10 МПа (1450 фунтов на кв. Дюйм) как функция максимального размера агрегата. CEB фактически указывает значение G F0 как 5,8 для 32-мм (1,26 дюйма) агрегата, но оно было заменено на 3,8, чтобы привести G F в соответствие с табличными значениями CEB.Подгонка квадратного уравнения к этим значениям G F0 как функция размера агрегата в мм составляет A P = 0,000520833 см / кПа, B P = 0,75 см и C P = 1,9334 КПа-см. Энергии разрушения при растяжении, рассчитанные по уравнению на Рисунке 82 для пяти удельных значений прочности бетона, приведены в Таблице 10. Таблица 10. Энергия разрушения при растяжении, приведенная в CEB в зависимости от прочности бетона. Предел прочности на сжатие МПа (фунт / кв. Дюйм) Совокупный размер 8 мм (0,31 дюйма) КПа-см (фунт / кв. Дюйм) Совокупный размер 16 мм (0,62 дюйма) КПа-см (фунт / дюйм2) Совокупное 32 мм (1,26 дюйма) КПа-см (фунт / дюйм2) 20 (2,901) 4,0 5,0 6,5 28 (4061) 5.0 6,0 8,0 38 (5 511) 6,5 7,5 9,5 48 (6962) 7,0 9,0 1,15 58 (8 412) 8,5 1,05 1,30 1 кПа-см = 0,05710 фунтов на квадратный дюйм Модель бетонного материала требует указания энергии разрушения в одноосном растягивающем напряжении, одноосном напряжении сжатия и чистом напряжении сдвига.Значения по умолчанию для энергии разрушения при растяжении задаются уравнением на Рисунке 82. Значения по умолчанию для энергии разрушения при сжатии устанавливаются равными 100-кратной энергии разрушения при растяжении. Значения по умолчанию для энергии разрушения при сдвиге установлены равными энергии разрушения при растяжении. Другие требуемые входные параметры: пороги хрупкого и вязкого повреждения и максимальные уровни повреждения: Каждый порог повреждения устанавливает уровень энергии упругой деформации, при котором начинается разупрочнение.Порог хрупкого повреждения устанавливается равным уровню энергии упругой деформации при неограниченном растяжении при пиковом напряжении. Порог вязкого разрушения устанавливается равным уровню энергии упругой деформации при неограниченном сжатии при пиковом напряжении. Форма кривых смягчения задается параметрами B и D . Значение B = 100,0 установлено при сжатии для постепенного начального размягчения (плоская вершина). Значение D = 0,1 установлено при растяжении для хрупкого начального размягчения (заостренный верх). Параметры максимального повреждения устанавливают максимальные уровни повреждений, достигаемые при неограниченном сжатии и растяжении. Максимальные уровни повреждений установлены равными 0,99 как для хрупких, так и для вязких составов. Параметры скорости деформации Бетон демонстрирует увеличение прочности с увеличением скорости деформации (см. Рисунок 13 и Рисунок 14). Данные обычно представляются в виде отношения динамической прочности к статической, называемого коэффициентом динамического увеличения (DIF).CEB предоставляет спецификации для DIF, как обсуждается в приложении D. Однако спецификации CEB не очень хорошо подходят для данных о растяжении, ранее показанных на рисунке 14. Таким образом, DIF, используемый и показанный на рисунке 83, основан на опыте разработчика. различные оборонные контракты, особенно для бетона с прочностью около f ‘ c = 45 МПа (6 527 фунтов на кв. дюйм). Эти характеристики хорошо согласуются с данными о растяжении и сжатии, ранее показанными на рисунках 13 и 14. Спецификации DIF приблизительно соблюдаются путем выполнения многочисленных расчетов и выбора параметров эффектов скорости вязкости с помощью метода проб и ошибок. Вязкопластические параметры применяются к формулировкам пластичности, повреждения и энергии разрушения. Эти параметры: η 0t и n t для подбора данных по одноосному растягивающему напряжению и η 0c и n c для подбора данных одноосного сжатия.Коэффициенты квадратного уравнения зависят от прочности на неограниченное сжатие, но не зависят от размера заполнителя. Параметры по умолчанию при растяжении: n t = 0,48, с коэффициентами квадратного уравнения для η 0t из A P = 8.0614774E-13 , B P = 19E-9,777 -10 и C P = 5.0752351E-05 для времени в секундах и напряжения в фунтах на квадратный дюйм.Параметры сжатия по умолчанию: n c = 0,78, с коэффициентами квадратного уравнения для η 0c из A P = 1,2772337-11 , B P = −1.0613722E-07 , и C P = 3.203497-04. Параметры скоростных эффектов при чистом напряжении сдвига устанавливаются равными параметрам при растяжении с помощью параметра Srate = 1. Пределы перенапряжения при растяжении ( overc ) и сжатии ( overc ) ограничивают эффекты скорости при высоких скоростях деформации (> 100).Коэффициенты квадратного уравнения перенапряжения для overt равны A P = 1,309663E-02 МПа -1 , B P = -0,39 и C P = 21,45 МПа. Они обеспечивают пределы перенапряжения при растяжении и сжатии 21 МПа (3046 фунтов на квадратный дюйм) при прочности на неограниченное сжатие 30 МПа (4351 фунтов на квадратный дюйм). В литературе содержится противоречивая информация о том, зависит ли энергия разрушения от скорости деформации.Одна из возможностей — смоделировать энергию разрушения независимо от скорости деформации ( repow = 0). Другая возможность — увеличить энергию разрушения со скоростью деформации путем умножения статической энергии разрушения на DIF ( repow = 1). Опыт разработчика заключался в увеличении значения энергии разрушения со скоростью деформации; следовательно, repow = 1 — значение по умолчанию. Это значение обеспечивает хорошую корреляцию с данными испытаний для большинства проблем, проанализированных и обсуждаемых в сопроводительном отчете об оценке конкретной модели. (1) Тем не менее, моделирование рельсов моста Texas T4 лучше всего коррелирует с данными, если энергия разрушения увеличивается пропорционально квадратному корню из скорости деформации ( repow = 0,5). Рисунок 83. LEAVE A REPLY Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Рубрики Газобетон Дом Разное Своими руками Советы Строительство Схема