Что означает буква E на калькуляторе: полное руководство по экспоненциальной записи

Что означает буква E на дисплее калькулятора

Буква E (или e) на дисплее калькулятора обозначает экспоненциальную запись числа. Она используется для компактного представления очень больших или очень маленьких чисел.

Экспоненциальная запись имеет следующий вид:

• a.bbbE±cc

Где:

• a.bbb — мантисса (значащие цифры числа)
• E — обозначение экспоненты
• ±cc — порядок (показатель степени 10)

Например, число 1 500 000 в экспоненциальной записи будет выглядеть как:

• 1.5E+06

А число 0.000015 запишется как:

• 1.5E-05

Почему используется экспоненциальная запись чисел

Экспоненциальная запись позволяет компактно представлять очень большие и очень маленькие числа. Это удобно по нескольким причинам:

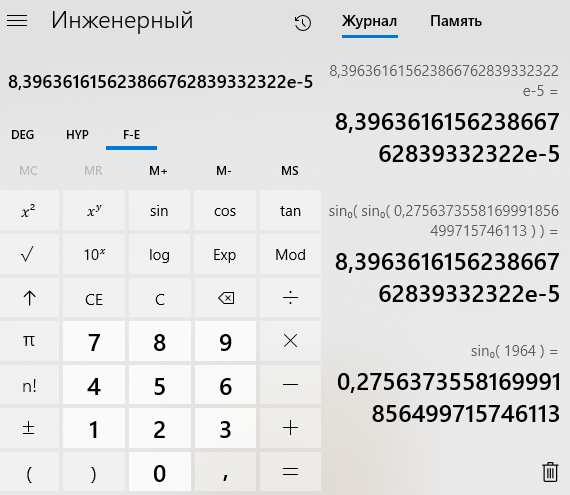
1. Экономия места на дисплее калькулятора
2. Упрощение записи длинных чисел
3. Удобство выполнения математических операций
4. Наглядное представление порядка числа

Благодаря экспоненциальной записи на калькуляторе можно работать с числами в диапазоне от 10^-99 до 10^99.

Как читать числа в экспоненциальной записи

Чтобы правильно интерпретировать число в экспоненциальной записи, нужно:

1. Взять мантиссу (часть до E)
2. Умножить ее на 10 в степени, указанной после E

Например:

• 2.5E+06 = 2.5 * 10^6 = 2 500 000
• 3.8E-04 = 3.8 * 10^(-4) = 0.00038

При положительном показателе степени десятичная точка сдвигается вправо, при отрицательном — влево.

Научная и инженерная нотация

Существует два основных формата экспоненциальной записи:

Научная нотация

В научной нотации мантисса всегда находится в диапазоне от 1 до 9.999…

Примеры:

• 1.234E+05
• 5.678E-03

Инженерная нотация

В инженерной нотации показатель степени всегда кратен 3. Мантисса находится в диапазоне от 1 до 999.999…

Примеры:

• 123.4E+03
• 5.678E-06

Инженерная нотация удобна при работе с единицами измерения, так как соответствует стандартным приставкам (кило-, мега-, милли- и т.д.).

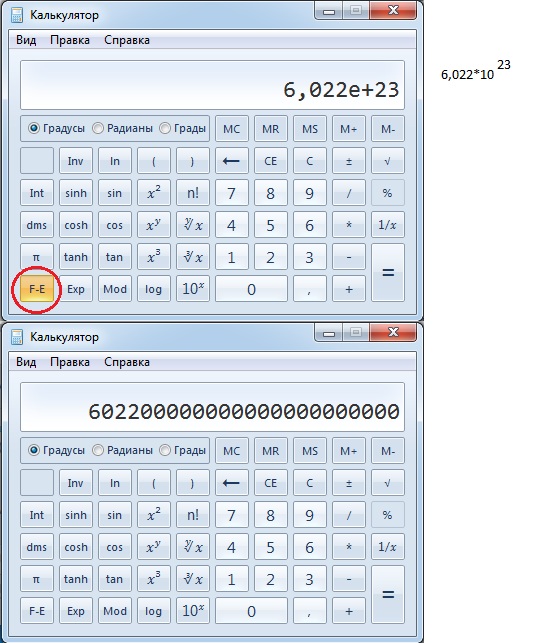
Как вводить числа в экспоненциальной записи

На большинстве калькуляторов для ввода чисел в экспоненциальной форме используется следующий порядок действий:

1. Ввести мантиссу числа
2. Нажать клавишу EE или EXP
3. Ввести показатель степени

Например, чтобы ввести число 2.5E+06:

1. Набрать 2.5
2. Нажать EE
3. Набрать 6

На экране отобразится 2.5E+06 или 2.5E6.

Операции с числами в экспоненциальной записи

При выполнении математических операций с числами в экспоненциальной форме действуют следующие правила:

Сложение и вычитание

Числа нужно привести к одинаковому порядку, а затем выполнить операцию с мантиссами.

Пример:

• 2.5E+05 + 3.7E+04 = 2.5E+05 + 0.37E+05 = 2.87E+05

Умножение и деление

Мантиссы умножаются/делятся, а показатели степени складываются/вычитаются.

Пример:

• 2.5E+03 * 4.0E-02 = (2.5 * 4.0)E(3 + (-2)) = 10E+01 = 1.0E+02

Возведение в степень

Мантисса возводится в степень, а показатель умножается на эту степень.

Пример:

• (2.0E+03)^2 = (2.0^2)E(3*2) = 4.0E+06

Преимущества использования экспоненциальной записи

Экспоненциальная запись чисел имеет ряд преимуществ:

1. Позволяет работать с очень большими и очень маленькими числами
2. Упрощает выполнение математических операций
3. Экономит место на дисплее калькулятора
4. Наглядно показывает порядок величины числа
5. Уменьшает вероятность ошибок при вводе длинных чисел

Типичные ошибки при работе с экспоненциальной записью

При использовании экспоненциальной записи чисел следует избегать следующих ошибок:

• Неправильная интерпретация знака показателя степени
• Путаница между научной и инженерной нотацией
• Ошибки при сложении/вычитании чисел разных порядков
• Неверный учет порядка при умножении/делении
• Забывание про нормализацию результата (приведение к стандартному виду)

Когда лучше не использовать экспоненциальную запись

Экспоненциальная запись не всегда оптимальна. Ее не рекомендуется применять в следующих случаях:

• Для чисел, близких к 1 (от 0.01 до 100)
• В финансовых расчетах, где важна точность до копеек
• При работе с целыми числами небольшого порядка
• Когда важна наглядность представления для неподготовленной аудитории

Заключение

Экспоненциальная запись чисел — мощный инструмент для работы с очень большими и очень маленькими величинами. Правильное понимание значения буквы E на калькуляторе позволяет эффективно использовать этот формат в научных и инженерных расчетах.

Освоив принципы работы с экспоненциальной записью, вы сможете легко оперировать числами в диапазоне от субатомных частиц до размеров Вселенной.