Бревно оцилиндрованное размеры: Оцилиндрованное бревно – характеристики, размеры, плюсы и минусы
Размеры оцилиндрованного бревна и его предназначение
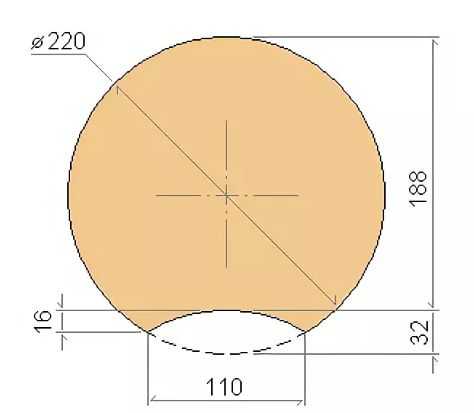
Размеры оцилиндрованного бревна подчиненны следующим стандартам: 180; 200; 220; 240; 260; 280 мм. Многие фирмы-производители имеют возможность производить пиломатериал и больших размеров, но такой заказ обычно обговаривается отдельно и более детально.
Размеры оцилиндрованного бревна.
Оцилиндрованное бревно и его предназначение
Бревна, имеющие оцилиндровку 180 мм, отлично подходят для возведения небольших строений, а именно беседок или маленьких бань. Но чаще всего такой размер не имеет большого спроса, так как конструкция, полученная в результате его применения, не имеет особой устойчивости и запаса прочности. И еще, из-за малого диаметра такие строения недостаточно эффектно выглядят. Поэтому если вы хотите получить прочную и надежную конструкцию, то лучше выбрать оцилиндрованное бревно диаметром 200-220 мм.
Опытные строители утверждают, что оцилиндрованное бревно, имеющее диаметр 200-220 мм, идеально подходят для постройки бань и домов, в которых планируется временное проживание в летний сезон.
А вот для построек, в которых будут жить круглый год, необходим материал, имеющий большую оцилиндровку – 240 мм и больше.
Как видите, существуют специальные условия строительства, которые напрямую влияют на выбор размеров оцилиндрованного бревна. Это:
Виды бревен и их размеры.
- Назначение дома. То есть, как уже выше говорилось, какое проживание планируется в таком доме. Если сезонное, то можно выбрать диаметр 200-220 мм, а если вы строите капитальный загородный дом, то лучше выбирать бревно размером 240, а еще лучше 260 мм.
- Общий стиль и габариты дома. Как это ни странно, но чем больше размер бревна, тем массивней и основательней кажется постройка. И это на самом деле так: чем толще бревно, тем меньше оно подвержено порче и лучше удержит тепло в доме. Не забывайте и о размерах строения. Для большого дома нужно использовать пиломатериал с большим диаметром, в противном случае строение будет наталкивать вас на мысль, что оно построено из карандашей.

- Общий бюджет, выделяемый на строительство. Чем выше размеры дерева, там оно дороже.
Вернуться к оглавлению
Как строят дом из оцилиндрованного бревна
Схема конструкции сруба.
Процесс возведения такого дома моментами похож на этапы строительства дома из бруса. А заключается он следующих шагах:
- Закладка фундамента.
- Возведение коробки (из бревен).
- Укладка кровли.
- Установка окон и дверей.
- Финишная отделка.
Стоит отметить, что после возведения стен и укладки кровли дом должен постоять какое-то время без отделки. Этот период может составить от полугода и выше. За этот отрезок времени строение даст так называемую усадку, а дерево приобретет оптимальную влажность. Все это не позволит в дальнейшем иметь каких-либо проблем во внутренней и внешней отделке.
Стены дома начинают собирать с закладки первого венца. Его монтируют на фундамент, предварительно установив на него обработанную антисептиками доску, толщина которой должна быть около 5 см.
Вертикальные опоры и столбцы монтируют с использованием специальных домкратов. Их наличие позволяет давать дому равномерную усадку. Каждый деревянный элемент дома должен быть подвергнут обработке антисептиком. А во время установки кровли и стропил необходимо обязательно учитывать подвижность деревянных строений и будущую усадку. Иначе вы рискуете оказаться в ситуации, когда крыша дома будет выглядеть больше, чем сам дом.
Оцилиндрованное бревно
Главная / Продукция / Оцилиндрованное бревно
ОЦИЛИНДРОВАННОЕ БРЕВНО
Наша компания занимается производством оцилиндрованного бревна из отборного зимнего леса (100% сосна) диаметром от 160 до 240 мм.
| Цена за домокомплект из оцилиндрованнного бревна | ||||||||||
| Размер высоты сруба 2,00 м | ||||||||||
| Диаметр бревна | 3*3 | 3*4 | 3*6 | 3*6+1 | 4*6 | 4*6+1 | 6*6 | 6*6+1 | Цена,п. м. м. | Ряд |
| 160 | 44430 | 51960 | 60960 | 74910 | 68280 | 86640 | 76860 | 98760 | 210 | 15 |
| 180 | 47335 | 55946 | 66200 | 80435 | 74546 | 93604 | 84270 | 107540 | 265 | 13 |
| 200 | 53310 | 63528 | 75660 | 91140 | 85548 | 106572 | 97020 | 123180 | 330 | 12 |
| 220 | 58400 | 70020 | 83800 | 100300 | 95020 | 117680 | 108000 | 136600 | 400 | 11 |
| 240 | 62425 | 75200 | 90350 | 107600 | 102650 | 126550 | 116850 | 147350 | 475 | 10 |
| Размер высоты сруба 2,20 м | ||||||||||
| Диаметр бревна | 3*3 | 3*4 | 3*6 | 3*6+1 | 4*6 | 4*6+1 | 6*6 | 6*6+1 | Цена,п. м. м. | Ряд |
| 160 | 47350 | 55368 | 64940 | 79820 | 72748 | 92332 | 81900 | 105260 | 210 | 16 |
| 180 | 50915 | 60168 | 71170 | 86500 | 80158 | 100682 | 90630 | 115690 | 265 | 14 |
| 200 | 57670 | 68712 | 81800 | 98570 | 92512 | 115288 | 104940 | 133280 | 330 | 13 |
| 220 | 63600 | 76240 | 91200 | 109200 | 103440 | 128160 | 117600 | 148800 | 400 | 12 |
| 240 | 68525 | 82530 | 99100 | 118075 | 112630 | 138920 | 128250 | 161800 | 475 | 11 |
| Размер высоты сруба 2,50 м | ||||||||||
| Диаметр бревна | 3*3 | 3*4 | 3*6 | 3*6+1 | 4*6 | 4*6+1 | 6*6 | 6*6+1 | Цена,п. м. м. | Ряд |
| 160 | 53190 | 62184 | 72900 | 89640 | 81684 | 103716 | 91980 | 118260 | 210 | 18 |
| 180 | 58075 | 68612 | 81110 | 98630 | 91382 | 114838 | 103350 | 131990 | 265 | 16 |
| 200 | 62030 | 73896 | 87940 | 106000 | 99476 | 124004 | 112860 | 143380 | 330 | 14 |
| 220 | 68800 | 82460 | 98600 | 118100 | 111860 | 138640 | 127200 | 161000 | 400 | 13 |
| 240 | 74625 | 89860 | 107850 | 128550 | 122610 | 151290 | 139650 | 475 | 12 | |
| Размер высоты сруба 2,70 м | ||||||||||
| Диаметр бревна | 3*3 | 3*4 | 3*6 | 3*6+1 | 4*6 | 4*6+1 | 6*6 | 6*6+1 | Цена,п. м. м. | Ряд |
| 160 | 59030 | 69000 | 80860 | 99460 | 90620 | 115100 | 102060 | 131260 | 210 | 20 |
| 180 | 61655 | 72834 | 86080 | 104695 | 96994 | 121916 | 109710 | 140140 | 265 | 17 |
| 200 | 66390 | 79080 | 94080 | 113430 | 106440 | 132720 | 120780 | 153480 | 330 | 15 |
| 220 | 74000 | 88680 | 106000 | 127000 | 120280 | 149120 | 136800 | 173200 | 400 | 14 |
| 240 | 80725 | 97190 | 116600 | 139025 | 132590 | 163660 | 151050 | 190700 | 475 | 13 |
Также при заказе сруба или стройкомплекта Вы получаете СКИДКУ НА ПИЛОМАТЕРИАЛ!
Компания «Уральский лес» так же реализует строительную доску и брус, погонажные изделия:
евровагонку, плинтуса, полки для парных, палубную, террасную и шпунтованную доску из различных пород дерева сосны, осины, лиственницы.
Любые вопросы вы можете уточнить по телефонам:
+7 (3435) 407-987
+7 (900) 200-32-82
Склад и производство находятся по адресу:
Нижний Тагил, Свердловская область, улица Юности, 5
Оформить заказ >>
Используя это! — Округление размеров — Заглядывая под капот… — Блоги коллег
Первоначально опубликовано 4 февраля 2015 г.
У нас было несколько вопросов об округлении размеров до ближайших 5 мм. В настоящее время это недоступно в диалоговом окне «Стили размеров», но теперь есть методы, доступные как для CONNECT Edition, так и для V8i.
CONNECT Edition:
Функциональность вычисления изменилась в CONNECT Edition, поэтому обходной путь V8i недоступен (как обсуждается в комментариях ниже), но мой коллега Йонг Ан Фу написал приложение MDL, которое обеспечивает гораздо более простое решение.
Внимание! Прежде чем использовать это, имейте в виду, что наличие округления явно не очевидно ни в свойствах элемента, ни в диалоговом окне Размерные стили. Также имейте в виду, что округление применяется к каждому отдельному измерению, поэтому общее измерение не может быть округлено до суммы подразмеров, как показано здесь:
Также имейте в виду, что округление применяется к каждому отдельному измерению, поэтому общее измерение не может быть округлено до суммы подразмеров, как показано здесь:
Наилучший подход к использованию этого MDL — использовать его только для создания измерения. стили названы так, чтобы четко определить, что они округлены. Я бы не стал делать это доступным для всех пользователей, поскольку применение округления к отдельным измерениям неуправляемо и может вызвать путаницу в дальнейшем.
Использовать:
Извлеките содержимое этого файла в C:\Program Files\Bentley\MicroStation CONNECT Edition\MicroStation\Mdlapps или в папку Mdlapps в пользовательской конфигурации, которая доступна только администраторам САПР.
6507.SetDimRound.zip
Keyin MDL LOAD SetDimRound n для применения значения округления к активному текущему размерному стилю. Значение относится к активным рабочим единицам. Например:
для округления до 5 мм с активными рабочими единицами, установленными на 9 мм.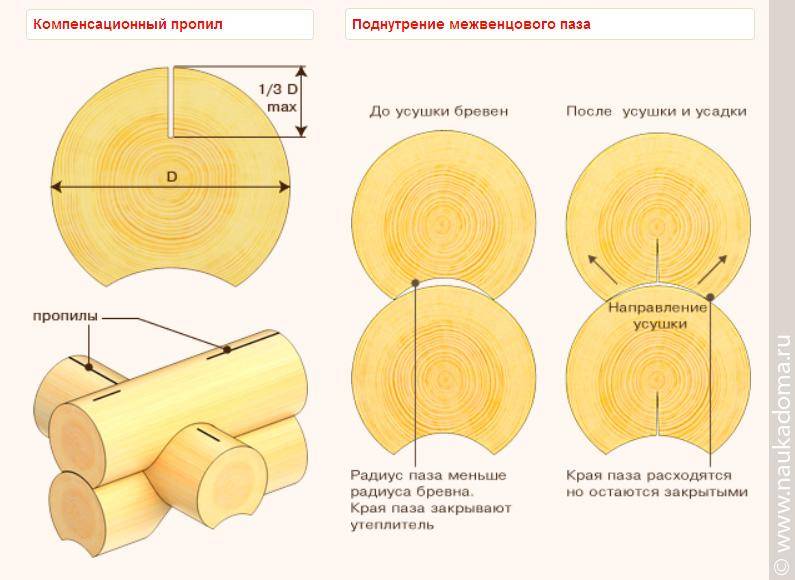 0005
0005
MDL LOAD SetDimRound 5.0
для применения скругления на 10 мм -in:
MDL LOAD LOAD SetDimRound (без аргумента)
Это приложение MDL запустится, а затем выгрузится само, его не нужно запускать в фоновом режиме, оно просто выполняет свою работу и оставляет запись двух строк в центре сообщений:
Создайте размерные стили с соответствующими именами и сохраните их в измерении. стили DGNLIB (предпочтительно указывается в MS_DGNLIBLIST_DIMENSIONSTYLES, обычно полезно упорядочивать ресурсы DGNLIB, используя определенную переменную, если она доступна).
Рекомендуйте пользователям использовать округление только с помощью размерных стилей, так как имя стиля сделает округление очевидным для последующих редакторов.
Округление можно удалить из существующих размеров с помощью инструмента «Изменить размер», чтобы применить стиль без округления.
Примеры:
Пример с рабочими единицами, установленными в мм (размеры округлены красным):
и установленными в м:
Дальнейшее развитие:
Дефект 1073871 «Размеры не могут быть округлены off to the ближайший 5mm» был подан, чтобы отслеживать требование для этой функциональности. Пожалуйста, отправьте запрос на обслуживание, указав этот номер дефекта, если вы хотите, чтобы эта возможность была добавлена к основным функциям CONNECT Edition.
Пожалуйста, отправьте запрос на обслуживание, указав этот номер дефекта, если вы хотите, чтобы эта возможность была добавлена к основным функциям CONNECT Edition.
Только V8i:
Используйте ввод с клавиатуры, описанный ниже, для изменения существующего размерного стиля. Вы можете протестировать это в любом файле проекта, не затрагивая стандарты, а затем скопировать измененный размерный стиль в свои стандарты DGNLIB.
- Открыть диалоговое окно размерных стилей
- Скопируйте существующий стиль и переименуйте с закругленным суффиксом (или любым другим соглашением об имени, которое вы предпочитаете/требуете).
- Сделать скопированный стиль активным
- На вкладке «Единицы» > набор «Основные единицы»
- Точность 0,1
- Убрать конечные нули
- в диалоговом окне введите:
- лей Расчет нагрузки; калькулятор mdlDimStyle_setDoubleProp(mdlDimStyle_getActive(), 5.
 0, 1083)
0, 1083) - Сохраните измененный размерный стиль.
[обратите внимание, что начальная часть командной строки — calculat , без «e» в конце! 8-символьные имена файлов DOS продолжают жить.]
На этом рисунке к строке меньшего размера применено округление.
Вы также можете использовать командную строку в качестве временного переопределения без изменения или создания каких-либо библиотечных стилей, и в этом случае обновление стиля из библиотеки приведет к его сбросу до стандарта компании и удалению параметра округления.
Также обратите внимание, что если размер с округлением существует, вы также можете использовать инструмент сопоставления текстовых атрибутов, чтобы выбрать настройку округления.
Фон
‘mdl load calculat’ запускается C:\Program Files (x86)\Bentley\AECOsimBuildingDesigner V8i Ss5\AECOsimBuildingDesigner\mdlsys\asneeded\calculat.ma
В данном случае он используется для доступа к команде mdl через API mdlDimStyle. Если вы хотите узнать больше об этой теме, вы можете:
Если вы хотите узнать больше об этой теме, вы можете:
- загрузить MicroStation V8i SDK и документацию к нему
- присоединяйтесь к обсуждениям на форуме программирования MicroStation
Найдите в справке MicroStation строку «Calculator/Preprocessor», чтобы получить рекомендации по более общим функциям, доступным на сайте calculate.ma.
Точность и прецизионность
Подраздел 1.2.1 Пояснение
Рисунок 1.2.1. Введение в точность и аккуратностьПри работе с измерениями мы заботимся о достоверности результатов. Это приводит нас к двум концепциям.
Определение 1.2.2. Точность.
Точность измерения показывает, насколько близко измерение к фактическому значению.
Заметьте, если мы что-то измеряем, то только потому, что не знаем фактического значения. Таким образом, мы не можем определить точное значение многих видов данных. Вместо этого мы довольствуемся повторяемостью. Если мы будем получать один и тот же результат достаточно часто, мы сможем убедить себя, что он достаточно точен.
Определение 1.2.3. Точность.
Точность измерения – это размер наименьшей его единицы.
Обратите внимание, что мы можем иметь высокую точность при низкой точности. То есть то, что мы пишем много знаков после запятой, не означает, что они близки к реальному значению.
Подраздел 1.2.2 Значимые цифры
При записи измерений нам нужен способ указать, насколько точны измерения. Значащие цифры , также называемые значащих цифр или просто «значащие цифры» — способ сделать это.
Правила записи чисел со значащими цифрами состоят из двух частей: ненулевых цифр и нулевых цифр.
Все ненулевые цифры являются значащими.
Нули между ненулевыми значениями имеют значение.
Любые нули, записанные справа от десятичной точки, являются значащими.
Если предполагается, что нули между ненулевыми цифрами (слева) и десятичной точкой (справа) являются значащими, поверх последней значащей цифры рисуется линия.

Для чисел меньше 1 нули между десятичной точкой (слева) и ненулевыми цифрами (справа) не имеют значения.
Эти правила можно резюмировать так: пишите только те цифры, которые вы имеете в виду, а если неясно, уточняйте.
Пример 1.2.4. Написание значащих цифр.
Каждый из этих номеров состоит из пяти (5) значащих цифр.
\(\displaystyle 10267\)
\(\displaystyle 1.2400\)
\(\displaystyle 7201\бар{0}\)
\(\displaystyle 2834100\)
\(\displaystyle 0.0010527\)
КПП 1.2.5.
Сколько значащих цифр имеет \(203\)?
Сколько значащих цифр имеет \(20\bar{0}0\)?
Ответ 1. Ответ 2. Решение.Поскольку 203 заканчивается ненулевой цифрой, все три цифры являются значащими.
Поскольку 0 в разряде десятков помечен как значащий (черта), имеется 3 значащих цифры
Нам также нужны правила арифметики со значащими цифрами.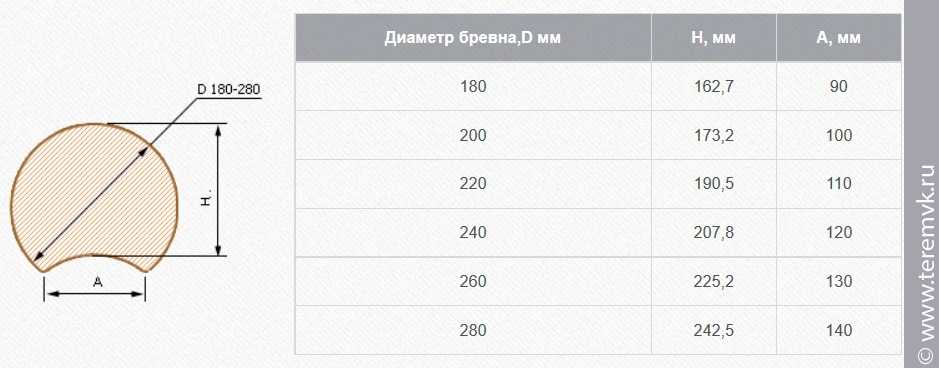 Они основаны на двух принципах
Они основаны на двух принципах
Результат арифметики не может быть более точным, чем наименее точное измерение.
Количество значащих цифр не может увеличиваться.
При сложении и вычитании результат (сумма или разность) имеет ту же точность, что и наименее точное число, которое прибавляется или вычитается. После сложения или вычитания мы округляем до крайней левой, последней значащей цифры.
Пример 1.2.6. Вычитание со значащими цифрами.
\(11050-723=10330\text{.}\) Это связано с тем, что последняя значащая цифра \(11050\) является позицией 10 (с 5 в ней), тогда как последняя значащая цифра \(723\ ) — это позиция 1 (с 3 в ней). Мы не знаем позицию 1 числа 11050, поэтому мы не можем знать позицию 1 в результате.
Пример 1.2.7. Сложение со значащими цифрами.
\(311+8310+202200=210800\text{.}\) Это связано с тем, что крайняя левая, последняя значащая цифра находится в позиции 100 в 202200. Дополнительная точность двух других чисел бесполезна.
Правило сложения/вычитания значащих цифр в основном говорит о том, что добавление точных данных к неточным данным не увеличивает точность неточных данных. Подробное объяснение в этом видео.
КПП 1.2.8.
Вычислить \(646+21.12+120\text{:}\)
Вычислить \(63.97-21\text{:}\)
Ответ 1.\(790\)
Ответ 2. 9 0002 \(43\) Решение.\(646+21,12+120=787,12 \приблизительно 790\), потому что \(120\) имеет значение только для позиции 10 (остальные более точны).
\(63,97-21=42,97 \приблизительно 43\), потому что \(21\) имеет значение только для позиции 1 (другая более точная).
При умножении и делении результат (произведение или частное) имеет то же количество значащих цифр, что и наименьшее количество введенных чисел.
Пример 1.2.9. Деление со значащими цифрами.
\(11050/722=15.3\text{.}\) Это потому, что \(722\) имеет только 3 значащие цифры.
Пример 1.2.10. Умножение со значащими цифрами.

\(17 \times 14\bar{0} \times 3.178= 7600\text{.}\) Это потому, что \(17\) имеет только две значащие цифры.
Правило умножения/деления значащих цифр в основном говорит о том, что цифры, которые были умножены на неточные данные, не могут быть точными. Объяснение того, почему это правило работает, в этом видео.
КПП 1.2.11.
Вычислить \(646 \times 21.12\text{:}\)
Вычислить \(63.97/21\text{:}\)
Ответ 1.\(13600\)
Ответ 2. Решение.\(646\times 21,12=13643,52\приблизительно 13600\), потому что \(646\) имеет только 3 значащих цифры (у другого больше).
\(63,97/21=3,0461
\приблизительно 3,0\), потому что \(21\) имеет только 2 значащие цифры (у другого больше). Правила значащих цифр должны применяться на каждом шаге. То есть, если у нас есть сочетание сложения, вычитания, умножения и деления, то мы выполняем одну операцию за раз и применяем соответствующее правило значащих цифр перед выполнением следующего арифметического шага.
Пример 1.2.12. Многошаговая арифметика со значащими цифрами.
Рассмотрим
\begin{equation*} 11 728+39(17,9+1,23). \end{equation*}
По порядку операций мы сначала вычисляем \(17,9+1,23 \приблизительно 19,1.\) Затем по порядку операций мы вычисляем \(39 \times 19,1 = 740.\) Наконец, мы вычисляем \(11,728 +740=12 470.\)
Подраздел 1.2.3 Округление
По разным причинам в приложениях нам нужно округлить число, то есть игнорировать некоторый уровень точности.
Таблица 1.2.13. Причины округления| Реальные ограничения | Например, мы не можем покупать частичные пакеты или иметь частичных людей |
| Удалить деталь | Например, при описании населения страны |
| Ошибка управления | При использовании в значащих цифрах |
Причина округления определяет, как мы это делаем. Рассмотрим следующие ограничения реальности, требующие округления. Например, если нам нужно 21 яйцо, а яйца продаются в коробках по одной дюжине (12) яиц, нам нужно \(21/12=1,75\) коробок. Поскольку мы не можем купить часть коробки, мы должны округлить 1,75 до 2 и купить 2 коробки.
Например, если нам нужно 21 яйцо, а яйца продаются в коробках по одной дюжине (12) яиц, нам нужно \(21/12=1,75\) коробок. Поскольку мы не можем купить часть коробки, мы должны округлить 1,75 до 2 и купить 2 коробки.
Обратите внимание, что в этом примере реальность требует округления до ближайшего целого числа. Мы округляем до целого числа, потому что мы не можем покупать дробные коробки яиц. Нам пришлось округлить, потому что округление в меньшую сторону оставило бы нам недостаточное количество яиц (а мы голодны).
Предположим, у вас есть банковский счет, содержащий 11 410 долларов США, на который начисляются 1,65% годовых. По расчетам банка, платеж должен быть равен \(\$11410\cdot 0,0165 = \$188,265\text{.}\) Банк выплатит вам $188,26. Они округляются до сотых, потому что центы — это единица, которой можно заплатить. Они округляют в меньшую сторону, потому что любят платить меньше.
Для удаления деталей рассмотрите отчет о населении страны. Мы можем сообщить о населении в 9 миллионов, а не в 9 904 607 человек. Мы делаем это, потому что нам не нужно точное число, которое, вероятно, меняется каждый день. Сообщая о диапазонах заработной платы, мы можем указать диапазон от 60 000 до 80 000 долларов США. То, что на самом деле диапазон составляет 61 233,57 и 80 290,11 долларов, вряд ли изменит решение. Обычно удаление деталей используется, когда мы заботимся о масштабе вещей, а не о количестве.
Мы делаем это, потому что нам не нужно точное число, которое, вероятно, меняется каждый день. Сообщая о диапазонах заработной платы, мы можем указать диапазон от 60 000 до 80 000 долларов США. То, что на самом деле диапазон составляет 61 233,57 и 80 290,11 долларов, вряд ли изменит решение. Обычно удаление деталей используется, когда мы заботимся о масштабе вещей, а не о количестве.
Округление для контроля ошибки — это использование значащих цифр.
Мы можем округлить до любой цифры. Мы можем округлить вверх, вниз или просто «округлить». Контекст или инструкции будут указывать, какая цифра и какой тип округления.
Пример 1.2.14. Округление вверх/вниз.
(а)
Округлите 72481 до ближайшей сотни.
Раствор.72400 округляется в меньшую сторону: оставляем 4 (сотню) в покое и «обрезаем» (превращаем в 0) все цифры вправо. Примечание \(72400 \le 72481\text{.}\)
(б)
Округлите 72481 до ближайшей сотни.
Раствор.
72500 округляется в большую сторону: мы увеличиваем 4 до 5 и «обрезаем» (превращаем в 0) все цифры вправо. Примечание \(72500 \ge 72481\text{.}\)
(c)
округлить 72481 до ближайшей сотни.
Раствор.Поскольку 72481 ближе к 72500, чем к 72400, мы округляем до 72500. Мы понимаем, что должны округлять в большую сторону, потому что позиция десятков равна \(8\ge 5\), что делает ее ближе к увеличению. Мы могли бы также признать необходимость округления, вычислив \(500-481=19\) и \(481-400=81\) и заметив, что \(81 \ge 19\text{.}\)
Пример 1.2.15. Округление вверх/вниз.
(а)
Округлите 72481 до ближайшей тысячи.
Раствор.72000 округляется в меньшую сторону: мы оставляем 2 (разряд тысяч) в покое и «обрезаем» (превращаем в 0) все цифры вправо. Примечание \(72000 \le 72481\text{.}\)
(b)
Округлите 72481 до ближайшей тысячи.
Раствор. 73000 округляется: мы увеличиваем 2 до 3 и «обрезаем» (превращаем в 0) все цифры вправо. Примечание \(73000 \ge 72481\text{.}\)
Примечание \(73000 \ge 72481\text{.}\)
(с)
Округлите 72481 до ближайшей тысячи.
Раствор.Поскольку 72481 ближе к 72000, чем к 73000, мы округляем до 72000. Мы понимаем, что должны округлять в большую сторону, потому что положение сотен равно \(4 < 5\), что делает его ближе к уменьшению. Мы могли бы также признать необходимость округления, вычислив \(3000-2481=519\) и \(2481-2000=481\) и заметив, что \(481 < 519\text{.}\)
Пример 1.2.16. Округление до различной точности.
Округлите 72321.83 до указанной точности.
Тысячи: 72000
Единицы: 72322
Десятки: 72321.8
КПП 1.2.17.
Округлить 812 247 до десятка:
Округлить 812 247 до сотни:
Ответ 1.\(812250\)
Ответ 2.\(812200\)
Подраздел 1.2.4 Максимально возможная ошибка
Когда мы пишем число со значащими цифрами или округляем число, мы пишем число, в котором есть ошибка. Например, если за день выпало 0,86 дюйма дождя, а мы пишем 0,9дюймов, есть погрешность 0,4. Важный вопрос: «Насколько велика может быть ошибка?».
Например, если за день выпало 0,86 дюйма дождя, а мы пишем 0,9дюймов, есть погрешность 0,4. Важный вопрос: «Насколько велика может быть ошибка?».
Поскольку наше правило округления состоит в том, что цифры 0–4 округляются вниз, округляются вверх, а цифры 5–9 округляются, округление всегда будет иметь максимально возможную ошибку, равную 5. Рассмотрим пример 1.2.18.
Пример 1.2.18.
Какова наибольшая возможная ошибка, если 130 округлить до ближайших 10?
Раствор.Возможно, число 130 было округлено в меньшую сторону. Тогда исходное число было одним из 130, 131, 132, 133 или 134. 134 — это самое дальнее число от 130 в точке \(134-130=4\text{.}\)
Другая возможность состоит в том, что 130 были собраны. Тогда исходное число было одним из 125, 126, 127, 128 или 129. 125 находится дальше всего в \(130-125=5\text{.}\)
Таким образом, наибольшая возможная ошибка была 5 из случая что 125 было собрано.
Обратите внимание, что в этом решении мы предполагали, что округленное число является целым числом. Однако, если бы мы разрешили 134,927 и 125,01, результат был бы таким же. дополнительные цифры не меняют округление.
Однако, если бы мы разрешили 134,927 и 125,01, результат был бы таким же. дополнительные цифры не меняют округление.
Пример 1.2.19.
Какова наибольшая возможная ошибка, если 9,31 округлить до сотых?
Раствор.Наибольшая возможная ошибка, если 9,31 было округлено от 9,305. Таким образом, наибольшая возможная ошибка составляет 5 тысячных.
Пример 1.2.20.
Какова наибольшая возможная ошибка, если 223 округлить до ближайшего значения?
Раствор.223 можно было бы округлить от 222.1. Но это также могло быть округлено от 222.01 или чего-то еще. Таким образом, максимально возможная ошибка меньше 1 (\(223-222=1\)).
Заметьте, мы должны знать, какой тип округления использовался. В большинстве измерений (т. е. значащих цифр) будет использоваться стандартное округление. Например, подумайте об измерении на линейке: если объект не находится точно на одной из линий, вы выберете ближайшую. Ближайший требует округления.
КПП 1.
 2.21.
2.21.Какова наибольшая возможная ошибка, если 8120 округлить до ближайших десяти?
Ответ. Раствор.Это может быть любое число от 8115 до 8124. Таким образом, максимально возможная ошибка равна 5,9.0005
КПП 1.2.22.
Какова наибольшая возможная ошибка в результате \(934\bar{0}00\text{?}\)
Ответ.\(50\)
Раствор.Наименьшая точная цифра — это разряд сотен, обозначенный полосой. Таким образом, номер может быть любым от 933950 до 934049. Таким образом, максимально возможная ошибка равна 50.
Подраздел 1.2.5 Цели округления
Упражнения 1.2.6 Упражнения
1. Значащие цифры.
2. Подсчитайте значащие цифры.
3. Подсчитайте значащие цифры.
4. Подсчитайте значащие цифры.
5. Подсчитайте значащие цифры.
6. Подсчитайте значащие цифры.
7. Арифметика значащих цифр.
8. Арифметика значащих цифр.
9.



 0, 1083)
0, 1083) 